Design and Characteristic Research on Variable Displacement Mechanism of Two-Dimensional (2D) Bivariable Pump
Abstract
1. Introduction
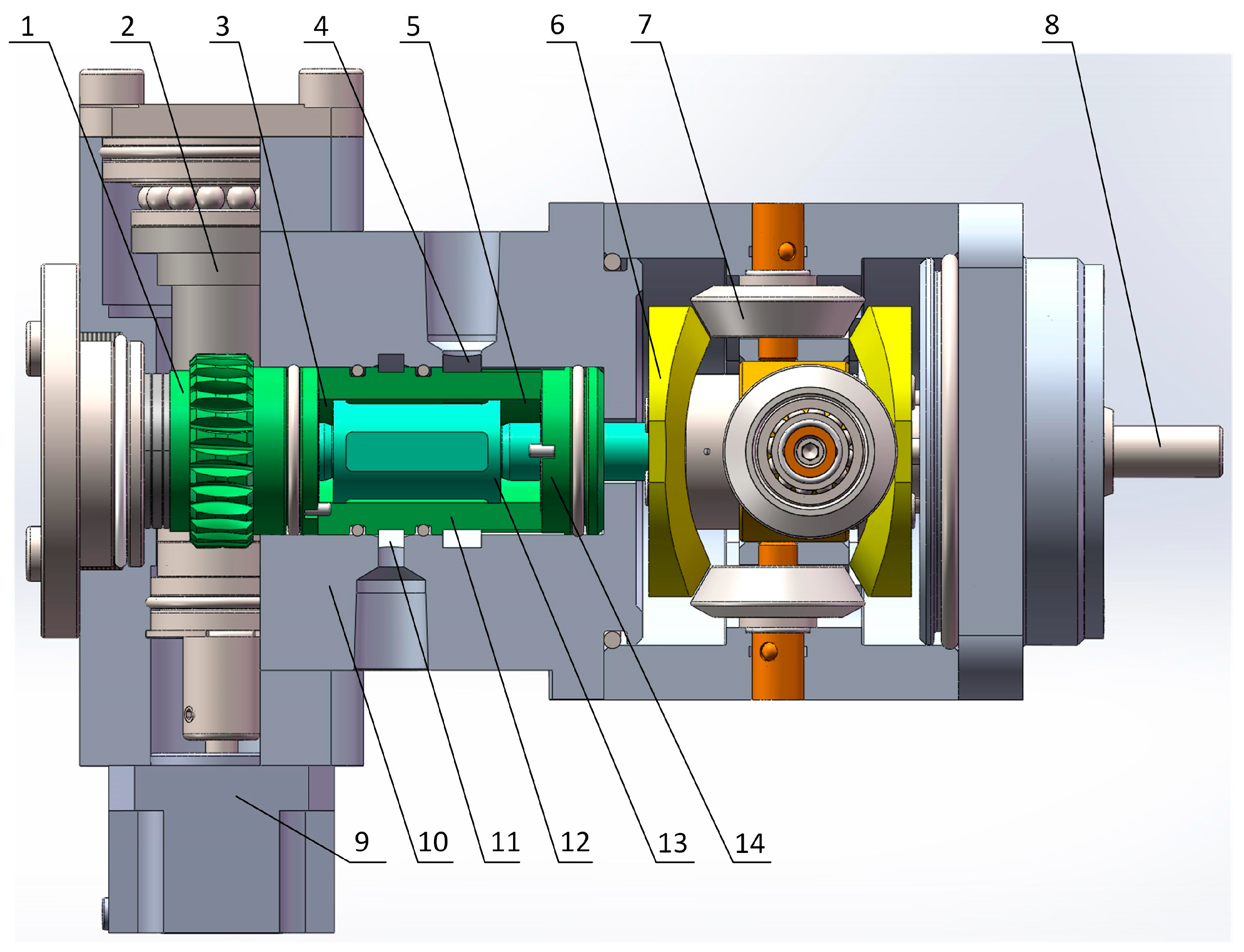
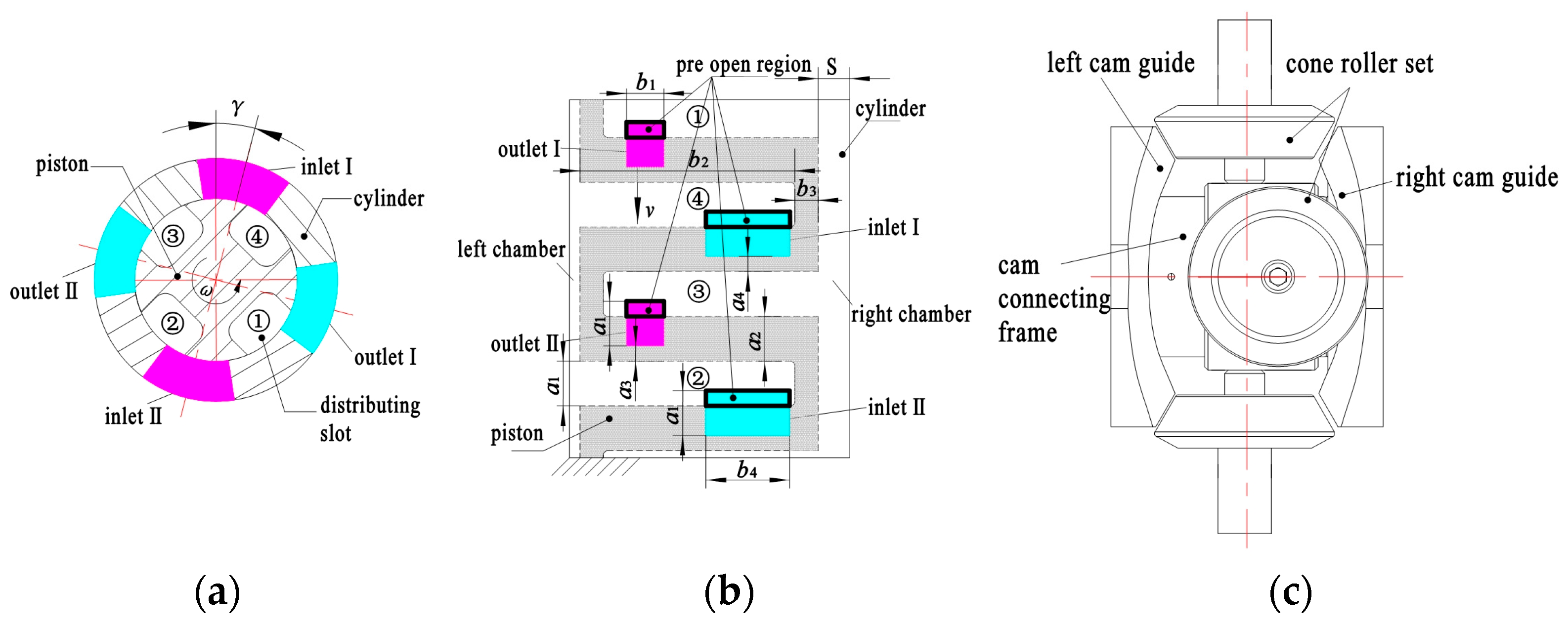
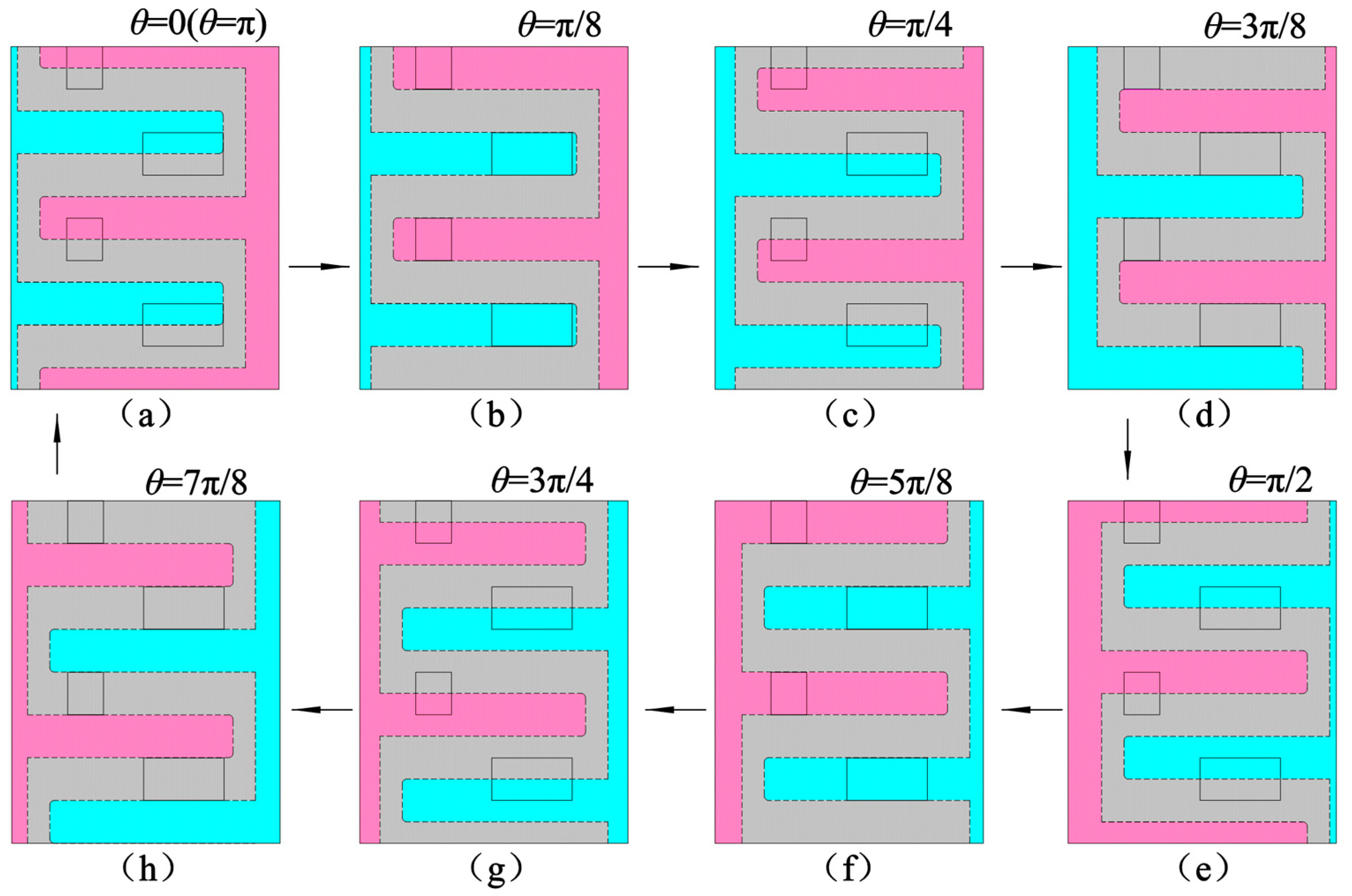
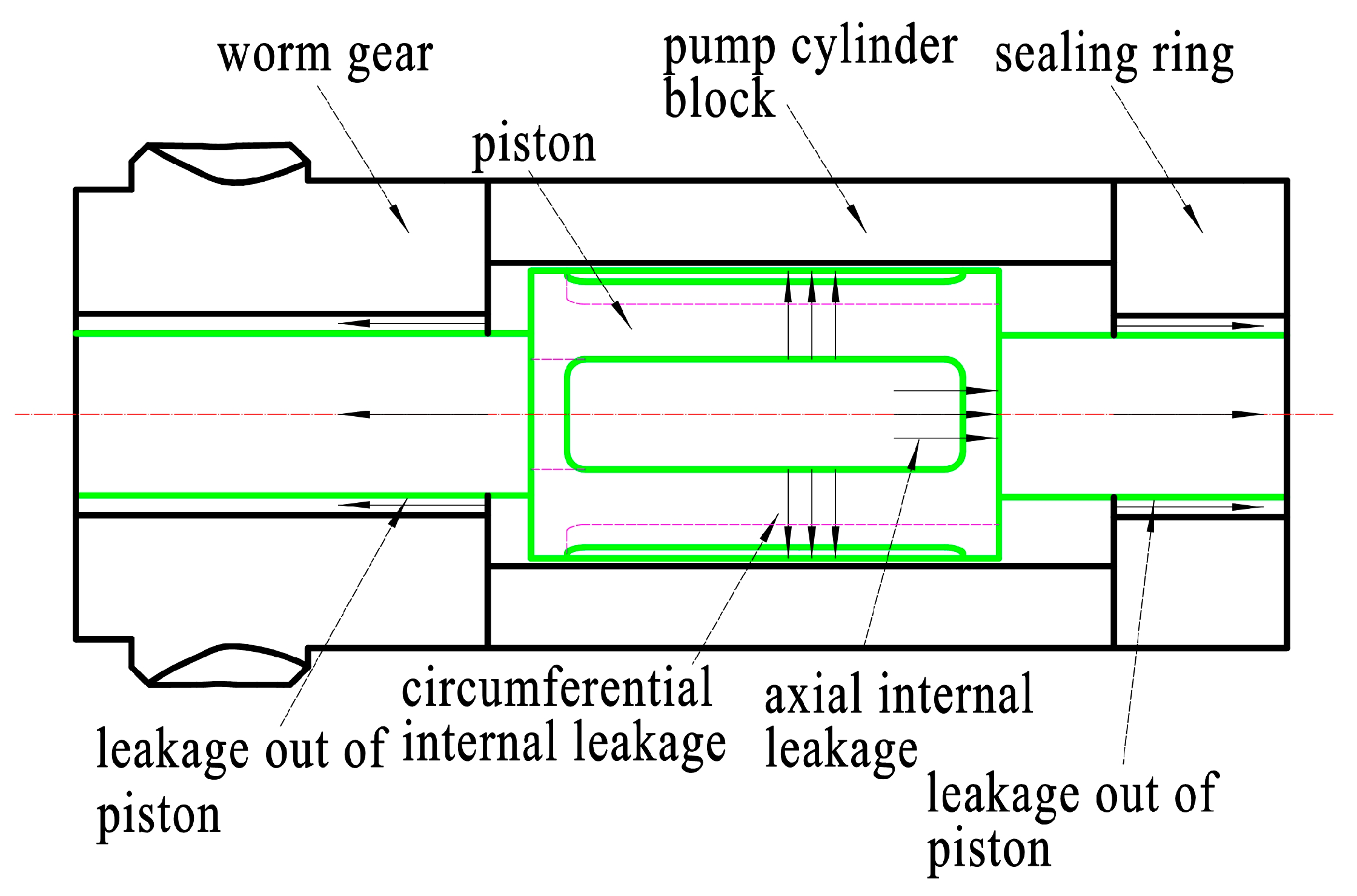
2. Mechanism and Working Principle
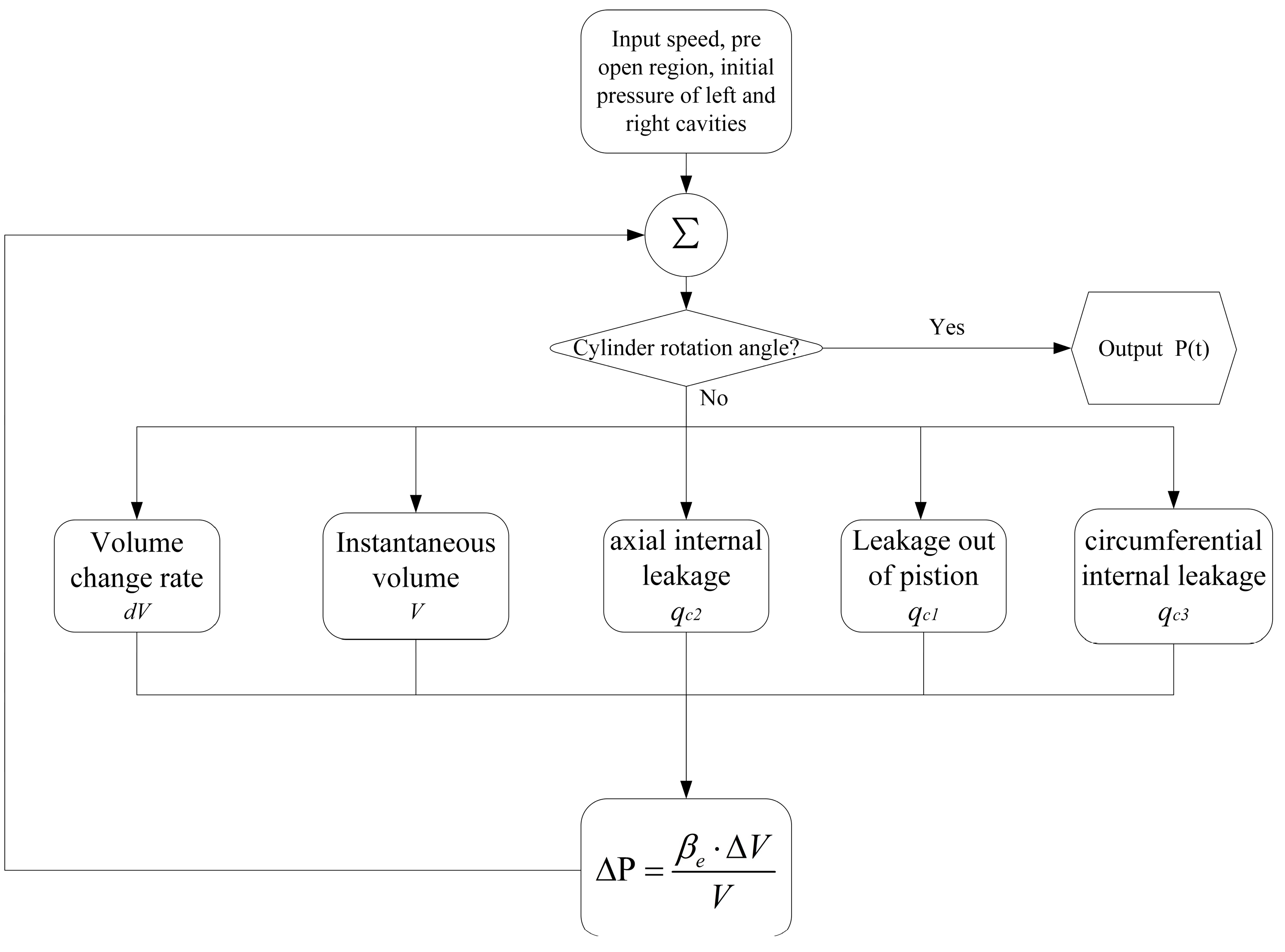
3. Mathematical Model
4. Matlab Simulation Analysis
5. Test
6. Conclusions
- (1)
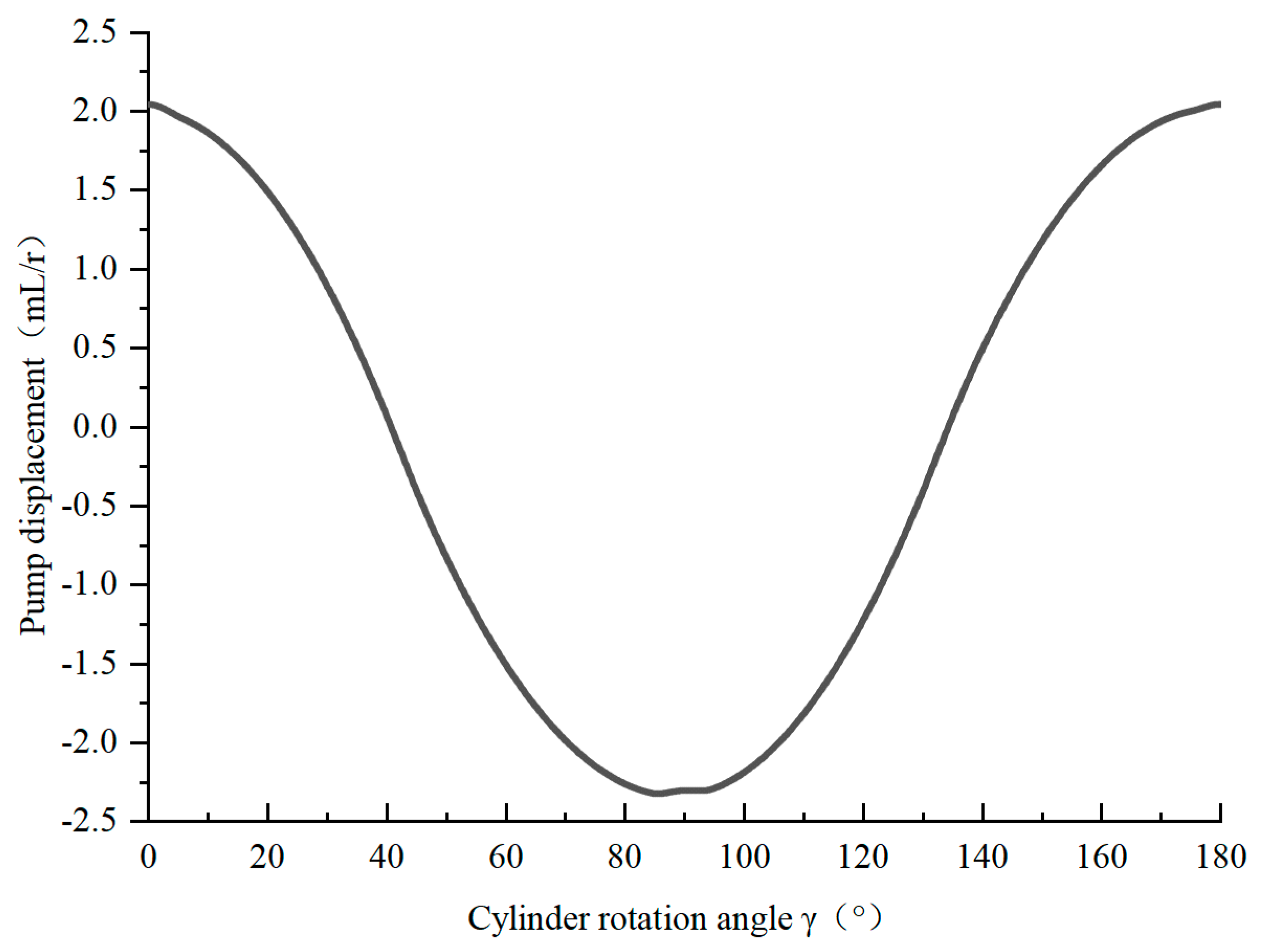
- For the 2D pump with the piston groove distribution structure, the displacement of the pump can be changed by rotating the cylinder block, and bidirectional variables can be realized. When the 2D pump cylinder rotation angle increases from 0° to 45°, the theoretical displacement decreases from 2.2 mL/r to 0, the cylinder rotation angle continues to increase, the pump is reversed until the cylinder rotation angle is 90°, and the displacement reaches the maximum.
- (2)
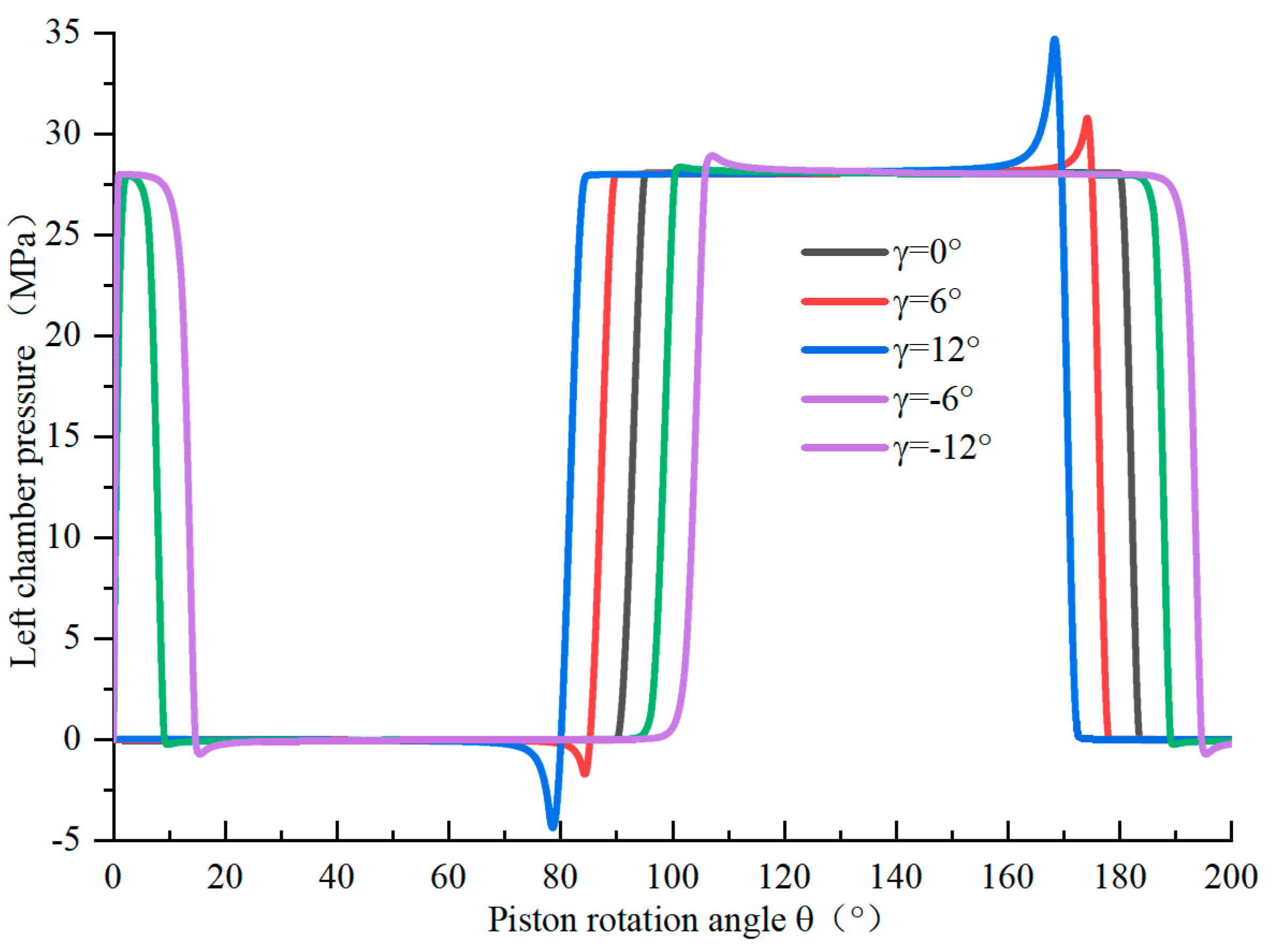
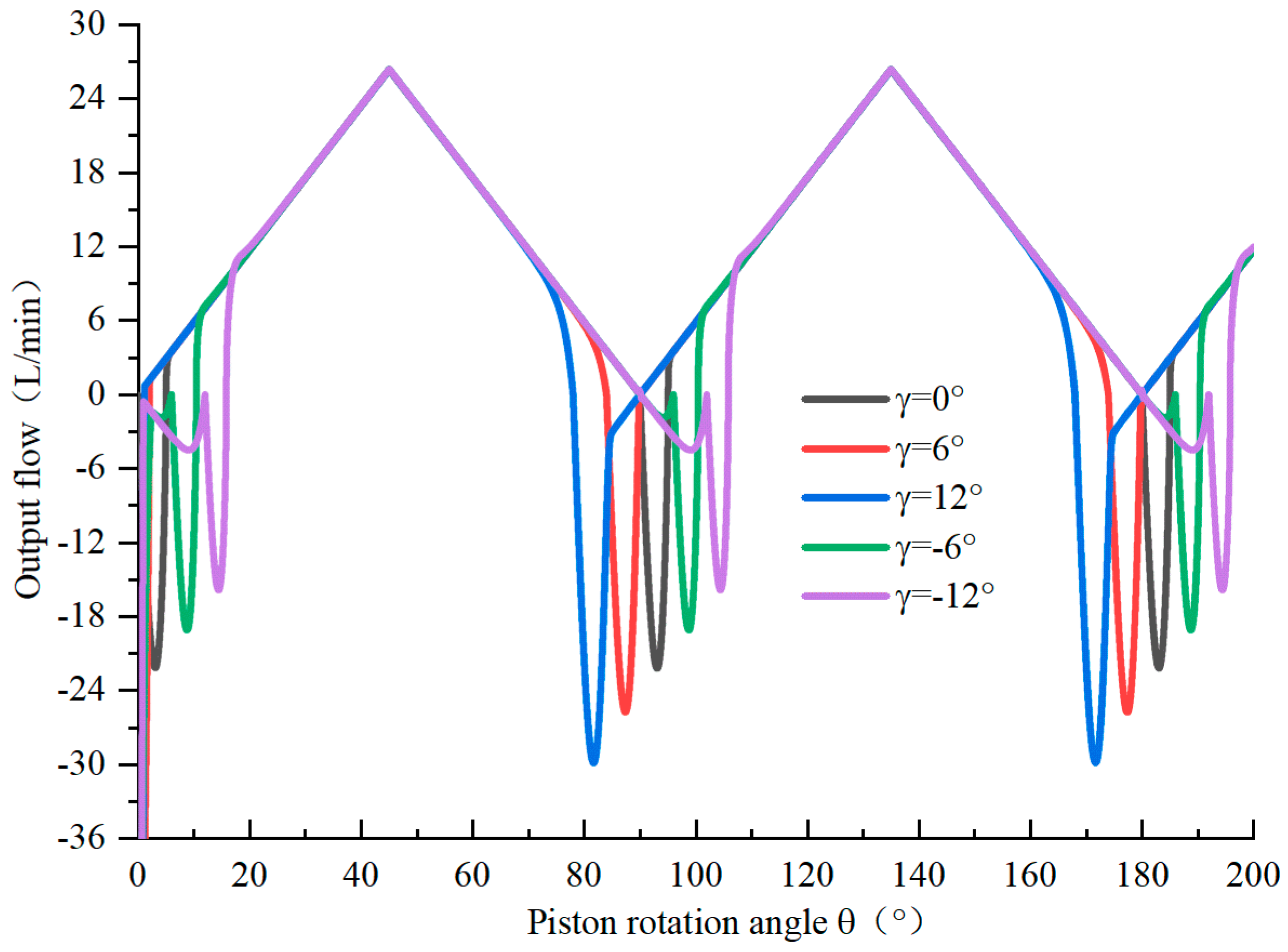
- According to the simulation analysis, when the cylinder rotation angle is negative, that is, when the rotation direction of the cylinder is the same as that of the pump, the flow backflow can be reduced, and the pressure pulsation can also be reduced when the flow distribution window switches. If the cylinder rotation angle is positive, increasing the cylinder rotation angle will increase the flow backflow and pressure pulsation.
- (3)
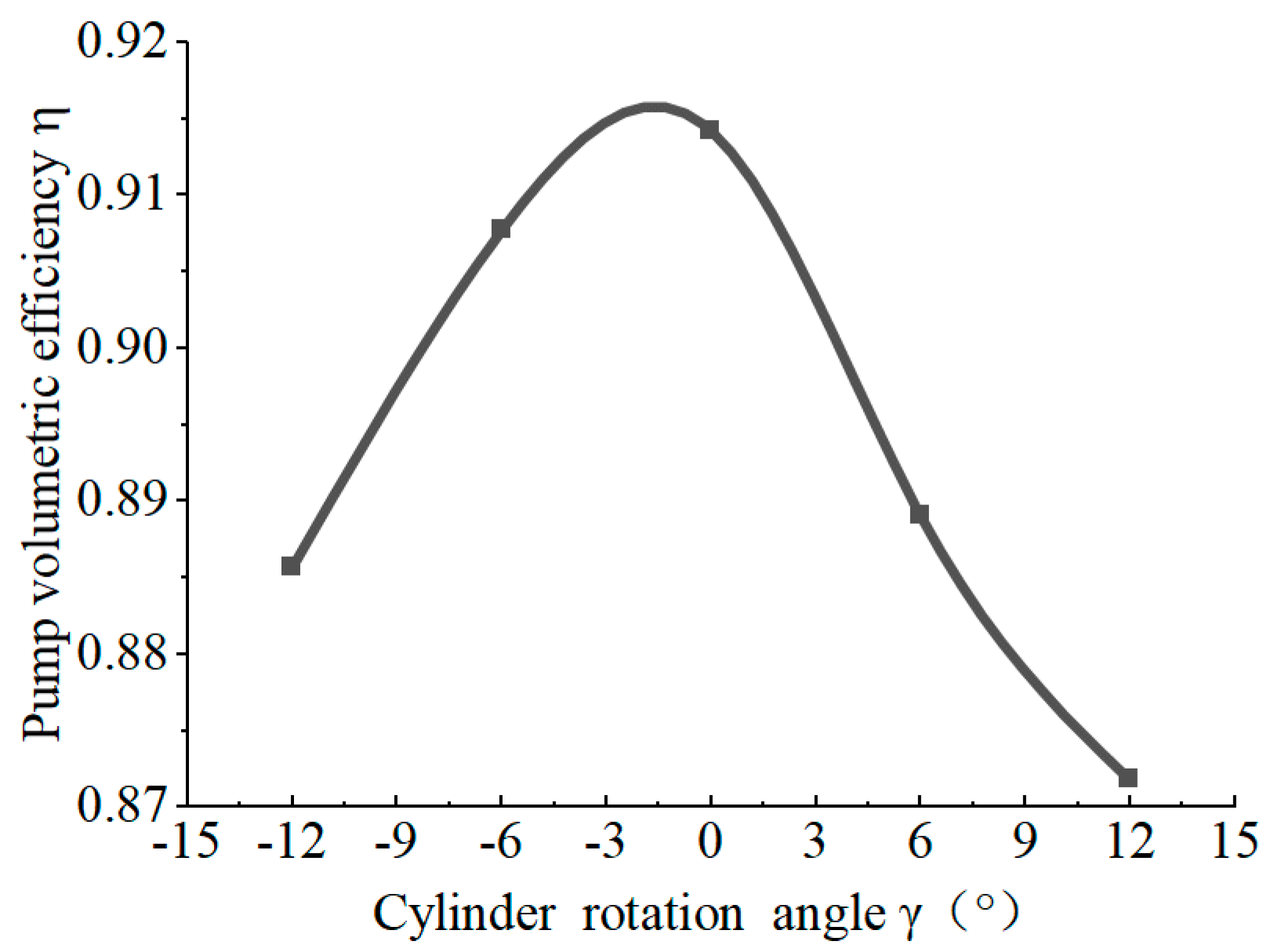
- When the pump displacement is reduced by changing the cylinder rotation angle, the volumetric efficiency and mechanical efficiency will decrease. Experiments show that when the cylinder rotation angle increases to 12°, the volumetric efficiency is reduced by approximately 2% and the mechanical efficiency is reduced by approximately 5%. It can be seen that the cylinder rotation angle also has an upper limit, and studying the appropriate rotation angle range is also a future research direction.
- (4)
- A cylinder rotation control mechanism is added to the 2D pump, which can only change the displacement by adjusting the motor speed so a variable displacement mode is added to the 2D pump and a bivariable 2D pump that can adapt to more working conditions is obtained. When the 2D pump works with small displacement, the motor speed need not be reduced too much to avoid the adverse effects of low-speed operation of the motor.
- (5)
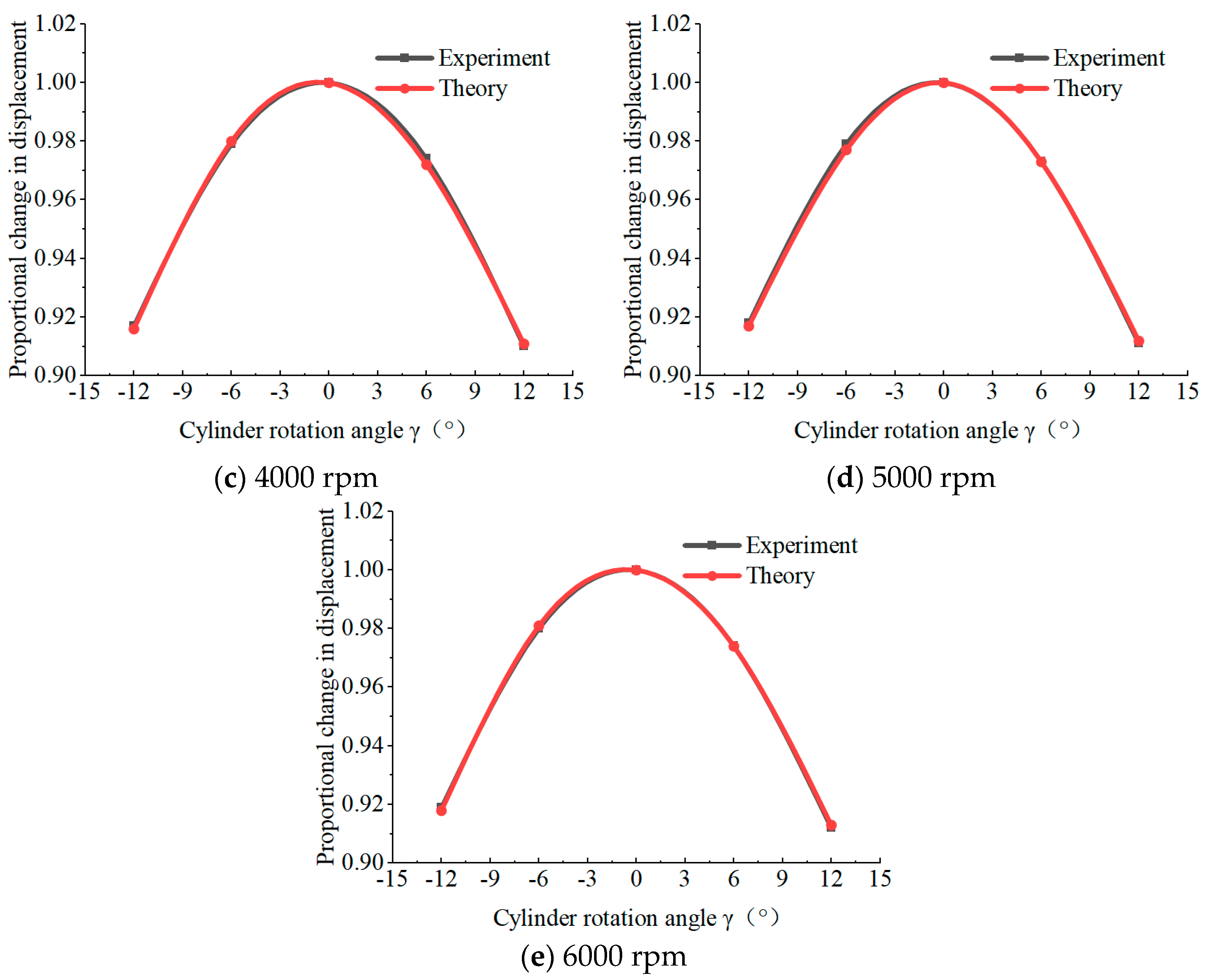
- The experiment is completed by adding gaskets to change the cylinder rotation angle, and the load experimental results of the variable displacement characteristics of the bivariable 2D pump are obtained. Compared with the simulation analysis results, the experimental data are essentially consistent with the simulation, and the relationship curve between the cylinder rotation angle and the pump displacement is verified.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| p1 | Instantaneous pressure of the left Chamber, MPa |
| βe | Bulk modulus of the oil |
| q | Flow in or out of the left lumen, m3/s |
| qc | Leakage flow, m3/s |
| V | Instantaneous volume of the left lumen, m3 |
| n | Rotation speed, r/min |
| D | Outer diameter of piston, m |
| d | Inner diameter of piston, m |
| γ | Cylinder rotation Angle (clockwise rotation is positive direction), ° |
| Vmin | Volume of the cavity at the left limit position of the piston, m3 |
| B | Total width of the constant length slot, B = 2b2 − b1 − b4, m |
| b1 | Axial length of drain window, m |
| b2 | Length flow distribution slot |
| b3 | Minimum axial seal length between left and right cavities of piston, m |
| b4 | Axial length of oil absorption window, m |
| Cd | Flow coefficient |
| A | Flow area of the distribution window, m2 |
| pin | Suction port pressure, MPa |
| pout | Oil drain pressure, MPa |
| ρ | Oil density, kg/m3 |
| l0 | Maximum seal length of left piston rod, m |
| s | Piston displacement, m |
| δ | Gap between piston and cylinder block, m |
| v | Piston velocity, m/s |
| p2 | Instantaneous pressure of the right Chamber, MPa |
| a1 | The length of the cylinder window circumference, m |
| a2 | Seal width between piston slots, m |
| a3 | Circumferential variable seal width for outlet leakage into low pressure chamber, m |
| a4 | Circumferential variable seal width for high pressure cavity leakage to the suction port, m |
References
- Lou, Q.S.; Zhu, L.S.; Niu, K.; Si, S.C. Research on Control System of Hydraulic Bionic Quadruped Robot. Microcontroll. Embed. Syst. 2015, 15, 37–40. [Google Scholar]
- Jiao, Y.S. The development and prospect of hydraulic power system in civil aircrafts. Aeronaut. Sci. Technol. 2019, 30, 1–6. [Google Scholar]
- Zhang, S.Z.; Liu, Y.; Li, S.; Zhang, X.F. Single and Double Pump Controlled Distributed Hydraulic System of Excavator Using Active Disturbance Rejection Control. Chin. Hydraul. Pneum. 2023, 47, 42–50. [Google Scholar]
- Hong, Y.S.; Doh, Y.H. Analysis on the friction losses of a bent-axis type hydraulic piston pump. KSME Int. J. 2004, 18, 1668–1679. [Google Scholar] [CrossRef]
- Li, J.; Fu, Y.L.; Wang, Z.L. Present Development Status and Key Technology Research of Airborne Electro-Hydrostatic Actuation System. Aeronaut. Manuf. Technol. 2005, 48, 73–77. [Google Scholar]
- Qiu, X.S. Research on the Advanced Actuators Technique. Aeronaut. Sci. Technol. 2009, 04, 6–8. [Google Scholar]
- Xin, H.T.; Wang, S.P.; Jiao, Z.X. Multidisciplinary Modeling Technology for Virtual Test and Simulation Platform of Electro-hydraulic Actuator. Mach. Tool Hydraul. 2008, 10, 122–126+143. [Google Scholar]
- Lv, F.; Xu, B.; Zhang, J.H. Simulative Analysis of Piston Posture and Piston/Cylinder Interface Leakage of EHA Pumps by the Influence of Rotating Speed. J. Mech. Eng. 2018, 54, 123–130. [Google Scholar] [CrossRef]
- Yang, H.Y.; Zhang, B.; Xu, B. Development of Axial Piston Pump/motor Technology. J. Mech. Eng. 2008, 44, 1–8. [Google Scholar] [CrossRef]
- Ouyang, X.P.; Wang, T.Z.; Fang, X. Research Status of the High Speed Aircraft Piston Pump. Chin. Hydraul. Pneum. 2018, 2, 1–8. [Google Scholar]
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A Review of High-Speed Electro-Hydrostatic Actuator Pumps in Aerospace Applications: Challenges and Solutions. J. Mech. Des. 2019, 141, 050801. [Google Scholar] [CrossRef]
- Wiegand, C. F-35 Air Vehicle Technology Overview. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018; AIAA AVIATION Forum. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Robbins, D.; Bobalik, J.; Stena, D.D.; Martin, N.; Plag, K.; Rail, K.; Wall, K. F-35 Subsystems Design, Development and Verification. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018; AIAA AVIATION Forum. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Eaton Aerospace Group. A Descriptive Summary of Vickers:Inline Pumps and Their Application. Available online: https://www.eaton.com.cn/cn/en-us/products/pumps.html (accessed on 25 June 2016).
- Guo, S.R.; Chen, J.H.; Lu, Y.L.; Wang, Y.; Dong, H.K. Hydraulic piston pump in civil aircraft: Current status, future directions and critical technologies. Chin. J. Aeronaut. 2020, 33, 16–30. [Google Scholar] [CrossRef]
- Ernst, M.; Ivantysynova, M.; Vacca, A. Shaping the Piston-Cylinder Interfaces of Axial Piston Machines for Running in the High-Pressure Regime with Water as the Hydraulic Fluid. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 095440622110686. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.Q.; Guo, S.R.; Lu, Y.L.; Liu, S. Fatigue analysis and life prediction method for cylinder block of aviation piston pump. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 1314–1321. [Google Scholar]
- Chao, Q.; Zhang, J.; Xu, B.; Wang, Q.; Lyu, F.; Li, K. Integrated slipper retainer mechanism to eliminate slipper wear in high-speed axial piston pumps. Front. Mech. Eng. 2022, 17, 1. [Google Scholar] [CrossRef]
- Ouyang, X.P. Modern Hydraulics for Aircrafts; Zhejiang University Press: Hangzhou, China, 2016. [Google Scholar]
- Zhang, Z.Y.; Zhang, C.C.; Lu, C.; Ruan, J. Design of 2D Hydraulic Plunger Pump. Chin. Hydraul. Pneum. 2017, 107–111. [Google Scholar]
- Ruan, J.; Li, J.Y.; Jin, D.C. Research and feasibility verification of two-dimensional (2D) piston pump. J. Zhejiang Univ. Technol. 2017, 45, 264–269. [Google Scholar]
- Wu, H. Two Kinds of Transmission Structure Miniature Water Pump Design and Research. Master’s Thesis, Zhejiang University of Technology, Hangzhou, China, 2022. [Google Scholar]
- Huang, Y. Research on the Efficiency Characteristics of High-Speed Two-Dimensional Piston Pumps. Ph.D. Thesis, Zhejiang University of Technology, Hangzhou, China, 2020. [Google Scholar]
- Ruan, J.; Jin, D.C.; Shentu, S.N.; Wu, C.S. Research and feasibility verification of two–dimensional (2D) tandem pump. Chin. Hydraul. Pneum. 2017, 11, 1–5. [Google Scholar]
- Wang, H.Y.; Ding, C.; Huang, Y.; Li, S.; Ruan, J. Design and research of 2D piston pumps with a stacked cone roller set. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2022, 236, 5. [Google Scholar] [CrossRef]
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors: Principles, Design, Performance, Modelling, Analysis, Control and Testing; Tech Books International: New Delhi, India, 2003. [Google Scholar]


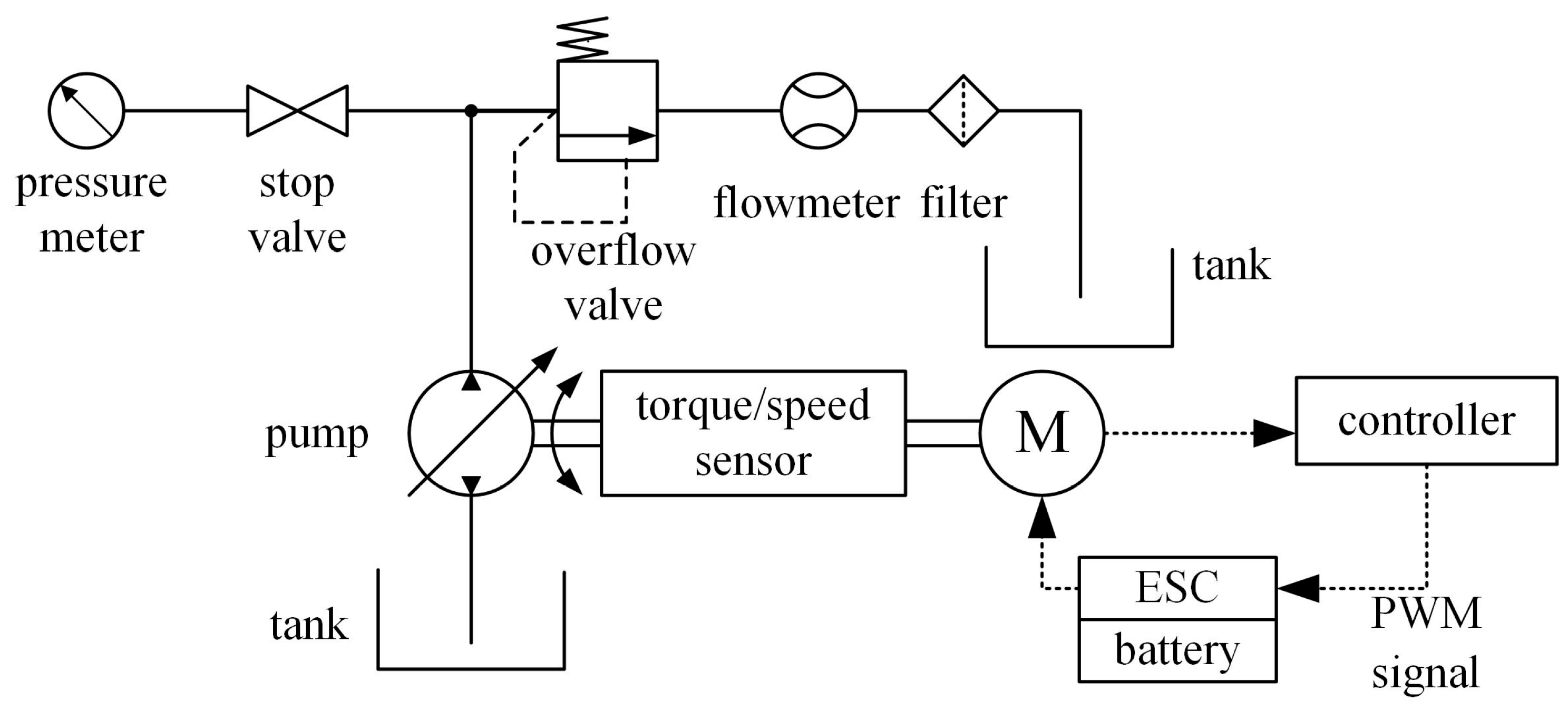



| Description | Value | Description | Value |
|---|---|---|---|
| Rotation speed n (rpm) | 6000 | Oil dynamic viscosity μ (Pa∙s) | 0.02 |
| Loading pressure (MPa) | 27 | Gap between piston and cylinder block δ (m) | 5 × 10−6 |
| Piston stroke h (m) | 0.004 | Maximum seal length of left piston rod (m) | 0.01 |
| Bulk modulus of the oil (Pa) | 0.95 × 109 | Axial length of oil absorption window (m) | 0.006 |
| Outer diameter of piston D (m) | 0.016 | Axial length of drain window (m) | 0.004 |
| Inner diameter of piston d (m) | 0.009 | Flow coefficient | 0.62 |
| Tank pressure (Pa) | 0 | Minimum axial seal length between left and right cavities of piston (m) | 0.002 |
| Length flow distribution slot (m) | 0.022 | Oil density ρ () | 833 |
| Minimum volume of piston chamber () | 1.35 × 10−6 |
| Name | Parameter |
|---|---|
| Kistler 4503B strain type torque/speed sensor | torque 0–20 N∙m, precision ± 0.05% rotational speed 0–18,000 r/min |
| MIK-P300 pressure sensor | pressure 0–10 Mpa, precision ± 0.3% |
| VSE-58809 flow meter | range 0.05–80 L/min, precision ± 0.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, T.; Ji, X.; Yang, Z.; Ruan, J. Design and Characteristic Research on Variable Displacement Mechanism of Two-Dimensional (2D) Bivariable Pump. Energies 2024, 17, 1725. https://doi.org/10.3390/en17071725
Xing T, Ji X, Yang Z, Ruan J. Design and Characteristic Research on Variable Displacement Mechanism of Two-Dimensional (2D) Bivariable Pump. Energies. 2024; 17(7):1725. https://doi.org/10.3390/en17071725
Chicago/Turabian StyleXing, Tong, Xu Ji, Zeri Yang, and Jian Ruan. 2024. "Design and Characteristic Research on Variable Displacement Mechanism of Two-Dimensional (2D) Bivariable Pump" Energies 17, no. 7: 1725. https://doi.org/10.3390/en17071725
APA StyleXing, T., Ji, X., Yang, Z., & Ruan, J. (2024). Design and Characteristic Research on Variable Displacement Mechanism of Two-Dimensional (2D) Bivariable Pump. Energies, 17(7), 1725. https://doi.org/10.3390/en17071725






