An Adaptive Modeling Method for the Prognostics of Lithium-Ion Batteries on Capacity Degradation and Regeneration
Abstract
1. Introduction
2. Related Work
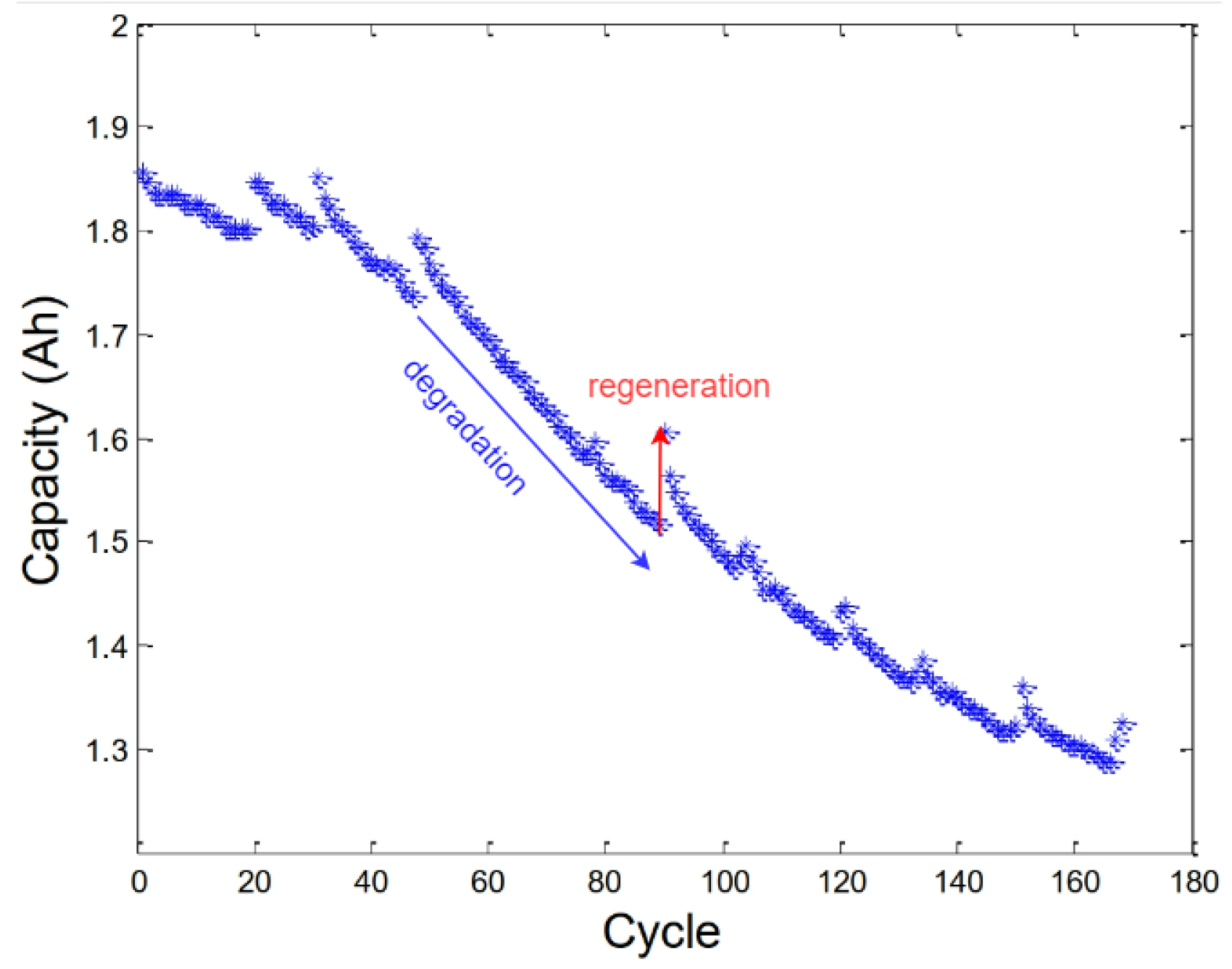
2.1. Battery Degradation
2.2. Regeneration Phenomenon
3. Model Development, Identification, and Prediction
3.1. Proposed Model
3.2. Particle Filtering Method
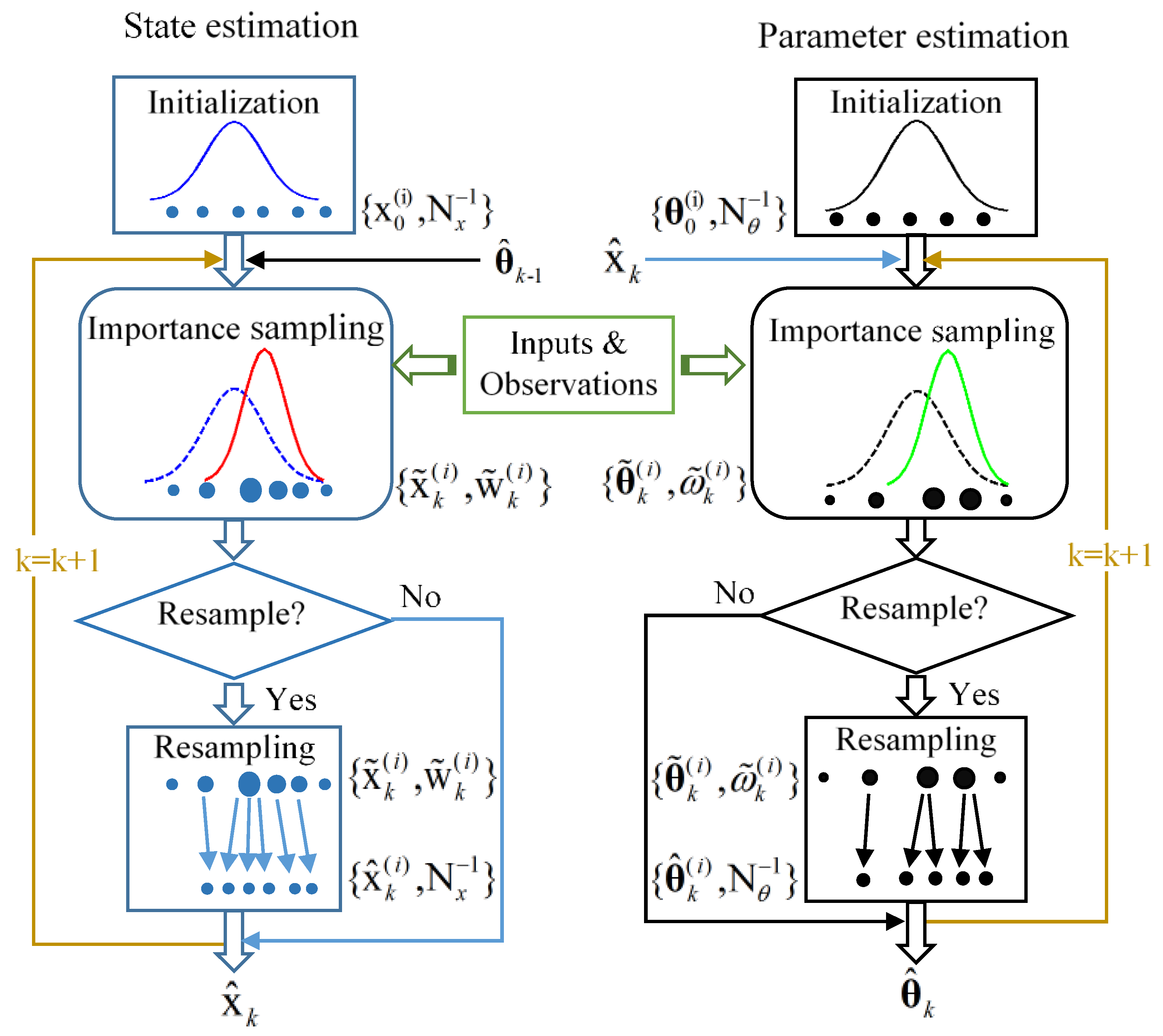
3.3. Dual Estimation
| Algorithm 1: Dual-particle filter algorithm. |
|
3.4. Kernel Smoothing
3.5. Remaining Useful Life Prediction
4. Experiment Comparisons
4.1. Experiment Settings
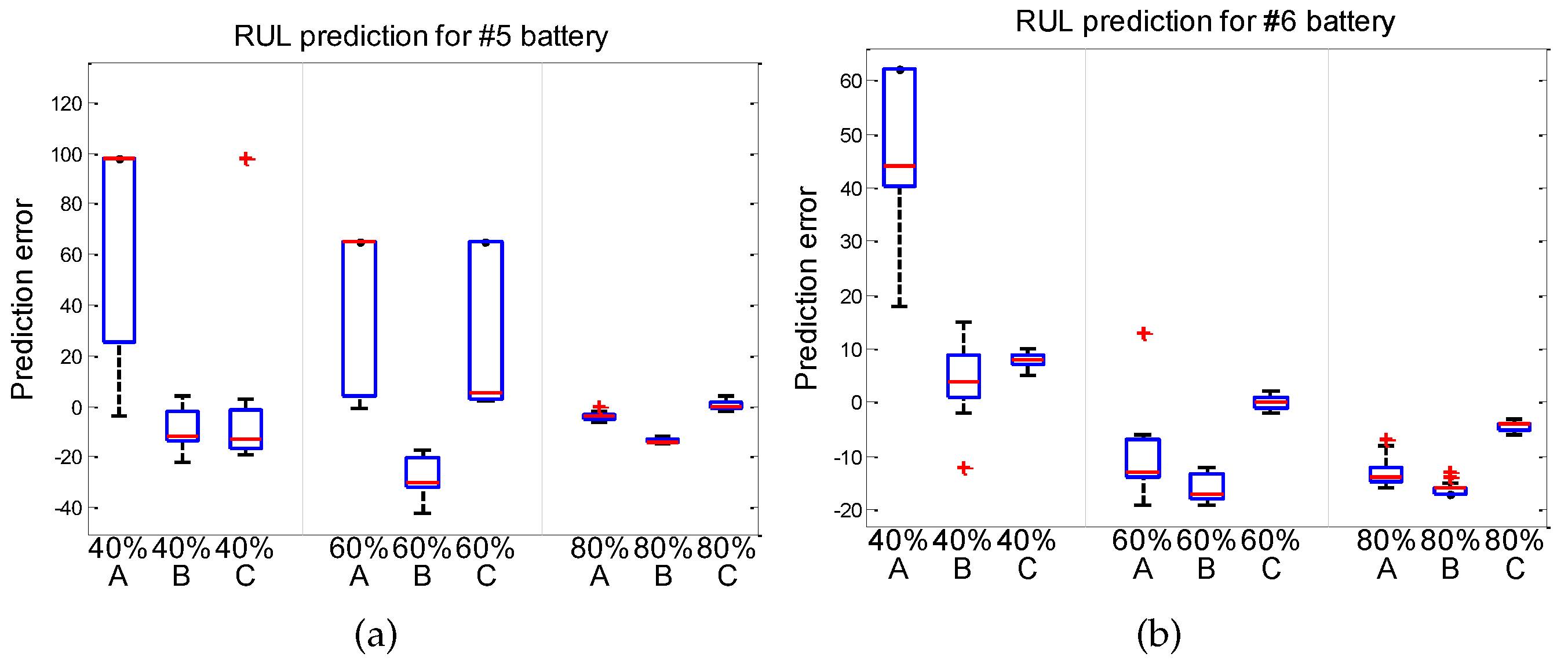
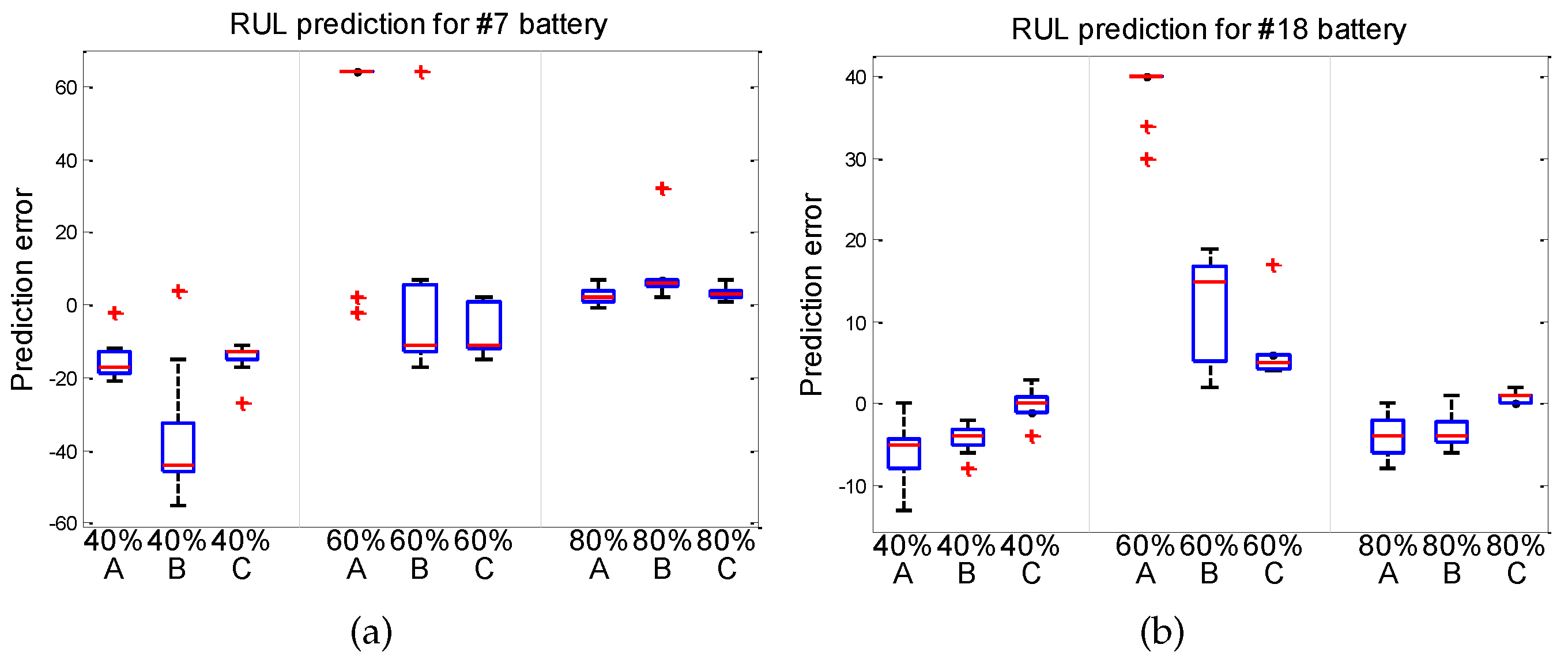
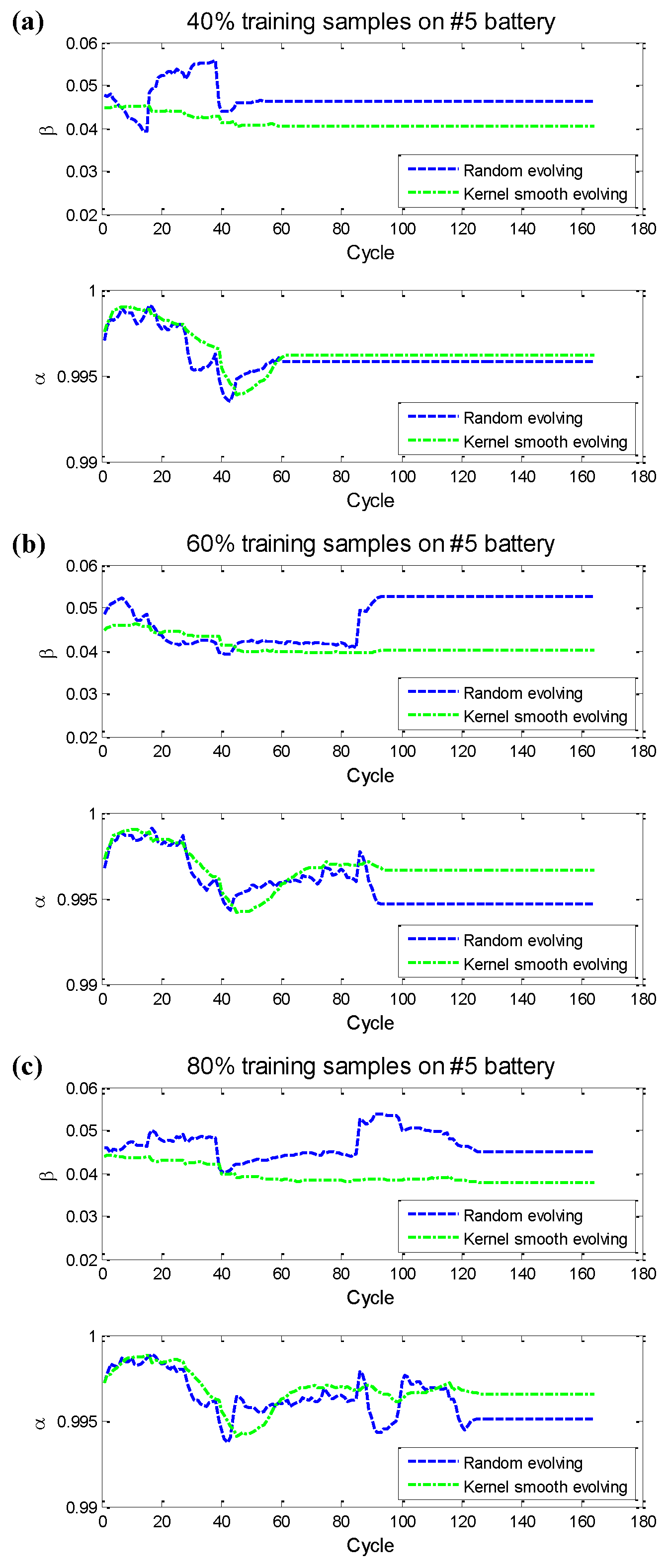
4.2. Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Equivalent Proof
References
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Huggins, R. Advanced Batteries: Materials Science Aspects; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Liu, K.; Hu, X.; Yang, Z.; Xie, Y.; Feng, S. Lithium-ion battery charging management considering economic costs of electrical energy loss and battery degradation. Energy Convers. Manag. 2019, 195, 167–179. [Google Scholar] [CrossRef]
- Li, W.; Fan, Y.; Ringbeck, F.; Jöst, D.; Sauer, D.U. Unlocking electrochemical model-based online power prediction for lithium-ion batteries via Gaussian process regression. Appl. Energy 2022, 306, 118114. [Google Scholar] [CrossRef]
- Xu, J.; Sun, C.; Ni, Y.; Lyu, C.; Wu, C.; Zhang, H.; Yang, Q.; Feng, F. Fast identification of micro-health parameters for retired batteries based on a simplified P2D model by using padé approximation. Batteries 2023, 9, 64. [Google Scholar] [CrossRef]
- You, G.w.; Park, S.; Oh, D. Real-time state-of-health estimation for electric vehicle batteries: A data-driven approach. Appl. Energy 2016, 176, 92–103. [Google Scholar] [CrossRef]
- Remmlinger, J.; Buchholz, M.; Meiler, M.; Bernreuter, P.; Dietmayer, K. State-of-health monitoring of lithium-ion batteries in electric vehicles by on-board internal resistance estimation. J. Power Sources 2011, 196, 5357–5363. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Woirgard, E.; Vinassa, J.M. Remaining useful life prediction of lithium batteries in calendar ageing for automotive applications. Microelectron. Reliab. 2012, 52, 2438–2442. [Google Scholar] [CrossRef]
- Ng, S.S.; Xing, Y.; Tsui, K.L. A naive Bayes model for robust remaining useful life prediction of lithium-ion battery. Appl. Energy 2014, 118, 114–123. [Google Scholar] [CrossRef]
- Yang, F.; Wang, D.; Xing, Y.; Tsui, K.L. Prognostics of Li(NiMnCo)O2-based lithium-ion batteries using a novel battery degradation model. Microelectron. Reliab. 2017, 70, 70–78. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Peng, Y.; Pecht, M. Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression. Microelectron. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; Gomadam, P.M.; White, R.; Popov, B.N. Development of first principles capacity fade model for Li-ion cells. J. Electrochem. Soc. 2004, 151, A196–A203. [Google Scholar] [CrossRef]
- Chen, Z.; Shen, W.; Chen, L.; Wang, S. Adaptive online capacity prediction based on transfer learning for fast charging lithium-ion batteries. Energy 2022, 248, 123537. [Google Scholar] [CrossRef]
- Liu, K.; Li, Y.; Hu, X.; Lucu, M.; Widanage, W.D. Gaussian Process Regression With Automatic Relevance Determination Kernel for Calendar Aging Prediction of Lithium-Ion Batteries. IEEE Trans. Ind. Inf. 2020, 16, 3767–3777. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, L.; Ma, Z.; Xu, K.; Zhou, Y.; Shen, W. Joint modeling for early predictions of Li-ion battery cycle life and degradation trajectory. Energy 2023, 277, 127633. [Google Scholar] [CrossRef]
- Liu, D.; Luo, Y.; Liu, J.; Peng, Y.; Guo, L.; Pecht, M. Lithium-ion battery remaining useful life estimation based on fusion nonlinear degradation AR model and RPF algorithm. Neural Comput. Appl. 2014, 25, 557–572. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.; Tsui, K.L.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K.; Christophersen, J. Comparison of prognostic algorithms for estimating remaining useful life of batteries. Trans. Inst. Meas. Control. 2009, 31, 293–308. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Modeling Li-ion battery capacity depletion in a particle filtering framework. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, CA, USA, 27 September–1 October 2009; pp. 2909–2924. [Google Scholar]
- Saha, B.; Goebel, K.; Poll, S.; Christophersen, J. Prognostics methods for battery health monitoring using a Bayesian framework. IEEE Trans. Instrum. Meas. 2009, 58, 291–296. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Vinassa, J.M. Lithium-ion battery performance improvement based on capacity recovery exploitation. Electrochim. Acta 2013, 114, 750–757. [Google Scholar] [CrossRef]
- Deng, L.; Shen, W.; Wang, H.; Wang, S. A rest-time-based prognostic model for remaining useful life prediction of lithium-ion battery. Neural Comput. Appl. 2021, 33, 2035–2046. [Google Scholar] [CrossRef]
- Jin, G.; Matthews, D.E.; Zhou, Z. A Bayesian framework for on-line degradation assessment and residual life prediction of secondary batteries inspacecraft. Reliab. Eng. Syst. Saf. 2013, 113, 7–20. [Google Scholar] [CrossRef]
- Tang, S.; Yu, C.; Wang, X.; Guo, X.; Si, X. Remaining useful life prediction of lithium-ion batteries based on the wiener process with measurement error. Energies 2014, 7, 520–547. [Google Scholar] [CrossRef]
- Olivares, B.E.; Munoz, M.A.C.; Orchard, M.E.; Silva, J.F. Particle-filtering-based prognosis framework for energy storage devices with a statistical characterization of state-of-health regeneration phenomena. IEEE Trans. Instrum. Meas. 2013, 62, 364–376. [Google Scholar] [CrossRef]
- Orchard, M.E.; Lacalle, M.S.; Olivares, B.E.; Silva, J.F.; Palma-Behnke, R.; Estévez, P.A.; Severino, B.; Calderon-Muñoz, W.; Cortés-Carmona, M. Information-theoretic measures and sequential monte carlo methods for detection of regeneration phenomena in the degradation of lithium-ion battery cells. IEEE Trans. Reliab. 2015, 64, 701–709. [Google Scholar] [CrossRef]
- Qin, T.; Zeng, S.; Guo, J.; Skaf, Z. A Rest Time-Based Prognostic Framework for State of Health Estimation of Lithium-Ion Batteries with Regeneration Phenomena. Energies 2016, 9, 896. [Google Scholar] [CrossRef]
- Pang, X.; Huang, R.; Wen, J.; Shi, Y.; Jia, J.; Zeng, J. A lithium-ion battery RUL prediction method considering the capacity regeneration phenomenon. Energies 2019, 12, 2247. [Google Scholar] [CrossRef]
- Ma, Q.; Zheng, Y.; Yang, W.; Zhang, Y.; Zhang, H. Remaining useful life prediction of lithium battery based on capacity regeneration point detection. Energy 2021, 234, 121233. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, Y.; Li, X.; Luo, H.; Yin, S.; Kaynak, O. Remaining useful life prediction of lithium-ion battery with adaptive noise estimation and capacity regeneration detection. IEEE/ASME Trans. Mechatron. 2022, 28, 632–643. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Y.; Cheng, J. A hybrid method for remaining useful life estimation of lithium-ion battery with regeneration phenomena. Appl. Sci. 2019, 9, 1890. [Google Scholar] [CrossRef]
- Yang, F.; Wang, D.; Zhao, Y.; Tsui, K.L.; Bae, S. A study of the relationship between Coulombic efficiency and capacity degradation of commercial lithium-ion batteries. Energy 2018, 145, 486–495. [Google Scholar] [CrossRef]
- Yang, F.; Song, X.; Dong, G.; Tsui, K.L. A Coulombic efficiency-based model for prognostics and health estimation of lithium-ion batteries. Energy 2019, 171, 1173–1182. [Google Scholar] [CrossRef]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEEE Proc. F Radar Signal Process. 1993, 140, 107–113. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Van Der Merwe, R.; Doucet, A.; De Freitas, N.; Wan, E.A. The unscented particle filter. In Advances in Neural Information Processing Systems 13: Proceedings of the 2000 Conference; The MIT Press: Cambridge, MA, USA, 2001; pp. 584–590. [Google Scholar]
- Wan, E.A.; Nelson, A.T. Dual extended Kalman filter methods. In Kalman Filtering and Neural Networks; John Wiley & Sons, Inc.: New York, NY, USA, 2001; pp. 123–173. [Google Scholar]
- Storvik, G. Particle filters for state-space models with the presence of unknown static parameters. IEEE Trans. Signal Process. 2002, 50, 281–289. [Google Scholar] [CrossRef]
- Daroogheh, N.; Meskin, N.; Khorasani, K. A Dual Particle Filter-Based Fault Diagnosis Scheme for Nonlinear Systems. IEEE Trans. Control. Syst. Technol. 2017, 26, 1317–1334. [Google Scholar] [CrossRef]
- West, M. Mixture models, Monte Carlo, Bayesian updating, and dynamic models. Comput. Sci. Stat. 1993, 24, 325–333. [Google Scholar]
- Liu, J.; West, M. Combined parameter and state estimation in simulation-based filtering. In Sequential Monte Carlo Methods in Practice; Springer: New York, NY, USA, 2001; pp. 197–223. [Google Scholar]
- Deng, L.M.; Hsu, Y.C.; Li, H.X. An improved model for remaining useful life prediction on capacity degradation and regeneration of lithium-ion battery. In Proceedings of the 9th Annual Conference of the Prognostics and Health Management Society 2017 (PHM 2017), St. Petersburg, FL, USA, 2–5 October 2017. [Google Scholar]
- Saha, B.; Goebel, K. Battery Data Set. 2007. Available online: https://ti.arc.nasa.gov/tech/dash/pcoe/prognostic-data-repository/#battery (accessed on 3 May 2016).


| Battery No. | True RUL | Method A | Method B | Method C | |||
|---|---|---|---|---|---|---|---|
| Median Prediction | Absolute Error | Median Prediction | Absolute Error | Median Prediction | Absolute Error | ||
| B0005 | 98 | 196 | 98 | 86 | 12 | 85 | 13 |
| 65 | 130 | 65 | 35 | 30 | 70 | 5 | |
| 33 | 29 | 4 | 19 | 14 | 33 | 0 | |
| B0006 | 62 | 106 | 44 | 66 | 4 | 70 | 8 |
| 41 | 28 | 13 | 24 | 17 | 41 | 0 | |
| 21 | 7 | 14 | 5 | 16 | 17 | 4 | |
| B0007 | 96 | 83 | 13 | 52 | 44 | 82 | 14 |
| 64 | 128 | 64 | 68 | 4 | 53 | 11 | |
| 32 | 35 | 3 | 36 | 4 | 35 | 3 | |
| B0018 | 60 | 55 | 5 | 56 | 4 | 60 | 0 |
| 40 | 80 | 40 | 55 | 15 | 45 | 5 | |
| 20 | 16 | 4 | 16 | 4 | 21 | 1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, L.; Shen, W.; Xu, K.; Zhang, X. An Adaptive Modeling Method for the Prognostics of Lithium-Ion Batteries on Capacity Degradation and Regeneration. Energies 2024, 17, 1679. https://doi.org/10.3390/en17071679
Deng L, Shen W, Xu K, Zhang X. An Adaptive Modeling Method for the Prognostics of Lithium-Ion Batteries on Capacity Degradation and Regeneration. Energies. 2024; 17(7):1679. https://doi.org/10.3390/en17071679
Chicago/Turabian StyleDeng, Liming, Wenjing Shen, Kangkang Xu, and Xuhui Zhang. 2024. "An Adaptive Modeling Method for the Prognostics of Lithium-Ion Batteries on Capacity Degradation and Regeneration" Energies 17, no. 7: 1679. https://doi.org/10.3390/en17071679
APA StyleDeng, L., Shen, W., Xu, K., & Zhang, X. (2024). An Adaptive Modeling Method for the Prognostics of Lithium-Ion Batteries on Capacity Degradation and Regeneration. Energies, 17(7), 1679. https://doi.org/10.3390/en17071679







