Analysis of Sediment Erosion in Pelton Nozzles and Needles Affected by Particle Size
Abstract
1. Introduction
2. Numerical Model and Mathematical Model
2.1. Computational Domain and Mesh
2.2. Numerical Mesh
2.3. Sediment Particle Diameter and Concentration
2.4. Boundary Conditions and Erosion Model
3. Analysis of the Three-Phase Flow Behavior and Erosion
3.1. Three-Phase Flow Behaviors
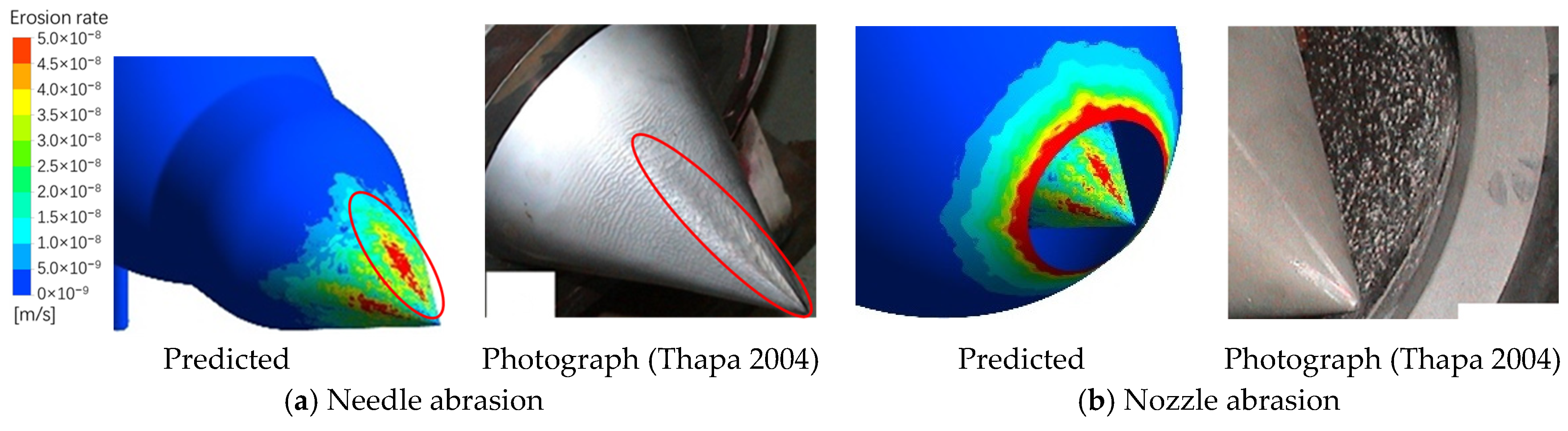
3.2. Predicted Erosion Distribution and Comparison
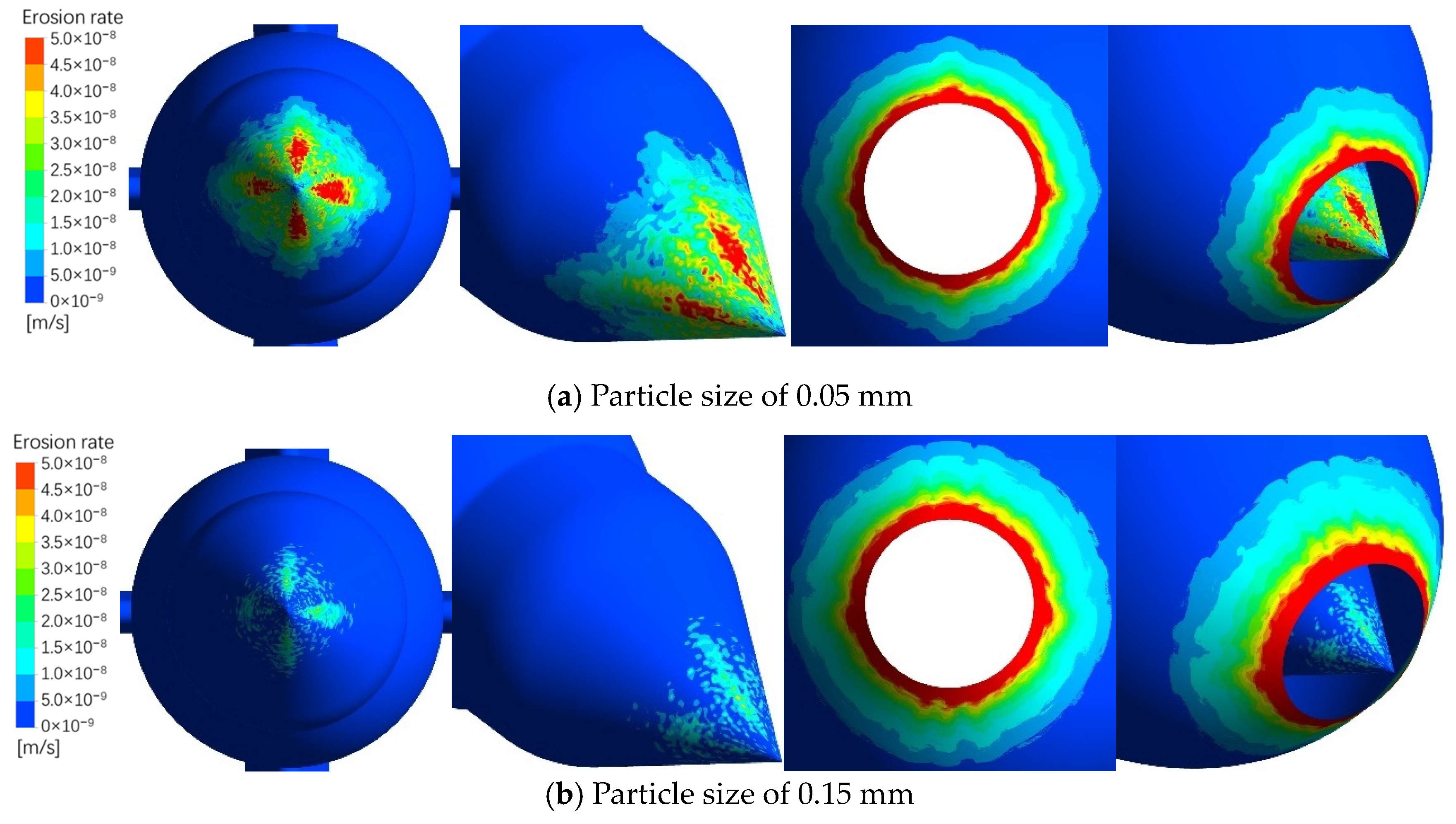
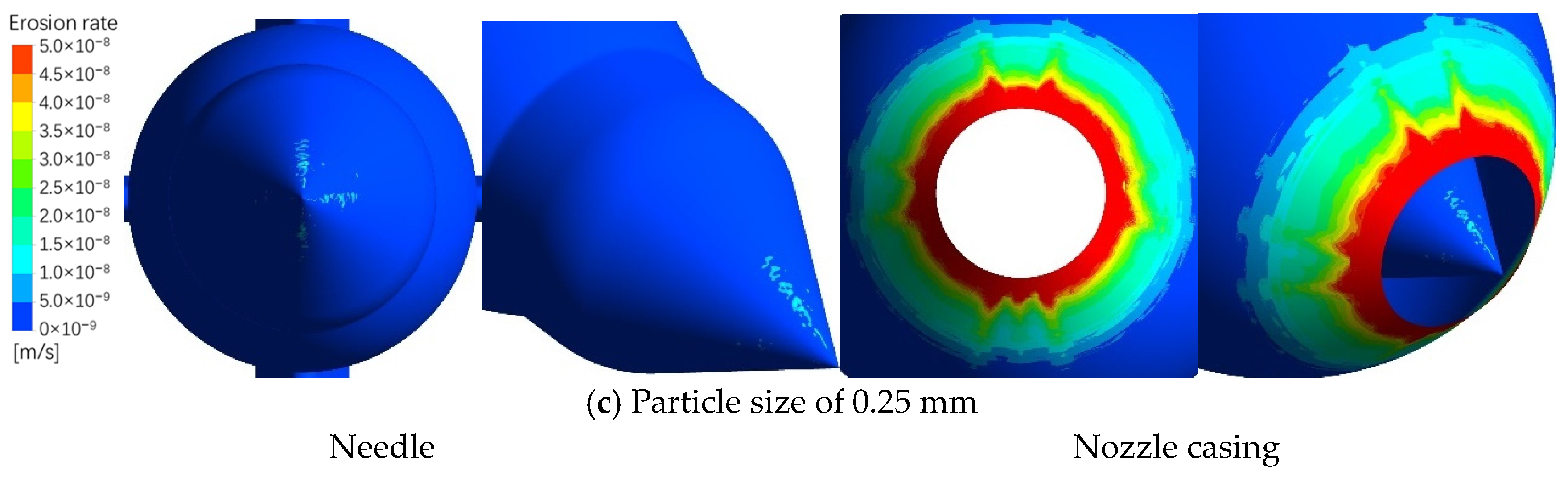
3.3. The Effect of Particle Size on Injector Erosion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, J.; Ge, X.F.; Zhou, Y.; Liu, D.; Liu, J.; Li, G.; Zheng, Y. Research on synergistic erosion by cavitation and sediment: A review. Ultrason. Sonochem. 2023, 95, 106399. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wu, J.; Ma, F. Cavitation–silt erosion in sand suspensions. J. Mech. Sci. Technol. 2018, 32, 5697–5702. [Google Scholar] [CrossRef]
- Rai, A.K.; Kumar, A.; Staubli, T. Analytical modelling and mechanism of hydro-abrasive erosion in Pelton buckets. Wear 2019, 436, 203003. [Google Scholar] [CrossRef]
- Zhang, Z. Pelton Turbine; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Nag, S.; Lee, K.Y. Network and Reserve Constrained Economic Analysis of Conventional, Adjustable-Speed and Ternary Pumped-Storage Hydropower. Energies 2020, 13, 4140. [Google Scholar] [CrossRef]
- Rai, A.K.; Kumar, A.; Staubli, T. Hydro-abrasive erosion in Pelton buckets: Classification and field study. Wear 2017, 392–393, 8–20. [Google Scholar] [CrossRef]
- Padhy, M.K.; Saini, R.P. Study of silt erosion on performance of a Pelton turbine. Energy 2011, 36, 141–147. [Google Scholar] [CrossRef]
- Morales, A.M.B.; Pachón, I.F.; Loboguerrero, J.U.; Medina, J.A.; Escobar, J.A.G. Development of a test rig to evaluate abrasive wear on Pelton turbine nozzles. A case study of Chivor hydropower. Wear 2017, 372–373, 208–215. [Google Scholar] [CrossRef]
- Din, U.D.; Mohammad, Z.; Harmain, G.A. Assessment of erosive wear of Pelton turbine injector: Nozzle and spear combination—A study of Chenani hydro-power plant. Eng. Fail. Anal. 2020, 116, 104695. [Google Scholar] [CrossRef]
- Sangal, S.; Singhal, M.K.; Saini, R.P. Hydro-abrasive erosion in hydro turbines: A review. Int. J. Green Energy 2018, 15, 232–253. [Google Scholar] [CrossRef]
- Abgottspon, A.; Staubli, T.; Felix, D. Erosion of Pelton buckets and changes in turbine efficiency measured in the HPP Fieschertal. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 122008. [Google Scholar] [CrossRef]
- Felix, D.; Albayrak, I.; Abgottspon, A.; Boes, R.M. Hydro-abrasive erosion of hydraulic turbines caused by sediment—A century of research and development. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 122001. [Google Scholar] [CrossRef]
- Felix, D. Experimental Investigation on Suspended Sediment, Hydro-Abrasive Erosion and Efficiency Reductions of Coated Pelton Turbines. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2017. [Google Scholar]
- Rai, A.K.; Kumar, A. Continuous measurement of suspended sediment concentration: Technological advancement and future outlook. Measurement 2015, 76, 209–227. [Google Scholar] [CrossRef]
- Thapa, B. Sand Erosion in Hydraulic Machinery. Ph.D. Thesis, Norwegian University of Science and Technology (NTNU), Trondheim, Norway, 2004. [Google Scholar]
- Rai, A.K.; Kumar, A.; Staubli, T.; Xiao, Y. Interpretation and application of the hydro-abrasive erosion model from IEC 62364 (2013) for Pelton turbines. Renew. Energy 2020, 160, 396–408. [Google Scholar] [CrossRef]
- Bajracharya, T.; Acharya, B.; Joshi, C.; Saini, R.; Dahlhaug, O. Sand erosion of Pelton turbine nozzles and buckets: A case study of Chilime Hydropower Plant. Wear 2008, 264, 177–184. [Google Scholar] [CrossRef]
- Nozaki, T. Estimation of Repair Cycle of Turbine Due to Abrasion Caused by Suspended Sand and Determination of Desilting Basin Capacity; Japan International Cooperation Agency: Tokyo, Japan, 1990. [Google Scholar]
- Sulzer Hydro. Ein Semi-Empirisches Abrasionsmodell zur Vorhersage von Hydro-Abrasivem Verschleiß an X5 CrNi 13/4 Stahl (a Semi-empirical Model to Predict Hydro-Abrasive Wear on Strainless Turbine Steel); Bericht Nr. STT.TB94.020; partially published in 2006; DWA: Hennef, Germany, 1996. (In German) [Google Scholar]
- Winkler, K.; Parkinson, E.; Dekumbis, R.; Rentschler, M.; Garcin, H. Understanding Hydro-Abrasive Erosion. In Proceedings of the Hydro Conference, Prague, Czech Republic, 17–19 October 2011. [Google Scholar]
- Padhy, M.K.; Saini, R.P. Effect of size and concentration of silt particles on erosion of Pelton turbine buckets. Energy 2009, 34, 1477–1483. [Google Scholar] [CrossRef]
- Zeng, C.J.; Xiao, Y.X.; Zhu, W.; Yao YYCal, L.; Wang, Z.W. Pelton turbine Needle erosion prediction based on 3D three- phase flow simulation. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 052019. [Google Scholar]
- Messa, G.V.; Mandelli, S.; Malavasi, S. Hydro-abrasive erosion in Pelton turbine injectors: A numerical study. Renew. Energy 2019, 130, 474–488. [Google Scholar] [CrossRef]
- Ge, X.F.; Sun, J.; Li, Y.; Wu, D.; Zhang, L.; Hua, H. Numerical simulation of silt erosion characteristics of an injector of Pelton turbine. J. Hydraul. Eng. 2020, 51, 1486–1494. [Google Scholar]
- Guo, B.; Xiao, Y.X.; Rai, A.K.; Zhang, J.; Liang, Q. Sediment-laden flow and erosion modeling in a Pelton turbine injector. Renew. Energy 2020, 162, 30–42. [Google Scholar] [CrossRef]
- Guo, B.; Xiao, Y.; Rai, A.K.; Liang, Q.; Liu, J. Analysis of the air-water-sediment flow behavior in Pelton buckets using a Eulerian-Lagrangian approach. Energy 2021, 218, 119522. [Google Scholar] [CrossRef]
- Xiao, Y.X.; Guo, B.; Rai, A.K.; Liang, Q.W.; Liu, J.; Zhang, J. Analysis of hydro-abrasive erosion in Pelton buckets using a Eulerian-Lagrangian approach. Renew. Energy 2022, 197, 472–485. [Google Scholar] [CrossRef]
- Shrivastava, N.; Rai, A.K.; Abbas, A.; Xiao, Y. Analysis of hydro-abrasive erosion in a high-head Pelton turbine injector using a Eulerian-Lagrangian approach. Proc. Inst. Mech. Eng. Part A J. Power Energy 2024. [Google Scholar] [CrossRef]
- Leguizamón, S.; Alimirzazadeh, S.; Jahanbakhsh, E.; Avellan, F. Multiscale simulation of erosive wear in a prototype-scale Pelton runner. Renew. Energy 2020, 151, 204–215. [Google Scholar] [CrossRef]
- Tarodiya, R.; Khullar, S.; Levy, A. Particulate flow and erosion modeling of a Pelton turbine injector using CFD-DEM simulations. Powder Technol. 2022, 399, 117168. [Google Scholar] [CrossRef]
- Tarodiya, R.; Khullar, S.; Levy, A. Assessment of erosive wear performance of Pelton turbine injectors using CFD-DEM simulations. Powder Technol. 2022, 408, 117763. [Google Scholar] [CrossRef]
- Liu, J.; Pang, J.; Liu, X.; Huang, Y.; Deng, H. Analysis of Sediment and Water Flow and Erosion Characteristics of Large Pelton Turbine Injector. Processes 2023, 11, 1011. [Google Scholar] [CrossRef]
- IEC 62364:2013; Hydraulic Turbines-Guide for Dealing with Hydro-Abrsive Erosion in Kaplan, Francis and Pelton Turbines. International Electrotechnical Commission: Geneva, Switzerland, 2013.
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Grant, G.; Tabakoff, W. Erosion Prediction in Turbomachinery Resulting from Environmental Solid Particles. J. Aircr. 1975, 12, 471–478. [Google Scholar] [CrossRef]
- Zhang, J.; Darihaki, F.; Shirazi, S.A. A comprehensive CFD-based erosion prediction for sharp bend geometry with examination of grid effect. Wear 2019, 430–431, 191–201. [Google Scholar] [CrossRef]
- Zhang, J.; McLaury, B.S.; Shirazi, S.A. Modeling sand fines erosion in elbows mounted in series. Wear 2018, 402–403, 196–206. [Google Scholar] [CrossRef]
- Padhy, M.K.; Saini, R.P. Study of silt erosion mechanism in Pelton turbine buckets. Energy 2012, 39, 286–293. [Google Scholar] [CrossRef]
- Oka, Y.I.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Vieira, R.E.; Mansouri, A.; McLaury, B.S.; Shirazi, S.A. Experimental and computational study of erosion in elbows due to sand particles in air flow. Powder Technol. 2016, 288, 339–353. [Google Scholar] [CrossRef]
- Nguyen, V.; Nguyen, Q.; Zhang, Y.; Lim, C.; Khoo, B. Effect of particle size on erosion characteristics. Wear 2016, 348–349, 126–137. [Google Scholar] [CrossRef]
- Zhao, X.; Luo, Y.; Wang, Z.; Xiao, Y.; Avellan, F. Unsteady Flow Numerical Simulations on Internal Energy Dissipation for a Low-Head Centrifugal Pump at Part-Load Operating Conditions. Energies 2019, 12, 2013. [Google Scholar] [CrossRef]
- Benzon, D.; Židonis, A.; Panagiotopoulos, A.; Aggidis, G.A.; Anagnostopoulos, J.S.; Papantonis, D.E. Impulse Turbine Injector Design Improvement Using Computational Fluid Dynamics. J. Fluids Eng. 2015, 137, 041106. [Google Scholar] [CrossRef]
- Semlitsch, B. Effect of inflow disturbances in Pelton turbine distributor lines on the water jet quality. Int. J. Multiph. Flow 2024, 174, 104786. [Google Scholar] [CrossRef]
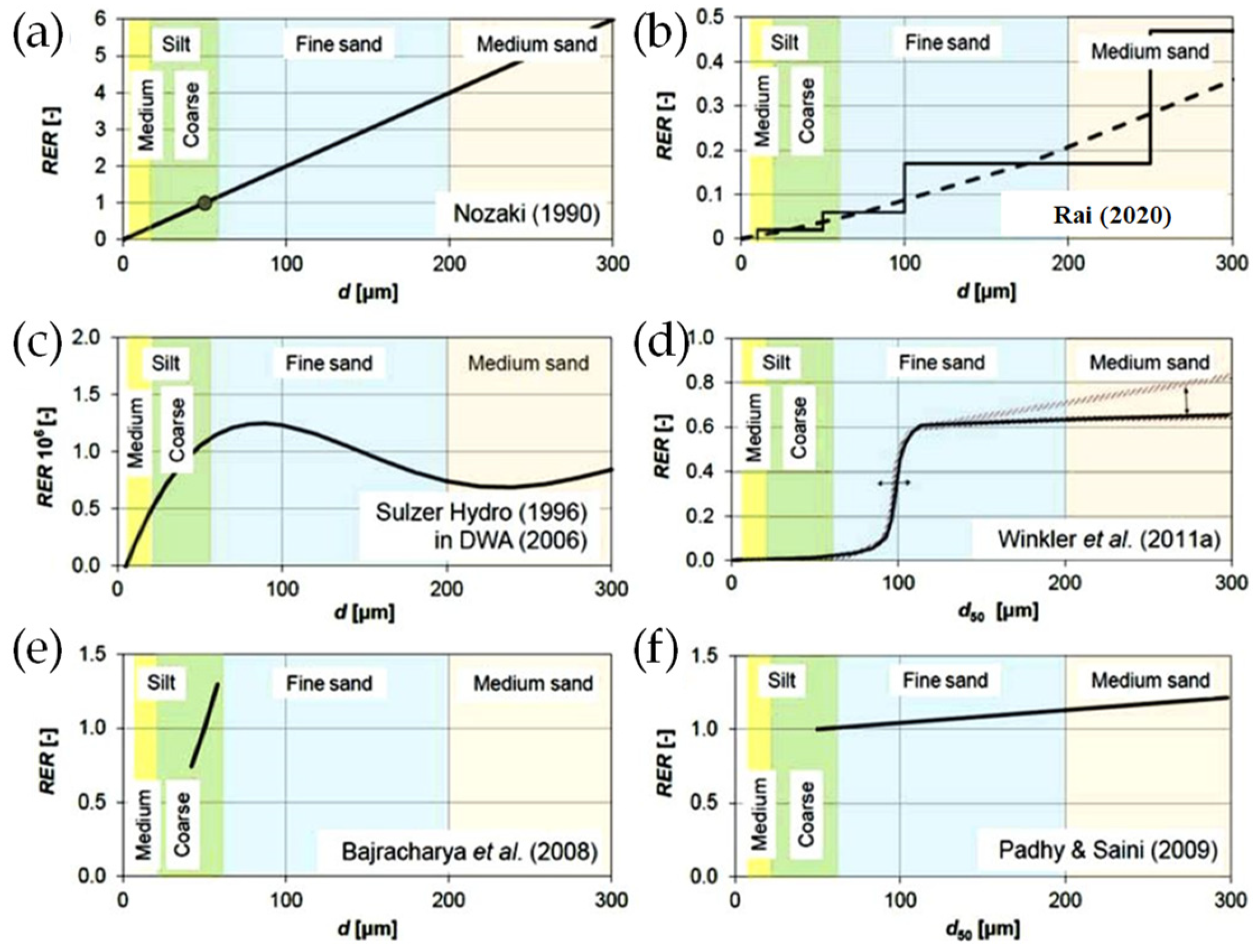

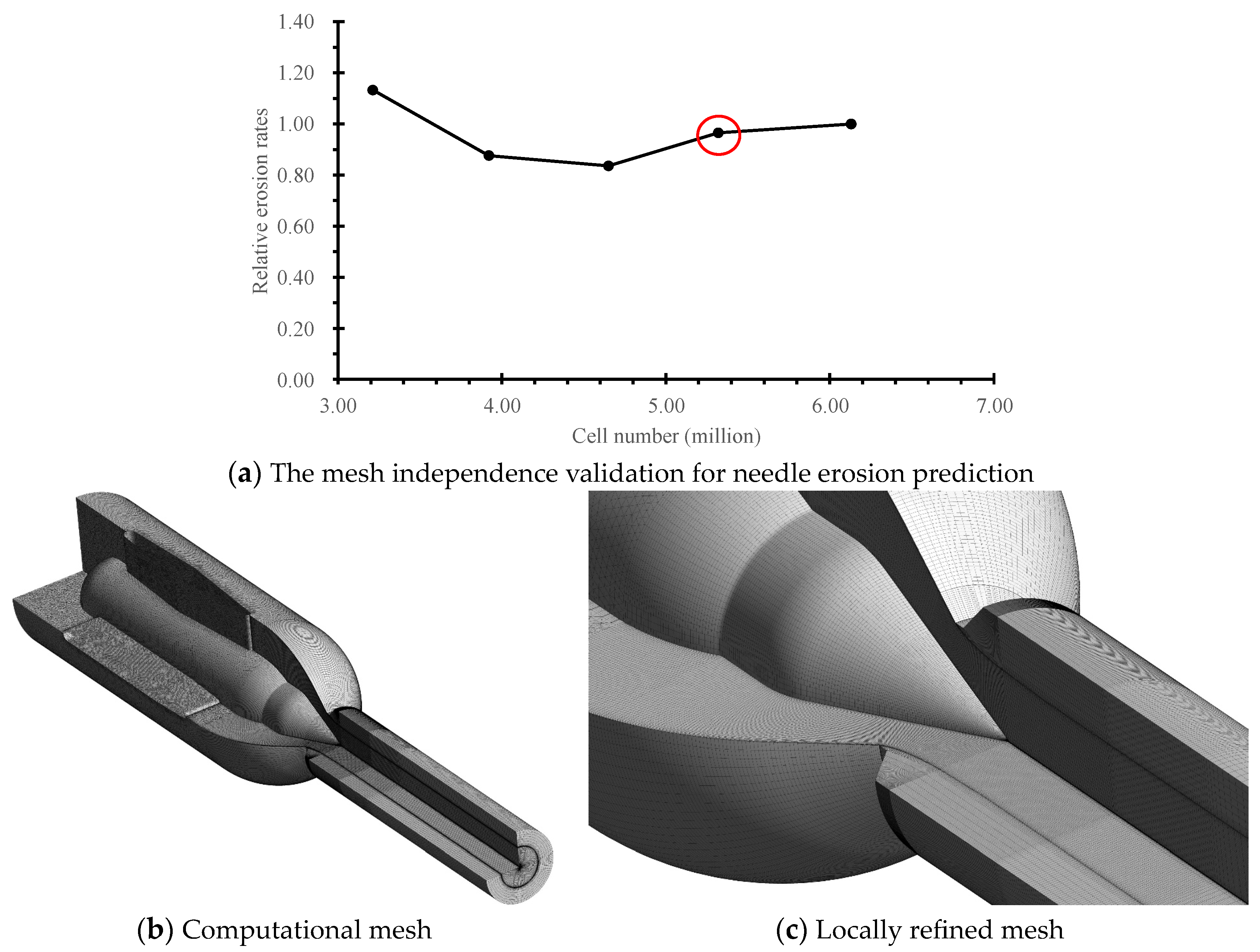
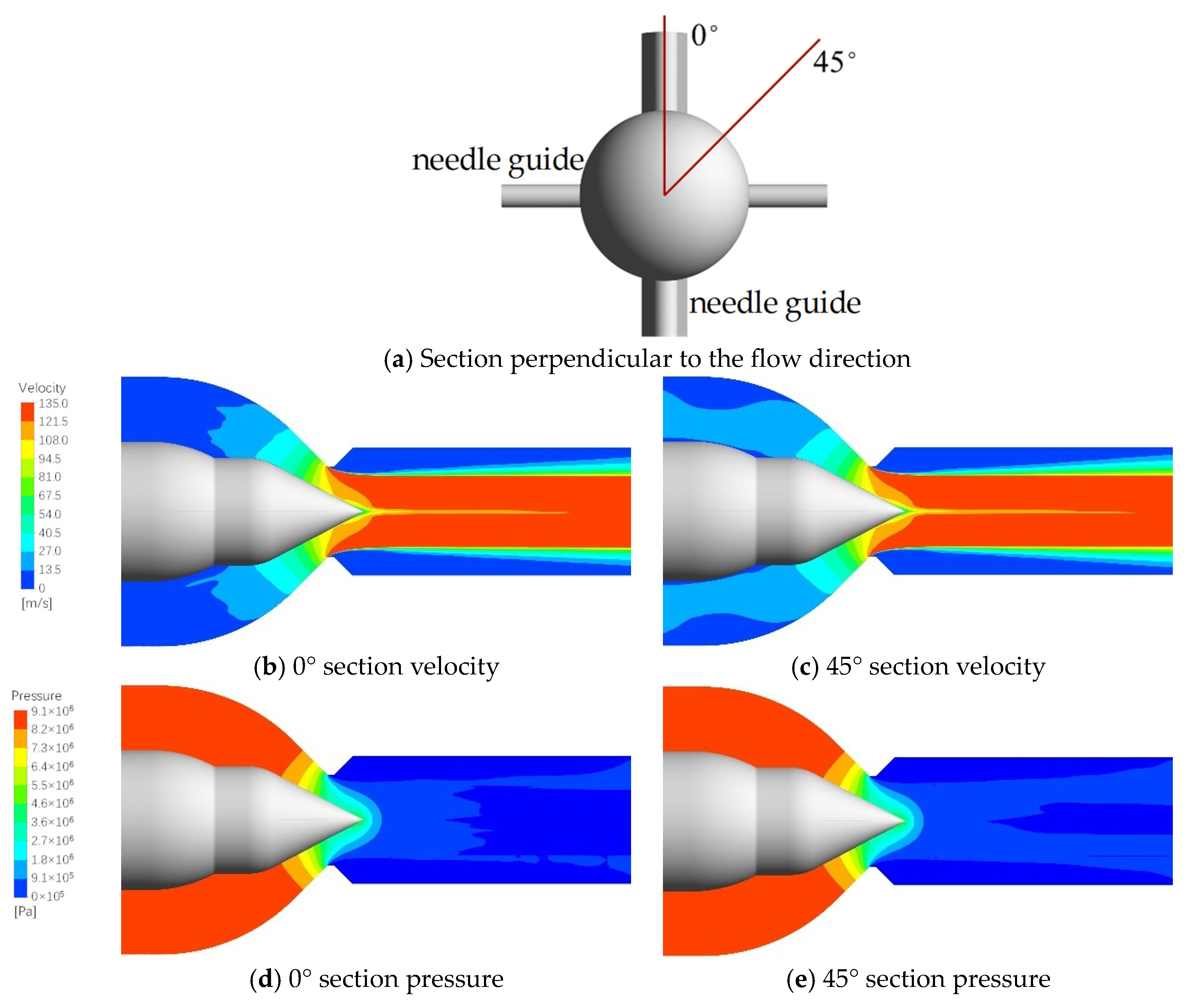
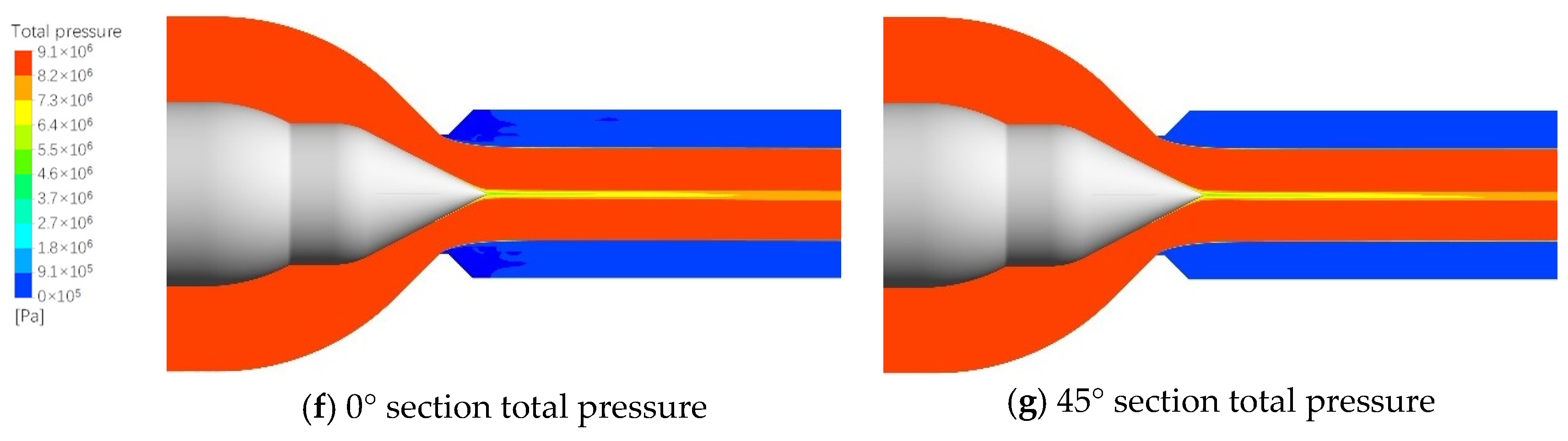

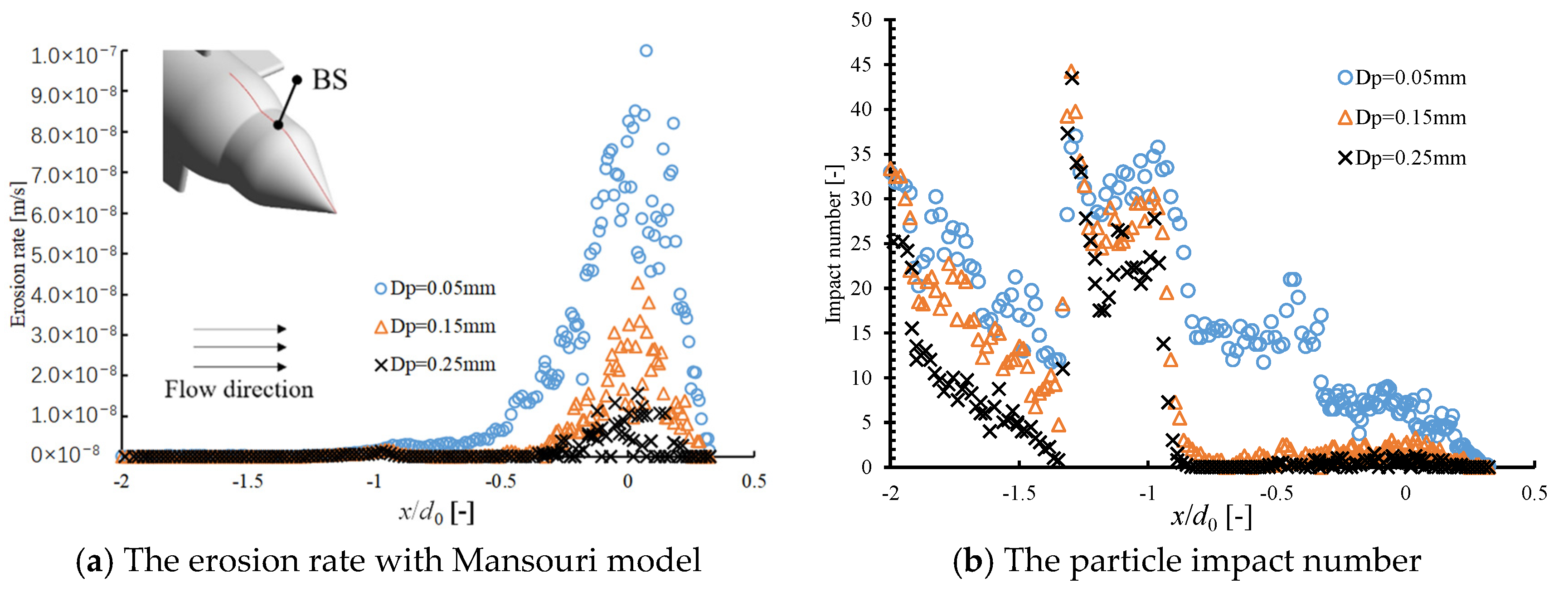
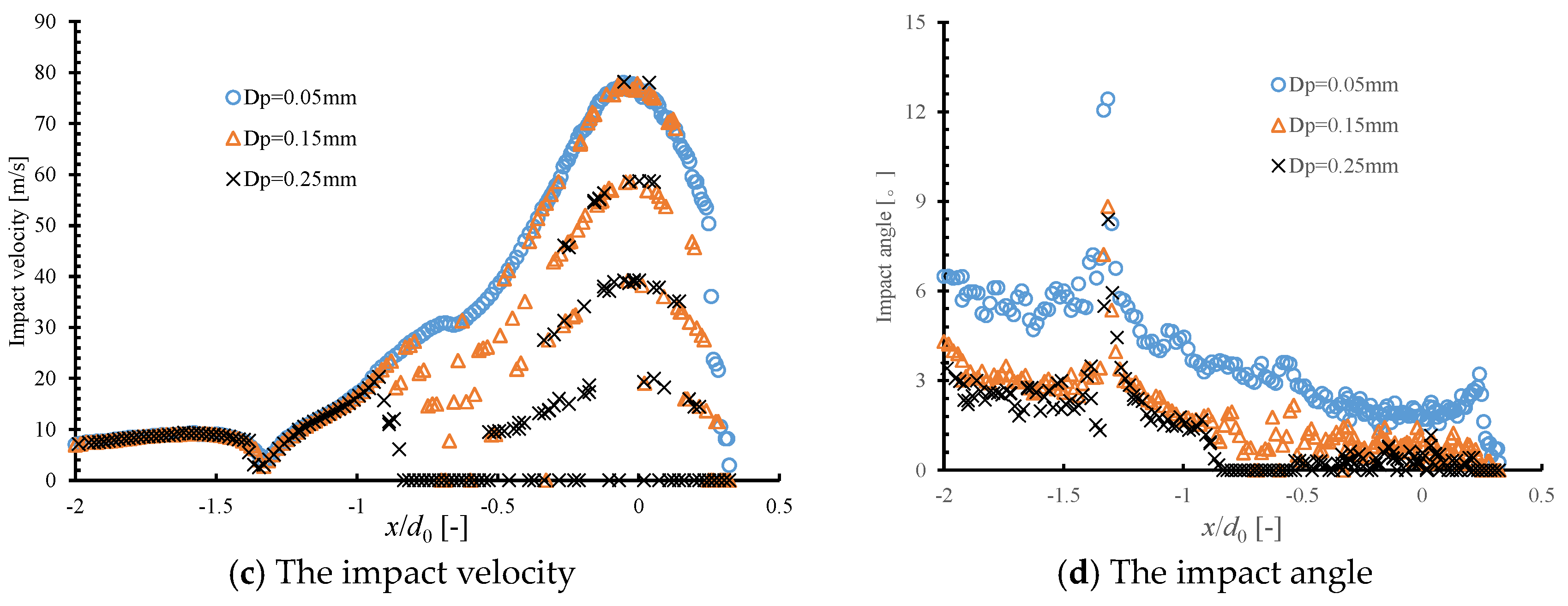

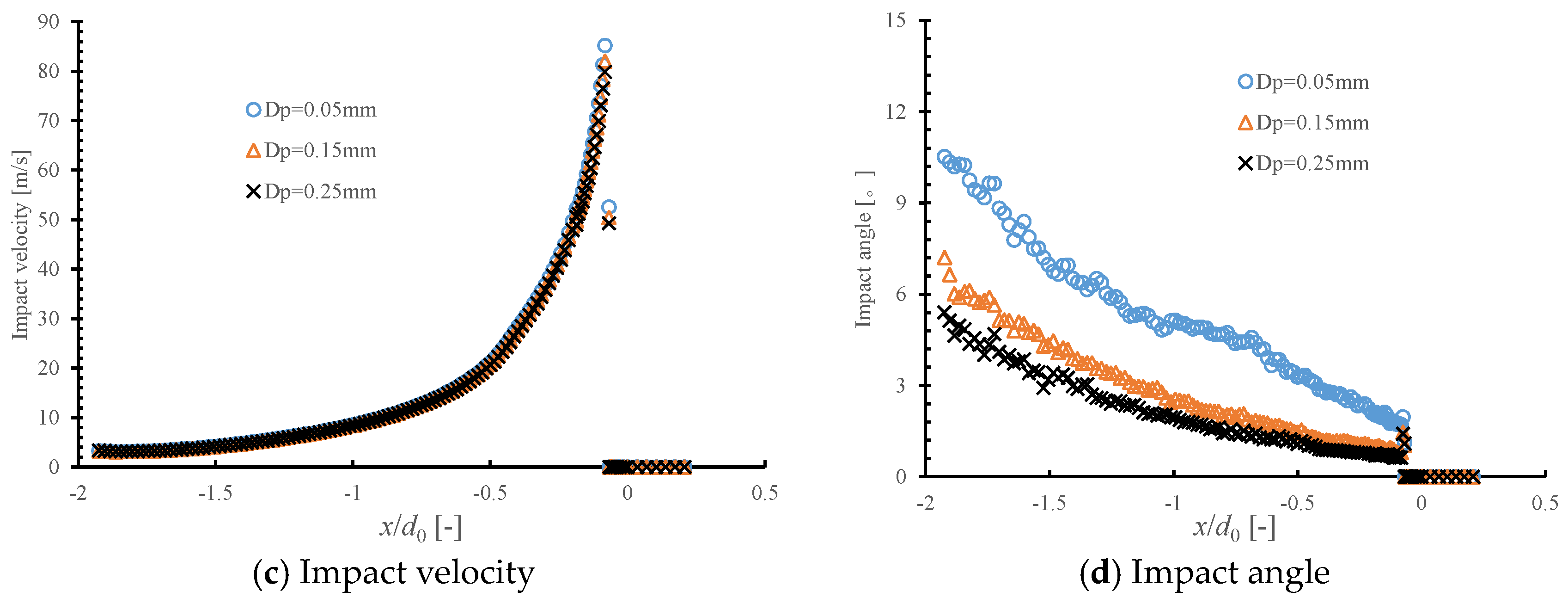
| Parameter | Description (Unit) |
|---|---|
| Injector number | 6 (-) |
| Angle of injector casing | 90 (°) |
| Output power | 900 MW |
| Bucket number | 22 (-) |
| Rotational speed | 214.3 (rpm) |
| Operating head | 1000 (m) |
| Unit speed | 39.86 (rpm) |
| Material | Stainless steel (-) |
| Average Value | Needle Surface | Nozzle Casing | ||||
|---|---|---|---|---|---|---|
| Particles size | 0.05 mm | 0.15 mm | 0.25 mm | 0.05 mm | 0.15 mm | 0.25 mm |
| Erosion rate (m/s) | 2.09 × 10−8 | 5.68 × 10−9 | 1.47 × 10−9 | 1.65 × 10−8 | 2.47 × 10−8 | 3.51 × 10−8 |
| Impact velocity vp (m/s) | 37.5 | 28.0 | 13.4 | 19.3 | 18.9 | 18.6 |
| Impact number nimp | 14.9 | 8.62 | 5.45 | 75.8 | 108 | 121 |
| Impact angle θ (°) | 3.49 | 1.62 | 1.07 | 4.26 | 2.32 | 1.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhu, Y.; Liang, Q.; Xiao, Y.; Liu, Z.; Li, H.; Ye, J.; Yang, N.; Deng, H.; Du, Q. Analysis of Sediment Erosion in Pelton Nozzles and Needles Affected by Particle Size. Energies 2024, 17, 1635. https://doi.org/10.3390/en17071635
Liu J, Zhu Y, Liang Q, Xiao Y, Liu Z, Li H, Ye J, Yang N, Deng H, Du Q. Analysis of Sediment Erosion in Pelton Nozzles and Needles Affected by Particle Size. Energies. 2024; 17(7):1635. https://doi.org/10.3390/en17071635
Chicago/Turabian StyleLiu, Jie, Yilin Zhu, Quanwei Liang, Yexiang Xiao, Zhengshu Liu, Haijun Li, Jian Ye, Nianhao Yang, Haifeng Deng, and Qingpin Du. 2024. "Analysis of Sediment Erosion in Pelton Nozzles and Needles Affected by Particle Size" Energies 17, no. 7: 1635. https://doi.org/10.3390/en17071635
APA StyleLiu, J., Zhu, Y., Liang, Q., Xiao, Y., Liu, Z., Li, H., Ye, J., Yang, N., Deng, H., & Du, Q. (2024). Analysis of Sediment Erosion in Pelton Nozzles and Needles Affected by Particle Size. Energies, 17(7), 1635. https://doi.org/10.3390/en17071635









