Design and Assessment of Track Structures in High-Frequency Planar Inductors

Abstract

This paper investigates the effect of different designs and arrangements of conductors on the operational parameters of a planar inductor. Accordingly, it is suggested that there is no one-size-fits-all design that can achieve all desired parameters in every application, and the best design should be determined by the needs of the application. In order to have a comprehensive study, four different structures are considered and compared. Numerous design parameters such as track width, track length, location of the conductors between the central limb and the lateral limb, and number of transposition points among subtracks for both air-core and ferrite-core inductors are considered. Each structure is evaluated according to AC resistance, $R_{AC}/R_{DC}$, and inductance. Measurement results reveal that it is critical to take into account all three characteristics when deciding the suitable structure for the conductors. Studies are carried out based on measurement results for experimental prototypes in the frequency range of 10 Hz–1 MHz, and a set of guidelines is provided with regard to the design of planar inductors to achieve desired characteristics.

1. Introduction

The emergence of high power density, high operating frequencies, and low profile power converters has posed a number of challenges for wire-wound magnetic structures [1]. In contrast, planar magnetics are particularly suited by virtue of their more advantageous thermal characteristics than conventional magnetics [2], their low profile [3], compact design, modularity, manufacturing simplicity [4], higher reliability [5], and predictable parasitic elements [6].

This paper focuses on planar inductors as one of the important families in planar magnetics. They are widely used in a variety of applications, ranging from heaters [7], to custom filters in power electronic converters [8], to wireless implantable medical devices [9]. To optimize planar inductors, it is imperative that inductance is achieved in accordance with the requirements of the application while simultaneously minimizing copper and core losses [10]. Designing a planar inductor involves selecting the core dimensions, number of turns, and inductance value, as well as conducting a comprehensive parameter sweep to determine the generalized design limits. Optimising the inductor for specific operating points and considering the trade-offs between loss and volume metrics should be the goal of the design. To achieve the desired performance metrics, the design process involves a hierarchical two-step optimization process, which considers factors such as spacing to air gap and fringing effects [11]. A key objective of this paper is to investigate the effects of different structures on the inductor parameters.

According to studies of the conductor arrangement in planar inductors, the AC resistance and, thus, the power loss of the inductor are greatly influenced by the configuration of the conductors on the printed circuit board (PCB). One of the primary reasons for the increased AC resistance at high frequencies is the skin effect caused by eddy currents generated inside the conductor as a result of the internal magnetic fields. Dividing a solid track into multiple smaller tracks reduces the cross-sectional area and helps eliminate the unwanted effects of eddy currents caused by skin effect [12]. As well as the skin effect, the proximity effect also creates a higher AC resistance due to a magnetic field that is produced by adjacent tracks. In order to compensate for the proximity effect, Litz structures appear to be the most promising solution [13]. The Litz structure minimizes the effect of an external magnetic field by utilizing the radial and azimuthal movements of the various conductor strands/tracks along the entire path [14].

In [15], a new scheme was presented for arranging the tracks in each turn. This method involves the use of vias on a PCB to twist different tracks around a path in order to produce a structure similar to that of a Litz conductor. In terms of AC resistance, the new structure exceeds the solid conductor in the frequency range of 20 kHz to 700 kHz. A study [16] compared the $R_{AC}/R_{DC}$ values for a spiral planar inductor with solid, multitrack, and Litz structures in the frequency range of up to 1 MHz.

In the latter two cases, the number of tracks was changed to investigate the impact of this parameter on the resistance of the inductor. During the construction of a Litz structure, only four transposition points are considered, which is insufficient in comparison with that of a Litz wire, where the strands are continuously transposed throughout the conductor path. In [13], this issue was addressed by providing more transposition points along the entire conductor path. Authors in [17] mentioned high manufacturing cost and low reliability as two main drawbacks of using more transposition points in planar inductors. Accordingly, using the filed profile of the planar windings, the minimization of the number of transposition points without significant reduction of performance was discussed. In addition to the number of transpositions, the number of the subtracks is another parameter that affects the characteristics of the inductor. In [7], the authors applied a crude method for separating conduction losses and induction losses in order to determine the optimal number of strands in Litz structures.

In order to extract the characteristics of the planar inductors with Litz structure, several methods are discussed and developed in the literature. The arrangement of the tracks in Litz structures necessitates the use of 3D finite element modelling (FEM); consequently, 2D simulations cannot yield accurate results. The implementation of 3D analysis of a planar magnetic device with Litz structure poses two main challenges: high processing time and power required for the hardware to simulate the model, and providing accurate geometric representations of the structure [18]. One important issue related to the latter problem is the numerous vias used in the structure of a Litz planar inductor. Vias have a significant effect on the DC and AC resistance, and any approximation in modelling vias in the simulation will result in deviations from the accurate values. Alternatively, analytical methods can be used to determine the AC resistance in planar magnetic devices with Litz structures, as discussed in [19,20,21]. In [19], for two components of AC resistance, namely, proximity and conduction components, respectively, two terms, ${\varphi }_{conduction}$ and ${\varphi }_{proximity}$, are defined that represent frequency and geometry dependency. In addition, Ref. [20] presented a 2-D analytical model for estimating the high-frequency winding loss of multilayer air-core PCB planar inductors with one turn per layer, based on the Maxwell equations. As a result of the proposed model, the edge-effect and the 2-D distribution of magnetic field at the edges of the rectangular cross-section of the coreless inductor were taken into account. In order to develop the models for the magnetic field boundary values, a linear current distribution approach was proposed based on the data derived from the FEM analysis. These terms should be extracted from the FEM simulation results. Then, the issues discussed earlier for FEM simulations are also valid for these analytical methods. Using the power losses determined by coupling two methods, the authors in [21] calculated the frequency-dependent resistance of a Litz structure. To calculate the magnetic field distribution on a solid conductor in different cut sections, the standard FEM method is applied. Then, these values serve as boundary conditions for partial element equivalent circuits (PEECs). In the case of planar inductors, since the movements of subtracks are not consistently distributed along the conductor, the method mentioned above will provide inaccurate results.

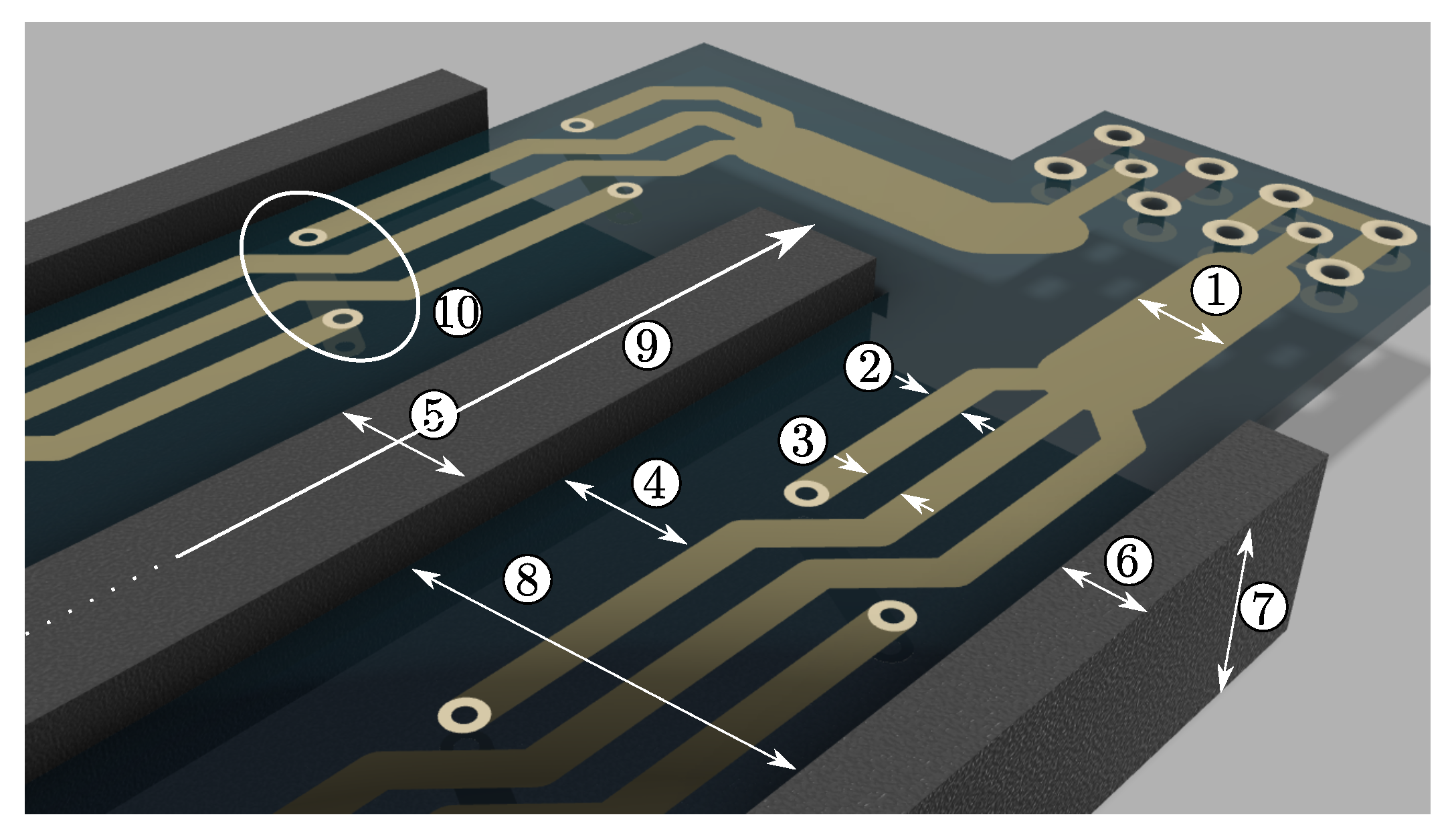
This paper investigates the effect of design parameters in planar inductors in order to provide instructions about optimum selection of these parameters to design an inductor with better characteristics. These parameters include the allocation of the conductors in the space between the central and lateral limbs of the core and also the number of transposition points for in-layer twisted and Litz structures. For this purpose, this paper presents four configurations of a planar inductor, as shown in Figure 1, namely, solid track, multitrack, in-layer twisted track, and track with a Litz structure. Within each structure, three conditions for the placement of conductors are defined, namely, the inside-edge, middle-edge, and outside-edge, that indicate the distance between the most inner track and the central limb of the core. All measurements were conducted on both air-core and ferrite-core prototypes.

The ratio of $R_{AC}/R_{DC}$ value is usually taken into account as the basis for comparing different structures in most studies of planar inductors. In essence, the $R_{AC}/R_{DC}$ value represents the sensitivity of the resistance of the structure to frequency; however, for operation and to minimize power loss, the resistance or $R_{AC}$ value is of primary importance. This paper demonstrates that a structure with a lower $R_{AC}/R_{DC}$ is not necessarily the one with a lower resistance at all the frequency values, since it may have a higher DC resistance. Moreover, when using inductors in power electronic applications, the value of inductance is important to reach the intended function in the circuit. Hence, the inductance of planar inductors is another key parameter which has not been examined thoroughly in previous studies. In this study, AC resistance, $R_{AC}/R_{DC}$, and inductance values will be measured for each structure at frequencies between 10 Hz and 1 MHz, and results obtained from experimental prototypes will be utilized to evaluate the characteristics of each structure.

2. Different Conductor Structures

This section is devoted to explaining various types of structures examined in this article, including solid, multitrack, twisted in-layer, and Litz structures (Figure 1). Each structure has different variants depending on the design parameters. A simplified structure of a single-turn planar inductor is illustrated in Figure 2 to introduce the parameters that are supposed to be investigated. Different variants are distinguished based on the distance of the most inner track from the central limb. Variants with closest and furthest conductors from the central limb are called inside edge and outside edge, respectively, and variants with conductors placed in between are addressed as middle edge. It should be mentioned that the number of turns in all the inductors is four turns.

2.1. Solid Track Structure

Solid tracks are the most straightforward way to arrange the conductors in a planar inductor, in which each turn comprises a single track. Five variations of solid structure, as shown in Figure 3, are studied in this work.The widest possible track width is illustrated in Figure 3a, in which all of the space between the central and lateral limbs of the core is occupied by the conductors. Because of some practical considerations, in most of the cases, the width of the tracks has to be less than maximum value. For instance, if there is an air-gap in the core, due to the fringing effect, it is preferred to place the conductors at a distance from the air-gap to keep the current density uniform [22]. Consequently, a portion of the space between the central and lateral limbs will remain unoccupied. In these cases, by placing the most inner turn at different distances from the central limb, different arrangements can be realized. In order to investigate the effect of this parameter, three conditions, inside-, middle-, and outside-edge, are considered, as shown in Figure 3b–d, respectively. An additional structure is considered, as shown in Figure 3e, which contains a middle-edge type with a smaller track width to examine the effects of track width on the parameters of the inductor.

2.2. Multitrack Structure

Using this structure, each solid track is divided into three subtracks one-third the width of the solid track, thereby alleviating the issues associated with the skin effect. Accordingly, three conditions for multitrack structures, namely, the inside-, middle-, and outside edges, as demonstrated in Figure 4a–c, are considered.

2.3. In-Layer Twisted Structure

This structure introduces an in-layer horizontal movement between the subtracks in each turn, as shown in Figure 1c. In this structure, the subtracks are placed in different layers of the PCB, in which only horizontal movement of tracks within each layer is considered to mimic the twisting feature. The main design variable in this case is the number of twisting points. Several twisting cases with 10, 30, and 60 twisting points are investigated. Similar to the previous structures, for each condition, three cases, inside-, middle-, and outside-edge, are regarded (Figure 5a–c). In-layer twisted structures should address some of the problems caused by proximity effects.

2.4. Litz Structure

To mitigate the effects of external magnetic fields in a more efficient way, in addition to the horizontal movements, it is preferable to bring vertical movements as well for the subtracks. For planar inductors, improvements have been reported with regard to reduced resistance by utilizing Litz structures in [23]. For this purpose, in this paper, a Litz structure, as shown in Figure 1d is considered in which the horizontal and vertical movements of the subtracks are realized by in-layer movements and interlayer movements (by vias), respectively. An increased number of transposition points tends to improve the Litz structure of the planar inductor, though it should be noted that vias in the transposition points will increase the path length inevitably, which is particularly crucial at low frequencies [13,16]. For the purpose of investigating the Litz structure, different prototypes will be examined with 10, 30, and 60 transposition points. Similar to the previous structures, the study of the Litz structure is carried out for inside-, middle-, and outside-edge prototypes, as shown in Figure 6.

3. Measurement Setup

The measurements are performed using high-precision Newton 4th PSM1735 [24] with the four-wire measurement method, as shown in Figure 7. A major determinant of the integrity of an LCR measurement is the nature and quality of the electrical connection between the measuring instrument and the device under test (DUT). In the four-wire measurement method, independent conductors are used for the signal source circuit (Power ±) and the measurement circuit (Sense ±) of a measurement instrument. In this way, it is guaranteed that the measured signal only reflects the voltage applied to the DUT, without taking into account any voltage drop across the supply cable. An advantage of the use of this connection technique is usually apparent when the DUT impedance is low and the measured frequency range is less than 1 MHz. The impact of parasitic components associated with the four-wire cable connection can become dominant as the DUT impedance and measurement frequency increase. In these circumstances, the conversion to a two-wire connection technique will achieve more repeatable and accurate measurements [25]. Therefore, due to the intended frequency range, i.e., 10 Hz–1 MHz, tests were carried out with both two-wire and four-wire measurements, in which the results were proved to be the same. Consequently, all the results reported in this paper are obtained by four-wire measurements.

4. Experimental Results

Experimental results as measured values for resistance and the inductance of 52 planar inductors with different conductor structures discussed in Section 2 for both air-core and ferrite-core conditions are presented in this section. For each structure, the AC resistance, $R_{AC}/R_{DC}$, and inductance values are reported. Discussions about the results are given and, at the end, to draw an analogy among different structures, the optimum structures with the middle-edge type from each structure are chosen and different characteristics are compared with each other.

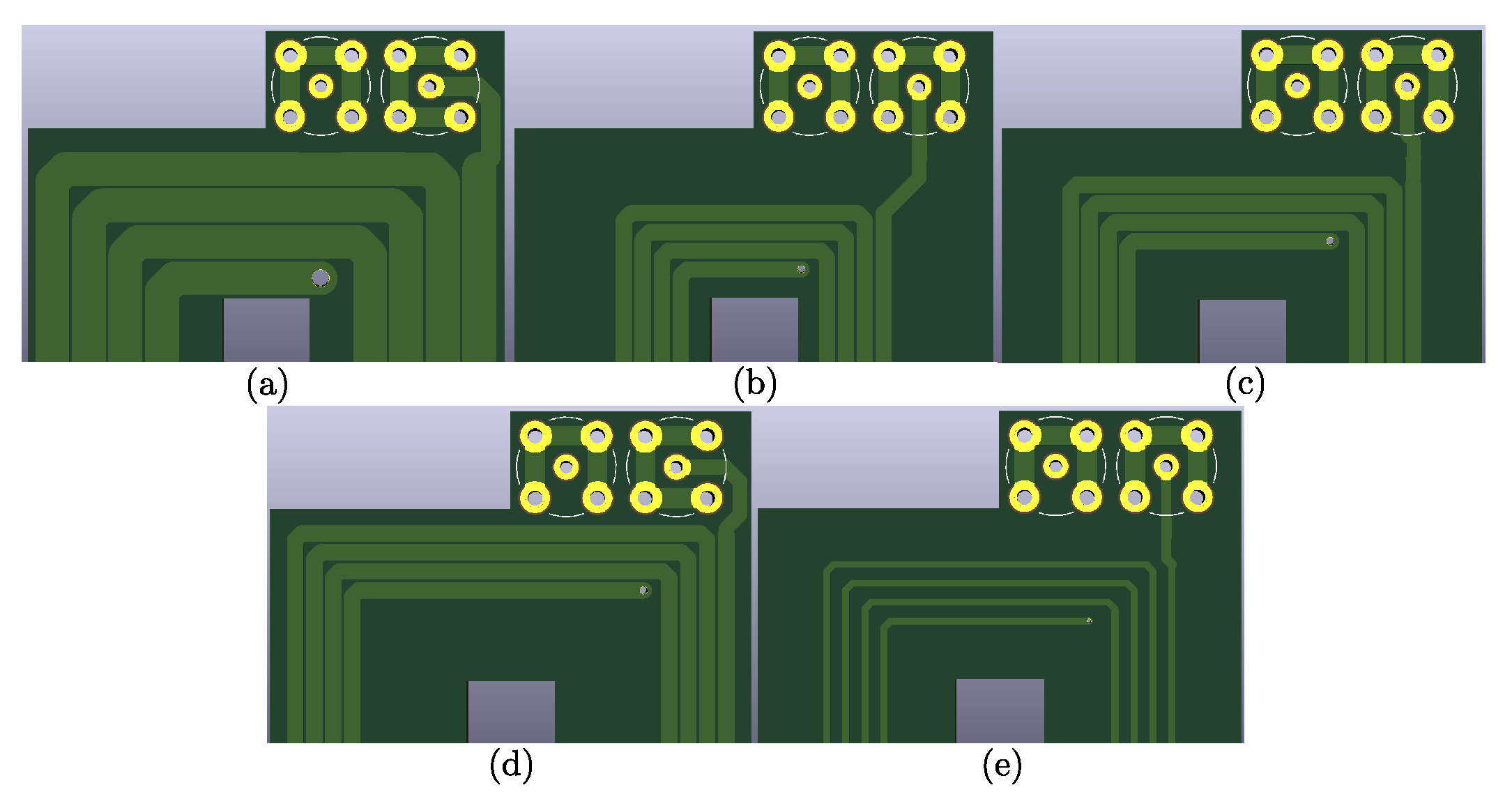
4.1. Solid Track Structure

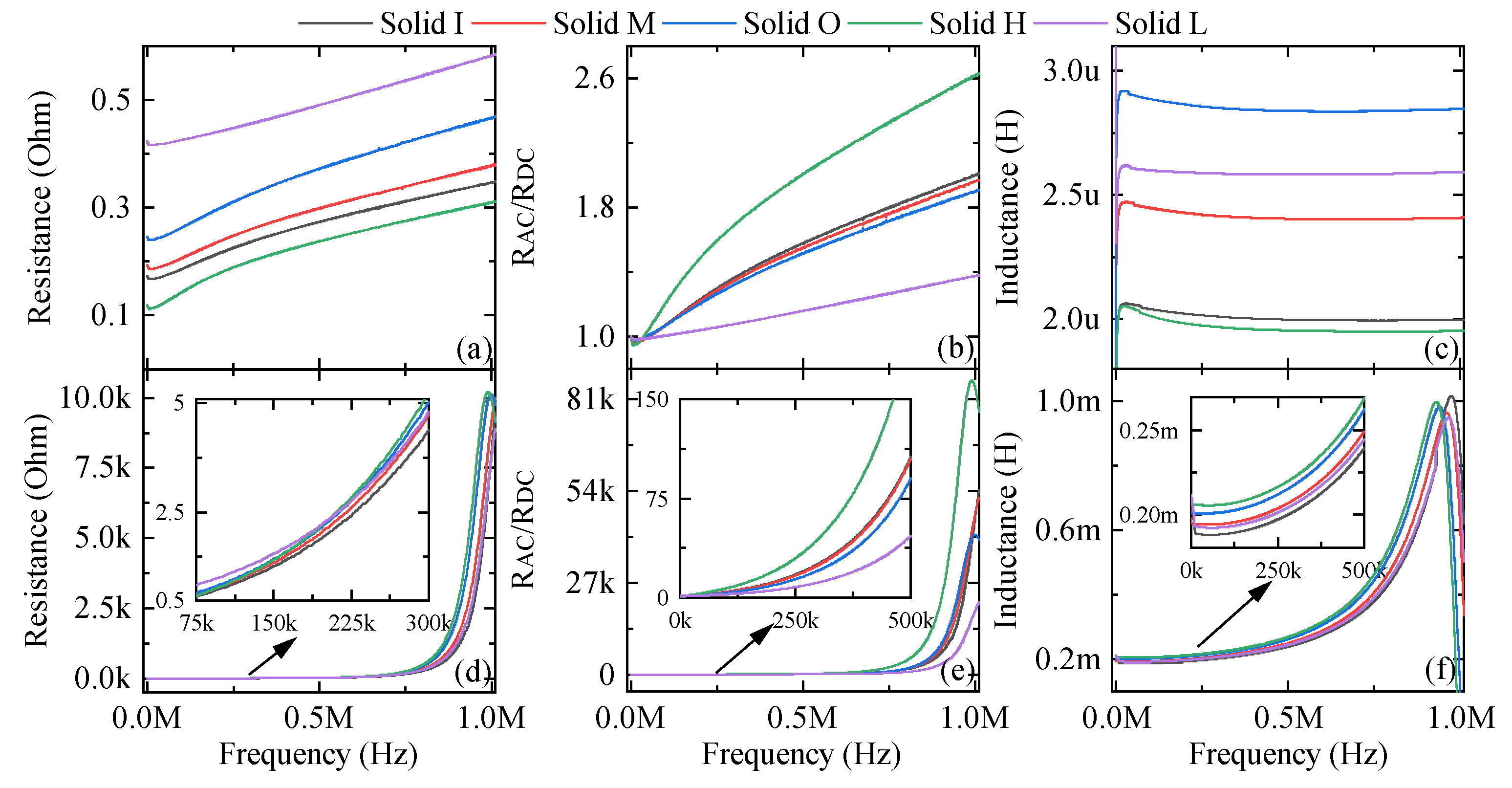
Considering the solid track structure, five different arrangements of the track were considered, including a solid track in the middle, outside edge, and inside edge, as well as the widest and smallest track width, respectively.

4.1.1. Air-Core Inductors

Figure 8 represents the measurement results for the air-core prototypes with solid structures. Considering Figure 8a, the thick-track and thin-track structures have the lowest and the highest resistance values, respectively. Also, it can be concluded that for similar track widths, lower resistances can be achieved by placing the conductors near the central limb as the inside-edge structure has less resistance compared to the middle- and outside-edge ones. This was expected since the conductor length is less for inside-edge type structures. The increase in the resistance values at high frequencies is due to the skin effect and the proximity effect.

Figure 8b shows that the slope of the $R_{AC}/R_{DC}$ curve is higher for the thick-track structure. It can be concluded that as the track-width increases, the resistance of the inductor becomes more sensitive to the frequency. For structures with the same track width, as the diameter of the inductor becomes smaller, the inner turns experience a higher portion of the magnetic field generated by the outer turns. Consequently, the proximity effect will be more significant. The inside-edge structure thus exhibits higher sensitivity to frequency as compared to the middle- and outside-edge structures.

A representation of the inductance values can be found in Figure 8c. It is expected that the structures with a larger cross-sectional area will have a lower inductance. These results confirm that the thick-track structure brings the overall lowest inductance. In addition, comparing the middle-edge type with medium track width and thin-track width structures, which almost share the same lengths, the thin-track structure shows a higher inductance. Additionally, the conductor length contributes to inductance, as it is likely that a structure with a longer length will have higher inductance. It can be also observed that the inductance is increased by increasing the conductor length, as the outside edge has a higher inductance than the other two prototypes.

4.1.2. Ferrite-Core Inductors

According to Figure 8, measurement results for ferrite-core inductors show a specific frequency at which the inductor resonates with the parasitic capacitance, and for values above that frequency, the element behaves as a capacitor and can no longer be used as an inductor. When using ferrite-core, as opposed to air-core, the proximity effect has a substantial effect. According to Figure 8d, the thick-track structure has the lowest resistance in the operating frequency range up to 60 kHz. Upon reaching 60 kHz, the inside-edge structure represents lower resistance than the thick-track structure, while it has lower track width. The proximity effect is more severe for the thick-track structure and at frequency values around 100 kHz, 160 kHz, and 200 kHz, its resistance exceeds the resistance of middle-, outside-edge, and thin-layer structures, respectively, and represents the highest resistance for frequency range above 200 kHz. The same phenomenon happens for the middle-edge medium-track and thin-track structures, as until 340 kHz, the medium-track inductor has lower resistance, but above this frequency, the situation is changed.

Figure 8e illustrates that for the low frequencies, the resistance of the thin-layer structure is the least sensitive to the frequency, but its resistance is the highest. Upon passing frequencies of 200 kHz, 220 kHz, and 340 kHz, its resistance becomes lower than that of thick-track, outside-edge, and middle-edge structures, respectively. Based on the results, for structures with the same track widths, the sensitivity of the resistance to the frequency will be similar, as $R_{AC}/R_{DC}$ values are close to each other for inside-, middle-, and outside-edge structures. But, unlike air-core inductors, ferrite-core inductors have a higher frequency sensitivity for the outside edge structure for frequencies above 750 kHz.

Figure 8f illustrates the inductance values for ferrite-core inductors with solid tracks. Due to their similar width, the inside-edge, middle, and outside-edge prototypes were considered when analysing the effect of track length on inductance. The prototype with outside-edge inductor has the highest inductance value, whereas the one with inside-edge track has the lowest value. In order to examine the effect of track width on inductance, thick-track, middle-edge, and thin-track prototypes were considered as their lengths are approximately the same. It can be seen that, in contrast to the air-core inductors, expanding the track width results in a higher inductance.

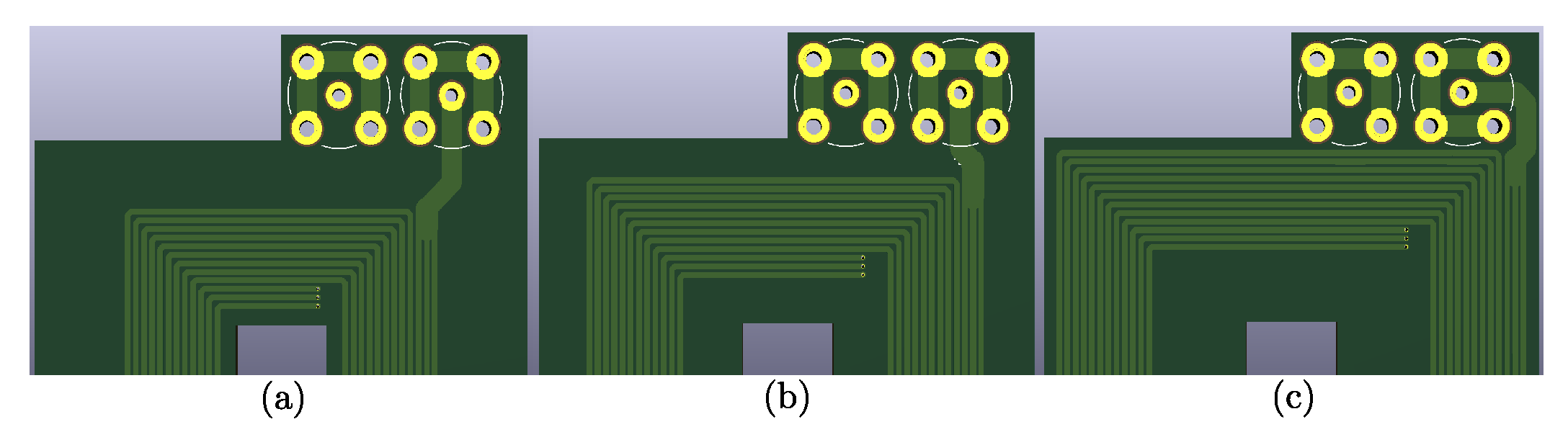
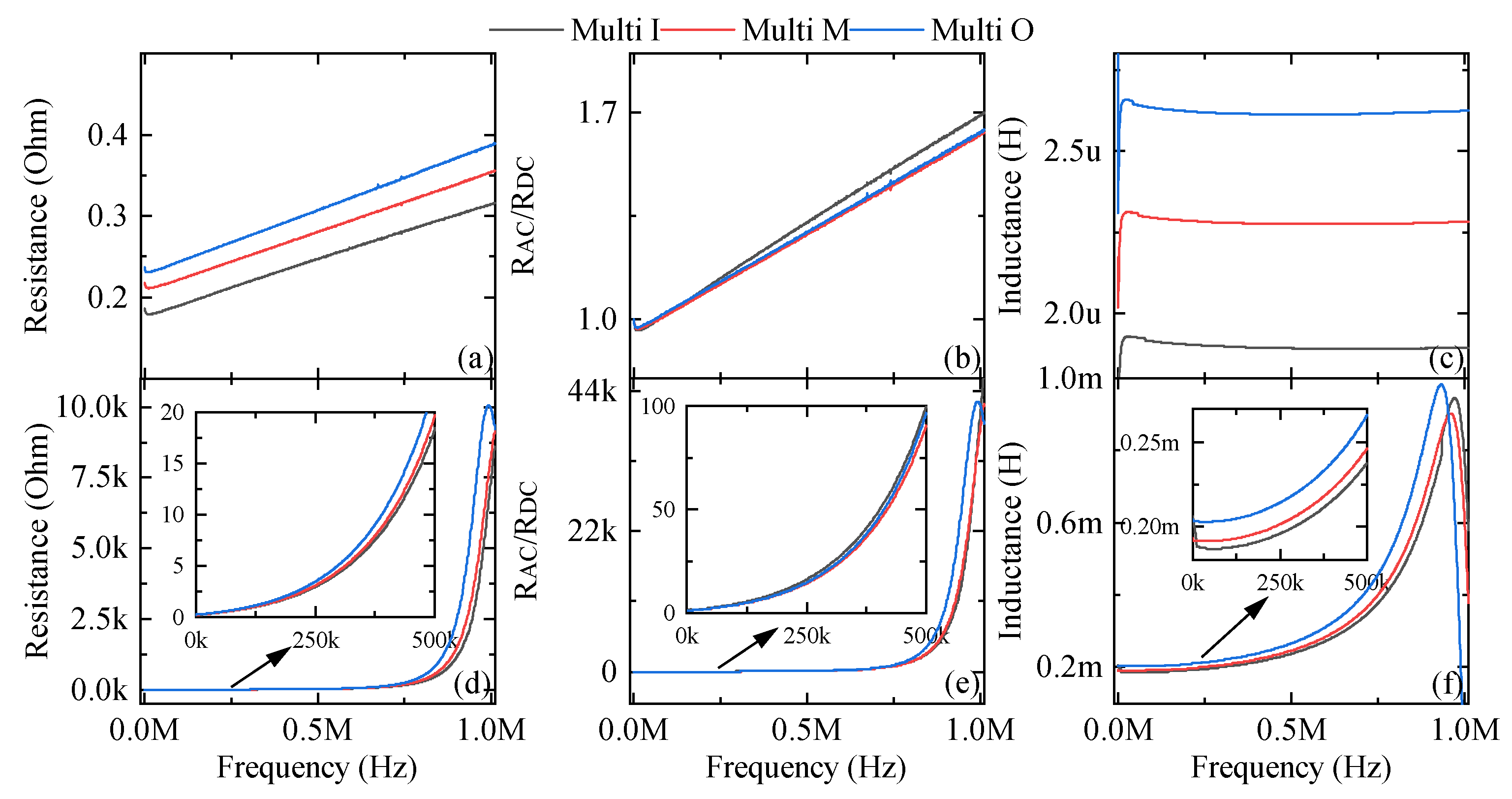
4.2. Multitrack Structure

There are only three types of structures compared in the multitrack structure: middle, outside edge, and inside edge.

4.2.1. Air-Core Inductors

Figure 9 represents the measurement results for the air-core multitrack structures. As expected, according to Figure 9a, the outside-edge and the inside-edge structures have the highest and the lowest resistance due to the highest and lowest conductor lengths, respectively. As the frequency is increased for all structures, resistance values are increasing due to the skin effect and proximity effect. According to Figure 9b, the sensitivity of the resistance to the frequency is similar for three cases; however, for the inside edge, the sensitivity is a little higher as inner turns experience more portion of the flux of outer turns and the proximity effect becomes more severe. Since all three structures have the same track width, the only parameter that affects the inductance is the conductor length, and consequently, the highest inductance belongs to the outside-edge structure, as shown in Figure 9c.

4.2.2. Ferrite-Core Inductors

As shown in Figure 9, the self-resonance occurs at a frequency of approximately 1 MHz. The lowest and the highest resistance values belong to the inside-edge and the outside-edge structures, respectively, due to their conductor length, as shown in Figure 9d. Figure 9e shows that for ferrite-core inductors up to 600 kHz, the resistance of the inside-edge structure is the most sensitive one to the frequency. Like the air-core inductors, the conductor length is the only factor affecting the inductance and, as represented in Figure 9f, it is highest for the outside-edge structure.

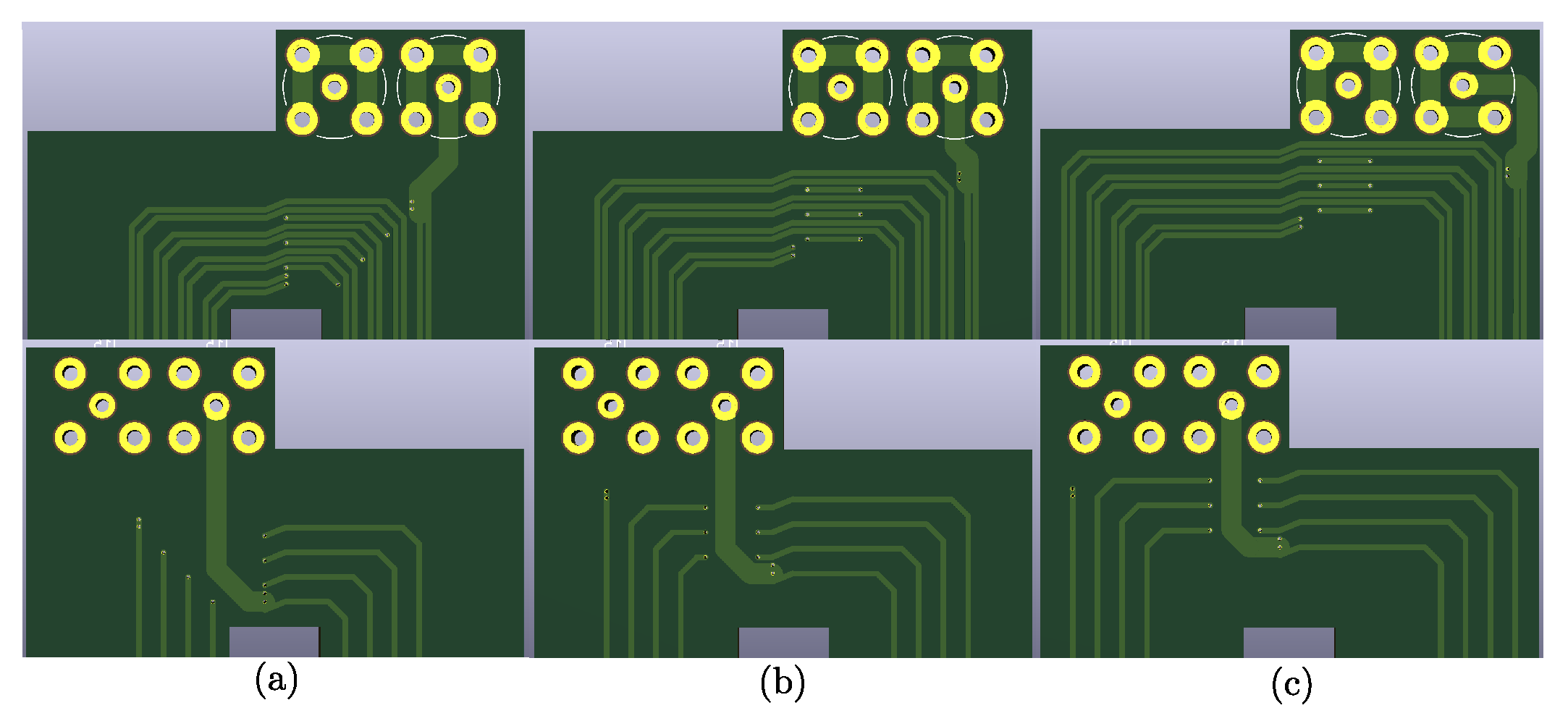
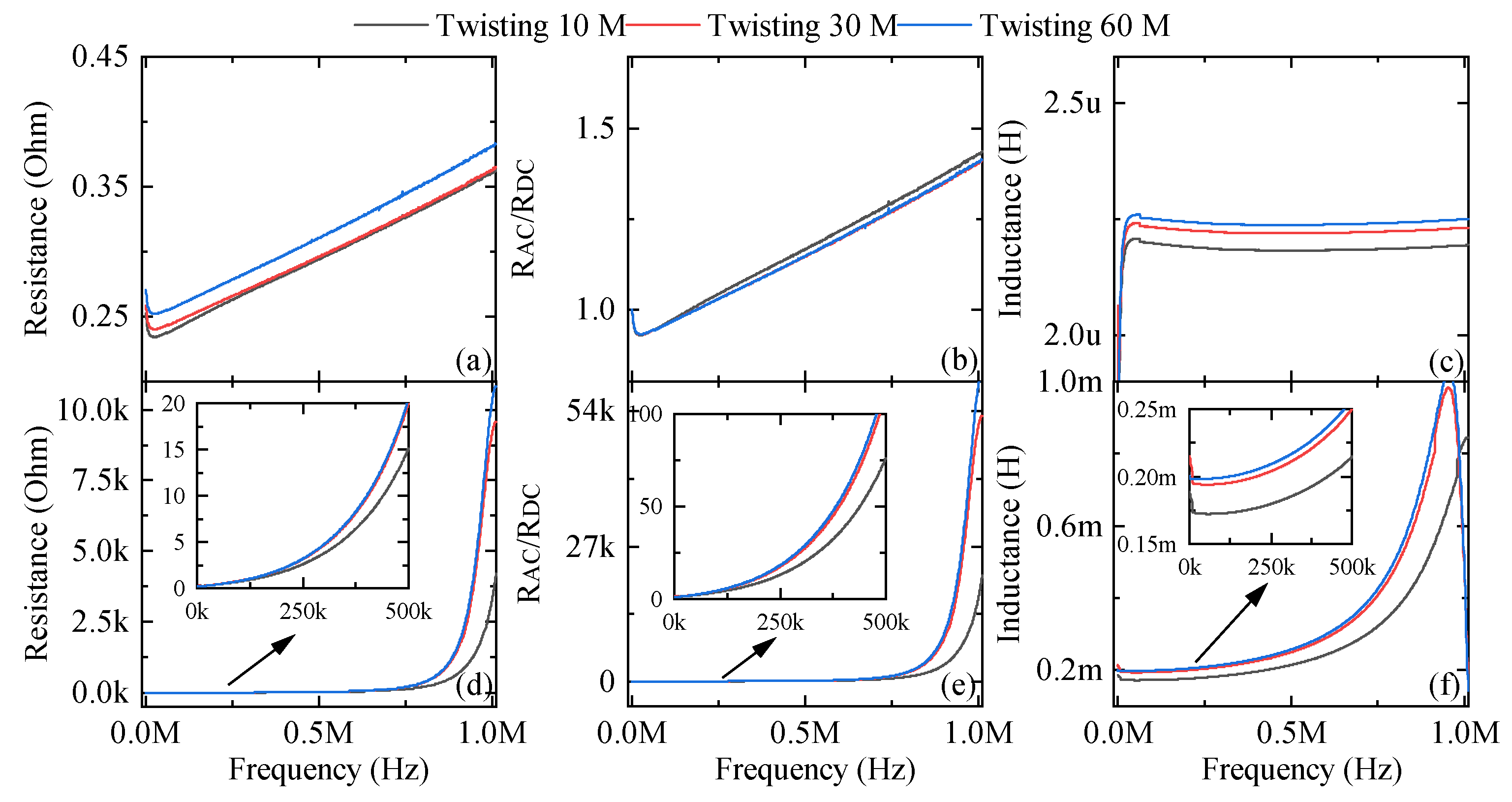
4.3. In-Layer Twisted Structure

Three case studies are examined in terms of structures that have 10, 30, and 60 twisting points within the in-layer twisted structure. For each structure, inside-, middle-, and outside-edge prototypes were tested, and the results followed a similar route to the solid and the multilayer structures. In other words, the lowest resistance and highest inductance in each case were realized by inside-edge and outside-edge structures, respectively. Hence, in this subsection, only the results for middle-edge prototypes are discussed.

4.3.1. Air-Core Inductors

Figure 10 illustrates the measurement results for in-layer twisted structures with air core. According to Figure 10a, in-layer twisting is not useful in mitigating proximity effect at high frequencies, as structures with a greater number of twisting points represent higher resistance values across the entire frequency range. A similar conclusion can be drawn from Figure 10b regarding the insufficiency of in-layer twisting for air-core inductors in reducing resistance sensitivity to frequency, as the slope of $R_{AC}/R_{DC}$ is almost the same for all three prototypes with 10, 30, and 60 twisting points.

The length of conductor is the decisive parameter when it comes to inductance, and measurement results show that in-layer twisting by itself does not have a noticeable effect. Considering Figure 10c, the prototypes with 60 and 10 twisting points exhibit the highest and the lowest inductances, respectively. This is due to the increase in length of a conductor which is a result of bringing more twisting points.

4.3.2. Ferrite-Core Inductors

Figure 10 represents the measurement results for the middle-edge twisted structures with different twisting points. It is intended to determine whether only the horizontal movement of tracks can mitigate a portion of the impact of the proximity effect.

According to Figure 10d, even for ferrite-core inductors, bringing in-layer twisted structures does not assist in coping with increased resistance at high frequencies as a result of the proximity effect. As can be seen in Figure 10d, the prototypes with 60 and 10 twisting points have the highest and lowest resistances for the entire frequency range, respectively. To evaluate the functionality of the in-layer twisting method, Figure 10e should be considered, in which it can be seen that there is no improvement, even with $R_{AC}/R_{DC}$. The resistance becomes even more sensitive to the frequency with the increase in twisting points.

Similar to the air-core prototypes, the introduction of the in-layer structure appears to have little effect on inductance, and the only parameter that affects inductance is the conductor length. According to Figure 10f, prototypes with 60 points (longest conductor length) and 10 points (shortest conductor length) will result in the highest and lowest inductance values, respectively.

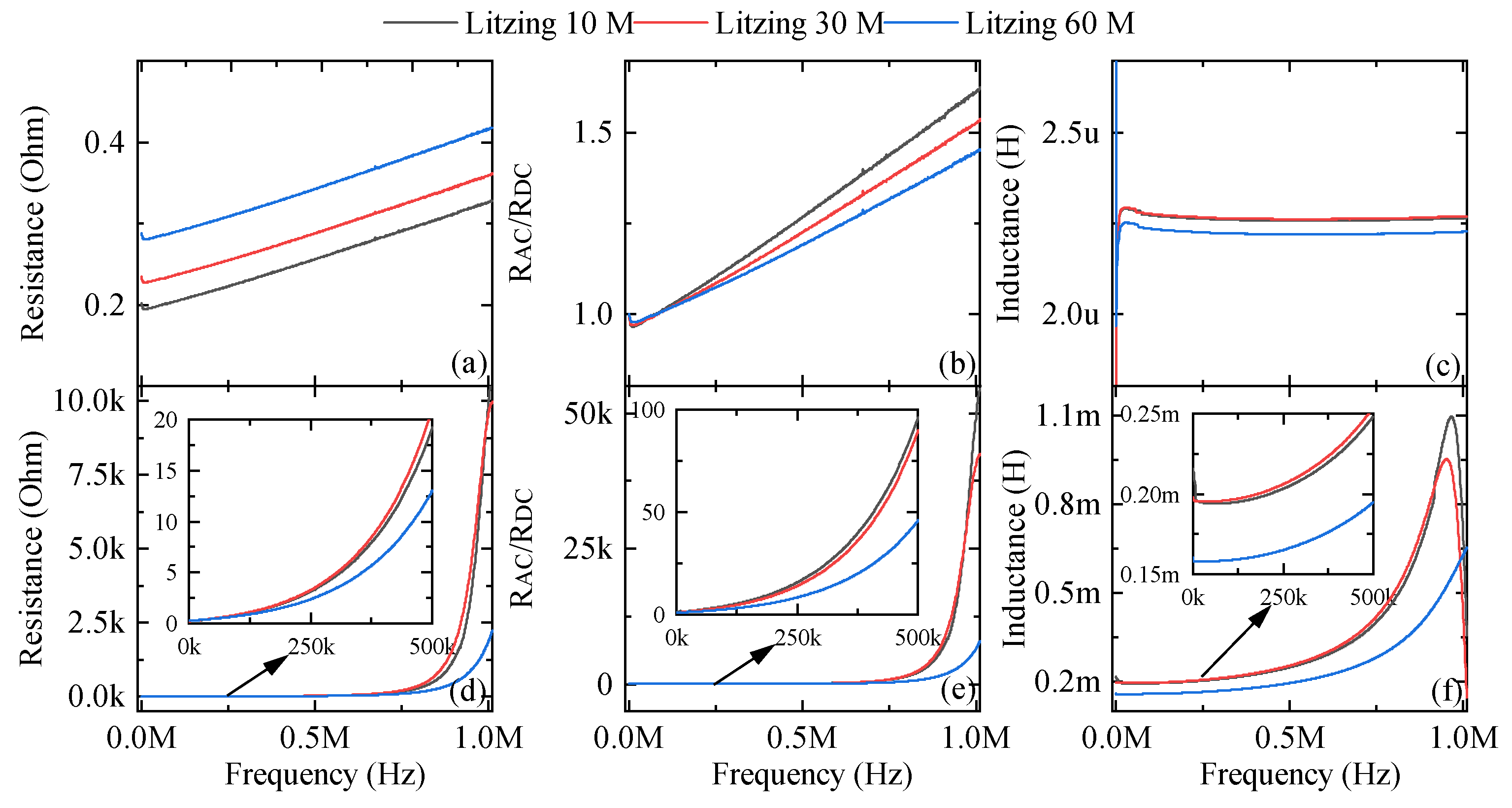
4.4. Litz Structure

To examine the functionality of the Litz structure, different prototypes with 10, 30, and 60 transposition points with inside-, middle-, and outside-edge structures are considered. As with the in-layer twisting structure, the effect of placing conductors at different distances from the central limb can also be predicted based on the analysis provided in the previous subsections. As a result, the following discussion focuses only on the results for the middle-edge structures.

4.4.1. Air-Core Inductors

Figure 11 shows the results of the measurements for the air-core prototypes with the Litz structure. Figure 11a indicates that for the air-core inductors the improvement brought by the Litz structure is not significant at frequencies up to 1 MHz. Increased DC resistance due to longer conductor length and more vias outweighs the proximity effect mitigation provided by the Litz structure. However, the improvement brought about by the Litz structure in reducing the sensitivity of resistance to the frequency can be seen in Figure 11b. As shown in Figure 11b, the slope of the $R_{AC}/R_{DC}$ curve for structures with 10 and 60 transposition points is the highest and the lowest, respectively. Figure 11c illustrates that inserting more transposition points results in reduced inductance values. The prototype with 60 transposition points has the lowest inductance value despite its longer conductor path, due to the increased number of vias.

4.4.2. Ferrite-Core Inductors

Measurement results for the inductors with the Litz structure and ferrite-core are shown in Figure 11. A Litz structure is an effective method for reducing the effects of proximity effect on resistance at high frequencies, as shown in Figure 11d. In contrast to air-core prototypes, the improvements brought about by the Litz method compensate for the high DC resistance resulting from the use of more vias in ferrite-core prototypes. The prototype with 60 transposition points has the highest resistance at frequencies up to 25 kHz. Alternatively, the prototype with 10 transposition points exhibits the lowest resistance for frequencies up to 40 kHz. For the frequency range above 40 kHz, the prototype with 60 transposition points represents the lowest resistance. Figure 11d illustrates the importance of selecting the correct number of transposition points since the structure with 30 transposition points shows higher resistance than the one with 10 points for the entire measurement frequency range. Due to the longer conductor path, the improvement gained by inserting 30 transposition points cannot alleviate the resistance increase.

Figure 11e is helpful for understanding the improvement made by the Litz structure. For the same frequency values, as shown in Figure 11e, the slope of $R_{AC}/R_{DC}$ will be lower for the structure with higher transposition points. For the structure with 10 transposition points, the $R_{AC}/R_{DC}$ ratio is twice that of the structure with 60 transposition points at a frequency of 500 kHz, whereas this ratio is 1.06 for the air-core inductors. Given the higher resistance of ferrite-core inductors, this improvement is of even greater significance.

Figure 11f illustrates how the Litz structure reduces inductance. Inductances for structures with 10 and 30 transposition points are close to each other; however, inductances for structures with 60 transposition points are considerably lower, and the difference increases with frequency. For the frequency range up to 500 kHz, the difference is around 40 $\mu$H, while for 700 kHz, this difference reaches 100 $\mu$H.

4.5. Comparative Study of Structures

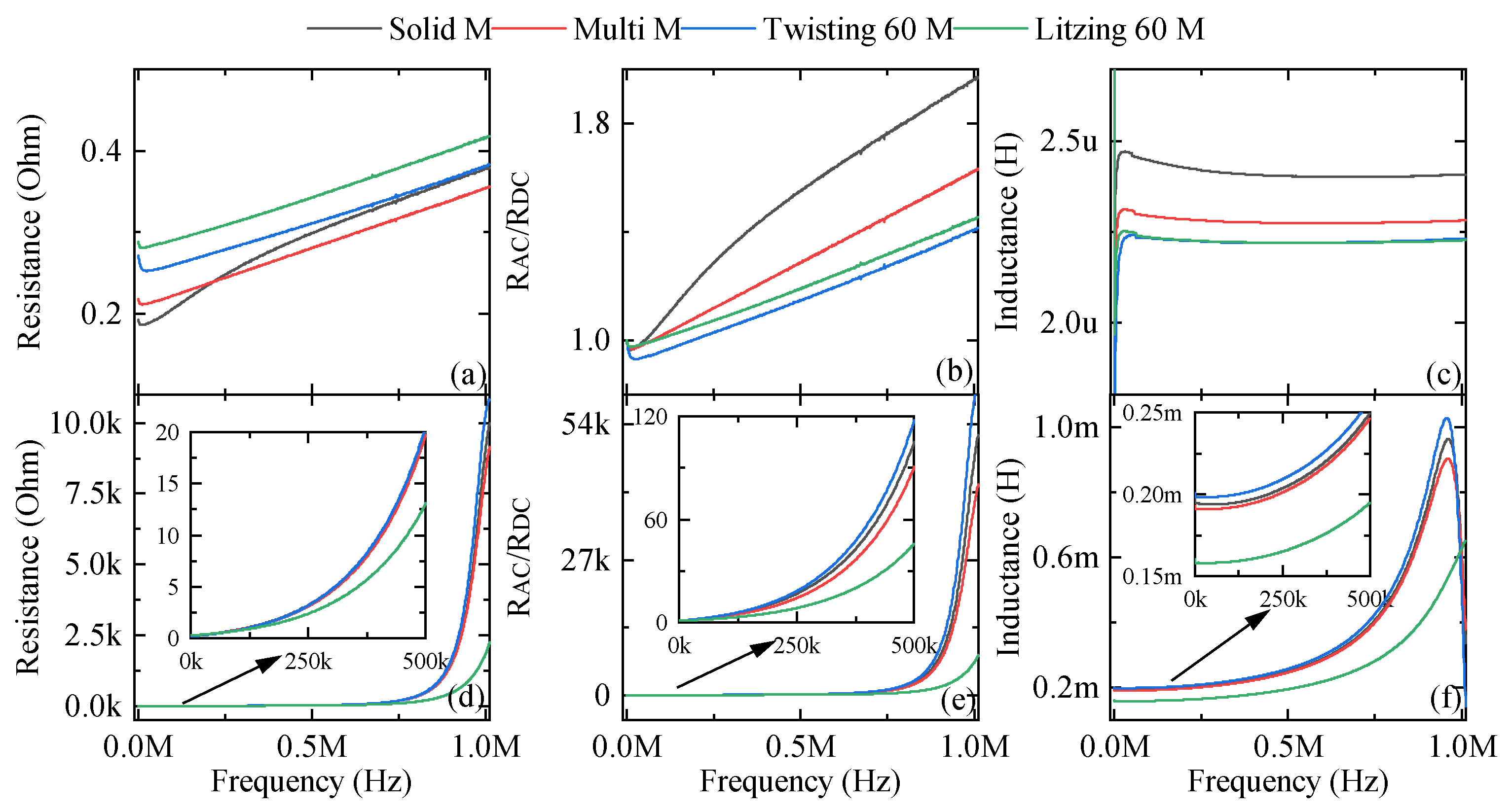
A review of the measurement results for the middle-edge prototypes of each structure at high frequencies is provided in this subsection.

4.5.1. Air-Core Inductors

Measurement results of the air-core middle-edge inductors with solid, multitrack, in-layer twisted, and Litz structures are presented in Figure 12. In Figure 12a, resistance values are represented and it can be concluded that the mentioned solutions can assist with only the skin effect issues and not the proximity effect issues. It was inferred that the resistance was decreased by dividing the solid track into multiple subtracks, as the multitrack structure has the lowest resistance of all. The Litz and twisting structures, which are supposed to help deal with the impacts of the proximity effect, are not useful, since their longer conductor lengths result in higher resistances than the others. Up to the frequency of 200 kHz, the multitrack structure has higher resistance than the solid structure. When the frequency exceeds 200 kHz, the resistance of the solid structure will be greater than the multitrack structure due to the skin effect. In general, resistance values in air-core inductors are low, and the frequency dependency is small, so the effect of different conductor arrangements is not significant.

Figure 12b provides more information regarding the improvements brought about by each method. Based on Figure 12b, inductor structures with Litz and in-layer twisting have the lowest sensitivity to frequency given their slopes on $R_{AC}/R_{DC}$ curves. However, it is noteworthy that for air-core inductors, when using Litz and in-layer twisting, the increase in the DC resistance outweighs the mitigation against proximity effect. It should be noted that, due to the lack of precautions for mitigating either the proximity or skin effect, the resistance of the solid structure is the most susceptible to frequency variation. As a result of using thinner tracks, the multitrack structure is less sensitive to frequency changes. In air-core inductors, the differences in $R_{AC}/R_{DC}$ are not significant compared to the ferrite-core inductors that will be discussed later. It can be seen that at 1 MHz, the lowest and highest values belong to Litz and solid structures, respectively, and that the difference between them is insignificant.

Inductance values measured for different structures are shown in Figure 12c. In the full frequency range, the solid structure has the highest inductance. At the frequency of 500 kHz, the inductance for the solid structure is 2.41 $\mu$H, while using a multitrack structure reduces the inductance value to 2.27 $\mu$H. It is expected that the Litz structure would have a lower inductance than the in-layer twisted structure; however, because of the additional vias and longer conductors in the Litz structure, the in-layer twisted structure will have a lower inductance. For instance, at the frequency of 500 kHz, the inductance value is 2.21 $\mu$H and 2.13 $\mu$H for Litz and in-layer structures, respectively.

4.5.2. Ferrite-Core Inductors

Figure 12 represents the measurement results for different conductor structures of ferrite-core inductors. The resistance values measured for the ferrite-core inductors are presented in Figure 12d. For frequencies less than 100 kHz, the resistance values of the various structures are almost similar, with the Litz structure having the highest value as a consequence of its longer conductors. Solid structures exhibit a lower resistance than multitrack structures until 40 kHz, after which the multitrack structures become more advantageous due to the skin effect cancellation. Among all the structures, the Litz structure exhibits the lowest resistance above 60 kHz despite having the highest resistance up to 50 kHz. As the operating frequency increases, the proximity effect mitigation provided by the Litz structure becomes more significant. As an example, the inductor with the Litz structure has a resistance of 13 $\Omega$ at 500 kHz, while the resistance for inductors with other structures is approximately 20 $\Omega$. As shown in Figure 12e, the Litz structure has the lowest dependency and the in-layer twisted and solid structure has the highest dependency on the frequency for their resistance. For ferrite-core inductors, using the in-layer twisted structure results in worse performance, with higher resistance sensitivity than when using a solid structure. The multitrack structure is better than the solid structure, but has higher dependency compared to the Litz structure since it only deals with the skin effect. Unlike air-core inductors, ferrite-core inductors require careful consideration of the conductor arrangement, as the $R_{AC}/R_{DC}$ values for different structures are not close to each other. As an example, at 400 kHz, the $R_{AC}/R_{DC}$ value is 50.8 for a solid structure, while it is 23.6 for a Litz structure, which is less than half of the solid structure value. With an increase in frequency, the difference between the frequency dependency of resistance for different structures becomes greater, and the selection of conductor structure becomes more critical. As a result, the solid and Litz structures represent 1746 and 528 $R_{AC}/R_{DC}$ values at 800 kHz, respectively.

As shown in Figure 12f, the in-layer twisted structures have the highest inductance over the full frequency range in the measurements. The inductance value for multitrack structure is lower than solid/in-layer twisted structures by almost 3 $\mu$H for different frequency values. The inductor with a Litz structure has considerably lower inductance for all frequencies. At the frequency of 100 kHz, the inductance of the Litz structure is 158 $\mu$H, which is 33 $\mu$H lower than the multitrack structure. For higher frequencies like 800 kHz, this difference is more noticeable as the inductance for solid, multitrack, and in-layer twisted structures is around 480 $\mu$H, while the Litz structure represents 317 $\mu$H inductance.

5. Discussions

In power electronics, inductors are used in a variety of applications, each with a unique requirement.

Table 1. Comparison of air-core and ferrite-core inductors in terms of resonance frequency, inductance range, AC resistance, and Q factor.

Feature	Air-Core Inductors	Ferrite-Core Inductors
Magnetic material	Air	Ferrite
Resonance frequency range	High	Medium
Inductance range	Low to medium	Medium to high
AC Resistance	Low to medium	Medium to high
Q Factor	Low to medium	High
Applications	RF circuits, tuning	Power electronics, converters

provides a comparison of air-core inductors and ferrite-core inductors with some applications included. Using a systematic set of experiments performed on prototypes, this section provides guidance on how to achieve the desired characteristics for inductors. In Figure 13, functionality is represented for each of the arrangements discussed in previous sections for air-core and ferrite-core inductors at low frequency (50 kHz) and high frequency (600 kHz). According to Figure 13a,b, using Litzing and twisting methods to reduce resistance can be ineffective for air-core inductors within the studied frequency range. However, these methods will result in reduced inductance values and higher DC resistance because of the longer path caused by vias and twisting points. For low-frequency applications, as shown in Figure 13a, the solid-track structure has the superior performance, providing high inductance and low resistance. Nevertheless, as frequency increases, the resistance of multitrack structures decreases, as can be inferred from Figure 13b. For ferrite-core inductors, Figure 13c,d illustrate the importance of twisting and Litzing. For the full range of frequencies, the Litzing structure exhibits significantly better resistance to frequency sensitivity reduction than all other structures. However, one of the most critical points is the poor performance of the Litzing method in the case of DC resistance. As a result of their higher DC resistance, inductors with Litzing structures are not necessarily the most appropriate choice for all applications. As shown in Figure 13c, a twisting structure is preferable to a Litzing structure for low-frequency ferrite-core inductors. To reach the lowest resistance in high-frequency applications, however, the Litzing structure is the most efficient method, as depicted in Figure 13d. As shown in Figure 13c,d, another practical point concerning the sufficiency of Litzing structures is their lack of ability to provide high inductance when compared to other structures. As a result, an inductor with a Litzing structure will require more turns to achieve the same inductance value, which will increase the resistance of the inductor.

The following conclusions can be substantiated for both air-core and ferrite-core inductors:

• As the track width increases, the resistance will become more sensitive to frequency changes;
• It has been demonstrated that the length of the conductors, or the location of the conductors in the space between the central and lateral limbs, has no significant effect on the sensitivity of the resistance to the frequency;
• By incorporating more transposition points, the Litz structure helps mitigate proximity effect and reduces resistance sensitivity to frequency;
• In order to achieve lower resistance values, the conductors should be positioned closest to the centre of the inductor or central limb;
• Using air-core inductors, low resistance can be achieved, less than 1 $\Omega$, at all frequencies up to 1 MHz. In contrast, ferrite-core inductors have considerably higher resistance. For instance, at 500 kHz for middle-edge prototypes, the resistance of the ferrite-core inductors will be approximately 20 $\Omega$;
• In order to achieve higher inductance values, it is preferred to place the tracks away from the central limb because outside-edge structures offer higher inductance values than middle- or inside-edge structures;
• The inductance value increases considerably when ferrite-core inductors are used. Inductors with air cores have approximately 2.3 $\mu$H inductance at 500 kHz, whereas ferrite cores can have 250 $\mu$H inductance at the same frequency.

The following inferences can be drawn from the measurements of the air-core inductors:

• While the frequency dependency of the resistance is lower for structures with thinner tracks, the impact of initial high DC resistance is much more significant compared to thick track structures. This is because the thick track structures have the lowest resistance in the full range of frequencies, despite their higher sensitivity to frequency;
• By dividing a solid track into smaller subtracks, resistance can be reduced for higher frequencies, 200 kHz for the prototypes presented in this study. As compared to the solid structure, this reduction is approximately 2% for frequencies around 250 kHz and 6% for frequencies above 500 kHz;
• Using a Litz structure does not reduce resistance in the intended frequency range. By increasing the number of transposition points, the resistance will increase as a result of more vias and longer conductor lengths, making the problem even worse. Despite the improvements provided by the Litz structure, the increase in DC resistance cannot be overcome. In the case of a Litz structure with 60 transposition points, the resistance will increase by 25%, 14%, and 11% for frequencies of 250 kHz, 500 kHz, and 800 kHz, respectively, compared to a solid structure at the same condition;
• Solid track structures provide the highest inductance. For instance, a solid track structure has an inductance of 2.4 $\mu$H at 500 kHz and this value is reduced by 5.5%, 12.5%, and 7.5% using multitrack, in-layer twisted, and Litz structures, respectively.

Measurement results for the ferrite-core inductors lead to the following deductions:

• For the ferrite-core inductors, self-resonance occurs at lower frequencies around 1 MHz and the device cannot be used as an inductor above this frequency.
• The track width of the ferrite-core inductors should be carefully considered. A wider track width can cause even higher resistance at high frequencies since the skin effect and proximity effect are more severe.
• The Litz structure is the most efficient option when it comes to achieving the lowest resistance in ferrite-core inductors. For frequencies up to 500 kHz, multitrack and in-layer twisted structures are effective, but not as much as Litz structures. For frequencies above 500 kHz, multitrack and in-layer twisted structures will yield higher resistance values than solid structures. The measured resistances for the solid structure at 100 kHz, 250 kHz, 500 kHz, and 800 kHz are $0.833$ $\Omega$, $3.22$ $\Omega$, $20.2$ $\Omega$, and 335 $\Omega$, respectively. With the use of the multitrack structure, the resistance is reduced by 4%, 3.7%, and 2.3% for the three former frequencies, respectively, while the resistance is increased by 1.7% for 800 kHz. Similarly, the in-layer twisted structure exhibits 6.3%, 2.8%, and 1% reductions at the first three frequencies, while at 800 kHz, the resistance is 2.6% higher than the solid structure. But the Litz structure is superior in this instance, since it reduces the resistance at the aforementioned frequencies by 13.5%, 26%, 35.6%, and 55%, respectively.
• When using the Litz structure for planar inductors with ferrite-core, it should be noted that this scheme reduces the sensitivity of the resistance to the frequency, but increases the DC resistance at the same time. With a low number of transposition points, the increase in DC resistance will be low, as well as the improvement in mitigating the impact of the proximity effect. Increasing the number of transposition points mitigates the proximity effect more effectively. When the optimum number of transposition points is considered, the improvement brought about by the Litz structure in mitigating impact of the proximity effect is dominant compared to the increased DC resistance caused by the use of vias. While the ability to mitigate the proximity effect does not increase linearly by increasing the number of transposition points, the increase in DC resistance does increase quite linearly. Therefore, the optimal number of transposition points is not necessarily the maximum number possible. Consequently, proper decisions should be made concerning the number of transposition points for each design. A conclusion can be drawn from the study of both $R_{AC}/R_{DC}$ and resistance characteristics. If only the $R_{AC}/R_{DC}$ curve is observed, the Litz structure would be recommended by any number of transposition points, which is incorrect.
• Inductance values for solid and multitrack structures are almost the same throughout the entire frequency range. These structures have 192 $\mu$H, 201 $\mu$H, 245 $\mu$H, and 482 $\mu$H inductances at 100 kHz, 250 kHz, 500 kHz, and 800 kHz frequencies, respectively. The in-layer twisted structure also exhibits a similar inductance to these structures, but represents a higher inductance only at high frequencies, although it is only $2.1\%$ higher at 800 kHz. With the Litz structure, the inductance is reduced by $17.7\%$, $17.9\%$, $20.8\%$, and $34.4\%$ for the frequencies mentioned above.

6. Conclusions

This paper discusses the evaluation of conductor arrangements in planar inductors for power electronic applications. Four topologies were examined: solid track, multitrack, in-layer twisted, and Litz structures, under various conditions. The study encompasses alterations in twisting/transposition points and considers both air-core and ferrite-core inductors. Experimental results were utilized for analysis. While the $R_{AC}/R_{DC}$ ratio dominates discussions in the existing literature, this study also emphasizes AC resistance and inductance values for a comprehensive evaluation.

One of the key contributions of this paper is to demonstrate that $R_{AC}/R_{DC}$ does not suffice to evaluate an arrangement, as arrangements with lower $R_{AC}/R_{DC}$ values could have a higher loss as a consequence of a higher $R_{DC}$. Different layouts may be more suitable in reality even if they produce greater $R_{AC}/R_{DC}$ values, despite the fact that certain arrangements may result in lower $R_{AC}/R_{DC}$ values due to higher DC resistance.

Regarding inductors, inductance is the primary parameter that must be met. According to the findings, different configurations represent different inductance values. Although solid-track layouts have higher resistance, they offer higher inductance as well. In this respect, they can be considered as candidates for some designs since the same inductance can be achieved with a greater number of turns with other arrangements. Other considerations regarding track arrangement are also discussed in this paper, showing the importance of reviewing all specifications and layouts for custom designs thoroughly.