Abstract
The detection and deterrence of collusive agreements among firms, such as price-fixing cartels, remain pivotal in maintaining market competition. This study investigates the application of machine learning methodologies in the behavioral screening process for detecting collusion, with a specific focus on parallel pricing behaviors in the wholesale fuel market. By employing unsupervised learning techniques, this research aims to identify patterns indicative of collusion—referred to as collusion markers—within time series data. This paper outlines a comprehensive screening research plan based on the CRISP-DM model, detailing phases from business understanding to monitoring. It emphasizes the significance of machine learning methods, including distance measures, motifs, discords, and semantic segmentation, in uncovering these patterns. A case study of the Polish wholesale fuel market illustrates the practical application of these techniques, demonstrating how anomalies and regime changes in price behavior can signal potential collusion. The findings suggest that unsupervised machine learning methods offer a robust alternative to traditional statistical and econometric tools, particularly due to their ability to process large and complex datasets without predefined models. This research concludes that these methods can significantly enhance the detection of collusive behaviors, providing valuable insights for antitrust authorities.
1. Introduction
Any collusive agreements among firms to set prices, divide markets, or restrict competition in other ways are considered universally unlawful across antitrust jurisdictions in most countries. In the European Union, Article 101 of the Treaty on the Functioning of the European Union (TFEU) prohibits “all agreements […] and concerted practices […] which have as their object or effect the prevention, restriction or distortion of competition within the internal market”. In the US, Section 1 of the Sherman Act declares “every contract, combination in the form of trust or otherwise, or conspiracy […] in restraint of trade or commerce.” to be illegal. Collusive agreements cause actual harm to consumer welfare. If we consider only price-fixing cartels, between 1990 and 2016, nominal affected sales by international cartels of that type exceeded USD 50 trillion. Gross cartel overcharges exceeded USD 1.5 trillion. More than 100,000 firms were liable for international price fixing [1]. However, collusive agreements can not only be overt (or hardcore) cartels where actual communication and agreements between players take place, but they can also be an outcome of the strategic behavior of rational players not involving explicit communication or another form of coordination of decisions. The idea of a market outcome in which prices and/or other characteristics differ from the competitive level and where the outcome is reached only by some unilateral strategic decisions of the players is well known in economics. From Stigler’s work [2] to contemporary models of strategic interactions, all of these outcomes are motivated by the equilibria of proper game theory models (especially repeated games with infinite horizon) and are usually called tacit collusion (for a comprehensive review, see [3,4,5]). Tacit collusion is also recognized by antitrust law but is not directly defined in the jurisdiction. However, specific formulations in EU and US law in this regard and case law also introduce the possibility of controlling “tacit coordination”, which is the EU law equivalent of the expression “tacit collusion” used in economics [6]. The main difference in understanding “tacit agreement” is that in a ground of law, one would think of anti-competitive conduct that was hard to prove (typically concerted practices or “conspiracies”). In contrast, most economists would think of non-competitive parallel conduct derived from oligopolistic interdependence, where there are no significant differences between a cartel and “tacit collusion” because both market states generate observable values of prices, supply, or other variables located between perfect competition and complete monopoly (based on the interpretation of antitrust law, Posner [7] also stated the equivalence of both market states). Therefore, regardless of the origins of the collusion (overt or tacit collusion), it seems that the common denominators in both cases are the following statements:
- -
- The agreement is horizontal;
- -
- Parallel conduct of the players is observed regarding some observable strategic variables;
- -
- Such an agreement should be detected and analyzed due to possible anti-competitive effects within the meaning of antitrust law.
This paper concentrates on the quantitative detection of overt or tacit collusion with the application of machine learning. Further in the text, the term “collusion” will be used, regardless of its origins. In this article, we want to point out a broader perspective on the use of machine learning methodology in the behavioral screening process and propose using certain unsupervised learning methods to detect patterns known as collusion markers. The structure of this paper is as follows. Section 2 provides a short background of antitrust screening and its connection with the algorithmic approach to data analysis. It also contains a review of works related to machine learning in screening. Section 3, Section 4 and Section 5 contain novel and original contributions of this paper. Section 3 outlines a universal screening research plan based on data mining the CRISP-DM model. In Section 4, we propose some terminological and methodological connections between the taxonomy presented in [8] and the objects of exploration of unsupervised learning. Necessary definitions, methods, and data patterns are introduced. Finally, in Section 5, we present a short case study on the use of the presented methods in the analysis of parallel price behavior in the wholesale fuel market. In our research, we focus on collusion markers based on an analysis of the time series of product and service prices and valuations of price drivers. These variables (as well as bids) provide the most considerable publicly available amount of data and are most often used in analyses related to behavioral screening, especially in the previously mentioned works in which machine learning was used.
2. Screening and Algorithmic Methods
Collusion deterrence is challenging due to the information asymmetry between colluding parties and antitrust authorities. Competition agencies use both reactive and proactive methods to detect collusion. Reactive methods rely on third-party information, while proactive methods include media monitoring, participation in trade associations, and empirical economic analysis. Screening, a key proactive tool, is a quantitative approach to collusion detection, analyzing economic data to identify potential collusion. Key references include [9,10,11,12].
Screening approaches are categorized into structural and behavioral approaches. Structural screening identifies market features that facilitate collusion, while behavioral screening detects firms’ strategic behavior indicative of collusion. The behavioral approach focuses on identifying firms’ strategic behaviors or market outcomes that may suggest collusion. It examines the market impact of coordination, with suspicions arising from patterns in prices, quantities, or other market behaviors. These patterns, known as collusion markers, are disturbances typical of collusive agreements, often linked to the relationships between players’ prices and changes in the demand on the market, the stability of prices and market shares, and the relationships between players’ prices and investments made in production potential [13]. Collusion markers are identified using quantitative models of firm interactions. As defined by Abrantes-Metz in [14], a screen is a statistical test based on econometric models to detect collusion, manipulation, or other cheating behaviors. Behavioral screening aims to detect transitions from non-collusion to collusion or differences between competitive and collusive phases. Unlike structural screening, which identifies vulnerable markets beforehand, behavioral screening can be used both to monitor markets and as an ex post tool for economic evidence of collusion.
The academic literature contains proposals for using diverse quantitative methods to detect collusion markers. Until recently, these were statistical and econometric methods related to adopting specific assumptions regarding the process of generating data, constructing an appropriate econometric model and estimating its parameters, and verifying statistical hypotheses regarding the process and/or its parameters. A good review of the earlier works includes [3,15].
In developing behavioral screening methods, several factors should be considered: the ongoing digitization of the economy, leading to increased data availability, and enhanced data processing capabilities due to advancements in hardware and data architecture. Screening data, often in the form of time series, present specific challenges like dependencies, non-stationarity, various temporal patterns, and high-frequency observations. These characteristics result in complex and non-linear data-generating mechanisms, which have driven interest in analytical methods that do not require traditional assumptions. This shift from “data modeling culture” to “algorithmic modeling culture”, as Breiman noted in [16], suggests that machine learning should be a key method for future behavioral screening.
Machine learning is understood as inductive learning, where knowledge is acquired through reasoning based on examples. A learning mechanism, or algorithm, generates predictions using a specific loss function to optimize information from new data [17]. The concept of “learning machines” is rooted in early work on artificial intelligence and the perceptron [18,19], with significant advancements made by [20,21]. Machine learning primarily focuses on predicting the value of a target variable using predictors (supervised learning) and extracting information without labels (unsupervised learning). Despite advancements in areas like reinforcement and active learning, the supervised–unsupervised dichotomy remains central.
To assess whether machine learning is suitable for collusion detection, we refer to two key papers. Abrantes-Metz and Metz in [22] suggest that flexible, unstructured algorithms can effectively identify anomalous data patterns for further investigation. However, the explainability of algorithmic methods remains a concern, as noted in [23], which necessitates caution in applying machine learning to a simple “collusion” vs. “no collusion” classification task. As [22] highlights, determining collusion is more complex than mere numerical detection; it requires understanding how likely it is that the observed data result from collusion rather than competition, based on an economic model of market interactions. The second paper, ref. [8], focuses on detecting bid-rigging cartels with machine learning, observing that if algorithms cannot directly classify collusion, screening should focus on identifying collusive markers, structural breaks, and anomalies. The authors define a collusive marker as a pattern in the data that is more consistent with collusion than the competition, a structural break as an abrupt change in the data-generating process, and an anomaly as a pattern in the data that is inexplicable or inconsistent with competition but may ultimately be found consistent with collusion. The taxonomy of phenomena we look for in behavioral screening is very well reflected in specific unsupervised learning tasks, as shown below. There are relatively few papers that address the use of machine learning in applied screening. A summary of the work can be found in [15]; among the relevant works is [24], which utilizes logistic regression, ridge regression, LASSO, neural networks (as part of an ensemble approach), and random forests; ref. [25], which uses LASSO, neural networks, bagged regression trees, random forests, and an ensemble approach; ref. [26], which applies LASSO, neural networks, bagged regression trees, random forests, and an ensemble approach; and ref. [27], which utilizes neural networks, support vector machines, random forests, and an ensemble approach. The authors of [28] use neural networks (as part of an ensemble approach), support vector machines, and random forests; ref. [29] employs neural networks, bagged regression trees, random forests, and an ensemble approach; ref. [30] uses an unsupervised network approach; and [31] utilizes convolutional neural networks.
3. Behavioral Screening Process with Machine Learning
We focus on behavioral screening here, as it is inherently quantitative, but the methods shown can be used in structural screening if they contain quantitative stages. Further, in this text, we refer to it as screening for simplicity.
Generally speaking, all screening applications, according to various definitions, have a form of quantitative empirical research based on an economic understanding of the market or industry, where one uses carefully selected quantitative data and proper statistical/econometric tools to detect the existence of specific phenomena from data. We can see a general scientific approach here but no systematic plan for such research. Some advice on screen design can be found in [10], and we use this to show correspondence between screening and the CRISP-DM general process.
If we think about screening as a data exploration task, we can use a ready-to-go data-centric process template in our research, which is one of the Knowledge Discovery and Data Mining process models (for a review, see [32]). We use a process model widely known in data science, the CRISP-DM, [33], as a best-practice schema. According to this process, research contains the following phases: Business Understanding, Data Understanding, Data Preparation, Modeling, Evaluation, Deployment, and Monitoring. In the context of screening research, these stages may correspond to the following steps.
Business Understanding should include understanding the industry or market at hand, including the nature of internal strategic interactions. A theoretical model of players’ interactions can be formulated at this stage. Utilizing that model and/or additional information (e.g., delivered by competition authorities, public opinion), some hypotheses on how collusive agreement will affect market outcomes should be formulated. Finally, on the basis of the above, collusion markers (what we are looking for in the data) should be clearly declared. The period of research should be stated.
Data Understanding should contain an analysis of quantitative data sources. A list of variables that may be useful in the detection of collusion markers should be prepared. Then, one needs to verify the availability of the data, encompassing the previously stated period of research, in the public domain. All available data should be extracted from sources, loaded to any data exploration tool, and initially checked and described. One has to check the format, number of records, frequency, and units of measure of the data. Initial exploration (in a field of data science called IDA (Initial Data Analysis)) should contain a visualization of the data and verification of their quality (checking for errors in data, missing data, and outliers). Basic descriptive statistics should also be calculated in this phase.
The Data Preparation phase uses information from previous phases to select a set of available variables and data records for further research, clean the data (treat missing values and outliers, remove errors), and integrate, unify, and transform data (e.g., aggregate/disaggregate, unify units of measures, normalize data). In this stage, additional variables can be constructed from the given ones, and proxy variables can be obtained in place of those that are not available/not usable. As the whole CRISP-DM process is circular rather than linear, data preparation tasks are likely to be performed multiple times and not in any prescribed order, directed partly by choice made in the Modeling phase.
In the Modeling phase, various quantitative (statistical, econometric, machine learning) techniques that are usable for the detection of collusion markers are selected and applied. Some techniques have specific requirements for the form of data. Therefore, stepping back to the Data Preparation phase is often necessary. Before one actually uses any tool, one must identify the mechanism to test the tool’s quality and validity. For example, in supervised data mining tasks, where there is a target variable, it is common to use error rates as quality measures for data mining models. Therefore, we typically randomly separate the dataset into estimation and validation subsets, build the model on the estimation set, and estimate its quality on the validation set. Statistical or econometric tools also have well-defined quality and validity measures, which should be checked. According to this technical (not economic, yet) assessment, the proper tool should be chosen for the research.
The Evaluation and Deployment phases of the original CRISP-DM process can be combined in the context of screening because, in this step, the economic results of the tools selected in the Modeling phase are verified. It should be assessed whether the detected phenomena may indicate the occurrence of collusion markers and whether these markers actually indicate the occurrence of collusion. In this phase, the results obtained should be compared with the economic hypothesis formulated in the first phase, and the possible alternative scenarios to collusion leading to these results should be critically analyzed.
The Monitoring phase is an additional phase of CRISP-DM, intended to recalibrate models when new information is obtained. In screening research, this phase can be used to construct real-time screening mechanisms for a particular type of market or industry on the basis of the results of previous steps that have been positively verified. A machine learning approach should be used here, as it is suitable for such online learning tasks.
Since this article focuses on the applications of machine learning in screening, it should be emphasized that in each of the above phases, it is possible to use machine learning methods together with standard statistical and econometric tools. We will provide an example later in the text.
4. Similarity Explorations in Screening for Price-Based Markers
As mentioned earlier, we focus on collusion markers based on prices in this paper. Hüschelrath [13], based on Harrington [11], lists the following patterns as price-based collusion markers: higher list (or regular) price and reduced variation in prices across customers; a series of steady price increases preceded by steep price declines; price rises and import declines; firms’ prices being strongly positively related (parallel pricing); a high degree of uniformity across firms in product price and other dimensions, including the prices for ancillary services; low price variance; and prices being subject to regime changes.
Taking into account price time series analysis and referring to the taxonomy of Harrington and Imhof from [8], but focusing on machine learning methodology, we can say that screening can be considered to be a time series mining task [34], or a form of time series similarity exploration, which can be considered to be a generalization of such tasks. Generally, one can observe various kinds of meaningful patterns in univariate and multivariate time series, such as trends, seasonality, cyclical changes, drifts, change points, and regime changes in mean, variance, or probability distribution, which classical statistical and econometric models describe well.
On the other hand, time series similarity exploration aims to find similar time series sequences within a dataset or between different datasets. This task is crucial for clustering, classification, and anomaly detection in general. It is considered an unsupervised machine learning problem if one searches for unknown patterns, which is the case in the context of behavioral screening. The most common types of patterns which we consider usable in screening are the following:
- -
- Distance;
- -
- Motifs;
- -
- Discord;
- -
- Semantic segments (regimes).
To define the above objects briefly, let us focus on univariate or bivariate time series. We formulate definitions without extensive formal notation, as such notation can be found in the cited papers. We aim to provide an intuition instead which allows us to better understand the potential applications of each object in screening tasks.
The distance measures for time series aim to provide a measure of the general similarity of bivariate time series. Given two time series, T1 and T2, the particular similarity function Dist calculates the distance between the two time series, denoted by Dist(T1, T2). There are dozens of propositions for the Dist function (for a comparison, see [35]). However, one can focus on representatives of Dist encompassing three distinct approaches to distance calculation: a comparison of the i-th point of one time series with the i-th point of another (e.g., Lp norms and all methods based on one of the Lp norms, like LB_Keogh, which is a DTW indexing method but can be used as a distance measure), a comparison of one-to-many points (e.g., Dynamic Time Warping, DTW) and one-to-many/one-to-none point comparisons (e.g., Largest Common Subsequence, LCSS). Figure 1 presents an example of DTW—a DTW-based measure of similarity between the spot price of Brent crude oil (lagged 4) and the wholesale price of standard 95 octane gasoline offered by the Polish company LOTOS.
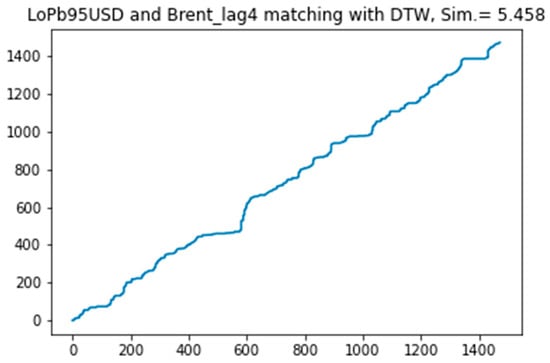
Figure 1.
DTW alignment path and similarity. Source: own calculation.
Time series motifs are approximately repeated subsequences found within a longer time series. Being able to say that a subsequence is “approximately repeated” requires that you be able to compare subsequences to each other. A formal definition can be found in [36]. The main challenges and benefits are discovering motifs of unknown length and shape, which is an unsupervised learning task. The general learning task is finding non-overlapping subsequences at all lengths with k or more (approximate) matches. Figure 2 presents the idea of the motif in a time series using synthetic data. Subsequences learned as motifs are marked in red, green and yellow color.
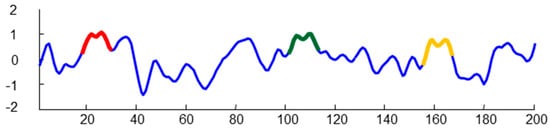
Figure 2.
Time series motifs. Source: Own preparation based on [36].
In the context of time series mining, a discord is a subsequence considered the most unusual or least similar to all other subsequences within a given time series. In other words, it is an anomalous pattern that does not match well with any other time series segment. See [37] for a formal definition. The idea of time series discord is depicted in Figure 3.

Figure 3.
Time series discord. Source: [37].
The detection of discords is sometimes associated with change point detection in time series, but the goals of both mining tasks are different. Change point detection is the problem of finding abrupt changes in data when a property of the time series changes (for a survey on this topic, see [38]; for its application in a fuel market, see [39]) and, defined as a machine learning task, it is similar to the problem of semantic segment detection defined in the next paragraph.
Unsupervised semantic segmentation in the time series domain can be defined as dividing a time series into internally consistent regimes or clustering the time series with the additional constraint that the elements in each cluster are contiguous in time [40]. Such a machine learning task is very useful in practice because it can detect unexpected regularities and regimes in poorly understood data. Figure 4 presents the idea of segments (regimes) in economic time series where one of the specific methods, the FLUSS/FLOSS (Fast Lowcost Online Semantic Segmentation) algorithm introduced in [40], was used.
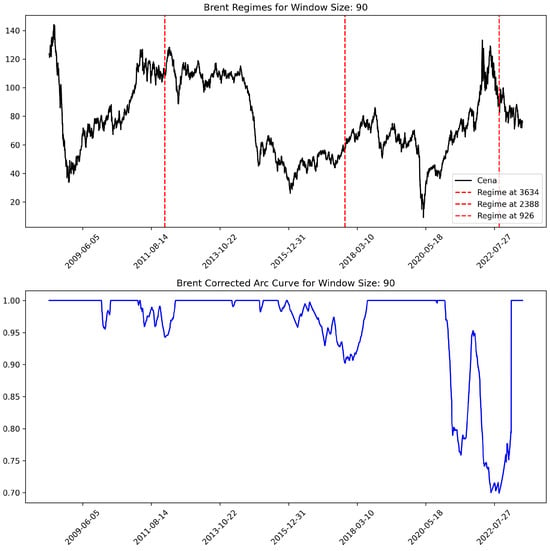
Figure 4.
Time series regimes. Source: own preparation.
Figure 4 contains the results of regime detection in the time series of Brent crude oil spot price (in the upper part, three points of change in the behavior of the time series are detected and marked by a red dotted line, and the lower part depicts the so-called CAC used in regime detection).
It should be emphasized here that semantic segmentation belongs to the model-agnostic, algorithmic method (according to Breiman’s definition, it represents algorithmic culture) and should be distinguished from the well-known statistical and econometric methods of detecting time series regimes. These methods concern detecting changes in specific parameters of the stochastic process, such as variance or mean, and require estimating the values of these moments directly or indirectly via a proper econometric model. For more information on the use of these methods in cartel screening, see [9,41,42,43].
In our view, distance, motifs, discords, and semantic segment explorations correspond closely to many numerical tasks described as collusion marker detection, especially in view of [8]’s classification of such tasks.
5. Empirical Case Study
One of the price-based collusion markers is parallel pricing. However, observed parallel conduct can result from mere oligopolistic interdependence and hence can not be treated as a signal of collusion. It is worth noting that the court annulled the only cartel case that relied exclusively on indirect evidence in the form of parallel pricing (see Woodpulp Judgment of the Court of 31 March 1993, A. Ahlström Osakeyhtiö and others v Commission, joined cases C-89/85, C-104/85, C-114/85, C-116/85, C-117/85 and C-125/85 to-129/85). Therefore, there is a need for tools to verify whether the observed parallel pricing strategies can be considered a marker of collusion. It seems that the unsupervised machine learning methods presented in the first part of this article, aimed at detecting specific patterns in the data, may be effective in quickly verifying this problem. The presented empirical example concerns the detection of patterns and changes in the competitive behavior of players present in the industry of producers and suppliers of wholesale liquid fuels in Poland in a specific time horizon, where competitive behavior is understood as the pricing strategies of wholesale prices in relation to the strategies implied by the pricing model Import Parity Pricing and changes in related pricing factors. This case study was constructed following the proposed screening research plan based on the CRISP-DM model. As this case study serves to present the possibilities of using machine learning methods and the CRISP-DM-based research plan itself, each stage will be characterized synthetically and without unnecessary technical details. All of the details can be found in the cited sources. Similarly, details of empirical examination (sources of data, details of transformations, descriptive statistics, etc.) will be omitted, as this paper is not devoted to referring to empirical study but to showing some ideas of unsupervised learning in screening supported by selected results of broader research.
Business Understanding. The aim of this study is to detect specific patterns and the compliance of these patterns in the competitive behavior of two dominant players in the industry of producers and suppliers of wholesale liquid fuels in Poland, PKN Orlen and LOTOS. The period covered by this study is from 1 January 2015 to 31 December 2021. A brief view of the Polish refining industry (it is important to limit the research scope to the period 2015–2021, as on 1 August 2022 LOTOS was merged into and became a part of PKN Orlen; however, as the wholesale prices of fuels will be published by LOTOS until 31 December 2025, it is obvious that from the merger date the structure of the market has changed to a monopolistic one), the liquid fuels’ wholesale market, and the price creation policy is provided in [39]. The pricing strategy is understood as the levels of wholesale prices of fuels (products) set by the player and their relationship with the price levels of price drivers. The price driver is a predictor implied by the IPP formula, the price of which (probably lagged) affects the current wholesale price of fuel on the examined market. A theoretical model of interaction, which is the basis of this research, is formulated in [44]. The model implies that, by treating the product-specific IPP price (latent variable) as the focal price, the strategies of both players replicating this price are strategies in subgame perfect equilibrium. Therefore, an external observer should observe natural parallel pricing strategies related to that focal price, and indirectly to the IPP price drivers. An empirical consequence of such equilibrium strategies is that the pricing strategy of the player is linked to the price drivers in a “constant and similar” way over time. Moving on to the definition of markers, the theoretical hypothesis implies that the observable time series of prices and price drivers should demonstrate the following characteristics:
- (a)
- Wholesale price paths and price driver paths should maintain constant similarity (distance) over time.
- (b)
- Anomalies or regimes detected in price drivers should be transferred to wholesale prices in a similar way, with similar lag and without any difference between players.
Points (a) and (b) allow for the construction of workable markers to look for in data. We will learn the following from the data:
- -
- Distance over time between wholesale price time series and price driver time series;
- -
- Discords in wholesale price time series and price driver time series;
- -
- Regimes in wholesale price time series and price driver time series;
- -
- Discords and regimes will be further analyzed to assess the similarity of their occurrence in both types of time series.
Data Understanding. In this stage, a preliminary selection of the time series of the wholesale prices of refining products announced by both players and price drivers from the set defined based on the IPP hypothesis was made. We had to consider other information needed in this research as well. The following time series were selected: wholesale prices from both players—the price of unleaded standard 95 octane gasoline in PLN per m3, the price of standard diesel oil for road transport in PLN per m3; and price drivers—the Brent crude oil spot price in USD per m3, New York Harbor Regular Gasoline spot price in USD per gallon, and New York Harbor Ultra-Low Sulfur No 2 Diesel spot price in USD per gallon. As we want to accommodate the impact of the USD exchange rate on domestic prices, the USD/PLN exchange rate was also listed as additional information. All listed time series were identified as possible to obtain from the public sources for the research period and downloaded as raw data format files. IDA was performed, and its conclusions were passed on to the next stage.
Data Preparation. The necessary data cleaning and transformations took place in this step. At first, daily observations were synchronized with the working week, missing observations were processed, and data normalization was performed (the primary tool for working with data was the Python programming language and the appropriate libraries of this language, containing the machine learning algorithms used in this study). Next, an additional time series of predictors was generated: a lagged series of price drivers (up to 14 lags) and one-hot encoded predictors from data stamps (e.g., day of a week, month of a year). Additionally, the wholesale prices of products were expressed in USD at the exchange rate on day t-1 relative to the price observation on day t. The final and most crucial part of this phase was the selection from the set of predictors of those variables that had the most significant impact on wholesale product prices. Based on the economic hypothesis, possible predictors were initially selected in the Data Understanding phase. However, at this stage, it was necessary to select from among 50 time series, which constituted the set created in the current stage. Focusing on machine learning methods in this paper, we decided to use two strictly algorithmic predictors’ selection methods. Fitting a regression random forest model for each of the four wholesale prices and using one of the Variable Importance Metrics [45,46] was chosen as the leading selection method. A random forest [46,47] is an ensemble (or forest) of decision trees grown from a randomized variant of the tree induction algorithm. It can be used in supervised learning tasks, like regression or classification.
A Mean Decrease Impurity (MDI; defined in [48]) measure was utilized to rank the relative significance of the predictor variables. MDI is one of the VIMs that is suitable for regression tree-based algorithms. MDI is based on the total decrease in node impurity from splitting on the variable, averaged over all trees. The standard for the supervised learning tuning of hyperparameters was conducted by a grid search on the training set (containing about 70% of each target sample), using the time series k-fold cross-validation. Finally, the MDI measure’s values were calculated. It was decided to use the similarity measurement between wholesale prices and predictors as a comparative and confirmatory method for selecting predictors. As an unsupervised method, it is based on a straightforward assumption that the course of the time series related to each other should be similar. The following distance (similarity) measures between time series were applied: Longest Common Subsequence (LCSS, defined in [49]) and LB_Keogh [50]. An example of the results of the predictors’ selection stage is shown in Table 1.

Table 1.
Results of predictors’ selection stage with algorithmic methods.
In the presented fragment of this study, the values of the MDI measure indicated the choice of the NYH price lagged by one day (in reference to the target price) as the most important price driver (which is consistent with the IPP valuation hypothesis). Measuring the similarity of the time series confirmed this finding. Figure 5 presents both raw time series (with prices in USD on the Y axes).

Figure 5.
Examined time series. Source: own preparation.
Attention should also be paid to the values of similarity measures between the price of 95 LOTOS gasoline and 95 Orlen gasoline, which are additionally presented in Table 1. These measures indicate the extreme similarity of both time series, which confirms parallel behavior. However, the question is whether it is natural for the duopoly (following the focal price hypothesis) or not. The next phase of the study may provide answers to this question.
Modeling. In this phase, tools appropriate for detecting the patterns specified in the Business Understanding phase were selected, allowing for the verification of the type of equilibrium. One can use various statistical and econometric methods to examine the relationship between the wholesale price and price driver defined in point (a). However, we want to show the usability of fast and simple, pure algorithmic methods, so we decided to use the distance measures introduced in Section 4. One can interpret distance calculated over time as a quasi-margin if one of the time series has a price-setting nature. That is precisely the case here, because we determined the distance between the wholesale price of fuel and the price driver implied by the IPP valuation. Figure 6 shows the result of the distance examination with the LB_Keogh measure. The graph presents the distance, calculated over time, between standard gasoline 95 sold by LOTOS and its price driver (NYH gasoline) selected in the previous phase.

Figure 6.
Result of the distance examination with the LB_Keogh measure. Source: own preparation.
The next screening step, following point (b), contains the discovery of discords in a price’s path. There are many unsupervised machine learning algorithms designed for such tasks. Some of the most popular tools are those based on the Symbolic Aggregate approXimation (SAX) transformation. SAX is a dimensionality reduction method that transforms a time series into a symbolic representation [51]. It applies Piecewise Aggregate Approximation (PAA) to reduce the dimensionality of the time series and maps the PAA segments to symbols. For discord discovery with SAX representation of time series, we used the HOTSAX algorithm [37]. The HOTSAX (Heuristically Optimized Time Series using SAX) algorithm is a time series anomaly detection algorithm that extends the SAX technique. The algorithm is designed to identify discords or anomalies efficiently within a given time series dataset. A Python implementation of HOTSAX, included in the library SAXPY [52], was used. Figure 7 shows the results of the discords’ discovery and depicts the distance (in working days) between each pair of the nearest discords detected in both time series. For example, there are discords placed about the data point 400 in both series, and one can see that the placement of those discords is nearly the same. The distance between those discords, shown in Figure 7, is six days.
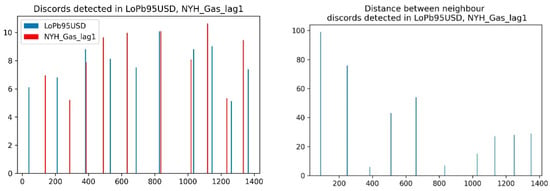
Figure 7.
Result of the discord examination. Source: own preparation.
According to point (b), the last pattern to discover is the semantic segments or time series regimes. We used another unsupervised machine learning tool, the matrix profile, to learn regimes from data. The matrix profile is a data structure with associated algorithms designed to analyze and discover time series data patterns. It was introduced in [53]. The matrix profile methodology is based on creating two meta time series, the matrix profile and the matrix profile index, to annotate a time series T with the distance and location of all its subsequences’ nearest neighbors within itself. Matrix profile-based algorithms enable unsupervised searches for various patterns in data, like motifs, discords, and regimes. Time series regime discovery with matrix profile and matrix profile index is based on the so-called Corrected Arc Curve (CAC). The Arc Curve (AC) for a time series T of length n is itself a time series of length n containing non-negative integer values. The i-th index in the AC specifies how many nearest neighbor arcs from the matrix profile index spatially cross over location i. To compensate for the edge effect bias in the Arc Curve, for each location i, we consider the actual number of observed arc crossings relative to the number of expected arc crossings predicted by the Idealized Arc Curve (IAC) parabolic model (inverted parabola with unique maximum at 0.5 * n), to obtain the Corrected Arc Curve (CAC) with the following values:
CACi = min (IACi/ACi, 1)
Regime detection based on CAC utilizes the simple observation that if a time series T has a regime change at location i, one would expect few arcs to cross i, as most subsequences will find their nearest neighbor within their host regime. Thus, the height of the CAC should be the lowest at the location of the boundary between the change in regimes/states.
All algorithms based on a matrix profile need to pass, among other things, two of the most important parameters: the length of the subsequence (window size) and the number of “matches” we look for in data. In the presented empirical case study, we examined times series with window sizes of 14 and 30 days, looking for up to three regimes. The Python 3 matrix profile library version 1.1.10 [54] was used for calculation. Figure 8 shows the results for the time series selected to present the empirical example.
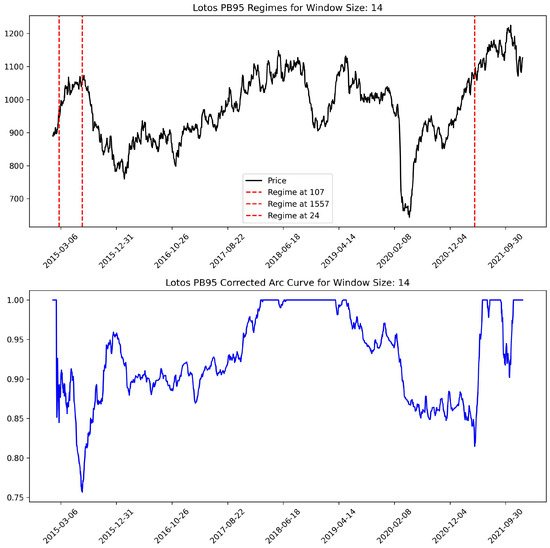
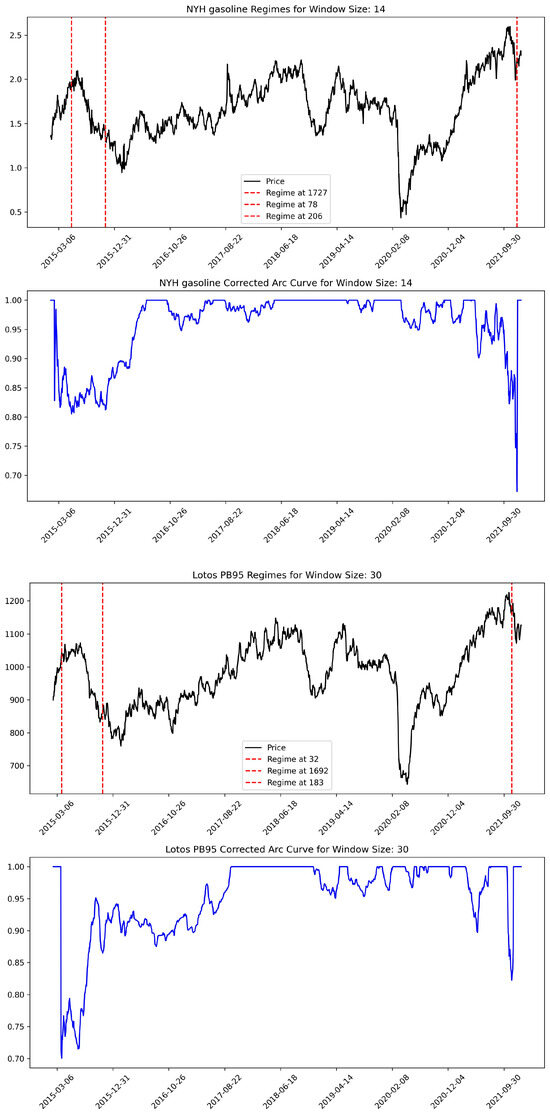
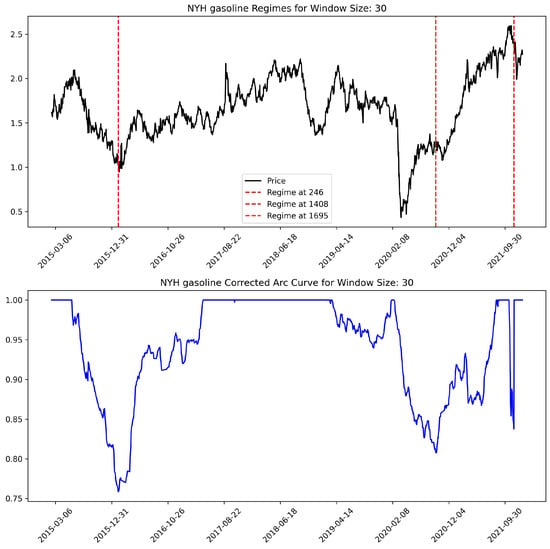
Figure 8.
Results of the regimes’ discovery. Source: own preparation.
The local minima of the CAC indicate regime change points, which means that the general behavior of time series before and after such points is different.
Concluding the description of the modeling phase, it should be added that the detected patterns for the wholesale price of gasoline of the second player, Orlen, were almost identical due to the high similarity of the course of both time series (see Table 1).
Evaluation. In this final step, it should be assessed whether the detected phenomena indicate the occurrence of collusion markers and whether these markers actually indicate the occurrence of collusion. The results obtained should also be compared with the economic hypothesis formulated in the Business Understanding phase. In the context of the presented empirical example, the following can be said:
- -
- The measurement of the distance between the wholesale price series and its price driver revealed that this distance changed significantly during the sample period. If we treat the price driver as a focal price in the sense of the theoretical hypothesis, it can be concluded that the distance from the focal price increased.
- -
- Discord discovery revealed interesting features of the disturbance occurrences in both time series. If we treat anomalies in the price driver series as specific shocks, the transfer of these shocks to the wholesale price of gasoline varied during the sample period. It can be noted that for most of the analyzed period, there was no regularity in the transfer of discords between time series. The distances between adjacent anomalies vary greatly, which excludes compliance with the focal price strategy. Only at the end of the sample does regularity appear in the distances, which indicates the transfer of disturbances from the price driver to the wholesale price of gasoline with a constant delay of about 28 days.
- -
- The discovery of regimes revealed their different distributions in both time series. This situation does not support the theoretical hypothesis about implementing the focal price strategy. If this were the case, the moments of changes in the general characteristics of the time series should be related. We also propose analyzing the CACs for both time series. They are clearly different between window 14 and window 30, which is confirmed by the lack of a clear transfer of patterns from the price driver to the wholesale price.
In our summary of the evaluation phase in the case of the presented example, one can state that the unsupervised learning methods used led to detecting the patterns indicated in the Business Understanding phase. Based on this analysis, one should question whether players use the equilibrium strategies specified in the theoretical hypothesis. This means that in the period under consideration, parallel pricing was not a consequence of the expected strategic interaction of duopolists but resulted from other reasons, including collusion. The implications of this research can serve as a “plus factor” (in a sense presented in [55]) in a more general assessment of the behavior of the players.
6. Conclusions
The presented article aims to indicate the connection between the typical tasks of behavioral screening and the problems of time series exploration and mining using algorithmic methods, especially unsupervised machine learning methods. This article shows that objects that are the subject of machine learning tasks, generally defined as similarity searches, such as distances, motifs, discords, or regimes, can be used as search patterns and markers confirming or denying the existence of collusion.
This article indicates that machine learning methods can be an interesting alternative or complement to standard statistical and econometric tools. The undoubted advantages of machine learning in screening tests are:
- -
- No assumptions as to the form of the model or the properties of the data-generating process;
- -
- The possibility of easy implementation for mass and streaming data;
- -
- It is natural for unsupervised learning to search for unknown patterns in the data, which is precisely the task faced by screening methods.
This article’s second aim is to organize and structure research aimed at screening. The CRISP-DM model was adopted as the template, but the individual phases of the process were redefined and adapted to the needs of the screening study. The described process can, of course, be used for any quantitative methods, not only data mining and machine learning methods.
This empirical case study presents proposed concepts in practice. It includes a screening study that was carried out according to the process proposed in the paper based on the CRISP-DM model. This study shows the possibilities of using machine learning methods in two process phases. It shows the use of patterns such as discords or semantic segments in constructing and verifying parallel pricing markers on the wholesale fuel market.
Funding
This research was financed by the National Science Centre project 2019/35/B/HS4/00642 entitled ‘Forecasting financial markets using a machine learning approach’.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflict of interest.
References
- Connor, J.M. The Private International Cartels (PIC) Data Set: Guide and Summary Statistics, 1990–July 2016 (Revised 2nd Edition). 2016. Available online: https://ssrn.com/abstract=2821254 (accessed on 18 May 2024).
- Stigler, G. A theory of oligopoly. J. Political Econ. 1964, 72, 44–61. [Google Scholar] [CrossRef]
- Bejger, S. Detection, Measurement and Assessment of Strategic, Horizontal Anticompetitive Behavior of Market Players: Quantitative Analysis; Wydawnictwo Naukowe Uniwersytetu Mikołaja Kopernika: Toruń, Poland, 2016. [Google Scholar]
- Tirole, J. The Theory of Industrial Organization; MIT Press: London, UK, 1998. [Google Scholar]
- Vives, X. Oligopoly Pricing: Old Ideas and New Tools; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Blanco, L.O. Market Power in EU Antitrust Law; Hart Publishing: Oxford, UK, 2012. [Google Scholar]
- Posner, R. Antitrust Law: An Economic Analysis; University of Chicago Press: Chicago, IL, USA, 1976. [Google Scholar]
- Harrington, J.; Imhof, D. Cartel Screening and Machine Learning. Stanf. Comput. Antitrust 2022, 2, 133–154. [Google Scholar]
- Abrantes-Metz, R.; Metz, A.D. How Far Can Screens Go in Detecting Explicit Collusion? New Evidence From the Libor Setting. In Competition Policy International Antitrust Chronicle; Competition Policy International, Inc.: Boston, MA, USA, 2012; Volume 1. [Google Scholar]
- Abrantes-Metz, R. Design and Implementation of Screens and Their Use by Defendants. In Competition Policy International Antitrust Chronicle; Competition Policy International, Inc.: Boston, MA, USA, 2011. [Google Scholar]
- Harrington, J.E. Behavioral Screening and the Detection of Cartels. In European Competition Law Annual; Hart Publishing: Oxford, UK, 2006. [Google Scholar]
- Harrington, J.E. Detecting Cartels. In Handbook in Antitrust Economics; Buccirossi, P., Ed.; MIT Press: Cambridge, MA, USA, 2008; pp. 213–258. [Google Scholar]
- Hüschelrath, R. How Are Cartels Detected? The Increasing Use of Pro-active Methods to Establish Antitrust Infringements. J. Eur. Compet. Law Pract. 2010, 1, 522–528. [Google Scholar] [CrossRef]
- OECD. Ex Officio Cartel Investigations and the Use of Screens to Detect Cartels; Competition Committee 2013 DAF/COMP(2013)27; OECD: Paris, France, 2013. [Google Scholar]
- OECD. Data Screening Tools in Competition Investigations; OECD Competition Policy Roundtable Background Note; OECD: Paris, France, 2022. [Google Scholar]
- Breiman, L. Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–215. [Google Scholar] [CrossRef]
- Vapnik, N.V. The Nature of Statistical Learning Theory; Springer Science and Business Media: New York, NY, USA, 2000. [Google Scholar]
- Minsky, M.; Papert, S. Perceptrons; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Michalski, R.S.; Carbonell, J.G.; Mitchell, T.M. Machine Learning: An Artificial Intelligence Approach; Tioga Publishing: Palo Alto, CA, USA, 1983. [Google Scholar]
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Abrantes-Metz, R.M.; Metz, A. Can Machine Learning Aide in Cartel Detection? In Competition Policy International Antitrust Chronicle; Competition Policy International, Inc.: Boston, MA, USA, 2018; Available online: https://ssrn.com/abstract=3291633 (accessed on 10 June 2024).
- Bejger, S.; Elster, S. Artificial Intelligence in economic decision making: How to assure a trust? Èkon. Prawo 2020, 19, 411–434. [Google Scholar] [CrossRef]
- Silveira, D.; Vasconcelos, S.; Resende, M.; Cajueiro, D.O. Won’t Get Fooled Again: A supervised machine learning approach for screening gasoline cartels. Energy Econ. 2021, 105, 105711. [Google Scholar] [CrossRef]
- Imhof, D. Empirical Methods for Detecting Bid-Rigging Cartels, Université Bourgogne Franche-Comté. 2018. Available online: https://tel.archives-ouvertes.fr/tel-01963076/document (accessed on 15 June 2024).
- Wallimann, H.; Imhof, D.; Huber, M. A Machine Learning Approach for Flagging Incomplete Bid-Rigging Cartels. Comput. Econ. 2022, 62, 1669–1720. [Google Scholar] [CrossRef]
- Imhof, D.; Wallimann, H. Detecting bid-rigging coalitions in different countries and auction formats. Int. Rev. Law Econ. 2021, 68, 106016. [Google Scholar] [CrossRef]
- Rodríguez, M.J.G.; Rodríguez-Montequín, V.; Ballesteros-Pérez, P.; Love, P.E.; Signor, R. Collusion detection in public procurement auctions with machine learning algorithms. Autom. Constr. 2021, 133, 104047. [Google Scholar] [CrossRef]
- Huber, M.; Imhof, D.; Ishii, R. Transnational Machine Learning with Screens for Flagging Bid-Rigging Cartels. J. R. Stat. Soc. Ser. A Stat. Soc. 2022, 185, 1074–1114. [Google Scholar] [CrossRef]
- Wachs, J.; Kertész, J. A network approach to cartel detection in public auction markets. Sci. Rep. 2019, 9, 10818. [Google Scholar] [CrossRef] [PubMed]
- Huber, M.; Imhof, D. Deep learning for detecting bid rigging: Flagging cartel participants based on convolutional neural networks. arXiv 2021, arXiv:2104.11142. [Google Scholar]
- Kurgan, L.A.; Musilek, P. A survey of Knowledge Discovery and Data Mining process models. Knowl. Eng. Rev. 2006, 21, 1–24. [Google Scholar] [CrossRef]
- Chapman, P. CRISP-DM 1.0: Step-By-Step Data Mining Guide; SPSS Inc.: Chicago, IL, USA, 2000. [Google Scholar]
- Lin, J.; Keogh, E.; Lonardi, S.; Chiu, B. A Symbolic Representation of Time Series, with Implications for Streaming Algorithms. In Proceedings of the 8th ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, San Diego, CA, USA, 13 June 2003. [Google Scholar]
- Ding, H.; Trajcevski, G.; Scheuermann, P.; Wang, X.; Keogh, E. Querying and Mining of Time Series Data: Experimental Comparison of Representations and Distance Measures. In Proceedings of the VLDB 2008, Auckland, New Zealand, 23–28 August 2008. [Google Scholar]
- Lin, J.; Keogh, E.; Lonardi, S.; Patel, P. Finding Motifs in Time Series. In Proceedings of the 2nd Workshop on Temporal Data Mining, at the 8th ACM SIGKDD Int’l Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 53–68. [Google Scholar]
- Keogh, E.; Lin, J.; Fu, A. HOT SAX: Efficiently Finding the Most Unusual Time Series Subsequence. In Proceedings of the IEEE International Conference on Data Mining, Houston, TX, USA, 27–30 November 2005; pp. 226–233. [Google Scholar]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef] [PubMed]
- Bejger, S. Competition in a Wholesale Fuel Market—The Impact of the Structural Changes Caused by COVID-19. Energies 2021, 14, 4211. [Google Scholar] [CrossRef]
- Gharghabi, S.; Ding, Y.; Yeh, C.; Kamgar, K.; Ulanova, L.; Keogh, E. Domain Agnostic Online Semantic Segmentation at Superhuman Performance Levels. In Proceedings of the ICDM 2017, New Orleans, LA, USA, 18–21 November 2017. [Google Scholar]
- Bejger, S. Econometric Tools for Detection of Collusion Equilibrium in the Industry. Dyn. Econ. Model. 2009, 9, 27–38. [Google Scholar] [CrossRef][Green Version]
- Bolotova, Y.; Connor, J.M.; Miller, D.J. The impact of collusion on price behavior: Empirical results from two recent cases. Int. J. Ind. Organ. 2008, 26, 1290–1307. [Google Scholar] [CrossRef]
- Jimenez, J.L.; Perdiguero, L. Could Transport Costs be Lower? The Use of a Variance Screen to Evaluate Competition in the Petrol Market in Spain. Int. J. Transp. Econ. 2011, 38, 265–284. [Google Scholar]
- Bejger, S. Theoretical Model of Pricing Behavior on the Polish Wholesale Fuel Market. Folia Oeconomica Stetin. 2016, 16, 286–300. [Google Scholar] [CrossRef][Green Version]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Breiman, L. Setting Up, Using, and Understanding Random Forests V3.1. 2003. Available online: https://www.stat.berkeley.edu/~breiman/Using_random_forests_V3.1.pdf (accessed on 1 January 2024).
- Vlachos, M.; Gunopoulos, D.; Kollios, G. Discovering Similar Multidimensional Trajectories. In Proceedings of the 18th International Conference on Data Engineering, San Jose, CA, USA, 26 February–1 March 2002; p. 673. [Google Scholar]
- Keogh, E.; Ratanamahatana, C.A. Exact indexing of dynamic time warping. Knowl. Inf. Syst. 2005, 7, 358–386. [Google Scholar] [CrossRef]
- Lin, J.; Keogh, E.; Wei, L.; Lonardi, S. Experiencing SAX: A novel symbolic representation of time series. Data Min. Knowl. Discov. 2007, 15, 107–144. [Google Scholar] [CrossRef]
- Senin, P.; Lin, J.; Wang, X.; Oates, T.; Gandhi, S.; Boedihardjo, A.P.; Chen, C.; Frankenstein, S.; Lerner, M. GrammarViz 2.0: A tool for grammar-based pattern discovery in time series. In Proceedings of the ECML/PKDD Conference 2014, Nancy, France, 14–18 September 2014. [Google Scholar]
- Yeh, C.; Zhu, Y.; Ulanova, L.; Begum, N.; Ding, Y.; Dau, H.; Silva, D.; Mueen, A.; Keogh, E. Matrix Profile I: All Pairs Similarity Joins for Time Series: A Unifying View that Includes Motifs, Discords and Shapelets. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016. [Google Scholar]
- Van Benschoten, A.; Ouyang, A.; Bischoff, F.; Marrs, T. MPA: A novel cross-language API for time series analysis. J. Open Source Softw. 2020, 5, 2179. [Google Scholar] [CrossRef]
- Posner, R.A. Antitrust Law, 2nd ed.; University of Chicago Press: Chicago, IL, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).