A Study on the Effect of Turbulence Intensity on Dual Vertical-Axis Wind Turbine Aerodynamic Performance
Abstract
1. Introduction
2. Numerical Model of Wind Turbines
2.1. Theoretical Equation
2.2. Numerical Model
3. Numerical Methods
3.1. Computational Domain and Boundary Conditions
3.2. Solver Settings
4. Model Validation and Result Analysis
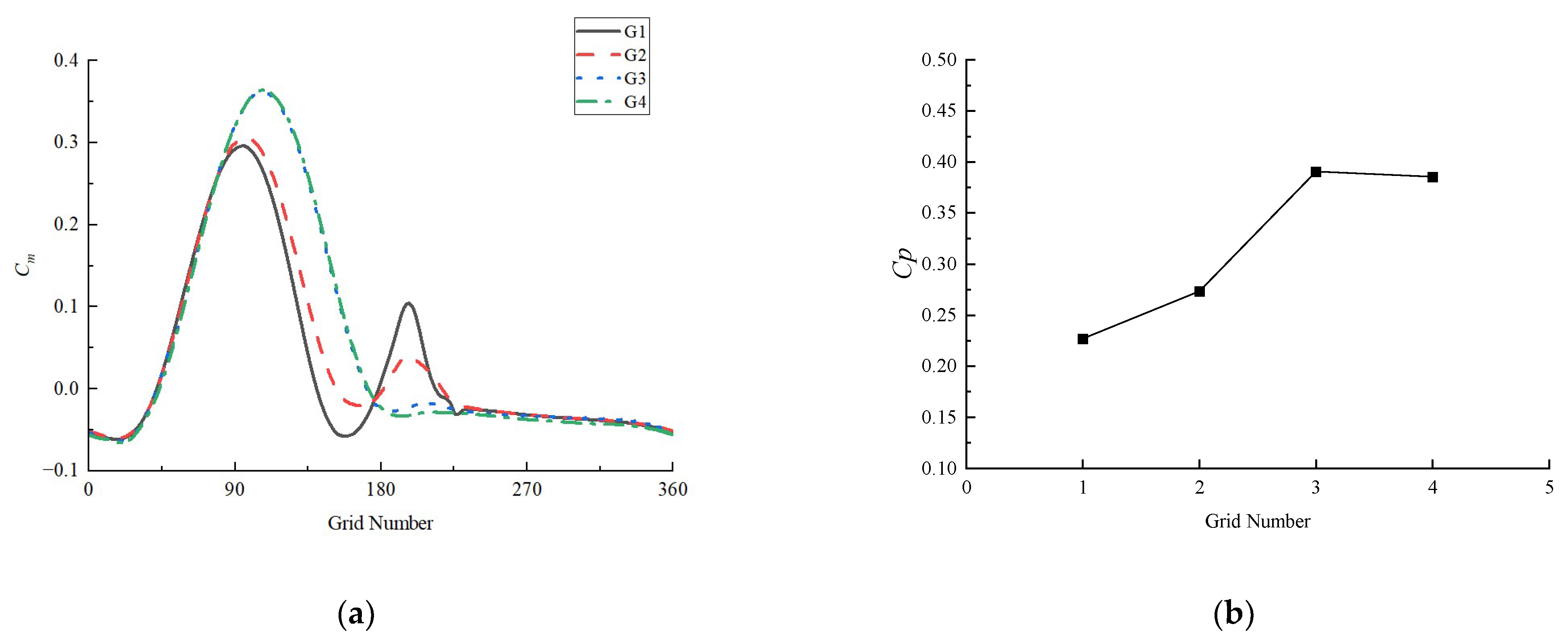
4.1. Grid Independence Study
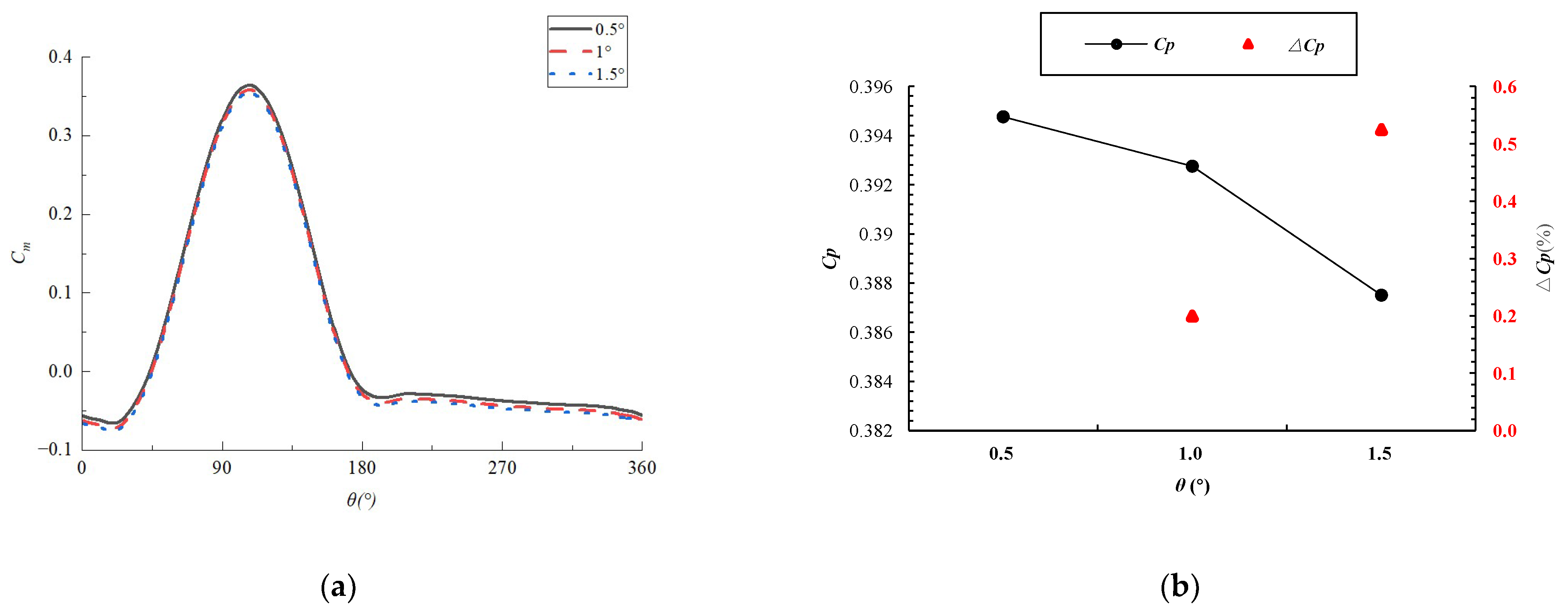
4.2. Time Step Independence Study
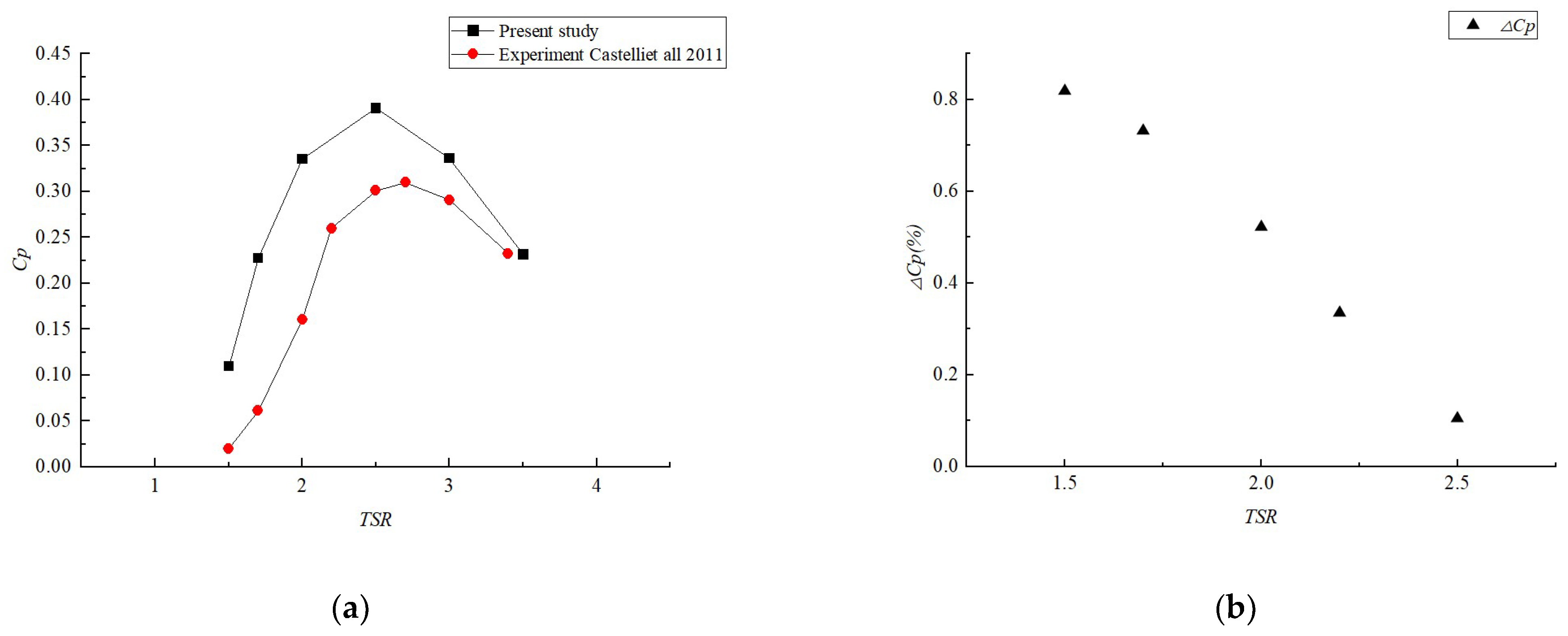
4.3. Model Validation
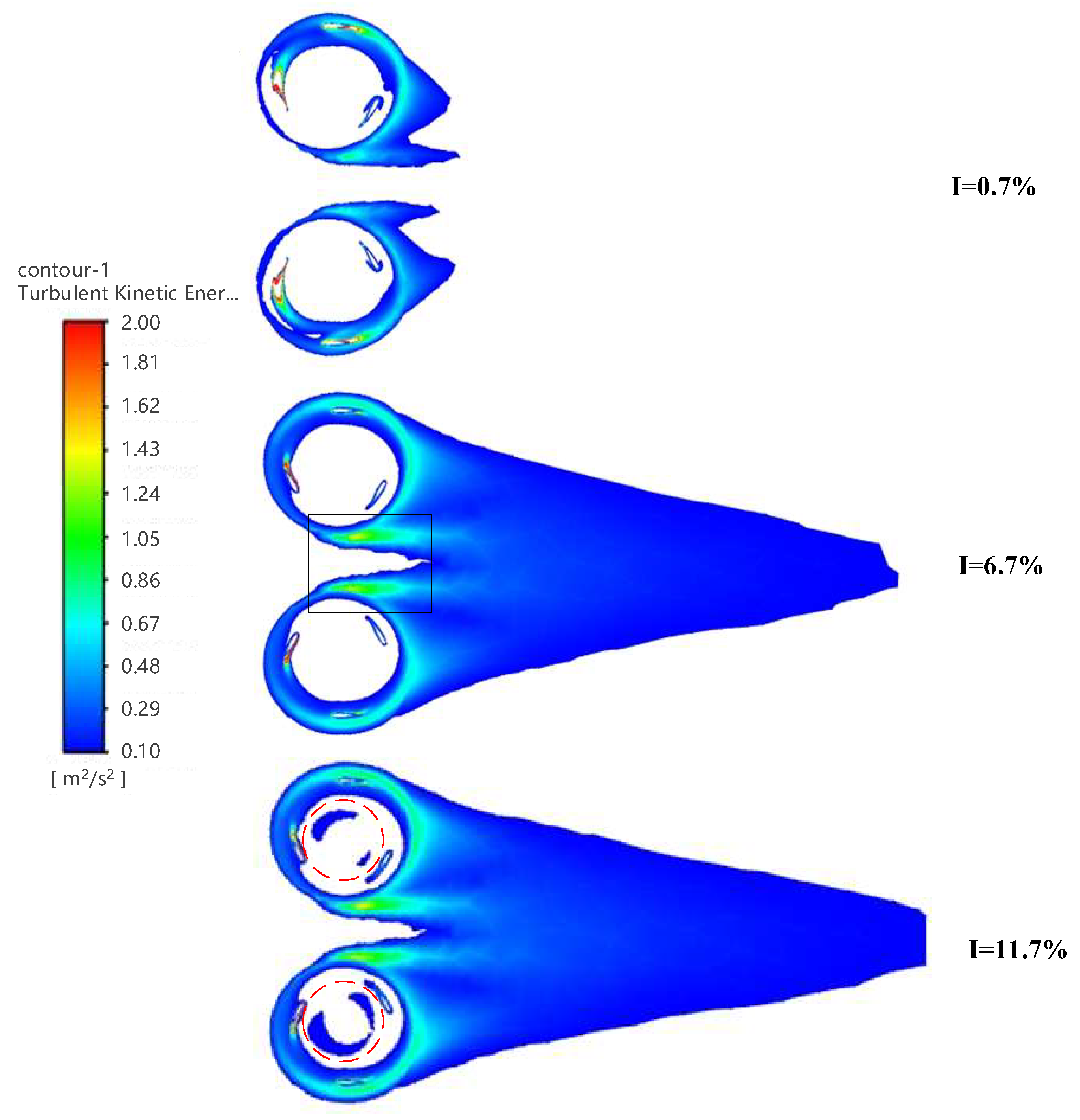
4.4. Effect of Turbulence Intensity
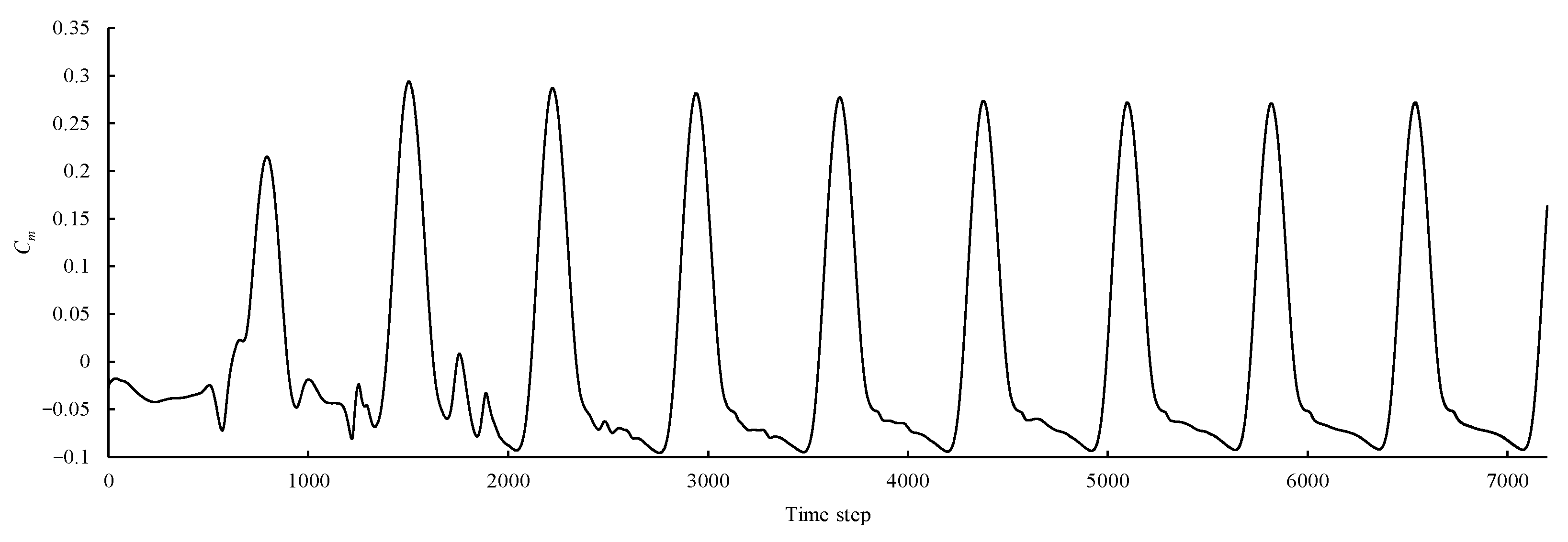
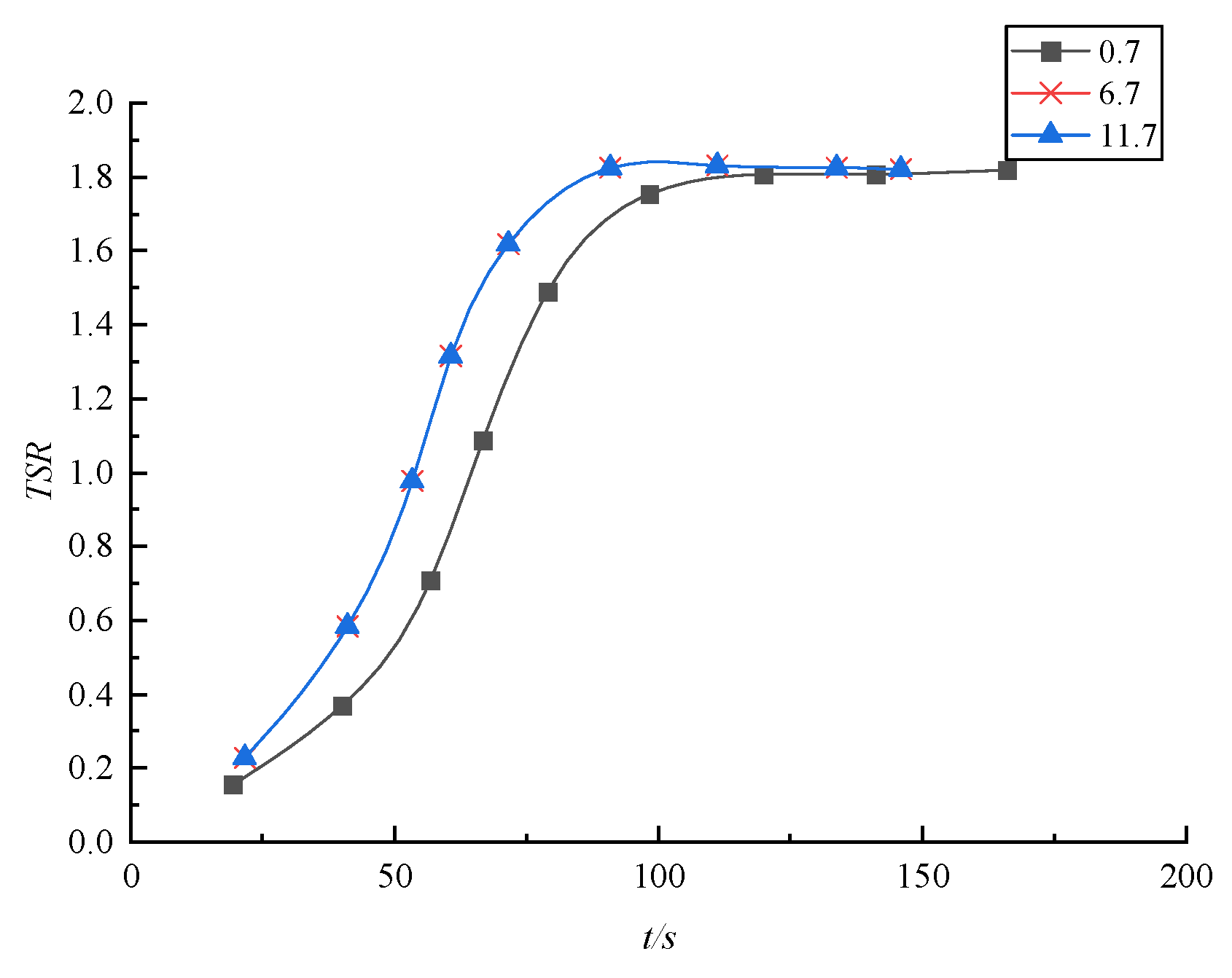
4.4.1. Self-Start Time
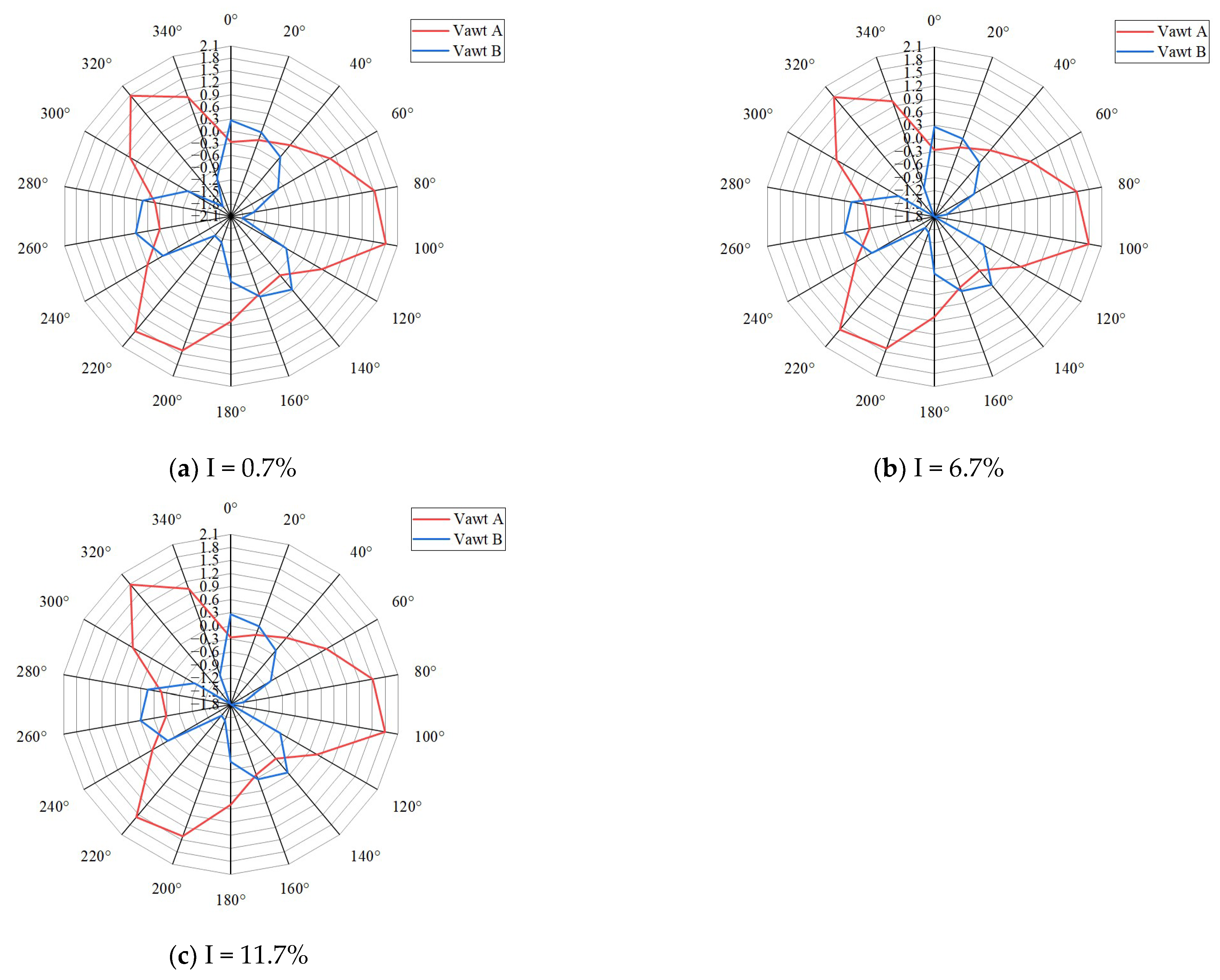
4.4.2. Power (Cp)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tasnim, M.; Rifa, T.I.; Shahriar, T.; Habib, M.A. Wind Energy Deployment in Bangladesh: Investigating Feasible Locations and Their Characteristics. Energy Rep. 2024, 11, 4338–4355. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, W.; Wang, Y.; Wang, H.; Yang, H.; Yao, P.; Zhu, Z. Distribution Characteristics and Assessment of Wind Energy Resources in the Coastal Areas of Guangdong. Sustain. Horizons 2024, 9, 100081. [Google Scholar] [CrossRef]
- Bonthu, S.; Purvaja, R.; Singh, K.S.; Ganguly, D.; Muruganandam, R.; Paul, T.; Ramesh, R. Offshore Wind Energy Potential along the Indian Coast Considering Ecological Safeguards. Ocean Coast. Manag. 2024, 249, 107017. [Google Scholar] [CrossRef]
- Barzegar-Kalashani, M.; Seyedmahmoudian, M.; Mekhilef, S.; Stojcevski, A.; Horan, B. Small-Scale Wind Turbine Control in High-Speed Wind Conditions: A Review. Sustain. Energy Technol. Assessments 2023, 60, 103577. [Google Scholar] [CrossRef]
- Eltayesh, A.; Castellani, F.; Natili, F.; Burlando, M.; Khedr, A. Aerodynamic Upgrades of a Darrieus Vertical Axis Small Wind Turbine. Energy Sustain. Dev. 2023, 73, 126–143. [Google Scholar] [CrossRef]
- Sun, S.; Liu, H.; Peng, H. Power Performance and Self-Starting Features of H-Rotor and Helical Vertical Axis Wind Turbines with Different Airfoils in Turbulence. Energy Convers. Manag. 2023, 292, 117405. [Google Scholar] [CrossRef]
- Molina, A.C.; De Troyer, T.; Massai, T.; Vergaerde, A.; Runacres, M.C.; Bartoli, G. Effect of Turbulence on the Performance of VAWTs: An Experimental Study in Two Different Wind Tunnels. J. Wind. Eng. Ind. Aerodyn. 2019, 193, 103969. [Google Scholar] [CrossRef]
- Abdolahifar, A.; Karimian, S. A Comprehensive Three-Dimensional Study on Darrieus Vertical Axis Wind Turbine with Slotted Blade to Reduce Flow Separation. Energy 2022, 248, 123632. [Google Scholar] [CrossRef]
- Abdalrahman, G.; Melek, W.; Lien, F.S. Pitch Angle Control for a Small-Scale Darrieus Vertical Axis Wind Turbine with Straight Blades (H-Type VAWT). Renew. Energy 2017, 114, 1353–1362. [Google Scholar] [CrossRef]
- Ni, L.; Miao, W.; Li, C.; Liu, Q. Impacts of Gurney Flap and Solidity on the Aerodynamic Performance of Vertical Axis Wind Turbines in Array Configurations. Energy 2020, 215, 118915. [Google Scholar] [CrossRef]
- Hezaveh, S.H.; Bou-Zeid, E.; Dabiri, J.; Kinzel, M.; Cortina, G.; Martinelli, L. Increasing the Power Production of Vertical-Axis Wind-Turbine Farms Using Synergistic Clustering. Bound. -Layer Meteorol. 2018, 169, 275–296. [Google Scholar] [CrossRef]
- Kusuma, Y.F.; Fuadi, A.P.; Al Hakim, B.; Sasmito, C.; Nugroho, A.C.P.T.; Khoirudin, M.H.; Priatno, D.H.; Tjolleng, A.; Wiranto, I.B.; Al Fikri, I.R.; et al. Navigating Challenges on the Path to Net Zero Emissions: A Comprehensive Review of Wind Turbine Technology for Implementation in Indonesia. Results Eng. 2024, 22, 102008. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Li, J.; Huang, H.; Huang, L. Research on Dynamic Characteristics of Vertical Axis Wind Turbine Extended to the Outside of Buildings. Energy 2023, 272, 127182. [Google Scholar] [CrossRef]
- Dabiri, J.O. Potential Order-of-Magnitude Enhancement of Wind Farm Power Density via Counter-Rotating Vertical-Axis Wind Turbine Arrays. J. Renew. Sustain. Energy 2011, 3, 043104. [Google Scholar] [CrossRef]
- Golarcheh, A.; Anbarsooz, M.; Benini, E. An Actuator Line Method for Performance Prediction of HAWTs at Urban Flow Conditions: A Case Study of Rooftop Wind Turbines. Energy 2024, 292, 130268. [Google Scholar] [CrossRef]
- Bianchini, A.; Balduzzi, F.; Bachant, P.; Ferrara, G.; Ferrari, L. Effectiveness of Two-Dimensional CFD Simulations for Darrieus VAWTs: A Combined Numerical and Experimental Assessment. Energy Convers. Manag. 2017, 136, 318–328. [Google Scholar] [CrossRef]
- Fertahi, S.E.-D.; Samaouali, A.; Kadiri, I. CFD Comparison of 2D and 3D Aerodynamics in H-Darrieus Prototype Wake. E-Prime Adv. Electr. Eng. Electron. Energy 2023, 4, 100178. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, L.; Shi, Y.; Zhang, K.; Liu, K.; Wang, S.; Hu, F. Analysis of Urban Turbulence Intensity Observed by Beijing 325-m Tower and Comparison with the IEC Turbulence Model for Small Wind Turbines. J. Wind. Eng. Ind. Aerodyn. 2023, 241, 105511. [Google Scholar] [CrossRef]
- Maalouly, M.; Souaiby, M.; ElCheikh, A.; Issa, J.; Elkhoury, M. Transient analysis of H-type Vertical Axis Wind Turbines using CFD. Energy Rep. 2022, 8, 4570–4588. [Google Scholar] [CrossRef]
- Shen, Z.; Gong, S.; Xie, G.; Lu, H.; Guo, W. Investigation of the Effect of Critical Structural Parameters on the Aerodynamic Performance of the Double Darrieus Vertical Axis Wind Turbine. Energy 2023, 290, 130156. [Google Scholar] [CrossRef]
- Ye, M.; Zhao, Y.; Chen, H.C.; Wan, D. Quantification of Numerical Uncertainties of CFD-Predicted Wind Turbine Performance with Overset Grids. Ocean. Eng. 2024, 298, 117231. [Google Scholar] [CrossRef]
- Shukla, S.; Ramanan, C.; Bora, B.J.; Deo, A.; Alom, N. Numerical analysis of vertical axis wind turbine blades in ANSYS Fluent. Mater. Today Proc. 2022, 59, 1781–1785. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Khedr, A.; Castellani, F. Critical Issues in the Moving Reference Frame CFD Simulation of Small Horizontal Axis Wind Turbines. Energy Convers. Manag. X 2024, 22, 100551. [Google Scholar] [CrossRef]
- Mahato, A.; Singh, R.K.; Barnwal, R.; Rana, S.C. Aerodynamic Characteristics of NACA 0012 vs. NACA 4418 Airfoil for Wind Turbine Applications through CFD Simulation. Mater. Today Proc. 2023, 22, 53–69. [Google Scholar] [CrossRef]
- Castelli, M.R.; Englaro, A.; Benini, E. The Darrieus Wind Turbine: Proposal for a New Performance Prediction Model Based on CFD. Energy 2011, 36, 4919–4934. [Google Scholar] [CrossRef]
- Chegini, S.; Asadbeigi, M.; Ghafoorian, F.; Mehrpooya, M. An Investigation into the Self-Starting of Darrieus-Savonius Hybrid Wind Turbine and Performance Enhancement through Innovative Deflectors: A CFD Approach. Ocean Eng. 2023, 287, 115910. [Google Scholar] [CrossRef]
- Li, L.; Wang, B.; Ge, M.; Huang, Z.; Li, X.; Liu, Y. A Novel Superposition Method for Streamwise Turbulence Intensity of Wind-Turbine Wakes. Energy 2023, 276, 127491. [Google Scholar] [CrossRef]
- Yossri, W.; Ben Ayed, S.; Abdelkefi, A. Evaluation of the Efficiency of Bioinspired Blade Designs for Low-Speed Small-Scale Wind Turbines with the Presence of Inflow Turbulence Effects. Energy 2023, 273, 127210. [Google Scholar] [CrossRef]
- Liu, S.; Li, Q.; Lu, B.; He, J. Analysis of NREL-5MW Wind Turbine Wake under Varied Incoming Turbulence Conditions. Renew. Energy 2024, 224, 120136. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Liu, X.; Sotiropoulos, F.; Yang, X. Turbulence in Waked Wind Turbine Wakes: Similarity and Empirical Formulae. Renew. Energy 2023, 209, 27–41. [Google Scholar] [CrossRef]






| Feature | Value |
|---|---|
| Airfoil | NACA0018 |
| Chord (c) | 0.172 m |
| Number of blades (N) | 3 |
| Rotor diameter (D) | 0.68 m |
| Grid Number | Internal Rotation Domain | External Stationary Domain | Entire Computational Domain |
|---|---|---|---|
| G1 | 59,850 | 35,150 | 95,000 |
| G2 | 108,819 | 65,181 | 174,000 |
| G3 | 289,088 | 170,512 | 459,600 |
| G4 | 837,199 | 493,801 | 1,331,000 |
| Grid Number | Cp | GCI | (%) |
|---|---|---|---|
| G1 | 0.227 | 0.0365 (16.07%) | 8.1 |
| G2 | 0.273 | 0.0924 (33.8%) | 17.14 |
| G3 | 0.389 | 0.0041 (1.05%) | 1.41 |
| G4 | 0.386 | - | - |
| Time Step (s) | Rotation Angle (°) | Number of Time Steps in a Cycle |
|---|---|---|
| 0.000 244 348 | 0.5 | 720 |
| 0.000 305 432 | 1 | 360 |
| 0.000 407 243 | 1.5 | 240 |
| The Time Step Corresponds to the Rotation Angle (°) | Cp | ∆Cp (%) | (%) |
|---|---|---|---|
| 0.5 | 0.394 | 0.2 | 0.989 |
| 1 | 0.392 | 0.525 | 1.647 |
| 1.5 | 0.387 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Cao, Y.; Qian, Z.; Wang, J.; Zhu, Y.; Chen, X.; Zhang, W.; Wang, Y.; Wu, G.; Chen, S. A Study on the Effect of Turbulence Intensity on Dual Vertical-Axis Wind Turbine Aerodynamic Performance. Energies 2024, 17, 4124. https://doi.org/10.3390/en17164124
Yang Y, Cao Y, Qian Z, Wang J, Zhu Y, Chen X, Zhang W, Wang Y, Wu G, Chen S. A Study on the Effect of Turbulence Intensity on Dual Vertical-Axis Wind Turbine Aerodynamic Performance. Energies. 2024; 17(16):4124. https://doi.org/10.3390/en17164124
Chicago/Turabian StyleYang, Yanan, Yang Cao, Zhong Qian, Jian Wang, Yixian Zhu, Xia Chen, Wendong Zhang, Yujie Wang, Guoqing Wu, and Shaohua Chen. 2024. "A Study on the Effect of Turbulence Intensity on Dual Vertical-Axis Wind Turbine Aerodynamic Performance" Energies 17, no. 16: 4124. https://doi.org/10.3390/en17164124
APA StyleYang, Y., Cao, Y., Qian, Z., Wang, J., Zhu, Y., Chen, X., Zhang, W., Wang, Y., Wu, G., & Chen, S. (2024). A Study on the Effect of Turbulence Intensity on Dual Vertical-Axis Wind Turbine Aerodynamic Performance. Energies, 17(16), 4124. https://doi.org/10.3390/en17164124






