The Development of a Malleable Model for Critical System Supervision Integration
Abstract
1. Introduction
2. Theoretical Reference
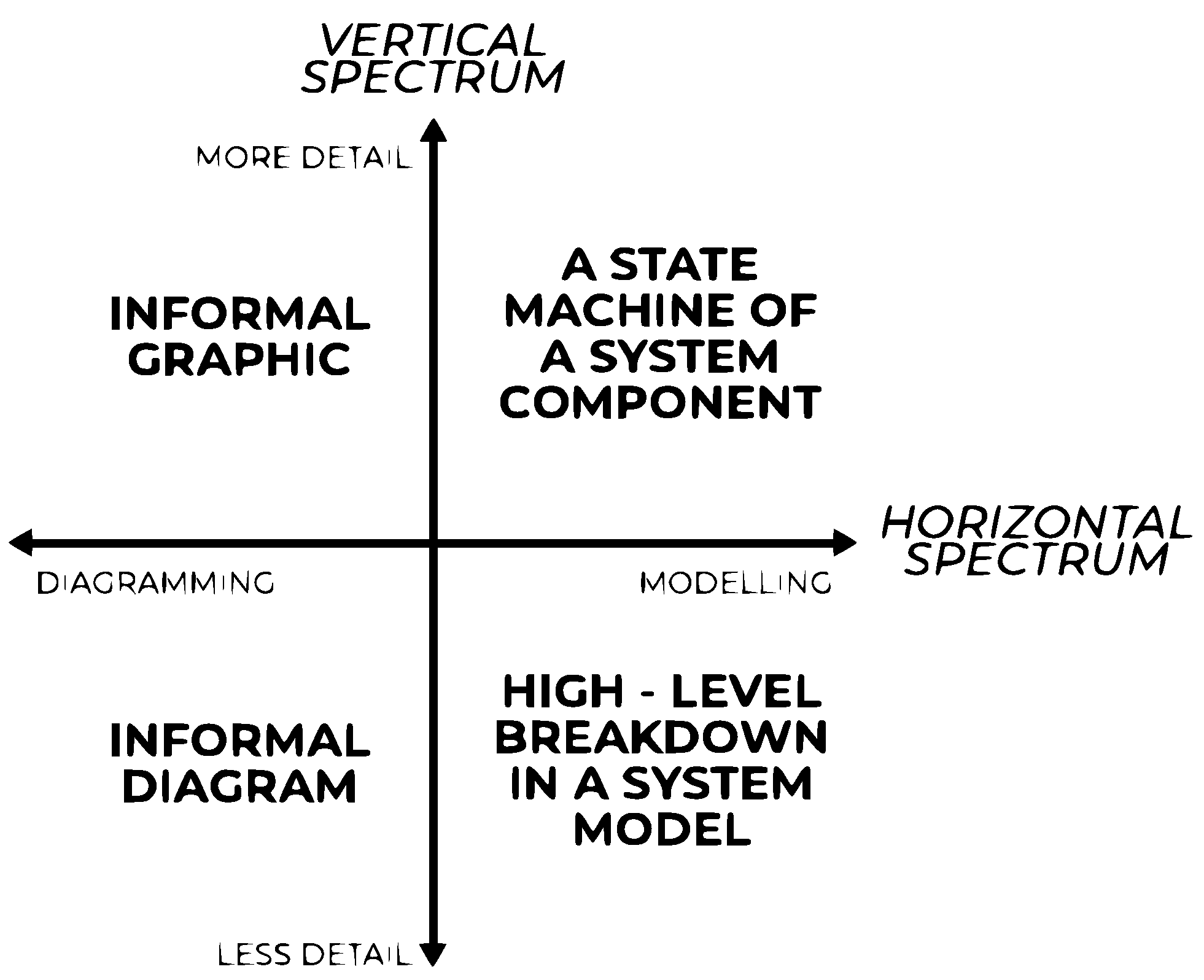
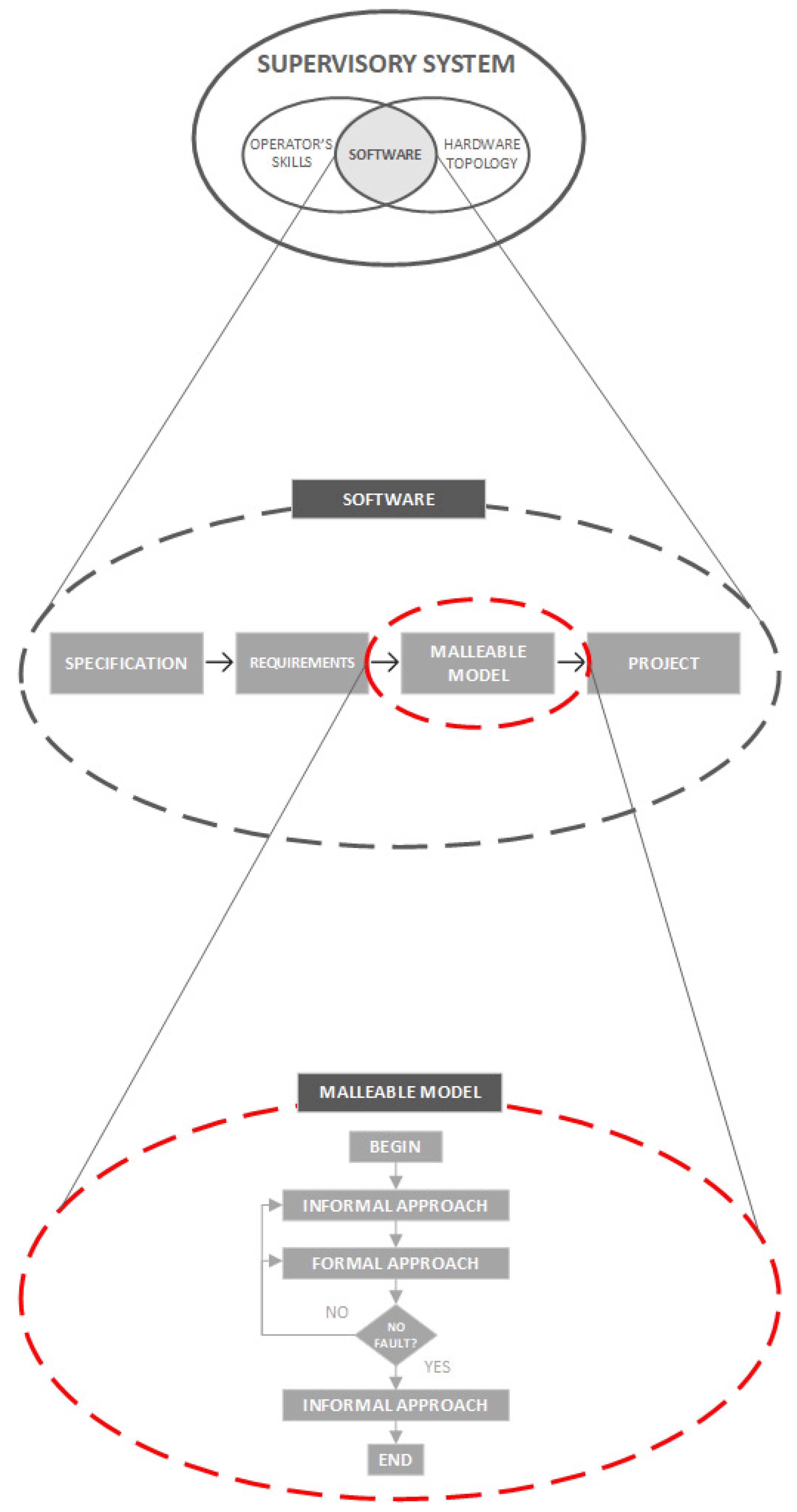
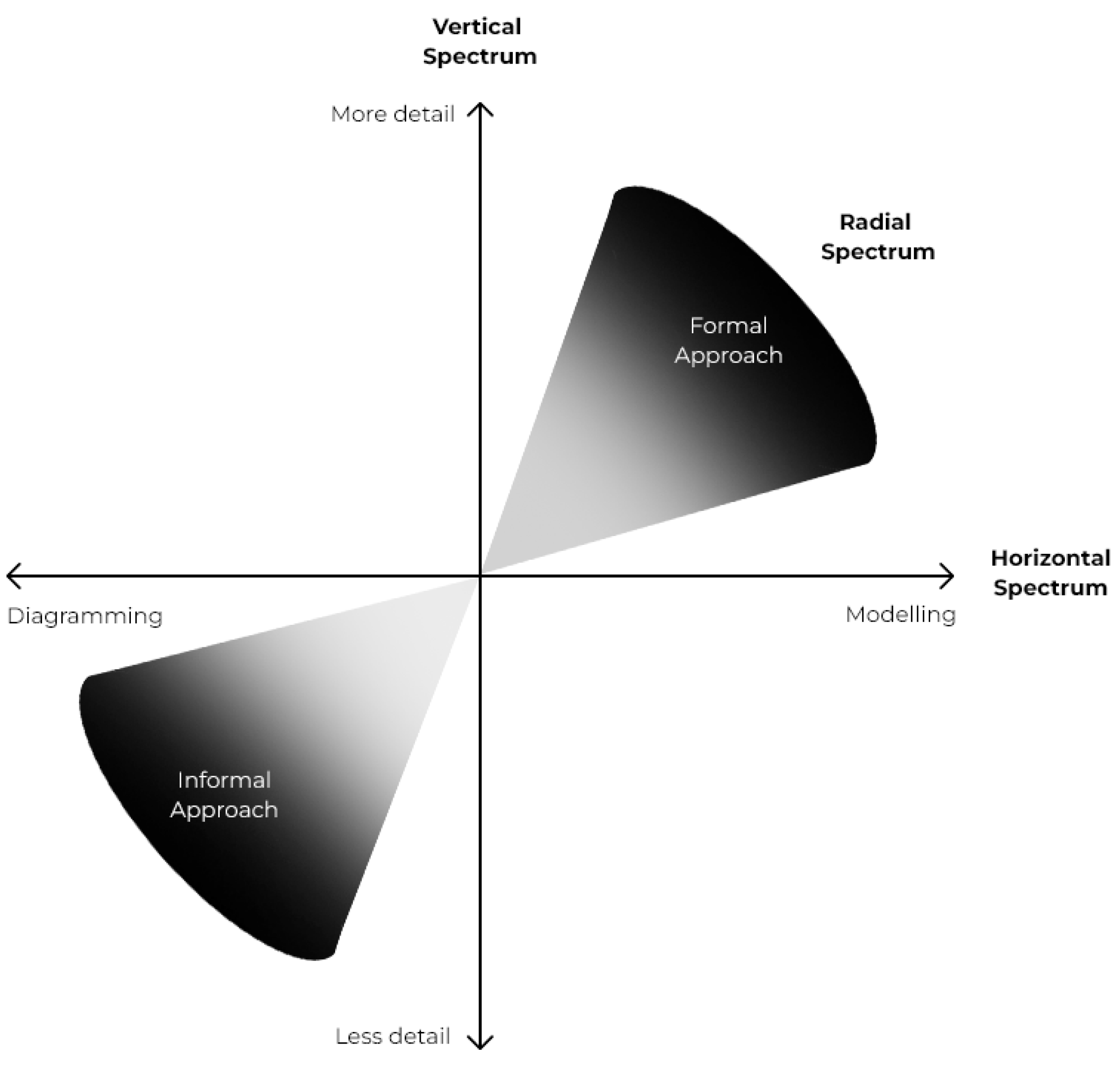
2.1. Malleable Model
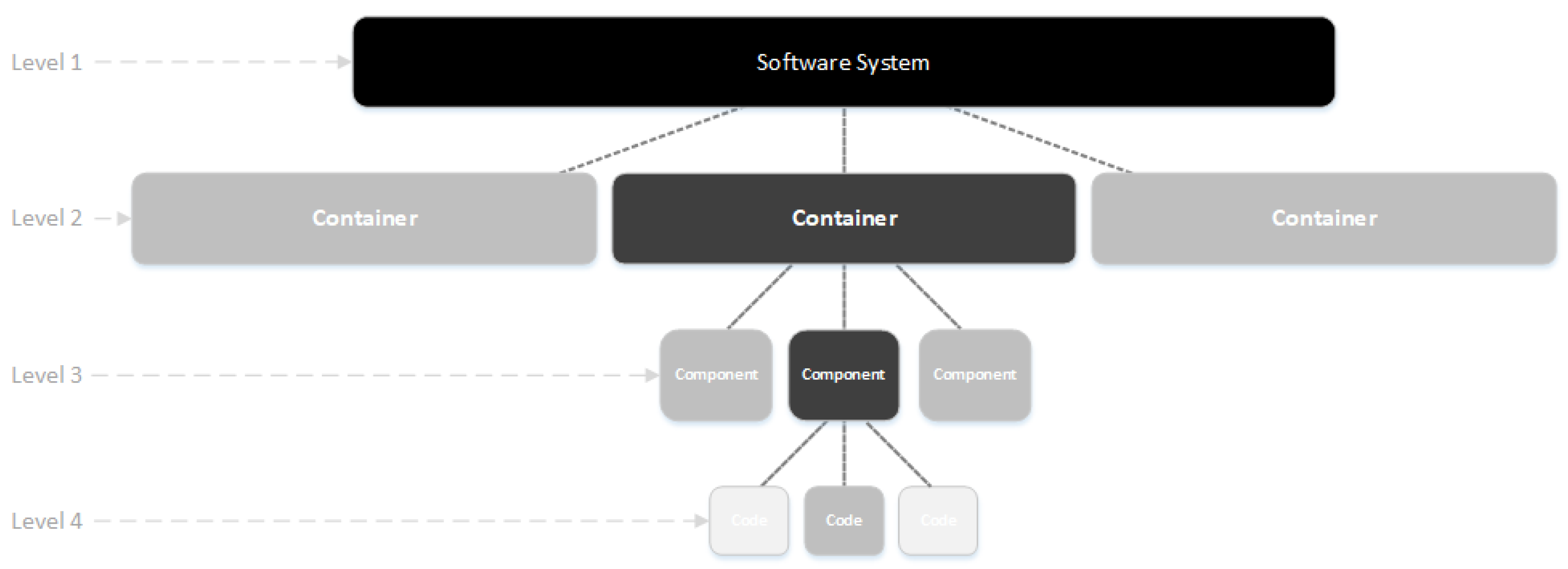
2.1.1. C4 Diagram Informal Approach
- Level 1 (software system context diagram): the highest level, referring to definitions of the key elements of the system under consideration;
- Level 2 (container diagram): the intermediate level, with descriptions of function and relationships among subsystems;
- Level 3 (components diagram): the intermediate level, with abstractions of the components needed for each container;
- Level 4 (code diagram): the lowest level, referring to diagram code described in the previous levels using appropriate language close to that of the actual implementation.
2.1.2. Basic Principles of Hierarchical Colored Petri Nets Formal Approach
- is a finite set of non-empty color sets (types).
- P is the finite set of all places.
- T is the finite set of all transitions.
- A is the finite set of all arcs such that P ∩ T = P ∩ A = T ∩ A = ∅.
- N is the node function such that N: A → P × T ∪ T × P.
- C is the color function such that C: P→.
- G is the guard expression function such that G: T→ Expr (Expr is the set of expressions provided by the CPN’s ML inscription language which specifies declarations and net inscriptions. This language is an extension of the functional programming language Standard ML) and ∀ t ∈T: [ Type(G(t)) (Type(e) is the type of an expression e∈ Expr, i.e., the type of Var(e) (the values obtained when evaluating e)) = Bool ∧ Type(Var(G(t))) ⊆].
- E is the arc expression function such that E: A→ Expr and ∀ a ∈A: [ Type(E(a)) = C(p(a))MS (the subscript MS denotes the multi-set of the associated place) ∧ Type(Var(E(a))) ⊆], where p(a) is the place of N(a).
- I is the initialization function such that I: P→ Expr and ∀ p ∈P: [ Type(I(p)) = C(p)MS].
- = is a non-hierarchical CPN.
- ⊆T is a set of substitution transitions.
- ⊆P is a set of port places.
- :→ is a port type function that assigns a port type to each port place.
- S is a finite set of modules. Each module is a CPN module s = ((, , , ,, , , , ), , , ), and it is necessary that (∪ ) ∩ (∪ ) = ∅ for all , ∈ S such that ≠.
- : →S is a submodule function that assigns a submodule to each substitution transition. It is required that the module hierarchy is acyclic.
- is a port-socket relation function that assigns a port-socket relation ⊆× to each substitution transition t, and it is required that = , = , and 〉 = 〉 for all ∈ and all t∈.
- ⊆ is a set of non-empty fusion sets such that = and 〉 = 〉 for all ∈ and all ∈.
3. Methodology
3.1. Malleable Model Framework
3.1.1. Coding Techniques
3.1.2. Performance Analysis
- Reachability→ This refers to the concept of a specific marking M being classified as reachable in a system, whereby there is a sequence of firing transitions that enables the system to move from the initial marking to the desired marking M. This concept can be formally expressed as M, belonging to the set of reachable markings R(N, ).
- Deadlocks→ They occur in a CPN model when a marking M is considered dead due to the absence of any enabled transition. A CPN model is deemed deadlock-free when every reachable marking within it enables at least one transition.
- Dead transitions→ A transition becomes categorized as inactive when it lacks a reachable marking where the transition can be executed.
- Liveness→ This property pertains to a transition t being classified as live when, given any marking M∈ R(), there is a series of transitions enabled from M including t, to be precise, for all M∈ R(N, ) where there exists M∈ R(N, M): ≤. The concept of liveness serves to guarantee that the CPN model will never experience blocking.
- Boundedness→ A specific location P is deemed k-bounded for a given natural number k if, for every reachable marking, place P does not exceed k tokens at any point, formally expressed as ∀M∈ R(N, ): ≤k. The concept of boundedness plays a crucial role in guaranteeing that the quantity of workpieces in progress remains within a certain limit, consequently contributing to the overall stability of the CPN model.
- Dead markings→ The information pertaining to dead markings provides insight into markings that lack enabled transitions.
4. Case Study
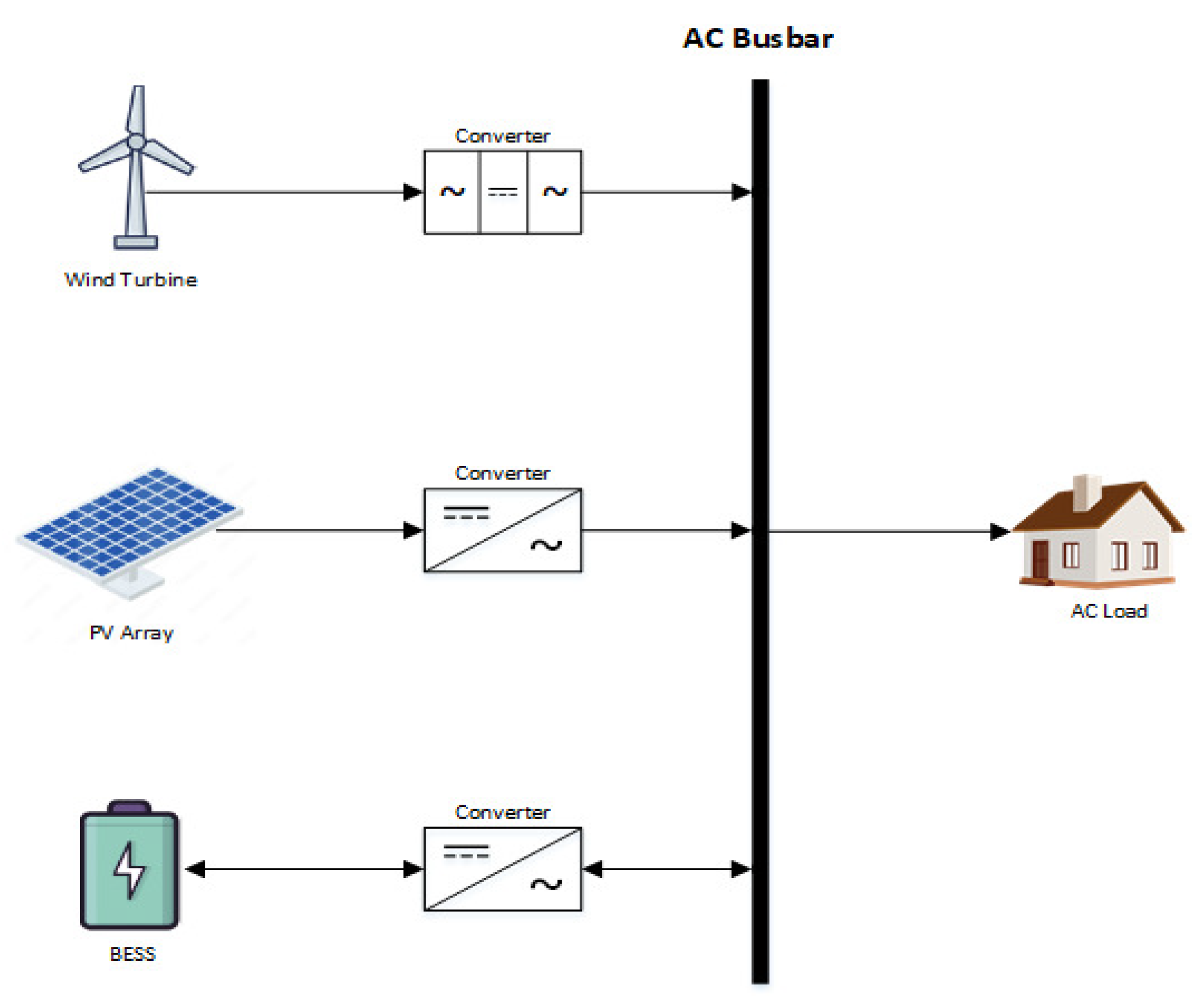
4.1. Eletrobras Chesf Hybrid Power Plant
- Layer 1 (local controllers): HPP assets have local controllers that are responsible for managing the generator unit subsystems in which they are inserted as well as receiving set points from external systems to adjust power generation. This layer also includes the protection relays, which are responsible for ensuring some safety conditions during system operation, acting when short circuits occur.
- Layer 2 (RTU): Each of the local controllers communicates with the RTU, which is responsible for managing asset operation and controlling and supervising the HPP. The RTU is also responsible for receiving orders from Layer 3 and communicating with Layer 1.
- Layer 3 (SCADA system): This has an interface with HPP assets, displaying values of electrical measurements and their operating states. In this layer, acquired data from meteorological stations are available, manual commands are made by the operator, and information from Layer 4 reaches Layer 2 and vice versa.
- Layer 4 (PIMS): This is the system that acquires process data from several sources, stores them in a historical database, and makes them available by means of several representation forms.
- Layer 5 (intelligence software): This is an artificial intelligence (AI)-based algorithm that relies on weather forecasts received from Layer 3 and shared with other layers, as well as time-varying energy pricing (PLD—its acronym in Portuguese), which are used to contribute to decision making regarding energy dispatch. This dispatch is made through performed maneuvers on the plant, such as energy supply made available only by BESS discharge when there is low wind or sun incidence in the region.
4.2. Malleable Model Development
4.2.1. STEP 1 (INFORMAL): Obtaining Part of C4 Diagram
- FR1 (operational vision structure): The SCADA system in its operational view must follow the pattern of three frames with defined dimensions, dividing the screen horizontally. These frames will be named “menu frame”, “main frame”, and “alarm frame”.
- FR2 (overview screen renewable generation system): The SCADA system must have a screen for monitoring the main electrical measurements of the IEDs for each HPP asset.
- FR3 (renewable generation system command screen): The SCADA system must have a screen that allows the operator to issue IED remote controls (for example, open/close, increase/decrease) initiated by operators.
- FR4 (renewable generation system monitoring screen): The system must have a screen for monitoring the main electrical quantities and states from IEDs.
- FR5 (alarm and event processing): The SCADA system must be provided with resources and logic functions to perform the classification, filtering, routing, annunciation, formatting, and archiving of alarm messages and events in general, which occur in the electrical system or in the control system itself.
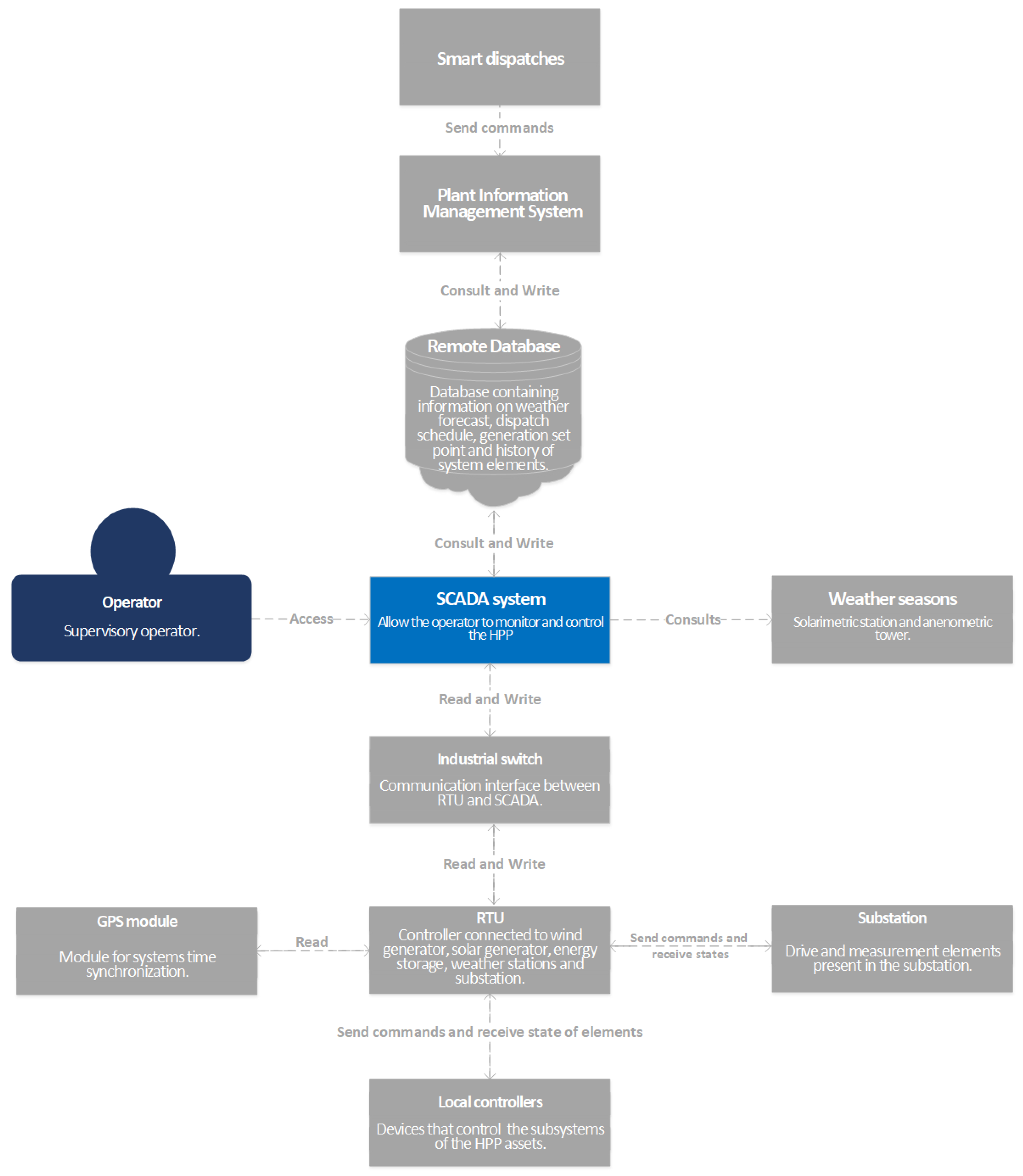
- Remote database: This contains the information history collected by the SCADA system to access the PIMS and smart dispatches. It also contains information about the WF, PV, BESS, weather forecast, proposed local control set point, and load dispatch schedule made by the Operator.
- Weather seasons: They are located in the HPP and connected to the SCADA system, sending information about weather conditions.
- Industrial switch: This refers to the system or equipment that acts as an interface for the communication network between the RTU and SCADA system, providing great capacity in data traffic and robustness to environments with extreme temperature variations. After capturing the information about the asset states, the switch sends it to the SCADA system, which processes data.
- Access control: This container is responsible for verifying the hierarchy level and allowing user access to the supervisory system. It consists of the login screen, which verifies the user’s hierarchy through an algorithm and allows the user to access operation and monitoring screens.
- History screens: This is the container of the set of screens and algorithms containing the screens of the system elements’ state history and the function for generating reports. This system has integration with the local SCADA system database, where such histories are stored.
- Local database: This is the database container, containing the history of the WF elements, PV, weather stations, BESS, and alarms. This information is collected from the operator’s actions on the SCADA system through queries to the remote database and RTU information.
- Supervision and control screens: This is the container of the set of screens, objects, and algorithms, which allows for the supervision and control of the elements contained in the SCADA system.
4.2.2. STEP 2 (FORMAL): Building HCPN Model
Components and Causal Relationships
- IED in operation: Event “PV PR in Ready”.
- IED communication fail: Event “PV PR Communication Fail”.
- IED energized: Event “PV PR Energized”.
Global Model
Generalization
4.2.3. STEP 3 (INFORMAL): Inserting the Global Model and Deploying the Proposed Code Diagrams as an Application Programming Interface
- Case 1 (OPENED): There is no fault and Energized IED (“Data.IEDEnergized”) equals 1; IED Communication (“Data.IEDCommunication”) equals 1; Ready IED (“Data.IEDReady”) equals 1; and 1 breaker opening supervision (“Data.BR2.Status”) equals 0.
- Case 2 (NOT OPENED): There is no fault and Energized IED (“Data.IEDEnergized”) equals 1; IED Communication (“Data.IEDCommunication”) equals 1; Ready IED (“Data.IEDReady”) equals 1; and 1 breaker opening supervision (“Data.BR2.Status”) equals 1.
- Case 3 (FAULT): There is at least a fault; that is, the other possible conditions beyond these ones presented to Cases 1 (OPENED) and 2 (NOT OPENED), whose whole pre-conditions to accomplish 1 breaker opening supervision with functional correctness are not met.
4.3. Modeling Results
4.3.1. Validation
- PV IED state turned on;
- Need to perform 1 breaker opening supervision with functional correctness.
- Start 1 breaker opening supervision;
- Analyze PV IED state information;
- Execute 1 breaker opening supervision reliably.
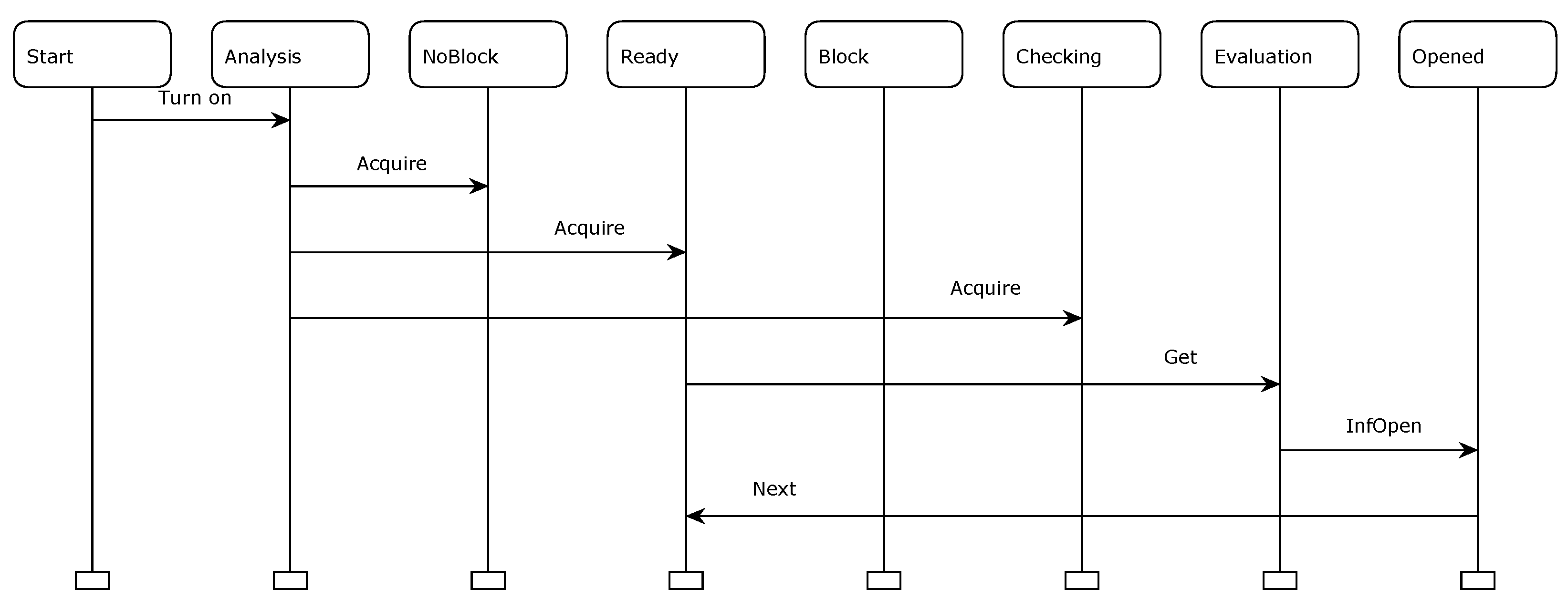
- Report generated: Sat May 11 21:08:23 2024
- 1 0 Turn_on @ (1:Initiating)
- - b = br(2)
- - c = false
- 2 0 Acquire @ (1:Initiating)
- - c = false
- - b = br(2)
- 3 0 Get @ (1:Evaluating)
- - c = false
- - b = br(2)
- - h = false
- 4 0 InfOpen @ (1:Evaluating)
- - h = false
- - c = false
- - b = br(2)
- 5 0 Next @ (1:Evaluating)
- - h = false
- - c = false
- - b = br(2)
- Report generated: Sat May 11 21:09:57 2024
- 1 0 Turn_on @ (1:Initiating)
- - b = br(2)
- - c = false
- 2 0 Acquire @ (1:Initiating)
- - c = false
- - b = br(2)
- 3 0 Get @ (1:Evaluating)
- - c = false
- - b = br(2)
- - h = true
- 4 0 InfNOpen @ (1:Evaluating)
- - h = true
- - c = false
- - b = br(2)
4.3.2. Checking
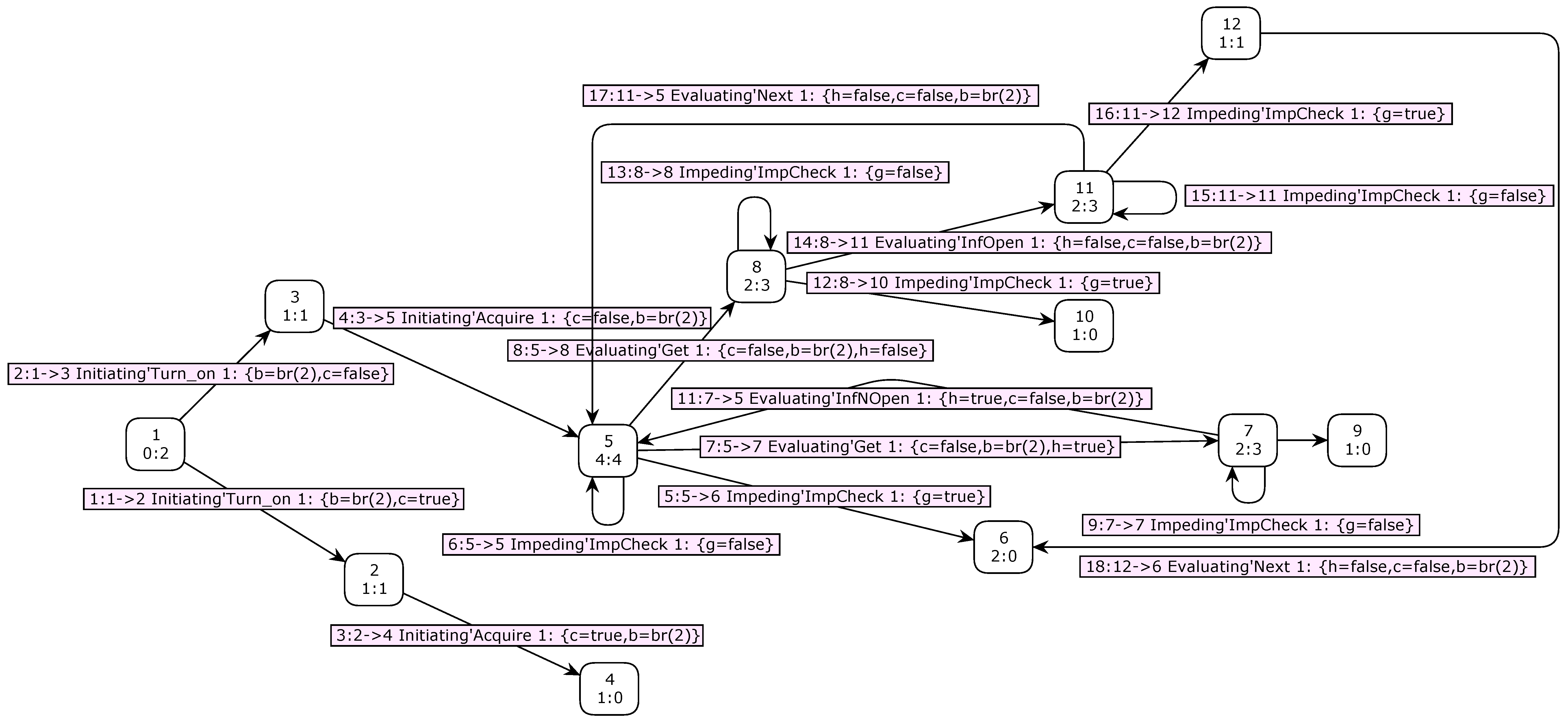
- Query 1:
- Reachable (11,5)
- Answer 1:
- val it = true: bool
- Query 1 and its corresponding response indicate marking 5 can be reached from marking 11.
- Query 2:
- AllReachable ()
- Answer 2:
- val it = false: bool
- Query 2 and its corresponding response indicate not all markings are reachable one from the other.
5. Discussion
- Construct and examine occurrence graphs through the utilization of computational tools and also use techniques to reduce occurrence graphs while preserving a significant amount of information;
- Employ a hierarchical approach to enhance system management efficiency and avoid unnecessary states.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Full State-Space Analysis Report
1 Breaker Opening Supervision Model
| Statistics | ||
| State Space | ||
| Nodes: 12 | ||
| Arcs: 18 | ||
| Secs: 0 | ||
| Status: Full | ||
| Scc Graph | ||
| Nodes: 9 | ||
| Arcs: 9 | ||
| Secs: 0 | ||
| Boundedness Properties | ||
| Best Integer Bounds | ||
| Upper | Lower | |
| Evaluating’Evaluation 1 | 1 | 0 |
| Evaluating’NoBlock 1 | 1 | 0 |
| Evaluating’Opened 1 | 1 | 0 |
| Evaluating’Ready 1 | 1 | 0 |
| Impeding’Block 1 | 1 | 0 |
| Impeding’Checking 1 | 1 | 0 |
| Impeding’NoBlock 1 | 1 | 0 |
| Initiating’Analysis 1 | 1 | 0 |
| Initiating’Block 1 | 1 | 0 |
| Initiating’Checking 1 | 1 | 0 |
| Initiating’NoBlock 1 | 1 | 0 |
| Initiating’Ready 1 | 1 | 0 |
| Initiating’Start 1 | 1 | 0 |
| Best Upper Multi-set Bounds | ||
| Evaluating’Evaluation 1 1‘(br(2),false,false)++ 1‘(br(2),false,true) | ||
| Evaluating’NoBlock 1 1‘a | ||
| Evaluating’Opened 1 1‘(br(2),false,false) | ||
| Evaluating’Ready 1 1‘(br(2),false) | ||
| Impeding’Block 1 1‘a | ||
| Impeding’Checking 1 1‘a | ||
| Impeding’NoBlock 1 1‘a | ||
| Initiating’Analysis 1 1‘(br(2),false)++ 1‘(br(2),true) | ||
| Initiating’Block 1 1‘a | ||
| Initiating’Checking 1 1‘a | ||
| Initiating’NoBlock 1 1‘a | ||
| Initiating’Ready 1 1‘(br(2),false) | ||
| Initiating’Start 1 1‘a | ||
| Best Lower Multi-set Bounds | ||
| Evaluating’Evaluation 1 empty | ||
| Evaluating’NoBlock 1 empty | ||
| Evaluating’Opened 1 empty | ||
| Evaluating’Ready 1 empty | ||
| Impeding’Block 1 empty | ||
| Impeding’Checking 1 empty | ||
| Impeding’NoBlock 1 empty | ||
| Initiating’Analysis 1 empty | ||
| Initiating’Block 1 empty | ||
| Initiating’Checking 1 empty | ||
| Initiating’NoBlock 1 empty | ||
| Initiating’Ready 1 empty | ||
| Initiating’Start 1 empty | ||
| Home Properties | ||
| Home Markings | ||
| None | ||
| Liveness Properties | ||
| Dead Markings | ||
| [4,6,9,10] | ||
| Dead Transition Instances | ||
| None | ||
| Live Transition Instances | ||
| None | ||
| Fairness Properties | ||
| Impartial Transition Instances | ||
| None | ||
| Fair Transition Instances | ||
| Initiating’Acquire 1 | ||
| Initiating’Turn_on 1 | ||
| Just Transition Instances | ||
| None | ||
| Transition Instances with No Fairness | ||
| Evaluating’Get 1 | ||
| Evaluating’InfNOpen 1 | ||
| Evaluating’InfOpen 1 | ||
| Evaluating’Next 1 | ||
| Impeding’ImpCheck 1 | ||
References
- Huang, J.; Meng, T.; Deng, Y.; Huang, F. Catching Critical Transition in Engineered Systems. Math. Probl. Eng. 2021, 2021, 5589429. [Google Scholar] [CrossRef]
- Zielinski, O.; Nicklas, D.; Colonius, H.; Siegel, M.; Hahn, A.; Meike, J.; Köster, F.; Lemmer, K. Interdisciplinary Research Center on Critical Systems Engineering for Socio-Technical Systems; Progress Report (Unpublished); German Aerospace Center: Braunschweig, Germany, 2015; pp. 1–59. [Google Scholar]
- SCIENCE—Complex Systems and Networks. Science 2009, 325, 357–504. Available online: https://www.sciencemag.org/content/325/5939.toc (accessed on 14 August 2024).
- Federal Energy Regulatory Comission (FERC); North American Electric Reliability Corporation (NERC); Regional Entities (Midwest Reliability Organization, Northeast Power Coordinating Council, Reliability First Corporation, SERC Corporation, Texas Reliability Entity and Western Electricity Coordinating Council). FERC, NERC and Regional Entity Staff Report. The February 2021 Cold Weather Outages in Texas and the South Central United States. 2021. Available online: https://www.ferc.gov/media/february-2021-cold-weather-outages-texas-and-south-central-united-states-ferc-nerc-and (accessed on 14 August 2024).
- Board, N.T.S. Pipeline Accident Report; NTSB/PAR-12/01 PB2012-916501; N. T. S. Board: Washington, DC, USA, 2010. [Google Scholar]
- Cherifi, T.; Hamami, L. A Practical Implementation of Unconditional Security for the IEC 60780-5-101 SCADA Protocol. Int. J. Crit. Infrastruct. Prot. 2018, 20, 68–84. [Google Scholar] [CrossRef]
- Nasr, P.M. Toward Modeling Alarm Handling in SCADA System: A Colored Petri Nets Approach. IEEE Trans. Power Syst. 2019, 34, 4525–4532. [Google Scholar] [CrossRef]
- Salehi, F.; Keypour, R.; Lee, W. Reliability Assessment of Automated Substation and Functional Integration. In Proceedings of the 2016 IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016; pp. 1–7. [Google Scholar]
- Taj, S.J.; Rizwan, S.M. Reliability Modeling and Analysis of Complex industrial systems—A Review. Manag. J. Math. 2019, 8, 43–60. [Google Scholar]
- Mamdikar, M.R.; Kumar, V.; Bharti, S.; Singh, P. Reliability Analysis of Safety-Critical Systems Using Optimized Petri Nets. Prog. Nucl. Energy 2023, 164, 104841. [Google Scholar] [CrossRef]
- Jongeling, R.; Ciccozzi, F. Towards Supporting Malleable Architecture Models. In Proceedings of the 2023 IEEE 20th International Conference on Software Architecture Companion (ICSA-C), L’Aquila, Italy, 13–17 March 2023; pp. 272–275. [Google Scholar]
- Lamsweerde, A.V. Requirements Engineering: From System Goals to UML Models to Software; John Wiley & Sons: Chichester, UK, 2009. [Google Scholar]
- Stevens, P.; Pooley, R. Using UML: Software Engineering with Objects and Components, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2006. [Google Scholar]
- Brown, S. The C4 Diagram for Software Architecture. 2018. Available online: http://c4model.com/ (accessed on 14 August 2024).
- Brown, S. Documentation C4 Diagram to Software Architecture. Available online: https://www.infoq.com/br/articles/C4-architecture-model/ (accessed on 14 August 2024). (In Portuguese).
- Jensen, K. Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use, Volume 1, 2nd ed.; The American Mathematical Monthly: New York, NY, USA, 1997. [Google Scholar]
- Jensen, K. Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use, Volume 2, 2nd ed.; The American Mathematical Monthly: New York, NY, USA, 1997. [Google Scholar]
- Ullman, J.D. Elements of ML Programming, ML 97 Edition, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1998. [Google Scholar]
- An, Y.; Wu, N.; Zhao, X.; Li, X.; Chein, P. Hierarchical Colored Petri Nets for modeling and Analysis of Transit Signal Priority Control Systems. Appl. Sci. 2018, 8, 141. [Google Scholar] [CrossRef]
- Jensen, K.; Christensen, S.; Kristensen, L. CPN Tools State Space Manual, University of Aarhus; Department of Computer Science, University of Aarhus: Aarhus, Denmark, 2006. [Google Scholar]
- Christensen, S.; Mortensen, K. Design/CPN ASK-CTL Manual Version 0.9; Department of Computer Science, University of Aarhus: Aarhus, Denmark, 1996. [Google Scholar]
- Lopez, R.; Moore, A.; Gillerman, J. A Model-Driven Approach to Smart Substation Automation and Integration for Comision Federal de Electricidad. In Proceedings of the IEEE PES T&D 2010, New Orleans, LA, USA, 19–22 April 2010; pp. 1–8. [Google Scholar]
- Neis, P.; Wehrmeister, A.A.; Mendes, M.F.; Pesente, J.R. Applying a Model-Driven Approach to the Development of Power Plant SCADA/EMS Software. Int. J. Electr. Power Energy Syst. 2023, 153, 109336. [Google Scholar] [CrossRef]
- Yang, C.W.; Vyatkin, V.; Pang, C. Service-Oriented Extension of IEC 61850 for Model-Driven Smart Grid Automation Design. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society (IECON), Beijing, China, 29 October–1 November 2017; pp. 5489–5496. [Google Scholar]
- Zhou, N.; Li, D.; Vyatkin, V.; Dubinin, V.; Liu, C. Toward Dependable Model-Driven Design of Low-Level Industrial Automation Control Systems. IEEE Trans. Autom. Sci. Eng. 2022, 19, 425–440. [Google Scholar] [CrossRef]
- Lisboa, L.A.C.; Lima, A.M.N.; Silva, L.D. Using Hierarchical Coloured Petri Net to Support Substation Restoration. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–9. [Google Scholar]
- Liang, X.; Hou, Y.; Zhao, M. Modeling and Analysis of Microgrid Energy Scheduling Based on Colored Petri Net. In Proceedings of the 2022 IEEE International Conference on Networking, Sensing and Control (ICNSC), Shanghai, China, 15–18 December 2022; pp. 1–6. [Google Scholar]
- Liu, X.; Zhao, M.; Wei, Z.; Lu, M. The Energy Management and Economic Optimization Scheduling of Microgrid based on Colored Petri Net and Quantum-PSO Algorithm. Sustain. Energy Technol. Assess. 2022, 53, 102670. [Google Scholar] [CrossRef]
- Clarke, E.; Grumberg, O.; Jha, S.; Lu, Y.; Veith, H. Progress on the State Explosion Problem in Model Checking. In Informatics: 10 Years Back, 10 Years Ahead; Springer: Berlin/Heidelberg, Germany, 2001; pp. 176–194. [Google Scholar]
- Valmari, A. The State Explosion Problem. In Proceedings of the Advanced Course on Petri Nets, Dagstuhl Castle, Germany, 7–18 October 1996; pp. 429–528. [Google Scholar]












| Declarations for 1 Breaker Opening Supervision | |||
|---|---|---|---|
| Name | Type | Definition | Meaning |
| iedboot | val | 20 | Estimated time in seconds to the IED boot |
| tmr | val | 1 | Timer value in seconds |
| n | val | 2 | Value used to define breaker 2 |
| IB | Colset | int with 1..iedboot | Integer data from 1 to iedboot |
| A | Colset | with a | Logical data |
| BOOL | Colset | bool | Boolean data |
| BR | Colset | index br with 2..n | Data to define breakers |
| BRxBOOL | Colset | product BR*BOOL 1 | Product data BRxBOOL |
| BRxBOOLxBOOL | Colset | product BR*BOOL*BOOL | Product data BRxBOOLxBOOL |
| INT | Colset | int | Integer data |
| TIMER | Colset | int with 1..tmr | Integer data from 1 to tmr |
| c, g, h | var | BOOL | Boolean variables |
| ib | var | IB | IB variable |
| t | var | TIMER | TIMER variable |
| b | var | BR | BR variable |
| Page Initiating for 1 Breaker Opening Supervision | ||
|---|---|---|
| Element | Type | Meaning |
| Start | Place | A token a in this place indicates the 1 breaker opening supervision needs to be started. |
| Analysis | Place | According to the information that “authorizes” starting 1 breaker opening supervision, there is a token in this place if the supervision must be started or a token if the supervision must not be started. |
| NoBlock | Place | A token a in this place means there is no block pre-condition to the 1 breaker opening supervision. |
| Ready | Place | A token in this place means the 1 breaker opening supervision is ready to start. |
| Block | Place | A token a in this place means the 1 breaker opening supervision is blocked and supervision cannot be achieved due to reliability criteria of the proposed code approach. |
| Checking | Place | A token a in this place means some posterior checking needs to be conducted from this point. |
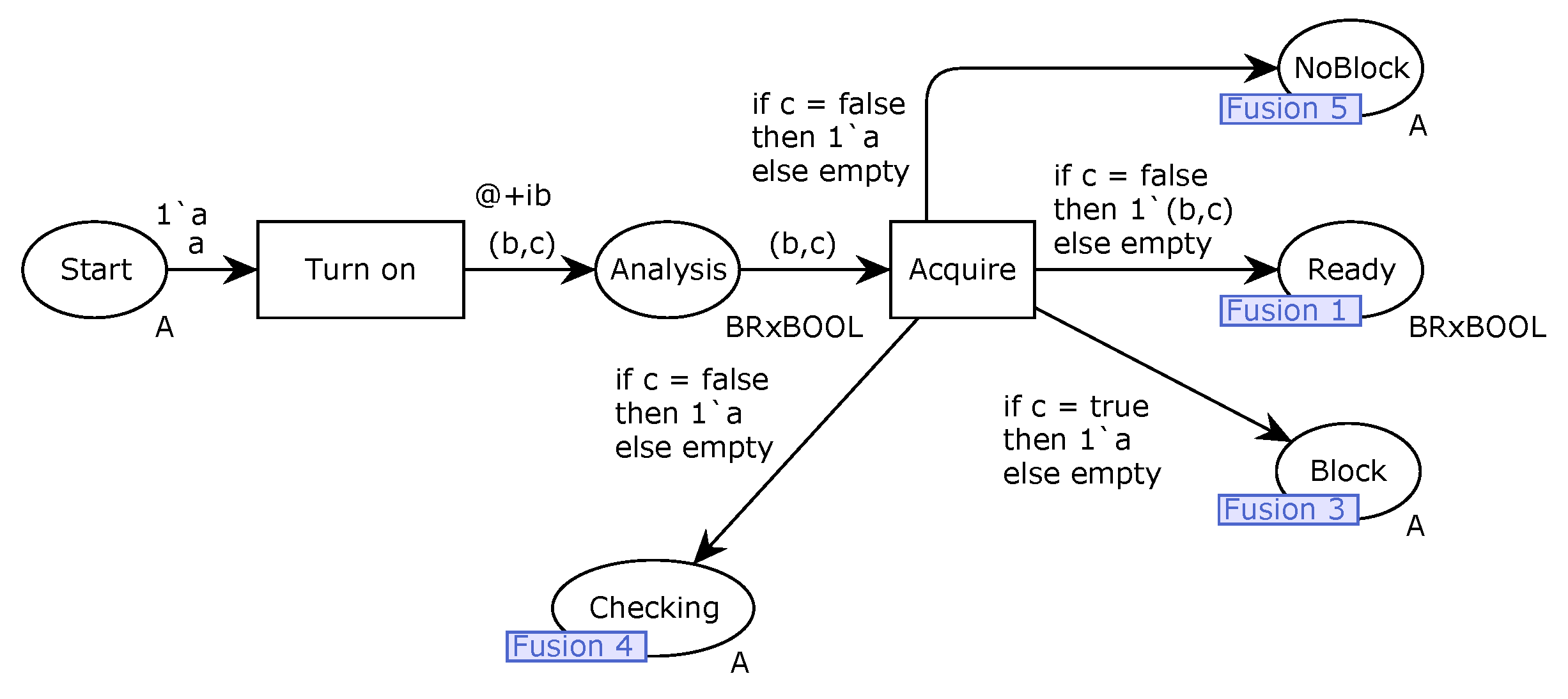
| Turn on | Transition | A token a in place Start enables this transition. When this transition fires, after a timer , if the 1 breaker opening supervision must be started, the value is returned from the HPP. Otherwise, information is returned from the HPP. The Boolean logical function associated with this transition, , is described by , where is the Boolean logical function associated with the pre-condition “Analysis” of the PV IED status. |
| Acquire | Transition | This transition evaluates the obtained information about the “authorization” to start the 1 breaker opening supervision. This information is needed to start the execution in a reliable way. The location Analysis enables this transition. If the supervision must be started, a token is in the location Analysis. In this condition, when this transition fires, a token is added to the location Ready. Moreover, a token a is added to the location NoBlock and a token a is added to the location Checking, indicating that there is no block pre-condition to the supervision and some posterior checking needs to be conducted from this point. On the other hand, if the supervision must not be started, a token is in the location Analysis. In this condition, when this transition fires, a token a is added to the location Block, indicating a block of the supervision, and supervision cannot be achieved due to the reliability criteria of the proposed code approach. |
| Page Evaluating for 1 Breaker Opening Supervision | ||
|---|---|---|
| Element | Type | Meaning |
| Ready | Place | See Table 2. |
| Evaluation | Place | This transition evaluates 1 breaker status. When the transition Get fires, there is a token in this location if the breaker is opened or a token if the breaker is not opened. |
| NoBlock | Place | See Table 2. |
| Opened | Place | After transition InfOpen to fire, there is a token in this location if the breaker is opened. |
| Get | Transition | A token in the location Ready enables this transition, indicating the 1 breaker opening supervision is ready to start. When this transition fires, if the breaker is opened, the value is returned from the HPP. Otherwise, the value is returned from the HPP. The Boolean logical function associated with this transition, , is described by , where is the Boolean logical function associated with the pre-condition breaker status. |
| InfNOpen | Transition | A token in the location Evaluation enables this transition. When this transition fires, a token is removed from the location Evaluation, and a token is added to the location Ready. |
| InfOpen | Transition | A token in the location Evaluation enables this transition. When this transition fires, a token is removed from the location Evaluation, and a token is added to the location Opened. |
| Next | Transition | A token in the location Opened enables this transition. When this transition fires, a token is removed from the location Opened, a token is added to the location Ready, and a breaker opening supervision alarm is generated. |
| Page Impeding for 1 Breaker | ||
|---|---|---|
| Element | Type | Meaning |
| Checking | Place | See Table 2. |
| NoBlock | Place | See Table 2. |
| Block | Place | See Table 2. |
| ImpCheck | Transition | This transition evaluates whether there is a condition that impedes 1 breaker opening supervision. A token a in the location Checking and a token a in the location NoBlock enable this transition. When this transition fires, after a timer t, if there is a condition that impedes 1 breaker opening supervision, the value is returned from the HPP. Then, a token a is removed from place Checking, a token a is removed from NoBlock, and a token a is added to the place Block, indicating a block of the 1 breaker opening supervision. On the other hand, if there is no condition that impedes 1 breaker opening supervision, the value is returned from the HPP. Thus, a token a is removed from the location Checking, and a token a is added to the location Checking, enabling transition ImpCheck. The Boolean logical function associated with this transition, , is described by , where is the Boolean logical function associated with the pre-condition breaker impeding. |
| Declarations for 4 Breakers Opening Supervisions | |||
|---|---|---|---|
| Name | Type | Definition | Meaning |
| n | val | 4 | Value used to define breakers 1, 2, 3, and 4 |
| BR | Colset | index br with 1..n | Data to define breakers |
| Conditions of Case 1 (OPENED) | ||
|---|---|---|
| Pre-Conditions | Variables | Values |
| Energized IED | Data.IEDEnergized | 1 |
| IED Communication | Data.IEDCommunication | 1 |
| Ready IED | Data.IEDReady | 1 |
| Breaker 2 | Data.BR2.Status | 0 |
| Conditions of Case 2 (NOT OPENED) | ||
|---|---|---|
| Pre-Conditions | Variables | Values |
| Energized IED | Data.IEDEnergized | 1 |
| IED Communication | Data.IEDCommunication | 1 |
| Ready IED | Data.IEDReady | 1 |
| Breaker 2 | Data.BR2.Status | 1 |
| Conditions of Case 3 (FAULT) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Pre-Conditions | Variables | Values | ||||||
| Energized IED | Data.IEDEnergized | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| IED Communication | Data.IEDCommunication | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| Ready IED | Data.IEDReady | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Breaker 2 | Data.BR2.Status | X 1 | X | X | X | X | X | X |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisboa, L.A.C.; Melo, T.R.; Campos, I.G.S.A.; Aragão, M.B.; Ribeiro, A.S.; Silva, L.C.; da Silva, V.L.; Lima, A.M.N.; Santos, A.A.B. The Development of a Malleable Model for Critical System Supervision Integration. Energies 2024, 17, 4094. https://doi.org/10.3390/en17164094
Lisboa LAC, Melo TR, Campos IGSA, Aragão MB, Ribeiro AS, Silva LC, da Silva VL, Lima AMN, Santos AAB. The Development of a Malleable Model for Critical System Supervision Integration. Energies. 2024; 17(16):4094. https://doi.org/10.3390/en17164094
Chicago/Turabian StyleLisboa, Luciano A. C., Thamiles R. Melo, Ikaro G. S. A. Campos, Matheus B. Aragão, Alexandre S. Ribeiro, Lucas C. Silva, Valéria L. da Silva, Antonio M. N. Lima, and Alex A. B. Santos. 2024. "The Development of a Malleable Model for Critical System Supervision Integration" Energies 17, no. 16: 4094. https://doi.org/10.3390/en17164094
APA StyleLisboa, L. A. C., Melo, T. R., Campos, I. G. S. A., Aragão, M. B., Ribeiro, A. S., Silva, L. C., da Silva, V. L., Lima, A. M. N., & Santos, A. A. B. (2024). The Development of a Malleable Model for Critical System Supervision Integration. Energies, 17(16), 4094. https://doi.org/10.3390/en17164094







