An Enhanced Forecasting Method of Daily Solar Irradiance in Southwestern France: A Hybrid Nonlinear Autoregressive with Exogenous Inputs with Long Short-Term Memory Approach

Abstract

The increasing global reliance on renewable energy sources, particularly solar energy, underscores the critical importance of accurate solar irradiance forecasting. As solar capacity continues to grow, precise predictions of solar irradiance become essential for optimizing the performance and reliability of photovoltaic (PV) systems. This study introduces a novel hybrid forecasting model that integrates Nonlinear Autoregressive with Exogenous Inputs (NARX) with Long Short-Term Memory (LSTM) networks. The purpose is to enhance the precision of predicting daily solar irradiance in fluctuating meteorological scenarios, particularly in southwestern France. The hybrid model employs the NARX model’s capacity to handle complex non-linear relationships and the LSTM’s aptitude to manage long-term dependencies in time-series data. The performance metrics of the hybrid NARX-LSTM model were thoroughly assessed, revealing a mean absolute error (MAE) of 9.58 W/m², a root mean square error (RMSE) of 16.30 W/m², and a Coefficient of Determination (R²) of 0.997. Consequently, the proposed hybrid model outperforms the benchmark model in all metrics, showing a significant improvement in prediction accuracy and better alignment with the observed data. These results highlight the model’s effectiveness in enhancing forecasting accuracy under unpredictable conditions, improving solar energy integration into power systems, and ensuring more reliable energy predictions.

1. Introduction

The escalating demand for energy sources in many sectors, such as transportation, residential, and industry, along with the adverse environmental effects of fossil fuels, has led to the emergence of renewable energy sources as a viable alternative, such as wind, geothermal, biomass, solar, and hydropower energy [1,2,3,4]. In the year 2022, the worldwide renewable energy capacity amounted to 3381 GW. Among these renewable sources, solar energy emerged as the second most extensively implemented, with a capacity of 1053 GW. It is positioned second after hydropower, which leads with a total capacity of 1392 GW [5,6]. Solar energy refers to the process of harnessing sunlight to generate electricity. Solar energy is widely recognized as a highly significant form of renewable energy on a global scale, owing to its abundant availability and environmentally advantageous characteristics [7,8,9,10]. The global installed solar energy capacity has had a significant growth, rising from 140,514 MW to 1053 GW over the course of the past decade (2013–2022) [11]. The predicted capacity for solar photovoltaic (PV) power generation is expected to reach 7000 terawatt-hours (TWh) by the year 2050. Multiple variables, including solar irradiance, wind speed, ambient and module temperatures, cloud cover, and humidity, influence solar power production. The generation of solar power is directly tied to solar irradiance, as higher levels of sunlight exposure result in increased energy output from solar panels. Therefore, precise predictions of solar irradiance are essential for assessing the solar energy potential in regions with fluctuating environmental conditions, such as France [12]. France is positioned as the fifth-ranked nation in Europe and the thirteenth-ranked nation in the world in terms of its significant solar energy capacity, trailing behind Germany, Italy, Spain, and the Netherlands. Over the past decade, the nation has witnessed a threefold increase in its cumulative installed solar energy capacity, rising from 5277 MW to 17,419 MW [11]. Figure 1 provides a graphical representation of the growth in solar energy capacity from 2013 to 2022, comparing the growth of France’s solar infrastructure with the global trend. This visual comparison highlights France’s role in the global solar market, with a consistent growth in installed capacity throughout the decade. This growth reflects France’s dedication to expanding its renewable energy resources. Simultaneously, the global capacity has shown a significant rise, indicating a robust worldwide shift towards solar energy.

The research on solar irradiance forecasting has gained significant attention, driven by the growing demand for renewable and environmentally friendly energy sources. Hence, the accurate prediction of solar irradiance is crucial for enhancing the effectiveness and reliability of solar power systems, and numerous techniques have been developed to meet this requirement [13,14,15,16]. Statistical techniques [17] like autoregressive integrated moving average (ARIMA) use past data to forecast future levels of irradiance, providing accurate predictions for short-term forecasts. Numerical weather prediction (NWP) models [18], which employ the principles of atmospheric physics to make accurate predictions, are well-suited for forecasting weather patterns over a time frame ranging from medium- to long-term, particularly in regions with complex weather patterns. Additionally, support vector machines (SVMs) [19], artificial neural networks (ANNs) [20], and random forests (RFs) [21] are machine learning approaches that have become popular because of their capacity to handle nonlinear relationships and adjust to various geographical situations. They have proven to be useful in both short-term and intra-day forecasting [22,23,24,25]. Furthermore, recent studies have developed hybrid models that combine different forecasting techniques to take advantage of their strengths and minimize their weaknesses, resulting in improved accuracy and reliability of forecasts [26].

Nevertheless, models frequently have difficulties in dealing with the fundamental instability of weather conditions. Severe weather phenomena, such as cloud cover and storms, have the potential to rapidly decrease the amount of sun radiation, making precise and consistent prediction difficult [27].

This study presents an advanced hybrid Nonlinear Autoregressive Network with Exogenous Inputs Long Short-Term Memory (NARX-LSTM) model to address the increasing demand for accurate daily solar irradiance forecasting, particularly in unstable weather conditions in southwestern France. The utilization of a NARX-LSTM hybrid model for predicting solar irradiance in areas with unpredictable environmental variables is significant progress in this study. By integrating the autoregressive capabilities of the NARX model with the long-term memory functions of the LSTM, this approach effectively addresses the complexity of environmental variability. The robustness of the NARX-LSTM model not only contributes to more precise energy planning and management but also ensures better operational efficiency of solar energy systems in regions where traditional models fail to perform adequately. This combination has the potential to establish a new benchmark model for accurate forecasting in locations with unpredictable environmental conditions.

The present paper is structured as follows: Section 2 provides an overview of the existing literature on the topic of solar energy forecasting. Section 3 provides a thorough explanation of the materials and the methodologies used in the present study. The findings of the simulation are analyzed and presented in Section 4. Section 5 presents the concluding remarks.

2. Related Works

Several studies have been undertaken to predict solar radiation through various methodologies. In other words, some research opted to employ a single methodological approach, while others combined many methodologies in a hybrid strategy to improve the accuracy and reliability of the network’s predictions.

In their study, Rangel et al. [28] proposed several NARX models for three sites. The focus of the study was to enhance the performance of NARX models for forecasting solar radiation an hour in advance by appropriately configuring input vectors. The study employed Engle–Granger causality tests to investigate collinearity among meteorological variables in databases from Chihuahua, Temixco, and Zacatecas, three Mexican cities characterized by distinct climates. The authors discovered that using input vectors containing only solar radiation and temperature data was sufficient for accurately predicting solar radiation. Including pressure, wind speed, and relative humidity data did not significantly improve the accuracy of the forecasts. The comparison of forecasting accuracy between the improved NARX models and the smart persistence model revealed notable enhancements in accuracy with the NARX models across all three cities.

Additionally, Hissou et al. [29] introduced a novel method for predicting solar radiation using a multivariate time series (MVTS) model that employed recursive feature elimination (RFE) with various models such as decision tree (DT), logistic regression (LogR), gradient boosting models (GBMs), Pearson correlation (Pr), and RF to improve the accuracy of forecasting by identifying the most important features. The LogR model particularly stands out, showing excellent performance with a low root mean square error (RMSE) (0.003) and a high R² score (0.002), while other models also demonstrate promising results with consistently high accuracy. The paper demonstrates how different machine learning approaches contribute to refining solar radiation forecasts by handling multiple variables and their complex relationships. This comprehensive approach not only enhances the precision and effectiveness of solar radiation forecasts but also provides a valuable understanding of the most influential meteorological variables that impact solar radiation levels, such as temperature and humidity.

Furthermore, Natava et al. [30] proposed a novel approach to forecast daily global solar radiation in Dumaguete using a NARX-LSTM hybrid network. The study discovered that the optimized Gaussian Process Regression (GPR) model and NARX were successful in accurately predicting outcomes using limited datasets. Despite their inherent inaccuracies, incorporating these models into an LSTM network enhanced their predictive precision. The LSTM model alone was highly effective with minimal losses, suggesting its robustness in predicting global solar radiation with just six variables. The hybrid NARX-LSTM model improved the results by achieving an RMSE of about 0.10, potentially decreasing the inconsistency and unpredictability in the output of PV cells.

Another study by Ref. [25] introduced a novel hybrid model for predicting solar radiation, combining the strengths of autoregressive and moving average (ARMA) and NARX models. Initially, the ARMA model is employed to predict solar radiation for specific winter and summer days, as well as to estimate daily and weekly averages. The hybrid approach benefits from ARMA’s initial predictive accuracy and NARX’s capabilities, aiming to deliver highly accurate and efficient solar radiation forecasts. The choice of models for the hybrid system is strategically determined by their simplicity, adaptability, and performance. Each model undergoes individual testing to verify its usefulness before being integrated. Therefore, the study confirms that while the ARMA model is effective in predicting weekly solar radiation averages when variations are under 10%, its performance declines with larger fluctuations. In such cases, the NARX model is employed, utilizing temperature and historical solar radiation data as inputs to handle higher variability (over 10%). The effectiveness of the resulting hybrid model is evaluated using metrics such as mean square error (MSE), mean absolute error (MAE), and RMSE. These metrics demonstrate improved performance in comparison to several prior research, highlighting the proposed model’s capacity to estimate weekly averages of solar radiation with more accuracy.

Moreover, Ref. [31] developed a hybrid algorithm combining k-means clustering and support vector regression (SVR) to predict daily global solar radiation. The model’s effectiveness was assessed using six years of meteorological data from Ibadan (2010–2015) to predict solar radiation for 2016 and 2017. The model was compared to three well-established models, namely ANN, Angstrom-Prescott, and ARMA, using a range of statistical tests, including RMSE, relative root mean square error (RRMSE), mean absolute percentage error (MAPE), and R². The results demonstrated the k-means-SVR model’s excellent accuracy and reliability, surpassing the performance of other current models. This indicates that the k-means-SVR model has great potential as a tool for energy planning.

Mutavhatsindi et al. [7] employed machine learning models to predict hourly solar irradiation. The performance of LSTM, SVR, and feed-forward neural networks (FFNNs) was evaluated and compared to the principal component regression model (PCR). The process of selecting variables was performed using the least absolute shrinkage and selection operator (Lasso). Based on the data, the FFNN model outperformed the other two machine learning models in terms of forecast accuracy, as measured by MAE and RMSE. The study found that when combining forecasts from machine learning models using both the convex combination approach and quantile regression averaging (QRA), QRA proved to be the superior method. It exceeded other models in all statistical tests and forecast accuracy measures employed.

The study conducted by Huang et al. [32] at Ganzhou station used historical meteorological data spanning from 1980 to 2016; twelve machine learning model networks (extreme gradient boosting (XGBoost), multiple linear regression (MLR), radial basis function neural network (RBFNN), RF, DT, back-propagation algorithm-based neural network (BPNN), extreme learning machine (ELM), GPR, gradient boosting regression tree (GBRT), adaptive boosting (AdaBoost), k-nearest neighbor (KNN), and SVR) were assessed for their effectiveness in predicting solar radiation both daily and monthly. The most frequently utilized models were GBRT, XGBoost, GPR, and RF, compared to the other models. These models were assessed using metrics such as R², RMSE, MAE, and BIAS. They found that GBRT showed the highest level of accuracy when it came to daily forecasts, although XGBoost outperformed other models for monthly predictions. Additionally, they conducted experiments with a stacking model that integrated these models. This stacking model demonstrated enhanced accuracy in daily radiation predictions. However, its effectiveness in monthly predictions was diminished, most likely due to limited data. This comprehensive investigation by Huang et al. demonstrated the potential of advanced machine learning methods, including hybrid approaches like stacking models, to significantly enhance the predictive accuracy of solar radiation, which is critical for strategic energy sector management. In their results, they determined that the XGBoost model excels at predicting solar radiation values, recommending the use of either the XGBoost or a stacking fusion model when handling large datasets.

The researchers of Ref. [21] focused on enhancing solar radiation prediction using the RF algorithm, comparing it to models like AdaBoost, linear regression (LR), and recurrent neural networks (RNNs). The study found that optimizing RF’s hyperparameters led to a significant accuracy improvement of 95.98%, surpassing other approaches. The favorable and consistent climate in Queretaro contributed to the high accuracy of the predictive models. The study also investigated the correlations among solar radiation, temperature, and humidity, confirming that humidity has a major influence on this relationship.

Chodakowska et al. [33] examined the use of ARIMA models to predict solar radiation using data from Jordan and Poland. The study evaluated the efficiency of ARIMA models under diverse meteorological conditions and for different time intervals, including monthly and hourly periods. The models had robust prediction skills, particularly under stable weather circumstances, and were observed to possess a high level of accuracy in Jordan owing to the persistent presence of sunlight. Nevertheless, the effectiveness of these methods showed inconsistencies in Warsaw, indicating limitations in less stable circumstances. This study highlights the significance of adjusting ARIMA models to geographic and climatic circumstances to enhance the accuracy of solar radiation predictions. This is essential for effective management and planning of energy systems.

In their study, Woldegiyorgis et al. [34] conducted a comprehensive analysis on forecasting daily and monthly averaged horizontal global solar radiation (HGSR) in Fiche town, Ethiopia, by employing various ANN models. They used ANN models like cascade-forward back-propagation (CFBP), feed-forward back-propagation (FFBP), Elman back-propagation (EBP), and layer recurrence (LayR) to estimate HGSR, analyzing their performance through metrics such as MAPE, MSE, and RMSE. The findings suggest that ANN models are capable of accurately forecasting solar radiation levels, although the level of accuracy may vary among different models.

Overall, these studies collectively contribute to the understanding of solar radiation forecasting by employing diverse methodological frameworks that adapt to the specifics of the datasets and environmental conditions they study. This review highlights the potential of combining traditional forecasting models with advanced machine learning techniques to enhance predictive accuracy and reliability.

Table 1. Previous studies on solar radiation forecasting.

Ref.	Year	Input Parameters	Forecasting Model	Region	Forecasting Results
[31]	2019	Clearness index, evaporation, sunshine duration, maximum temperature, sunshine hours, difference between max and min temperature, average of max and min temperature	Hybridized k-means and SVR	Ibadan, Nigeria	For 2016: R2 = 0.9816 RMSE = 0.4275 RRMSE = 2.6515% MAPE = 1.7928% For 2017: R2 = 0.9842 RMSE = 0.434 RRMSE = 2.7498% MAPE = 1.795%
[28]	2020	Solar radiation, wind speed, relative humidity, pressure, temperature	Persistence model, NARX	Three cities in Mexico	%Forecast skill: 11.5% in Chihuahua 5.7% in Temixco 27.2% in Zacatecas
[7]	2020	wind speed, wind direction standard deviation, rainfall, relative humidity, barometric pressure, temperature, hour, month, a non-linear trend, a lagged hourly solar irradiance at lags 1 and 2.	LSTM, SVR, FFNN, PCR, Convex model, QRA model		RMSE = 88.6, MAE = 52.034
[25]	2021	Historical solar radiation, temperature	ARMA, NARX, Hybrid model of ARMA and NARX	Spain	MSE = 0.0340 MAE = 0.1270 RMSE = 0.1863
[32]	2021	sunshine duration, mean wind speed, mean ground temperature, mean relative humidity, minimum temperature, maximum temperature, mean temperature, mean precipitation, mean pressure, visibility	XGBoost, ELM, DT, RF, GBRT, BPNN, AdaBoost, KNN, SVR, GPR, MLR, RBFNN	Ganzhou, China	R2 = 0.944 RMSE = 1.131 MJ/m2 MAE = 0.870 MJ/m2
[21]	2022	Solar radiation, humidity, wind direction, wind speed, temperature, barometric pressure, sunshine hours	LR, RNN, SVR, RF, AdaBoost, Optimization RF, Optimization AdaBoost	Juriquilla, Queretaro, Mexico	MSE = 5011.19 RMSE = 70.78 MAE = 33.44 R2 = 0.95 MAPE = 1.596019 × 1013 Accuracy % = 95.98
[30]	2023	Rainfall, wind direction, wind speed, relative humidity, temperature, sunshine duration, predicted global solar radiation	Optimized GPR, NARX, NARX-LSTM	Dumaguete, Philippines	RMSE = 0.10
[33]	2023	Historical solar irradiance	ARIMA	Amman, Jordan Warsaw, Poland	R2 = 99.9% RMSE = 13.53 MSE = 183.18 MAPE = 2.79% Std. Error = 14.14
[29]	2023	Maximum and minimum temperature, wind speed, relative humidity, precipitation	RF, DT, LR, Pr, GBM	-	RMSE = 0.003 R2 = 0.002
[34]	2023	Maximum and minimum temperature, relative humidity, surface pressure, wind speed, latitude, longitude, elevation	FFBP, LayR, CFBP, EBP	Fiche town, Oromia, Ethiopia	MSE = 0.0079 RMSE = 0.0889 MAPE = 1.2075

provides a concise summary of the various forecasting models discussed in the literature review. It outlines the models employed, input parameters, geographical location of the studies, and significant conclusions.

3. Materials and Methods

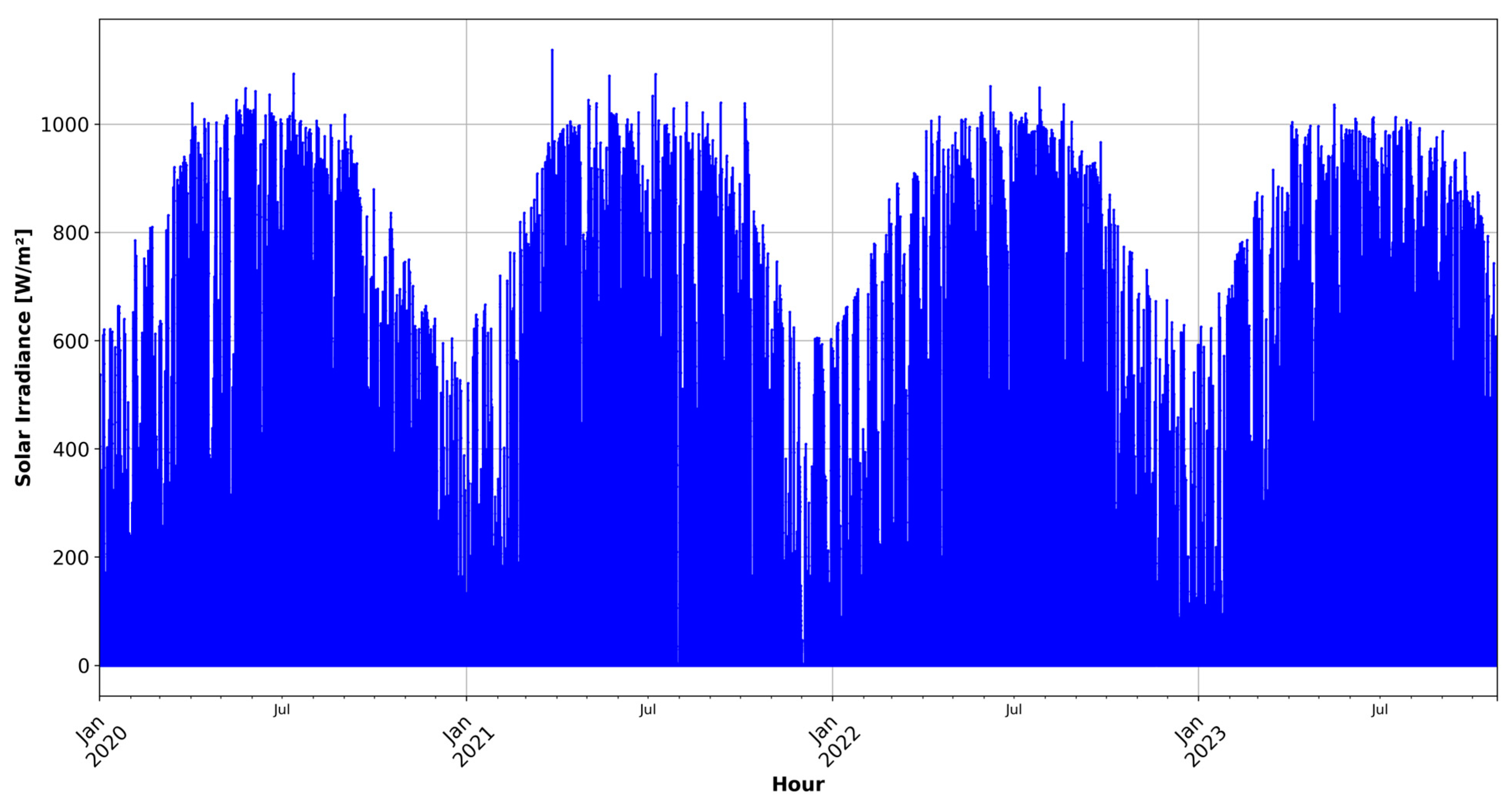
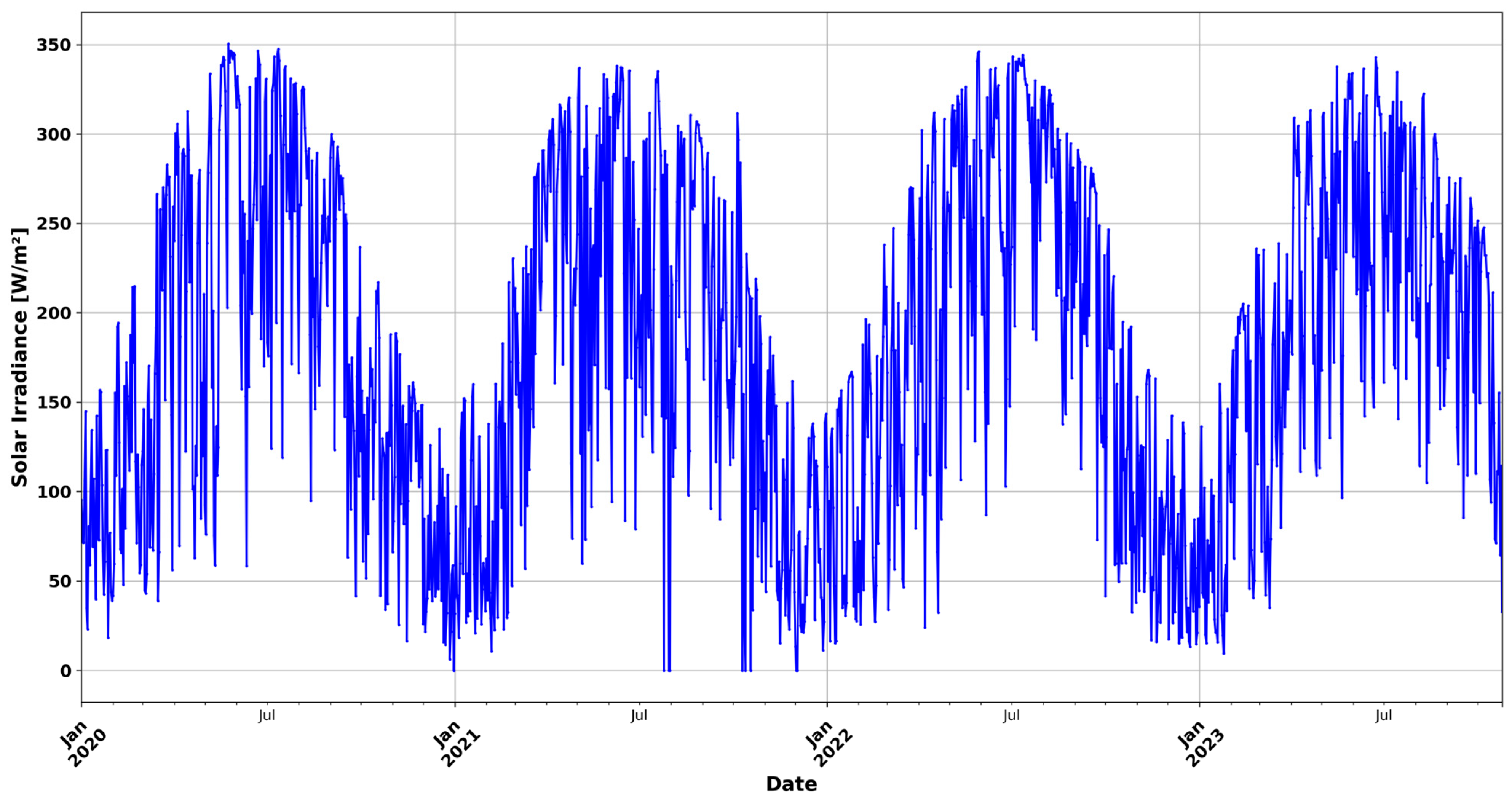
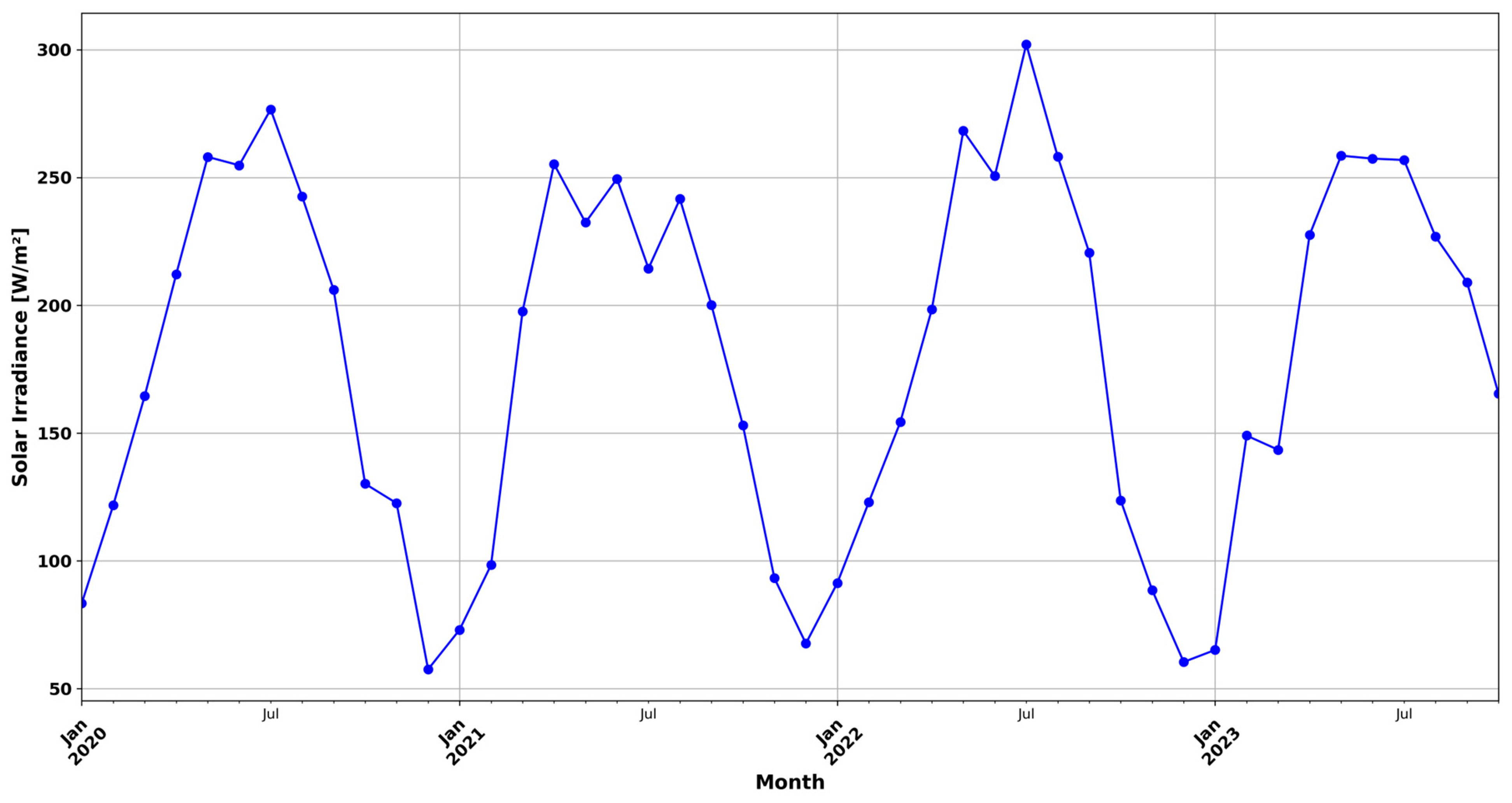
3.1. Site Assessment and Dataset

The solar farm is situated in southwestern France with a total capacity of 41.2 MWp of ground-mounted installation. The project comprises four PV plants; however, our study focuses exclusively on one specific part, namely Project A, with a capacity of 11.1 MW, as illustrated in Figure 2. The project has a prolonged wet season that lasts for 8.5 months, starting in September and ending in June. During this period, there is a minimum 25% chance of rainfall occurring every day. Simultaneously, this period is marked by substantial cloud cover. Precise prediction of solar irradiance is crucial for maximizing the incorporation of solar energy into the power grid and reducing uncertainty related to solar power generation.

The study employs a dataset consisting of solar power generation data collected from 1 January 2020 to 25 October 2023. The dataset has 33,456 observations that were recorded at hourly intervals. The data comprises the following variables:

• Date_Time: The exact date and time of each observation, formatted in “DD/MM/YYYY HH:MM”;
• T01-t Solar Irradiance [W/m²]: Solar irradiance of Transformer 1;
• T01-t Module Temperature [°C]: Temperature of the solar module of Transformer 1;
• T03-Ta Ambient Temperature [°C]: Ambient temperature of Transformer 3;
• T03-Wind Speed [m/s]: Wind speed of Transformer 3.

3.2. Data Preprocessing

The preprocessing phase is crucial for ensuring that the dataset is properly prepared for further analysis and modeling. Preprocessing involves making efforts to improve the quality and integrity of the data, as well as configuring the dataset to better align with the requirements of the forecasting models. Here, this section will present a comprehensive description of each step included in the preprocessing procedure.

Data Cleaning:

• Handling Missing Values: Due to the continuous nature of solar irradiance and related environmental data, missing values can significantly impact the performance of predictive models. We employed an interpolation method to replace the missing data points.

Feature Engineering:

• Lagged Features: Historical data of the variables can provide context for current values, helping to capture trends and inertia in the data. We created lagged features for up to 24 h prior for the variables.
• Integration of Exogenous Variables: In the NARX framework, the exogenous variables (ambient temperature, surface temperature, and wind speed) are treated as external inputs that provide additional context to the model. These are integrated into the input feature set alongside the historical values of the target variable (solar irradiance).

Feature Scaling:

• Normalization: This was employed to standardize the values of distinct features, which had a broad range, in order to make them similar. This process improved the stability and performance of the machine learning models. Min-max scaling was used to rescale all features so that they fall within the range of 0 to 1.

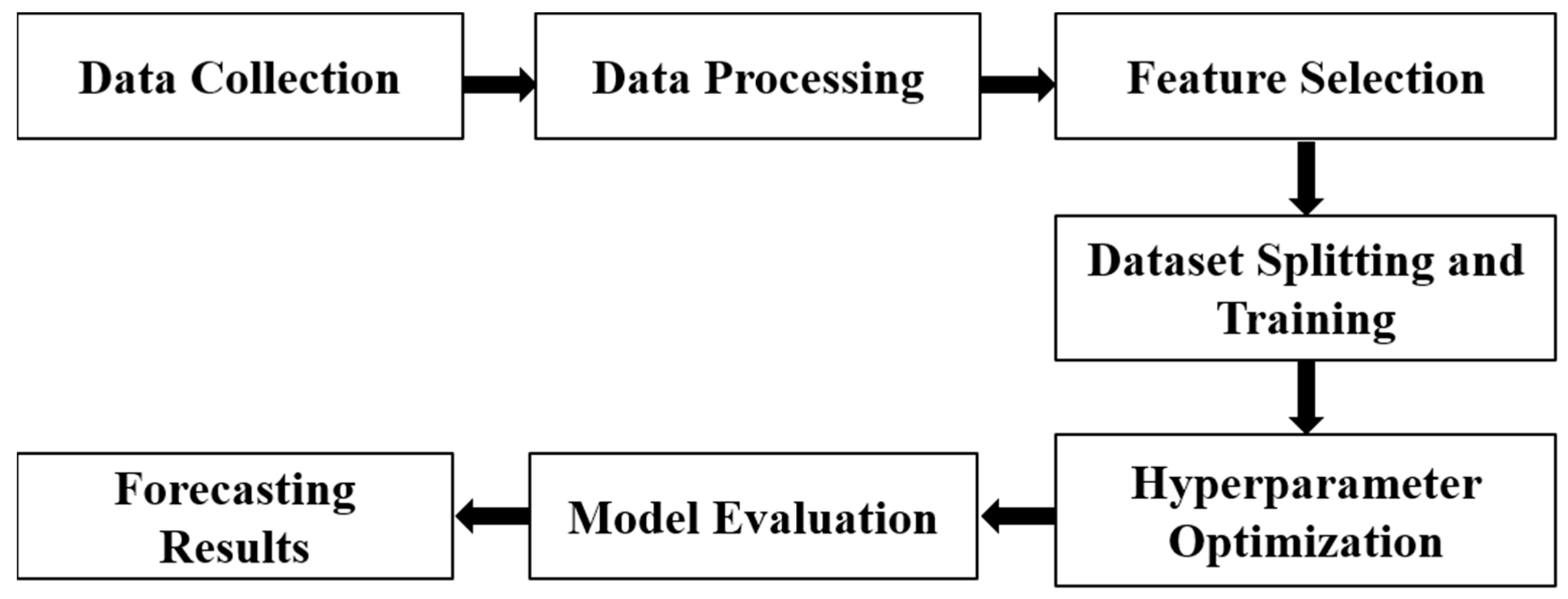
3.3. Proposed Methodology

This section provides a comprehensive explanation of the method that will be employed to carry out the investigation. Forecasting solar irradiance using a Nonlinear Autoregressive Network with Exogenous Inputs (NARX) combined with a Long Short-Term Memory (LSTM) neural network, which is a type of recurrent neural network (RNN), involves several steps. This approach utilizes the memory capacity of LSTM networks to effectively manage complicated time-series data, where previous values (autoregression) and additional variables (exogenous inputs) impact the target predictions. The following steps give a comprehensive outline of the methods employed in this study, where Figure 3 illustrates the overall flowchart of the study.

• Feature Selection: For the development of a robust hybrid NARX-LSTM model aimed at forecasting solar irradiance, it is critical to carefully select and prepare input features that capture the underlying dynamics affecting solar power generation. In this context, features such as wind speed and ambient and surface temperatures are selected using the Pearson correlation coefficient due to their direct influence on solar irradiance levels.
• Data Segmentation: After the feature selection, the preprocessed dataset was divided into three subsets: 80% for training, 10% for validation, and 10% for testing. The training set is used to enable the model to acquire knowledge from a significant historical context. The validation set is employed for model parameter fine-tuning and overfitting prevention. Finally, the testing set assesses the model’s performance on unseen data. Table 2 presents the division of data across different periods and the number of samples in each dataset.
  Table 2. Training, validation, and test sets.

  Datasets	Time Periods	Number of Samples
  Training set	1 January 2020–20 January 2023	26765
  Validation set	20 January 2023–06 August 2023	3346
  Testing set	6 August 2023–25 October 2023	3345

  Table 2. Training, validation, and test sets.

  Datasets	Time Periods	Number of Samples
  Training set	1 January 2020–20 January 2023	26765
  Validation set	20 January 2023–06 August 2023	3346
  Testing set	6 August 2023–25 October 2023	3345

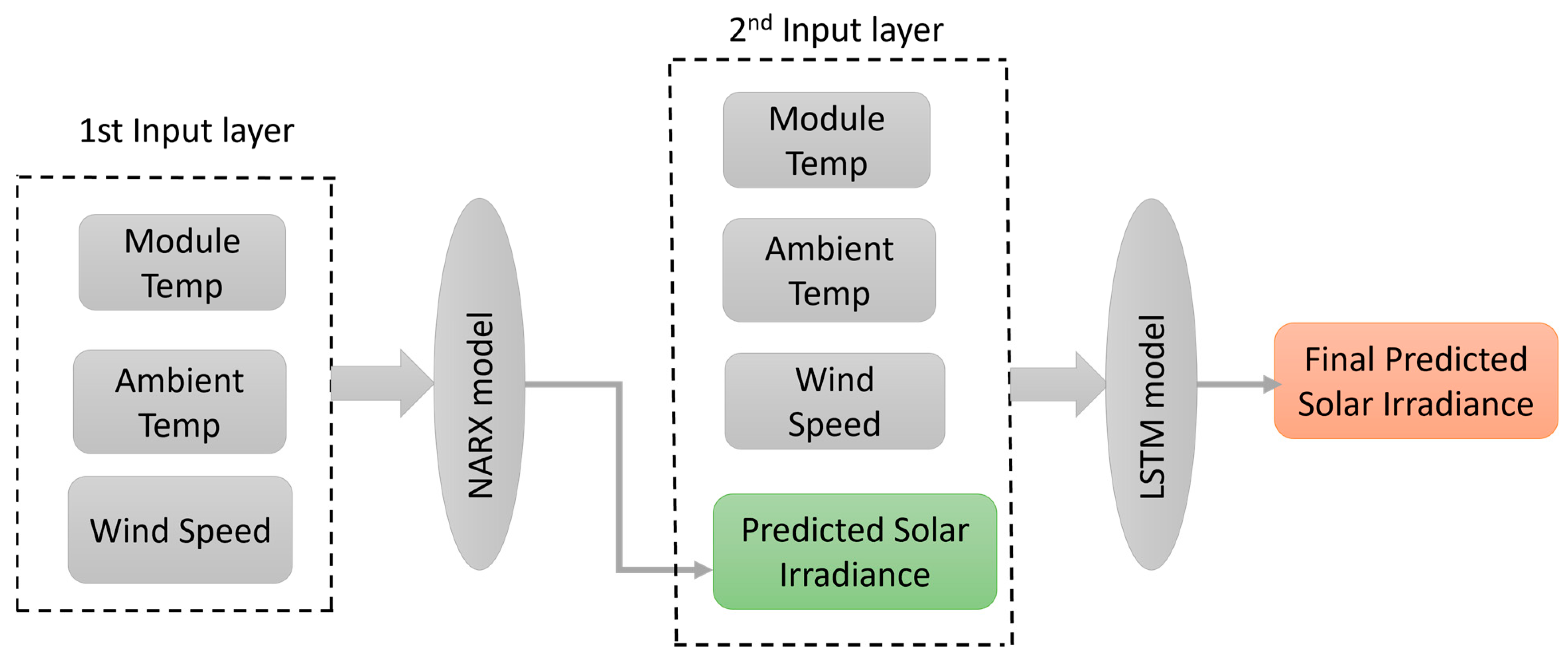
• Model Architecture: The architecture of the hybrid NARX-LSTM model is shown in Figure 4.
  Figure 4. Hybrid NARX-LSTM proposed model structure.

  Figure 4. Hybrid NARX-LSTM proposed model structure.
• Hyperparameter Optimization: Hyperparameter optimization for LSTM networks is an essential technique focused on adjusting the parameters that control the model’s learning process and structure. Our study utilizes the Optuna package to do hyperparameter optimization when building an LSTM-based neural network with Keras. The crucial hyperparameters that were optimized were the number of LSTM layers, the number of units per layer, the dropout rate, and the learning rate. Optuna’s efficient search algorithms are used to change these parameters. The algorithms recommend values for the number of units and dropout rates within specified ranges, and they also utilize a logarithmic scale for the learning rate with an ADAM optimizer to efficiently explore a wider range of values. The model architecture is dynamically constructed based on these parameters, incorporating dropouts after each LSTM layer to prevent overfitting. During model training, early stopping is used to end the training process if the validation loss does not improve. This helps increase training efficiency and prevents overfitting. This approach is particularly effective for managing the complexities of time-series predictions where the tuning of network architecture and learning parameters can greatly influence model accuracy and generalization. The optimized hyperparameters of this study are displayed in Table 3.
  Table 3. Best hyperparameters for LSTM model.

  Hyperparameter	Value	Search Interval
  LSTM layers	2	1–5
  Hidden units	192	12–200
  Learning rate	0.0008	0.0001–0.1
  Number of epochs	350	100–1500
  Dropout rate	0.3559	0.2–0.6

  Table 3. Best hyperparameters for LSTM model.

  Hyperparameter	Value	Search Interval
  LSTM layers	2	1–5
  Hidden units	192	12–200
  Learning rate	0.0008	0.0001–0.1
  Number of epochs	350	100–1500
  Dropout rate	0.3559	0.2–0.6

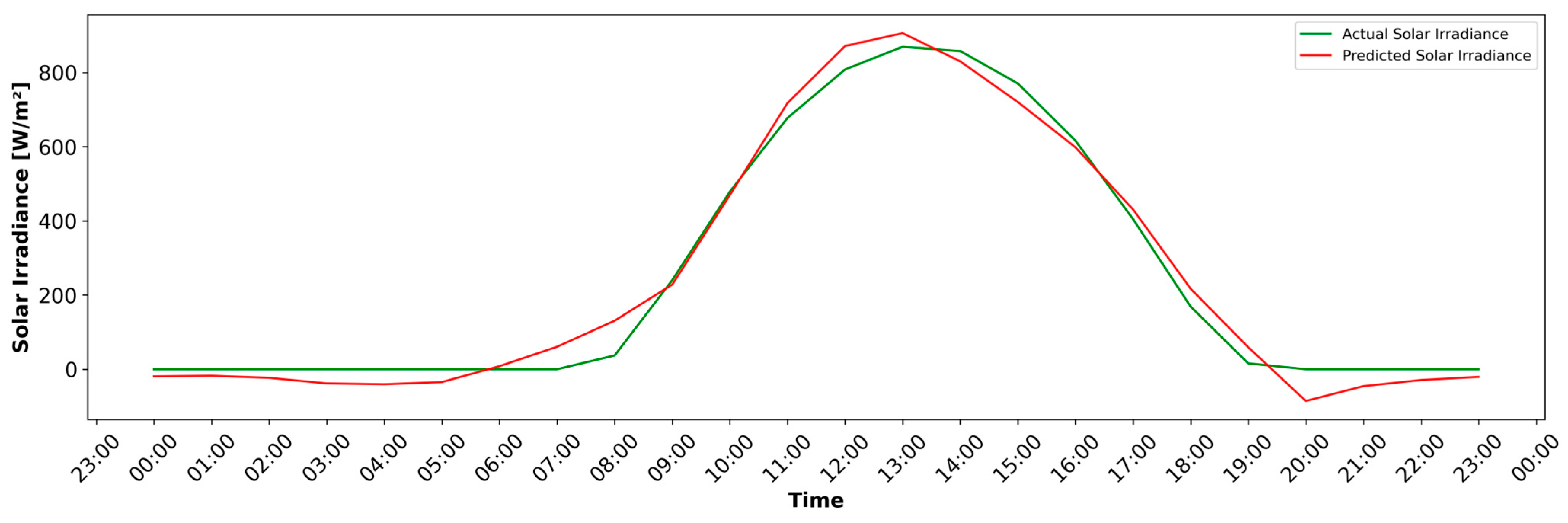
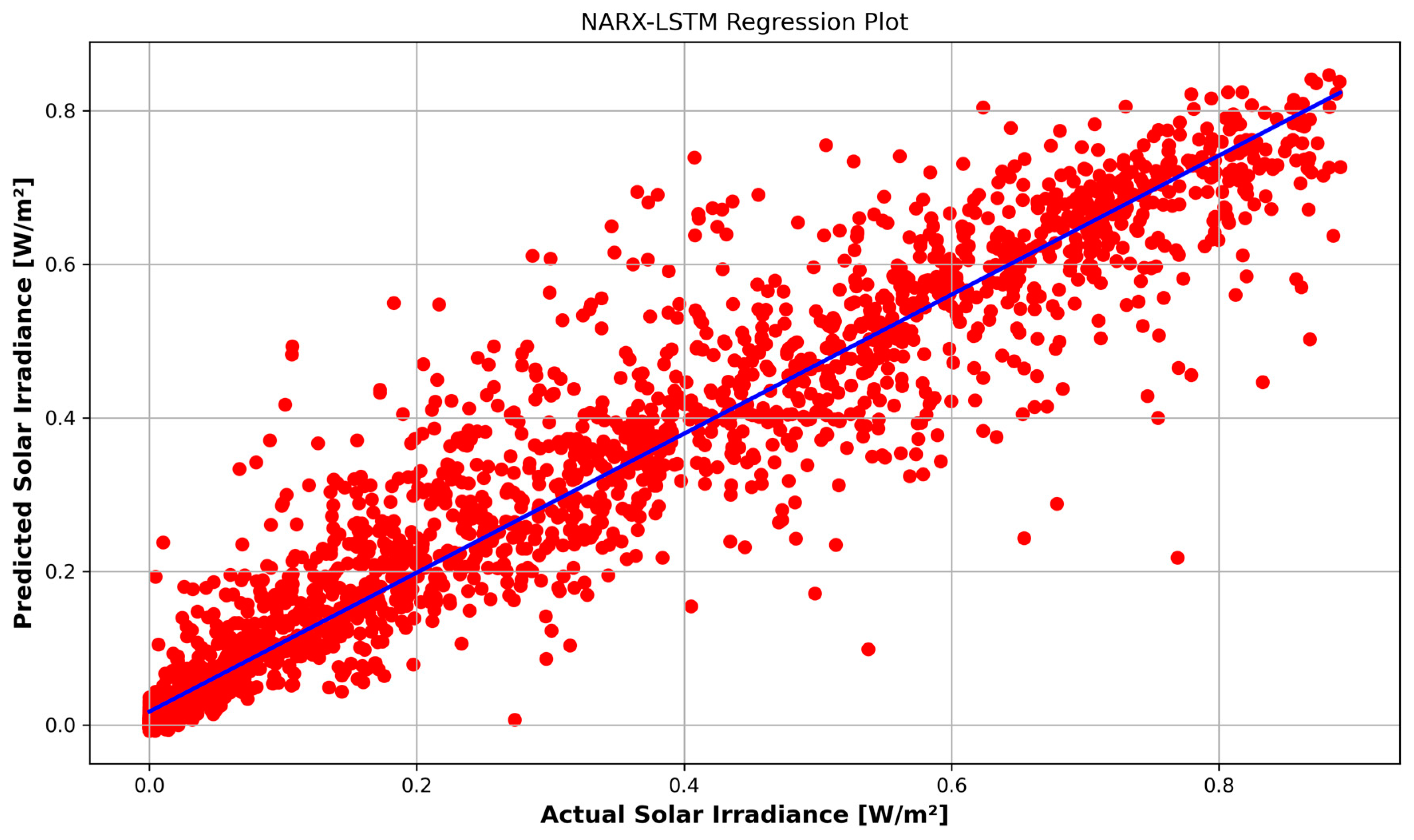
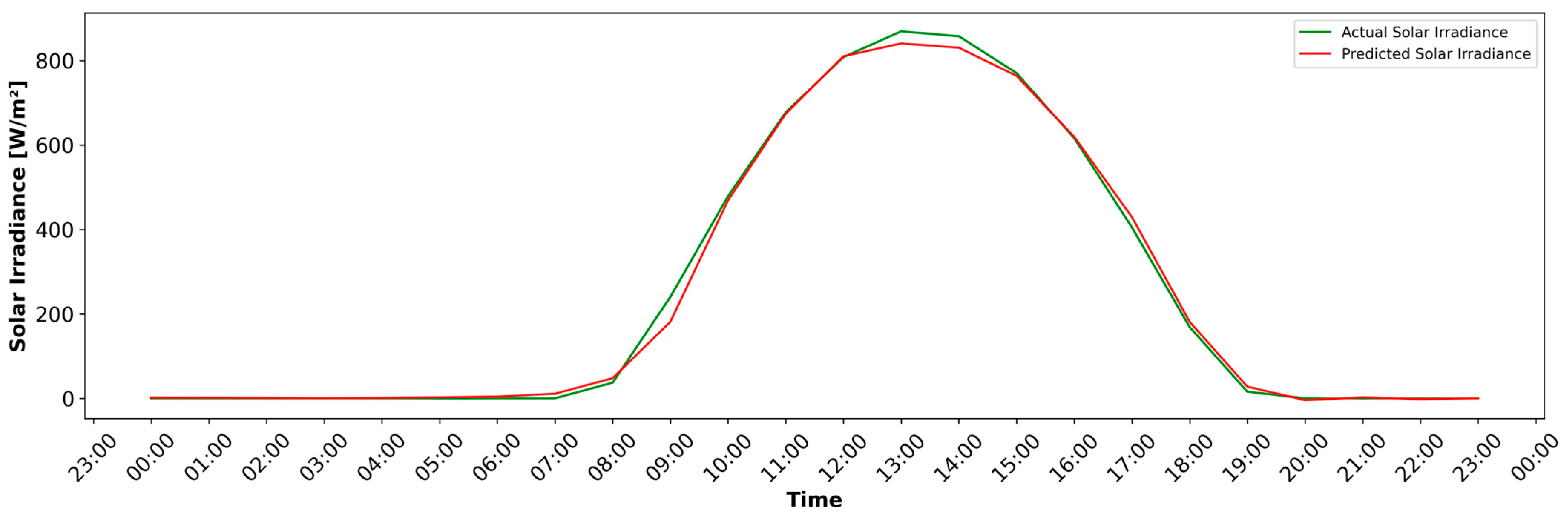
• Model Evaluation: The evaluation of the hybrid NARX-LSTM model for forecasting solar irradiance is conducted using MAE, RMSE, and R² performance metrics to ensure a comprehensive assessment of its predictive accuracy and reliability.

The data preprocessing, analysis, and model creation tasks were performed using Python, utilizing libraries such as Pandas for data manipulation, Sklearn for machine learning methods, Keras for deep learning models, and Matplotlib for data visualization.

3.4. Statistical Performance Metrics

In order to assess the precision and predictive capability of the solar irradiance forecasting of the proposed model, three primary performance metrics were employed: Coefficient of Determination (R²), root mean square error (RMSE), and mean absolute error (MAE). These metrics offer a thorough evaluation of the accuracy of predictions and the model’s ability to explain the data, enabling a strong assessment of the model’s performance [35,36].

The Coefficient of Determination, denoted as R², measures the proportion of variance in the dependent variable that is predictable from the independent variables. It provides an indication of how well the model can predict unseen data by indicating the quality of fit. The R² value ranges from 0 to 1, where 1 indicates perfect prediction. It is calculated using the formula:

$$R^2=1-{\displaystyle \frac{\sum {(y_i-\widehat{y})}^2}{\sum {(y_i-\overline{y})}^2}}$$

(1)

where $y_i$ is the actual value, $\widehat{y}$ is the predicted value, and $\overline{y}$ is the mean of the actual values.

RMSE is a frequently used measure of the differences between values predicted by a model and the values observed from the environment that is being modeled. It is particularly useful when large errors are particularly undesirable. The RMSE of an estimator with respect to an estimated variable is defined as the square root of the mean squared error:

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N(y_i-\widehat{y}{)}^2}$$

(2)

Here:

• N represents the number of observations.

MAE measures the average magnitude of the errors in a set of predictions without considering their direction. It is the average over the test sample of the absolute differences between prediction and actual observation, where all individual differences have equal weight:

$$MAE={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\left|y_i-\widehat{y}\right|$$

(3)

4. Results and Discussion

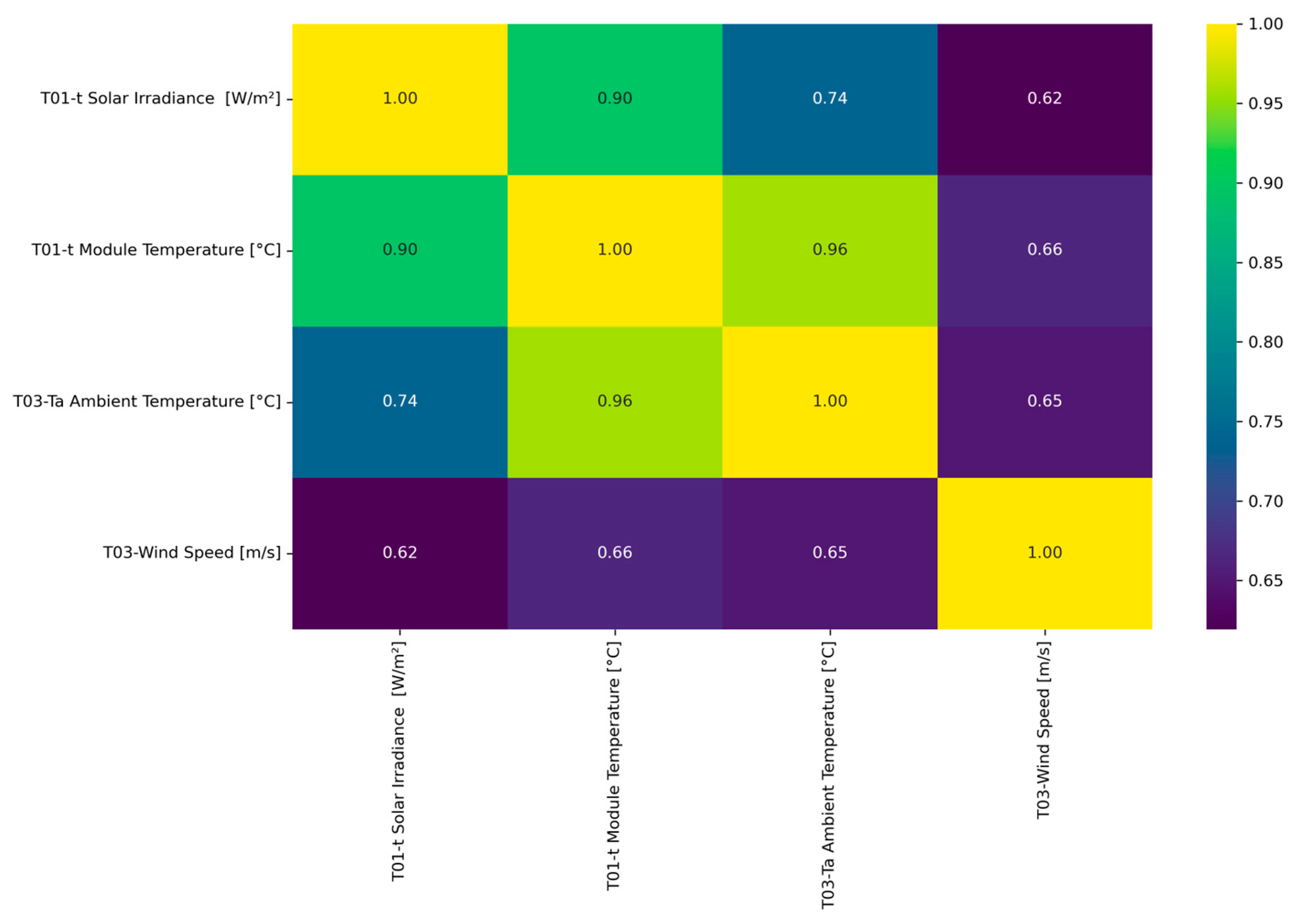
4.1. Correlation Coefficient

After the preprocessing stage, the Pearson correlation coefficient is generated to visually represent the connections between the most important variables. The Pearson correlation coefficient is a statistical metric that precisely defines the magnitude and direction of a linear relationship between two variables. It ranges from −1 to +1, where +1 indicates a perfect positive linear correlation, −1 indicates a perfect negative linear correlation, and 0 indicates no linear correlation. A positive number indicates a direct relationship, where an increase in one variable will be followed by an increase in the other variable. Conversely, a negative value indicates an inverse relationship, where an increase in one variable is preceded by a reduction in the other variable [37].

Figure 5 presents a correlation heatmap that measures the relationships between solar irradiance and several environmental factors, including module temperature, ambient temperature, and wind speed. These relationships are crucial for understanding the dynamics of solar energy generation and are central to enhancing forecasting accuracy.

The following deductions can be derived from this heatmap analysis:

• Solar Irradiance and Module Temperature: The correlation coefficient between solar irradiance and module temperature is high, indicating a strong positive relationship. As solar irradiance increases, module temperature typically rises, affecting the efficiency of PV cells. This relationship underscores the need for thermal management in solar PV systems, especially in regions with high solar irradiance.
• Solar Irradiance and Ambient Temperature: There is also a significant positive correlation between solar irradiance and ambient temperature. This relationship is expected, as higher solar irradiance leads to increased temperatures. Ambient temperature can influence the performance of solar PV installations by affecting the physical properties of the materials involved in energy conversion. This phenomenon can be attributed to the overall rise in temperature that occurs during bright weather.
• Solar Irradiance and Wind Speed: The correlation between solar irradiance and wind speed is moderately positive. While less intuitive, this relationship suggests that in certain geographical regions, higher solar irradiance days might also experience higher wind speeds, possibly due to local climatic conditions. Wind speed can play a role in cooling solar panels, potentially improving their performance on very sunny days.

This detailed analysis helps to highlight the complex relationship of these environmental variables with solar irradiance. By understanding these correlations, we can better predict the performance of solar energy systems under various environmental conditions. Furthermore, the insights gained from this analysis are crucial for designing more robust solar energy systems that are more robust and can effectively employ particular climatic circumstances.

4.2. Nonlinear Autoregressive with Exogenous Inputs (NARX) Prediction Model

The Nonlinear Autoregressive with Exogenous Inputs (NARX) model is a recurrent dynamic neural network specifically designed for the accurate prediction of time-series data. This model depicts the relationships between the previous values of a target variable and the previous values of external or exogenous inputs. NARX models are widely used in diverse domains, including signal processing, financial forecasting, weather prediction, and energy-related projections. The usefulness of the NARX model in forecasting and system identification comes from its inherent structure and functionality, enabling it to accurately capture complex nonlinear relationships present in time-series data [38,39]. The NARX methodology operates by utilizing a systematic analysis, as given below:

• Nonlinear Autoregressive (NAR): This aspect of the model signifies that the future values of a series are predicted based on past values of the same series but with a nonlinear relationship. In traditional linear models, future values are a linear combination of past values; in NARX, these relationships are modeled using nonlinear functions, typically represented by a neural network.
• Exogenous Inputs (X): These are external variables that influence the target variable but are not influenced by it within the model framework. For example, in the case of solar irradiance forecasting, exogenous inputs might include temperature, humidity, or cloud cover.

The NARX model is characterized by the following mathematical equation:

$$y\left(t\right)=f[y\left(t-1\right), y\left(t-2\right), \dots , y\left(t-d_y\right); u\left(t-1\right), u\left(t-2\right), \dots , u\left(t-d_u\right)]$$

(4)

where $y\left(t\right)$ is the target variable at time t, $u\left(t\right)$ represents the exogenous inputs, $d_y$ and $d_u$ are the delays for the target and the exogenous inputs, respectively, and f represents a nonlinear function.

Moreover, the nonlinear function f is commonly represented by a neural network, although other nonlinear estimators such as polynomial models, radial basis functions, or SVM may be employed, depending on the system’s complexity and the available data. In the context of this study, neural networks are used to implement the nonlinear function f in NARX model. Hence, the nonlinear function f would be given as:

$$f\left(\bullet \right)=W_o\mathrm{\varnothing }\left(W_i\left[y\left(t-1\right), \dots ,y\left(t-n_y\right), u\left(t-1\right), \dots , u\left(t-n_u\right)\right]+b_i\right)+b_o$$

(5)

Here:

• $\mathrm{\varnothing }$ is the nonlinear activation function (tanh for this study).
• $W_i$ and $W_o$ are the weight matrices for the input and output layers, respectively.
• $b_i$ and $b_o$ are bias vectors for the input and output layers, respectively.

In this study, NARX is used as a benchmark model to compare performance metrics with the proposed model. After the training and the hyperparameter optimization, the performance metrics results of the benchmark model are as follows: an R² of 0.983, an RMSE of 43.02, and an MAE of 37.18.

Additionally, Figure 6 illustrates the predicted solar irradiance for 7 October 2023, using the NARX model, which was specifically selected to evaluate its performance in predicting solar irradiance on rainy days.

4.3. Hybrid NARX-LSTM Prediction Model

In this study, the hybrid NARX-LSTM prediction model is proposed, which is a sophisticated hybrid neural network that combines the NARX model and LSTM networks to enhance time-series forecasting accuracy. The NARX model initially captures the nonlinear relationships between the target variable and its past values, along with exogenous inputs, effectively handling the dependencies influenced by historical data and external conditions. Afterwards, the LSTM component, known for its ability to effectively understand long-term dependencies, handles the outputs from the NARX model (see Appendix A). The utilization of a two-stage technique enables the NARX-LSTM model to exploit the initial predictions and enhance them by incorporating more complex temporal patterns that may be neglected by the NARX model alone. An integrated model is especially advantageous in complicated forecasting scenarios, such as solar irradiance prediction, where both short-term variations and long-term trends significantly affect the accuracy of predictions.

Figure 7, Figure 8 and Figure 9 illustrate the hourly, daily average, and monthly average of solar irradiance, respectively. Figure 7 presents the hourly observations of solar irradiance taken from 1 January 2020 to 25 October 2023. The vertical peaks correspond to the magnitude of solar irradiation, quantified in watts per square meter. Irradiance peaks are observed during daylight hours. The general pattern exhibits seasonal fluctuations, with greater levels of irradiance observed during the summer months. Furthermore, Figure 8 shows the daily mean solar irradiation throughout the same time period. Each vertical bar corresponds to the mean irradiance value for a specific day. The graph exhibits a distinct seasonal pattern, matching the hourly data, with elevated values in the summer and diminished values in the winter. The daily variation is also evident, affected by meteorological conditions and atmospheric transparency. Finally, Figure 9 displays the mean monthly solar irradiance. The y-axis quantifies solar irradiance in units of watts per square meter, while the x-axis corresponds to the months. The graph demonstrates a clear seasonal pattern, with irradiance reaching its highest point during the summer months and its lowest point during the winter, reflecting the previous figures. This pattern reflects the impact of the Earth’s axial tilt on sun exposure.

Additionally, the regression plot of predicted and actual solar irradiance has been constructed, as shown in Figure 10. This scatter plot depicts the correlation between forecasted and observed sun irradiance values. Each red dot corresponds to a pair of real and forecasted irradiance values, with the real values plotted on the x-axis and the forecasted values on the y-axis. The blue line indicates the optimal scenario in which the anticipated values precisely correspond to the actual values. The proximity of the red dots to the blue line demonstrates the precision of the forecasts. In general, the plot displays a robust linear correlation, indicating that the predictions are reasonably precise, although there are occasional variations, particularly at higher levels of irradiation.

Furthermore, the hybrid NARX-LSTM solar irradiance prediction model shown in Figure 11 demonstrated exceptional performance on 7 October 2023, specifically chosen to assess its effectiveness during wet days. Wet days are known to present difficulties in predicting solar irradiance due to the fluctuating cloud cover and precipitation, as mentioned in Section 3.1. The graph shows an excellent alignment between the predicted and actual solar irradiance values throughout the daylight hours, demonstrating the model’s high effectiveness under unfavorable weather conditions. This ability to closely track the actual irradiance during wet conditions underscores the robustness of the model. The precision with which the predicted curve follows the actual data during peak solar hours indicates that the model has successfully captured the complex dynamics influenced by intermittent cloud cover and varying sunlight availability. Such precision in adverse weather conditions is crucial for optimizing the operation and energy output of solar power systems, as it ensures reliable forecasting essential for grid management and energy planning in regions experiencing frequent wet weather. As a result, the hybrid model’s performance metrics include an MAE of 9.58 W/m², an RMSE of 16.30 W/m², and an R² of 0.997.

Table 4. Comparison of the proposed model with prior studies.

Reference	Models	Optimal Model	Performance Metrics
			RMSE (W/m2)	MAE (W/m2)	R2
[40]	SVR, GPR, MLP, ELM	ELM	60.60	-	0.96
[41]	LSTM, SVM, MLANN	LSTM	41.05	21.99	0.98
[42]	WPD–CNN–LSTM-MLP, BPNN, SVM, RNN, LSTM, Clim-Pers	WPD–CNN–LSTM-MLP	32.1006	14.3523	0.994
[43]	Persistence, LSTM, LR, BPNN	LSTM	76.245	-	-
[38]	NN, LR, AdaBoost, RF	RF	66	33	0.96
[44]	LSTM-RNN, FFNN, NARX	LSTM-RNN	60.31	36.90	-
Present Study	NARX, Hybrid NARX-LSTM	Hybrid NARX-LSTM	16.30	9.58	0.997

represents the comparison between the results obtained from this study and the prior studies on solar irradiance prediction models. The present study has compared its performance metrics with those of previous studies. The study in ref. [40] effectively shows that machine learning techniques can improve the accuracy of solar radiation predictions compared to standard physics-based models. The ELM method demonstrated superior performance in multiple scenarios, achieving an RMSE of 60.60 W/m² and an R² value of 0.96. Similarly, ref. [41] examines the effectiveness of machine learning models in predicting solar radiation in different climatic regions of Morocco. By employing models such as LSTM, SVM regression, and Multilayer Artificial Neural Networks (MLANNs), it emphasizes the LSTM model’s exceptional performance in terms of forecasting accuracy, as evidenced by its RMSE of 41.05 W/m², MAE of 21.99 W/m², and R² of 0.98. Moreover, a novel multivariate hybrid WPD-CNN-LSTM-MLP has been proposed by ref. [42] that is designed for forecasting solar irradiance. This model combines wavelet packet decomposition (WPD), CNN, LSTM networks, and multi-layer perceptron (MLP) to improve prediction accuracy. It achieves this by analyzing multiple variables, such as hourly solar irradiance, temperature, relative humidity, and wind speed. The findings demonstrated a significant enhancement in forecasting accuracy using the WPD-CNN-LSTM-MLP model. This model outperformed traditional models in predicting hourly irradiance, exhibiting lower error rates and higher precision. The performance metrics, namely RMSE and MAE, were measured at 32.1006 W/m² and 14.3523 W/m², respectively. Additionally, the R² value was determined to be 0.994. Focusing on the needs of distributed photovoltaic generation systems, Ref. [43] employs LSTM to model hourly day-ahead solar irradiance using readily available weather forecasting data. The LSTM model exhibited exceptional performance, outperforming conventional methods such as persistence algorithms, linear regression, and simple neural networks, achieving a good RMSE of 76.245 W/m². Finally, ref. [44] developed a novel forecasting model that uses commonly available weather data instead of historical solar irradiance data to predict solar power output for microgrids. Utilizing a deep LSTM-RNN, the model was compared against a traditional FFNN across six experiments involving weather stations located in Germany, USA, Switzerland, and South Korea. The findings demonstrated that the LSTM-RNN model had superior performance compared to the FFNN, attaining an RMSE of 60.31 W/m² and an MAE of 36.90 W/m².

The proposed hybrid NARX-LSTM model demonstrated superior performance compared to previous models, as seen by its lower RMSE of 16.30 W/m², MAE of 9.58 W/m², and high R² of 0.997. This proposed model shows a notable enhancement compared to other sophisticated models such as WPD–CNN–LSTM-MLP, which previously held the best reported performance among the prior studies, with an RMSE and MAE of 32.1006 W/m² and 14.3523 W/m², respectively, and an R² of 0.994. The enhanced accuracy of the hybrid NARX-LSTM model not only showcases the effectiveness of combining NARX and LSTM architectures but also highlights its promise for practical solar irradiance prediction in uncertain environmental situations. Despite its complexity, the obvious improvements in prediction accuracy justify the model’s employment, suggesting that its integration could enhance operational efficiency in renewable energy management.

5. Conclusions and Future Perspectives

The research findings validate the effectiveness of the hybrid NARX-LSTM model in significantly enhancing the precision of daily solar irradiance forecasts for southwestern France. The hybrid NARX-LSTM model demonstrated superior performance, evidenced by an MAE of 9.58 W/m², an RMSE of 16.30 W/m², and an R² of 0.997. These metrics demonstrate a significant enhancement compared to conventional forecasting (benchmark model) and validate the hybrid model’s capacity to successfully manage the complexity of solar irradiance data. The effective implementation of this model offers useful insights for optimizing and planning the operations of solar power plants, leading to potential cost reductions and enhanced energy reliability. This study enhances the field of renewable energy forecasting by showcasing the potential of using advanced neural network designs to improve the accuracy of predictions in areas with unpredictable climate variables. Future studies could investigate the possibility of applying this model to additional geographical areas or alternative tasks related to predicting renewable energy, thereby confirming its usefulness and flexibility in various environmental and operational contexts.