4.2. Case Study and Discussion
In this paper, Monte Carlo [
51,
52] is used to simulate the distribution of on-station EVs in 24 h. The 2022 white paper on China’s electric vehicle users’ charging behavior [
53] selected the main peak (nighttime) and the secondary peak (midday) to simulate the EV charging load distribution. It is assumed that 100 EVs are charged on the station throughout the day. In the main peak during nighttime, the charging start time of each EV satisfies the normal distribution
. In the secondary peak during midday, the charging start time of each EV satisfies the normal distribution
. According to [
50], it is assumed that the ratio of EVs choosing fast and slow charging is 6:4. Based on the fast/slow charging habits of EVs, it is assumed that the number of EVs choosing fast charging at midday and nighttime accounts for 80% and 20% of the total number of fast charging EVs, respectively. The number of EVs choosing slow charging at midday and nighttime accounts for 20% and 80% of the total number of slow-charging EVs, respectively. The initial SOC is assumed to obey a normal distribution of
N(0.5,
). The power of EVs charging at the station is shown in
Figure 14. The number of charging EVs is set to be the same as that of idle EVs.
In this paper, the forecasting results of AHA-LSSVM are compared with LSSVM and BP to verify the feasibility and validity of AHA-LSSVM, and the results are shown in
Figure 15 with cloudy weather as an example.
All three models, namely, the AHA-LSSVM, LSSVM, and BP, have a good performance in PV forecasting. The mean absolute error (MAE) and root mean square error (RMSE) of the PV output of each model are given in
Table 4. In
Table 4, the RMSE of the LSSVM is reduced by 5.8%, and the MAE is reduced by 3.8% compared with BP. The RMSE of the AHA-LSSVM is reduced by 12.7% compared with BP and 7.3% compared with the LSSVM, and the MAE is reduced by 18.8% compared with BP and 15.3% compared with the LSSVM. The increase in predictive accuracy achieved by the LSSVM over BP is relatively subtle (MAE reduction of 0.08%). In contrast, the enhancement in predictive accuracy realized by the AHA-LSSVM compared to the LSSVM is remarkably substantial (MAE reduction by 0.32%), signifying a threefold improvement. The results show that the accuracy of the LSSVM in PV forecasting is better than that of BP, and the improved AHA-LSSVM in PV forecasting has much better accuracy regarding forecasting results compared to the LSSVM.
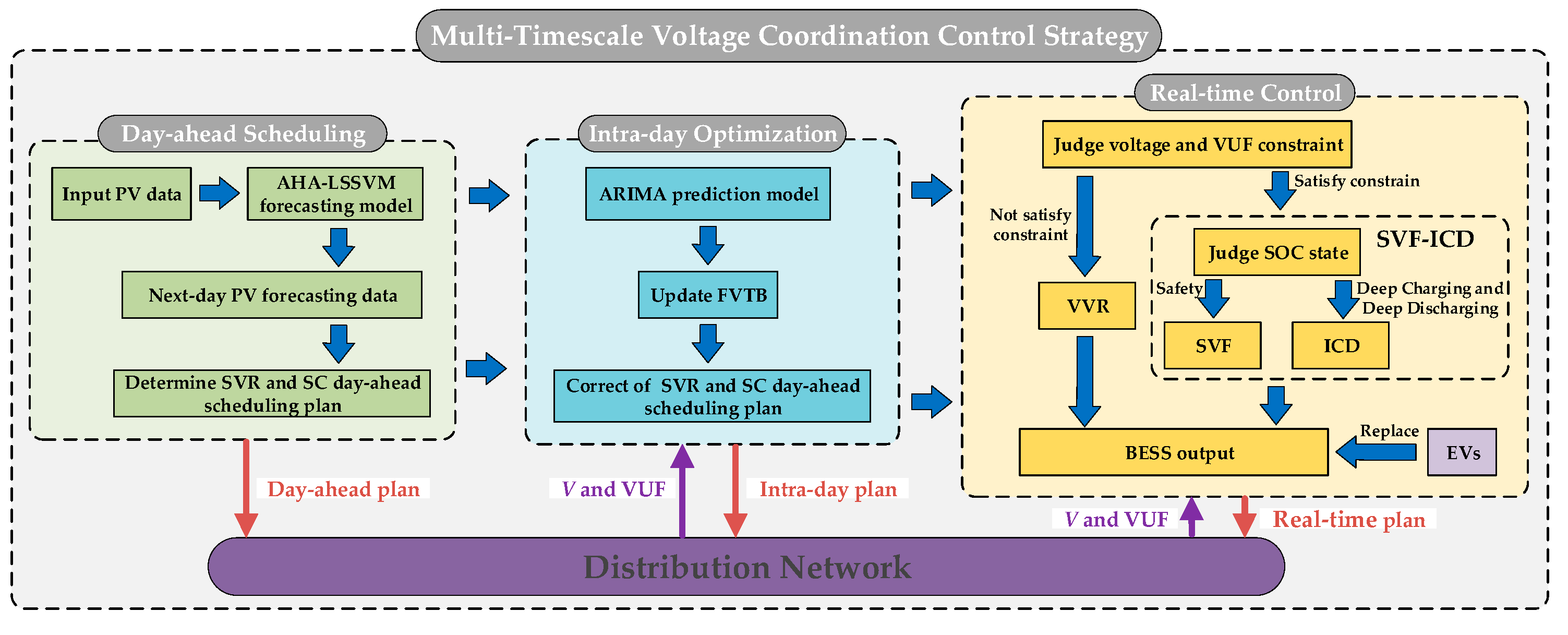
Eleven cases involved in three timescales are designed to analyze and verify the feasibility and effectiveness of the proposed multi-timescale voltage regulation via a coordinated control strategy, as shown in
Table 5.
In the day-ahead stage, the time interval is 5 min. In Case 1-1, the PV output by the AHA-LSSVM is used to obtain the day-ahead voltage and VUF. In Case 1-2, the voltage and VUF of Case 1-1 are adjusted by the proposed day-ahead coordinated control of the SVR and SC to verify the effectiveness.
In the intra-day stage, the time interval is 1 min. Case 2-1 applies the coordinated control in Case 1-2 to the intra-day stage to verify its effectiveness. Case 2-2 and Case 2-3 use dead-band control and FVTB control to modify the control strategy in Case 1-2, respectively. The effectiveness of the proposed FVTB control strategy is verified.
In real-time control, the time interval is 2 s. Case 3-1 implements the control strategy of Case 2-3 to verify the effectiveness of intra-day scheduling in the real-time stage. BESS participates in voltage regulation in Case 3-2 for real-time control. Case 3-3 uses AVOA to optimize the BESS output to achieve accurate voltage regulation as well as reduce the BESS output for capacity curtailment. Case 3-4 implements a strategy to suppress voltage fluctuations. Case 3-5 implements the ICD strategy to mitigate BESS deep charging/discharging as well as curtail the BESS capacity. Case 3-6 further optimizes Case 3-5 by replacing part of the BESS with EVs.
In Case 1-1, the forecasting output of PV is brought into power flow calculation to obtain the voltages at nodes 18 and 33, as shown in
Figure 16a,b. The maximum VUF at node 33 is shown in
Figure 16c.
In
Figure 16a,b, the voltage exceeds the lower limit during the 5:00–8:30 and 17:00–1:00 periods when there is no PV output or less PV output, which is about 43.8% of the whole day’s length. Particularly during the 19:00–20:30 period, with regular loads and demands for charging EVs, the voltage exceeds the lower limit to 0.905 pu.
With the increase in the PV output, the voltage exceeds the upper limit frequently during the 11:00–16:00 period, which is about 15.6% of the whole day’s length. During the peak period of PV output (13:00–14:00), the voltage exceeds the upper limit by up to 1.087 pu.
From
Figure 16c, with single-phase load and single-phase PV, the degree of voltage unbalance increases and exceeds the limit during the 11:00–15:30 period, which accounts for about 11.5% of the whole day’s length, and the VUF reaches a maximum of 2.47%.
As shown in
Figure 17a,b, neglecting the mechanical delays of the SVR and SC, the day-ahead scheduling strategy regulates the voltage within the threshold. The VUF is smaller than 2% throughout the day, as shown in
Figure 17c. It indicates the effectiveness of the day-ahead scheduling strategy proposed in this paper.
In
Figure 18a,b, the SVR and SC operations are in accordance with the day-ahead scheduling strategy. When the voltage exceeds the limit, the SVR operates first to adjust the voltage amplitude. When the SVR cannot adjust the voltage back to the threshold or the VUF is larger than 2%, the SC participates in regulation for coordinated control. In
Figure 18b, before 11:15, the VUF is within the threshold, and only the SVR operates for voltage regulation. After 11:15, the VUF is larger than 2%, SC2 at node 33 operates to provide reactive power to suppress the VUF, and it reaches 75 kVar at 12:15. SC2 at node 33 perfectly regulates the VUF back to its limit, and therefore, SC1 has no operation. The proposed day-ahead scheduling strategy successfully regulates the voltage and VUF within the threshold.
In Case 2-1, as seen in
Figure 19a,b, the voltage exceeds the upper/lower limits during the 9:30–11:30 and 16:30–19:00 periods, respectively. The voltage violation accounts for 3% of the whole day’s length. In
Figure 19c, the VUF also frequently exceeds the limit during the 11:00–12:30 period. This is because there is an error in the intra-day PV output compared with day-ahead forecasting, and it is impossible to control the voltage and VUF well within the thresholds when executing the day-ahead scheduling plan in intra-day optimization. Therefore, intra-day optimization is required.
The voltage and VUF profiles with voltage dead-band control are shown in
Figure 20.
As shown in
Figure 20a,b, the high penetration of PV, SVR, and SC (neglecting the mechanical delay) without soft control capability cannot eliminate the voltage violation caused by the PV output, and the voltage exceeds the dead-band at 13:00 and 14:30. The voltage violation accounts for 1.3% of the whole day’s length. The VUF in
Figure 20c is smaller than 2% throughout the day after dead-band control. As seen in
Figure 20, dead-band control successfully regulates the voltage and VUF within the threshold [0.95, 1.05], but compared with Case 1-2, the narrow range of voltage dead-band leads to the excessive operations of the SVR and SC, as shown in
Figure 21. In
Figure 21, the operation numbers significantly increase for the regulation of the voltage and VUF.
In this paper, the FVTB control strategy is proposed as an alternative to voltage dead-band control to mitigate the frequent SVR and SC operations and alleviate the frequent voltage violations. The voltage and VUF profiles in FVTB control are shown in
Figure 22.
As seen in
Figure 22a,b, the voltage is basically within the FVTB; however, like in Case 2-2, there is a voltage violation during the 11:30–13:30 period subject to SVR and SC regulation capability, but the voltage violation only accounts for 0.6% of the whole day’s length, which is much smaller than that in dead-band control. As seen in
Figure 22c, the VUF is controlled well within 2% for the whole day in FVTB control.
The SVR and SC operations are shown in
Figure 23. In
Figure 23a,b, the SC operations with FVTB control rise in comparison with dead-band control. In
Figure 23c, the number of SVR operations in FVTB control is significantly reduced compared to that in dead-band control, especially during the peak period of PV output. The numbers of SVR and SC operations in voltage dead-band control and FVTB control are given in
Table 6.
As shown in
Table 6, compared to dead-band control, the number of SVR operations in FVTB control is reduced by 45 times, which is only 42.3% of that in dead-band control. The number of SC operations in FVTB control is increased to 25, improving the participation of SC. Therefore, FVTB control effectively reduces the number of SVR operations and increases SC involvement.
In the real-time stage, the timescale is 2 s. After accounting for the mechanical delays of SVR and SC, the voltage and VUF curves in the real-time stage are shown in
Figure 24 with intra-day scheduling in Case 2-3.
In
Figure 24a,b, the voltage exceeds its limit due to the mechanical delay of SVR/SC and ultra-short-term fluctuations in PV, and it accounts for about 5.4% of the whole day’s length. As shown in
Figure 24c, the VUF is always smaller than 2% throughout the day. Therefore, in the real-time control stage, the SVR and SC cannot cope with the voltage violation problem, as shown in
Figure 24, and a BESS is employed for real-time operation with flexible control ability.
In
Figure 25, the BESS’s participation in voltage regulation maintains the voltage and VUF within the thresholds throughout the day, indicating that the BESS eliminates the voltage violation caused by the mechanical delay of SVR/SC and PV fluctuation in the real-time stage, as seen in comparison with
Figure 24a–c. The BESS output and SOC are given in
Figure 26.
In
Figure 26a, the maximum charging power of the BESS is close to 200 kW, and the maximum discharging power is about 100 kW. At around 6:00, the voltage slightly exceeds the lower limit due to the mechanical delay of the SVR and SC, and the BESS is capable of adjusting the voltage back to its threshold by briefly discharging. In
Figure 26b, before the peak of the PV output, the SOC rises to a maximum of 78.86%. The voltage slightly exceeds the lower limit around 14:45, and the BESS discharges as the SOC decreases by 0.2%.
In
Figure 27, the AVOA is utilized to optimize the BESS output to achieve accurate voltage regulation and reduce the BESS output. This is in contrast to
Figure 25a,b, where the adjusted voltage does not closely track the threshold boundary due to over-regulation, resulting in an increase in the BESS output.
In
Figure 27a,b, the BESS output by AVOA precisely regulates the exceeding voltage to the threshold boundary. In
Figure 27c, the VUF also does not exceed the threshold. The BESS output and SOC profile by AVOA are shown in
Figure 28.
Figure 28a shows the BESS output by AVOA. Compared with Case 3-2, the maximum value of the SOC decreases from 78.86% to 75.54% in
Figure 28b. In this paper, the BESS capacity is set to be 350 kWh, and the initial SOC is 50%; according to Equation (91), the curtailment of the BESS capacity reaches 11.51% by AVOA compared to Case 3-2.
The evaluation of the curtailment of the BESS capacity is expressed by Equation (91):
where
is the BESS capacity curtailment rate.
are the changes in the SOC before and after the utilization of the AVOA, respectively.
The intensity of voltage fluctuation,
, is etched by the voltage fluctuation rate, as shown in Equation (92):
where
is the number of nodes in DN.
is coefficient.
In
Figure 28a, the BESS is idle most of the time, and the operation time is only about 5% of the whole day.
Figure 27a,b show that the voltage fluctuation is very drastic, and
, which is calculated according to Equation (92), reaches 12.39%. To suppress the voltage fluctuation and improve the utilization rate of the BESS, the BESS is mobilized in an idle period, and the voltage and VUF profiles are shown in
Figure 29.
In
Figure 29a,b, voltage fluctuation is obviously alleviated by SFTB, and
is reduced to 7.97%, which is a 35.7% reduction in
compared to 12.39% in Case 3-3. The voltage and VUF are within the threshold throughout the day. The comparison before and after the SVF of node 18 is taken as an example and illustrated in
Figure 30.
In
Figure 30, the SFTB effectively suppresses voltage fluctuation compared to Case 3-3. During the period of voltage violation, the prior objective of the BESS is to deal with the voltage violation problem, so there are voltages that have not converged into the SFTB. The BESS output and SOC profile are shown in
Figure 31.
In
Figure 31a, the BESS operation time is significantly increased, and the utilization rate is improved. Around the 19:00–6:00 period, voltage fluctuation suppression is not performed without the PV output. In
Figure 31b, with the increase in the PV output, the overall voltage tends to rise and exceed the upper limit of the SFTB. The BESS adjusts the voltage by charging, which leads to the rise in the SOC to the maximum value of about 82.75% at about 13:25. After the peak time of PV, the voltage tends to descend and exceed the lower limit of the SFTB. The BESS adjusts the voltage by discharging, which leads to a decrease in the SOC to the minimum value of about 49.81% at about 7:00. During the 12:00–13:30 period, the SOC exceeds the upper limit, leading to the deep charging of the BESS. In
Figure 31a, the maximum charging power of the BESS is close to 350 kWh, and the maximum discharging power is about 500 kW. The calculated capacity of the BESS is 1.5 MWh.
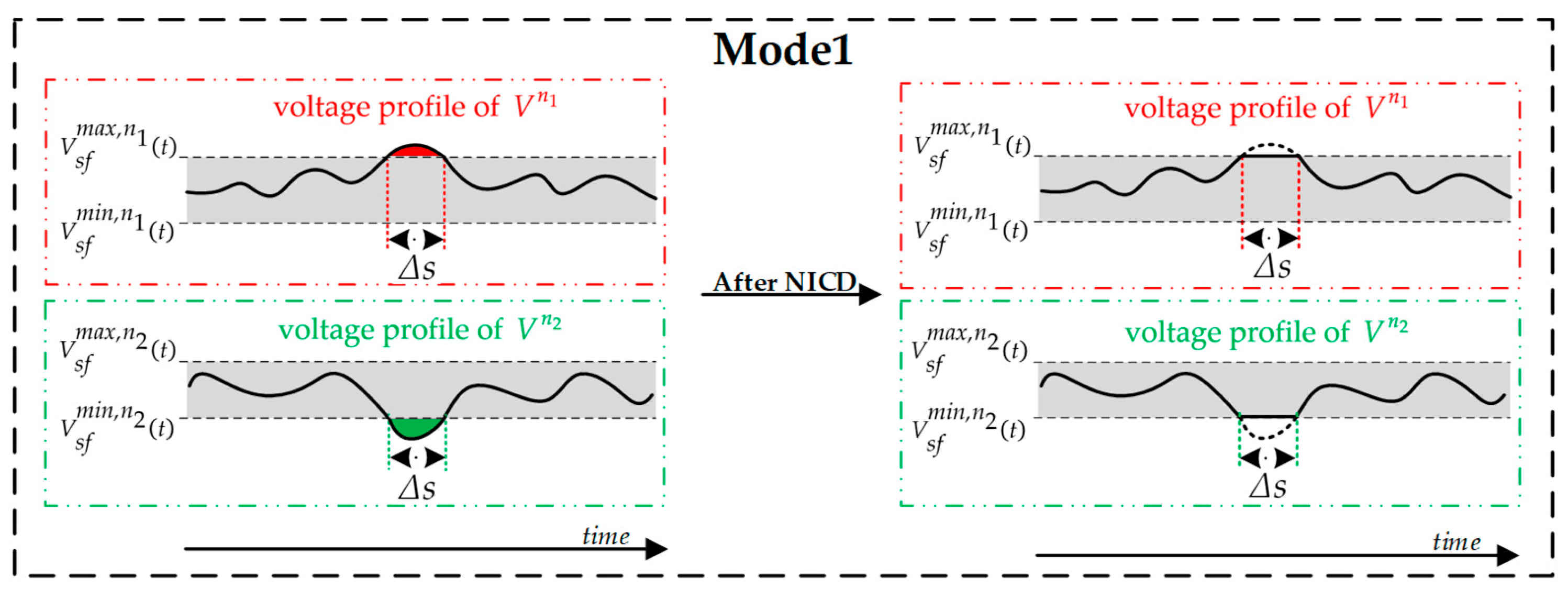
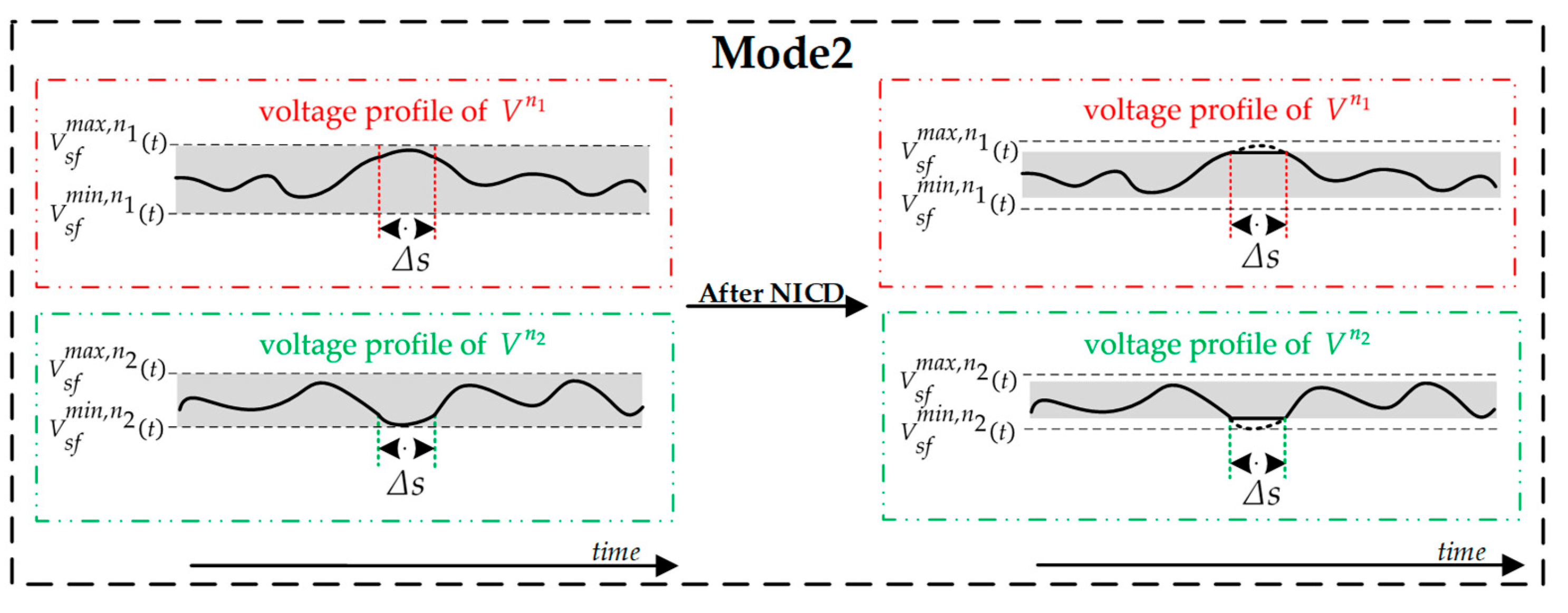
In Case 3-4, the effectiveness of voltage fluctuation suppression is significant, and the utilization of the BESS is also improved, but the required BESS capacity and PCS are greatly increased, and the BESS also suffers from the problem of deep charging. Therefore, in this case, we propose the ICD strategy for the BESS to realize the curtailment of the BESS capacity as well as suppress the voltage fluctuation and avoid the deep charging/discharging of the BESS.
As shown in
Figure 32, the voltage and VUF are within the threshold throughout the day with the ICD strategy. The voltage fluctuation is significantly diminished, and
is reduced to 9.14%. Although the voltage suppression effect is slightly inferior compared to Case 3-4, the capacity of the BESS is reduced to 350 kWh through the ICD strategy, and the maximum output of the BESS is 200 kW, as shown in
Figure 33a. The maximum SOC is about 76.93%, as shown in
Figure 33b. The results verify that the ICD strategy realizes BESS capacity curtailment and solves the deep charging problem while suppressing voltage fluctuation and improving BESS utilization.
EVs are used in this paper to replace BESSs for the further curtailment of the BESS capacity. The profiles of the voltage, VUF, BESS output, SOC variation, and EV charging/discharging power after EV replacement are shown in
Figure 34 and
Figure 35.
In
Figure 34a–c, the voltage and VUF are within the thresholds throughout the day. Compared to the ICD strategy, after replacing part of the BESS with EVs, the BESS output and operation period decrease, and the maximum value of the SOC decreases to 72.17%.
Figure 35c shows the charging/discharging power of EVs. The BESS capacity required in Case 3-6 is scaled down by 13.09% compared to that in the ICD strategy.
The comparison of each case is shown in
Table 7. The AVOA realizes the accurate output of the BESS and voltage regulation. The proposed SVF significantly moderates the voltage fluctuation. The proposed ICD realizes the great curtailment of the BESS’s capacity. Ultimately, the application of EVs further improves the curtailment of the BESS capacity with user participation in the voltage regulation of DN.