Abstract
In recent years, the energy industry has increased the proportion of renewable energy sources, which are sustainable and carbon-free. However, the increase in renewable energy sources has led to grid instability due to factors such as the intermittent power generation of renewable sources, forecasting inaccuracies, and the lack of metering for small-scale power sources. Various studies have been carried out to address these issues. Among these, research on Virtual Power Plants (VPP) has focused on integrating unmanaged renewable energy sources into a unified system to improve their visibility. This research is now being applied in the energy trading market. However, the purpose of VPP aggregators has been to maximize profits. As a result, they have not considered the impact on distribution networks and have bid all available distributed resources into the energy market. While this approach has increased the visibility of renewables, an additional method is needed to deal with the grid instability caused by the increase in renewables. Consequently, grid operators have tried to address these issues by diversifying the energy market. As regulatory method, they have introduced real-time energy markets, imbalance penalty fees, and limitations on the output of distributed energy resources (DERs), in addition to the existing day-ahead market. In response, this paper proposes an optimal scheduling method for VPP aggregators that adapts to the diversifying energy market and enhances the operational benefits of VPPs by using two Mixed-Integer Linear Programming (MILP) models. The validity of the proposed model and algorithm is verified through a case study analysis.
1. Introduction
Recently, energy policies considering carbon-free energy and the enhancement of sustainable energy are being established worldwide [1,2]. Thus, the share of renewable energy sources that are carbon-free and sustainable is expected to increase further [3]. However, due to certain characteristics of renewable energy sources, such as their decentralization, intermittency, and uncertainty, the integration of renewable energy generation with high performance remains a challenging task [4,5]. One of the aspects that researchers are studying to address this issue is the development of VPPs based on the concept of distributed energy generation aggregation [6,7,8,9]. VPPs can be categorized into Commercial Virtual Power Plants (CVPPs) and Technical Virtual Power Plants (TVPPs) based on their operational objectives. CVPPs are designed to contribute to the demand balance of the transmission system. They have no regional constraints on resource aggregation and enable various business opportunities through participation in the energy market [10,11]. As a result, aggregators can recruit distributed resources and encourage their participation in the energy market, thereby increasing the visibility of distributed resources and improving the efficiency of grid operations. However, the primary objective of a VPP is profit maximization. So, they often bid all distributed resources into the energy market without considering the impact on the distribution network. This fact increases the potential for grid instability, voltage imbalances, frequency fluctuations, short-circuit currents, and harmonics, due to the arbitrary generation by aggregators [12]. As a result, grid operators are now implementing real-time energy markets and imbalance penalties in addition to the existing day-ahead market as regulatory measures [13]. Furthermore, in order to maintain real-time power balance, the output from distributed energy resources (DERs) has been constrained through the implementation of real-time constraints [14,15]. In the context of a real-time market, real-time prices are provided as the market reflects supply–demand balance conditions, thereby offering short-term price signals. As the trading intervals decrease from 1 h to 30 min, 15 min, and 5 min, flexible resources are likely to receive relatively greater rewards. The imbalance penalty calculates the difference between the planned generation amounts in the day-ahead market and the actual generation in real time at real-time prices. This provides an incentive for VPPs to adhere to their bid amounts in the day-ahead market.
On the other hand, limiting the output power of DERs due to the power balance is a major factor that reduces the revenue of VPP aggregators. Various studies have been conducted to solve these power curtailments and maximize the benefits for aggregators. Ref. [16] adjusts scheduling by considering the predicted grid operating conditions and those provided by the DSO. After this, they adjust the scheduling by considering penalties for real-time non-compliance with the day-ahead scheduling. Ref. [17] describes a method for determining the power bidding curve of a VPP, considering power consumption, the probability of renewable energy generation uncertainty, and the cost of deploying flexible resources. These aforementioned cases can be managed by considering the capabilities of the participants. However, when considering power curtailment, scheduling adjustments for specific participants may be enforced. Ref. [18] presents a method for controlling the generation of PV systems and the charging speed of electric vehicles at each bus to satisfy voltage stability conditions. Additionally, Refs. [19,20] propose operational strategies for participating in DR services to enhance the economic benefits for prosumers. The above method shows that all participants cooperate with power curtailment, but it is necessary to consider the profitability of participants who incur losses during the cooperation process. There is also an approach that involves conducting P2P transactions to mitigate the uncertainty of renewable energy generation. Ref. [21] demonstrates a method for considering the uncertainty of renewable energy generation by placing energy market bids and simultaneously conducting P2P transactions among participants. Refs. [22,23,24] describe a method where P2P transactions are conducted first, considering the uncertainty of renewable energy, and the remaining electricity is then bid into the energy market. These methods effectively manage the uncertainty of renewable energy generation, increase flexibility among market participants, and enhance the overall stability of the energy system. However, the feasibility of such P2P transactions can be limited by regulations of the energy market structures. Additionally, there are challenges related to data communication and processing delays due to technical issues, as well as the need for significant initial investments. Another approach involves current studies on microgrid systems that integrate RES to manage the uncertainties in renewable energy output, which can be applied to VPP research. For example, Ref. [25] proposes a new concept called the Committed Carbon Emission Operation Region (CCEOR) for integrated energy systems, which considers the uncertainties in renewable energy output and the characteristics of low-carbon sequential operations. Ref. [26] suggests a probabilistic triple-layer game method for multi-energy trading in integrated energy markets that include various multi-energy microgrids (MEMGs). The algorithm proposed in [27] applies a two-stage robust optimization (TSRO) method that omits discrete variables and constraints of ESS to effectively compensate for the variability and uncertainty of RES power output. While these techniques excel in ensuring energy self-sufficiency and reducing carbon emissions in small regions by utilizing multiple complex resources, additional robust optimization methods need to be applied for maximizing commercial profit and optimizing energy markets, which are among the primary operational objectives of VPPs. In this context, research has been conducted on optimal bidding strategies to maximize commercial profits in the VPP energy market. First, Refs. [28,29] use neural networks such as LSTM and GAN models to predict uncertainties in load, energy market prices, and DERs, significantly enhancing the operational stability of VPP operators. However, these methods have high computational loads and their prediction accuracy is influenced by the quality and quantity of historical operational data. Refs. [30,31] integrate various types of RES resources and use linear and nonlinear programming techniques such as Mixed-Integer Nonlinear Programming (MINLP) and Mixed-Integer Linear Programming (MILP) to derive optimal profits for VPP operators by participating in multiple energy markets. Nevertheless, these studies only consider day-ahead market bidding, and there is a need to secure additional profitability through the consideration of real-time bidding markets. Another approach for optimizing VPPs is the Optimal Virtual Power Plant Management method using the Model Predictive Control (MPC) approach, as proposed in [32,33]. This method models internal resources and uses a three-tiered structure to optimize VPP generation by effectively controlling internal resources for both day-ahead and real-time market errors. However, this method also only considers day-ahead market bids, necessitating the need to secure profitability through real-time additional bidding.
This paper presents an energy optimization algorithm for VPP aggregators operating PV, WT, and ESS systems. This paper addresses the integration of real-time energy markets, imbalance penalties, and power curtailment in addition to the existing day-ahead energy market. In order to achieve this objective, two MILP (Mixed-Integer Linear Programming) models are employed. The initial MILP model is concerned with the minimization of imbalance penalties that arise from excess generation by a VPP. This is achieved by scheduling the available resources in a more effective manner when the actual awarded bid quantity is less than the submitted bid quantity. This model considers various constraints and parameters such as the forecasted generation, the submitted bids, and the real-time bid quantities to optimize resource allocation and minimize penalties. The second MILP model is designed to maximize profit in the real-time market. It identifies the optimal generation amounts that should be bid during the most profitable time periods. This model considers real-time market prices, the state of charge of the ESS, and other operational constraints to determine the best times to discharge the ESS and sell electricity in the real-time market. This strategy enhances real-time scheduling and resource management within the VPP, leading to improvements in profit maximization and penalty minimization. Specifically, the proposed “Dual-MILP” algorithm schedules DERs every 15 min, considering curtailment areas and generation errors. This allows the Dual-MILP approach to dynamically adjust to real-time market conditions and generation forecasts, providing a solution to the challenges posed by the integration of renewable energy sources and the variability of real-time energy markets.
The remainder of this paper is organized into five sections. Section 2 describes the definition and operational framework of the proposed VPP. Section 3 presents the mathematical formulation of the optimal VPP operation model, which aims to maximize the VPP’s profit in various market environments. In Section 4, case studies are presented to verify the proposed optimal operation model. Finally, the conclusions are presented in Section 5.
2. Description and Framework of the VPP and Energy Market
The structure of the energy market is based on the timelines of the day-ahead market and the real-time market. In this context, the VPP forecasts the next day’s generation power before the day-ahead market closure and places bids in the energy market. In this study, bidding for supply was considered in the power wholesale market, which means that the VPP only performs bidding as a seller. The day-ahead market operates from 08:00 to 11:00 on the day prior to the operational day, with bidding closing at 11:00. Then, at 18:00 on the same day, the results of the day-ahead market are received. Based on the bid results, the VPP determines the availability of surplus renewable energy and formulates generation schedule plans accordingly. For example, when the bid quantity is determined to be lower than the expected quantity, this indicates the occurrence of surplus power. In such cases, the VPP must formulate strategies to either curtail the output to manage the surplus renewable energy or utilize its resources to mitigate the excess. The real-time market is assumed to be held at 22:00–22:45 the previous day, and the real-time market is repeated every 15 min. In order to bid in the real-time market, this paper assumes that the amount of error between the predicted power generation of renewable energy and the successful bid result of the day-ahead market is calculated. Then, it calculates the amount of error compared to the successful bid result of the day-ahead market. It establishes a bidding plan considering the market penalty criteria to be imposed later. In other words, the VPP operator is assumed to be fully responsible for the day-ahead schedule. If errors arise in the bidding results, the operator is subject to market penalties. The structure of the energy market and the basic configuration of the VPP are illustrated in Figure 1.
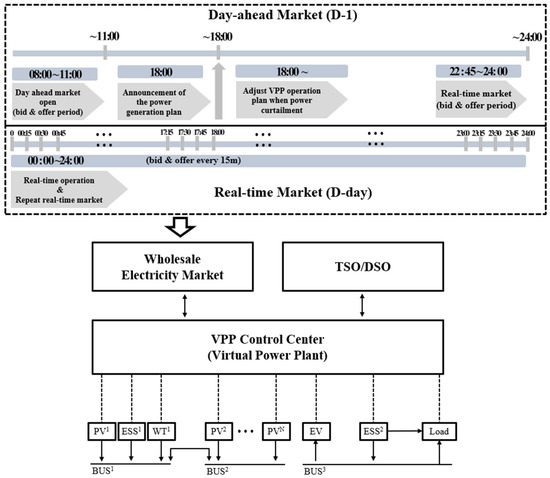
Figure 1.
The structure of the energy market.
3. Optimal Scheduling of VPP Using the Dual-MILP Approaches
3.1. Day-Ahead Market Scheduling
In this section, the mathematical modeling of VPP scheduling in a multi-energy market environment are conducted. The optimization model for VPP operation is divided into the formulation of the day-ahead market scheduling, real-time market scheduling, and additional bidding in the real-time market, following the market processes of the wholesale energy market. In this context, the day-ahead market scheduling optimization model is designed to minimize VPP over-generation by utilizing the ESS to respond to the power curtailment instructions from the grid operator.
The bidding sequence for participation in the day-ahead market is illustrated in Figure 2, where t represents the one-hour set of periods for the VPP day-ahead market operation scheduling, and , denote the estimate generation quantities for PV and WT in each period. , represent the bid quantity for the day-ahead generation plan and the actual confirmed bid quantity from the grid operator. It is assumed that before the closure of the day-ahead market, the VPP bids 100% of the predicted generation power of the RES resources, as follows:
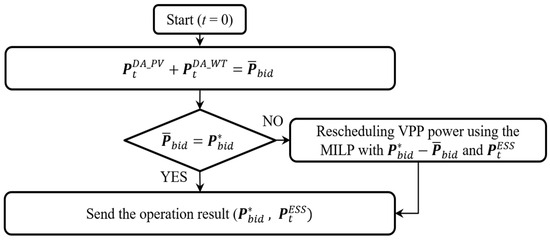
Figure 2.
Bidding sequence for the day-ahead market.
The VPP operator can be bid the entire generation quantity submitted in the day-ahead market. However, the grid operator may request the VPP generator to reduce a certain portion of the bid quantity based on the day-ahead estimate supply–demand balance. In this case, if the day-ahead estimate generation power of the RES is accurate, the VPP must stop or reduce a certain amount of generation to avoid penalties for over-generation, which can result in losses for the VPP. To address this issue, the proposed day-ahead market bid sequence involves establishing an adjustment plan to mitigate profit losses, considering the available ESS resources, or determining whether to curtail the renewable energy output if the bid result is not 100% of the bid plan. The objective function for this is defined by the following formula in Equation (2).
where denote the ESS charging/discharging plan and the day-ahead market price. To prevent excessive ESS operation and ensure ESS stability, the ESS is operated on a daily basis with multiple specified constraints, including the battery capacity, PCS capacity, and SOC levels. The first constraint is designed to maintain an appropriate SOC at the end of each day to prepare for the next day’s operation or emergency support. The formulation for this is provided below [34].
where s represents the unique identifier of the ESS, and denote the minimum SOC, the real-time ESS SOC, and the maximum SOC. The value in Equation (4) is determined based on Equation (5), where , , represent the charging capacity and charging efficiency and the discharging capacity and discharging efficiency. , denote the ESS rated capacity (kWh) and the ESS control period, respectively. The second constraint ensures operation within the rated capacity of the PCS for charging and discharging, as shown in Equations (6) and (7).
In addition, the equation for constraining simultaneous charging and discharging is as follows:
where , represent the state binary variables for the charging mode and discharging mode, respectively.
3.2. Real-Time Market Scheduling
In the real-time market, a VPP is penalized based on the real-time market price, which is taken as the penalty rate. Therefore, the negative error penalty for each time period can be calculated by multiplying the negative error amount by the real-time market price. Similarly, the positive penalty can be calculated by multiplying the positive error amount exceeded by the real-time market price. The market penalty function for generation error is defined as follows:
where represents a 15 min set of periods for the VPP day-ahead market operation plan; , denote the penalty costs for positive and negative error in the real-time market; and represents the expected revenue in the real-time market. Specifically, the positive penalty function for the real-time market is optimized under the assumption that penalties are only imposed on amounts exceeding 5% of the day-ahead market bid quantity. For this purpose, the constant representing the percentage of error is used in Equation (11). Equation (12) represents the MILP objective function for real-time market scheduling. The MILP objective function in Equation (11), which includes the penalty cost and the use of ESS resources within the VPP, aims to optimize the VPP to maximize operational profit by addressing error from the bid results.
For the case of real-time market scheduling, the constraints are the same as those used for the day-ahead market, but because it operates every 15 min, the inequality constraint matrix A and the equality constraint matrix Aeq for MILP application are much more complex, and constraints must be applied at 15 min intervals. First, the constraint matrix for the SOC of ESS in the real-time market is as follows:
where to denote the discharge amounts of the ESS at each time interval. Since the scheduling is carried out in 15 min intervals over 24 h, the 24 h period is divided into 96 columns, forming the matrix . The SOC constraints corresponding to the discharge amounts are also structured in the same manner as those shown in Equation (14). Secondly, the constraint matrix used to prevent simultaneous charging and discharging of the ESS is constructed as follows:
where each include binary conditions that take on values of 0 or 1. The constraint matrix is constructed to prevent simultaneous charging and discharging by multiplying the values of at each time interval by the maximum and minimum charging and discharging amounts of the ESS. Additionally, to incorporate penalties for over-generation and under-generation, the equality matrix is as follows:
Finally, the sequence of the proposed MILP scheduling algorithm, which includes the above constraints in the real-time market, is illustrated in Figure 3.
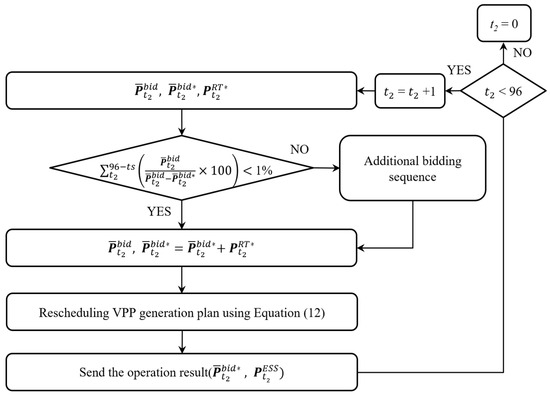
Figure 3.
Bidding sequence for the real-time market.
3.3. Optimal Additional Bidding in the Real-Time Market
Through the MILP optimization in Equation (12), the VPP schedules its daily generation plan in real time to minimize penalties by utilizing its available resources. However, since the ESS capacity within the VPP is finite and must maintain a certain SOC level, limitations arise if the VPP operates only based on the grid operator commands. For example, if a command to reduce generation is received for a specific time period, the VPP uses its ESS resources to charge excess generation. However, if the over-generation exceeds the ESS capacity, it becomes challenging to fully accommodate the over-generation, and additional methods must be employed to discharge the ESS to ensure operation the following day. To address these issues, this paper proposes a sequence for additional bidding in the real-time market. For this purpose, the function in Equations (10) and (11) is modified as follows:
where represents the additional bid capacity in the real-time market. If the total amount of in Equation (20) is modified, the value of the MILP optimization in Equation (12), which uses this variable, will change accordingly. This means that by finding and applying the optimal value of , it can be used in the real-time market optimization algorithm in Equation (12). For this purpose, additional MILP modeling is performed, and the cost function is as follows:
The sequence for additional bidding in the real-time market is illustrated in Figure 4.
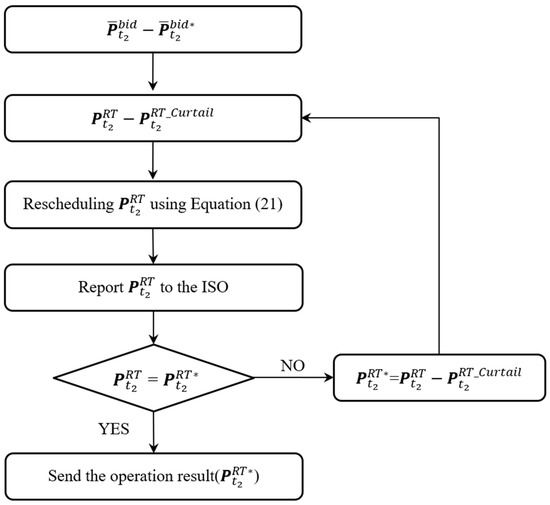
Figure 4.
Operational sequence for real-time additional bidding.
In Figure 4, represents the real-time additional bid quantity not approved by the system operator. The overall flow of the algorithm can be summarized as follows: The VPP operator adjusts the scheduling of the RES and submits it to the DSO. If the DSO notices that the scheduling does not meet the supply–demand balance, it provides a new bid quantity to the VPP. Then, the VPP attempts to offset the power curtailment as much as possible using internal resources. If it cannot be fully offset, the operator proceeds with output curtailment while considering penalties to maximize operation profit. After this, through the real-time market, the VPP platform operator adjusts the generation by placing additional real-time bids.
4. Simulation Analysis and Comparison
4.1. Definition of Simulation Scenarios
This section investigates the performance of the proposed Dual-MILP bidding strategy for VPPs based on the various case studies. The main contribution of the proposed Dual-MILP method is that it allows real-time scheduling of VPP generation in a real-time market. Specifically, it aims to maximize VPP profit through the real-time scheduling of RES resources within the VPP in response to (1) generation errors within the VPP or (2) sudden output adjustment requests from the DSO/ISO leading to changes in . To achieve this, each RES resource sends newly updated generation forecasts to the MILP Control Center every 15 min. These values are compared with the actual bid value to obtain or . Based on this comparison, the generation of RES resources owned by the VPP is scheduled in the day-ahead market. The detailed simulation setup is shown in Figure 5 and Figure 6 below.
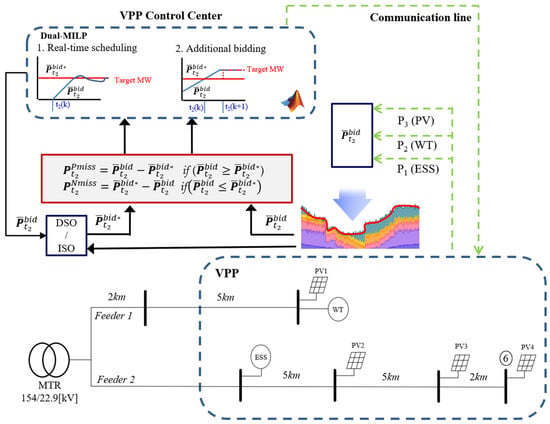
Figure 5.
System configuration for simulation.
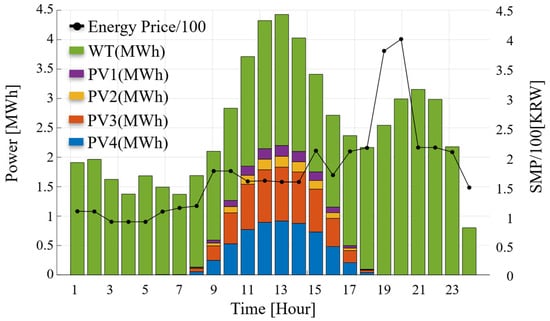
Figure 6.
Day-ahead forecasted RES generation and hourly electricity prices.
The case scenarios compare the scheduling and cost results of four additional cases based on the basic case, which only involves preliminary scheduling, as shown in Table 1. The scenarios include three cases: First, the day-ahead generation and bid values differ without re-scheduling, Second, the day-ahead generation and bid values differ with ESS re-scheduling, Third, additional real-time bidding is performed. In these scenarios, the rated power of the available ESS resource is assumed to be 500 kW, the rated capacity is 5000 kWh, and the initial SOC is 50%.

Table 1.
Scenario configuration table.
4.2. Simulation Results
As explained in Section 1 and Section 2, the grid operator requests the VPP to adjust its generation output according to the demand–supply balance. To validate this scenario, scenario 1 is designed to impose a 20% power curtailment on the bid quantity submitted during peak generation periods. In Figure 7, the black waveform and blue waveform represent the submitted VPP generation plan and the bid quantity, respectively, while the green waveform represents the real-time energy price. The red blocks and blue blocks represent the expected income and actual income, respectively. As shown in Figure 7, during the over-generation periods where penalties occur, it is evident that there is a significant discrepancy between the actual income and the forecasted income if no additional re-scheduling is performed. To ensure the accuracy and reliability of our simulation results, the following hardware configuration was used: CPU: [12th Gen Intel(R) Core(TM) i5-1240P 1.70 GHz], RAM: [16.0 GB], GPU: [Intel Iris Xe], Operating System: [Windows 11 Pro].
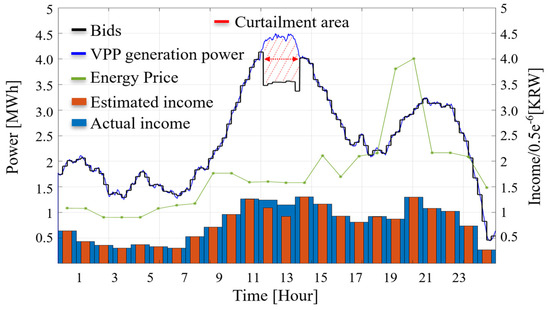
Figure 7.
Results of scenario 1 without the proposed method (Case 1).
Figure 8 illustrates the scenario when the VPP uses its ESS and the proposed algorithm to mitigate penalties from over-generation. According to the ESS capacity assumptions defined in Section 4.1, the SOC is limited to operate within 0.3 to 0.7. Due to these constraints, if there is no additional discharge scenario, the ESS cannot fully absorb the entire over-generation, and only a portion is compensated. In this case, although the penalties are reduced compared to the scenario in Figure 7, the actual income is still lowered due to over-generation penalties.
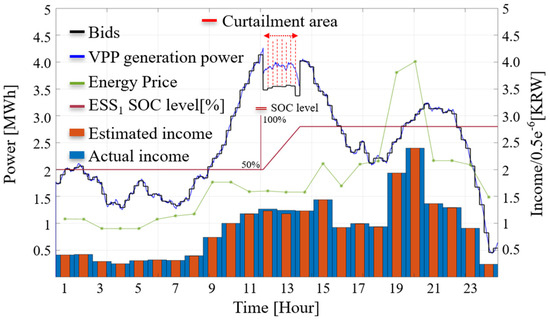
Figure 8.
Results of scenario 1 when the proposed method is used without additional bidding in the real-time market (Case 2).
To overcome the limitations illustrated in Figure 8, this paper proposes the Dual-MILP approach explained in Section 3. The proposed Dual-MILP algorithm performs additional bidding in areas where the optimal profit can be achieved, based on the values updated every 15 min. The algorithm process can be summarized as follows: First, if a curtailment area occurs, the algorithm schedules the ESS to minimize the penalty for over-generation. Next, using the SOC capacity of the ESS charged through the curtailment area and the remaining time intervals over 24 h, the algorithm calculates the areas where additional bidding can yield profit, using Equation (14), and reflects this in the VPP generation scheduling. The simulation results following this sequence can be seen in Figure 9. In the real-time market within the curtailment areas, the algorithm reduces the penalty for over-generation by charging the ESS and additional bid quantities through the additional bidding algorithm, marked with the yellow dashed line. This approach achieves higher income compared to simple over-generation compensation methods, while also improving the SOC capacity through discharges to address over-generation on the following day. The proposed method has the drawback of requiring accurate real-time energy price data. To mitigate this, it is advisable to update the energy price data needed for the optimization algorithm at least every 15 min.
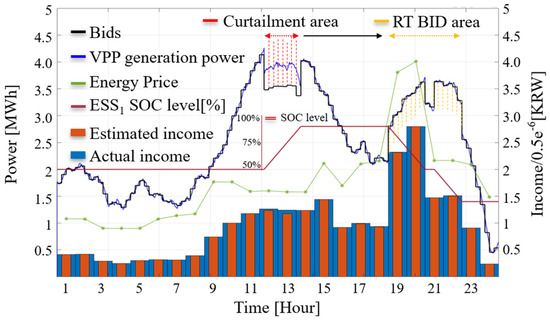
Figure 9.
Results of scenario 2 when the proposed method is used with additional bidding in the real-time market (Case 3).
Finally, if the penalties for over-generation cannot be overcome through additional generation bidding and ESS scheduling in the real-time market, as shown in Figure 10, the final way to mitigate penalties is to control the renewable energy generation resources within the VPP. This approach minimizes penalties by reducing over-generation. However, since this method negatively impacts the profit of VPP operators who generate income from renewable energy, it is considered a last-resort process.
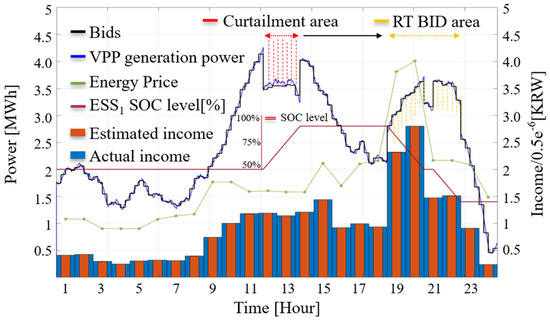
Figure 10.
Results of scenario 3 when the proposed method is used with additional bidding in the real-time market and RES curtailment (Case 4).
The simulation results for scenario 4 are shown in Figure 11. In scenario 4, since the generation power curtailment is lower than the charging capacity limit of the ESS within the VPP, all of the over-generation capacity can be absorbed without an additional curtailment area. It can be observed that the proposed method maximizes the VPP’s profitability by bidding for additional generation in the real-time market during the peak energy price period from 19:00 to 20:00.
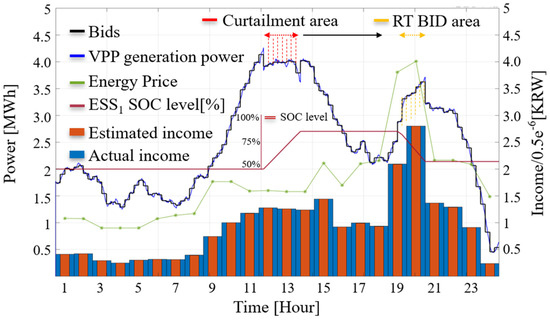
Figure 11.
Results of scenario 4 when the proposed method is used with additional bidding in the real-time market (Case 5).
The results of the simulations for each scenario are presented in Table 2. The effectiveness of the algorithm is demonstrated by key parameters such as the penalty cost for over-generation, the actual income for curtailment areas, the ratio of penalties to income, and income from additional real-time bidding. As evidenced by the simulation results, the proposed algorithm yields a lower ratio of penalties to income. Furthermore, it can be observed that the income generated by the VPP is increased by the additional bidding.

Table 2.
The impact of varying operational scenarios on VPP income.
5. Conclusions
This paper presents an optimal scheduling model for VPPs as a solution to renewable energy power curtailment, considering the characteristics of renewable energy sources such as decentralization, intermittency, and uncertainty. In order to achieve this objective, this paper focuses on VPP aggregators that operate PV, WT, and ESS, which constitute the majority of renewable energy resources. Furthermore, this paper presents an energy optimization scheduling technique that utilizes resources within the VPP in the complex energy market environment, including the day-ahead market, the real-time energy market, imbalance, and power curtailment. In order to achieve this goal, this study analyzed a VPP one-day market bidding model, a real-time market scheduling model, and a real-time market additional bidding model by applying step-by-step modeling techniques. In order to derive the optimal value of the operation model, a MILP technique was employed.
The results of the case study analysis demonstrate that, in the context of power curtailment commands, the proposed algorithm achieved a reduction in operational losses of approximately 3–15% in comparison to a traditional VPP. Furthermore, real-time additional bidding yielded an increase in VPP profit of over 21%. Based on the numerical results of this case study, the main conclusions of this paper are as follows:
- (1)
- The proposed Dual-MILP algorithm schedules ESS generation every 15 min, considering curtailment areas and generation errors. Additionally, it performs real-time supplementary bidding for the area that can achieve optimal profit in the next time slot.
- (2)
- Through this, the VPP configuration using PV, WT systems, and ESS demonstrated higher profitability in the complex energy market structure compared to standalone systems, thereby confirming the economic attractiveness of this VPP setup.
- (3)
- Additionally, it was demonstrated that a VPP based on an uncertain renewable energy resource can be characterized and quantified to provide flexibility and ancillary services. This interaction can assist grid system operators in managing and planning the transmission system.
- (4)
- The proposed strategy was formulated as a MILP model and simulated on a multi-energy system, demonstrating the effectiveness and applicability of the model.
- (5)
- In scenarios involving more dynamic markets within larger systems, computational efficiency becomes critical. To address this, it can be advantageous to use commercial solvers such as Gurobi, CPLEX, or CBC instead of the intlprog solver used here in the MATLAB (version R2020a) simulations in Section 4.
Lastly, in this work, there are also some parts that could be improved. Firstly, future research could consider the maximization of profit assuming various grid support services, which have recently diversified [33,34,35,36] (from the day-ahead scale of the market to almost-instantaneous frequency regulation). The proposed model only considers the real-time market and additional bidding market, thus failing to leverage revenue generation through grid support services. Given the above research limitations, future studies could utilize a hierarchical structure like that used in [26,32] to schedule resources in real time while also enabling profit generation from various grid support services.
Author Contributions
S.-J.Y.: conceptualization, methodology, analysis, writing—original draft preparation; K.-S.R., C.K., and Y.-H.N.: investigation, data curation, model analysis, writing; D.-J.K. and B.K.: writing—review and editing, resources, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was conducted under the framework of a research-and-development program of the Korea Institute of Energy Research (C4–2422–01). This research was funded by the Ministry of Trade, Industry, and Energy and supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) (grant number: [No. 20223030020110]).
Data Availability Statement
The data used to support the findings of this study are included in this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, Y.; Su, Q.; Li, B.; Zhang, Y.; Wang, X.; Zhao, H.; Guo, S. Have those countries declaring “zero carbon” or “carbon neutral” climate goals achieved carbon emissions-economic growth decoupling? J. Clean. Prod. 2022, 363, 132450. [Google Scholar] [CrossRef]
- Shabani, M.J.; Moghaddas-Tafreshi, S.M. Fully-decentralized coordination for simultaneous hydrogen, power, and heat interaction in a multi-carrier-energy system considering private ownership. Electr. Power Syst. Res. 2020, 180, 106099. [Google Scholar] [CrossRef]
- Breyer, C.; Khalili, S.; Bogdanov, D.; Ram, M.; Oyewo, A.S.; Aghahosseini, A.; Sovacool, B.K. On the history and future of 100% renewable energy systems research. IEEE Access 2022, 10, 78176–78218. [Google Scholar] [CrossRef]
- Shafiekhani, M.; Ahmadi, A.; Homaee, O.; Shafie-khah, M.; Catalão, J.P. Optimal bidding strategy of a renewable-based virtual power plant including wind and solar units and dispatchable loads. Energy 2022, 239, 122379. [Google Scholar] [CrossRef]
- Ela, E.; Diakov, V.; Ibanez, E.; Heaney, M. Impacts of variability and uncertainty in solar photovoltaic generation at multiple timescales. In Technical Report NREL; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2013. [Google Scholar]
- Zhou, Y.; Wei, Z.; Sun, G.; Cheung, K.W.; Zang, H.; Chen, S. A robust optimization approach for integrated community energy system in energy and ancillary service markets. Energy 2018, 148, 1–15. [Google Scholar] [CrossRef]
- Vicente-Pastor, A.; Nieto-Martin, J.; Bunn, D.W.; Laur, A. Evaluation of flexibility markets for retailer–DSO–TSO coordination. IEEE Trans. Power Syst. 2018, 34, 2003–2012. [Google Scholar] [CrossRef]
- de Cerio Mendaza, I.D.; Szczesny, I.G.; Pillai, J.R.; Bak-Jensen, B. Demand response control in low voltage grids for technical and commercial aggregation services. IEEE Trans. Smart Grid 2015, 7, 2771–2780. [Google Scholar] [CrossRef]
- Nasiri, N.; Zeynali, S.; Ravadanegh, S.N.; Marzband, M. A hybrid robust-stochastic approach for strategic scheduling of a multi-energy system as a price-maker player in day-ahead wholesale market. Energy 2021, 235, 121398. [Google Scholar] [CrossRef]
- Amissah, J.; Abdel-Rahim, O.; Mansour, D.E.A.; Bajaj, M.; Zaitsev, I.; Abdelkader, S. Developing a three stage coordinated approach to enhance efficiency and reliability of virtual power plants. Sci. Rep. 2024, 14, 13105. [Google Scholar] [CrossRef]
- Li, S.; Huo, X.; Zhang, X.; Li, G.; Kong, X.; Zhang, S. A Multi-Agent Optimal Bidding Strategy in Multi-Operator VPPs Based on SGHSA. Int. Trans. Electr. Energy Syst. 2022, 1, 7584424. [Google Scholar] [CrossRef]
- Husin, H.; Zaki, M. A critical review of the integration of renewable energy sources with various technologies. Prot. Control Mod. Power Syst. 2021, 6, 1–18. [Google Scholar]
- Joos, M.; Staffell, I. Short-term integration costs of variable renewable energy: Wind curtailment and balancing in Britain and Germany. Renew. Sustain. Energy Rev. 2018, 86, 45–65. [Google Scholar] [CrossRef]
- Kane, L.; Ault, G. A review and analysis of renewable energy curtailment schemes and Principles of Access: Transitioning towards business as usual. Energy Policy 2014, 72, 67–77. [Google Scholar] [CrossRef]
- Bird, L.; Cochran, J.; Wang, X. Wind and solar energy curtailment: Experience and practices in the United States (No. NREL/TP-6A20-60983). In Technical Report NREL; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2014. [Google Scholar]
- Park, S.Y.; Park, S.W.; Son, S.Y. Optimal VPP Operation Considering Network Constraint Uncertainty of DSO. IEEE Access 2023, 11, 8523–8530. [Google Scholar] [CrossRef]
- Ghanuni, A.; Sharifi, R.; Farahani, H.F. A risk-based multi-objective energy scheduling and bidding strategy for a technical virtual power plant. Electr. Power Syst. Res. 2023, 220, 109344. [Google Scholar] [CrossRef]
- Meng, Y.; Qiu, J.; Zhang, C.; Lei, G.; Zhu, J. A Holistic P2P market for active and reactive energy trading in VPPs considering both financial benefits and network constraints. Appl. Energy 2024, 356, 122396. [Google Scholar] [CrossRef]
- Maeyaert, L.; Vandevelde, L.; Döring, T. Battery storage for ancillary services in smart distribution grids. J. Energy Storage 2020, 30, 101524. [Google Scholar] [CrossRef]
- Sasidharan, N.; Singh, J.G.; Ongsakul, W. Real time active power ancillary service using DC community grid with electric vehicles and demand response. Procedia Technol. 2015, 21, 41–48. [Google Scholar] [CrossRef]
- Lin, W.T.; Chen, G.; Li, C. Risk-averse energy trading among peer-to-peer based virtual power plants: A stochastic game approach. Int. J. Electr. Power Energy Syst. 2021, 132, 107145. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Liu, X.; Chen, G.; Dong, Z.Y. Two-stage community energy trading under end-edge-cloud orchestration. IEEE Internet Things J. 2022, 10, 1961–1972. [Google Scholar] [CrossRef]
- Seven, S.; Yao, G.; Soran, A.; Onen, A.; Muyeen, S.M. Peer-to-peer energy trading in virtual power plant based on blockchain smart contracts. IEEE Access 2020, 8, 175713–175726. [Google Scholar] [CrossRef]
- Aguilar, J.; Bordons, C.; Arce, A.; Galán, R. Intent profile strategy for virtual power plant participation in simultaneous energy markets with dynamic storage management. IEEE Access 2022, 10, 22599–22609. [Google Scholar] [CrossRef]
- Jiang, Y.; Ren, Z.; Li, W. Committed carbon emission operation region for integrated energy systems: Concepts and analyses. IEEE Trans. Sustain. Energy 2023, 15, 1194–1209. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Xu, Y.; Wang, L.; Yang, N. Distributed tri-layer risk-averse stochastic game approach for energy trading among multi-energy microgrids. Appl. Energy 2023, 331, 120282. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Y.; Li, Z.; Jiang, T.; Li, X. Two-stage robust operation of electricity-gas-heat integrated multi-energy microgrids considering heterogeneous uncertainties. Appl. Energy 2024, 371, 123690. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y.; Bo, W.; Wang, D.; Zhang, D.; Shi, J. Optimal Scheduling of Virtual Power Plant Considering Revenue Risk with High-Proportion Renewable Energy Penetration. Electronics 2023, 12, 4387. [Google Scholar] [CrossRef]
- Ghasemi-Olanlari, F.; Moradi-Sepahvand, M.; Amraee, T. Two-stage risk-constrained stochastic optimal bidding strategy of virtual power plant considering distributed generation outage. IET Gener. Transm. Distrib. 2023, 17, 1884–1901. [Google Scholar] [CrossRef]
- Wu, Q.; Li, C.; Bai, J. Optimal bidding strategy for multi-energy virtual power plant participating in coupled energy, frequency regulation and carbon trading markets. Int. J. Hydrogen Energy 2024, 73, 430–442. [Google Scholar]
- Yang, C.; Du, X.; Xu, D.; Tang, J.; Lin, X.; Xie, K.; Li, W. Optimal bidding strategy of renewable-based virtual power plant in the day-ahead market. Int. J. Electr. Power Energy Syst. 2023, 144, 108557. [Google Scholar] [CrossRef]
- Mei, S.; Tan, Q.; Liu, Y.; Trivedi, A.; Srinivasan, D. Optimal bidding strategy for virtual power plant participating in combined electricity and ancillary services market considering dynamic demand response price and integrated consumption satisfaction. Energy 2023, 284, 128592. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Carli, R.; Dotoli, M. Robust Optimal Demand Response of Energy-efficient Commercial Buildings. In Proceedings of the 2022 European Control Conference (ECC), London, UK, 12–15 July 2022; pp. 1–6. [Google Scholar]
- Dang, J. SoC Feedback Control for Wind and ESS Hybrid Power System Frequency Regulation. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 2, 79–86. [Google Scholar] [CrossRef]
- Bolzoni, A.; Parisio, A.; Todd, R.; Forsyth, A.J. Optimal virtual power plant management for multiple grid support services. IEEE Trans. Energy Convers. 2020, 36, 1479–1490. [Google Scholar] [CrossRef]
- Jiang, Y.; Dong, J.; Huang, H. Optimal bidding strategy for the price-maker virtual power plant in the day-ahead market based on multi-agent twin delayed deep deterministic policy gradient algorithm. Energy 2024, 306, 132388. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).