Application of Dynamic Weight Mixture Model Based on Dual Sliding Windows in Carbon Price Forecasting

Abstract

As global climate change intensifies, nations around the world are implementing policies aimed at reducing emissions, with carbon-trading mechanisms emerging as a key market-based tool. China has launched carbon-trading markets in several cities, achieving significant trading volumes. Carbon-trading mechanisms encompass cap-and-trade markets and voluntary markets, influenced by various factors, including policy changes, economic conditions, energy prices, and climate fluctuations. The complexity of these factors, coupled with the nonlinear and non-stationary nature of carbon prices, makes forecasting a substantial challenge. This paper proposes a dynamic weight hybrid forecasting model based on a dual sliding window approach, effectively integrating multiple forecasting models such as LSTM, Random Forests, and LASSO. This model facilitates a thorough analysis of the influences of policy, market dynamics, technological advancements, and climatic conditions on carbon pricing. It serves as a potent tool for predicting carbon market price fluctuations and offers valuable decision support to stakeholders in the carbon market, ultimately aiding in the global efforts towards emission reduction and achieving sustainable development goals.

1. Introduction

As the impact of global climate change intensifies and the emphasis on sustainable development goals escalates, the management and mitigation of carbon emissions have risen to prominence within the international agenda. Governments worldwide acknowledge the critical need to curtail carbon emissions and are actively devising policies that foster carbon reduction initiatives. The 1997 Kyoto Protocol specified the targets for reducing greenhouse gases for industrialized countries from 2005 to 2020 and pro-posed three mechanisms for emission reduction: carbon emissions trading, joint fulfillment, and the Clean Development Mechanism [1]. Among these, the carbon-trading mechanism serves as an effective market-based tool aimed at incentivizing reduction behaviors through the pricing of carbon emissions, incentivizing reduction efforts through the monetization of carbon emissions and serving as a fundamental strategy to meet greenhouse gas reduction targets [2]. In 2020, China announced its dual carbon goals, underscoring the necessity to establish and refine market mechanisms and to harness the role of the national carbon emission trading market. Presently, China has operational carbon-trading markets in multiple cities including Beijing, Shanghai, and Guangzhou, with the cumulative transaction volume reaching 440 million tons and a transaction value of CNY 24.9 billion by the end of 2023, reflecting a dynamically evolving carbon market [3].

The carbon market plays a crucial role in achieving global and regional climate goals. By pricing carbon emissions, it creates financial incentives for businesses and industrial sectors to reduce their carbon footprints [4]. Carbon trading is categorized into two systems: cap-and-trade markets and voluntary markets. Cap-and-trade markets involve the allocation of carbon quotas by governments, usually distributed to businesses through auctions or free allocations and subsequently traded in the market. These quotas, often based on historical emissions and industry benchmarks, enable enterprises to actively participate in buying and selling [5]. This mechanism is mandatory in regions like the European Union, the United States’ California, and China [6]. Conversely, voluntary markets allow enterprises to engage in the trading of carbon credits voluntarily, often through participation in certified emission reduction projects, which are active in countries such as Canada and Australia [7]. This market-driven approach encourages innovation and investment in clean technologies, promoting the transition to a low-carbon economy. These systems not only ensure the achievement of emission reduction targets but also provide businesses with the flexibility to comply in a cost-effective manner. By integrating various market products such as low-carbon investment funds and carbon credit futures, the carbon market offers multiple pathways for investors to support emission reduction efforts.

The carbon price, a pivotal element in the carbon market, is subject to influences from policy shifts, economic activity, energy price fluctuations, and climatic extremes. This complexity renders carbon price forecasting a formidable task. Accurate carbon price pre-dictions are vital for establishing a robust price discovery mechanism and for guiding decisions in production, management, and investment. The nonlinear, non-stationary, and multifaceted nature of carbon prices, coupled with the intrinsic risks distinct from traditional financial assets like stocks, necessitates a sophisticated approach to forecasting [8,9,10].

Practically, precise carbon price forecasting is essential for enabling businesses and policymakers to make informed decisions. For businesses, it improves risk management, optimizes investment strategies, and facilitates efficient resource allocation. For governments, understanding carbon price dynamics helps in formulating more effective environmental policies, driving emission reductions, and advancing global climate objectives. Thus, the forecasting model presented in this paper is not only a theoretical innovation but also holds considerable potential for practical application, contributing significantly to the advancement of global sustainable development.

Accurate forecasting of carbon prices is imperative for informed decision-making by governments. The pricing mechanism serves as a pivotal component within the intricate carbon market system, significantly influenced by diverse factors such as energy prices, abnormal weather patterns, and political decisions [11]. Early studies of the carbon market predominantly focused on elucidating the operational mechanisms of carbon trading, garnering substantial scholarly attention. For instance, Jesper and Rasmussen utilized a general equilibrium model to explore various methods of allocating tradable carbon emission rights, highlighting the potential compensatory benefits of emission rights [12]. Similarly, Benz and Truck simulated different approaches to EU emission allowance returns, uncovering fluctuations in the demand for CO₂ quotas under distinct trading mechanisms [13]. Tavoni et al. employed a comprehensive model to quantify the impacts of carbon-trading mechanisms on different regions, showcasing the efficiency and equity of the carbon market in promoting clean energy investments [14]. Meanwhile, Daskalakis assessed the market efficiency of EU carbon futures, observing a gradual maturation of the EU ETS [15]. These studies laid the theoretical foundation for the carbon market, emphasizing the important role of carbon-trading mechanisms in emission reduction and economic benefits. However, there remains a significant gap in the area of carbon price forecasting.

While acknowledging the carbon-trading market’s evolution towards resembling a financial market, recent research has delved into forecasting carbon prices to maintain market stability and inform investor strategies [16]. This shift has seen the emergence of various forecasting methodologies, including traditional econometric models, emerging machine learning algorithms, and composite models. Chevallier pioneered the application of non-parametric models in carbon price forecasting, highlighting the nonlinear nature of carbon spot price data and their effectiveness through empirical evidence [17]. Conversely, Koop and Tole utilized Dynamic Moving Average (DMA) to describe the characteristics of carbon prices, providing policy and statistical insights by flexibly capturing the dynamic changes in time series data [18]. Byun and Cho used the GARCH model to handle the volatility in time series data and identified significant predictors of carbon prices, emphasizing the roles of electricity, coal, and Brent crude oil prices [19]. Additionally, Han et al. used a Distributed Lag Model to forecast EU carbon prices, demonstrating the effectiveness of the GA-ridge algorithm in selecting predictive variables [20].

The advent of machine learning has further revolutionized carbon price forecasting, utilizing powerful data analysis capabilities to capture nonlinear data characteristics. Atsalakis proposed computational intelligence techniques such as the hybrid neuro-fuzzy controller (PATSOS), artificial neural networks (ANN), and adaptive neuro-fuzzy inference system (ANFIS), which combine neural networks and fuzzy logic to capture the complex nonlinear features in carbon price data. Among these, PATSOS demonstrated the highest prediction accuracy [21]. Abdi and Taghipour constructed a probabilistic model based on Bayesian neural networks (BNN), incorporating energy prices, economic growth, and weather conditions. Using Bayesian statistics to handle uncertainty and prior information, they improved the robustness and accuracy of carbon price predictions in the Western Climate Initiative market [22]. Simultaneously, Jaramillo-Morán and García-García developed a multi-layer perceptron neural network (MLP) model, which processes complex nonlinear relationships through a multi-layer network structure to forecast carbon quota prices and examine the spatiotemporal relationships between electricity, steel, and carbon prices [23]. Yahşi et al. explored various forecasting models and found that the Random Forest algorithm performed excellently in predicting EU carbon prices. The Random Forest approach constructs multiple decision trees and integrates the results of various models, enhancing the stability and accuracy of predictions [24]. Additionally, Adekoya compared forecasting models using the Feasible Generalized Least Squares (FQGLS) estimation, which addressed heteroscedasticity and autocorrelation issues, highlighting the effectiveness of asymmetric models and the significance of energy prices in carbon price forecasting [25].

In this context, this paper considers the impacts of policy, market, technology, and climate on the carbon market. By integrating traditional algorithms such as LASSO, LSTM, and RFR with a dynamic weighting hybrid strategy, and using Python 3.8 software, a superior carbon price forecasting algorithm is developed. The primary goal is to enhance the accuracy and robustness of carbon price predictions. By providing more accurate and reliable carbon price data, this model helps reduce market uncertainty and improve the scientific and effective nature of the decision-making process. This not only helps businesses remain competitive in a complex and volatile market environment but also assists policymakers in formulating more flexible and precise carbon emission policies, thus advancing global and regional climate goals. For businesses, accurate carbon price forecasts can optimize investment decisions, improve risk management, and facilitate efficient resource allocation. Policymakers can use carbon price forecasting models to create more targeted environmental policies, effectively promoting emission reduction goals. Investors can conduct more precise market analyses using the model, making more informed low-carbon investment choices. Additionally, regulatory bodies can use this model to monitor market dynamics, ensuring the stability and transparency of the carbon market, thereby enhancing market trust and participation.

The structure of this paper is as follows: Section 2 details the materials and methods used, including data preprocessing and the hybrid forecasting model. Section 3 presents the results and their analysis. Section 4 compares the performance of various models. Finally, Section 5 discusses the conclusions and future work directions.

2. Materials and Methods

2.1. ICEEMDAN Model

Data preprocessing is essential to ensure the quality of the original data, reduce noise, and make the data more suitable for creating forecasting models. In carbon price forecasting, the reasons for data preprocessing include ensuring data integrity and accuracy, capturing key features, and reducing the impact of external factors.

This paper employs the Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN), an enhanced version of the Empirical Mode Decomposition (EMD) method that is adaptive and efficient [26,27,28], particularly suitable for nonlinear and non-stationary time series data [29,30]. The advantages of using ICEEMDAN for preprocessing include the following:

Adaptivity: ICEEMDAN can better adapt to data characteristics of different scales and frequencies, automatically adjusting decomposition layers to extract more meaningful modes.

Effective denoising: by incorporating noise-assisted components, ICEEMDAN better suppresses the effects of noise during decomposition, improving the separation of signal from noise.

Reduced modal coupling: the improved ensemble method helps reduce the interaction between modes, enhancing the independence of the modes.

Preprocessing is crucial for establishing an accurate carbon price forecasting model. Original data may have missing or outlier values, and using such data directly can lead to inaccuracies and instabilities in model training. Different influencing factors have different units of measurement; to eliminate the impact of scale differences on the model, data normalization is required. Additionally, time series data often contain trends and seasonality, and the forecasting model needs to better reveal the intrinsic patterns of the data, making detrending and deseasonalization necessary preprocessing steps. In handling these steps, the use of Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN) offers significant advantages. ICEEMDAN introduces adaptively controlled amplitude of white noise to avoid mode mixing issues, enhancing the robustness of modal decomposition. Also, by integrating multiple decomposition results, ICEEMDAN reduces the variance of the decomposition results, making them more stable. This method better adapts to the nonlinear and non-stationary nature of carbon price data, providing a reliable foundation for subsequent modeling and forecasting.

Empirical Mode Decomposition (EMD) was proposed by Huang et al. [25] to smooth signals with nonlinear and non-stationary characteristics. The EMD technique decomposes original data into intrinsic mode functions with different scale oscillations. However, due to the discontinuities in the original signal, it includes mode mixing issues. To address the problems in EMD, Wu and Huang [27] proposed the Ensemble Empirical Mode Decomposition (EEMD) technique. Although EEMD can solve mode mixing issues, it does not completely eliminate residual noise. Therefore, Torres et al. [28] proposed an improved method called Ensemble Empirical Mode Decomposition with Adaptive Noise. However, the improved algorithm still had some issues, such as potential residual noise in the modes and possible spurious modes. To resolve these issues, Colominas et al. [31] proposed an advanced method called Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, or ICEEMDAN.

Using the EMD decomposition method, $E_k\left(·\right)$ is defined as the $k$-th order mode; the details of the ICEEMDAN method are as follows:

Step one: Add $E_1\left(w^{\left(i\right)}\right)$ to the initial signal $x$:

$$x^{\left(i\right)}=x+{\beta }_0{E}_1\left(w^{\left(i\right)}\right)$$

(1)

where $w^{\left(i\right)}$ is Gaussian white noise with a mean of zero, and ${\beta }_0$ represents the amplitude coefficient of the added noise.

Step two: Use EMD to determine the local mean of signal $x^{\left(i\right)}$ to obtain the first residual:

$$r_1=〈M\left(x^{\left(i\right)}\right)〉$$

(2)

where $M\left(·\right)$ represents the operator that generates the local average.

Step three: Identify the first mode ${IMF}_1$ when $k=1$:

$${IMF}_1=x-r_1$$

(3)

Step four: Identify the second mode ${IMF}_2$

$${IMF}_2=r_1-r_2$$

(4)

$$r_2=〈M\left(r_1+{\beta }_1{E}_2\left(w^{\left(i\right)}\right)\right)〉$$

(5)

Step five: Identify the $k$-th mode ${IMF}_k$:

$${IMF}_k=r_{k-1}-r_k, k=3, 4, \cdots , K$$

(6)

$$r_k=〈M\left(r_{k-1}+{\beta }_{k-1}{E}_k\left(w^{\left(i\right)}\right)\right)〉$$

(7)

Step six: Repeat step five for the next iteration.

Through the preprocessing with ICEEMDAN, key features of the carbon price data can be better preserved, and noise interference can be minimized, providing more reliable inputs for subsequent model training.

2.2. Mixed Forecasting Algorithm Model

2.2.1. Least Absolute Shrinkage and Selection Operator (LASSO) Model

LASSO is a variable selection method with high model stability capable of effective feature extraction. It continuously compresses coefficients by introducing a penalty term into the model estimation to simplify the model while effectively addressing issues of overfitting and multicollinearity [32]. The LASSO model refines the model by constructing a penalty function aimed at compressing regression coefficients, making it a biased estimator for dealing with data that exhibit complex collinearity [33]. While ridge regression cannot reduce model complexity, LASSO regression optimizes on the basis of ridge regression by potentially compressing coefficients to zero, thus reducing model complexity [34]. The objective function of LASSO regression can be expressed as follows:

$$L\left(b|\mathit{X},y\right)=\sum {\left(y-\mathit{X}b\right)}^2+\lambda {‖b‖}_1=\sum {\left(y-\mathit{X}b\right)}^2+\sum \lambda \left|b\right|$$

(8)

where $\lambda {‖b‖}_1$ is the penalty term of the function, $\lambda$ is the penalty coefficient; and ${‖b‖}_1$ is the regularization of the regression coefficients, representing the sum of the absolute values of all regression coefficients. In the cross-validation curve, choose $\lambda$ where the bias is minimized, under which the LASSO regression model has the best fit. LASSO is suitable for datasets with a large number of features, effectively performing feature selection to prevent overfitting.

Assume that there is carbon price data $Z_0$, and other influencing factor data $Z_1$, $Z_2$, … $Z_M$. $Z_0$ obtains $K_0$ IMFs from the ICEEMDAN method (Formulas (1)–(7)) as $\left[{IMF}_1^{Z_0},{IMF}_2^{Z_0},\cdots ,{IMF}_{K_0}^{Z_0}\right]$. In this paper, a total of 9 influencing factors were selected (see

Table 1. Data indicator description.

Indicator		Unit	Mean	Std	Min.	Max.	Data Source
Predicted data	($Z_0$)	CNY/ton	61.04	6.97	50.52	81.67	[35]
Financial market indicators	($Z_1$)	-	12.87	1.93	9.03	17.41	[17,19,25,35]
	($Z_2$)	USD /CNY	688.64	28	630.1	725.5	[11,17,19]
	($Z_3$)	EUR/CNY	735.72	34.6	675	808.8	[11,17,19]
	($Z_4$)	-	100.7	3.55	95.5	106.4	[18,20,35]
Energy market indicators	($Z_5$)	(CNY/barrel)	614	71.9	481.5	806.6	[18,23,35,36]
	($Z_6$)	(CNY/ton)	6365.3	1401.26	4148	9415	[11,18,35]
	($Z_7$)	(CNY/cubic meter)	3.6	0.181	3.2	3.85	[11,18,24,35]
	($Z_8$)	(CNY/ton)	731.765	8.0434	715	759	[11,18,35]

), namely M = 8. (Please refer to Appendix A for the relevant data sources).

$Z_1$, $Z_2$, … $Z_8$ obtains $K_1,K_2,\cdots ,K_8$ IMFs from the ICEEMDAN method as $\left[{IMF}_1^{Z_1},{IMF}_2^{Z_1},\cdots ,{IMF}_{K_1}^{Z_1}\right],\left[{IMF}_1^{Z_2},{IMF}_2^{Z_2},\cdots ,{IMF}_{K_2}^{Z_2}\right],\cdots \left[{IMF}_1^{Z_M},{IMF}_2^{Z_8},\cdots ,{IMF}_{K_8}^{Z_8}\right]$.

They are used as input features of the prediction model, denoted as:

$$X=\left[{IMF}_1^{Z_0},\cdots ,{IMF}_{K_0}^{Z_0},{IMF}_1^{Z_1},\cdots ,{IMF}_{K_1}^{Z_1},{IMF}_1^{Z_M},\cdots ,{IMF}_{K_M}^{Z_M}\right]$$

(9)

Because each input feature is a series of time series, let $T$ represent the total length of the time series, and use $t$ to represent the $t$-th data in the time series. Therefore, dataset $X$ can be represented as follows:

$$X=\left[\begin{array}{c}{IMF}_{1,0}^{Z_0},\cdots ,{IMF}_{K_0,0}^{Z_0},{IMF}_{1,0}^{Z_1},\cdots ,{IMF}_{K_1,0}^{Z_1},\cdots ,{IMF}_{1,0}^{Z_8},\cdots ,{IMF}_{K_8,0}^{Z_8}\\ ⋮\\ {IMF}_{1,t}^{Z_0},\cdots ,{IMF}_{K_0,t}^{Z_0},{IMF}_{1,t}^{Z_1},\cdots ,{IMF}_{K_1,t}^{Z_1},\cdots ,{IMF}_{1,t}^{Z_8},\cdots ,{IMF}_{K_8,t}^{Z_8}\\ ⋮\\ {IMF}_{1,T}^{Z_0},\cdots ,{IMF}_{K_0,T}^{Z_0},{IMF}_{1,T}^{Z_1},\cdots ,{IMF}_{K_1,T}^{Z_1},\cdots ,{IMF}_{1,T}^{Z_8},\cdots ,{IMF}_{K_8,T}^{Z_8}\end{array}\right]$$

(10)

Similarly, this article represents the carbon price dataset as follows:

$$Y={\left[Z_{0,0},\cdots ,Z_{0,t},\cdots ,Z_{0,T}\right]}^T$$

(11)

Therefore, in order to better train the model proposed in this paper, we processed the dataset into a training set and a testing set, where the features $X_{train}$ and target $Y_{train}$ of the training set and the features $X_{test}$ and target $Y_{test}$ of the testing set are represented as follows:

$$\begin{gathered} X_{train}=\left[X_0^{∆T},\cdots ,X_t^{∆T},\cdots ,X_k^{∆T}\right],Y_{train}={\left[Y_{∆T}^D,\cdots ,Y_{t+∆T}^D,\cdots ,Y_{k+∆T}^D\right]}^T \\ {X}_{test}=\left[X_k^{∆T},\cdots ,X_{T-∆T}^{∆T}\right],Y_{test}={\left[Y_{k+∆T}^D,\cdots ,Y_T^D\right]}^T \end{gathered}$$

(12)

Among them, $∆T$ represents the length of the time series used for prediction, and $D$ represents the time span for predicting the future. In the third section of this article, $∆T=5$, $D=1$, that is:

$$\begin{gathered} X_t^{∆T}=\left[\begin{array}{c}{IMF}_{1,t}^{Z_0},\cdots ,{IMF}_{K_0,t}^{Z_0},\cdots ,{IMF}_{1,t}^{Z_8},\cdots ,{IMF}_{K_8,t}^{Z_8}\\ ⋮\\ {IMF}_{1,t+∆T}^{Z_0},\cdots ,{IMF}_{K_0,t+∆T}^{Z_0},\cdots ,{IMF}_{1,t+∆T}^{Z_8},\cdots ,{IMF}_{K_8,t+∆T}^{Z_8}\end{array}\right] \\ {Y}_{t+∆T}^D={\left[Z_{0,t+∆T},\cdots ,Z_{0,t+∆T+D}\right]}^T \end{gathered}$$

(13)

Then according to Formula (8), the prediction model that can be constructed is as follows:

$$Y_{LASSO}=LASSO\left(X_{test}\right)=X_{test}b,whereb\in \arg \min L\left(b|X_{train},Y_{train}\right)$$

(14)

2.2.2. Long Short-Term Memory Model (LSTM)

Hochreiter and Schmidhuber [37] first introduced Long Short-Term Memory (LSTM), which is designed based on Recurrent Neural Networks (RNNs) with added memory characteristics to avoid the long dependency problem. LSTM can maintain long-term memory in neural networks, making the model also well-suited for carbon price forecasting.

For RNNs, as the network layers update information unrestrictedly, information becomes jumbled and prone to disappearance, leading to the problem of vanishing gradients [38]. However, LSTM networks incorporate forget and memory cells in the hidden layers, discarding secondary information when new information is input, and retaining important information in long-term memory. These cells are known as gates in LSTM, and the gating mechanism fundamentally includes a cell and three gates, such as the input gate, output gate, and forget gate.

LSTM neural networks include multiple gates: the input gate i determines how much of the current timestep’s input is saved in the cell state. Sometimes, the input gate is also called the update gate; the forget gate f decides how much of the previous timestep’s cell state is retained to the current timestep, or possibly not retained at all; the output gate o determines how much of the cell state is outputted to the current output value of the hidden state.

Compared to RNNs, which have only one type of transmission state, LSTMs have two transmission states, namely the cell state $C_t$ and the hidden state $h_t$ The key to LSTM is the cell state c, which acts like a conveyor belt running directly through the entire chain framework with only minimal linear interactions, making it easy for each cell’s information to circulate and remain unchanged across the network. Moreover, to address the problem of vanishing gradients, LSTMs do not simply apply element-wise nonlinear affine transformations to internal self-loops, but instead use a gating mechanism to control the flow of information within the LSTM. Gates typically include pointwise multiplication used for addition and are governed by sigmoid functions $tanh\left(x\right)=(e^x-e^{-x})∕(e^x+e^{-x})$ to determine how much information can be passed.

Equations (15)–(20) detail the computational formulas for LSTM, where lowercase variables represent vectors, and uppercase variables represent vector matrices.

$$f_t=\sigma \left(W_f{x}_t+U_f{h}_{t-1}+b_f\right)$$

(15)

$$i_t=\sigma \left(W_i{x}_i+U_i{h}_{t-1}+b_i\right)$$

(16)

$${\tilde{c}}_t=tanh\left(W_c{x}_t+U_c{h}_{t-1}+b_c\right)$$

(17)

$${\tilde{c}}_t=tanh\left(W_c{x}_t+U_c{h}_{t-1}+b_c\right)$$

(18)

$$o_t=\sigma \left(W_o{x}_t+U_o{h}_{t-1}+b_o\right)$$

(19)

$$h_t=o_t\circ tanh\left(c_t\right)$$

(20)

In this context, $x_t\in {\mathbb{R}}^m$ is the input vector to the LSTM cell; $h_t\in {\left(-1,1\right)}^n$ is the hidden state vector of the LSTM cell; $f_t\in {\left(0,1\right)}^n$ is the activation vector of the forget gate; $i_t\in {\left(0,1\right)}^n$ is the activation vector of the input gate; ${\tilde{c}}_t\in {\left(-1,1\right)}^n$ is the cell input activation vector; $c_t\in {\mathbb{R}}^n$ is the cell state vector; and $o_t\in {\left(0,1\right)}^n$ is the activation vector of the output gate, where the superscripts m and n, respectively, indicate the number of input features and hidden units. $\circ$ represents the Hadamard product. For $W_k\in {\mathbb{R}}^{n\times m},U_k\in {\mathbb{R}}^{n\times n},b_k\in {\mathbb{R}}^n$, k = f, i, c, o, these represent the weight matrices of the input vector $x_t$, the weight matrices of the hidden vector state $h_t$, and the bias vector parameters, each corresponding to different gates or cell states f, i, c, o. Additionally, special vector notation is used to better elucidate, for example, the cell state vector $c_t\in {\mathbb{R}}^n$, which contains information not only about one cell in the LSTM neural network but also about n LSTM cells. In practical calculations, the Adam optimization algorithm [39] is commonly used, which is a method of gradient descent because it adaptively adjusts the learning rate. Adam combines the advantages of the AdaGrad and RMSProp optimization algorithms, offering simplicity, high computational efficiency, and low resource usage. As the updates of its parameters are unaffected by gradient transformations, it is suitable for datasets with noisy, unstable, or sparse gradients. Furthermore, as overfitting is a common issue when training neural networks, it is necessary to implement a Dropout mechanism [40].

Let the LSTM model calculation process represented by Formulas (11)–(16) be represented by function $LSTM\left(X\right)$. As in Formula (9), in this section, the input variable in the LSTM model training process is also $\mathit{X}$, the output variable is $Z_0$, the carbon price to be predicted is represented by $Y_{LSTM}$, and the feature variable input in the prediction process is $X_{new}$. Then, the prediction process can be expressed as follows:

$$Y_{LSTM}=LSTM\left(X_{test}\right)=W_y{h}_t+b_y,where{W}_y,b_y\in \arg \min LSTM\left(W_y,b_y|X_{train},Y_{train}\right)$$

(21)

where $W_y$ and $b_y$ are the weights and biases of the output layer.

2.2.3. Random Forest Regression Model (RFR)

Random Forest is an ensemble learning method that enhances overall model performance and robustness by constructing multiple decision trees and synthesizing the results of multiple models through voting or averaging. Specific construction methods and examples of the Random Forest regression model can be found in the literature [41]. The Random Forest regression model can be mathematically summarized as follows: Given a data sample $X$ and prediction set $Y$, a forest dependent on random variables is planted, forming tree predictors $h\left(x,{\theta }_k\right)$ that output numerical results. The Random Forest predictor is obtained by averaging these trees $\left\{h\left(x,{\theta }_k\right)\right\}$ with respect to $k$. The training set consists of samples $Y,X$ drawn independently and distributed according to a random variable. The mean squared generalization error for any tree predictor $h{E}_{X,Y}{\left(Y-h\left(X\right)\right)}^2$. When the number of trees in the forest increases indefinitely, $E_{X,Y}{\left(Y-{av}_{k}h\left(X,{\theta }_k\right)\right)}^2\to E_{X,Y}{\left(Y-E_{\theta }h\left(X,\theta \right)\right)}^2$ holds everywhere.

Thus, the Random Forest regression function is $Y=E_{\theta }h\left(X,\theta \right)$, and in practice, it is often replaced by the approximation formula $Y={av}_{k}h\left(X,{\theta }_k\right)$ when $k$ is sufficiently large. The error analysis is as follows:

$${PE}^{\mathrm{*}}\left(tree\right)=E_{\theta }{E}_{X,Y}{\left(Y-h\left(X,\theta \right)\right)}^2$$

(22)

where ${PE}^{\mathrm{*}}$ represents the average generalization error of the Random Forest. Assuming that for all $\theta$, $E\left(Y\right)=E_{X}h\left(X,\theta \right)$ holds, then:

$${PE}^{\mathrm{*}}\left(forest\right)\le \overline{y}{PE}^{\mathrm{*}}\left(tree\right)$$

(23)

where $\overline{y}$ is the weighted correlation coefficient between $Y-h\left(X,\theta \right)$ and the remainder $Y-h\left(X,{\theta }^{\prime }\right)$, and $\theta$ and ${\theta }^{\prime }$ are independent of each other. This demonstrates that the generalization error of the Random Forest is $\overline{y}$ times lower than that of individual trees, and the introduction of random variables $\theta$ and ${\theta }^{\prime }$ is intended to reduce $\overline{y}$.

According to the calculation process of the Random Forest Regression Model expressed in Formulas (22) and (23), assuming that there are $M$ trees in the Random Forest, the prediction model of the $m$th tree is $h_m\left(·\right)$. Then, given the feature data set $X_{test}$, the carbon price prediction result can be expressed as follows:

$$Y_{RFR}=RFR\left(X_{test}\right)={\displaystyle \frac{1}{M}}{\sum }_{m=1}^M{h}_m\left(X_{test}\right)$$

(24)

2.2.4. Hybrid Forecasting Model Weighting Rules

This paper employs a dynamic weighting hybrid forecasting model based on dual sliding windows. For the prediction results of each algorithm, the average absolute error (MAE), root mean square error (RMSE), symmetric mean absolute percentage error (SMAPE), and accuracy (Accuracy) from the Least Absolute Shrinkage and Selection Operator (LASSO), Long Short-Term Memory model (LSTM), and Random Forest Regression (RFR) algorithms are used as weighting coefficients.

The formula for calculating the hybrid weights is as follows:

To test the predictive effectiveness of the designed hybrid forecasting framework, this study considers four commonly used metrics: mean absolute error (MAE), root mean square error (RMSE), symmetric mean absolute percentage error (SMAPE), and accuracy (Accuracy). Lower values of the first three indicators signify higher predictive accuracy, while a higher value of the last indicator indicates greater predictive accuracy. The specific formulas are shown below, where N represents the number of samples, and $R_n$ and $P_n$, respectively, represent the actual ($Y_{test}$) and predicted values at the $n$-th time node.

The formula for mean absolute error (MAE) is given by:

$$MAE={\displaystyle \frac{1}{N}}{\sum }_{n=1}^N\left|R_n-P_n\right|$$

(25)

The formula for root mean square error (RMSE) is given by:

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{n=1}^N{\left(R_n-P_n\right)}^2}$$

(26)

The formula for symmetric mean absolute percentage error (SMAPE) is given by:

$$SMAPE={\displaystyle \frac{100\mathrm{\%}}{N}}{\sum }_{n=1}^N{\displaystyle \frac{\left|R_n-P_n\right|}{\left(\left|R_n\right|+\left|P_n\right|\right)/2}}$$

(27)

The formula for accuracy (Accuracy) is given by:

$$Accuracy=\left(1-100\mathrm{\%}\times {\displaystyle \frac{\left|R_n-P_n\right|}{R_n}}\right)$$

(28)

Because lower values of mean absolute error, root mean square error, and symmetric mean absolute percentage error indicate better model performance, and higher values of accuracy indicate better model performance, this research uses the reciprocals of the MAE, RMSE, SMAPE, and accuracy derived from the Least Absolute Shrinkage and Selection Operator (LASSO), Long Short-Term Memory model (LSTM), and Random Forest Regression (RFR) algorithms as follows: $w_{ij}$, where, $i\in \{LASSO,LSTM,RFR\}$, $j\in \{MAE,RMSE,SMAPE,ACCUARCY\}$.

Therefore, the hybrid weight of algorithm $i\in \{LASSO,LSTM,RFR\}$ can be defined as $W_i$:

$$W_i={\displaystyle \frac{{\sum }_j{w_{ij}}^{-1}}{{\sum }_i{\sum }_j{w_{ij}}^{-1}}}$$

(29)

According to Formulas (13), (20), (24) and (29), the prediction model proposed in this paper can be expressed as follows:

$$Y=W_{LASSO}{Y}_{LASSO}+W_{LSTM}{Y}_{LSTM}+W_{RFR}{Y}_{RFR}=W_{LASSO}LASSO\left(X_{test}\right)+W_{LSTM}LSTM\left(X_{test}\right)+W_{RFR}RFR\left(X_{test}\right)$$

(30)

By integrating the LASSO, LSTM, and Random Forest algorithms, this study is able to fully leverage the strengths of each algorithm, compensate for the deficiencies of single models under specific conditions, and enhance the comprehensiveness and robustness of the forecasts. The adoption of a dynamic weight adjustment strategy allows for flexible adjustments to each algorithm based on the performance of different forecasting indicators, improving the model’s adaptability to various aspects. The use of dual sliding windows makes the model more sensitive to the diversity and complexity of carbon price changes, more accurately capturing the dynamic characteristics of the market. By considering multiple performance indicators, including MAE, RMSE, SMAPE, and Accuracy, a comprehensive evaluation of the algorithms is conducted to ensure that the model achieves good predictive results in all aspects.

3. Results

3.1. Example Selection

This study primarily utilizes carbon price data from the National Carbon Market (China). Predicting carbon prices is a complex process influenced by various factors. To more accurately predict carbon prices, we need to consider a series of relevant market indicators. Given that changes in carbon prices are closely related to the energy and financial markets, we must take these into account. The supply–demand relationship and price fluctuations in the energy market directly impact the demand for carbon emissions rights and investment decisions, thereby affecting carbon prices. Simultaneously, the financial market significantly influences carbon prices through financial innovation, capital flows, and policy and regulatory measures. Therefore, when predicting and analyzing carbon prices ($Z_0$), it is essential to comprehensively consider various factors from both markets.

The financial market indicators include the Shanghai Stock Exchange Composite Index ($Z_1$), the midpoints of the USD to CNY ($Z_2$) and EUR to CNY ($Z_3$) exchange rates, and the China Enterprise Commodity Price Index ($Z_4$). These indicators reflect the performance of the domestic stock market, exchange rate changes, and commodity price fluctuations, which impact the carbon market’s capital flows, investor sentiment, and supply–demand relationship. The energy market indicators include the closing price of crude oil futures ($Z_5$), the price of liquefied natural gas ($Z_6$), the price of industrial natural gas ($Z_7$), and the Bohai Rim Steam Coal Price Index ($Z_8$). The fluctuations in these energy prices directly or indirectly affect the supply–demand relationship and pricing in the carbon market, as shown in Table 1.

In carbon price forecasting, the theoretical output results typically manifest as predicted carbon prices at a future point in time (such as the next day), and the model’s training process aims to align these predictions as closely as possible with actual observed values. The form of the output results can be flexible, either as a single day’s forecast or as a series of predicted values for future points in time, depending on the design of the model and specific requirements of the task. The expected accuracy of the forecasts is influenced by several factors, including the chosen model, the volume of training, data quality, and the complexity of the problem. Common metrics used to measure model performance include Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Symmetric Mean Absolute Percentage Error (SMAPE), and accuracy. A comprehensive consideration of these indicators helps to assess the overall performance of the model and improve the accuracy of future carbon price changes.

The model and related procedures defined in this study allow for the training and prediction time series length to be set according to real-world conditions. For simplicity, this study selected an example using 5 days’ worth of data (a working week) as input, aimed at predicting the carbon price for the next day. The input data include carbon price data from the past 5 days, as well as other energy and financial market indicator factors. Regarding the output data, this report predicts the carbon price for the next day. The selection of this example is well justified. Firstly, using a shorter range of data can more sensitively reflect the short-term fluctuations in carbon prices, thus testing the model’s ability to capture market dynamics. Secondly, predicting the carbon price for the next day is a common task in practical scenarios and a focus of interest for investors and decision-makers; thus, it is representative of practical applications. Finally, the example includes multiple influencing factors, allowing the model to make predictions in more complex situations and verifying its robustness under the influence of multiple factors.

The object of the trial calculation’s verification is to compare the model’s predicted carbon price for the next day with the actual observed data. By comparing with actual data, the accuracy and reliability of the model in this short-term prediction task can be assessed. This verification object directly relates to the algorithm’s effectiveness in real-market applications, providing strong support for the model’s practicality. By choosing this example, this study aims to demonstrate the application effect of the carbon price prediction algorithm in real scenarios and provide a solid basis for validating the model’s performance.

Furthermore, to more comprehensively demonstrate the advantages of the proposed forecasting model, this study selected a complete dataset spanning from 4 January 2022 to 30 December 2023 for step-by-step prediction validation. The choice of such an extended time span aims to thoroughly evaluate the model’s adaptability to different seasons, cycles, and external factors, verifying its stability and robustness in long-term forecasting tasks. Through step-by-step prediction validation using the full-year data, this study can more comprehensively assess the model’s ability to capture carbon price fluctuations, further validating its feasibility and practicality in real market environments. This also helps reveal the model’s performance in long-term forecasting, providing decision-makers with more reliable market trend references.

To determine the optimal exogenous parameter settings in the proposed model, this study employed the GridSearchCV method, which optimizes model parameters by traversing a given parameter grid, in conjunction with cross-validation to identify the best parameter combinations. Specifically, we set a fine parameter grid ranging from 0 to 1 with an interval of 0.01 for the key parameter (regularization parameter) of the LASSO model. For the LSTM model, detailed parameter grids were set for the training batch size ([32, 64, 128]), the number of network layers ([1, 2, 3, 4]), and the number of neurons ([20, 40, 60, 80, 100, 120]). For the Random Forest model, we meticulously set parameter grids for the number of decision trees ([100, 200, 300]) and the maximum depth of each tree ([None, 10, 20, 30]).

Ultimately, through rigorous cross-validation, we selected the best-performing parameter combinations: the regularization parameter for the LASSO model was set at 0.1; the LSTM network structure was determined to be 3 layers with 100 hidden layer neurons; and the Random Forest model was set with 100 decision trees, each with a depth of 20. These key exogenous parameter settings provide strong support for the accuracy and reliability of the model in this study.

3.2. Results Analysis

To verify the predictive accuracy of the trial calculation example and to assess whether the hybrid algorithm offers an advantage, we can calculate four predictive accuracy indicators (RMSE, MAE, SMAPE, Accuracy) and make comparisons, as shown in Figure 1.

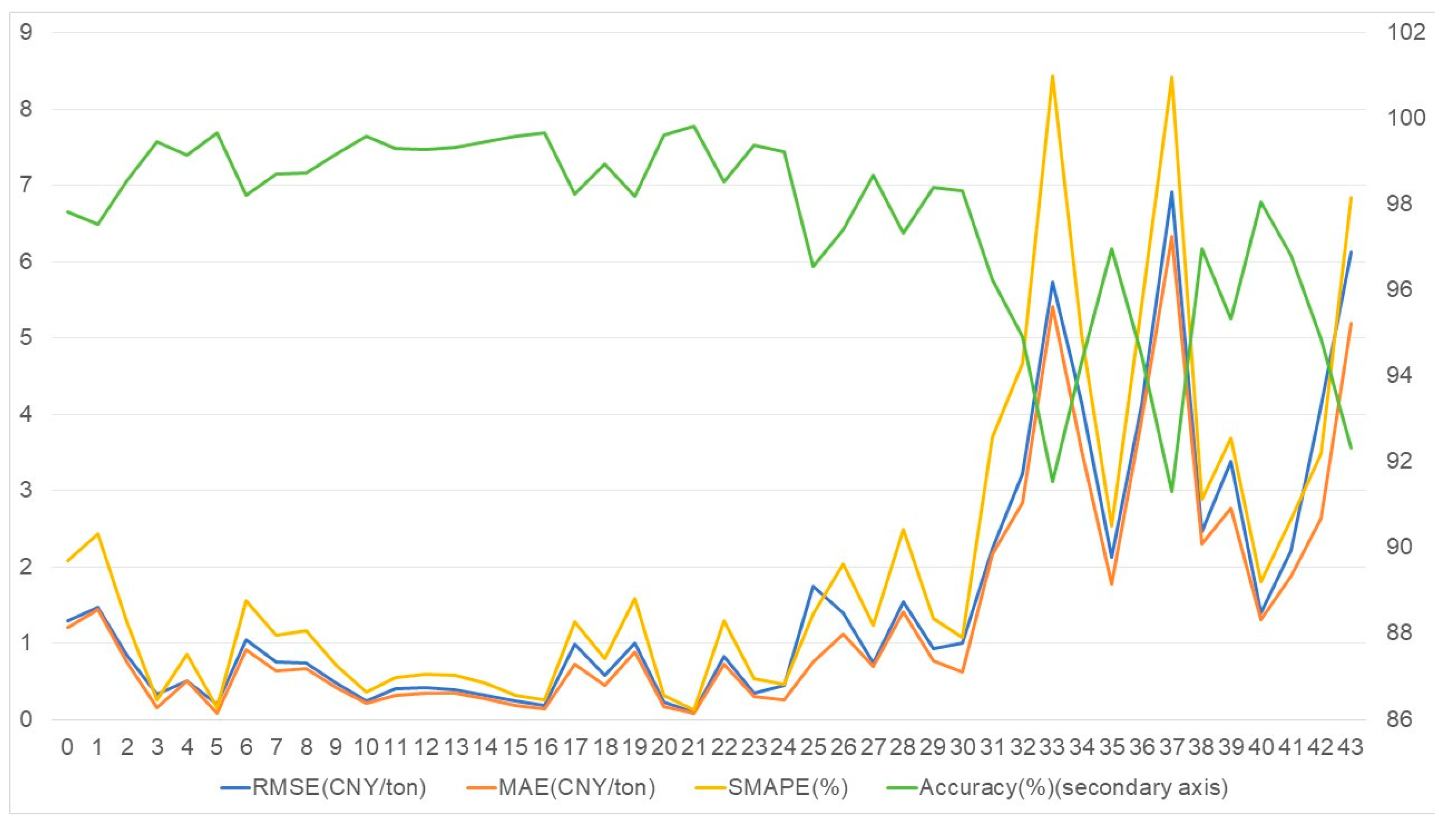
Figure 1 presents four evaluation metrics of the hybrid algorithm in carbon price prediction: RMSE, MAE, SMAPE, and Accuracy. The blue line represents RMSE, the orange line represents MAE, the yellow line represents SMAPE, and the green line represents Accuracy (right Y-axis). As shown in the figure, the maximum values of RMSE and MAE are 6.1242 CNY/ton and 5.1882 CNY/ton, respectively. For most of the time, they remain below 1, with minimum values reaching 0.2352 CNY/ton and 0.2071 CNY/ton, indicating that the prediction error of the model is relatively small. The maximum value of SMAPE is 6.8337%, but it stays below 2 for most of the time, also indicating a relatively small error. The minimum value of Accuracy is 92.33%, and it remains above 95% for most of the time, indicating a high prediction accuracy of the model. Overall, these metrics demonstrate the effectiveness and reliability of the proposed hybrid algorithm in carbon price prediction.

Before proceeding with the comparative analysis, it is necessary to understand the range or standards of the indicators predetermined by the research objectives. Generally, lower values of RMSE, MAE, and SMAPE, along with a higher Accuracy value, indicate better predictive accuracy. We can initially compare the performance of the hybrid algorithm against three separate algorithms on these indicators to verify whether the hybrid algorithm has advantages across multiple metrics. The comparison between the prediction results and the original data is shown in Figure 2.

Figure 2 shows the comparison between actual carbon prices and predicted carbon prices. The blue line represents actual carbon prices (CNY/ton), and the orange line represents the carbon prices predicted by the proposed algorithm (CNY/ton). The actual carbon prices underwent several significant phases from January 2022 to December 2023: slight fluctuations in early 2022, but generally stable between 55 and 60 CNY/ton; relatively stable from mid-2022 to early 2023, maintaining the same range of 55–60 CNY/ton; an upward trend from early 2023 to mid-2023, peaking at over 80 CNY/ton in mid-2023; and significant volatility from mid-2023 to the end of 2023, with a sharp decline followed by a recovery, stabilizing between 70 and 80 CNY/ton. The predicted carbon prices closely align with the actual prices. Overall, the proposed algorithm performs well in predicting carbon prices. Although there are slight delays or deviations in some periods, the overall trend is consistent with the actual prices. Especially in early 2022 and early 2023, the prediction results closely match the actual results. During periods of significant price volatility, the predictions still accurately reflect the actual price trends, demonstrating the model’s effectiveness and high prediction accuracy.

This study’s predictions perform generally well as the model successfully captures the overall fluctuation trend of carbon prices and achieves satisfactory predictive accuracy on many dates. Facing various complex market scenarios, the model demonstrates strong adaptability and successfully predicts changes in carbon prices. These results indicate that the hybrid forecasting algorithm in this study possesses high accuracy and robustness in predicting carbon prices, meeting the predetermined indicators of the research objectives and providing reliable decision support for handling uncertainties in the carbon market.

Despite significant progress in carbon price prediction, we must acknowledge the presence of some anomalies that were not predicted. These anomalies may be influenced by various unexpected events, policy adjustments, or other unpredictable factors, contributing to market volatility uncertainties. While adjusting model parameters can increase sensitivity to outliers, this often comes at the expense of overall predictive accuracy. Tuning the model to better capture outliers might make it more sensitive to noise or short-term fluctuations, thereby reducing its ability to accurately capture overall trends. When balancing the model’s sensitivity and stability, we need to weigh the response to outliers against the grasp of overall market trends.

Although the presence of unpredicted outliers does not affect the model’s reliability in general situations, we recommend integrating the model’s outputs with other market analysis tools in practical applications to fully understand the dynamics of the carbon market. Additionally, regularly monitoring model performance and making necessary adjustments based on market changes are key to maintaining the model’s accuracy and robustness.

Overall, the hybrid forecasting algorithm in this study demonstrates a relatively high level of accuracy and robustness in predicting carbon prices, providing decision-makers with a reliable decision support tool. However, we must remain cautious in using the model, recognize the presence of outliers, and adjust the model flexibly to adapt to dynamic market changes.

4. Comparison of Algorithmic Advantages

4.1. Logical Advantages

The carbon price forecasting algorithm developed in this study demonstrates several advantages in its logical design. First, it adopts a comprehensive algorithmic architecture that integrates various mature forecasting algorithms such as Lasso, LSTM, and RFR, making full use of their strengths in time series data analysis, feature capture, and nonlinear relationship modeling. Secondly, by introducing a dynamic weight mixing strategy, it flexibly adjusts the weights of each algorithm, thus better adapting to the dynamic changes in the carbon market. Most notably, the use of a dual sliding window enhances the model’s sensitivity to changes in carbon prices, enabling it to better adapt to the instantaneous fluctuations and long-term trends of the market.

4.2. Performance Advantages

In our comparative analysis, we conducted a comprehensive evaluation of the independent applications of the Lasso, LSTM, and RFR algorithms against the dynamic weight mixing forecast model proposed in this paper. The results from

Table 2. Comparative analysis.

Algorithm Names	RMSE (CNY/ton)	MAE (CNY/ton)	SMAPE (%)	Accuracy (%)
Lasso Algorithm	3.3767	1.983	3.00855	91.94%
LSTM Algorithm	2.2301	1.2754	1.9516	97.11%
RFR Algorithm	2.36218	1.3016	1.96005	97.31%
ARIMA	2.3696	1.909	2.878	91.29%
Exponential Smoothing Algorithm	2.4243	1.9522	2.9515	91.14%
The proposed algorithm	1.5882	1.35423	2.049	97.64%

clearly show that the dynamic weight mixing forecast model in this study significantly outperforms the other forecasting algorithms when applied independently in terms of various evaluation metrics and overall accuracy.

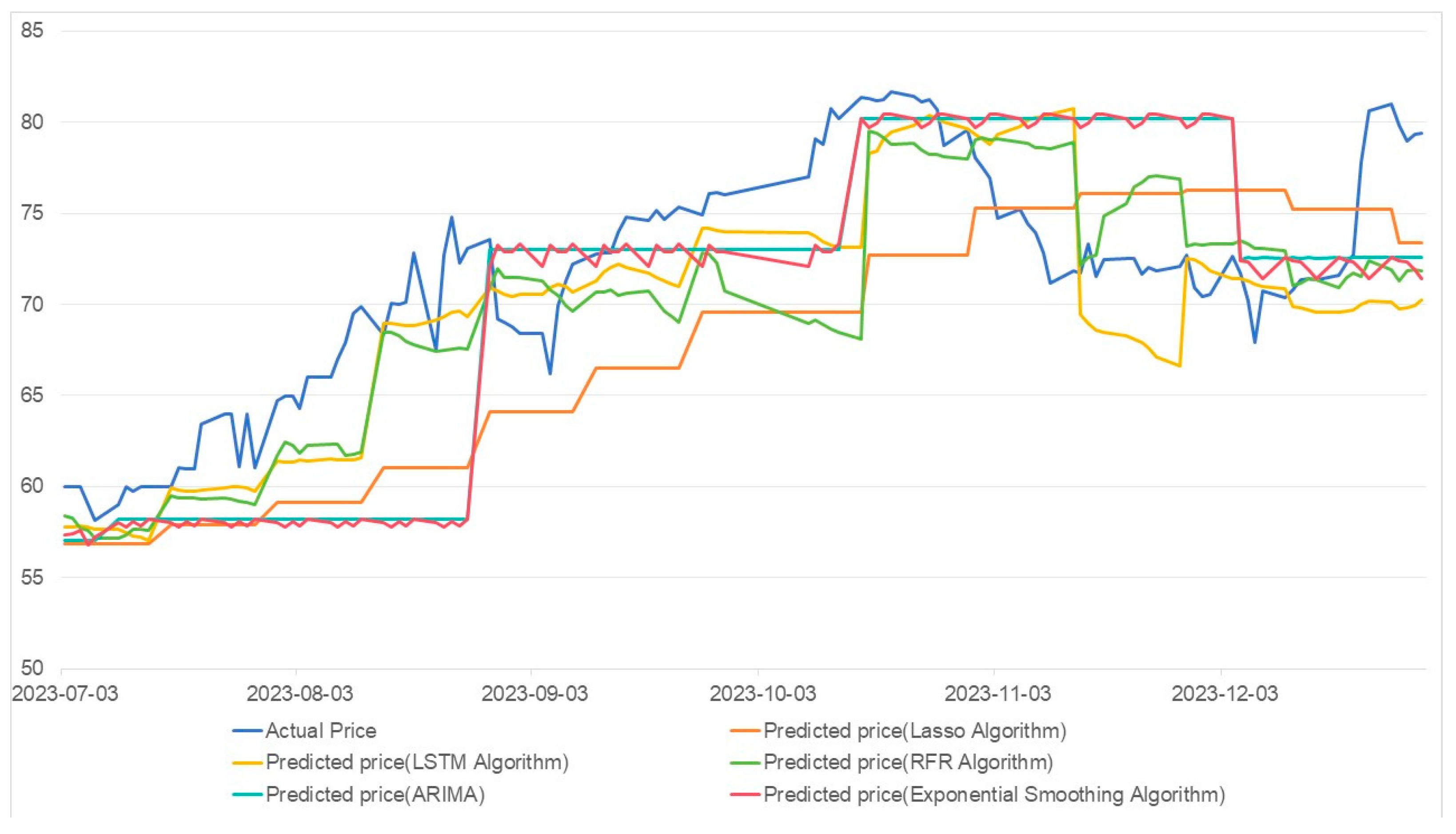
Specifically, the Lasso algorithm’s RMSE (3.3767), MAE (1.983), and SMAPE (3.00855) values are relatively high, with an accuracy of only 91.94%. In contrast, the LSTM algorithm and RFR algorithm perform better on these metrics, but still not as well as the hybrid model developed in this study. The Autoregressive Integrated Moving Average (ARIMA) model and Exponential Smoothing algorithm perform even worse on these metrics, as shown in Figure 3.

The LSTM algorithm shows shortcomings in handling sudden changes in carbon prices, as evidenced by its poor performance during the sudden price drop in November 2023 and the sudden price rise in December 2023. The Lasso algorithm also lacks in capturing price volatility. The RFR algorithm sometimes fails to accurately capture changes in carbon prices; for example, when actual prices were rising in October 2023, the algorithm predicted a downward trend. Both the ARIMA model and the Exponential Smoothing algorithm can capture overall trends in carbon prices, but they fall short in addressing short-term price fluctuations.

The dynamic weighted hybrid prediction model proposed in this paper achieves RMSE, MAE, and SMAPE values of 1.5882, 1.35423, and 2.049, respectively, with an accuracy of 97.64%. This indicates that our model significantly surpasses traditional algorithms in terms of accuracy and robustness in carbon price prediction. By leveraging the strengths of the Lasso, LSTM, and RFR algorithms through a dynamic weighting strategy, our model provides more realistic predictions, offering more reliable decision support for carbon market participants. This significant performance improvement demonstrates the effectiveness and superiority of the hybrid prediction strategy adopted in this study.

In order to more comprehensively evaluate the performance of the model, we used a method of gradually eliminating indicators and carefully observed the changes in the prediction results of indicators such as mean absolute error (MAE), root mean square error (RMSE), symmetrical mean absolute percentage error (SMAPE), and accuracy. This allowed us to more accurately grasp the impact of each indicator on the prediction results.

In Table 2, we learn that the algorithm model proposed in this article has scores of 1.5882, 1.35423, 2.049, and 97.64% in terms of RMSE, MAE, SMAPE, and accuracy, respectively. In

Table 3. Analysis of influencing factors.

Excluded Indicators	RMSE (CNY/ton)	MAE (CNY/ton)	SMAPE (%)	Accuracy (%)
$Z_1$	+0.030256	+0.049426	+0.086384	−0.05973
$Z_2$	+0.00529	+0.004948	+0.026189	−0.01317
$Z_3$	+0.05739	+0.05374	+0.06414	−0.008354
$Z_4$	+0.07542	−0.06647	+0.07692	−0.001763
$Z_5$	+0.04562	+0.03691	−0.04131	−0.047854
$Z_6$	+0.062752	+0.063913	+0.111424	−0.11018
$Z_7$	+0.04613	−0.03466	+0.04591	−0.054055
$Z_8$	+0.02987	+0.02466	−0.02377	−0.010903

, we show the changes in the model’s RMSE after removing each metric. The “−” sign indicates a decrease in the corresponding value compared to the above scores, while the “+” sign indicates an increase in the corresponding value compared to the above scores.

From the analysis results of Table 3, it is evident that price indicators have significant economic and managerial implications for the carbon market. Specifically, the price of liquefied natural gas ($Z_6$) has the greatest impact on carbon price changes, as indicated by an increase in RMSE by 0.062752, in MAE by 0.063991, and in SMAPE by 0.111424, and a decrease in accuracy by 0.110185. This suggests that the price of liquefied natural gas is one of the most critical variables in carbon market pricing. Managers should closely monitor the fluctuations in the liquefied natural gas market and its impact on carbon prices, and develop corresponding risk management strategies. Conversely, the USD to CNY exchange rate midpoints ($Z_2$) have the least impact, with RMSE increasing by only 0.00529, MAE by 0.004948, and SMAPE by 0.026189, and accuracy decreasing by 0.01317. This indicates that exchange rate fluctuations have a relatively minor impact on carbon market prices. When formulating carbon market policies and conducting market forecasts, less attention can be given to exchange rate changes, allowing more resources to be allocated to monitoring and analyzing energy prices, especially the price of liquefied natural gas, to improve the accuracy of prediction models and the effectiveness of management decisions.

4.3. Other Advantages

Beyond performance improvements, the algorithms in this study also possess other significant advantages. First, the algorithm fully utilizes information from different algorithms during the training phase and effectively avoids the limitations of a single algorithm under specific conditions through dynamic weight mixing. Secondly, detailed analysis of influencing factors and data preprocessing enable the algorithm to better adapt to the complexities of the carbon market, enhancing the adaptability of the model. Overall, the advantages of the algorithms in this study lie not only in their outstanding performance but also in their comprehensive consideration of multiple factors in their design, making them more practical and reliable. This provides decision-makers with a more comprehensive reference for carbon market trends, holding significant value for practical applications.

5. Conclusions

This study is dedicated to developing a superior carbon price forecasting algorithm by integrating traditional methods (such as Lasso, LSTM, and RFR) with a dynamic weight hybrid strategy. The goal is to comprehensively and accurately grasp the future trends of the carbon market. Through an in-depth analysis of factors influencing the carbon market, meticulous data preprocessing, and extensive validation, this research has achieved significant results. Comparative analysis reveals that the proposed dynamic weight hybrid forecasting model significantly outperforms traditional algorithms in various evaluation metrics (RMSE, MAE, and SMAPE) and overall accuracy. It performs exceptionally well in handling sudden changes in carbon prices and short-term price fluctuations, as shown in Figure 2 and Figure 3.

The scientific novelty of this research lies in the innovative integration of multiple algorithms through a dynamic weighting approach, which harnesses the strengths of each method to deliver superior predictive performance. This novel hybrid model provides a more nuanced and accurate understanding of carbon market dynamics, demonstrating its practical significance in offering reliable decision support to market participants.

However, it is worth noting that the integration of multiple algorithms to enhance predictive performance may increase the computational complexity of the model, leading to an extended runtime. Despite the thorough analysis of the carbon market’s influencing factors, this study may not have comprehensively covered all key elements. Given the continuous development of the carbon market and the evolving policy environment, new influencing factors are bound to emerge.

Further improvement in the carbon price forecasting algorithm needs to ensure the adaptation of this algorithm to the ever-changing market environment. For this, it is necessary to solve the following main tasks:

(1)

Incorporate more factors: Include additional influencing factors in the model, such as social factors and policy changes. These factors can significantly impact carbon market dynamics, and their inclusion can enhance the model’s comprehensiveness and predictive capability.

(2)

Research more complex algorithm structures and deep learning models: Conduct in-depth research and application of more complex algorithm structures and deep learning models. This will help to more accurately capture the nonlinear and time-varying characteristics of the carbon market, thereby improving prediction accuracy.

(3)

Balance model prediction accuracy and computational efficiency: Carefully balance model prediction accuracy and computational efficiency during development. By optimizing algorithm combinations and reasonably allocating computational resources, we can find the optimal balance between performance and efficiency, thereby enhancing the model’s practical value.

(4)

Expand the dataset and improve data quality: Further expand the scope of the dataset and improve data quality. High-quality and diverse data will enhance the model’s stability and generalization ability, ensuring good predictive performance under different market conditions.