A Generalized Load Model Considering the Fault Ride-Through Capability of Distributed PV Generation System
Abstract
1. Introduction
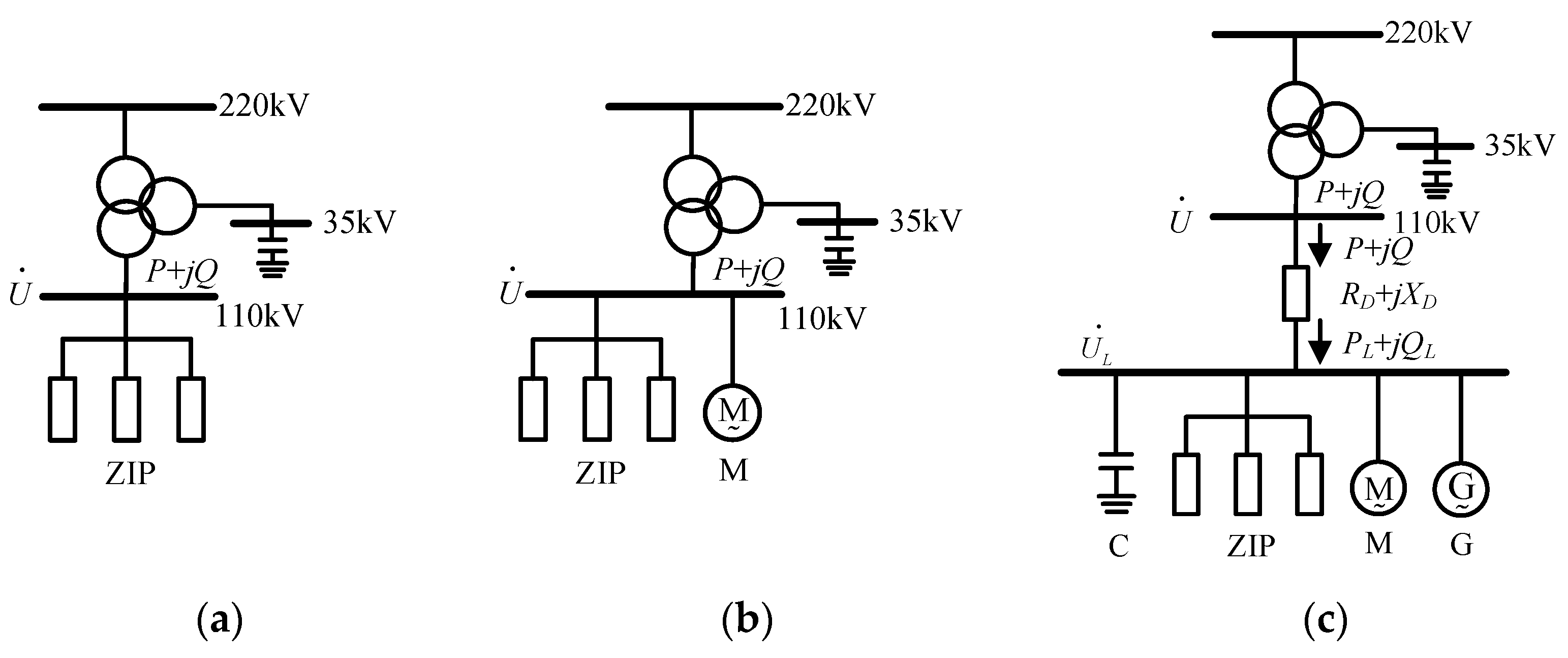
2. Generalized Load Model Structure
2.1. Traditional Load Model
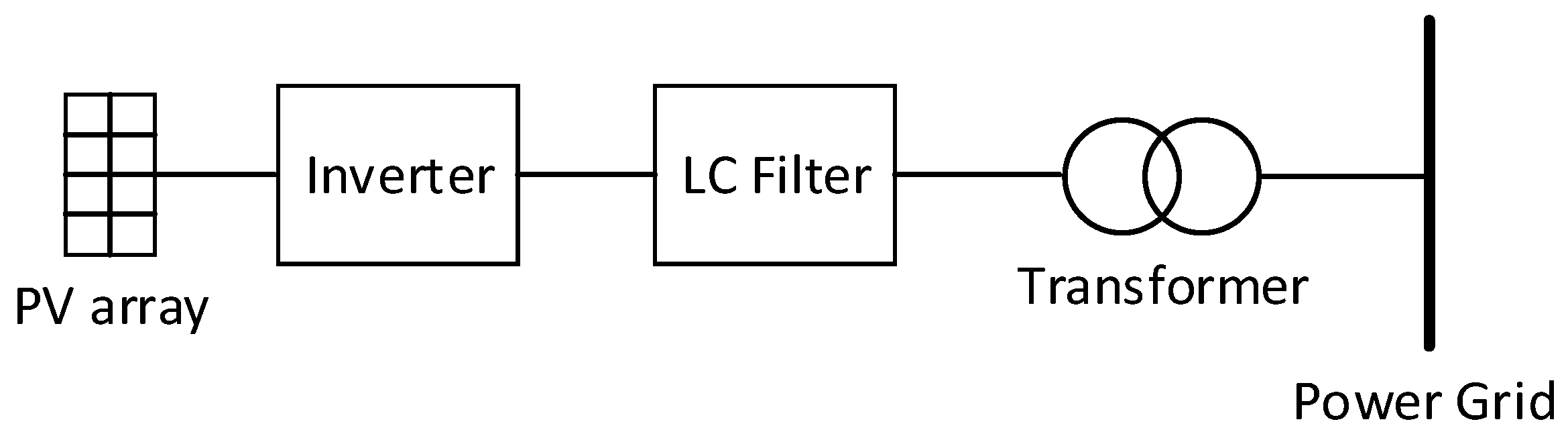
2.2. PV Power System Model and Grid-Connected Control
2.3. Generalized Load Model
3. HVRT and LVRT of PV Inverters
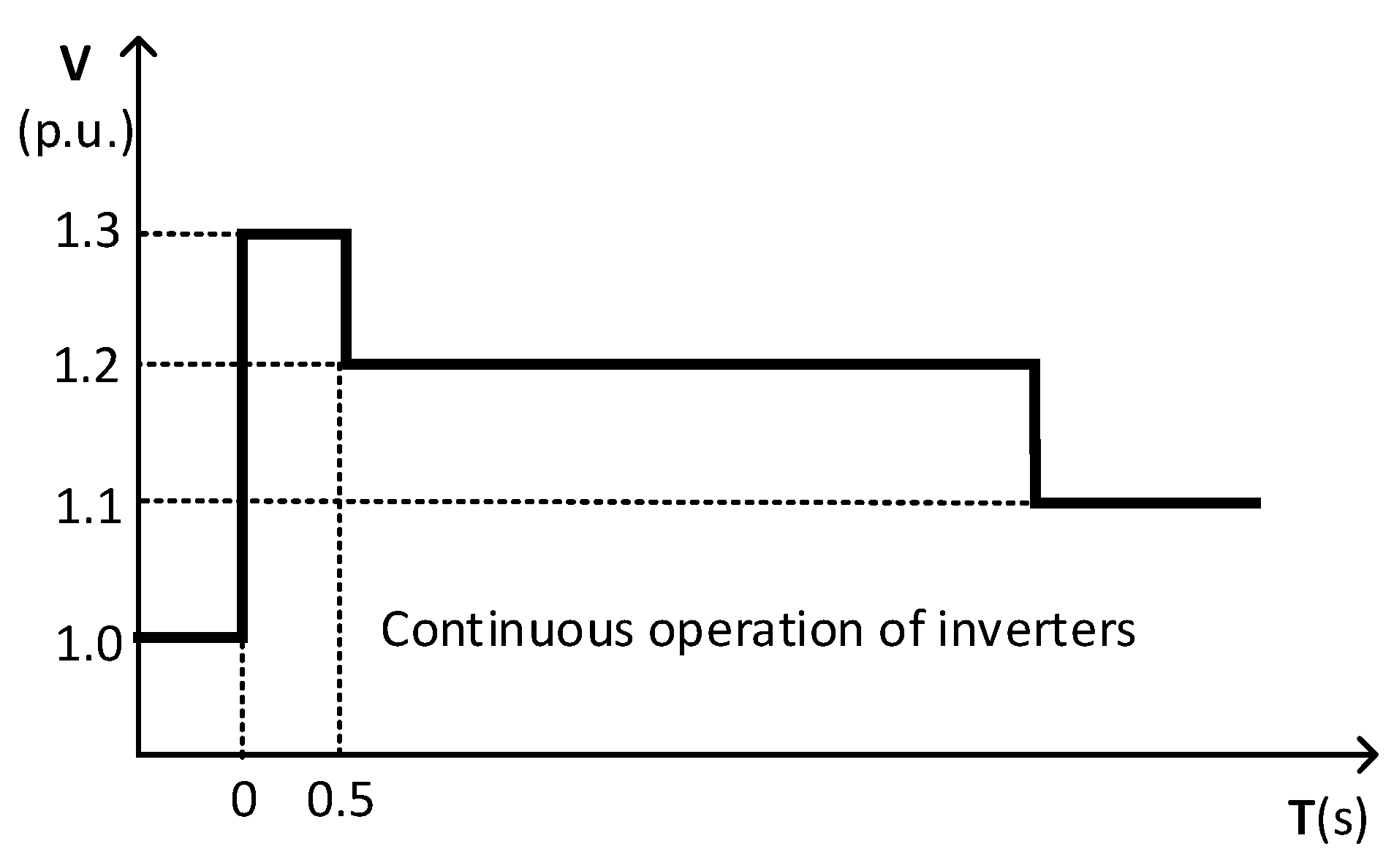
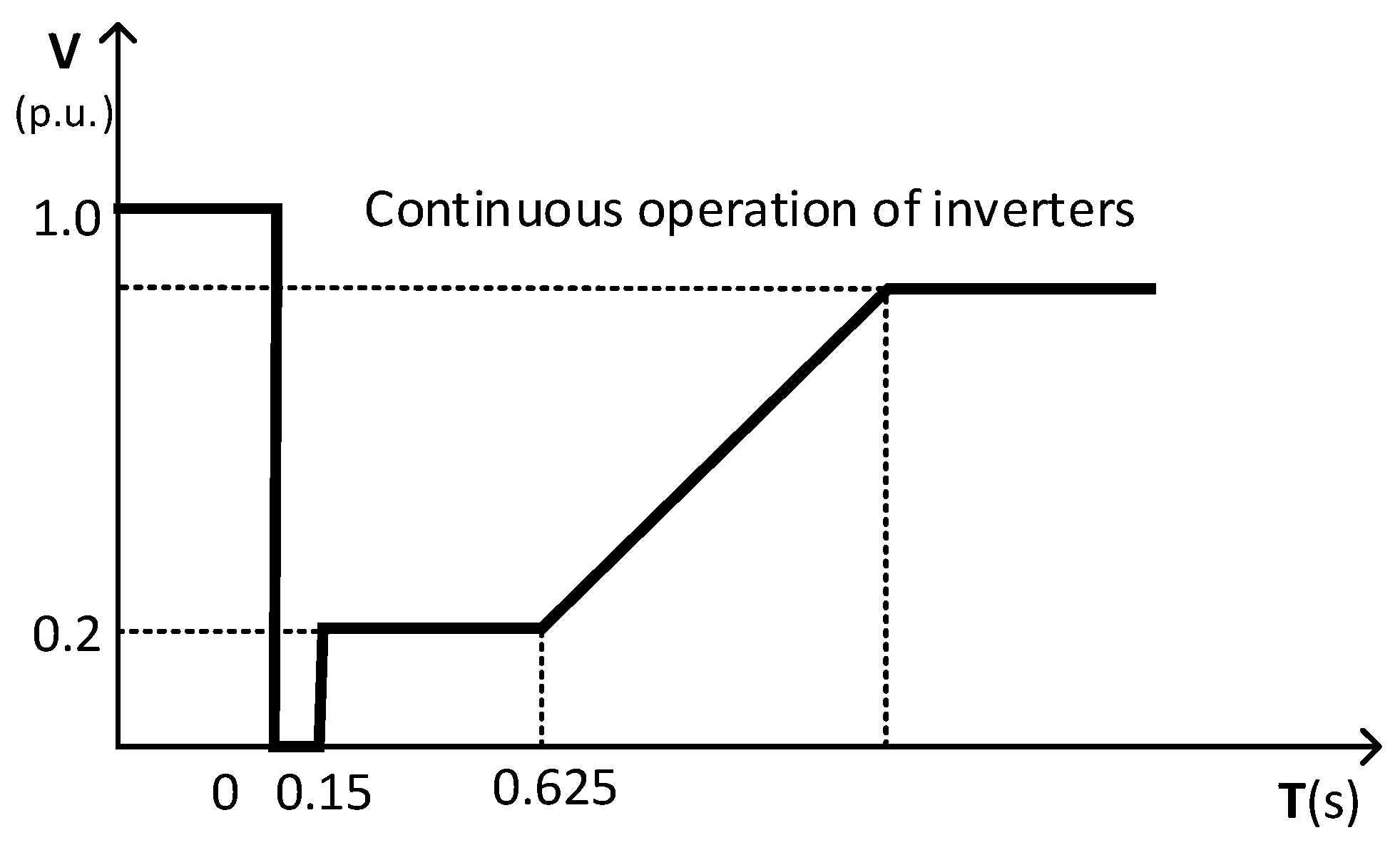
3.1. HVRT and LVRT Requirements of Distributed PV System
3.2. HVRT and LVRT Strategies of PV Inverters
4. Parameters Identification and Simulation Verification for Generalized Load Model
4.1. Parameter Extraction for Generalized Load Models
4.2. Sensitivity Analysis of the Parameters
- Set up a three-phase symmetrical voltage dip fault at the parallel network point POC so that its duration is 0.5 s and the voltage dip amplitude is 20%, record the active power P0 and reactive power Q0 output from the parallel network point.
- Increase the jth parameter by a factor of 0.1 and change the corresponding parameter in each element in the distribution network, set the same fault conditions as in the previous step, and record the active power Pj and reactive power Qj at the output of the grid point.
- The active and reactive sensitivities are calculated separately through Equation (2). The average trajectory sensitivity is obtained by calculating the average of the two.
4.3. Identification of the Parameters
- On the one hand, the external input parameters of the generalized load model are determined according to the actual situation. On the other hand, determine the values of voltage, active, and reactive power at each node under normal operation and the occurrence of voltage dip faults at fixed locations through the detailed PSCAD model. These values are used as determinants to inform the parameter identification process.
- The parameter identification follows the order of sensitivity from highest to lowest. Set the parameter to be recognized to an initial value and the rest to typical values.
- A nonlinear least squares method based on the trust domain reflection algorithm is used to identify high-sensitivity parameters in a generalized load model. Calculating the sum of squares of the deviations of the operating results of the system containing the generalized load model from the test samples and using it as an objective function for optimization of the parameters to be identified.
- Run the simulation with the identified results and compare the obtained results with the actual results, the identified parameter values can be accepted under the range of error operation, otherwise, re-identification is carried out.
4.4. Simulation Validation of the Generalized Load Model
4.4.1. Detailed Distribution Network Model Calibration Based on Measured Data
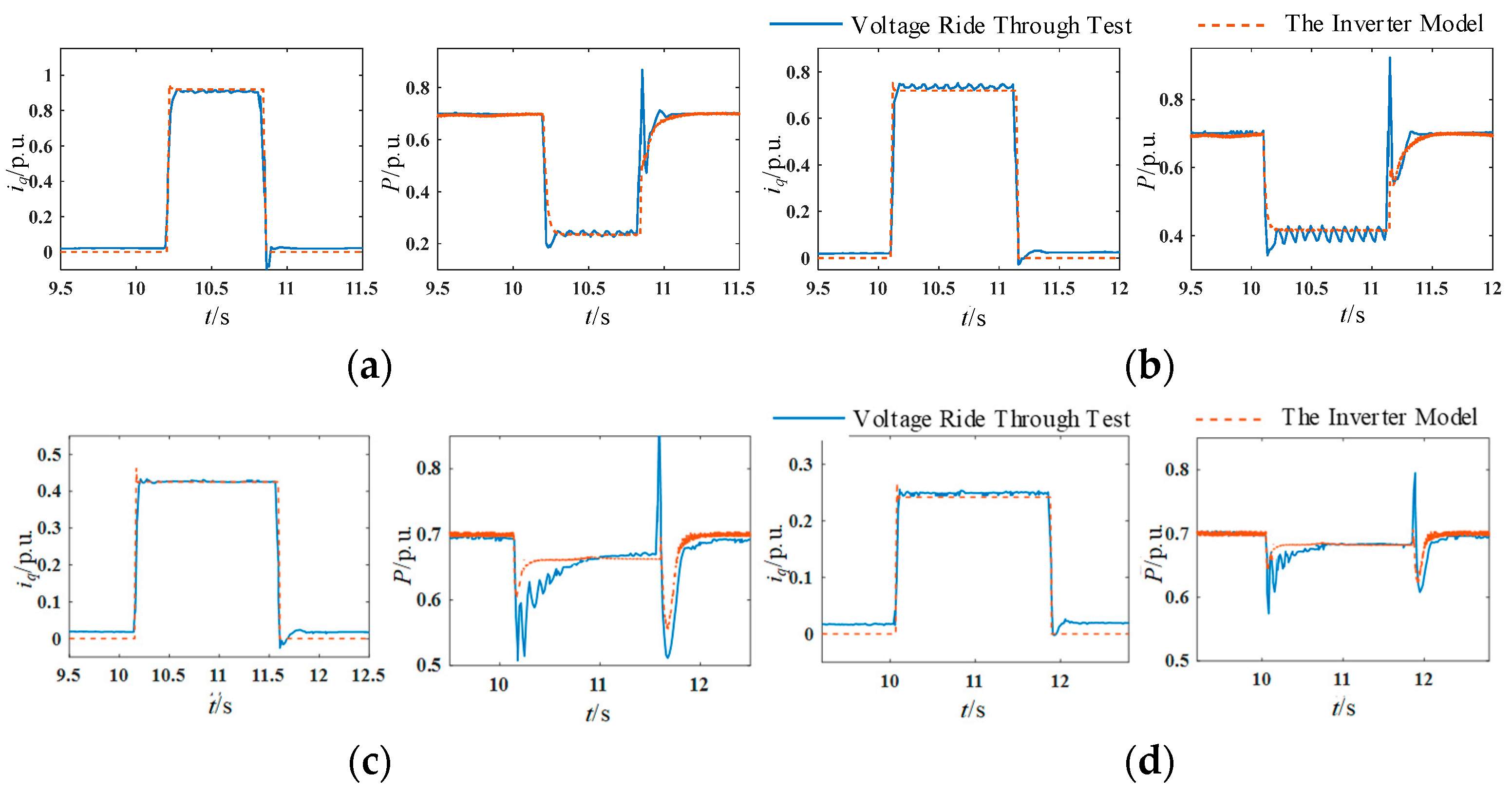
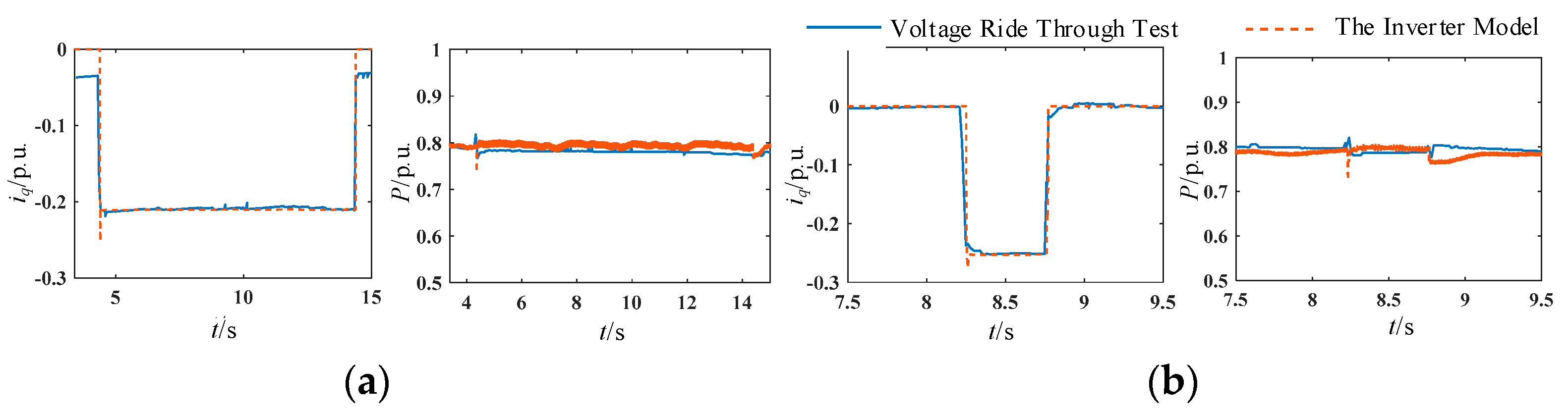
- During the fault transient, the detailed electromagnetic transient model of the PV grid-connected inverter is calibrated based on the PV grid-connected inverter low-voltage and high-voltage ride-through test data to verify its accuracy.
- During stable operation, based on the actual grid measurement data at a certain moment, combined with the light and temperature conditions at that moment, the PV grid-connected system detailed electromagnetic transient model of the PV output, and the steady state currents of each grid-connected point are calibrated.
- With small errors, the detailed simulation model can reflect the operational state of the actual power grid. Subsequently, it can provide sufficient current data for the parameter identification of the generalized load model.
4.4.2. Generalized Load Model Calibration
- Time period A starts 2 s before the voltage dip.
- The first 20 ms of the voltage drop to 0.9 p.u. is the end of the A period and the beginning of the B period.
- The first 20 ms of the start time of disturbance removal is the end of the B time period and the start of the C time period.
- After the disturbance is cleared, 2 s after the system’s active power starts to stabilize its output is the end of the C time period.
- The average deviation in the steady state interval (F1) represents the arithmetic mean of the deviations between the detailed electromagnetic transient model and the generalized load model in the steady state interval.
- The average deviation over the transient interval (F2) is the arithmetic mean of the deviations between the detailed electromagnetic transient model and the generalized load model over the transient interval.
- The maximum deviation in the steady state interval (F3) is the maximum value of the deviation between the detailed electromagnetic transient model and the generalized load model in the steady state interval.
5. Conclusions
- A generalized load model that includes a detailed PV system structure and considers PV high and low voltage fault ride-through capability is developed. Compared with other load models, this model takes into account the PV high and low voltage ride-through characteristics, which are more adapted to the load characteristics of the real distribution network at present.
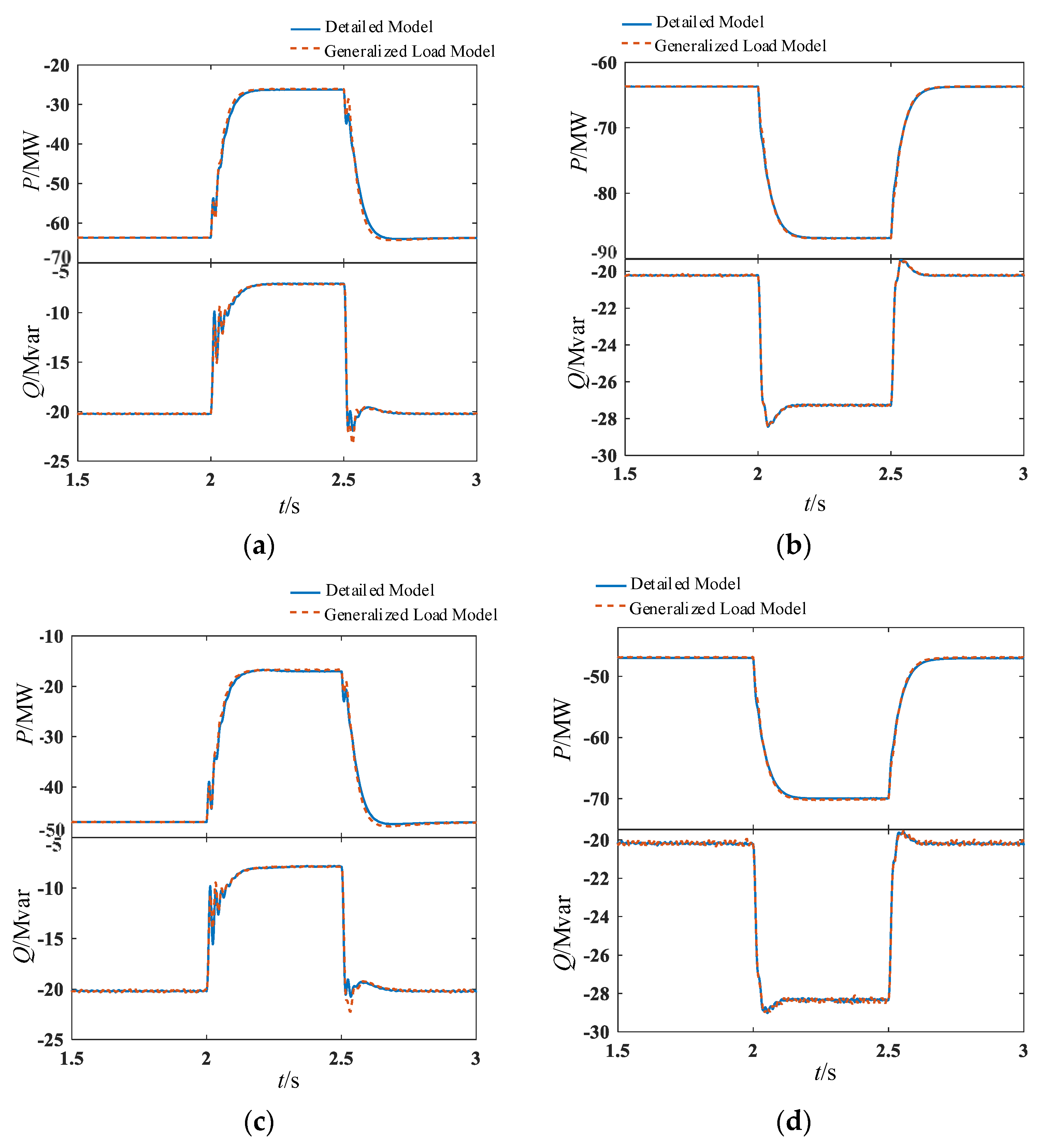
- In the model calibration section, a detailed model calibration of the distribution network based on measured data is proposed. Considering that it is difficult to obtain the parameters of the actual grid fault, the detailed model based on measured data is first established to check its ability to express the stable operation and fault transient characteristics of the actual distribution network. From the simulation results, the error between the actual current and the detailed model is less than 1%, and it can be considered that the model can reflect the actual operation state of the grid. The grid-connected data can be used as the benchmark data for the parameter identification of the generalized load model.
- After the parameter identification is completed, the generalized load model and the detailed model will be simulated. By comparing the simulation results under four groups of different PV penetration rates and different operating conditions, the errors of the corresponding physical quantities of the two models are calculated, and the resulting errors are less than 1%. The model fits well with the distributed PV access to the distribution network.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karimi, M.; Mokhlis, H.; Naidu, K.; Uddin, S.; Bakar, A. Photovoltaic penetration issues and impacts in distribution network–A review. Renew. Sustain. Energy Rev. 2016, 53, 594–605. [Google Scholar] [CrossRef]
- Rahman, A.; Farrok, O.; Haque, M.M. Environmental impact of renewable energy source based electrical power plants: Solar, wind, hydroelectric, biomass, geothermal, tidal, ocean, and osmotic. Renew. Sustain. Energy Rev. 2022, 161, 112279. [Google Scholar] [CrossRef]
- Alsafasfeh, Q.; Saraereh, O.A.; Khan, I.; Kim, S. Solar PV grid power flow analysis. Sustainability 2019, 11, 1744. [Google Scholar] [CrossRef]
- Ding, M.; Wang, W.; Wang, X.; Song, Y.T.; Chen, D.Z.; Sun, M. A Review on the Effect of Large-scale PV Generation on Power Systems. Proc. CSEE 2014, 34, 1–14. [Google Scholar]
- Huang, W.; Dong, X.; Lei, J.; Yu, L. Integrated Impact of Large-capacity Distributed Photovoltaic on Power Grid. Proc. CSU-EPSA 2016, 28, 44–49. [Google Scholar]
- Zheng, W.; Xiong, X. A model identification method for photovoltaic grid-connected inverters based on the Wiener model. Proc. CSEE 2013, 33, 18–26. [Google Scholar]
- Liu, Z.; Wu, H.; Jin, W.; Xu, B.; Ji, Y.; Wu, M. Two-step method for identifying photovoltaic grid-connected inverter controller parameters based on the adaptive differential evolution algorithm. IET Gener. Transm. Distrib. 2017, 11, 4282–4290. [Google Scholar] [CrossRef]
- Paulescu, M.; Brabec, M.; Boata, R.; Badescu, V. Structured, physically inspired (gray box) models versus black box modeling for forecasting the output power of photovoltaic plants. Energy 2017, 121, 792–802. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, J.; Wu, H. Research on the identification and adaptation of generalized load modeling based on distributed generators. Power Syst. Prot. Control 2013, 41, 105–111. [Google Scholar]
- Ma, Y.; Li, X.; Cao, J. Integrated load modeling with inverter-containing distributed power. J. Sol. Energy 2015, 36, 1869–1875. [Google Scholar]
- Samadi, A.; Soder, L.; Shayesteh, E.; Eriksson, R. Static equivalent of distribution grids with high penetration of PV systems. IEEE Trans. Smart Grid 2015, 6, 1763–1774. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, Y. Impact of three-phase single-stage photovoltaic system on distribution network load modeling. Autom. Electr. Power Syst. 2011, 35, 73–78. [Google Scholar]
- Guan, L.; Zhao, Q.; Zhou, B.; Lyu, Y.; Zhao, W.; Yao, W. Multi-scale clustering analysis based modeling of photovoltaic power characteristics and its application in prediction. Autom. Electr. Power Syst. 2018, 42, 24–30. [Google Scholar]
- Qu, X.; Li, X.; Sheng, Y.; Su, Z.; Zhao, Y. Research on equivalent modeling of PV generation system for generalized load. Power Syst. Technol. 2020, 44, 2143–2150. [Google Scholar]
- Stetz, T.; Marten, F.; Braun, M. Improved low voltage grid-integration of photovoltaic systems in Germany. IEEE Trans. Sustain. Energy 2013, 4, 534–542. [Google Scholar] [CrossRef]
- Ju, P.; Ma, D. Power System Load Modeling, 2nd ed.; China Electric Power Press: Beijing, China, 2008; pp. 144–145. [Google Scholar]
- Zhang, R.; Chao, L.; Ying, W. A two-stage framework for ambient signal based load model parameter identification. Int. J. Electr. Power Energy Syst. 2020, 121, 106064. [Google Scholar] [CrossRef]
- Arif, A.; Wang, Z.; Wang, J.; Mather, B.; Bashualdo, H.; Zhao, D. Load modeling—A review. IEEE Trans. Smart Grid 2017, 9, 5986–5999. [Google Scholar] [CrossRef]
- China Electric Power Research Institute. Power System Analysis Synthesis Program Version 6. 0 User Manual; China Electric Power Research Institute: Beijing, China, 2000; pp. 1–200. [Google Scholar]
- Kabir, M.N.; Mishra, Y.; Ledwich, G.; Dong, Z.Y.; Wong, K.P. Coordinated control of grid-connected photovoltaic reactive power and battery energy storage systems to improve the voltage profile of a residential distribution feeder. IEEE Trans. Ind. Inform. 2014, 10, 967–977. [Google Scholar] [CrossRef]
- Kumary, S.V.S.; Oo, V.A.A.M.T.; Shafiullah, G.M.; Stojcevski, A. Modelling and power quality analysis of a grid-connected solar PV system. In Proceedings of the 2014 Australasian Universities Power Engineering Conference (AUPEC), Perth, Australia, 28 September–1 October 2014; pp. 1–6. [Google Scholar]
- Jin, X.; Wen, S.; Ni, H.; Yang, Y.; Wen, Y. Review of maximum power point tracking of photovoltaic system. Chin. J. Power Sources 2019, 43, 532–535. [Google Scholar]
- Rajlaxmi, E.; Behera, S.; Panda, S.K. Comparison of Inverter Control by SPWM and SVPWM Method in Standalone PV System. In Proceedings of the 2020 IEEE International Symposium on Sustainable Energy, Signal Processing and Cyber Security (iSSSC), Gunupur Odisha, India, 16–17 December 2020. [Google Scholar]
- Hassaine, L.; Olias, E.; Quintero, J.; Salas, V. Overview of power inverter topologies and control structures for grid connected photovoltaic systems. Renew. Sustain. Energy Rev. 2014, 30, 796–807. [Google Scholar] [CrossRef]
- Li, F.; Liu, M.; Wang, Y.; Zhang, X. Research on HIL-based HVRT and LVRT automated test system for photovoltaic inverters. Energy Rep. 2021, 7, 405–412. [Google Scholar] [CrossRef]
- Al-Shetwi Ali, Q.; Sujod, M.Z.; Blaabjerg, F. Low voltage ride-through capability control for single-stage inverter-based grid-connected photovoltaic power plant. Sol. Energy 2018, 159, 665–681. [Google Scholar] [CrossRef]
- Guo, L.; Meng, Z.; Sun, Y.; Wang, L. Parameter identification and sensitivity analysis of solar cell models with cat swarm optimization algorithm. Energy Convers. Manag. 2016, 108, 520–528. [Google Scholar] [CrossRef]





| NO. | Parameter | Notation |
|---|---|---|
| 1 | Active Power of Static Loads and Dynamic Loads | P |
| 2 | Number of PV units | nPV |
| 3 | Intensity of light | S |
| 4 | Celsius temperature | T |
| NO. | Parameter | Notation |
|---|---|---|
| 1 | Ration of Active Power for Static Loads | kL |
| 2 | Power Factor of ZIP Loads | θ |
| 3 | Stator Resistance for Dynamic Loads | RS |
| 4 | Stator Reactance for Dynamic Loads | XS |
| 5 | Rotor Resistance for Dynamic Loads | Rr |
| 6 | Rotor Reactance for Dynamic Loads | Xr |
| 7 | Excitation Reactance for Dynamic Loads | Xm |
| 8 | Rated turndown for Dynamic Loads | sN |
| 9 | Inductance at Inverter Exit | L |
| 10 | Proportional Coefficient of External Segment | KE |
| 11 | Integral Time Constant of External Segment | TE |
| 12 | Proportional Coefficient of Internal Segment | KI |
| 13 | Integral Time Constant of Internal Segment | TI |
| 14 | Dynamic Reactive Power Support Factor | K |
| Parameter | Active Power | Reactive Power | Averages |
|---|---|---|---|
| K | 0.0090 | 6.8972 | 3.4531 |
| θ | 0.1054 | 4.3658 | 2.2356 |
| sN | 0.2995 | 3.8111 | 2.0553 |
| Rr | 0.2624 | 3.1256 | 1.6940 |
| kL | 1.7563 | 0.5122 | 1.1343 |
| Xm | 0.0336 | 1.9356 | 0.9846 |
| XS | 0.0551 | 0.2129 | 0.6340 |
| RS | 0.0119 | 0.3864 | 0.1992 |
| Xr | 0.0056 | 0.3039 | 0.1547 |
| L | 0.0241 | 0.2384 | 0.1312 |
| TE | 0.0407 | 0.1066 | 0.0736 |
| KE | 0.0309 | 0.1035 | 0.0672 |
| TI | 0.0015 | 0.0873 | 0.0444 |
| KI | 0.0015 | 0.0627 | 0.0321 |
| NO. | Parameter | Averages |
|---|---|---|
| 1 | K | 1.5742 |
| 2 | KL | 0.8432 |
| 3 | θ | 0.9776 |
| 4 | sN | 0.9634 |
| 5 | Rr | 0.0301 |
| 6 | Xm | 2.4124 |
| 7 | XS | 0.1677 |
| 8 | RS | 0.0282 |
| 9 | Xr | 0.0253 |
| 10 | L | 0.0994 |
| 11 | TE | 0.0980 |
| 12 | KE | 3 |
| 13 | TI | 0.012 |
| 14 | KI | 0.2 |
| Point | Measurement Data | Simulation Data | Relative Error | |||
|---|---|---|---|---|---|---|
| P/MW | Q/MVar | P/MW | Q/MVar | P/MW | Q/MVar | |
| 1 | 6.78 | — | 6.71 | — | 1.03 | — |
| 2 | 2.45 | — | 2.49 | — | 1.63 | — |
| 3 | 2.24 | 2.15 | 2.25 | 2.16 | 0.446 | 0.465 |
| 4 | 4.66 | 0 | 4.67 | 0.005 | 0.214 | 0.497 |
| 5 | 9.53 | 2.04 | 9.56 | 2.04 | 0.314 | 0 |
| Sample | Conditions | PV Penetration |
|---|---|---|
| 1 | Voltage dropped by 20% | 0.15 |
| 2 | Voltage increased by 15% | 0.15 |
| 3 | Voltage dropped by 20% | 0.30 |
| 4 | Voltage increased by 15% | 0.30 |
| Sample | KL | θ | Rr/p.u. | Xm/p.u. | SN | K |
|---|---|---|---|---|---|---|
| 1 | 0.7761 | 0.9810 | 0.0345 | 2.5379 | 0.9598 | 1.6248 |
| 2 | 0.7942 | 0.9793 | 0.0267 | 2.5456 | 0.9690 | 1.1186 |
| 3 | 0.8144 | 0.9801 | 0.0278 | 2.7280 | 0.9675 | 1.3866 |
| 4 | 0.8068 | 0.9804 | 0.0261 | 2.7686 | 0.9697 | 0.9650 |
| F1/F2 | F3 | Weighted Deviations | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U | I | P | Q | U | I | P | Q | U | I | P | Q | ||
| Sample1 | A | 0.0002 | 0.0001 | 0.0001 | 0.0002 | 0.0013 | 0.0003 | 0.0006 | 0.0011 | 0.0003 | 0.0012 | 0.0019 | 0.0004 |
| B1 | 0.0007 | 0.0041 | 0.0039 | 0.0003 | — | — | — | — | |||||
| B2 | 0.0002 | 0.0006 | 0.0016 | 0.0007 | 0.0010 | 0.0009 | 0.0021 | 0.0012 | |||||
| C1 | 0.0004 | 0.0067 | 0.0097 | 0.00001 | — | — | — | — | |||||
| C2 | 0.0002 | 0.0001 | 0.0001 | 0.0002 | 0.0013 | 0.0004 | 0.0015 | 0.0011 | |||||
| Sample2 | A | 0.0003 | 0.0001 | 0.0004 | 0.0001 | 0.0013 | 0.0005 | 0.0008 | 0.00115 | 0.0015 | 0.0006 | 0.0006 | 0.0002 |
| B1 | 0.0010 | 0.0039 | 0.0001 | 0.0002 | — | — | — | — | |||||
| B2 | 0.0003 | 0.0001 | 0.0006 | 0.00009 | 0.0015 | 0.0004 | 0.0012 | 0.0015 | |||||
| C1 | 0.0022 | 0.0021 | 0.0008 | 0.0002 | — | — | — | — | |||||
| C2 | 0.0003 | 0.0002 | 0.0007 | 0.0001 | 0.0013 | 0.0006 | 0.0012 | 0.0011 | |||||
| Sample3 | A | 0.0001 | 0.00006 | 0.0003 | 0.0004 | 0.0013 | 0.0009 | 0.0015 | 0.0036 | 0.0024 | 0.0019 | 0.0024 | 0.0004 |
| B1 | 0.0035 | 0.0090 | 0.0066 | 0.0005 | — | — | — | — | |||||
| B2 | 0.0001 | 0.0011 | 0.0032 | 0.0004 | 0.0010 | 0.0021 | 0.0046 | 0.0022 | |||||
| C1 | 0.0052 | 0.0048 | 0.0003 | 0.0010 | — | — | — | — | |||||
| C2 | 0.0001 | 0.0001 | 0.0002 | 0.0002 | 0.0013 | 0.0010 | 0.0023 | 0.0032 | |||||
| Sample4 | A | 0.0001 | 0.0006 | 0.0017 | 0.0005 | 0.0013 | 0.0015 | 0.0031 | 0.0038 | 0.0026 | 0.0013 | 0.0021 | 0.0003 |
| B1 | 0.0038 | 0.0052 | 0.0022 | 0.0003 | — | — | — | — | |||||
| B2 | 0.0002 | 0.0004 | 0.0019 | 0.0001 | 0.0016 | 0.0012 | 0.0037 | 0.0041 | |||||
| C1 | 0.0020 | 0.0028 | 0.0017 | 0.0002 | — | — | — | — | |||||
| C2 | 0.0001 | 0.0010 | 0.0027 | 0.0006 | 0.0014 | 0.0019 | 0.0043 | 0.0038 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Chen, Q.; Zhang, L.; Yin, X.; Cui, H.; Zhang, Z.; Wei, H.; Chen, X. A Generalized Load Model Considering the Fault Ride-Through Capability of Distributed PV Generation System. Energies 2024, 17, 3595. https://doi.org/10.3390/en17143595
Wang H, Chen Q, Zhang L, Yin X, Cui H, Zhang Z, Wei H, Chen X. A Generalized Load Model Considering the Fault Ride-Through Capability of Distributed PV Generation System. Energies. 2024; 17(14):3595. https://doi.org/10.3390/en17143595
Chicago/Turabian StyleWang, Haiyun, Qian Chen, Linyu Zhang, Xiyu Yin, Han Cui, Zhijian Zhang, Huayue Wei, and Xiaoyue Chen. 2024. "A Generalized Load Model Considering the Fault Ride-Through Capability of Distributed PV Generation System" Energies 17, no. 14: 3595. https://doi.org/10.3390/en17143595
APA StyleWang, H., Chen, Q., Zhang, L., Yin, X., Cui, H., Zhang, Z., Wei, H., & Chen, X. (2024). A Generalized Load Model Considering the Fault Ride-Through Capability of Distributed PV Generation System. Energies, 17(14), 3595. https://doi.org/10.3390/en17143595





