Prediction of Pipe Failure Rate in Heating Networks Using Machine Learning Methods
Abstract
1. Introduction
2. Current State of the Research Area
2.1. Traditional Evaluation Models
2.2. Intelligent Predictive Models
- linear: K(x, x′) = (x · x′);
- polynomial: K(x, x′) = (x · x′)d;
- radial basis function: for γ > 0;
- sigmoid: K(x, x′) = tanh(κx · x′ + c), for almost every κ > 0 and c > 0.
3. Materials and Methods
- Multilayer perceptron (MLP);
- Support vector machine (SVM);
- Gradient boosting regression tree (GBRT);
- Random forest (RF).
- mean absolute error (MAE), as follows:
- mean absolute percentage error (MAPE), as follows:
- mean squared error (MSE), as follows:
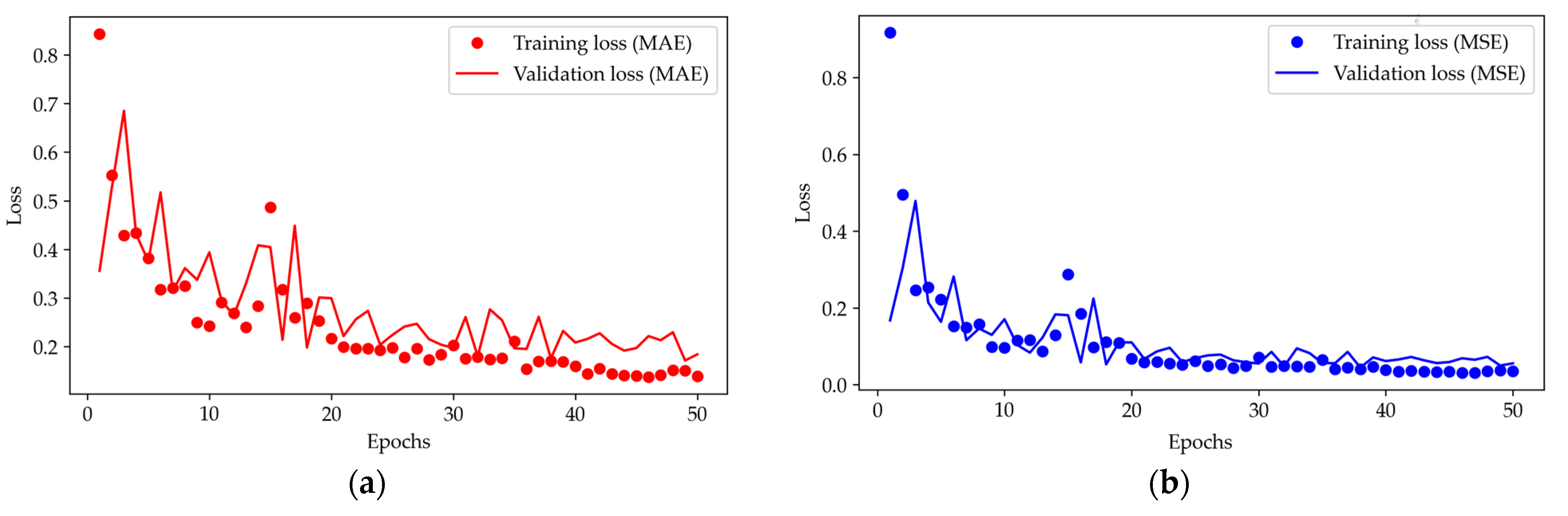
4. Results
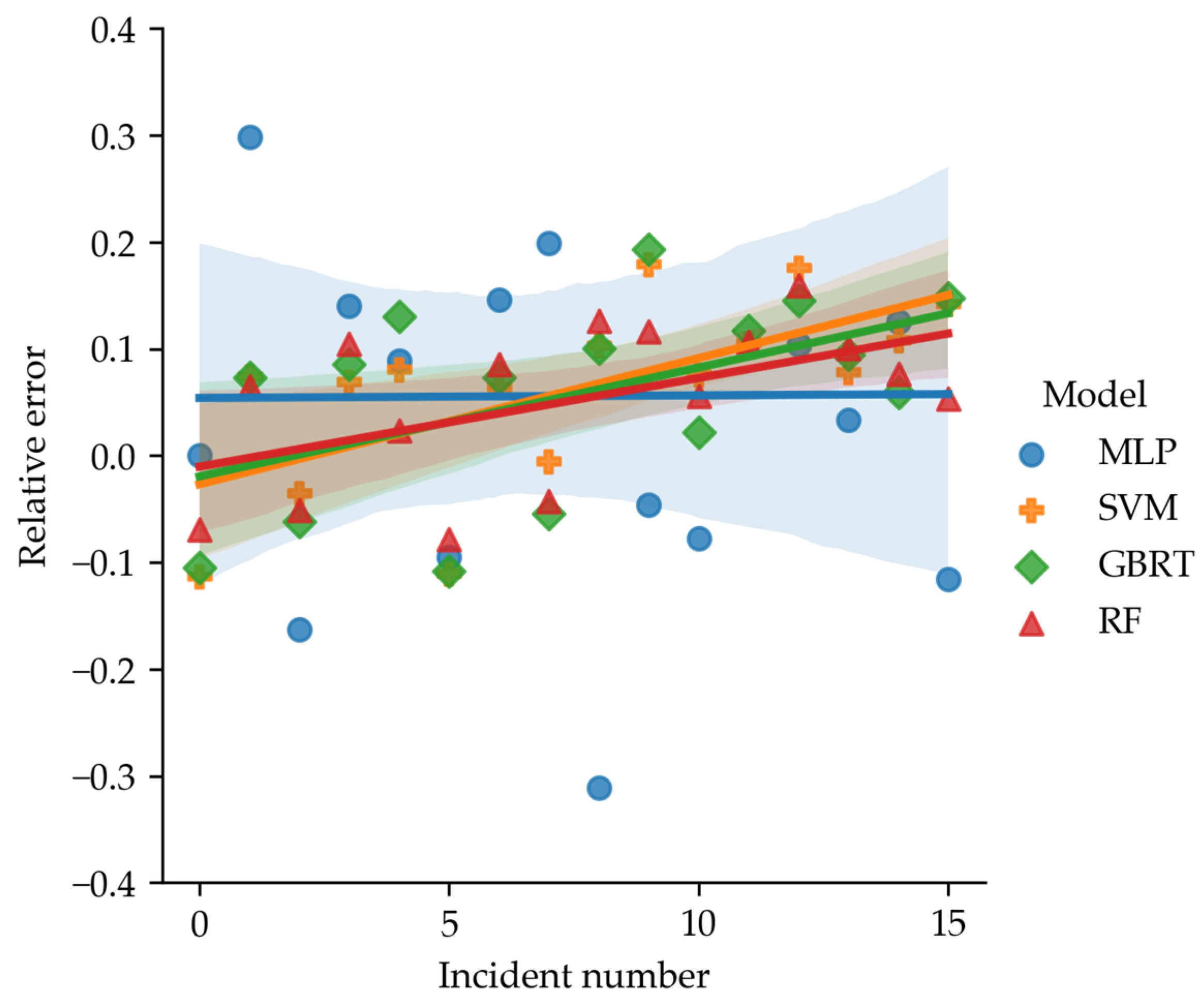
- There is no significant correlation between the target feature and significant factors (Figure 5);
5. Discussion
6. Conclusions
- The distribution of the Ki coefficient actual values within the general population of data is close to the normal Gauss–Laplace distribution, which indicates the representativeness of the source data;
- The most significant factors when assessing the condition of underground steel pipelines are wall thinning (K1) and soil corrosion (K3);
- Previous incidents on the pipeline section (K2) are the least significant factor, and their exclusion from the training set leads to an increase in the accuracy of the models;
- The MLP model showed the worst results and is therefore not suitable for solving such tasks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Notations | |
| α | coefficient taking into account the duration of the pipeline section operation |
| γ | kernel constant |
| ε | the insensitivity of the loss function |
| λ | the failure rate of heating network elements, (km·h)−1 |
| λ0 | initial failure rate of 1 km of single-line heat pipeline, obtained from the Weibull distribution equation, 5.7·10−6 (km·h)−1 |
| ξ | slack variables |
| σf | flow stress, MPa |
| τ | pipeline service life |
| C | the regularization constant |
| d | depth of the corrosion zone, m |
| D | outside diameter of the pipeline, m |
| gm | negative gradient |
| K1 | residual pipeline wall thickness, % |
| K2 | previous incidents on the pipeline section |
| K3 | soil corrosion activity |
| K4 | flooding (traces of flooding) of the channel |
| K5 | presence of intersections with communications |
| l | length of the corrosion zone, m |
| L | loss function |
| M | Folias bulging coefficient |
| pb | burst pressure, MPa |
| Pi | predicted values |
| Ri | calculated (actual) values |
| Rt0.5 | the minimum yield strength, MPa |
| t | wall thickness of the pipeline, m |
| Abbreviations | |
| AGA | American Natural Gas Association |
| ANN | Artificial neural networks |
| API | American Petroleum Institute |
| ASME | American Society of Mechanical Engineers |
| AVP | Average validity percentage |
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| CONCAWE | Conservation of Clean Air and Water in Europe |
| CPU | Central processing unit |
| EGIG | European Gas Pipeline Incident Data Group |
| EL | Ensemble learning |
| FL | Fuzzy logic |
| GBRT | Gradient boosting regression tree |
| GCN | Graph convolutional neural network |
| GPU | Graphics processing unit |
| IPSO | Improved particle swarm optimization |
| JSC | Joint-stock company |
| LR | Linear regression |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| MNL | Multinomial logistic regression |
| MSE | Mean squared error |
| RBF | Radial basis function |
| ReLU | Rectified linear unit |
| RF | Random forest |
| SVM | Support vector machine |
References
- EGIG. Available online: https://www.egig.eu/reports (accessed on 18 June 2024).
- Li, H.; Huang, K.; Zeng, Q.; Sun, C. Residual Strength Assessment and Residual Life Prediction of Corroded Pipelines: A Decade Review. Energies 2022, 15, 726. [Google Scholar] [CrossRef]
- Akhmetova, I.G.; Akhmetov, T.R. Analysis of Additional Factors in Determining the Failure Rate of Heat Network Pipelines. Therm. Eng. 2019, 66, 730–736. [Google Scholar] [CrossRef]
- Zhu, X.-K. Recent Advances in Corrosion Assessment Models for Buried Transmission Pipelines. CivilEng 2023, 4, 391–415. [Google Scholar] [CrossRef]
- Law, M.; Bowie, G. Prediction of failure strain and burst pressure in high yield-to-tensile strength ratio line pipes. Int. J. Press. Vessel. Pip. 2007, 84, 487–492. [Google Scholar] [CrossRef]
- Lyons, C.J.; Race, J.M.; Chang, E.; Cosham, A.; Barnett, J. Validation of the ng-18 equations for thick walled pipelines. EFA 2020, 112, 104494. [Google Scholar] [CrossRef]
- API Specification 5L. Lin Pipe, 46th ed.; American Petroleum Institute: Washington, DC, USA, 2018. [Google Scholar]
- Zhou, R.; Gu, X.; Luo, X. Residual strength prediction of X80 steel pipelines containing group corrosion defects. Ocean. Eng. 2023, 274, 114077. [Google Scholar] [CrossRef]
- Methodology and Algorithm for Calculating Reliability Indicators of Heat Supply to Consumers and Redundancy of Heat Networks when Developing Heat Supply Schemes. Available online: https://www.rosteplo.ru/Tech_stat/stat_shablon.php?id=2781 (accessed on 18 June 2024).
- Cai, J.; Jiang, X.; Yang, Y.; Lodewijks, G.; Wang, M. Data-driven methods to predict the burst strength of corroded line pipelines subjected to internal pressure. J. Mar. Sci. Appl. 2022, 21, 115–132. [Google Scholar] [CrossRef]
- Soomro, A.A.; Mokhtar, A.A.; Hussin, H.B.; Lashari, N.; Oladosu, T.L.; Jameel, S.M.; Inayat, M. Analysis of machine learning models and data sources to forecast burst pressure of petroleum corroded pipelines: A comprehensive review. EFA 2024, 155, 107747. [Google Scholar] [CrossRef]
- Rahmanifard, H.; Plaksina, T. Application of artificial intelligence techniques in the petroleum industry: A review. Artif. Intell. Rev. 2019, 52, 2295–2318. [Google Scholar] [CrossRef]
- Bagheri, M.; Zhu, S.P.; Ben Seghier, M.E.A.; Keshtegar, B.; Trung, N.T. Hybrid intelligent method for fuzzy reliability analysis of corroded X100 steel pipelines. Eng. Comput. 2020, 37, 2559–2573. [Google Scholar] [CrossRef]
- Liang, Q. Pressure pipeline leakage risk research based on trapezoidal membership degree fuzzy mathematics. GST 2019, 24, 48–53. [Google Scholar]
- Mishra, M.; Keshavarzzadeh, V.; Noshadravan, A. Reliability-based lifecycle management for corroding pipelines. Struct. Saf. 2019, 76, 1–14. [Google Scholar] [CrossRef]
- Sakamoto, S.; Ghanem, R. Polynomial chaos decomposition for the simulation of non-Gaussian nonstationary stochastic processes. J. Eng. Mech. 2002, 128, 190–201. [Google Scholar] [CrossRef]
- Robles-Velasco, A.; Cortés, P.; Muñuzuri, J.; Onieva, L. Prediction of pipe failures in water supply networks using logistic regression and support vector classification. Reliab. Eng. Syst. Saf. 2020, 196, 106754. [Google Scholar] [CrossRef]
- Nie, F.; Zhu, W.; Li, X. Decision Tree SVM: An extension of linear SVM for non-linear classification. Neurocomputing 2020, 401, 153–159. [Google Scholar] [CrossRef]
- Seghier, M.E.A.B.; Höche, D.; Zheludkevich, M. Prediction of the internal corrosion rate for oil and gas pipeline: Implementation of ensemble learning techniques. J. Nat. Gas. Sci. Eng. 2022, 99, 104425. [Google Scholar] [CrossRef]
- Foroozand, H.; Weijs, S. Entropy ensemble filter: A modified bootstrap aggregating (bagging) procedure to improve efficiency in ensemble model simulation. Entropy 2017, 19, 520. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Ossai, C.I. Corrosion defect modelling of aged pipelines with a feed-forward multi-layer neural network for leak and burst failure estimation. EFA 2020, 110, 104397. [Google Scholar] [CrossRef]
- MDK 4-01.2001; Recommended Practice for Investigation and Recordkeeping of Technical Violations in Public Energy Utility Systems and in the Operation of Public Energy Utility Organizations. State Unitary Enterprise «Center for Design Products in Construction»: Moscow, Russia, 2001.
- Elshaboury, N.; Al-Sakkaf, A.; Alfalah, G.; Abdelkader, E.M. Data-Driven Models for Forecasting Failure Modes in Oil and Gas Pipes. Processes 2022, 10, 400. [Google Scholar] [CrossRef]
- Xu, L.; Yu, J.; Zhu, Z.; Man, J.; Yu, P.; Li, C.; Wang, X.; Zhao, Y. Research and Application for Corrosion Rate Prediction of Natural Gas Pipelines Based on a Novel Hybrid Machine Learning Approach. Coatings 2023, 13, 856. [Google Scholar] [CrossRef]
- Sahin, E.; Yüce, H. Prediction of Water Leakage in Pipeline Networks Using Graph Convolutional Network Method. Appl. Sci. 2023, 13, 7427. [Google Scholar] [CrossRef]
- Shang, Y.; Li, S. FedPT-V2G: Security enhanced federated transformer learning for real-time V2G dispatch with non-IID data. Appl. Energy 2024, 358, 122626. [Google Scholar] [CrossRef]
- Pang, B.; Nijkamp, E.; Wu, Y.N. Deep learning with tensorflow: A review. J. Educ. Behav. Stat. 2020, 45, 227–248. [Google Scholar] [CrossRef]
- Zhang, Z. Improved Adam Optimizer for Deep Neural Networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018. [Google Scholar] [CrossRef]
- Kramer, O. Scikit-Learn; Springer: New York, NY, USA, 2016; pp. 45–53. [Google Scholar] [CrossRef]
- Çetin, V.; Yildiz, O. A comprehensive review on data preprocessing techniques in data analysis. Pamukkale Üniversitesi Mühendislik Bilim. Derg. 2022, 28, 299–312. [Google Scholar] [CrossRef]
- Islam, M.R. Sample size and its role in Central Limit Theorem (CLT). J. Computat. Appl. Math. 2018, 4, 1–7. [Google Scholar]








| Number of Records | Length, m | Diameter, mm | Wall thinning (K1), % | Previous Incidents (K2) | Corrosion Activity (K3) | Flooding Traces (K4) | Intersection with Communications (K5) |
|---|---|---|---|---|---|---|---|
| 1 | 30 | 50 | 60.0 | no | average | no | no |
| 2 | 75 | 50 | 45.7 | no | low | yes | да |
| 3 | 50 | 100 | 32.5 | no | low | no | no |
| 4 | 30 | 50 | 62.9 | no | low | no | yes |
| 5 | 170 | 200 | 24.7 | yes | average | yes | yes |
| 6 | 270 | 150 | 53.3 | yes | high | yes | yes |
| Metrics | Statistics of the Results of 71 Models from [2] | Author’s Result | ||
|---|---|---|---|---|
| Minimum | Maximum | Average | ||
| Sample size | 15 | 259 | 188 | 111 |
| Number of significant factors | 2 | 11 | 6 | 5(4) |
| Number of target features | 1 | 1 | 1 | 1 |
| MAPE | 0.0123 | 0.1499 | 0.0708 | 0.06069 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beloev, H.I.; Saitov, S.R.; Filimonova, A.A.; Chichirova, N.D.; Babikov, O.E.; Iliev, I.K. Prediction of Pipe Failure Rate in Heating Networks Using Machine Learning Methods. Energies 2024, 17, 3511. https://doi.org/10.3390/en17143511
Beloev HI, Saitov SR, Filimonova AA, Chichirova ND, Babikov OE, Iliev IK. Prediction of Pipe Failure Rate in Heating Networks Using Machine Learning Methods. Energies. 2024; 17(14):3511. https://doi.org/10.3390/en17143511
Chicago/Turabian StyleBeloev, Hristo Ivanov, Stanislav Radikovich Saitov, Antonina Andreevna Filimonova, Natalia Dmitrievna Chichirova, Oleg Evgenievich Babikov, and Iliya Krastev Iliev. 2024. "Prediction of Pipe Failure Rate in Heating Networks Using Machine Learning Methods" Energies 17, no. 14: 3511. https://doi.org/10.3390/en17143511
APA StyleBeloev, H. I., Saitov, S. R., Filimonova, A. A., Chichirova, N. D., Babikov, O. E., & Iliev, I. K. (2024). Prediction of Pipe Failure Rate in Heating Networks Using Machine Learning Methods. Energies, 17(14), 3511. https://doi.org/10.3390/en17143511







