Uninterruptible Power Supply Topology Based on Single-Phase Matrix Converter with Active Power Filter Functionality
Abstract
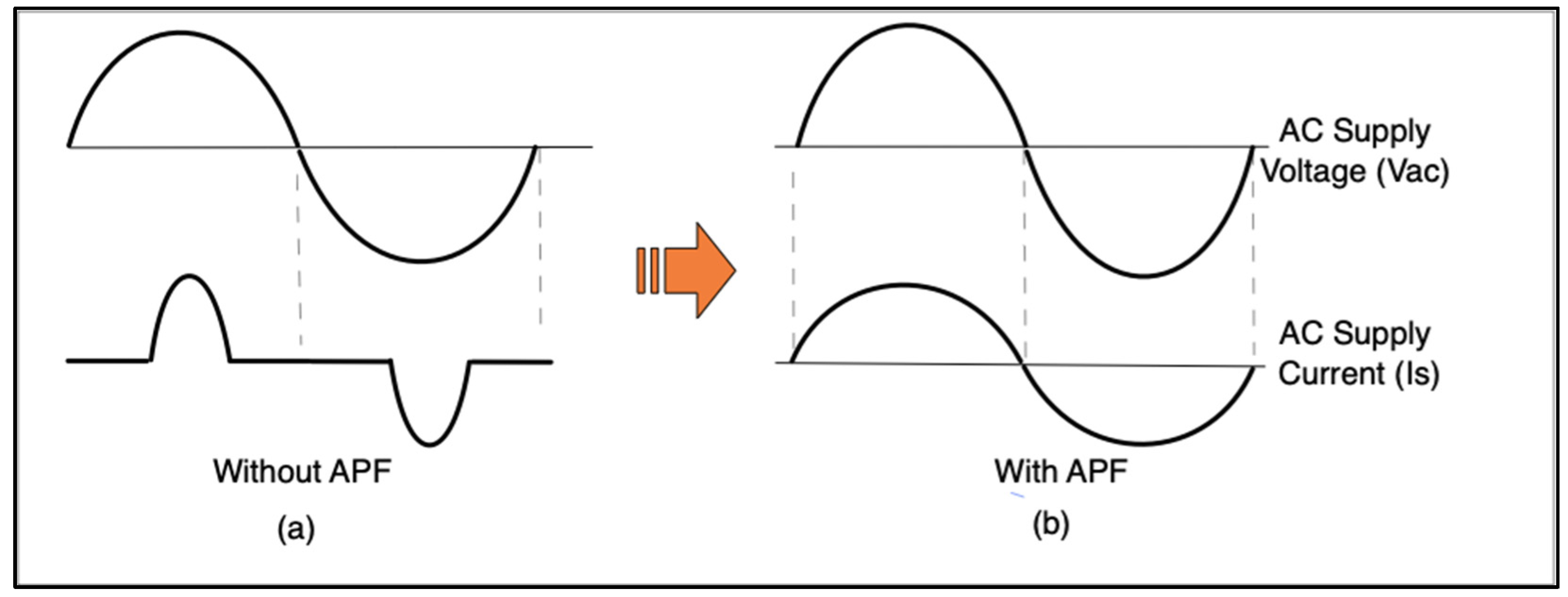
1. Introduction
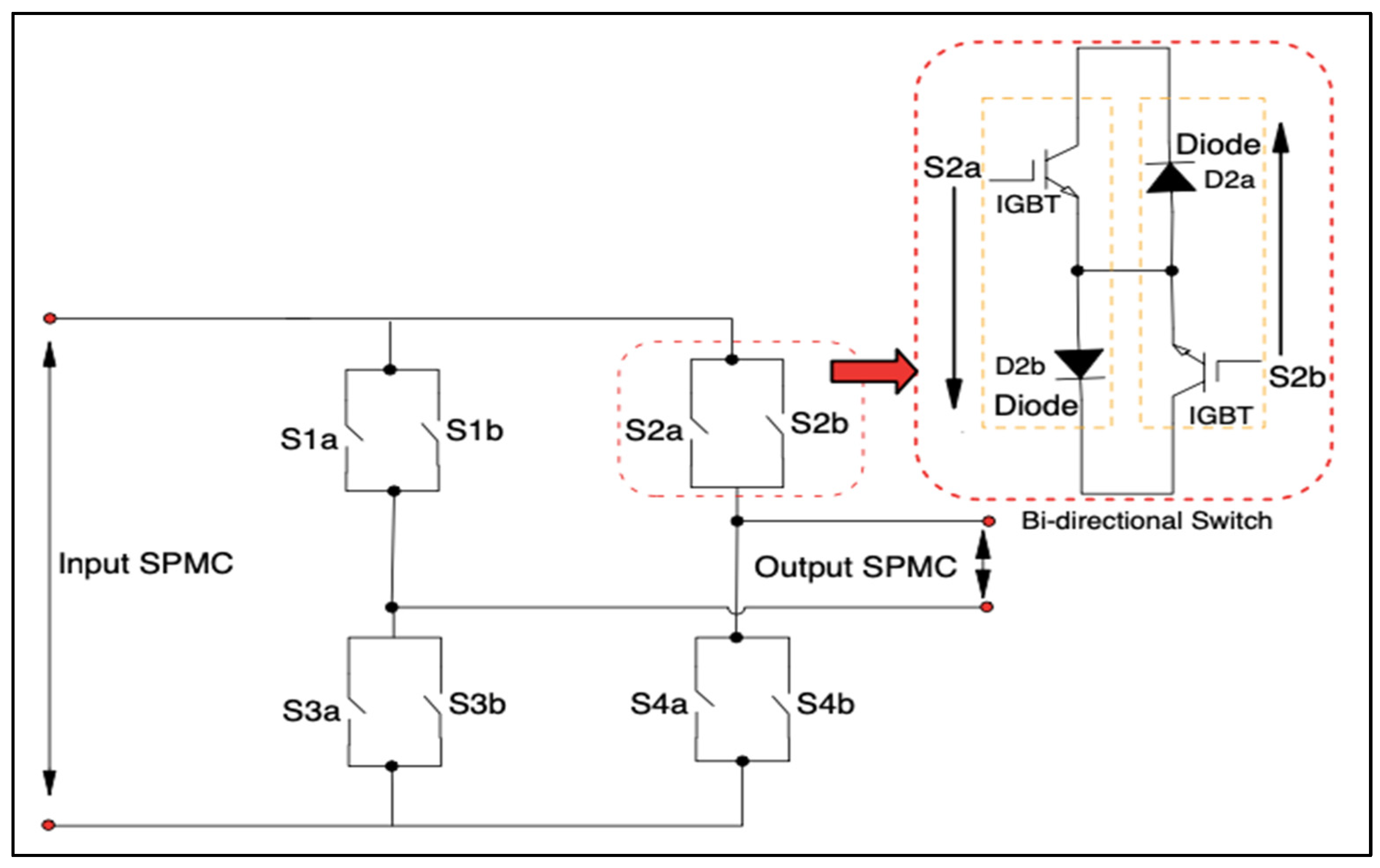
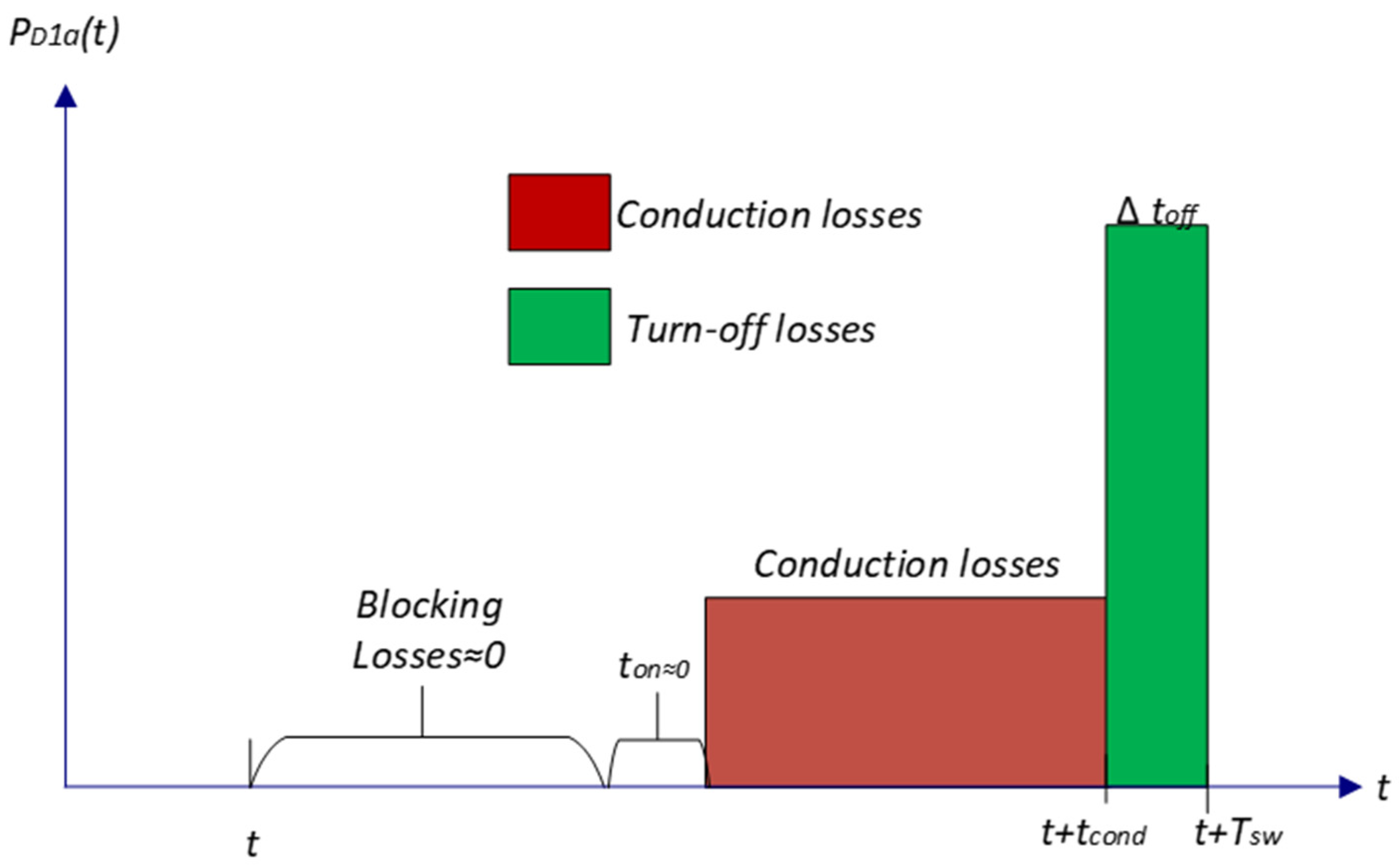
2. Bidirectional Switch Power Losses
- is devices instantaneous dissipated power.
- is fundamental output current period.
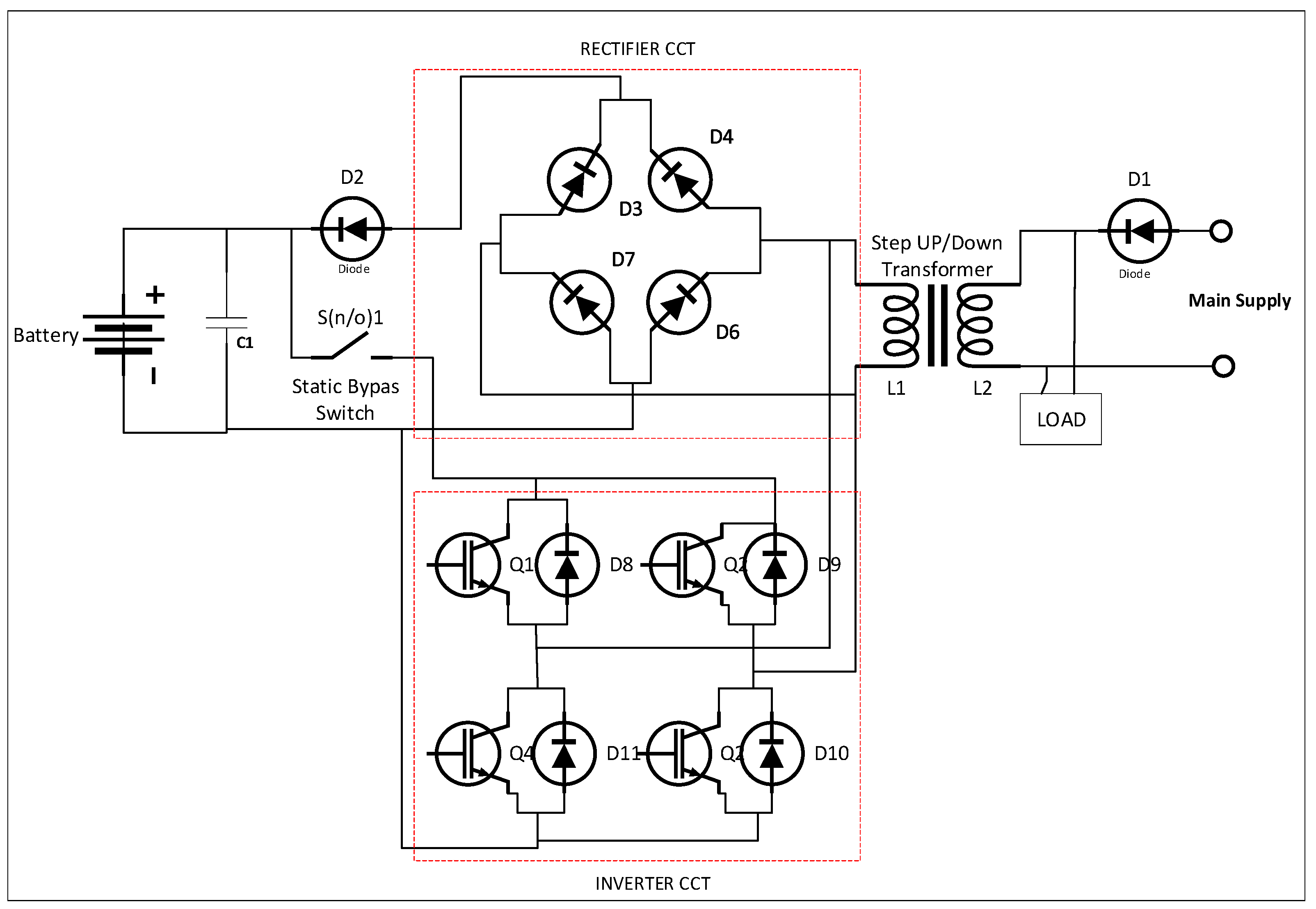
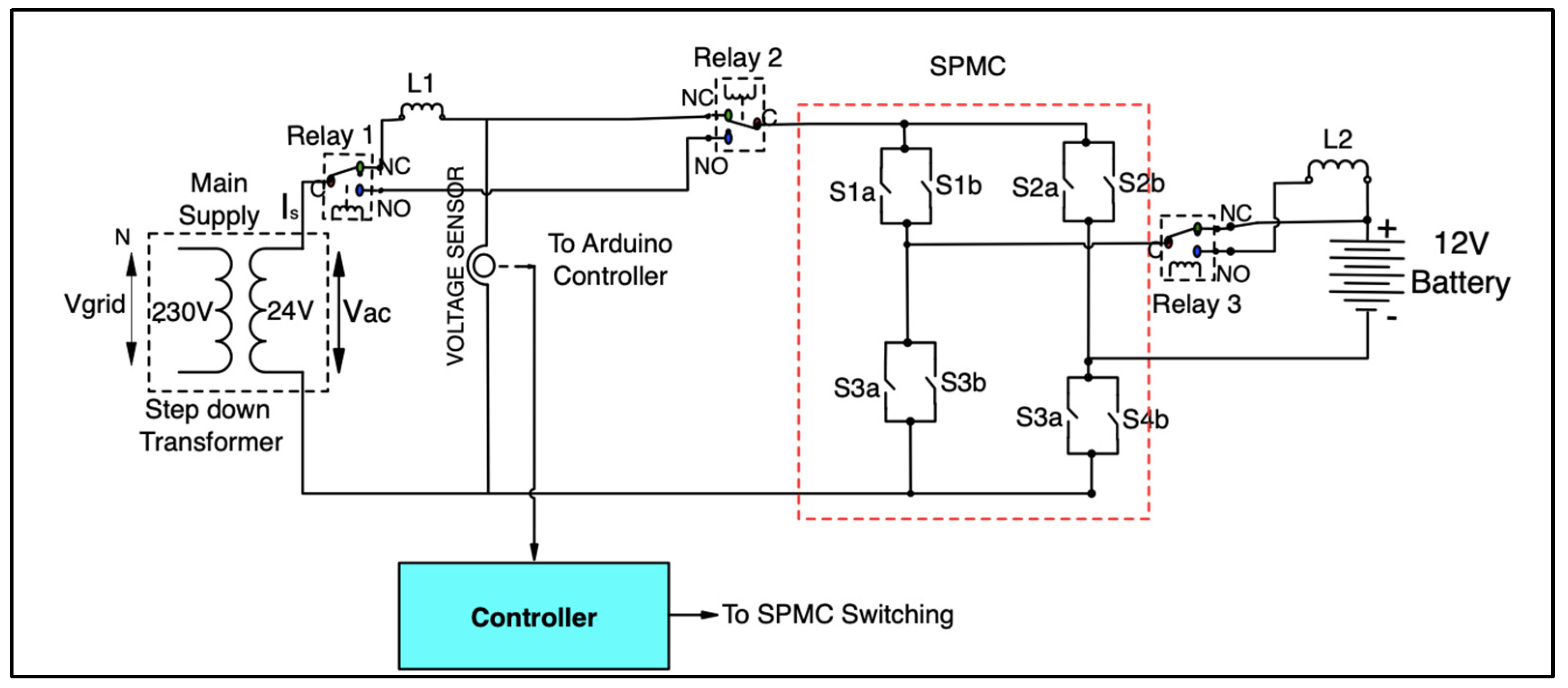
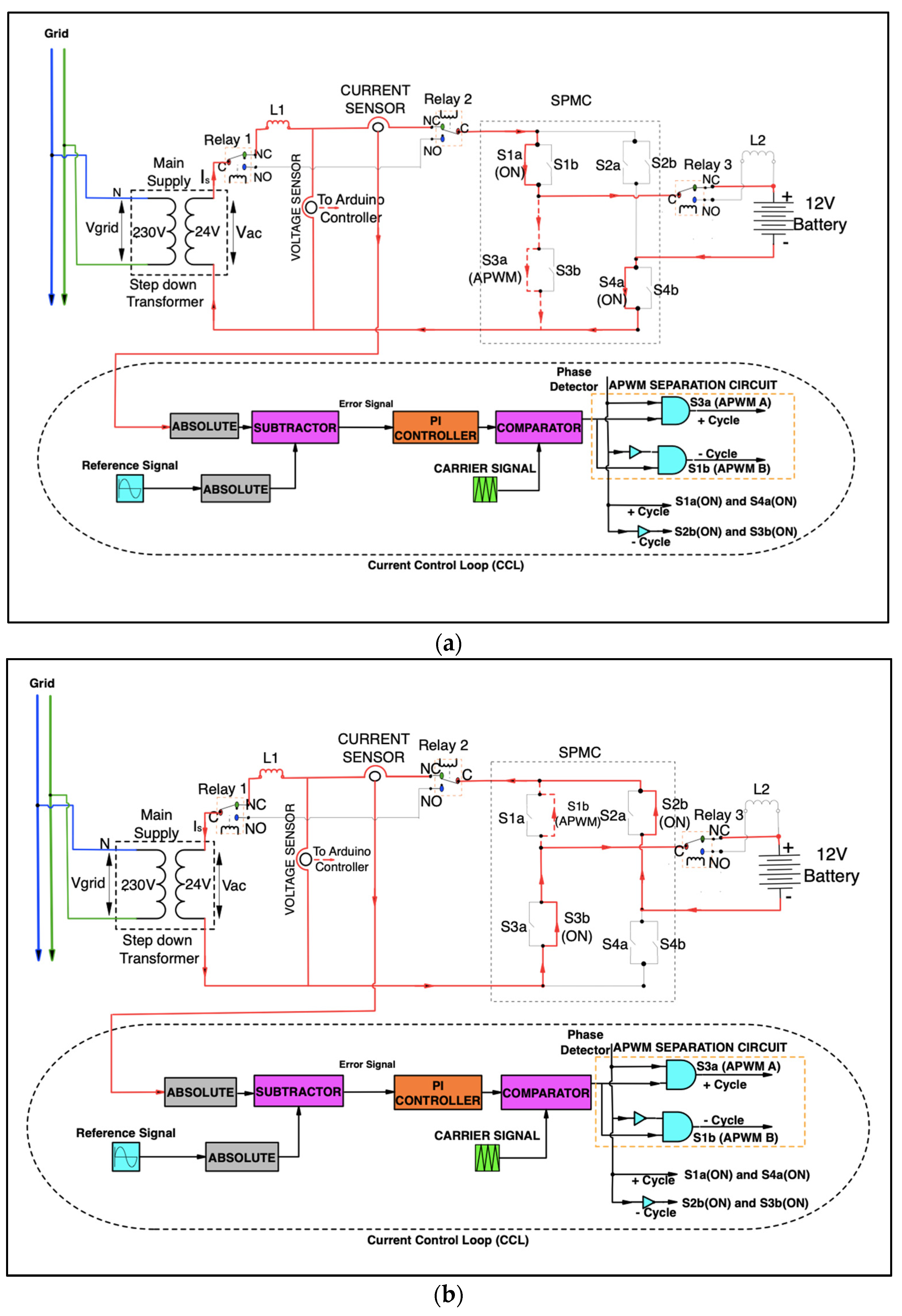
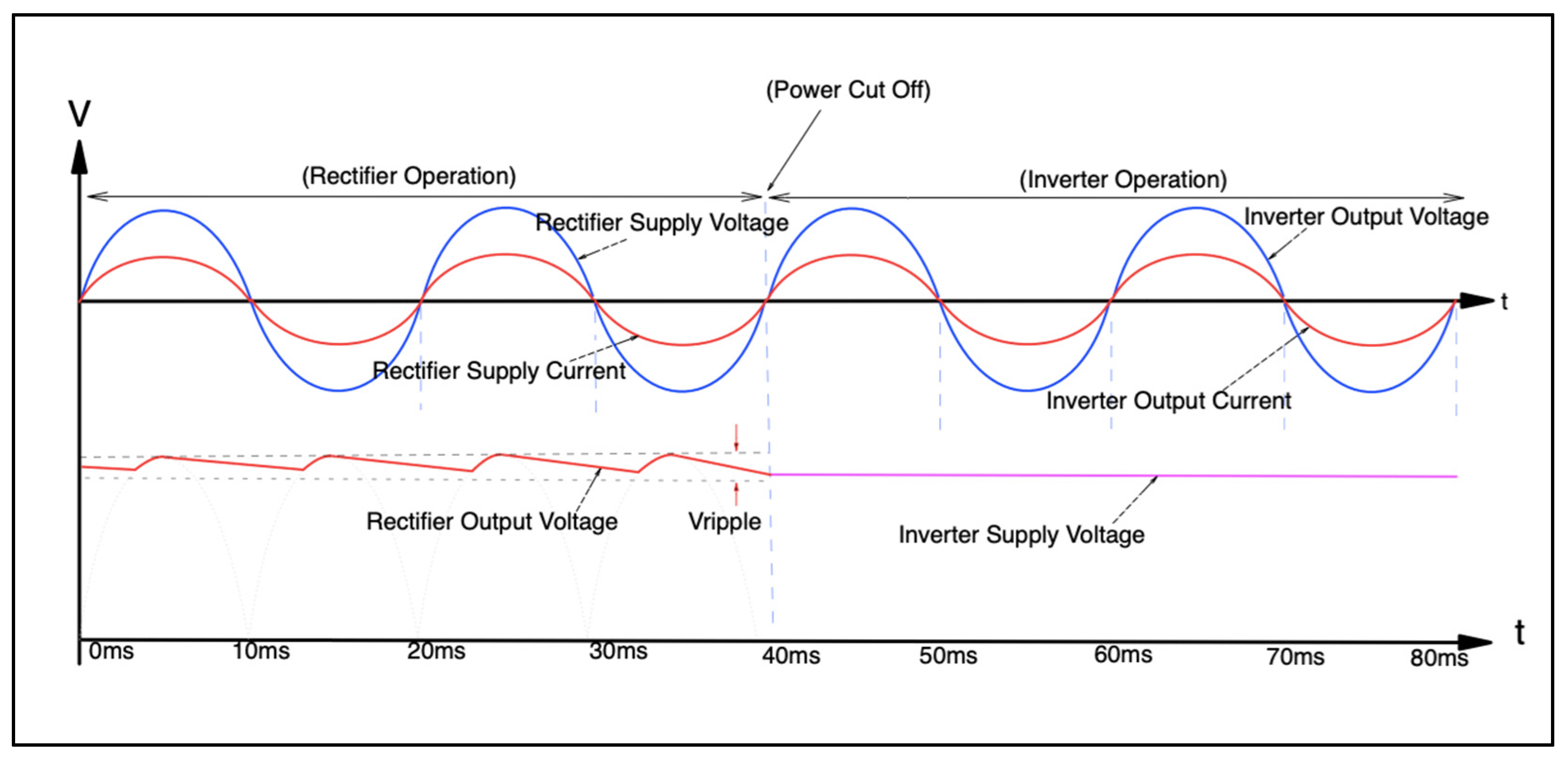
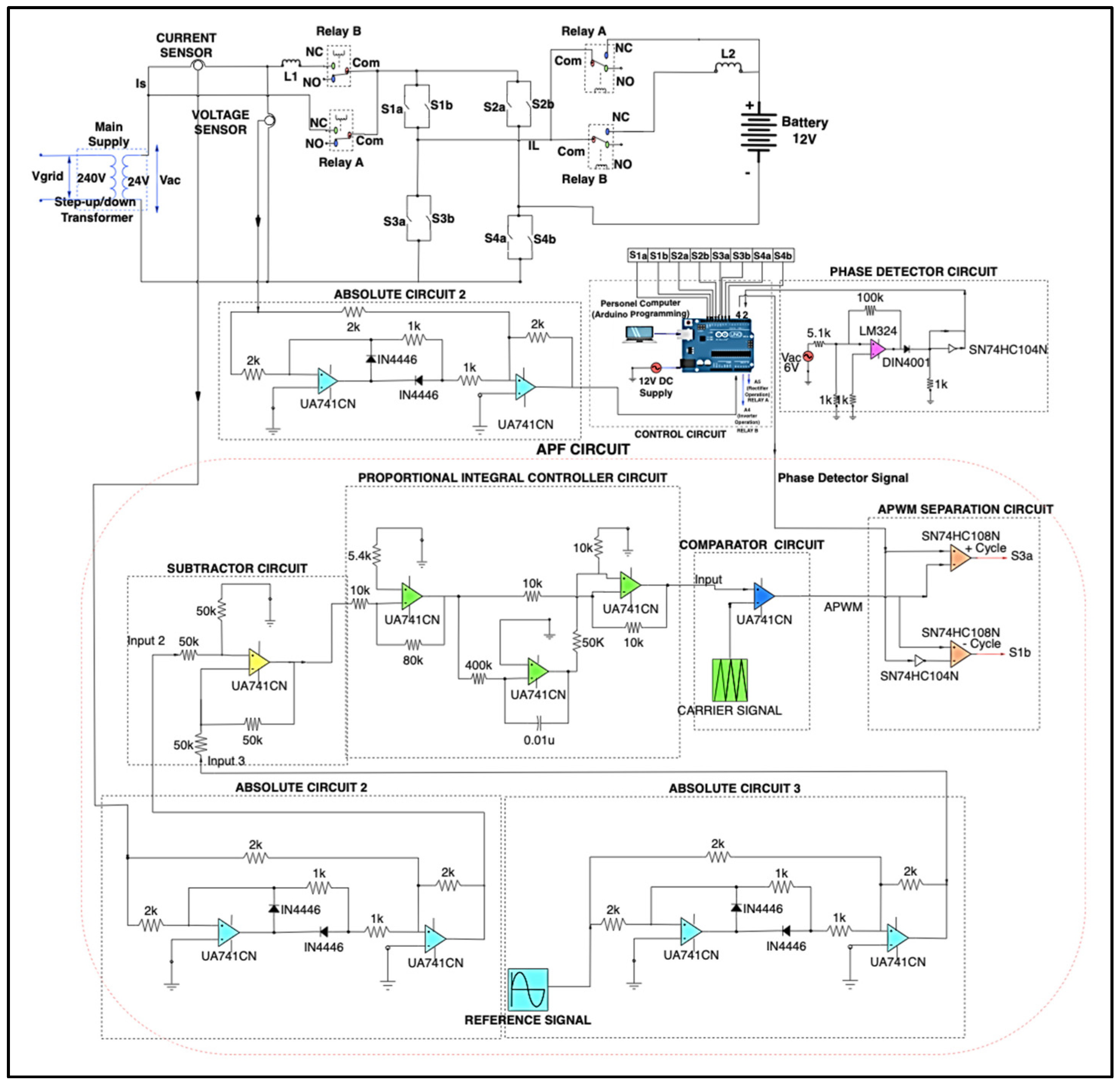
3. Topology of UPS System
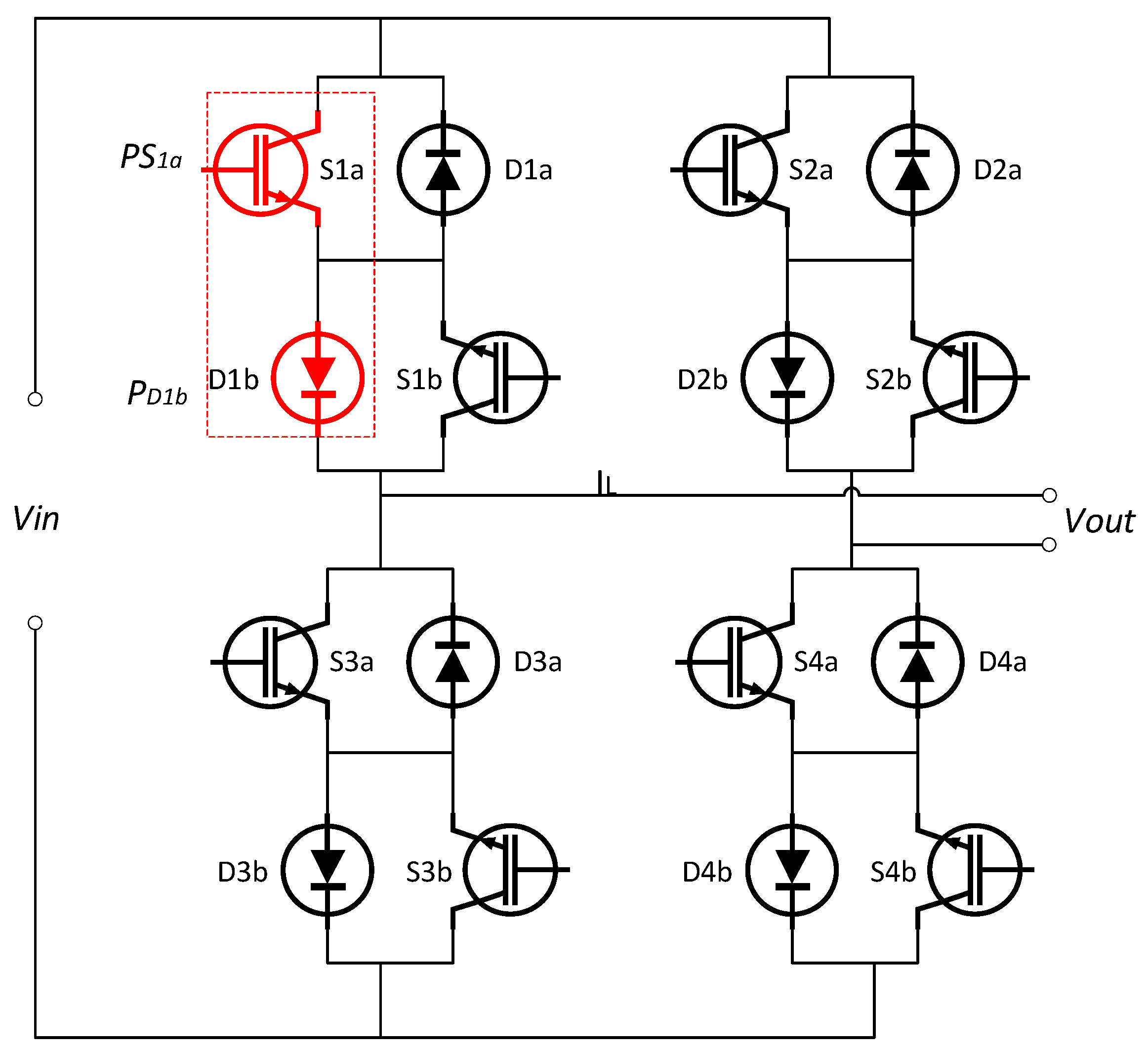
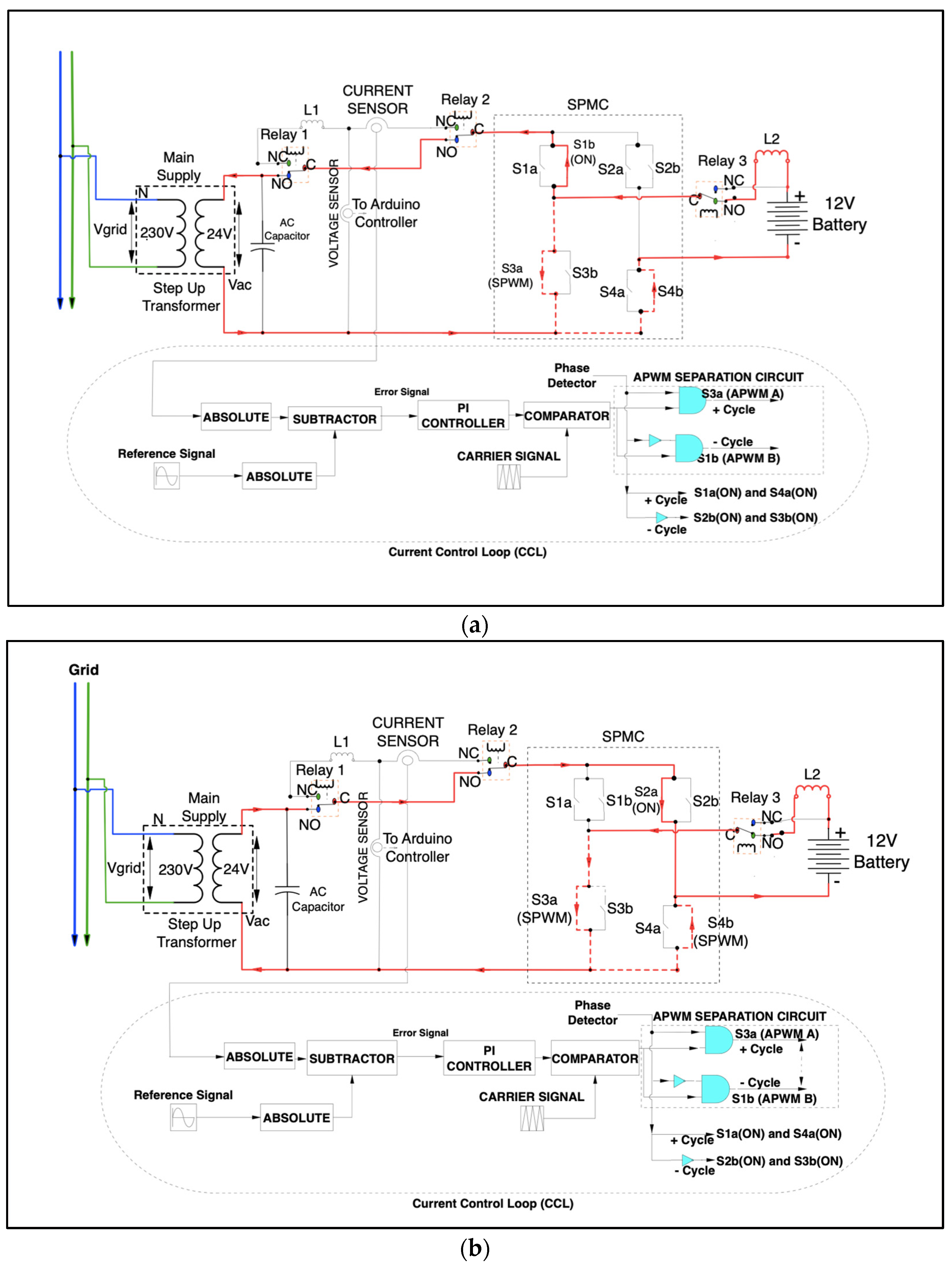
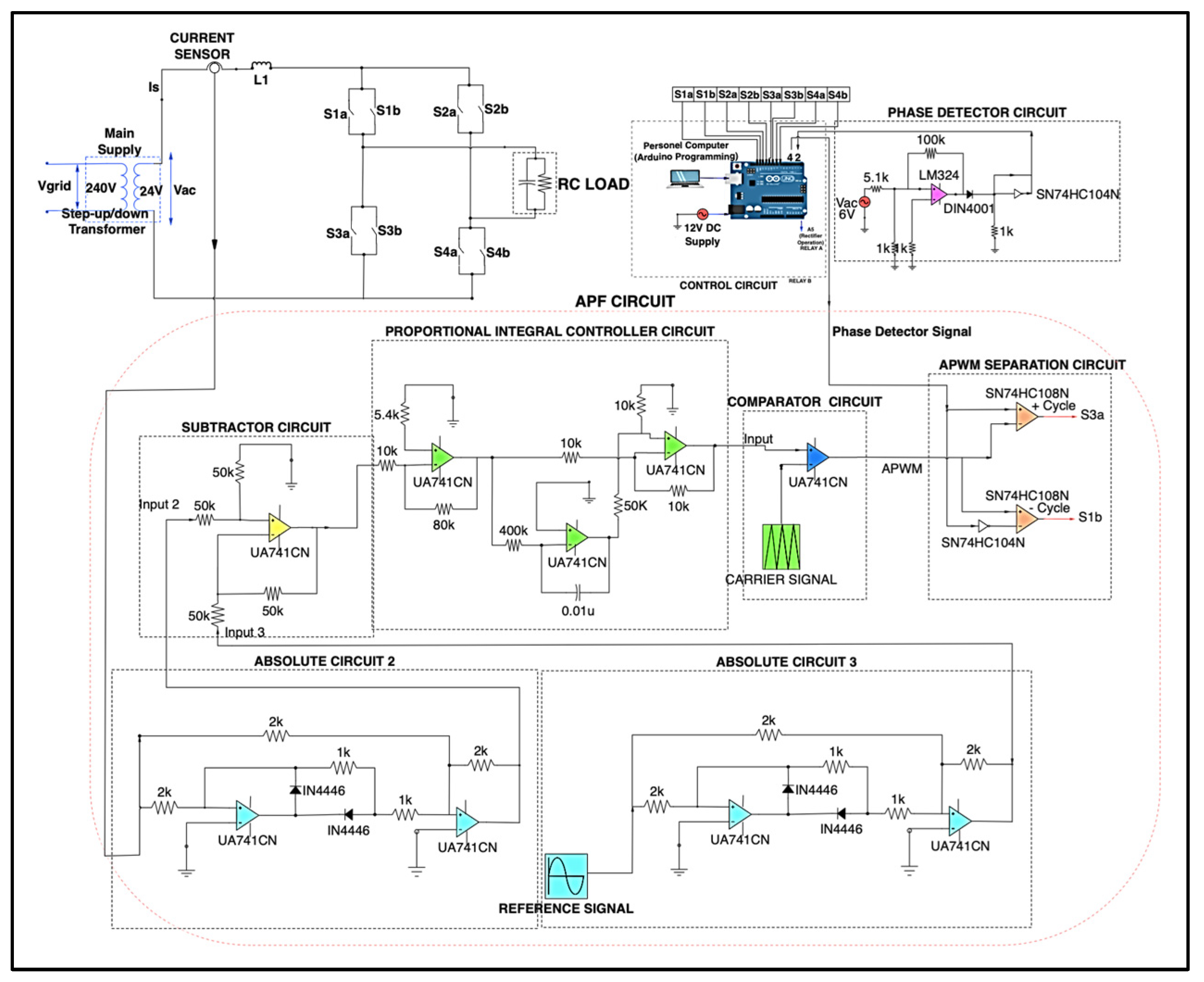
4. Topology of UPS System with APF Functionality
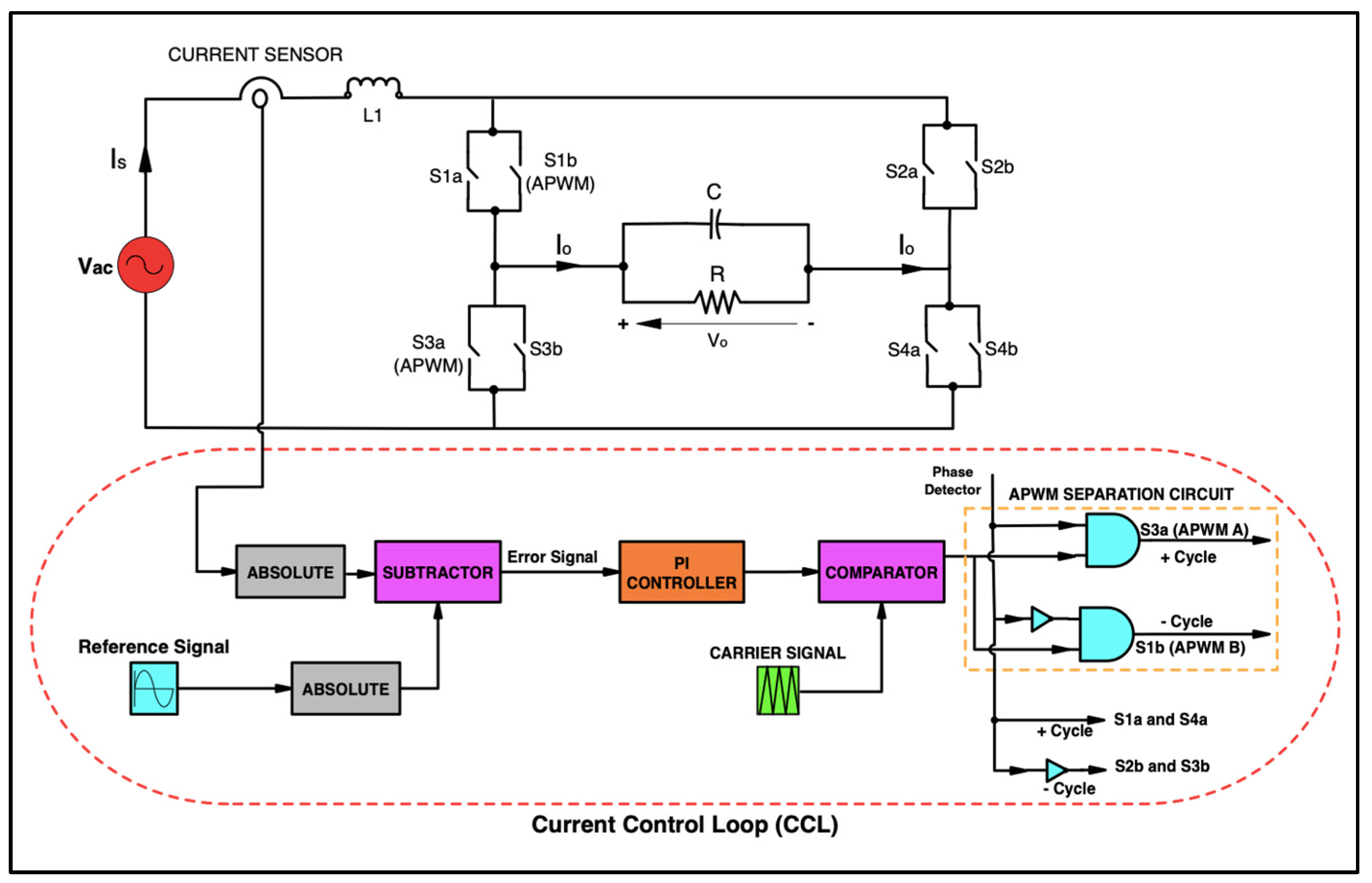
4.1. APF Mathematical Treatment Modeling
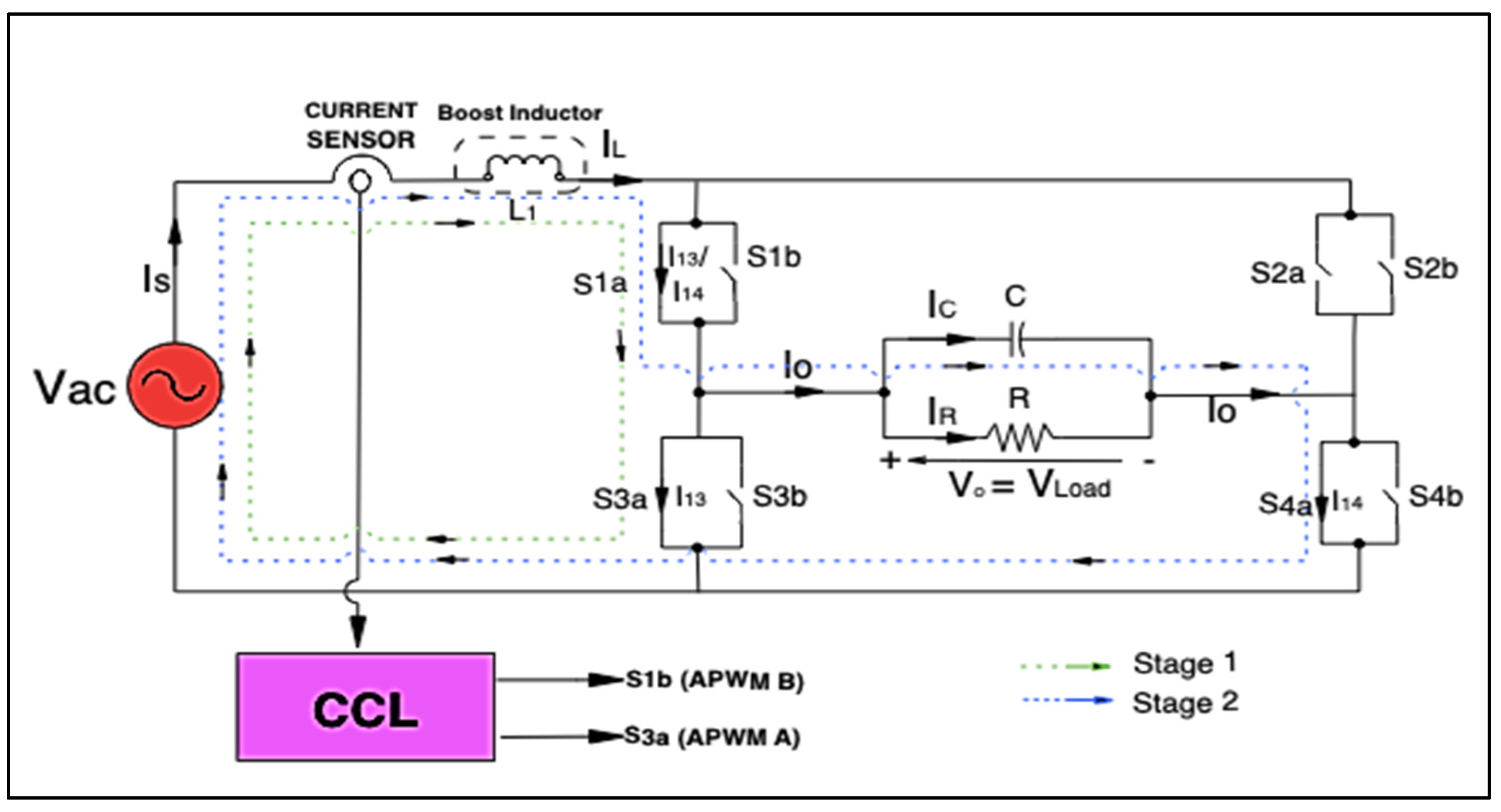
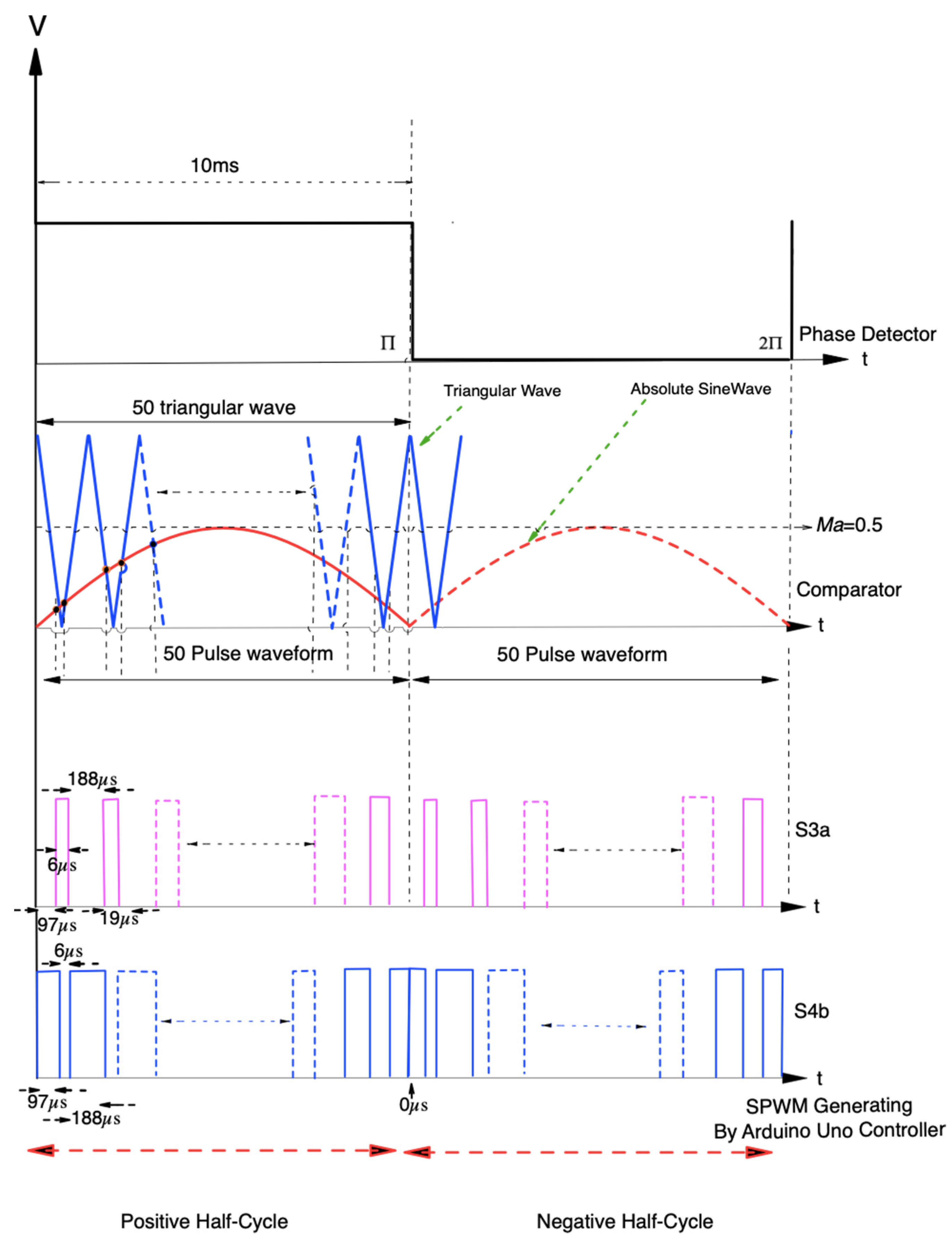
4.2. Controlled Rectifier Mode (Charging Mode)
- Step 1 (Positive Cycle):
- Step 2 (Positive Cycle):
- Step 3 (Negative Cycle):
- Step 4 (Negative Cycle):
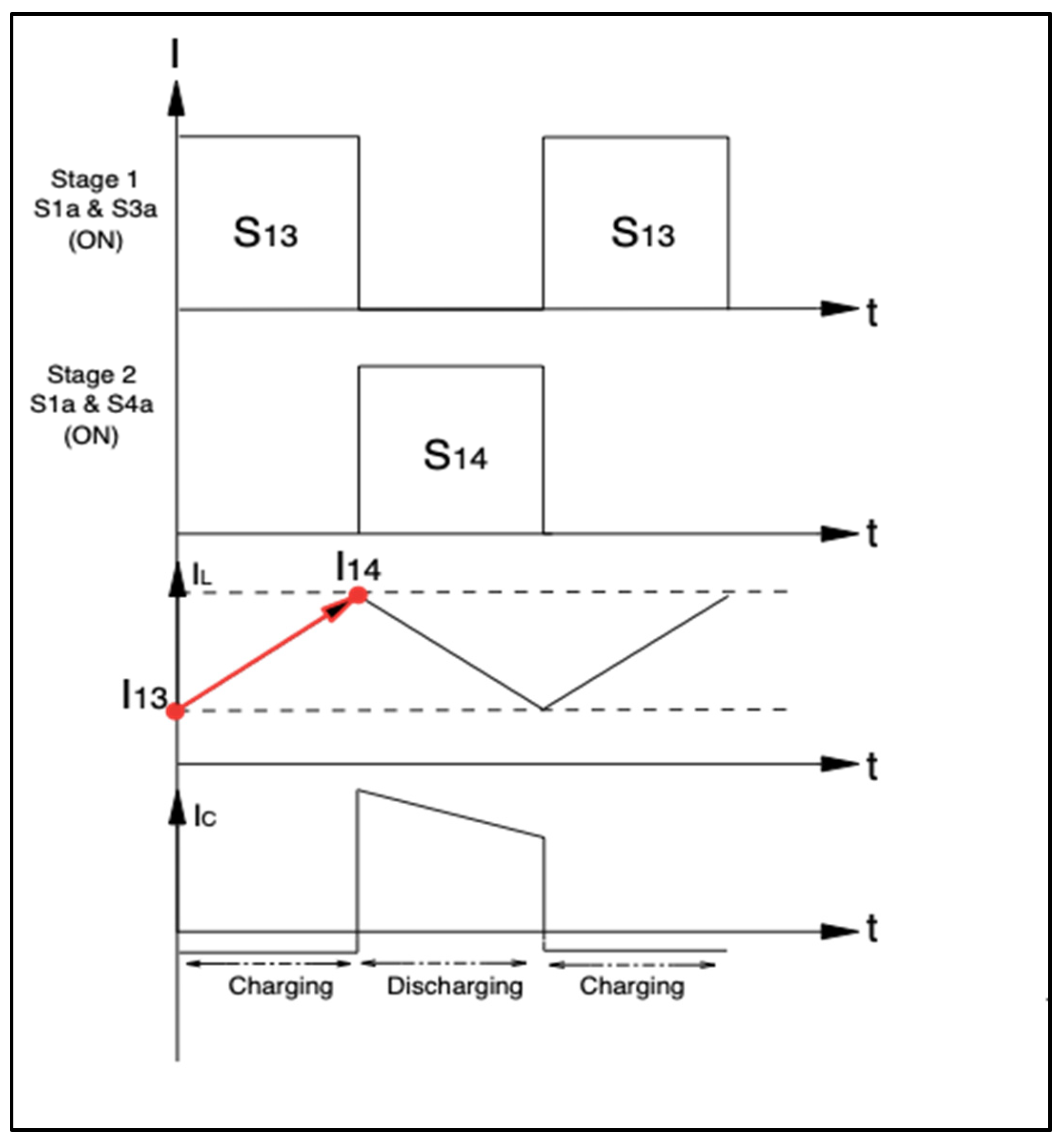
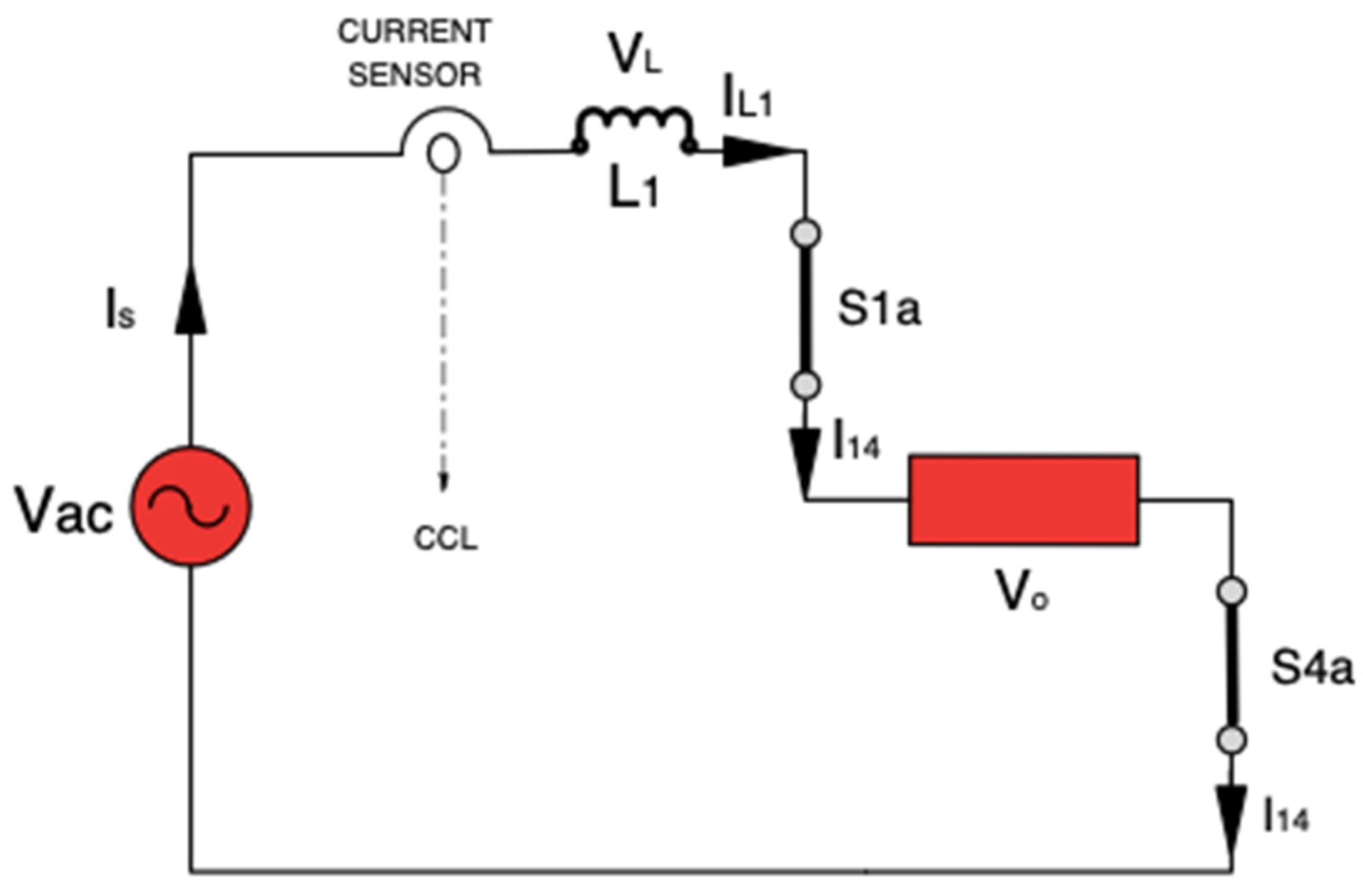
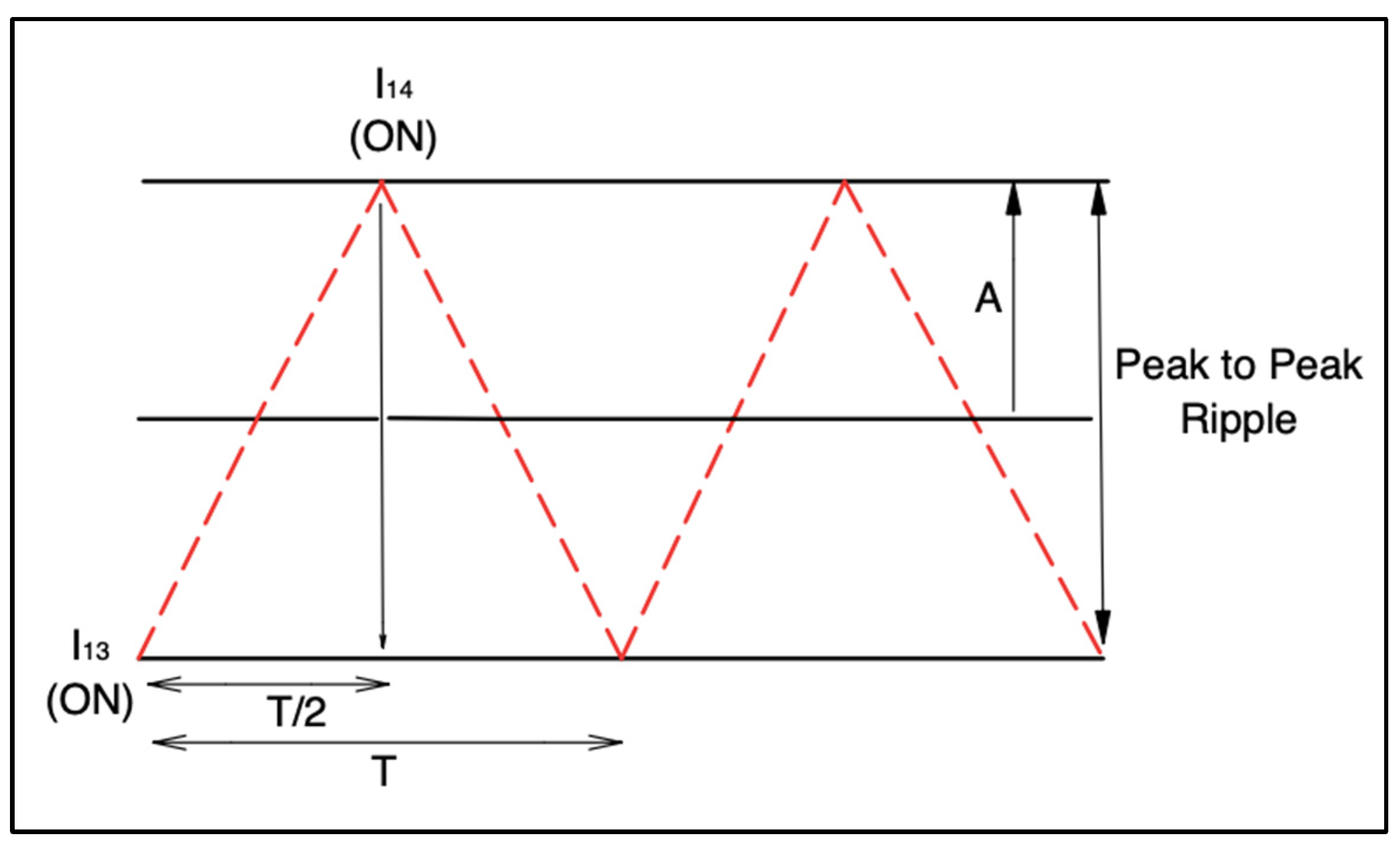
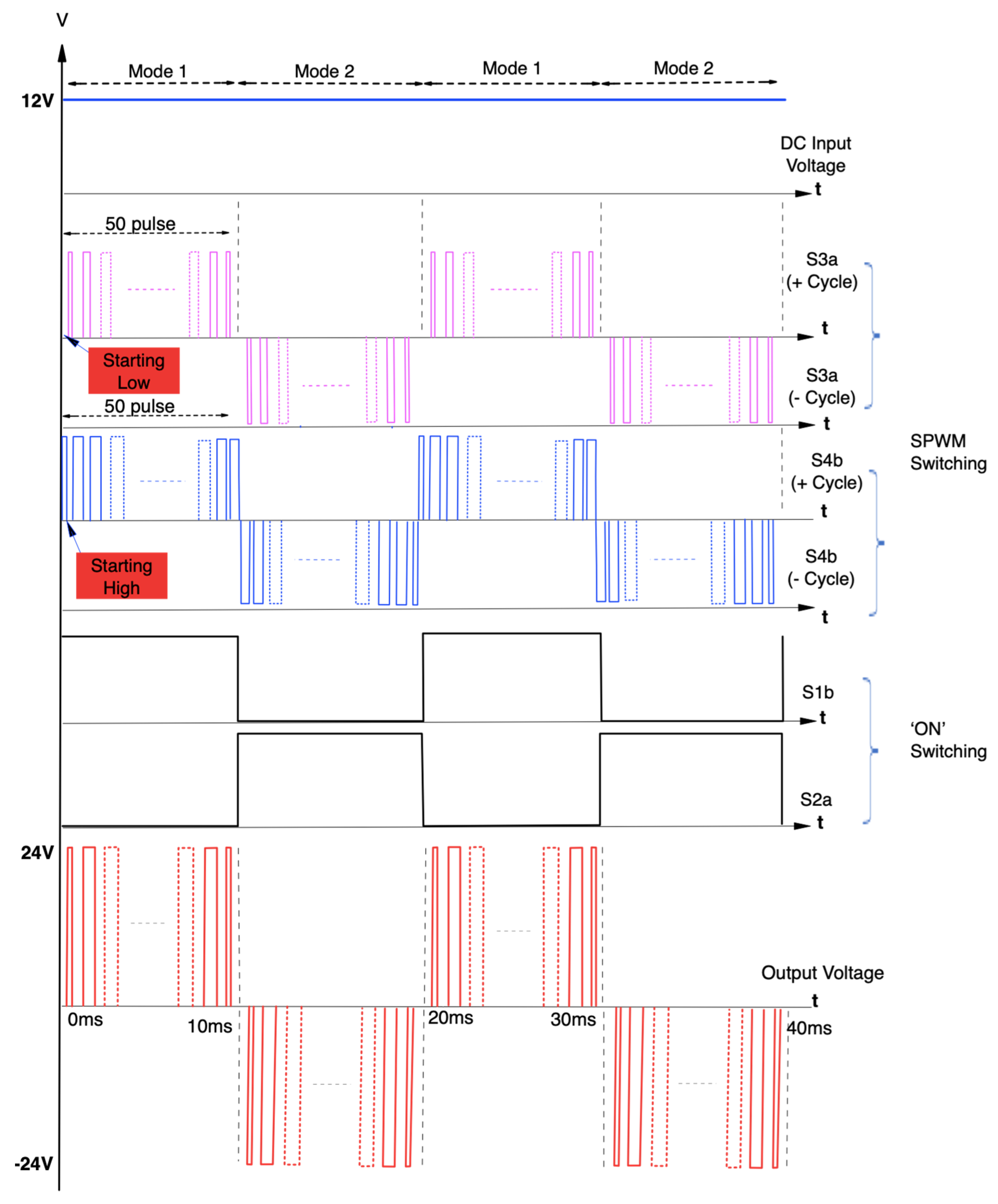
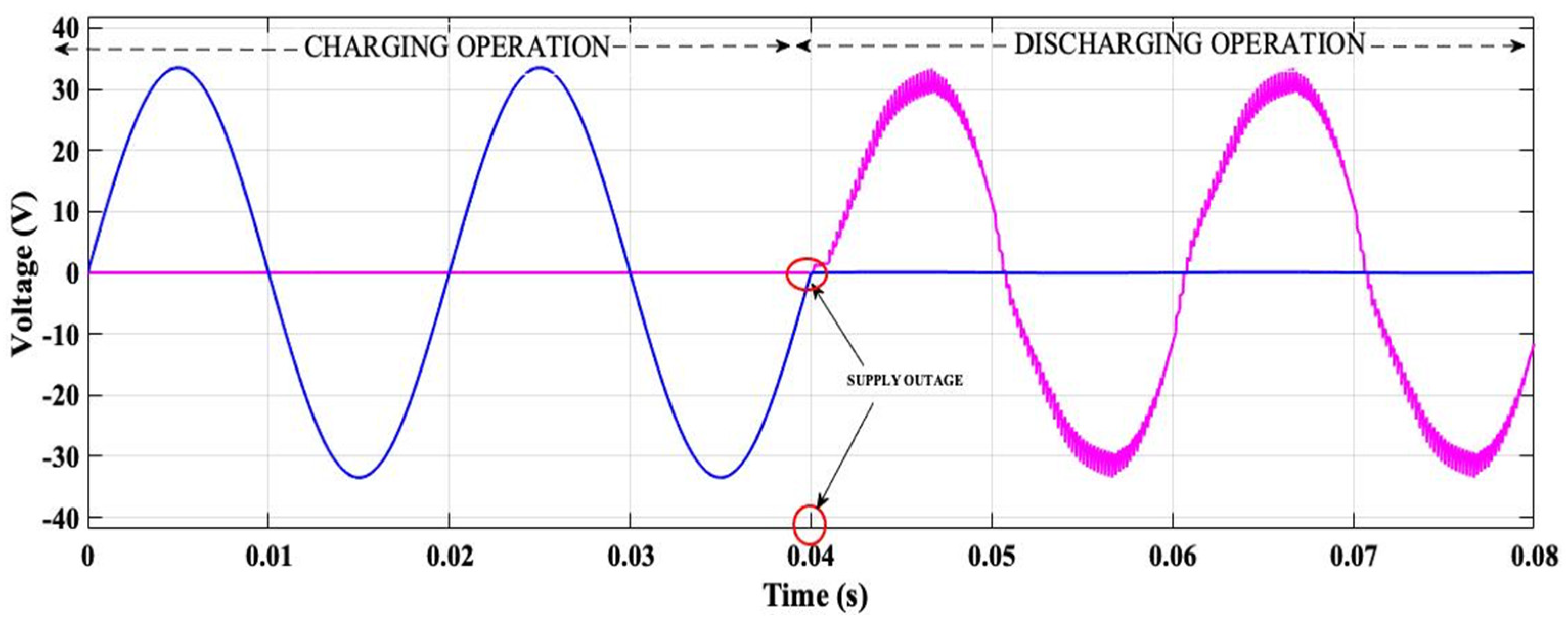
4.3. Managed Inverter Phase (Energy Release Mode)
- Positive cycle:
- Negative cycle:
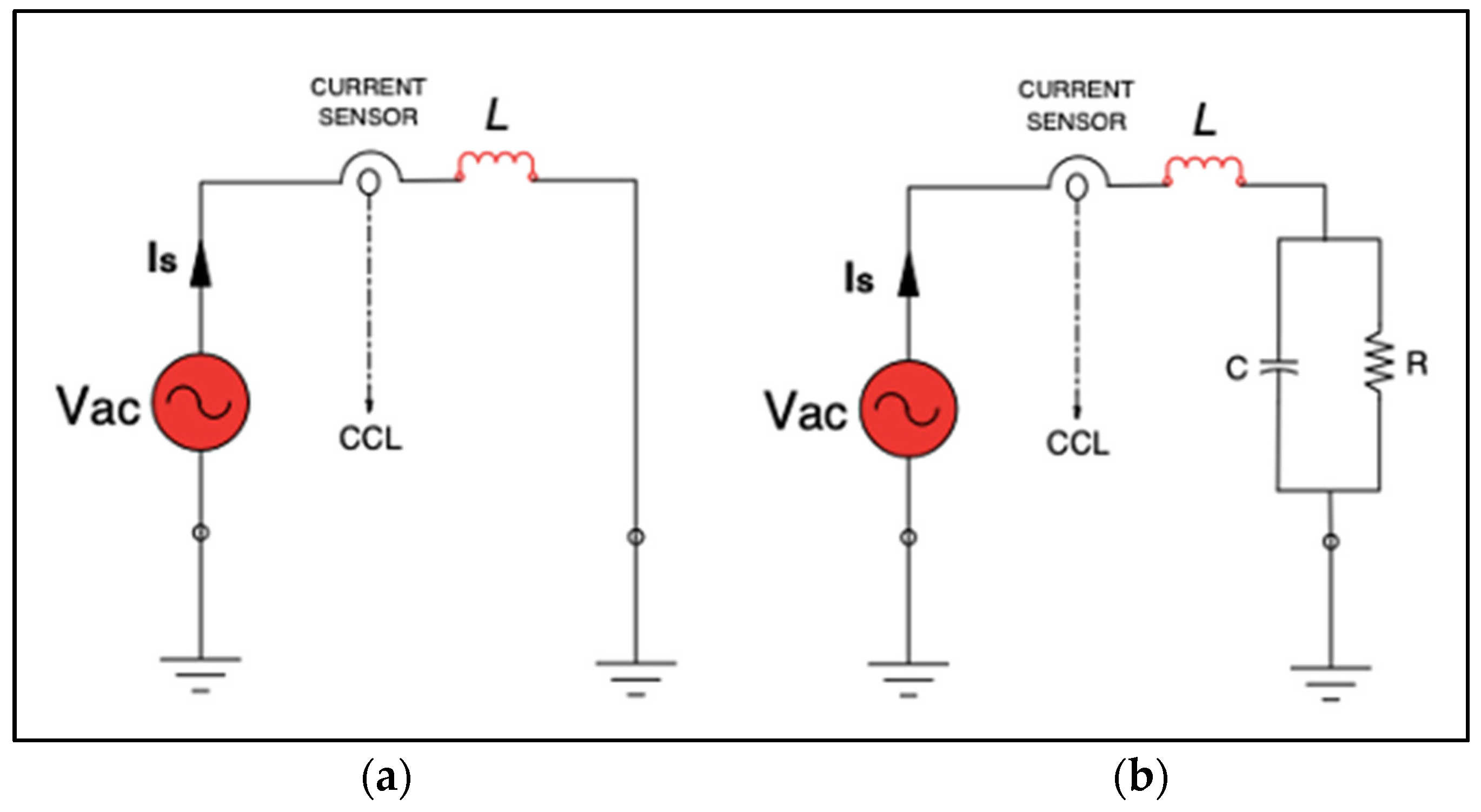
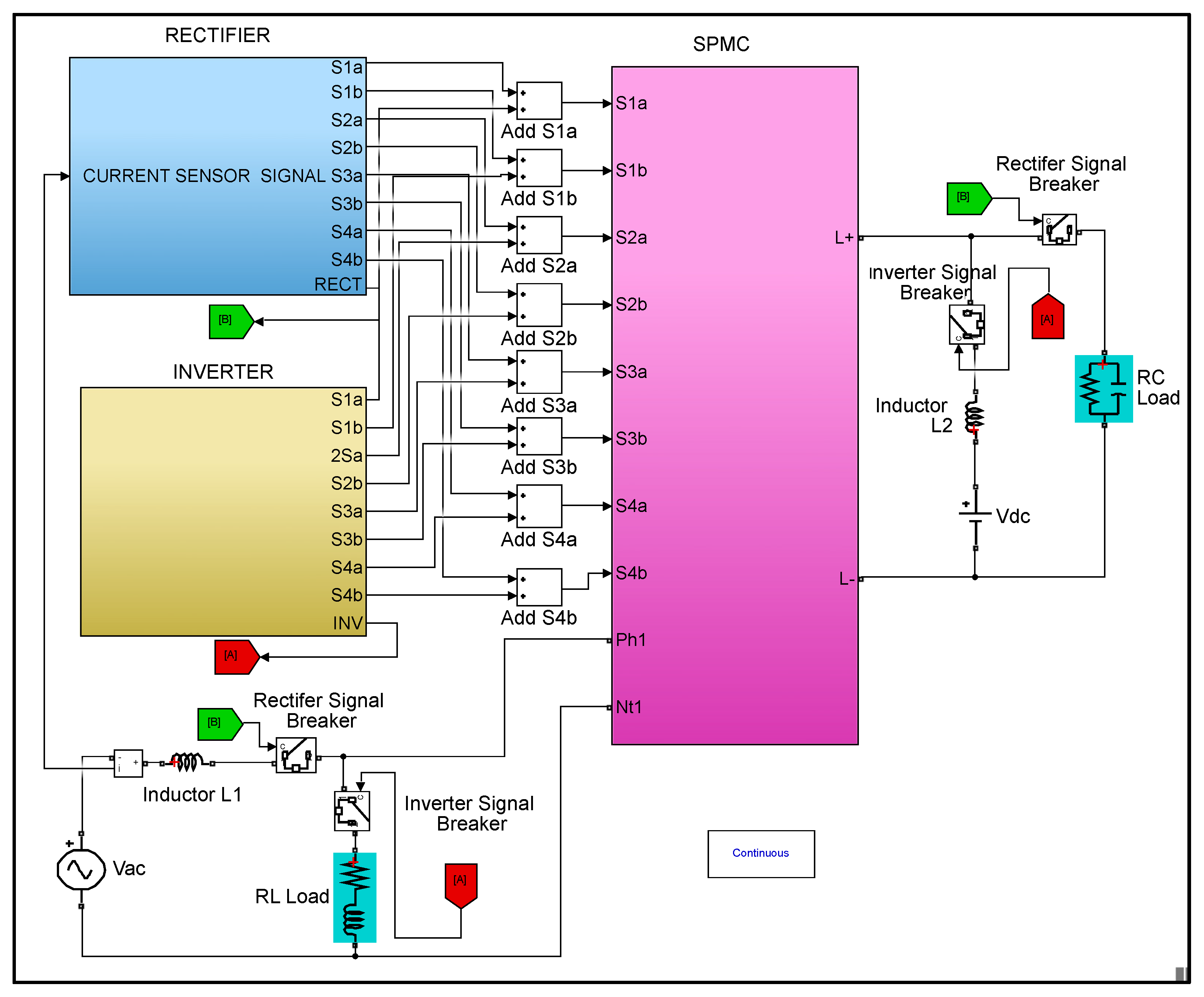
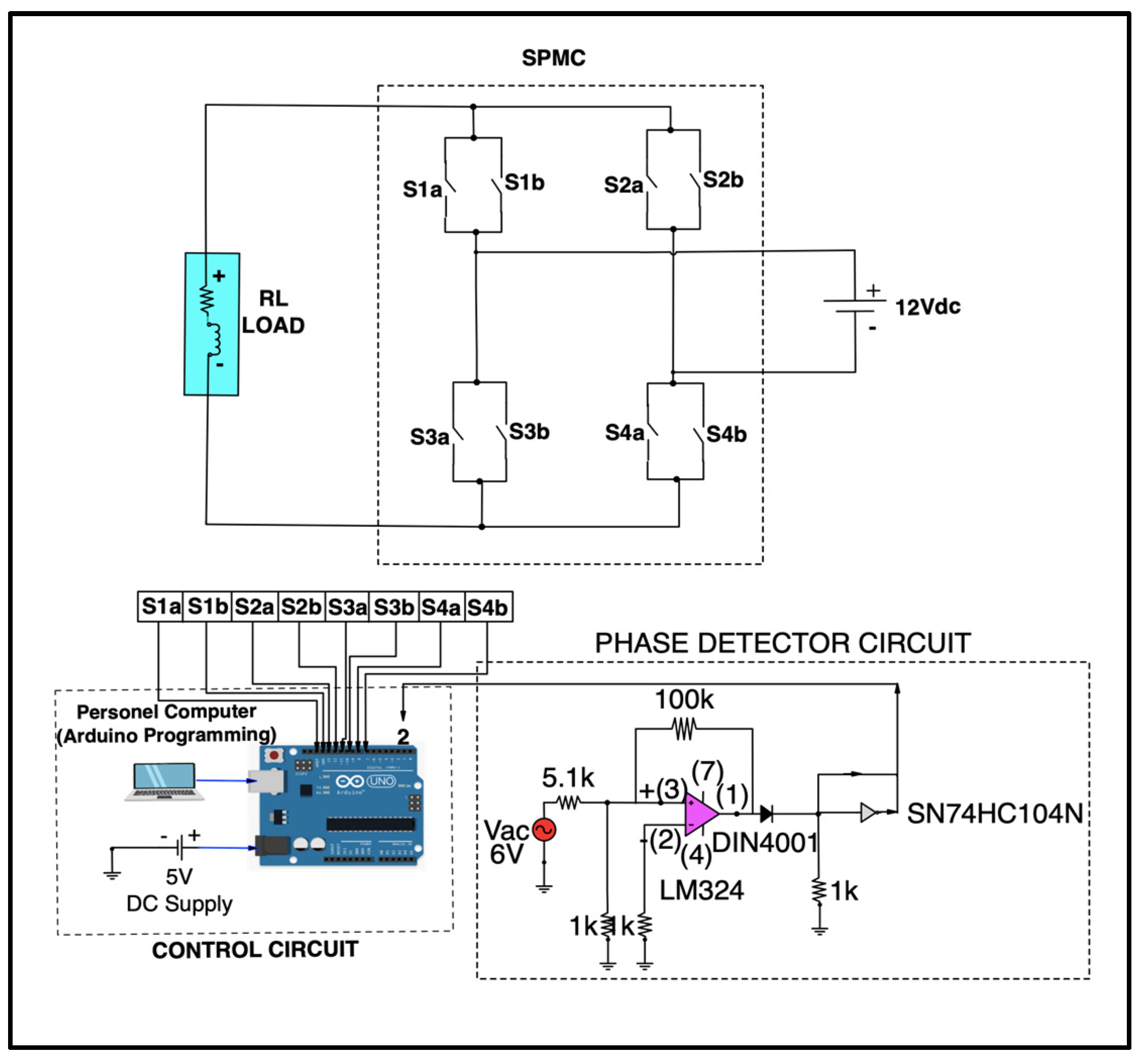
5. Simulation Model and Experimental Test Rig
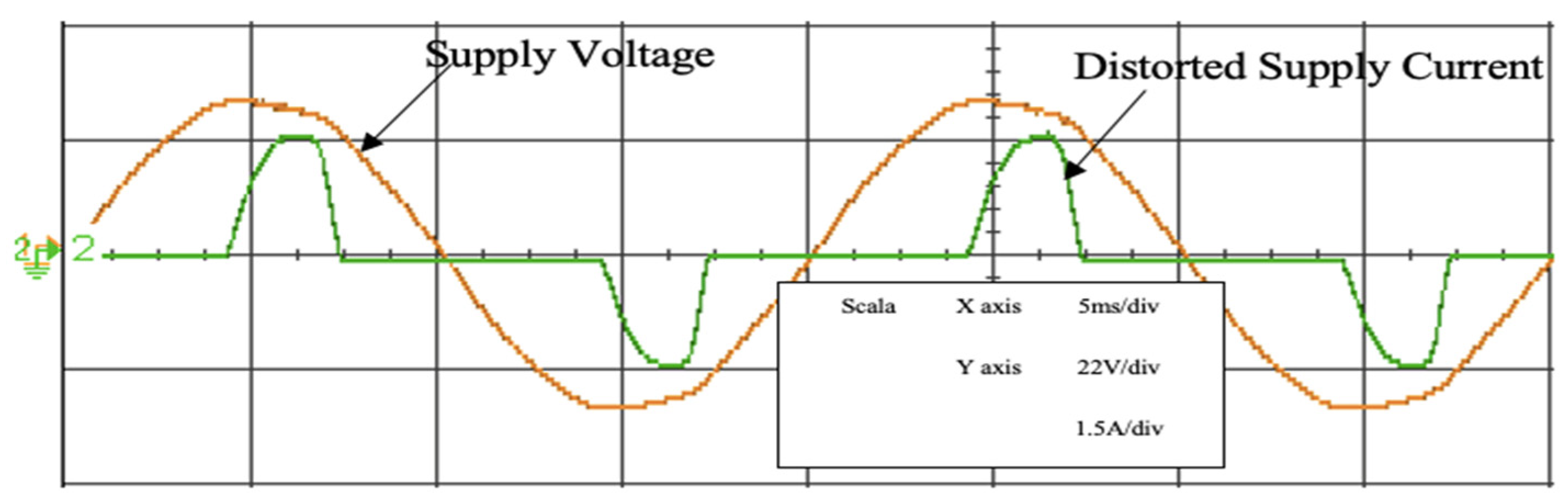
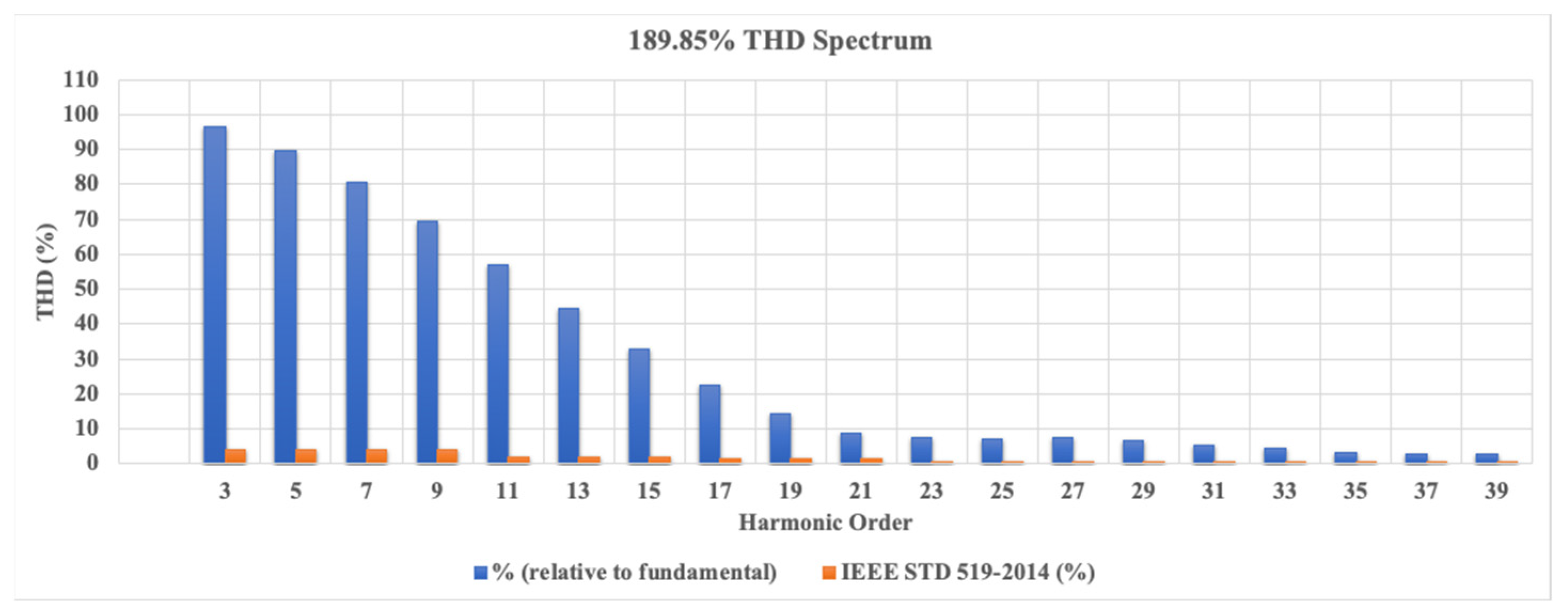
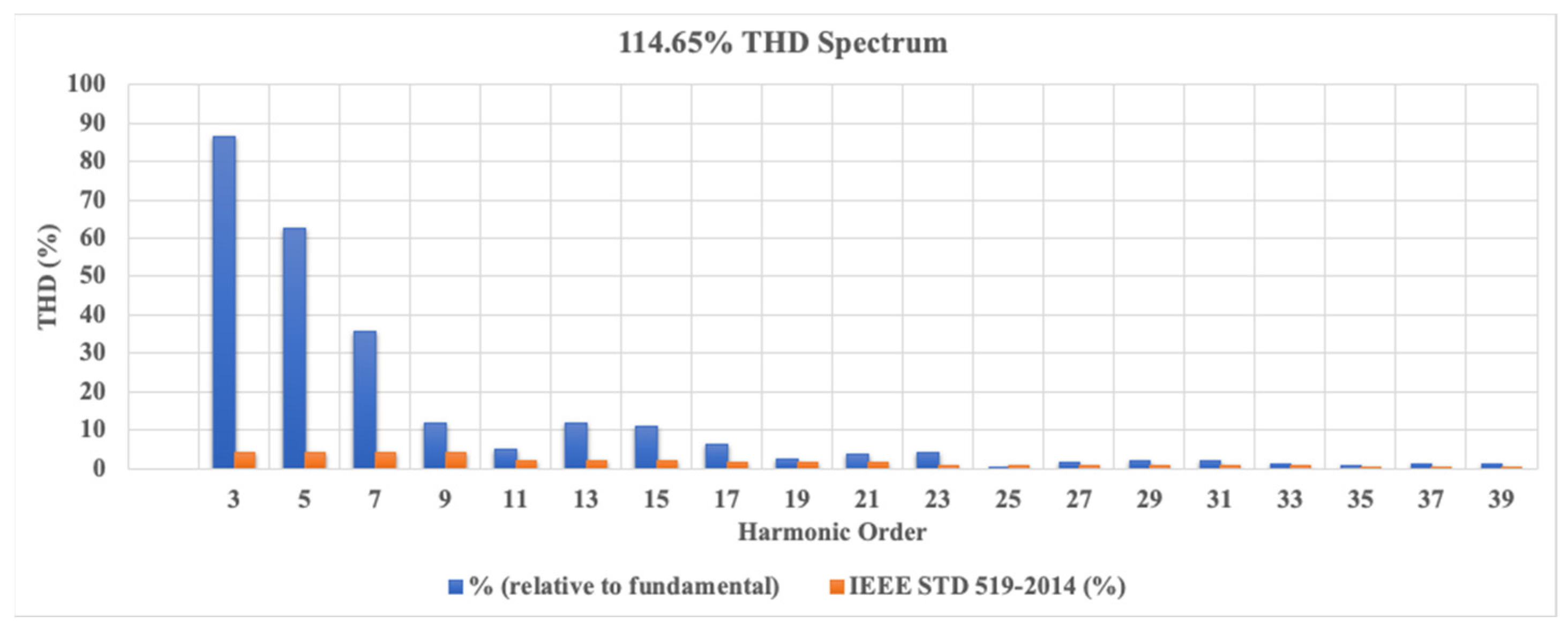
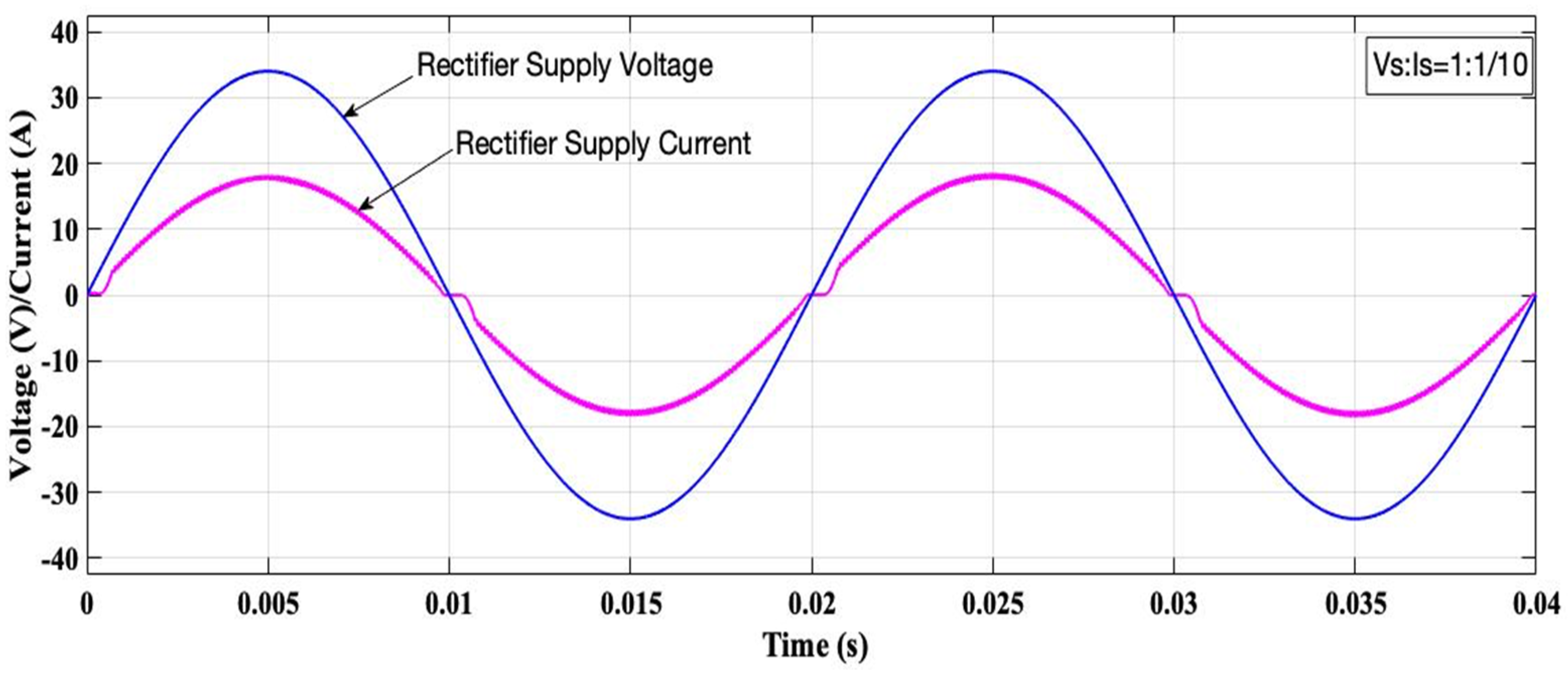
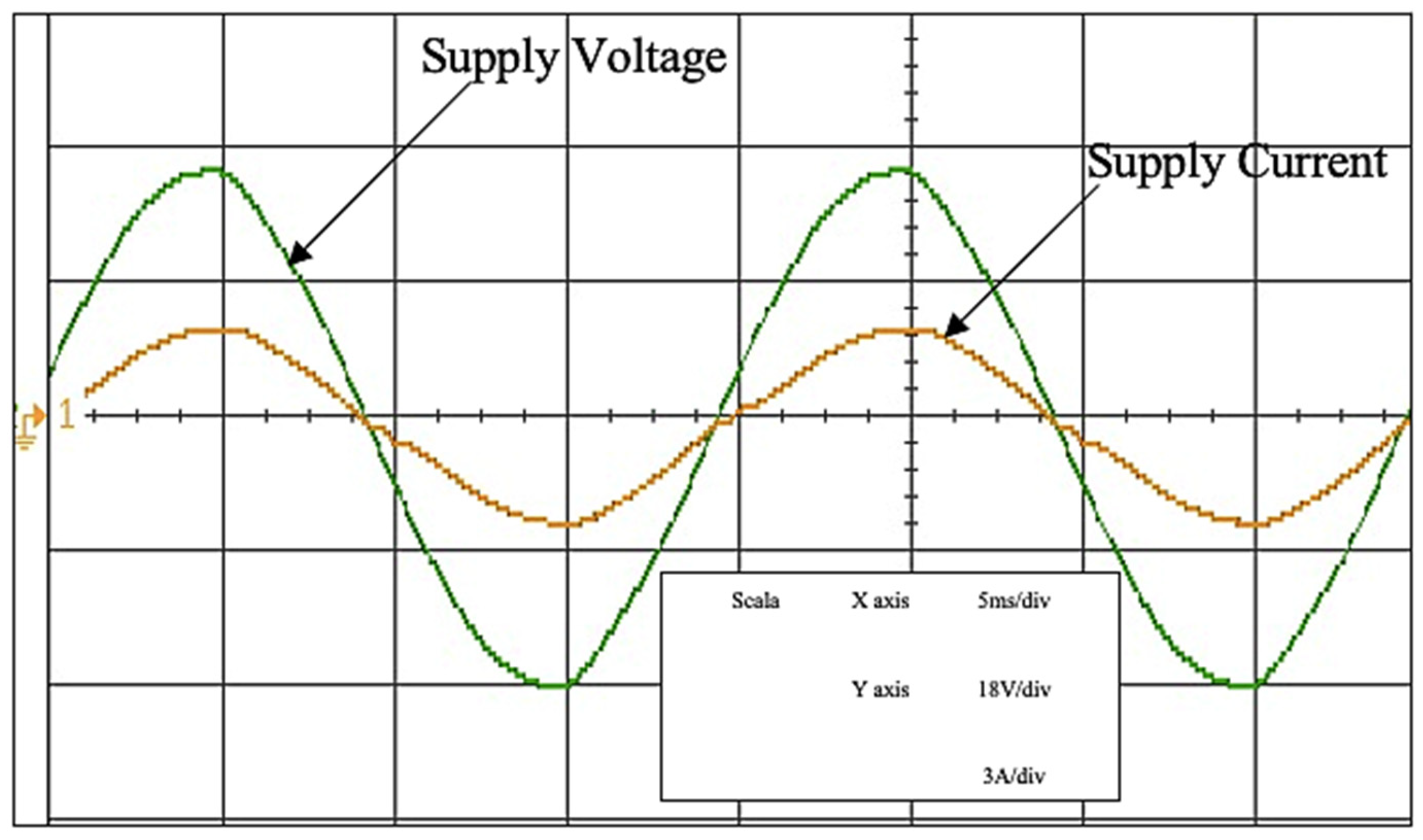
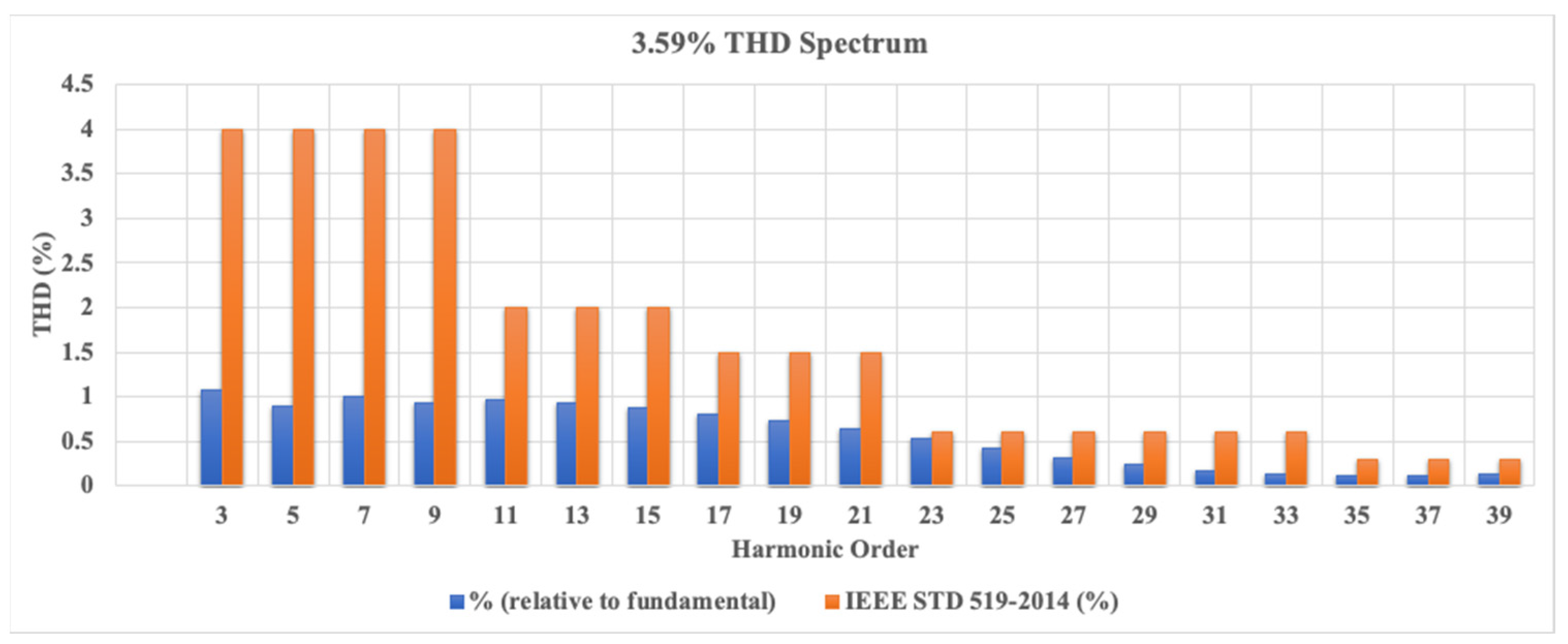
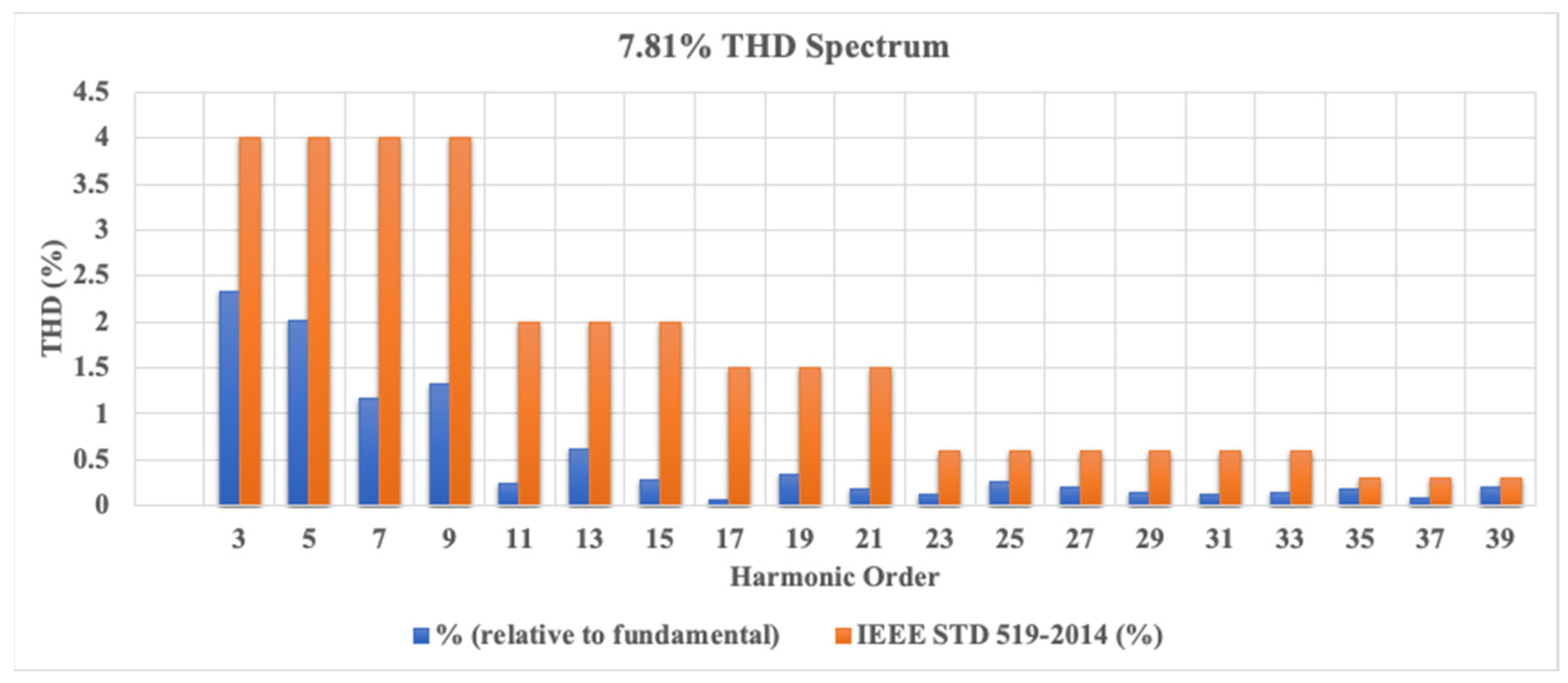
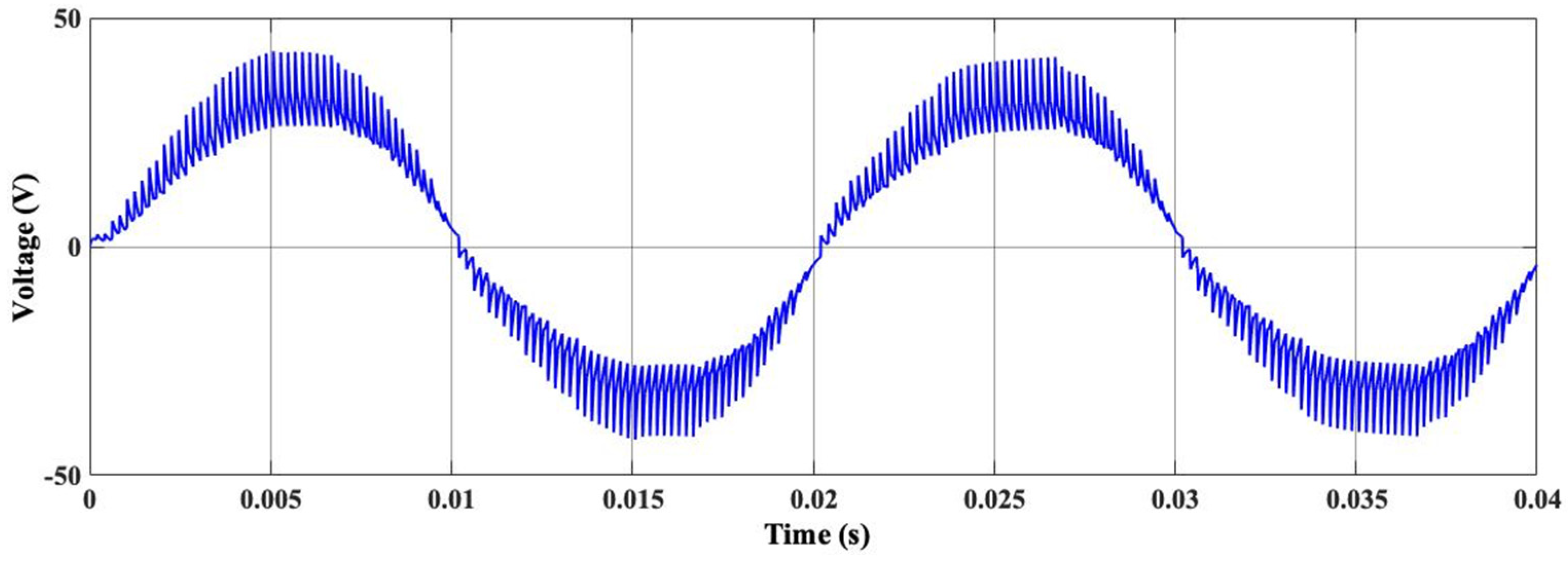
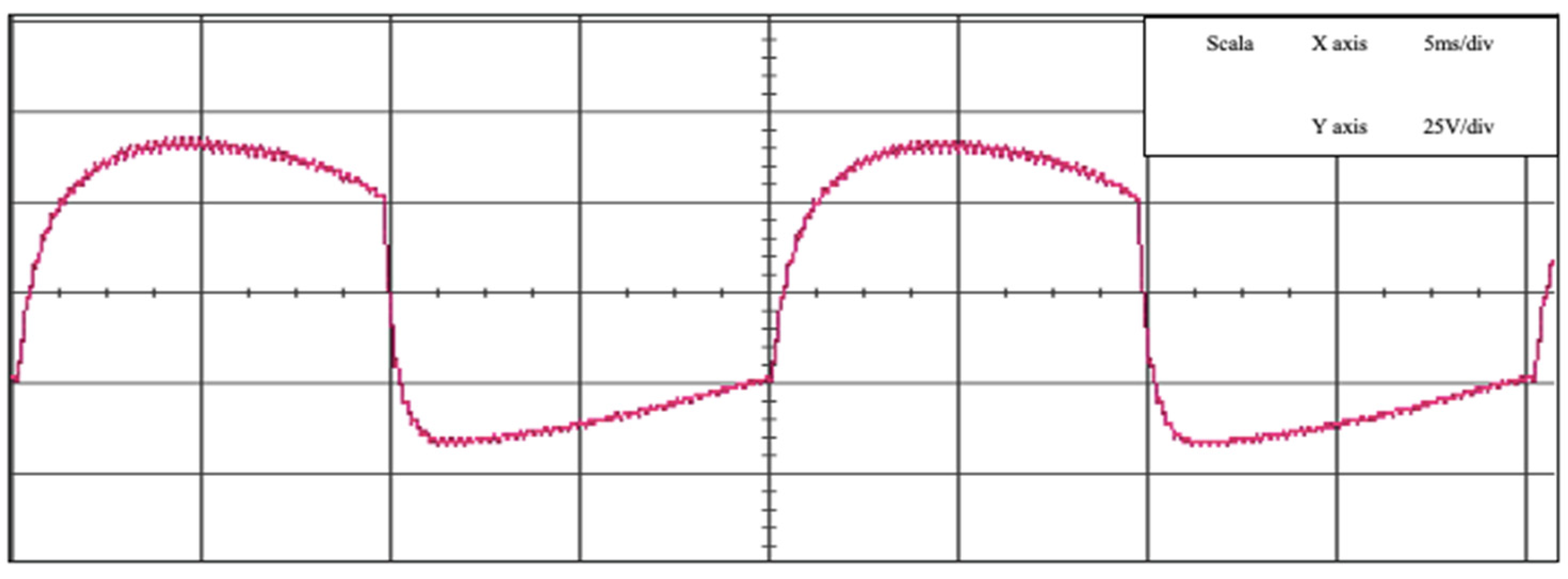
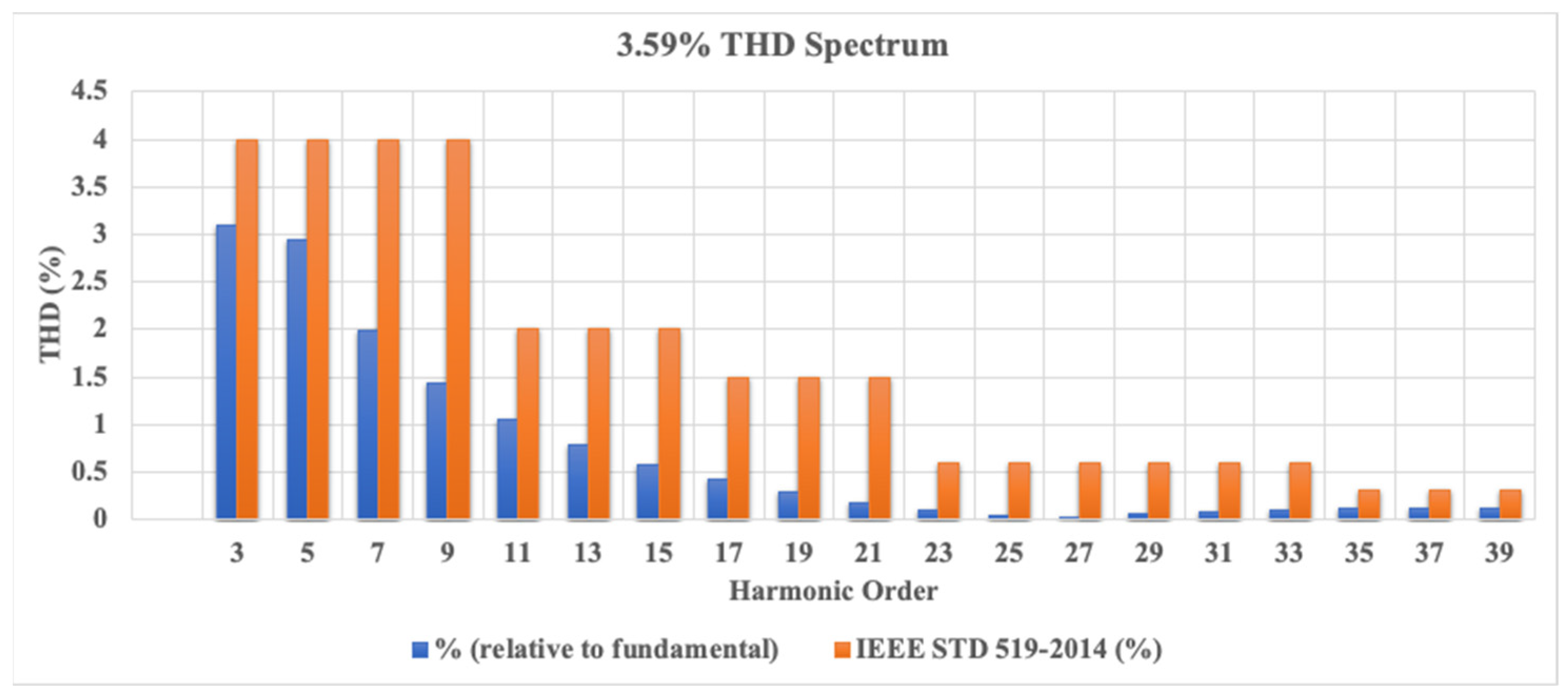
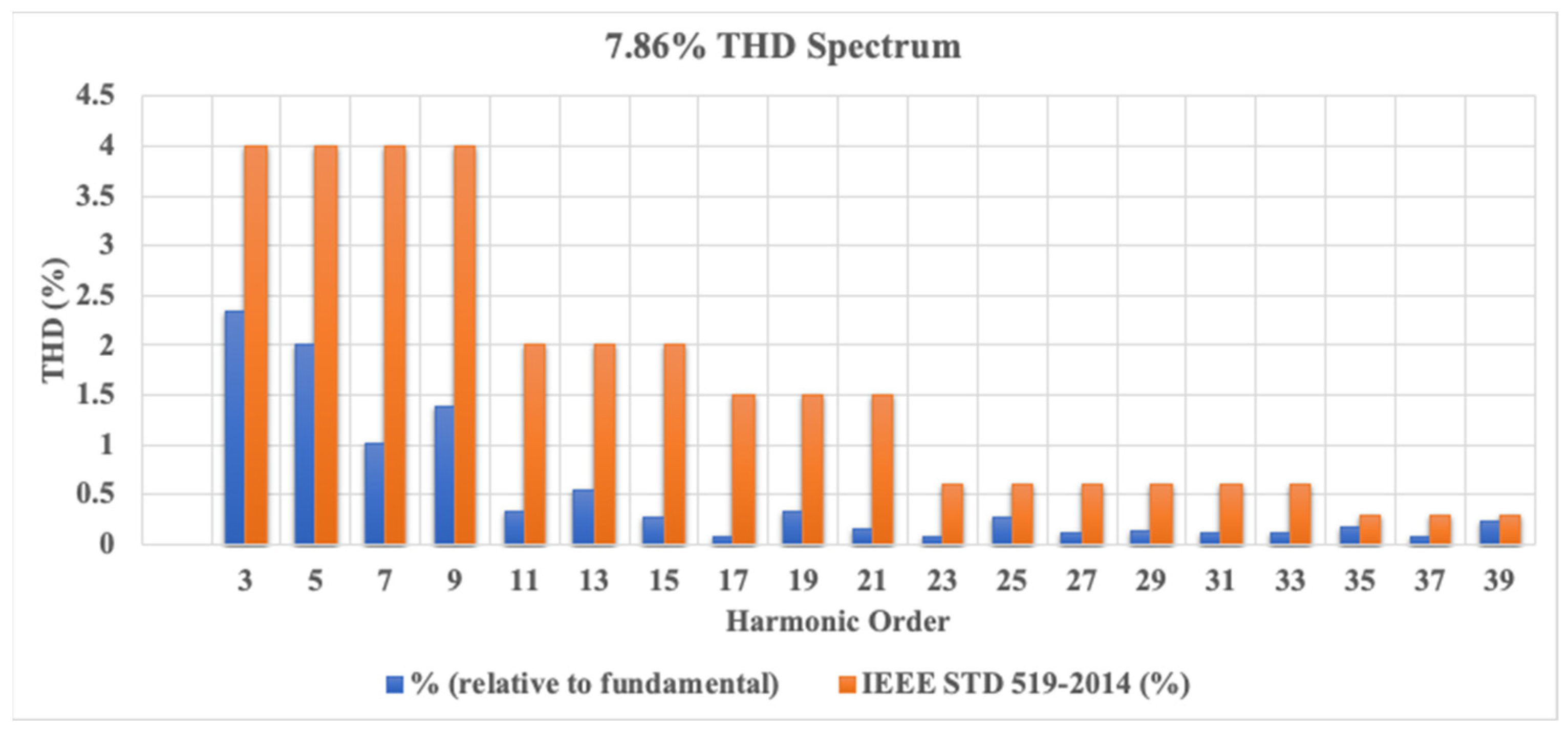
6. Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. of Pulse | Positive Cycle (μs) | No. of Pulse | Positive Cycle (μs) | No. of Pulse | Negative Cycle (μs) | No. of Pulse | Negative Cycle (μs) |
|---|---|---|---|---|---|---|---|
| 1 | 97 | 26 | 141 | 51 | 0 | 76 | 132 |
| 2 | 6 | 27 | 54 | 52 | 199 | 77 | 73 |
| 3 | 188 | 28 | 150 | 53 | 2 | 78 | 123 |
| 4 | 19 | 29 | 46 | 54 | 197 | 79 | 83 |
| 5 | 175 | 30 | 158 | 55 | 4 | 80 | 112 |
| 6 | 31 | 31 | 38 | 56 | 195 | 81 | 93 |
| 7 | 163 | 32 | 165 | 57 | 6 | 82 | 102 |
| 8 | 44 | 33 | 31 | 58 | 192 | 83 | 104 |
| 9 | 150 | 34 | 172 | 59 | 10 | 84 | 91 |
| 10 | 56 | 35 | 25 | 60 | 188 | 85 | 115 |
| 11 | 138 | 36 | 178 | 61 | 14 | 86 | 79 |
| 12 | 68 | 37 | 19 | 62 | 184 | 87 | 126 |
| 13 | 126 | 38 | 184 | 63 | 19 | 88 | 68 |
| 14 | 79 | 39 | 14 | 64 | 178 | 89 | 138 |
| 15 | 115 | 40 | 188 | 65 | 25 | 90 | 56 |
| 16 | 91 | 41 | 10 | 66 | 172 | 91 | 150 |
| 17 | 104 | 42 | 192 | 67 | 31 | 92 | 44 |
| 18 | 102 | 43 | 6 | 68 | 165 | 93 | 163 |
| 19 | 93 | 44 | 195 | 69 | 38 | 94 | 31 |
| 20 | 112 | 45 | 4 | 70 | 158 | 95 | 175 |
| 21 | 83 | 46 | 197 | 71 | 46 | 96 | 19 |
| 22 | 123 | 47 | 2 | 72 | 150 | 97 | 188 |
| 23 | 73 | 48 | 199 | 73 | 54 | 98 | 6 |
| 24 | 132 | 49 | 0 | 74 | 141 | 99 | 97 |
| 25 | 63 | 50 | 400 | 75 | 63 | 100 | 0 |
Appendix B
| Frequency (Hz) | Harmonic Number | % (Relative to Fundamental) | Frequency (Hz) | Harmonic Number | % (Relative to Fundamental) |
|---|---|---|---|---|---|
| 0 | 0 | 3.40 | 1000 | 20 | 0.13 |
| 50 | 1 | 100.00 | 1050 | 21 | 0.16 |
| 100 | 2 | 1.03 | 1100 | 22 | 0.21 |
| 150 | 3 | 2.34 | 1150 | 23 | 0.08 |
| 200 | 4 | 1.86 | 1200 | 24 | 0.26 |
| 250 | 5 | 2.01 | 1250 | 25 | 0.27 |
| 300 | 6 | 0.89 | 1300 | 26 | 0.22 |
| 350 | 7 | 1.02 | 1350 | 27 | 0.11 |
| 400 | 8 | 0.59 | 1400 | 28 | 0.14 |
| 450 | 9 | 1.39 | 1450 | 29 | 0.13 |
| 500 | 10 | 0.52 | 1500 | 30 | 0.14 |
| 550 | 11 | 0.34 | 1550 | 31 | 0.11 |
| 600 | 12 | 0.31 | 1600 | 32 | 0.21 |
| 650 | 13 | 0.54 | 1650 | 33 | 0.12 |
| 700 | 14 | 0.57 | 1700 | 34 | 0.08 |
| 750 | 15 | 0.28 | 1750 | 35 | 0.17 |
| 800 | 16 | 0.18 | 1800 | 36 | 0.09 |
| 850 | 17 | 0.07 | 1850 | 37 | 0.07 |
| 900 | 18 | 0.20 | 1900 | 38 | 0.22 |
| 950 | 19 | 0.34 | 1950 | 39 | 0.23 |
Appendix C
| Frequency (Hz) | Harmonic Number | % (Relative to Fundamental) | Frequency (Hz) | Harmonic Number | % (Relative to Fundamental) |
|---|---|---|---|---|---|
| 0 | 0 | 0.48 | 1000 | 20 | 0.05 |
| 50 | 1 | 100.00 | 1050 | 21 | 0.63 |
| 100 | 2 | 0.13 | 1100 | 22 | 0.03 |
| 150 | 3 | 1.07 | 1150 | 23 | 0.53 |
| 200 | 4 | 0.23 | 1200 | 24 | 0.02 |
| 250 | 5 | 0.89 | 1250 | 25 | 0.42 |
| 300 | 6 | 0.12 | 1300 | 26 | 0.01 |
| 350 | 7 | 1.00 | 1350 | 27 | 0.32 |
| 400 | 8 | 0.15 | 1400 | 28 | 0.00 |
| 450 | 9 | 0.93 | 1450 | 29 | 0.24 |
| 500 | 10 | 0.13 | 1500 | 30 | 0.01 |
| 550 | 11 | 0.96 | 1550 | 31 | 0.17 |
| 600 | 12 | 0.10 | 1600 | 32 | 0.02 |
| 650 | 13 | 0.92 | 1650 | 33 | 0.13 |
| 700 | 14 | 0.10 | 1700 | 34 | 0.03 |
| 750 | 15 | 0.88 | 1750 | 35 | 0.11 |
| 800 | 16 | 0.08 | 1800 | 36 | 0.03 |
| 850 | 17 | 0.81 | 1850 | 37 | 0.12 |
| 900 | 18 | 0.06 | 1900 | 38 | 0.03 |
| 950 | 19 | 0.73 | 1950 | 39 | 0.13 |
Appendix D
- is devices instantaneous dissipated power.
- is fundamental output current period.
- is the output current amplitude.
- M is the modulation depth index whose value is between 0 to 1.
- is the output frequency pulsation.
References
- Popa, G.N. Electric Power Quality through Analysis and Experiment. Energies 2022, 15, 7947. [Google Scholar] [CrossRef]
- Prado, E.O.; Bolsi, P.C.; Sartori, H.C.; Pinheiro, J.R. Comparative Analysis of Modulation Techniques on the Losses and Thermal Limits of Uninterruptible Power Supply Systems. Micromachines 2022, 13, 1708. [Google Scholar] [CrossRef] [PubMed]
- Godoy, M.P.; Uberti, V.A.; da Rosa Abaide, A.; Guidali, G.D.; Prade, L.R.; Keller, A.L. Identifying and reducing harmonic distortion in an industrial uninterruptible power supply system. In Proceedings of the 2020 6th International Conference on Electric Power and Energy Conversion Systems (EPECS), Istanbul, Turkey, 5–7 October 2020; pp. 34–39. [Google Scholar]
- Abaray, S.; Beaver, S.; Nguyen, C. How reliable is your ups? Eliminating single points of failure. In Proceedings of the 2017 Petroleum and Chemical Industry Technical Conference (PCIC), Calgary, AB, Canada, 18–20 September 2017; pp. 311–316. [Google Scholar]
- Srivastava, M.; Goyal, S.K.; Saraswat, A.; Shekhawat, R.S.; Gangil, G. A Review on Power Quality Problems, Causes and Mitigation Techniques. In Proceedings of the 2022 1st International Conference on Sustainable Technology for Power and Energy Systems (STPES), SRINAGAR, India, 4–6 July 2022; pp. 1–6. [Google Scholar]
- Gerber, D.L.; Ghatpande, O.A.; Nazir, M.; Heredia, W.G.B.; Feng, W.; Brown, R.E. Energy and power quality measurement for electrical distribution in AC and DC microgrid buildings. Appl. Energy 2022, 308, 118308. [Google Scholar] [CrossRef]
- Gong, S.; Huang, J.; He, G. Research on ADRC controller design for three-phase UPS with multi-disturbances. J. Eng. 2019, 2019, 8409–8413. [Google Scholar] [CrossRef]
- Kim, J.; Choi, H.H.; Jung, J.W. MRAC-Based voltage controller for three-phase CVCF inverters to attenuate parameter uncertainties under critical load conditions. IEEE Trans. Power Electron. 2020, 35, 1002–1013. [Google Scholar] [CrossRef]
- Kumar, M.; Uqaili, M.A.; Memon, Z.A.; Das, B. Experimental Harmonics Analysis of UPS (Uninterrupted Power Supply) System and Mitigation Using Single-Phase Half-Bridge HAPF (Hybrid Active Power Filter) Based on Novel Fuzzy Logic Current Controller (FLCC) for Reference Current Extraction (RCE). Adv. Fuzzy Syst. 2022, 2022, 5466268. [Google Scholar] [CrossRef]
- Vyas, M.; Vyas, S. Matrix Converter: A Solution for Electric Drives and Control Applications. In Optimal Planning of Smart Grid With Renewable Energy Resources; IGI Global: Hershey, PA, USA, 2022; pp. 219–244. [Google Scholar]
- Burhanudin, J.; Hasim, A.S.A.; Ishak, A.M.; Fairuz, S.M.; Dardin, S.M.; Azid, A.A.; Burhanudin, J. Simulation of AC/ AC Converter using Single Phase Matrix Converter for Wave Energy Converter. In Proceedings of the 2022 IEEE International Conference in Power Engineering Application (ICPEA), Shah Alam, Malaysia, 7–8 March 2022; pp. 1–6. [Google Scholar]
- Osheba, M.S.; Lashine, A.E.; Mansour, A.S. Design, implementation and performance evaluation of multi-function boost converter. Sci. Rep. 2023, 13, 4276. [Google Scholar] [CrossRef] [PubMed]
- Gyugyi, B.; Pelly, L. Static Power Chargers, Theory, Performance and Application; John Wiley & Son Inc.: Hoboken, NJ, USA, 1976; Volume 1. [Google Scholar]
- Narwal, R.; Rawat, S.; Kanale, A.; Cheng, T.H.; Agarwal, A.; Bhattacharya, S.; Baliga, B.J.; Hopkins, D.C. Analysis and Characterization of Four-quadrant Switches based Commutation Cell. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; pp. 209–216. [Google Scholar]
- Rahman, K. Matrix converter and its probable applications. In DC Microgrids: Advances, Challenges, and Applications; Wiley: Hoboken, NJ, USA, 2021; pp. 273–298. [Google Scholar]
- Zuckerberger, A.; Weinstock, D.; Aiexandrovitz, A. Single-phase matrix converter. IEE Proceeding Electr. Power Appl. 1997, 144, 235–240. [Google Scholar] [CrossRef]
- Burany, N. Safe control of four-quadrant switches. In Proceedings of the Conference Record of the IEEE Industry Applications Society Annual Meeting, San Diego, CA, USA, 1–5 October 1989; Volume 1, pp. 1190–1194. [Google Scholar]
- Baharom, R.; Hamzah, M.K. A New Single-Phase Controlled Rectifier Using Single-Phase Matrix Converter Topology Incorporating Active Power Filter. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; pp. 874–879. [Google Scholar]
- Osman, D.A.A.; Baharom, R.; Johari, D.; Hidayat, M.N.; Muhammad, K.S. Development of active power filter using rectifier boost technique. Int. J. Power Electron. Drive Syst. 2019, 10, 1446–1453. [Google Scholar] [CrossRef]
- Vázquez, N.; Aguilar, C.; Arau, J.; Cáceres, R.O.; Barbi, I.; Gallegos, J.A. A novel uninterruptible power supply system with active power factor correction. IEEE Trans. Power Electron. 2002, 17, 405–412. [Google Scholar] [CrossRef]
- Hamzah, M.K.; Saidon, M.F.; Noor, S.Z.M. Application of Single-Phase Matrix Converter Topology in Uninterruptible Power Supply Circuit incorporating Unity Power Factor Control. In Proceedings of the 2006 1ST IEEE Conference on Industrial Electronics and Applications, Singapore, 24–26 May 2006; pp. 1–6. [Google Scholar]
- Baharom, R.; Rawi, M.S.M.; Rahman, N.F.A. Uninterruptible Power Supply Employing Single-Phase Matrix Converter Topology. In Proceedings of the 2020 IEEE International Conference on Power and Energy (PECon), Penang, Malaysia, 7–8 December 2020; pp. 19–23. [Google Scholar]
- Rawi, M.M.S.; Baharom, R.; Radzi, M.A.M. Simulation Model of Uninterruptible Wireless Power Supply Based on Single-Phase Matrix Converter with Active Power Filter Functionality. In Proceedings of the 2023 IEEE Industrial Electronics and Applications Conference (IEACon), Penang, Malaysia, 6–7 November 2023; pp. 157–162. [Google Scholar]
- Rawi, M.S.M.; Baharom, R.; Rahman, N.F.A. Computer Simulation Model of Unity Power Factor Uninterruptible Power Supply Topology using Single Phase Matrix Converter; International Journal of Power Electronics and Drive Systems (IJPEDS): Yogyakarta, Indonesia, 2022; Volume 12, pp. 969–979. [Google Scholar]
- Wang, B.; Venkataramanan, G. Analytical modeling of semiconductor losses in matrix converters. In Proceedings of the Conference Proceedings—IPEMC 2006: CES/IEEE 5th International Power Electronics and Motion Control Conference, Shanghai, China, 14–16 August 2006; Volume 1, pp. 1–8. [Google Scholar]
- Robinson, F.V.P. Power electronics converters, applications and design. Microelectronics J. 1997, 28, 105–106. [Google Scholar] [CrossRef]
- Clemente, S. Application characterization of IGBTs. In Application Note AN-990, IGBT Design Manual; International Rectifier: El Segundo, CA, USA, 1994. [Google Scholar]
- PEM, “Power Electronic Measurement. Available online: Https://www.pemuk.com (accessed on 18 June 2024).
- Casanellas, F. Losses in PWM inverters using IGBTs. IEE Proc. Electr. Power Appl. 1994, 141, 235–239. [Google Scholar] [CrossRef]
- Dalai, S.K.; Dash, D.K. Analysis of single-phase matrix converter with regenerative capabilities of Single phase induction motor. In Proceedings of the 2017 International Conference on Smart Technologies for Smart Nation (SmartTechCon), Bengaluru, India, 17–19 August 2017; pp. 465–469. [Google Scholar]
- Baharom, R.; Hashim, N.; Hamzah, M.K. Implementation of controlled rectifier with power factor correction using single-phase matrix converter. In Proceedings of the 2009 International Conference on Power Electronics and Drive Systems (PEDS), Taipei, Taiwan, 2–5 November 2009; pp. 1020–1025. [Google Scholar]
- Ramesh, R.D.K.K.S. An Investigation on Performance Characteristics of Sealed Lead Acid Battery. In Proceedings of the 2022 4th International Conference on Smart Systems and Inventive Technology (ICSSIT), Penang, Malaysia, 6–7 November 2023; pp. 563–568. [Google Scholar]
- Bradley, A. DC-UPS with Integrated Battery-24V, 10A; Rockwell Automation Publication: Milwaukee, WI, USA, 2019; 1606-RM003A-EN-P; Available online: https://literature.rockwellautomation.com/idc/groups/literature/documents/rm/1606-rm003_-en-p.pdf (accessed on 18 June 2024).
- Youssef, M. Simulation and Design of A Single Phase Inverter with Digital PWM Issued by An Arduino Board. Int. J. Eng. Res. Technol. 2020, 9, 560–566. [Google Scholar]
- Li, J. Measuring and Understanding the Output Voltage Ripple of A Boost Converter; Texas Instruments Inc.: Dallas, TX, USA, 2021. [Google Scholar]
- Zin, M.F.M.; Baharom, R.; Yassin, I.M. Development of boost inverter using single phase matrix converter topology. Int. J. Eng. Technol. 2018, 7, 241–245. [Google Scholar]
- IEEE Std 519™-2022; IEEE Standard for Harmonic Control in Electric Power Systems. The Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2022.
- IEC62040-3 Standard; Uninterruptible Power Systems (UPS)-Part 3: Method of Specifying the Performance and Test Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2021.


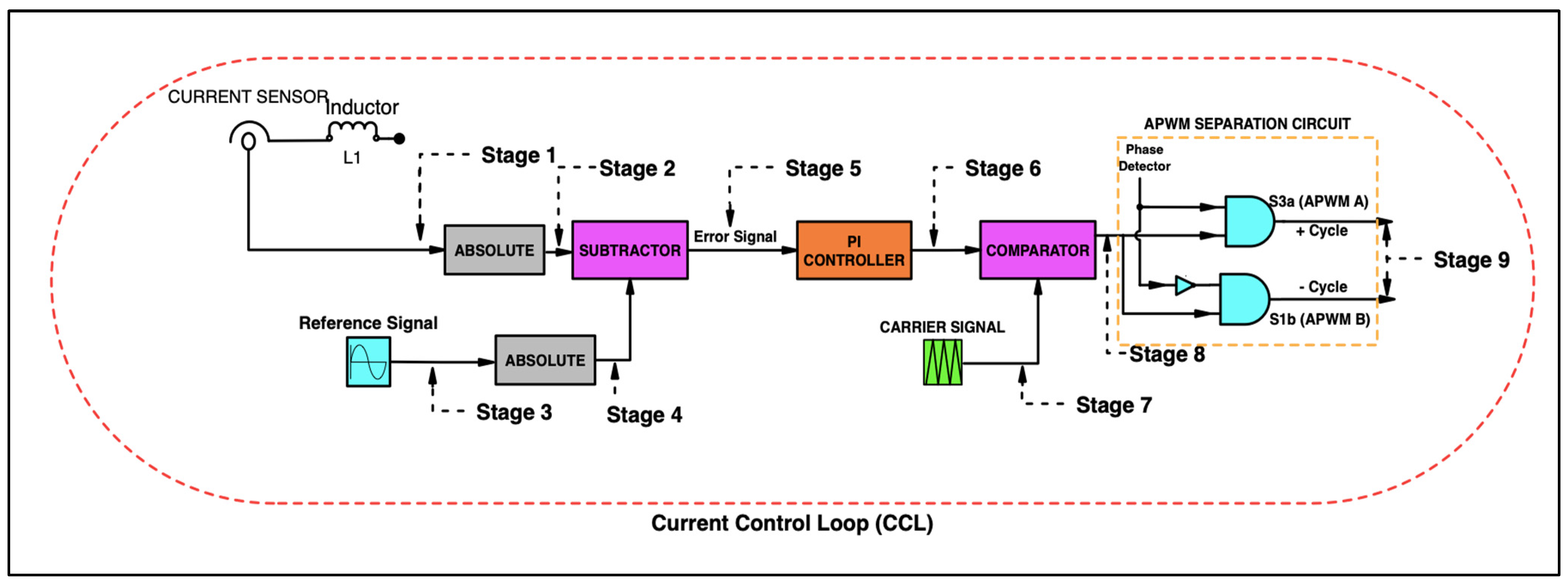
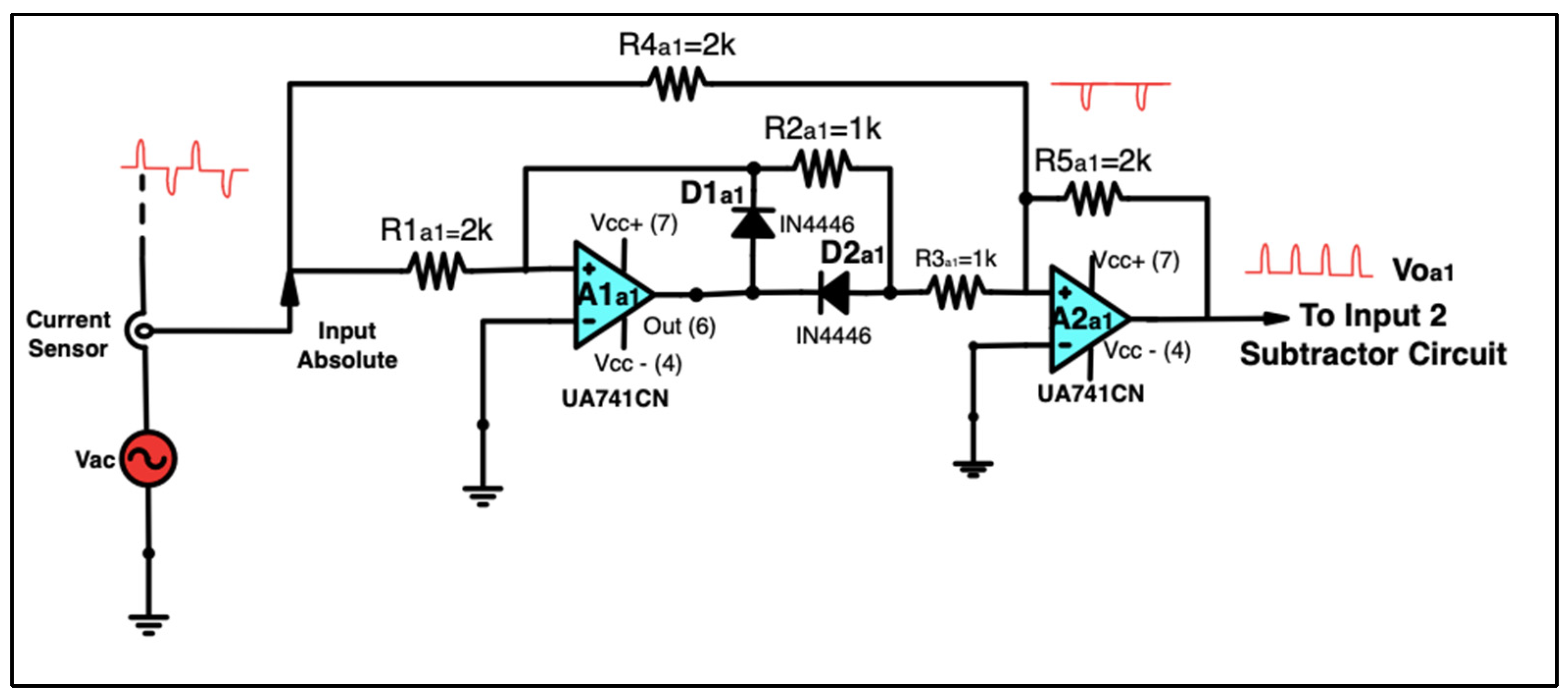
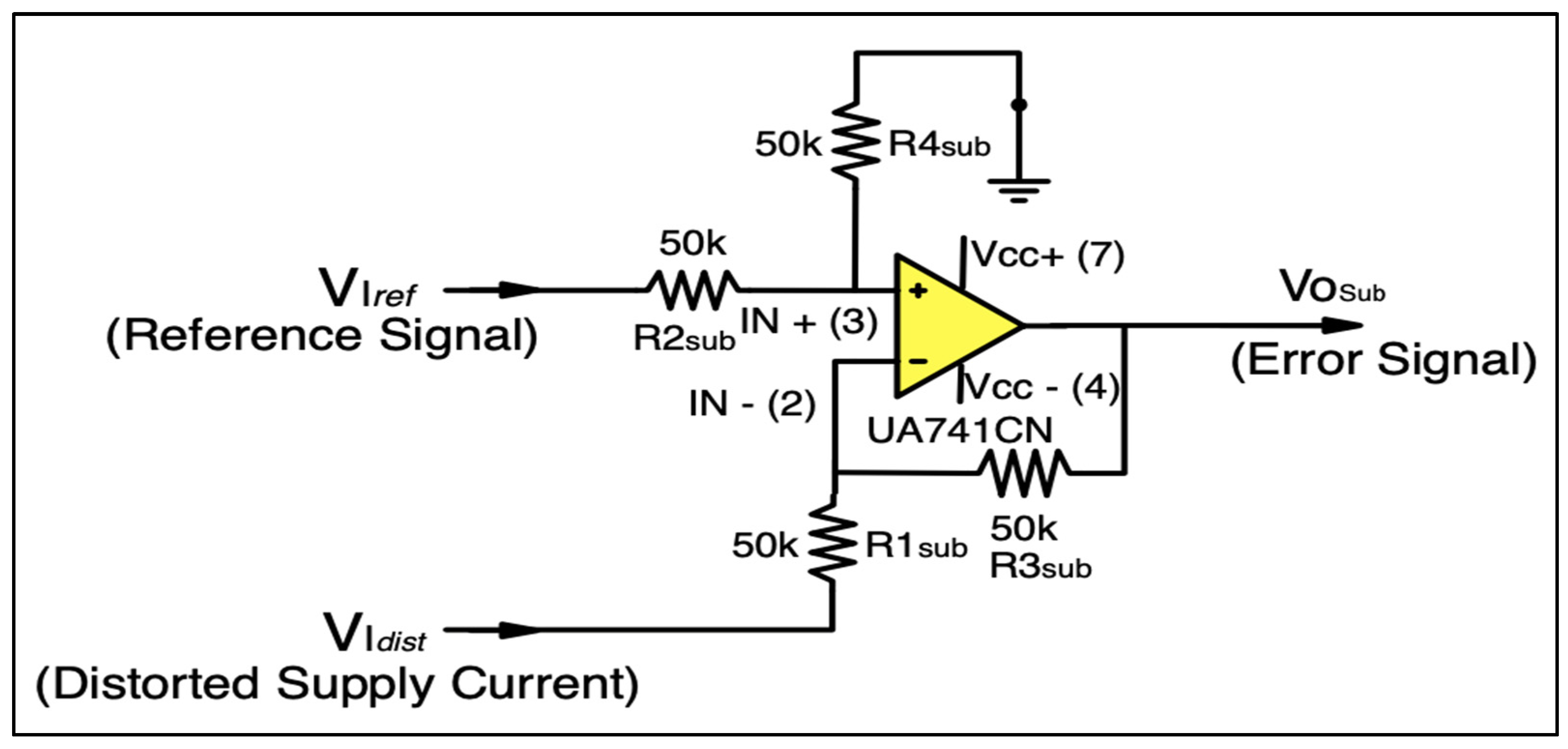
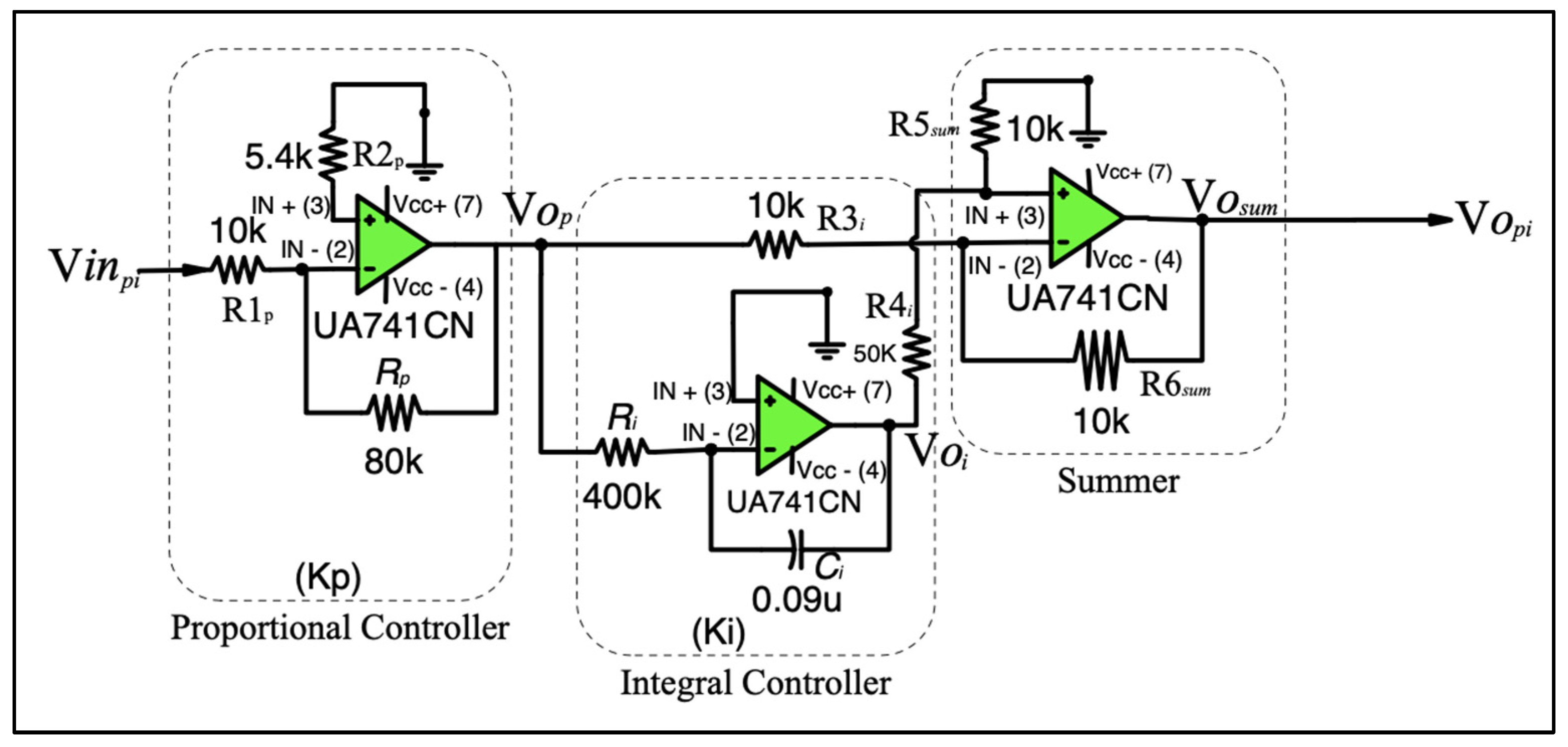


| State | IGBT Parameters | Diode Parameter |
|---|---|---|
| On-state | ||
| Turn-on | , , | - |
| Turn-off | , | = 25, |
| Applied voltage | ||
| Fundamental frequency | ||
| Switching frequency | ||
| Modulation | ||
| Peak current | ||
| Power factor | ||
| Device | Total Losses/Device | Proposed UPS | Typical UPS |
|---|---|---|---|
| Number of Devices (Losses) | Number of Devices (Losses) | ||
| IGBT | 41.45 W | 8 (331.6 W) | 4 (165.8 W) |
| DIODE | 15.50 W | 8 (124 W) | 8 (124 W) |
| Total Losses | 56.95 W | 455.6 W | 289.8 W |
| Switch | Rectifier Mode | |
|---|---|---|
| Positive Cycle | Negative Cycle | |
| S1a | ON | Off |
| S1b | Off | APWM |
| S2a | Off | Off |
| S2b | Off | ON |
| S3a | APWM | Off |
| S3b | Off | ON |
| S4a | ON | Off |
| S4b | Off | Off |
| Inverter Operation | Positive Cycle | Negative Cycle | ||
|---|---|---|---|---|
| Switching | Starting Pulse | Switching | Starting Pulse | |
| S1a | Off | Off | Off | Off |
| S1b | ON | High | Off | Off |
| S2a | Off | Off | ON | High |
| S2b | Off | Off | Off | Off |
| S3a | SPWM | Low | SPWM | High |
| S3b | Off | Off | Off | Off |
| S4a | Off | Off | Off | Off |
| S4b | SPWM | Low | SPWM | High |
| Parameter | Value |
|---|---|
| AC supply voltage, Vac | 24 V |
| DC supply voltage, Vdc | 12 V |
| Boost inductor, Ls | 2 mH |
| Inductor load, LL | 5 mH |
| Capacitor load, CL | 1000 μF |
| Resistive load, RL | 300 Ω |
| Switching frequency for rectifier, fs | 10 kHz |
| Switching frequency for inverter, fs | 5 kHz |
| Proportional gain, Kp | 8 |
| Integral gain, Ki | 27 |
| Strategies | THD (%) | Power Factor (pf) | |
|---|---|---|---|
| Rectifier without APF | Simulation | 189.85 | 0.6248 |
| Experimental test rig | 114.65 | 0.6391 | |
| Rectifier with APF | Simulation | 3.59 | 0.9996 |
| Experimental test rig | 7.81 | 0.9725 | |
| UPS with APF | Simulation | 3.59 | 0.9996 |
| Experimental test rig | 7.86 | 0.9715 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamad Rawi, M.S.; Baharom, R.; Mohd Radzi, M.A. Uninterruptible Power Supply Topology Based on Single-Phase Matrix Converter with Active Power Filter Functionality. Energies 2024, 17, 3441. https://doi.org/10.3390/en17143441
Mohamad Rawi MS, Baharom R, Mohd Radzi MA. Uninterruptible Power Supply Topology Based on Single-Phase Matrix Converter with Active Power Filter Functionality. Energies. 2024; 17(14):3441. https://doi.org/10.3390/en17143441
Chicago/Turabian StyleMohamad Rawi, Muhammad Shawwal, Rahimi Baharom, and Mohd Amran Mohd Radzi. 2024. "Uninterruptible Power Supply Topology Based on Single-Phase Matrix Converter with Active Power Filter Functionality" Energies 17, no. 14: 3441. https://doi.org/10.3390/en17143441
APA StyleMohamad Rawi, M. S., Baharom, R., & Mohd Radzi, M. A. (2024). Uninterruptible Power Supply Topology Based on Single-Phase Matrix Converter with Active Power Filter Functionality. Energies, 17(14), 3441. https://doi.org/10.3390/en17143441






