Study on Heat and Mass Transfer Performance of Ultra-Thin Micro-Heat Pipes
Abstract
1. Introduction
2. Establishing the Ultra-Thin MHP Model
2.1. Establishing the Heat and Mass Transfer Performance Test Platform
2.2. Establishing the Three-Dimensional Model
2.3. Settings of Governing Equations and Boundary Conditions
- (1)
- The heat pipe does not fail under different heating powers.
- (2)
- The evaporation and condensation occur at the gas–liquid interface. The radiative heat transfer is ignored, and only conductive and convective heat transfer are considered.
- (3)
- The flow states of liquid and gaseous working media are both laminar, and the fluids are incompressible.
- (4)
- The wick is an isotropic porous medium filled with a liquid working medium.
- (5)
- The vapor pressure inside the heat pipe equals the saturated vapor pressure at the corresponding temperature.
2.4. Settings of the Modified Parameter
2.5. Grid Independence Test
3. Heat and Mass Transfer Performance Analysis of the Ultra-Thin MHP
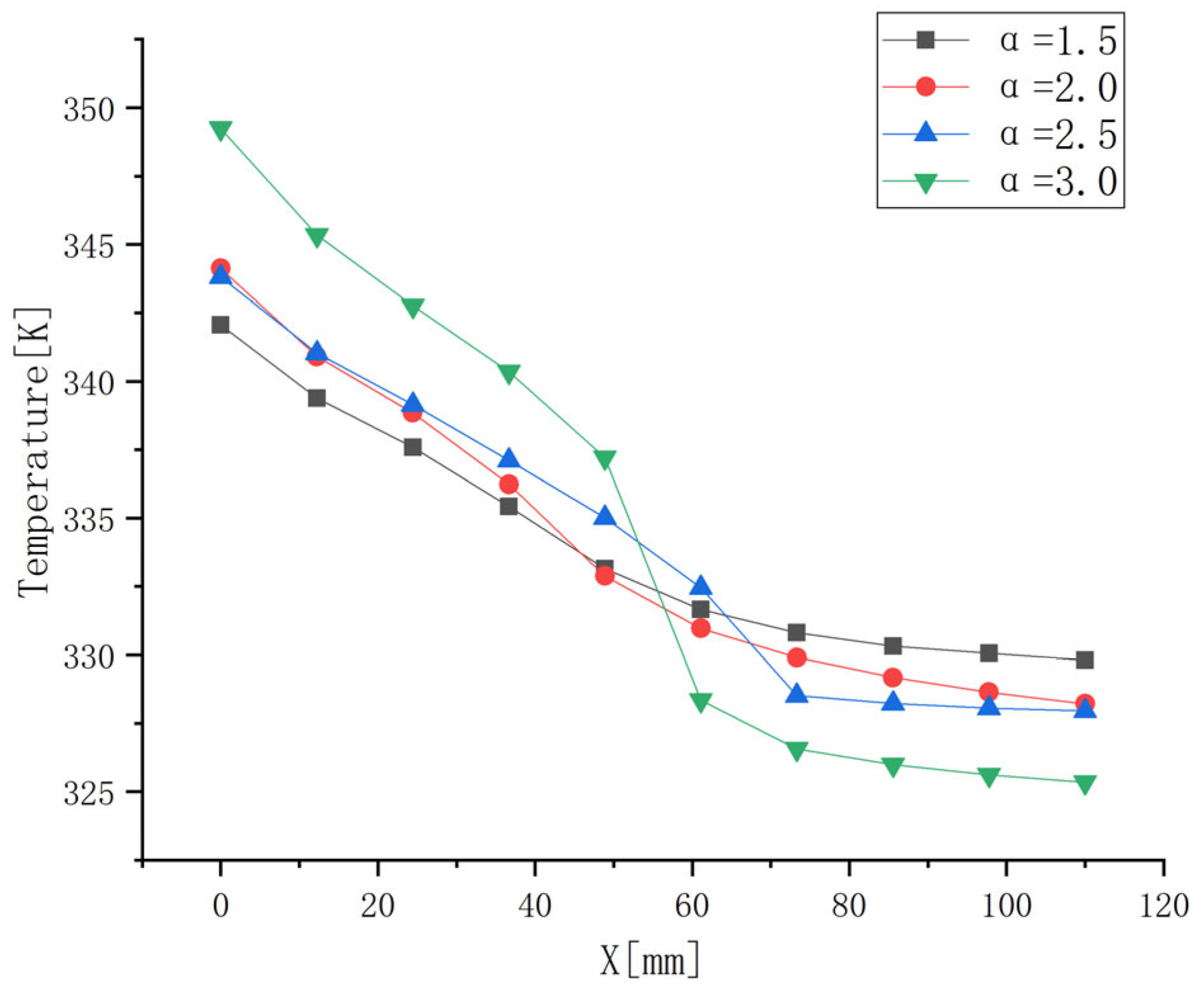
3.1. Influences of α on Temperature Distribution
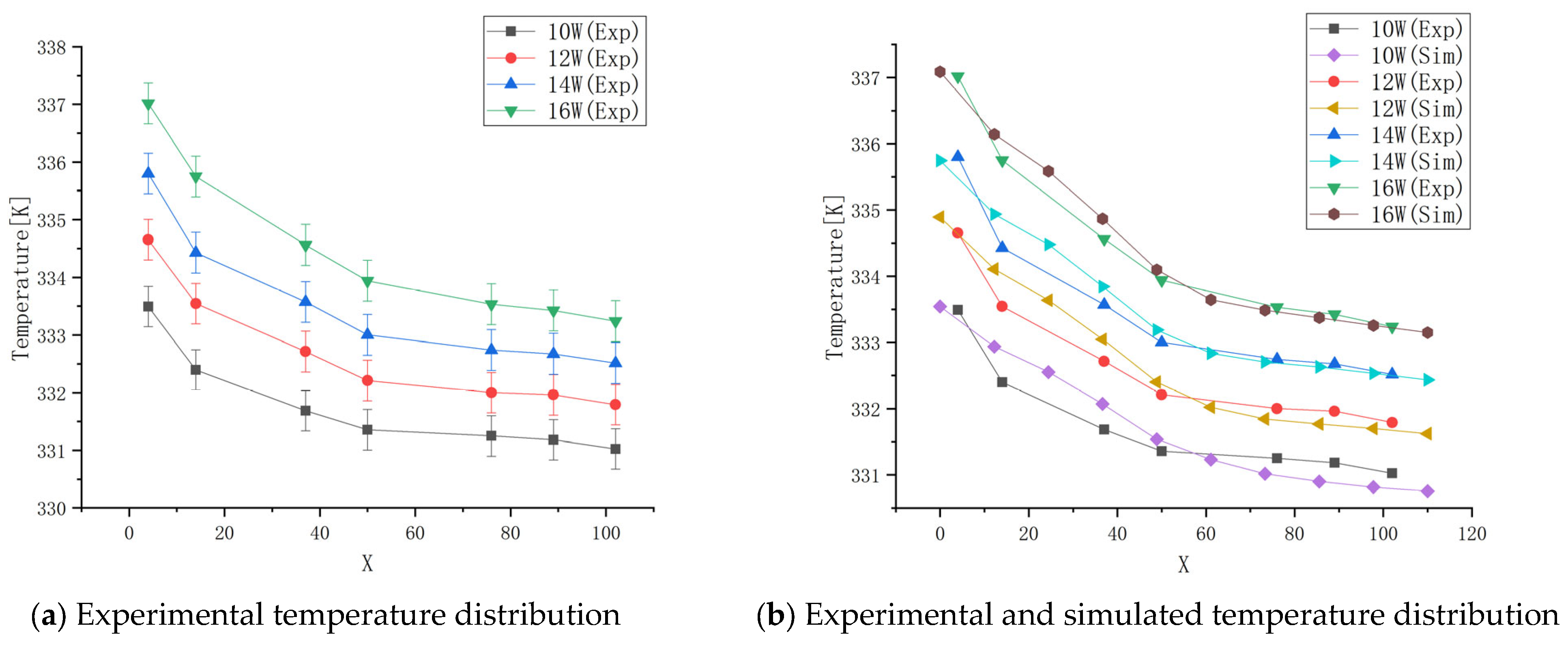
3.2. Model Reliability Analysis
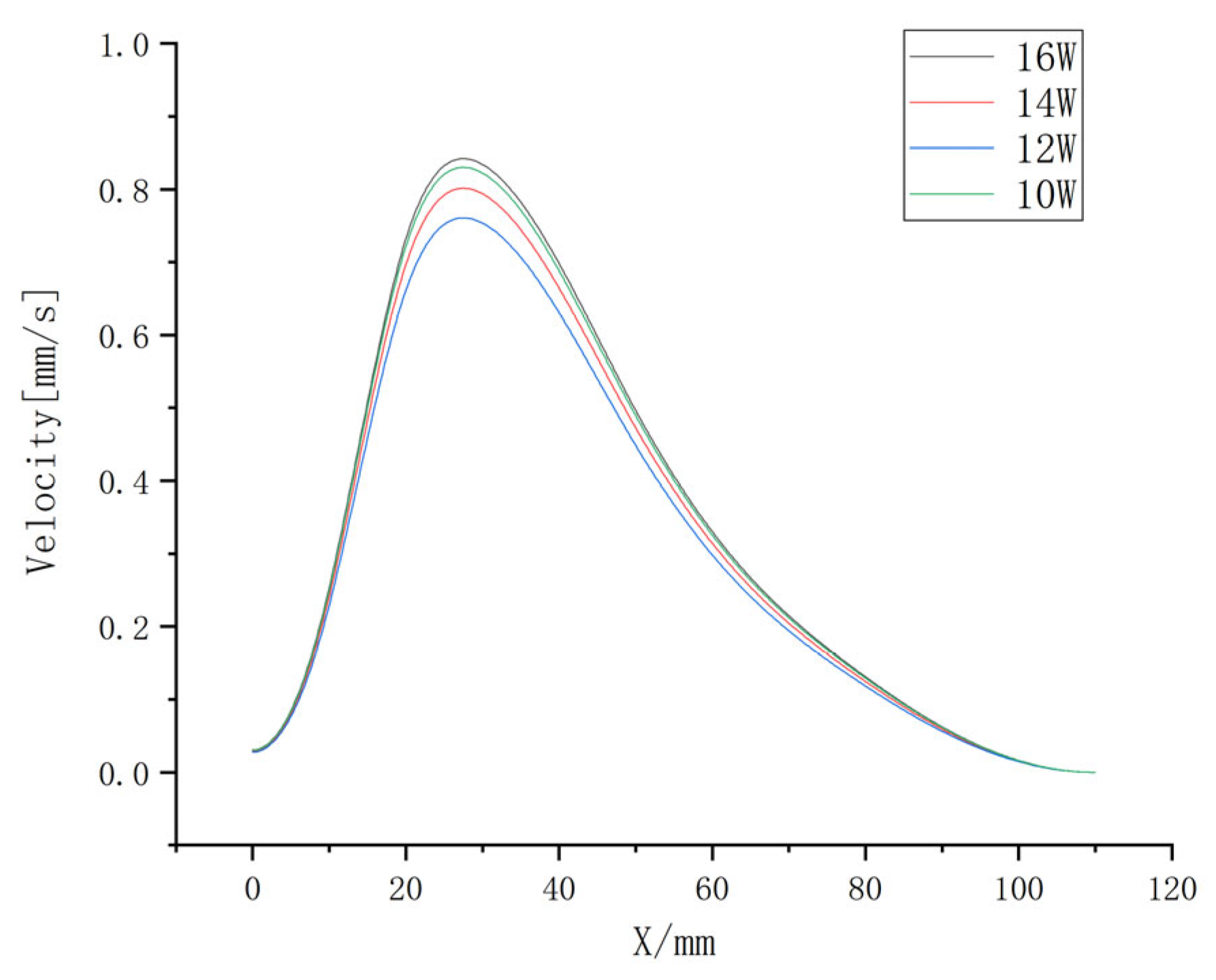
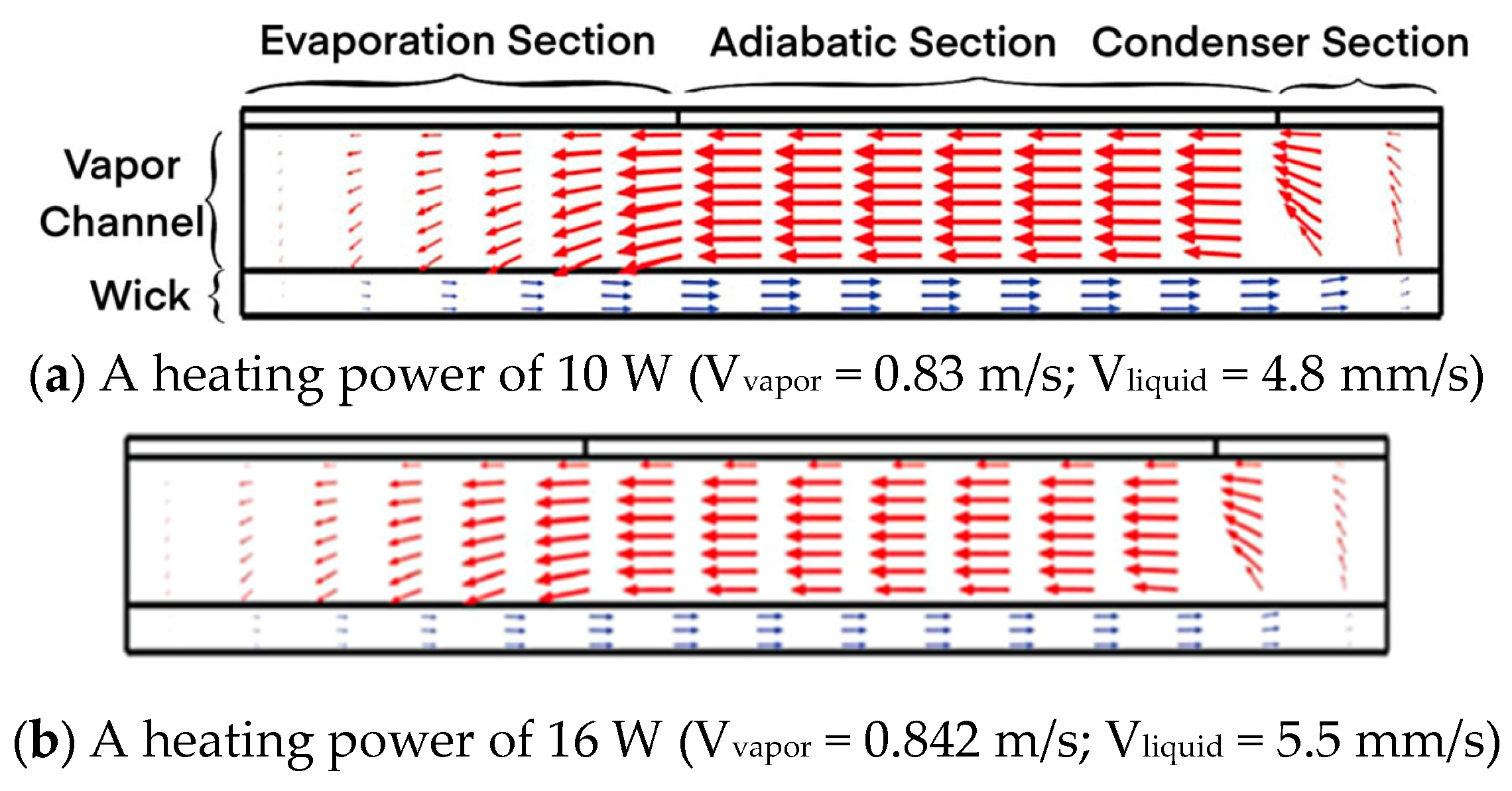
3.3. Influences of Heating Power on the Vapor Velocity Distribution
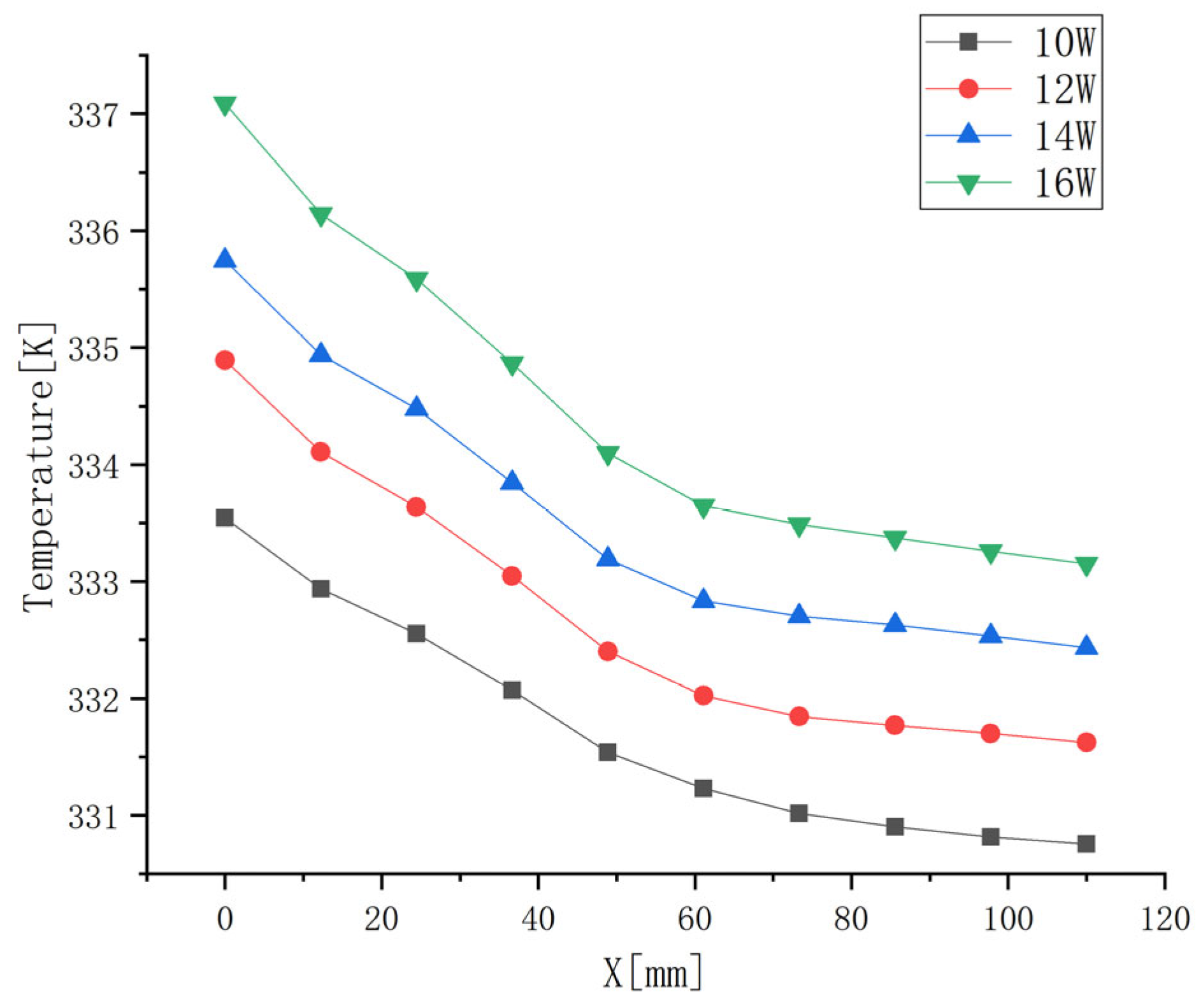
3.4. Influences of Heating Power on Temperature Distribution
4. Discussion
5. Conclusions
- (1)
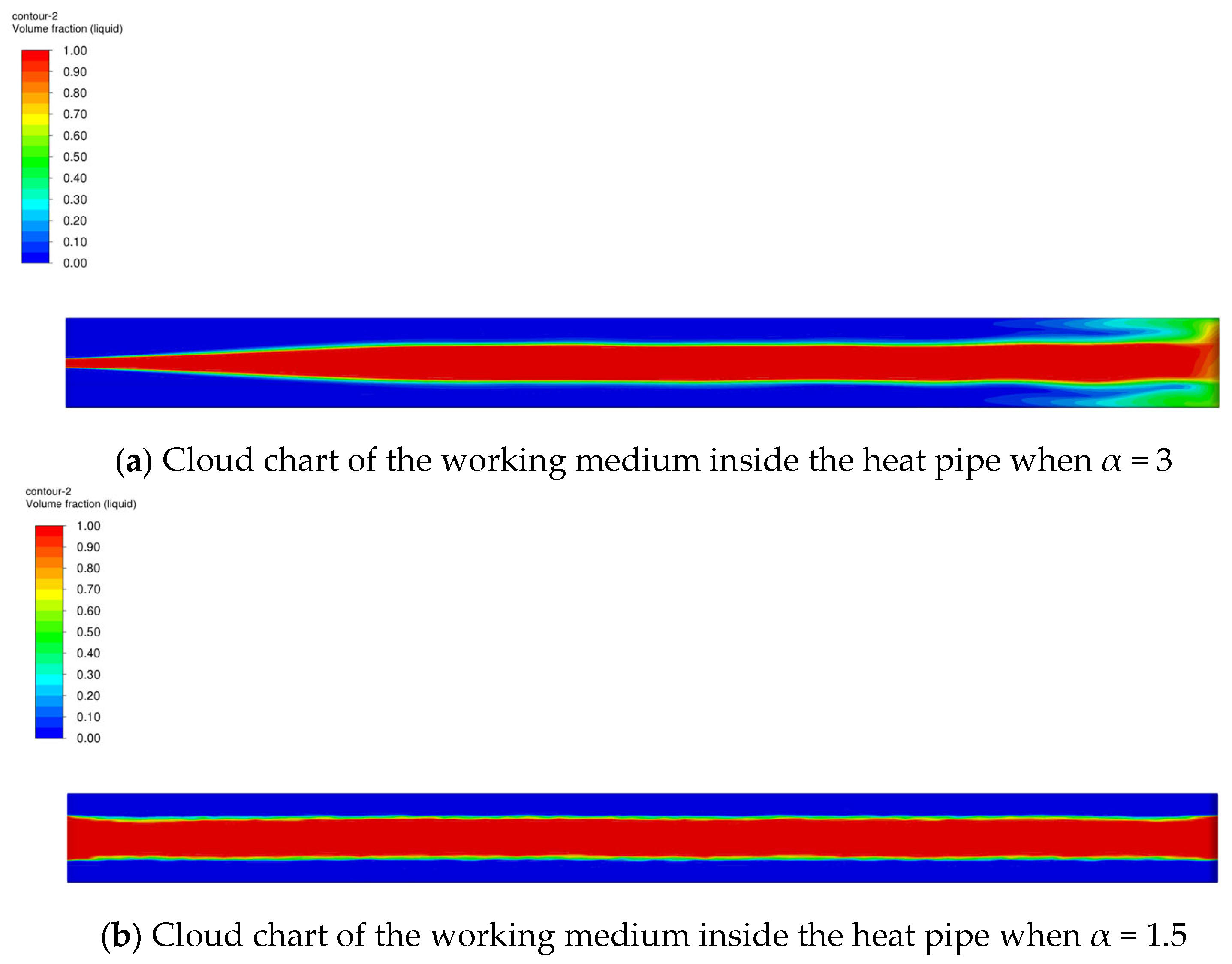
- Although the wick porous medium model presents a better transport capacity for the liquid working medium, an excessive α value significantly affects the calculation accuracy and stability of the model. In the given range of α values, when α = 3, the “liquid accumulation” phenomenon appears on the heat pipe model, significantly decreasing the temperature equalization property, which does not meet the temperature requirements. When α = 1.5, the heat pipe model meets the temperature requirements to the best degree; this parameter value was selected for subsequent analysis.
- (2)
- An experimental platform was built to conduct heat transfer performance experiments on ultra-thin MHP samples. The model’s reliability was verified by fitting the heat pipe samples’ surface temperature to the simulation model’s surface temperature under the same heating powers. It was found that the error between the experimental value and the simulation value decreases gradually with an increase in heating power. The deviation value is caused by the heat resistance between the wick and the pipe wall, the heat resistance between the pipe surface and the thermocouple, and the heat dissipation in the adiabatic section.
- (3)
- The flow states of the inner vapor working medium under different heating powers were analyzed by using the established ultra-thin MHP model. Under different heating powers, the vapor velocity in the inner cavity of the heat pipe model always increases first and then decreases; the maximum vapor velocity appears at the junction of the heating section and the adiabatic section. The working medium in the heating section is heated to evaporate, and a large amount of vapor is accumulated in the evaporation section. Therefore, the flow rate also reaches the maximum value. The maximum vapor velocity reaches 0.842 m/s under the heating power of 16 W. In addition, the flow rate drops to 0 m/s when approaching the central position of the condensation section.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, H.; Tang, Y.; Wan, Z.; Li, J.; Yuan, W.; Lu, L.; Tang, K. Review of applications and developments of ultra-thin micro heat pipes for electronic cooling. Appl. Energy 2018, 223, 383–400. [Google Scholar] [CrossRef]
- Gan, Y.H.; Xiong, T.; Luo, Q.L.; Liang, J.L.; Dong, D.W.; Li, Y. Influence of Vapor-Liquid Passage Structure on the Performance of an Ultra-Thin Heat Pipe. J. Tianjin Univ. (Sci. Technol.) 2022, 55, 965–972. [Google Scholar]
- Guptaa, N.K.; Arun, K.T.; Subrata, K.G. Heat transfer mechanisms in heat pipes using nanofluids—A review. Exp. Therm. Fluid Sci. 2018, 90, 80–100. [Google Scholar] [CrossRef]
- Li, P.; Chen, C.; Qin, Q.; Tian, X.; Yan, R.; Fang, Y.; Jun, J.; Zhi, M. Sintering microstructure and properties of copper powder prepared by electrolyzation and atomization. J. Cent. South Univ. 2021, 28, 1966–1977. [Google Scholar] [CrossRef]
- Huang, D.; Jia, L. Study on the Capillary Performance of Sintered Copper Powder Wick. J. Eng. Thermophys. 2021, 42, 494–503. [Google Scholar]
- Yan, W.; Yang, X.; Liu, T.; Wang, S. Numerical Simulation of Heat Transfer Performance for Ultra-Thin Flat Heat Pipe. J. Therm. Sci. 2023, 32, 643–649. [Google Scholar] [CrossRef]
- Meijie, L. Study on Capillary Driving and Heat Transfer Performance of Micro Heat Pipe Based on Different Channels. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, April 2021. [Google Scholar]
- Yi, F.; Gan, Y.; Xin, Z.; Li, Y.; Chen, H. Experimental study on thermal performance of ultra-thin heat pipe with a novel composite wick structure. Int. J. Therm. Sci. 2023, 193, 108539. [Google Scholar] [CrossRef]
- Huang, Z.; Tang, X.; Luo, Q.; Gan, Y.; Liang, J.; Li, R.; Xiong, T.; Liu, J.; Ma, L.; Dong, D.; et al. Numerical analysis on heat transfer characteristics of a multi-vapor channel vapor chamber with novel ultra-thin composite wick. Case Stud. Therm. Eng. 2021, 26, 101035. [Google Scholar] [CrossRef]
- Jung, E.G.; Booj, H. A numerical modeling for the steady-state performance of a micro heat pipe using thin liquid film theory. Int. J. Heat Mass Transf. 2018, 126, 557–566. [Google Scholar] [CrossRef]
- Koito, Y. Numerical analyses on heat transfer characteristics of ultra-thin heat pipes: Fundamental studies with a three-dimensional thermal-fluid model. Appl. Therm. Eng. 2019, 148, 430–437. [Google Scholar] [CrossRef]
- Koito, Y. A numerical analysis on the effect of deviation from a centered wick structure in an ultra-thin flattened heat pipe. Front. Heat Mass Transf. 2021, 16, 1–7. [Google Scholar] [CrossRef]
- Ming, Z.; Zhongliang, L.; Guoyuan, M. The experimental and numerical investigation of a grooved vapor chamber. Appl. Therm. Eng. 2009, 29, 422–430. [Google Scholar] [CrossRef]
- Lu, L.; Xie, Y.; Zhang, F.; Liao, H.; Liu, X.; Tang, Y. Influence of a sintered central column on the thermal hydraulic performance of a vapor chamber: A numerical analysis. Appl. Therm. Eng. 2016, 103, 1176–1185. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, H.; Xu, Z.; Li, J.; Deng, D. Numerical analysis on the thermal hydraulic performance of a composite porous vapor chamber with uniform radial grooves. Int. J. Heat Mass Transf. 2019, 142, 118458. [Google Scholar] [CrossRef]
- Fang, W. Numerical simulations of the liquid-vapor phase change dynamic processes in a flat micro heat pipe. Int. J. Heat Mass Transf. 2020, 147, 119022. [Google Scholar] [CrossRef]
- Huang, Z.; Li, D.; Zhao, J.; Jian, Q. Thermal and hydraulic analysis of ultra-thin vapor chamber with copper columns considering Marangoni effect. Int. J. Heat Mass Transf. 2022, 184, 122343. [Google Scholar] [CrossRef]
- Patankar, G.; Weibel, J.A.; Garimella, S.V. On the transient thermal response of thin vapor chamber heat spreaders: Governing mechanisms and performance relative to metal spreaders. Int. J. Heat Mass Transf. 2019, 136, 995–1005. [Google Scholar] [CrossRef]
- Gaurav, P.; Weibel, J.A.; Garimella, S.V. On the transient thermal response of thin vapor chamber heat spreaders: Optimized design and fluid selection. Int. J. Heat Mass Transf. 2020, 148, 119106. [Google Scholar]
- Rabiee, R.; Rajabloo, B.; Désilets, M.; Proulx, P. Heat transfer analysis of boiling and condensation inside a horizontal heat pipe. Int. J. Heat Mass Transf. 2019, 139, 526–536. [Google Scholar] [CrossRef]
- Liu, T.; Dunham, M.T.; Jung, K.W.; Chen, B.; Asheghi, M.; Goodson, K.E. Characterization and thermal modeling of a miniature silicon vapor chamber for die-level heat redistribution. Int. J. Heat Mass Transf. 2020, 152, 119569. [Google Scholar] [CrossRef]
- Özisik, M.N.; Orlande, H.R.B. Inverse Heat Transfer: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Shuang, L. Active Cooling Mechanism and Cooling Capacity Evaluation of Thermal Protection Systems for Hypersonic Vehicle. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, June 2010. [Google Scholar]
- Chang, M.H.; Cheng, C.H. Non-destructive inverse method for determination of irregular internal temperature distribution in PEMFCs. J. Power Sources 2005, 142, 200–210. [Google Scholar] [CrossRef]
- Bu, Z.; Li, S.; Jiao, B.; Wang, B.; Gan, Z. Visualization study on a nitrogen pulsating heat pipe under different condenser temperatures. Chem. Ind. Eng. Prog. 2023, 42, 4167–4181. [Google Scholar]
- Yong, Y.; Yang, H.; Lu, X.; Zhang, M. Research on visualization mechanism of pulsating heat pipe based on surfactant aqueous solution. Energy Conserv. 2023, 42, 37–42. [Google Scholar]
- Zhao, J.; Wang, Z.; Xu, W.; Liu, Y. Investigation on the Flow Pattern Evolution and Heat Transfer Characteristics of an Embedded Heat Pipe. J. Eng. Thermophys. 2022, 43, 2659–2666. [Google Scholar]
- Yu, F.; Yu, C.; Cao, J.; Chen, Y. Experimental analysis of the evaporation regimes of an axially grooved heat pipe at small tilt angles. Int. J. Heat Mass Transf. 2018, 126, 334–341. [Google Scholar] [CrossRef]
- Wang, C.; Yao, F.; Shi, J.; Wu, L.; Zhang, M. Visualization Study on Thermo-Hydrodynamic Behaviors of a Flat Two-Phase Thermosyphon. Energies 2018, 11, 2295. [Google Scholar] [CrossRef]
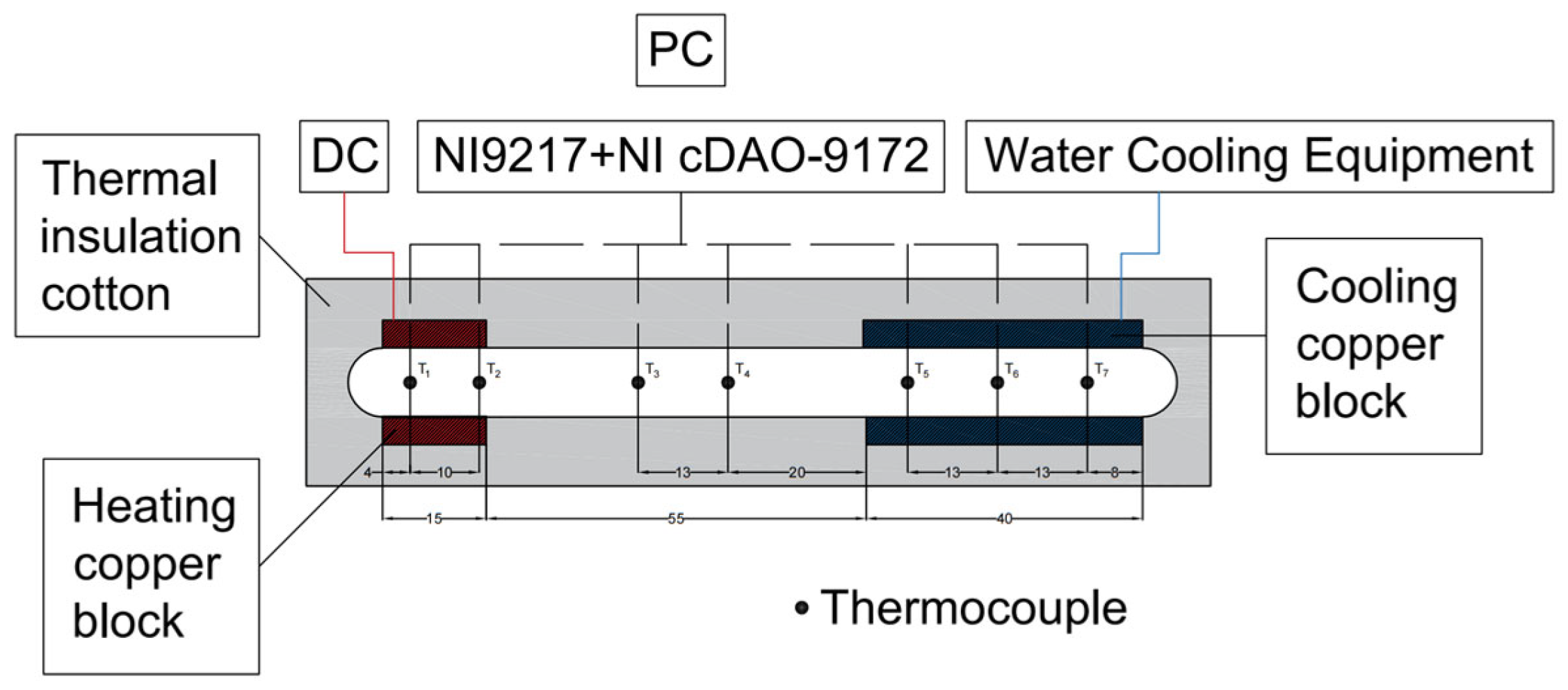
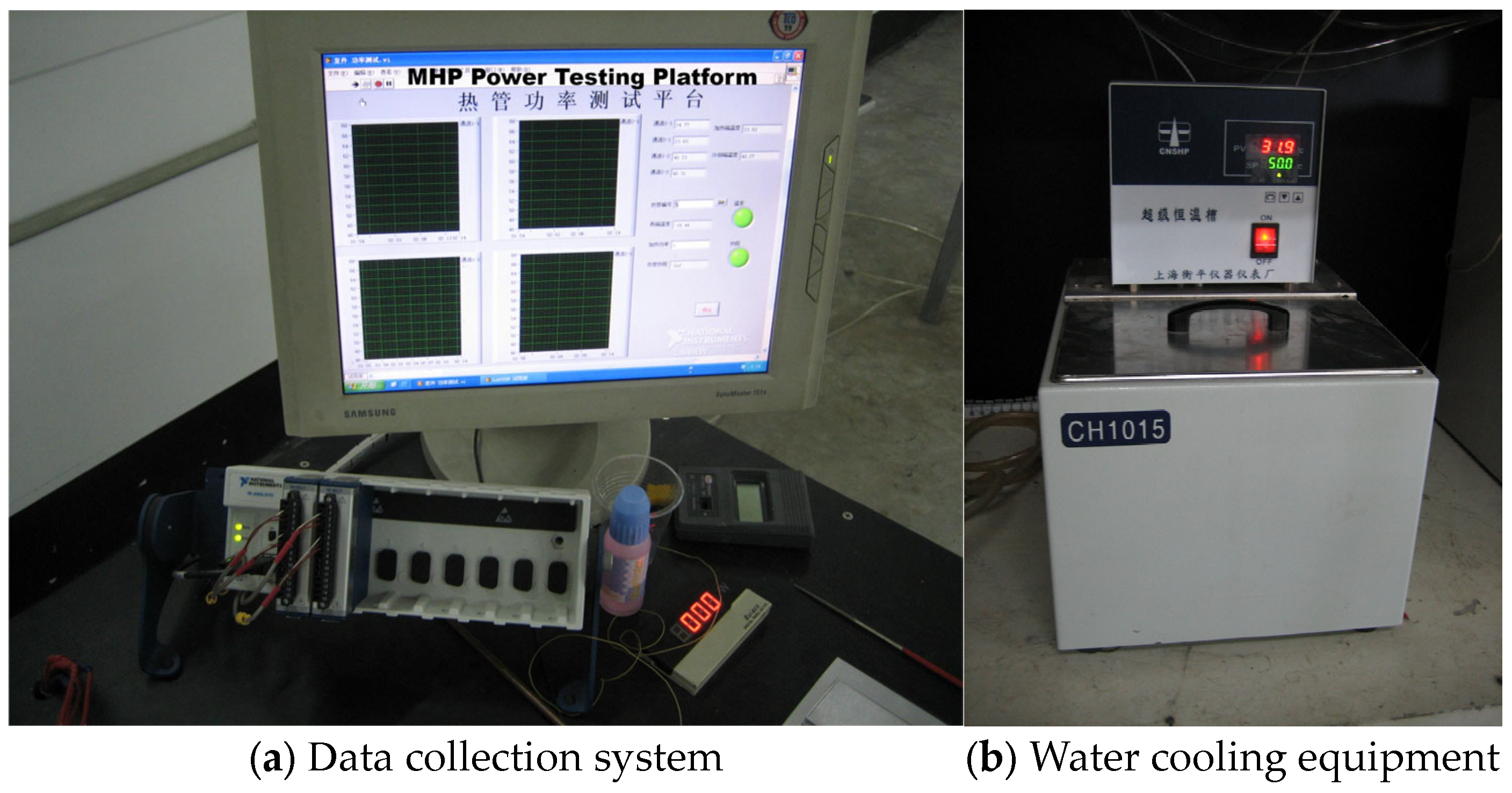


| Parameter | Value |
|---|---|
| Density | 998.2 [kg·m−3] |
| Specific heat capacity | 4.102 [J·(kg·K)−1] |
| Heat conductivity | 0.602 [W·(m·K)−1] |
| Viscosity | 1.0015 [mPa·S] |
| Surface tension | 0.073 [N·m−1] |
| Parameter | Value |
|---|---|
| Length | 110.0 [mm] |
| Thickness | 1.0 [mm] |
| Width | 10.0 [mm] |
| Wall thickness | 0.2 [mm] |
| Evaporator section length | 15.0 [mm] |
| Condenser section length | 40.0 [mm] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Y.; Sun, Y.; Li, G.; Liu, X.; Liu, L.; Zhao, F.; Li, X. Study on Heat and Mass Transfer Performance of Ultra-Thin Micro-Heat Pipes. Energies 2024, 17, 3426. https://doi.org/10.3390/en17143426
Xiang Y, Sun Y, Li G, Liu X, Liu L, Zhao F, Li X. Study on Heat and Mass Transfer Performance of Ultra-Thin Micro-Heat Pipes. Energies. 2024; 17(14):3426. https://doi.org/10.3390/en17143426
Chicago/Turabian StyleXiang, Yuming, Yonghua Sun, Guolin Li, Xiangjuan Liu, Lin Liu, Fangwei Zhao, and Xibing Li. 2024. "Study on Heat and Mass Transfer Performance of Ultra-Thin Micro-Heat Pipes" Energies 17, no. 14: 3426. https://doi.org/10.3390/en17143426
APA StyleXiang, Y., Sun, Y., Li, G., Liu, X., Liu, L., Zhao, F., & Li, X. (2024). Study on Heat and Mass Transfer Performance of Ultra-Thin Micro-Heat Pipes. Energies, 17(14), 3426. https://doi.org/10.3390/en17143426








