On the Necessity of Including the Dissociation Kinetics When Modelling Gas Hydrate Pipeline Plug Dissociation

Abstract

Gas hydrate plugs in petroleum fluid pipelines are a major flow assurance problem and thus, it is important for industry to have reliable mathematical models for estimating the time required to dissociate a hydrate pipeline plug. The existing mathematical models for modelling hydrate plug dissociation treat the problem as a pure heat transfer problem. However, an early study by Jamaluddin et al. speculated that the kinetics of gas hydrate dissociation could become the rate-limiting factor under certain operating conditions. In this short communication, a rigorous 2D model couples the equations of heat transfer and fluid flow with Clarke and Bishnoi’s model for the kinetics of hydrate dissociation. A distinguishing feature of the current work is the ability to predict the shape of the dissociating hydrate–gas interface. The model is used to correlate experimental data for both sI and sII hydrate plug dissociation, via single-sided depressurization and double-sided depressurization. As a preliminary examination on the necessity of including dissociation kinetics, this work is limited to conditions for which hydrate dissociation rate constants are available; kinetic rate constants for hydrate dissociation are available at temperatures above 273.15 K. Over the range of conditions that were investigated, it was found that including the intrinsic kinetics of hydrate dissociation led to only a very small improvement in the accuracy of the predictions of the cumulative gas volumes collected during dissociation. By contrast, a sensitivity study showed that the predictions of hydrate plug dissociation are very sensitive to the value of the porosity. Thus, it is concluded that unless values of the thermophysical properties of a hydrate plug are known, accounting for the dissociation kinetics need not be a priority.

1. Introduction

In 1934, a Texoma Natural Gas Company Engineer named E.G. Hammerschmidt wrote “Solid compounds, resembling snow or ice in appearance, are formed with methane, ethane, propane and isobutane in the presence of water at elevated pressures and temperatures” [1]. Those solids which resembled snow or ice turned out to be gas hydrates and the petroleum industry has since spent vast sums of money trying to avoid their formation [2]. Gas hydrates are crystalline compounds in which cage networks of water molecules trap gas molecules. Depending on the gas molecules involved, gas hydrates that are found in nature will usually be found in one of three crystal forms: sI (cubic), sII (cubic) or sH (hexagonal). Smaller molecules such as methane or ethane will form sI hydrates, whereas propane and other similar sized molecules will form sII hydrates. sH hydrates require the presence of both a large molecule and a smaller “helper” molecule and as such, they are only very rarely found in nature [2].

Since Hammerschmidt’s seminal paper, the flow assurance industry has been established to ensure that petroleum fluids can flow without being obstructed by gas hydrates, waxes or asphaltenes [3]. Historically, flow assurance as applied to gas hydrates has involved injecting large quantities of thermodynamic hydrate inhibitors, such as methanol, into pipelines. The addition of these compounds extends the thermodynamic limits for hydrate-free operation. However, thermodynamic inhibitors are expensive and they are not environmentally benign. Additionally, as offshore oil and gas production moves into deeper water, the higher pressures push the required amount of methanol past the point of being economically feasible [4].

Parallel to field developments in hydrate prevention and management, the last thirty years have also seen the development of computer tools to predict the formation and dissociation of hydrate pipeline plugs. Modelling the formation and dissociation of a hydrate pipeline plug requires the simultaneous solution of the heat/mass/momentum balance equations as well as the appropriate thermodynamic and kinetic equations. As such, these problems are computationally-intensive and it has only been since the late 1980s that computers have been powerful enough to tackle even the most simplistic cases.

Over the last thirty years several groups tackled the problem of predicting hydrate plug formation [5,6,7,8,9,10,11,12,13,14,15]; however, less attention has been paid to predicting hydrate plug dissociation. The first serious attempt to model the dissociation of a gas hydrate plug came from Ullerich et al. [16] who proposed a 1D moving boundary heat transfer model. Their model [16] considered the hydrate to be a rectangular 1D semi-infinite solid, in which a constant heat flux is applied at one of the boundaries. Additionally, their model treated the dissociating hydrate as an ablation problem; in an ablation problem the evolved gas blows the water away from the dissociating hydrate surface. The model [16] was solved analytically and the results were compared to experimental results [16] for hydrate mass loss measurements. They [16] were able to predict the quantitative behavior of the dissociating hydrate plug; however, they consistently underpredicted the mass of the collected gas by up to 10%. It should be noted that in 1987, not all of the thermophysical properties of methane hydrates were known and, as such, errors of 10% were acceptable. Even though this work presented no attempt at addressing hydrate dissociation by pressure reduction it was an important first step towards modelling hydrate pipeline plug dissociation.

Two years later, Jamaluddin et al. [17] modelled the dissociation of a semi-infinite gas hydrate plug by combining 1D heat transfer with the kinetics of hydrate dissociation. As was done by Ullerich et al. [16], their model [17] treated the dissociating hydrate as an ablation problem. However, the inclusion of dissociation kinetics resulted in a boundary condition that was non-linear in temperature. Thus, a numerical solution was necessary. The results of the simulations [17] predicted that changes in the system pressure were sufficient to transition hydrate dissociation from a heat-transfer-controlled process to a kinetics-controlled process. In the region of kinetics control, it was further seen that the value of the activation energy and the hydrate surface roughness have a significant effect on the observed rate of hydrate dissociation. Although these results predicted a transition from heat transfer control to kinetic control, the authors were not able to compare their predictions to experimental data.

Kelkar et al. [18] derived a heat-conduction-based model for gas hydrate plug dissociation via double-sided depressurization. In their model, the radial dissociation of the hydrate plug was modelled as a 1D moving boundary heat conduction problem in rectangular coordinates. Since they used rectangular coordinates and since they assumed that there was no axial hydrate dissociation, Kelkar et al. [18] were able to derive an analytical expression for the position of the dissociating hydrate interface, as a function of time. Their [18] results predicted that a rapid double-sided depressurization of the hydrate plug could result in the hydrate plug becoming coated by a layer of ice. Interestingly, Kelkar et al. [18] also predicted that the time for complete plug dissociation went through a minimum at −5 °C. Unfortunately, Kelkar et al. [18] were not able to compare their predictions to any experimental data.

While Kelkar’s model [18] suffered from several questionable assumptions, such as the dissociating hydrate being surrounded by a stagnant layer of water, it became the starting point for several subsequent attempts at modelling hydrate plug dissociation. In 2003, Bollavaram and Sloan [19] presented experimental results and modelling results for hydrate dissociation by single-sided and double-sided depressurization. In the experiments, hydrate plugs were formed in 36” by 1” cylindrical vessels and then subsequently dissociated by either single- or double-sided depressurization. In modelling the results for the double-sided depressurization, Bollavaram and Sloan [19] transformed Kelkar’s model [18] to cylindrical coordinates. A key observation of their work [19] was to confirm Kelkar’s [18] assumption that axial dissociation is negligible during double-sided depressurization.

Bollavaram and Sloan [19] also described a model for single-sided hydrate dissociation; however, in their 2003 work [19] they only described the equations in words. The full set of equations for single-sided depressurization was eventually presented by Davies et al. [20] in 2006. Their model [20] consists of four successive steps: (1) the computation of the axial pressure profile, (2) the computation of the gas flow velocity through the hydrate plug, (3) the computation of the axial temperature profile and (4) the successive radial dissociation of small sections of the hydrate plug. When used to correlate experimental data [20], the model can capture the trend of the single-sided depressurization process. Additionally, Davies et al. [20] also correlated experimental results for the case of hydrate pipeline plug dissociation via electrical heating. Like the case of double-sided dissociation, they [20] observed that dissociation via electrical heating primarily proceeded in the radial direction.

Despite the successes of their model [20], the derivation of the model leads to two issues that warrant mention. First, it was assumed [20] that each of the axial slices of the hydrate plug are at a constant temperature. This gives rise to a temperature discontinuity at the hydrate–pipe interface, which in turn can create numerical challenges when implementing the model. Second, as each of the axial slices dissociates, it was assumed that they were surrounded by a stagnant layer of water. This assumption is questionable since the pressure gradient will likely cause the water to flow downstream. Finally, it should also be noted that Davies et al. [20] mentioned that the effect of kinetics should be studied; however, they [20] did not provide any insight into how kinetics should be incorporated into their model.

Since 2006 there have been no further studies, at least in the open literature, that attempt to model the dissociation of a hydrate pipeline plug. However, there have been a handful of related studies that bear mentioning in the context of the current work. The first is that of Sean et al. [21] who proposed a kinetic model to describe the dissociation of a spherical pellet of methane hydrate suspended in a vertical downward flow of water. This model [21] was not presented in the context of hydrate pipeline plug dissociation; however, it illustrated a method to couple hydrate dissociation kinetics and transport equations. In their model, Sean et al. [21] expressed the driving force for hydrate dissociation in terms of the Gibbs energy difference between the hydrate and the liquid phases. A limitation of expressing the driving force in this manner is that it requires knowledge of the liquid phase mole fraction of methane, at equilibrium and at the system conditions; the mole fraction of methane at the system conditions was not known and thus, was fit to the experimental data. Subsequently the model was verified with experimental data in which a 1 cm diameter methane hydrate pellet was suspended in a stream of flowing water and dissociated at a pressure of 9 MPa and temperatures ranging from (276 to 284) K.

In 2007, Nazridoust and Ahmadi [22] performed a computational fluid dynamics (CFD) simulation of methane hydrate dissociation within a sandstone core. In their model [22] the energy balance on the dissociating hydrate is coupled with the dissociation kinetics model of Kim et al. [23]. It was noted [22] that the rate of dissociation is affected by the heat transfer from the environment as well as by the temperature/pressure conditions in the core holder. Unfortunately, in 2007, the experimental data needed to verify the modelling results were not available.

Also in 2007, Sean et al. [24] extended their earlier work [21] to dissociation by both depressurization and by temperature increase. Their generalized model [24] was used to correlate experimental data on the dissociation of a hydrate-encrusted methane bubble. While the model was able to correlate the results, it suffered from the same limitations as their previous work [22]; specifically, the dissociation driving force was expressed in terms of quantities that had to be fit to the experimental data.

Kumar et al. [25], in 2013, proposed a model to describe the dissociation of CO₂ hydrates formed in a bed of glass beads. Their model [25] combined hydrate dissociation with heat and mass flow in porous media. Subsequently, the model was used to correlate lab data on the dissociation of CO₂ hydrates formed in glass beads. In their model [25], the kinetics of hydrate dissociation were described by the model of Kim et al. [23]. While this work presented a methodology for including hydrate dissociation kinetics in modelling the dissociation of in situ hydrates, it did not address the question of whether the kinetics were significant. In other words, the results [25] with the kinetics were not compared to the case of dissociation as a heat-transfer-controlled process. Almost a half-decade after the work of Kumar et al. [25], Yu et al. [26] used CFD to study the flow of methane through a porous mixture of sediment and dissociating methane hydrate. Their proposed model included the hydrate dissociation kinetics term proposed by Sean et al. [21]. Of possible relevance to the current study is their observation that the inclusion of kinetics becomes important as the porosity decreases.

Finally, in 2021, Li et al. [27] proposed an integral heat conduction model with Neumann boundary conditions. Of relevance to the current study, Li et al. [27] presented the Stefan boundary conditions in a generalized vector form. The model was subsequently applied to a semi-infinite hydrate reservoir and it was seen that the model was able to track the location of the dissociating interface. The authors [27] did not present any results for hydrate dissociation by depressurization; however, they did allude to how their model could be extended to such cases.

In the current study, a 2D axisymmetric model for hydrate plug dissociation is developed and implemented with COMSOL (Version 6.2) [28], a commercially available CFD software package. Like the models of Bollavaram and Sloan [19] and Davies et al. [20], the current study considers the solid hydrate plug to be porous. However, the current model also includes the additional resistances of the kinetics of dissociation and the heat conduction through the wall of the pipe. Furthermore, the current study solves the 2D partial differential equations of heat/mass/momentum using a fully coupled solver whereas the previous works [19,20] computed the pressure, velocity, and temperature profiles sequentially.

2. Theory

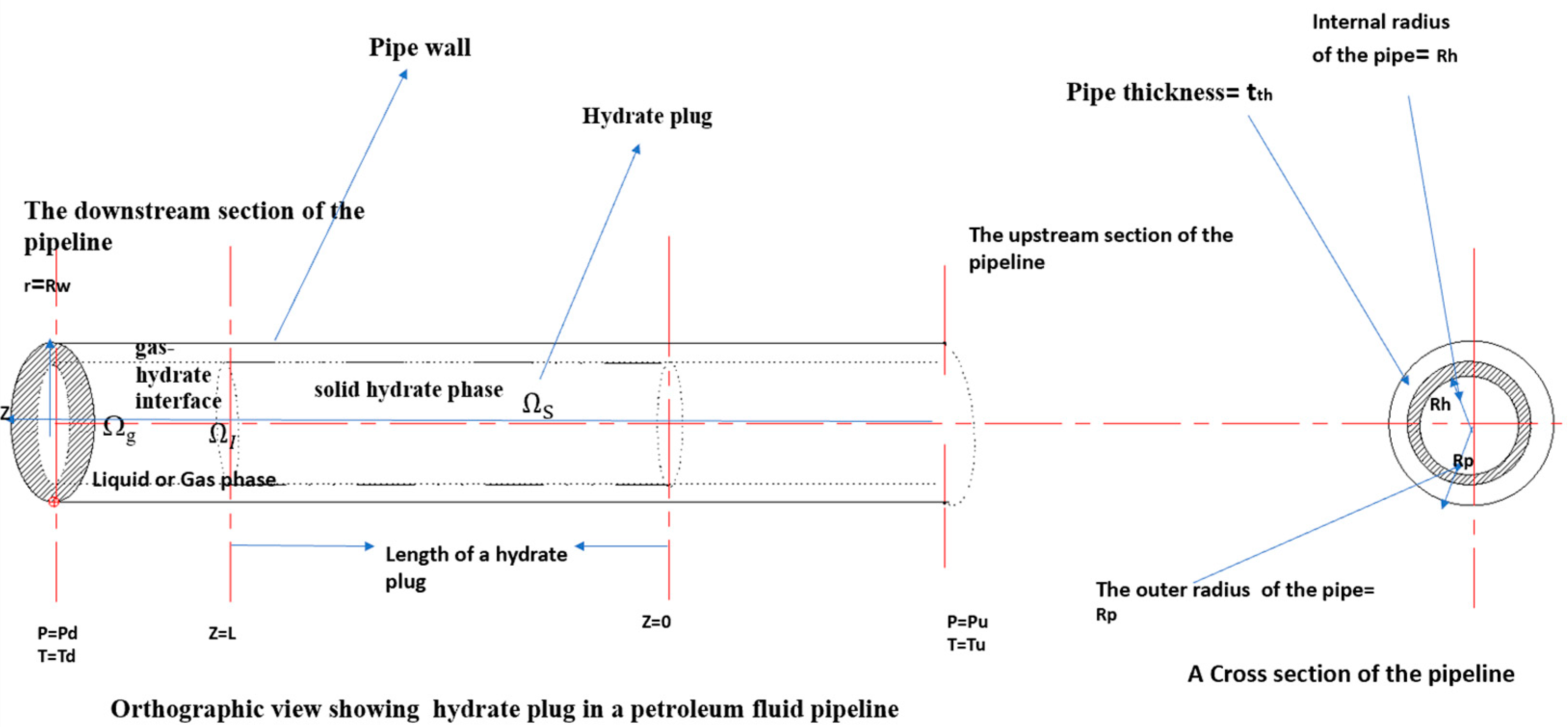
This section presents a 2D axisymmetric model for the dissociation of a gas hydrate plug in a natural gas pipeline. Figure 1 shows a schematic of a dissociating hydrate plug in a gas pipeline. In Figure 1, the region containing the solid gas hydrate is denoted as Ω_h, the region containing the solid pipeline wall is denoted as ${\Omega }_{wall}$, the region that forms the interface between the hydrate phase and the gas phase is denoted as Ω_I and the region downstream of the hydrate plug is denoted as Ω_g.

At t = 0, a region of the pipeline of length L is filled with a porous gas hydrate plug. It is also assumed that there is no free liquid water present before dissociation begins. Hydrate dissociation can proceed by either single-sided or double-sided depressurization and the dissociation will result in a moving boundary problem. At the dissociating hydrate interface, it will be assumed that the hydrate surface temperature is equal to the three-phase equilibrium temperature at the downstream pressure. Furthermore, radiative effects, viscous dissipation and the work done by pressure changes are assumed to be negligible.

The model will compute the relevant temperature, pressure and phase fraction profiles by solving the coupled continuity, heat transfer, momentum transfer and hydrate dissociation kinetic equations. The equations will be solved using COMSOL (Version 6.2) [28], which is a commercially available finite element method (FEM) solver. In the following sections, the equations for continuity, momentum transfer, heat transfer and hydrate dissociation kinetics will be presented, for each of the domains.

2.1. Continuity Equation

The continuity equation describes the conservation of mass within a given region. Within the hydrate region, the hydrate plug has a finite porosity and permeability, which is assumed to remain constant with respect to both time and position. As noted by Bollavaram and Sloan [19], the single-sided depressurization of a sufficiently porous plug can result in gas flow through the plug. Even though gas may be able to flow through the plug it is assumed that free water can only be liberated at the hydrate–gas interface. Hence, there is no need to explicitly write a continuity equation for water flow within the hydrate. Within the porous solid hydrate, the conservation of mass equation for compressible gas flow can be written as follows:

$$\frac{\partial \phi {\rho }_g}{\partial t}+\nabla ·\left({\rho }_g\mathit{u}\right)=Q_g \left(r,z\right)\in {\Omega }_h$$

(1)

where u is the fluid velocity vector, ${\rho }_g$ is the gas density and ${\mathrm{Q}}_{\mathrm{g}}$is the volumetric flow rate of gas that is evolved from the dissociating hydrate. The volumetric flow rate of gas evolved from the dissociating hydrate is computed with the hydrate dissociation kinetic model of Clarke and Bishnoi [29], which will be detailed in a later section. The gas density is computed with the Peng Robinson Equation of State [30].

At the dissociating hydrate surface, it is assumed that the evolved gas ‘blows’ the water away from the hydrate, and that the pressure gradient subsequently carries the gas and the water away from the hydrate. As noted earlier, this assumption was also invoked by Jamaluddin et al. [17] and by Ullerich et al. [16]. For the sake of simplicity, it is assumed that the flow characteristics in this region can be approximated as a single-phase gas. In future works, the presence of additional fluids (oils and non-aqueous liquids) and solids may be considered. In such cases it will be necessary to perform a rigorous multi-phase flow simulation in this region; however, in the current work, the continuity equation in this region is simply the following:

$$\frac{\partial {\rho }_g}{\partial t}+\nabla ·\left({\rho }_g\mathit{u}\right)=Q_g \left(r,z\right)\in {\Omega }_G$$

(2)

In the initial state, the gas velocity is zero since it is assumed that there is no pressure gradient along the length of the hydrate plug.

2.2. Momentum Conservation for the Gas Flowing through the Hydrate Plug

During dissociation by depressurization, gas can flow through the porous hydrate plug if a pressure gradient exists. It is assumed that radial pressure gradients are negligible compared to the axial pressure gradient. In the model of Bollavaram and Sloan [19] it was assumed that the gas flow through the porous hydrate plug was slow enough as to obey Darcy’s law. However, in the current study this assumption is relaxed and the full Brinkman equation [31] will instead be used to describe the gas flow within the porous hydrate plug:

$$\frac{\rho }{\phi }\lceil \frac{\mathit{\partial }\mathit{u}}{\partial t}+\left(\frac{\left(\mathit{u}·\nabla \right)\mathit{u}}{\phi }\right)\rceil =\nabla ·\left[-P\mathit{I}+\mathit{K}\right]-\left(\frac{{\mu }_f}{k}+\beta \rho \left|\mathit{u}\right|+\frac{Q_m}{{\phi }^2}\right)\mathit{u} +\mathit{F} \left(r,z\right)\in {\Omega }_h$$

(3)

where F is the body force vector or external force on gas per unit volume, I is the identity matrix, ρ is the gas density, μ is the dynamic viscosity of the gas, $P$ is the pressure, $Q_m$ is a mass source per unit volume of the porous medium and K is the stress tensor, which is given by the following:

$$\mathit{K}=\mu \frac{1}{\phi }\left(\nabla \mathit{u}+{\left(\nabla \mathit{u}\right)}^T\right)-\frac{2}{3}\mu \frac{1}{\phi }$$

(4)

2.3. Momentum Conservation for the Free-Flowing Gas

As previously noted, the water and gas that are evolved from the dissociating hydrate are assumed to flow downstream due to the downstream pressure gradient. This assumption is consistent with the works of Ullerich et al. [16] and Jamaluddin et al. [17], who treated hydrate dissociation as an ablation problem. This assumption is also in contrast to what was done by Bollavaram and Sloan [19], who assumed that the evolved water forms a stagnant liquid layer surrounding the dissociating hydrate. In the current work, the result for the momentum balance for this region is as follows:

$$\rho \frac{\partial \mathit{u}}{\partial t} +\rho \left(\nabla ·\mathit{u}\right)\mathit{u}=[\nabla ·\mathit{K}]-\nabla P +\mathit{F} \left(r,z\right)\in {\Omega }_G$$

(5)

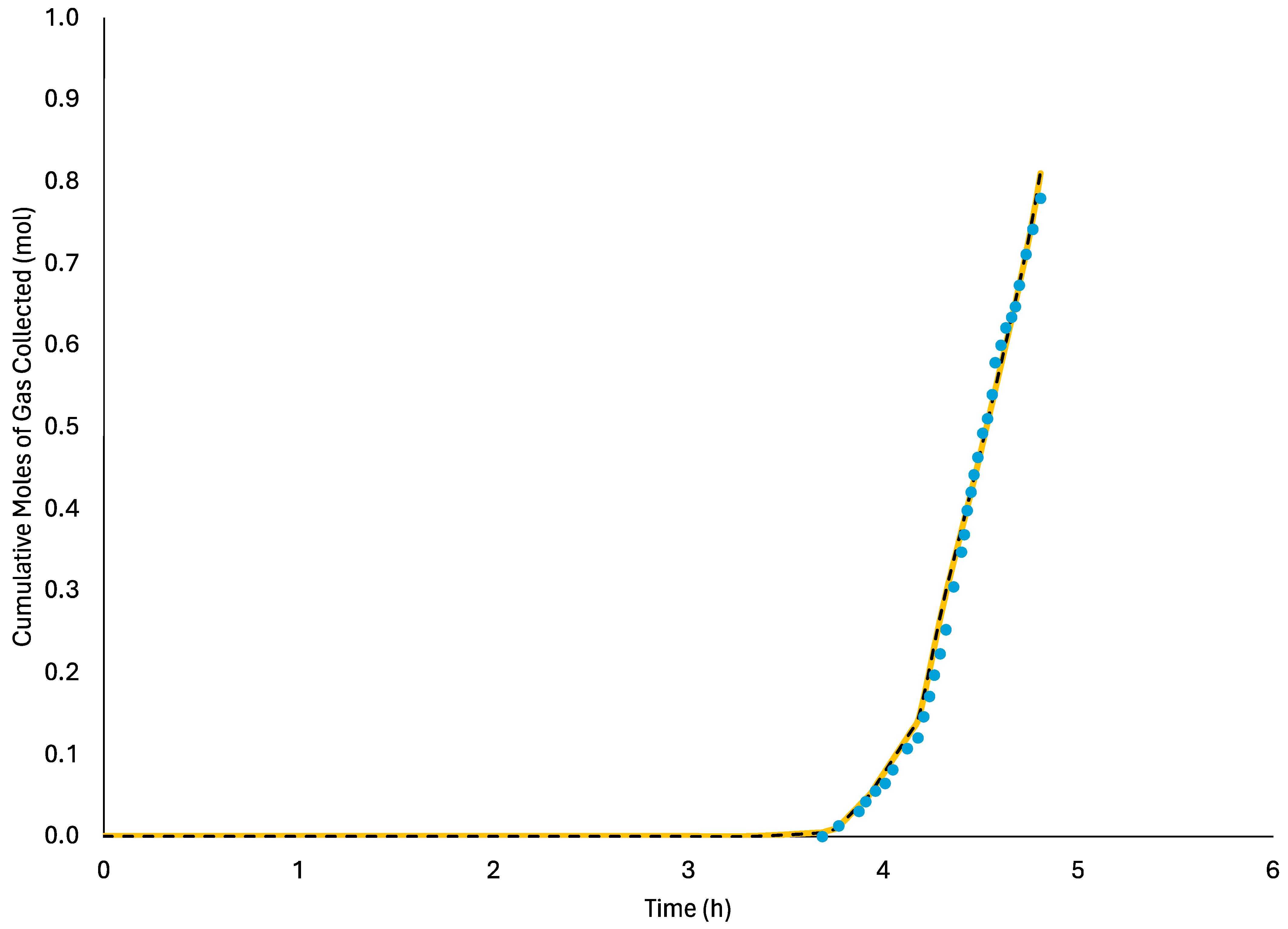
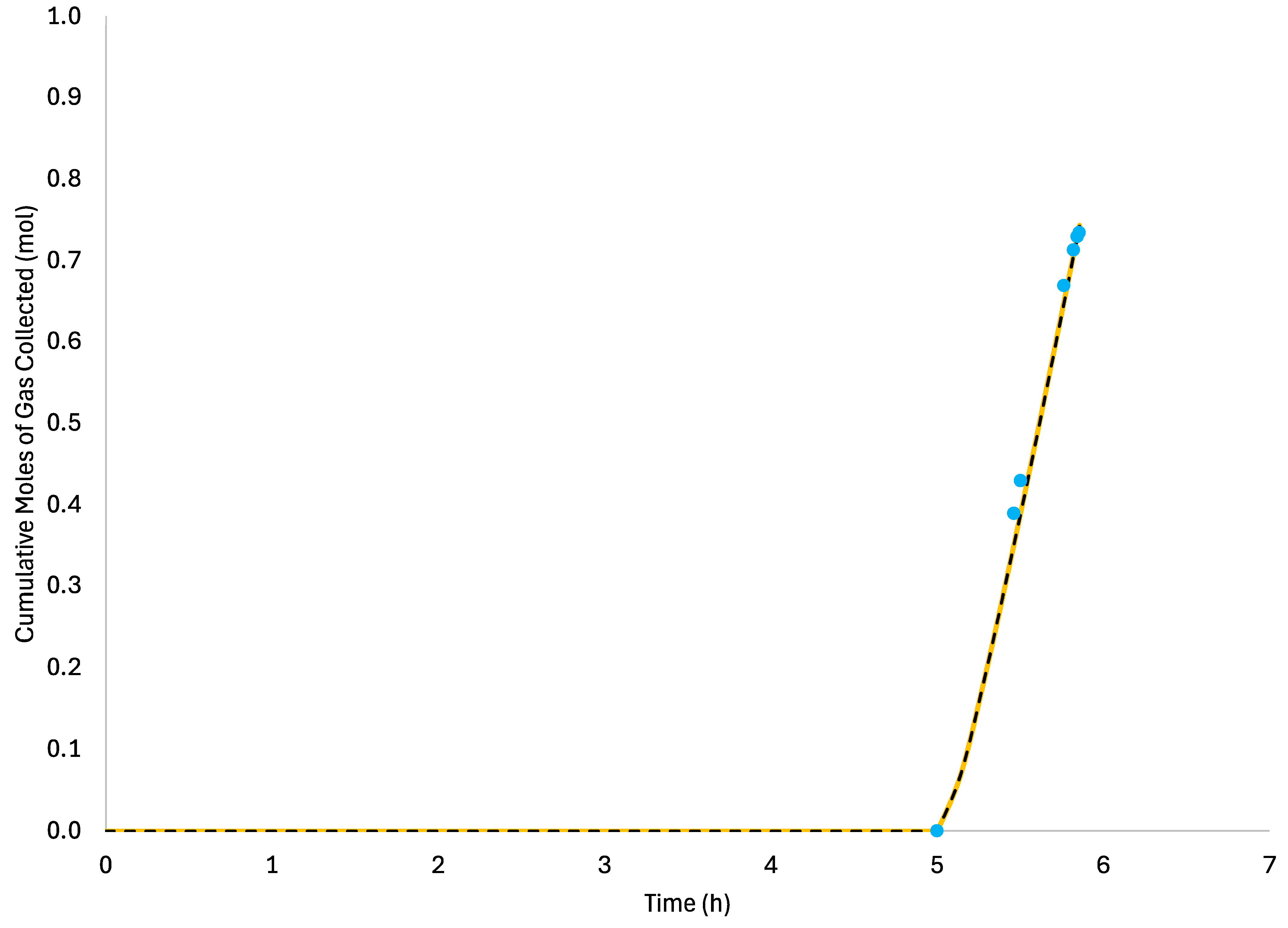
In this region, the initial gas velocity is taken to be zero since the pressure is assumed to be constant. For model verification, it will be assumed that the pressure is changed in step changes since the experimental pressure changes [19,20] are approximately step changes. It should be noted, however, that the current model can also consider other upstream and downstream pressure change functions by changing the appropriate pressure boundary conditions.

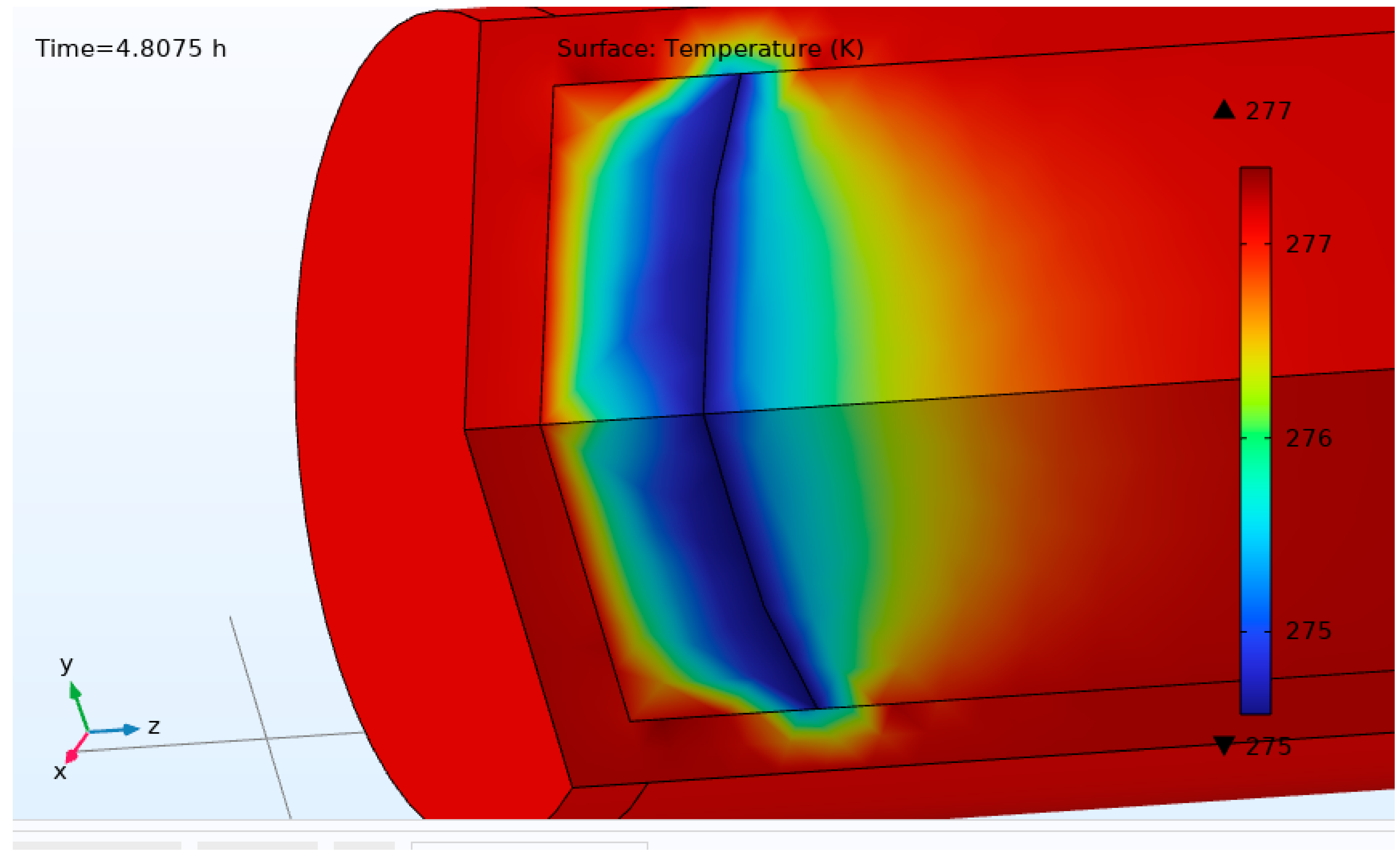
2.4. Energy Balance within the Solid Hydrate Plug

At t = 0, it is assumed that the temperature of the hydrate and its surroundings (i.e., the pipe wall) are uniform. Once the downstream pressure is reduced, the resulting pressure gradient gives rise to a temperature gradient. Within the hydrate there may be heat transfer between the pipe wall and the hydrate as well as between the hydrate and the flowing gas. As noted by Bollavaram and Sloan [19], the one-sided depressurization problem is effectively forced convection flow through a porous medium. Based on the experimental observations of Bollavaram and Sloan [19], this work assumes that local thermal equilibrium exists between the gas and the hydrate phase. As a result, the energy balance for the hydrate phase and for the gas phase reduces to the following single equation:

$${(\rho Cp)}_{eff}\frac{\partial T}{\partial t}+{(\rho Cp)}_{eff}\mathit{u}·\nabla T=\nabla ·\left(K_{eff} \nabla T\right) \left(r,z\right)\in {\Omega }_h$$

(6)

where

$${(\rho Cp)}_{eff}=\phi \left({\rho }_g{C}_{pg}\right)+\left(1-\phi \right)\left({\rho }_h{C}_{ph}\right)$$

(7)

$$K_{eff}=\left(1-\phi \right)\left(K_h\right)+\phi K_g$$

(8)

At the interface between the dissociating hydrate and the gas, the temperature of the hydrate is assumed to be equal to the three-phase equilibrium temperature, at the gas pressure.

2.5. Energy Balance within the Free-Flowing Gas Region

In the case of dissociation by depressurization, gas can flow downstream from the dissociating hydrate plug. This region was not considered by Bollavaram and Sloan [19] but it is being considered in this work because the temperature gradient at the interface may affect the rate of hydrate dissociation. In this region, the energy balance is given by Equation (9):

$$\left({\rho }_g{C}_{pg}\right)\frac{\partial T_g}{\partial t}+\left({\rho }_g{C}_{pg}\right)\mathit{u}·\nabla T_g=\nabla ·\left(K_g \nabla T_g\right) \left(r,z\right)\in {\Omega }_g$$

(9)

where the subscript g refers to the free-flowing gas, $C_{pg}$ is the specific heat capacity at a constant pressure of the gas, $K_g$ is the thermal conductivity of gas, ${\rho }_g$ is density of gas and $T_g$ is temperature of gas. At the interface between the dissociating hydrate and the free-flowing gas, the temperature of the gas is the same on both sides of the interface.

2.6. Energy Balance at the Dissociating Hydrate Interface

At the interface between the dissociating hydrate phase and the gas, the energy balance is given by the Stefan equation [32]:

$$K_h\frac{\partial {\mathit{T}}_{\mathit{h}}}{\partial \stackrel{\rightharpoonup }{\mathit{n}}}-K_g\frac{\partial {\mathit{T}}_{\mathit{g}}}{\partial \stackrel{\rightharpoonup }{\mathit{n}}}={\rho }_h{\lambda }_h\stackrel{\rightharpoonup }{\mathit{V}}·\stackrel{\rightharpoonup }{\mathit{n}} \left(r,z\right)\in {\Omega }_I t>0$$

(10)

where $\stackrel{\rightharpoonup }{\mathit{V}}$ is the velocity vector of the dissociating hydrate interface, $\stackrel{\rightharpoonup }{\mathit{n}}$ is the unit normal vector, K is the thermal conductivity, T is the temperature, λ is the heat of dissociation and the subscripts h and g represent the hydrate and gas phases, respectively. When Equation (10) is used in conjunction with Equations (1)–(9) it becomes possible to track the location of the dissociating hydrate interface, as a function of time.

To account for the kinetics of hydrate dissociation at the interface, the work of Jamaluddin et al. [1] will be generalized to a 2D hydrate. The rate of hydrate dissociation is given by the model of Kim et al. [23]:

$$-{\left(\frac{dn}{dt}\right)}_p=A{{\displaystyle \sum }}_j{K}_{d,j} {\left(f_{eq}-f_g\right)}_j$$

(11)

where A is the surface area of the dissociating hydrate, K_d is the hydrate dissociation rate constant, f is the fugacity and the subscripts eq, g and j refer to the three-phase equilibrium condition, the gas phase and component j, respectively. In the current work, the model of Kim et al. [23] is chosen due to the availability of rate constants for a relatively large number of compounds and due to the driving force being expressed in terms of quantities that are easily computed. As noted by Kim et al. [23] and by Clarke and Bishnoi [29], the rate constants for hydrate dissociation follow an Arrhenius relationship, as given in Equation (13):

$$K_d=K_o{e}^{-\left(\frac{E}{R{T}_S}\right)}$$

(12)

where K_o is the intrinsic rate constant of hydrate dissociation, E is the activation energy of hydrate dissociation and R is the universal gas constant. In the current study, only hydrate dissociation at temperatures above 273.15 K will be studied since intrinsic rate constants and activation energies are currently only available at those conditions.

To relate the molar rate of hydrate dissociation to the energy balance at the hydrate–gas interface, Jamaluddin et al. [17] performed a mass balance around the 1D dissociating hydrate surface. When generalized to a 2D hydrate plug, the mass balance of Jamaluddin et al. [17] becomes the following:

$$-\left(\frac{dn}{dt}\right)=A_{geo}{\rho }_h\stackrel{\rightharpoonup }{\mathit{V}}·\stackrel{\rightharpoonup }{\mathit{n}}$$

(13)

where A_geo is the geometric area of the dissociating hydrate plug. By combining Equations (13), (11) and (10), the Stefan boundary condition can be re-written in terms of the hydrate dissociation rate parameters:

$$k_h\frac{\partial {\mathit{T}}_{\mathit{h}}}{\partial \stackrel{\rightharpoonup }{\mathit{n}}}-k_g\frac{\partial {\mathit{T}}_{\mathit{g}}}{\partial \stackrel{\rightharpoonup }{\mathit{n}}}=\psi {\lambda }_h{{\displaystyle \sum }}_j{K}_{d,j} {\left(f_{eq}-f_g\right)}_j \left(r,z\right)\in {\Omega }_I t>0$$

(14)

where the surface roughness, $\psi$, is an adjustable parameter which is defined as follows:

$$\psi =\frac{A}{A_{geo}}$$

(15)

2.7. Energy Conservation within the Pipe Wall

In the experimental model of Bollavaram and Sloan [19], heat conduction through the pipeline wall was not considered. In the current work, this additional resistance is considered to avoid the potential for encountering temperature discontinuities at the interface between the hydrate and the pipe inner wall. The energy balance within the pipe is given by the following equation:

$${\rho }_{wall}{C}_{p_{wall}}\frac{\partial T_{wall}}{\partial t}=\nabla ·\left(k_{wall}\nabla T_{wall}\right) \left(r,z\right)\in {\Omega }_{wall}$$

(16)

At the interface between the hydrate and the inner pipe wall, the temperature on both sides of the interface must be equal. Similarly, at the interface between the inner pipe wall and the free gas phase, the temperature also must be equal on both sides of the interface. The temperature boundary condition on the outer pipe wall can be set to either a constant temperature, a time varying temperature or a constant heat flux, depending on the scenario under consideration.

3. Results

3.1. Verification and Validation of the Numerical Method

To verify the capability of the new numerical model, the mesh dependency and convergence criterion were first examined. For the verification study, the kinetics of hydrate dissociation were not considered, since the introduction of hydrate dissociation kinetics introduces an adjustable parameter (i.e., the surface roughness). In other words, the boundary condition at the dissociating hydrate interface was taken to be Equation (10) rather than Equation (14).

The model was used to correlate the experimental data of Bollavaram and Sloan [19] for the dissociation of an sI methane hydrate plug. Briefly, Bollavaram and Sloan [19] formed a methane hydrate plug in a horizontal cylindrical pressure vessel (1” diameter, 36” length). The cell was immersed in a temperature bath, which kept the outer surface of the cell at 277.15 K. The early stages of the depressurization occurred via single-step depressurization whereas double-sided depressurization occurred in the later stages of the experiment, after the pressure gradient had equilibrated. In the very final stage of their experiment [19], the downstream pressure was such that the surface temperature of the dissociating hydrate was below the freezing point of water. As previously noted, a limitation of the current work is that dissociation rate constants are only available for temperatures above the freezing point of water. Hence, this work will not examine the model’s ability to model hydrate dissociation at temperatures below 273.15 K. This limitation may be addressed in a future work once the appropriate rate constants become available. The model parameters are given in

Table 1. Parameter values used in model verification.

Parameter	Value	Source
The heat of dissociation for sI (λh)	460.24 (kJ/kg)	[21]
Porosity (φ)	0.5	[21]
Permeability (k)	0.1 (mD)	[18]
Thermal conductivity of methane hydrate (Kh)	0.68 (W/mK)	[33]
Thermal conductivity of water (Kw)	0.55 W/(mK)	[16]
Heat capacity of methane hydrate (Kh)	2510.4 J/(kgK)	[16]
Heat capacity of water (Kw)	4200 J/(kgK)	[16]
Density of methane hydrate (ρh)	914 (kg/m3)	[16]
Density of water at 277.15 K (ρw)	1000 kg/m3	[16]

.

In the verification stage, the effect of both the mesh density and the convergence criterion were examined. To quantify these effects, the root mean square of the error (RMSE) between the experimental data [19] and the model predictions were computed. In addition, since it was not known a priori if the convergence criterion and the mesh density could be varied independently, a full factorial design was used for the study. For the mesh density, the levels were coarse, fine and extra-fine whereas for the convergence criterion, values of 10⁻², 10⁻⁴ and 10⁻⁶ were used. The RMSEs for the simulations are given in

Table 2. Results of the model verification study.

Convergence Criterion Value	Mesh Density	RMSE (%)
10−2	Coarse	14.43
10−2	Fine	9.91
10−4	Extra-Fine	6.4
10−4	Coarse	10.11
10−4	Fine	9.03
10−4	Extra-Fine	6.04
10−6	Coarse	8.68
10−6	Fine	8.34
10−6	Extra-Fine	5.94

. Figure 2 and Figure 3 present a plot of moles versus time for one of the runs as well as the temperature profile at the last time step, respectively.

The results in Table 2 show that when the convergence criterion value is held constant, the use of an extra-fine mesh has a noticeable improvement compared to when a coarse mesh or fine mesh are used. On the other hand, decreasing the convergence criterion from 10⁻⁴ to 10⁻⁶ for the fine and extra-fine mesh only led to a small improvement in the RMSE; however, the run times increased by up to 21%. Thus, an extra-fine mesh with a convergence criterion of 10⁻⁴ was used for all subsequent simulations.

In Figure 2, it is seen that the model correlates the experimental data [19] with sufficient accuracy. The change in slope that is seen at roughly 4.3 h is due to the downstream pressure being changed [19]. Bollavaram and Sloan [19] noted that the experimental data [19] were not able to account for all of the gas that was consumed during hydrate formation, due to difficulties with the experimental operation. Additionally, Bollavaram and Sloan [19] noted that tetradecane was used as a pore filling agent; however, they were not able to say if the presence of the tetradecane affected any of the hydrate’s thermophysical properties. Thus, given these uncertainties, an RMSE of 6.04% is acceptable.

Figure 3 shows the corresponding temperature profile of the dissociating methane hydrate towards the end of the experiment. It can be seen in Figure 3 that the model is able to predict curvature at the interface. The small amount of interface curvature can be explained by considering the conditions under investigation. As previously noted, the current work is limited to temperatures above 273.15 K. As a result, the rate of heat conduction from the pipe wall to the hydrate is relatively small. It is suspected that a larger temperature difference between the hydrate and the pipe wall would lead to more significant interface curvature. Two other noteworthy points, in Figure 3, are related to the temperature gradients. In the hydrate phase, radial temperature gradients, at any axial location, are small. Similarly, the temperature gradient in the pipeline wall, adjacent to the hydrate–gas interface, is also relatively small. Thus, the assumptions made by Bollavaram and Sloan [19], regarding radial temperature variations, are likely acceptable for the specific case of an underwater pipeline (i.e., a constant outer wall temperature). In the case of a hydrate pipeline blockage in a land-based pipeline, the outer wall temperature may vary with time. In that case, it would be necessary to account for the thermal momentum of the pipeline wall. This will be investigated in a future study.

3.2. Effects of Including the Dissociation Kinetics in the Boundary Condition

To examine the effects of the dissociation kinetics, the experimental data of Bollavaram and Sloan [19] were correlated, for both sI and sII hydrate plug dissociation. However, the boundary condition at the hydrate–gas interface was changed from Equation (10) to Equation (14). The experimental data for the dissociation of an sI pipeline plug are the same data that were correlated in the previous section, whereas the sII hydrate dissociation data came from the dissociation of a hydrate plug formed from a synthetic natural gas. The composition of that synthetic gas is given in

Table 3. Composition of the synthetic natural gas used to form sII hydrates [19].

Gas	Composition (Mole %)
Methane	83.80
Ethane	7.01
Propane	1.60
i-Butane	0.05
n-Butane	0.02
Pentane	0.02
Hexane	0.003
Heptanes	0.003
Nitrogen	4.85
Carbon Dioxide	1.84

[20]. The experimental procedure with the sII hydrates was the same as with sI; however, the upstream and downstream pressures were different in the two sets of experiments [19].

The kinetic rate constants that were used with Equation (12) are given in

Table 4. Parameter values used in model verification.

Gas	E (kJ/mol)	Ko (mol m−2 Pa−1 s −1)	Source
Carbon dioxide in sI	102.88	1.83 × 108	[34]
Methane, in sI	81.0	3.60 × 104	[35]
Methane in sII	77.3	8.06 × 103	[29]
Ethane in sI and sII	104.0	2.56 × 108	[29]

. To correlate the experimental data for the dissociation of the sII hydrate plug [19] it was also necessary to make two additional assumptions. First, since the only rate constant available for CO₂ hydrate dissociation is for sI hydrates [34], it was assumed that the value for the sII dissociation rate constant is the same. Second, since rate constants are currently only available for methane, ethane and CO₂, it was assumed that these were the only gases to participate in the hydrate formation. The authors expect that propane and possibly i-butane would also participate in sII hydrate formation at the given conditions; however, hydrate dissociation rate constants for those components are not available.

In Equation (14) the surface roughness, φ, is unknown; thus, a sensitivity study was performed. For the surface roughness sensitivity study, there are no experimental measurements available in the literature to suggest which values to use; however, Jamaluddin et al. [17] suggested values of 1, 8, 64 and 100. The results of the sensitivity study are given in Figure 4 and Figure 5.

Table 5. RMSE versus surface roughness, for the dissociation of sI methane hydrates.

Surface Roughness	RMSE (%)
1	5.93
8	5.95
64	5.97
100	6.02

and

Table 6. RMSE versus surface roughness, for the dissociation of sII natural gas hydrates.

Surface Roughness	RMSE (%)
1	5.64
8	5.65
64	5.65
100	5.79

also present the statistical summary of the surface roughness sensitivity study. Since the results are almost completely overlapping, Figure 4 only shows the results with surface roughness values of one and one hundred. The two figures and the two tables show that, at the given experimental conditions, the model is relatively insensitive to the surface roughness; in other words, the process is heat-transfer controlled. It is believed that the insensitivity to the value of the surface roughness is due to the relatively small surface area per unit volume of a solid hydrate plug. Based on the cell dimensions, the plugs formed by Bollavaram and Sloan [19] would have had a surface area per unit volume on the order of 10¹ m²/m³. By contrast, in the hydrate dissociation experiments of Clarke and Bishnoi [29,33] hydrates were in the form of discrete particles and the measured hydrate surface area per unit volume was on the order of 10³ m²/m³. Hence, it comes as little surprise that the effect of surface area is less significant for a hydrate plug than it is for discrete hydrate particles.

In their work, Jamaluddin et al. [17] concluded that hydrate dissociation kinetics are the rate-limiting step whenever the value of (E/R) is greater than 7600 K. In all of the predictions in this work, the value of (E/R) was greater than 7600 K yet the processes are seen to be controlled by heat transfer. This result is contrary to that which would have been expected from the results of Jamaluddin et al. [17]. It needs to be emphasized, however, that Jamaluddin et al. [17] did not take porosity into account. Thus, to shed more light on the discrepancies between the results of the current work and those of Jamaluddin et al. [17], a porosity sensitivity study was also performed.

The results of the porosity sensitivity study are presented in

Table 7. RMSE versus porosity for surface roughness values of one and one hundred, for the dissociation of sI methane hydrates. An upward pointing arrow (↑) means that the model is over-predicting the data whereas a downward pointing arrow (↓) indicates that the model is under-predicting the data.

Porosity (%)	RMSE, at φ = 1 (%)	RMSE, at φ = 100 (%)
25	10.40 ↓	10.57 ↓
50	5.93 ↑	6.02 ↑
75	9.44 ↑	9.42 ↑

and

Table 8. RMSE versus porosity for surface roughness values of one and one hundred, for the dissociation of sII natural gas hydrates. An upward pointing arrow (↑) means that the model is over-predicting the data whereas a downward pointing arrow (↓) indicates that the model is under-predicting the data.

Porosity (%)	RMSE, at φ = 1 (%)	RMSE, at φ = 100 (%)
25	37.72 ↓	37.74 ↓
50	5.64 ↑	5.79 ↑
75	27.92 ↑	27.93 ↑

for sI and sII hydrates, respectively. In both cases, the predictions of the cumulative gas consumptions are seen to be strongly dependent upon the value of the porosity. For all of the chosen values of porosity, the prediction of the dissociation of sII hydrates shows noticeably higher RMSE values than the sI hydrates. This may be an indication that the assumptions made regarding the values of sII rate constants for CO₂, C₃H₈, and possibly i-C₄H₁₀, were not accurate. Comparing the results in Table 7 and Table 8 with the results in Table 5 and Table 6 reveals that the model is much more sensitive to the value of the porosity than it is to the kinetics of hydrate dissociation; in other words, the dissociation of these hydrate plugs [19] was heat-transfer limited at the experimental conditions.

As previously noted, this observation runs contrary to Jamaluddin’s [17] assertion that dissociation switches to kinetic control when (E/R) > 7600 K; this indicates that the geometry and physical properties of a hydrate plug must be taken into consideration to ascertain whether dissociation will be heat-transfer controlled or kinetics controlled. Thus, given that the model is much more sensitive to the value of the porosity than it is to the value of the hydrate dissociation rate constant, and given that the porosity of a hydrate plug is likely unknown, it is concluded that accounting for the hydrate dissociation kinetics need only be prioritized if all of the thermophysical properties of the hydrate pipeline plug are accurately known.

It may be the case that the hydrate dissociation kinetics become significant when hydrates are formed in the presence of condensable hydrocarbons or when plug dissociation is aided by the injection of a hydrate inhibitor. However, without supporting experimental observations these remarks are only speculative. It is the authors’ hope that this work can be a motivation for future experimental studies on hydrate pipeline plug dissociation and on hydrate dissociation kinetics.

4. Conclusions

In this work, COMSOL (Version 6.2) [28] was used to model the 2D axisymmetric dissociation of a gas hydrate pipeline plug. The focus of the study was both to evaluate the capability of COMSOL (Version 6.2) [28] for solving the 2D moving boundary problem as well as to provide insight into the relative importance of gas hydrate dissociation kinetics in such a problem. Given the limited conditions at which dissociation rate constants are available, the results for this study were only able to cover a limited range of operating conditions; specifically, hydrate dissociation rate constants are only available for temperatures above 273.15 K. Nonetheless, the results provide useful insights into modelling the dissociation of a hydrate pipeline plug. First, within the temperature and pressure range of this study, the modelling results are far more sensitive to the value of the porosity than they are to the rate of hydrate dissociation. Given this, the authors conclude that, at least when hydrates are formed only in the presence of non-condensable gases, the improvement that can be gained by including the dissociation kinetics is far less than what can be gained from having a more accurate knowledge of the hydrate’s thermophysical properties. Second, when the driving force for hydrate dissociation is not large, the radial temperature gradient in the hydrate phase is seen to be small. Thus, the much simpler model of Bollavaram and Sloan [19] will be sufficiently accurate. It is important to note, though, that there may still be situations where the inclusion of the dissociation kinetics term is warranted. These situations could include when the hydrate plug is formed in an oil pipeline or when hydrate dissociation is aided by the addition of a hydrate inhibitor.