Calculation Method of Three-Phase Productivity of Horizontal Well in Water-Bearing Condensate Gas Reservoir
Abstract
1. Introduction
2. Methodology
2.1. Basic Assumptions
- (1)
- The reservoir is horizontal and with uniform thickness;
- (2)
- The gravity force and the capillary force are neglected;
- (3)
- The flow of reservoir fluids is assumed to be isothermal;
- (4)
- Gas and water are immiscible with each other; gas and oil are miscible with each other;
- (5)
- The horizontal well is producing at a constant mass flow rate at the surface condition.
2.2. Mathematical Modeling of Three-Phase Flow
2.2.1. Governing Equations
2.2.2. Constraint Conditions
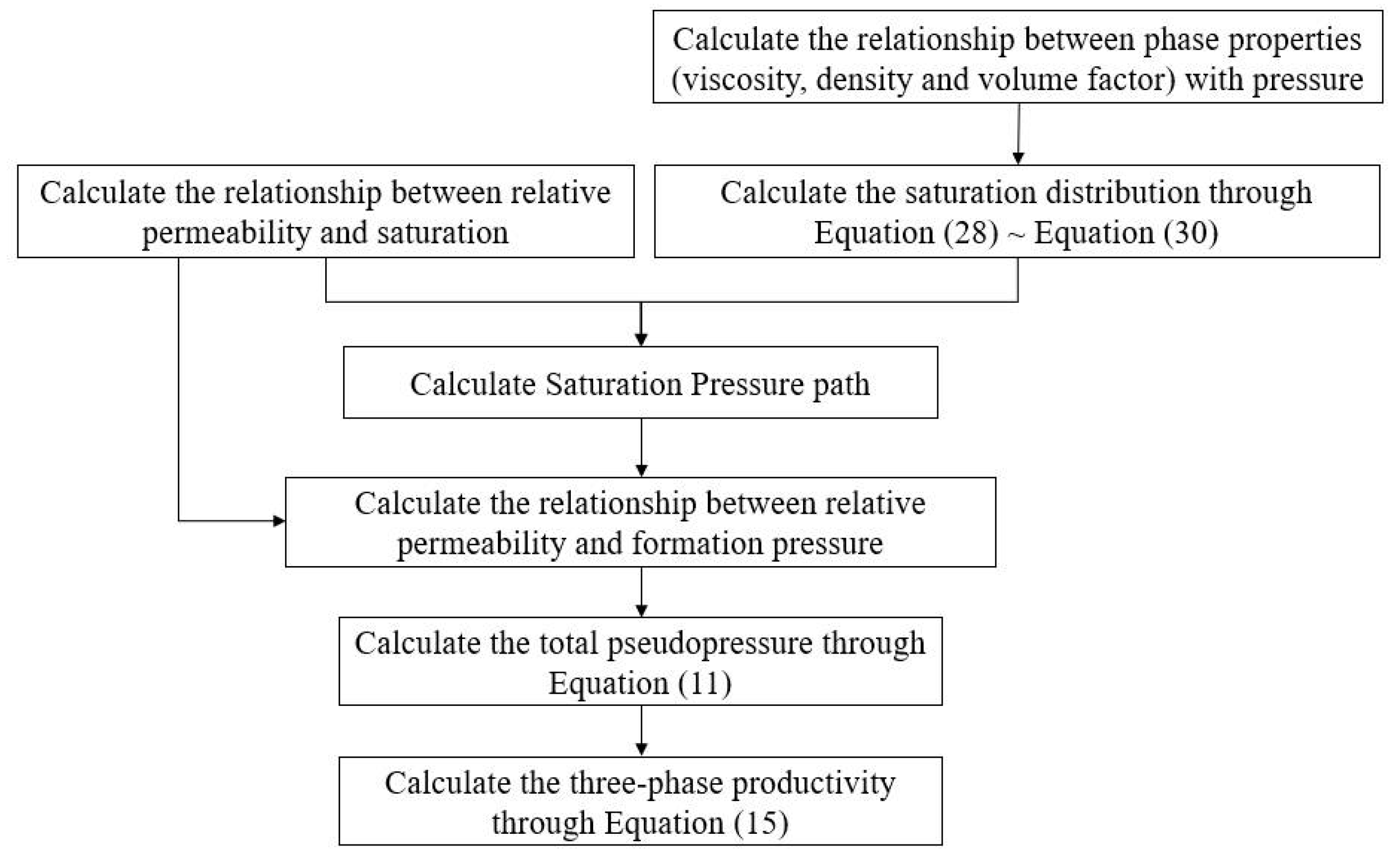
3. Model Solution
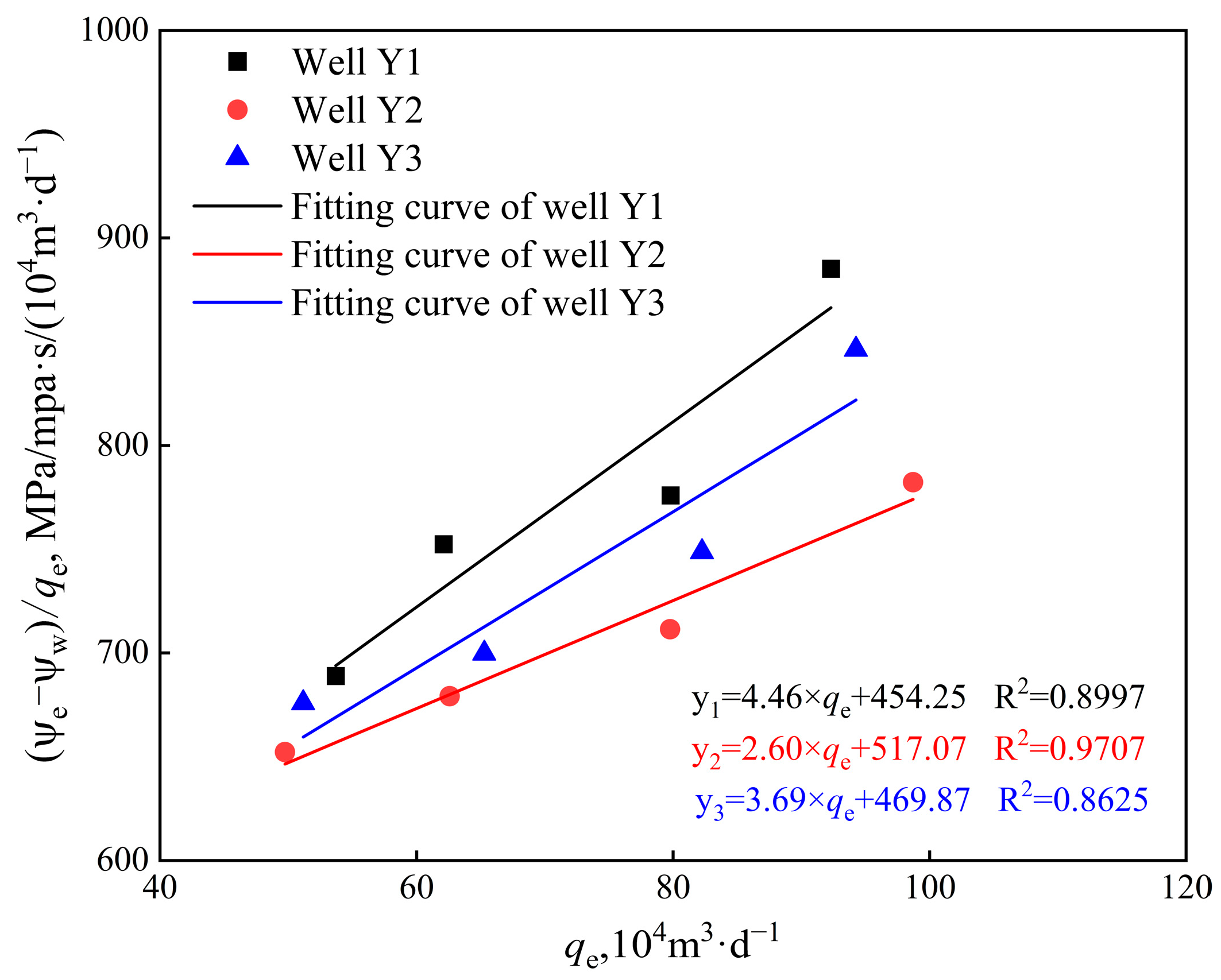
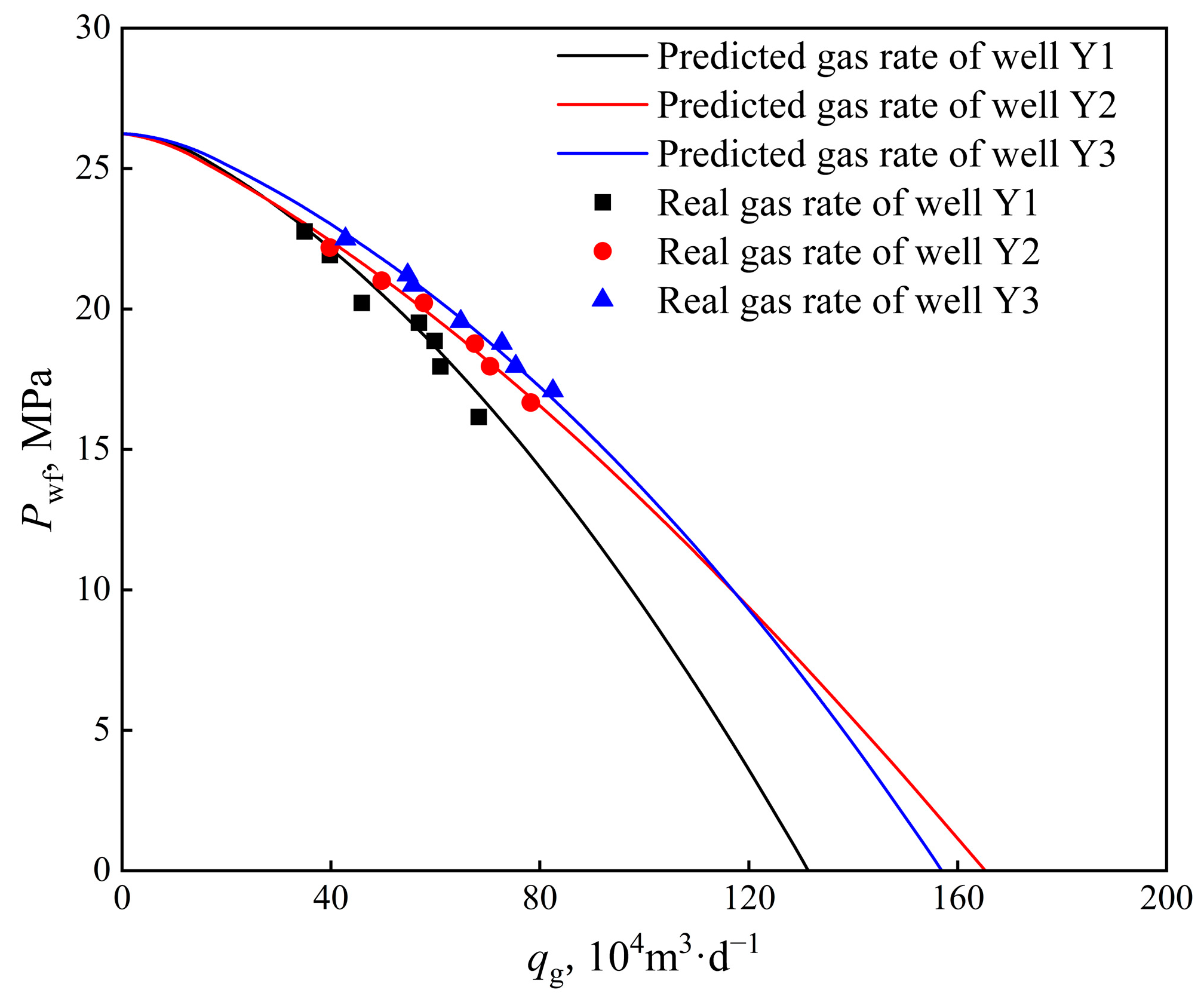
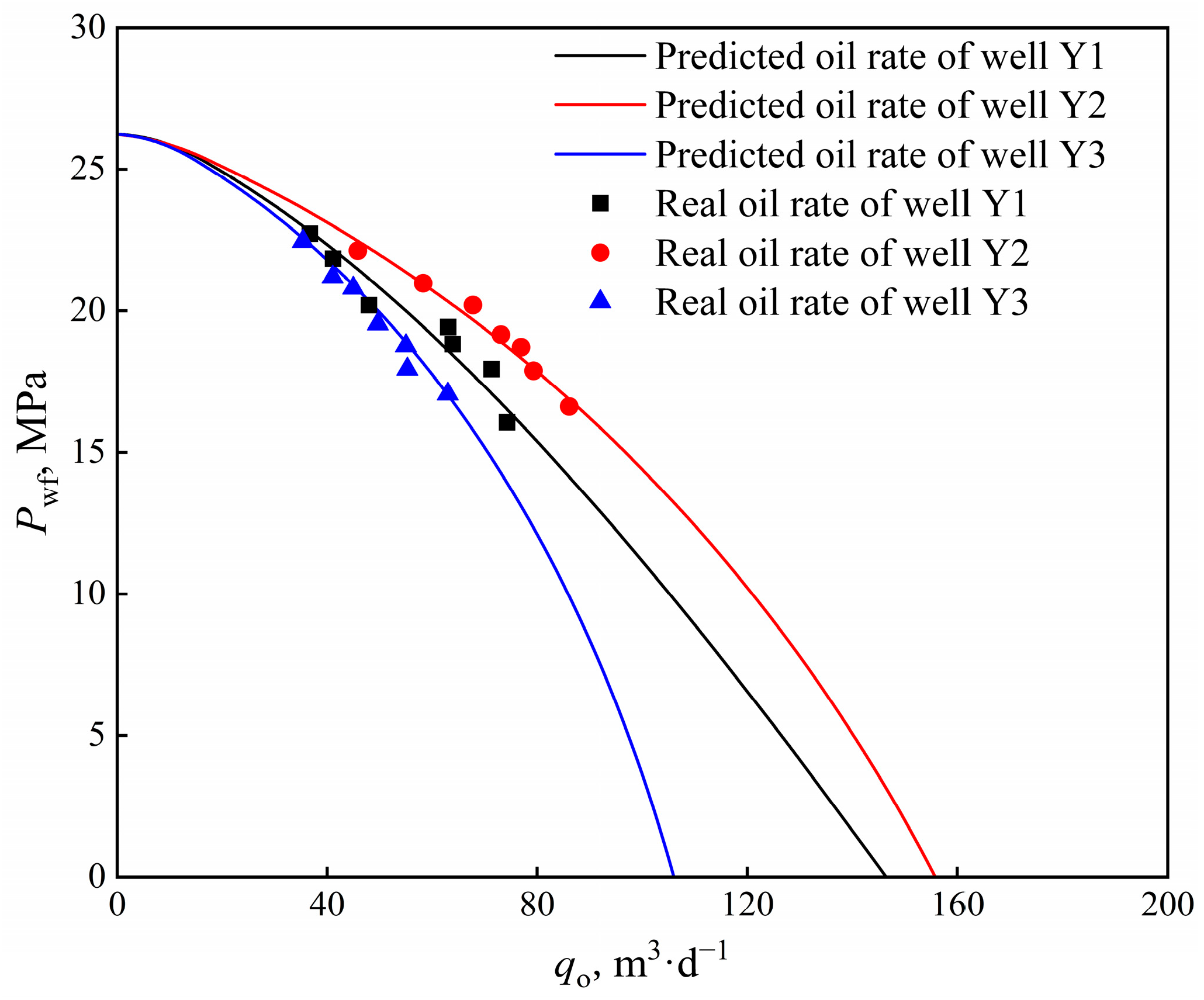
4. Case Validation and Discussion
5. Conclusions
- (1)
- In this paper, a three-phase productivity calculation model for horizontal wells in water-bearing condensate gas reservoirs is proposed, which considers the non-Darcy effect. The total pseudopressure and the equivalent total flow are defined to solve the multiphase nonlinear problem in the oil–gas–water three-phase control flow equation, and to establish a three-phase productivity equation.
- (2)
- The key to the productivity model proposed in this paper is to solve the total pseudopressure. Based on the relationship between the saturation and pressure, combined with the relative permeability curve, the relationship between the saturation and pressure is established, and the total pseudopressure function is solved using the numerical integration method. Combined with the equivalent total flow, the productivity equation is determined by regression.
- (3)
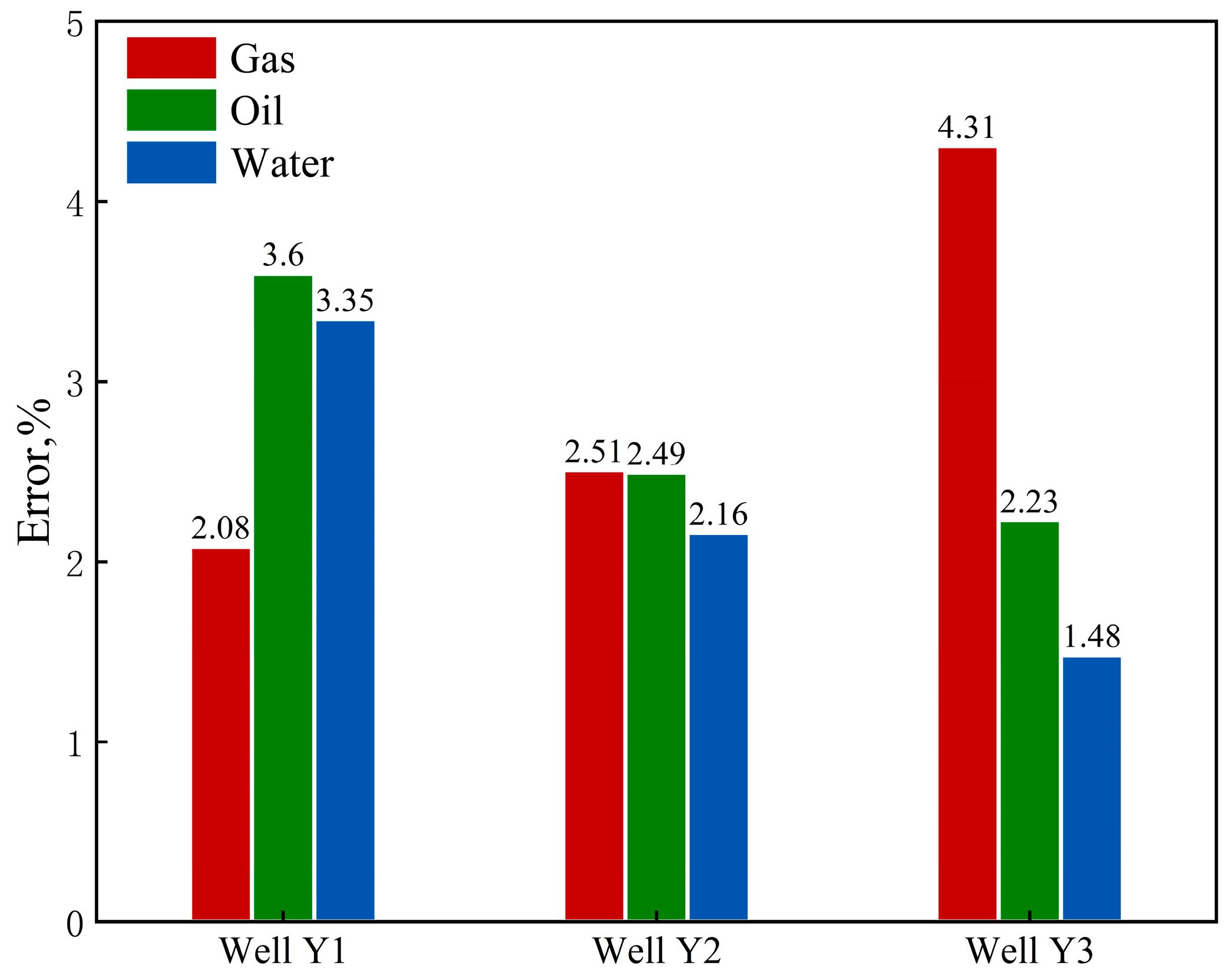
- The field cases and error analysis of three horizontal wells in a condensate gas reservoir show that the proposed model can fit the actual production data better. The results show that except for the gas production error of Well Y3, the average error of the production data of the other gas wells is below 4%. The fitting effect of Well Y2 is better than that of the other two horizontal wells, and the average error of the oil, gas, and water phases is below 3%.
- (4)
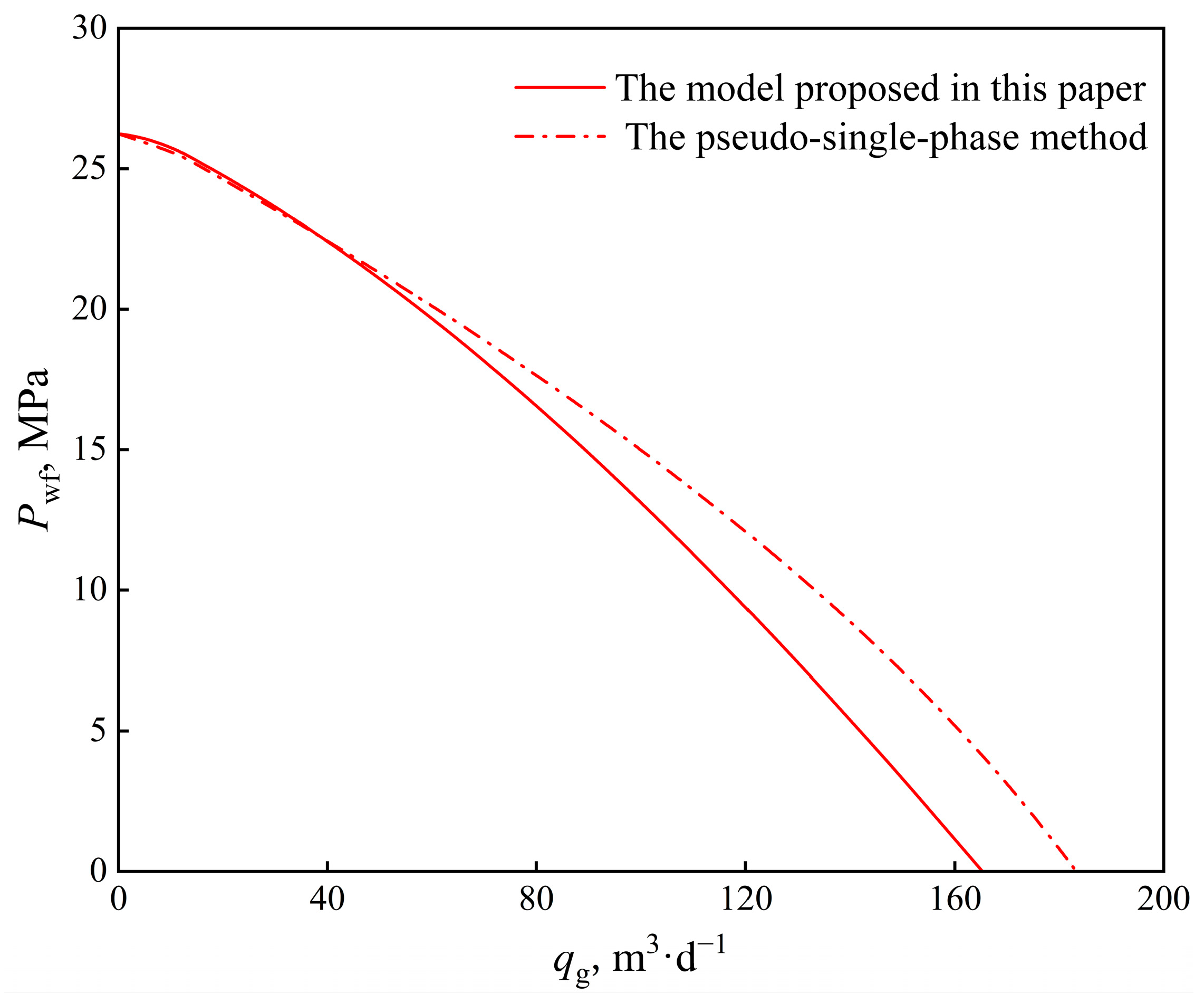
- The pseudo-single-phase method has a large error when the pressure difference is large, and the three-phase flow production equation proposed in this paper can more accurately calculate the production capacity of horizontal wells in condensate reservoirs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Behmanesh, H.; Mattar, L.; Thompson, J.M.; Anderson, D.M.; Nakaska, D.W.; Clarkson, C.R. Treatment of Rate-Transient Analysis During Boundary-Dominated Flow. SPE J. 2018, 23, 1145–1165. [Google Scholar] [CrossRef]
- Ghahri, P.; Jamiolahmady, M.; Sohrabi, M. Gas condensate flow around deviated and horizontal wells. In Proceedings of the SPE Europec featured at EAGE Conference and Exhibition, Vienna, Austria, 23–27 May 2011. [Google Scholar]
- Abad, A.R.B.; Mousavi, S.; Mohamadian, N.; Wood, D.A.; Ghorbani, H.; Davoodi, S.; Alvar, M.A.; Shahbazi, K. Hybrid machine learning algorithms to predict condensate viscosity in the near wellbore regions of gas condensate reservoirs. J. Nat. Gas Sci. Eng. 2021, 95, 104210. [Google Scholar] [CrossRef]
- Afidick, D.; Kaczorowski, N.J.; Bette, S. Production performance of a retrograde gas reservoir: A case study of the Arun field. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Melbourne, Australia, 7–10 November 1994; SPE: Richardson, TX, USA, 1994; p. SPE-28749. [Google Scholar]
- Zhang, W.; Cui, Y.; Jiang, R.; Xu, J.; Qiao, X.; Jiang, Y.; Zhang, H.; Wang, X. Production performance analysis for horizontal wells in gas condensate reservoir using three-region model. J. Nat. Gas Sci. Eng. 2019, 61, 226–236. [Google Scholar] [CrossRef]
- Jun, J.; Kang, J.; Jeong, D.; Lee, H. An efficient approach for optimizing full field development plan using Monte-Carlo simulation coupled with genetic algorithm and new variable setting method for well placement applied to gas condensate field in Vietnam. Energy Explor. Exploit. 2017, 35, 75–102. [Google Scholar] [CrossRef]
- Saleh, A.M.; Stewart, G. Interpretation of gas condensate well tests with field examples. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992; SPE: Richardson, TX, USA, 1992; p. SPE-24719. [Google Scholar]
- Daungkaew, S.; Ross, F.; Gringarten, A.C. Well test analysis of condensate drop-out behavior in a North Sea len gas condensate reservoir. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002; p. 77548. [Google Scholar]
- Marhaendrajana, T.; Kaczorowski, N.J.; Blasingame, T.A. Analysis and interpretation of well test performance at Arun field, Indonesia. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999; SPE: Richardson, TX, USA, 1999; p. SPE-56487. [Google Scholar]
- Bonyadi, M.; Rahimpour, M.R.; Esmaeilzadeh, F. A new fast technique for calculation of gas condensate well productivity by using pseudopressure method. J. Nat. Gas Sci. Eng. 2012, 4, 35–43. [Google Scholar] [CrossRef]
- Dahim, S.; Taghavinejad, A.; Razghandi, M.; Rigi, H.R.; Moeini, K.; Jamshidi, S.; Sharifi, M. Pressure and rate transient modeling of multi fractured horizontal wells in shale gas condensate reservoirs. J. Pet. Sci. Eng. 2020, 185, 106566. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Al-Lamki, A.; Daungkaew, S.; Mott, R.; Whittle, T.M. Well test analysis in gas-condensate reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Fussell, D.D. Single-well performance predictions for gas condensate reservoirs. J. Pet. Technol. 1973, 25, 860–870. [Google Scholar] [CrossRef]
- Yin, F.; Cheng, S.; Liu, X.; Zhang, L.; Liu, H.; Bai, W.; Shi, D.; Wang, Y. Semianalytical Modeling for Multiphase Flow in a Fractured Low-Permeability Gas Condensate Reservoir. ACS Omega 2023, 8, 32892–32906. [Google Scholar] [CrossRef] [PubMed]
- Shaoul, J.R.; Park, J.; Boucher, A.; Tkachuk, I.; Veeken, C.; Salmi, S.; Bahri, K.; Rashdi, M.; Nazaruk, D. Evaluating the Performance of Horizontal Multi-Frac Wells in a Depleted Gas Condensate Reservoir in Sultanate of Oman. In Proceedings of the SPE International Hydraulic Fracturing Technology Conference and Exhibition, Muscat, Oman, 11–13 January 2022; SPE: Richardson, TX, USA, 2022; p. D031S013R004. [Google Scholar]
- Daneshfar, R.; Keivanimehr, F.; Mohammadi-Khanaposhtani, M.; Baghban, A. A neural computing strategy to estimate dew-point pressure of gas condensate reservoirs. Pet. Sci. Technol. 2020, 38, 706–712. [Google Scholar] [CrossRef]
- Bai, W.; Cheng, S.; Wang, Y.; Cai, D.; Guo, X.; Guo, Q. A transient production prediction method for tight condensate gas wells with multiphase flow. Pet. Explor. Dev. 2024, 51, 1–7. [Google Scholar] [CrossRef]
- Dehane, A.; Tiab, D.; Osisanya, S.O. Comparison of the performance of vertical and horizontal wells in gas-condensate reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000; SPE: Richardson, TX, USA, 2000; p. SPE-63164. [Google Scholar]
- Ertekin, T. Neuro-simulation analysis of pressure maintenance operations in gas condensate reservoirs. J. Pet. Sci. Eng. 2007, 58, 207–226. [Google Scholar]
- Kniazeff, V.J.; Naville, S.A. Two-phase flow of volatile hydrocarbons. Soc. Pet. Eng. J. 1965, 5, 37–44. [Google Scholar] [CrossRef]
- Mokhtari, R.; Varzandeh, F.; Rahimpour, M.R. Well productivity in an Iranian gas-condensate reservoir: A case study. J. Nat. Gas Sci. Eng. 2013, 14, 66–76. [Google Scholar] [CrossRef]
- Mott, R. Engineering calculations of gas-condensate-well productivity. SPE Reserv. Eval. Eng. 2003, 6, 298–306. [Google Scholar] [CrossRef]
- Muladi, A.; Pinczewski, W.V. Application of horizontal well in heterogeneity gas condensate reservoir. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 20–22 April 1999; SPE: Richardson, TX, USA, 1999; p. SPE-54351. [Google Scholar]
- Behmanesh, H.; Hamdi, H.; Clarkson, C.R. Production data analysis of tight gas condensate reservoirs. J. Nat. Gas Sci. Eng. 2015, 22, 22–34. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, H.; Gao, Y.; Feng, N.; Yu, H. Evaluation of Liquid Production and Water Injection Profiles of Horizontal Well by Pressure-Transient Analysis: Field Cases. Energy Fuels 2023, 37, 18890–18898. [Google Scholar] [CrossRef]
- Stewart, G. Wireline Formation Testing and Well Deliverability; PennWell: Tulsa, OK, USA, 2012. [Google Scholar]
- Zhang, H.; Lu, J.; Cao, W.; Sun, H. Usual productivity equation of gas well on various units of measurement. Well Test. 2017, 26, 1–7. [Google Scholar]
- Muskat, M. Some theoretical aspect s of cycling–Part 2: Retrograde condensation about well bores. Oil Gas J. 1950, 48, 53–55. [Google Scholar]
- Thompson, L.G.; Niu, J.G.; Reynoalds, A.C. Well testing for gas condensate reservoirs. In Proceedings of the SPE Asia Pacific Oil and Gas Conference, Singapore, 8–10 February 1993; p. SPE-25371. [Google Scholar]
- Liu, X.; Chen, H.; Chen, Z.; Yang, R.; Song, L.; Bai, M.; Qiu, P.; Zuo, M.; Li, B.; Yang, B.; et al. Study on characterization and distribution of four regions of tight sandstone condensate gas reservoirs in the depletion development process. Fuel 2024, 358, 130267. [Google Scholar] [CrossRef]
- Ghahri, P.; Jamiolahmadi, M.; Alatefi, E.; Wilkinson, D.; Sedighi Dehkordi, F.; Hamidi, H. A new and simple model for the prediction of horizontal well productivity in gas condensate reservoirs. Fuel 2018, 223, 431–450. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, X.; Gao, X.; Chen, P.; Guo, K. A Novel Method for the Quantitative Evaluation of Retrograde Condensate Pollution in Condensate Gas Reservoirs. Processes 2024, 12, 522. [Google Scholar] [CrossRef]
- Walsh, M.; Lake, L.W. A Generalized Approach to Primary Hydrocarbon Recovery; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Lal, R.R. Well Testing in Gas-Condensate Reservoirs. Master’s Thesis, Department of Petroleum Engineering of Stanford University, Stanford, CA, USA, 2003. [Google Scholar]
- Zhou, C.; Wu, X.; Li, H.; Lin, H.; Liu, X.; Cao, M. Optimization of methods for liquid loading prediction in deep condensate gas wells. J. Pet. Sci. Eng. 2016, 146, 71–80. [Google Scholar] [CrossRef]
- Li, J.; Zhao, G.; Jia, X.; Yuan, W. Integrated study of gas condensate reservoir characterization through pressure transient analysis. J. Nat. Gas Sci. Eng. 2017, 46, 160–171. [Google Scholar] [CrossRef]
- Liu, H.; Xie, B.; Xin, X.; Zhao, H.; Liu, Y. Investigation on the Extent of Retrograde Condensation of Qianshao Gas Condensate Reservoir Using PVT Experiments and Compositional Reservoir Simulation. Processes 2024, 12, 503. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, F.; Liang, B.; Cheng, S.; Wang, Y. Pressure Transient Analysis for the Fractured Gas Condensate Reservoir. Energies 2022, 15, 9442. [Google Scholar] [CrossRef]
- Fevang, O.; Whitson, C.H. Modeling gas-condensate well deliverability. SPE Reserv. Eng. 1996, 11, 221–230. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Original reservoir pressure Pe (MPa) | 26.2 |
| Reservoir thickness h (m) | 8.54 |
| Reservoir porosity Φ | 0.16 |
| Original formation permeability ki (10−3 μm2) | 39.7 |
| Reservoir temperature T (K) | 346 |
| Gas density under standard conditions ρgsc (kg/m3) | 0.76 |
| Oil density under standard conditions ρosc (kg/m3) | 728 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Chen, Y.; Xu, A.; He, J.; Luo, E.; Liu, Y.; Zeng, X.; Jiang, L. Calculation Method of Three-Phase Productivity of Horizontal Well in Water-Bearing Condensate Gas Reservoir. Energies 2024, 17, 2932. https://doi.org/10.3390/en17122932
Zhang Y, Chen Y, Xu A, He J, Luo E, Liu Y, Zeng X, Jiang L. Calculation Method of Three-Phase Productivity of Horizontal Well in Water-Bearing Condensate Gas Reservoir. Energies. 2024; 17(12):2932. https://doi.org/10.3390/en17122932
Chicago/Turabian StyleZhang, Yufeng, Yefei Chen, Anzhu Xu, Jun He, Erhui Luo, Yunyang Liu, Xing Zeng, and Luyang Jiang. 2024. "Calculation Method of Three-Phase Productivity of Horizontal Well in Water-Bearing Condensate Gas Reservoir" Energies 17, no. 12: 2932. https://doi.org/10.3390/en17122932
APA StyleZhang, Y., Chen, Y., Xu, A., He, J., Luo, E., Liu, Y., Zeng, X., & Jiang, L. (2024). Calculation Method of Three-Phase Productivity of Horizontal Well in Water-Bearing Condensate Gas Reservoir. Energies, 17(12), 2932. https://doi.org/10.3390/en17122932





