A Dynamic Tanks-in-Series Model for a High-Temperature PEM Fuel Cell
Abstract
1. Introduction
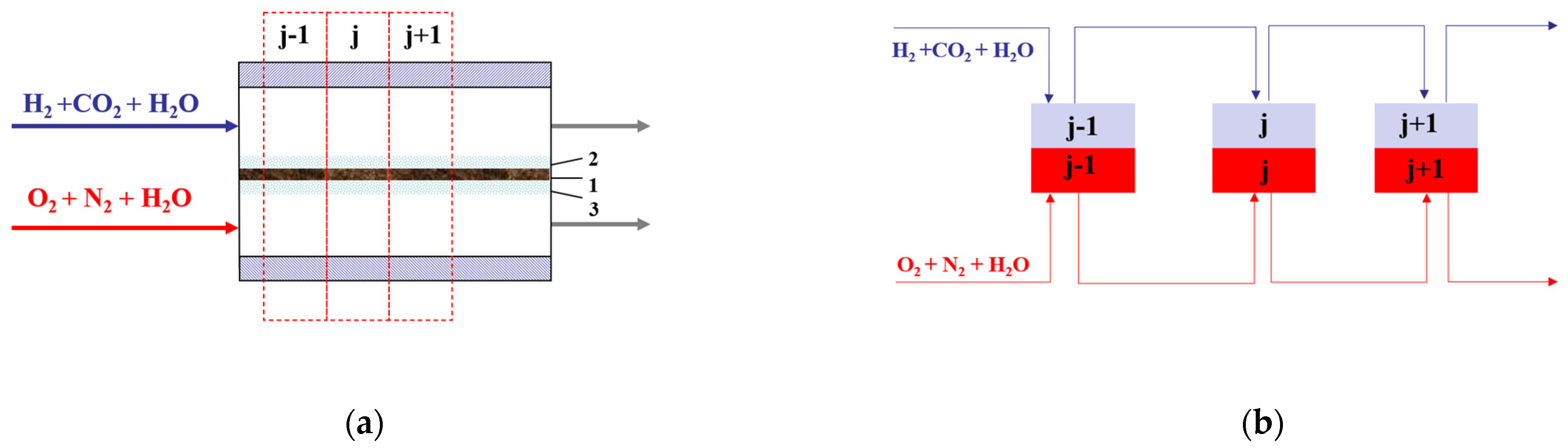
2. Tanks-in-Series Model for HT-PEMFC
- (i)
- There is complete mixing in a tank with a step change in variables from tank to tank;
- (ii)
- Anode electrochemical reaction occurs at the anode electrode/membrane interface;
- (iii)
- Cathode electrochemical reaction occurs at the cathode electrode/membrane interface;
- (iv)
- There is uniform gas flow distribution in the anode and cathode channels and there are pseudo-three-component reformate gas flows in the anode channels (H2 + CO2 + H2O);
- (v)
- There is a Chilton–Colburn analogy between heat and mass transfer.
2.1. Charge Balance
2.2. Electrode Current
2.3. Electrolyte Current
2.4. Electrochemical Reactions
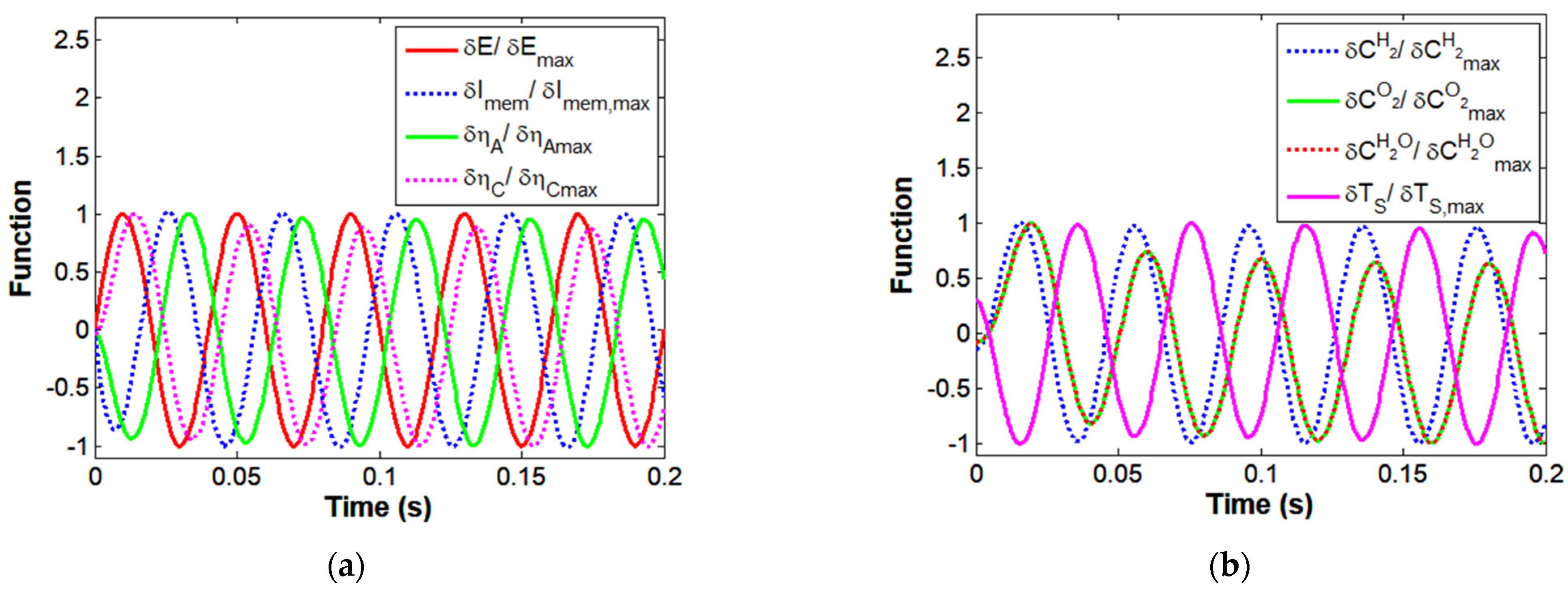
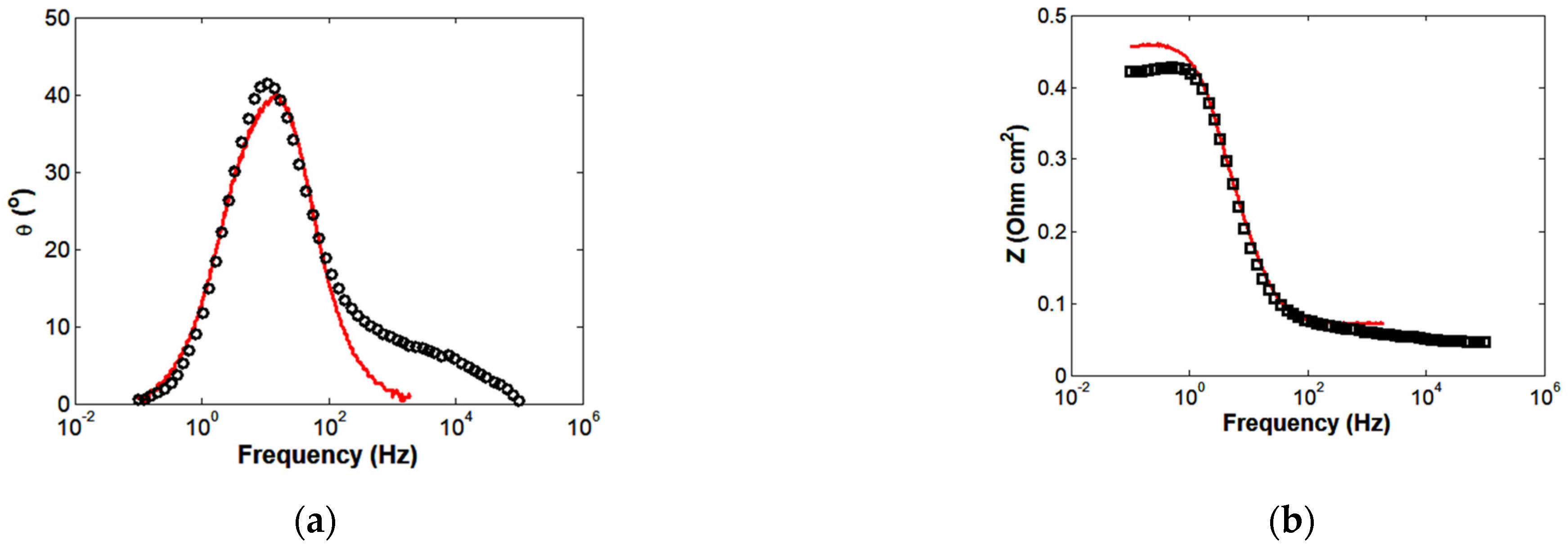
3. Electrochemical Impedance Model
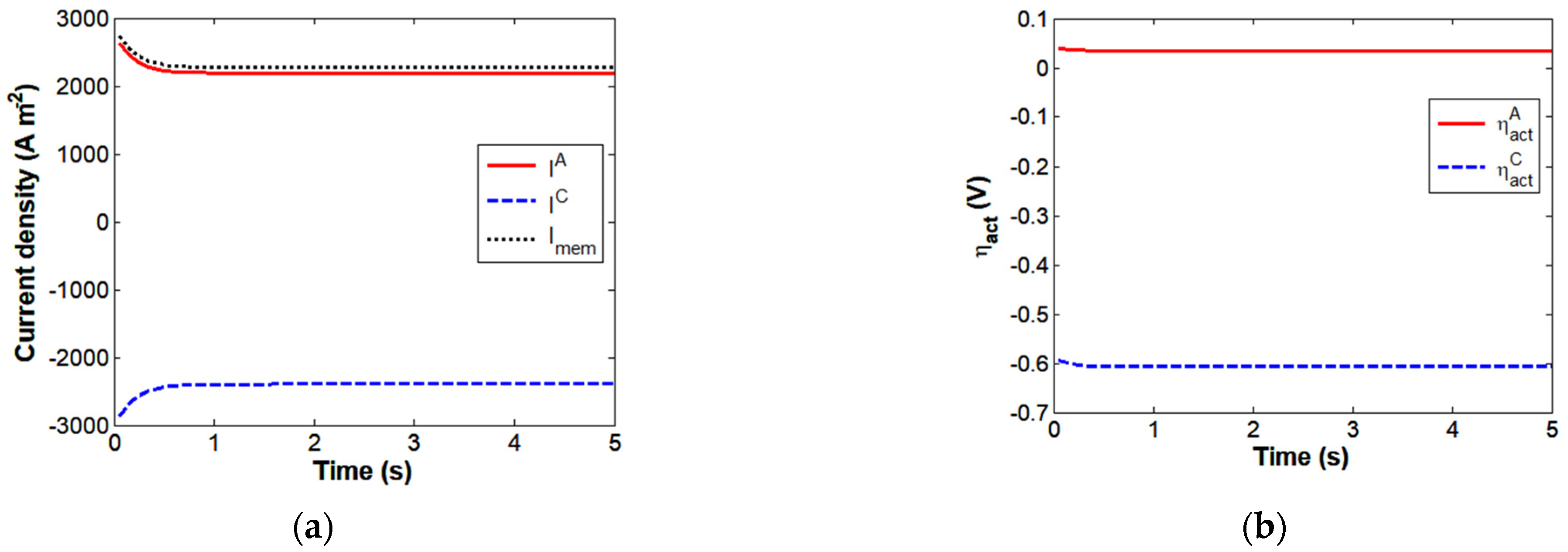
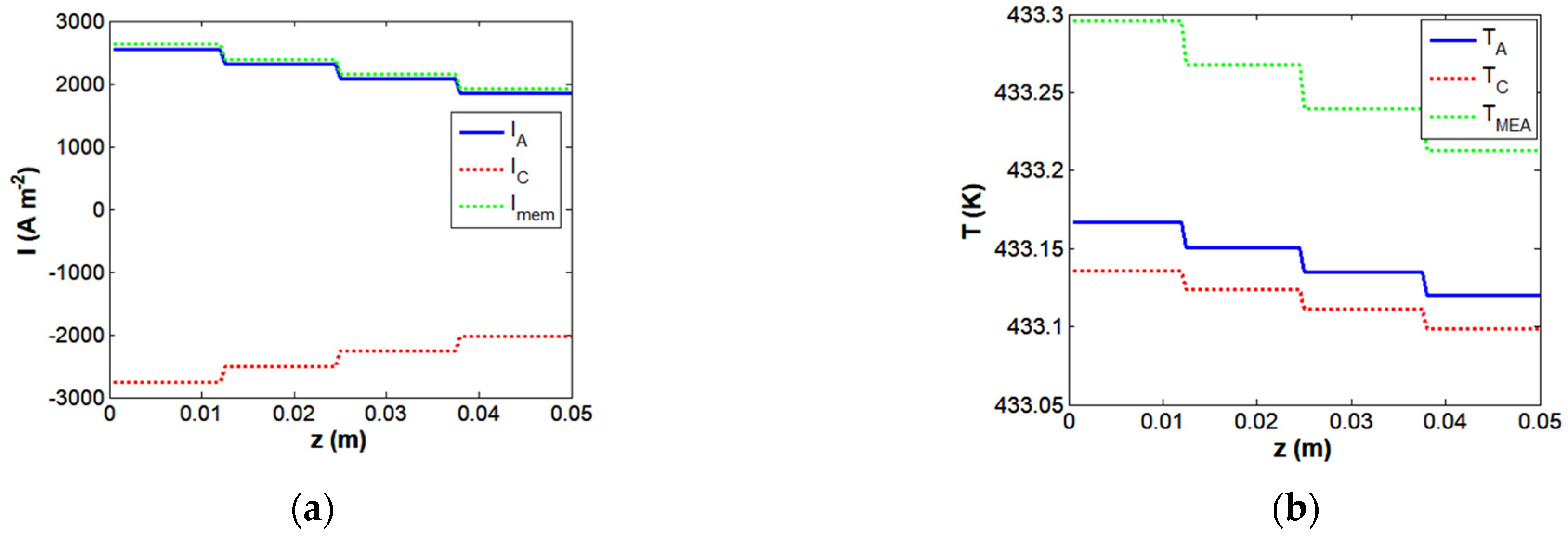
4. Results
4.1. Modeling of Transfer Processes
4.2. Simulation of HT-PEMFC Impedance Spectrum
- Electrochemical oxidation of hydrogen in the anode catalyst layer;
- Electrochemical reduction of oxygen in the cathode catalyst layer;
- Charge balances at the electrode/membrane interfaces;
- Energy balances in the gas channels and catalyst layer (HT-MEA);
- Anode and cathode parasitic currents.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| C | Molar concentration (mol m−3) |
| CdL | Double layer capacitance (C m−2) |
| Cp | Specific heat (J mol−1 K−1) |
| Ecell | Cell voltage (V) |
| E0 | Theoretical potential (V) |
| Ea | Activation energy (J mol−1) |
| FA,FC | Anode and cathode volumetric flow rate (m3 s−1) |
| F | Faraday’s constant (C mol−1) |
| kmem | Membrane conductivity (S m−1) |
| Kp | Permeability coefficient (mol s−1 m−2 Pa−1) |
| H | Henry constant (mol m−3 Pa−1) |
| h | Enthalpy (J mol−1) |
| I | Current density (A m−2) |
| I0 | Exchange current density (A m−2) |
| N | Component molar flux (mol s−1) |
| NTSR | Number of tanks |
| ne | Number of electrons |
| P | Pressure (Pa) |
| r | Mass source term (mol s−1) |
| R | Ideal gas constant (J mol−1 K−1) |
| Rmem | Ohmic resistance (Ω m2 ) |
| q | Energy source term (J s−1) |
| S | Electrode area (m2) |
| t | Time (s) |
| T | Temperature (K) |
| V | Volume (m3) |
| y | Mole fraction in the gas phase |
| Greek letters | |
| α | Heat transfer coefficient (W m−2 K−1) |
| Anodic charge transfer coefficients for anode | |
| Cathodic charge transfer coefficients for anode | |
| Anodic charge transfer coefficients for cathode | |
| Cathodic charge transfer coefficients for cathode | |
| βeff | Effective mass transfer coefficient (m s−1) |
| δmem | Membrane thickness (m) |
| δcat | Catalyst thickness (m) |
| η | Potential difference (V) |
| ηact | Activation overpotential (V) |
| θCO | Surface coverage of carbon monoxide |
| ν | Stoichiometry coefficient |
| ρmol | Molar density (mol m−3) |
| Subscripts/superscripts | |
| act | Activation |
| eff | Effective |
| eq | Equilibrium |
| j | J tank |
| A | Anode |
| C | Cathode |
| cat | Catalyst |
| cell | Fuel cell |
| cross | Crossover |
| G | Gas phase |
| L | Liquid phase |
| mol | Molar |
| mem | Membrane |
| ref | Reference |
| S | Solid |
| H2 | Hydrogen |
| O2 | Oxygen |
| H2O | Water |
| N2 | Nitrogen |
| CO | Carbon monoxide |
| CO2 | Carbon dioxide |
| Abbreviation | |
| CFD | Computational fluid dynamics |
| HT-PEMFC | High-temperature proton exchange membrane fuel cell |
| HT-MEA | High-temperature membrane electrode assembly |
| MEA | Membrane electrode assembly |
| ODE | Ordinary differential equation |
Appendix A
| Coefficient | Value | Unit |
|---|---|---|
| 0.993 | - | |
| −4.75 × 10−3 | A−1 | |
| −1.74 × 10−2 | K−1 | |
| −0.829 | ||
| −1.76 × 10−2 | ||
| 1.16 | ||
| 5.98 × 10−2 | ||
| 6.35 × 10−4 | K−1 | |
| −4.67 × 10−4 | A−1 |
| Model | Polarization Curve | EIS | Comments |
|---|---|---|---|
| 3D CFD model | 714 s | 1763 s | Single channel [55] |
| TSR model | 16.7 s | 111.7 s | 25 cm2 HT-PEMFC |
References
- Samsun, R.C.; Wiethege, C.; Pasel, J.; Janßen, H.; Lehnert, W.; Peters, R. HT-PEFC systems operating with diesel and kerosene for APU application. Energy Procedia 2012, 29, 541–551. [Google Scholar] [CrossRef][Green Version]
- Samsun, R.C.; Pasel, J.; Janßen, H.; Lehnert, W.; Peters, R.; Stolten, D. Design and test of a 5 kW e high-temperature polymer electrolyte fuel cell system operated with diesel and kerosene. Appl. Energy 2014, 114, 238–249. [Google Scholar] [CrossRef]
- Rosli, R.E.; Sulong, A.B.; Daud, W.R.W.; Zulkifley, M.A.; Husaini, T.; Rosli, M.I.; Haque, M.A. A review of high-temperature proton exchange membrane fuel cell (HT-PEMFC) system. Int. J. Hydrogen Energy 2017, 42, 9293–9314. [Google Scholar] [CrossRef]
- Mamlouk, M.; Sousa, T.; Scott, K. A high-temperature polymer electrolyte membrane fuel cell model for reformate gas. Int. J. Electrochem. 2011, 2011, 1–18. [Google Scholar] [CrossRef]
- Shamardina, O.; Kulikovsky, A.A.; Chertovich, A.V.; Khokhlov, A.R. A model for high-temperature PEM fuel cell: The role of transport in the cathode catalyst layer. Fuel Cells 2012, 12, 577–582. [Google Scholar] [CrossRef]
- Doubek, G.; Robalinho, E.; Cunha, E.F.; Cekinski, E.; Linardi, M. Application of CFD techniques in the modelling and simulation of PBI PEMFC. Fuel Cells 2011, 11, 764–774. [Google Scholar] [CrossRef]
- Chippar, P.; Oh, K.; Kim, D.; Hong, T.W.; Kim, W.; Ju, H. Coupled mechanical stress and multi-dimensional CFD analysis for high-temperature proton exchange membrane fuel cells (HT-PEMFCs). Int. J. Hydrogen Energy 2013, 38, 7715–7724. [Google Scholar] [CrossRef]
- Jiao, K.; Alaefour, I.E.; Li, X. Three-dimensional non-isothermal modeling of carbon monoxide poisoning in high temperature proton exchange membrane fuel cells with phosphoric acid doped polybenzimidazole membranes. Fuel 2011, 90, 568–582. [Google Scholar] [CrossRef]
- Krastev, V.K.; Falcucci, G.; Jannelli, E.; Minutillo, M.; Cozzolino, R. 3D CFD modeling and experimental characterization of HT PEM fuel cells at different anode gas compositions. Int. J. Hydrogen Energy 2014, 39, 21663–21672. [Google Scholar] [CrossRef]
- Caglayan, D.G.; Sezgin, B.; Devrim, Y.; Eroglu, I. Three-dimensional modeling of a high temperature polymer electrolyte membrane fuel cell at different operation temperatures. Int. J. Hydrogen Energy 2016, 41, 10060–10070. [Google Scholar] [CrossRef]
- Siegel, C.; Bandlamudi, G.; Heinzel, A. Systematic characterization of a PBI/H3PO4 sol-gel membrane-Modeling and simulation. J. Power Sources 2011, 196, 2735–2749. [Google Scholar] [CrossRef]
- Sezgin, B.; Caglayan, D.G.; Devrim, Y.; Steenberg, T.; Eroglu, I. Modeling and sensitivity analysis of high temperature PEM fuel cells by using Comsol Multiphysics. Int. J. Hydrogen Energy 2016, 41, 10001–10009. [Google Scholar] [CrossRef]
- Kvesić, M.; Reimer, U.; Froning, D.; Lüke, L.; Lehnert, W.; Stolten, D. 3D modeling of an HT-PEFC stack using reformate gas. Int. J. Hydrogen Energy 2012, 37, 12438–12450. [Google Scholar] [CrossRef]
- Vang, J.R.; Andreasen, S.J.; Kær, S.K. A transient fuel cell model to simulate HTPEM fuel cell impedance spectra. In Proceedings of the International Conference on Fuel Cell Science, Engineering and Technology, Washington, DC, USA, 7–10 August 2011; pp. 817–830. [Google Scholar]
- Baricci, A.; Zago, M.; Casalegno, A. A quasi 2D model of a high temperature polymer fuel cell for the interpretation of impedance spectra. Fuel Cells 2014, 14, 926–937. [Google Scholar] [CrossRef]
- Vivona, D.; Casalegno, A.; Baricci, A. Validation of a pseudo 2D analytical model for high temperature PEM fuel cell impedance valid at typical operative conditions. Electrochim. Acta 2019, 310, 122–135. [Google Scholar] [CrossRef]
- Shamardina, O.; Kondratenko, M.S.; Chertovich, A.V.; Kulikovsky, A.A. A simple transient model for a high temperature PEM fuel cell impedance. Int. J. Hydrogen Energy 2014, 39, 2224–2235. [Google Scholar] [CrossRef]
- Shahin, H.; Danilov, V.A.; Vijay, P.; Tade, M.O. An improved tank in series model for the planar solid oxide fuel cell. Ind. Eng. Chem. Res. 2011, 50, 1056–1069. [Google Scholar]
- Bozbiyik, B.; Danilov, V.A.; Denayer, J.F. An improved tank in series model for PEMFC. Int. J. Hydrogen Energy 2011, 36, 14552–14561. [Google Scholar] [CrossRef]
- Danilov, V.A.; Denayer, J.F.; Moon, I. An improved tank in series model for the Direct Methanol Fuel Cell. Int. J. Electrochem. 2011, 2011, 1–9. [Google Scholar] [CrossRef][Green Version]
- Schepper, P.; Danilov, V.A.; Denayer, J.F. A tank in series model for Alkaline Fuel Cell in cogeneration of hydrogen peroxide and electricity. Int. J. Hydrogen Energy 2012, 37, 17258–17267. [Google Scholar] [CrossRef]
- Danilov, V.A.; Schepper, P.; Denayer, J.F. A TSR model for direct propane fuel cell with equilibrium adsorption and desorption processes. Renew. Energy 2015, 83, 1084–1096. [Google Scholar] [CrossRef]
- Danilov, V.A.; Kolb, G.; Cremers, C. Tanks-in-series model for high-temperature electrochemical hydrogen pump. Int. J. Hydrogen Energy 2021, 46, 11536–11543. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Siegel, C.; Lang, S.; Fontes, E.; Beckhaus, P. Approaches for the modeling of PBI/H3PO4 based HT-PEM fuel cells. In High Temperature Polymer Electrolyte Membrane Fuel Cells; Springer: Cham, Switzerland, 2016; pp. 387–424. [Google Scholar]
- Olapade, P.O.; Meyers, J.P.; Borup, R.L.; Mukundan, R. Parametric study of the morphological proprieties of HT-PEMFC components for effective membrane hydration. J. Electrochem Soc. 2011, 158, B639–B649. [Google Scholar] [CrossRef]
- Häffelin, A.; Joos, J.; Ender, M.; Weber, A.; Ivers-Tiffée, E. Time-dependent 3D impedance model of mixed-conducting solid oxide fuel cell cathodes. J. Electrochem. Soc. 2013, 160, F867. [Google Scholar] [CrossRef]
- Pinar, F.J.; Rastedt, M.; Pilinski, N.; Wagner, P.; Dyck, A. Demonstrating feasibility of a high temperature polymer electrolyte membrane fuel cell operation with natural gas reformate composition. Int. J. Hydrogen Energy 2017, 42, 13860–13875. [Google Scholar] [CrossRef]
- Rau, M.; Niedergesäß, A.; Cremers, C.; Alfaro, S.; Steenberg, T.; Hjuler, H.A. Characterization of membrane electrode assemblies for high-temperature PEM fuel cells. Fuel Cells 2016, 16, 577–583. [Google Scholar] [CrossRef]
- Pinar, F.J.; Pilinski, N.; Rastedt, M.; Wagner, P. Performance of a high-temperature PEM fuel cell operated with oxygen enriched cathode air and hydrogen from synthetic reformate. Int. J. Hydrogen Energy 2015, 40, 5432–5438. [Google Scholar] [CrossRef]
- Boillot, M.; Didierjean, S.; Lapicque, F. Residence time distributions of gases in lab-scale polymer electrolyte membrane fuel cells (PEMFC). Chem. Eng. Sci. 2005, 60, 1187–1192. [Google Scholar] [CrossRef]
- Daletou, M.K.; Kallitsis, J.K.; Voyiatzis, G.; Neophytides, S.G. The interaction of water vapors with H3PO4 imbibed electrolyte based on PBI/polysulfone copolymer blends. J. Membr. Sci. 2009, 326, 76–83. [Google Scholar] [CrossRef]
- Lobato, J.; Cañizares, P.; Rodrigo, M.A.; Linares, J.J.; Ubeda, D.; Pinar, F.J. Study of the catalytic layer in polybenzimidazole-based high temperature PEMFC: Effect of platinum content on the carbon support. Fuel Cells 2010, 10, 312–319. [Google Scholar] [CrossRef]
- Linares, J.J.; Sanches, C.; Paganin, V.A.; Gonzalez, E.R. Performance of a poly(2,5-benzimidazole)-based polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2012, 37, 7212–7220. [Google Scholar] [CrossRef]
- Reimer, U.; Ehlert, J.; Janßen, H.; Lehnert, W. Water distribution in high temperature polymer electrolyte fuel cells. Int. J. Hydrogen Energy 2016, 41, 1837–1845. [Google Scholar] [CrossRef]
- Bezmalinović, D.; Strahl, S.; Roda, V.; Husar, A. Water transport study in a high temperature proton exchange membrane fuel cell stack. Int. J. Hydrogen Energy 2014, 39, 10627–10640. [Google Scholar] [CrossRef]
- Waller, M.G.; Walluk, M.R.; Trabold, T.A. Performance of high temperature PEM fuel cell materials. Part 1: Effects of temperature, pressure and anode dilution. Int. J. Hydrogen Energy 2016, 41, 2944–2954. [Google Scholar] [CrossRef]
- Søndergaard, T.; Cleemann, L.N.; Becker, H.; Steenberg, T.; Hjuler, H.A.; Seerup, L.; Jensen, J.O. Long-term durability of PBI-based HT-PEM fuel cells: Effect of operating parameters. J. Electrochem. Soc. 2018, 165, F3053–F3062. [Google Scholar] [CrossRef]
- Søndergaard, S.; Cleemann, L.N.; Jensen, J.O.; Bjerrum, N.J. Influence of oxygen on the cathode in HT-PEM fuel cells. Int. J. Hydrogen Energy 2019, 44, 20379–20388. [Google Scholar] [CrossRef]
- Thomas, S.; Araya, S.S.; Frensch, S.H.; Steenberg, T.; Kær, S.K. Hydrogen mass transport resistance changes in a high temperature polymer membrane fuel cell as a function of current density and acid doping. Electrochim. Acta 2019, 317, 521–527. [Google Scholar] [CrossRef]
- Lobato, J.; Cañizares, P.; Rodrigo, M.A.; Pinar, F.J.; Úbeda, D. Study of flow channel geometry using current distribution measurement in a high temperature polymer electrolyte membrane fuel cell. J. Power Sources 2011, 196, 4209–4217. [Google Scholar] [CrossRef]
- Jespersen, J.L.; Schaltz, E.; Kær, S.K. Electrochemical characterization of a polybenzimidazole-based high temperature proton exchange membrane unit cell. J. Power Sources 2009, 191, 289–296. [Google Scholar] [CrossRef]
- Mack, F.; Laukenmann, R.; Galbiati, S.; Kerres, J.A.; Zeis, R. Electrochemical impedance spectroscopy as a diagnostic tool for high-temperature PEM fuel cells. ECS Trans. 2015, 69, 1075–1087. [Google Scholar] [CrossRef]
- Mamlouk, M.; Scott, K. Analysis of high temperature polymer electrolyte membrane fuel cell electrodes using electrochemical impedance spectroscopy. Electrochim. Acta 2011, 56, 5493–5512. [Google Scholar] [CrossRef]
- Buffham, B.A.; Gibilaro, L.G. A generalization of the tanks-in-series mixing model. AIChE J. 1968, 14, 805–806. [Google Scholar] [CrossRef]
- Stokes, R.L.; Nauman, E.B. Residence time distribution functions for stirred tanks in series. Can. J. Chem. Eng. 1970, 48, 723–725. [Google Scholar] [CrossRef]
- Aris, R. Ends and beginnings in the mathematical modelling of chemical engineering systems. Chem. Eng. Sci. 1993, 48, 2507–2517. [Google Scholar] [CrossRef]
- Van Hasselt, B.W.; Calis, H.P.A.; Sie, S.T.; Van den Bleek, C.M. Gas-and liquid-phase residence time distribution in the three-levels-of-porosity reactor. Chem. Eng. Sci. 1999, 54, 5047–5053. [Google Scholar] [CrossRef]
- Commenge, J.M.; Falk, L.; Corriou, J.P.; Matlosz, M. Analysis of microstructured reactor characteristics for process miniaturization and intensification. Chem. Eng. Technol. Ind. Chem. -Plant Equip. -Process Eng. -Biotechnol. 2005, 28, 446–458. [Google Scholar] [CrossRef]
- Rodrigues, A.; Amphlett, J.C.; Mann, R.F.; Peppley, B.A.; Roberge, P.R. Carbon monoxide poisoning of proton-exchange membrane fuel cells. In Proceedings of the Thirty-Second Intersociety Energy Conversion Engineering Conference, Honolulu, HI, USA, 27 July–1 August 1997; pp. 768–773. [Google Scholar]
- Levenspiel, O. The tanks-in-series model. In Tracer Technology; Springer: New York, NY, USA, 2012; pp. 81–97. [Google Scholar]
- Ponzi, E.N.; Gonzalez, M.G. Comparison between the dispersion and tanks in series models. Chem. Eng. Sci. 1980, 35, 1804–1806. [Google Scholar]
- Taylor, G.I. Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1953, 219, 186–203. [Google Scholar]
- Aris, R. On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 235, 67–77. [Google Scholar]
- Mass Transport Analysis of a High Temperature PEM Fuel Cell. Available online: https://www.comsol.com/model/mass-transport-analysis-of-a-high-temperature-pem-fuel-cell-8550 (accessed on 28 May 2024).

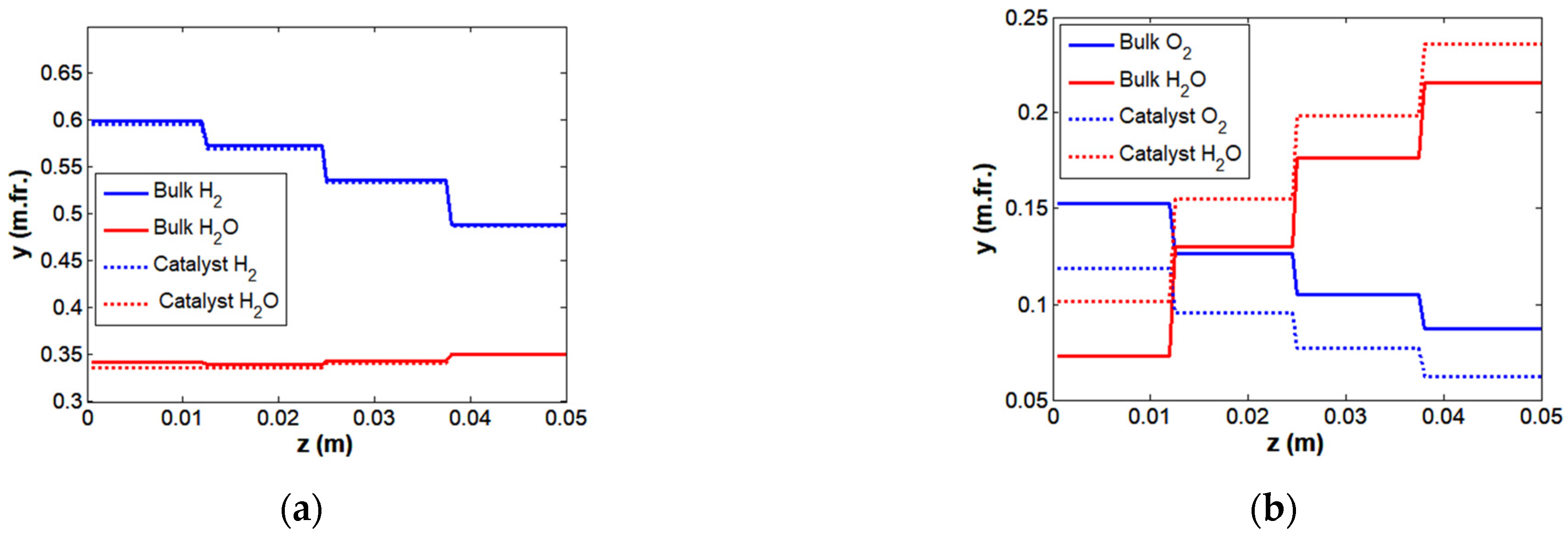
| Parameter | G1 | G2 | G3 | G4 | C1 | C2 | S1 |
|---|---|---|---|---|---|---|---|
| H2 stoichiometric ratio | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| O2 stoichiometric ratio | 2 | 2 | 2 | 2 | 2 | 2 | 6 |
| Temperature (K) | 433 | 433 | 433 | 433 | 433 | 433 | 433 |
| Pressure (atm) | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| H2 mole fraction | 1.00 | 0.78 | 0.54 | 0.54 | 1.00 | 0.33 | 1.00 |
| CO2 mole fraction | 0 | 0.22 | 0.15 | 0.14 | 0 | 0.2 | 0 |
| H2O mole fraction | 0 | 0 | 0.31 | 0.31 | 0 | 0.46 | 0 |
| CO mole fraction | 0 | 0 | 0 | 0.01 | 0 | 0.01 | 0 |
| Reference | [28] | [28] | [28] | [28] | [29] | [29] | [17] |
| Parameter | Units | Symbol | G1–G4 | C1,C2 | S1 |
|---|---|---|---|---|---|
| Reference exchange current | (A m−2) | 1.44 × 103 | 1.44 × 103 | 1.44 × 103 | |
| Activation energy | (J mol−1) | 1.69 × 104 | 1.69 × 104 | 1.69 × 104 | |
| Reference temperature | (K) | 433 | 433 | 433 | |
| Reference concentration | (mol m−3) | 3.93 × 10−3 | 3.93 × 10−3 | 3.93 × 10−3 | |
| Charge transfer coefficient | 1 | 1 | 1 | ||
| Charge transfer coefficient | 1 | 1 | 1 | ||
| Reference exchange current | (A m−2) | 7.89 × 10−4 | 7.89 × 10−4 | 7.89 × 10−4 | |
| Activation energy | (J mol−1) | 7.24 × 104 | 7.24 × 104 | 7.24 × 104 | |
| Reference temperature | (K) | 423 | 423 | 423 | |
| Reference concentration | (mol m−3) | 1.5 × 10−3 | 1.5 × 10−3 | 1.5 × 10−3 | |
| Charge transfer coefficient | 1 | 1 | 1 | ||
| Charge transfer coefficient | 1 | 1 | 1 | ||
| Channel height | (m) | h | 1 × 10−3 | 1 × 10−3 | 1 × 10−3 |
| Electrode area | (m2) | S | 25 × 10−4 | 21 × 10−4 | 5 × 10−4 |
| Membrane width | (m) | 60 × 10−6 | 40 × 10−6 | 60 × 10−6 | |
| Catalyst width | (m) | 20 × 10−6 | 20 × 10−6 | 50 × 10−6 | |
| Double layer capacitance | (mF cm2) | Cdl | 150 | 150 | 150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danilov, V.A.; Kolb, G.; Cremers, C. A Dynamic Tanks-in-Series Model for a High-Temperature PEM Fuel Cell. Energies 2024, 17, 2841. https://doi.org/10.3390/en17122841
Danilov VA, Kolb G, Cremers C. A Dynamic Tanks-in-Series Model for a High-Temperature PEM Fuel Cell. Energies. 2024; 17(12):2841. https://doi.org/10.3390/en17122841
Chicago/Turabian StyleDanilov, Valery A., Gunther Kolb, and Carsten Cremers. 2024. "A Dynamic Tanks-in-Series Model for a High-Temperature PEM Fuel Cell" Energies 17, no. 12: 2841. https://doi.org/10.3390/en17122841
APA StyleDanilov, V. A., Kolb, G., & Cremers, C. (2024). A Dynamic Tanks-in-Series Model for a High-Temperature PEM Fuel Cell. Energies, 17(12), 2841. https://doi.org/10.3390/en17122841







