Cost-Optimality Assessment of a Solar Trigeneration System for Tertiary Sector Buildings in Greece

Abstract

To pave the way towards buildings’ decarbonization in the context of the European Union’s (EU) policy, the methodology of cost-optimality assessment based on regulation 244/2012/EU is a useful tool to explore and foster the application of energy technologies in buildings. Meanwhile, the fostering of concentrated solar power is included in the EU solar energy strategy. In this study, the cost-optimal methodology is employed for the techno-economic assessment of the integration of a novel solar, multi-purpose energy technology, namely a parabolic trough collector-based trigeneration system, in two building types with different characteristics, namely an office and a hospital, in Greece, thus allowing the evaluation of the cost-optimal system design and the impact of the building type on the system’s techno-economic performance. Reference buildings are defined and their energy demand is calculated through dynamic energy simulations. The trigeneration system’s performance for different design scenarios is then parametrically investigated using a simulation model. For each scenario, energy, environmental and economic indicators are calculated and the cost-optimal designs are extracted. In the cost-optimal implementation, the system covered 18.19–36.39% and 3.58–15.71% of the heating and cooling demand, respectively, while the reduction of the primary energy consumption and emissions was estimated at 10–14% and 10–16%, respectively. However, differences between the buildings related to the operation schedule and the loads led to the implementation of the system being economically more attractive in the hospital, while for the office, financial support is necessary for a viable investment.

1. Introduction

Decarbonization of buildings is of paramount significance in the European Union (EU) environmental policy, considering that buildings in the EU consume 40% of the total energy and emit 36% of the greenhouse gases [1]. The Energy Performance of Buildings Directive (EPBD) 2010/31/EU urges member states to decarbonize the building sector through the integration of local renewable energy sources (RES), among other measures. Meanwhile, the EU Renovation Wave aims at the renovation of the public and private building stock, along with the increase of the share of local RES in heating and cooling [2]. Moreover, the revised Renewable Energy Directive (EU) 2023/2413 included the target for an average annual increase in the share of renewables in heating and cooling by 0.8% and 1.1% during the years 2021–2025 and 2026–2030 [3]. Owing to its abundance, solar energy is at the core of the EU solar energy strategy [4] and Strategic Energy Technology (SET) Plan [5], which aim at supporting photovoltaics (PV), solar heating, as well as solar thermal (including concentrated solar power (CSP)) technologies in buildings.

Compared to commercially established PV-driven systems, solar thermal trigeneration systems for the production of heating, cooling and electricity have a series of advantages. Firstly, they are associated with higher overall conversion efficiencies of solar radiation; thus they can yield more final energy per unit of utilized area [6]. Secondly, thermal energy storage (TES) is less expensive than electrical energy storage through batteries [7]. Furthermore, through solar thermal trigeneration systems, it is easier to produce at the same time electricity, heating and cooling [8,9], compared to the use of PVs with heat pumps, which typically have a single operating mode at a given time. Finally, solar thermal trigeneration systems can be hybridized with alternative heat sources such as geothermal, waste heat and biomass [8,9] and are thus more relevant in the context of sector coupling.

Solar thermal systems can be based on different types of collectors, the most prominent being flat plate, evacuated tube and parabolic trough collectors (PTCs). The main advantage of concentrating PTCs is their capability of operating at higher temperatures that range from around 150 °C to 400 °C [6,10,11], which enables higher conversion efficiencies into electricity and cooling as well as improved energy densities and hence flexibility if coupled with high-temperature sensible TES systems.

The most commonly investigated type of solar thermal trigeneration system driven by PTCs is based on an Organic Rankine Cycle (ORC) that is coupled with a thermally activated chiller. Overall, different technologies of thermally activated chillers have been proposed along with various ways of integrating them with ORCs. The most widely considered options are based on absorption chillers [8,10] as well as ejector cooling cycles (ECCs) [9,12,13] in various configurations. In general, thermal cooling based on ejector has advantages over absorption chillers such as lower capital expenses and operation and maintenance costs, less complicated design and more flexibility in the choice of the working fluid, even though their coefficient of performance (COP) is lower than absorption chillers [7]. Another advantage of the combination of ORC with ECC is that some parts of the configuration can be common (generator, condenser, pump, etc.). Finally, this combination has the possibility of producing cooling and electricity as well as heating from low temperature sources [7]. Most studies on such solar thermal trigeneration systems based on integrated ORCs with ECCs (ORC-ECCs) primarily focus on the analysis and optimization of the ORC-ECC system itself, without considering the demand side, i.e., the building. As a result, the impact that the properties of the building have on the performance and the optimal size of the system are not thoroughly analyzed.

Taking into account the energy demands of the building is also very significant in the context of the EPBD Directive 2010/31/EU, which introduced the concept of cost-optimal levels of energy consumption, which refers to the implementation of energy efficiency (EE) or RES measures that would lead to a reduction of the energy consumption but also to the minimization of the global cost (GC) in the lifetime of the building. The methodological steps for building cost-optimality assessments are provided in the supplementary Directive 244/2012/EU [14] and its accompanying guidelines [15]. Apart from its implementation by the EU member states for the revision of their minimum energy performance requirements [16], the methodology has been also widely used to calculate the optimal sizing of individual elements for EE (for example, thickness of insulation) or RES measures in buildings [17,18,19,20]. An analysis based on this methodology was conducted for the evaluation of the implementation of different combinations of EE and RES interventions in the case of residential [21] and office buildings [22] in Greece considering various combinations of insulation, energy systems, integration of solar energy, etc., in different climate zones (CZs).

Concerning the application of the cost-optimal methodology, it can be concluded that it offers the possibility to assess not only the optimal combination of a package of measures but also the optimal implementation of individual measures in a specific building type. Although much research has been done in employing the cost-optimality methodology, most of the studies focus on single-purpose energy measures such as thermal insulation, PVs and heat pumps. Moreover, most studies on cost-optimality focus on either residential or office buildings. Nevertheless, regarding non-residential buildings, differences exist between the different building types, such as the operation schedule and the energy loads, which may affect the cost-optimal implementation of energy measures. The ongoing encouraging research findings on trigeneration implementation in terms of energy performance and the lack of extensive application of the cost-optimality methodology for all tertiary-sector building types under different climatic conditions raise the research interest on the investigation of the cost-optimal sizing of such combinatorial systems in a wider spectrum of building types and CZs.

Triggered by the above conclusion, the current study investigates the cost-optimal integration of a solar trigeneration system consisting of PTCs, TES and ORC-ECC in two tertiary sector buildings with different operation schedules and energy loads, namely a hospital building and an office building. An extensive cost-optimality assessment of different design scenarios of the trigeneration system is conducted, for the assessment of the optimal size of the trigeneration system in each building. Based on that, conclusions regarding the optimal implementation of solar trigeneration in buildings are extracted. Moreover, the impact of the operation schedule and energy demands of the two examined building types on the performance of the trigeneration system is investigated. The environmental impact of the integration of the trigeneration system is studied through the detailed calculation of GHG emissions. Moreover, through the calculation of investment KPIs, the economic viability of the integration of the technology in buildings is investigated, and insights regarding the requirements for an acceptable economic performance are provided and discussed. Finally, the effect of the different CZs is studied by simulating the operation and estimating the cost-optimal scenario in two different CZs in Greece. To achieve the objectives of the study, initially, reference office and hospital buildings were defined by elaborating building-features’ data of the Greek building stock, followed by the calculation of their energy loads in the two CZs based on dynamic energy simulations. A model for the simulation of the operation of the trigeneration system was then created, which allowed the calculation of the system’s performance under different values of its design parameters, and several alternative design scenarios for the trigeneration system were established for each building. For each scenario, the system’s techno-economic and environmental performance was calculated by utilizing the results from the building and the trigeneration system’s simulation and by including all relevant costs.

2. Materials and Methods

A flow chart of the inputs, calculations and simulation models used in this work and the steps leading to the calculation of the cost-optimal trigeneration system’s design scenario for a reference building in a specific CZ is presented in Figure 1. As shown in Figure 1, the characteristics of the reference building, along with weather data for the chosen CZ, are fed to the dynamic simulation model of the building, which provides the building’s loads. For each building, several design scenarios for the trigeneration system have been defined. The building’s loads, together with the weather data and the design parameters of the trigeneration system for each defined design scenario, are fed into the trigeneration system’s simulation model, which returns the production of heating, cooling and electricity from the system. By combining the latter with the building’s demand, the building’s energy consumption and primary energy consumption (PEC) after the integration of the trigeneration system under the examined design scenario can be calculated, as well as the GHG emissions related to the building. Finally, by considering cost data regarding the trigeneration system and the cost related to the energy consumption of the building, the necessary economic indicators can be calculated. The described process is repeated for all defined design scenarios, leading to the evaluation of the cost-optimal scenario. The inputs, calculations and simulation models are analyzed in detail in the following sections.

2.1. Definition of Reference Buildings

In the guidelines provided by the EU regarding the cost-optimal methodology, a main step is the definition of the reference buildings [15]. The thermophysical properties and technical properties of the systems stand for the most widely used ones, to characterize the building stock. In such studies, for each building use existing in the stock, one or more reference buildings are defined. The definition of the reference building can either be based on the selection of a real building that is considered representative or on the creation of a theoretical reference one, whose characteristics are those that are most common in the buildings of the same use in the country [15,23]. The first option requires access to extensive information on the building stock, whilst the second option can be implemented by utilizing available data from statistics and other sources. In this study, the second option was chosen. Data on the building stock were gathered from the following sources:

• The building stock census from the Hellenic Statistical Authority (ELSTAT) [24], which recorded several characteristics of the building stock. Based on that, the characteristics that appear in the majority of buildings in Greece were considered.
• Published data from energy performance certificates (EPCs) per building type in Greece [25,26]. The data in ref. [26] are also provided per period of construction as well as per CZ.
• The guidelines of the Greek EPBD [27], which were used for the calculation of some properties based on characteristics collected from the other two sources. Also, the guidelines provide typical values for the operation schedule, number of occupants, etc. depending on the building use.

The building operation schedule can be decisive in the assessment of energy investments in buildings, as it affects the building’s energy demand. Thus, two representative building types are used as test-beds in the current study, which cover a high proportion of the operation schedule diversity of tertiary buildings in Greece, namely an office building and a hospital building. A basic difference between the two building types is the operation schedule, which is normally intermittent and continuous for the office and the hospital, respectively. It should be also mentioned that office buildings are the only category of tertiary buildings that must be included in the cost-optimal calculations, according to the EU guidelines [14]. Also, they constitute the largest category of tertiary domain buildings in Greece according to the ELSTAT [24]. Hospitals have continuous operation and higher energy demands than other types of buildings.

From the analysis of the data from the building stock census, it was found that for both building categories, the two regions with most buildings are Attica (23.15% of the offices and 26.87% of the hospitals in Greece) and Central Macedonia (12.8% of offices and 16.41% of hospitals in Greece) [24]. These are the regions where the two largest cities of Greece, Athens and Thessaloniki, are found, which suggests that both types of buildings are more likely to be found within cities, where the population is denser. Also, Attica and Central Macedonia belong to CZ B and CZ C, respectively, according to the classification of Greek EPBD [27]. The thermal transmittance of roofs and walls is estimated based on the Greek EPBD guidelines regarding the construction material and the period of construction that defines the insulation level of the building [27]. According to statistical data from the ELSTAT, the majority of the considered building types were constructed before 1980, when insulation was not obligatory for new building constructions [27], while the main construction material is reinforced concrete and bricks. As for the windows, average thermal transmittance values were in available EPCs found in ref. [26]. Moreover, to account for realistic test-beds size, the following assumptions were made:

• For the office building, according to the official national report on the minimum energy performance requirements [28], two typologies are indicated as representative: a 1-floor office building for small cities and a 5-floor office building for large cities. Considering that the majority of office buildings are located in larger cities, then a 5-floor office is selected herein, which in fact is more realistic for a trigeneration system application due to the required large heating and cooling demands.
• Most hospital buildings in Greece have one floor according to ELSTAT. However, in the Region of Attica, which concentrates the highest hospital building stock, most hospitals have 3–5 floors. Therefore, a 5-floor building is considered. Regarding the floor area, the average hospital building area based on data from EPCs in Greece is equal to 10,211.55 m² [25]. Nevertheless, in ref. [29], the areas of hospitals in the 1st Health Region (that includes the Region of Attica) are presented, wherein sizes from 10,000 to 80,000 m² are mentioned, with an average size of 25,821.21 m². Therefore, combining the above information and considering that hospitals may consist of several buildings, a hospital building complex is considered with a total area of 30,634.65 m², consisting of 3 buildings, each with a floor area of 10,211.55 m². All buildings of the complex are assumed to have the same heating and cooling systems.

To calculate the buildings’ windows area, the window-to-wall ratio, i.e., the ratio of the total area of windows to the total area of external walls of the building, was assumed equal to 20% in both buildings, based on the building information presented in [22].

Regarding the characteristics of buildings’ heating, cooling, domestic hot water (DHW) and lighting systems, average values from EPCs for the respective building use and period of construction were taken from ref. [26]. The operation schedule, number of occupants, desirable temperature levels, fresh air requirements, DHW consumption and internal heat gains from appliances were taken from the guidelines of the Greek EPBD for the respective building use [27].

In

Table 1. Characteristics of the representative test-bed buildings.

Characteristic of Building	Office	Hospital
Thermal transmittance values	Uroof = 2.7 W/m2K Uwall = 2.4 W/m2K Uwindows = 4.6 W/m2K Ufloor = 3.1 W/m2K	Uroof = 2.7 W/m2K Uwall = 2.4 W/m2K Uwindows = 3.7 W/m2K Ufloor = 3.1 W/m2K
Number of floors	6 (Ground floor + 5 floors)	6 (Ground floor + 5 floors)
Building area (m2)	2504.5 m2	30,634.65 m2
Window-to-wall ratio	20%	20%
Heating system and efficiency	Oil boiler, eff = 0.83	Oil boiler, eff = 0.83
Cooling system and efficiency	Heat pump, COP = 2.7	Heat pump, COP = 2.6
DHW system and efficiency	Does not exist	Oil boiler, eff = 0.83
Lighting system installed power	20.2 W/m2	14.2 W/m2
Schedule	10 h/day, 5 days/week, 12 months/year	24 h/day, 7 days/week, 12 months/year
Occupants	10 people/100 m2	30 people/100 m2
Temperature setpoint (°C)	Winter 20 °C, Summer 26 °C	Winter 22 °C, Summer 26 °C
Fresh air requirements	3 m3/h/m2	10.5 m3/h/m2
DHW consumption	No DHW consumption	120 lt/person/day
Internal heat gains from appliances	15 W/m2	15 W/m2

, the key building features produced by the above-mentioned elaboration of literature data are presented. These parameters synthesize the test-bed buildings and are used as input conditions in the building energy models (BEM) in the calculation procedure.

Finally, as mentioned in the Introduction, the calculations of the energy performance of the two reference buildings were conducted for two different CZs, i.e., CZ B and CZ C, as the majority of office and hospital buildings in Greece exist in the regions of Attica and Central Macedonia.

2.2. Energy Simulations and Calculation of Primary Energy

The steps leading to the calculation of the PEC of a trigeneration system’s design scenario for a reference building are presented in Figure 1 and analyzed in the following subsections.

2.2.1. Building Energy Model

For the calculation of the building energy performance of the formulated reference buildings, a BEM is constructed for dynamic energy simulations, as per the guidelines for cost-optimal calculations [15]. Building energy models are developed using EnergyPlus (24.1.0), using the parameters of Table 1 as input conditions. Regarding the weather data, .epw files for the cities of Athens and Thessaloniki are used [30]. Athens (CZ B) has higher temperatures than Thessaloniki (CZ C) [27,30]; thus, lower heating and higher cooling loads are expected in CZ B. The energy indicators that were calculated from the BEM are the energy loads and energy consumption by energy carrier, i.e., oil and electricity, as well as energy loads and energy consumption by end-use. These results were then used for the techno-economic assessment of the implementation of proposed technology in each building and, ultimately, for the cost-optimality assessment.

2.2.2. Trigeneration System’s Simulation Model

The layout of the overall investigated system is shown in Figure 2. The main components of the system include the PTCs, the TES and the ORC-ECC system.

The main components and mathematical representation of related physical processes and properties of the trigeneration system are described below.

PTC field operation and thermal power production were simulated based on the calculation of the PTC efficiency, ${\eta }_{PTC}$, from the Equation (1) [11]:

$${\eta }_{PTC}=c_0\ast K\left(\theta \right)-c_1\frac{T_{PTC}-T_{amb}}{I_{sol}}-c_2{\left(\frac{T_{PTC}-T_{amb}}{I_{sol}}\right)}^2$$

(1)

where:

• I_sol is the direct normal irradiance (DNI) in W/m²;
• T_PTC is the collector’s temperature in °C, which was considered equal to the average of the heat transfer fluid’s (HTF) inlet and outlet temperature;
• T_amb is the ambient temperature in °C.

Hourly data for the DNI and the ambient temperature are fed into the simulation from the .epw files that were also used for the building simulation [30].

Regarding the coefficients $c_0$, ${ c}_1$ and $c_2$, different values can be used that correspond to different collectors’ designs. In this study, the coefficients are considered equal to 0.673, 0.2243 and 0, respectively, according to a previous scientific study [11].

Even though a tracking system is often used in PTC systems, the DNI cannot be always normal to the collector; therefore, the incident angle modifier $K\left(\theta \right)$ is used. Assuming a north–south orientation for the PTCs and the ability for tracking on the east–west axis, the incident angle modifier for the Eurotrough collector is fairly calculated from Equation (2) below [31]:

$$K\left(\theta \right)=\cos \left(\theta \right)-5.25\ast {10}^{-4}\ast \theta -2.859\ast {10}^{-5}\ast {\theta }^2$$

(2)

where:

• θ is the incident angle in degrees (^o) for an east–west tracking collector [32].

Based on the calculation described for the PTC efficiency, the solar heat $Q_{PTC},$which is produced by the PTC system in Watt, can be calculated from Equation (3):

$$Q_{PTC}={\eta }_{PTC}\ast A_{PTC}\ast I_{sol}$$

(3)

where:

• A_PTC is the PTC aperture area in m².

Based on that, the enthalpy difference (and based on the temperature difference) of the HTF before and after the collector is calculated as follows:

$$h_{PTC,out}-h_{PTC,in}=\frac{Q_{PTC}}{{\dot{m}}_{col}}$$

(4)

where:

• ${\dot{m}}_{col}$ is the mass flow rate of HTF in the PTC (in kg/s). This is assumed equal to 2% of the PTC aperture area [33].

The HTF is considered to be heated to temperatures up to 400 °C.

Based on the equations described above, the aperture area of the PTC field is inserted in the calculation through Equation (3), and for given DNI and ambient temperature data on an hourly basis, the thermal power from the PTC field with a specific collectors’ area is obtained.

As for the TES, a concrete TES is assumed, due to its ability to operate at higher temperatures, up to 400 °C [34,35], as well as due to its lower cost compared to other TES types [36]. The TES is modeled as follows:

The heat absorbed (or delivered) by the TES results in the change of the TES enthalpy (and temperature), based on the following equation.

$${\mathsf{\Delta }H}_{TES}=\frac{Q_{TES}\ast \mathsf{\Delta }t}{M_{TES}}$$

(5)

where:

• Q_TES is the heat absorbed or delivered by the TES in W;
• Δt is the timestep considered in the calculation in s;
• M_TES is the mass of the TES in kg.

Regarding the concrete TES’ properties, its maximum and minimum temperatures were considered 400 °C and 150 °C, respectively. Its average heat capacity and density were considered equal to 1050 J/kg and 2400 kg/m³, respectively, based on the data presented in ref. [35], while its energy density is equal to 175 kWh/m³.

Moreover, the heat losses from the TES that may occur due to the temperature difference between the TES and the ambient are also envisaged in the model as follows:

$$Q_L=U_L\ast A_{TES}\ast (T_{TES}-T_{amb})$$

(6)

where:

• U_L is the heat loss coefficient of the TES to its surroundings in W/m²K, which is taken equal to 2.5 W/m²K, as proposed in similar studies [11,32];
• A_TES is the area of the TES in m².

Regarding the ORC-ECC, the thermodynamic analysis, numerical modeling and optimization of ORC [37] and ECC cycles [7,38] including the numerical analysis of the performance of ejector devices [39] have been extensively discussed in the literature. Therefore, in the present study, only the most relevant information is presented.

Heat is supplied to the whole system by the heat source in a heat exchanger, which functions at the same time as an ORC evaporator and a ECC generator (see Figure 2). The superheated vapor that is produced in the ORC evaporator/ECC generator can be supplied to the ejectors (primary flow) for cooling production (ECC) or to the expander (ORC) to produce electricity, depending on the operating mode.

A critical operational parameter of ECCs is the ejector backpressure, which is the same as the condensation pressure. The condensation pressure is determined by the condensation temperature, which is in turn affected by the temperature and flow rate of the cooling water in the condenser. Ultimately, the latter is determined by the ambient air temperature, since the water is cooled down in the dry cooler of the system. Because of the significant variability of the ambient temperature throughout the year and considering the high dependence of the ejector performance on the condensation pressure, the system includes two ejectors. The first ejector is optimized for a lower condensation pressure (and hence ambient temperatures that correspond to the spring period), while the second ejector is optimized for higher condensation pressure (and hence ambient temperatures that correspond to the summer period).

The investigated ORC-ECC has four operating modes: (1) electricity-only, (2) combined heat and power (CHP), (3) cooling-only (spring ejector) and (4) cooling-only (summer ejector). In the first two modes, only the ORC is operational, while in the third and fourth modes, only the ECC is operational. In the electricity-only mode, the ORC working fluid is heated in the ORC evaporator, passes through the expander, the recuperator hot-side and subsequently the condenser and subcooler, exiting it as subcooled liquid that is then discharged by the ORC pump to the recuperator’s cold-side. The CHP mode is similar; however, in this mode, the recuperator is bypassed and the condenser pressure/temperature is raised to produce heat at a higher temperature. In cooling mode, the working fluid exiting the ECC generator is driven to the high-pressure inlet port of one of the ejectors. It is highlighted that only one of the ejectors is operational at any given time.

As it was discussed in the previous section, the heat source of the ORC-ECC will be HTF provided by the PTCs that can be up to 400 °C. Theoretically, such a high temperature would enable the operation of the ORC-ECC with a very high cycle temperature of up to 200–300 °C, which is the typical range of high-temperature commercial ORC systems for biomass and waste heat recovery applications. Under this maximum temperature, the thermal efficiency of the ORC as well as the coefficient of performance of the ECC would be high. However, for technical, practical and economic reasons for the present analysis, the maximum temperature that was considered for the design of the ORC-ECC had to be significantly reduced. There are three main reasons for this:

• Working fluids that are suitable for high-temperature operation include natural hydrocarbons such as cyclopentane or siloxanes. While these fluids are used in commercial refrigeration and ORC applications, they have very high flammability and are toxic. Considering that the scope of the study is focused on non-industrial applications, it is important to minimize the aforementioned risks.
• In order to achieve the operation of small-scale ORC systems at very high temperatures above 140 °C, specialized components (piping, valves, vessels) suitable for high-temperature application would have to be used, which could have a very negative impact on the cost-effectiveness of the system. On the other hand, by maintaining the operating temperature of the prototype below 140 °C, it is possible to use off-the-shelf components used in common refrigeration and heating applications, thus maintaining the cost of the system at reasonable ranges.
• Most importantly, because of the scope of the analysis, the scale of the system is relatively small. While turboexpanders are used in high-temperature (>200 °C) ORCs at very large scales (in the range of hundreds of MWs), they are not commercially mature for small-scale systems (in the hundreds of kWs), for which screw machines are commercially mature. Therefore, to make the analysis more realistic considering the present status of the expander technology, a lower temperature had to be considered, with which screw expanders are compatible.

Following the above considerations, the maximum operating temperature of the ORC-ECC system is set to 135 °C. Given the necessity of using low-flammability, non-toxic substances suitable for low-temperature (<140 °C) applications as working fluids, the selected refrigerant is hydrofluoroolefin (HFO) R1233zd(E). The reasons for selecting this working fluid are the following:

• Because of its critical pressures and temperature, it is suitable for use within the heat source/heat sink temperature ranges of the system.
• It has zero or low flammability and the lowest toxicity (A1 and A2L ASHRAE safety group). This is an important criterion considering that the system is addressed to non-industrial settings, as previously mentioned.
• It has zero ozone depletion potential (ODP) and ultra-low (<1) global warming potential (GWP). These characteristics are dictated by the Montreal [40] and Kyoto Protocols [41], as well as the F-gases regulations [42].
• It is commercially available.

The thermodynamic assumptions and specifications of the simulated ORC-ECC system are summarized in

Table 2. Overview of ORC-ECC thermodynamic assumptions and specifications.

Parameter	Electricity-Only (Winter)	Electricity-Only (Summer)	CHP	ECC (Cooling) Summer/Spring
Expander isentropic efficiency (%)	65 [45,46,47] 1
Pump isentropic efficiency (%)	65 [48,49]
Expander generator efficiency (%)	96 [50]
Pump motor efficiency (%)	85 [50,51]
Working fluid	R1233zd(E)
Temperature at expander/ejector inlet (°C)	135
Superheating degree at expander/ejector inlet (K)	5
Pressure at expander/ejector inlet (bar)	19.08
Evaporation temperature at ECC cooling evaporator (only in ECC cooling mode) (°C)	5
Evaporation pressure at ECC cooling evaporator (only in ECC cooling mode) (bar)	0.60
Superheating degree at ECC cooling evaporator outlet (K)	2
Subcooling degree at pump inlet (K)	5
Pinch point in condenser (K)	3
Pinch point in ECC cooling evaporator (K)	3
Pinch point in recuperator (recuperative ORC in electricity-only mode) (K)	10
Chilled water temperature drop in ECC cooling evaporator (K)	5
Chilled water temperature at ECC cooling evaporator inlet (°C)	13
Cooling water temperature rise in condenser (K)	5
Cooling water temperature at condenser inlet (°C)	13	37	47	37/30
Condensation temperature (°C)	20.80	44.80	54.18	43.98/37.08
Condensation pressure (bar)	1.11	2.51	3.32	2.44/1.96
Ejector entrainment ratio	-	-	-	0.13/0.31
ORC electric efficiency (%)	13.6	10.7	8.9	-
ORC heating efficiency (%)	-	-	87.4	-
ECC thermal COP (-)	-	-	-	0.10/0.21

¹ A single value per row refers to the same value being assumed for all the considered operational modes.

. The thermophysical properties have been calculated using REFPROP [43]. Ejector modeling is based on the 1D model by Huang et al. [39] using the semi-empirical equations from [44].

The ORC electric efficiency, heating efficiency and ECC thermal COP are used for converting the heat input to the ORC-ECC system to net electric power output ($P_{e,net}$), useful heating output (${\dot{Q}}_{heating}$) and cooling output (${\dot{Q}}_{cool}$), respectively, according to the following equations:

$${\eta }_{e,ORC}=\frac{P_{e,net}}{{\dot{Q}}_{ORC-ECC}}$$

(7)

$${\eta }_{h,ORC}=\frac{{\dot{Q}}_{heating}}{{\dot{Q}}_{ORC-ECC}}$$

(8)

$${COP}_{th,ECC}=\frac{{\dot{Q}}_{cool}}{{\dot{Q}}_{ORC-ECC}}$$

(9)

The operation strategy of the ORC-ECC is demand-driven. When there is neither heating nor cooling demand, it operates in electricity-only mode. In this case, all heat recovered from the condenser is rejected to the ambient. When there is heating demand, the ORC-ECC operates in CHP mode. In this case, the cooling water leaving the condenser at 52 °C is used to cover the heating demand. When the heating output is higher than the demand, a part of the heat of the cooling water leaving the condenser is rejected to the ambient. When there is cooling demand, the ORC-ECC operates in ECC mode. The chilled water leaving the ECC cooling evaporator at 8 °C is used to cover part of the cooling demand. Because the cooling produced by the ORC-ECC system is much smaller than the cooling demand of the building, all cooling produced by the ECC is fully utilized.

Finally, as for the simulation of the operation of the overall system, the heat balance of the overall system is represented by the following Equation (10):

$$Q_{TES}=Q_{PTC}-Q_L-Q_{ORC-ECC}$$

(10)

It should be noted that the temperature at the TES must remain within its operation temperature range. Therefore, some of the solar heat may not be absorbed by the TES, if the temperature is already at its maximum level. Finally, a cut-off threshold for the ORC-ECC generator was assumed at 75% of the design thermal input for CHP and electricity mode. For the cooling mode, the respective threshold was considered as 100%. Therefore, if the available solar heat is lower than these thresholds, the ORC-ECC does not operate and the building’s loads are not covered. As a result, higher ORC size may result in fewer hours of operation due to the unavailability of solar heat, especially in the winter. Also, in case of building loads lower than the ORC-ECC cut-off threshold, the ORC-ECC would produce a higher amount of heating or cooling than the required and the surplus would be dumped to the environment. Thus, the utilization of the heating and cooling produced by the trigeneration system could be lower than 100%, and part of the solar heat would be wasted.

The physical model described above is developed in Python 3.9.12 and the simulations are executed with an hourly time step and for a whole year. The results from the building simulations were utilized as inputs to this model, as they define the demand from the ORC-ECC system at each hour. It must be mentioned that the available DNI in Athens (CZ B) and Thessaloniki (CZ C) is equal to 2104.61 kW/m² and 1806.29 kW/m², respectively [30].

2.2.3. Trigeneration System’s Design Scenarios

The most influential design parameters of the trigeneration system that are treated as manipulation variables in the cost-optimal calculations to test their impact are:

• The aperture area of the PTCs;
• The capacity of the TES;
• The size of the ORC-ECC generator.

The rationale for defining the alternative values of the above variables in the framework of the parametric analysis is as follows:

• PTC field aperture area: Regarding the size of the PTC field, larger sizes are usually encountered, since they are more beneficial due to lower specific cost and better efficiency [52]. However, small-scale PTC applications are reported in the literature in building applications [10]. Based on the data presented in [10,52], an aperture area of 300 m² is considered as the minimum. Starting from the latter, the investigation continued with higher sizes, which were multiples of the starting one, up to the point that the results were meaningful in terms of the building’s demand coverage and economic performance. For the office, areas in the ranges of 300–1200 m² with an increasing step of 300 m² were tested. For the hospital, in addition to the latter range, areas in the range of 1200–13,200 m² with an increasing step of 1200 m² were tested.
• ORC generator size: For a given PTC field size, the examined sizes of the ORC generator were defined as a percentage of the peak PTC thermal output. The theoretical thermal output from the PTC field for each examined aperture area was simulated on an hourly basis based on Equations (1)–(4), and the peak output for each CZ is presented in

  Table 3. Theoretical peak thermal output from the PTC field for each examined aperture area.

  Examined PTC Aperture Area (m2)	Peak PTC Thermal Output in CZ B (kW)	Peak PTC Thermal Output in CZ C (kW)
  300	154.01	146.38
  600	316.18	300.36
  900	470.43	460.70
  1200	632.42	605.81
  2400	1252.16	1213.08
  3600	1896.98	1804.53
  4800	2526.18	2451.30
  6000	3130.31	3035.12
  7200	3765.35	3630.30
  8400	4453.44	4267.64
  9600	5054.93	4868.93
  10,800	5692.26	5459.50
  12,000	6308.87	6093.91
  13,200	6950.30	6739.21

  . Considering that the peak output occurs only for a few hours per year, the examined scenarios for the size of the ORC generator were defined as a percentage of the peak thermal output from the PTC field and more specifically from 10% to 60% with a step of 10%.
• TES capacities: For each PTC aperture size and ORC generator capacity, the TES capacity was defined as a multiple of the ORC generator size on the basis of the discharge hours of the TES, therefore allowing for the calculation of the optimal discharge duration. A duration from 3 up to 13 discharge hours per day was considered.

2.2.4. Primary Energy Calculations

From the combined BEM-trigeneration system modeling, the following energy indicators are obtained:

• Energy demand (heating, cooling, DHW);
• Energy use (heating, cooling, DHW, lighting);
• Renewable energy production;
• Delivered energy (consumption of oil and electricity).

Based on the above, the calculation of the PEC from the delivered energy carriers is possible by applying the appropriate primary energy factors, which are 2.9 for electricity and 1.1 for oil [27].

2.3. Environmental Footprint

Based on the energy indicators, the reduction of GHG emissions in terms of carbon dioxide equivalent (CO_2,eq) after the integration of the trigeneration system is calculated (see Figure 1). The final energy consumption per carrier is multiplied by the respective GHG emissions conversion factors as follows:

• CO₂: 0.264 kg/kWh for heating oil [27] and 0.42 for electricity [53]
• CH₄: 1.54 × 10⁻⁵ kg_CH4/kWh for heating oil and 1.12 × 10⁻⁵ kg/kWh for electricity [54]
• N₂O: 7.23 × 10⁻⁶ kg_N2O/kWh for heating oil and 4.173 × 10⁻⁶ kg/kWh for electricity [54]

To calculate the CO_2,eq emissions, the emissions of the CH₄ and N₂O are multiplied by the GWP of each gas, i.e., 1 kg_CO2/kg_CO2 for CO₂, 28 kg_CH4/kg_CO2 for CH₄ and 265 kg_N2O/kg_CO2 for N₂O [54].

2.4. Calculation of Cost Indicators

Within the cost-optimality programming code, a subroutine undertaking the calculation of cost indicators is also included. The steps leading to the calculation of the GC and investment indicators of a trigeneration system’s design scenario for a reference building are presented in Figure 1.

For each combination of the design parameters, the cost indicators presented in the following subsections are computed based on the energy performance indicators.

2.4.1. Calculation of Global Cost

According to the EU’s supplementary regulation on cost-optimality [14], the following equation is used for the calculation of the GC in the case of the alternative designs of the trigeneration system:

$$C_g\left(\tau \right)={CAPEX}_I+\sum _{i=1}^{\tau }\left(C_{\alpha ,i}\ast {\left(\frac{1}{1+\frac{r}{100}}\right)}^i \right)$$

(11)

where:

• τ is the calculation period (years);
• C_g(τ) is the GC over the calculation period (EUR);
• r is the discount rate, considered equal to 3%, as proposed in the Greek guide for conducting energy renovation plans [55];
• CAPEX_I are the capital expenses of the trigeneration system (EUR);
• C_α,i is the annual cost during year i.

The latter consists of the annual energy cost, related to the operation of the building, and the annual operation and maintenance (O&M) cost of the trigeneration system. The capital expenses (CAPEX), the O&M cost and the energy costs of the building are presented in the following subsections. The calculation period is considered equal to 20 years, as recommended in ref. [14].

2.4.2. Trigeneration System’s Techno-Economic Data

The economic data of the system, i.e., the CAPEX and O&M costs of the system’s components, are presented below.

The CAPEX of all components is converted to 2023 economic data (${CAPEX}_{2023}$) from the initially reported value (${CAPEX}_{ref}$) using the Chemical Engineering Plant Cost Index ($CEPCI$) of 2023 (${CEPCI}_{2023}$) and of the reference year corresponding to its component (${CEPCI}_{ref}$), according to the following equation:

$${CAPEX}_{2023}={CAPEX}_{ref}\frac{{CEPCI}_{2023}}{{CEPCI}_{ref}}$$

(12)

The CEPCI values are retrieved from [56].

As for the PTC, a CAPEX of 260 USD₂₀₁₈/m² is considered based on [57], which includes the collectors’ and HTF circuit’s costs and other auxiliary costs. For the TES, a cost of 25 USD₂₀₁₈/kWh_th is retrieved from [36]. Both costs are converted to EUR considering an exchange rate of 0.8475 (average of 2018). The considered values are presented in

Table 4. Considered CAPEX values for the trigeneration system’s components.

PTC	TES	ORC-ECC
300 EUR/m2	30 EUR/kWhth	$\mathrm{10,356.42}\ast P_{e.ORC }^{0.826}$

.

The CAPEX of the ORC-ECC is calculated as a function of the ORC electric power output ($P_{e.ORC}$), using a cost-correlation for ORC modules that was presented by Braimakis [58] taking into account cost data reported in the literature and past studies [59] that was adapted to the year 2022:

$${CAPEX}_{ORC,2022}=\mathrm{10,553}\ast P_{e.ORC }^{0.826}$$

(13)

Considering that the ORC-ECC has very few additional components compared to an ORC (namely ejector and cooling evaporator), Equation (13) can be used to calculate the cost of the whole ORC-ECC system with sufficient accuracy. The considered CAPEX value for the ORC-ECC is presented in Table 4.

The integration of the system into the building heating and cooling distribution network is highly location- and site-specific. For the present study, the integration cost is calculated based on economic data for the integration cost of heat pumps that had been provided by private companies and trade associations of the Greek market and adapted to 2023. Ultimately, the integration cost is calculated from the nominal heat input of the system (${\dot{Q}}_{heating}$) from the following equation:

$$C_{integration,2023}=-0.1028{{\dot{Q}}_{heating}}^2+195.58{\dot{Q}}_{heating}+1055.9$$

(14)

The O&M cost of the system was considered equal to 2% of the CAPEX [11,60]. Finally, the lifetime of the equipment was considered equal to 20 years, which coincides with the calculation period considered in Equation (11). Therefore, no residual value for the equipment was considered in Equation (11). In addition, no equipment replacement cost was considered.

2.4.3. Energy Costs

The energy costs are estimated as follows (considering recent energy prices from August 2022 to July 2023):

• Electricity cost: The calculation was based on the existing electricity charging mechanism in Greece, as presented in ref. [61]. The Greek Public Power Corporation (PPC) issues monthly data regarding fixed and variable electricity charges for different electricity supply bundles, which were used to calculate the electricity costs. The chosen bundle for this study is the G22, which is used in non-residential infrastructure with installed capacity from 25 kVA up to 250 kVA [62]. For the examined buildings, the cost is equal to 0.2695 EUR/kWh.
• Electricity cost reduction in case of local RES production: In Greece, in the case of buildings where electricity from RES or CHP plants is produced locally, the electricity costs are avoided through the implementation of energy-sharing schemes [61]. The produced electricity is consumed locally, while any excess electricity flows to the grid and the owner is compensated by means of avoiding part of the electricity cost. In this study, the trigeneration system’s ability to produce electricity was treated as a RES plant that operates in an energy-sharing scheme, thus reducing the electricity charges of the building. The existing energy-sharing scheme in Greece in the case of local electricity production from RES, as presented in ref. [61], was implemented.
• Oil cost: The oil cost in Greece is published in the Liquid Fuel Price Observatory of the Greek Ministry of Development and Investment on a weekly or daily basis [63]. The average value for the considered period was calculated equal to 1.2432 EUR/lt, including VAT and other taxes. This corresponds to a value of 0.124 EUR/kWh.

Consequently, after the integration of the trigeneration system, a reduction of the electricity consumption and electricity cost is expected, due to the coverage of cooling and possibly heating loads from the system. An additional reduction of the electricity cost is expected due to the local electricity production.

Finally, according to the EU supplementary regulation 244/2012/EU, the evolution of energy prices must be also considered [14]. This refers to the annual increase rate of future energy prices. A typical value of 2.8% is adopted in the current study [19,21,28].

2.4.4. Calculation of Additional Investment Performance Indicators

In addition to the GC, the following key performance indicators (KPIs) are also calculated:

• Discounted payback period (PBP): It is calculated as the year at which the cumulative cash flow (which comes from the annual cost reductions) becomes positive, considering the discounted annual cash flow.
• Net present value (NPV): It is calculated as follows:

$$NPV=-CAPEX+\sum _{i=1}^N\frac{{NCF}_i}{{\left(1+r\right)}^i}$$

(15)

where:

• i is the ongoing year after the implementation of the investment;
• N is the lifespan of the investment, in years, equal to 20 years;
• NCF is the net annual cash flow at year i, in EUR. It is equal to the annual energy cost reductions that are achieved due to the reduction of the heating, DHW and cooling demand and the local production of electricity, after subtracting the O&M cost of the trigeneration system;
• It is noted that a positive NPV indicates a theoretically viable investment.

• Internal rate of return (IRR) is the discount rate at which the NPV equals zero. An IRR greater than the assumed discount rate indicates a viable investment.

3. Results

In this section, initially, the simulation results from the buildings simulation are presented for the two examined buildings in the two CZs, along with the results from the trigeneration system’s simulation for a specific design scenario, to demonstrate the results from both simulation models and the differences between the examined buildings. Then, a sensitivity analysis of the design parameters of the trigeneration system for the two buildings is presented, which leads to conclusions regarding the effect of each design parameter on the performance of the system. After that, the results from the cost-optimality assessment for the two buildings are presented. Based on the latter, an investigation of the economic viability focused on the office building is presented.

3.1. Building and Trigeneration System Simulation Results

The results from the dynamic BEM regarding the buildings’ loads, developed using EnergyPlus, which were retrieved in the form of loads per end use on an hourly basis for a whole year for the office and the hospital building, are presented in Figure 3 and Figure 4, respectively. These results were then fed into the trigeneration system’s simulation model. The peak and average heating and cooling loads for the two buildings in the two CZs are presented in

Table 5. Buildings’ peak and average loads.

Building	Max Heating Load (kW)	Average Heating Load (kW)	Max Cooling Load (kW)	Average Cooling Load (kW)
Office CZ B	258.12	34.46	260.30	124.57
Office CZ C	316.96	63.10	256.61	103.67
Hospital CZ B	3467.08	638.22	3195.25	663.51
Hospital CZ C	4036.58	783.75	3129.55	603.61

. Both buildings have heating and cooling loads in the winter and in the summer, respectively, and lighting and devices loads all over the year. As expected, in both buildings, the heating loads are higher in CZ C and the cooling loads are higher in CZ B. The demands in the hospital building are almost continuous, due to the operation schedule of the building, while there are only a few hours in the winter and in the summer when no heating and no cooling demand exists, respectively. In addition, the demand for DHW is constant throughout the year. On the other hand, the demands of the office building are intermittent due to the intermittent operation schedule. Finally, the demands in the hospital building are much higher than in the office building, as expected due to its larger size and continuous operation schedule. This is also confirmed in

Table 6. Energy indicators for the office and the hospital building.

Energy Indicator	Office CZ B		Office CZ C		Hospital CZ Β		Hospital CZ C
	Absolute Value (kWh)	Normalized Value (kWh/m2)	Absolute Value (kWh)	Normalized Value (kWh/m2)	Absolute Value (kWh)	Normalized Value (kWh/m2)	Absolute Value (kWh)	Normalized Value (kWh/m2)
Energy consumption for heating	29,435.66	11.75	84,992.10	33.94	1,437,130.71	46.91	2,973,139.02	97.05
Energy consumption for cooling	59,609.00	23.80	41,814.75	16.70	1,135,872.41	37.08	843,427.56	27.53
Energy consumption for DHW	0.00	0.00	0.00	0.00	5,298,753.63	172.97	5,298,753.63	172.97
Energy consumption for lighting	121,984.00	48.71	121,984.59	48.71	1,991,157.79	65.00	1,991,157.79	65.00
Energy consumption for devices	27,446.40	10.96	27,446.40	10.96	659,730.63	21.54	659,730.63	21.54
Total oil consumption	29,435.66	11.75	84,992.10	33.94	6,735,884.34	219.88	8,271,892.65	270.02
Total electricity consumption	209,039.4	83.46552	1,912,45.87	76.36	3,786,760.84	123.61	3,494,315.99	114.06
Delivered fuel primary energy	32,379.23	12.93	93,491.31	37.33	7,409,472.78	241.87	9,099,081.91	297.02
Delivered electric primary energy	606,214.26	242.05	554,613.01	221.45	10,981,606.42	358.47	10,133,516.36	330.79
PEC	638,593.48	254.98	648,104.32	258.78	18,391,079.20	600.34	19,232,598.28	627.81

and

Table 7. Annual CO_2,eq emissions for the office and the hospital building.

	Office CZ B		Office CZ C		Hospital CZ Β		Hospital CZ C
	Absolute Value (kg)	Normalized Value (kg/m2)	Absolute Value (kg)	Normalized Value (kg/m2)	Absolute Value (kg)	Normalized Value (kg/m2)	Absolute Value (kg)	Normalized Value (kg/m2)
Annual CO2,eq emissions	95,933.43	38.30	103,232.12	41.22	3,389,892.51	110.66	3,675,760.20	119.99

, where the annual values of several energy indicators and of CO_2,eq emissions, respectively, are presented for the two buildings. In terms of normalized values, the normalized energy demand per each end use in the hospital is higher than the office, which is expected due to its continuous operation. As a result, the PEC and the CO_2,eq emissions are higher for the case of the hospital. Finally, for both buildings, both the PEC and the emissions are slightly higher in Zone C.

Following the feeding of the simulated buildings’ loads in the physical model of the trigeneration system, the performance of the system is computed for various design parameters’ values. Indicatively, to better understand the introduced simulation procedure and the consequent computed indicators, the modeling results for a specific design, i.e., PTC aperture area of 300 m², an ORC size equal to 20% of the peak PTC thermal output (i.e., 31 kW and 29 kW in CZ B and CZ C, respectively) and a TES capacity capable of 13h of discharge (i.e., 400 kWh and 380 kWh in CZ B and CZ C, respectively), are presented in Figure 5 and

Table 8. Main annual energy results from the trigeneration system’s simulation for the two examined buildings in the two CZs.

Building	Office CZ B	Office CZ C	Hospital CZ B	Hospital CZ B
Solar heat from PTCs (MWh)	208.42	177.04	208.99	177.77
Produced heating (MWh)/Heating demand coverage (%)	7.39/30.27	12.84/18.19	42.22/3.54	45.86/1.86
Produced cooling (MWh)/Cooling demand coverage (%)	5.75/3.58	4.27/3.78	19.11/0.65	13.82/0.63
Produced electricity (MWh)/Electricity demand coverage (%)	18.95/9.07	15.92/8.32	6.55/0.17	6.44/0.18
Produced DHW (MWh)/DHW demand coverage (%)	-/-	-/-	15.17/0.34	10.60/0.24
ORC heat utilization (%)	65.36	82.72	100.00	100.00
ORC cool utilization (%)	94.89	94.69	98.31	98.17

. Considering the ORC-ECC efficiencies and COP (see Table 2), the trigeneration system has a nominal heating capacity of 27 kW and 25 kW in CZ B and CZ C, respectively. The cooling capacity in the summer is equal to 3.1 kW and 2.9 kW in CZ B and CZ C, respectively, while it is higher in the spring and autumn due to the higher COP (see Table 2). Moreover, the minimum heating capacity (i.e., 75% of the nominal) is 20.25 kW and 18.75 kW in CZ B and CZ C, respectively, while the minimum cooling capacity is the same as the nominal.

Figure 5 depicts the outputs from the trigeneration system in each building. In the case of the office building, both the heating and the cooling output are intermittent, following the demand of the building. Electricity is produced during the hours with no heating or cooling demand, if there is available thermal energy, as well as during the hours when the system operates in CHP mode. On the contrary, in the case of the hospital, the heating and cooling output is almost continuous during the winter and the summer months, respectively, due to the building’s continuous heating demand, while during spring and autumn, there are several hours when there is no demand for heating or cooling. In these hours, DHW is produced, as its demand is continuous throughout the year. As a result, the system never operates in electricity-only mode. Finally, it can be observed that the heating capacity (27 kW) is close to the average heating load of the office building, while it is much lower than the average heating load of the hospital building (see Table 5).

The difference in the operation of the trigeneration system in the two buildings can be also deducted from Table 8, where annual results describing the operation of the trigeneration system in the examined buildings and CZs are presented. It is observed that the distribution of the heat produced by the collectors is different in the two buildings, based on their demands. Solar heat is mainly utilized for heating and cooling in the case of the hospital building, as the produced heating and cooling is higher than the office building. Thus, in the latter, more electricity is produced. As for DHW production in the hospital building, it is lower than heating since heating is prioritized over DHW. The demand coverage in the case of the hospital is lower, due to the building’s high loads compared to the trigeneration system’s heating and cooling capacity. Nevertheless, the latter results in a complete utilization of the heating and cooling produced by the trigeneration system. In the case of the office, the minimum heating output (20.25 kW) is higher than the heating load at some hours (see Figure 3). At these hours, the produced heat is higher than the heating demand of the building, and thus the surplus heat is dumped. The cooling output is generally lower than the respective building’s loads, and therefore the utilization of the cooling output is high. Concerning differences due to location, Table 8 dictates that the annual production of solar heat is lower in the case of CZ C, due to the lower availability of DNI. Moreover, in both buildings, more heating and less cooling are produced by the trigeneration system in CZ C, as expected, while the production of DHW in the hospital building in CZ B is higher. The electricity production is similar in both CZs.

Concerning the impacts at the building level, the results are presented in

Table 9. Main annual energy results after the integration of the trigeneration system for the two examined buildings in the two CZs.

	Office CZ B	Office CZ C	Hospital CZ B	Hospital CZ B
Reduction in oil consumption (MWh/%)	8.91/30.26	15.46/18.19	69.14/1.03	68.04/0.82
Reduction in electricity consumption (MWh/%)	19.08/9.13	15.81/8.27	11.61/0.31	9.84/0.28
PEC reduction (kWh/m2/%)	26.02/10.20	25.11/9.70	43.81/0.59	41.28/0.54
CO2,eq emissions reduction (tn/%)	10.41/10.86	10.78/10.45	23.31/0.69	22.27/0.61

. As expected, the reduction of oil consumption is higher in the case of the hospital, as the trigeneration system produces more heating, as well as DHW, while the electricity consumption reduction is higher in the case of the office building. The reduction of both the PEC and the emissions is higher in the case of the hospital building. This shows that the implementation of the same system has a higher impact on the PEC and emissions reduction in the case of the hospital. Regarding the differences between the CZs, the PEC and emissions reduction are similar, even though there are differences in the reduction of oil and electricity.

Finally, the economic assessment of the trigeneration system in the examined buildings is presented in

Table 10. Economic and investment indicators regarding the integration of the trigeneration system in the two examined buildings in the two CZs.

	Office CZ B	Office CZ C	Hospital CZ B	Hospital CZ B
GC (EUR)	1,165,915.49	1,207,615.97	33,882,585.78	36,138,979.12
CAPEX (EUR)	142,071.07	139,833.76	14,2071.07	139,833.76
Oil cost reduction in the first year	1105.99	1920.00	8583.50	8446.03
Electricity cost reduction in the first year	4000.83	3313.41	2925.61	2463.26
Cash flow in the first year (EUR)	2390.32	2556.59	8792.62	8232.48
NPV (EUR)	−86,004.38	−80,605.78	34,330.08	26,189.17
IRR (%)	−4.53	−4.04	5.20	4.72
Discounted PBP (years)	75.77	63.31	16.19	16.92

. The GC is calculated based on Equation (11). The annual cash flow in the case of the hospital is higher than that of the office, due to the higher reduction in oil costs. Moreover, based on the NPV, IRR and discounted PBP, the integration of the system in the office building is a non-viable investment, contrary to the hospital building, for which the indicators suggest a viable investment.

Overall, it can be concluded that the implementation of the same trigeneration system has a higher impact on the PEC and emissions reduction and a higher economic performance in the case of the hospital. Two factors leading to that result can be identified:

• The continuous demand for heating from the hospital building, which causes longer operation of the ORC-ECC in CHP mode instead of electricity-only mode in the winter. In

  Table 11. PEC, emissions and energy cost reduction per kWh of solar heat in the different operating modes of the ORC-ECC.

  Operating Mode of ORC-ECC	Produced Heating (kWh)	Produced Cooling (kWh)	Produced Electricity (kWh)	PEC Reduction (kWh)	Emissions Reduction (kg)	Energy Cost Reduction (EUR)
  CHP	0.870	0.000	0.089	1.411	0.317	0.154
  Electricity-only	0.000	0.000	0.136	0.394	0.057	0.037
  Cooling-only (summer)	0.000	0.100	0.000	0.112	0.016	0.010
  Cooling-only (spring)	0.000	0.210	0.000	0.234	0.034	0.022

  , the PEC, emissions and energy cost reduction at each operating mode of the ORC-ECC is calculated, considering the primary energy and emission factors, the efficiency of the heating and cooling systems (see Table 1), the efficiencies of the ORC-ECC (see Table 2) and the energy costs. As shown, the highest reduction of all indicators is achieved in CHP mode. Thus, the operation in CHP mode, which is constant in the hospital building during winter, is the most beneficial mode of operation.
• The lower utilization of the heat produced from the ORC in the case of the office. A higher utilization would lead to higher PEC and emissions reduction and higher annual cash flow.

As for cooling, the operation in cooling-only mode has the lowest performance. As a result, the hospital building’s almost constant cooling demand during summer leads to a worse performance compared to the office, where the system operates in cooling mode only during the operation schedule of the building. However, this is counterbalanced by the better performance in the winter.

3.2. Sensitivity Analysis of the Design Parameters

In this section, indicative results from the two buildings that demonstrate the differences between the examined scenarios and the impact of the design parameters on the system’s performance are presented. The results correspond to indicative PTC sizes for the two buildings. In Figure 6, Figure 7, Figure 8 and Figure 9, the variation of energy, environmental and economic indicators for different ORC and TES sizes is presented, for a PTC size of 300 m² for the office and 7200 m² for the hospital building, both in CZ B.

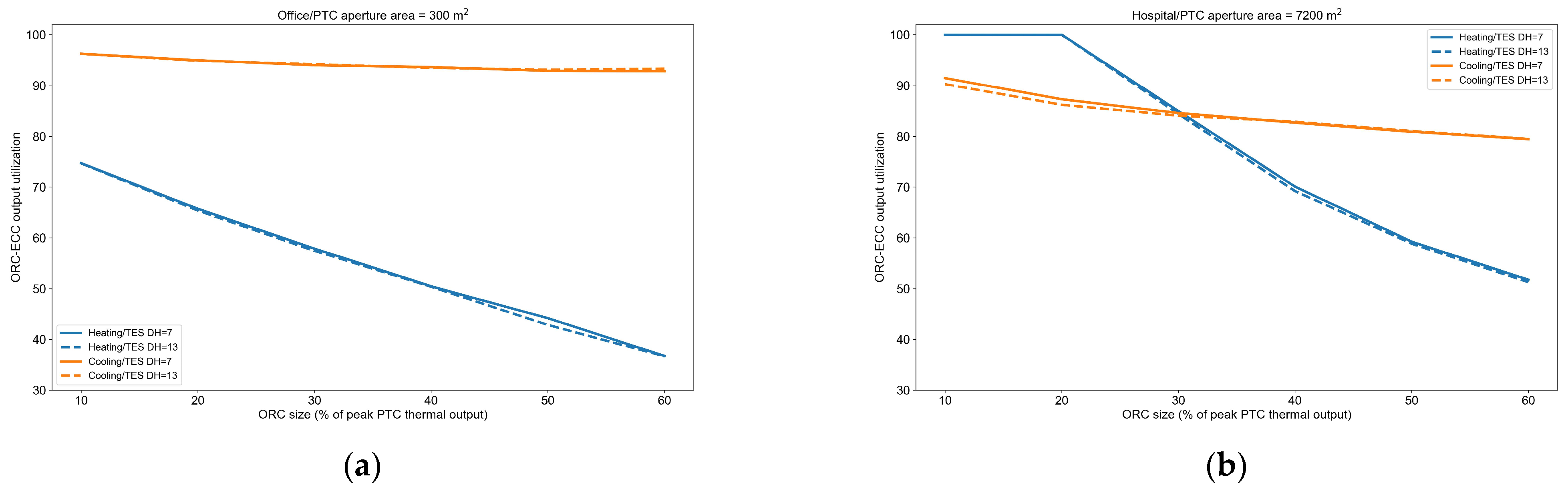
In Figure 6, the variation of the PEC and the GC of the building for increasing ORC size is presented, for two different sizes of the TES. For smaller ORC sizes, the increase in the size leads to a decrease in both the PEC and the GC, as the trigeneration system produces more output, leading to the minimum GC. A further increase in the ORC size results in a further decrease of the PEC, while the GC increases, as the higher CAPEX cannot be counterbalanced by the additional benefit. Finally, a further increase in the ORC size results in an increase of both the GC and the PEC, suggesting a decrease in the energy production from the system. This is related to the cut-off threshold of the ORC-ECC, which, as the ORC size increases, results in fewer hours of operation and lower utilization of the solar heat, as explained above. The lower utilization of the ORC-ECC outputs for an increasing ORC size can be also verified from Figure 7, where the utilization of the ORC-ECC outputs for an increasing ORC size is presented. The impact is lower in the utilization of cooling since the cooling output is much lower than the cooling demand due to the low COP. As for the TES capacity, its increase results in more beneficial values of PEC and GC for lower ORC sizes, as more heat can be stored, while for larger ORC sizes, the increase of the TES capacity is not beneficial. Moreover, the TES size has a low impact on the outputs’ utilization.

Regarding the NPV (Figure 8), in the case of the office building, only negative values are obtained, while positive values appear for the hospital. The optimal NPV is achieved for medium ORC sizes, while the increase of the TES capacity leads to higher NPV values. Moreover, as expected, for each TES size, the optimal NPV value occurs for the same ORC size as the one for the optimal GC. Finally, the CO_2,eq emissions reduction (Figure 9) is inversely proportional to the PEC reduction, as expected, and is higher for higher TES capacity. A maximum of around 14% and 16% emission reduction is observed for the office and the hospital building, respectively.

From the above, it can be concluded that the increase in the ORC size is beneficial only up to a certain point, while the increase in the TES size leads to more beneficial PEC and GC values at lower ORC sizes.

In Figure 10, the GC-PEC plots for the two buildings are presented for indicative consecutive values of the examined PTC sizes. For a specific PTC size, the variation of the GC and PEC that was presented in Figure 6 can be observed. Furthermore, as the PTC size increases, higher reduction of the PEC can be achieved as more solar heat is available. In the case of the office, this leads to a higher GC. In the case of the hospital, the medium PTC size presented (7200 m²) shows lower GC values than the other sizes. This difference between the buildings is related to the building loads.

3.3. Cost-Optimality Assessment

In the following sections, the cost-optimality assessment results are presented for the two examined buildings. The results are presented mainly in the form of the GC-PEC plot, which allows the identification of the cost-optimal scenario and its respective PEC level. In these plots, the scenarios with a negative NPV are marked with a red circle. Also, to better demonstrate the effect of a different PTC size, a line is depicted in the plots, which shows the scenarios with the minimum GC for each examined PTC size. Finally, the cost-optimal scenario is marked with yellow.

3.3.1. Office Building

The GC-PEC plots for the office building in the two CZs are presented in Figure 11. The optimal scenario in both CZs is observed for the lowest examined PTC size, as expected. Moreover, in all examined scenarios, the NPV is negative, suggesting a non-viable investment. Regarding the comparison between the CZs, in CZ C the points are shifted towards higher PEC and GC values, due to the higher PEC of the building in CZ C. Other than that, the variation of the points is similar in the two CZs. In addition, in Figure 12, the GC and PEC, which correspond to the line frontiers of cost minima of Figure 11, together with the NPV are presented for CZ B. As the PTC size increases, the GC and the PEC vary inversely, while the NPV decreases, remaining negative in all scenarios. This suggests that the increase of the PTC size is not beneficial in the case of the office, as for larger sizes the additional energy cost reduction is not enough to counterbalance the higher CAPEX.

The design characteristics of the cost-optimal scenarios in the two CZs are presented in

Table 12. Design characteristics of the cost-optimal scenarios for the office building.

CZ	PEC (kWh/m2)	GC (EUR/m2)	PTC Size (m2)	ORC Size (kW)	ORC Size (% of Peak PTC Thermal Output)	TES Size (kWh)	TES Discharge Hours
B	228.96	465.53	300	31	20	400	13
C	233.67	482.18	300	29	20	380	13

, while the trigeneration system performance in these design scenarios is presented in

Table 13. Energy, environmental and economic indicators of the trigeneration system at the cost-optimal scenarios for office building.

CZ	B	C
Thermal energy from PTC (MWh)	208.42	177.04
Produced heat (MWh)	7.39	12.84
Produced cooling (MWh)	5.75	4.27
Produced electricity (MWh)	18.95	15.92
ORC heat utilization (%)	65.36	82.72
ORC cooling utilization (%)	94.89	94.69
PEC reduction (MWh)	65.17	62.88
PEC reduction (%)	10.20	9.70
Emissions reduction (tn)	10.41	10.78
Emissions reduction (%)	10.86	10.45
CAPEX (EUR)	142,071.07	139,833.76
Cash flow at 1st year	2390.32	2556.59
NPV (EUR)	−86,004.38	−80,605.78
IRR (%)	−4.53	−4.04
Discounted PBP (years)	75.77	63.31

. The cost-optimal PTC size, ORC size as a percentage of the peak PTC thermal output and TES discharge hours are the same in the two CZs. As for the trigeneration system’s performance, the produced heating and cooling is balanced in CZ B, while more heating is produced in CZ C, due to the higher heating load. Overall, the reduction of PEC and emissions is around 10–11% in both CZs. The economic indicators are not acceptable in both cases, while their values are slightly better in CZ C. Finally, the utilization of the outputs from the trigeneration system is higher in the case of cooling compared to heating. This is because the ORC size, and thus the heating capacity of the system, is higher than the building’s heating loads at some hours (see Figure 3). The latter confirms the observation made in Figure 12 regarding the higher GC and lower NPV at higher PTC sizes. More specifically, higher PTC size entails higher ORC and heating capacity, which in turn results in lower utilization of the heat from the ORC. This leads to lower economic performance.

3.3.2. Hospital Building

The GC-PEC plots for the hospital building in the two CZs are presented in Figure 13. In this case, many scenarios present a positive NPV. Comparing performances between the CZs, similar conclusions as in the case of the office can be drawn, while the variation of the points in the plot is similar in the two CZs. Moreover, in Figure 14, the GC and PEC and the NPV of the scenario with the minimum GC for each examined PTC field aperture area are presented. As the PTC size increases, the GC initially decreases, reaching its optimal value for a PTC size of 7200 m². After this point, the GC increases, as the additional energy cost reduction is not enough to counterbalance the impact of the CAPEX on the GC. The NPV has an inverse variation, reaching its optimal value at the same PTC size, while it remains positive in all cases. On the other hand, the PEC constantly decreases as the PTC size increases, as more solar heat is produced from the trigeneration system. The above findings suggest that a larger PTC field is beneficial for the hospital up to a certain point, as the higher PEC reduction can result in a reduction of the GC.

The design parameters’ values of the cost-optimal scenarios in the two CZs are presented in

Table 14. Design characteristics of the cost-optimal scenarios for the hospital building.

CZ	PEC (kWh/m2)	GC (EUR/m2)	PTC Size (m2)	ORC Size (kW)	ORC Size (% of Peak PTC Thermal Output)	TES Size (kWh)	TES Discharge Hours
B	517.78	1070.30	7200	753	20	9790	13
C	537.19	1145.81	8400	854	20	11,096	13

, while the trigeneration system’s performance indicators in these scenarios are presented in

Table 15. Energy, environmental and economic indicators of the trigeneration system at the cost-optimal scenarios for the hospital building.

CZ	B	C
Thermal energy from PTC (MWh)	4949.32	4972.37
Produced heat (MWh)	434.13	724.47
Produced DHW (MWh)	912.73	809.43
Produced cooling (MWh)	411.28	344.55
Produced electricity (MWh)	153.62	178.54
ORC heat utilization (%)	100.00	97.99
ORC cooling utilization (%)	86.21	83.90
PEC reduction (MWh)	2529.07	2775.97
PEC reduction (%)	13.75	14.43
Emissions reduction (tn)	540.34	600.23
Emissions reduction (%)	15.94	16.33
CAPEX (EUR)	3,012,948	3,468,277
Cash flow at 1st year	207,350.5	225,743.1
NPV (EUR)	1,128,542	1,063,690
IRR (%)	6.31	5.75
Discounted PBP (years)	14.64	15.40

. The optimal PTC size is higher in the case of CZ B, while the annual thermal energy produced from the collectors is similar. The cost-optimal ORC size as a percentage of the peak PTC thermal output and the TES discharge hours are the same in the two CZs. As for the trigeneration system’s performance, the distribution of heating and cooling is different, with more heating and electricity produced in CZ C and more cooling and DHW in CZ B. However, the reduction of PEC and emissions is similar, around 14% and 16%, respectively, in both CZs. Also, the economic indicators are acceptable and slightly better in CZ B. Finally, in contrast to the office building case, the utilization of both outputs from the trigeneration system is high.

3.3.3. Cost-Optimal Design Compared to the Building Energy Demand

To further analyze the cost-optimal design, in

Table 16. Buildings’ loads and cost-optimal values of the design parameters.

	Office CZ B	Office CZ C	Hospital CZ B	Hospital CZ C
Heating capacity of trigeneration system (kW)	27.09	25.35	658.12	746.40
Heating capacity of trigeneration system (% of max building load)	10.49	8.00	18.98	18.49
Cooling capacity of trigeneration system (kW)	3.10	2.90	75.30	85.40
Cooling capacity of trigeneration system (% of max building load)	1.19	1.13	2.36	2.73

, the heating and cooling capacity at the cost-optimal scenario is compared to the building’s maximum and average loads (see Table 5), while the building’s demand coverage from the trigeneration system is presented in

Table 17. Coverage of building’s demands at cost-optimal scenario.

	Office CZ B	Office CZ C	Hospital CZ B	Hospital CZ C
Heating demand coverage (%)	30.27	18.19	36.39	29.36
Cooling demand coverage (%)	3.58	4.27	13.92	15.71
DHW demand coverage (%)	-	-	20.75	18.40
Electricity demand coverage (%)	9.07	8.32	4.17	5.23

. In the case of the hospital, the heating load corresponds to the sum of the heating and DHW load of the building. The cost-optimal heating and cooling capacity in terms of a percentage of the maximum buildings’ loads in the examined buildings and CZs is equal to 8–19% of the maximum heating load and 1–3% of the maximum cooling load of the building. Also, in both buildings, the system’s heating capacity is similar to the average heating load of the building (see Table 5). Moreover, the heating demand coverage is higher in the buildings in CZ B (see Table 17). Meanwhile, the cooling demand coverage is higher in the hospital building and electricity demand coverage is higher in the office building. However, in all cases, the demand coverage in the cost-optimal scenario is limited to a rather low value.

Overall, it can be concluded that despite the differences between the buildings, the heating and cooling capacity in terms of a percentage of the maximum buildings’ loads and the heating demand coverage are similar in the examined buildings and CZs.

3.4. Economic Viability in the Office Building

As presented in the previous sections, the economic indicators in the case of the office building suggest a non-viable investment, even in the cost-optimal scenario. Two parameters that could improve the viability are identified, namely the utilization of the produced heat, which could be higher, and the CAPEX, whose reduction would improve the economic indicators. The influence that those parameters could have on the economic viability is investigated below.

3.4.1. Higher Utilization of Produced Heat

As presented in the cost-optimal results of the office building, the utilization of the heat produced by the ORC is lower than 100% in both CZs (see Table 13). To investigate the influence of higher heat utilization, the calculation of the economic indicators of the cost-optimal scenarios in CZ B and CZ C was repeated, considering a full utilization of the heat produced by the ORC. More specifically, the surplus of heat was considered to be utilized, resulting in an additional income. The economic indicators are presented in

Table 18. Energy and economic indicators at the cost-optimal scenario.

CZ	Surplus Heat (kWh)	Additional Annual Income in the First Year (EUR)	Cash Flow in the First Year (EUR)	NPV (EUR)	IRR (%)	Discounted PBP (Years)	GC (EUR/m2)
B	3918.05	585.35	2975.667	−77,295.90	−3.578	56.40	462.05
C	2680.93	400.52	2957.11	−74,647.00	−3.40	53.37	479.80

. The effect of the full utilization of the surplus heat is important, as an additional annual income of 400–600 EUR resulted in an improvement of the economic indicators compared to those in Table 13. However, the economic indicators’ values still suggest a non-viable investment.

3.4.2. CAPEX Reduction

The non-beneficial economic indicators in the case of the office occurred mainly because of the high CAPEX, which is not compensated by the cost reductions achieved after the implementation of the system. Thus, reductions in the CAPEX could lead to a viable investment. To investigate that, the CAPEX value that would lead to NPV equal to zero was calculated for the cost-optimal scenario. The results are presented in

Table 19. Necessary CAPEX reduction for viable investment in the cost-optimal scenario of the office building.

Building	Initial CAPEX (EUR)	CAPEX for NPV = 0 (NPV)	Necessary Reduction of CAPEX (%)
Office CZ Β	142,071.10	56,067.03	60.53
Office CZ C	139,833.76	59,227.90	57.64

. Based on the results, the minimum reduction of the CAPEX to achieve economic viability is around 58–61%.

4. Discussion

In the cost-optimal scenarios, the ORC size as a percentage of the peak PTC thermal output and the TES discharge hours were found to be the same in all buildings and CZs, despite the differences between the buildings and CZs. This was expected based on the results presented in Figure 6 and Figure 8, which show that a smaller ORC size and a large TES size result in more beneficial economic indicators in both buildings. Nevertheless, the cost-optimal PTC size and absolute ORC and TES size were different. The increase in the PTC area was not beneficial for the office (see Figure 12), while an increase up to a certain point was beneficial for the hospital (see Figure 14). The latter was also affected by the lower cost per kW of the ORC-ECC at higher ORC sizes (see Table 4). Moreover, in both examined buildings and both CZs, the heating and cooling capacities were found to be a fraction of the maximum loads of the building (see Table 16). Also, in both buildings, the trigeneration system covered part of the building’s demand (see Table 17). Regarding heating, this is expected because, in the winter, the availability of solar energy is low in some hours, also depending on the region. Thus, a large system would be required to cover the whole demand. Regarding cooling, the low COP of the ECC would also require a large system to cover the whole cooling demand, which would not be viable. From the above, it can be concluded that in the cost-optimal scenario, the proposed system covers part of the building’s demand, thus reducing the energy consumption, cost and emissions, but does not fully replace the building’s heating and cooling system. Due to that fact, the proposed trigeneration system requires auxiliary heating and cooling systems, something that is also mentioned in other studies regarding solar trigeneration systems [9,64]. In addition, even though the cost-optimal scenario was different in the two buildings, the heating and cooling capacity as a percentage of the buildings’ loads was similar, at 8–19% for heating and 1–3% for cooling (see Table 16). Also, in both buildings, even though the absolute reduction of PEC and emissions was different, the percentage of reduction was similar at around 10–14% and 10–16% for PEC and emissions reduction, respectively (see Table 13 and Table 15). The PEC and GC at the cost-optimal scenario of the office building (see Table 12) are higher than those reported in the Greek official national report on the minimum energy performance requirements for office buildings [28] and in a relevant study on office buildings in Greece [22], where values as low as 114.4 kWh/m² and 358.35 EUR/m² for the PEC and GC, respectively, are mentioned at the cost-optimal scenario for the office building in CZ B [28]. However, these more cost-efficient results are obtained by combinations of several EE and RES measures and not regarding a single intervention as obtained in this study. Overall, despite the differences between the two building types, the cost-optimal system size corresponds to a similar percentage of the building’s loads, while the expected relative reduction of PEC and emissions is also similar.

Regarding the operation of the trigeneration system, two parameters were found to be different between the two buildings, i.e., the operating mode of the ORC-ECC system and the degree of utilization of the heat produced by the ORC. Both affected the cost-optimal scenario and the profitability of the trigeneration system. The operating mode of the ORC-ECC was found to be related to the building’s operation schedule. In the hospital building, CHP operation occurs more often than in the office in the winter, due to the almost continuous heating demand and the continuous DHW demand that stem from the continuous schedule. This resulted in better energy and economic performance, as CHP mode was found to have the best performance among the ORC-ECC operating modes (see Table 11). The more frequent operation in cooling-only mode in the hospital compared to the office had a negative effect, as cooling-only was found to have the lowest performance. However, overall, the positive effect of the operation in CHP mode dominated, resulting in acceptable economic performance in the hospital, contrary to the office. From that, it can be concluded that the building schedule affects the performance of the system, with a continuous schedule being more beneficial.

The second parameter, i.e., the utilization of the heat produced by the ORC, was found to be related to the scale of the heating loads of the building in comparison to the size of the trigeneration system, which depends on the building’s size. In the office, at the minimum examined PTC aperture area, the utilization of the produced heat was lower than 100% (see Figure 7), due to the building’s heating loads being lower than the minimum trigeneration system’s heating output for some hours. At higher PTC sizes, the heating capacity is higher, and thus the heat utilization is lower, which negatively affects the economic performance. The heat utilization could be improved with a PTC size lower than the minimum examined, which is, however, not realistic. On the other hand, in the hospital, at PTC sizes larger than the minimum size, the heat utilization was almost complete (see Figure 7), due to the building’s high loads. That resulted in acceptable economic indicators at larger PTC sizes. Overall, considering the minimum PTC size, it can be concluded that the integration of the proposed system in buildings with higher loads would be more beneficial. Furthermore, regarding the effect of the two parameters, it was shown that even if the surplus heat were fully utilized, the economic indicators would remain unacceptable, even though they would be improved (see Table 18). Thus, the negative effect of the intermittent operation schedule of the office would not be counterbalanced. Finally, it must be mentioned that, as for the cooling loads, their scale is not as important, since due to the low COP of cooling, the trigeneration system’s minimum cooling capacity was found to be lower than the cooling demand for most of the hours.

From the economic assessment, it was found that the hospital building is a suitable facility for integrating the proposed trigeneration system in terms of economic performance, mainly due to its continuous operation schedule and high demand for heating and cooling. Viable economic performance has also been reported in the literature for solar trigeneration systems [64]. Based on that, buildings with high and continuous heating and cooling demands, such as year-round hotels, would be the most suitable candidates along with hospitals. Moreover, residential buildings with high loads, such as multi-family houses, or district heating applications could be suitable, due to their continuous demand. On the other hand, in the office building, less beneficial economic indicators were calculated compared to those obtained by the cost-optimality survey for combinations of various EE and RES technologies in office buildings in Greece [22,28]. It was found that a reduction of the CAPEX is required in the case of the office building to achieve acceptable investment indicators, due to its intermittent operation and lower demands. Such reductions could be expected in the future, as the involved technologies become more widespread and mature and benefit from economies of scale [65]. However, in the current environment, some form of financial support is required. This support could be provided in the form of subsidies that would decrease the CAPEX. In addition, subsidies are a common measure of promoting the deployment of new technologies, as proposed in ref. [66]. Moreover, public buildings generally constitute a suitable category of buildings for implementing new energy technologies due to the exemplary role that public buildings should have in the demonstration of new technologies, according to the EU directives [66,67]. Thus, they could be eligible to receive subsidies to implement the proposed trigeneration system. Therefore, public offices, education buildings, sports halls, medical facilities and multi-purpose buildings could be considered suitable demonstration buildings, as the implementation of the system in these buildings could become viable through subsidies.

Based on the results from this study, it can be expected that in larger-scale building applications, the cost-optimal design would lead to a larger system as well as to a similar percentage of PEC and emissions reduction. Regarding the economic performance, a higher performance could be expected in larger applications. PTC systems are usually implemented in large-scale applications [10], since they can benefit from economies of scale that exist for larger plants and have lower specific costs, as well as higher efficiency [52,57,65]. In addition, the lower specific cost of the ORC and integration cost at larger sizes (see Equations (13) and (14)) would have a beneficial effect on the economic performance of the system.

The implementation of the proposed system requires the consideration of several, technical challenges The issue of area availability is important, especially in the case of the hospital building, in which the cost-optimal system consists of a PTC field with a substantial aperture area, while an even larger area would be required to install the whole system, considering the spaces between the PTCs rows and space required for the TES and ORC-ECC equipment. Thus, the area availability requirements could pose a challenge in the deployment of the system, especially in buildings located in urban areas. Moreover, even if the required area is available, alternative uses of this space could be considered by the buildings’ managers. The installation of the PTC field on the rooftop of the examined building could be investigated. However, in this case, issues such as the available rooftop area, wind protection and the securing of integrity of the bearing structure should be addressed and may result in additional costs. Furthermore, the integration of the trigeneration system into the building’s heating and cooling distribution network is site-specific, requires additional equipment (pipes, heat exchangers, pumps, etc.) and could be challenging. Finally, factors such as the availability of suitable commercial expanders, the higher cost of piping, valves and vessels and the flammability of the ORC-ECC working fluid can be limiting factors, especially in the case that the implementation of a high-temperature ORC-ECC system in a building is considered.

Finally, as for the limitations of the study, both the buildings’ heating, cooling and electricity loads and the thermal power production from the PTC field were calculated from simulations based on typical meteorological weather data rather than utilizing actual measurements from both the buildings and from an existing PTC system. The latter could provide more realistic results regarding the energy and economic performance of the system. Moreover, in the calculations, the off-design operation of the trigeneration system, e.g., the part-load operation of the ORC-ECC’s pump or expander, was not considered. Thus, regarding future work, a pilot implementation of the proposed system in a building would provide measurements, allow a more realistic calculation of the system’s performance and reveal the most important technical challenges of the system’s implementation. Moreover, regarding the ORC-ECC, the techno-economic performance of a trigeneration system with a high-temperature ORC-ECC, which would better exploit the high temperature of the PTC field and could achieve a higher thermal efficiency and COP, should be investigated. It must be mentioned that the methodology that was described and implemented in this study could be replicated for the case of different regions, by considering the weather data, typical building characteristics and economic environment of the region. Therefore, an investigation of the system’s techno-economic performance in different regions, as well as for different building types, e.g., hotels, multi-family houses or district heating applications, would allow the assessment of the potential of the proposed system to contribute to the decarbonization of the building sector. Finally, the methodology that was presented in this study could be implemented for the assessment of the techno-economic performance of other novel energy technologies.

5. Conclusions

In this study, the 244/2012/EU regulation’s cost-optimal methodology was implemented for the assessment of a solar trigeneration system consisting of PTCs, TES and ORC-ECC in tertiary sector buildings in Greece. The chosen building types were an office and a hospital, due to the differences in their operation schedule. For each building type, a reference building was established based on features that are mostly encountered in the Greek building stock, while its energy loads and demand were calculated on an hourly basis by means of a dynamic energy simulation. Moreover, a model for the simulation of the trigeneration system’s operation and performance was developed. By varying the system’s design parameters, different design scenarios were defined and indicators related to the energy, environmental and economic performance of the system at each scenario were calculated, leading to the identification of the cost-optimal scenario at each building. The assessment was conducted for two CZs that are the most populated by the considered building types in Greece.

The dynamic energy simulation of the buildings revealed that the hospital building has higher PEC, CO_2,eq emissions and energy loads compared to the office, due to its continuous operation schedule and larger size. A key finding from the study was that these two characteristics are decisive in the profitability of the implementation of the system in each building. As for the operation schedule, the continuous heating demand of the hospital resulted in longer operation of the ORC-ECC in CHP mode, which was found to be the most efficient mode, contrary to the office where the system operated in CHP mode only during its operation schedule. Also, the higher heating loads of the hospital resulted in higher utilization of the heat produced by the ORC, contrary to the office, where an amount of surplus heat was dumped. As for cooling, due to the low COP of the ORC-ECC in cooling mode, the utilization of the produced cooling was high in both buildings.

Furthermore, significant findings occurred regarding the cost-optimal size of the trigeneration system and the PEC and emissions reduction. As for the cost-optimal scenario, in the investigated size range, an ORC size corresponding to 20% of the peak PTC thermal output was found to be optimal. As for the TES capacity, 13 h of discharge was found to be optimal in all examined buildings and CZs. Finally, the cost-optimal PTC size was found within the examined range, being the minimum examined size, i.e., 300 m² for the office, as the increase of the size was not beneficial. In the hospital, the cost-optimal PTC aperture area was equal to 7200 m² in CZ B and 8400 m² in CZ C. Despite the differences in the cost-optimal scenario, the heating and cooling capacity as a percentage of the building’s peak heating and cooling load was found to be similar in both buildings, being 8–19% for the heating capacity and 1–3% for the cooling capacity. The coverage of the heating demand in the two buildings ranged from 18 to 36%, while the cooling demand coverage, which was higher in the hospital, remained below 16% in all examined cases. As a result, the existence of auxiliary heating and cooling systems is necessary. Furthermore, the integration of the trigeneration system in the office reduced the PEC by 62.88–65.17 MWh and the CO_2,eq emissions by 10.41–10.78 tn, depending on the CZ. The respective reduction in the hospital was higher, being 2529.07–2775.97 MWh for the PEC and 540.34–600.23 tn for the CO_2,eq emissions. Nevertheless, the relative reduction of these indicators was similar in the two buildings, with the PEC reduction being around 10% in the office and 14% in the hospital and the CO_2,eq reduction being 10% in the office and 16% in the hospital. In addition, the different weather conditions in CZ B and C resulted in different heating and cooling loads, which resulted in a different cost-optimal scenario in the hospital. However, the energy, environmental and economic indicators were similar between the examined CZs.

Finally, the economic performance of the system in the hospital building was found to be acceptable, with a discounted PBP of around 15 years. On the contrary, for the office, the economic indicators suggested a non-viable investment. Therefore, subsidies of at least 58–61% of the CAPEX would be necessary for implementing the suggested system in an office.

Overall, the main implication of the results of this study is that the implementation of the examined solar trigeneration system can contribute to the decarbonization of buildings, due to its potential for decreasing emissions and PEC, as well as energy costs. Provided that the necessary investment financing is available, the presented calculations suggest that the proposed system would be indeed a viable investment for building decarbonization purposes. Meanwhile, maintaining the conventional heating and cooling systems of the building as auxiliary systems remains necessary.