ANN for Temperature and Irradiation Prediction and Maximum Power Point Tracking Using MRP-SMC
Highlights
- The study introduces a hybrid approach that integrates Artificial Neural Networks (ANNs) for precise weather forecasting with the Minimum-Risk Problem and Sliding Mode Control (MRP-SMC) algorithm. This method optimizes the performance of photovoltaic (PV) panels by dynamically adjusting the Maximum Power Point (MPP) based on environmental predictions, leading to improved energy recovery efficiency.
- The model, trained on extensive temperature and solar radiation data, shows high accuracy in energy forecasting, enhancing reliability in real-time energy output predictions. This contributes to optimized energy distribution, reduced reliance on conventional energy, and better integration of renewable energy into the grid.
- The study's method offers a significant leap in autonomous photovoltaic (PV) system optimization by integrating advanced AI-based predictions with robust control mechanisms. This eliminates the need for additional hardware, simplifying the system design while maintaining high accuracy and adaptability to environmental changes.
- The successful implementation of the proposed method creates new possibilities for the future of Maximum Power Point Tracking (MPPT) in solar systems. By developing a robust monitoring system integrated with intelligent real-time error detection and correction, the efficiency and reliability of solar energy systems can be further enhanced, potentially leading to more widespread and effective deployment of solar technology.
Abstract
1. Introduction
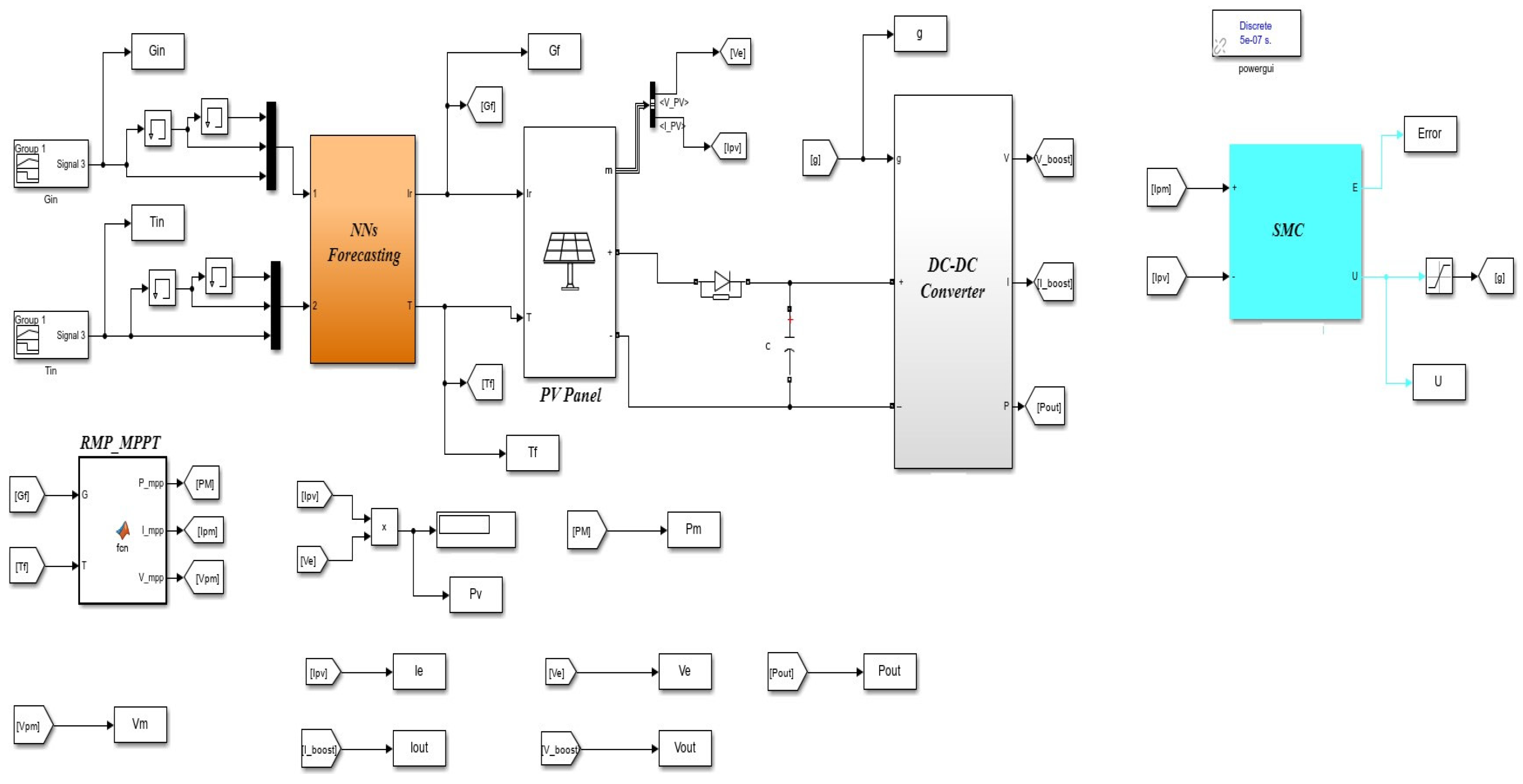
2. Methodology
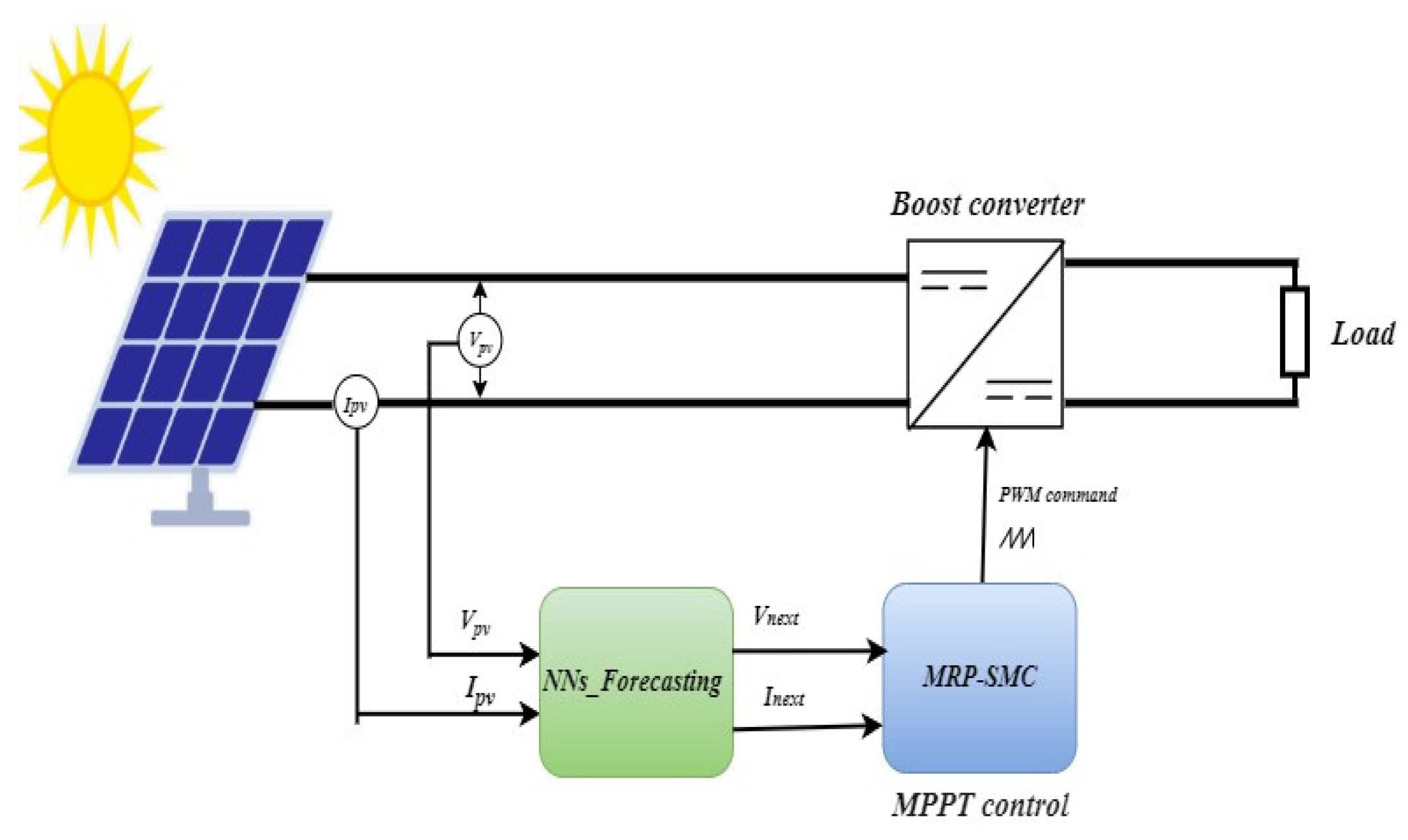
2.1. PV Panel Modeling
2.2. Hybrid MPPT Control
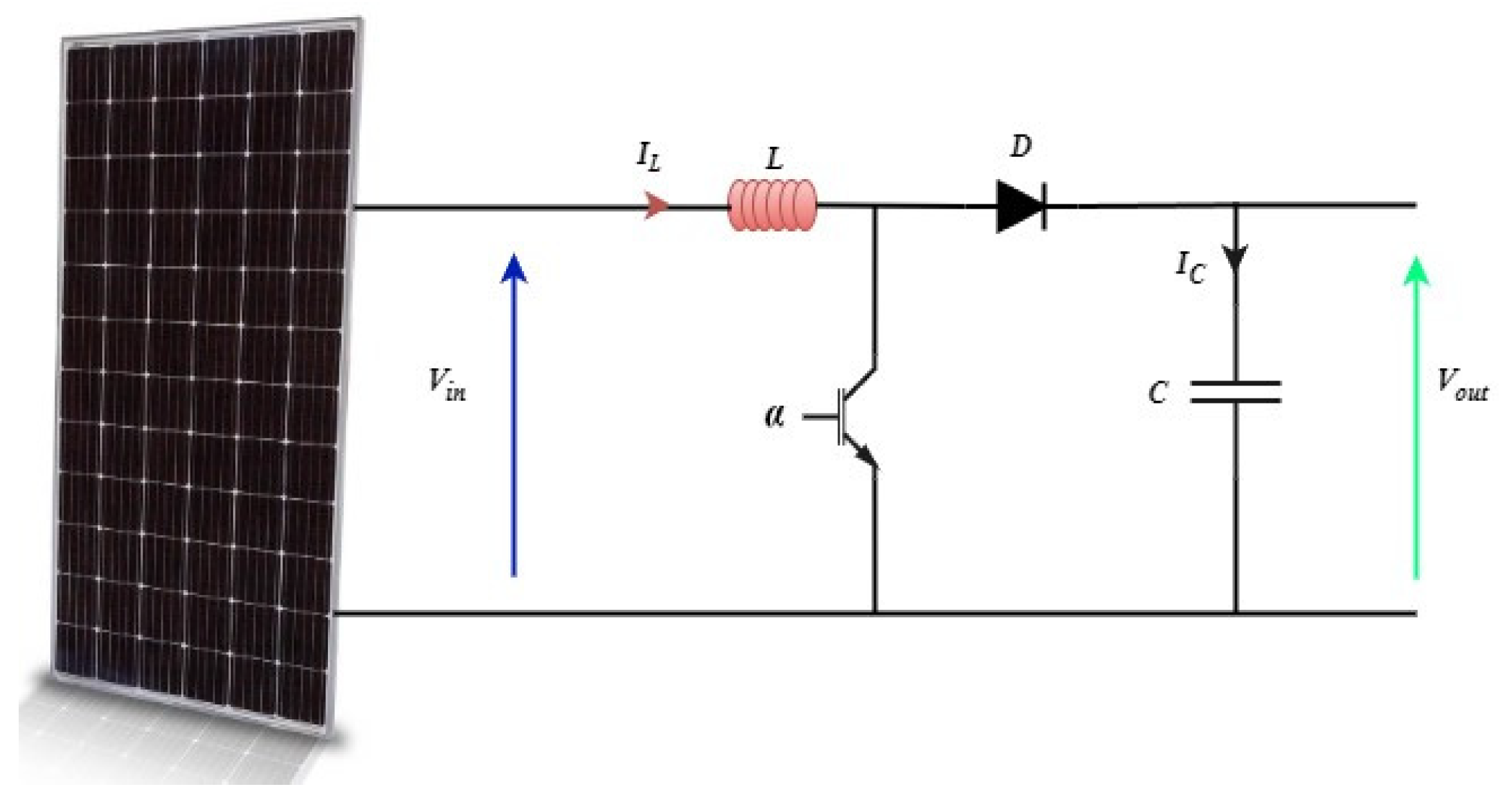
2.2.1. Boost Converter Model
2.2.2. MRP-SMC Hybrid MPPT Control
- The MPPT approach
- 2.
- Sliding Mode Controller
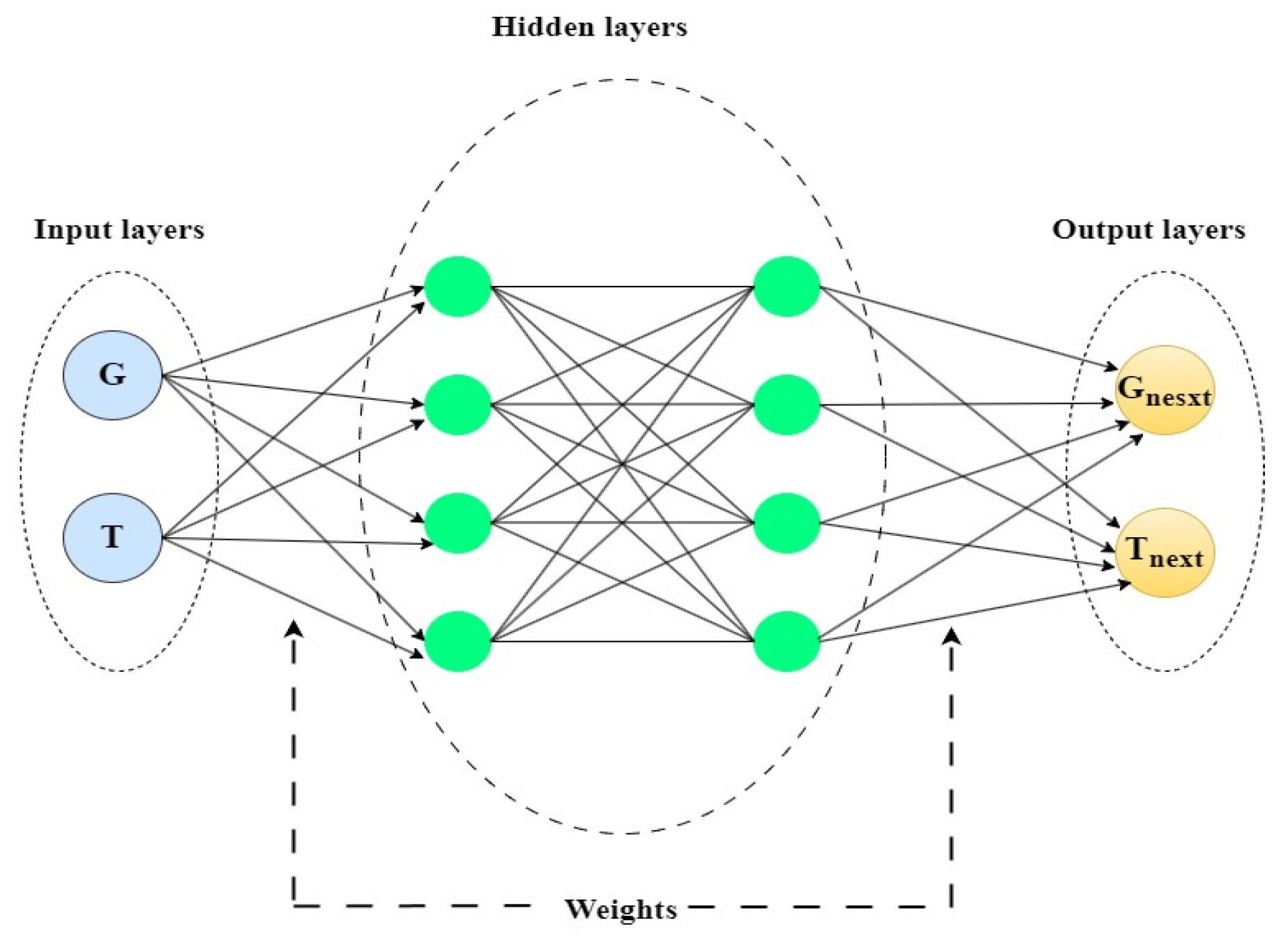
3. Neural-Network-Based Predictive Models
- Y: the output layer;
- σ: The activation function;
- Wi,j represents the weight linking the ith neuron in the preceding layer to the jth neuron in the current layer;
- Xj: The output of the ith neuron in the previous layer;
- β: Biases.
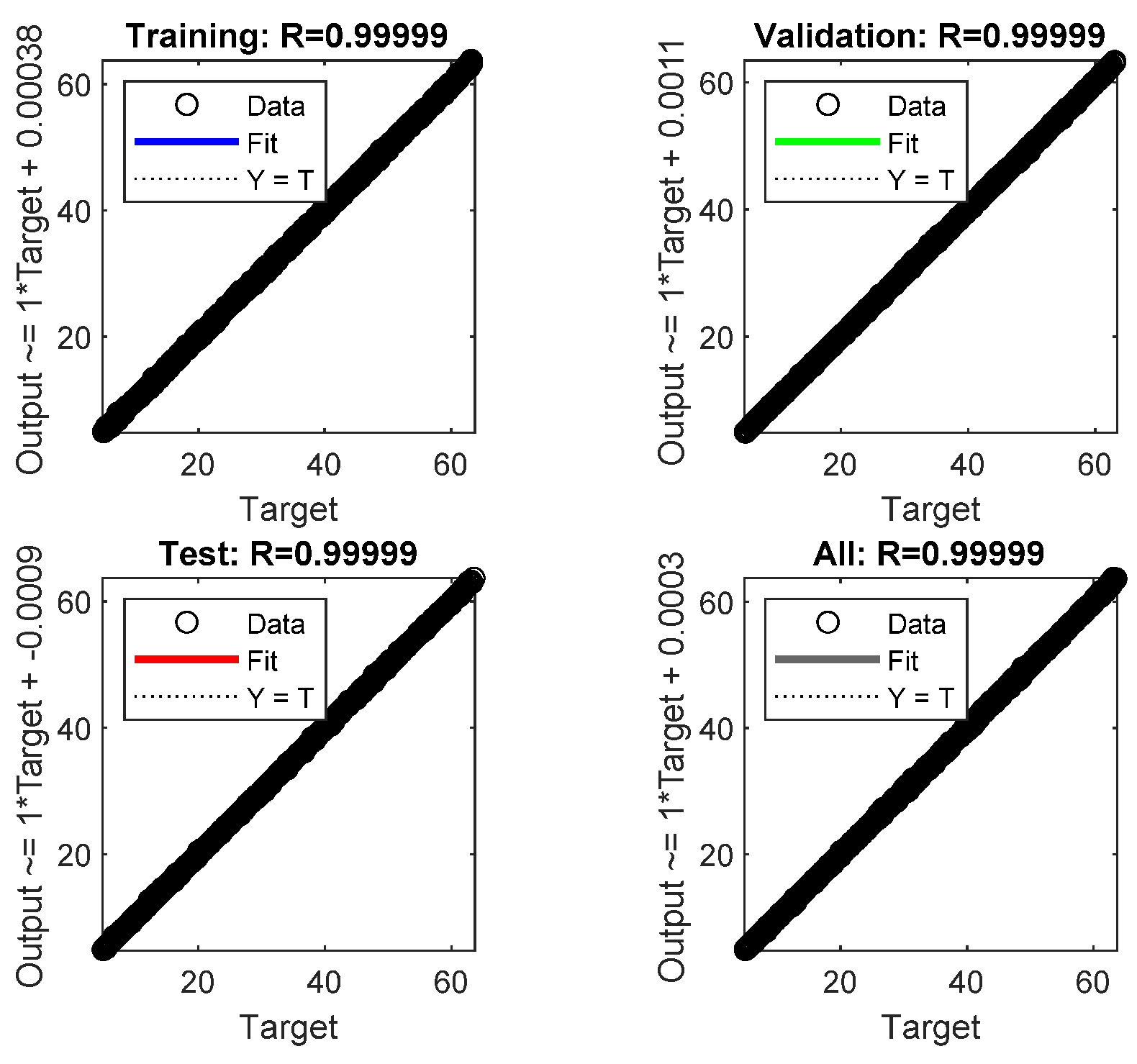
4. Results
5. Comparative Study
5.1. Forecasting Method Comparison
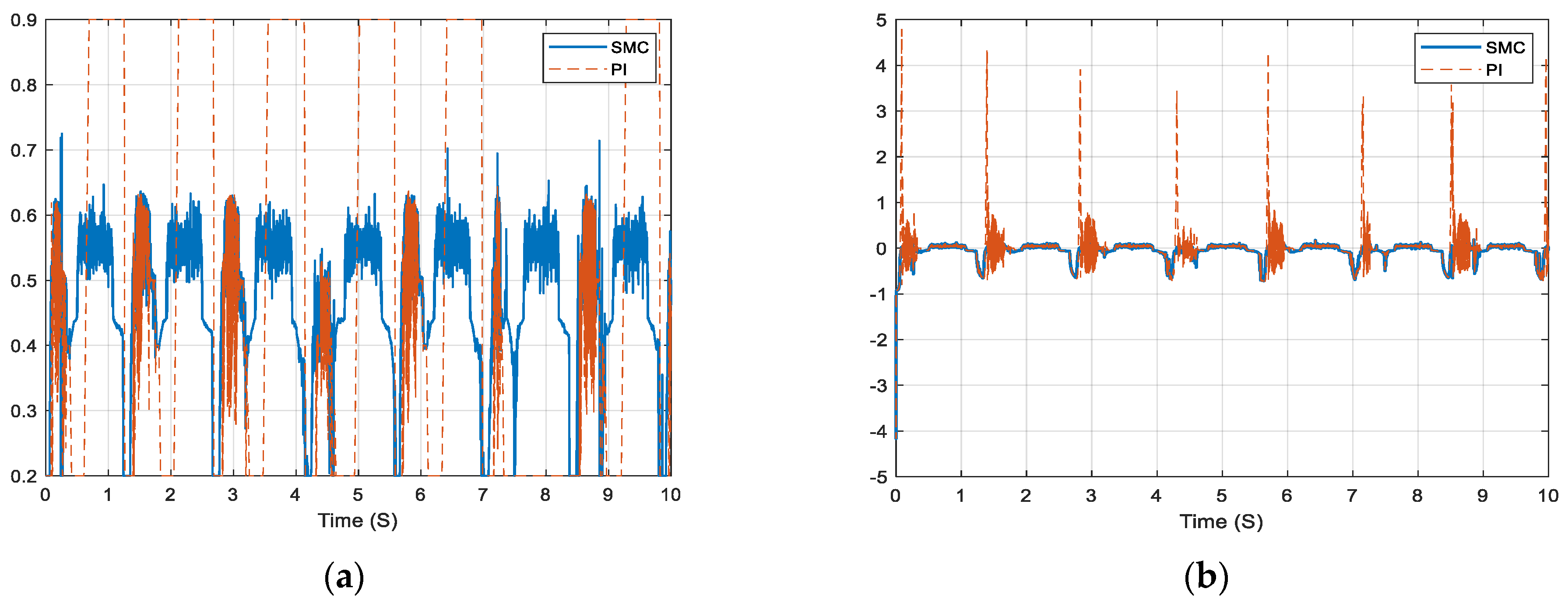
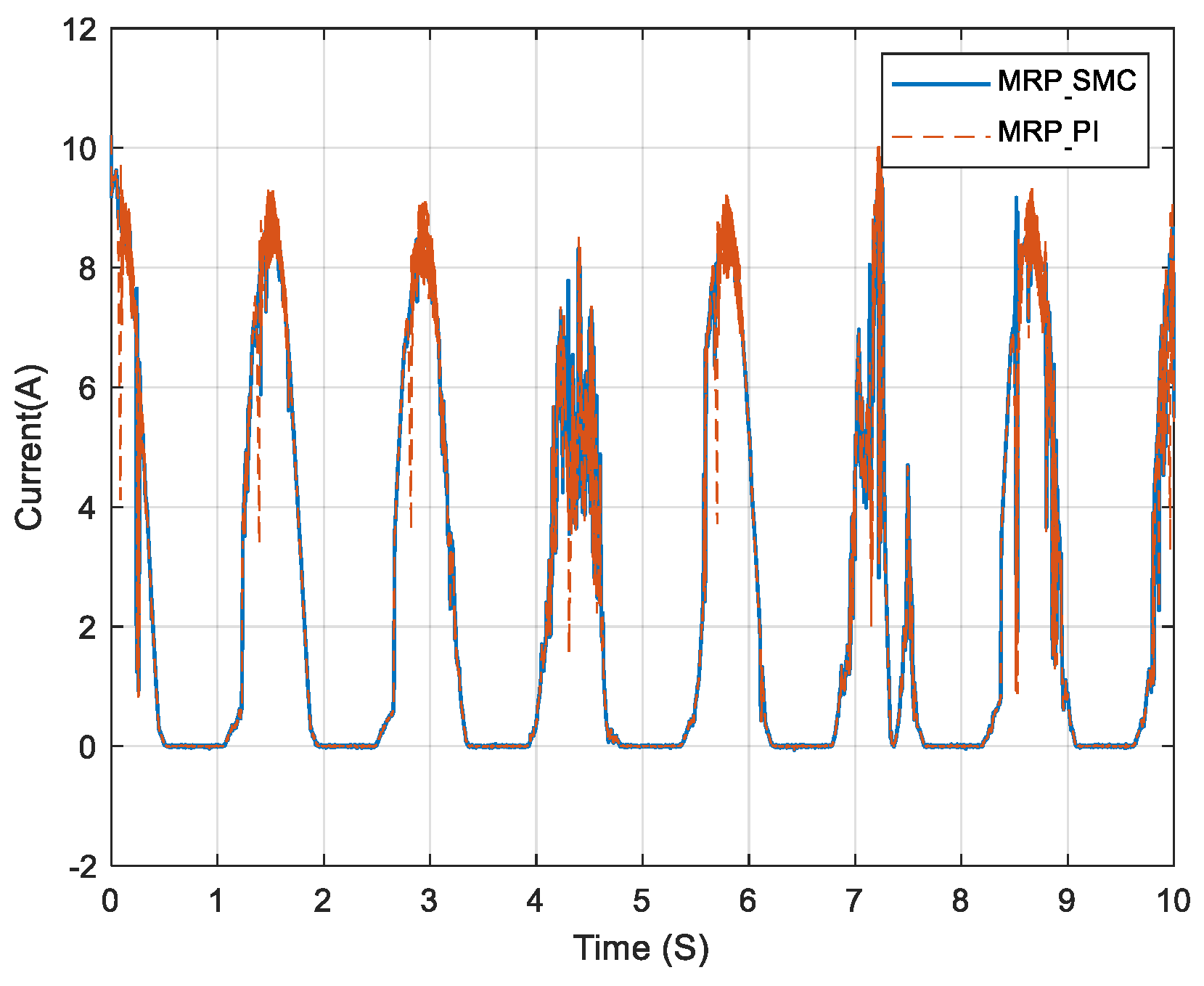
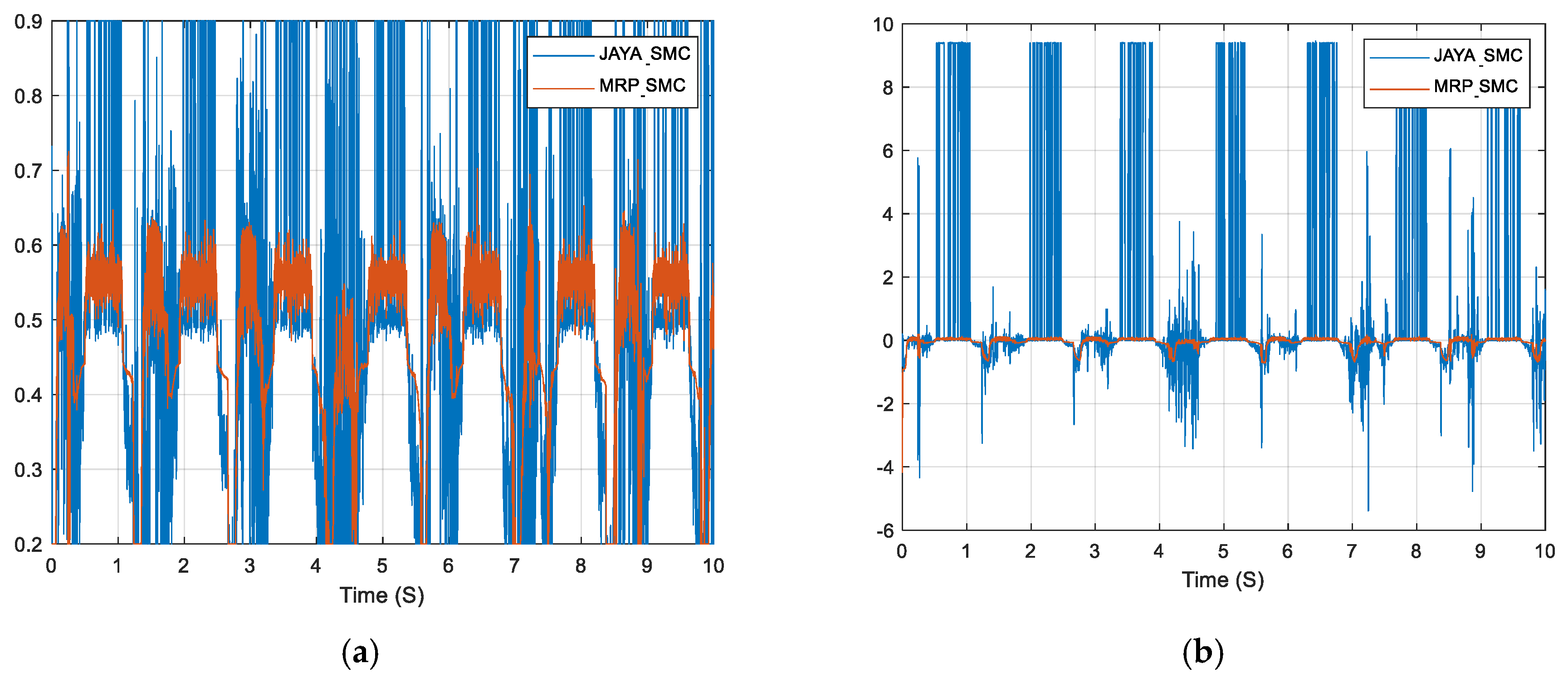
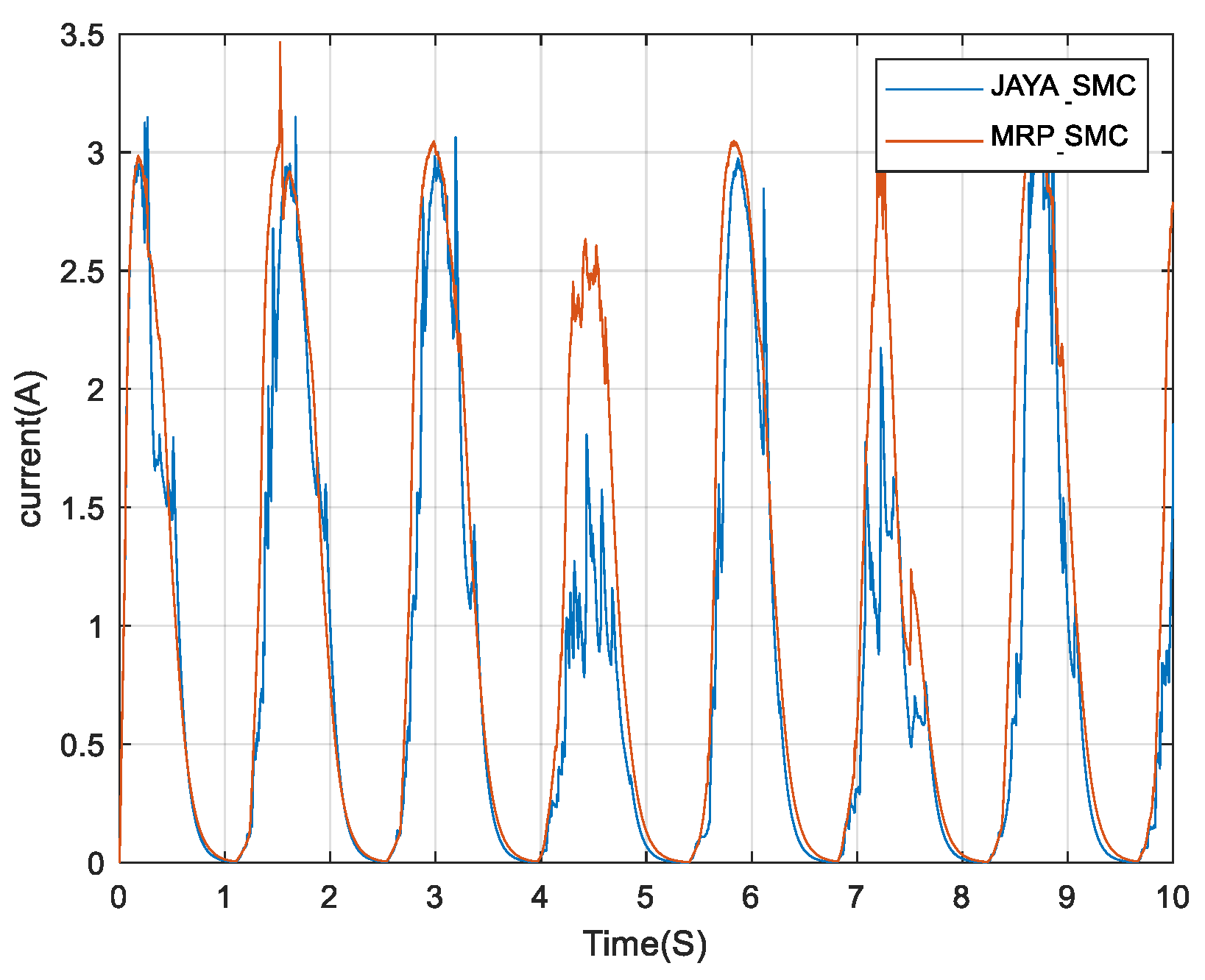
5.2. MPPT Approach Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| AI | Artificial Intelligence |
| NN | Neural Network |
| R | Regression |
| MSE | Mean Squared Error |
| MPP | Maximum Power Point |
| MPPT | Maximum Power Point Tracking |
| PV | Photovoltaic |
| P&O | Perturb and Observe |
| Tanh | Hyperbolic Tangent |
| OCV | Open-Circuit Voltage |
| SCC | Short-Circuit Current |
| SMC | Sliding Mode Control |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| PI | Proportional Integral |
| DC | Direct Current |
| IC | Incremental Conductance |
| QSVM | Quadratic Support Vector Machine |
| CNN-BILSTM | Convolution Neural Network–Bi-Direction Long Short-Term Memory |
| ANFIS | Adaptive Neuron Fuzzy Inference System |
| GMDH | Group Method of Data Handling |
| ANFIS-PSO | Adaptive Neuron Fuzzy Inference System–Particle Swarm Optimization |
| SCG | Scaled Conjugate Gradient |
| SOP | Stochastic Optimization Problem |
Appendix A. Sensor Specifications
| Properties | Values |
| Voltage | 12–28 V |
| Irradiance measurement range | Up to 1500 W/m2 |
| Temperature measurement range | −40 to 90 °C |
Appendix B. PV Panel Parameters
| Maximum power (Pmax) | 340 W |
| Voltage at Pmax (Vmp) | 36.7 V |
| Current at Pmax (Imp) | 9.28 A |
| Open-circuit voltage (Voc) | 45.2 V |
| Short circuit current (Isc) | 9.9 A |
Appendix C. The Boost Specifications
| Properties | Values |
| Switching frequency | 20 kHz |
| Maximum input voltage | 60 V |
| Maximum output voltage | 250 V |
| Maximum input current | 30 A |
| Maximum output current | 30 A |
Appendix D. JAYA Algorithm
|
References
- Song, D.; Liu, Y.; Qin, T.; Gu, H.; Cao, Y.; Shi, H. Overview of the policy instruments for renewable energy development in China. Energies 2022, 15, 6513. [Google Scholar] [CrossRef]
- Asif, M.H.; Zhongfu, T.; Ahmad, B.; Irfan, M.; Razzaq, A.; Ameer, W. Influencing factors of consumers’ buying intention of solar energy: A structural equation modeling approach. Environ. Sci. Pollut. Res. 2023, 30, 30017–30032. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, D.; Odyuo, Y. An ab initio issues on renewable energy system integration to grid. Int. J. Sustain. Energy Plan. Manag. 2019, 23. [Google Scholar] [CrossRef]
- Azarpour, A.; Mohammadzadeh, O.; Rezaei, N.; Zendehboudi, S. Current status and future prospects of renewable and sustainable energy in North America: Progress and challenges. Energy Convers. Manag. 2022, 269, 115945. [Google Scholar] [CrossRef]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A comprehensive review of maximum power point tracking (mppt) techniques used in solar pv systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Nkambule, M.S.; Hasan, A.N.; Ali, A.; Hong, J.; Geem, Z.W. Comprehensive evaluation of machine learning MPPT algorithms for a PV system under different weather conditions. J. Electr. Eng. Technol. 2021, 16, 411–427. [Google Scholar] [CrossRef]
- Verma, D.; Nema, S.; Agrawal, R.; Sawle, Y.; Kumar, A. A different approach for maximum power point tracking (MPPT) using impedance matching through non-isolated DC-DC converters in solar photovoltaic systems. Electronics 2022, 11, 1053. [Google Scholar] [CrossRef]
- Khodair, D.; Motahhir, S.; Mostafa, H.H.; Shaker, A.; Munim, H.A.E.; Abouelatta, M.; Saeed, A. Modeling and Simulation of modified MPPT techniques under varying operating climatic conditions. Energies 2023, 16, 549. [Google Scholar] [CrossRef]
- Radia, M.A.; El Nimr, M.K.; Atlam, A.S. IoT-based wireless data acquisition and control system for photovoltaic module performance analysis. E-Prime-Adv. Electr. Eng. Electron. Energy 2023, 6, 100348. [Google Scholar] [CrossRef]
- Rojek, I.; Mikołajewski, D.; Mroziński, A.; Macko, M. Machine Learning-and Artificial Intelligence-Derived Prediction for Home Smart Energy Systems with PV Installation and Battery Energy Storage. Energies 2023, 16, 6613. [Google Scholar] [CrossRef]
- Sharma, A.K.; Pachauri, R.K.; Choudhury, S.; Minai, A.F.; Alotaibi, M.A.; Malik, H.; Márquez, F.P.G. Role of metaheuristic approaches for implementation of integrated MPPT-PV systems: A comprehensive study. Mathematics 2023, 11, 269. [Google Scholar] [CrossRef]
- Mehazzem, F.; André, M.; Calif, R. Efficient Output Photovoltaic Power Prediction Based on MPPT Fuzzy Logic Technique and Solar Spatio-Temporal Forecasting Approach in a Tropical Insular Region. Energies 2022, 15, 8671. [Google Scholar] [CrossRef]
- Koeva, D.; Kutkarska, R.; Zinoviev, V. High Penetration of Renewable Energy Sources and Power Market Formation for Countries in Energy Transition: Assessment via Price Analysis and Energy Forecasting. Energies 2023, 16, 7788. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Sajid, I.; Gautam, A.; Sarwar, A.; Tariq, M.; Liu, H.D.; Ahmad, S.; Sayed, A.E. Optimizing Photovoltaic Power Production in Partial Shading Conditions Using Dandelion Optimizer (DO)-Based MPPT Method. Processes 2023, 11, 2493. [Google Scholar] [CrossRef]
- Akman, D.V.; Malekipirbazari, M.; Yenice, Z.D.; Yeo, A.; Adhikari, N.; Wong, Y.K.; Gumus, A.T. k-best feature selection and ranking via stochastic approximation. Expert Syst. Appl. 2023, 213, 118864. [Google Scholar] [CrossRef]
- Triki, Y.; Bechouche, A.; Seddiki, H.; Abdeslam, D.O. An improved incremental conductance based MPPT algorithm for photovoltaic systems. In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Thirunavukkarasu, G.S.; Seyedmahmoudian, M.; Jamei, E.; Horan, B.; Mekhilef, S.; Stojcevski, A. Role of optimization techniques in microgrid energy management systems—A review. Energy Strategy Rev. 2022, 43, 100899. [Google Scholar] [CrossRef]
- Du, Y.; Xu, F. A hybrid multi-step probability selection particle swarm optimization with dynamic chaotic inertial weight and acceleration coefficients for numerical function optimization. Symmetry 2020, 12, 922. [Google Scholar] [CrossRef]
- Jlidi, M.; Hamidi, F.; Abdelkrim, M.N.; Jerbi, H.; Abbassi, R.; Kchaou, M. Synthesis of an Advanced Maximum Power Point Tracking Method for a Photovoltaic System: A Chaotic Jaya Logistic Approach. In Proceedings of the 2022 4th International Conference on Applied Automation and Industrial Diagnostics (ICAAID), Hail, Saudi Arabia, 29–31 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Chaitanya, K.; Somayajulu, D.V.; Krishna, P.R. Memory-based approaches for eliminating premature convergence in particle swarm optimization. Appl. Intell. 2021, 51, 4575–4608. [Google Scholar] [CrossRef]
- Alshammari, B.M.; Farah, A.; Alqunun, K.; Guesmi, T. Robust design of dual-input power system stabilizer using chaotic Jaya algorithm. Energies 2021, 14, 5294. [Google Scholar] [CrossRef]
- Yang, J.; Hu, Y.; Zhang, K.; Wu, Y. An improved evolution algorithm using population competition genetic algorithm and self-correction BP neural network based on fitness landscape. Soft Comput. 2021, 25, 1751–1776. [Google Scholar] [CrossRef]
- Zafar, M.H.; Khan, N.M.; Mirza, A.F.; Mansoor, M.; Akhtar, N.; Qadir, M.U.; Moosavi, S.K.R. A novel meta-heuristic optimization algorithm based MPPT control technique for PV systems under complex partial shading condition. Sustain. Energy Technol. Assess. 2021, 47, 101367. [Google Scholar] [CrossRef]
- Colbu, Ş.C.; Popescu, D.; Băncilă, D.M.; Mone, M.A.; Petrescu-Niţă, A. Stochastic Optimization and Risk Problems for Engineering Applications. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; pp. 775–779. [Google Scholar] [CrossRef]
- Ampountolas, A. Modeling and forecasting daily hotel demand: A comparison based on sarimax, neural networks, and garch models. Forecasting 2021, 3, 580–595. [Google Scholar] [CrossRef]
- Kurani, A.; Doshi, P.; Vakharia, A.; Shah, M. A comprehensive comparative study of artificial neural network (ANN) and support vector machines (SVM) on stock forecasting. Ann. Data Sci. 2023, 10, 183–208. [Google Scholar] [CrossRef]
- Gourvenec, S.; Sturt, F.; Reid, E.; Trigos, F. Global assessment of historical, current and forecast ocean energy infrastructure: Implications for marine space planning, sustainable design and end-of-engineered-life management. Renew. Sustain. Energy Rev. 2022, 154, 111794. [Google Scholar] [CrossRef]
- Acharya, S.K.; Wi, Y.M.; Lee, J. Day-ahead forecasting for small-scale photovoltaic power based on similar day detection with selective weather variables. Electronics 2020, 9, 1117. [Google Scholar] [CrossRef]
- Ellahi, M.; Usman, M.R.; Arif, W.; Usman, H.F.; Khan, W.A.; Satrya, G.B.; Shabbir, N. Forecasting of Wind Speed and Power through FFNN and CFNN Using HPSOBA and MHPSO-BAACs Techniques. Electronics 2022, 11, 4193. [Google Scholar] [CrossRef]
- Jlidi, M.; Hamidi, F.; Barambones, O.; Abbassi, R.; Jerbi, H.; Aoun, M.; Karami-Mollaee, A. An Artificial Neural Network for Solar Energy Prediction and Control Using Jaya-SMC. Electronics 2023, 12, 592. [Google Scholar] [CrossRef]
- Kabilan, R.; Chandran, V.; Yogapriya, J.; Karthick, A.; Gandhi, P.P.; Mohanavel, V.; Manoharan, S. Short-term power prediction of building integrated photovoltaic (BIPV) system based on machine learning algorithms. Int. J. Photoenergy 2021, 2021, 5582418. [Google Scholar] [CrossRef]
- Rai, A.; Shrivastava, A.; Jana, K.C. A CNN-BiLSTM based deep learning model for mid-term solar radiation prediction. Int. Trans. Electr. Energy Syst. 2021, 31, e12664. [Google Scholar] [CrossRef]
- Obiora, C.N.; Ali, A.; Hasan, A.N. Estimation of hourly global solar radiation using deep learning algorithms. In Proceedings of the 2020 11th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 29–31 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Petković, D. Adaptive neuro-fuzzy approach for solar radiation prediction in Nigeria. Renew. Sustain. Energy Rev. 2015, 51, 1784–1791. [Google Scholar] [CrossRef]
- Khosravi, A.; Nunes, R.O.; Assad, M.E.H.; Machado, L. Comparison of artificial intelligence methods in estimation of daily global solar radiation. J. Clean. Prod. 2018, 194, 342–358. [Google Scholar] [CrossRef]
- Halabi, L.M.; Mekhilef, S.; Hossain, M. Performance evaluation of hybrid adaptive neuro-fuzzy inference system models for predicting monthly global solar radiation. Appl. Energy 2018, 213, 247–261. [Google Scholar] [CrossRef]
- Yilmaz, U.; Kircay, A.; Borekci, S. PV system fuzzy logic MPPT method and PI control as a charge controller. Renew. Sustain. Energy Rev. 2018, 81, 994–1001. [Google Scholar] [CrossRef]
- Idrissi, Y.E.A.; Assalaou, K.; Elmahni, L.; Aitiaz, E. New improved MPPT based on artificial neural network and PI controller for photovoltaic applications. Int. J. Power Electron. Drive Syst. 2022, 13, 1791. [Google Scholar] [CrossRef]
- Tang, J.; Ni, H.; Peng, R.L.; Wang, N.; Zuo, L. A review on energy conversion using hybrid photovoltaic and thermoelectric systems. J. Power Sources 2023, 562, 232785. [Google Scholar] [CrossRef]
- Geethamahalakshmi, G.; Kalaiarasi, N.; Nageswari, D. Fuzzy based MPPT and solar power forecasting using artificial intelligence. Intell. Autom. Soft Comput. 2022, 32, 1667–1685. [Google Scholar] [CrossRef]
- Hamidi, F.; Olteanu, S.C.; Popescu, D.; Jerbi, H.; Dincă, I.; Ben Aoun, S.; Abbassi, R. Model Based Optimisation Algorithm for Maximum Power Point Tracking in Photovoltaic Panels. Energies 2020, 13, 4798. [Google Scholar] [CrossRef]
- Al-Masri, H.M.; Magableh, S.K.; Abuelrub, A.; Saadeh, O.; Ehsani, M. Impact of different photovoltaic models on the design of a combined solar array and pumped hydro storage system. Appl. Sci. 2020, 10, 3650. [Google Scholar] [CrossRef]
- Nguyen-Duc, T.; Nguyen-Duc, H.; Le-Viet, T.; Takano, H. Single-diode models of PV modules: A comparison of conventional approaches and proposal of a novel model. Energies 2020, 13, 1296. [Google Scholar] [CrossRef]
- Rusirawan, D.; Farkas, I. Identification of model parameters of the photovoltaic solar cells. Energy Procedia 2014, 57, 39–46. [Google Scholar] [CrossRef]
- Anani, N.; Ibrahim, H. Adjusting the single-diode model parameters of a photovoltaic module with irradiance and temperature. Energies 2020, 13, 3226. [Google Scholar] [CrossRef]
- Escamilla-García, A.; Soto-Zarazúa, G.M.; Toledano-Ayala, M.; Rivas-Araiza, E.; Gastélum-Barrios, A. Applications of artificial neural networks in greenhouse technology and overview for smart agriculture development. Appl. Sci. 2020, 10, 3835. [Google Scholar] [CrossRef]
- Sajjad, U.; Hussain, I.; Raza, W.; Sultan, M.; Alarifi, I.M.; Wang, C.C. On the critical heat flux assessment of micro-and nanoscale roughened surfaces. Nanomaterials 2022, 12, 3256. [Google Scholar] [CrossRef]
- Gaspar, A.; Oliva, D.; Cuevas, E.; Zaldívar, D.; Pérez, M.; Pajares, G. Hyperparameter optimization in a convolutional neural network using metaheuristic algorithms. In Metaheuristics in Machine Learning: Theory and Applications; Springer International Publishing: Cham, Switzerland, 2021; pp. 37–59. [Google Scholar] [CrossRef]


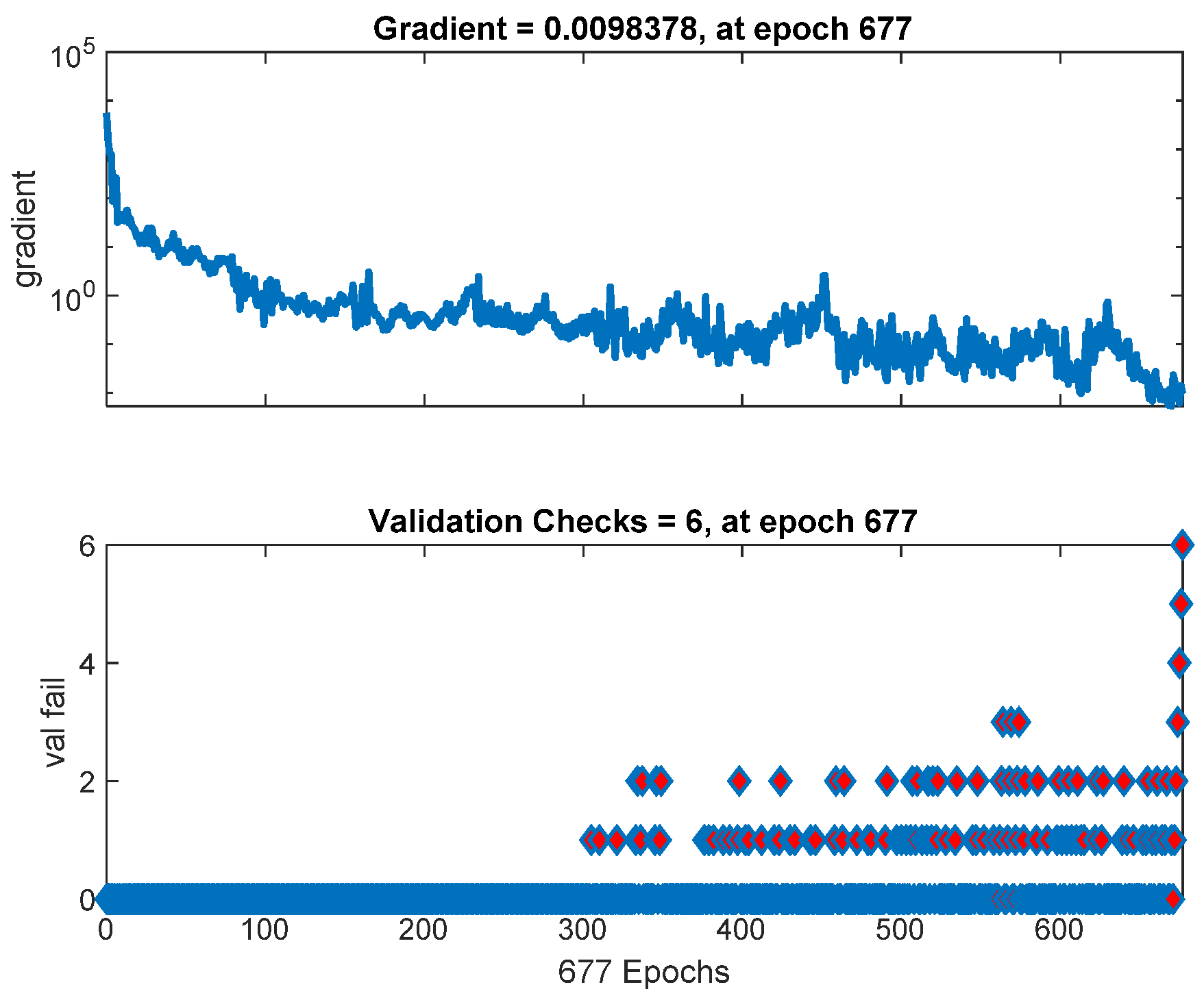
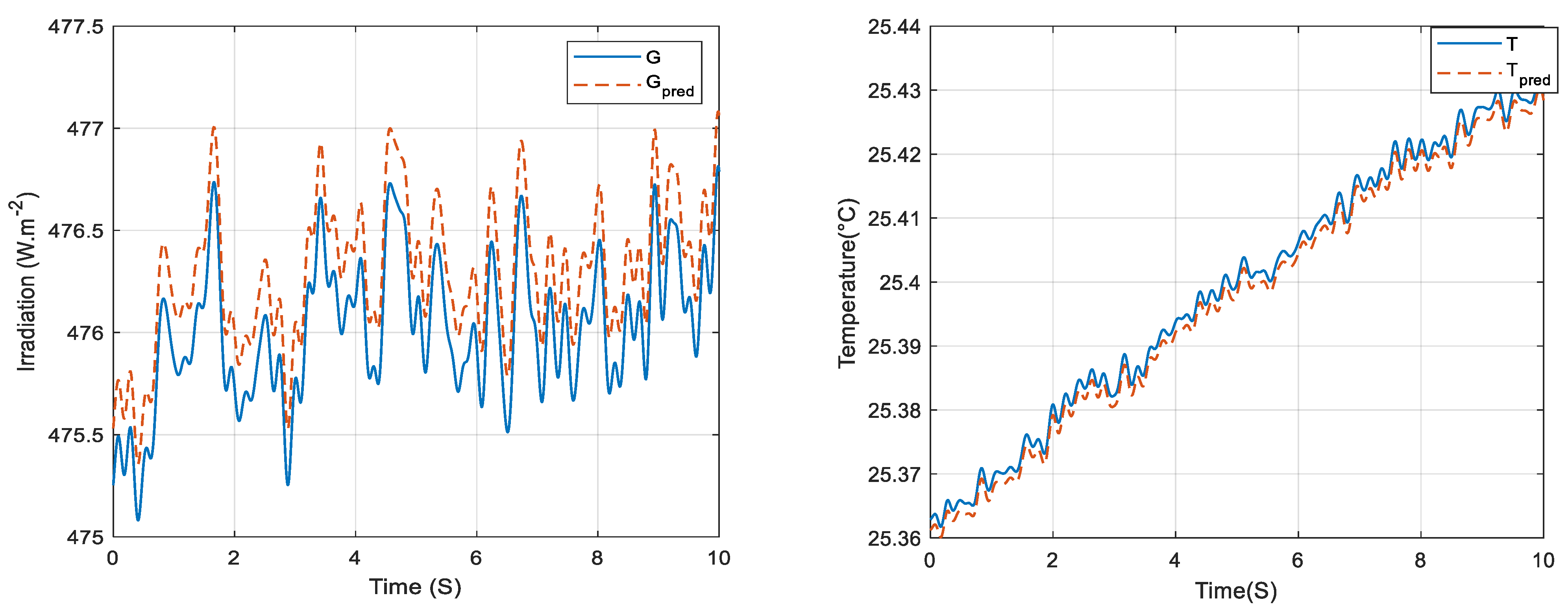
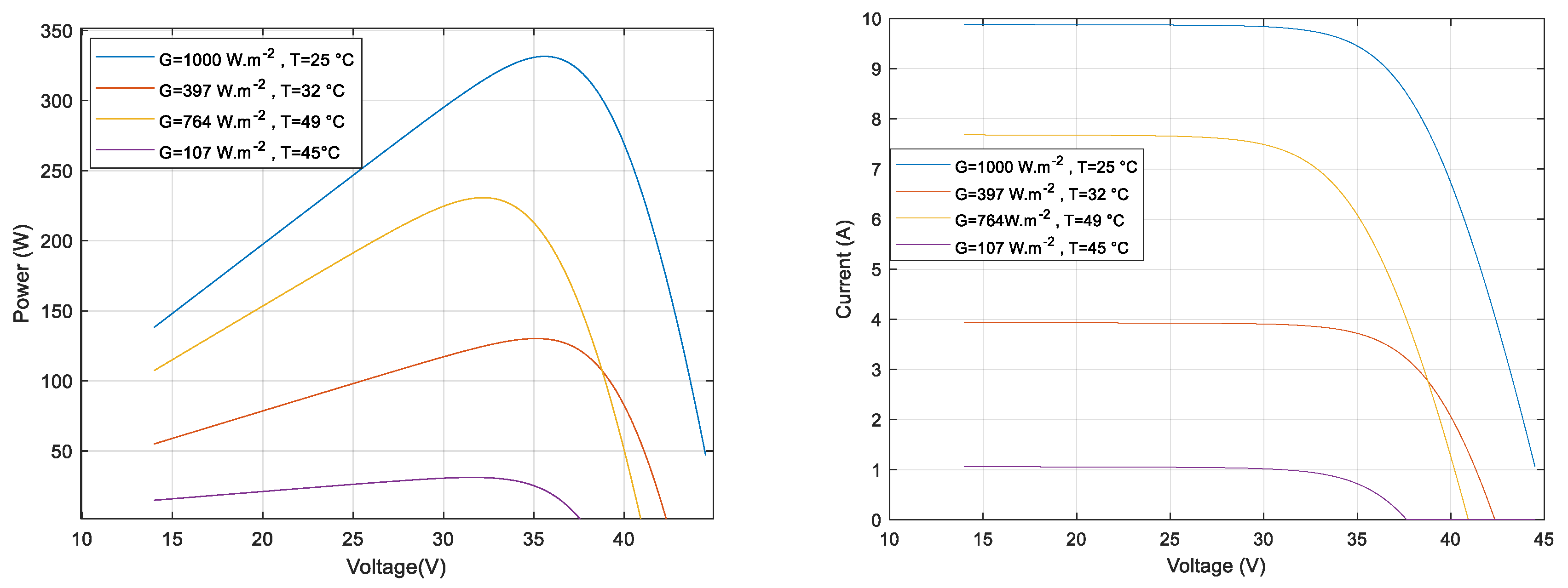
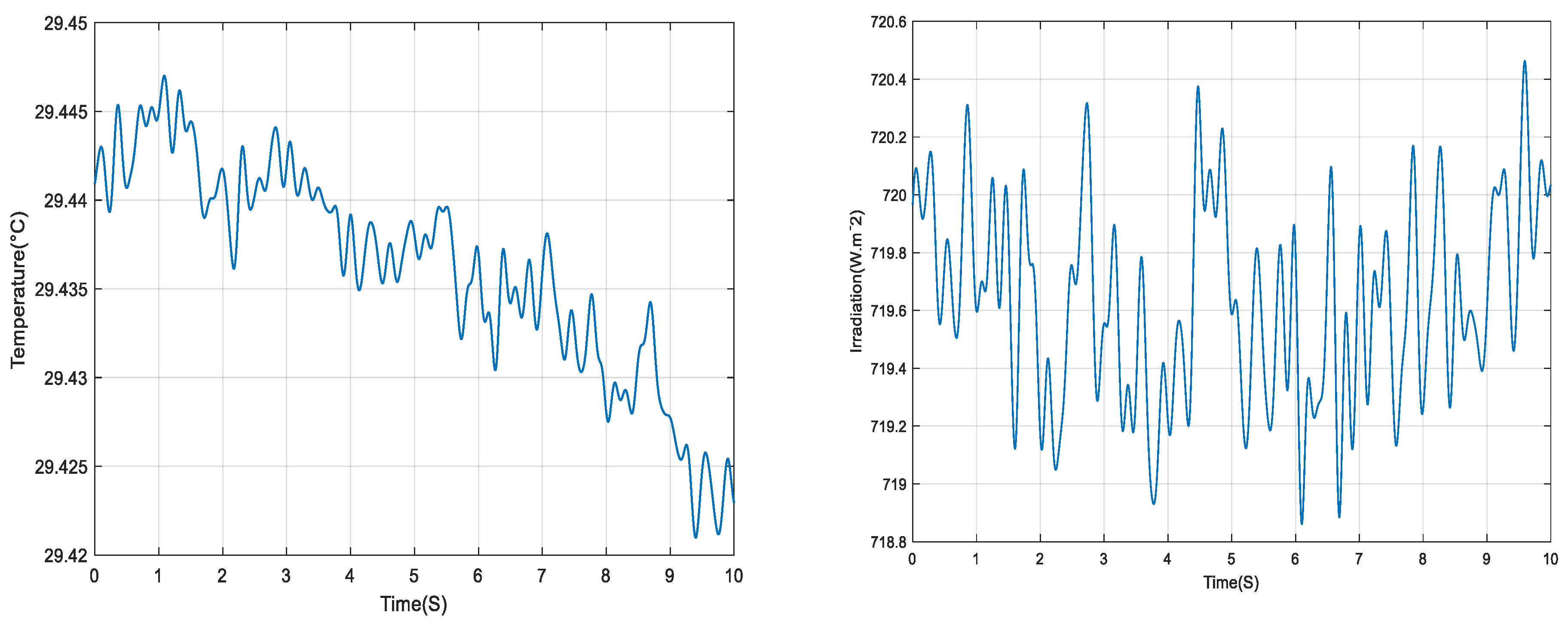
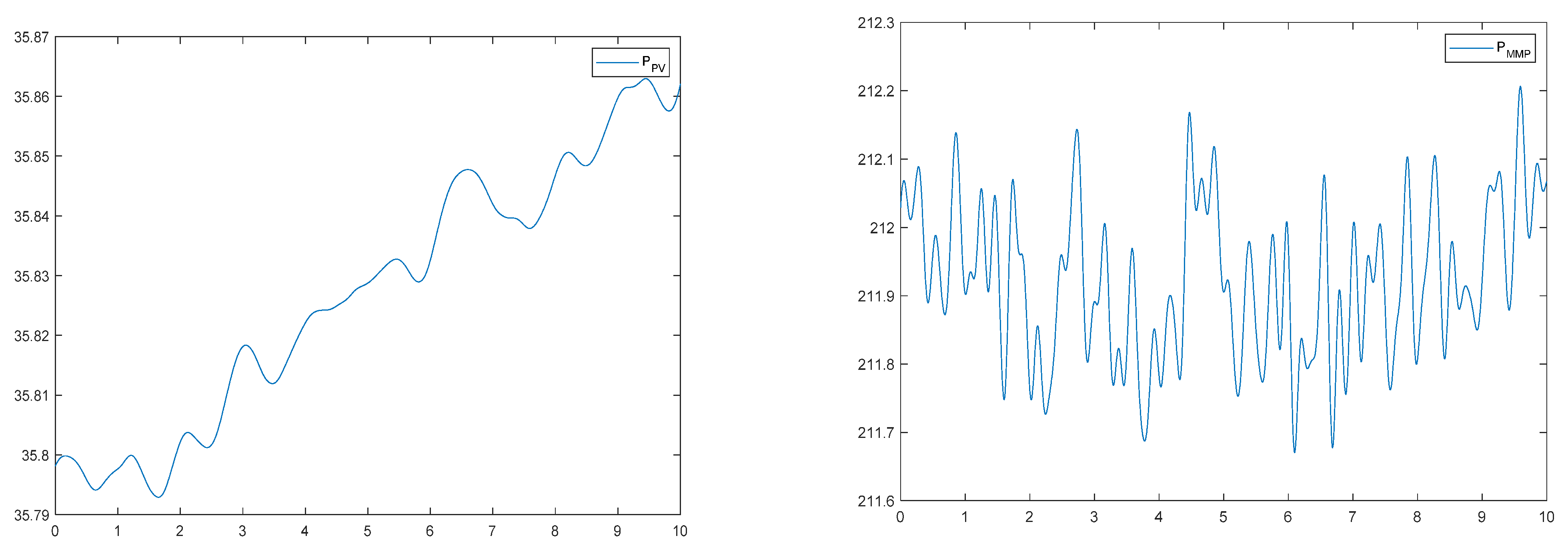
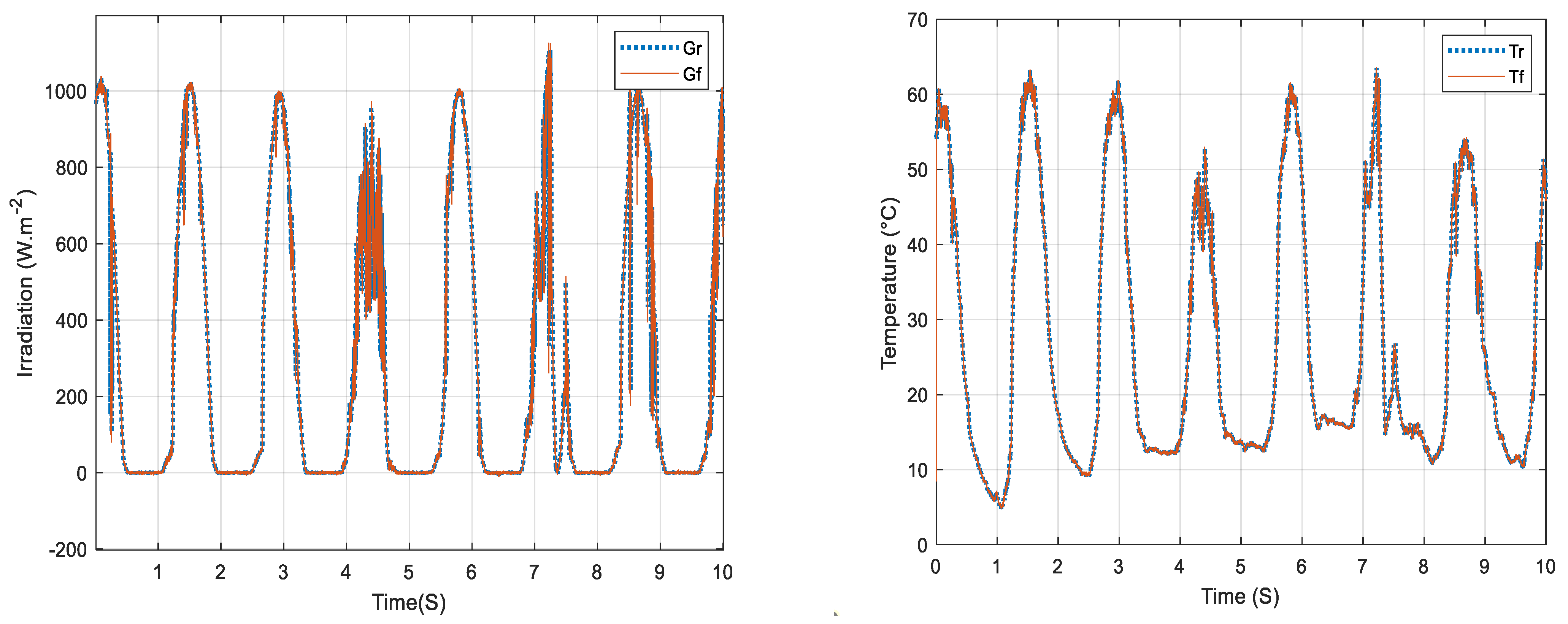
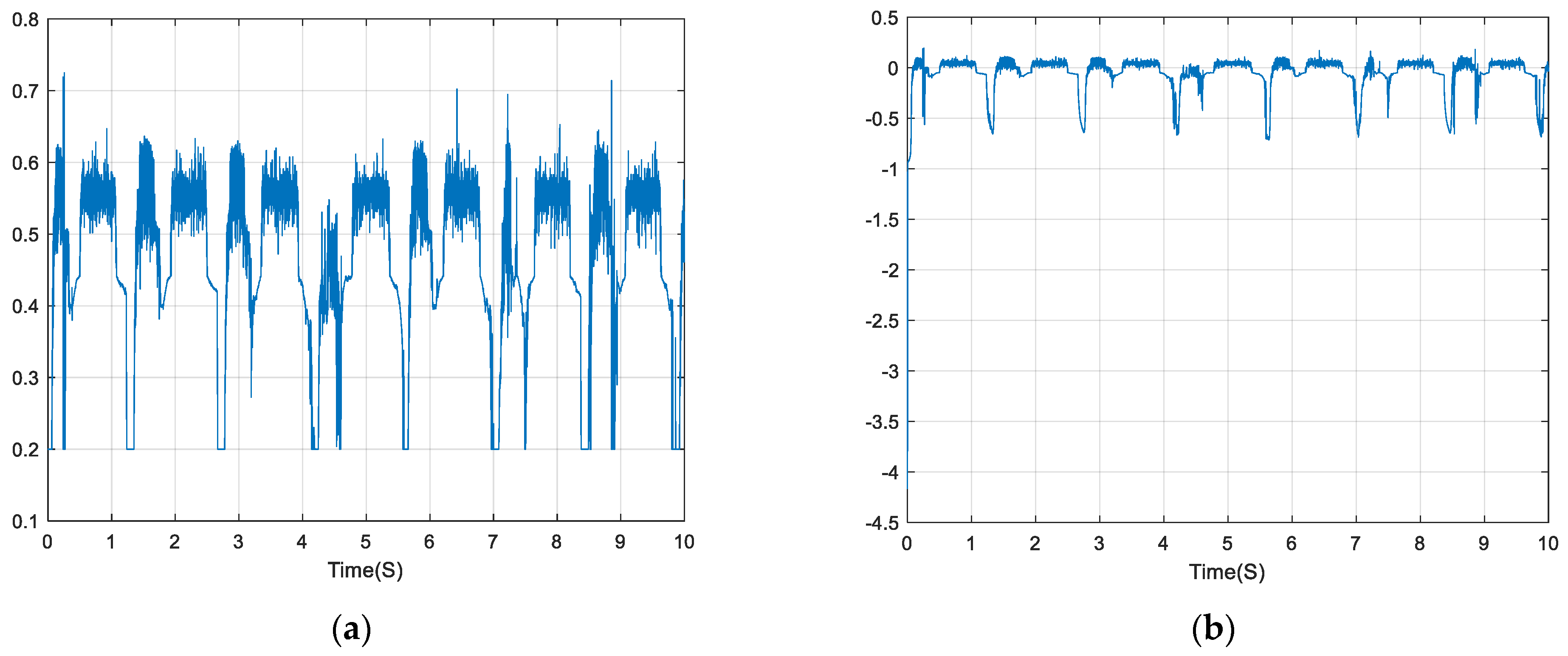
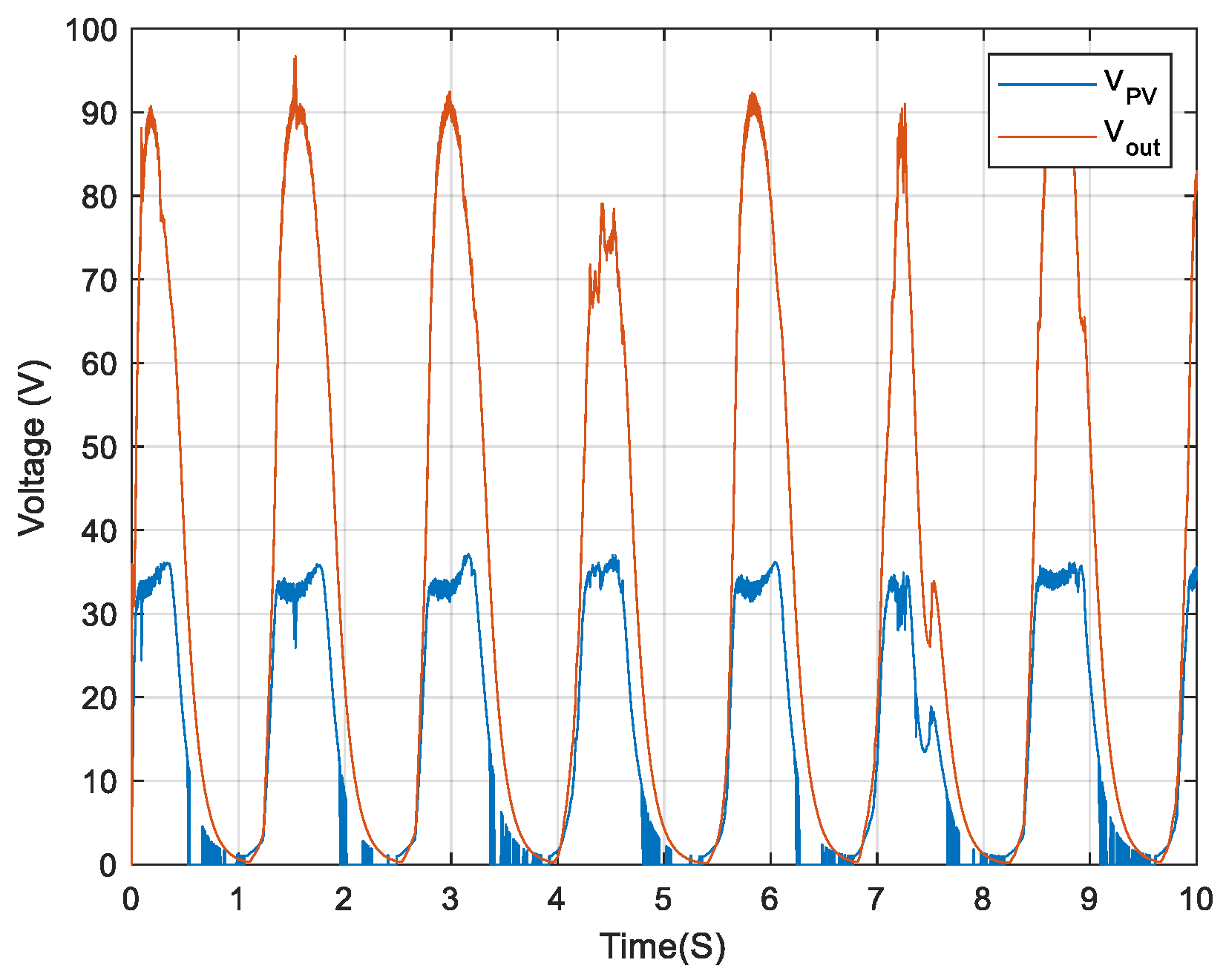
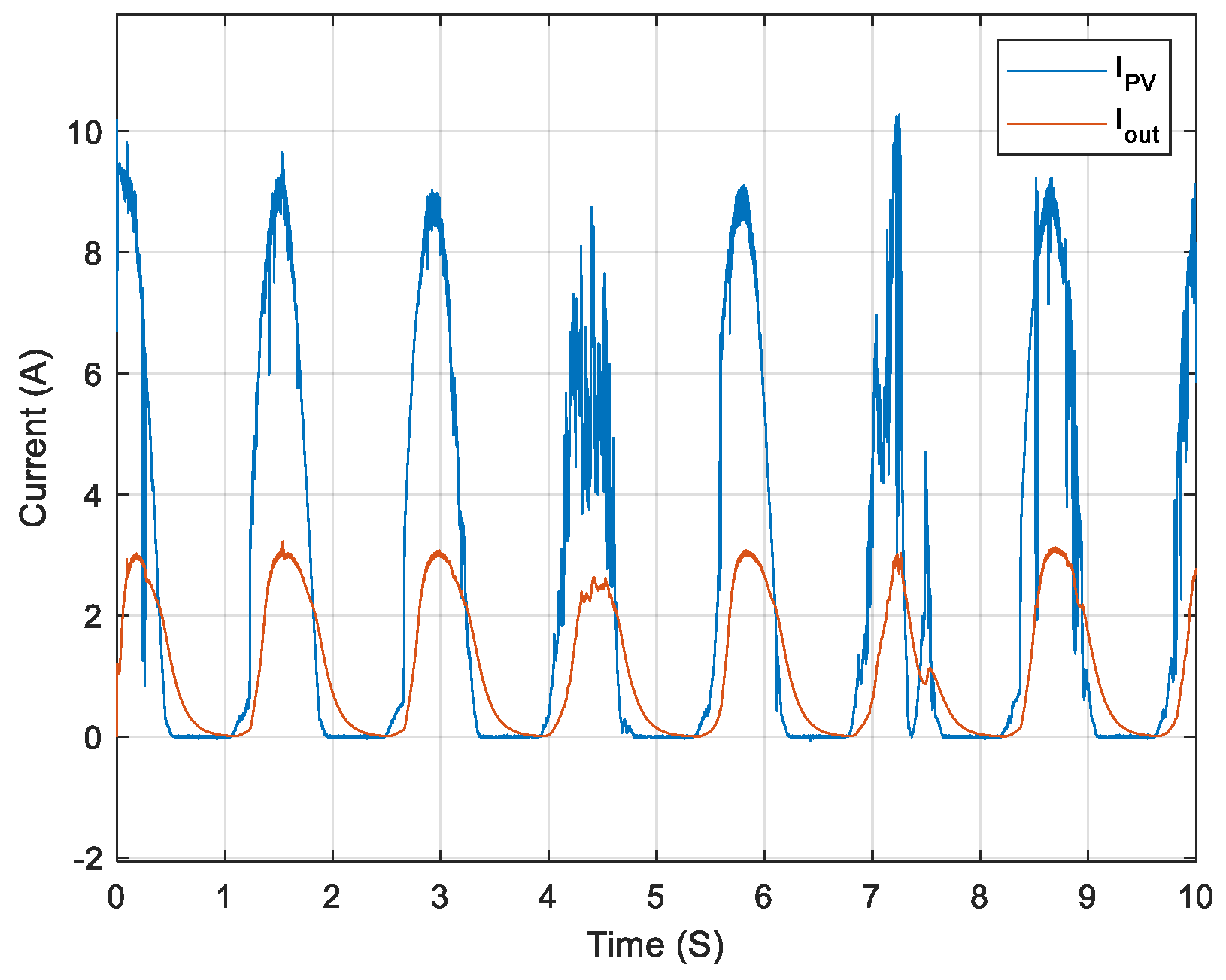
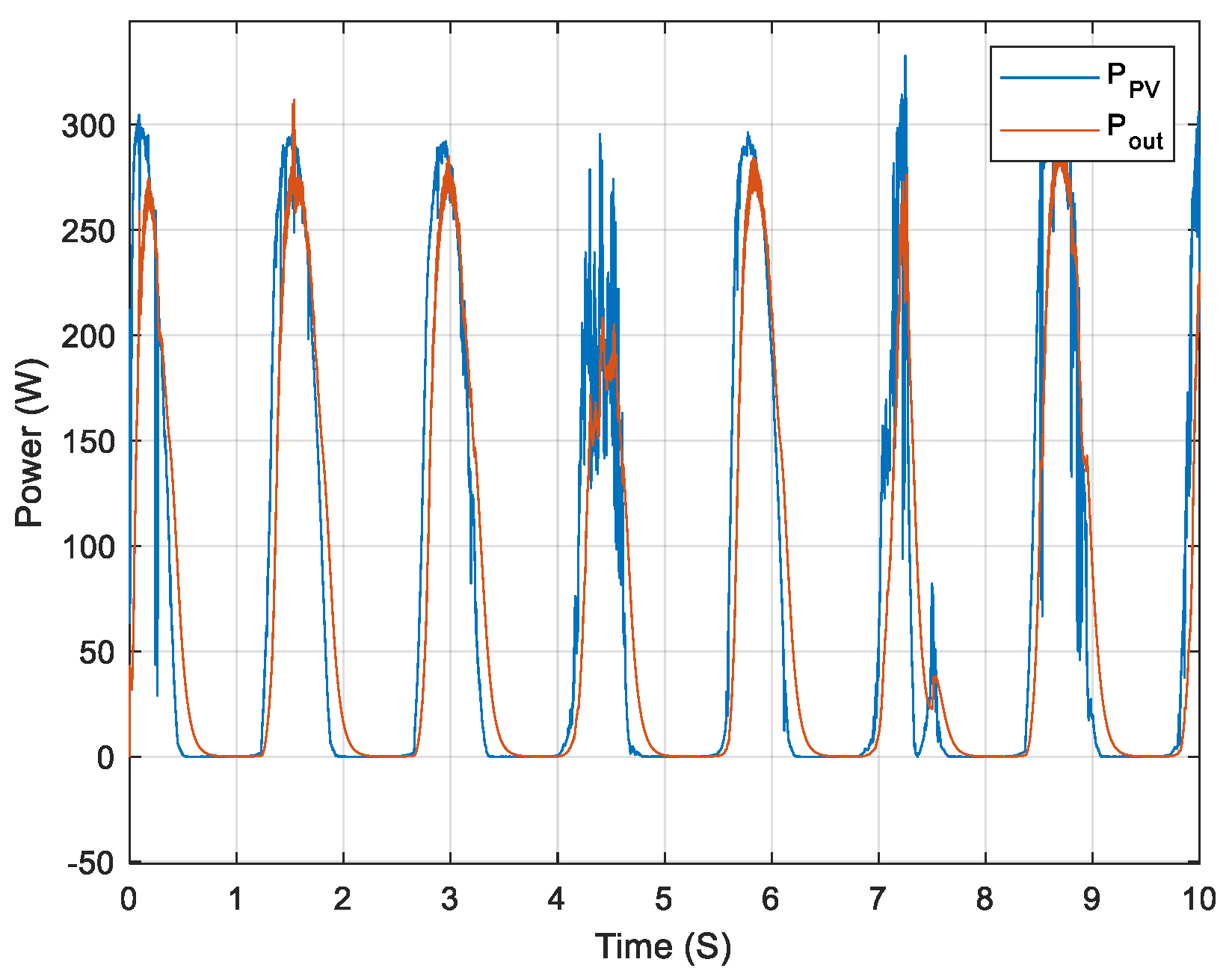
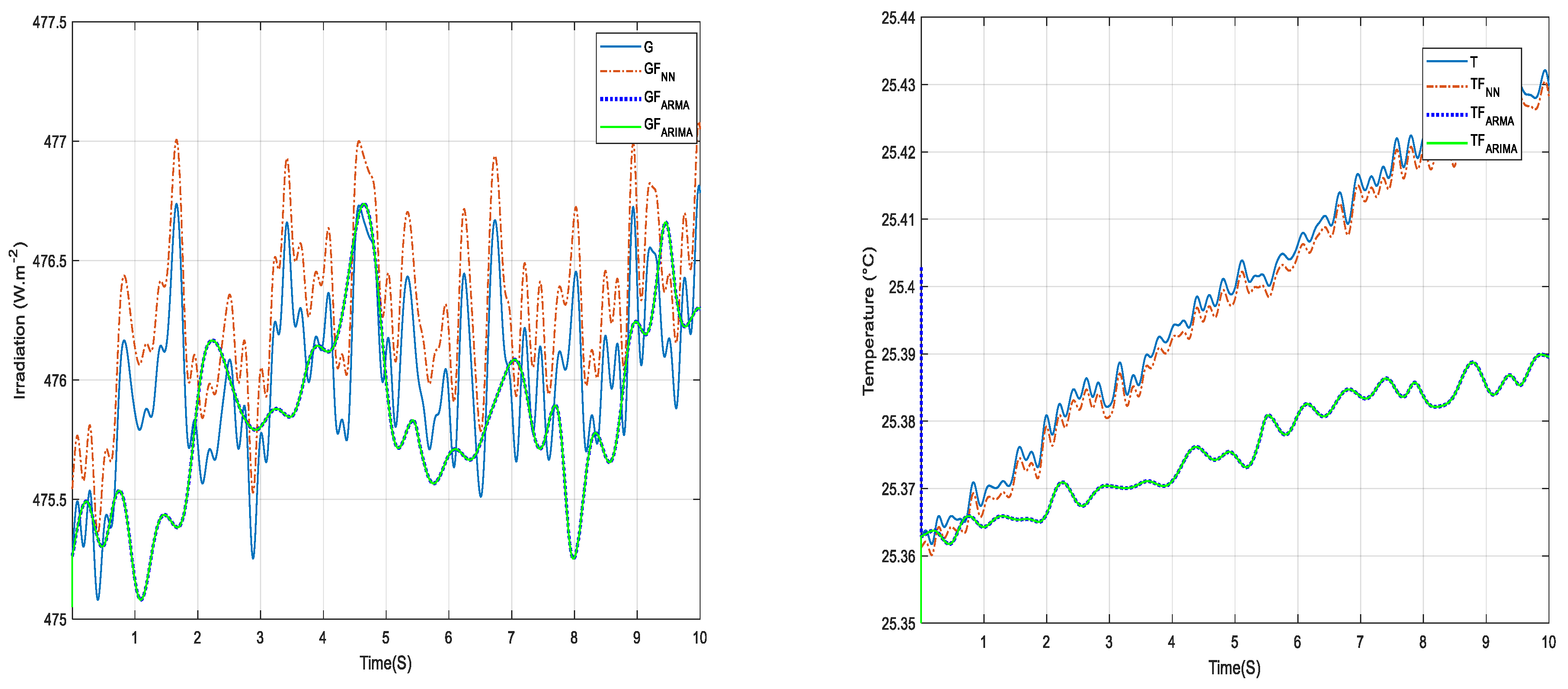


| Model | R2 | MSE | RMSE | MAE | Neural N° | Training Data (%) |
|---|---|---|---|---|---|---|
| ANN | 0.98 | 0.0044 | 0.066 | 0.033 | 15 | 70 |
| ARIMA | 0.99 | 0.29 | 0.47 | 0.088 | - | 70 |
| ARMA | 0.99 | 0.22 | 0.47 | 0.081 | - | 70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jlidi, M.; Barambones, O.; Hamidi, F.; Aoun, M. ANN for Temperature and Irradiation Prediction and Maximum Power Point Tracking Using MRP-SMC. Energies 2024, 17, 2802. https://doi.org/10.3390/en17122802
Jlidi M, Barambones O, Hamidi F, Aoun M. ANN for Temperature and Irradiation Prediction and Maximum Power Point Tracking Using MRP-SMC. Energies. 2024; 17(12):2802. https://doi.org/10.3390/en17122802
Chicago/Turabian StyleJlidi, Mokhtar, Oscar Barambones, Faiçal Hamidi, and Mohamed Aoun. 2024. "ANN for Temperature and Irradiation Prediction and Maximum Power Point Tracking Using MRP-SMC" Energies 17, no. 12: 2802. https://doi.org/10.3390/en17122802
APA StyleJlidi, M., Barambones, O., Hamidi, F., & Aoun, M. (2024). ANN for Temperature and Irradiation Prediction and Maximum Power Point Tracking Using MRP-SMC. Energies, 17(12), 2802. https://doi.org/10.3390/en17122802







