New Advances in Materials, Applications, and Design Optimization of Thermocline Heat Storage: Comprehensive Review
Abstract
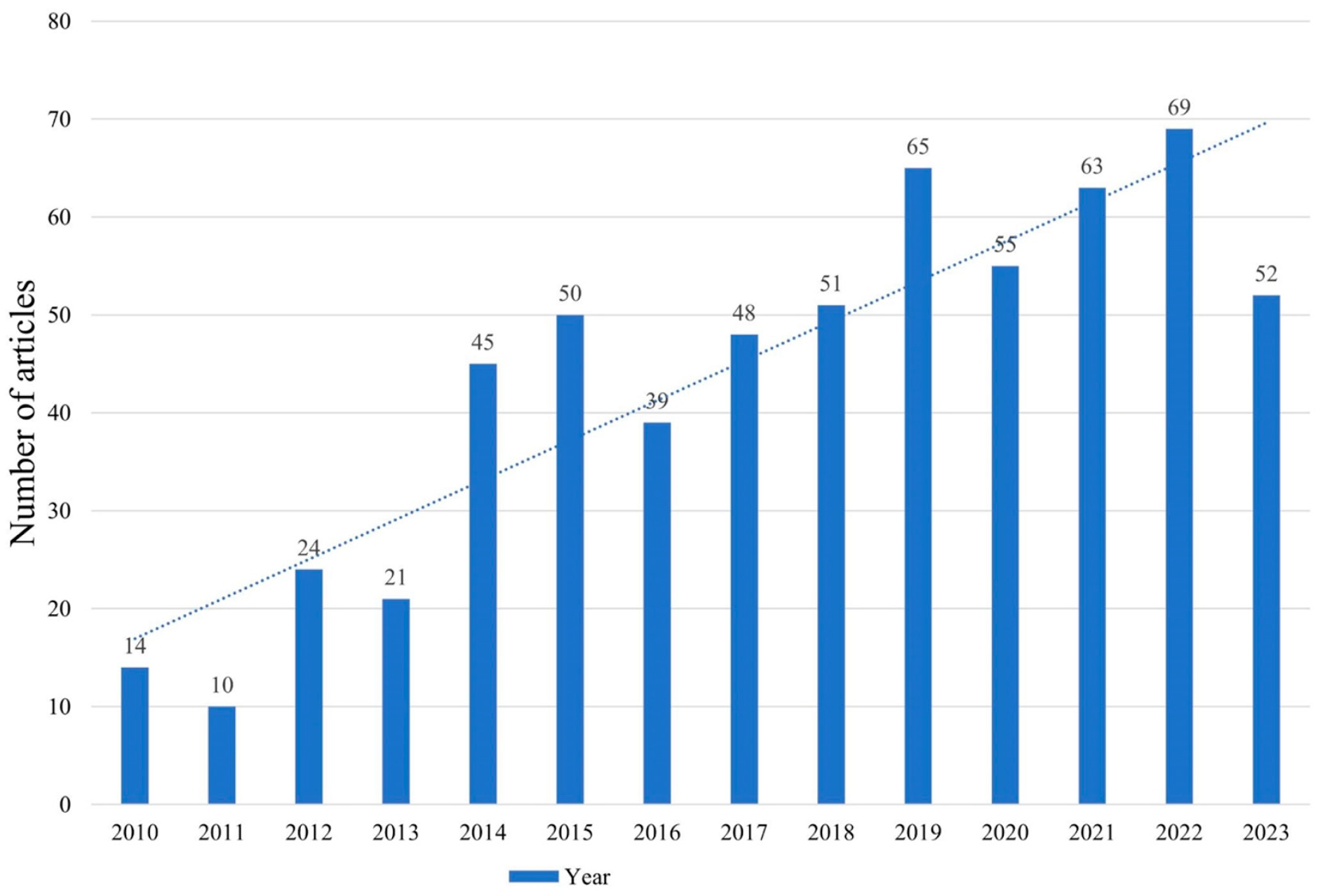
1. Introduction
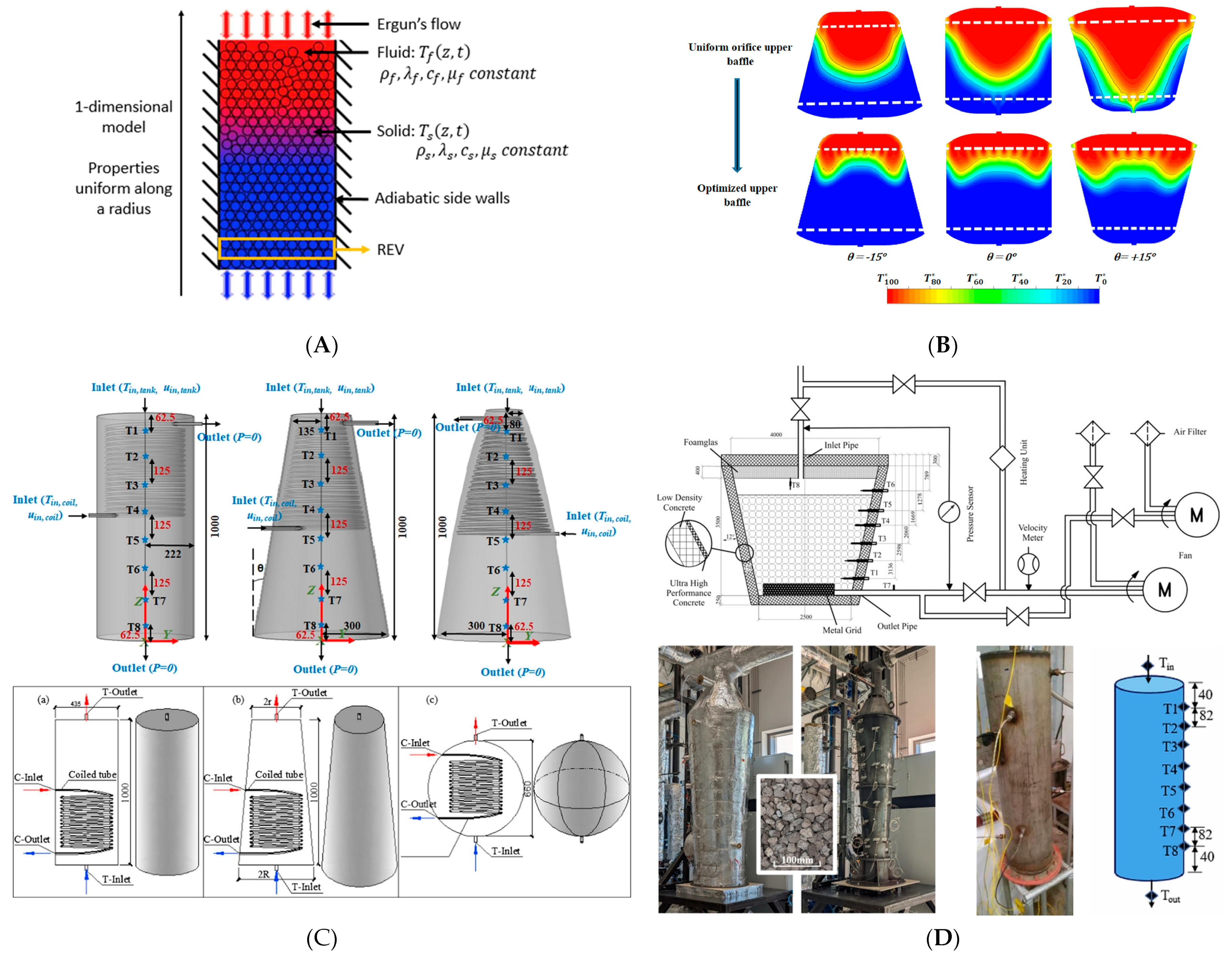
2. Thermocline Heat Storage Principles
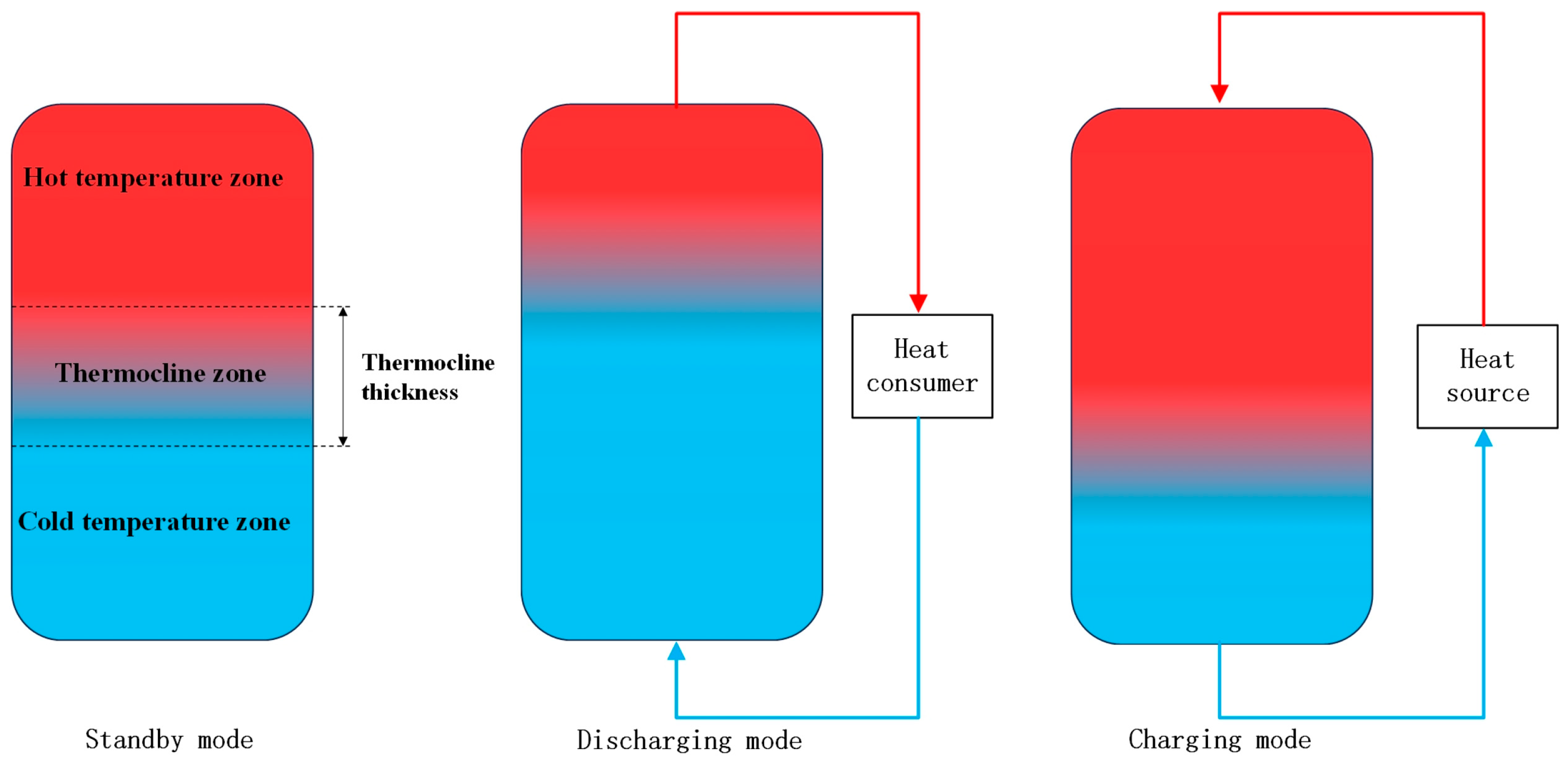
2.1. Basic Principles
2.2. Classification of Thermocline Heat Storage
2.3. Thermocline Heat Storage Process
2.4. Thermal Ratchet Phenomenon
2.5. Dimensionless Numbers and Performance Indicators
2.5.1. Dimensionless Numbers
- Stratification number
- Dimensionless temperature
- Reynolds number
- Richardson number
- Froude number
- Peclet number
- Stanton number
- MIX number
2.5.2. Performance Indicators
2.5.3. Economic Indicators
2.5.4. Environmental Indicators
- Cumulative Energy Demand (CED), measured in MJ, associated with the energy impact category.
- Global Warming Potential (GWP), measured in kgCO2, associated with the climate change impact category.
- The Abiotic Depletion Potential (ADP) of minerals, fossil, and renewable resources, measured in kgSb, associated with the resource depletion impact category.
- Particulate Matter (PM), measured in kgPM2.5, associated with the human health impact category.
3. Thermal Energy Storage Materials for Thermocline Heat Storage
- Thermal indicators: specific heat capacity, melting point, thermal conductivity, thermal capacity heat transfer coefficient, and long-term thermal stability.
- Physics indicators: high physical stability and low expansion rate.
- Chemical indicators: high chemical stability, non-degradation, non-corrosiveness, non-toxicity, non-flammability, and non-explosiveness.
- Economic and environmental indicators: easy availability, cost-effectiveness, and environmental friendliness.
| Material | Density | Specific Heat | Thermal Conductivity | Thermal Capacity | Thermal Diffusivity m2/s] | Thermal Effusivity J/(m2Ks1/2)] |
|---|---|---|---|---|---|---|
| Alumina [29,38,49] | 3600–4000 | 0.780–1.023 | 21–30 | 2810–4092 | - | 8.88 |
| Alumina ceramics [39,60] | 2200–3750 | 0.780–1.100 | 1.06–30.10 | 1716–2925 | - | - |
| Aluminum [40,41,45] | 2700 | 0.945–0.951 | 204–238.4 | 2419–2551 | 84.10–93.3 | 24.66 |
| Basalt [51] | 2210–3011 | 0.717–0.900 | 2–5.7 | 1750–2500 | - | 2.29 |
| Bauxite [33] | 3005 | 1.076 | 4.0 | 3233 | - | 3.59 |
| Brick (dry) [40,45] | 1500–1800 | 0.84–1.008 | 0.50 | 1417–1512 | 0.33 | 0.87 |
| Ceramic [51,61,62] | 2090–3120 | 0.837–1.076 | 3.982–17 | 1749–3357 | - | 1.52–2.37 |
| Chalk brick [45] | 3000 | 1.130 | 5.07 | 3390 | 1.9416 | - |
| Cipolin [51] | 2610–2870 | 0.800–1.470 | 3.2 | 1680–2520 | - | - |
| Concrete [40,41,45] | 2200 | 0.72–1.29 | 0.9–2.65 | 1680–3005 | 0.356–0.94 | 1.52 |
| Copper [40,41,45] | 8300–8960 | 0.385–0.419 | 372–385 | 3178–3729 | 107–112.3 | 35.97 |
| Copper foam [39] | 2700 | 0.800 | 126 | 2160 | - | - |
| Gabbro [63,64] | 2900–3500 | 0.710–0.980 | 2.19 | 2485–2842 | - | - |
| Glue [62] | 1730 | 1.0087 | 0.299 | 1745 | - | - |
| Gneiss [65,66] | 2590–2700 | 0.770–0.979 | 2.7–3.1 | 2008–2640 | 0.94–6.80 | - |
| Granite [40,41,51] | 2530–2750 | 0.600–12 | 2.2–2.9 | 1440–2880 | 1.18 | 2.67 |
| Graphite [40,41] | 2200–2400 | 0.61–0.660 | 30.40–155 | 882–1378 | 120 | 14.41 |
| Hornfels [51,63] | 2400–2800 | 0.700–0.900 | 1.5 | 2560–2880 | - | - |
| High-temp concrete [39] | 2750 | 0.916 | 1.0 | 2519 | - | - |
| Iron [40] | 7850 | 0.465 | 59.3 | 3348–6612 | 16.3 | 14.7 |
| Lead [40,41] | 11340 | 0.131 | 35.25 | 1485 | 23.6 | 7.24 |
| Limestone [40,41] | 2500 | 0.74–0.90 | 1.26–2.2 | 1584–2506 | 0.56–1.19 | 2.02 |
| Magnesia [24] | 1800 | 1.862 | 27.60 | 3352 | - | - |
| Marble [45,51] | 2560–2670 | 0.800–1.521 | 2.07–3.20 | 1680–2520 | 0.995–1.413 | - |
| Mica [62] | 2800 | 0.880 | 0.58 | 2464 | - | - |
| Nichrome [62] | 8400 | 0.460 | 16.75 | 3864 | - | - |
| Pebbles [67] | 1680 | 0.880 | 1.2 | 1479 | - | - |
| Quartzite [42,51] | 2320–2860 | 0.700–1.185 | 5.69–29.3 | 2002–3822 | - | 3.44 |
| Quartz sand [62] | 1730 | 1.2059 | 0.272 | 2086 | - | - |
| Silicon carbide [39] | 3210 | 0.750–1.043 | 9.01–120 | 2408–3348 | - | - |
| Slag [40] | 2700–2850 | 0.84–0.94 | 0.57–1.5 | 2268–2679 | 0.25 | 1.13 |
| Sodium chloride [40] | 2165 | 0.86 | 6.5 | 1836–1861 | 3.5 | 3.5 |
| Sodium carbonate [41] | 2510 | 1.090 | - | 2736 | - | - |
| Soil (clay) [40] | 1450 | 0.88 | 1.28 | 1276 | 1.0 | 1.28 |
| Soil (gravelly) [40] | 2040 | 1.84 | 0.59 | 3754 | 0.16 | 1.49 |
| Stainless steel [49] | 8030 | 0.50248 | 16 | 4035 | - | - |
| Steel slag [68] | 3430 | 0.877 | 1.47 | 3008 | - | - |
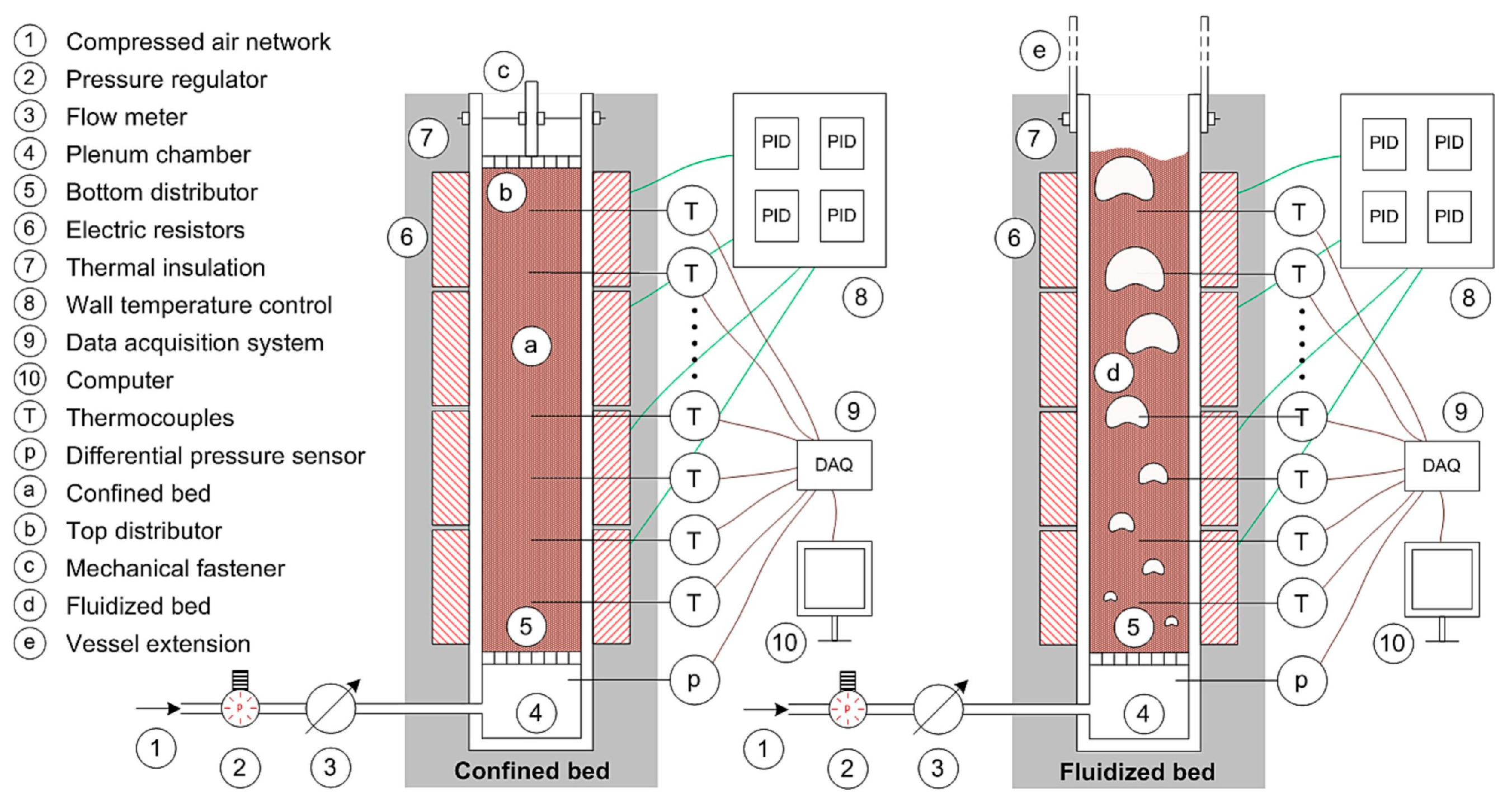
4. Application of Thermocline Heat Storage
5. Optimization of Thermocline Heat Storage
5.1. Optimization of Thermocline Heat Storage System Design
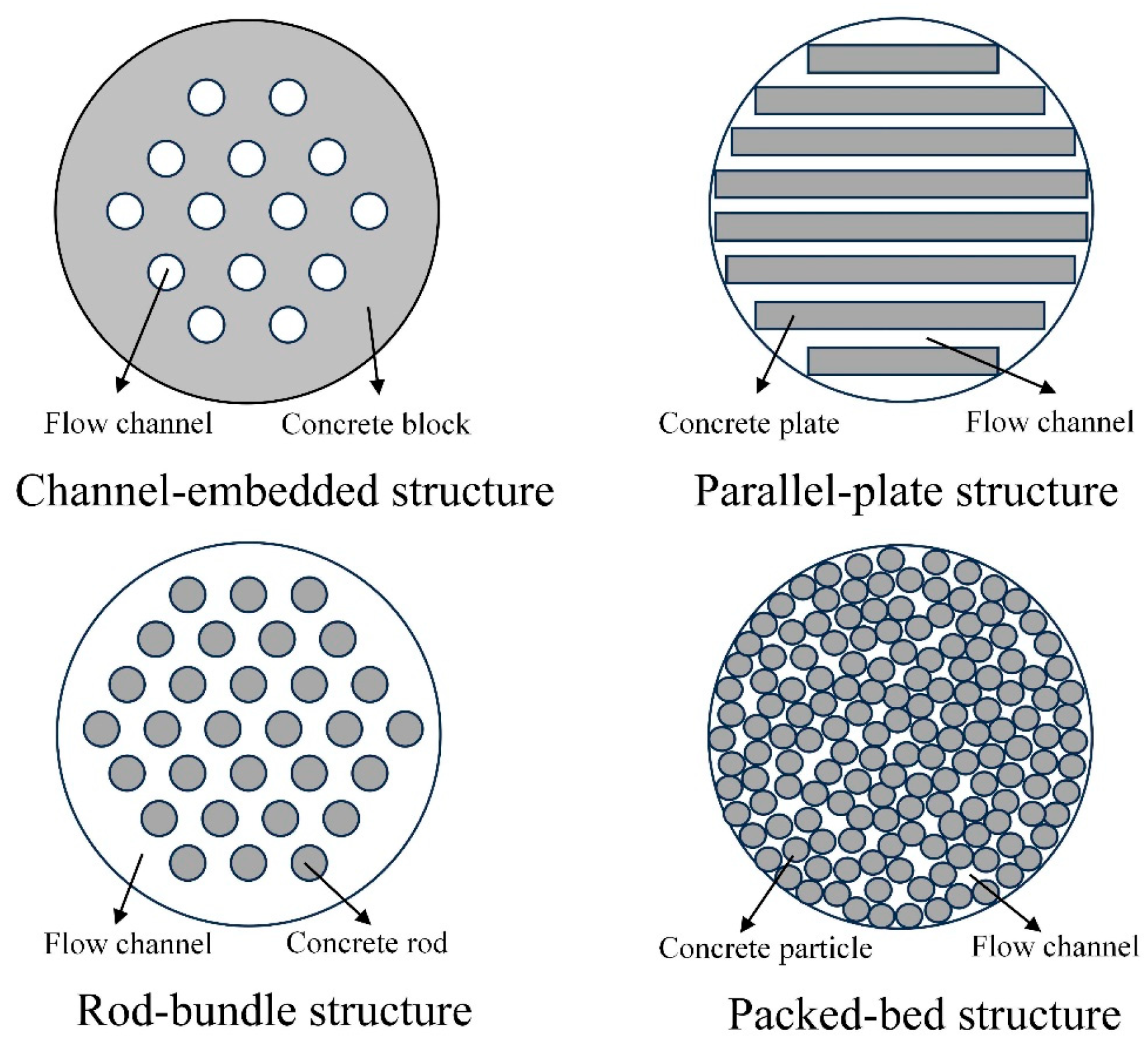
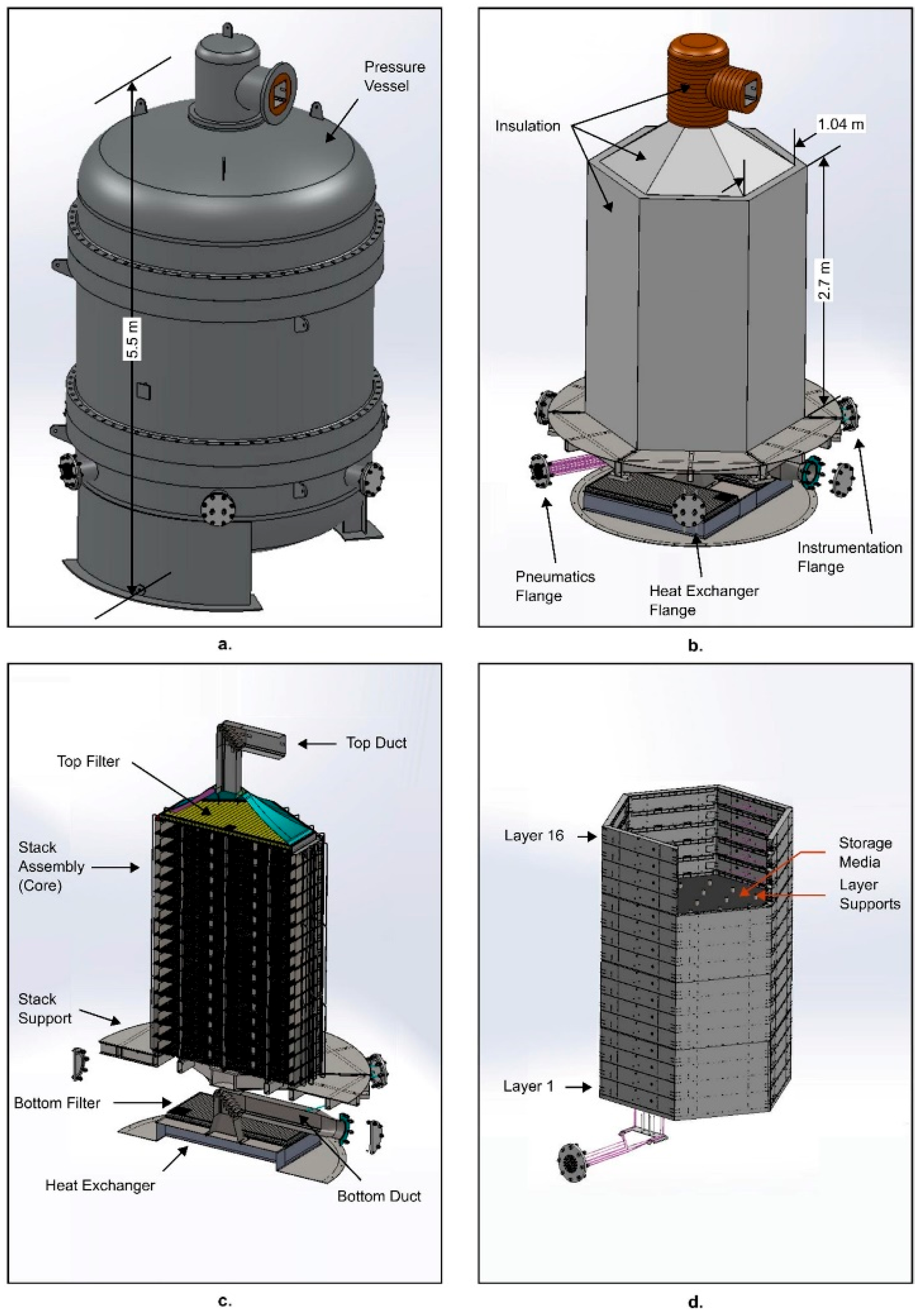
5.1.1. Tank Structure
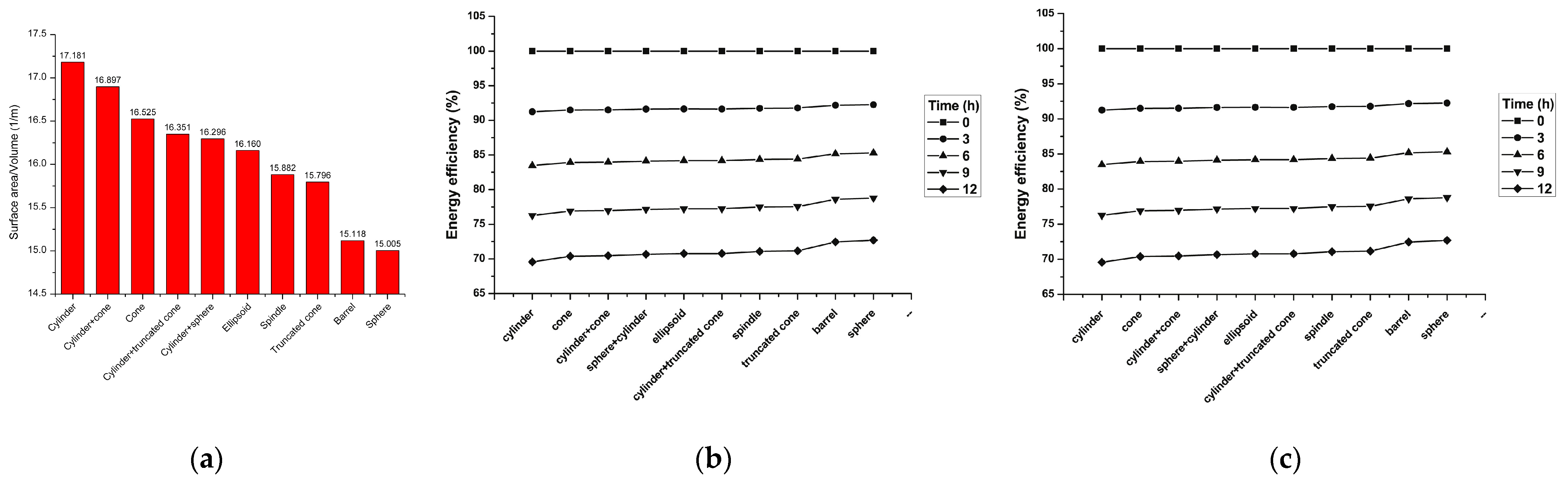
Tank Shape
Aspect Ratio
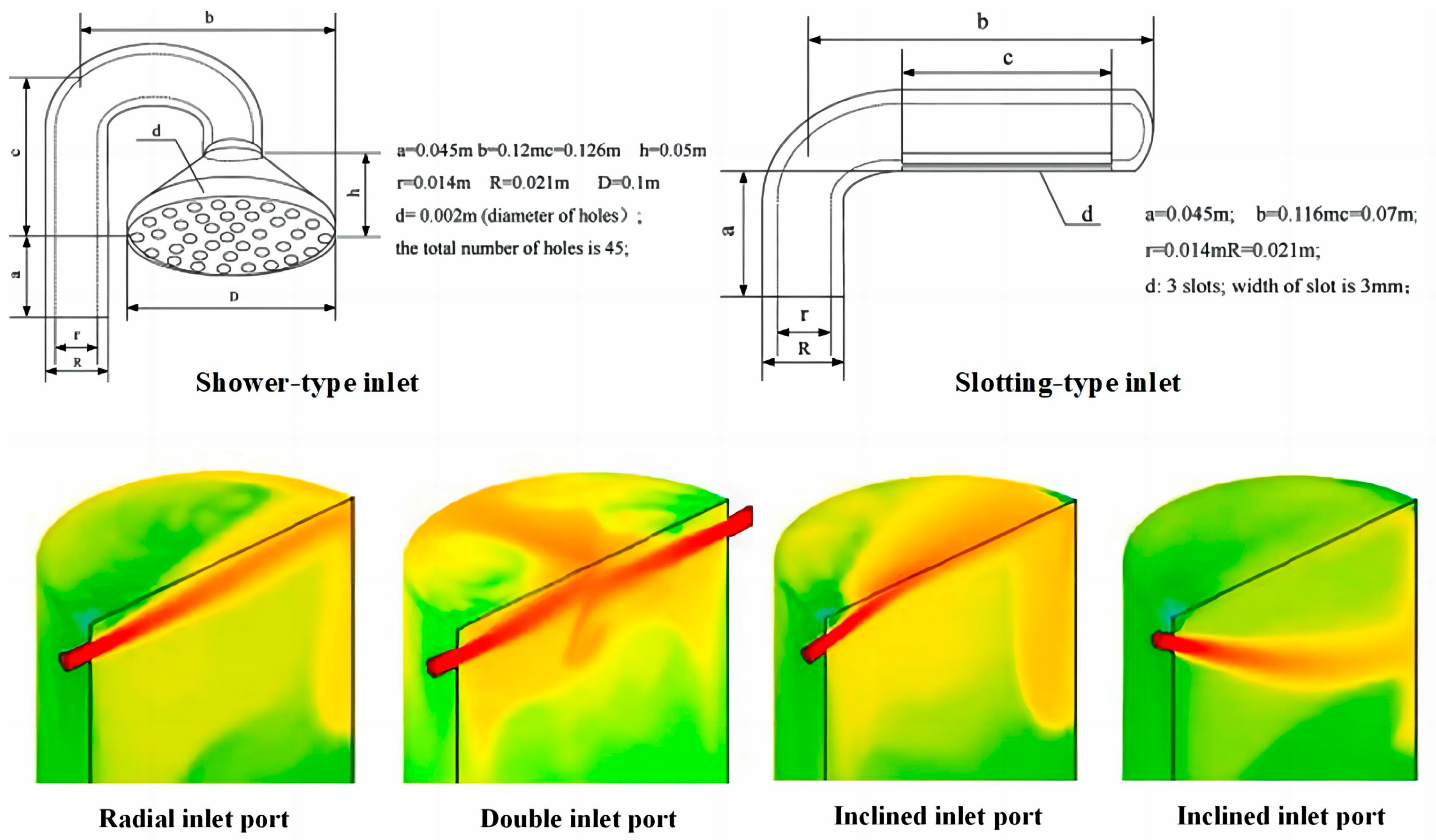
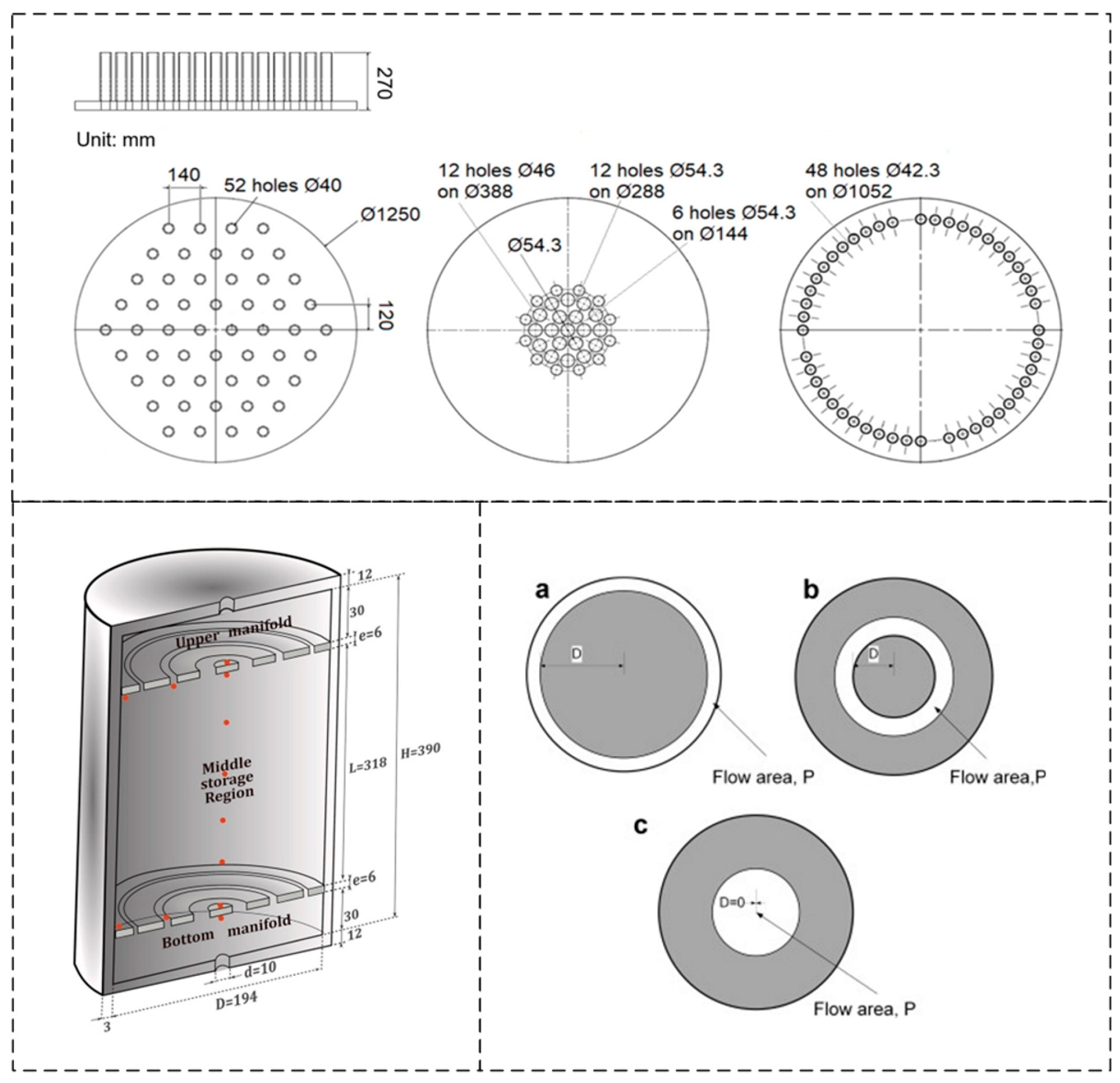
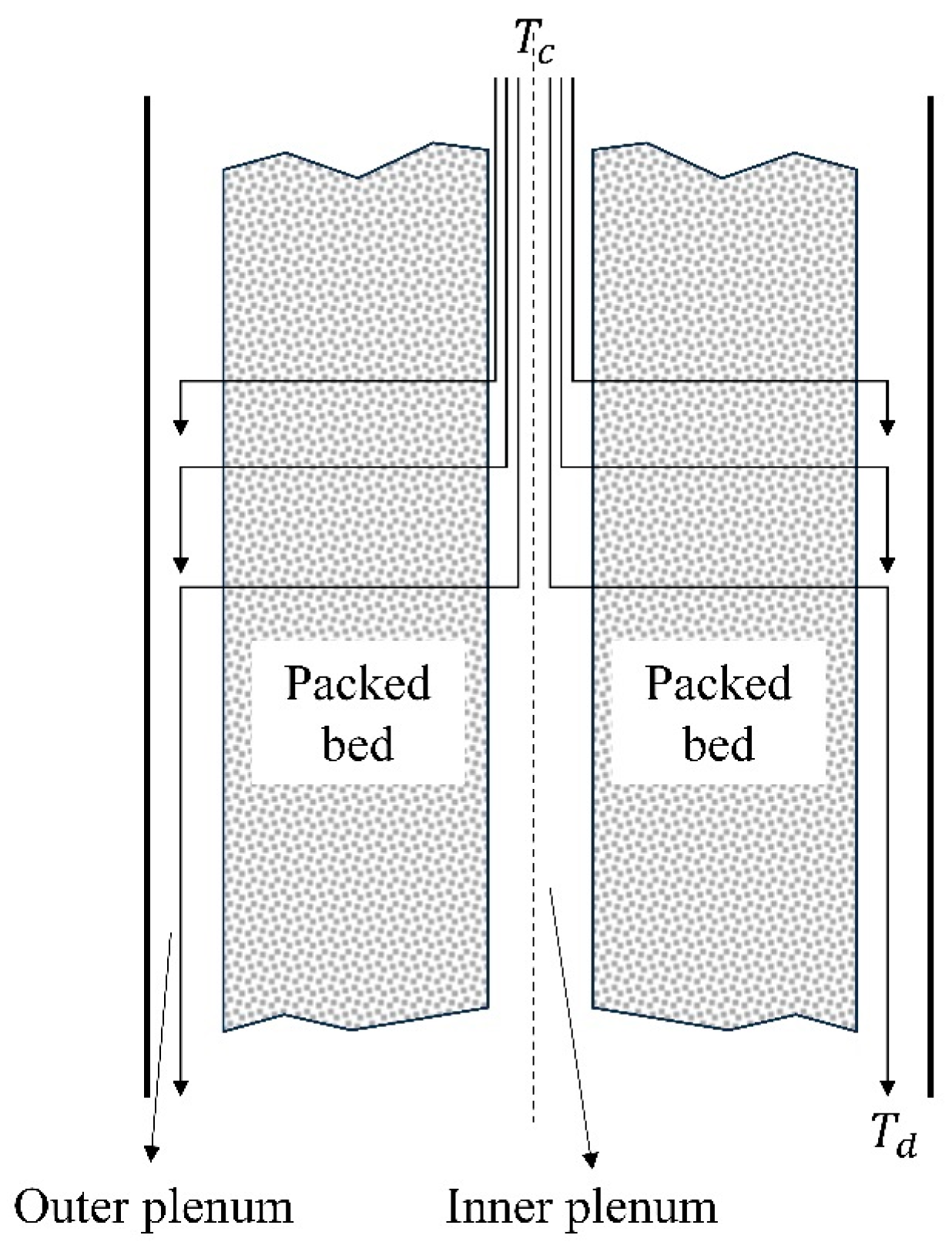
Inlet and Outlet Configuration
Flow Direction
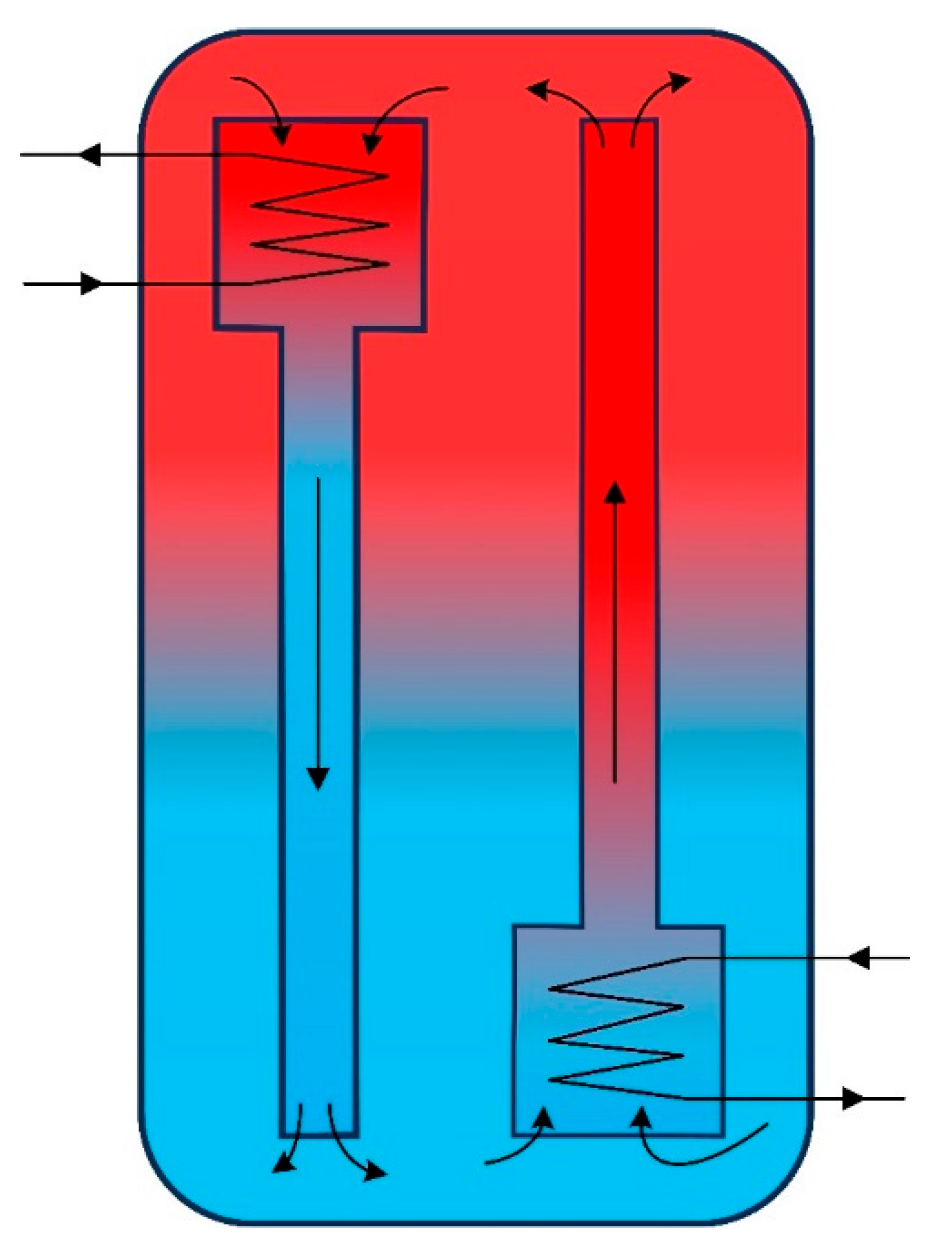
Heat Exchanger Configuration
5.1.2. Arrangement of Solid Thermal Energy Storage Materials
Ordered Packing Configuration
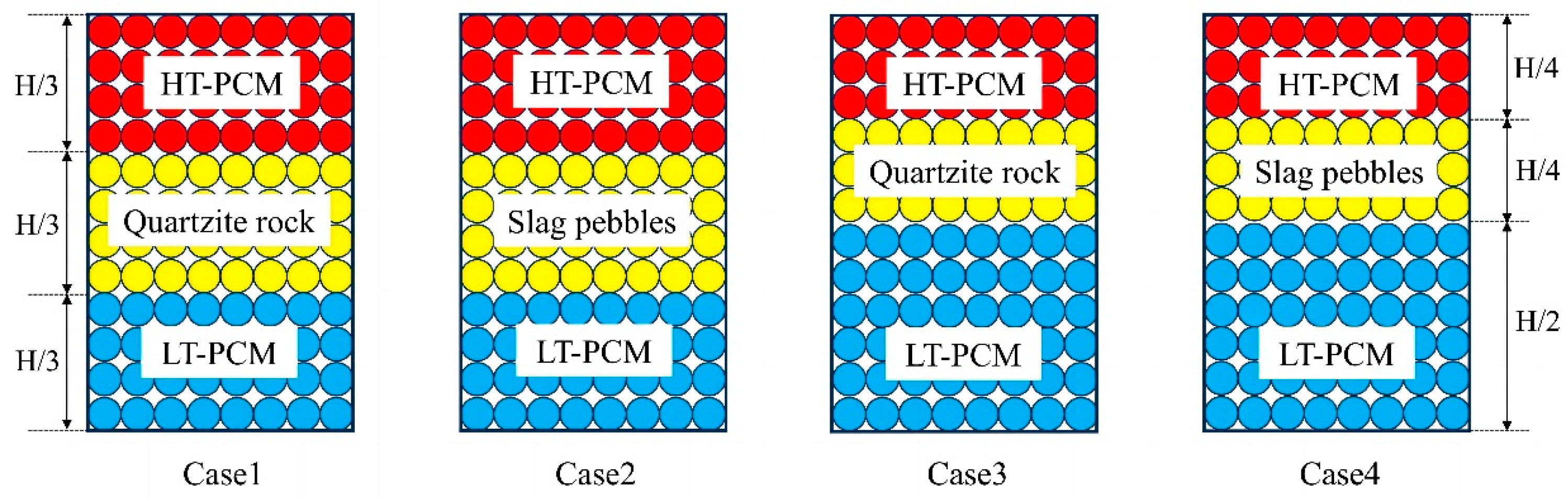
Cascaded Configuration
Structured Configuration
Particle Diameter
5.2. Optimization of Operating Strategies for Thermocline Heat Storage Systems
5.2.1. Flow Velocity
5.2.2. Temperature
5.2.3. Charging and Discharging Strategies
5.3. Optimization of Thermocline Heat Storage System Numerical Model
6. Conclusions and Perspectives
- SMTHS systems are structurally simple and easy-to-maintain but have lower thermal storage capacity, making them suitable for domestic applications. Distributors are needed to mitigate the impact of the inlet jet on thermal performance.
- DMTHS systems offer large thermal storage capacity and stable performance but require special attention to the thermal ratcheting issue. Strategies such as composite walls, conical storage tanks, and structured tanks can be used to reduce the risk of structural failure. Due to mechanical limitations, the maximum height for packed bed THS systems is 16 m.
- Increasing the aspect ratio can reduce the diffusion of the thermocline zone but may increase heat loss. During long standby modes, spherical and barrel-shaped tanks are the most efficient; parabolic tanks perform better in charge–discharge modes.
- When selecting TESMs, multiple requirements must be considered. Utilizing local natural materials and industrial waste can reduce costs and address waste management issues, but stability and compatibility must be considered.
- The ordered packing of solid TESMs can enhance thermal stratification stability and reduce pressure drop. The cascaded configuration using both sensible and latent heat TESMs can improve the system’s thermal performance and efficiency; three–five levels are recommended based on cost and structural considerations.
- Axial downward flow from the top of the tank is the optimal flow direction. For tanks requiring a reverse flow design, distributors should be used to limit the movement of solid particles within the tank to maintain a fixed bed state. Radial flow packed bed structures have low pressure drop and self-insulation properties but lower efficiency.
- Multi-objective optimization is necessary in THS system design. Excessively small particle sizes and high flow rates can significantly reduce THS system performance, and insulation treatment is crucial in any design.
- For multi-tank THS systems, a series configuration is recommended to achieve stable outlet temperatures and reduce the diffusion of thermal gradients.
- Charging and discharging strategies significantly affect the overall efficiency of THS, especially for continuous cyclic operation. Numerical studies of large-scale or seasonal systems require one-dimensional models to accelerate computation speed.
- THS has bright application prospects in fields such as hydrogen storage and waste heat recovery, with both environmental and economic benefits.
- The arrangement of solid TESMs in structured THS tanks needs to be optimized to improve heat transfer efficiency and thermal efficiency.
- There is a lack of experimental research to verify the effectiveness and feasibility for orderly bed-type THS tanks.
- Research on the thermal cycling and long-term operation of THS systems is scarce, and attention should be paid to the cycling efficiency and long-term performance of THS heating systems under different operating strategies.
- Further in-depth research on the thermal ratcheting issue of packed bed THS systems is needed to determine the specific conditions that may lead to structural damage.
Funding
Data Availability Statement
Conflicts of Interest
References
- Brockway, P.E.; Owen, A.; Brand-Correa, L.I.; Hardt, L. Estimation of global final-stage energy-return-on-investment for fossil fuels with comparison to renewable energy sources. Nat. Energy 2019, 4, 612–621. [Google Scholar] [CrossRef]
- Manowska, A.; Nowrot, A. The Importance of Heat Emission Caused by Global Energy Production in Terms of Climate Impact. Energies 2019, 12, 3069. [Google Scholar] [CrossRef]
- Koohi-Fayegh, S.; Rosen, M.A. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Suresh, C.; Saini, R.P. Thermal performance of sensible and latent heat thermal energy storage systems. Int. J. Energy Res. 2020, 44, 4743–4758. [Google Scholar] [CrossRef]
- Pizzolato, A.; Donato, F.; Verda, V.; Santarelli, M.; Sciacovelli, A. CSP plants with thermocline thermal energy storage and integrated steam generator–Techno-economic modeling and design optimization. Energy 2017, 139, 231–246. [Google Scholar] [CrossRef]
- Angelini, G.; Lucchini, A.; Manzolini, G. Comparison of Thermocline Molten Salt Storage Performances to Commercial Two-tank Configuration. Energy Procedia 2014, 49, 694–704. [Google Scholar] [CrossRef]
- Cascetta, M.; Petrollese, M.; Oyekale, J.; Cau, G. Thermocline vs. two-tank direct thermal storage system for concentrating solar power plants: A comparative techno-economic assessment. Int. J. Energy Res. 2021, 45, 17721–17737. [Google Scholar] [CrossRef]
- Alesbe, I.; Abdul Wahhab, H.A.; Aljabair, S. Transient study of thermal stratification of full-scale chilled water storage tank during optimum discharge condition. J. Energy Storage 2023, 65, 107236. [Google Scholar] [CrossRef]
- Xi, X.; Zhang, Z.; Wei, H.; Chen, Z.; Du, X. Experimental Study of Simultaneous Charging and Discharging Process in Thermocline Phase Change Heat Storage System Based on Solar Energy. Sustainability 2023, 15, 7322. [Google Scholar] [CrossRef]
- Armfield, S.W.; Kirkpatrick, M.P.; Milton-McGurk, L.; Williamson, N. Characterising entrainment in fountains and negatively buoyant jets. J. Fluid Mech. 2022, 939, A29. [Google Scholar] [CrossRef]
- Advaith, S.; Parida, D.R.; Aswathi, K.T.; Dani, N.; Chetia, U.K.; Chattopadhyay, K.; Basu, S. Experimental investigation on single-medium stratified thermal energy storage system. Renew. Energy 2021, 164, 146–155. [Google Scholar] [CrossRef]
- Zachár, A. Analytic solution for convection dominant heat transport induced by buoyant jet entrainment inside hot fluid storage tanks. Sol. Energy 2020, 195, 239–248. [Google Scholar] [CrossRef]
- Yi, Y.; Nakayama, A. An analytical study on transient thermal behavior of a packed-bed molten salt thermocline thermal storage. Int. J. Heat Mass Transf. 2023, 209, 124095. [Google Scholar] [CrossRef]
- Li, M.-J.; Qiu, Y.; Li, M.-J. Cyclic thermal performance analysis of a traditional Single-Layered and of a novel Multi-Layered Packed-Bed molten salt Thermocline Tank. Renew. Energy 2018, 118, 565–578. [Google Scholar] [CrossRef]
- Xie, B.; Baudin, N.; Soto, J.; Fan, Y.; Luo, L. Experimental and numerical study on the thermocline behavior of packed-bed storage tank with sensible fillers. Renew. Energy 2023, 209, 106–121. [Google Scholar] [CrossRef]
- He, Z.; Qian, Y.; Xu, C.; Yang, L.; Du, X. Static and dynamic thermocline evolution in the water thermocline storage tank. Energy Procedia 2019, 158, 4471–4476. [Google Scholar] [CrossRef]
- Flueckiger, S.; Yang, Z.; Garimella, S.V. An integrated thermal and mechanical investigation of molten-salt thermocline energy storage. Appl. Energy 2011, 88, 2098–2105. [Google Scholar] [CrossRef]
- Elfeky, K.E.; Mohammed, A.G.; Ahmed, N.; Wang, Q. Thermo-mechanical investigation of the multi-layer thermocline tank for parabolic trough power plants. Energy 2023, 268, 126749. [Google Scholar] [CrossRef]
- González, I.; Pérez-Segarra, C.D.; Lehmkuhl, O.; Torras, S.; Oliva, A. Thermo-mechanical parametric analysis of packed-bed thermocline energy storage tanks. Appl. Energy 2016, 179, 1106–1122. [Google Scholar] [CrossRef]
- Wang, G.; Yu, S.; Niu, S.; Chen, Z.; Hu, P. A comprehensive parametric study on integrated thermal and mechanical performances of molten-salt-based thermocline tank. Appl. Therm. Eng. 2020, 170, 115010. [Google Scholar] [CrossRef]
- Motte, F.; Bugler-Lamb, S.L.; Falcoz, Q.; Py, X. Numerical Study of a Structured Thermocline Storage Tank Using Vitrified Waste as Filler Material. Energy Procedia 2014, 49, 935–944. [Google Scholar] [CrossRef]
- Mawire, A.; Taole, S.H. A comparison of experimental thermal stratification parameters for an oil/pebble-bed thermal energy storage (TES) system during charging. Appl. Energy 2011, 88, 4766–4778. [Google Scholar] [CrossRef]
- Castell, A.; Medrano, M.; Solé, C.; Cabeza, L.F. Dimensionless numbers used to characterize stratification in water tanks for discharging at low flow rates. Renew. Energy 2010, 35, 2192–2199. [Google Scholar] [CrossRef]
- Pradeep, N.; Reddy, K.S. Performance enhancement of packed bed thermal energy storage system for solar cogeneration of power and potable water production. J. Clean. Prod. 2023, 404, 136754. [Google Scholar] [CrossRef]
- Rendall, J.; Abu-Heiba, A.; Gluesenkamp, K.; Nawaz, K.; Worek, W.; Elatar, A. Nondimensional convection numbers modeling thermally stratified storage tanks: Richardson’s number and hot-water tanks. Renew. Sustain. Energy Rev. 2021, 150, 111471. [Google Scholar] [CrossRef]
- Raccanello, J.; Rech, S.; Lazzaretto, A. Simplified dynamic modeling of single-tank thermal energy storage systems. Energy 2019, 182, 1154–1172. [Google Scholar] [CrossRef]
- Ortega-Fernández, I.; Loroño, I.; Faik, A.; Uriz, I.; Rodríguez-Aseguinolaza, J.; D’Aguanno, B. Parametric analysis of a packed bed thermal energy storage system. AIP Conf. Proc. 2017, 1850, 080021. [Google Scholar] [CrossRef]
- Haller, M.Y.; Cruickshank, C.A.; Streicher, W.; Harrison, S.J.; Andersen, E.; Furbo, S. Methods to determine stratification efficiency of thermal energy storage processes–Review and theoretical comparison. Sol. Energy 2009, 83, 1847–1860. [Google Scholar] [CrossRef]
- Vannerem, S.; Neveu, P.; Falcoz, Q. Thermal cycle performance of thermocline storage: Numerical and experimental exergy analysis. Energy 2023, 278, 127647. [Google Scholar] [CrossRef]
- Ameen, M.T.; Ma, Z.; Smallbone, A.; Norman, R.; Roskilly, A.P. Experimental study and analysis of a novel layered packed-bed for thermal energy storage applications: A proof of concept. Energy Convers. Manag. 2023, 277, 116648. [Google Scholar] [CrossRef]
- Cárdenas, B.; Davenne, T.R.; Wang, J.; Ding, Y.; Jin, Y.; Chen, H.; Wu, Y.; Garvey, S.D. Techno-economic optimization of a packed-bed for utility-scale energy storage. Appl. Therm. Eng. 2019, 153, 206–220. [Google Scholar] [CrossRef]
- Ingenhoven, P.; Lee, L.; Saw, W.; Rafique, M.M.; Potter, D.; Nathan, G.J. Techno-economic assessment from a transient simulation of a concentrated solar thermal plant to deliver high-temperature industrial process heat. Renew. Sustain. Energy Rev. 2023, 185, 113626. [Google Scholar] [CrossRef]
- Le Roux, D.; Olivès, R.; Neveu, P. Combining entropy weight and TOPSIS method for selection of tank geometry and filler material of a packed-bed thermal energy storage system. J. Clean. Prod. 2023, 414, 137588. [Google Scholar] [CrossRef]
- Ingenhoven, P.; Saw, W.; Chinnici, A.; Potter, D.; Nathan, G.; Rafique, M.M.; Lee, K.L.; Jafarian, M. Energetic Assessment of a High Temperature Packed Bed Storage System in Combination with a Solar Expanding-Vortex Particle Receiver. In Proceedings of the ISES Solar World Congress 2021, Online, 25–29 October 2021; pp. 1–10. [Google Scholar]
- Singh, P.L.; Deshpandey, S.D.; Jena, P.C. Thermal performance of packed bed heat storage system for solar air heaters. Energy Sustain. Dev. 2015, 29, 112–117. [Google Scholar] [CrossRef]
- Andharia, J.K.; Markam, B.; Dzhonova, D.; Maiti, S. A comparative performance analysis of sensible and latent heat based storage in a small-scale solar thermal dryer. J. Energy Storage 2022, 45, 103764. [Google Scholar] [CrossRef]
- Cascetta, M.; Licheri, F.; Merchán, R.P.; Petrollese, M. Operating performance of a Joule-Brayton pumped thermal energy storage system integrated with a concentrated solar power plant. J. Energy Storage 2023, 73, 108865. [Google Scholar] [CrossRef]
- Junli, C.; Yanping, Z.; Chongzhe, Z.; Yulong, X.; Yuming, O. Thermal performance analysis of a thermocline storage tank with integrated annular distributors. Front. Energy Res. 2023, 11. [Google Scholar] [CrossRef]
- Wang, G.; Xie, Z.; Wang, B.; Lin, J. Comparison study on operation and mechanical characteristics of liquid sodium thermoclinic heat storage tank using different solid filling materials. Case Stud. Therm. Eng. 2023, 49, 103415. [Google Scholar] [CrossRef]
- Aggarwal, A.; Goyal, N.; Kumar, A. Thermal characteristics of sensible heat storage materials applicable for concentrated solar power systems. Mater. Today Proc. 2021, 47, 5812–5817. [Google Scholar] [CrossRef]
- Ding, Z.; Wu, W.; Leung, M. Advanced/hybrid thermal energy storage technology: Material, cycle, system and perspective. Renew. Sustain. Energy Rev. 2021, 145, 111088. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, Y.; Li, J.; Ma, X.; Li, Q.; Yang, M.; Zhao, X.; Zhu, Y. Simulation and economic analysis of an innovative indoor solar cooking system with energy storage. Sol. Energy 2023, 263, 111816. [Google Scholar] [CrossRef]
- Ushak, S.; Fernández, A.G.; Prieto, C.; Grageda, M. 3-Advances in molten salt storage systems using other liquid sensible storage media for heat storage. In Advances in Thermal Energy Storage Systems, 2nd ed.; Cabeza, L.F., Ed.; Woodhead Publishing: Duxford, UK, 2021; pp. 55–81. [Google Scholar]
- Abedigamba, O.P.; Mndeme, F.S.; Mawire, A.; Bahadur, I. Thermo-physical properties and thermal energy storage performance of two vegetable oils. J. Energy Storage 2023, 61, 106774. [Google Scholar] [CrossRef]
- Chekifi, T.; Boukraa, M. Thermocline storage for concentrated solar power plants: Descriptive review and critical analysis. J. Energy Storage 2022, 55, 105773. [Google Scholar] [CrossRef]
- Lou, W.; Xie, B.; Aubril, J.; Fan, Y.; Luo, L.; Arrivé, A. Optimized flow distributor for stabilized thermal stratification in a single-medium thermocline storage tank: A numerical and experimental study. Energy 2023, 263, 125709. [Google Scholar] [CrossRef]
- Cagnoli, M.; Gaggioli, W.; Liberatore, R.; Russo, V.; Zanino, R. CFD modelling of an indirect thermocline energy storage prototype for CSP applications. Sol. Energy 2023, 259, 86–98. [Google Scholar] [CrossRef]
- Odenthal, C.; Tombrink, J.; Klasing, F.; Bauer, T. Comparative study of models for packed bed molten salt storage systems. Appl. Therm. Eng. 2023, 226, 120245. [Google Scholar] [CrossRef]
- Al-Azawii, M.M.S.; Alhamdi, S.F.H.; Braun, S.; Hoffmann, J.-F.; Calvet, N.; Anderson, R. Thermocline in packed bed thermal energy storage during charge-discharge cycle using recycled ceramic materials-Commercial scale designs at high temperature. J. Energy Storage 2023, 64, 107209. [Google Scholar] [CrossRef]
- Wu, M.; Li, M.; Xu, C.; He, Y.; Tao, W. The impact of concrete structure on the thermal performance of the dual-media thermocline thermal storage tank using concrete as the solid medium. Appl. Energy 2014, 113, 1363–1371. [Google Scholar] [CrossRef]
- Grirate, H.; Agalit, H.; Zari, N.; Elmchaouri, A.; Molina, S.; Couturier, R. Experimental and numerical investigation of potential filler materials for thermal oil thermocline storage. Sol. Energy 2016, 131, 260–274. [Google Scholar] [CrossRef]
- Elouali, A.; Kousksou, T.; El Rhafiki, T.; Hamdaoui, S.; Mahdaoui, M.; Allouhi, A.; Zeraouli, Y. Physical models for packed bed: Sensible heat storage systems. J. Energy Storage 2019, 23, 69–78. [Google Scholar] [CrossRef]
- Elfeky, K.E.; Mohammed, A.G.; Wang, Q. Thermo-economic evaluation of PCM layer thickness change on the performance of the hybrid heat storage tank for concentrating solar power plants. Energy 2022, 253, 124128. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, C.; Liu, J.; Fang, X.; Zhang, Z. Highly stable graphite nanoparticle-dispersed phase change emulsions with little supercooling and high thermal conductivity for cold energy storage. Appl. Energy 2017, 188, 97–106. [Google Scholar] [CrossRef]
- Huang, X.; Lin, Y.; Alva, G.; Fang, G. Thermal properties and thermal conductivity enhancement of composite phase change materials using myristyl alcohol/metal foam for solar thermal storage. Sol. Energy Mater. Sol. Cells 2017, 170, 68–76. [Google Scholar] [CrossRef]
- Rostami, S.; Afrand, M.; Shahsavar, A.; Sheikholeslami, M.; Kalbasi, R.; Aghakhani, S.; Shadloo, M.S.; Oztop, H.F. A review of melting and freezing processes of PCM/nano-PCM and their application in energy storage. Energy 2020, 211, 118698. [Google Scholar] [CrossRef]
- Zahid, M.S.; Ahmed, N.; Qaisrani, M.A.; Mahmood, M.; Ali, M.; Waqas, A.; Assadi, M. Charging and discharging characterization of a novel combined sensible-latent heat thermal energy storage system by experimental investigations for medium temperature applications. J. Energy Storage 2022, 55, 105612. [Google Scholar] [CrossRef]
- Ali, H.M.; Rehman, T.-u.; Arıcı, M.; Said, Z.; Duraković, B.; Mohammed, H.I.; Kumar, R.; Rathod, M.K.; Buyukdagli, O.; Teggar, M. Advances in thermal energy storage: Fundamentals and applications. Prog. Energy Combust. Sci. 2024, 100, 101109. [Google Scholar] [CrossRef]
- Chen, J.; Feng, B.; Wang, W.; Liang, Y.; Zhang, W.; Li, X.; Li, C.; Wang, N.; Shi, Z. Cobalt nanoparticles supported on nitrogen-doped carbon nanotubes for the efficient oxygen reduction reaction in Mg-air battery. J. Alloys Compd. 2024, 983, 173878. [Google Scholar] [CrossRef]
- Molina, S.; Haillot, D.; Deydier, A.; Bedecarrats, J.-P. Material screening and compatibility for thermocline storage systems using thermal oil. Appl. Therm. Eng. 2019, 146, 252–259. [Google Scholar] [CrossRef]
- Mahammod, B.P.; Barua, E.; Deb, P.; Deoghare, A.B.; Pandey, K.M. Investigation of Physico-mechanical Behavior, Permeability and Wall Shear Stress of Porous HA/PMMA Composite Bone Scaffold. Arab. J. Sci. Eng. 2020, 45, 5505–5515. [Google Scholar] [CrossRef]
- Yu, S.; Han, D.; He, W.; Zhou, M.; Zhu, L.; Gao, Y.; Cui, G.; Peng, T. Analysis and optimization of transient heat dissipation characteristics of high power resistors with a sensible heat storage method. Appl. Therm. Eng. 2023, 226, 120246. [Google Scholar] [CrossRef]
- Tiskatine, R.; Aharoune, A.; Bouirden, L.; Ihlal, A. Identification of suitable storage materials for solar thermal power plant using selection methodology. Appl. Therm. Eng. 2017, 117, 591–608. [Google Scholar] [CrossRef]
- Amiri, L.; Ermagan, H.; Kurnia, J.C.; Hassani, F.; Sasmito, A.P. Progress on rock thermal energy storage (RTES): A state of the art review. Energy Sci. Eng. 2024, 12, 410–437. [Google Scholar] [CrossRef]
- Jemmal, Y.; Zari, N.; Maaroufi, M. Thermophysical and chemical analysis of gneiss rock as low cost candidate material for thermal energy storage in concentrated solar power plants. Sol. Energy Mater. Sol. Cells 2016, 157, 377–382. [Google Scholar] [CrossRef]
- El Alami, K.; Asbik, M.; Agalit, H. Identification of natural rocks as storage materials in thermal energy storage (TES) system of concentrated solar power (CSP) plants—A review. Sol. Energy Mater. Sol. Cells 2020, 217, 110599. [Google Scholar] [CrossRef]
- Katekar, V.P.; Rao, A.B.; Sardeshpande, V.R. An experimental investigation to optimise pebbles-based sensible heat storage system: An exploration to improve thermal efficiency of solar devices. J. Energy Storage 2023, 73, 108964. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Y. Exploration of steel slag for thermal energy storage and enhancement by Na2CO3 modification. J. Clean. Prod. 2023, 395, 136289. [Google Scholar] [CrossRef]
- Yang, X.; Cai, Z. An analysis of a packed bed thermal energy storage system using sensible heat and phase change materials. Int. J. Heat Mass Transf. 2019, 144, 118651. [Google Scholar] [CrossRef]
- Canneto, G.; Tizzoni, A.C.; Sau, S.; Mansi, E.; Gaggioli, W.; Spadoni, A.; Corsaro, N.; Capocelli, M.; Caputo, G.; Galindo, F.; et al. Thermocline Thermal Storage for Concentrated Solar Power Applications: Characterization of Novel Nitrate Salt Mixtures. J. Sol. Energy Eng. 2023, 145, 031001. [Google Scholar] [CrossRef]
- Lucio-Martin, T.; Martin, M.; Guerreiro, L.; Villardón, R.S.; Lopez, J.; Alonso, M.C. Thermal performance of a hybrid steel-concrete tank section for thermal energy storage in concentrated solar power plants. J. Energy Storage 2023, 60, 106630. [Google Scholar] [CrossRef]
- El Kouihen, F.; Filali Baba, Y.; AitOusaleh, H.; Elharrak, A.; Elalami, K.; Bennouna, E.; Faik, A. Investigation of thermal energy storage system based on mining by-products for the recovery of Moroccan mining industrial waste heat. Appl. Therm. Eng. 2023, 230, 120708. [Google Scholar] [CrossRef]
- Al-Azawii, M.M.S.; Alhamdi, S.F.H.; Braun, S.; Hoffmann, J.-F.; Calvet, N.; Anderson, R. Experimental study on packed-bed thermal energy storage using recycled ceramic as filler materials. J. Energy Storage 2021, 44, 103375. [Google Scholar] [CrossRef]
- Hong, D.; Yin, Z.; Yan, S.; Xu, W. Fine grained Al2O3/SiC composite ceramic tool material prepared by two-step microwave sintering. Ceram. Int. 2019, 45, 11826–11832. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Li, Y.; Ren, N.; Zhi, R.-P.; Ma, C.-F. Experimental study on the thermal stability of a new molten salt with low melting point for thermal energy storage applications. Sol. Energy Mater. Sol. Cells 2018, 176, 181–189. [Google Scholar] [CrossRef]
- Li, Q.; Cong, L.; Zhang, X.; Dong, B.; Zou, B.; Du, Z.; Xiong, Y.; Li, C. Fabrication and thermal properties investigation of aluminium based composite phase change material for medium and high temperature thermal energy storage. Sol. Energy Mater. Sol. Cells 2020, 211, 110511. [Google Scholar] [CrossRef]
- Fernández, Á.G.; Pineda, F.; Fuentealba, E.; Jullian, D.; Mallco, A.; Walczak, M. Compatibility of alumina forming alloys with LiNO3-containing molten salts for solar thermal plants. J. Energy Storage 2022, 48, 103988. [Google Scholar] [CrossRef]
- Lincu, D.; Ioniţǎ, S.; Mocioiu, O.C.; Berger, D.; Matei, C.; Mitran, R.A. Aluminum doping of mesoporous silica as a promising strategy for increasing the energy storage of shape stabilized phase change materials containing molten NaNO3: KNO3 eutectic mixture. J. Energy Storage 2022, 49, 104188. [Google Scholar] [CrossRef]
- Nualsing, D.; Pannucharoenwong, N.; Echaroj, S.; Rattanadecho, P. Investigation of molten salts incorporated with anodic aluminum oxide as thermal energy storage fluid on heat transfer efficiency. Case Stud. Therm. Eng. 2023, 49, 103258. [Google Scholar] [CrossRef]
- Wang, G.; Wang, T.; Han, W. Cyclic and standby behavior evaluations of liquid lead-bismuth eutectic thermal energy storage tank for concentrated solar power. Case Stud. Therm. Eng. 2022, 29, 101729. [Google Scholar] [CrossRef]
- Suresh, C.; Saini, R.P. An experimental study on the performance evaluation of a combined sensible-latent heat thermal energy storage. Int. J. Energy Res. 2021, 45, 5730–5746. [Google Scholar] [CrossRef]
- Spur, R.; Fiala, D.; Nevrala, D.; Probert, D. Performances of modern domestic hot-water stores. Appl. Energy 2006, 83, 893–910. [Google Scholar] [CrossRef]
- Mawire, A.; Taole, S.H.; Van den Heetkamp, R.R.J. Experimental investigation on simultaneous charging and discharging of an oil storage tank. Energy Convers. Manag. 2013, 65, 245–254. [Google Scholar] [CrossRef]
- He, W.; Wang, J.; Wang, Y.; Ding, Y.; Chen, H.; Wu, Y.; Garvey, S. Study of cycle-to-cycle dynamic characteristics of adiabatic Compressed Air Energy Storage using packed bed Thermal Energy Storage. Energy 2017, 141, 2120–2134. [Google Scholar] [CrossRef]
- Peng, H.; Shan, X.; Yang, Y.; Ling, X. A study on performance of a liquid air energy storage system with packed bed units. Appl. Energy 2018, 211, 126–135. [Google Scholar] [CrossRef]
- Wang, L.; Lin, X.; Chai, L.; Peng, L.; Yu, D.; Liu, J.; Chen, H. Unbalanced mass flow rate of packed bed thermal energy storage and its influence on the Joule-Brayton based Pumped Thermal Electricity Storage. Energy Convers. Manag. 2019, 185, 593–602. [Google Scholar] [CrossRef]
- Daschner, R.; Binder, S.; Mocker, M. Pebble bed regenerator and storage system for high temperature use. Appl. Energy 2013, 109, 394–401. [Google Scholar] [CrossRef]
- Schwarzmayr, P.; Birkelbach, F.; Walter, H.; Javernik, F.; Schwaiger, M.; Hofmann, R. Packed bed thermal energy storage for waste heat recovery in the iron and steel industry: A cold model study on powder hold-up and pressure drop. J. Energy Storage 2024, 75, 109735. [Google Scholar] [CrossRef]
- Li, G.; Zheng, X. Thermal energy storage system integration forms for a sustainable future. Renew. Sustain. Energy Rev. 2016, 62, 736–757. [Google Scholar] [CrossRef]
- Petrollese, M.; Cascetta, M.; Tola, V.; Cocco, D.; Cau, G. Pumped thermal energy storage systems integrated with a concentrating solar power section: Conceptual design and performance evaluation. Energy 2022, 247, 123516. [Google Scholar] [CrossRef]
- Chandra, Y.P.; Matuska, T. Stratification analysis of domestic hot water storage tanks: A comprehensive review. Energy Build. 2019, 187, 110–131. [Google Scholar] [CrossRef]
- Gaggioli, W.; Fabrizi, F.; Tarquini, P.; Rinaldi, L. Experimental Validation of the Innovative Thermal Energy Storage Based on an Integrated System “Storage Tank/Steam Generator”. Energy Procedia 2015, 69, 822–831. [Google Scholar] [CrossRef]
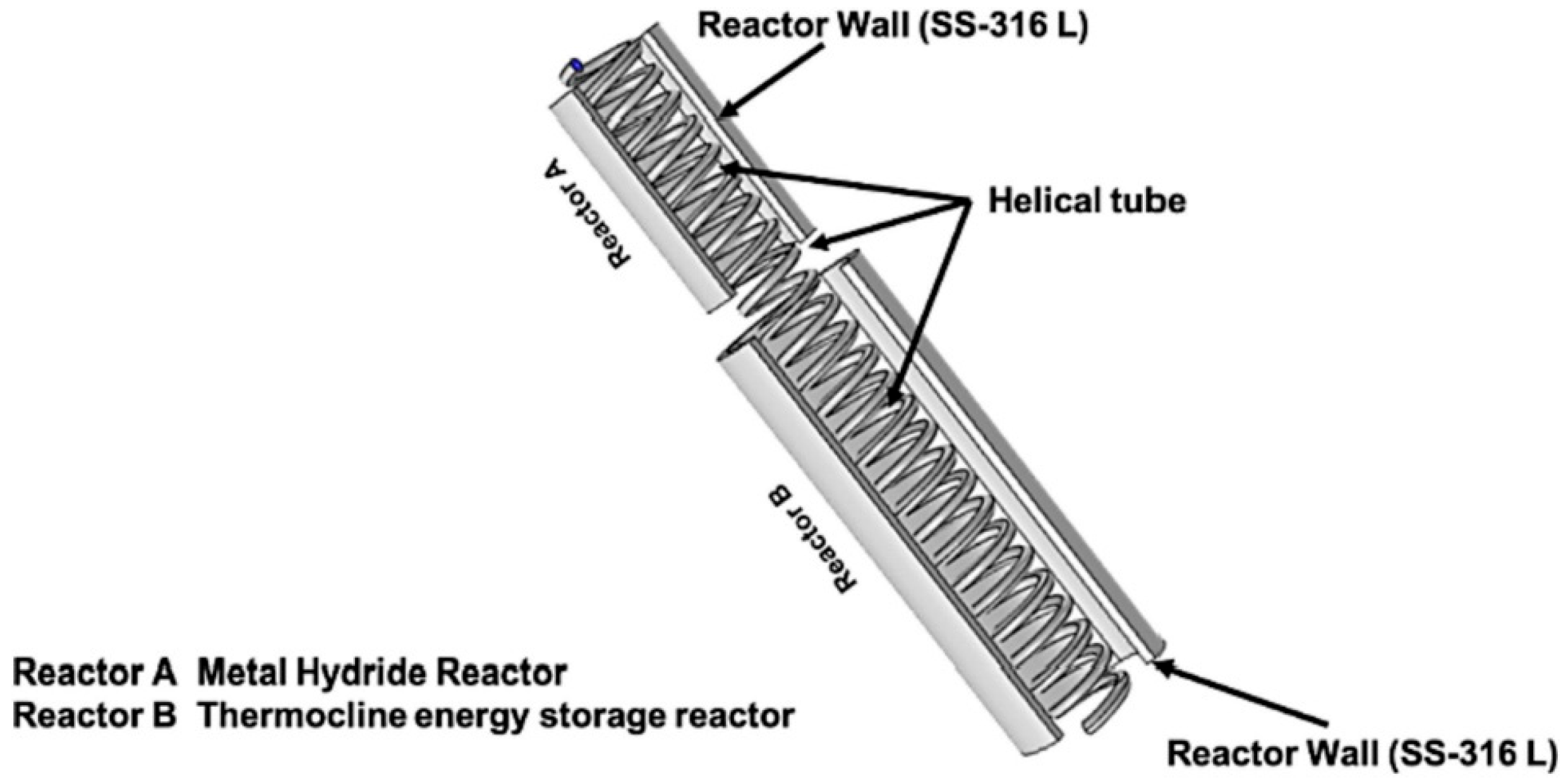
- Tiwari, S.; Sharma, P. Integration of metal hydride reactor with thermocline based heat storage system. J. Energy Storage 2023, 59, 106506. [Google Scholar] [CrossRef]
- Li, A.; Cao, F.; Zhang, W.; Shi, B.; Li, H. Effects of different thermal storage tank structures on temperature stratification and thermal efficiency during charging. Sol. Energy 2018, 173, 882–892. [Google Scholar] [CrossRef]
- Lou, W.; Fan, Y.; Luo, L. Single-tank thermal energy storage systems for concentrated solar power: Flow distribution optimization for thermocline evolution management. J. Energy Storage 2020, 32, 101749. [Google Scholar] [CrossRef]
- Khurana, H.; Majumdar, R.; Saha, S.K. Thermal stratification characteristics during simultaneous charging and discharging for different storage tank geometries with immersed discharging coil. Appl. Therm. Eng. 2023, 225, 120235. [Google Scholar] [CrossRef]
- Khurana, H.; Tiwari, S.; Majumdar, R.; Saha, S.K. Comparative Evaluation of Circular Truncated-Cone and Paraboloid Shapes for Thermal Energy Storage Tank based on Thermal Stratification Performance. J. Energy Storage 2021, 34, 102191. [Google Scholar] [CrossRef]
- Schwarzmayr, P.; Birkelbach, F.; Walter, H.; Hofmann, R. Standby efficiency and thermocline degradation of a packed bed thermal energy storage: An experimental study. Appl. Energy 2023, 337, 120917. [Google Scholar] [CrossRef]
- Zanganeh, G.; Pedretti, A.; Zavattoni, S.; Barbato, M.; Steinfeld, A. Packed-bed thermal storage for concentrated solar power–Pilot-scale demonstration and industrial-scale design. Sol. Energy 2012, 86, 3084–3098. [Google Scholar] [CrossRef]
- Le Roux, D.; Lalau, Y.; Rebouillat, B.; Neveu, P.; Olivès, R. Thermocline thermal energy storage optimisation combining exergy and life cycle assessment. Energy Convers. Manag. 2021, 248, 114787. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, H.; Wang, L.; Sheng, Y.; Wang, Y. Comparative study of the influences of different water tank shapes on thermal energy storage capacity and thermal stratification. Renew. Energy 2016, 85, 31–44. [Google Scholar] [CrossRef]
- Kurşun, B.; Ökten, K. Effect of rectangular hot water tank position and aspect ratio on thermal stratification enhancement. Renew. Energy 2018, 116, 639–646. [Google Scholar] [CrossRef]
- Marti, J.; Geissbühler, L.; Becattini, V.; Haselbacher, A.; Steinfeld, A. Constrained multi-objective optimization of thermocline packed-bed thermal-energy storage. Appl. Energy 2018, 216, 694–708. [Google Scholar] [CrossRef]
- Nandi, B.R.; Bandyopadhyay, S.; Banerjee, R. Numerical modeling and analysis of dual medium thermocline thermal energy storage. J. Energy Storage 2018, 16, 218–230. [Google Scholar] [CrossRef]
- Shaikh, W.; Wadegaonkar, A.; Kedare, S.B.; Bose, M. Numerical simulation of single media thermocline based storage system. Sol. Energy 2018, 174, 207–217. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, M.; Wang, Z.; Li, X.; Chen, L. Thermal stratification in a cylindrical tank due to heat losses while in standby mode. Sol. Energy 2019, 185, 222–234. [Google Scholar] [CrossRef]
- Skuntz, M.E.; Elander, R.; Al Azawii, M.; Bueno, P.; Anderson, R. System efficiency of packed bed TES with radial flow vs. axial flow-Influence of aspect ratio. J. Energy Storage 2023, 72, 6. [Google Scholar] [CrossRef]
- Esence, T.; Bruch, A.; Molina, S.; Stutz, B.; Fourmigué, J.-F. A review on experience feedback and numerical modeling of packed-bed thermal energy storage systems. Sol. Energy 2017, 153, 628–654. [Google Scholar] [CrossRef]
- Lou, W.; Baudin, N.; Roux, S.; Fan, Y.; Luo, L. Impact of buoyant jet entrainment on the thermocline behavior in a single-medium thermal energy storage tank. J. Energy Storage 2023, 71, 108017. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Z.; Duan, Y. Influence of flow distribution on the thermal performance of dual-media thermocline energy storage systems. Appl. Energy 2015, 142, 283–292. [Google Scholar] [CrossRef]
- Li, S.-H.; Zhang, Y.-X.; Li, Y.; Zhang, X.-S. Experimental study of inlet structure on the discharging performance of a solar water storage tank. Energy Build. 2014, 70, 490–496. [Google Scholar] [CrossRef]
- Shafieian, A.; Bahrami, H.-R.; Roostaee, A.; Feyzi, S.S. Effects of different inlet configurations on the performance of solar storage tanks: A three-dimensional unsteady CFD simulation. Case Stud. Therm. Eng. 2023, 45, 103019. [Google Scholar] [CrossRef]
- Vannerem, S.; Neveu, P.; Falcoz, Q. Experimental investigation of the impact of fluid distribution on thermocline storage performance. J. Energy Storage 2022, 52, 104864. [Google Scholar] [CrossRef]
- Bellenot, G. Study on the Influence of Fluid’s Distribution over the Thermohydraulic Behaviour of a Single-Tank Dual-Media Thermal storageEtude de L’influence de la Distribution de Fluide sur le Comportement Thermohydraulique d’un Réservoir de Stockage Thermique Mono-Cuve Dual-Media; Université Grenoble Alpes: Grenoble, French, 2020. [Google Scholar]
- Soria-Verdugo, A.; Cano-Pleite, E.; Panahi, A.; Ghoniem, A.F. Partitioning of a wide bubbling fluidized bed with vertical internals to improve local mixing and bed material circulation. Powder Technol. 2022, 408, 117771. [Google Scholar] [CrossRef]
- Morato-Godino, A.; Sánchez-Delgado, S.; García-Hernando, N.; Soria-Verdugo, A. Pyrolysis of Cynara cardunculus L. samples–Effect of operating conditions and bed stage on the evolution of the conversion. Chem. Eng. J. 2018, 351, 371–381. [Google Scholar] [CrossRef]
- Hernández-Jiménez, F.; Soria-Verdugo, A.; Acosta-Iborra, A.; Santana, D. Exergy recovery from solar heated particles to supercritical CO2. Appl. Therm. Eng. 2019, 146, 469–481. [Google Scholar] [CrossRef]
- Cano-Pleite, E.; Hernández-Jiménez, F.; García-Gutiérrez, L.M.; Soria-Verdugo, A. Thermo-economic optimization of a novel confined thermal energy storage system based on granular material. Appl. Therm. Eng. 2023, 224, 120123. [Google Scholar] [CrossRef]
- Soria-Verdugo, A.; Guil-Pedrosa, J.F.; Hernández-Jiménez, F.; García-Gutiérrez, L.M.; Cano-Pleite, E.; García-Hernando, N. Experimental analysis of a novel confined bed system for thermal energy storage. J. Energy Storage 2023, 69, 107972. [Google Scholar] [CrossRef]
- McTigue, J.D.; White, A.J. A comparison of radial-flow and axial-flow packed beds for thermal energy storage. Appl. Energy 2018, 227, 533–541. [Google Scholar] [CrossRef]
- Capocelli, M.; Caputo, G.; De Falco, M.; Mazzei, D.; Piemonte, V. Two-Channels Thermal Energy Storage Tank: Experiments and Short-Cut Modelling. Zenodo 2017, 10008164. [Google Scholar] [CrossRef]
- Capocelli, M.; Caputo, G.; De Falco, M.; Balog, I.; Piemonte, V. Numerical Modeling of a Novel Thermocline Thermal Storage for Concentrated Solar Power. J. Sol. Energy Eng. 2019, 141, 051001. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, P.; Wang, R.Z. Numerical heat transfer analysis of the packed bed latent heat storage system based on an effective packed bed model. Energy 2010, 35, 2022–2032. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, Y. Pore scale numerical simulation of heat transfer and flow in porous volumetric solar receivers. Appl. Therm. Eng. 2017, 120, 150–159. [Google Scholar] [CrossRef]
- Guo, X.; Dai, R. Numerical simulation of flow and heat transfer in a random packed bed. Particuology 2010, 8, 293–299. [Google Scholar] [CrossRef]
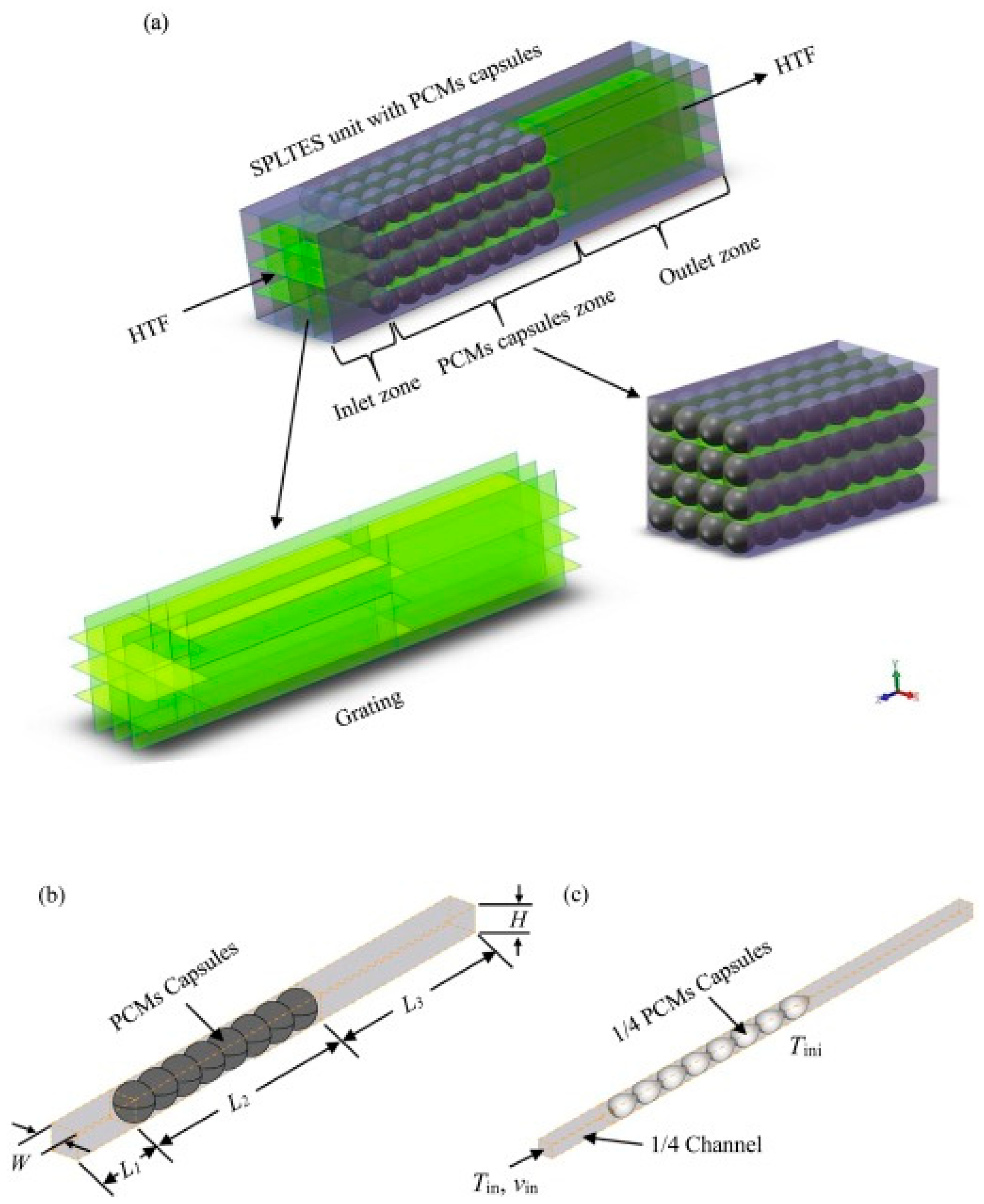
- Zhang, Z.; Yu, C.; Ci, Z.; Cao, L. A numerical study on the thermal storage properties of packer bed under different arrangements of PCM capsules. Therm. Sci. 2022, 26, 1345–1356. [Google Scholar] [CrossRef]
- Lv, P.; Liu, L.; Lei, G.; Dong, H. Pore-scale numerical investigation on the thermal storage properties of packed-bed systems with phase change material microcapsules. J. Clean. Prod. 2023, 405, 137071. [Google Scholar] [CrossRef]
- Flueckiger, S.M.; Garimella, S.V. Latent heat augmentation of thermocline energy storage for concentrating solar power—A system-level assessment. Appl. Energy 2014, 116, 278–287. [Google Scholar] [CrossRef]
- Cheng, X.; Zhai, X. Thermal performance analysis and optimization of a cascaded packed bed cool thermal energy storage unit using multiple phase change materials. Appl. Energy 2018, 215, 566–576. [Google Scholar] [CrossRef]
- Elfeky, K.E.; Ahmed, N.; Wang, Q. Numerical comparison between single PCM and multi-stage PCM based high temperature thermal energy storage for CSP tower plants. Appl. Therm. Eng. 2018, 139, 609–622. [Google Scholar] [CrossRef]
- Elfeky, K.E.; Li, X.; Ahmed, N.; Lu, L.; Wang, Q. Optimization of thermal performance in thermocline tank thermal energy storage system with the multilayered PCM(s) for CSP tower plants. Appl. Energy 2019, 243, 175–190. [Google Scholar] [CrossRef]
- Elfeky, K.E.; Mohammed, A.G.; Ahmed, N.; Wang, Q. Thermal performance of cascaded and combined sensible-latent heat storage tank under fluctuations in sunlight and electric demand. Appl. Therm. Eng. 2023, 229, 120575. [Google Scholar] [CrossRef]
- Elsihy, E.S.; Mokhtar, O.; Xu, C.; Du, X.; Adel, M. Cyclic performance characterization of a high-temperature thermal energy storage system packed with rock/slag pebbles granules combined with encapsulated phase change materials. Appl. Energy 2023, 331, 120380. [Google Scholar] [CrossRef]
- John, E.E.; Hale, W.M.; Selvam, R.P.; Brown, B.; Asme. Development and Performance Evaluation of High Temperature Concrete for Thermal Energy Storage for Solar Power Generation. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition (IMECE), Denver, CO, USA, 11–17 November 2011; pp. 1207–1213. [Google Scholar]
- Motte, F.; Bugler-Lamb, S.L.; Falcoz, Q. Thermocline Storage Filled with Structured Ceramics. Numerical Consistency of the Developed Numerical Model and First Observations. High Temp. Mater. Process. 2015, 34, 353–365. [Google Scholar] [CrossRef]
- Strasser, M.N.; Selvam, R.P. A cost and performance comparison of packed bed and structured thermocline thermal energy storage systems. Sol. Energy 2014, 108, 390–402. [Google Scholar] [CrossRef]
- Yu, C.; Qian, J.; Cao, D.; Chen, D.; Wu, L.; Zhang, C. Charging performance of structured packed-bed latent thermal energy storage unit with phase change material capsules. J. Energy Storage 2023, 71, 108157. [Google Scholar] [CrossRef]
- Elsihy, E.S.; Liao, Z.; Xu, C.; Du, X. Dynamic characteristics of solid packed-bed thermocline tank using molten-salt as a heat transfer fluid. Int. J. Heat Mass Transf. 2021, 165, 120677. [Google Scholar] [CrossRef]
- Xu, C.; Li, X.; Wang, Z.; He, Y.; Bai, F. Effects of solid particle properties on the thermal performance of a packed-bed molten-salt thermocline thermal storage system. Appl. Therm. Eng. 2013, 57, 69–80. [Google Scholar] [CrossRef]
- Khurana, H.; Majumdar, R.; Saha, S.K. Experimental investigation of heat dispatch controllability through simultaneous charging-discharging and stand-alone discharging operations in vertical cylindrical sensible heat storage tank. J. Energy Storage 2022, 54, 105268. [Google Scholar] [CrossRef]
- Yaïci, W.; Ghorab, M.; Entchev, E.; Hayden, S. Three-dimensional unsteady CFD simulations of a thermal storage tank performance for optimum design. Appl. Therm. Eng. 2013, 60, 152–163. [Google Scholar] [CrossRef]
- Fernández-Seara, J.; Uhía, F.J.; Sieres, J. Experimental analysis of a domestic electric hot water storage tank. Part I: Static mode of operation. Appl. Therm. Eng. 2007, 27, 129–136. [Google Scholar] [CrossRef]
- Dickinson, R.M.; Cruickshank, C.A.; Harrison, S.J. Charge and discharge strategies for a multi-tank thermal energy storage. Appl. Energy 2013, 109, 366–373. [Google Scholar] [CrossRef]
- Szczęśniak, A.; Milewski, J.; Dybiński, O.; Futyma, K.; Skibiński, J.; Martsinchyk, A. Dynamic simulation of a four tank 200 m3 seasonal thermal energy storage system oriented to air conditioning at a dietary supplements factory. Energy 2023, 264, 126106. [Google Scholar] [CrossRef]
- Crandall, D.M.; Thacher, E.F. Segmented thermal storage. Sol. Energy 2004, 77, 435–440. [Google Scholar] [CrossRef]
- McTigue, J.D.; White, A.J. Segmented packed beds for improved thermal energy storage performance. IET Renew. Power Gener. 2016, 10, 1498–1505. [Google Scholar] [CrossRef]
- Biencinto, M.; Bayón, R.; Rojas, E.; González, L. Simulation and assessment of operation strategies for solar thermal power plants with a thermocline storage tank. Sol. Energy 2014, 103, 456–472. [Google Scholar] [CrossRef]
- Palomba, V.; Frazzica, A. Application of numerical methods for the design of thermocline thermal energy storage: Literature review and critical analysis. J. Energy Storage 2022, 46, 103875. [Google Scholar] [CrossRef]
- Szczęśniak, A.; Milewski, J.; Dybiński, O.; Futyma, K.; Skibiński, J.; Martsinchyk, A.; Szabłowski, Ł. Determination of Thermocline Heat Transfer Coefficient by Using CFD Simulation. Energies 2023, 16, 3150. [Google Scholar] [CrossRef]
- Untrau, A.; Sochard, S.; Marias, F.; Reneaume, J.-M.; Le Roux, G.A.C.; Serra, S. A fast and accurate 1-dimensional model for dynamic simulation and optimization of a stratified thermal energy storage. Appl. Energy 2023, 333, 120614. [Google Scholar] [CrossRef]
- Hoffmann, J.F.; Fasquelle, T.; Goetz, V.; Py, X. A thermocline thermal energy storage system with filler materials for concentrated solar power plants: Experimental data and numerical model sensitivity to different experimental tank scales. Appl. Therm. Eng. 2016, 100, 753–761. [Google Scholar] [CrossRef]
- Cortés, E.; Gaviño, D.; Calderón-Vásquez, I.; García, J.; Estay, D.; Cardemil, J.M.; Barraza, R. Application of layer view factor method in high temperature thermal storage packed bed. Appl. Therm. Eng. 2024, 236, 121471. [Google Scholar] [CrossRef]
- Ruiz, G.; Ripoll, N.; Fedorova, N.; Zbogar-Rasic, A.; Jovicic, V.; Delgado, A.; Toledo, M. Experimental and numerical analysis of the heat transfer in a packed bed exposed to the high thermal radiation flux. Int. J. Heat Mass Transf. 2019, 136, 383–392. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.; Moscardini, M.; Kamlah, M.; Liu, S. A DEM-based heat transfer model for the evaluation of effective thermal conductivity of packed beds filled with stagnant fluid: Thermal contact theory and numerical simulation. Int. J. Heat Mass Transf. 2019, 132, 331–346. [Google Scholar] [CrossRef]
- Sedighi, M.; Padilla, R.V.; Alamdari, P.; Lake, M.; Rose, A.; Izadgoshasb, I.; Taylor, R.A. A novel high-temperature (>700 °C), volumetric receiver with a packed bed of transparent and absorbing spheres. Appl. Energy 2020, 264, 114705. [Google Scholar] [CrossRef]
- Johnson, E.; Tarı, İ.; Baker, D. A Monte Carlo method to solve for radiative effective thermal conductivity for particle beds of various solid fractions and emissivities. J. Quant. Spectrosc. Radiat. Transf. 2020, 250, 107014. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, H.; Hao, Z.; Liu, F.; Niu, F. A non-linear transform approach for conduction-radiation heat transfer in the extended thermal discrete element method. Int. J. Heat Mass Transf. 2021, 176, 121432. [Google Scholar] [CrossRef]
- Khurana, H.; Majumdar, R.; Saha, S.K. Response Surface Methodology-based prediction model for working fluid temperature during stand-alone operation of vertical cylindrical thermal energy storage tank. Renew. Energy 2022, 188, 619–636. [Google Scholar] [CrossRef]
- Trevisan, S.; Jemmal, Y.; Guedez, R.; Laumert, B. Packed bed thermal energy storage: A novel design methodology including quasi-dynamic boundary conditions and techno-economic optimization. J. Energy Storage 2021, 36, 102441. [Google Scholar] [CrossRef]

| Material | Density | Specific Heat | Thermal Conductivity | Thermal Capacity | Viscosity ] |
|---|---|---|---|---|---|
| Water (20 °C) [40,41] | 998 | 4.183 | 0.598 | 4174 | - |
| Silicon Oil (Ak250) [40] | 900–970 | 1.465 | 0.168 | 1421–2100 | - |
| Transformer Oil (60 °C) [40] | 842 | 2.090 | 0.122 | 1760 | - |
| Therminol [24] | 1056 | 1.575 | 0.135 | 1663 | 0.0030 |
| Thermal Oil T55 [42] | 766 | 2.455 | 0.11 | 1880 | 0.001021 |
| Mineral Oil [41,43] | 770–800 | 2.60 | 0.12 | 2080–2600 | - |
| Synthetic Oil [41,43] | 900 | 2.10–2.30 | 0.11 | 1890–2300 | - |
| Rapeseed Oil [38] | 781 | 3.385 | 0.217 | 2643 | 0.00291 |
| Sunflower Oil [44] | 915–920 | 1.863–2.439 | 0.139–0.163 | 1705–2232 | 0.057 |
| Roki Oil [44] | 909–950 | 1.888–2.404 | 0.153–0.170 | 1716–2280 | 0.08220 |
| K-NaNO3 (230 °C) [40] | 1950 | 1.57 | 0.50 | 3062 | - |
| Paraffin (20 °C) [40] | 900 | 2.13 | 0.26 | 1917 | - |
| Molten Salts [40,41] | 500–2600 | 1.50 | 0.2–2.0 | 1350–3900 | - |
| CaloriaHT 42 [45] | 695 | 2.700 | - | 1877 | - |
| Liquid Sodium (100 °C) [40] | 927 | 1.385 | 85.84 | 1105 | - |
| Material | Thermal Properties | |
|---|---|---|
| Water [46] | Density [kg/m3] | |
| Specific Heat [J/(kg∙k)] | ||
| Thermal Conductivity [W/(m∙k)] | ||
| Viscosity [Pa∙s] | ||
| Solar Salt [18] | Density [kg/m3] | |
| Specific Heat [J/(kg∙k)] | ||
| Thermal Conductivity [W/(m∙k)] | ||
| Viscosity [Ns∙m−2] | ||
| Hitex XL [47] | Density [kg/m3] | |
| Specific Heat [J/(kg∙k)] | ||
| Thermal Conductivity [W/(m∙k)] | 0.519 | |
| Viscosity [Pa∙s] | ||
| Jarysol Oil [29] | Density [kg/m3] | |
| Specific Heat [J/(kg∙k)] | ||
| Thermal Conductivity [W/(m∙k)] | ||
| Viscosity [Pa∙s] |
| Reference | Optimized Packing Method | Description | Characteristics |
|---|---|---|---|
| [112,113] | Ordered packing | Filled with TESM particles in a certain order | The pressure drop in ordered packing is lower than that of disordered packing, and the temperature field is more uniform. Multi-layered ordered packing with particles of different sizes is superior to single-layered ordered packing because it can effectively shorten charging time and reduce thermocline degradation. |
| [45,114,115,116,117,118,119] | Cascaded configuration | Filled with multiple layers of different TESM particles | Matching the thermal properties of TESMs with the HTF temperature curve along the bed gives the cascade configuration better thermal performance and higher overall efficiency than the single-layer configuration and shortens the charging time. Among multiple cascade configurations, the sensible–latent heat hybrid cascade configuration has higher charging and discharging efficiency and utilization rate. It is economical to replace some PCMs with sensible TESMs. |
| [21,42,49,120,121,122,123] | Structured configuration | Arrange TESMs in a certain shape or pattern in the THS tank | Avoiding the risk of thermal ratcheting and solving the problem of excessive pressure drop in packed bed configurations under high flow rates. Compared to the packed bed configuration, the capacity cost of the structured configuration is lower, but the efficiency is also slightly reduced. |
| Reference | Strategy | Type | Approach | Characteristics |
|---|---|---|---|---|
| [65] | Dynamic dual mode | SMTHS | Ex | Describe the thermal stratification phenomenon of THS storage tanks used for cooking under three different SCAD modes. |
| [126] | Dynamic dual mode | Indirect SMTHS | Ex/Nu | The initial thermocline zone split into primary and secondary thermocline zones, which expand with time and increasing coil flow rate. |
| [9] | Dynamic dual mode | DMTHS | Ex | The increase in discharge flow increases the overall charge–discharge time, thickening the thermocline, and there exists a “perfect flow” that maximizes discharge efficiency and utilization rate. |
| [84] | Standby mode, reverse charging method, and forward charging method | DMTHS | Ex | In long standby mode, reverse charging has twice the exergy loss of forward charging, with significantly lower energy and exergy efficiency than forward charging. |
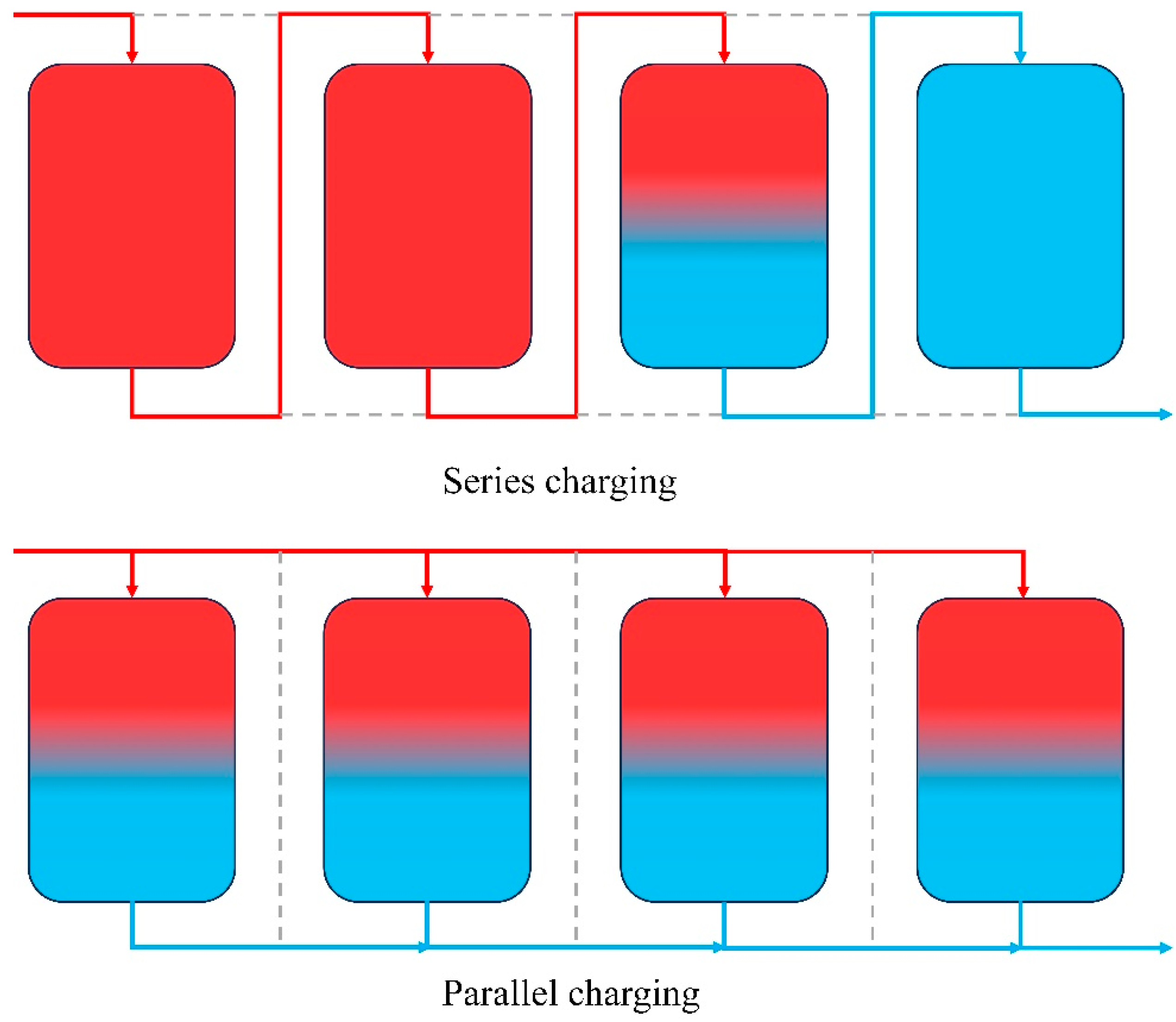
| [129] | Series charging and discharging method, parallel charging and discharging method, and series charging combined with parallel discharging method | Multi-tank indirect SMTHS | Ex/Nu | The parallel charging and discharging method has lower discharge temperatures, and the series–parallel combination method results in unequal discharge temperatures of the three tanks, with the series charging and discharging method being the best strategy. |
| [130] | Series charging method | Multi-tank SMTHS | Nu | The thermocline zone can move between multiple tanks connected in series, and the multi-tank THS reduces thermocline energy loss. |
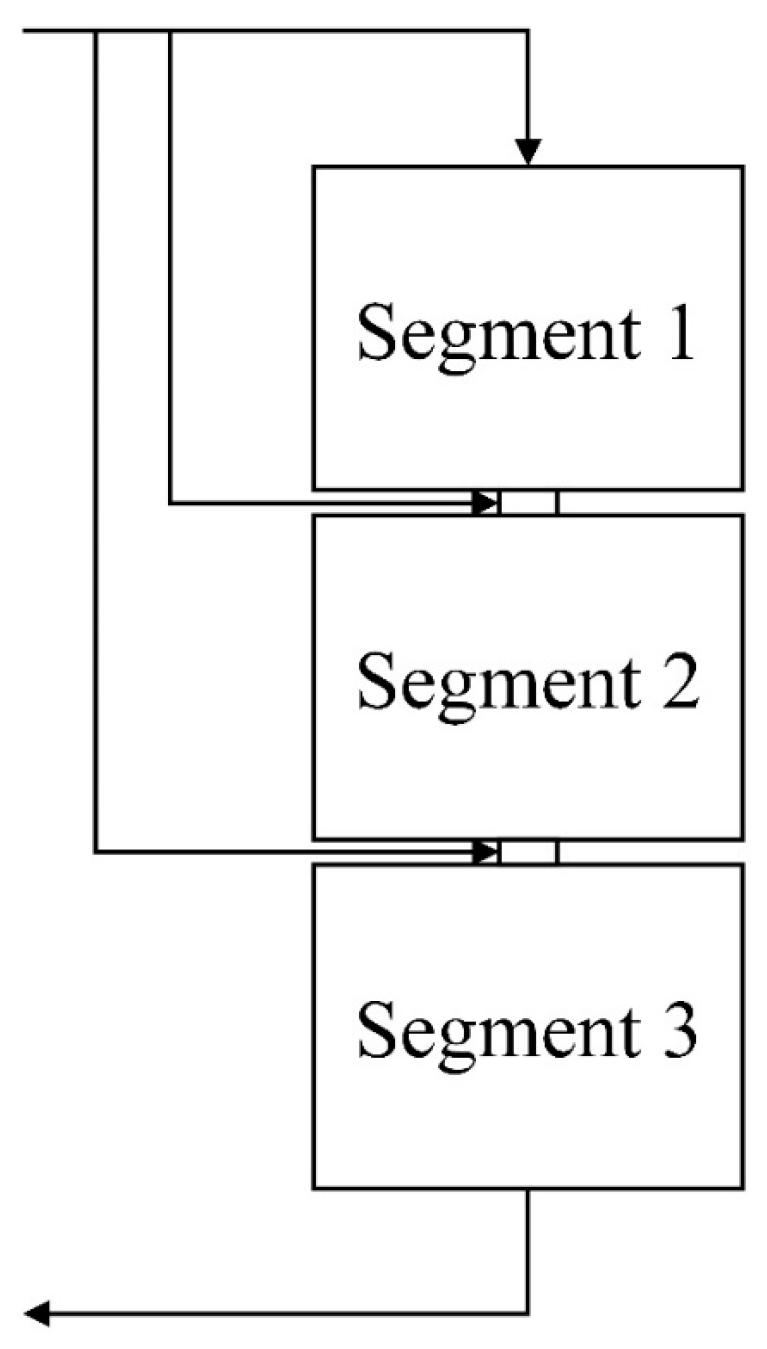
| [131] | Segmented charging method | Segmented bed | Nu | Segmented charging can control the movement of thermal fronts and maintain thermal stratification, and the segmented position has a slight impact on the maximum energy storage capacity of the system. |
| [105,132] | Segmented charging and discharging method | Segmented bed | Nu | Segmentation reduces conduction losses during the charging mode, and segmented THS tanks have better performance and economics than radial flow THS tanks and axial flow THS tanks. |
| [30] | Two cycle control scenarios: time-based and temperature-based | Layered bed | Ex | Layering reduces pressure loss by about 64% while producing a narrower thermocline. In the time-based scenario, the layered and simple modes have comparable thermal performance, with lower exit loss in the layered mode. In the temperature-based scenario, the layered mode reaches the steady state earlier and has better performance. |
| [118] | Full charge–partial discharge scheme, partial charge–partial discharge scheme | Combined sensible–latent THS, cascaded THS | Nu | The overall efficiency of the full charge–partial discharge scheme is much higher than the partial charge–partial discharge scheme. |
| [133] | Seven charging and discharging strategies consisting of four charging strategies and five discharging strategies | Two-tank TES, indirect two-tank TES, DMTHS, indirect DMTHS | Nu | The annual electricity production of a solar thermal power plant with a THS system is always lower than that of the same plant with a two-tank system. The electricity yield and fossil fuel consumption for the seven strategies analyzed show similar behavior in direct and indirect configurations. The optimal strategy for the charging process is to partially extract the thermocline region to feed the solar field to the maximum allowable inlet temperature. The best strategies for discharge technology are to completely extract the thermocline region, and the feeding sequence to various components of the power plant varies according to the annual power generation or annual fossil fuel consumption. |
| Approach | Schematic | Principle | Computational Time |
|---|---|---|---|
| 0D modeling approach |  | The system is considered as a unique fully mixed region having uniform temperature. The dynamic behavior of the storage is described by the time profile of the uniform temperature inside the tank calculated by solving a single energy balance ordinary differential equation. | 5 s |
| quasi-1D modeling approach |  | The internal volume is subdivided into a hot and a cold region, having uniform temperature and variable boundaries over time. The storage operation is described by the time profiles of the temperatures and masses of the two regions calculated using two energy and mass balance ordinary differential equations. | 12 s |
| 1D modeling approach | 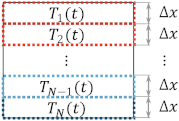 | and uniform temperature, where the layer at the top is defined as layer number 1. The thickness is known by dividing the tank height by the chosen number of layers. energy balance ordinary differential equations are required to calculate the temperature stratification inside the storage tank as a function of time. | 13 s |
| Type of Model | Main Features | Motivation for Choosing the Model |
|---|---|---|
| 1D | Low computational effort, 2 phases assumed. | Simple geometry of the tank, with no effect of radiant gradient, especially suited for coupling with optimization methods. |
| 2D 1-phase | 1 heat equation for both filler and HTF, reduced computational effort. | Systems in which Biot body approximation can be applied. This occurs for small-size filler particles or low Reynolds numbers in the fluid. |
| 2D 2-phase | 2 heat equations for filler and HTF. | Suitable for a wide variety of systems, including solid or PCM fillers, vast literature data available, proven reliability and accuracy. |
| 3D | Higher computational effort compared to 1D and 2D cases, higher accuracy. | The evaluation of localized phenomena, the evaluation of complex geometries, i.e., in the distributors. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Guo, Y.; Zhu, J.; Yuan, W.; Zhao, F. New Advances in Materials, Applications, and Design Optimization of Thermocline Heat Storage: Comprehensive Review. Energies 2024, 17, 2403. https://doi.org/10.3390/en17102403
Zhang Y, Guo Y, Zhu J, Yuan W, Zhao F. New Advances in Materials, Applications, and Design Optimization of Thermocline Heat Storage: Comprehensive Review. Energies. 2024; 17(10):2403. https://doi.org/10.3390/en17102403
Chicago/Turabian StyleZhang, Yunshen, Yun Guo, Jiaao Zhu, Weijian Yuan, and Feng Zhao. 2024. "New Advances in Materials, Applications, and Design Optimization of Thermocline Heat Storage: Comprehensive Review" Energies 17, no. 10: 2403. https://doi.org/10.3390/en17102403
APA StyleZhang, Y., Guo, Y., Zhu, J., Yuan, W., & Zhao, F. (2024). New Advances in Materials, Applications, and Design Optimization of Thermocline Heat Storage: Comprehensive Review. Energies, 17(10), 2403. https://doi.org/10.3390/en17102403