Abstract
Accurate wind power forecasting (WPF) is critical in optimizing grid operations and efficiently managing wind energy resources. Challenges arise from the inherent volatility and non-stationarity of wind data, particularly in short-to-medium-term WPF, which extends to longer forecast horizons. To address these challenges, this study introduces a novel model that integrates Improved Empirical Mode Decomposition (IEMD) with an enhanced Transformer called TransIEMD. TransIEMD begins by decomposing the wind speed into Intrinsic Mode Functions (IMFs) using IEMD, transforming the scalar wind speed into a vector form that enriches the input data to reveal hidden temporal dynamics. Each IMF is then processed with channel attention, embedding, and positional encoding to prepare inputs for an enhanced Transformer. The Direct Embedding Module (DEM) provides an alternative viewpoint on the input data. The distinctive perspectives of IEMD and DEM offer interaction through cross-attention within the encoder, significantly enhancing the ability to capture dynamic wind patterns. By combining cross-attention and self-attention within the encoder–decoder structure, TransIEMD demonstrates enhanced proficiency in detecting and leveraging long-range dependencies and dynamic wind patterns, improving the forecasting precision. Extensive evaluations on a publicly available dataset from the National Renewable Energy Laboratory (NREL) demonstrate that TransIEMD significantly improves the forecasting accuracy across multiple horizons of 4, 8, 16, and 24 h. Specifically, at the 24 h forecast horizon, TransIEMD achieves reductions in the normalized mean absolute error and root mean square error of 4.24% and 4.37%, respectively, compared to the traditional Transformer. These results confirm the efficacy of integrating IEMD with attention mechanisms to enhance the accuracy of WPF.
1. Introduction
The contemporary world faces the dual challenges of fossil fuel depletion and climate catastrophes caused by the greenhouse effect []. The large-scale development and application of green and clean energy sources are crucial in addressing these challenges []. Among various new energy sources, wind power generation has emerged as an important renewable energy source with its advantages of a low cost, environmental sustainability, and significant scale benefits [].
To achieve the climate goal of limiting global warming within 1.5 degrees Celsius, it is crucial to triple the renewable energy capacity by 2030, where wind energy plays a pivotal role []. The Global Wind Energy Council (GWEC) anticipates that new wind energy installations will reach 130 GW in 2024, with a projected addition of 791 GW over the next five years [].
Governments worldwide are actively progressing toward this ambitious renewable energy goal. In the European Union, wind energy emerged as the dominant form of renewable energy for the first time in 2018, generating 362.4 TWh and accounting for 24% of all renewable energy installations []. Similarly, China is on course to exceed its renewable energy target, with a record 290 GW installed in 2023 alone, aiming for renewables to make up over 50% of the new electricity consumption by 2025 []. Furthermore, Peru’s varied geography and extensive coastline make it an ideal location for wind power, offering potential capacities of 20.5 GW onshore and 347 GW offshore [].
Due to temperature, altitude, terrain, and air pressure influences, wind energy is characterized by variability, randomness, and non-stationarity. Moreover, the operational efficiency of wind turbines is closely related to changes in wind speed (WS) [], posing certain challenges to power grid scheduling with large-scale wind power integration []. Accurate wind power forecasting (WPF) can effectively improve the peak-adjusting capabilities of the power grid, enhance its wind power acceptance, and improve the safety and economic efficiency of the operation of the power system, which is vital for the integrated use of wind power and the stability of the power system [].
According to prediction timescales, WPF models can be grouped into ultra-short-term, short-term, medium-term, and long-term models []. Specifically, short-term models are designed to predict wind power generation from 30 min to up to six hours in advance. In contrast, medium-term models extend their forecasting capabilities from six hours to a full day ahead. This paper concentrates on developing and analyzing short-to-medium-term WPF models, which are critical for applications in power dispatch, energy trading, and overall power system management.
WPF methods can be broadly classified into four principal categories based on their foundational modeling approaches []: physical, statistical, artificial intelligence (AI)-based, and hybrid models. Within AI-based methodologies, a distinction is made between those founded on traditional machine learning techniques and those employing advanced deep learning (DL) [] strategies. Leveraging mathematical frameworks akin to statistical models, machine learning-based WPF approaches demonstrate performance that rivals that of statistical methods. However, the remarkable progress in DL has established it as a central pillar of WPF research, and it is the primary emphasis of this paper.
Recurrent Neural Networks (RNNs) [], one of the major DL architectures, are distinguished for their capability to process sequential data, making them particularly suitable for WPF, which requires an understanding of temporal dynamics. The RNN and its variants, such as Long Short-Term Memory (LSTM) [] and Gated Recurrent Units (GRU) [], have significantly influenced WPF by offering an enhanced time series data model. Sun et al. [] employ Variational Mode Decomposition (VMD) [] alongside Convolutional LSTM (ConvLSTM) to refine short-term WPF, achieving superior performance over traditional models. Similarly, Liu et al. [] innovate with a stacked RNN featuring parametric sine activation functions (PSAF), leading to notable improvements in the forecasting accuracy. Zhou et al. [] and Wu et al. [] explore the synergy between VMD and LSTM to enhance the forecasting capabilities. Zhou et al. [] leverage Numerical Weather Prediction (NWP) data for WPF refinement. Wu et al. [] integrate Convolutional Neural Networks (CNNs) [] with LSTM, significantly reducing noise and extracting meaningful wind speed and power features. Wu et al. [] apply CNN-LSTM to make predictions for wind farm clusters, highlighting the critical role of spatial correlations among NWP data across wind farms in the forecasting accuracy. Liu et al. [] propose a hybrid model combining Complementary Ensemble Empirical Mode Decomposition (CEEMDAN), Bidirectional LSTM, and Markov Chains, effectively navigating the uncertainty and variability characteristic of wind power. Lastly, Hossain et al. [] significantly improve the accuracy of very-short-term WPF by integrating of CEEMDAN, LSTM, and monarch butterfly optimization.
Through advanced data processing techniques, RNNs have also been utilized in WS forecasting and correction to improve the accuracy, as demonstrated by Liu et al. [] and Lv et al. []. Additionally, their use extends to photovoltaic (PV) power generation forecasting, with Huang et al. [] leveraging LSTM networks for accurate energy output predictions.
Transformers [] have notably advanced long-term time series forecasting [,], overcoming the challenges faced by RNNs in capturing long-range dependencies and enhancing the training efficiency. Utilizing self-attention mechanisms, Transformers efficiently process input data in parallel, thus providing insights into the relationships within complex data essential for accurate long-term forecasts. Transformers have demonstrated significant utility in the realm of WPF and related areas. Research indicates that combining Temporal Fusion Transformers (TFT) [] with VMD significantly improves the WPF accuracy and effectively addresses the uncertainties inherent in wind patterns []. Furthermore, the development of interpretable models that combine VMD and TFT has advanced WS forecasting, offering deep insights into wind dynamics []. Introducing hybrid models, such as H-Transformer, which integrates the traditional Autoregressive Integrated Moving Average (ARIMA) with a Transformer, further highlights the transformative impact of Transformers in accurately forecasting renewable energy production [].
Beyond DL architectures, time series decomposition may significantly improve the forecasting accuracy. Empirical Mode Decomposition (EMD) [,], Ensemble EMD [,], and VMD [,,] have been thoroughly integrated with RNNs and are receiving extensive attention. Abedinia et al. [] developed Improved EMD (IEMD), merging bagging neural networks and K-means clustering for WPF and achieving improved accuracy over various forecast horizons. Decomposition techniques have also been shown to enhance the forecasting accuracy in conjunction with Transformers []. Wu et al. [] combined VMD with TFT for a 10-step WS forecast. However, accurate short-to-medium-term WPF, particularly for forecast horizons spanning up to 24 h—a challenge that typically involves forecasting hundreds of steps—has yet to be extensively explored.
This paper investigates how to enhance the accuracy of short-to-medium-term WPF given the inherent volatility and non-stationarity of wind energy. We introduce the TransIEMD model, which combines IEMD [] with the Transformer architecture [], to tackle this issue. This model leverages IEMD to decompose WS into Intrinsic Mode Functions (IMFs), enriching the input with temporal insights. Coupled with a Direct Embedding Module (DEM) that employs a cross-attention mechanism, TransIEMD surpasses the limitations of traditional Transformers [] in capturing temporal features. Fusing IEMD with channel attention stabilizes the input sequences and effectively extracts essential trends and features in wind series data, significantly improving the forecasting accuracy.
The core contributions of our study are outlined as follows.
- By integrating IEMD with channel attention, the TransIEMD model stabilizes the input sequences and transforms WS into multivariate vectors rich in temporal context. This approach enhances the ability to accurately capture and interpret the complex dynamics and inter-variable relationships among meteorological variables, especially wind patterns, leading to a notable improvement in the forecasting accuracy.
- We enhance the encoder–decoder in Transformer by incorporating cross-attention and self-attention mechanisms with DEM. This enhancement strengthens the proficiency of the model in identifying and leveraging long-range dependencies and evolving data patterns, substantially elevating the forecasting precision.
The forecasting performance of our TransIEMD model is thoroughly evaluated over forecast horizons of 4, 8, 16, and 24 h, utilizing a publicly available dataset from the National Renewable Energy Laboratory (NREL) [] in the United States. Our comprehensive evaluation demonstrates the exceptional predictive capabilities of the proposed model across various forecast horizons.
The rest of this paper is structured as follows. Section 2 outlines essential background theories on IEMD and the attention mechanism. Section 3 delves into the detailed description of the TransIEMD model. Section 4 presents the results of a series of experiments conducted to validate the performance of the proposed TransIEMD model. Section 5 discusses comparisons with existing WPF models, extended applications, and future works on the TransIEMD model. Finally, Section 6 summarizes the findings and contributions of this study.
2. Theoretical Framework
2.1. Self-Attention Mechanism
The attention mechanism was initially proposed to improve long sequence processing in RNN []. It provides a mechanism for the decoder to determine and select the most important tokens in a specific context. The study [] abandoned the RNN structure and used the self-attention mechanism for the same purpose, becoming a mainstream structure in natural language processing, image and video analysis, and time series analysis [].
The self-attention in Transformer operates on matrices of query , key , and value tokens, which are extracted from the input series with linear transformations. Each matrix represents a set of tokens, with individual rows corresponding to a separate query, key, and value token. These transformations are defined as
where matrices , , and are parameters to be learned in self-attention. The calculation of self-attention is expressed as
where is the resulting context matrix that conveys information about the input series. This matrix expression allows self-attention to perform parallelized sequence learning, avoiding the iterative processing employed by RNNs. Figure 1 visualizes this process, where the weighting step corresponds to the operation in Equation (2).
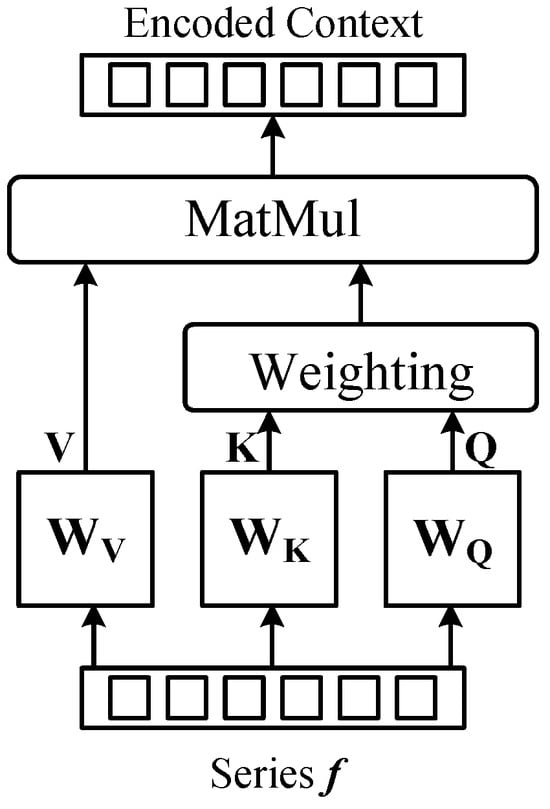
Figure 1.
The computing process of self-attention.
2.2. Improved Empirical Mode Decomposition
EMD is an adaptive signal decomposition method using the Hilbert–Huang transform [], which can decompose a nonlinear and non-stationary time series into a finite number of IMFs. The instantaneous frequency obtained from the Hilbert transform of the decomposed IMFs has clear physical meaning, enabling a better representation of local signal phase changes []. IMFs, being stationary and more predictable than the original series, enhance the prediction accuracy of time series and are widely used in WPF [].
The EMD of a time signal can be expressed as
where represents the IMFs, with subscript m distinguishing different modes, and is the residual after decomposition. The m-th order IMF is obtained by repeatedly applying a sifting process to the decomposition residuals. For the -th residual of the m-th order IMF decomposition, denoted as , the sifting process initiates by locating the local maxima and minima of . It proceeds by fitting upper and lower envelopes with cubic spline functions and calculates their means, represented as . The decomposition iterates the following sifting process:
until achieves Cauchy-like convergence in terms of the normalized squared error, which is calculated as
The m-th order IMF decomposition starts with the residual , where the initial residual is the original signal to be decomposed, i.e., .
In practice, the results obtained from EMD may produce spurious components due to insufficient sampling rates or improper spline interpolation. Therefore, the decomposed modes are selectively retained in IEMD by discarding spurious components and preserving only those that reflect the true IMFs of the signal. A component is filtered out if it satisfies the following condition:
where ∨ represents the logical OR, is the correlation coefficient of the component with the original signal, is the threshold for selecting the correlation coefficient, and denotes the two-sample Kolmogorov–Smirnov (KS) test []. The threshold is set to , where . Components with a correlation coefficient smaller than are ignored. The KS test is used to ascertain the correlation of each modal component with Gaussian noise, thereby ignoring components close to noise. After filtering with (6) proposed by IEMD, the number of IMFs is reduced from to M.
3. Methodology
In this study, we tackle the task of predicting a sequence of wind power outputs , covering a continuous forecast horizon of H time steps beyond time t. The inputs to the WPF model are meteorological variables observed within a lookback window of length L leading up to time t, which we denote as . The operation of the WPF model can be succinctly formalized as
where represents the forecast power output, and denotes learnable parameters.
3.1. TransIEMD Architecture Overview
Transformer [] generalizes the conventional encoder–decoder structure [] by introducing self-attention. In a Transformer, the encoder converts an input sequence into some contextual representations, which the decoder then uses to generate the output sequence. The encoder comprises a stack of identical blocks, each consisting a self-attention layer and a multi-layer perceptron (MLP). Both layers are enhanced with residual connections [] and layer normalization for training stability and convergence. Like the encoder, the decoder block includes an additional attention layer over the encoder output. Due to self-attention, Transformers are effective in learning long-range dependencies in sequence-to-sequence tasks, a critical aspect for time series forecasting that improves the performance and model interpretability.
To address the challenge of accurate short-to-medium-term WPF, particularly due to the variability and non-stationarity of wind, this paper proposes the TransIEMD model. This model combines IEMD [] with the attention mechanism []. The architecture, shown in Figure 2, comprises six components: the tokenizer, DEM, encoder, decoder, query generation, and prediction Output.
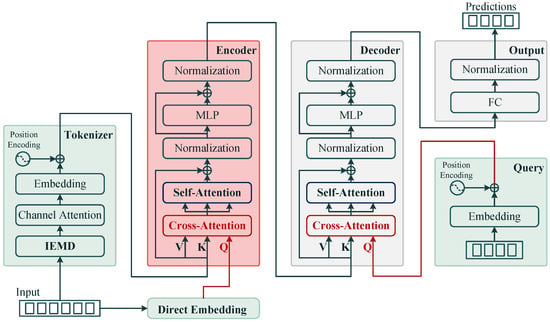
Figure 2.
The architecture of TransIEMD for short-to-medium-term WPF.
Figure 2 depicts the data flow within TransIEMD. The input meteorological sequence passes through both the tokenizer and DEM. The input sequence is tokenized via IEMD [], aligning it with positional encoding (PE) to form a structure amenable to attention mechanisms. Simultaneously, the DEM transforms the inputs to create query vectors for the encoder. The encoder then applies cross-attention and self-attention in succession, utilizing the tokenized key–value pairs and DEM queries to capture the temporal dependencies within the meteorological data, especially the decomposed WS. This process enriches the encoded contexts, which are subsequently decoded using additional position-encoded queries to focus on the forecasting targets. The output module transforms the decoded context features into the final forecast, specifying the WPF for upcoming time steps.
TransIEMD refines the standard Transformer with a blend of IEMD and a dual-attention mechanism, comprising both cross-attention and self-attention. This structure excels in extracting predictable patterns from meteorological data, significantly enhancing the feature extraction process. Additionally, DEM aids in crafting robust contextual representations that resonate with the inherent characteristics of the input. By enabling the encoder and decoder to process diverse query tokens via cross-attention, TransIEMD provides a refined forecasting approach that is well suited for the fluctuating dynamics of wind energy data.
3.2. Tokenization Based on IEMD
In TransIEMD, tokenization, a technique originally utilized in natural language processing to break down text into digestible tokens, is ingeniously adapted for the transformation of meteorological inputs into analyzable tokens. This adaptation is pivotal in harnessing the attention mechanism and tailoring Transformer models to the intricacies of WPF. Following the application of IEMD, wind data are decomposed into multiple IMFs, , for . Each IMF, marked by enhanced predictability and stability, lays the groundwork for the generation of tokens that improve the forecasting capabilities.
The model employs channel attention to recognize the disparate forecasting impacts of each IMF and the additional meteorological variables that extend beyond wind feature decomposition. This strategy dynamically adjusts the significance of each component to refine the forecasting acumen. The mechanism processes the decomposed features via global max and average pooling operations, succeeded by an MLP with shared parameters and sigmoid activation, yielding the channel attention vector as expressed in
where denotes the sigmoid function; encapsulates both the M IMFs and the additional D meteorological features exclusive of the decomposed wind signals. After channel attention modulation, is subject to embedding and PE, culminating in , which serves as the key–value pair for the encoder. The methodology for the conversion of into key–value pairs mirrors that of the query generation module, detailed in Section 3.4.
3.3. Encoder and Decoder Modules
The proposed TransIEMD architecture improves the original Transformer by enhancing the encoder and decoder modules for superior feature extraction and analysis. Central to this model, these modules employ layers of cross-attention, self-attention, and feedforward networks to symmetrically encode and decode the input data, ensuring a balanced processing mechanism.
As depicted in Figure 3, the cross-attention mechanism facilitates interaction between two sequences. The key and value tokens are derived from sequence , which is the same as the self-attention shown in Figure 1 and Equation (1). The query tokens are derived from sequence as follows:
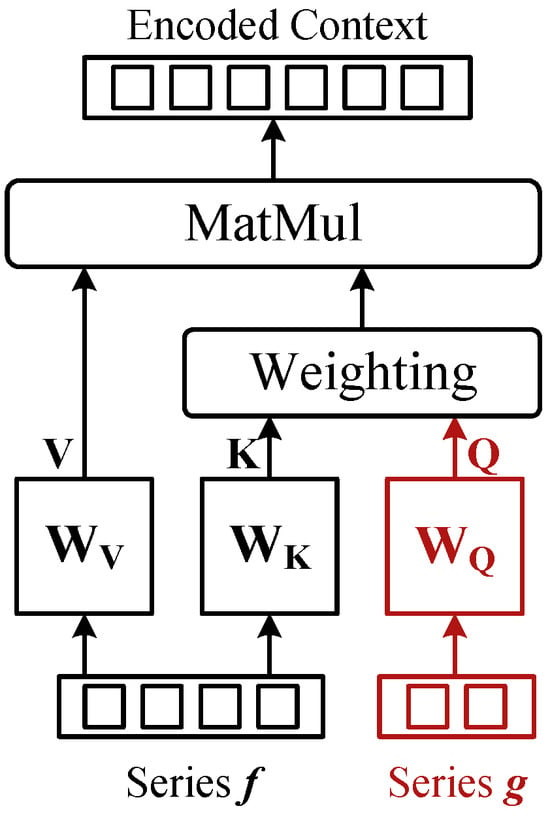
Figure 3.
Calculation process of cross-attention.
As illustrated in Figure 2, the encoder and decoder apply cross-attention but with different sources for their query sequences. The encoder uses the -series derived from the DEM. DEM performs nonlinear transformations on the original input sequences, allowing subsequent cross-attention to establish correlations across different data views by querying the transformed sequences against the IEMD sequences. Equipped with convolution layers with bias terms and a ReLU activation layer, DEM can efficiently extract local features and learn dependencies within various time ranges, enhancing the understanding of dynamic meteorological processes.
In contrast, the decoder employs placeholder sequences for its queries, using the encoded features to generate predictive contexts for upcoming time intervals. This difference in the query sequences between the encoder and decoder is critical in capturing the dynamic and complex patterns inherent in wind data, enabling precise forecasting.
Residual connections and normalization layers are integrated within both mechanisms and the feedforward network to fortify the learning efficacy. To systematically differentiate between the attention layers within both modules, a superscript notation , where , labels their parameters, , , and , and outputs, aligning with the sequential direction of the data flow. According to Equation (2), the context is obtained by the attention mechanism as a linear combination of the corresponding input values . The effectiveness of both the encoder and decoder is thus rooted in the IEMD-based tokenization strategy.
3.4. Query Generation and Prediction Output Modules
In TransIEMD, addressing temporal relationships is crucial due to the potential loss of time series continuity through tokenization. To preserve the temporal integrity, PE is added to the data before they are processed by the encoder and decoder. This strategy injects the time step information lost during tokenization, allowing the model to interpret the temporal dynamics effectively. Specifically, in the encoder, PE is applied post-embedding for key–value tokens.
For embedding, each input token is transformed into a d-dimensional vector, reshaping the data from a sequence into a matrix format, which is crucial for parallel processing with an attention mechanism. PE marks each time step uniquely with sine and cosine, providing a distinct positional signature as detailed below:
where t denotes the time step in the input sequence, i is the dimension in the embedding, and 10,000, enhancing the model’s sensitivity to the temporal ordering.
The objective function to optimize TransIEMD is formulated as -norm minimization to enhance the robustness against outliers [], favoring more stable and reliable predictions. The objective function is expressed as
indicating the aggregate deviation of the predicted from the actual wind power outputs over the dataset . Our comprehensive parameter set encompasses learnable weights within the components of TransIEMD, all of which are optimized to enhance the accuracy and reliability of WPF.
3.5. Pseudocode
To enhance the clarity and reproducibility of the TransIEMD model, the detailed pseudocode for the main components and the overall model is presented in Algorithm 1. The pseudocode begins with the Tokenizer and Encoder. The Tokenizer processes the input meteorological data, applying IEMD to the wind data, followed by channel attention, embedding, and PE. The Encoder then processes these tokens through cross-attention and self-attention mechanisms, which are crucial in capturing temporal dependencies. Because of its structural similarity to the encoder, the decoder can be implemented by mirroring the Encoder procedure, with minor modifications. The whole procedure of TransIEMD is illustrated to ensure the streamlined computation of the model, efficiently incorporating both output and query components. This pseudocode serves as a guide for the recreation of the TransIEMD model.
| Algorithm 1 Pseudocode for the implementation of TransIEMD |
|
4. Results
In this section, comprehensive experiments are conducted to validate the efficacy of our proposed TransIEMD model against state-of-the-art approaches, including GRU [], Informer [], and Transformer []. Informer, developed by Zhou et al. [], enhances Transformer’s efficiency with ProbSparse self-attention, reducing the complexity to for long-sequence tasks. This section presents a structured description, including dataset specifics, model configurations, and evaluation metrics to ensure transparency and replicability. Comparative analyses alongside error distribution assessments demonstrate the superior forecasting accuracy of TransIEMD. An ablation study further elucidates the benefits derived from integrating IEMD and DEM.
4.1. Dataset
To evaluate the efficacy of TransIEMD, this paper conducts comprehensive comparative experiments on a publicly available wind power dataset [] from the National Renewable Energy Laboratory (NREL), United States. The chosen dataset contains 736,416 observations recorded at wind farm ID 126684, covering 2007 to 2013. Data points were captured at 5 min intervals, yielding 288 observations per day, with a maximum installed capacity of 16 megawatts (). For each time instance, the data point includes five meteorological variables, which are the WS measured in meters per second (m/s), the wind direction (WD) in degrees (°), the temperature in degrees Celsius (°C), the humidity in percent (%), and the pressure in hectopascals (hPa), along with the wind power in megawatts (MW). Among the equations of the proposed model, (7) and (11) output values in the same unit of measurement as the wind power, MW. However, other equations, such as (8)–(10), are not constrained by units of measurement.
Constructed with the WIND tool [], the NREL dataset undergoes rigorous correction and validation processes, including multi-station comparisons and meteorological data integration, which ensures its accuracy and reliability. The dataset is an exemplary resource for WPF research [], because it has been validated against actual production patterns to ensure its usability and is free from human-induced noise []. Please refer to ref. [] for more details.
For this investigation, the dataset is divided into a training set , a validation set , and a test set , adhering to a 7:1:2 partition ratio. This division facilitates thorough training, fine-tuning, and evaluation phases for the TransIEMD model. Employing a sliding window technique with a step size of one, the methodology ensures the maximal exploitation of the training set, thereby augmenting the predictive performance of the model. The input of the model is sequences of length , derived from a predetermined lookback window, optimizing the model’s capacity to predict wind power generation accurately.
4.2. Model Configurations
The architecture of TransIEMD is thoroughly engineered to optimize the forecasting performance, balancing complexity with precision. The output dimension of the tokenizer is set at 512, which is a critical aspect in determining the model size. The output dimensions of the DEM and query module align with this setting, ensuring seamless integration within the model framework. The encoder and decoder are key parts of the Transformer architecture and have the same structure in TransIEMD. Both use self-attention and cross-attention with dimensionality of 512 and a two-layer MLP, with matrices configured to and . This uniformity creates a consistent data processing environment in the model and enables sophisticated feature transformations. The prediction output module employs a fully connected (FC) layer capable of transforming 512-dimensional feature vectors into a one-dimensional output, essential for delivering precise forecasting results.
In pursuit of an equitable comparison, the hidden layer feature dimensions of all baseline models, including Transformer [], Informer [], and GRU [], are uniformly set to 512 in the experiments. Such settings aim to eliminate potential biases in the performance evaluation arising from model parameter variances, thereby ensuring a fair and direct comparison across all models.
In training TransIEMD, the optimizer employs the Adam method with momentum to ensure training stability. The training process includes 30 epochs, with a batch size of 256, carefully calibrated to balance the computational demands with effective model optimization.
The adaptability and efficacy of TransIEMD are rigorously evaluated through four forecasting tasks with horizons H of 48, 96, 192, and 288, corresponding to 4, 8, 16, and 24 h, respectively. This varied approach assesses the flexibility of TransIEMD across different time frames. In the meantime, TransIEMD can generate predictions for multiple time points concurrently, significantly enhancing its practical utility in real-world applications.
4.3. Evaluation Metrics
To rigorously evaluate the performance of the WPF models, we employ several key metrics on the test set , namely the mean absolute error (MAE) and root mean square error (RMSE), alongside the relative RMSE (rRMSE) and the coefficient of determination (). These metrics are crucial in quantifying the differences between the forecast values and actual observations, offering a comprehensive assessment of the prediction accuracy.
The MAE is defined to capture the average magnitude of absolute errors:
where is the total number of data samples within the test set, with and denoting the predicted and actual power values at time t, respectively. The RMSE measures the average magnitude of the squared errors and is expressed as
which penalizes larger errors more than the MAE. The unit for both the MAE and RMSE is MW, which is consistent with the unit used to measure the wind power. For comparability across different scales, the rRMSE adjusts the RMSE relative to the average observed value:
where represents the average true wind power across the test set. The coefficient of determination, , evaluates the proportion of variance in the actual data that is predictable from the model:
Lastly, we adopt normalized relative errors, denoted by the Greek letter , to assess the percentage of error reduction achieved by TransIEMD compared to the Transformer:
where can be the MAE or RMSE, and represents the maximum installed capacity. This comparative method quantitatively converts the performance differential between the models into a percentage of installed capacity, offering a clear and direct measure for the evaluation of performance enhancements.
By adopting these metrics, our analysis ensures a comprehensive and equitable evaluation of the forecasting models under consideration, effectively highlighting their performance nuances in wind power prediction tasks.
4.4. Comparison with Existing Models
To accurately evaluate the performance of the proposed TransIEMD model in short-term WPF, three representative deep learning models were chosen as baselines for comparison. These baseline models included (1) the classical RNN network model GRU [] for time series forecasting; (2) the Transformer [], a foundational sequence processing model based on the self-attention mechanism; and (3) Informer [], optimized for long-sequence forecasting. These models were selected due to their widely recognized effectiveness in the field of time series analysis. Due to their poorer multi-step forecasting performance, the comparison did not include traditional machine learning methods like random forest and support vector machine regression. The selection of baseline models ensures that the experimental results comprehensively reflect the performance of TransIEMD.
4.4.1. Comparative Analysis of WPF Models
Table 1 provides a detailed comparison of the forecasting performance between the proposed TransIEMD model and the three baseline models across all four tested forecast horizons (4, 8, 16, and 24 h). The evaluation metrics include the MAE, RMSE, rRMSE, and , which collectively offer a nuanced insight into the accuracy, efficiency, and predictive power of each model in short-term WPF.

Table 1.
Forecasting performance comparison across models. In this table, bold values highlight the top performance and italics indicate the second-best across each forecast horizon and metric.
TransIEMD exhibits superior forecasting accuracy across all horizons, as highlighted by its lower MAE and RMSE values. This superiority is especially marked for longer forecasts of up to 24 h, indicating the robustness of TransIEMD in capturing the inherent variability of the input NWP. The performance gap widens with the forecast horizon, underlining the ability of TransIEMD to handle long temporal dependencies and non-stationarities in data effectively.
The rRMSE metric further emphasizes the consistency and reliability of TransIEMD in forecasting. The rRMSE values of TransIEMD are markedly lower than those of the competing models, indicating a smaller error magnitude relative to the mean observed values and superior model performance across varying lengths of forecast horizons.
Moreover, the values are highest for TransIEMD across all forecast horizons. This suggests that TransIEMD excels in explaining the variability in wind power data, highlighting its effectiveness in capturing the underlying patterns and dynamics critical for operational planning in the wind energy sector.
In essence, the TransIEMD model not only offers a notable improvement in forecasting accuracy but also showcases a significant reduction in errors and an enhanced ability to elucidate the dynamics of wind power generation. This makes TransIEMD a valuable tool in enhancing the efficiency and reliability of WPF, which is essential for grid management and operational decision-making in the renewable energy industry.
4.4.2. Visual Comparison
The visual representation of the WPF results in Figure 4 spans seven days of test set data. Each subplot illustrates how the different models perform over four forecast horizons. The ground truth (GT) values of wind power are indicated by grey lines, and the various colors distinguish the forecasts from each model. Dark grey vertical lines mark the transitions between the different forecast horizons.
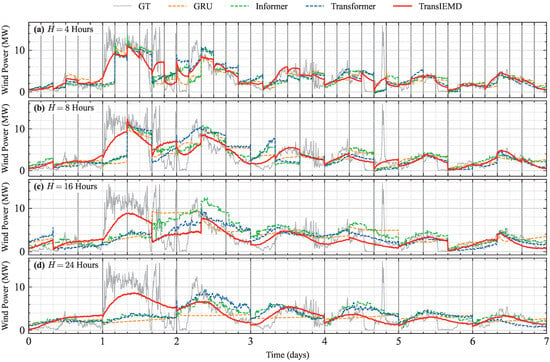
Figure 4.
Comparative analysis of WPF performance: seven-day visualization across multiple forecast horizons. (a) Forecast results for the 4 h horizon. (b) Forecast results for the 8 h horizon. (c) Forecast results for the 16 h horizon. (d) Forecast results for the 24 h horizon.
A close examination of Figure 4 reveals that the forecasts of TransIEMD closely match the GT throughout all forecast horizons, efficiently capturing both the highs and lows of the wind power output. This contrasts with the competing models, which often produce overly smooth forecasts, especially at critical peaks and troughs, resulting in inaccurate predictions. The distinct performance advantage of TransIEMD is consistent across all forecast horizons. It can be attributed to its utilization of cross-attention and self-attention mechanisms, which facilitate the in-depth synthesis of the original signal with the decomposed IMFs. This integration allows TransIEMD to harness essential temporal features in the data, leading to significantly improved accuracy in the complex domain of WPF.
The strength of TransIEMD is even more pronounced when dealing with longer forecast horizons. At the 24 h mark, the predictions of TransIEMD exhibit impressive alignment with the GT data, highlighting its capacity for reliable extended-range forecasting. This is essential for strategic energy grid management and planning in the wind energy industry.
The graphical analysis in Figure 4 highlights the precision and reliability of TransIEMD, showcasing its potential to serve as a robust tool for industry applications. Its capability to deliver accurate longer multiple-step forecasts can greatly enhance wind energy’s integration into power systems, signifying a notable advancement over the models being compared.
4.4.3. Computational Complexity Analysis
The model sizes, training, and inference speeds are crucial factors that influence the cost-effectiveness of applying a WPF model. These computational demands are compared in Table 2, which provides insights into the operational efficiencies of the models. The results were obtained using a high-performance computing setup equipped with dual 2.50 GHz Xeon E5-2678 CPUs (Intel, USA) and 4 NVIDIA RTX 3090 GPUs (Gigabyte Technology, New Taipei City, Taiwan), with each model utilizing only one GPU during both the training and testing stages.

Table 2.
Comparative overview of model complexity and training efficiency.
According to Table 2, TransIEMD exhibits a marginally larger parameter size and slightly slower training and inference speeds than Transformer and Informer. The IEMD computation stage in TransIEMD introduces an additional, though negligible, 8.00 s to the total training time. Despite these minor increases, the substantial accuracy improvements provided by TransIEMD justify the slight rise in computational resource usage. These data confirm the feasibility of TransIEMD in terms of computational complexity, making it a cost-effective solution, particularly in scenarios where accuracy is important.
4.5. Error Analysis
The performance of the forecasting models is examined through two types of error distribution: the overall RMSE distribution and the time-step-specific MAE distribution.
4.5.1. Overall RMSE Distributions
Figure 5 presents the RMSE values in boxplot form, visually assessing the central tendency and variability for forecast horizons of 4, 8, 16, and 24 h.
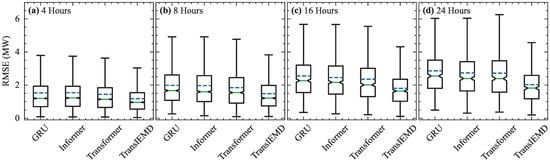
Figure 5.
Boxplots depict the RMSE distributions on four forecast horizons. The green line and blue dashed lines show the median and mean RMSE for each model, respectively. (a) Boxplot of forecast RMSE for the 4 h horizon. (b) Boxplot of forecast RMSE for the 8 h horizon. (c) Boxplot of forecast RMSE for the 16 h horizon. (d) Boxplot of forecast RMSE for the 24 h horizon.
According to Figure 5, TransIEMD demonstrates the lowest median (solid green lines) and mean (blue dashed lines) RMSE across all horizons, indicating its consistent prediction accuracy and robustness across different conditions. The RMSE boxplots of TransIEMD show a narrower interquartile range (heights of the boxes) and shorter whiskers, implying higher consistency. This suggests that TransIEMD provides a more reliable forecast, especially as the horizon lengthens (16 and 24 h), where the forecasting challenge is inherently greater. These error distributions emphasize the advantages of incorporating IEMD into the Transformer model for WPF.
4.5.2. Time-Step-Specific MAE Distribution
Figure 6 shows the distribution of the MAE at each forecast time step in three forecast horizons. The solid lines in the figure represent the median MAE of each model at different time steps in the 8, 16, and 24 h forecasting tasks. At the same time, the colored shaded areas reflect the distribution of the MAE from the 25th to the 75th percentile, validating the consistency and reliability range of errors. For clarity and readability, the MAE distributions of GRU [] and Transformer [] are not shown in Figure 6 as they are not significantly different from those of the Informer model. In Figure 6, the progression of the MAE interquartile ranges for each forecast time step elucidates the increasing difficulty of WPF as the forecasting horizon expands.
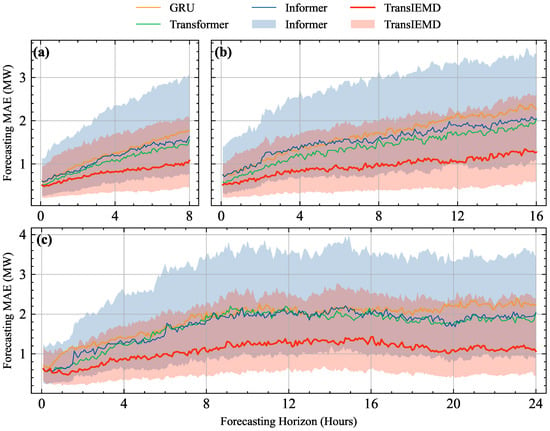
Figure 6.
The percentile ranges of the MAE at each forecasting time step for forecast horizons of 8, 16, and 24 h. Each line represents the median MAE across the forecasting horizon for each model, and the shaded area indicates the 25th to 75th percentile range of the MAE for Informer and TransIEMD for clarity. (a) Forecast results for the 8 h horizon. (b) Forecast results for the 16 h horizon. (c) Forecast results for the 24 h horizon.
The TransIEMD model, delineated by the red median line and associated shaded area, demonstrates a gradual increase in the median MAE with the advancing time step, indicative of the inherent challenge in long-range forecasting. Despite this, TransIEMD maintains a consistently lower and more compact percentile range than Informer []. This reflects the superior accuracy of TransIEMD and its consistent performance over time.
As the forecast time increases, the broadening percentile ranges for Informer [] signal a rise in error spread and highlight the increasing complexity encountered. TransIEMD has relatively steady percentile ranges, even at later time steps. This underscores its ability to sustain its prediction reliability over extended forecast horizons, a decisive factor for operational efficiency in wind power management.
4.6. Ablation Analysis of IEMD and DEM
With the pivotal role of WS and WD in short-term WPF, this study focuses exclusively on these meteorological variables, employing IEMD decomposition to elucidate their complex dynamics. The ablation study, detailed in Table 3, assesses the incremental impact of these decomposed features, individually and in combination with DEM, on the performance of the TransIEMD model. Without DEM, TransIEMD falls back to the basic Transformer [], implementing a query with conventional self-attention. The IEMD processing of WS provides a robust foundation, as indicated by the consistent reduction in the MAE and RMSE across all forecast horizons. For the IEMD-decomposed WS, we have IMFs and additional meteorological variables. When incorporating both the decomposed WS and WD with IMFs, the count of the other meteorological variables reduces to , as illustrated in Figure 7.

Table 3.
Ablation study results for IEMD-decomposed wind speed and direction. In this table, bold values highlight the top performance and italics indicate the second-best across each forecast horizon and metric. Checkmarks, √, indicate whether the IEMD-decomposed WS and/or WD is used in the model and whether the DEM is adopted.
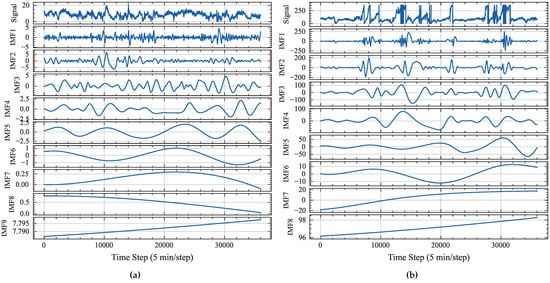
Figure 7.
IMFs of wind speed and direction obtained through IEMD. (a) IMFs derived from IEMD of wind speed data. (b) IMFs derived from IEMD of wind direction data.
Incorporating DEM with the IEMD-processed WS further refines the forecasting capabilities. Realizing optimal improvements, this configuration consistently outperforms others across all metrics and forecast horizons. This result suggests that the querying mechanism implemented with cross-attention can better capture the evolving meteorological complexity compared to standard self-attention. When both the WS and WD are decomposed, including DEM also significantly elevates the performance of TransIEMD. The ability of DEM to leverage the temporal patterns in the data is further evidenced by the enhanced forecasting precision and increased values. The improvements facilitated by DEM can be attributed to the efficacy in querying the decomposed IMFs with the original input features brought by DEM, effectively capturing the dynamic complexity of meteorological data.
The integration of the decomposed WD with the WS offers mixed results, whether using DEM or not. While the forecast accuracy slightly diminishes for shorter horizons, it is beneficial for longer forecast horizons, implying the increased relevance of the WD over extended durations. The potential decline in performance upon integrating the decomposed WD can be attributed to discontinuities in the WD signal, as shown in Figure 7b, which induces high-frequency fluctuations that complicate the extraction of coherent patterns during the IEMD decomposition process.
This ablation study substantiates the potential of the proposed approach in advancing WPF, validating the integration of feature decomposition and embedding techniques as critical to enhancing the model accuracy and reliability for short-to-medium-term forecasting.
IEMD of Wind Features
Figure 7 demonstrates the decomposition of wind speed and direction signals into a series of IMFs via IEMD, addressing their inherent complexity and stochastic nature. IEMD strategically segregates these signals into components reflecting distinct frequency bands and behavioral trends. The initial IMFs capture the immediate, high-frequency oscillations, predominantly representing noise and short-lived perturbations in wind behavior. Successive IMFs reveal progressively lower-frequency oscillations, delineating more substantial and coherent trends vital for accurate prediction in WPF.
IEMD converts the WS and WD from scalar measurements to multivariate vectors with extended temporal contexts. Upon entry into the TransIEMD encoder, these vectors enhance the contextual encoding, significantly improving the forecast efficacy. Consequently, DEM is leveraged to clarify the inter-variable correlations and the complex temporal contexts conveyed by the IEMD-derived vectors. Focusing on the deterministic traits revealed by the IMFs, TransIEMD improves the forecast precision.
One reason for the decreased performance when utilizing the IMFs of both the WS and WD is the discontinuities (such as at the time step of 10,000) in the WD signal. As shown in Figure 7b, abrupt changes introduce extra high-frequency components, making IEMD difficult to process. Despite the comprehensive depiction of wind dynamics through IEMD, these discontinuities introduce complexities that hinder the learning process, particularly impacting its capacity to handle directional shifts effectively.
5. Discussion
5.1. Comparison with Existing WPF Models
A comparative analysis with other established WPF models is beneficial in contextualizing the performance of TransIEMD within the landscape of WPF. However, direct comparisons are complicated due to disparities in the datasets and forecast horizons. For a balanced comparison across different models, we use the normalized MAE (nMAE) and normalized RMSE (nRMSE), which are adjusted relative to the maximum installed capacity . According to Table 4, TransIEMD shows competitive performance in terms of the nMAE and nRMSE for the 4 and 8 h forecast horizons, where the existing models are evaluated for only up to 1 h. Moreover, TransIEMD outperforms the stacked RNN PSAF model [] in terms of .

Table 4.
Performance comparison between TransIEMD and existing WPF models. Both metrics, nMAE and nRMSE, are calculated based on data from the referenced studies.
TransIEMD substantially enhances WPF by extending the forecast horizon up to 24 h, considerably longer than the existing models. Additionally, the model employs a non-autoregressive approach that outputs all forecast steps simultaneously, effectively reducing error propagation. TransIEMD integrates IEMD with cross-attention mechanisms. This allows the model to effectively capture the inherent volatility and non-stationarity of wind energy data, surpassing existing approaches. These features mark substantial theoretical and practical advancements in the field of WPF.
5.2. Extensions
The proposed TranIEMD model, designed for horizontal-axis wind turbines (HAWT), shows potential for adaptation to vertical-axis wind turbines (VAWT) [] due to its data-driven nature. The successful retraining of TransIEMD for VAWTs would require abundant data, including temporally aligned NWP and power outputs specific to VAWTs. Adapting TransIEMD to VAWTs will bring some challenges, such as addressing their capability to capture wind from all directions and the complexities involved in simulating such wind fields []. Consequently, conducting comprehensive studies to fine-tune the model is crucial in ensuring reliable WPF on VAWTs.
TransIEMD enhances the accuracy of WPF, thereby reducing the uncertainties associated with wind’s variability and potentially aiding in the assessment of the wind resource potential. This model offers an improvement over the conventional wind power curves used for energy estimation, as detailed in [], by incorporating more comprehensive meteorological observations for more precise results. However, despite these advancements, the current design and technical constraints of TransIEMD do not facilitate the direct integration of environmental impact assessments. Specifically, it does not evaluate the suitability of locations for wind farm development in terms of environmental impact.
5.3. Advantages and Limitations of TransIEMD
The TransIEMD model presents several advantages that enhance its utility in WPF. First, it integrates IEMD with the Transformer architecture, significantly improving the accuracy for short-to-medium-term predictions by skillfully capturing dynamic wind patterns. Second, TransIEMD scales effectively with large data volumes, making it suitable for industrial applications. Additionally, its versatility allows it to be adapted for various forecasting tasks beyond wind power.
However, deploying TransIEMD has its challenges. The computational demands are substantial, often requiring high-performance computing resources like GPUs, which may not be feasible for all applications. Moreover, the setup and tuning of TransIEMD demand technical expertise, potentially hindering its adoption by practitioners without extensive data science knowledge. Lastly, the performance of TransIEMD heavily relies on the quality and granularity of the training and input data, limiting its effectiveness in scenarios where high-quality data are scarce.
5.4. Future Works
To further improve the prediction accuracy of WPF, our future work will explore two main strategies. According to machine learning theory, only structural errors can be minimized and not those arising from noise. Thus, implementing an error correction approach could effectively improve the accuracy. We aim to identify distinct error patterns and develop specialized error correction models for each identified pattern, potentially employing ensemble models to enhance these efforts. Secondly, we intend to investigate state space models to more accurately capture the dynamic behaviors of wind. This approach differs from the methods used in previous studies, such as the one outlined in [], and promises a more nuanced understanding of the wind dynamics.
6. Conclusions
This study introduces and validates TransIEMD, a novel model for short-to-medium-term WPF. TransIEMD integrates IEMD with a cross-attention mechanism to address the challenges associated with grid integration and dispatching wind energy. An evaluation on the publicly accessible NREL dataset reveals that TransIEMD surpasses baseline models in terms of forecasting accuracy across forecast horizons of 4, 8, 16, and 24 h. These results affirm the effectiveness of TransIEMD in solving the key challenges of short-to-medium-term WPF, directly responding to the central research question of this study.
This research has yielded several important insights.
- The usage of IEMD for the decomposition of the WS notably improves the signal predictability, supported by the ablation analysis detailed in Section 4.6. The IEMD-based tokenizer is pivotal in boosting the accuracy and reliability of the model.
- DEM allows the model to capture the intrinsic dynamic patterns within the data, contributing to enhanced performance, as evidenced in Table 3. The distinct views provided by the tokenizer and DEM enable sophisticated interactions in cross-attention, improving the WPF accuracy.
- TransIEMD demonstrates superior and consistent forecasting performance across various tasks compared to other models. This advantage is demonstrated in the error distribution analysis in Section 4.5, where TransIEMD exhibits both lower median errors and narrower error distributions than its competitors.
In conclusion, TransIEMD presents a significant advancement in the accuracy of short-to-medium-term WPF, offering a refined methodological approach with substantial implications for future wind energy management strategies.
Author Contributions
Conceptualization, formal analysis, and writing—original draft preparation, J.H.; formal analysis, investigation, and data curation, L.D.; methodology, software, investigation, data curation, and visualization, Y.Z.; validation and data curation, S.J.; conceptualization, writing—review and editing, project administration, supervision, and funding acquisition, F.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (Key technology of self-adaptive grid connection and active synchronization of distributed photovoltaic power generation with extremely high penetration rate, 2022YFB2402905).
Data Availability Statement
The dataset used in this paper is publicly available at https://www.nrel.gov/grid/wind-toolkit.html, accessed on 26 March 2022.
Conflicts of Interest
Authors Jiafei Huan, Li Deng and Shangguang Jiang were employed by the North China Branch of State Grid Corporation of China. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ARIMA | Autoregressive Integrated Moving Average |
| EMD | Empirical Mode Decomposition |
| GRU | Gated Recurrent Unit |
| GT | Ground Truth |
| HAWT | Horizontal-Axis Wind Turbine |
| hPa | Hectopascals |
| IEMD | Improved Empirical Mode Decomposition |
| KS | Kolmogorov–Smirnov |
| MAE | Mean Absolute Error |
| MB | Megabytes |
| MLP | Multi-Layer Perceptron |
| MW | Megawatts |
| PSAF | Parametric Sine Activation Function |
| PV | Photovoltaic |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
| rRMSE | Relative RMSE |
| VAWT | Vertical-Axis Wind Turbine |
| VMD | Variational Mode Decomposition |
| WPF | Wind Power Forecasting |
| WD | Wind Direction |
| WS | Wind Speed |
References
- Singh, S. Energy Crisis and Climate Change: Global Concerns and Their Solutions. In Energy: Crises, Challenges and Solutions; Singh, P., Singh, S., Kumar, G., Baweja, P., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; Chapter 1; pp. 1–17. [Google Scholar] [CrossRef]
- Agrawal, S.; Soni, R. Renewable Energy: Sources, Importance and Prospects for Sustainable Future. In Energy: Crises, Challenges and Solutions; Singh, P., Singh, S., Kumar, G., Baweja, P., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; Chapter 7; pp. 131–150. [Google Scholar] [CrossRef]
- Kariniotakis, G. Renewable Energy Forecasting: From Models to Applications; Series in Energy; Woodhead Publishing: Duxford, UK, 2017. [Google Scholar]
- Lee, J.; Zhao, F. Global Wind Report 2024; Global Wind Energy Council: Brussels, Belgium, 2024. [Google Scholar]
- Wolniak, R.; Skotnicka-Zasadzień, B. Development of Wind Energy in EU Countries as an Alternative Resource to Fossil Fuels in the Years 2016–2022. Resources 2023, 12, 96. [Google Scholar] [CrossRef]
- Cacciuttolo, C.; Cano, D.; Guardia, X.; Villicaña, E. Renewable Energy from Wind Farm Power Plants in Peru: Recent Advances, Challenges, and Future Perspectives. Sustainability 2024, 16, 1589. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, M.; Hodge, B.M.; Florita, A.; Freedman, J. Ramp Forecasting Performance from Improved Short-Term Wind Power Forecasting over Multiple Spatial and Temporal Scales. Energy 2017, 122, 528–541. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Chen, J. Wind Power Forecasting Using Multi-Objective Evolutionary Algorithms for Wavelet Neural Network-Optimized Prediction Intervals. Appl. Sci. 2018, 8, 185. [Google Scholar] [CrossRef]
- Li, L.L.; Zhao, X.; Tseng, M.L.; Tan, R.R. Short-Term Wind Power Forecasting Based on Support Vector Machine with Improved Dragonfly Algorithm. J. Clean. Prod. 2020, 242, 118447. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, R.; Liu, F.; Zhang, L.; Liu, Q. A Review of Wind Speed and Wind Power Forecasting with Deep Neural Networks. Appl. Energy 2021, 304, 117766. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder–Decoder Approaches. In Proceedings of the SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, Doha, Qatar, 25 October 2014; Wu, D., Carpuat, M., Carreras, X., Vecchi, E.M., Eds.; Association for Computational Linguistics: Doha, Qatar, 2014; pp. 103–111. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, M. Short-Term Wind Power Forecasting Based on VMD Decomposition, ConvLSTM Networks and Error Analysis. IEEE Access 2020, 8, 134422–134434. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, J.; Qian, H. Short-Term Wind Power Forecasting by Stacked Recurrent Neural Networks with Parametric Sine Activation Function. Electr. Power Syst. Res. 2021, 192, 107011. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, C.; Luo, Y.; Wu, B.; Dong, N.; Xiao, T.; Zhu, H. Wind Power Forecast Based on Variational Mode Decomposition and Long Short Term Memory Attention Network. Energy Rep. 2022, 8, 922–931. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, S.; Lai, C.S.; Zhao, Z.; Lai, L.L. Short-Term Wind Power Prediction Based on Data Decomposition and Combined Deep Neural Network. Energies 2022, 15, 6734. [Google Scholar] [CrossRef]
- Wu, F.; Yang, M.; Shi, C. Short-Term Prediction of Wind Power Considering the Fusion of Multiple Spatial and Temporal Correlation Features. Front. Energy Res. 2022, 10, 878160. [Google Scholar] [CrossRef]
- Liu, Y.; He, J.; Wang, Y.; Liu, Z.; He, L.; Wang, Y. Short-Term Wind Power Prediction Based on CEEMDAN-SE and Bidirectional LSTM Neural Network with Markov Chain. Energies 2023, 16, 5476. [Google Scholar] [CrossRef]
- Hossain, M.A.; Gray, E.; Lu, J.; Islam, M.R.; Alam, M.S.; Chakrabortty, R.; Pota, H.R. Optimized Forecasting Model to Improve the Accuracy of Very Short-Term Wind Power Prediction. IEEE Trans. Ind. Inform. 2023, 19, 10145–10159. [Google Scholar] [CrossRef]
- Liu, M.D.; Ding, L.; Bai, Y.L. Application of Hybrid Model Based on Empirical Mode Decomposition, Novel Recurrent Neural Networks and the ARIMA to Wind Speed Prediction. Energy Convers. Manag. 2021, 233, 113917. [Google Scholar] [CrossRef]
- Lv, S.; Wang, L.; Wang, S. A Hybrid Neural Network Model for Short-Term Wind Speed Forecasting. Energies 2023, 16, 1841. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, J.; Min, J. SSA-LSTM: Short-Term Photovoltaic Power Prediction Based on Feature Matching. Energies 2022, 15, 7806. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30. [Google Scholar]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in Time Series: A Survey. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, Macao, China, 19–25 August 2023; Volume 6, pp. 6778–6786. [Google Scholar] [CrossRef]
- Ahmed, S.; Nielsen, I.E.; Tripathi, A.; Siddiqui, S.; Ramachandran, R.P.; Rasool, G. Transformers in Time-Series Analysis: A Tutorial. Circuits Syst. Signal Process. 2023, 42, 7433–7466. [Google Scholar] [CrossRef]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for Interpretable Multi-Horizon Time Series Forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Jiang, M.; Jiang, X.; Zhou, Q. Temporal Fusion Transformer Using Variational Mode Decomposition for Wind Power Forecasting. arXiv 2023, arXiv:2302.01222. [Google Scholar] [CrossRef]
- Wu, B.; Wang, L.; Zeng, Y.R. Interpretable Wind Speed Prediction with Multivariate Time Series and Temporal Fusion Transformers. Energy 2022, 252, 123990. [Google Scholar] [CrossRef]
- Galindo Padilha, G.A.; Ko, J.; Jung, J.J.; De Mattos Neto, P.S.G. Transformer-Based Hybrid Forecasting Model for Multivariate Renewable Energy. Appl. Sci. 2022, 12, 10985. [Google Scholar] [CrossRef]
- Liu, M.; Sun, X.; Wang, Q.; Deng, S. Short-Term Load Forecasting Using EMD with Feature Selection and TCN-Based Deep Learning Model. Energies 2022, 15, 7170. [Google Scholar] [CrossRef]
- Chen, Y.; Dong, Z.; Wang, Y.; Su, J.; Han, Z.; Zhou, D.; Zhang, K.; Zhao, Y.; Bao, Y. Short-Term Wind Speed Predicting Framework Based on EEMD-GA-LSTM Method under Large Scaled Wind History. Energy Convers. Manag. 2021, 227, 113559. [Google Scholar] [CrossRef]
- Abedinia, O.; Lotfi, M.; Bagheri, M.; Sobhani, B.; Shafie-khah, M.; Catalao, J.P.S. Improved EMD-Based Complex Prediction Model for Wind Power Forecasting. IEEE Trans. Sustain. Energy 2020, 11, 2790–2802. [Google Scholar] [CrossRef]
- Draxl, C.; Clifton, A.; Hodge, B.M.; McCaa, J. The Wind Integration National Dataset (WIND) Toolkit. Appl. Energy 2015, 151, 355–366. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A Review on Hilbert-Huang Transform: Method and Its Applications to Geophysical Studies. Rev. Geophys. 2008, 46, RG2006. [Google Scholar] [CrossRef]
- Naaman, M. On the Tight Constant in the Multivariate Dvoretzky–Kiefer–Wolfowitz Inequality. Stat. Probab. Lett. 2021, 173, 109088. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks. In Proceedings of the SIGIR’18: The 41st International ACM SIGIR Conference on Research and Development in Information Retrieval, Ann Arbor MI USA, 8–12 July 2018; ACM: New York, NY, USA, 2018; pp. 95–104. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Kumar, R.; Raahemifar, K.; Fung, A.S. A Critical Review of Vertical Axis Wind Turbines for Urban Applications. Renew. Sustain. Energy Rev. 2018, 89, 281–291. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, W. Wind Energy Potential Assessment Based on Wind Speed, Its Direction and Power Data. Sci. Rep. 2021, 11, 16879. [Google Scholar] [CrossRef]
- Duan, J.; Zuo, H.; Bai, Y.; Duan, J.; Chang, M.; Chen, B. Short-Term Wind Speed Forecasting Using Recurrent Neural Networks with Error Correction. Energy 2021, 217, 119397. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).