Evaluation of the Influence of Water Content in Oil on the Metrological Performance of Oil Flow Measurement Systems

Abstract

According to current Brazilian regulations, if the volumes of oil produced used as a reference for the payment of government shares and third parties contain a water content greater than 2% v/v, these volumes must be arbitrarily increased between 1.44% and 10.89% due exclusively to water content, which has caused operational problems for oil companies such as differences between volumes produced and volumes sold, and additional payments from government shares and third parties. This study aimed to evaluate the metrological performance of oil measurement systems with ultrasonic, Coriolis and positive displacement flow meters when subjected to varied water content, fluid temperature and flow rate conditions using the Design of Experiments and the Response Surface Methodology. The analysis of variance showed that the models presented good fits for the ultrasonic meter (coefficient of determination R² of 97.96%, p-value of 0.001, and a standard deviation of 5.89 × 10⁻⁵); Coriolis meter (R² of 90.91%, p-value of 0.037, and a standard deviation of 5.88 × 10⁻⁵); and positive displacement meter (R² of 99.07%, p-value of 0.000, and a standard deviation of 4.85 × 10⁻⁵). The results of the experiments carried out indicate that the contribution of each parameter analyzed to the metrological performance of the measurement system varies depending on the measurement technology used by the flow meter. However, the fluid temperature proved to be a relevant parameter common to all flow measurement technologies evaluated. All measuring technologies evaluated were influenced by water content in the range of 0% to 10% v/v, with the measurement error being less than 0.2% when compared to a standard positive displacement type meter in almost all experimental conditions. The Coriolis-type flow meter was the one that presented the smallest error among the measuring technologies evaluated.

1. Introduction

Globally, the oil and gas industry presents several challenges, especially in multiphase flow, where measurement uncertainties are due to different flow rates and BSW [1]; on the other hand, different operating conditions (flow and temperature) can be correlated with a maximum BSW content to ensure reliable measurements [2]. Furthermore, in offshore oil production, fluctuations in flow rates and BSW content can destabilize the process, resulting in operational losses and environmental fines [3].

Government participation generated by the exploration of oil and natural gas in Brazil is an important source of income for the development of Brazilian society, with these resources being allocated especially to education and health. In 2021, the amount collected by the Union in the form of government participation was more than USD 15.5 billion [4], which makes the quality of the measurement systems used to control the production of oil and natural gas and the existence of a robust measurement management system to guarantee the reliability of the results obtained.

In Brazil, the measurement systems used to control the production of oil and natural gas in an oil field are governed by the Technical Regulation for the Measurement of Oil and Natural Gas (RTM), approved by Joint Resolution ANP (Brazilian National Agency of Petroleum, Natural Gas and Biofuels) and INMETRO (Brazilian Institute for Metrology, Quality and Technology) 1/2013, which establishes the minimum technical, constructive and metrological conditions and requirements that these measuring systems must comply with, with a view to guaranteeing the credibility of the measurement results [5].

Online petroleum fiscal measurement systems must consist of at least the following equipment: a flow meter; an instrument for measuring temperature; an instrument for measuring static pressure; and a flow computer for correction of volumes based on flow, temperature and static pressure information.

As determined by this Brazilian regulation, fiscal petroleum measurement systems must be located immediately downstream of petroleum treatment systems to ensure that the measured petroleum is stabilized and does not contain a water content (BSW) greater than 1% v/v. Additionally, for events where the average BSW is greater than 2% v/v, the volumes of oil produced must be increased by a correction factor pre-defined by the ANP that can vary between 1.44% and 10.89% depending on exclusively from the average daily BSW [6].

The increase in the volumes of oil produced because of oil non-compliance events due to arbitrary factors can cause operational problems for oil companies. A one-day oil decommissioning event can result in an additional payment of USD 144,000 in government participation in Brazil.

The increase in produced volumes by arbitrary correction factors based exclusively on average BSW may not be sufficient to characterize the metrological performance of online fiscal petroleum measurement systems operating in high BSW conditions. Hallanger et al. [7] and Skea and Hall [8] indicate that constructive aspects of the measurement system, such as flow meter technology and characteristics of the measured oil, such as temperature, kinematic viscosity and density, can have an influence on the metrological performance of measurement systems oil in line operating under high BSW conditions.

Water content in crude oil is the subject of several studies in the most diverse areas, such as high-performance biodegradable [9], the development of new microwave sensors [10,11] and quality control [12].

Economically, it is important for the oil industry that the amount paid as government shares and to third parties reflects the volumes of oil produced and that there is consistency between these volumes and the volumes of oil sold. Thus, a gap was identified in the literature regarding the performance of a sensitivity study for the simultaneous assessment of factors influencing the metrological performance of online oil measurement systems.

This study aimed to evaluate, by means of the Design of Experiments and Response Surface Methodology, the influence of BSW, fluid temperature and flow rate on the metrological performance of oil measurement systems with ultrasonic, Coriolis and positive displacement flow meters.

2. Rationale

The Constitution of the Federative Republic of Brazil of 1988 determines that mineral resources, which include oil and natural gas deposits, constitute assets of the Union. In this sense, in the case of the exploitation of these non-renewable resources by authorized companies, financial compensation to the Union is provided for, which varies according to the exploration and production contract signed and which, generically, is called Government Participation (PGov).

Based on Brazilian laws, the following government and third-party participations are considered: signature bonus, royalties, special participation, payment for occupation or retention of area, payment to landowners, and surplus oil.

2.1. Technical Regulations for the Oil and Natural Gas Area

The Brazilian RTM established the minimum conditions and requirements for oil and natural gas measurement systems with a view to ensuring accurate and complete results in line with the criticality of the process of determining oil and natural gas production.

The Technical Regulation for Notification of Failures of Oil and Natural Gas Measurement Systems and Oil Framing Failures (RTNF), approved by ANP Resolution No. 18 of 27 March 2014, defined deadlines and procedures to be adopted with relation to the occurrence of failure events associated with the measurement systems provided for in the RTM [13].

To guarantee the Brazilian interests, this regulation established standardized methodologies for estimating the volumes affected in the event of a measurement failure event. For oil classification failure events, i.e., where volumes produced with average daily BSW greater than 1% v/v are measured, aiming to mitigate a potential increase in measurement uncertainty in a fiscal oil measurement system, it is mandatory to apply correction factors to the volume produced. Almeida et al. [14] concluded that BSW uncertainty and flow meter calibration factor uncertainty are the main sources of uncertainty for in-line petroleum measurement systems.

Table 1. Factors correction for events in failure in the framework of petroleum.

Average BSW Daily	Correction Factor
1% v/v < BSW ≤ 2% v/v	-
2% < BSW ≤ 30% v/v	1.14%
30% v/v < BSW ≤ 50% v/v	7.80%
BSW ≥ 50% v/v	10.89%

Source: adapted from ANP [6].

presents the correction factors for the volume of oil produced according to the average daily BSW predicted in Circular Letter No. 2/2021/NFP/ANP-e [6].

The Metrological Technical Regulation for Dynamic Measurement Systems equipped with meters for quantities of petroleum and its liquid derivatives, approved by INMETRO Ordinance No. 291 of 7 July 2021, established the metrological and technical requirements, such as accuracy class and maximum error permissible, which flow measurement systems must comply with for their use in determining the volumes of oil provided for in the RTM [15].

Fines are the main penalty applied to companies that produce oil and natural gas as part of the inspection process of measurement systems conducted by the ANP’s Production Inspection Center (NFP). Fines applicable to infractions associated with oil and natural gas measurement systems range from 5 thousand to 2 million reais. The value of the fine is defined by the dosimetry provided for in Decision No. 2/2021/NFP [6] and depends, among other factors, on the severity of the infraction, the offender’s background, and the volume of oil and natural gas moved in the installation as detailed in Equation (1).

$$VP=V_{min}+\left|\frac{600\times FGI\times FM+5\times FCEI+5\times FAI+FVA}{611}\right|\times \left(V_{max}-V_{min}\right)\times \left(1-A_{conf}-A_{rec}\right)$$

(1)

where VP is the value of the penalty in reais; V_min is the minimum value of the penalty in reais according to Law no. 9.847/99 in which the infraction was framed; V_max is the maximum value of the penalty in reais according to Law no. 9.847/99 in which the infraction was framed; FGI is the severity factor of the offense committed; FM is the production movement factor for the installation in which the infraction was committed; FCEI is the factor of the economic condition of the company responsible for operating the field where the infraction occurred; FAI is the background factor of the company responsible for operating the field where the infraction occurred; FVA is the economic advantage factor obtained by the company responsible for operating the field where the infraction occurred; A_conf is the mitigating factor due to spontaneous communication or confession of the infraction to the ANP; A_rec is the mitigating factor in the case of recalculation of the volumes affected by the occurrence of the infraction.

API MPMS [16] defines requirements for the application of liquid flow measurement systems. According to this standard, the volumetric flow of oil in the standard measurement condition, that is, at a temperature of 20 °C and a static pressure of 101.325 kPa, is given by Equation (2).

$$Q_b=Q\times MF\times CTL\times CPL\times \left(1-BSW\right)$$

(2)

where Q_b is volumetric oil flow in standard measurement conditions in m³/h, Q is the gross volumetric flow of oil in operating conditions in m³/h, MF is the meter factor, CTL is the conversion factor from the volume measured at the operating temperature to the volume at the standard temperature condition, CPL is the conversion factor from the volume measured at operating pressure to the volume at standard pressure condition and BSW is the water content in the oil in the operating condition in % v/v.

2.2. General Design of Experiments and Response Surface Methodology

An experiment or trial can be defined as a set of actions to analyze a process or system with the aim of obtaining new information, evaluating hypotheses, or reaffirming previously obtained results. The basic concept of an experiment is, based on the selection of control factors (process input), observing the response variable (process output) to analyze the relationship between them.

Depending on the process analyzed, an experiment can be complex and costly due to the high number of possible combinations between control factors and response variables. In this context, the use of a statistical tool such as the Design of Experiments (DoE) becomes critical for obtaining the most information at the lowest cost. Montgomery [17] cites the advantages of using the DoE tool, such as reducing cost and product development time and improving process performance. The DoE tool has been widely used in various branches of science and industry: Guerra et al. [18] used the Central Composite Design to optimize acceptance criteria for instrument calibration in oil and natural gas measurement systems; Sengel-Turk et al. [19] applied the DoE tool to evaluate new techniques for cancer treatment; Sibiya et al. [20] used DoE concepts to optimize water treatment; a central composite design was used for optimizing turbidity removal in a reactor system [21]; a Box–Behnken design was used to analyze the effects of pollutant interactions in pollutants oilfield [22]; a Box–Behnken design was used to identify optimum conditions in drilling and completion operations [23]; and a 3² factorial design was used for assessing the relevance of changing in test method for kinematic viscosity of opaque oils [24].

Montgomery [17] proposed a basic protocol for using the DoE approach as follows: (i) definition of the objectives of the experiment; (ii) parameter mapping; (iii) selection of control factors and response variables; (iv) definition of the experimental matrix; (v) carrying out the experiment; (vi) data analysis; and (vii) interpretation of results.

2.3. Box–Behnken Design

The Box–Behnken Design (BBD), which is connected to Response Surface Methodology (RSM), is a very powerful type of experimental design when considering a model with second-order adjustment. To use the BBD, there must be at least three control factors, and each factor must always be observed at three levels (minimum, medium and maximum). The experiment must be conducted so that each of the levels is positioned equidistant from the center of the model. In a BBD with three control factors, this is achieved by always fixing one of the levels at the midpoint and obtaining the response variables for each combination of the other factors at the minimum and maximum levels. Additionally, in BBD, observations are made at the central point, with all control factors at the average level, to determine the experimental error.

Manohar et al. [25] described the BBD as spherical since all points of the model are inscribed on a sphere of radius $\sqrt{2}$ and no points are located at the vertices of the area delimited by the minimum and maximum levels of each control factor.

Table 2. The headquarters experimental generic is for one BBD with three control factors and three center points (C).

Treatment	Factor x1	Factor x2	Factor x3	Response
1	−1	−1	0	y1
2	1	−1	0	y2
3	−1	1	0	y3
4	1	1	0	y4
5	−1	0	−1	y5
6	1	0	−1	y6
7	−1	0	1	y7
8	1	0	1	y8
9	0	−1	−1	y9
10	0	1	−1	y10
11	0	−1	1	y11
12	0	0	1	y12
C	0	0	0	y13
C	0	0	0	y14
C	0	0	0	y15

presents the generic experimental matrix for a BBD with three control factors and three central points.

The number of treatments for a BBD is defined by Equation (3) [25]:

$$N=2\times k\times \left(k-1\right)\times C_0$$

(3)

where N is the number of treatments for BBD; k is the number of control factors in the experiment; and C₀ is the number of observations of the response variable at the center point.

One advantage of BBD is that it requires fewer observations than other types of DoE, such as full factorial design. Additionally, in a BBD, extreme conditions—that is, when all control factors are at their minimum or maximum levels—are not necessary. On the other hand, this design is not suitable for experiments where the observation of control factors at their extreme levels may be relevant.

3. Experimental Procedure

To evaluate the metrological performance of oil flow measurement systems, a test bench was built especially for the experiment on the Technological Research Institute (IPT) premises in São Paulo, Brazil. This test bench consisted of a closed circuit with all flow meters to be evaluated arranged in series in a horizontal line.

Table 3. Evaluation of the flow meter rate in petroleum.

Technology	Nominal Diameter (mm)	Manufacturer	Model	Repeatability	Minimum Flow (m3/h)	Maximum Flow (m3/h)	Reference
BiRotor Plus *	150	Brodie	B291X	0.01%	9	272	[27]
Positive Displacement	100	Metroval	OAP250 AG-20/F2	0.05%	7.2	72.0	[28]
Ultrasonic	150	Krohne	UFS 500F/55Tr	0.02%	12.6	630.0	[29]
Coriolis	100	Micro Motion	CMF400K 436N282P222	0.025%	21.0	415.0	[30]

* Master meter.

presents the oil flow measurement technologies evaluated and the details of each meter model used in the experiment. All measurement systems were calibrated by accredited laboratories [26].

The schematic diagram of the closed circuit used as a test bench is shown in Figure 1.

3.1. Test Bench Validation

The Technological Research Institute has a bench accredited by ISO/IEC 17025 [26] for calibrating oil flow meters, which uses a compact tester-type reference standard for calibrations in the range of 0.8 to 800 m³/h with mineral oil with a kinematic viscosity between 7 and 350 cSt under standard measurement conditions (20 °C and 101.325 kPa).

The bench validation was carried out by comparing the results obtained for the ultrasonic and Coriolis type meters under evaluation and the standard positive displacement type meter with the results obtained on the accredited bench.

For comparison between benches, the normalized error E_n according to Equation (4). By this criterion, if $\left|E_n\right|\le 1$, the results can be considered compatible.

$$E_n=\frac{\left(X_{lab}-X_{ref}\right)}{\sqrt{U_{lab}^2+U_{ref}^2}}$$

(4)

where X_lab is the experiment’s result, X_ref is the reference value, U_lab is the expanded uncertainty associated with the experiment’s outcome, and U_ref is the expanded uncertainty associated with the reference value.

Table 4. Validation from the bench in test with an ultrasonic meter.

Bench in Test			Accredited Bench			Comparison
Qtest (m3/h)	Etest (%)	Utest (%)	QIPT (m3/h)	EIPT (%)	UIPT (%)	En
35.2	−0.27	0.13	32.7	−0.23	0.14	−0.24
50.5	−0.25	0.15	56.6	−0.11	0.19	−0.58
88.0	−0.17	0.11	86.6	−0.16	0.11	−0.11
125.4	−0.10	0.25	133.1	−0.23	0.16	0.43
151.8	−0.10	0.21	157.9	0.09	0.17	−0.68

,

Table 5. Validation from the bench in test with a Coriolis meter.

Bench in Test			Bench Accredited			Comparison
Qtest (m3/h)	Etest (%)	Utest (%)	QIPT (m3/h)	EIPT (%)	UIPT (%)	En
35.2	−0.41	0.5	35.0	−0.36	0.10	−0.11
50.5	−0.10	0.3	50.3	−0.03	0.11	−0.24
151.5	−0.03	0.09	150.6	0.08	0.09	−0.85

and

Table 6. Validation from the bench in test with a positive displacement meter (meter standard).

Bench in Test			Accredited Bench			Comparison
Qtest (m3/h)	Etest (%)	Utest (%)	QIPT (m3/h)	EIPT (%)	UIPT (%)	En
37.4	0.04	0.10	32.8	0.14	0.10	−0.67
55.0	0.11	0.10	56.0	0.20	0.10	−0.59
85.9	0.15	0.10	86.9	0.19	0.10	−0.29
130.7	0.15	0.10	133.0	0.19	0.10	−0.27
155.5	0.14	0.10	158.1	0.18	0.10	−0.25

present the comparison results for each meter.

For the Coriolis meter, it was only possible to evaluate three gradients due to operational limitations.

In Table 4, Table 5 and Table 6, Q_test is the flow rate of the meter on the test bench in m³/h; E_test is the average flow error of the meter on the test bench in %; U_test is the expanded uncertainty associated with the result of the flow measurement on the test bench in %; Q_IPT is the flow rate of the meter on the IPT accredited bench in m³/h; E_IPT is the average error of the meter flow on the IPT accredited bench in %; U_IPT is the expanded uncertainty associated with the result of the flow measurement on the IPT accredited bench in %; E_n is the normalized error.

Based on the results presented, given that the absolute normalized error $\left|E_n\right|$ was less than unity for all experimental conditions, the absence of systematic errors, the test bench built for the experiment, was considered validated.

3.2. Experimental Matrix

Using BBD, an experimental matrix was proposed for each flow meter to be evaluated, as presented in Table 2. The control factors chosen to evaluate the metrological performance of the flow meters were the BSW, the fluid temperature and the volumetric flow rate (

Table 7. Experimental conditions for flow meters.

		Displacement Positive Meter	Ultrasonic Meter	Coriolis Meter
BSW (%)	Temperature (°C)	Flow Rate (m3/h)
0	25	20	125	100
5	34	35	150	125
10	43	50	175	150

).

The levels for the BSW were defined considering the most frequent range of values from oil classification failure events in fiscal measurement systems communicated to the ANP. They were the same for all flow meters evaluated.

The fluid temperature levels considered for the experiment were chosen based on the average temperature conditions found in online petroleum fiscal measurement systems, and, like BSW, they were the same for all oil flow meters evaluated.

Finally, the flow rate levels are different for each meter evaluated and were chosen considering the test bench’s flow rate limit (200 m³/h) and the flow limits of each meter, as detailed in Table 3.

Due to the logistical difficulties of carrying out the experiment with oil in the laboratory, mineral oil with a viscosity like that produced in the Brazilian pre-salt fields (20 cSt under standard measurement conditions, 20 °C and 101.325 kPa) was decided upon.

Initially, the closed circuit was filled with pure mineral oil, that is, with BSW equal to 0% v/v. The volume of mineral oil inserted into the closed circuit was calculated based on the fluid’s density, and the fluid’s mass was determined using a scale.

3.3. Fluid Change

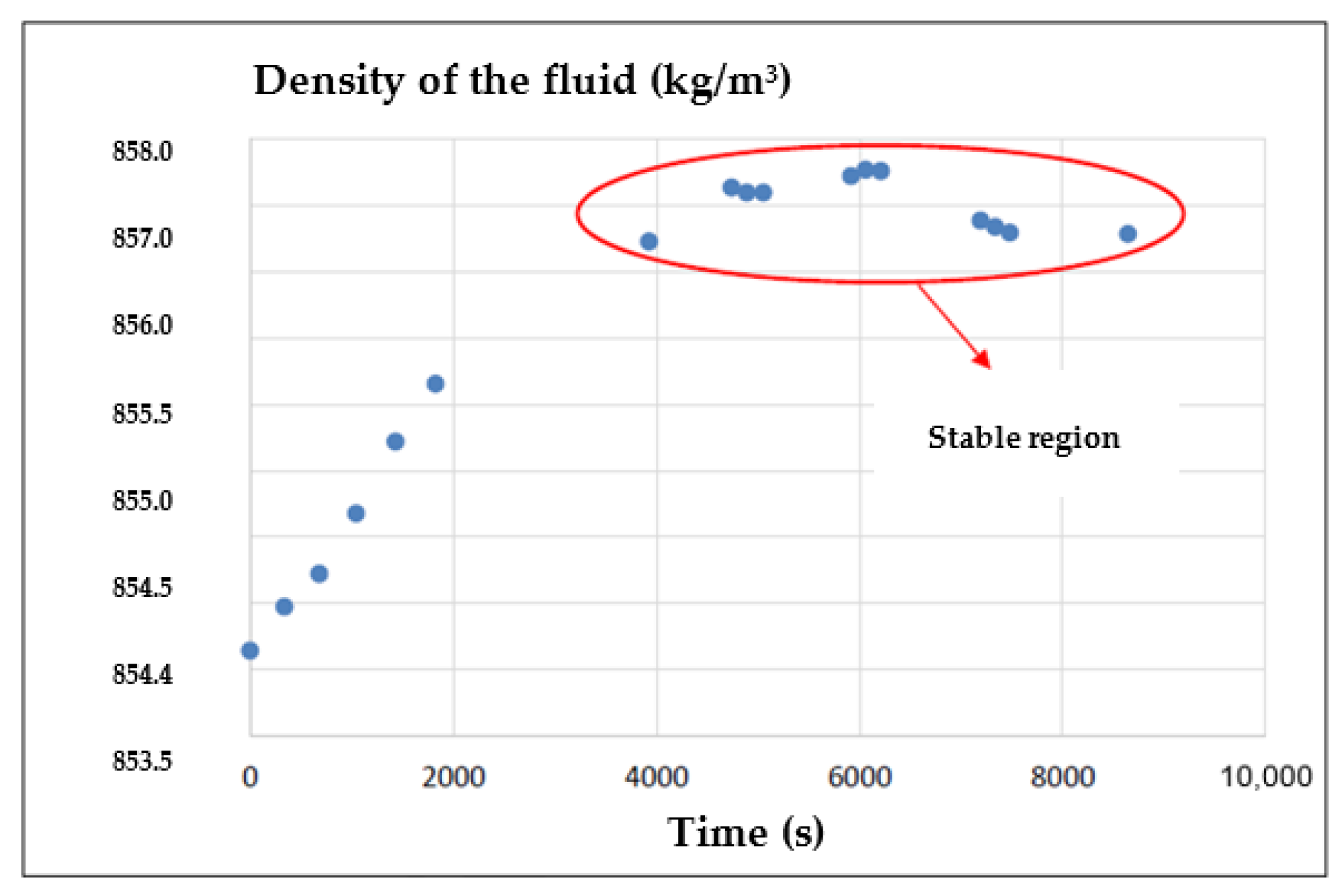
The change in the BSW level was evaluated by inserting water into the closed circuit. Figure 2 shows the monitoring of the results of measuring the density of the fluid using the Coriolis flow meter. After the insertion of water into the circuit, until the fluid is homogenized, the density tends to vary until it reaches a region of stability where it is possible to continue with the other stages of the experiment.

4. Results and Discussion

The objective of the experiment was to evaluate the impact of different measurement technologies on the metrological performance of oil flow measurement systems calibrated under different conditions of BSW, fluid temperature and flow rate (control factors).

For this analysis, the response variable of the experiment was the absolute error between the difference in the volumetric flow rate indicated by meters with different technologies and the volumetric flow rate of the standard meter as defined in Equation (5):

$$Error=\left|\frac{Q_{meter}-Q_{standard}}{Q_{standard}}\right|$$

(5)

where Q_meter is the corrected flow indicated by the flow meter being evaluated in m³/h, and Q_standard is the corrected flow indicated by the standard flow meter in m³/h.

The corrected flow rates Q_meter and Q_standard are expressed in the standard measurement condition provided for in the RTM, that is, at a temperature of 20 °C and a static pressure of 101.325 kPa. The gross flow rates recorded by the flow meters were corrected using the temperature correction factors (CTL) and pressure correction factors (CPL) provided for in the API MPMS Chapter 11.1 standard [16].

Here, DoE is considered a 0.05 significance level. Next, the results for each oil flow meter technology evaluated from the experimental matrix for BBD using Minitab 19 software and Microsoft Excel 365 are presented, and the analysis of variance (ANOVA) method and the surface methodology response (RSM) are applied.

The control factors and their interactions are detailed below: $x_1$ is the linear term of the fluid temperature; $x_2$ is the linear term of the flow rate;$x_3$ is the linear term of BSW; $x_1^2$ is the quadratic term of the fluid temperature; $x_2^2$ is the quadratic term of the flow rate; $x_3^2$ is the quadratic term of BSW; $x_1\times x_2$ is the linear interaction between fluid temperature and flow rate; $x_1\times x_3$ is the linear interaction between fluid temperature and BSW; and $x_2\times x_3$ is the linear interaction between the flow rate and the BSW.

4.1. Ultrasonic Meter

BBD was used with the control factors, and the response variable analyzed for the ultrasonic flow meter is presented in

Table 8. Experimental matrix and results obtained for the ultrasonic flow meter.

Treatment	$\mathbf{Factor}{\mathit{X}}_1$	$\mathbf{Factor}{\mathit{X}}_2$	$\mathbf{Factor}{\mathit{X}}_3$	Temperature (°C)	Flow Rate (m3/h)	BSW (% v/v)	Error
1	−1	−1	0	25	125	5	0.129%
2	1	−1	0	43	125	5	0.009%
3	−1	1	0	25	175	5	0.074%
4	1	1	0	43	175	5	0.116%
5	−1	0	−1	25	150	0	0.192%
6	1	0	−1	43	150	0	0.073%
7	−1	0	1	25	150	10	0.126%
8	1	0	1	43	150	10	0.119%
9	0	−1	−1	34	125	0	0.009%
10	0	1	−1	34	175	0	0.010%
11	0	−1	1	34	125	10	0.035%
12	0	1	1	34	175	10	0.043%
C	0	0	0	34	150	5	0.010%
C	0	0	0	34	150	5	0.014%
C	0	0	0	34	150	5	0.039%

below:

The effects of control factors and interactions between these factors on the response variable using ANOVA are presented in

Table 9. ANOVA for the ultrasonic flow meter.

Source			Degrees of Freedom	Contribution	p-Value
Model	-	-	9	97.96%	0.001
-	Linear	-	3	89.57%	0.000
-	-	${\mathrm{X}}_1$	1	87.91%	0.000
-	-	${\mathrm{X}}_2$	1	0.03%	0.791
-	-	${\mathrm{X}}_3$	1	1.63%	0.102
-	Quadratic	-	3	5.51%	0.069
-	-	${\mathrm{X}}_1^2$	1	4.85%	0.016
-	-	${\mathrm{X}}_2^2$	1	0.47%	0.312
-	-	${\mathrm{X}}_3^2$	1	0.19%	0.521
-	Interactions	-	3	2.88%	0.189
-	-	${\mathrm{X}}_1\ast {\mathrm{X}}_2$	1	0.08%	0.674
-	-	${\mathrm{X}}_1\ast {\mathrm{X}}_3$	1	1.09%	0.163
-	-	${\mathrm{X}}_2\ast {\mathrm{X}}_3$	1	1.71%	0.096
Error	-	-	5	2.04%
-	Lack of adjustment	-	3	0.93%	0.693
-	Error pure		2	1.11%
Total	-	-	14	100.00%

:

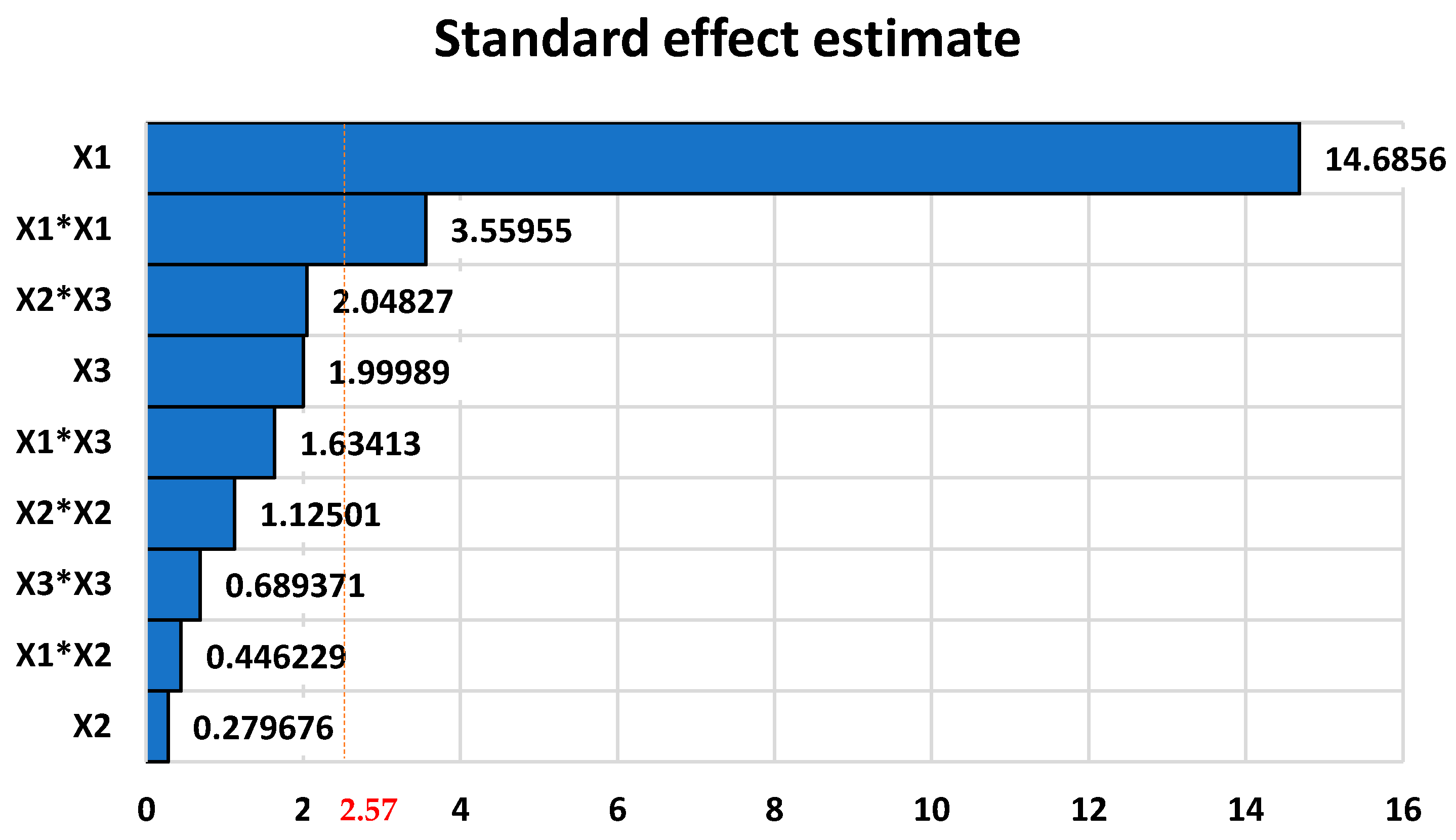
The Pareto chart for the estimated standardized effects is presented in Figure 3:

From Table 8 and Table 9 and Figure 3, the influence of the fluid temperature ($x_1$) in the response variable is statistically significant. This statement is also valid for the quadratic contribution ($x_1^2$) of this factor of control. The mathematical model, Equation (6) that describes the relationship between control factors and the variable in response obtained was as follows:

$$\begin{array}{cc}\hfill Error=& 0.001417-0.000306x_1+0.000006x_2+0.000042x_3\hfill \\ & +0.000109x_1^2-0.000035x_2^2+0.000021x_3^2\hfill \\ & +0.000013x_1{x}_2+0.000048x_1{x}_3+0.0000060x_2{x}_3\hfill \end{array}$$

(6)

This model presented a good fit with a coefficient of determination R² of 97.96% and a standard deviation of 5.89 × 10⁻⁵.

Using the RSM, it is possible to observe the response variable. Tables S1–S3 present the model’s results mathematically detailed in Equation (6) considering the variation from the fluid temperature and the flow rate for the BSW equals 0% v/v, 5% v/v and 10% v/v.

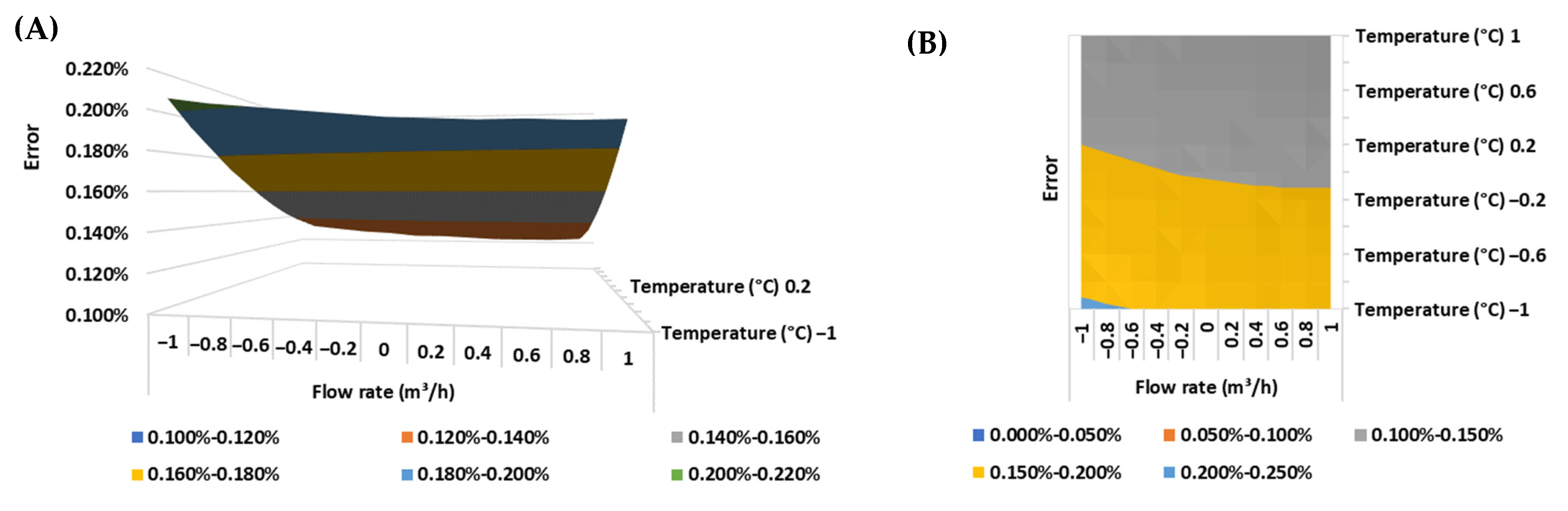
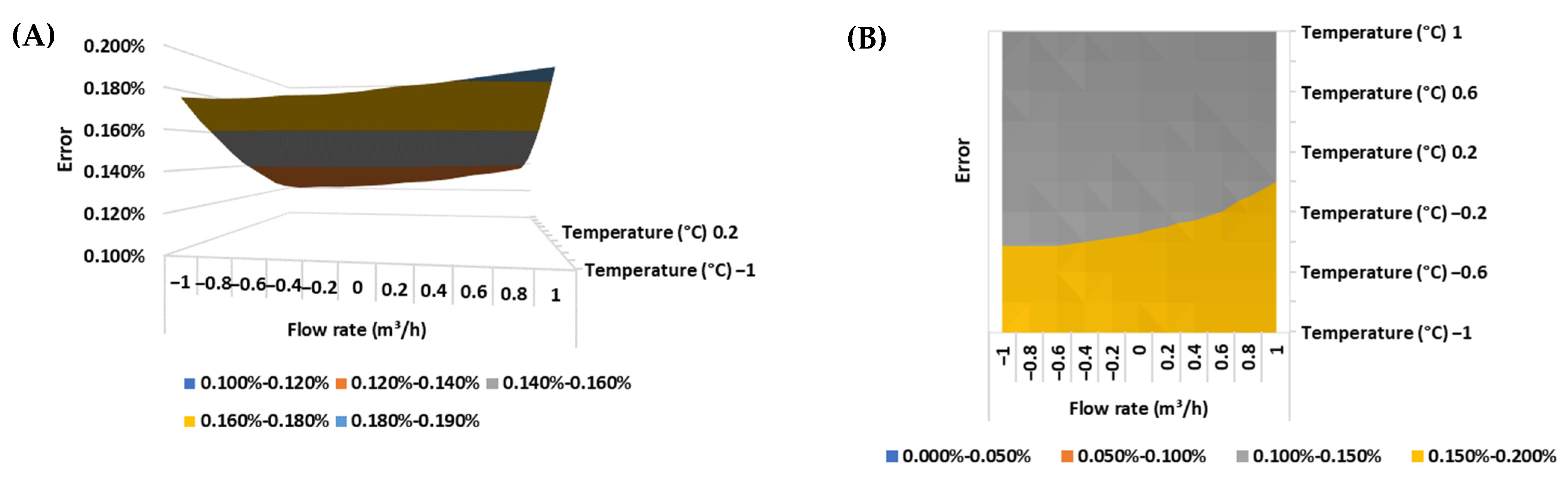
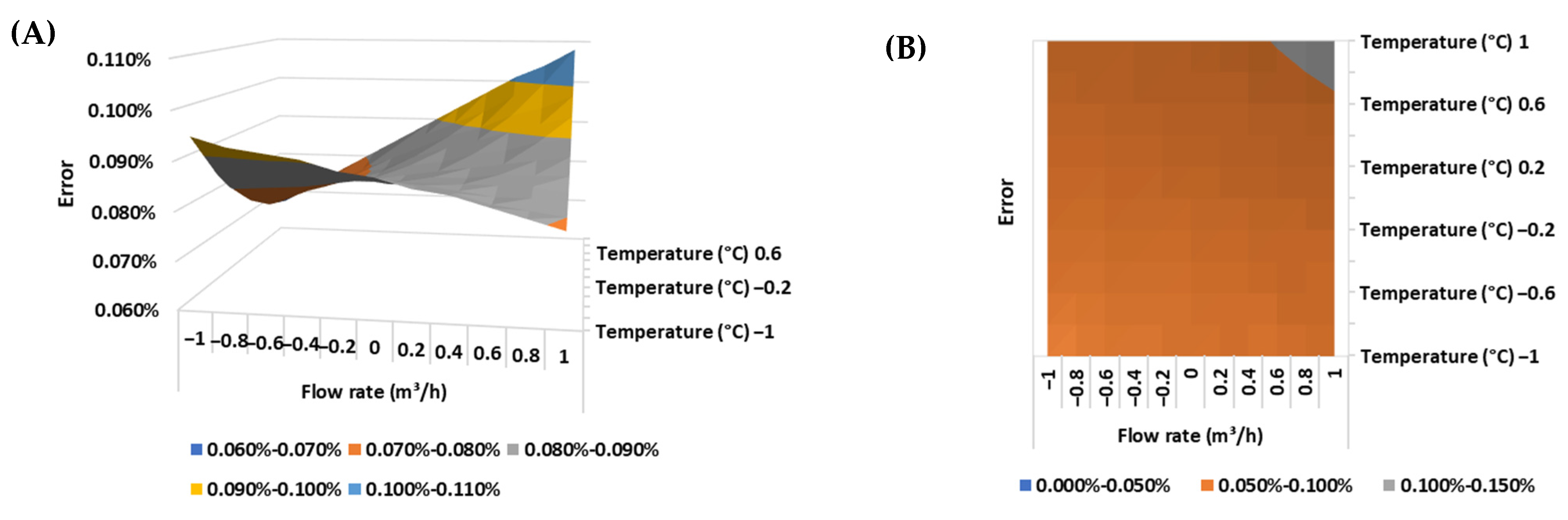
Below are presented the response surfaces and contour plots of the ultrasonic flow meter error for each BSW condition evaluated (Figure 4, Figure 5 and Figure 6).

The metrological performance of ultrasonic flow meters based on the transit time method, such as the flow meter evaluated in the experiment, is associated with the occurrence of a fully developed flow in a turbulent regime (Re > 4000). Since the lower the fluid temperature, the higher its viscosity and the higher the fluid viscosity, the lower the Reynolds number of the flow, it can be seen that the highest errors were observed close to the lowest levels for the fluid temperature (25 °C) and the flow rate (125 m³/h), which may be an indication that the meter is operating in non-ideal conditions (laminar regime).

Additionally, it is worth highlighting that these non-contact mechanical flow meters are recommended for clean and homogeneous fluids [31]. The presence of a two-phase flow can lead to the attenuation of the ultrasonic wave and, consequently, an increase in measurement error. This scenario can be evidenced by the increase in measurement error from the increase in BSW, as shown in Figure 4, Figure 5 and Figure 6 for a fully developed flow in a turbulent regime.

Table 10. Ultrasonic flowmeter error due to increased BSW.

Error		BSW (v/v)
Temp (°C)	Flow Rate (m3/h)	0	5	10
34	175	0.146%	0.146%	0.150%
43	175	0.123%	0.127%	0.136%

presents a comparison of the error for the same flow rate condition (175 m³/h) considering two different fluid temperature conditions (34 °C and 43 °C). The error increases as the BSW increases, which may be associated with the occurrence of a two-phase flow and an eventual attenuation of the ultrasonic wave in this system.

4.2. Coriolis Meter

The experimental matrix for BBD used with the control factors and the response variable analyzed for the Coriolis flow meter is presented in

Table 11. Experimental matrix and results obtained for the Coriolis flow meter.

Treatment	$\mathbf{Factor}{\mathit{X}}_1$	$\mathbf{Factor}{\mathit{X}}_2$	$\mathbf{Factor}{\mathit{X}}_3$	Temperature (°C)	Flow Rate (m3/h)	BSW (% v/v)	Error
1	−1	−1	0	25	100	5	0.105%
2	1	−1	0	43	100	5	0.088%
3	−1	1	0	25	150	5	0.078%
4	1	1	0	43	150	5	0.072%
5	−1	0	−1	25	125	0	0.106%
6	1	0	−1	43	125	0	0.091%
7	−1	0	1	25	125	10	0.079%
8	1	0	1	43	125	10	0.084%
9	0	−1	−1	34	100	0	0.085%
10	0	1	−1	34	150	0	0.070%
11	0	−1	1	34	100	10	0.084%
12	0	1	1	34	150	10	0.076%
C	0	0	0	34	125	5	0.068%
C	0	0	0	34	125	5	0.088%
C	0	0	0	34	125	5	0.098%

:

The effects of control factors and interactions between these factors on the response variable using ANOVA are presented in

Table 12. ANOVA for Coriolis flow meter.

Source			Degrees of Freedom	Contribution	p-Value
Model	-	-	9	90.91%	0.037
-	Linear	-	3	19.83%	0.099
-	-	${\mathrm{X}}_1$	1	18.41%	0.025
-	-	${\mathrm{X}}_2$	1	0.40%	0.661
-	-	${\mathrm{X}}_3$	1	1.02%	0.487
-	Quadratic	-	3	9.20%	0.284
-	-	${\mathrm{X}}_1^2$	1	8.67%	0.088
-	-	${\mathrm{X}}_2^2$	1	0.28%	0.694
-	-	${\mathrm{X}}_3^2$	1	0.25%	0.724
-	Interactions	-	3	61.88%	0.011
-	-	${\mathrm{X}}_1\ast {\mathrm{X}}_2$	1	11.24%	0.055
-	-	${\mathrm{X}}_1\ast {\mathrm{X}}_3$	1	38.64%	0.006
-	-	${\mathrm{X}}_2\ast {\mathrm{X}}_3$	1	12.01%	0.050
Error	-	-	5	9.09%
-	Lack of adjustment	-	3	7.99%	0.176
-	Error pure		2	1.10%
Total	-	-	14	100.00%

:

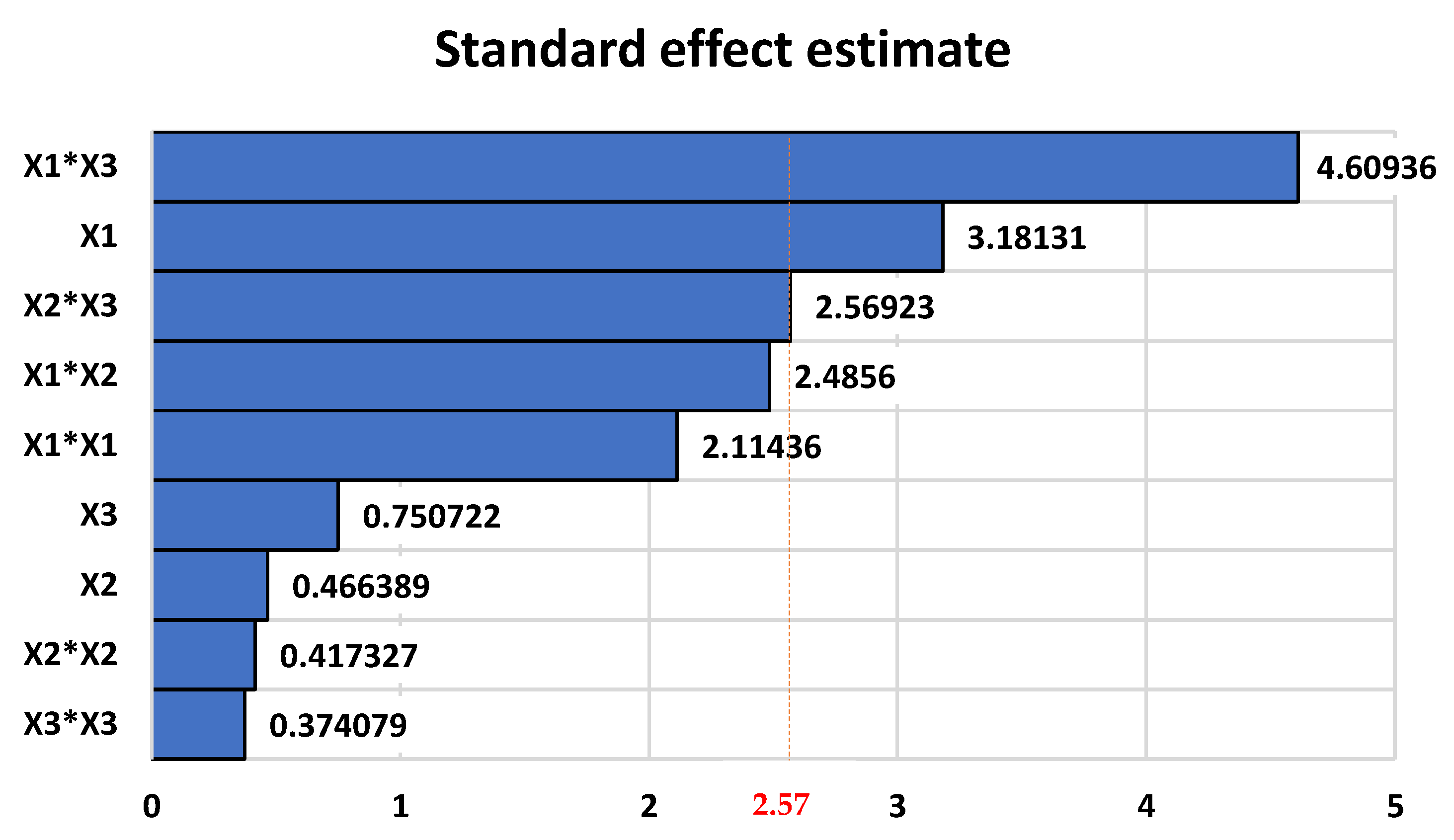
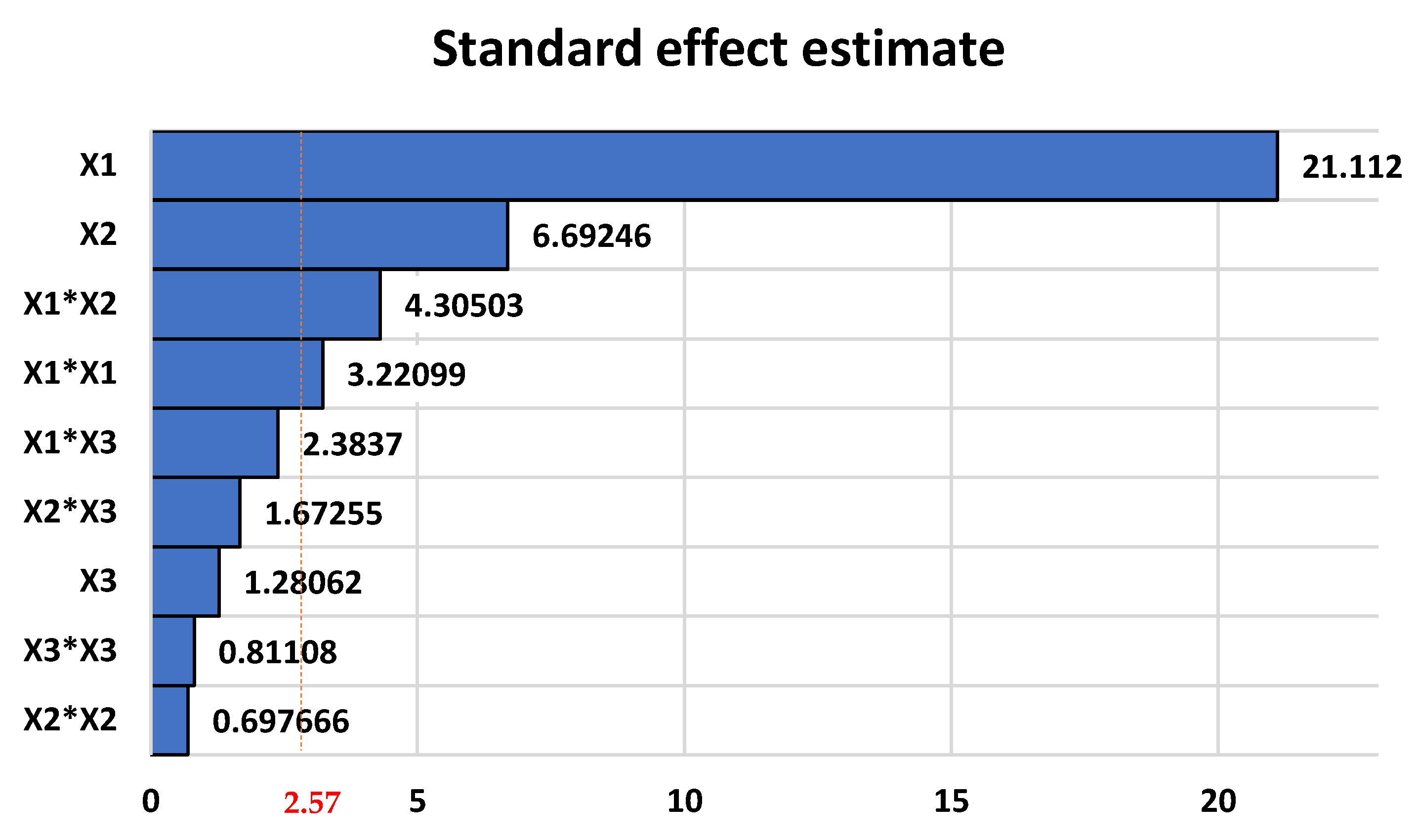
The Pareto chart for the estimated standardized effects is presented in Figure 7:

From Table 11 and Table 12 and Figure 7, the influence of fluid temperature ($x_1$) and its interaction with BSW ($x_1\times x_3$) on the response variable are statistically significant. The mathematical model that described the relationship between control factors and variables in response obtained was as follows:

$$\begin{array}{cc}\hfill Error=& 0.000825-0.000066x_1+0.000010x_2-0.000016x_3\hfill \\ & +0.000065x_1^2-0.000013x_2^2-0.000011x_3^2\hfill \\ & +0.000073x_1{x}_2+0.000135x_1{x}_3+0.0000075x_2{x}_3\hfill \end{array}$$

(7)

This model presented a good fit with a coefficient of determination R² of 90.91% and a standard deviation of 5.88 × 10⁻⁵.

Using the RSM, it was possible to observe the response variable. Tables S4–S6 presented the results of the mathematical model detailed in Equation (7) considering the variation in fluid temperature and flow rate for the BSW equal to 0% v/v, 5% v/v and 10% v/v.

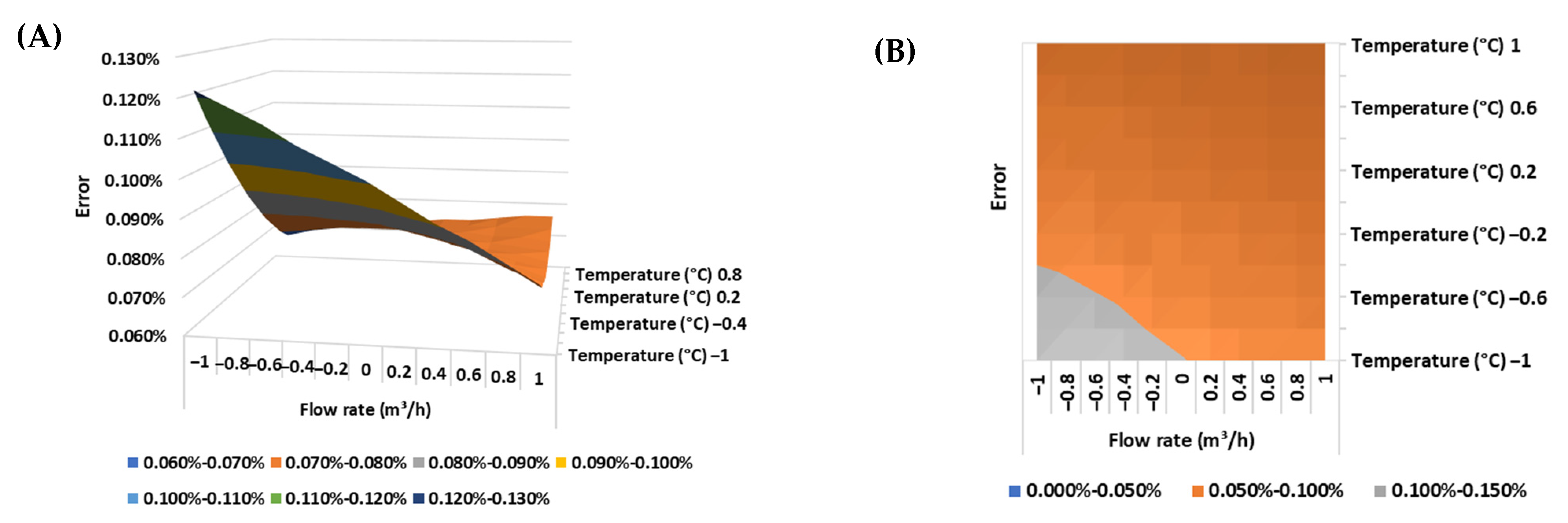
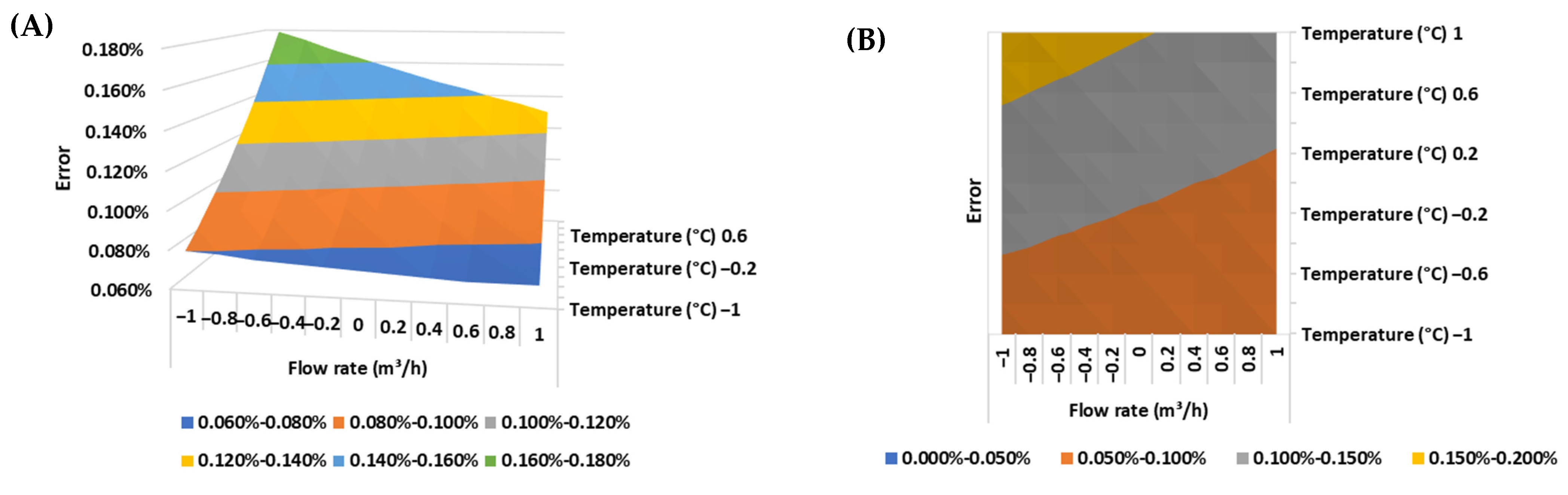
Below are presented the response surfaces and the contour plots of the error of the Coriolis meter for each of the BSW conditions evaluated (Figure 8, Figure 9 and Figure 10).

For higher BSW content, the error increases with extreme values of flow and temperature. Within the same BSW contents, the error increases for the smallest and largest values of flow and temperature.

Coriolis flow meters are mass meters; that is, they measure the mass flow rate of the flow. The volumetric flow rate of the flow is obtained by determining the density of the fluid using the flow meter itself. In this sense, this type of flow meter must be calibrated with a fluid like the one that was measured by it to minimize the error associated with the volumetric flow.

Based on Figure 2, changing the fluid’s BSW level causes a change in its density. Additionally, changes in fluid temperature lead to changes in its density. Such premises confirm the mathematical model described in Equation (7) and the results presented in Table 11 and Table 12 and Figure 7, which indicate the fluid temperature and its interaction with the BSW as the main sources of influence on the measurement error.

4.3. Positive Displacement Meter

The experimental matrix for BBD used with the control factors and the response variable analyzed for the positive displacement type flow meter is presented in

Table 13. Experimental matrix and results obtained for the positive displacement type flow meter.

Treatment	$\mathbf{Factor}{\mathit{X}}_1$	$\mathbf{Factor}{\mathit{X}}_2$	$\mathbf{Factor}{\mathit{X}}_3$	Temp (°C)	Flow Rate (m3/h)	BSW (% v/v)	Error
1	−1	−1	0	25	35	5	0.073%
2	1	−1	0	43	35	5	0.121%
3	−1	1	0	25	65	5	0.097%
4	1	1	0	43	65	5	0.150%
5	−1	0	−1	25	50	0	0.087%
6	1	0	−1	43	50	0	0.080%
7	−1	0	1	25	50	10	0.108%
8	1	0	1	43	50	10	0.110%
9	0	−1	−1	34	35	0	0.111%
10	0	1	−1	34	65	0	0.178%
11	0	−1	1	34	35	10	0.131%
12	0	1	1	34	65	10	0.092%
C	0	0	0	34	50	5	0.114%
C	0	0	0	34	50	5	0.106%
C	0	0	0	34	50	5	0.147%

:

The effects of control factors and interactions between these factors on the response variable using ANOVA are presented in

Table 14. ANOVA for positive displacement type flow meter.

Source			Degrees of Freedom	Contribution	p-Value
Model	-	-	9	99.07%	0.000
-	Linear	-	3	91.83%	0.000
-	-	${\mathrm{X}}_1$	1	83.17%	0.000
-	-	${\mathrm{X}}_2$	1	8.36%	0.001
-	-	${\mathrm{X}}_3$	1	0.31%	0.257
-	Quadratic	-	3	2.20%	0.088
-	-	${\mathrm{X}}_1^2$	1	1.97%	0.023
-	-	${\mathrm{X}}_2^2$	1	0.11%	0.516
-	-	${\mathrm{X}}_3^2$	1	0.12%	0.454
-	Interactions	-	3	5.04%	0.019
-	-	${\mathrm{X}}_1\ast {\mathrm{X}}_2$	1	3.46%	0.008
-	-	${\mathrm{X}}_1\ast {\mathrm{X}}_3$	1	1.06%	0.063
-	-	${\mathrm{X}}_2\ast {\mathrm{X}}_3$	1	0.52%	0.155
Error	-	-	5	0.93%
-	Lack of adjustment	-	3	0.89%	0.062
-	Error pure		2	0.04%
Total	-	-	14	100.00%

:

The Pareto chart for the estimated standardized effects is presented in Figure 11:

From Table 13 and Table 14 and Figure 11, the influence of fluid temperature $\left(x_1\right)$ and flow rate ${(x}_2)$ on the response variable is statistically significant. Additionally, the quadratic portion of the fluid temperature ($x_2^2$) and the interaction between the fluid temperature and the flow rate ($x_1\times x_2$) influence the second-order model estimated for the response variable.

The mathematical model that describes the relationship between the control factors and the response variable obtained was as follows:

$$\begin{array}{cc}\hfill Error=& 0.001097+0.000342x_1-0.000108x_2+0.000021x_3\hfill \\ & +0.000077x_1^2-0.000017x_2^2-0.000019x_3^2+0.000099x_2\hfill \\ & -0.000055x_1{x}_3+0.0000038x_2{x}_3\hfill \end{array}$$

(8)

This model presented a good fit with a coefficient of determination R² of 99.07% and a standard deviation of 4.58 × 10⁻⁵.

Using the RSM, the response variable can be observed. Tables S7–S9 present the results of the mathematical model detailed in Equation (8), considering the variation in fluid temperature and flow rate for the BSW, which is equal to 0% v/v, 5% v/v and 10% v/v.

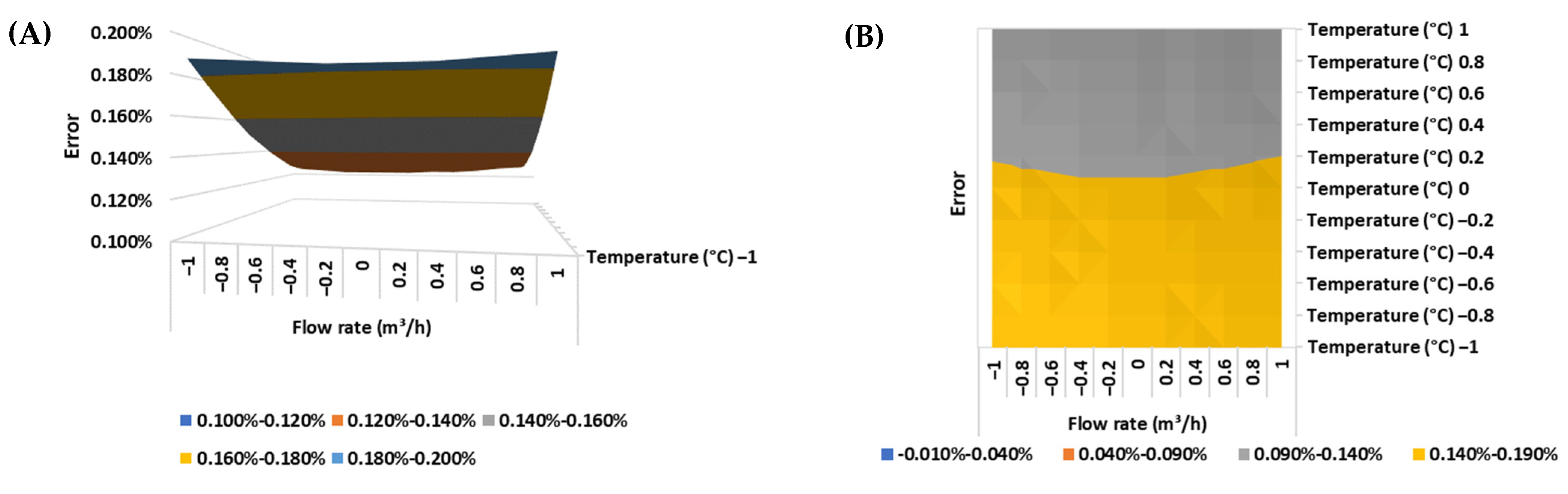
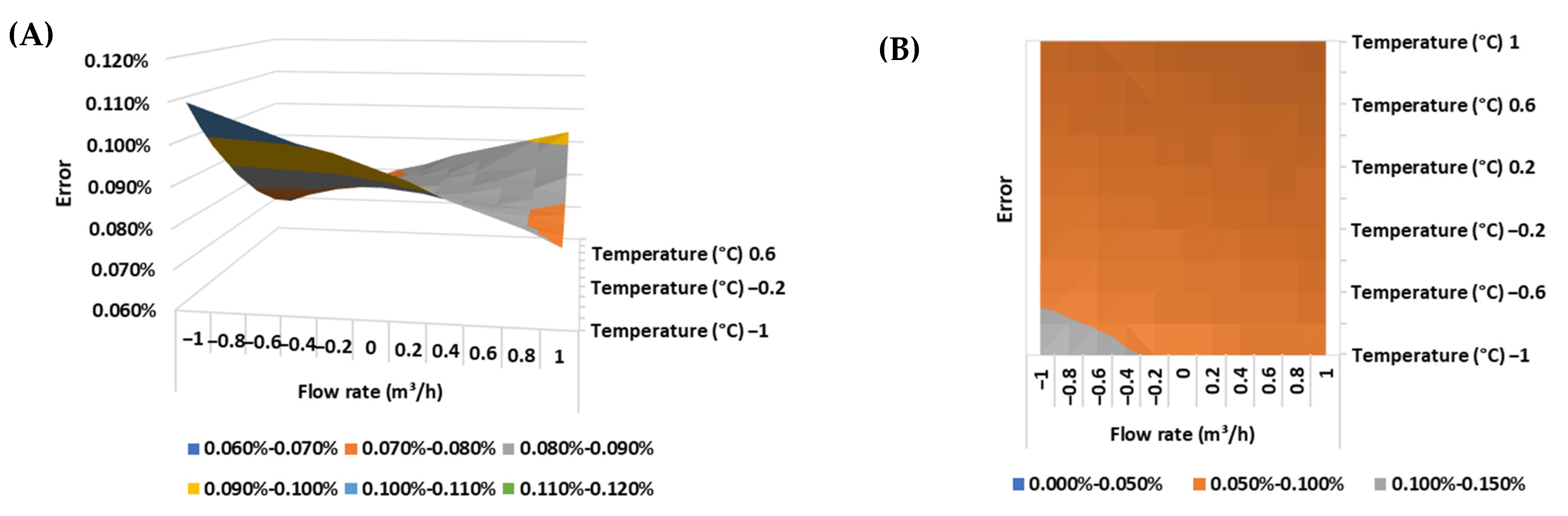
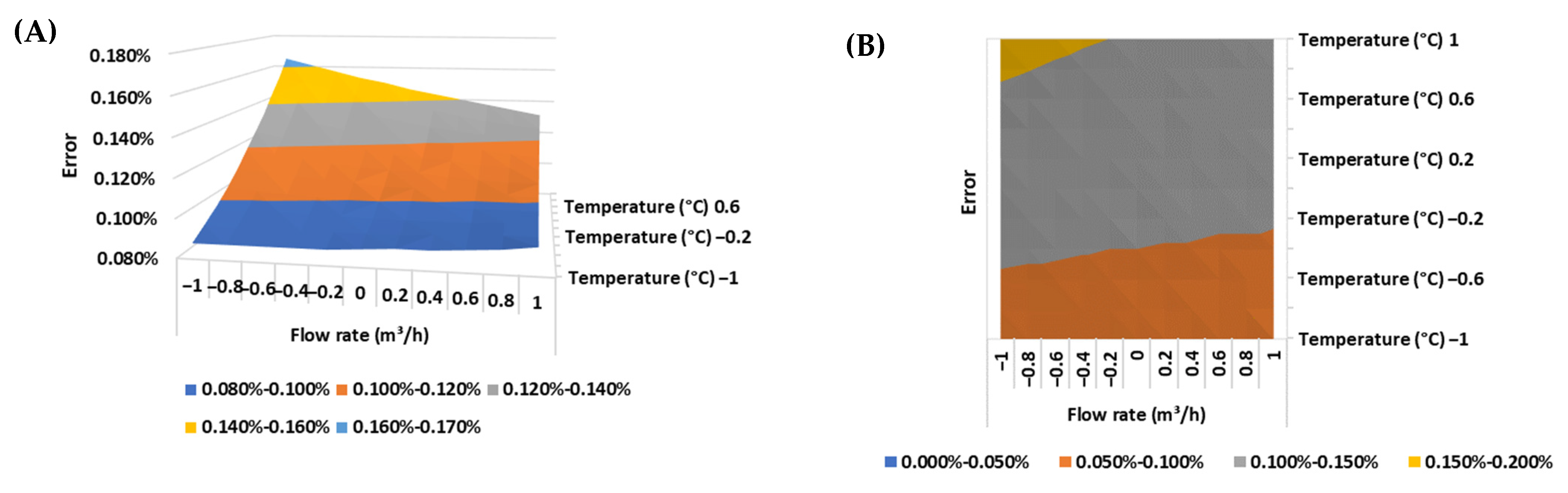
The response surfaces and the contour plots of the error of the positive displacement flow meter for each of the BSW conditions evaluated are presented in Figure 12, Figure 13 and Figure 14.

Positive displacement flow meters that use oval gears work by discretizing the flow into portions of known volume through the action of the flow on a rotating element. For the rotating element to fulfill its role, that is, to transport the discretized volume from the flow meter inlet to its outlet, it is necessary that the rotating element is not in contact with the meter shell, which can cause a small amount of volume (slide).

The greater the slip, the greater the measurement error. Slippage is directly proportional to the viscosity of the fluid and inversely proportional to the flow rate, especially when the meter operates close to the minimum flow limit for which it was designed.

Additionally, the measurement error can be impacted by physical changes in the flow meter due to the thermal expansion of the materials used, which leads to changes in the discretized volume with each rotation of the measuring element.

This premise is validated by the results obtained, as the mathematical model detailed in Equation (8) indicates that the main influencing factors are the fluid temperature (and its quadratic portion), the flow rate and the linear interaction between the fluid temperature and the flow rate, with the largest error (0.179%) being observed for the largest fluid temperature level (43 °C) and the lowest flow rate level (35 m³/h).

5. Conclusions

This study aimed to evaluate, using DoE and RSM, the metrological performance of oil measurement systems with ultrasonic flow meters, Coriolis and positive displacement when subjected to different BSW operating conditions, fluid temperature and flow rate.

From the execution of the experiment detailed in this study, it was found that all measuring technologies evaluated suffer low influence from BSW in the range of 0% to 10% v/v, with the measurement error being less than 0.2% in almost all operational conditions evaluated, when compared to a standard positive displacement type meter in almost all experimental conditions.

Additionally, it can be proven that the influence of the control factors evaluated on the response variable varies depending on the measurement technology used by the flow meter. However, it was found that fluid temperature is a relevant parameter in evaluating the metrological performance of oil flow measurement systems for all measurement technologies evaluated.

Finally, it is concluded that the Coriolis flow meter presented the lowest error among the measuring technologies evaluated. Additionally, ultrasonic flow meters should be avoided with flows that are not completely developed or in laminar flows.

To deepen discussions on the metrological performance of oil measurement systems, it is suggested to evaluate the issues by undertaking the following: (i) carry out other experiments using petroleum instead of mineral oil; (ii) evaluate the metrological performance of petroleum measurement systems with other measurement technologies, such as turbine-type flow meters; (iii) evaluate the metrological performance of oil measurement systems under more severe BSW conditions; (iv) carry out other experiments with different models of the same measurement technology; and (v) evaluate the influence of the Reynolds number on the metrology of oil measurement systems with ultrasonic flow meters.