Machine Learning Models for Regional Photovoltaic Power Generation Forecasting with Limited Plant-Specific Data

Abstract

Predicting electricity production from renewable energy sources, such as solar photovoltaic installations, is crucial for effective grid management and energy planning in the transition towards a sustainable future. This study proposes machine learning approaches for predicting electricity production from solar photovoltaic installations at a regional level in Italy, not using data on individual installations. Addressing the challenge of diverse data availability between pinpoint meteorological inputs and aggregated power data for entire regions, we propose leveraging meteorological data from the centroid of each Italian province within each region. Particular attention is given to the selection of the best input features, which leads to augmenting the input with 1-hour-lagged meteorological data and previous-hour power data. Several ML approaches were compared and examined, optimizing the hyperparameters through five-fold cross-validation. The hourly predictions encompass a time horizon ranging from 1 to 24 h. Among tested methods, Kernel Ridge Regression and Random Forest Regression emerge as the most effective models for our specific application. We also performed experiments to assess how frequently the models should be retrained and how frequently the hyperparameters should be optimized in order to comprise between accuracy and computational costs. Our results indicate that once trained, the model can provide accurate predictions for extended periods without frequent retraining, highlighting its long-term reliability.

1. Introduction

Renewable energy sources such as solar photovoltaic (PV) play a pivotal role in the transition to a sustainable and carbon-neutral future. However, the inherent variability and intermittency of these energy sources pose significant challenges to power grid operators and energy management systems [1]. To address this issue, machine learning (ML) techniques have emerged as powerful tools for accurately predicting electricity production from renewable energy sources installations [2].

In recent years, ML algorithms have demonstrated their ability to capture complex patterns and make accurate predictions based on historical data [3]. Furthermore, they have shown effectiveness in extrapolating insights not only from past instances of the same case but also from analogous cases, thereby extending their applicability to similar scenarios [4]. By leveraging the vast amount of data collected from PV installations, these approaches can provide valuable insights into future energy production, enabling better planning and optimization of renewable energy systems.

One of the primary applications of ML in the renewable energy domain is the prediction of electricity generation from solar PV systems. These systems are highly dependent on weather conditions, including solar irradiance and temperature. ML models can leverage historical weather data along with production data to learn the relationships between meteorological variables and electricity output. By considering factors such as cloud cover, shading, and panel orientation, ML algorithms can make accurate predictions of solar PV production, aiding in the effective integration of these systems into the grid [2].

In this article, we propose some machine learning approaches to predict electricity production from solar PV installations at the regional (i.e., market zone) level with limited data about the location or the dimension of the available power plants. Accurate predictions of electricity production from solar PV installations can facilitate effective grid management, enable better energy planning, and ultimately accelerate the transition to a sustainable energy future.

This level of prediction poses a significant challenge due to the limited availability of precise data pertaining to individual contributing installations. In most cases, the data provided only encompass the aggregated production of the entire zone. This lack of granularity makes it difficult to accurately predict the production of specific solar PV installations within the zone. The total production of the zone is influenced by numerous factors, including the combined output of various types and sizes of renewable energy installations, geographical variations, and localized weather conditions. Extracting precise information regarding the production of individual installations becomes a complex task due to the absence of detailed information regarding each contributing unit. Consequently, predicting zone-level production requires sophisticated modelling techniques that can effectively capture the collective behaviour of multiple installations and incorporate statistical methods to account for the inherent uncertainties in such predictions. Furthermore, it is crucial to emphasise the importance of predicting on a regional scale rather than solely focusing on large, comprehensive installations, as illustrated in the case of Italy. Small plants with a capacity below 20 kW represent around 93% of the total installed plants and 26% in terms of power [5]. Considering the contributions of these smaller installations is essential to achieving accurate predictions and effectively managing renewable energy resources. This specific condition of data scarcity is a topic relatively underexplored in the literature, despite being highly prevalent in real-world applications.

One of the key challenges in this problem lies in the design process regarding data selection, level of aggregation, and geographical representation. Choosing the appropriate data to train and validate machine learning approaches for predicting electricity production from solar PV installations is a complex task. While some models may require highly granular data at the individual installation level, often only aggregated data at the market zone or regional level are available. Balancing the trade-off between data granularity and model complexity is crucial. Additionally, geolocational considerations are essential, as the predictive models need to capture the specific characteristics of each geographic area, including variations in weather patterns, topography, and energy infrastructure. An example of limited data arises when information regarding the size, production, and location of many installations is unknown, yet the desired outcome is the total regional production. If all data regarding the production plants were available, it would be possible to perform a weighted average of the meteorological data based on location and production capacity, thereby making inputs and outputs more readily correlatable. Alternatively, it would be possible to obtain the aggregated prediction as the sum of individual predictions. Without this information, a discrepancy arises between available inputs and required outputs and leads to a significant challenge.

Innovatively, this article addresses the challenging problem of predicting electricity production from solar PV installations at the regional level, even in cases with limited data availability or an almost complete absence of granular information on individual contributing installations. While the prediction of electricity generation from renewable sources has been extensively explored, the scarcity of precise data at the individual installation level poses unique obstacles, and our proposed machine learning approaches aim to overcome these challenges to deliver accurate predictions at the market zone level.

The proposed approach entails the utilisation of supervised regression ML models. Innovatively, addressing the challenge of disparate data availability between pinpoint meteorological inputs and aggregated power data for entire regions, we propose leveraging geolocated meteorological data from centroid coordinates of provinces within each region. Another key contribution lies in the selection of features and inputs for these models. As previously mentioned, we propose using meteorological data corresponding to the coordinates of the provinces within the regions. Additionally, we suggest augmenting the input with 1-hour lagged meteorological data (i.e., the previous hour and the subsequent hour) and data on power production from the preceding hour. The output is the total regional production. The approach is validated through testing with data from Italian electricity market regions, and hyperparameter tuning is performed via five-fold cross-validation.

Another significant contribution of this work is the analysis of the effect of periodically retraining the models at different time distances, in order to assess how often the models should be retrained in order to accommodate for seasonal variations in the data. Moreover, we performed experiments to compare the effect of frequently optimising the hyperparameters, with respect to the case of fixing the optimal hyperparameters for a long time. These experiments enhance the practicality and relevance of the proposed methodology for real-world applications. The predictions have hourly resolution, and the models are trained on data spanning 60 days, with a time horizon ranging from 1 to 24 h. In particular, the test set is one week (168 h), and we follow a rolling approach, testing on 54 consecutive weeks comprehensively testing on a whole year of data.

The paper is organised as follows: In Section 2, we present an in-depth description of the main problem related to the prediction of electrical power from photovoltaic resources. Subsequently, Section 3 introduces the machine learning approaches proposed in this study for tackling the aforementioned problem. In Section 4, we present the results obtained by applying the proposed approaches to a carefully considered case study. Finally, in Section 5, we draw insightful conclusions based on the findings and outcomes of our research.

2. Theoretical Description

The surging demand for renewable energy sources has spurred remarkable progress in renewable power technologies. Among these, solar PV systems stand out as they skillfully harness the boundless power of sunlight to generate electricity through the photovoltaic effect.

2.1. Motivation

Accurate prediction of electricity production from PV sources holds significant importance for various stakeholders in the renewable energy sector. Firstly, for energy grid operators, precise predictions enable better management of the electricity grid by facilitating the integration of intermittent renewable energy sources. By knowing the expected electricity output, operators can make informed decisions regarding load balancing, grid stability, and optimal utilisation of conventional power generation resources [6]. Additionally, accurate predictions assist in optimising the dispatch of electricity, minimising imbalances, and reducing the reliance on costly backup power options. Moreover, accurate predictions of electricity production are crucial for energy trading and market participation. Energy traders can make more precise forecasts of supply and demand, allowing for effective bidding strategies in energy markets [7].

The utilisation of machine learning approaches for predicting electricity production from solar PV sources offers several advantages over traditional modelling methods. Machine learning algorithms excel at extracting complex patterns and relationships from large datasets, enabling them to capture the dynamics inherent in renewable energy generation. These approaches can leverage historical production data, weather variables, and other relevant inputs to create models that adapt and improve over time [2,8]. By learning from past patterns and incorporating real-time data, machine learning models can provide more accurate and reliable predictions compared to conventional analytical methods.

Machine learning also offers the flexibility to handle the nonlinear and highly dynamic nature of solar PV or other power generation. Traditional modelling techniques often rely on simplifying assumptions that may not capture the intricacies of these complex systems. In contrast, machine learning algorithms can capture non-linear relationships, identify subtle patterns, and adapt to changing conditions, allowing for more precise predictions [9].

In summary, leveraging machine learning approaches for predicting electricity production from solar PV sources offers the benefits of enhanced accuracy, flexibility, and the ability to handle complex and dynamic systems. These approaches have the potential to support various stakeholders in optimising renewable energy integration, planning resource allocation, and making informed decisions in the rapidly evolving energy landscape.

2.2. Analysis of the Problem

Solar irradiance consists of three main components: direct irradiance, diffuse irradiance, and reflected irradiance [10]. Among these components, direct and diffuse irradiances are the most significant for PV energy production [11]. Generally, the efficiency of solar cells decreases as temperature increases, which can lead to a reduction in electricity production [12]. In cases where precise data for the tilt and azimuth angles of individual installations are unknown, horizontal components of irradiance, which assume no inclination, are often considered as a simplified approach [13]. Therefore, a global horizontal irradiance $ghi$, as the sum of direct and diffuse irradiances is the most commonly used outcome of the weather forecast, and it will be used in this work as the main input data, as described in the following.

2.3. State of the Art

The state-of-the-art in photovoltaic power production prediction has been driven by the pressing need for accurate and reliable forecasts to facilitate the seamless integration of renewable energy sources into the global energy landscape. In this pursuit, a diverse array of approaches has been extensively studied and utilised, primarily categorised into physical models and statistical models [8,14].

Physical models represent a mechanistic approach to power prediction, grounded in fundamental principles governing solar cell behaviour and the interaction of solar radiation with PV modules. These models require detailed information about system specifications, atmospheric conditions, and solar irradiance patterns to generate accurate forecasts. Among physical models, numeric weather predictors have emerged as one of the most popular choices [15,16].

On the other hand, statistical techniques rely on historical data and correlations between PV power output and relevant meteorological parameters. Machine learning algorithms and time series analysis constitute data-driven methods that effectively capture complex patterns and variations in PV performance, without heavily relying on physical parameters [8].

Regarding time series predictions, widely used models include Autoregressive with exogenous input (ARX), Autoregressive Moving Average (ARMA), and Autoregressive Integrated Moving Average (ARIMA) [8,17,18]. Nevertheless, recent research has been exploring hybrid models that combine different time series prediction methods or integrate statistical approaches, such as machine learning. For example, Sansa et al. [19] proposed a combination of ARMA and Nonlinear Auto Regressive with eXogenous input (NARX), while Zhang et al. [20] developed a hybrid model combining fuzzy information granulation (FIG), improved long and short-term memory network (ILSTM), and ARIMA.

As for machine learning models, Support Vector Regression (SVR) [12], Gradient Boost Decision Tree [21], Convolutional Neural Networks (CNN), Gated Recurrent Units (GRU), Long Short-Term Memory (LSTM) [22,23], and generally Artificial Neural Networks (ANN) [24,25,26] have been widely explored. Recent advancements also include hybrid combinations of ML approaches, such as the combination of GRU and CNN proposed by Sabri et al. [23], or the combination of CNN and LSTM as explored by Almaghrabi et al. [27]. These hybrid models strive to leverage the strengths of different ML techniques to enhance the accuracy and robustness of PV power predictions, opening up new possibilities for further improvements in renewable energy integration.

In addition to forecasting photovoltaic power production, AI and ML techniques are increasingly playing a pivotal role in predicting other sources of renewable energy production, such as wind energy [28] or hydroelectric production [29]. These advanced methods have demonstrated remarkable efficacy in not only predicting renewable energy production but also in forecasting various other critical aspects relevant to renewable energy systems, including energy prices [30], demand loads [31], and maintenance requirements [29].

Another significant classification of the literature regarding the prediction of photovoltaic power involves the level of application detail. Researchers have tackled two main approaches: works focused on individual PV systems and those dealing with the aggregated power of multiple installations, such as at the regional or market zone level. The former category of applications aims to predict power output for specific, stand-alone PV systems, often considering detailed data such as the exact location and power capacity of each installation. For instance, in our previous study [32], we compared simple forecasting methodologies with more sophisticated ones over 32 photovoltaic (PV) plants of different sizes and technology over a whole year. Additionally, from this study, it was deduced that an enhancement in weather forecast accuracy could lead to up to a 1% improvement in predictions (from 3% to 2%).

Conversely, applications at the aggregated level encompass a broader scope, seeking to forecast power generation for groups of PV systems within a region or market zone. While there are several approaches available for solar PV power forecasting at the plant level, the number of studies dedicated to regional-level prediction remains limited. This problem proves challenging due to the vast heterogeneity of PV installations, each influenced by unique environmental conditions, orientations, and technology variations. Nonetheless, researchers have proposed innovative methodologies to handle the complexity inherent in aggregated predictions. Some studies aggregate data from individual installations based on their power capacity, allowing a more generalised forecast for the entire region. Others explore geolocation clustering techniques, grouping installations with similar environmental characteristics to enhance prediction accuracy at the aggregated level.

Regarding large-scale predictions, Refs. [33,34] propose forecasting methodologies that incorporate data on the location of PV systems or sites, as well as meteorological station records. In a similar context, Ref. [27] aggregate and normalise power data from individual PV plants to facilitate more comprehensive analyses. To further optimise their predictions, Ref. [12] employ clustering techniques, effectively grouping PV installations based on their power characteristics. Moreover, Ref. [25] also employs clustering strategies for PV installations while introducing an additional step to calculate centroids. These centroids represent the approximate average locations of the regions or clusters under consideration, further refining the prediction process.

3. Methodology

To address the difficult task of predicting electricity production from PV sources at regional levels, we employ a comprehensive set of machine learning models, each meticulously crafted to accommodate the unique characteristics of various market zones. The primary focus of our algorithm revolves around harnessing the predictive power of beam horizontal irradiance $b_{hi}$ and diffuse horizontal irradiance $d_{hi}$. data. Our approach involves testing and fine-tuning multiple ML models, including k-Nearest neighbours Regression (KNNR) [35], Decision Tree Regression (DTR) [36], Kernel Ridge Regression (KRR) [37], Linear Regression (LR) [38], Support Vector Regression (SVR) [12], Random Forest Regression (RFR) [37], Gradient Boosting (GB) [21], and an ensemble model combining KNNR, SVR, and GB, referred to as KSVRGB.

• k-Nearest neighbours Regression (KNNR): A non-parametric method that predicts the target variable by averaging the values of its k nearest neighbours in the feature space.
• Decision Tree Regression (DTR): A tree-based method that recursively splits the feature space into partitions to predict the target variable.
• Kernel Ridge Regression (KRR): A regularised version of linear regression that uses kernel methods to map the input features into a higher-dimensional space.
• Linear Regression (LR): A simple linear model that predicts the target variable as a linear combination of the input features.
• Support Vector Regression (SVR): A regression technique that uses support vector machines to find the optimal hyperplane in a projected space while fulfilling data constraints.
• Random Forest Regression (RFR): An ensemble learning method that combines multiple decision trees to improve prediction accuracy by reducing overfitting and variance.
• Gradient Boosting (GB): A machine learning technique that builds models sequentially by focusing on the errors made by previous weak models, thereby producing a strong predictive model.
• Ensemble model (KSVRGB): An ensemble model combining KNNR, SVR, and GB, designed to leverage the strengths of each individual model for improved predictive performance.

One of the distinguishing challenges in our predictive modelling framework is the incongruence between input and output data. The input features include a large number of irradiance predictions (one for each province as introduced later) within a given market zone while the output corresponds to the aggregated electrical production for that entire zone. This disparity necessitates a sophisticated adaptation of each model for the specificity of each market zone. Consequently, a tailored ML model is developed for every market area, ensuring that the predictive models capture the distinct characteristics and variations inherent in each region.

The selection of diverse machine learning models allows us to explore the potential strengths and weaknesses of each algorithm in capturing the relationships between irradiance predictions and aggregated electrical production. In the following, we will specifically highlight only a subset of machine learning models that have demonstrated more promising outcomes.

3.1. Data Selection

In the context of a specific electricity market region, the availability of meteorological data in aggregated form for the entire region is often lacking and sometimes meaningless. This poses a challenge, particularly in the absence of comprehensive information regarding the distribution and scale of facilities within the region. Without such details, it becomes impractical to perform a weighted average of local meteorological readings at individual facilities, where the weights are determined based on the respective capacities of these facilities.

To address this limitation, an alternative approach is proposed wherein geolocated meteorological readings from densely populated areas within the market region, such as provincial capital cities or other administrative divisions are leveraged. By focusing on these areas, which typically exhibit higher energy consumption and thus greater relevance to load forecasting, it is posited that more accurate predictions can be obtained. It is acknowledged that while this approach may be more reliable for load forecasting compared to production forecasting, its efficacy hinges on the availability of relevant data.

Empirical evidence supporting this hypothesis is derived from subsequent analyses, indicating that despite the absence of detailed facility-specific information, the approximation provided by utilising geolocated readings from populous regions yields satisfactory results. This underscores the pragmatic nature of the proposed approach in situations where comprehensive data may be lacking, offering a viable solution for enhancing prediction accuracy within the constraints of available resources and information. Indeed, it is important to specify that among the considered input data are meteorological readings related to beam horizontal irradiance $bhi$ and diffuse horizontal irradiance $dhi$, and temperatures. However, temperatures that exhibit significant variability, even with minor location approximations, will be excluded from further analysis in this article. Another considered input feature is temporality, where the proposed and tested models utilise the time of day as input. It is noteworthy to mention that the considered data are point values referring to the centroids of the provinces of the regions under consideration.

In particular, the predictions of the irradiance are obtained from a meteorological forecast model with a spatial resolution of 7 × 7 Km and temporal resolution of 15 min. The predictions are then spatially and temporally aggregated in order to obtain the average hourly irradiance in the geographical center of each Italian province

In each of the proposed ML methods and for each region, considering discretized data in time intervals of duration $\Delta t=1\left[h\right]$, the training input data X have dimensions of $n\times r$, where n represents the number of considered training observations (as consecutive input time intervals), and $r=(p·d_p)+d_r$ is the number of input variables, where p denotes the number of geolocated centres (i.e., centroids) or provinces within a single region, $d_p$ represents the number of features per province, and $d_r$ represents the number of features common to the entire region. On the other hand, the training output Y is the scalar value representing the regional global power [MW] over the aforementioned n training time intervals. Regarding the test set, we perform predictions on the subsequent m time intervals. The size of the training and test sets were selected using a continual learning approach described in the following.

3.2. Model Selection

To enhance the robustness of the proposed machine learning methods, we implemented a series of strategies primarily revolved around hyperparameter optimisation and input selection, both of which play pivotal roles in mitigating overfitting and fine-tuning model performance.

Leveraging the GridSearch technique with five-fold cross-validation, see Figure 1, we systematically explored a range of hyperparameter configurations to identify the optimal settings for each model variant. This exhaustive search process allowed us to navigate the complex landscape of hyperparameters and pinpoint combinations that maximised the predictive accuracy while minimising the risk of overfitting.

By meticulously optimising hyperparameters, we ensured that our models were finely tuned to extract meaningful insights from the data while maintaining robustness across diverse scenarios. This iterative refinement process played a crucial role in elevating the performance and reliability of our machine-learning models, ultimately enhancing their utility in real-world applications.

In our approach, the selection of input features was performed using a variable bagging algorithm, which was applied consistently across all methods. This technique involved randomly selecting subsets of features from the available pool and training models on each subset. Additionally, the results indicate that the selected variables include not only the current hour’s inputs but also inputs one hour forward, inputs one hour backward, and the previous hour’s output. Further details on the feature selection process will be provided in the following section.

4. Validation

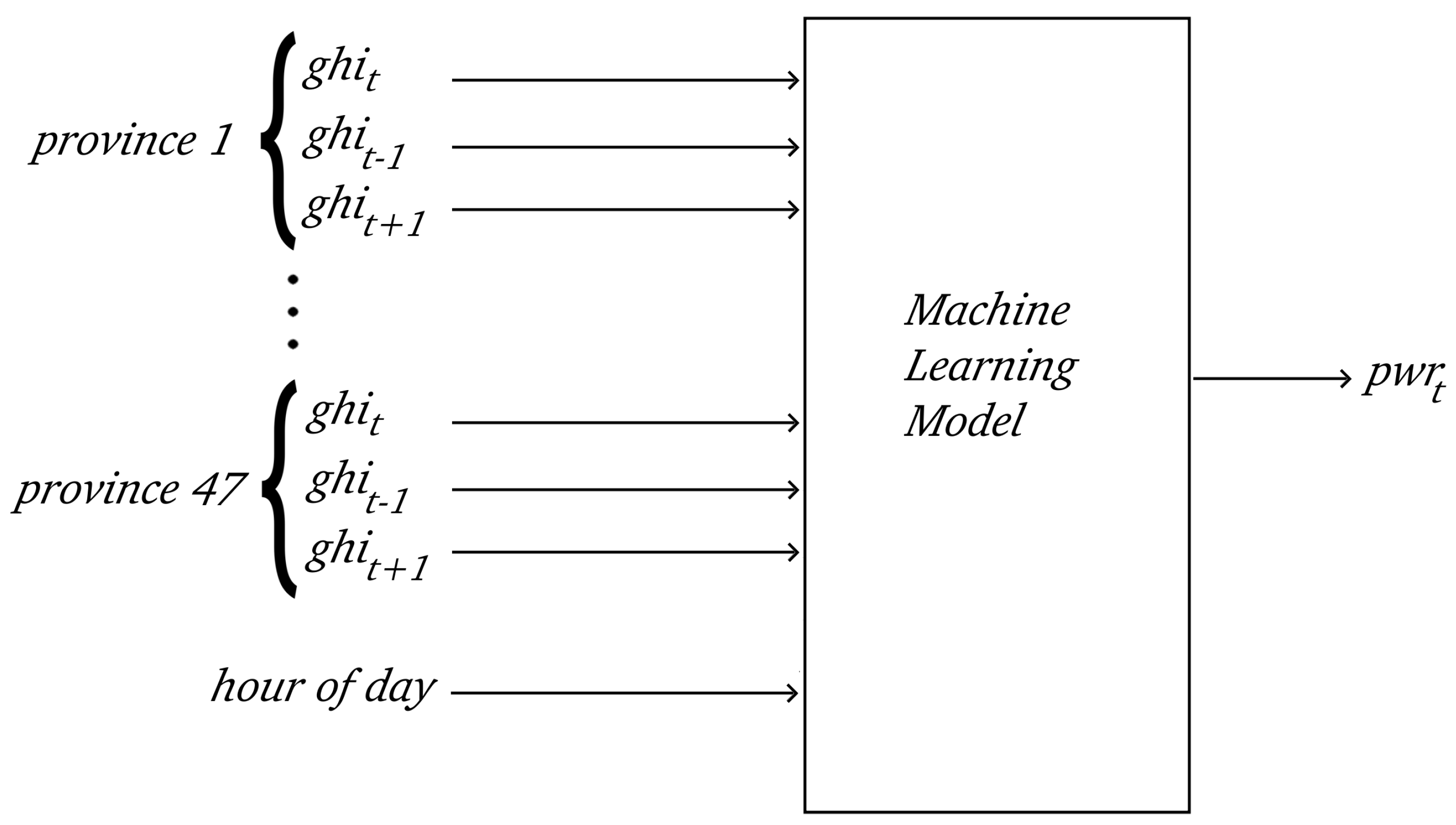
The proposed approach has been applied to the Italian electricity market, which is divided into seven market regions or zones, as shown in Figure 2. The Italian electricity market comprises a network of seven distinct market regions or zones, each characterised by its unique set of attributes and operational dynamics. These zones exhibit notable variations across multiple dimensions, including demographic composition, industrial infrastructure, energy consumption patterns, geographical features, and climatic conditions [39]. For instance, certain regions may be densely populated urban centres with high industrial activity, leading to pronounced peaks in energy demand during specific hours of the day. In contrast, other zones might encompass rural areas characterised by agrarian economies, where energy usage patterns differ significantly due to factors such as agricultural operations and seasonal variations. Additionally, geographical considerations, such as proximity to renewable energy sources like hydroelectric or solar power plants, play a pivotal role in shaping the energy generation mix and overall market dynamics within each zone. Furthermore, climatic variations across different regions influence factors such as solar availability, further contributing to the heterogeneity observed in energy production patterns. As delineated in Section 3.1, the input data dimensions of these networks are directly proportional to the number of provinces in each respective zone. These zones and their respective number of provinces are outlined in

Table 1. Italian Electricity Market Zones and Provinces.

Market Zone	Zone Number	Number of Provinces
Northern Italy	1	47
Central-Northern Italy	2	15
Central-Southern Italy	3	11
Southern Italy	4	15
Calabria	5	5
Sardinia	6	5
Sicily	7	9

.

The meteorological data utilised consist of hourly forecasts provided by the Italian Air Force–Aeronautica Militare [40], while the hourly production data are sourced from the European Network of Transmission System Operators for Electricity [41]. The available data spans from February 2022 to April 2023 inclusive and has granularity $\Delta t$ of 1 h. Data from 2 months (60 days) are used for training, and the testing phase utilises the following week (7 days). Additionally, each model is retrained weekly by shifting the data by one week to cover a prediction of an entire year, i.e., from April 2022 to March 2023, i.e., the training data span from February 2022 to February 2023. Furthermore, it is important to note that the meteorological data are provided at 00:00 of the preceding day, while the power data are assumed to be available for the preceding hour. In the experiments presented in the following section, the temporal horizon transitions from 24 h to 1 h in the case of using power data.

As previously mentioned, for each zone the input data X have dimensions of $n\times r$, where n represents the number of considered intervals, and $r=(p·d_p)+d_r$ denotes the total number of variables, p signifies the number of geolocated centers or provinces within the region, $d_p$ represents the number of geolocated features, and $d_r$ indicates the number of features common to the entire region.

For example, in zone 1, i.e., North, the number of training observations n is 60 × 24 = 1440, and the number of input variables r = 143. Where, $d_r$ = 2, signifying the hour of day information and the lagged production power $pw{r}_{t-1}$ of 1 h backward; p = 47, representing the number of provinces; and $d_p$ = 3, encompassing the current $gh{i}_t$ at time t, the lagged $gh{i}_{t-1}$ of 1 h backward, the lagged $gh{i}_{t+1}$ of 1 h forward, as depicted in Figure 3. Using the production power of the previous hour as input leads to a nowcast problem with 1 h ahead time horizon. In order to enlarge the time horizon to 24 h, we also tested a model with no lagged power as an input feature, as shown in Figure 4.

The test size m is 7 days × 24 h = 168 h. Using a rolling approach we test on 54 weeks of comprehending a whole year. This choice of a one-hour lag proved to be the most effective, suggesting that it strikes an optimal balance between capturing short-term fluctuations and preserving the overall temporal structure of the data. By leveraging this approach, our models demonstrate improved robustness and predictive accuracy, thus enhancing its utility in real-world applications.

Performances

The performance of the tested machine learning approaches, including implementations with data augmentation techniques and hyperparameters tuning as described in Section 3.2, in predicting electrical PV power across the different market zones was evaluated, with the Normalised Root Mean Square Error (NRMSE) serving as a key indicator. The NRMSE is defined as:

$$\mathrm{NRMSE}=\frac{\sqrt{\frac{1}{n}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}{y_{\max }-y_{\min }}\%,$$

(1)

where n is the number of observations, $y_i$ is the actual value, ${\widehat{y}}_i$ is the predicted value, and $y_{\max }-y_{\min }$ is the range of the observed values. The NRMSE normalises the Root Mean Square Error (RMSE) by dividing it by the range of the observed values, making it a dimensionless measure that ranges from 0 to 100%. In practice, this range corresponds to the maximum observed production across the entire dataset, including both training and testing data, as production can be zero. NRMSE is a commonly used metric that provides a standardised measure of the prediction error, accounting for the scale of the target variable in these kinds of problems.

As previously mentioned, the various regions exhibit significantly different characteristics. While the resolution approach remains consistent, we tailored a distinct set of hyperparameters for each region to optimise model performance. To achieve this, we conducted an extensive GridSearch process with a five-fold cross-validation, iterating over a range of hyperparameters for each region. The GridSearch technique systematically explores a predefined set of hyperparameters for a machine learning algorithm, evaluating the model’s performance across various combinations. Specifically, for each considered set of hyperparameters, we performed 54 individual trainings, spanning an entire year from the first week of April 2022 to the first week of March 2023. Each training cycle was followed by testing the model on the subsequent week, and this process was repeated for all weeks of the year. Subsequently, we averaged the test results over the entire year interval to assess the overall performance of each model. Notably, every individual training and resulting model had its unique optimal set of hyperparameters. For clarity of presentation, we showcase only the optimal hyperparameter values, determined by selecting those with the highest frequency of occurrence among the 54 training iterations for each model. These summarised outcomes are detailed in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9.

All of the considered models and hyperparameters’ names and definitions refer to the implementation of the Python library Scikit-learn [42], which was used in this work. All calculations were performed on a single machine equipped with an Intel Core i9-10900K processor clocked at 3.70 GHz with 10 cores and 32 GB RAM. The hyperparameters considered in the LR model, as shown in Table 2, are fit intercept and positive. The fit intercept hyperparameter determines whether an intercept term is included in the model equation, accounting for the constant term. Meanwhile, the positive hyperparameter imposes non-negativity constraints on the coefficients, fostering interpretability and enhancing model robustness, particularly in scenarios where negative relationships are deemed implausible.

Table 2. Hyperparameters for each zone for LR model.

Zone	Fit Intercept	Positive
1	True	True
2	False	False
3	False	False
4	False	False
5	False	False
6	True	False
7	True	False

Table 2. Hyperparameters for each zone for LR model.

Zone	Fit Intercept	Positive
1	True	True
2	False	False
3	False	False
4	False	False
5	False	False
6	True	False
7	True	False

The hyperparameters considered in the SVR model, as shown in Table 3, are C, $ϵ$, $\gamma$, and kernel. The kernel hyperparameter determines the type of kernel function used to transform the input space into a higher-dimensional feature space, allowing for nonlinear mappings. Common choices for the kernel function include linear, polynomial, radial basis function (rbf), and sigmoid. Another essential hyperparameter is C, which controls the regularisation strength by balancing the trade-off between maximising the margin and minimising the training error. Values between 0.1, 1, and 10 have been tested. Additionally, the epsilon hyperparameter specifies the margin of tolerance for errors in the training data. It defines a tube around the regression line within which no penalty is incurred, providing flexibility in accommodating deviations from the optimal solution. Values 0.1, 0.2, and 0.3 have been tested. Lastly, the $\gamma$ hyperparameter, applicable when using an RBF kernel, determines the influence of a single training. It represents the kernel coefficient, influencing the flexibility of the decision boundary. In the context of utilising Scikit-learn [42], it offers two strategies for selecting the $\gamma$ hyperparameter: auto and scale. The auto option dynamically adjusts $\gamma$ based on the inverse of the number of features, while the scale option still dynamically adjusts $\gamma$ based on the inverse of the number of features, but also takes into account the unit variance. Through the mentioned GridSearch approach, the most effective strategy for enhancing model performance was identified.

Table 3. Hyperparameters for each zone for SVR model.

Zone	C	$\mathit{ϵ}$	$\mathit{\gamma }$	Kernel
1	1	0.1	scale	rbf
2	1	0.1	auto	rbf
3	10	0.1	scale	rbf
4	1	0.1	scale	rbf
5	10	0.1	scale	rbf
6	10	0.1	auto	rbf
7	10	0.1	scale	rbf

Table 3. Hyperparameters for each zone for SVR model.

Zone	C	$\mathit{ϵ}$	$\mathit{\gamma }$	Kernel
1	1	0.1	scale	rbf
2	1	0.1	auto	rbf
3	10	0.1	scale	rbf
4	1	0.1	scale	rbf
5	10	0.1	scale	rbf
6	10	0.1	auto	rbf
7	10	0.1	scale	rbf

The hyperparameters considered in the DTR model, as shown in Table 4, are criterion, max depth, max features, min sample leaf, and min sample split. The criterion hyperparameter determines the function used to measure the quality of a split in the decision tree, with options such as Friedman mean squared error (mse), squared error, and absolute error. Meanwhile, the max depth hyperparameter specifies the maximum depth of the decision tree, allowing for the control of model complexity and overfitting. Value 5 and 10 have been tested, allowing for the None option for the default version. Additionally, the max features’ hyperparameter limits the number of features considered at each node, aiding in the prevention of overfitting by reducing the model’s complexity. The considered values are None, where it sets max features to the square root of the total number of features, and log2 where it sets max features to the base-2 logarithm of the total number of features. Furthermore, the min samples leaf hyperparameter sets the minimum number of samples required to be at a leaf node, while the min samples split hyperparameter determines the minimum number of samples required to split an internal node. A range of integer values from 1 to 4, and values 2, 5, and 10, have been explored, respectively.

Table 4. Hyperparameters for each zone for DTR model.

Zone	Criterion	Max Depth	Max Features	Min Sample Leaf	Min Sample Split
1	squared error	10	None	4	5
2	Friedman MSE	None	None	4	10
3	squared error	10	None	4	2
4	Friedman MSE	10	None	4	10
5	squared error	10	None	4	2
6	squared error	10	None	4	10
7	absolute error	10	None	4	5

Table 4. Hyperparameters for each zone for DTR model.

Zone	Criterion	Max Depth	Max Features	Min Sample Leaf	Min Sample Split
1	squared error	10	None	4	5
2	Friedman MSE	None	None	4	10
3	squared error	10	None	4	2
4	Friedman MSE	10	None	4	10
5	squared error	10	None	4	2
6	squared error	10	None	4	10
7	absolute error	10	None	4	5

The hyperparameters considered in the RFR model, as shown in Table 5, are max features and estimators. The max features hyperparameter determines the maximum number of features to consider when looking for the best split at each node in the decision trees that make up the random forest. The considered values are None, where it sets max features to the square root of the total number of features, and log2 where it sets max features to the base-2 logarithm of the total number of features. The estimators’ hyperparameter specifies the number of decision trees to be included in the random forest ensemble. A range of values from 100 to 500 with increments of 100 has been explored.

Table 5. Hyperparameters for each zone for RFR model.

Zone	Max Features	Estimators
1	log2	500
2	log2	500
3	None	500
4	log2	500
5	None	500
6	None	500
7	None	500

Table 5. Hyperparameters for each zone for RFR model.

Zone	Max Features	Estimators
1	log2	500
2	log2	500
3	None	500
4	log2	500
5	None	500
6	None	500
7	None	500

The hyperparameters considered in the KNNR model, as shown in Table 6, are metric, neighbours, and weights. The metric hyperparameter was tested with both Euclidean and Manhattan distance metrics to measure the distance between data points in the feature space. For the neighbours hyperparameter, values of 3, 9, 27, and 81 were tested to determine the number of nearest neighbours to consider when making predictions for a new data point. Additionally, the weights hyperparameter was explored with both uniform and distance weighting schemes. When set to uniform, all neighboring points contribute equally to the prediction, while distance weighting gives more weight to closer neighbours, inversely proportional to their distance.

Table 6. Hyperparameters for each zone for KNNR model.

Zone	Metric	Neighbours	Weights
1	Euclidean	9	distance
2	Euclidean	9	distance
3	Euclidean	9	distance
4	Euclidean	9	distance
5	Manhattan	9	distance
6	Euclidean	9	distance
7	Euclidean	9	distance

Table 6. Hyperparameters for each zone for KNNR model.

Zone	Metric	Neighbours	Weights
1	Euclidean	9	distance
2	Euclidean	9	distance
3	Euclidean	9	distance
4	Euclidean	9	distance
5	Manhattan	9	distance
6	Euclidean	9	distance
7	Euclidean	9	distance

The hyperparameters considered in the KRR model, as shown in Table 7, are $\alpha$, degree, $\gamma$ and kernel. The $\alpha$ hyperparameter controls the regularization strength, and values of 0.1, 1, and 10 were tested to explore the impact of different levels of regularisation. For the degree hyperparameter, polynomial degrees of 2, 3, and 4 were investigated to assess the polynomial complexity of the model. The $\gamma$ hyperparameter, which influences the kernel’s behaviour, was tested with values of None, 0.1, and 1.0. A value of None represents auto-selection. The SVR choice of kernel, includes linear, polynomial (poly), radial basis function (rbf), and sigmoid.

Table 7. Hyperparameters for each zone for KRR model.

Zone	$\mathit{\alpha }$	Degree	$\mathit{\gamma }$	Kernel
1	0.1	2	0.1	rbf
2	0.1	4	0.1	poly
3	1	4	0.1	poly
4	0.1	4	0.1	poly
5	0.1	3	None	poly
6	0.1	4	0.1	poly
7	0.1	4	0.1	poly

Table 7. Hyperparameters for each zone for KRR model.

Zone	$\mathit{\alpha }$	Degree	$\mathit{\gamma }$	Kernel
1	0.1	2	0.1	rbf
2	0.1	4	0.1	poly
3	1	4	0.1	poly
4	0.1	4	0.1	poly
5	0.1	3	None	poly
6	0.1	4	0.1	poly
7	0.1	4	0.1	poly

The hyperparameters considered in the GB model, as shown in Table 8, are learning rate, max depth, and estimators. For the learning rate hyperparameter, values of 0.05, 0.1, and 0.2 were tested to assess the impact of different rates of learning. Lower learning rates require more trees in the ensemble but can lead to better generalisation, while higher learning rates may result in faster learning but could overfit the training data. The max depth hyperparameter, which controls the maximum depth of each tree in the ensemble, was tested with depths of 3, 4, and 5. Deeper trees can capture more complex interactions in the data but may also lead to overfitting. Additionally, the n estimators hyperparameter, determining the number of boosting stages or trees in the ensemble, was explored with values of 50, 100, and 200. Increasing the number of estimators can lead to a more expressive model, but it also increases computational cost and the risk of overfitting.

Table 8. Hyperparameters for each zone for GB model.

Zone	Learning Rate	Max Depth	Estimators
1	0.05	3	200
2	0.05	4	200
3	0.1	3	200
4	0.1	3	200
5	0.1	4	200
6	0.1	4	200
7	0.1	4	200

Table 8. Hyperparameters for each zone for GB model.

Zone	Learning Rate	Max Depth	Estimators
1	0.05	3	200
2	0.05	4	200
3	0.1	3	200
4	0.1	3	200
5	0.1	4	200
6	0.1	4	200
7	0.1	4	200

The ensemble model implemented is a VotingRegressor, which combines predictions from three different regression models: KNNR, SVR, and GB. This ensemble is cooperative in nature, leveraging the predictions from each base model and aggregating them to produce a final prediction. The VotingRegressor is directly available in the Python library Scikit-learn [42], enabling seamless integration and straightforward implementation of the ensemble approach. The hyperparameters considered in the ensemble, as shown in Table 9, include weights which were tested with all possible combinations of values 1 and 2 for each of the three models. These weights reflect the relative importance assigned to each base model in the VotingRegressor ensemble. In this context, a weight of 1 signifies equal importance given to each model, while a weight of 2 implies a higher emphasis placed on a particular model compared to others.

Table 9. Hyperparameters for each zone for KSVRGB model.

Zone	KNNR Weight	SVR Weight	GB Weight
1	2	1	1
2	1	1	2
3	1	2	2
4	2	1	2
5	1	1	2
6	1	1	2
7	1	1	2

Table 9. Hyperparameters for each zone for KSVRGB model.

Zone	KNNR Weight	SVR Weight	GB Weight
1	2	1	1
2	1	1	2
3	1	2	2
4	2	1	2
5	1	1	2
6	1	1	2
7	1	1	2

We evaluated the computing time required for predicting outcomes across the seven zones using each of the proposed ML models. As already mentioned, for each model, we conducted experiments over the course of one year, periodically retraining them to account for evolving data patterns. In our study, we conducted two experiments, labelled Exp1 and Exp2, in which we trained prediction models on the aforementioned temporal data. In the case of Exp1, we executed a total of 54 iterations (one per week) for each model and each region, training and validating the models on each prediction week. Throughout this process, we employed the GridSearch to identify the optimal hyperparameters in each iteration. Subsequently, in Exp2 we retrained the models on the same time interval, again with 54 iterations, this time fixing the hyperparameters to the initial values identified through only the first two training months as conducted in Exp1. This allowed us to assess the computational and qualitative impact of the chosen hyperparameters solution.

Table 10. Computing time for the seven zones with each ML model, considering hyperparameter tuning and fixed hyperparameters.

Zone	LR		SVR		DTR		RFR		KNNR		KRR		GB		KSVRGB
	Exp1 (s)	Exp2 (s)	Exp1 (s)	Exp2 (s)	Exp1 (s)	Exp2 (s)	Exp1 (s)	Exp2 (s)	Exp1 (s)	Exp2 (s)	Exp1 (s)	Exp2 (s)	Exp1 (s)	T2 (s)	Exp1 (s)	Exp2 (s)
1	1.6	$6.8\times {10}^{-2}$	2.9	$2.4\times {10}^{-2}$	209.2	$1.1\times {10}^{-1}$	575.0	2.7	2.2	$3.3\times {10}^{-3}$	19.2	$7.3\times {10}^{-2}$	1602.3	19.4	318.9	9.7
2	$4.0\times {10}^{-1}$	$1.7\times {10}^{-2}$	7.5	$1.6\times {10}^{-2}$	67.8	$4.7\times {10}^{-2}$	210.7	0.5	1.3	$3.8\times {10}^{-5}$	17.5	$1.2\times {10}^{-1}$	513.3	8.1	103.4	3.1
3	$2.0\times {10}^{-1}$	$1.2\times {10}^{-2}$	3.1	$1.2\times {10}^{-2}$	54.0	$2.8\times {10}^{-2}$	173.1	8.2	1.2	$2.0\times {10}^{-3}$	17.5	$1.2\times {10}^{-1}$	382.7	6.3	79.7	2.3
4	$4.0\times {10}^{-1}$	$1.6\times {10}^{-2}$	2.8	$1.3\times {10}^{-2}$	70.0	$3.6\times {10}^{-3}$	211.8	1.3	1.3	$1.3\times {10}^{-3}$	17.7	$1.2\times {10}^{-1}$	509.4	6.3	102.6	3.2
5	$1.0\times {10}^{-1}$	$5.1\times {10}^{-3}$	35.7	$2.3\times {10}^{-2}$	27.1	$1.5\times {10}^{-2}$	94.4	1.9	1.0	$1.3\times {10}^{-3}$	17.0	$1.2\times {10}^{-1}$	178.5	2.9	37.6	1.1
6	$1.0\times {10}^{-1}$	$3.6\times {10}^{-3}$	8.6	$2.2\times {10}^{-2}$	27.8	$1.4\times {10}^{-2}$	96.1	3.9	1.0	$9.8\times {10}^{-4}$	16.9	$1.2\times {10}^{-1}$	180.1	3.5	37.6	1.1
7	$2.0\times {10}^{-1}$	$6.9\times {10}^{-3}$	8.9	$1.5\times {10}^{-2}$	44.5	$3.8\times {10}^{-1}$	144.1	3.3	1.1	$2.3\times {10}^{-3}$	17.4	$1.2\times {10}^{-1}$	315.1	5.0	64.3	1.9

presents the computational times for each experiment, each zone, and each model. The times, expressed in seconds, denote the average training time over the 54 weeks. The results, as expected, reveal a significant reduction in computing time when utilising fixed hyperparameters (Exp2) compared to the exhaustive tuning process (Exp1). In fact in calculating the training times, we include the process of searching the hyperparameters using the exhaustive GridSearch approach, which consists of calculating the five-fold cross-validation (training and testing the model five times) for each possible combination of the parameters inside the search ranges shown in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. Despite the efficiency gains achieved by fixing hyperparameters,

Table 11. Percentage NRMSE Values for the seven zones with every ML model each solved tuning the hyperparameters and with fixed hyperparameters.

Zone	LR		SVR		DTR		RFR		KNNR		KRR		GB		KSVRGB
	Exp1 (%)	Exp2 (%)	Exp1 (%)	Exp2 (%)	Exp1 (%)	Exp2 (%)	Exp1 (%)	Exp2 (%)	Exp1 (%)	Exp2 (%)	Exp1 (%)	Exp2 (%)	Exp1 (%)	Exp2 (%)	Exp1 (%)	Exp2 (%)
1	4.4	4.4	4.4	5.3	7.1	7.1	4.8	4.8	4.4	4.4	2.7	2.7	4.4	4.4	3.9	4.0
2	3.9	4.5	4.3	4.4	6.6	6.6	4.5	4.5	5.0	5.0	3.4	3.5	4.3	4.3	4.2	4.2
3	3.9	4.9	4.4	4.7	6.0	6.0	4.5	4.6	4.5	4.5	2.6	2.6	4.0	4.0	3.8	3.8
4	3.9	4.5	4.2	4.5	6.1	6.4	4.2	4.3	4.0	4.0	2.5	2.6	4.0	4.0	3.5	3.5
5	4.6	5.0	4.9	5.0	5.8	5.8	4.3	4.3	5.6	6.0	3.5	3.5	3.9	3.9	4.4	4.4
6	4.8	5.1	4.6	4.7	6.3	6.3	4.8	4.8	5.5	5.5	3.3	3.3	4.2	4.3	4.3	4.3
7	4.6	5.0	4.3	4.9	6.0	6.0	4.4	4.4	5.1	5.2	3.0	3.0	4.0	4.0	4.0	4.0
Average	4.3	4.8	4.4	4.8	6.3	6.3	4.5	4.5	4.9	4.9	3.0	3.0	4.1	4.1	4.0	4.0
$\sigma$	0.4	0.3	0.2	0.3	0.4	0.4	0.2	0.2	0.6	0.7	0.4	0.4	0.2	0.2	0.3	0.3

illustrates that the predictive performance, as quantified by the NRMSE percentage, remains relatively stable. Again, with the two scenarios Exp1, where hyperparameter tuning was performed at every retraining step, and Exp2, where the initial hyperparameters found were fixed for the remaining iterations. For each row and for each of the two experiments, the best value is highlighted in bold. Additionally, there are two extra final rows representing the average performance $\mu$ across different zones of the models and the standard deviation $\sigma$ of the performances is computed as $\sigma =\sqrt{\frac{1}{N}{\sum }_{i=1}^7{(NMRS{E}_i-\mu )}^2}$. This finding suggests that the performance degradation resulting from using fixed hyperparameters is generally acceptable across the majority of zones and ML models considered. Additionally, Table 11 reveals that Kernel Ridge Regression consistently outperformed other methods, yielding the lowest NRMSE values across all zones for Exp1 and in all cases for Exp2. This suggests that KRR effectively captures the underlying patterns and complexities of each market region, resulting in more accurate predictions. Furthermore, it is noteworthy that although the standard deviation is not the absolute lowest, it still maintains a very reasonable value of 0.4, indicating a consistent performance. These findings underscore the effectiveness of KRR as a robust modelling technique for electricity market forecasting, demonstrating its potential to enhance decision-making processes and optimise resource allocation strategies.

As previously mentioned, the use of production data with a one-hour lag as features constrains the temporal horizon to one hour. To extend the temporal horizon and demonstrate the utility of this feature, we introduce a third experiment (Exp3), wherein the same temporal data—specifically the 54 weeks of training data are utilised without the production-related features, i.e., the power produced at the previous hour. Not using the power at the previous hour as an input feature allows us to increase the forecast horizon to 24 h. Hyperparameters for all weeks are set to those obtained during the first two months of training, similar to Exp2.

Table 12. Percentage NRMSE Values for the seven zones with every ML model each solved with fixed hyperparameters without power data lagging.

Zone	LR	SVR	DTR	RFR	KNNR	KRR	GB	KSVRGB
	Exp3 (%)	Exp3 (%)	Exp3 (%)	Exp3 (%)	Exp3 (%)	Exp3 (%)	Exp3 (%)	Exp3 (%)
1	6.1	7.3	7.6	4.9	5.6	5.0	5.5	5.1
2	6.0	5.3	6.9	4.7	5.2	4.9	5.4	4.9
3	7.0	6.2	7.8	5.3	5.8	5.5	5.9	5.5
4	6.2	5.0	6.6	4.5	4.9	4.5	4.9	4.6
5	6.8	6.6	7.1	5.4	6.0	5.4	5.8	5.4
6	6.9	6.7	7.5	5.5	5.8	5.8	6.0	5.8
7	6.8	7.2	7.3	5.1	5.2	5.6	5.6	5.2
Average	6.5	6.3	7.3	5.1	5.5	5.2	5.6	5.2
$\sigma$	0.4	0.9	0.4	0.4	0.4	0.4	0.4	0.4

presents the predictive performance of Exp3 using the NRMSE percentage, where the best values are highlighted in bold. Without power features, the average error increases from 3% to 5.1%, while maintaining a consistent standard deviation of 0.4. This also alters the nature of the problem, with the most performing model in this case being, albeit marginally, the RFR rather than the KRR.

In Figure 5 and Figure 6 the performance results in terms of percentage NRMSE for each of the 54 weeks considered in every zone are illustrated. Figure 5 highlights the outcomes achieved with the KRR model, which exhibited the highest performance, for Experiment Exp2. Meanwhile, Figure 6 corresponds to Experiment Exp3, employing the RFR model. The main purpose of Figure 5 and Figure 6 relies on appreciating the behaviour of weekly test error during an entire year, highlighting a known seasonality effect (errors are lower during Spring, from March to April, and higher at the beginning of fall in September), and letting to appreciate the minimum and maximum weekly errors, as well as the average error (which is reported in Table 11 and Table 12), for all zones in the case of using the power as input, Figure 5, or not using the power as input, Figure 6.

Figure 7 and Figure 8 present an example of performance comparison for Zone 1, Northern Italy, which is considered the most complex and representative region. Each figure illustrates the predictive performance over a sample day of a 7-day forecast. Figure 7 depicts the resolution performance without lagging, meaning neither production data nor meteorological data with lagging are included, showcasing the predictive curves for each ML model alongside the actual realisation for comparison. The average NRMSE is 6.0%. Similar results are obtained for other zones.

In addition to evaluating the predictive performance for the upcoming week, we also assessed the degradation of prediction accuracy over a longer forecasting horizon. Using the same machine learning models, we extended the forecast period to three months, corresponding to nearly 13 weeks, without retraining. This experiment allowed us to investigate the degradation of the predictions with time as the models rely on an older training set with respect to the current data to be predicted. The results, depicted in Figure 9, showcase the percentage NRMSE for each ML model across each predicted week in an example where the training period spans 2 months, or more precisely, 60 days starting from 1 February 2022. This analysis demonstrates that while there is a gradual increase in prediction error over time, the degradation remains within acceptable bounds. Specifically, it suggests that it may not be necessary to retrain the models on a weekly basis. Instead, retraining them on a monthly basis appears to be sufficient to maintain satisfactory prediction accuracy. This finding offers practical insights into the frequency of model retraining required for effective long-term forecasting in electricity markets.

5. Conclusions

The proposed resolution approach has proven to be valid and efficient in addressing the challenge of predicting electrical production from photovoltaic installations at the regional level. The decision to use geolocated data at the centroids of provinces within electricity market zones has been pivotal, enabling accurate predictions even in the absence of precise information about individual installations and their locations. Among the models tested, Kernel Ridge Regression and Random Forest Regression emerged as the most effective for our specific application, achieving percentage NRMSE values of 3% in the case of lagged power used as input, corresponding to 1-h time horizon, and 5% in the case of no lagged power used as input, corresponding to 24 h time horizon.

Hyperparameter tuning played a crucial role in enhancing model performance, and fixing them across the test sets allowed us to significantly reduce resolution times without significantly compromising prediction accuracy. Once optimised, the fixed hyperparameters allowed for quick and reliable solutions.

Additionally, it has been demonstrated that once the model is trained, it can be used to obtain accurate predictions for extended periods without the need for frequent retraining. Results indicate that the model remains useful for obtaining accurate predictions for at least a month without further updates.

It is important to acknowledge that, like any other Machine Learning-based method, our approach is not devoid of prediction errors, albeit these may be minor. Furthermore, another limitation of our method is the limited time horizon, especially when using the entire set of proposed features. Additionally, the quality of available data presents another constraint. However, it is noteworthy that despite such limitations, the results remain promising. Particularly, we have observed that even without including the previous hour’s production, our model continues to provide accurately informed forecasts, indicating the potential of this approach in the context of electrical production from photovoltaic forecasting.

Overall, this work demonstrates that the use of innovative machine learning-based approaches and the adoption of appropriate data management strategies can overcome the challenges associated with predicting electrical production from photovoltaic installations at the regional level, thereby contributing to more efficient and reliable management of renewable energy resources.

In conclusion, there are several promising avenues for future research. For example, extending our approach to encompass additional renewable energy sources beyond electricity production, such as solar or wind energy, could provide a more holistic understanding of sustainable energy generation. Furthermore, the exploration of alternative sets of features may yield insights into previously unconsidered factors that could impact energy production and market dynamics.