1. Introduction
The environmental impact caused by the consumption of fossil fuels to generate heat and electricity has already reached a critical level, putting the world at risk of serious climate change. Industry and electricity generation are the sectors with the largest energy consumption and, as a consequence, with the largest carbon dioxide (CO
2) emissions as well [
1]. Among the different industrial sectors, the non-energy-intensive manufacturing sector is considered the largest consumer of energy worldwide [
2]. This sector comprises industries like pharmaceuticals, pulp and paper, textiles, food processing and beverages, paint and coatings, etc. Within these industries, there is a significant number of processes whose operating temperatures lie in the interval 40–260 °C [
3], which is suitable for well-developed and commercial solar thermal technologies such as flat plate collector (FPC), evacuated-tube collector (ETC), and parabolic trough collector (PTC) [
4].
In general, it has been estimated that 74% of the global consumption of energy by industry is heat, from which 30% corresponds to low-temperature heat (<150 °C), 22% to medium-temperature heat (150–400 °C), and 48% to high-temperature heat (>400 °C) [
5]. Provided that FPC and ETC collectors are capable of delivering low-temperature heat, and PTC collector delivers medium-temperature heat [
3,
6], there is an ideal scenario to promote the use of solar heat for industrial processes (SHIP), especially in the non-energy-intensive manufacturing sector, where the industry of beer production has strategic importance, given the fact that it is the most consumed alcoholic drink in the world [
7].
In a brewery, the demand for heat can exceed 70% of the total energy consumed [
8]. A significant portion of this heat is spent during the mashing and wort boiling processes [
7,
8,
9]. Mashing needs hot water between 71–82 °C [
7], temperatures easily attainable with a field of FPC or ETC collectors. On the other hand, the boiling of the wort occurs at around 100 °C [
9], thus it could be powered with steam of higher temperature, achievable with an arrangement of PTC collectors. Hot water and steam are also needed for other operations, such as washing, cleaning, and sterilization. Eiholzer et al. [
10] have made a detailed analysis of the amounts of heat and temperatures required by the different operations of a medium-sized brewery.
Just like for any other industrial process, the integration of solar heat into a brewing process can be performed at the supply level or process level. Supply-level integration is usually easier because the solar heat is supplied to the central boiler for hot water or steam production, providing more flexibility for the set temperature of the solar thermal system [
11]. In addition to the field of solar collectors, the integration project will also need a thermal energy storage system (TES) because solar radiation is intermittent by nature. The most straightforward way to store thermal energy is as sensible heat; however, it can also be stored as latent heat or thermochemically. These last two offer the advantage of considerably higher stored energy density. However, according to Koçak et al. [
2], only sensible thermal energy storage (STES) offers cost-effective solutions for medium- to high-temperature industrial applications. Nonetheless, it has the disadvantage of requiring large volumes to accumulate a given amount of heat [
2,
12]. Yet, expenses can be reduced if low-cost storage materials are employed.
The integration of solar heat at the supply level to feed the processes requiring hot water at 80 °C in a brewery located in Scotland, UK, has been studied by Eiholzer et al. [
10]. They analyzed the replacement of the central boiler by a field of either FPC or ETC collectors, a stratified hot water storage tank, and an auxiliary heater. Solar fractions of 6.8% and 7.7% were obtained for each collector type. They argued that without government restrictions on the solar plant capacity, the solar fraction with ETC collectors could rise to 13.6%. Mauthner et al. [
13] investigated the technical feasibility of integrating solar heat for the processes of mashing (58–78 °C), can pasteurizing (63–65 °C), and malt drying (35–55 °C) in three breweries located in Goess, Austria, Valencia, Spain, and Vialonga, Portugal. The integration was performed at the process level with FPC collectors and STES tanks, using water as heat transfer fluid (HTF) and storage material. Simulations produced solar fractions of 30%, 45%, and 20% for each process, correspondingly.
The number of studies dealing with the incorporation of solar heat into a brewing process is limited; however, additional works can be found on the use of solar heat in other food processing and beverages industries. At supply level integration, Silva et al. [
14] achieved an average annual solar fraction of 34.9% in the production of steam at 120 °C for a tomato preservation factory in Andalucía, Spain, making use of stratified STES and PTC collectors. Bolognese et al. [
15] obtained 23% of the solar fraction by combining PTC collectors with an STES tank to supply pressurized hot water at 135 °C for the drying process of a pasta factory in Molina, Italy. Biencinto et al. [
16] modeled the heat demand at 85 °C to pasteurize milk, employing PTC collectors and latent thermal energy storage (LTES) at two locations, Graz, Austria, and Almería, Spain, obtaining annual solar fractions of 27% and 52%, respectively.
It is evident from the works reviewed that both schemes of solar heat integration in the food processing and beverages industries can lead to important energy savings and reductions in CO
2 emissions as a consequence. Particularly for breweries, the use of FPC or ETC collectors to generate hot water has been addressed successfully; however, the simultaneous production of hot water and steam through a hybrid system composed of two types of collectors has not been conducted despite the potential benefits that it could convey, as demonstrated by Tian et al. [
17], who modeled a hybrid solar field made of FPC and PTC collectors for district heating. Therefore, it is the objective of this work to evaluate the capability of a hybrid solar plant composed of FPC and PTC collectors, stratified STES tanks, an economizer, and a steam generator to meet the hot water and steam requirements of the medium-sized brewery analyzed by Eiholzer et al. [
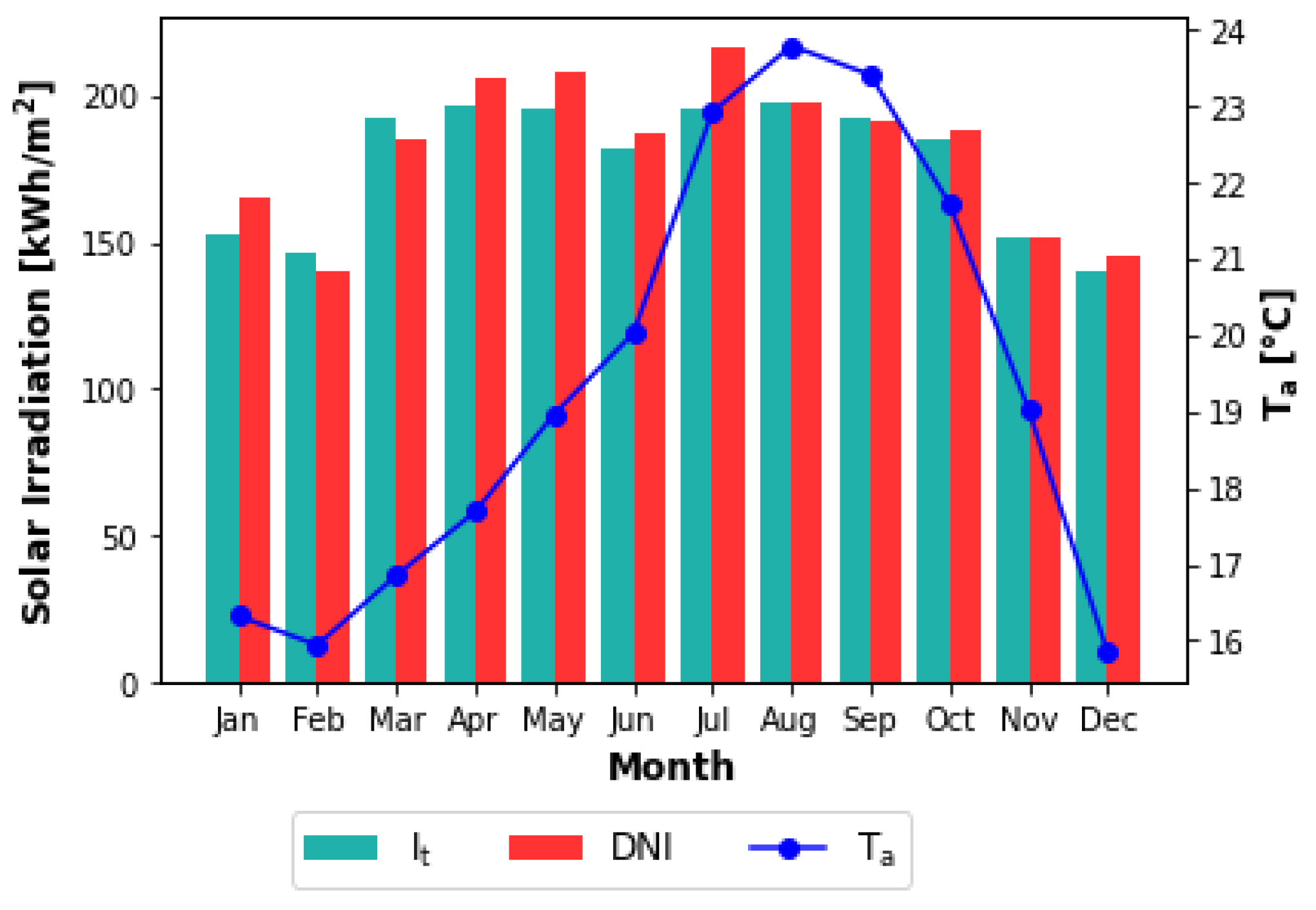
10], but at the weather conditions of Ensenada, Mexico, provided that this city hosts a flourishing brewing industry and experiences high levels of solar insolation. Stratified tanks were used for sensible heat storage as they provide a well-developed and practical solution in this type of industry, as well as a straightforward approach in terms of numerical implementation.
2. Heat Demand and Proposed Solar Plant
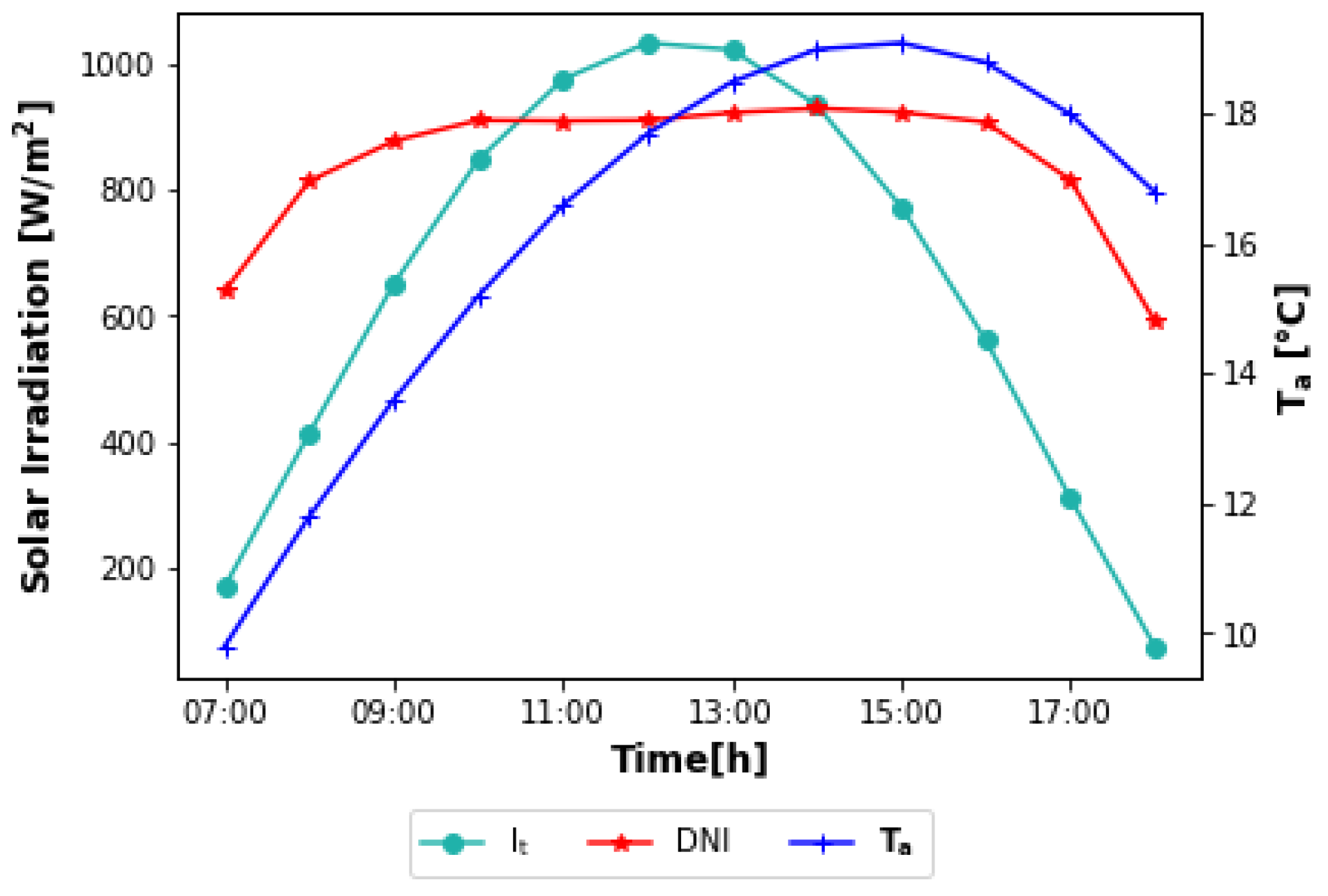
The description of each step of the brewing process selected for this study and the corresponding amounts of heat, mass flow rates, and temperatures required for each stream have already been given by Eiholzer et al. [
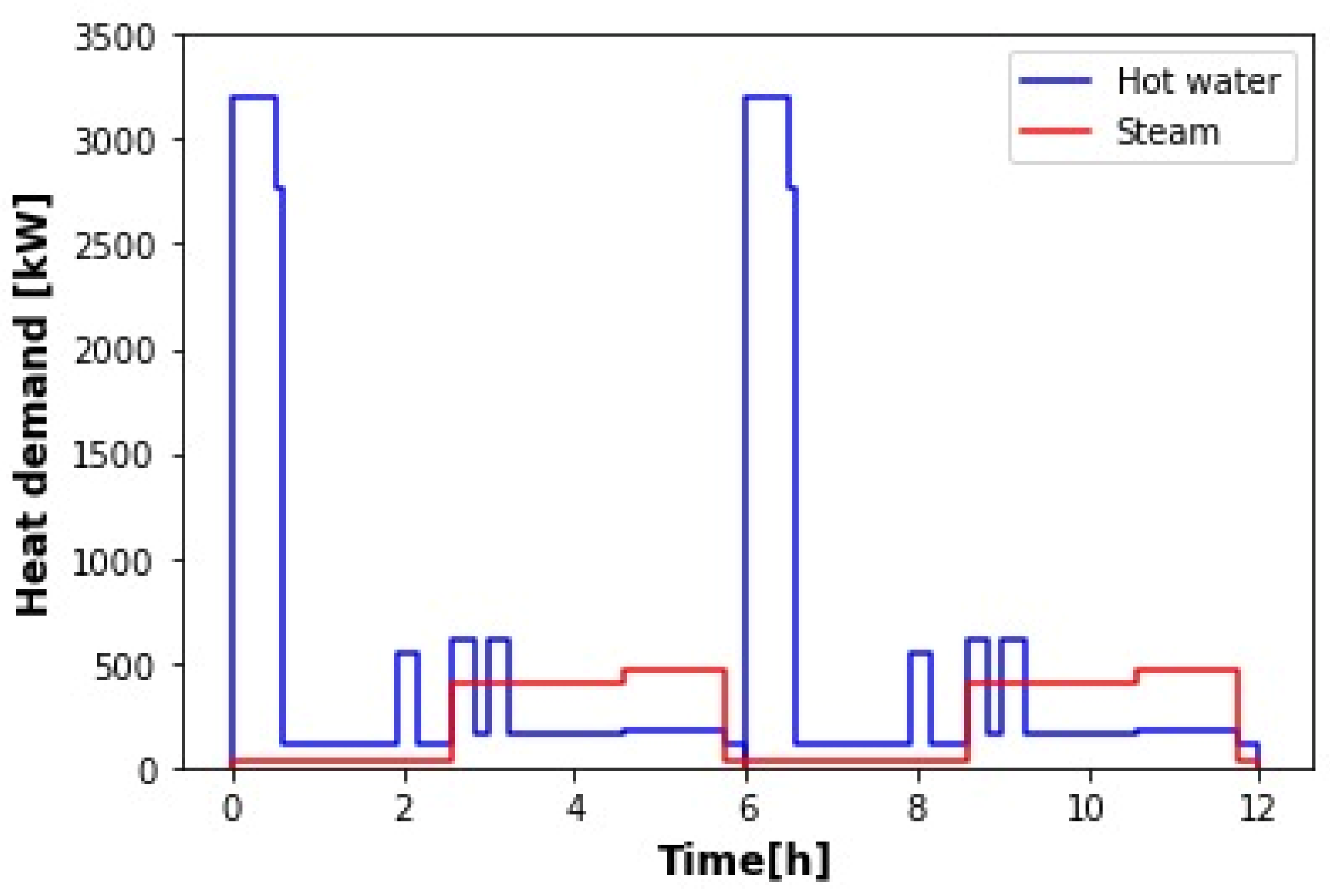
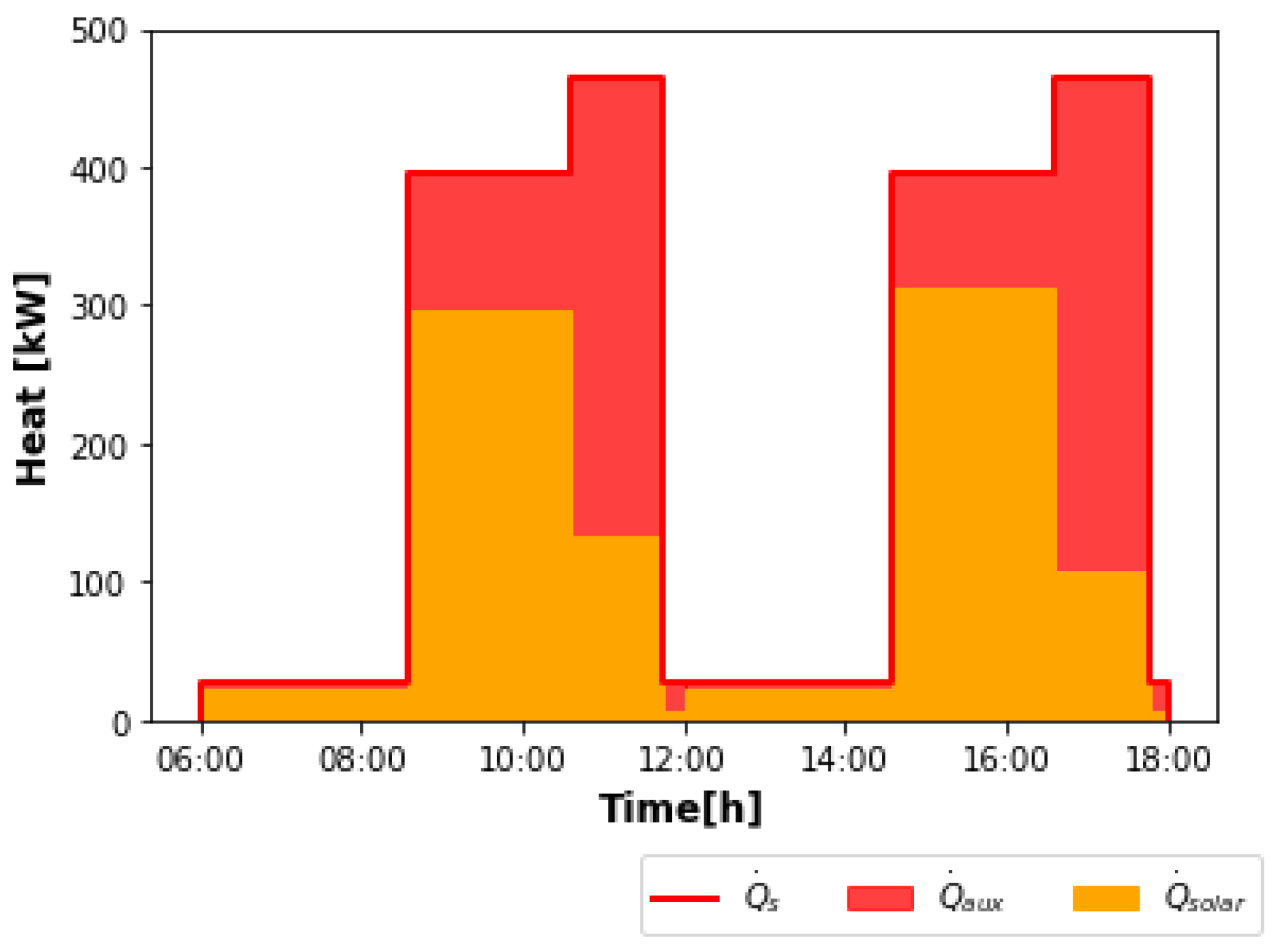
10]. The brewery works 300 days a year and processes four batches per day. Each batch is completed in 6 h. Considering only the operations that require heating (mashing, wort preheating and boiling, cleaning, and keg washing), the heat demand consists then of the production of hot water at 1 bar and 80 °C and saturated steam at 6 bar and 160 °C. The authors only examined the supply of hot water with solar energy. For steam generation, flue gas was used. As the purpose of this work is to produce both hot water and steam with solar energy, then, from the data provided by the authors, the curves of heat demand were determined. They are shown in
Figure 1. Only two batches were considered (diurnal operation), starting at 6 a.m. The times and mass flow rates (
) used to calculate the heat demands (
) per batch are listed in
Table 1.
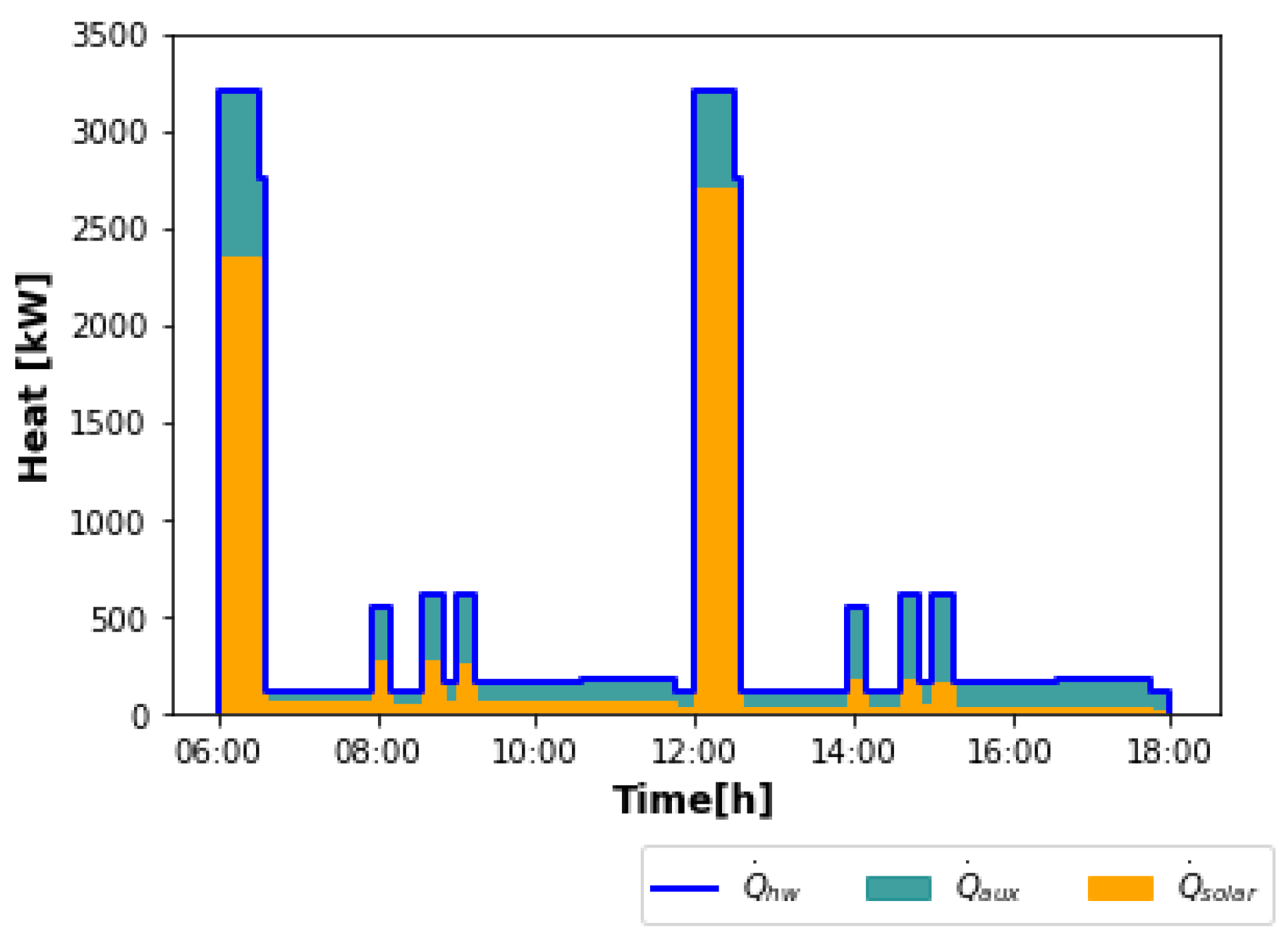
It can be observed in
Figure 1 that the hot water demand presents significant variations over time, with the highest peaks during mashing. The other peaks correspond to simultaneous cleaning and keg washing. Throughout the whole time period, hot water is also needed for cleaning. The total heat requirement for hot water production
for the two batches is 5837.5 kWh. Steam is also constantly demanded for keg washing. As in this work, the aim is to perform the operations of wort preheating and boiling with saturated steam instead of flue gas, the peaks shown in
Figure 1 correspond to these two processes. The total amount of heat needed for steam production
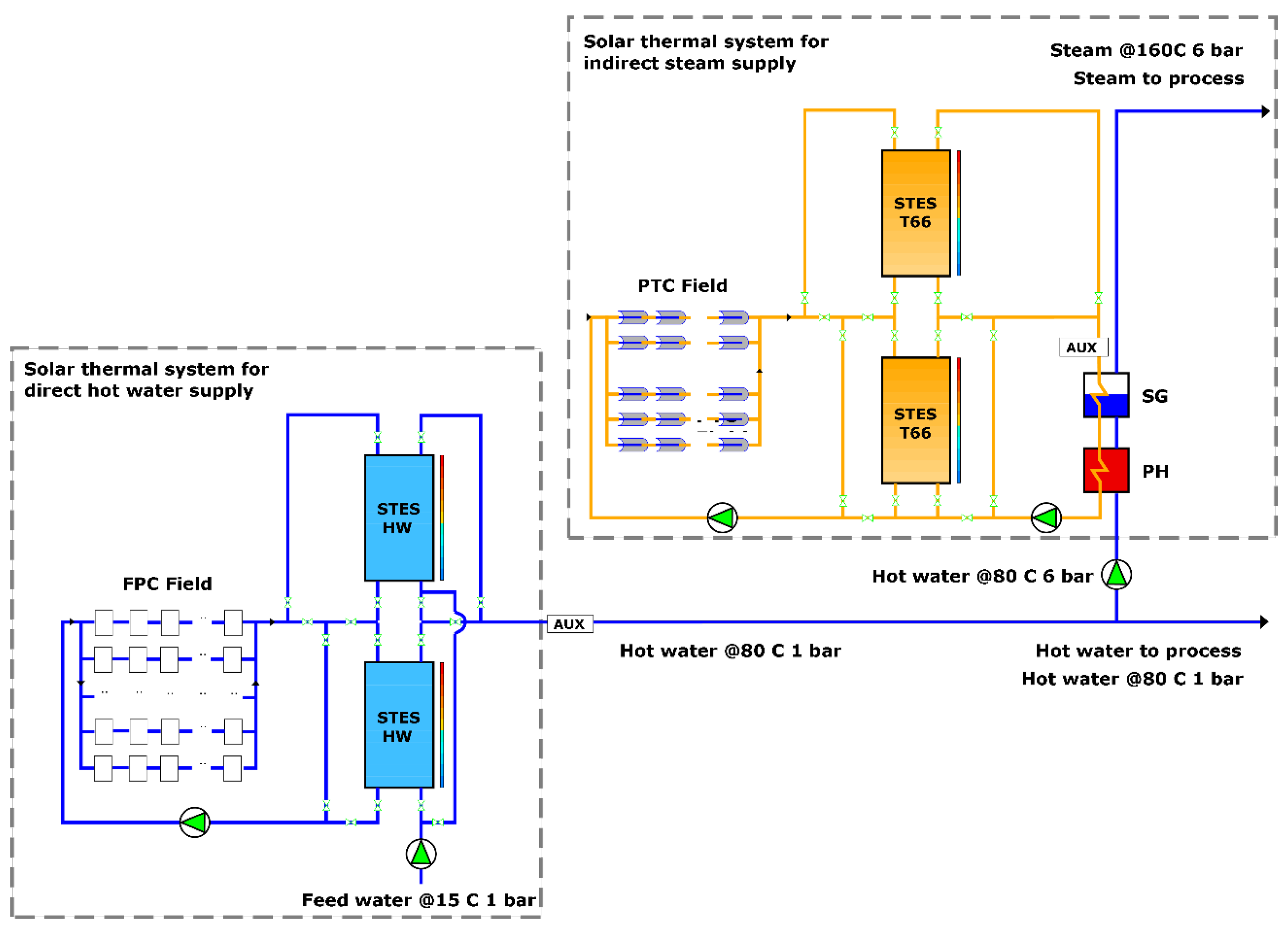
for the two batches is 2817.9 kWh. The solar plant proposed to meet the total heat demand is schematized in
Figure 2.
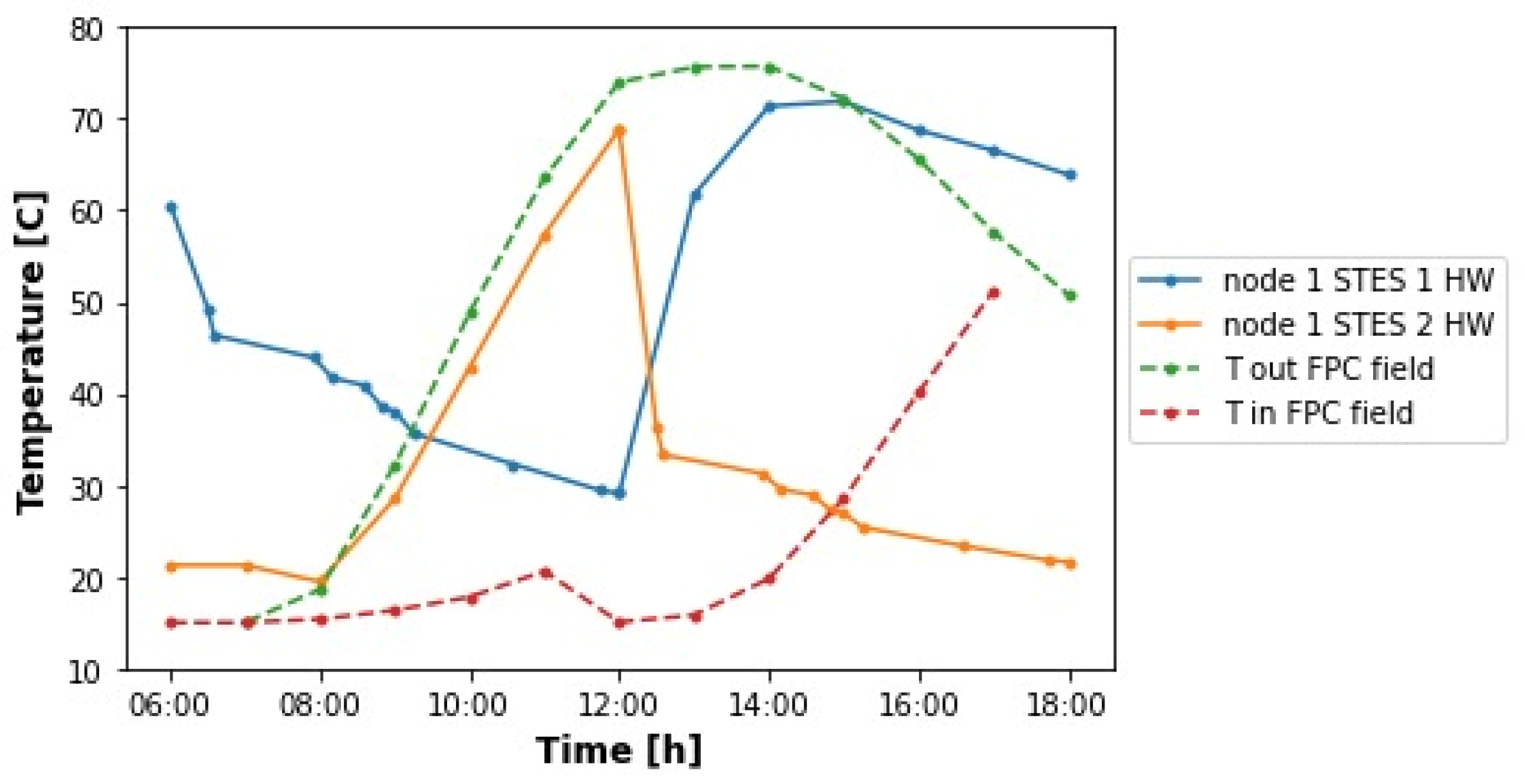
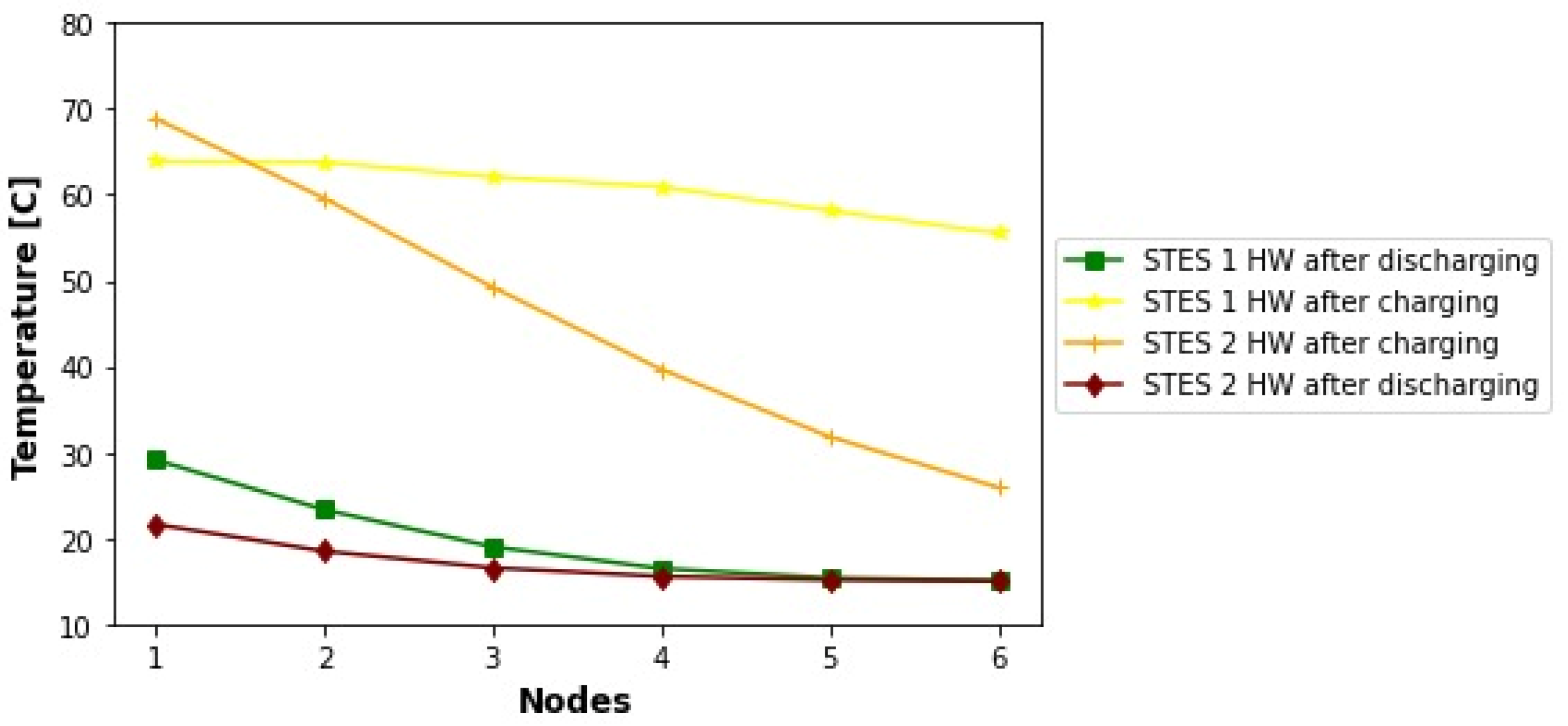
The plant is composed of two subsystems: one for hot water and one for saturated steam. The first subsystem also provides the water that is converted to steam. A total of 250 FPC collectors arranged in five parallel lines, each with ten sets of five collectors in series, two stratified STES tanks, two pumps, one auxiliary heating system, and a series of valves comprise the first subsystem. Water is employed as HTF and storage material. For the second subsystem, eight parallel lines of five PTC collectors in series, two stratified STES tanks, three pumps, one economizer (feedwater preheater, PH), one steam generator (SG), one auxiliary heating system, and a group of valves are used. Therminol 66
® (T66) is the HTF and storage material in this case. The suggestion of Silva et al. [
14] to use an economizer before the steam generator was implemented. The auxiliary heating systems help to reach the set temperatures when the solar plant cannot make it due to the inherent intermittency of solar radiation.
The FPC collector selected for this study is the SunEarth TR40 [
18]. The chosen PTC collector is the NEP PolyTrough 1800 [
19]. Their technical specifications are given in
Table 2. A shell-and-tube heat exchanger (HX) with one shell pass and two tube passes was used as a steam generator. Hot T66 oil flows inside the tubes while liquid saturated water at 6 bar and 160 °C is on the shell side. A plate-type, liquid-to-liquid HX in counterflow was employed to increase the feedwater temperature to saturation conditions. The design of both HXs was completed with the ε-NTU (effectiveness–number of transfer units) method [
20]. The analysis of the auxiliary heating systems, pumps, and piping systems was skipped for the moment.
5. Discussion
The annual solar heat coverages obtained in this work lay within the interval of solar fractions reported in the literature for projects involving food processing and beverages industries. In
Table 8, there is a comparison between the results attained here and those of the works mentioned in the literature review. In addition, since this work aimed to model the heat supply of the brewery analyzed by Eiholzer et al. [
10] at conditions of higher solar insolation, a more complete comparison is described in
Table 9. Provided that the size of the solar plant studied here is nearly three times larger, the simulation of meeting both heat demands (hot water and steam) produced nearly a fourfold improvement in fossil fuel savings and CO
2 emissions reductions.
From an economic standpoint, the UK renewable heat incentive (RHI) program, which offers 0.108 USD per kWh saved, allowed a yearly return of nearly 33,274 USD for the project of Eiholzer et al. [
10]. In addition, the fact that the natural gas price in the UK can be nearly twice that of Mexico [
36] permitted them to reach a short payback period of 6.5 years. On the other hand, for the project proposed here, the application of the 30% tax-deduction benefit of Mexico (mentioned in
Section 3.6) allowed a reduction in the installation cost to approximately 469,604 USD and a payback period of 15 years.
An additional comparison in terms of the LCOH between the results obtained here and other similar projects, including that of Eiholzer et al. [
10], is provided in
Table 10. Data from
Table 7 were used for the calculations. The influence of factors such as process temperature levels, demand continuity, project scale, solar insolation levels, and geographical location can be straightforwardly appreciated. Among all, it seems that the levels of solar insolation determined by the geographical location played the most crucial role in determining the viability of the solar plant. The timing of the study also had an important effect since the prices of solar technologies have decreased by 35% over the last decade [
33]. The competitive LCOH value of 0.032 USD/kWh achieved here demonstrates that the city of Ensenada, Mexico, can be seen as an ideal location to implement solar heat for industrial processes. Nonetheless, and despite the government incentives, the relatively low natural gas prices found in the region may pose an obstacle to a swift transition towards the use of renewable solar heat in industry.