Ensemble Machine Learning Approaches for Prediction of Türkiye’s Energy Demand
Abstract
:1. Introduction
2. Literature Review
2.1. Review of Energy Demand Forecasting in the World
2.2. Energy Demand Forecasting in Türkiye
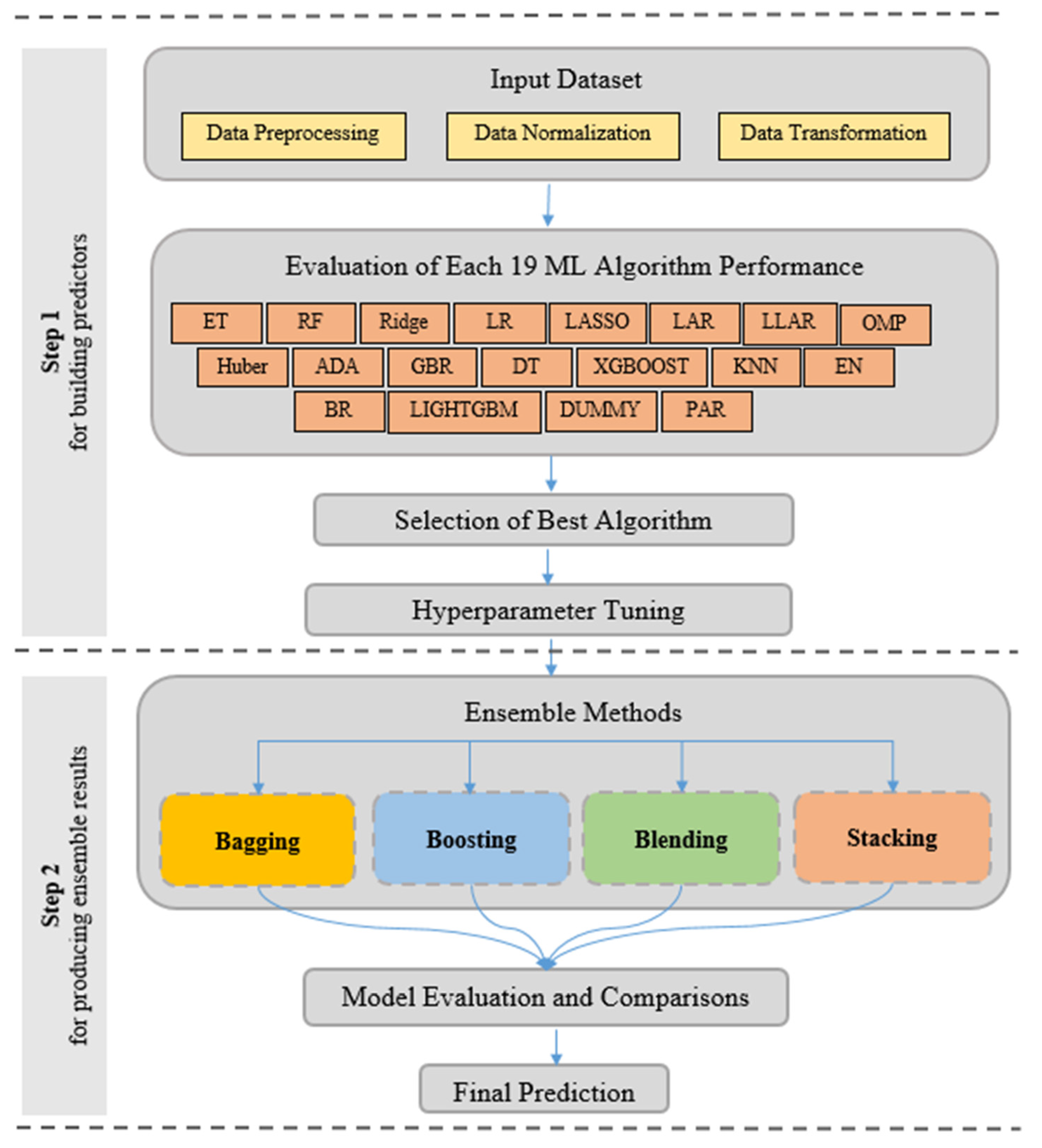
3. Materials and Methods
3.1. ML Algorithms
- Light Gradient Boosting Machine (LightGBM) [71]
- XGBoost [72]
- Extra Trees Regression [73]
- Passive Aggressive Regressor (PAR) [74]
- Elastic Net [75]
- Least Angle Regression (LARS) [76]
- Lasso Least Angle Regression [76]
- Orthogonal Matching Pursuit (OMP) [77]
- Random Forest Regressor [78]
- Gradient Boosting Regressor [32]
- AdaBoost Regressor [79]
- Linear Regression [80]
- Lasso Regression [81]
- K-Neighbors Regressor [82]
- Bayesian Ridge Regression [83]
- Decision Tree Regressor [84]
- Ridge Regression [85]
- Huber Regressor [86]
- Dummy Regressor
3.2. Structure of the Proposed Methods
3.2.1. k-Fold Cross-Validation
3.2.2. Model Hyperparameters Tuning
3.2.3. Performance Metrics
3.3. Data Collection
4. Results and Discussion
4.1. Implementation Setup
4.2. Feature Selection
4.3. Performance Evaluation
5. Conclusions
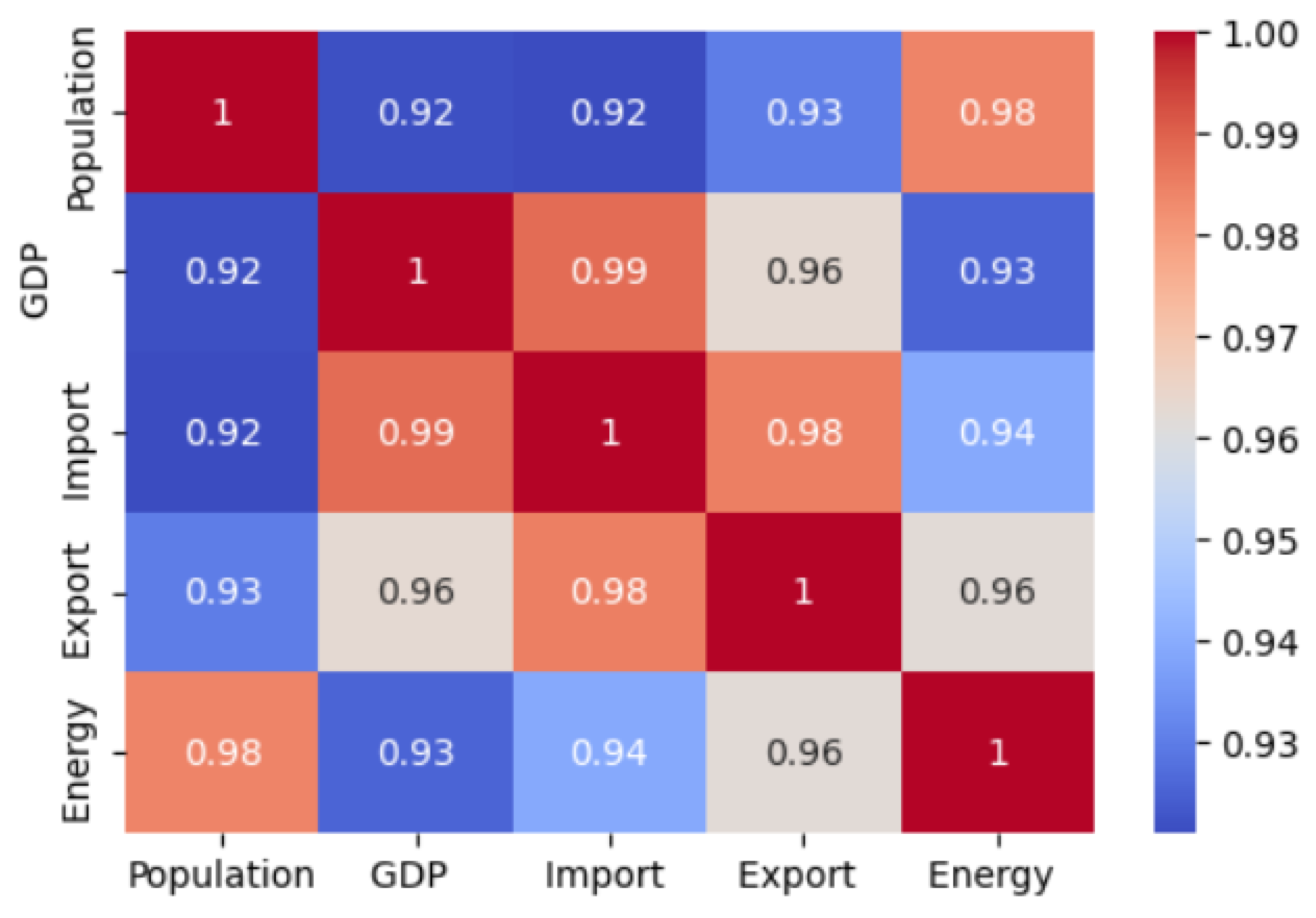
- The GDP, population, import, export, and energy data taken between 1979 and 2021 were used and it is observed that there is a strong correlation among them.
- Five statistical metrics are discussed to evaluate the performance of the algorithms in the forecast.
- A total of 19 machine learning algorithms were constructed and analyzed to select models for diverse ensemble combinations.
- Considering all metrics collectively, the stacking ensemble model utilizing Ridge Regressor as a meta-learner outperforms single ML algorithms as well as other bagging, boosting, and blending models.
- The predicted values reveal that the stacking ensemble model has delivered highly satisfactory outcomes in comparison to the actual energy demand outputs.
- These ensemble models can readily be adapted and recommended for future energy demand forecasts in other countries. Notably, the stacking ensemble model demonstrates statistically superior results compared to other models, making it a more suitable choice for accurate forecasting.
Funding
Data Availability Statement
Conflicts of Interest
References
- World Bank Data World Development Indicators. Available online: https://www.worldbank.org/en/country/turkey/overview (accessed on 15 June 2023).
- European Commission Eurostat. EU Energy and Climate Reports. 2023. Available online: https://commission.europa.eu/ (accessed on 4 May 2023).
- Republic of Türkiye, Ministry of Foreign Affairs. Türkiye’s International Energy Strategy. Available online: https://www.mfa.gov.tr/turkeys-energy-strategy.en.mfa (accessed on 18 June 2023).
- United Nations. Available online: https://sdgs.un.org/goals (accessed on 9 April 2023).
- Kong, K.G.H.; How, B.S.; Teng, S.Y.; Leong, W.D.; Foo, D.C.; Tan, R.R.; Sunarso, J. Towards data-driven process integration for renewable energy planning. Curr. Opin. Chem. Eng. 2021, 31, 100665. [Google Scholar] [CrossRef]
- Singh, S.; Bansal, P.; Hosen, M.; Bansal, S.K. Forecasting annual natural gas consumption in USA: Application of machine learning techniques-ANN and SVM. Resour. Policy 2023, 80, 103159. [Google Scholar] [CrossRef]
- Sözen, A. Future projection of the energy dependency of Turkey using artificial neural network. Energy Policy 2009, 37, 4827–4833. [Google Scholar] [CrossRef]
- Panklib, K.; Prakasvudhisarn, C.; Khummongkol, D. Electricity consumption forecasting in Thailand using an artificial neural network and multiple linear regression. Energy Sources Part B Econ. Plan. Policy 2005, 10, 427–434. [Google Scholar] [CrossRef]
- Murat, Y.S.; Ceylan, H. Use of artificial neural networks for transport energy demand modeling. Energy Policy 2006, 34, 3165–3172. [Google Scholar] [CrossRef]
- Sahraei, M.A.; Çodur, M.K. Prediction of transportation energy demand by novel hybrid meta-heuristic ANN. Energy 2022, 249, 123735. [Google Scholar] [CrossRef]
- Çodur, M.Y.; Ünal, A. An estimation of transport energy demand in Turkey via artificial neural networks. Promet-Traffic Transp. 2019, 31, 151–161. [Google Scholar] [CrossRef]
- Ferrero Bermejo, J.; Gómez Fernández, J.F.; Olivencia Polo, F.; Crespo Márquez, A. A review of the use of artificial neural network models for energy and reliability prediction. A study of the solar PV, hydraulic and wind energy sources. Appl. Sci. 2019, 9, 1844. [Google Scholar] [CrossRef]
- Kaya, T.; Kahraman, C. Multicriteria decision making in energy planning using a modified fuzzy TOPSIS methodology. Expert Syst. Appl. 2011, 38, 6577–6585. [Google Scholar] [CrossRef]
- Azadeh, A.; Asadzadeh, S.M.; Ghanbari, A. An adaptive network-based fuzzy inference system for short-term natural gas demand estimation: Uncertain and complex environments. Energy Policy 2010, 38, 1529–1536. [Google Scholar] [CrossRef]
- Guevara, E.; Babonneau, F.; Homem-de-Mello, T.; Moret, S. A machine learning and distributionally robust optimization framework for strategic energy planning under uncertainty. Appl. Energy 2020, 271, 115005. [Google Scholar] [CrossRef]
- Erdogdu, E. Electricity demand analysis using cointegration and ARIMA modelling: A case study of Turkey. Energy Policy 2007, 35, 1129–1146. [Google Scholar] [CrossRef]
- Ünler, A. Improvement of energy demand forecasts using swarm intelligence: The case of Turkey with projections to 2025. Energy Policy 2008, 36, 1937–1944. [Google Scholar] [CrossRef]
- Hamzaçebi, C. Forecasting of Turkey’s net electricity energy consumption on sectoral bases. Energy Policy 2007, 35, 2009–2016. [Google Scholar] [CrossRef]
- Kavaklioglu, K. Modeling and prediction of Turkey’s electricity consumption using Support Vector Regression. Appl. Energy 2011, 88, 368–375. [Google Scholar] [CrossRef]
- Hotunoglu, H.; Karakaya, E. Forecasting Turkey’s Energy Demand Using Artificial Neural Networks: Three Scenario Applications. Ege Acad. Rev. 2011, 11, 87–94. [Google Scholar]
- Utgikar, V.P.; Scott, J.P. Energy forecasting: Predictions, reality and analysis of causes of error. Energy Policy 2006, 34, 3087–3092. [Google Scholar] [CrossRef]
- El-Telbany, M.; El-Karmi, F. Short-term forecasting of Jordanian electricity demand using particle swarm optimization. Electr. Power Syst. Res. 2008, 78, 425–433. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, C.; Qu, S.; Chen, X. An explainable artificial intelligence approach for financial distress prediction. Inf. Process. Manag. 2022, 59, 102988. [Google Scholar] [CrossRef]
- Hewage, P.; Trovati, M.; Pereira, E.; Behera, A. Deep learning-based effective fine-grained weather forecasting model. Pattern Anal. Appl. 2021, 24, 343–366. [Google Scholar] [CrossRef]
- Suganthi, L.; Samuel, A.A. Energy models for demand forecasting—A review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Bao, Y.; Hilary, G.; Ke, B. Artificial intelligence and fraud detection. Innov. Technol. Interface Financ. Oper. 2022, 1, 223–247. [Google Scholar]
- Mohammed, A.; Kora, R. A comprehensive review on ensemble deep learning: Opportunities and challenges. J. King Saud Univ. -Comput. Inf. Sci. 2023, 35, 757–774. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Hategan, S.M.; Stefu, N.; Paulescu, M. An Ensemble Approach for Intra-Hour Forecasting of Solar Resource. Energies 2023, 16, 6608. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked Generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- World Energy Outlook IEA. International Energy Agency, Paris. 2022. Available online: https://www.iea.org/data-and-statistics/data-product/world-energybalances#energy-balances (accessed on 4 April 2022).
- Zhang, M.; Mu, H.; Li, G.; Ning, Y. Forecasting the transport energy demand based on PLSR method in China. Energy 2009, 34, 1396–1400. [Google Scholar] [CrossRef]
- Kumar, U.; Jain, V.K. Time series models (Grey-Markov, Grey Model with rolling mechanism and singular spectrum analysis) to forecast energy consumption in India. Energy 2010, 35, 1709–1716. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Rajasekar, E.; Natarajan, S.; McCullen, N.A. Comparative assessment of SARIMA, LSTM RNN and Fb Prophet models to forecast total and peak monthly energy demand for India. Energy Policy 2022, 168, 113097. [Google Scholar] [CrossRef]
- Sahraei, M.A.; Duman, H.; Çodur, M.Y.; Eyduran, E. Prediction of transportation energy demand: Multivariate adaptive regression splines. Energy 2021, 224, 120090. [Google Scholar] [CrossRef]
- Javanmard, M.E.; Ghaderi, S.F. Energy demand forecasting in seven sectors by an optimization model based on machine learning algorithms. Sustain. Cities Soc. 2023, 95, 104623. [Google Scholar] [CrossRef]
- Ye, J.; Dang, Y.; Ding, S.; Yang, Y. A novel energy consumption forecasting model combining an optimized DGM (1, 1) model with interval grey numbers. J. Clean. Prod. 2019, 229, 256–267. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, H. Fuzzy Wavelet Neural Networks for City Electric Energy Consumption Forecasting. Energy Procedia 2012, 17, 1332–1338. [Google Scholar] [CrossRef]
- Mason, K.; Duggan, J.; Howley, E. Forecasting energy demand, wind generation and carbon dioxide emissions in Ireland using evolutionary neural networks. Energy 2018, 155, 705–720. [Google Scholar] [CrossRef]
- Muralitharan, K.; Sakthivel, R.; Vishnuvarthan, R. Neural network based optimization approach for energy demand prediction in smart grid. Neurocomputing 2018, 273, 199–208. [Google Scholar] [CrossRef]
- Yu, S.; Zhu, K.; Zhang, X. Energy demand projection of China using a path-coefficient analysis and PSO–GA approach. Energy Convers. Manag. 2012, 53, 142–153. [Google Scholar] [CrossRef]
- Verwiebe, P.A.; Seim, S.; Burges, S.; Schulz, L.; Müller-Kirchenbauer, J. Modeling Energy Demand—A Systematic Literature Review. Energies 2021, 14, 7859. [Google Scholar] [CrossRef]
- Ghalehkhondabi, I.; Ardjmand, E.; Weckman, G.R.; Young, W.A. An overview of energy demand forecasting methods published in 2005–2015. Energy Syst. 2017, 8, 411–447. [Google Scholar] [CrossRef]
- Aslan, M. Archimedes optimization algorithm based approaches for solving energy demand estimation problem: A case study of Turkey. Neural Comput. Appl. 2023, 35, 19627–19649. [Google Scholar] [CrossRef]
- Korkmaz, E. Energy demand estimation in Turkey according to modes of transportation: Bezier search differential evolution and black widow optimization algorithms-based model development and application. Neural Comput. Appl. 2023, 35, 7125–7146. [Google Scholar] [CrossRef]
- Aslan, M.; Beşkirli, M. Realization of Turkey’s energy demand forecast with the improved arithmetic optimization algorithm. Energy Rep. 2022, 8, 18–32. [Google Scholar] [CrossRef]
- Ağbulut, Ü. Forecasting of transportation-related energy demand and CO2 emissions in Turkey with different machine learning algorithms. Sustain. Prod. Consum. 2022, 29, 141–157. [Google Scholar] [CrossRef]
- Özdemir, D.; Dörterler, S.; Aydın, D. A new modified artificial bee colony algorithm for energy demand forecasting problem. Neural Comput. Appl. 2022, 34, 17455–17471. [Google Scholar] [CrossRef]
- Özkış, A. A new model based on vortex search algorithm for estimating energy demand of Turkey. Pamukkale Univ. J. Eng. Sci. 2020, 26, 959–965. [Google Scholar] [CrossRef]
- Tefek, M.F.; Uğuz, H.; Güçyetmez, M. A new hybrid gravitational search–teaching–learning-based optimization method for energy demand estimation of Turkey. Neural Comput. Appl. 2019, 31, 2939–2954. [Google Scholar] [CrossRef]
- Beskirli, A.; Beskirli, M.; Hakli, H.; Uguz, H. Comparing energy demand estimation using artificial algae algorithm: The case of Turkey. J. Clean Energy Technol. 2018, 6, 349–352. [Google Scholar] [CrossRef]
- Cayir Ervural, B.; Ervural, B. Improvement of grey prediction models and their usage for energy demand forecasting. J. Intell. Fuzzy Syst. 2018, 34, 2679–2688. [Google Scholar] [CrossRef]
- Koç, İ.; Nureddin, R.; Kahramanlı, H. Implementation of GSA (Gravitation Search Algorithm) and IWO (Invasive Weed Optimization) for the Prediction of the Energy Demand in Turkey Using Linear Form. Selcuk. Univ. J. Eng. Sci. Technol. 2018, 6, 529–543. [Google Scholar]
- Özturk, S.; Özturk, F. Forecasting energy consumption of Turkey by Arima model. J. Asian Sci. Res. 2018, 8, 52. [Google Scholar] [CrossRef]
- Beskirli, M.; Hakli, H.; Kodaz, H. The energy demand estimation for Turkey using differential evolution algorithm. Sādhanā 2017, 42, 1705–1715. [Google Scholar] [CrossRef]
- Daş, G.S. Forecasting the energy demand of Turkey with a NN based on an improved Particle Swarm Optimization. Neural Comput. Appl. 2017, 28, 539–549. [Google Scholar] [CrossRef]
- Kankal, M.; Uzlu, E. Neural network approach with teaching–learning-based optimization for modeling and forecasting long-term electric energy demand in Turkey. Neural Comput. Appl. 2017, 28, 737–747. [Google Scholar] [CrossRef]
- Uguz, H.; Hakli, H.; Baykan, Ö.K. A new algorithm based on artificial bee colony algorithm for energy demand forecasting in Turkey. In Proceedings of the 2015 4th International Conference on Advanced Computer Science Applications and Technologies (ACSAT), Kuala Lumpur, Malaysia, 8–10 December 2015; pp. 56–61. [Google Scholar]
- Tutun, S.; Chou, C.A.; Canıyılmaz, E. A new forecasting for volatile behavior in net electricity consumption: A case study in Turkey. Energy 2015, 93, 2406–2422. [Google Scholar] [CrossRef]
- Kıran, M.S.; Özceylan, E.; Gündüz, M.; Paksoy, T. Swarm intelligence approaches to estimate electricity energy demand in Turkey. Knowl. Based Syst. 2012, 36, 93–103. [Google Scholar] [CrossRef]
- Kankal, M.; Akpınar, A.; Kömürcü, M.İ.; Özşahin, T.Ş. Modeling and forecasting of Turkey’s energy consumption using socio-economic and demographic variables. Appl. Energy 2011, 88, 1927–1939. [Google Scholar] [CrossRef]
- Ediger, V.S.; Akar, S. ARIMA forecasting of primary energy demand by fuel in Turkey. Energy Policy 2007, 35, 1701–1708. [Google Scholar] [CrossRef]
- Toksari, M.D. Ant colony optimization approach to estimate energy demand of Turkey. Energy Policy 2007, 35, 3984–3990. [Google Scholar] [CrossRef]
- Sözen, A.; Arcaklioğlu, E.; Özkaymak, M. Turkey’s net energy consumption. Appl. Energy 2005, 81, 209–221. [Google Scholar] [CrossRef]
- Canyurt, O.E.; Ceylan, H.; Ozturk, H.K.; Hepbasli, A. Energy demand estimation based on two-different genetic algorithm approaches. Energy Sources 2004, 26, 1313–1320. [Google Scholar] [CrossRef]
- Ceylan, H.; Ozturk, H.K. Estimating energy demand of Turkey based on economic indicators using genetic algorithm approach. Energy Convers. Manag. 2004, 45, 2525–2537. [Google Scholar] [CrossRef]
- Ceylan, H.; Ozturk, H.K.; Hepbasli, A.; Utlu, Z. Estimating energy and exergy production and consumption values using three different genetic algorithm approaches, part 2: Application and scenarios. Energy Sources 2005, 27, 629–639. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 3149–3157. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Crammer, K.; Dekel, O.; Keshet, J.; Shalev-Shwartz, S.; Singer, Y. Online Passive-Aggressive Algorithms. J. Mach. Learn. Res. 2006, 7, 551–585. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least Angle Regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Elad, M.; Bruckstein, A. A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Trans. Inf. Theory 2002, 48, 2558–2567. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the Machine Learning: Proceedings of the Thirteenth International Conference (ICML), Bari, Italy, 3–6 July 1996; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1996; Volume 96, pp. 148–156. [Google Scholar]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models, 4th ed.; Irwin: Huntersville, NC, USA, 1996. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Belhumeur, P.N.; Hespanha, J.P.; Kriegman, D.J. Eigenfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 711–720. [Google Scholar] [CrossRef]
- MacKay, D.J. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Chapman & Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 492–518. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Turkish Statistical Institute (Turkstat). Statistical Tables, Ankara, Türkiye. Available online: https://www.tuik.gov.tr/ (accessed on 8 June 2023).
- Turkish Ministry of Energy and Natural Resources (MENR). Ankara, Türkiye. Available online: https://enerji.gov.tr/eigm-raporlari (accessed on 8 June 2023).
- Krzywanski, J. Advanced AI Applications in Energy and Environmental Engineering Systems. Energies 2022, 15, 5621. [Google Scholar] [CrossRef]
- Huybrechts, T.; Reiter, P.; Mercelis, S.; Famaey, J.; Latré, S.; Hellinckx, P. Automated Testbench for Hybrid Machine Learning-Based Worst-Case Energy Consumption Analysis on Batteryless IoT Devices. Energies 2021, 14, 3914. [Google Scholar] [CrossRef]
- Toquica, D.; Agbossou, K.; Malhamé, R.; Henao, N.; Kelouwani, S.; Cardenas, A. Adaptive Machine Learning for Automated Modeling of Residential Prosumer Agents. Energies 2020, 13, 2250. [Google Scholar] [CrossRef]
| Author(s) | Year | Method Used | Dataset | Input Parameters | Performance Metric | Forecasting for |
|---|---|---|---|---|---|---|
| Aslan [47] | 2023 | Archimedes Optimization Algorithm | 1979–2005 1979–2011 | GDP, Population, Import, Export | The Amount of Error, Relative Error (%) | Energy |
| Korkmaz [48] | 2022 | Bezier Search Differential Evolution Black Widow Optimization (BWO) | 2000–2017 | Passenger-km, Freight-km, Carbon dioxide emissions, GDP, Infrastructure Investment | AE, APE, Std_AE, Std_APE, R2, Adj R2, MAE, MAPE, and RMSE | Transportation Energy |
| Aslan and Beşkirli [49] | 2022 | Improved Arithmetic Optimization Algorithm | 1979–2011 | GDP, Population, Import, Export | The Amount of Error, Relative Error (%) | Energy |
| Ağbulut [50] | 2022 | Deep Learning (DL) Support Vector Machine (SVM) Artificial Neural Network (ANN) | 1970–2016 | GDP, Population, Vehicle-km, Year | R2, RMSE, MAPE, MBE, rRMSE, and MABE | Transportation Energy |
| Özdemir et al. [51] | 2022 | Modified Artificial Bee Colony Algorithm | 1979–2005 | GDP, Population, Import, Export | AE, APE, Std_AE, Std_APE, R2, MAE, MAPE, and RMSE | Energy |
| Özkış [52] | 2020 | Vortex Search Algorithm (VS) | 1979–2005 1979–2011 | GDP, Population, Import, Export | The Amount of Error | Energy |
| Tefek et al. [53] | 2019 | Hybrid Gravitational Search, Teaching, Learning-Based Optimization Method | 1980–2014 | Population, Gross Generation, Net Consumption, GDP, Installed Power | R2, RMSE, MAPE | Energy |
| Beskirli et al. [54] | 2018 | Artificial Algae Algorithm (AAA) | 1979–2005 | GDP, Population, Import, Export | The Amount of Error, Relative Error (%) | Energy |
| Cayir Ervural and Ervural [55] | 2018 | Grey Prediction Model Based on GA Grey Prediction Model Based on PSO | 1996–2016 | Previous Annual Electricity Consumption Data | RMSE, MAPE | Electricity Energy consumption |
| Koç et al. [56] | 2018 | Gravity Search Algorithm (GSA), Invasive Weed Optimization Algorithm (IWO) | 1979–2011 | GDP, Population, Import, Export | The Amount of Error, Relative Error (%) | Energy |
| Öztürk and Öztürk [57] | 2018 | ARIMA | 1970–2015 | Previous Energy Consumption Data | AIC | Energy |
| Beskirli et al. [58] | 2017 | Differential Evolution Algorithm (DE) | 1979–2011 | GDP, Population, Import, Export | Mean Absolute Relative Error, Relative Error (%), Magnitude of Error | Energy |
| Daş [59] | 2017 | Neural Network Based on Particle Swarm Optimization | 1979–2005 | GDP, Population, Import, Export | Absolute Relative Error, Relative Error (%), R2, RMSE, MAPE, and MAD | Energy |
| Kankal and Uzlu [60] | 2017 | ANN | 1980–2012 | GDP, Population, Import, Export | Average Relative Error, RMSE, and MAE | Electricity Energy |
| Uguz et al. [61] | 2015 | Artificial Bee Colony with Variable Search Strategies (ABCVSS) | 1979–2005 | GDP, Population, Import, Export | The Amount of Error, Relative Error (%) | Energy |
| Tutun et al. [62] | 2015 | Regression and ANN | 1975–2010 | Import, Export, Gross generation, Transmitted energy | R2, RMSE, MAPE, MSE, MA, and SSE | Electricity Energy consumption |
| Kıran et al. [63] | 2012 | Hybrid Meta-Heuristic (Particle Swarm Optimization, Ant Colony Optimization) | 1979–2005 | GDP, Population, Import, Export | Relative Error (%), R2 | Electricity Energy consumption |
| Kankal et al. [64] | 2011 | Regression Analysis/ANN | 1980–2007 | GDP, Population, Import, Export, Employment | Relative Error (%), R2 and RMSE | Energy |
| Ünler [17] | 2008 | Particle Swarm Optimization | 1979–2005 | GDP, Population, Import, Export | The Amount of Error, Relative Error (%) | Energy |
| Ediger and Akar [65] | 2007 | Autoregressive Integrated Moving Average (ARIMA) and seasonal ARIMA (SARIMA) | 1950–2005 | Previous Energy Consumption Data | MSE and MAED | Energy |
| Toksarı [66] | 2007 | Ant Colony Optimization | 1970–2005 | Population, GDP, Import, Export | R2 | Energy |
| Sözen et al. [67] | 2005 | ANN | 1975–2003 | Population, Gross Generation, Installed Capacity, Import, Export | R2, RMSE, and MAPE | Energy |
| Canyurt et al. [68] | 2004 | Genetic Algorithm | 1970–2001 | GDP, Population, Import, Export | Relative Error (%) | Energy |
| Ceylan and Öztürk [69] | 2004 | Genetic Algorithm | 1970–2001 | GDP, Population, Import, Export | Relative Error (%), MSE, and R2 | Energy |
| Ceylan et al. [70] | 2004 | Genetic Algorithm | 1990–2001 | GDP, Population, Import, Export | Average Relative Error | Energy and exergy production and consumption |
| Variable | The Influencing Factors for Using This Variable |
|---|---|
| GDP | There exists a strong correlation between GDP and energy consumption, as the level of economic activity directly impacts the demand for energy. When the GDP of a country increases, it generally indicates a growth in industrial and commercial activities, leading to higher energy consumption. Considering the substantial impact of GDP on energy demand, GDP is often chosen as an independent variable in studies analyzing energy consumption patterns. |
| Population | Population growth directly affects the demand for energy in a country or region. As the population increases, there is a greater need for energy to meet the demands of the growing population, including residential, commercial, industrial, and transportation sectors. Understanding and considering population values as an independent variable is crucial for analyzing and planning energy resources. |
| Import | The relationship between imports and energy consumption is significant, as the availability and reliance on imported energy resources can directly impact a country’s energy demand. The import values of energy resources are chosen as independent variables in this study due to their influence on the overall energy consumption patterns. |
| Export | The relationship between exports and energy consumption is an important aspect of understanding a country’s energy demand. The export values of energy resources are chosen as independent variables in this study due to their potential impact on a country’s overall energy consumption patterns. |
| Years | Population (106) | GDP (USD 109) | Import (USD 109) | Export (USD 109) | Energy (Mtoe) |
|---|---|---|---|---|---|
| 1979 | 43.19 | 82.00 | 5.07 | 2.26 | 26.37 |
| 1980 | 44.09 | 68.82 | 7.91 | 2.91 | 27.51 |
| 1981 | 44.98 | 71.04 | 8.93 | 4.70 | 27.60 |
| 1982 | 45.95 | 64.55 | 8.84 | 5.75 | 29.59 |
| 1983 | 47.03 | 61.68 | 9.24 | 5.73 | 30.25 |
| 1984 | 48.11 | 59.99 | 10.76 | 7.13 | 31.75 |
| 1985 | 49.18 | 67.23 | 11.34 | 7.96 | 32.73 |
| 1986 | 50.22 | 75.73 | 11.10 | 7.46 | 34.59 |
| 1987 | 51.25 | 87.17 | 14.16 | 10.20 | 38.70 |
| 1988 | 52.28 | 90.85 | 14.34 | 11.66 | 39.73 |
| 1989 | 53.31 | 107.14 | 15.80 | 11.62 | 40.40 |
| 1990 | 54.32 | 150.68 | 22.30 | 12.96 | 42.24 |
| 1991 | 55.32 | 150.03 | 21.05 | 13.59 | 43.09 |
| 1992 | 56.30 | 158.46 | 22.87 | 14.71 | 44.70 |
| 1993 | 57.30 | 180.17 | 29.43 | 15.35 | 48.26 |
| 1994 | 58.31 | 130.69 | 23.27 | 18.11 | 45.77 |
| 1995 | 59.31 | 169.49 | 35.71 | 21.64 | 50.53 |
| 1996 | 60.29 | 181.48 | 43.63 | 23.22 | 54.85 |
| 1997 | 61.28 | 189.83 | 48.56 | 26.26 | 57.99 |
| 1998 | 62.24 | 275.97 | 45.92 | 26.97 | 57.12 |
| 1999 | 63.19 | 256.39 | 40.67 | 26.59 | 55.22 |
| 2000 | 64.11 | 274.30 | 54.50 | 27.77 | 61.60 |
| 2001 | 65.07 | 201.75 | 41.40 | 31.33 | 55.60 |
| 2002 | 65.99 | 240.25 | 51.55 | 36.06 | 59.49 |
| 2003 | 66.87 | 314.59 | 69.34 | 47.25 | 64.59 |
| 2004 | 67.79 | 408.88 | 97.54 | 63.17 | 68.24 |
| 2005 | 68.70 | 506.31 | 116.77 | 73.48 | 70.33 |
| 2006 | 69.60 | 557.06 | 139.58 | 85.53 | 74.82 |
| 2007 | 70.47 | 681.34 | 170.06 | 107.27 | 79.79 |
| 2008 | 71.32 | 770.46 | 201.96 | 132.03 | 77.76 |
| 2009 | 72.23 | 649.27 | 140.93 | 102.14 | 78.36 |
| 2010 | 73.20 | 776.99 | 185.54 | 113.88 | 79.84 |
| 2011 | 74.17 | 838.76 | 240.84 | 134.91 | 84.91 |
| 2012 | 75.28 | 880.56 | 236.55 | 152.46 | 88.84 |
| 2013 | 76.58 | 957.78 | 260.82 | 161.48 | 88.07 |
| 2014 | 78.11 | 938.95 | 251.14 | 166.50 | 89.25 |
| 2015 | 79.65 | 864.32 | 213.62 | 150.98 | 99.47 |
| 2016 | 81.02 | 869.69 | 202.19 | 149.25 | 104.57 |
| 2017 | 82.09 | 859.00 | 238.72 | 164.50 | 111.65 |
| 2018 | 82.81 | 778.47 | 231.15 | 177.17 | 109.44 |
| 2019 | 83.48 | 759.94 | 210.35 | 180.83 | 110.65 |
| 2020 | 84.14 | 720.30 | 219.52 | 169.64 | 113.70 |
| 2021 | 84.78 | 819.04 | 271.42 | 225.29 | 123.86 |
| Model | Input |
|---|---|
| M1 | GDP, Population |
| M2 | GDP, Import |
| M3 | GDP, Export |
| M4 | Population, Import |
| M5 | Population, Export |
| M6 | Import, Export |
| M7 | GDP, Population, Import |
| M8 | GDP, Population, Export |
| M9 | Population, Import, Export |
| M10 | GDP, Import, Export |
| M11 | * GDP, Population, Import, Export |
| Models | ML Algorithm | MAE | MSE | RMSE | R2 | MAPE |
|---|---|---|---|---|---|---|
| M1 | Extra Trees Regressor | 2743.27 | 14,435,527.00 | 3622.18 | 0.9751 | 0.0546 |
| Huber Regressor | 3419.46 | 20,734,897.00 | 4395.82 | 0.9642 | 0.0749 | |
| Extreme Gradient Boosting | 3725.91 | 22,807,495.50 | 4551.60 | 0.9625 | 0.0655 | |
| M2 | K-Neighbors Regressor | 6881.86 | 84,149,616.80 | 8596.44 | 0.8710 | 0.1104 |
| Random Forest Regressor | 6809.08 | 114,145,888.80 | 9963.98 | 0.8252 | 0.1167 | |
| Extra Trees Regressor | 6452.43 | 123,658,755.00 | 9929.56 | 0.8117 | 0.1178 | |
| M3 | Extra Trees Regressor | 3977.99 | 44,054,367.30 | 5730.78 | 0.9299 | 0.0695 |
| Random Forest Regressor | 4631.80 | 55,354,193.10 | 6583.28 | 0.9162 | 0.0797 | |
| Gradient Boosting Regressor | 5351.58 | 64,199,913.90 | 7220.71 | 0.9031 | 0.0901 | |
| M4 | Extra Trees Regressor | 3042.48 | 17,937,995.55 | 3844.90 | 0.9733 | 0.0591 |
| Random Forest Regressor | 3666.07 | 22,957,290.18 | 4448.29 | 0.9716 | 0.0685 | |
| Gradient Boosting Regressor | 4156.41 | 26,308,872.75 | 4930.11 | 0.9652 | 0.0742 | |
| M5 | Huber Regressor | 3864.21 | 36,775,418.87 | 5527.85 | 0.9541 | 0.0601 |
| Lasso Regression | 4003.55 | 36,200,997.00 | 5456.62 | 0.9530 | 0.0678 | |
| Least Angle Regression | 4003.72 | 36,196,280.60 | 5456.35 | 0.9530 | 0.0678 | |
| M6 | K-Neighbors Regressor | 5707.22 | 80,792,845.60 | 7992.88 | 0.8962 | 0.1035 |
| Random Forest Regressor | 5455.21 | 77,021,388.80 | 8193.73 | 0.8644 | 0.0930 | |
| Extra Trees Regressor | 5511.29 | 82,472,925.80 | 8300.80 | 0.8540 | 0.0950 | |
| M7 | Extra Trees Regressor | 2308.94 | 12,339,053.90 | 3277.79 | 0.9754 | 0.0488 |
| Random Forest Regressor | 2972.75 | 17,408,515.60 | 3854.32 | 0.9608 | 0.0576 | |
| AdaBoost Regressor | 3400.27 | 18,546,026.70 | 4014.45 | 0.9538 | 0.0640 | |
| M8 | Extra Trees Regressor | 3189.81 | 17,110,325.38 | 3874.79 | 0.9716 | 0.0537 |
| AdaBoost Regressor | 4293.89 | 29,715,232.81 | 5282.08 | 0.9475 | 0.0728 | |
| Random Forest Regressor | 4287.09 | 35,730,037.10 | 5185.02 | 0.9460 | 0.0700 | |
| M9 | Extra Trees Regressor | 3018.13 | 30,503,239.40 | 4394.13 | 0.9477 | 0.0407 |
| Random Forest Regressor | 3583.32 | 45,575,422.90 | 5273.91 | 0.9304 | 0.0473 | |
| AdaBoost Regressor | 4069.59 | 37,580,683.81 | 5358.08 | 0.9285 | 0.0609 | |
| M10 | K-Neighbors Regressor | 5670.51 | 74,121,506.00 | 7652.91 | 0.9017 | 0.1003 |
| Random Forest Regressor | 5372.22 | 75,187,291.90 | 7930.92 | 0.8896 | 0.0942 | |
| Ridge Regression | 7009.35 | 69,191,604.80 | 8277.45 | 0.8621 | 0.1643 | |
| M11 | Extra Trees Regressor | 2296.86 | 8,756,864.57 | 2932.96 | 0.9788 | 0.0464 |
| Random Forest Regressor | 3186.05 | 14,777,499.11 | 3817.37 | 0.9684 | 0.0658 | |
| Ridge Regression | 3676.12 | 21,641,675.00 | 4466.13 | 0.9655 | 0.0736 |
| ML Algorithm | MAE | MSE | RMSE | R2 | MAPE |
|---|---|---|---|---|---|
| Extra Trees Regressor | 2296.86 | 8,756,864.57 | 2932.96 | 0.9788 | 0.0464 |
| Random Forest Regressor | 3186.05 | 14,777,499.11 | 3817.37 | 0.9684 | 0.0658 |
| Ridge Regression | 3676.12 | 21,641,675.00 | 4466.14 | 0.9655 | 0.0736 |
| Linear Regression | 3780.00 | 23,739,669.80 | 4668.86 | 0.9635 | 0.0825 |
| Lasso Regression | 3779.85 | 23,736,214.80 | 4668.54 | 0.9635 | 0.0825 |
| Least Angle Regression | 3780.00 | 23,739,655.90 | 4668.86 | 0.9635 | 0.0825 |
| Lasso Least Angle Regression | 3779.85 | 23,736,205.30 | 4668.54 | 0.9635 | 0.0825 |
| Orthogonal Matching Pursuit | 3780.00 | 23,739,655.90 | 4668.86 | 0.9635 | 0.0825 |
| Huber Regressor | 3828.58 | 22,823,167.86 | 4595.40 | 0.9634 | 0.0785 |
| AdaBoost Regressor | 3575.50 | 15,583,915.43 | 3934.88 | 0.9611 | 0.0691 |
| Gradient Boosting Regressor | 3772.78 | 16,872,570.61 | 4096.12 | 0.9556 | 0.0707 |
| Decision Tree Regressor | 3768.74 | 16,856,622.84 | 4094.38 | 0.9554 | 0.0707 |
| Extreme Gradient Boosting | 3768.71 | 16,856,282.40 | 4094.34 | 0.9554 | 0.0706 |
| K-Neighbors Regressor | 3987.62 | 29,417,635.00 | 5274.57 | 0.9493 | 0.0848 |
| Elastic Net | 7402.15 | 81,150,325.20 | 8721.88 | 0.8666 | 0.1248 |
| Bayesian Ridge | 22,303.79 | 705,872,003.20 | 25,684.29 | −0.0970 | 0.4306 |
| Light Gradient Boosting Machine | 22,303.79 | 705,872,041.79 | 25,684.29 | −0.0970 | 0.4306 |
| Dummy Regressor | 22,303.79 | 705,872,041.60 | 25,684.29 | −0.0970 | 0.4306 |
| Passive Aggressive Regressor | 40,863.75 | 2,361,836,689.9 | 48,178.33 | −3.9041 | 0.5635 |
| ML Algorithm | MAE | MSE | RMSE | R2 | MAPE |
|---|---|---|---|---|---|
| Extra Trees Regressor | 2989.27 | 17,145,375.48 | 4140.6975 | 0.9811 | 0.0406 |
| Training | Test | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ensemble Methods | Fold | Base Learners | Meta Learner | MAE | MSE | RMSE | R2 | MAPE | MAE | MSE | RMSE | R2 | MAPE |
| 0 | 2384.30 | 10,532,299.28 | 3245.35 | 0.9855 | 0.0425 | ||||||||
| 1 | 2428.40 | 10,139,704.39 | 3184.29 | 0.9870 | 0.0583 | ||||||||
| 2 | 1320.12 | 4,588,805.18 | 2142.15 | 0.9606 | 0.0211 | ||||||||
| Bagging | 3 | ET | 2943.76 | 18,949,550.99 | 4353.11 | 0.9814 | 0.0811 | 3247.76 | 20,526,807.39 | 4530.65 | 0.9773 | 0.0476 | |
| 4 | 2833.04 | 10,421,373.56 | 3228.22 | 0.9859 | 0.0642 | ||||||||
| Mean | 2381.92 | 10,926,346.68 | 3230.62 | 0.9801 | 0.0534 | ||||||||
| Std | 574.24 | 4,594,895.36 | 699.59 | 0.0099 | 0.0204 | ||||||||
| 0 | 2324.68 | 10,142,168.21 | 3184.68 | 0.9861 | 0.0401 | ||||||||
| 1 | 2292.10 | 7,616,694.33 | 2759.84 | 0.9902 | 0.0526 | ||||||||
| 2 | 1591.23 | 6,141,944.75 | 2478.29 | 0.9473 | 0.0249 | ||||||||
| Boosting | 3 | ET | 2450.57 | 10,639,983.49 | 3261.90 | 0.9895 | 0.0582 | 2791.95 | 16,986,253.22 | 4121.44 | 0.9811 | 0.0367 | |
| 4 | 2256.76 | 6,211,550.01 | 2492.30 | 0.9916 | 0.0484 | ||||||||
| Mean | 2183.07 | 8,150,468.16 | 2835.41 | 0.9809 | 0.0448 | ||||||||
| Std | 303.05 | 1,910,132.98 | 333.12 | 0.0169 | 0.0116 | ||||||||
| 0 | 2621.68 | 13,996,026.78 | 3741.13 | 0.9808 | 0.0456 | ||||||||
| 1 | 2115.51 | 6,368,872.54 | 2523.66 | 0.9918 | 0.0388 | ||||||||
| 2 | ET | 1227.95 | 2,599,808.47 | 1612.39 | 0.9777 | 0.0213 | |||||||
| Blending | 3 | RF | 2266.80 | 7,245,254.56 | 2691.70 | 0.9929 | 0.0348 | 3138.73 | 20,627,053.08 | 4541.70 | 0.9772 | 0.0430 | |
| 4 | Ridge | 1783.21 | 4,566,049.47 | 2136.83 | 0.9938 | 0.0311 | |||||||
| Mean | 2003.03 | 6,955,202.36 | 2541.14 | 0.9874 | 0.0343 | ||||||||
| Std | 472.02 | 3,864,676.67 | 705.55 | 0.0068 | 0.0081 | ||||||||
| 0 | 2332.41 | 10,667,480.27 | 3266.11 | 0.9853 | 0.0383 | ||||||||
| 1 | 2359.09 | 6,559,821.14 | 2561.21 | 0.9916 | 0.0470 | ||||||||
| 2 | ET | 1133.61 | 2,887,446.54 | 1699.25 | 0.9752 | 0.0187 | |||||||
| Stacking | 3 | RF | Ridge | 2110.38 | 6,221,784.33 | 2494.35 | 0.9939 | 0.0343 | 2704.34 | 15,710,000.99 | 3963.58 | 0.9826 | 0.0359 |
| 4 | Ridge | 1520.56 | 3,762,509.98 | 1939.72 | 0.9949 | 0.0294 | |||||||
| Mean | 1891.21 | 6,019,808.45 | 2392.13 | 0.9882 | 0.0335 | ||||||||
| Std | 484.35 | 2,714,418.86 | 545.46 | 0.0073 | 0.0094 | ||||||||
| Years | Observed Energy Demand (Mtoe) | Predicted Energy Demand (Mtoe) | Amount of Errors | Relative Errors (%) |
|---|---|---|---|---|
| 1980 | 27.51 | 26.96 | 0.55 | 1.99 |
| 1983 | 30.25 | 28.97 | 1.28 | 4.23 |
| 1984 | 31.75 | 30.42 | 1.33 | 4.18 |
| 1988 | 39.73 | 38.69 | 1.04 | 2.62 |
| 1989 | 40.40 | 40.53 | −0.13 | −0.32 |
| 2002 | 59.49 | 62.74 | −3.25 | −5.46 |
| 2007 | 79.79 | 76.95 | 2.84 | 3.56 |
| 2010 | 79.84 | 81.93 | −2.09 | −2.62 |
| 2013 | 88.07 | 91.51 | −3.44 | −3.91 |
| 2014 | 89.25 | 96.05 | −6.80 | −7.62 |
| 2021 | 123.86 | 113.73 | 10.13 | 8.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kayacı Çodur, M. Ensemble Machine Learning Approaches for Prediction of Türkiye’s Energy Demand. Energies 2024, 17, 74. https://doi.org/10.3390/en17010074
Kayacı Çodur M. Ensemble Machine Learning Approaches for Prediction of Türkiye’s Energy Demand. Energies. 2024; 17(1):74. https://doi.org/10.3390/en17010074
Chicago/Turabian StyleKayacı Çodur, Merve. 2024. "Ensemble Machine Learning Approaches for Prediction of Türkiye’s Energy Demand" Energies 17, no. 1: 74. https://doi.org/10.3390/en17010074
APA StyleKayacı Çodur, M. (2024). Ensemble Machine Learning Approaches for Prediction of Türkiye’s Energy Demand. Energies, 17(1), 74. https://doi.org/10.3390/en17010074







