Abstract
This paper attempts to elucidate the transformative integration of computational techniques within power systems, underscoring their critical role in enhancing system modeling, control, and the efficient integration of renewable energy. It breaks down the two-sided nature of technological progress, highlighting both gains in operational efficiency and new challenges such as real-time processing, data management, and cybersecurity. Through meticulous analysis of query-based research patterns and mathematical frameworks, this study delves into the balancing act between specificity and breadth in scholarly inquiries while evaluating the impact and evolution of research trends through citation analysis. The convergence of interests and transient research trends is evident, particularly in Artificial Intelligence and optimization. This comprehensive narrative anticipates a sophisticated trajectory for power systems, advocating for continuous innovation and strategic research to foster sustainable, resilient, and intelligent energy networks.
1. Introduction
The advent of advanced computational methodologies has initiated a transformative era in the domain of power system operations. At the forefront of this transformation lies the seamless integration of state-of-the-art computational techniques, representing a pivotal milestone in the evolution of power networks into autonomous, self-regulating entities capable of optimization. In this context, Figure 1 provides a concise portrayal of a microgrid system. On the left, simplified icons depict photovoltaic solar panels and wind turbines. On the right, a basic icon represents a natural gas generation facility. At the bottom, an icon signifies energy storage batteries. Structures and charging stations are illustrated using basic geometric shapes, while a central icon symbolizes the core control system. This minimalist diagram effectively communicates the integration of renewable energy sources, backup natural gas generation, energy storage, and demand management within the microgrid, all orchestrated by the central control system.

Figure 1.
Schematic research showing the SG components.
This paper explores the profound implications of such technologies, ranging from machine learning algorithms to intricate control strategies. By meticulously analyzing the intricacies of these methods, this paper demonstrates their indispensability in enhancing accuracy, efficiency, and robustness in power system modeling and control [1].
Our methodological framework employs a comprehensive review of case studies and scholarly articles to navigate the complexities and the dynamic nature of modern power networks [2]. With an emphasis on the seamless incorporation of renewable energy sources, this paper sheds light on the essentiality of computational techniques in maintaining system stability and optimizing performance [3].
Furthermore, this paper delineates the multifaceted challenges accompanying these computational advancements, such as real-time data processing demands, voluminous data management, and cybersecurity [4]. Through a balanced inquiry into various queries, our analysis adheres to a mathematical marking framework, critically assessing the relevance, diversity, and citation impact of the research within this field [5].
In essence, a forward-looking perspective is presented and analyzed by empirical evidence and quantitative analysis to forecast the trajectory of power systems [6]. It stands on the precipice of a new era where power networks are more efficient, innovative, and responsive to the ever-evolving energy landscape [7].
2. The State of the Art
2.1. Historical Overview of Computational Techniques in Power Systems
The progression of computational methods has been pivotal to advancing power systems within electrical engineering, enhancing control and stability. Initially, linear control strategies were instrumental, setting a foundation for later advancements [8]. However, as power systems became more complex, the shortcomings of linear models led to the development of more advanced algorithms. Machine learning and optimization algorithms marked a significant shift, introducing dynamic responses to the nonlinear challenges in contemporary power systems [9]. For example, neural networks and fuzzy logic have notably improved the damping of oscillations, essential for system stability [10].
Later, heuristic approaches like Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO) emerged, offering robust solutions to the multifaceted optimization problems of power system control [11]. Research has shown GAs notably enhance stabilizer tuning [12]. The incorporation of renewable energy necessitated computational methods to manage new uncertainties. Techniques like Adaptive Neuro-Fuzzy Inference Systems (ANFISs) and Support Vector Machines (SVMs) were vital, with ANFISs demonstrating superior learning speed and adaptability [13]. Comparative studies underscored ANFISs’ advantages over SVMs in power system scenarios [14].
In real-time control and analysis, the advent of Real-Time Digital Simulators and Hardware-In-the-Loop (HIL) simulations has been transformative, allowing for practical validation of computational methods [15]. HIL simulations, in particular, provide a more interactive testing environment, essential for developing real-time strategies [16]. Entering the 21st century, computational intelligence and AI have become central to power system stability, with techniques like Deep Learning and Reinforcement Learning offering novel capabilities in pattern recognition and decision making [17]. Deep Learning’s application to power system stability indicates its revolutionary potential for predictive and adaptive control [18].
In [19], the paper explores day-ahead and real-time cooperative energy management challenges in multienergy systems comprising numerous energy entities. It introduces an event-triggered distributed algorithm characterized by distributed execution, asynchronous communication, and independent calculation to tackle these challenges.
2.2. Modern Computational Methods and Their Applications
The integration of contemporary computational approaches has markedly reshaped stability and control within power systems. These approaches, grounded in advanced analytics, are crucial for solving intricate optimization challenges in this domain. Notably, Particle Swarm Optimization (PSO), the Kidney-Inspired Algorithm (KA), and Adaptive Neuro-Fuzzy Inference Systems (ANFISs) stand out for their contributions to Power System Stabilizer (PSS) enhancement and precise demand prediction.
PSO, drawing from avian social patterns, has shown effectiveness in PSS parameter adjustment for complex multimachine systems. Verdejo et al. [20] confirmed PSO’s utility in substantial systems via implementation in DigSilent PowerFactory, yielding enhanced stability and adeptness at navigating the dynamics of extensive networks.
Conversely, the KA, taking cues from renal processes, has been harnessed for PSS optimization to bolster the damping of electromechanical modes. Investigations by Ekinci et al. [21] into a 16-machine, 68-bus system presented favorable outcomes over traditional approaches, with the KA surpassing others in computation speed, convergence, and solution quality.
Moreover, AI-driven Maximum Power Point Tracking (MPPT) methods have catalyzed a paradigm shift in solar energy, especially under varying shade conditions. Yap et al. [22] examined six AI-based MPPT methods, noting their swift convergence and high efficiency. A hybrid MPPT approach, merging traditional and AI methods, emerged as optimal for balancing complexity with performance.
In the realm of demand forecasting, pivotal for power system management, AI methodologies have proven advantageous. A thorough evaluation by Ahmad et al. [23] of various forecasting models, incorporating Machine Learning, Deep Learning, and AI, highlighted the precision of hybrid models in minimizing errors, thus aiding sector decision-makers in maintaining consistent power distribution.
These comparative assessments suggest a shift towards hybridized and specialized computational methods. While PSO is favored for its robustness in large-scale settings, the KA is recognized for its rapid convergence and efficiency. AI’s incorporation into MPPT and forecasting enhances performance and bolsters system reliability.
In the paper in [24], a novel approach to enhance heating systems and raw material preheating is proposed and validated by mathematical analysis and industrial experiments. The paper in [25] also explores aluminum electrolysis, developing a mathematical model for the Soderberg electrolyzer and analyzing primary aluminum production methods while reviewing computational models for electrolyzers’ thermal and electromagnetic fields. These studies highlight the complexities and innovative solutions in applying computational techniques.
2.3. Challenges in Implementing Computational Techniques
The deployment of computational techniques in power system operations is a testament to the field’s evolution. However, the path to seamless integration is laden with technical and infrastructural challenges. While enhancing real-time monitoring and control capabilities, the burgeoning Internet of Things (IoT) technology introduces complexities in managing the vast data streams and ensuring cybersecurity [26]. Bedi et al. [26] highlighted the transformative role of IoT in electric power and energy systems (EPESs), emphasizing the need for robust computational intelligence to manage the deluge of data and the associated security concerns.
Model Predictive Control (MPC), a sophisticated control methodology, has been increasingly applied in power electronics to improve performance and stability. Karamanakos et al. [27] extensively reviewed MPC techniques, discussing the trade-offs between direct and indirect MPC regarding design complexity and computational demands. The challenge lies in the real-time implementation of these algorithms, which requires high computational resources and advanced control platforms.
The innovative grid paradigm, focusing on optimization and simulation, presents another layer of complexity. Soares et al. [28] conducted a comprehensive analysis of the challenges in intelligent grid optimization, particularly in energy resource management. Integrating distributed renewable generation, demand response, and electric vehicles introduces uncertainty that traditional computational tools need help managing effectively.
Moreover, the real-time state estimation for Wide-Area Measurement Systems (WAMSs) is critical for the reliability of power grids. Li et al. [29] proposed an Event-Trigger Heterogeneous Nonlinear Filter (ET-HNF) to address the computational burden of particle filters and the data communication infrastructure challenges posed by Phasor Measurement Units (PMUs). Their work underscores the necessity for innovative solutions that can efficiently leverage computational power while maintaining high state estimation performance.
2.4. Case Studies Showcasing the Impact of Computational Methods on Power System Stability
The emergence of computational techniques has revolutionized power system stability analysis, allowing for enhanced precision in models, improved predictive capabilities, and superior control of intricate electrical grids. This segment offers a synopsis of case studies that exemplify the profound influence of these methodologies on maintaining power system equilibrium.
Wang et al. [30] addressed the complexities of simulating wind farms for stability evaluations by introducing a refined aggregate modeling technique. The paper employs a geometric template for turbine clustering and a multiobjective optimization algorithm; their method exemplifies how computational strategies can refine the accuracy of extensive power system analyses. In addressing load frequency control, Jin et al. [31] presented an innovative reconstructed model for PID controllers within wind power networks, skillfully harmonizing computational precision and efficiency—critical considerations given the unpredictable nature of wind power and resultant system latencies. Devarapalli et al. [32] delivered an exhaustive critique of computational techniques for power system stabilizers, accentuating their effectiveness in quelling power network fluctuations. This review illuminates the vast array of computational tools for fortifying power system stability. Lastly, He et al. [33] delved into the stability of DC distribution networks, suggesting a bus node impedance criterion for small-signal stability assessment. Their findings not only confront stability issues in distributed networks but also offer a relative assessment of existing criteria, marking the progress and implementation of computational techniques in contemporary power systems. These case studies collectively demonstrate the transformational role of computational methods in power system stability, showing that enhanced model precision, computational efficiency, and robust control mechanisms are crucial in managing the integration of renewables and system uncertainties. They further emphasize the continuous quest for novel computational strategies to meet the dynamic and evolving demands of power system stability.
The analysis of the methodologies employed in the selected papers, as summarized in Table 1, reveals significant insights into the prevalent computational techniques in power system stability and control. The PSS methodology appears to be the most frequently employed (cited in eight papers), indicating its prominence and possible effectiveness in this research area. Similarly, the term ‘power’ is referenced in six papers, suggesting its central role in the studies. The use of ‘algorithm’ and ‘performance’ in five papers each ([34,35,36,37,38] for ‘algorithm’ and [35,36,37,39,40] for ‘performance’) highlights their importance in the methodologies of power system analysis. ‘Simulations’ and ‘PSO’ are also notable, each mentioned in four different papers ([38,41,42,43] for ‘simulations’ and [35,37,39,44] for ‘PSO’), reflecting their utility in research methodologies. This distribution of methodologies across papers underscores the diverse yet focused approaches in the field, with specific techniques being more prevalent, possibly due to their proven effectiveness or suitability for specific types of analysis in power system stability and control.

Table 1.
Overview of Computational Methodologies in Power System Stability and Control Research.
PSO has become an essential tool in power system optimization and has gained significant prominence in state-of-the-art methodologies. Its ability to navigate complex, multidimensional search spaces efficiently makes it efficient for power system applications, including unit commitment, load forecasting, and renewable energy integration. PSO stands out from other optimization techniques because of its adaptability and robustness in handling nonlinear, dynamic power systems. Its versatility extends to solving intricate problems in power system stability, grid optimization, and demand-side management.
3. Methodology
The selection of search queries presented in Table 2 was meticulously crafted to encompass a broad spectrum of computational techniques applied to power system stability and control. The queries were designed to capture the intersection of advanced computational methods and their application in the dynamic field of power system engineering. This approach ensures a comprehensive retrieval of the literature that spans both theoretical and practical aspects of the domain, providing a rich dataset for subsequent analysis.

Table 2.
Search Queries for Computational Techniques in Power System Stability and Control.
Boolean expressions were utilized to formulate the queries to refine the search results. ‘AND’ narrows the focus to documents containing all the specified terms, ensuring relevance to the topic. Conversely, ‘OR’ broadens the search to include any listed terms, capturing a more comprehensive range of methodologies and applications. The strategic use of ‘NOT’ in certain queries excludes papers focusing on specific subtopics, such as machine learning, to avoid overshadowing other computational techniques. This Boolean logic is fundamental in database searching and is widely recognized for its effectiveness in information retrieval [51].
A comparative analysis of the queries reveals varying degrees of specificity and breadth. Queries such as Q1 and Q2 are broader and expected to yield more diverse papers. At the same time, Q3 introduces exclusivity, potentially limiting the scope but increasing the focus on non-machine-learning techniques. This nuanced approach allows for a layered understanding of the field, highlighting the multifaceted nature of computational applications in power system stability and control. The methodology behind these queries is supported by best practices in systematic literature reviews, ensuring a balanced and thorough exploration of the available research [52].
As shown in Table 3, the search queries for computational techniques in power system stability and control exhibit a range of advantages and disadvantages. Query Q1 offers the broadest coverage, potentially capturing a wide array of computational techniques, but it may also include less relevant papers due to its breadth [53]. Conversely, Q3 and Q5 provide a more focused lens, specifically excluding machine learning and emphasizing heuristic methods. This focus, while beneficial for specificity, may overlook significant advancements in machine learning (Q3) or nonheuristic computational techniques (Q5), representing a trade-off between breadth and specificity [54].

Table 3.
Comparative Analysis of Query Specificity, including Advantages, Scope, Possible trend and Gap.
The scope of research for each query, as detailed in Table 3, also varies significantly. Queries Q2 and Q6, which include machine learning, optimization algorithms, and renewable integration, are likely to yield results that span a broad spectrum of current and emerging technologies in power system control. This broad scope can be advantageous for a comprehensive review but may also result in a voluminous and diverse set of papers that require extensive filtering [55]. In contrast, Q4 and Q7, focusing on damping oscillations and power system stabilizers, respectively, offer a narrower scope that may facilitate a more targeted analysis but at the risk of missing out on broader contextual information.
The potential trend–theme and identified gaps highlighted in Table 3 reflect the evolving nature of the field. Queries such as Q1 and Q2 will likely capture papers on cutting-edge machine learning applications, a significant trend in power system stability and control. However, the possible identified gaps, such as the omission of newer computational methods in Q1 or the potential for too broad a capture in Q2, suggest that no single query is exhaustive. The careful construction of these queries aims to balance the capture of emerging trends with identifying gaps in the literature, ensuring a comprehensive understanding of the field’s trajectory.
The qualification score for a scientific query is encapsulated by Equation (1), which provides a systematic approach to evaluating literature searches’ effectiveness. This score is derived by averaging the weighted contributions of three critical factors: the relevance of each paper to the query (), the diversity of content across the papers (), and the citation count as an indicator of impact (). The weights , , and reflect the significance assigned to each of these factors, ensuring a balanced consideration of quality, breadth, and influence.
In the second paragraph, the diversity factor ensures a broad representation of research areas and methodologies, echoing the findings of Alimi and Ouahada [56], who highlight the necessity of methodological variety in comprehensive literature reviews. Citation count serves as a proxy for the scholarly recognition and influence of the work, with its inclusion in the qualification score grounded in the established practices of academic impact assessment. The normalization by the number of papers (N) allows for consistent comparison across searches with varying results. The components and their respective weights are detailed in Table 4, which underpins the calculation of the qualification score. This methodological framework ensures that the qualification score is a multifaceted reflection of the research’s quantity, pertinence, and impact within the field.

Table 4.
Parameters, Symbols and Description for Qualification Score Calculation.
The Algorithm 1 orchestrates a systematic methodology for selecting the most efficacious query for retrieving research papers pertinent to specific scientific inquiries. Initially, each proposed query undergoes a meticulous analysis to discern its intrinsic advantages, scope, prevailing trends, and identifiable gaps. After this analytical phase, the algorithm begins a retrieval process, sourcing papers from a consortium of open-access libraries, ensuring a comprehensive amalgamation of scholarly articles. Each retrieved paper is then subjected to a quantitative evaluation, wherein pivotal metrics such as the number of citations, diversity of content, and relevance to the initial query are assessed and quantified. A mathematical formulation is employed to synthesize these metrics, yielding a composite qualification score that encapsulates the overall efficacy of each query. This score is instrumental in facilitating an objective comparison of the queries, culminating in selecting the query that exhibits the highest degree of alignment with the research objectives. The algorithm’s design embodies a fusion of analytical rigor and computational proficiency, enabling it to adeptly navigate the vast scholarly landscape and isolate the queries most conducive to advancing scientific exploration.
| Algorithm 1 Research Paper Query Selection Algorithm |
|
4. Results and Discussion
As shown in Table 5, the strength of the queries varies significantly, reflecting the diverse computational techniques applied to power system stability and control. Query Q1 and Q2 demonstrate a broad scope, incorporating advanced computational techniques and machine learning, pivotal in modern power systems analysis [57]. In contrast, Q3 deliberately excludes machine learning to focus on alternative computational methods, which may limit its breadth but increase specificity [58]. The strength of a query is not solely determined by its breadth but also by its ability to yield targeted results, as broader queries may retrieve a high volume of less relevant papers.

Table 5.
Search Queries’ Strength, Thematic Relevance, Number of Papers in Scopus, and Corresponding Qualification Scores.
The thematic focus of the queries, as detailed in Table 5, ranges from general power system stability and control (Q1, Q2) to more specific aspects such as the exclusion of machine learning (Q3) or the inclusion of renewable integration (Q6). The expected number of papers for each query directly reflects the thematic scope, with broader themes like those in Q1 and Q2 likely to yield a larger body of work compared with the more narrowly focused Q3 [59]. This breadth versus specificity trade-off is a common challenge in designing search queries for literature reviews, as a broader theme can sometimes dilute the concentration of highly relevant papers.
The qualification of each query, as per the defined formula, considers the papers’ relevance, diversity, and citation impact. Queries Q1 and Q2, with a qualification score of 4, are considered highly effective due to their comprehensive nature and the significant citation counts of the retrieved papers, indicating their impact and importance in the field [60]. On the other hand, Q3’s more focused approach yields a lower qualification score of 2, suggesting a narrower but more in-depth exploration of the topic. This nuanced evaluation underscores the importance of a balanced methodology in query formulation, ensuring both breadth and depth are considered to achieve a comprehensive literature review [61].
The bar chart depicted in Figure 2 showcases the most cited papers from the query Q2, with the work of Fuller A. [62] achieving the highest citation count at 739. This significant number of citations reflects the paper’s impact on the field, likely resonating with contemporaneous and successive research inquiries. The accompanying table, labeled Table 6, provides a detailed synopsis of the top ten papers, elucidating the first authors, their citation, citation volume, and central keyword.
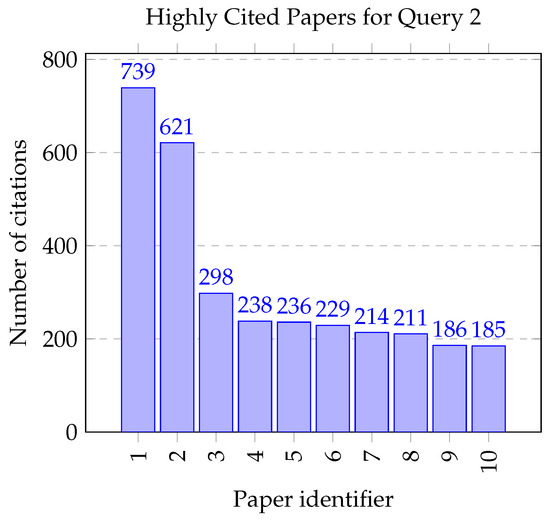
Figure 2.
Number of citations per paper for Query 2.

Table 6.
Most cited papers for query 2.
A discernible trend emerges from the analysis of these data: topics such as Deep Learning, Artificial Intelligence (AI), and various optimization techniques dominate the list of highly cited works. These subjects are pivotal in evolving computational methods applied to complex systems. The prominence of Artificial Intelligence, appearing in multiple entries, underscores its burgeoning influence across multiple research fronts.
The citation amounts present a steep initial descent from the apex citation count, suggesting a high variance in the recognition and influence of papers within the top ten. Such a pattern underscores the highly competitive nature of prominent research areas, where a few seminal works garner the bulk of citations. In contrast, others, despite their value, receive comparatively fewer citations. This hierarchy of scholarly impact is a testament to the dynamic nature of academic discourse within the domain defined by query Q2.
Figure 3 delineates the citation dynamics for three distinct research queries within power systems, as measured by normalized total citations. Query Q1, embracing advanced computational techniques, initially leads to citation impact, highlighting the scholarly emphasis on intricate methodologies for system stability and control. However, its influence recedes over time, suggesting a possible saturation or shift in research focus.
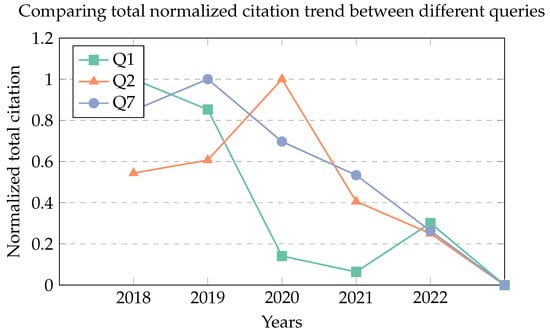
Figure 3.
Annual trends in normalized citation counts for distinct scopus queries.
In contrast, Query Q2, with its broader scope on computational techniques, including machine learning, ascends to citation prominence in 2020, underscoring the escalating relevance of data-centric algorithms in power systems research. This peak mirrors burgeoning trends toward Artificial Intelligence and optimization within the sector.
Query Q7, tightly linked to power system stabilizers, maintains a consistent citation presence, indicating sustained interest and ongoing discourse in optimizing system stability. The congruence of citation trajectories in 2022 implies a harmonization of research interests, reflecting a potential cross-pollination of ideas among the areas represented by the queries.
The bar graph in Figure 4 offers an insightful perspective on the normalized publication volume across three distinct queries within power system research. The visualization’s texture-rich bars each represent a unique query.
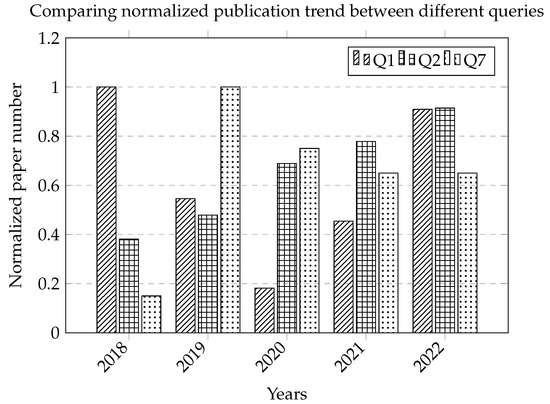
Figure 4.
Normalized publication number by year for different queries.
In the initial year showcased, Q1 captures a leading position, which could reflect the initial high interest or breakthroughs in advanced computational technologies applied to power systems. Over the years, however, the publications linked to Q1 and Q2 display a converging pattern, suggesting a possible cross-fertilization of ideas between computational techniques and machine learning within power system applications.
The graph’s uniform endpoint in 2022, where all queries align in normalized publication numbers, is particularly noteworthy. This convergence may imply a stabilization in research interest across the fields or a state of equilibrium achieved due to the saturation of the topics. Alternatively, it could indicate a collective shift in research focus towards emerging areas not captured by the existing queries.
Moreover, the steady performance of Q7 throughout the timeline signifies a consistent academic output, indicative of ongoing incremental advancements or a continuous reliance on established power system stabilizers and damping methods in the industry.
The scatter plot in Figure 5 eloquently illustrates the relationship between the year of publication and the normalized citation count for two distinct research queries within the power systems domain. An initial analysis reveals that publications from query Q7 garnered more citations in the earlier years, particularly in 2018 and 2019. This could indicate a robust foundational interest or the culmination of impactful research that resonated with contemporaneous academic efforts.
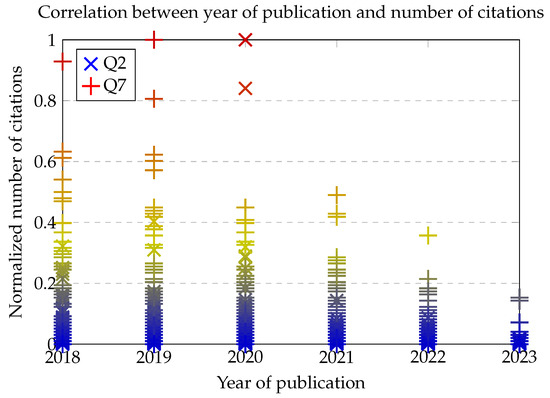
Figure 5.
Normalized number of citations by year of publication for queries Q2 and Q7.
In contrast, the upward citation trajectory for query Q2 beginning in 2020 suggests a shift in academic focus or delayed recognition of the relevance of these publications. The inflection point in 2020 may reflect emerging trends or technological advancements that increased the applicability of research related to Q2. As the body of literature grew, the intersection of computational techniques with power system stability and control began to yield more citable results, hence the increased citations.
While the normalized citation numbers offer a lens to measure the impact and relevance of research over time, they also hint at the evolving nature of scholarly priorities and interests. Despite the fluctuations, the consistent presence of citations throughout the years for both queries underscores the enduring significance of these topics in academic and practical applications. The data suggest an ecosystem where past research foundations pave the way for new explorations, with each query contributing to the progressive building of knowledge in the field.
Analyzing digital methods in power system monitoring and support highlights the field’s global research trends. This study’s geographical diversity, encompassing contributions from regions including the Middle East, North America, Europe, and Asia, offers a multifaceted view of technological advancements. This approach effectively addresses potential regional biases by transcending mere publication counts to consider research context and content. By integrating varied global perspectives and thematic analyses, this study provides a nuanced understanding of the evolving trends in this domain, accurately reflecting the current and future state of power system monitoring research.
5. Conclusions and Future Works
In conclusion, our analysis, underpinned by a meticulously structured methodology, goes beyond the simple quantification of publication numbers in digital methods for power system monitoring and support. Utilizing Boolean logic, our approach ensured a comprehensive and relevant collection of literature, capturing the intersection of critical areas in computational techniques and power system stability. This systematic process was not limited to counting publications but extended to a deeper evaluation of their relevance, diversity, and citation impact. The mathematical marking framework employed in our study was instrumental in quantitatively assessing the articles, providing a robust foundation for our analysis. This quantitative evaluation was complemented by a qualitative assessment, examining the impact and contribution of the publications to the field. Such a dual approach, blending quantitative retrieval with qualitative insights, forms the scientific backbone of our research. It offers a nuanced understanding of the trends and shifts in digital methods for power system monitoring and support, highlighting the popularity of these methods and their evolving significance and application in the field. This comprehensive analysis underscores the dynamic nature of technological advancements and their implications in power systems.
In power systems, integrating advanced computational techniques has marked a significant evolution, offering enhanced accuracy, efficiency, and robustness in system modeling and control. The exploration of various computational methods, from machine learning algorithms to sophisticated control strategies, has demonstrated their pivotal role in addressing the complexities of modern power networks. These methods have proven particularly effective in managing renewable energy integration challenges, ensuring system stability, and optimizing performance. The case studies reviewed underscore the transformative impact of these computational approaches, showcasing their ability to adapt to and efficiently manage the dynamic nature of power systems. This evolution points towards a future where power systems are more stable and efficient, innovative, and responsive to the changing energy landscape.
This comprehensive analysis of digital methods in power system monitoring and support, drawing from a diverse array of high-quality, peer-reviewed journals indexed in the SCOPUS database, significantly advances our understanding in this field. Prominent publications from IEEE, Elsevier, MDPI, and Springer highlight the interdisciplinary nature and evolving trends in power system stability and control. This research quantifies the prevalence of various methodologies and assesses their impact, offering valuable insights for future advancements in digital technologies for power systems.
The journey through the landscape of computational methods in power systems also highlights the challenges accompanying these technological advancements. Issues such as real-time processing, managing large volumes of data, and ensuring cybersecurity have emerged as critical areas requiring further innovation and research. The case studies and literature reviewed reveal that while computational methods have significantly advanced power system operations, the path forward involves addressing these challenges to harness their potential fully. The ongoing development of computational techniques, coupled with a deeper understanding of their implications for system stability and control, is essential for future power systems’ sustainable and efficient operation. This continuous evolution underscores the importance of research and development in this field, paving the way for more resilient and intelligent power networks.
The mathematical marking framework, applied to assess the effectiveness of each query, underscores the critical role of relevance, diversity, and citation impact in scholarly research. This quantitative approach reveals that while queries with a narrower focus, such as Q3 and Q5, offer high specificity, they risk overlooking critical advancements in the field. Conversely, broader queries, though capturing a wide range of studies, may dilute the focus. This analysis emphasizes the need for a balanced query design, aligning research scope with emerging trends and gaps in the field.
Analyzing citation trends and publication patterns within computational methods in power systems, as visualized through various graphs, reveals insightful patterns. The trend in normalized citations indicates a shifting academic focus, with particular research queries gaining prominence over others in specific years. For instance, query Q7’s papers were more cited in earlier years, while query Q2’s relevance surged later, highlighting evolving research interests. Similarly, the scatter plot analysis underscores the correlation between the year of publication and the number of citations, reflecting the dynamic nature of research impact over time. The bar chart of the most cited papers further illuminates the significant influence of specific topics, like Artificial Intelligence and Deep Learning, which dominate the top-cited research, indicating their pivotal role in shaping future research directions.
The comprehensive examination of citation and publication trends in power systems and computational methods offers an intriguing narrative of academic evolution. The uniform citation distribution in 2022 across different queries, as shown in the bar graph, suggests a convergence of research interest, possibly indicating a maturation of certain research areas or the emergence of unifying themes. This aspect, coupled with the distinct citation peaks for queries Q2 and Q7 in specific years, demonstrates the transient nature of research trends. Additionally, the analysis of the highly cited papers emphasizes the profound impact of innovative methodologies, particularly in Artificial Intelligence and optimization techniques. These insights portray a diverse and dynamic field, with research interests continually adapting to new challenges and technological advancements.
The analysis of queries for computational techniques in power system stability and control shows that striking a balance between specificity and breadth is crucial. Query Q2, which includes (‘Computational Techniques’ OR ‘Machine Learning’ OR ‘Optimization Algorithms’) AND (‘Power System Stability’ OR ‘Power System Control’) is the most effective methodology. It yielded 1097 papers and received the highest qualification score of 5. This query is an excellent example of the importance of encompassing a wide range of research areas while maintaining focus. It captures emerging trends in machine learning and optimization algorithms, alongside traditional computational techniques, making it an exemplary model for similar research endeavors. The success of Q2 in providing a comprehensive yet focused collection of literature underscores its significant contribution to the field. It positions it as a recommended approach for future studies seeking to explore the intersection of advanced computational methods and power system control.
Author Contributions
Conceptualization, methodology, software, resources, validation, and formal analysis, W.P., M.J. and J.C.V.; investigation and writing—original draft preparation, W.P.; writing—review and editing and supervision, M.J. and J.C.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Universidad Politécnica Salesiana-Ecuador.
Data Availability Statement
The datasets utilized in the paper “A Review of Modern Computational Techniques and Their Role in Power System Stability and Control” are publicly available for review and analysis. These datasets can be found at the following URL: http://wilsonpavon.info/datasets/ (accessed on 20 December 2023). This repository includes a series of datasets named as follows: scopusQ1.csv to scopusQ7.csv. Each file contains specific data used and analyzed in the study, contributing to the findings and conclusions. For further details regarding data handling and specifics, readers are encouraged to visit the provided link. The data provided at this location support the results reported in this study, allowing for the transparency and reproducibility of the research.
Acknowledgments
This paper presents partial results from the doctoral research undertaken within the PhD program at Università degli Studi di Ferrara, Italy. The research received support from Universidad Politécnica Salesiana and was further facilitated by the GIEHS (Grupo de Investigación de Entornos Habitables Sostenibles or Sustainable Living Environments Research Group) in 2023. Additionally, invaluable collaboration was provided by the Department of Energy at Aalborg University, Denmark. This multifaceted support and collaboration has been instrumental in advancing the research presented in this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dawood, K.; Komurgoz, G.; Isik, F. Evaluation of the Electromagnetic Forces in the Zigzag Transformer using a Computational Method. In Proceedings of the 2022 2nd International Conference on Digital Futures and Transformative Technologies, ICoDT2 2022, Rawalpindi, Pakistan, 24–26 May 2022; pp. 2–7. [Google Scholar]
- Alshammari, F.A.; Alshammari, G.A.; Guesmi, T.; Alzamil, A.A.; Alshammari, B.M.; Alshammari, A.S. Local Search-based Non-dominated Sorting Genetic Algorithm for Optimal Design of Multimachine Power System Stabilizers. Eng. Technol. Appl. Sci. Res. 2021, 11, 7283–7289. [Google Scholar] [CrossRef]
- Gani, S.M.A.; Islam, M.R.; Shafiullah, M.; Tayeb, J.H.; Hossain, M.I.; Ali, A. Equilibrium Optimizer for LFO Damping in Multimachine Power System Networks. In Proceedings of the 2022 International Conference on Advancement in Electrical and Electronic Engineering, ICAEEE 2022, Gazipur, Bangladesh, 24–26 February 2022; pp. 1–6. [Google Scholar]
- Latif, S.; Irshad, S.; Kamarposhti, M.A.; Shokouhandeh, H.; Colak, I.; Eguchi, K. Intelligent Design of Multi-Machine Power System Stabilizers (PSSs) Using Improved Particle Swarm Optimization. Electronics 2022, 11, 946. [Google Scholar] [CrossRef]
- Islam, M.S.; Islam, M.R.; Shafiullah, M.; Azam, M.S. Dragonfly Algorithm for Robust Tuning of Power System Stabilizers in Multimachine Networks. In Proceedings of the 2022 International Conference on Advancement in Electrical and Electronic Engineering, ICAEEE 2022, Gazipur, Bangladesh, 24–26 February 2022; pp. 1–6. [Google Scholar]
- Tabatabaeipour, S.M.; Blanke, M. Compositional finite-time stability analysis of nonlinear systems. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; American Automatic Control Council: New Orleans, LA, USA, 2014; pp. 1851–1857. [Google Scholar]
- Ghosh, S.; Isbeih, Y.J.; El Moursi, M.S.; El-Saadany, E.F. Cross-Gramian Model Reduction Approach for Tuning Power System Stabilizers in Large Power Networks. IEEE Trans. Power Syst. 2020, 35, 1911–1922. [Google Scholar] [CrossRef]
- Raibaudo, C.; Zhong, P.; Noack, B.R.; Martinuzzi, R. Machine learning strategies applied to the control of a fluidic pinball. Phys. Fluids 2020, 32, 015108. [Google Scholar] [CrossRef]
- Mohammed, O.; Kianfar, J. A Machine Learning Approach to Short-Term Traffic Flow Prediction: A Case Study of Interstate 64 in Missouri. In Proceedings of the IEEE International Smart Cities Conference (ISC2), Kansas City, MO, USA, 16–19 September 2018. [Google Scholar] [CrossRef]
- Nawaz, R.; Shahid, M.A.; Qureshi, I.; Mehmood, M. Machine learning based false data injection in smart grid. Int. J. Electr. Power Energy Syst. 2018, 130, 106819. [Google Scholar] [CrossRef]
- Andreou, A.; Mavromoustakis, C.; Mastorakis, G.; Mumtaz, S.; Batalla, J.M.; Pallis, E. Modified Machine Learning Technique for Curve Fitting on Regression Models for COVID-19 projections. In Proceedings of the IEEE 25th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), Pisa, Italy, 14–16 September 2020. [Google Scholar] [CrossRef]
- Alhelou, H.H.; Golshan, M.; Fini, M.H. Wind Driven Optimization Algorithm Application to Load Frequency Control in Interconnected Power Systems Considering GRC and GDB Nonlinearities. Electr. Power Components Syst. 2018, 46, 1223–1238. [Google Scholar] [CrossRef]
- Seck, G.S.; Krakowski, V.; Assoumou, E.; Maïzi, N.; Mazauric, V. Embedding power system’s reliability within a long-term Energy System Optimization Model: Linking high renewable energy integration and future grid stability for France by 2050. Appl. Energy 2020, 257, 114037. [Google Scholar] [CrossRef]
- Mohammadrezapour, O.; Piri, J.; Kisi, O. Comparison of SVM, ANFIS and GEP in modeling monthly potential evapotranspiration in an arid region (Case study: Sistan and Baluchestan Province, Iran). Water Sci. Technol. 2019, 19, 392–401. [Google Scholar] [CrossRef]
- Ren, H.; Pan, C.; Wang, K.; Xu, W.; Elkashlan, M.; Nallanathan, A. Joint Transmit Power and Placement Optimization for URLLC-Enabled UAV Relay Systems. IEEE Trans. Veh. Technol. 2020, 69, 8003–8007. [Google Scholar] [CrossRef]
- Yang, C.; Xue, Y.; Zhang, X.-P.; Zhang, Y.; Chen, Y. Real-Time FPGA-RTDS Co-Simulator for Power Systems. IEEE Access 2018, 6, 39576–39586. [Google Scholar] [CrossRef]
- Dawan, P.; Sriprapha, K.; Kittisontirak, S.; Boonraksa, T.; Junhuathon, N.; Titiroongruang, W.; Niemcharoen, S. Comparison of Power Output Forecasting on the Photovoltaic System Using Adaptive Neuro-Fuzzy Inference Systems and Particle Swarm Optimization-Artificial Neural Network Model. Energies 2020, 13, 351. [Google Scholar] [CrossRef]
- Lacroix, N.; Hellings, C.; Andersen, C.K.; Di Paolo, A.; Remm, A.; Lazar, S.; Krinner, S.; Norris, G.J.; Gabureac, M.; Heinsoo, J.; et al. Improving the Performance of Deep Quantum Optimization Algorithms with Continuous Gate Sets. PRX Quantum 2020, 1, 020304. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Liang, X.; Huang, B. Event-Triggered-Based Distributed Cooperative Energy Management for Multienergy Systems. IEEE Trans. Ind. Inform. 2019, 15, 2008–2022. [Google Scholar] [CrossRef]
- Verdejo, H.; Pino, V.; Kliemann, W.; Becker, C.; Delpiano, J. Implementation of Particle Swarm Optimization (PSO) Algorithm for Tuning of Power System Stabilizers in Multimachine Electric Power Systems. Energies 2020, 13, 2093. [Google Scholar] [CrossRef]
- Ekinci, S.; Demirören, A.; Hekimoğlu, B. Parameter optimization of power system stabilizers via kidney-inspired algorithm. Trans. Inst. Meas. Control 2018, 41, 1405–1417. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J. Artificial Intelligence Based MPPT Techniques for Solar Power System: A review. Mod. Power Syst. Clean Energy 2020, 8, 1043–1059. [Google Scholar] [CrossRef]
- Ahmad, N.; Ghadi, Y.; Adnan, M.; Ali, M. Load Forecasting Techniques for Power System: Research Challenges and Survey. IEEE Access 2022, 10, 71054–71090. [Google Scholar] [CrossRef]
- Eremeeva, A.; Ilyushin, Y. Automation of the control system for drying grain crops of the technological process for obtaining biodiesel fuels. Sci. Rep. 2023, 13, 14956. [Google Scholar] [CrossRef]
- Ilyushin, Y.; Kapostey, E. Developing a Comprehensive Mathematical Model for Aluminium Production in a Soderberg Electrolyser. Energies 2023, 16, 6313. [Google Scholar] [CrossRef]
- Bedi, G.; Venayagamoorthy, G.; Singh, R.; Brooks, R.R.; Wang, K.-C. Review of Internet of Things (IoT) in Electric Power and Energy Systems. IEEE Internet Things J. 2018, 5, 847–870. [Google Scholar] [CrossRef]
- Karamanakos, P.; Liegmann, E.; Geyer, T.; Kennel, R. Model Predictive Control of Power Electronic Systems: Methods, Results, and Challenges. IEEE Open J. Ind. Appl. 2020, 1, 172–186. [Google Scholar] [CrossRef]
- Soares, J.; Pinto, T.; Lezama, F.; Morais, H. Survey on Complex Optimization and Simulation for the New Power Systems Paradigm. Complexity 2018, 2018, 2340628. [Google Scholar] [CrossRef]
- Li, S.; Li, L.; Li, Z.; Chen, X.; Fernando, T.; Iu, H.; He, G.; Wang, Q.; Liu, X. Event-Trigger Heterogeneous Nonlinear Filter for Wide-Area Measurement Systems in Power Grid. IEEE Trans. Smart Grid 2019, 10, 3203–3212. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Z.; Huang, Q.; Wang, N.; Zhang, X.; Lee, W. Improved Wind Farm Aggregated Modeling Method for Large-Scale Power System Stability Studies. IEEE Trans. Power Syst. 2018, 33, 5958–5968. [Google Scholar] [CrossRef]
- Jin, L.; He, Y.; Zhang, C.-K.; Shangguan, X.-C.; Jiang, L.; Wu, M. Robust Delay-Dependent Load Frequency Control of Wind Power System Based on a Novel Reconstructed Model. IEEE Trans. Cybern. 2021, 51, 3100–3111. [Google Scholar] [CrossRef] [PubMed]
- Devarapalli, R.; Sinha, N.; Márquez, F.P.G. A Review on the Computational Methods of Power System Stabilizer for Damping Power Network Oscillations. Arch. Comput. Methods Eng. 2022, 29, 3713–3739. [Google Scholar] [CrossRef]
- He, B.; Chen, W.; Ruan, X.; Zhang, X.; Zou, Z.; Cao, W. A Generic Small-Signal Stability Criterion of DC Distribution Power System: Bus Node Impedance Criterion (BNIC). IEEE Trans. Power Electron. 2022, 37, 5741–5752. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, R.; Ashfaq, H.; Singh, S.K.; Badoni, M. Power system stability enhancement by damping and control of Sub-synchronous torsional oscillations using Whale optimization algorithm based Type-2 wind turbines. ISA Trans. 2021, 108, 240–256. [Google Scholar] [CrossRef]
- Acharya, D.; Das, D.K.; Rai, A. Particle Swarm Optimization (PSO) based 2-DoF-PID power system stabilizer design for damping out low frequency oscillations in power systems. In Proceedings of the 2nd International Conference on Innovations in Electronics, Signal Processing and Communication, IESC 2019, Shillong, India, 1–2 March 2019; pp. 148–153. [Google Scholar]
- Alshammari, B.M.; Guesmi, T. New Chaotic Sunflower Optimization Algorithm for Optimal Tuning of Power System Stabilizers. J. Electr. Eng. Technol. 2020, 15, 1985–1997. [Google Scholar] [CrossRef]
- Morsali, J. TID-based PSS2B to Overcome LFO Issue in Multi-machine Power Systems. In Proceedings of the 2022 30th International Conference on Electrical Engineering, ICEE 2022, Tehran, Iran, 17–19 May 2022; pp. 968–973. [Google Scholar]
- Abu-Fedda, A.; Feilat, E.A. Optimal Tuning of Power System Stabilizers Using Metaheuristic Optimization Algorithms: A Comparative Study. In Proceedings of the 2022 International Conference on Smart Systems and Power Management, IC2SPM 2022, Beirut, Lebanon, 10–12 November 2022; pp. 141–146. [Google Scholar]
- Tayeb, J.H.; Islam, M.R.; Shafiullah, M.; Gani, S.M.A.; Hossain, M.I. Robust Power System Stabilizer for Multi-machine Power Networks using Tunicate Swarm Algorithm. In Proceedings of the 2nd International Conference on Artificial Intelligence and Smart Energy, ICAIS 2022, Coimbatore, India, 23–25 February 2022; pp. 1761–1766. [Google Scholar]
- Shafiullah, M.; Rana, M.J.; Shahriar, M.S.; Al-Sulaiman, F.A.; Ahmed, S.D.; Ali, A. Extreme learning machine for real-time damping of LFO in power system networks. Electr. Eng. 2021, 103, 279–292. [Google Scholar] [CrossRef]
- Baerthlein, E.M.; Parolini, L.; Hartung, M.; Panosyan, A.; Serra, E.B.; Witzmann, R. Variable bandwidth computation for tap changer control in distribution grids. In Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference, Dallas, TX, USA, 3–5 May 2016; pp. 1–5. [Google Scholar]
- Aydin, B.; Poyrazoglu, G. Algorithmic Approaches for DER Sizing and Spatial Placement in Radial Networks. In Proceedings of the 2023 IEEE 5th Global Power, Energy and Communication Conference, GPECOM 2023, Nevsehir, Turkiye, 14–16 June 2023; pp. 364–369. [Google Scholar]
- Folly, K.A.; Mulumba, T.F. A Study on the Impact of DE Population Size on the Performance Power System Stabilizers. Adv. Distrib. Comput. Artif. Intell. J. 2022, 11, 97–109. [Google Scholar]
- Velasquez, R.M.A.; Ezcurra, T.T.P.; Aldon, L.F.V. Power System Stabilizer Design with meta-heuristic methods in a Peruvian case study. In Proceedings of the 2022 IEEE 29th International Conference on Electronics, Electrical Engineering and Computing, INTERCON 2022, Lima, Peru, 11–13 August 2022; pp. 4–7. [Google Scholar]
- Kasilingam, G.; Pasupuleti, J.; Kasirajan, S.K.; Nagarathinam, A.; Natesan, D. Optimal Design of Damping Control of Oscillations in Power System Using Power System Stabilizers with Novel Improved BBO Algorithm. Indones. J. Electr. Eng. Inform. 2022, 10, 879–890. [Google Scholar] [CrossRef]
- Sarkar, D.U.; Prakash, T. A Neural Network Approach to Design Power System Stabilizer for Damping Power Oscillations. In Proceedings of the 2022 22nd National Power Systems Conference, NPSC 2022, New Delhi, India, 17–19 December 2022; pp. 837–842. [Google Scholar]
- Sarkar, D.U.; Prakash, T. A Novel Design of Power System Stabilizer via GWO-tuned Radial-basis Function Neural Network for Damping Power Oscillations. In Proceedings of the 2022 IEEE 10th Power India International Conference, PIICON 2022, New Delhi, India, 25–27 November 2022; pp. 1–6. [Google Scholar]
- Mehta, D.; Molzahn, D.K.; Turitsyn, K. Recent advances in computational methods for the power flow equations. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016; American Automatic Control Council (AACC): New Orleans, LA, USA, 2016; pp. 1753–1765. [Google Scholar]
- El kashlan, A.; El kashlan, S. Pi Power System Controller: Eigenstructure—Based Design and Sensitivities. Int. J. Energy Environ. 2021, 15, 84–89. [Google Scholar] [CrossRef]
- Chen, T.; Mehta, D. On the Network Topology Dependent Solution Count of the Algebraic Load Flow Equations. IEEE Trans. Power Syst. 2018, 33, 1451–1460. [Google Scholar] [CrossRef]
- Wang, S.; Scells, H.; Koopman, B.; Zuccon, G. Can ChatGPT Write a Good Boolean Query for Systematic Review Literature Search? arXiv 2023, arXiv:2302.03495. [Google Scholar]
- Scells, H.; Zuccon, G.; Koopman, B. Automatic Boolean Query Refinement for Systematic Review Literature Search. In Proceedings of the WWW’19: The World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019. [Google Scholar] [CrossRef]
- Zhao, T.; Yue, M.; Wang, J. Robust Power System Stability Assessment Against Adversarial Machine Learning-Based Cyberattacks via Online Purification. IEEE Trans. Power Syst. 2023, 38, 5613–5622. [Google Scholar] [CrossRef]
- Gros, I.-C.; Lü, X.; Oprea, C.; Lu, T.; Pintilie, L. Artificial intelligence (AI)-based optimization of power electronic converters for improved power system stability and performance. In Proceedings of the 2023 IEEE 14th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Chania, Greece, 28–31 August 2023. [Google Scholar] [CrossRef]
- Yin, Z.; Dai, X.; Yang, Z.; Shen, Y.-W.; Hattab, G.; Zhao, H. Learning-based Control for PMSM Using Distributed Gaussian Processes with Optimal Aggregation Strategy. arXiv 2023. [Google Scholar] [CrossRef]
- Alimi, O.A.; Ouahada, K.; Abu-Mahfouz, A.M. A Review of Machine Learning Approaches to Power System Security and Stability. IEEE Access 2020, 8, 113512–113531. [Google Scholar] [CrossRef]
- Fu, X. Statistical machine learning model for capacitor planning considering uncertainties in photovoltaic power. Prot. Control Mod. Power Syst. 2022, 7, 5. [Google Scholar] [CrossRef]
- Verkerken, M.; D’hooge, L.; Wauters, T.; Volckaert, B.; De Turck, F. Towards Model Generalization for Intrusion Detection: Unsupervised Machine Learning Techniques. J. Netw. Syst. Manag. 2021, 30, 1–25. [Google Scholar] [CrossRef]
- Injeti, S.K.; Thunuguntla, V.K. Optimal integration of DGs into radial distribution network in the presence of plug-in electric vehicles to minimize daily active power losses and to improve the voltage profile of the system using bio-inspired optimization algorithms. Prot. Control Mod. Power Syst. 2020, 5, 1–15. [Google Scholar] [CrossRef]
- Meegahapola, L.; Sguarezi, A.; Bryant, J.S.; Gu, M.; Conde D, E.R.; Cunha, R.B. Power System Stability with Power-Electronic Converter Interfaced Renewable Power Generation: Present Issues and Future Trends. Energies 2020, 13, 3441. [Google Scholar] [CrossRef]
- Guerra, K.; Haro, P.; Gutiérrez, R.E.; Gómez-Barea, A. Facing the high share of variable renewable energy in the power system: Flexibility and stability requirements. Appl. Energy 2022, 310, 118561. [Google Scholar] [CrossRef]
- Fuller, A.; Fan, Z.; Day, C.; Barlow, C. Digital Twin: Enabling Technologies, Challenges and Open Research. IEEE Access 2020, 8, 108952–108971. [Google Scholar] [CrossRef]
- Rasheed, A.; San, O.; Kvamsdal, T. Digital twin: Values, challenges and enablers from a modeling perspective. IEEE Access 2020, 8, 21980–22012. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Kadir, S.J.A.; Rais, H.M.; Mirjalili, S.; Alhussian, H. Binary Optimization Using Hybrid Grey Wolf Optimization for Feature Selection. IEEE Access 2019, 7, 39496–39508. [Google Scholar] [CrossRef]
- James, J.Q.; Hill, D.J.; Lam, A.Y.; Gu, J.; Li, V.O. Intelligent time-adaptive transient stability assessment system. IEEE Trans. Power Syst. 2018, 33, 1049–1058. [Google Scholar] [CrossRef]
- Minerva, R.; Lee, G.M.; Crespi, N. Digital Twin in the IoT Context: A Survey on Technical Features, Scenarios, and Architectural Models. Proc. IEEE 2020, 108, 1785–1824. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Mosallanezhad, M.; Rashid, A.S.A.; Pradhan, B. Modification of landslide susceptibility mapping using optimized PSO-ANN technique. Eng. Comput. 2019, 35, 967–984. [Google Scholar] [CrossRef]
- Mythili, S.; Thiyagarajah, K.; Rajesh, P.; Shajin, F.H. Ideal position and size selection of unified power flow controllers (Upfcs) to upgrade the dynamic stability of systems: An antlion optimiser and invasive weed optimisation algorithm. HKIE Trans. 2020, 27, 25–37. [Google Scholar] [CrossRef]
- Duan, J.; Shi, D.; Diao, R.; Li, H.; Wang, Z.; Zhang, B.; Bian, D.; Yi, Z. Deep-Reinforcement-Learning-Based Autonomous Voltage Control for Power Grid Operations. IEEE Trans. Power Syst. 2020, 35, 814–817. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Y.; Wei, Q.; Liu, X. Residential energy scheduling for variable weather solar energy based on adaptive dynamic programming. IEEE/CAA J. Autom. Sin. 2018, 5, 36–46. [Google Scholar] [CrossRef]
- Luo, L.; Abdulkareem, S.S.; Rezvani, A.; Miveh, M.R.; Samad, S.; Aljojo, N.; Pazhoohesh, M. Optimal scheduling of a renewable based microgrid considering photovoltaic system and battery energy storage under uncertainty. J. Energy Storage 2020, 28, 101306. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).