FastInformer-HEMS: A Lightweight Optimization Algorithm for Home Energy Management Systems
Abstract
1. Introduction
- (a)
- A lightweight optimization algorithm called the FastInformer-HEMS is proposed, which introduces the E-Attn attention mechanism [21] and uses global average pooling to extract attention features and improve the accuracy of a battery energy level’s multi-step prediction and effectively reduce the computational complexity.
- (b)
- Considering the need for safe operation, self-consumption maximum (SCM) is introduced as the backup security policy for the first time to ensure that the executed strategy is safe and feasible.
- (c)
- The simulation results show that the proposed algorithm has lower electricity cost than the existing HEMS algorithms, and it has the lowest computational complexity among all algorithms.
2. Background of Home Energy Management
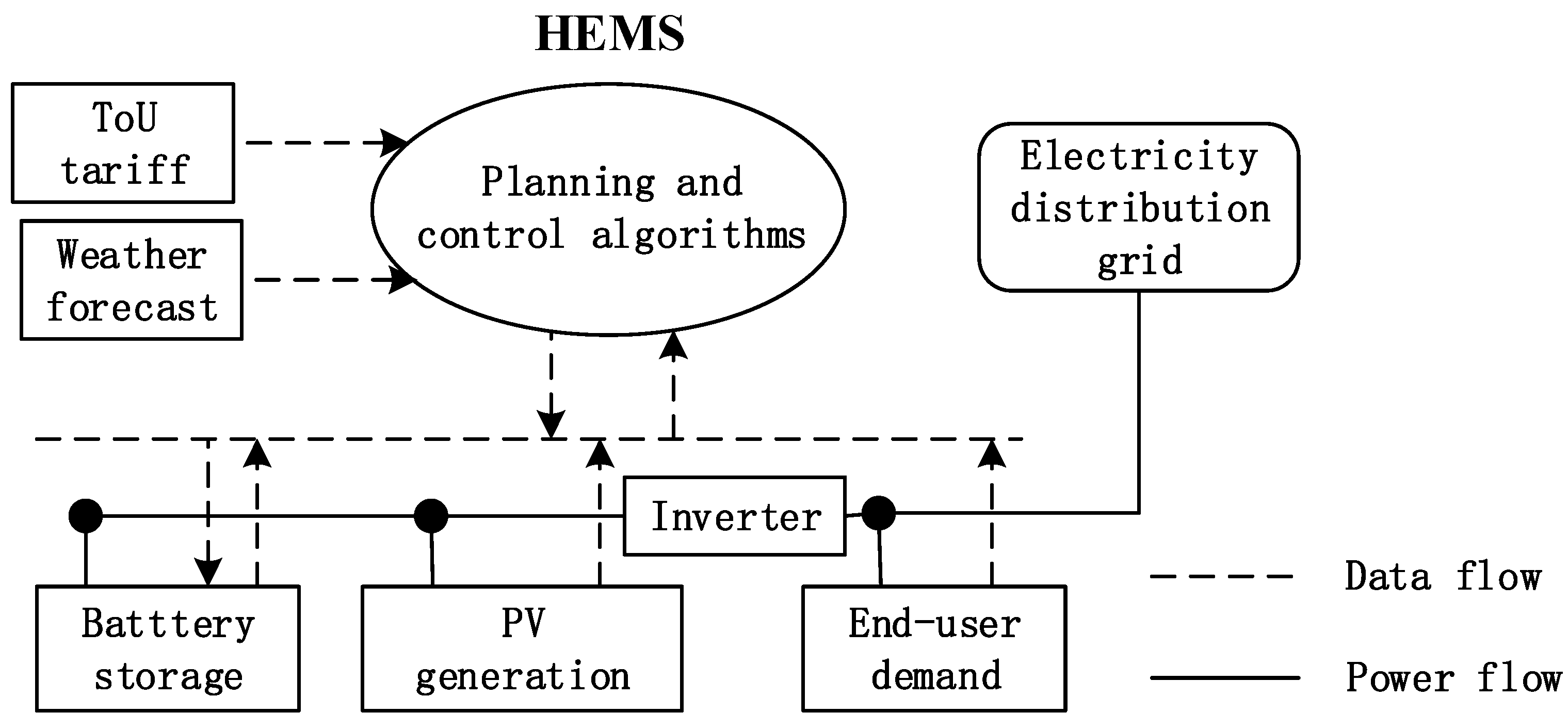
2.1. Structure of Home Energy System
2.2. Home Energy Management Optimization
2.3. Algorithm Based on Machine Learning for Home Energy Management System
3. FastInformer-HEMS Algorithm
3.1. Algorithm Framework
3.1.1. Prediction Module
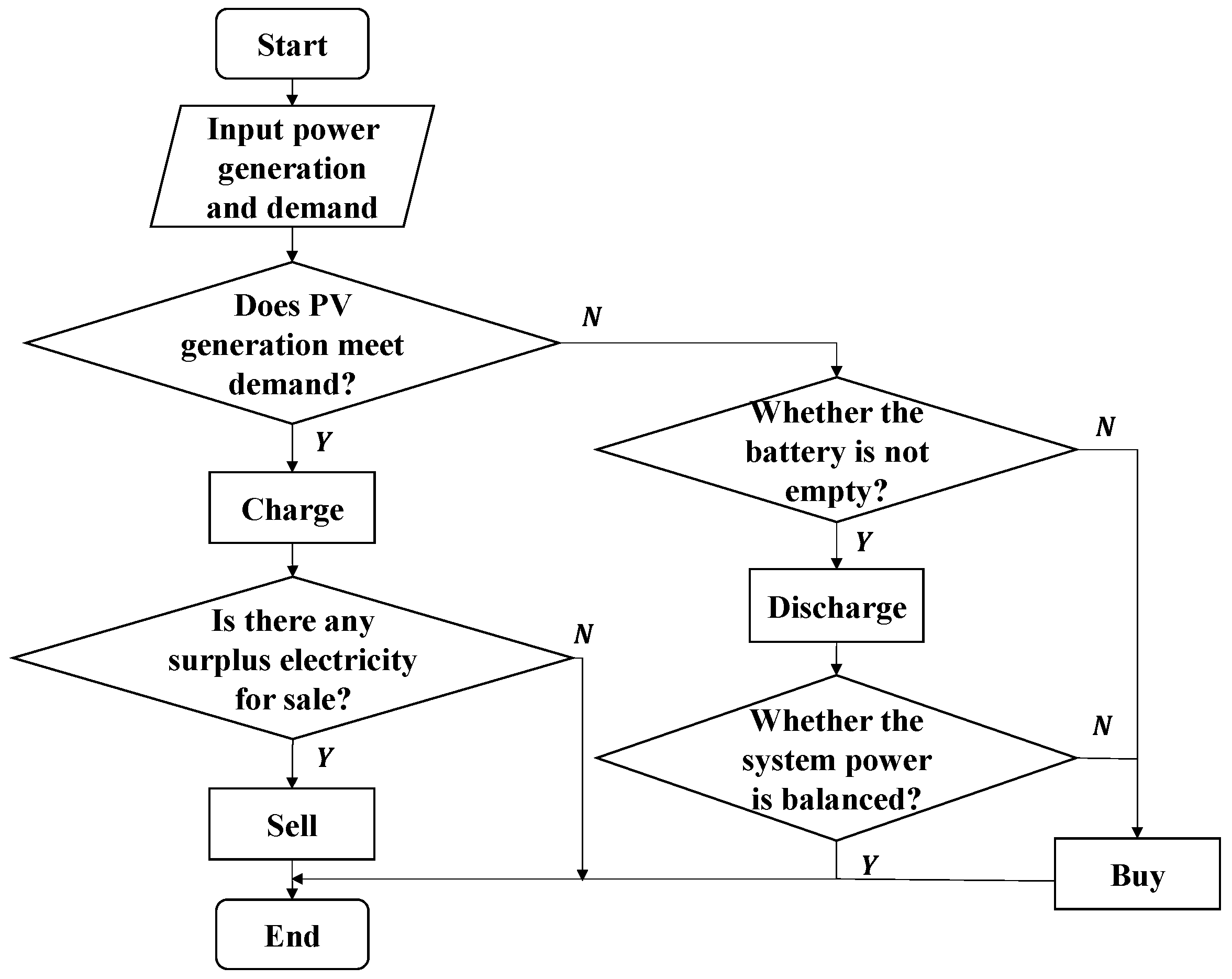
3.1.2. Safety Module
3.1.3. Strategy Generation Module
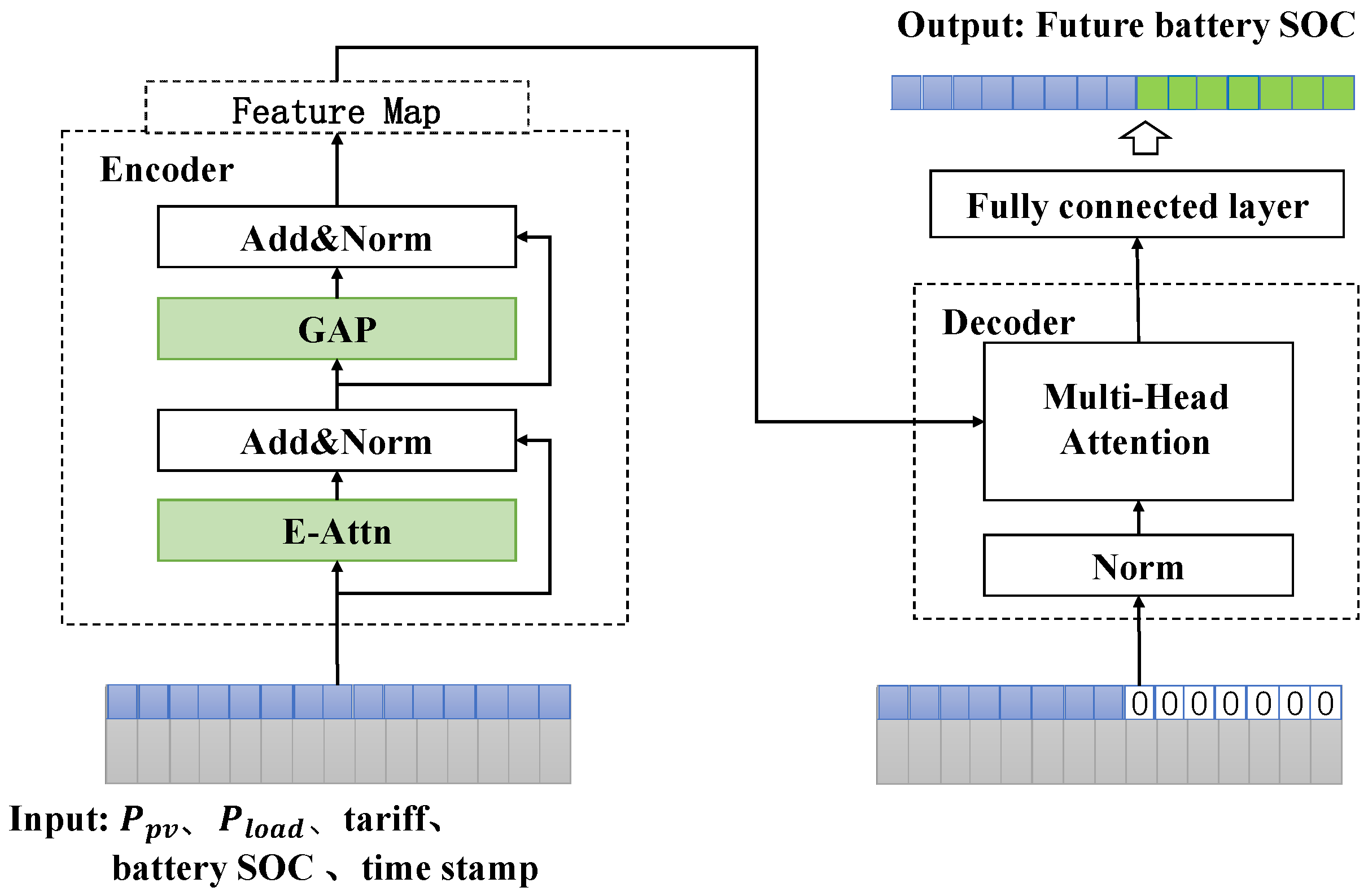
3.2. FastInformer Model
3.2.1. Encoder
3.2.2. Decoder
4. Results and Analysis
4.1. Dataset
4.2. Experiment Setup
4.3. Comparison Algorithm and Evaluation Index
- (a)
- The mixed integer linear programming algorithm (MILP), which assumes that the future PV and load demand are perfectly predictable so that its planning quality is the highest.
- (b)
- The HEMS algorithm based on LSTM (LSTM-HEMS), which is a good choice to avoid the high computational complexity of MILP at present. It adopts the LSTM model to predict decision variables step by step as shown in Figure 2a.
- (c)
- The Informer-based algorithm for an HEMS (Informer-HEMS), which introduces Informer to realize the multi-step prediction of the battery energy level.
4.4. Analysis of Experiment Results
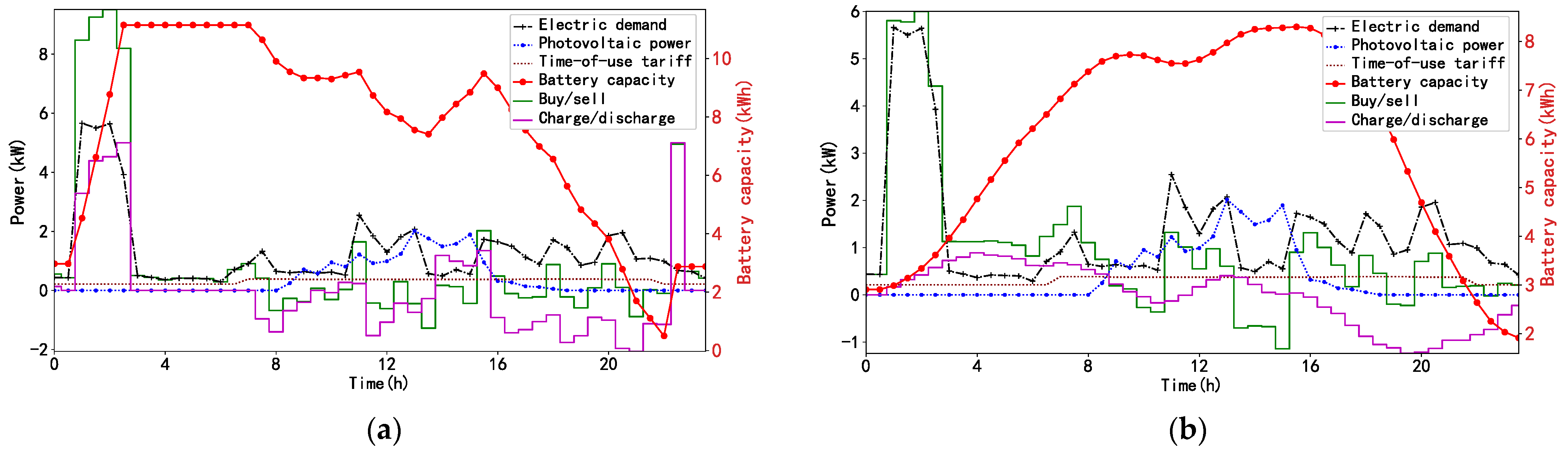
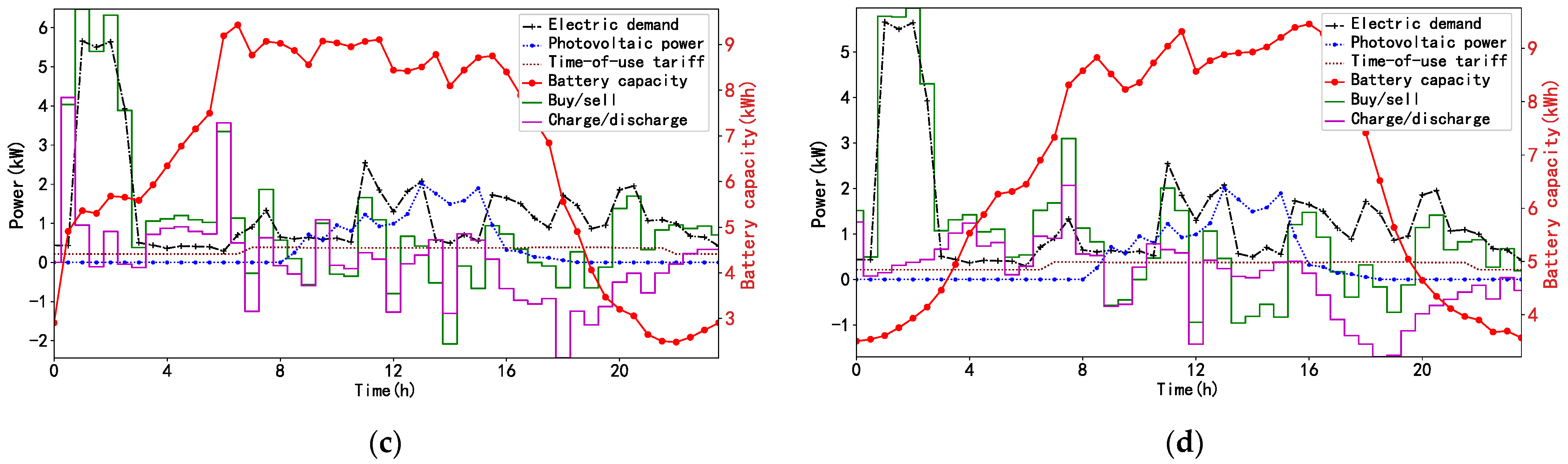
4.4.1. Quality of Strategies over a Day
4.4.2. Cost of Strategies over Several Days
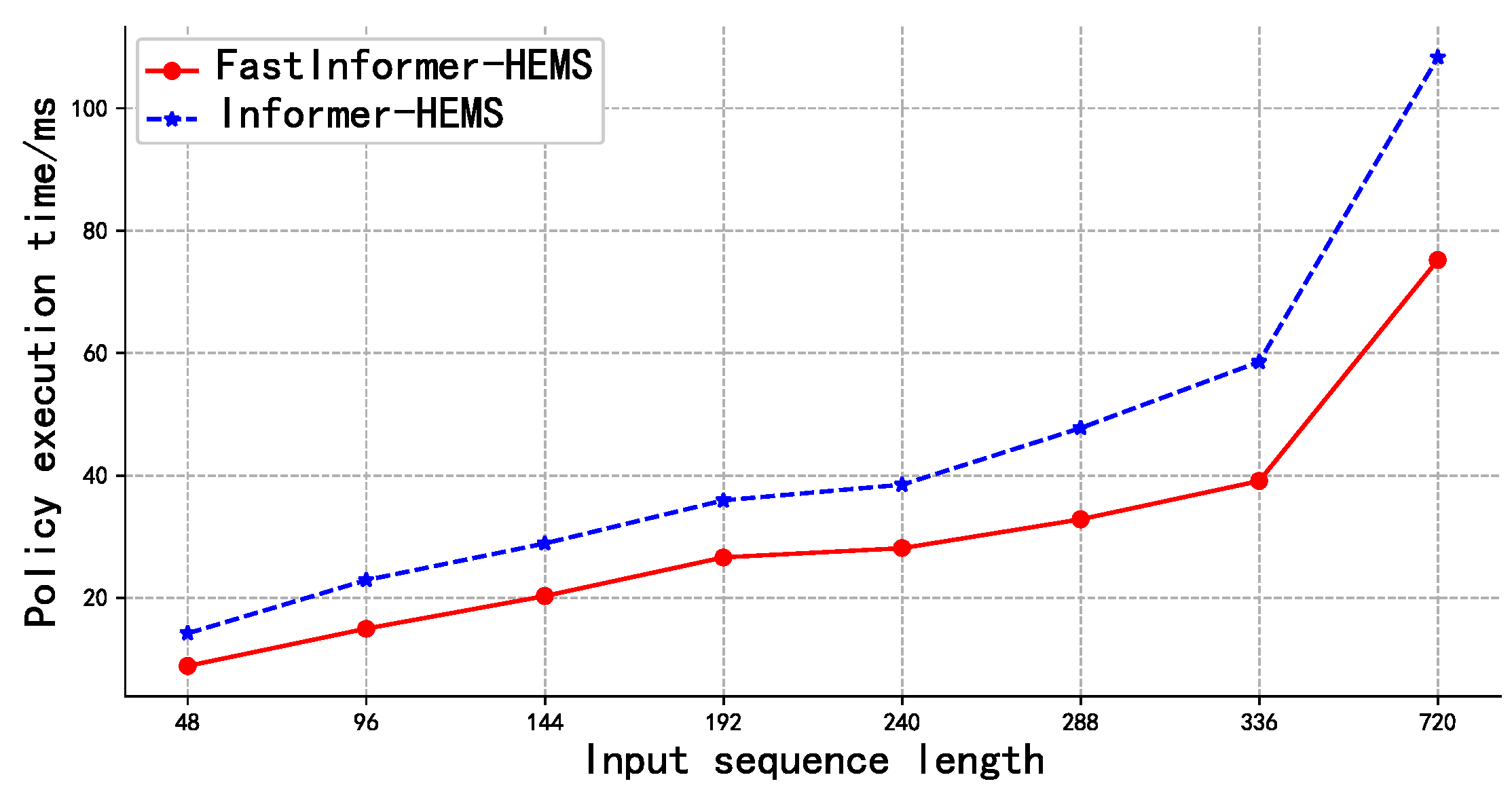
4.4.3. Execution Time of Strategies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paridari, K.; Nordstrom, L.; Sandels, C. Aggregator strategy for planning demand response resources under un-certainty based on load flexibility modeling. In Proceedings of the 2017 IEEE International Conference on Smart Grid Communications, Dresden, Germany, 23–27 October 2017; pp. 338–343. [Google Scholar]
- Kwac, J.; Flora, J.; Rajagopal, R. Household energy consumption segmentation using hourly data. IEEE Trans. Smart Grid 2014, 5, 420–430. [Google Scholar] [CrossRef]
- Azuatalam, D.; Paridari, K.; Ma, Y.; Förstl, M.; Chapman, A.C.; Verbič, G. Energy management of small-scale PV-battery systems: A systematic review considering practical implementation, computational requirements, quality of input data and battery degradation. Renew. Sustain. Energy Rev. 2019, 112, 555–570. [Google Scholar] [CrossRef]
- Bouakkaz, A.; Mena, A.J.G.; Haddad, S.; Ferrari, M.L. Efficient energy scheduling considering cost reduction and energy saving in hybrid energy system with energy storage. J. Energy Storage 2021, 33, 101887. [Google Scholar] [CrossRef]
- Ahmad, A.; Khan, A.; Javaid, N.; Hussain, H.M.; Abdul, W.; Almogren, A.; Alamri, A.; Niaz, I.A. An optimized home energy management system with integrated renewable energy and storage resources. Energies 2017, 10, 549. [Google Scholar] [CrossRef]
- Azuatalam, D.; Verbic, G.; Chapman, A. Impacts of net-work tariffs on distribution network power flows. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, VIC, Australia, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Keerthisinghe, C.; Verbič, G.; Chapman, A.C. A Fast Technique for Smart Home Management: ADP With Temporal Difference Learning. IEEE Trans. Smart Grid 2018, 9, 3291–3303. [Google Scholar] [CrossRef]
- Zhao, Z.; Keerthisinghe, C. A Fast and Optimal Smart Home Energy Management System: State-Space Approximate Dynamic Programming. IEEE Access 2020, 8, 184151–184159. [Google Scholar] [CrossRef]
- Keerthisinghe, C.; Verbič, G.; Chapman, A.C. Addressing the stochastic nature of energy management in smart homes. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar]
- Xu, X.; Jia, Y.; Xu, Y.; Xu, Z.; Chai, S.; Lai, C.S. A Multi-Agent Reinforcement Learning-Based Data-Driven Method for Home Energy Management. IEEE Trans. Smart Grid 2020, 11, 3201–3211. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Xie, W.; Xie, D.; Zou, Y.; Zhang, D.; Sun, Z.; Zhang, L.; Zhang, Y.; Jiang, T. Deep reinforcement learning for smart home energy management. IEEE Internet Things J. 2019, 7, 2751–2762. [Google Scholar] [CrossRef]
- Chen, S.; Wang, M.; Song, W.; Yang, Y.; Li, Y.; Fu, M. Stabilization approaches for reinforcement learning-based end-to-end autonomous driving. IEEE Trans. Veh. Technol. 2020, 69, 4740–4750. [Google Scholar] [CrossRef]
- Dinh, H.T.; Lee, K.-H.; Kim, D. Supervised-learning-based hour-ahead demand response for a behavior-based home energy management system approximating MILP optimization. Appl. Energy 2022, 321, 119382. [Google Scholar] [CrossRef]
- Kim, Y.J. A supervised-learning-based strategy for optimal demand response of an hvac system in a multi-zone office building. IEEE Trans. Smart Grid 2020, 11, 4212–4226. [Google Scholar] [CrossRef]
- Dinh, H.T.; Kim, D. Milp-based imitation learning for hvac control. IEEE Internet Things J. 2021, 9, 6107–6120. [Google Scholar] [CrossRef]
- Gao, S.; Xiang, C.; Yu, M.; Tan, K.T.; Lee, T.H. Online optimal power scheduling of a microgrid via imitation learning. IEEE Trans. Smart Grid 2021, 13, 861–876. [Google Scholar] [CrossRef]
- Paridari, K.; Azuatalam, D.; Chapman, A.C.; Verbič, G.; Nordström, L. A plug-and-play home energy management algorithm using optimization and machine learning techniques. In Proceedings of the 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids, Aalborg, Denmark, 29 October–1 November 2018; pp. 1–6. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence (AAAI-21), Virtual, 2–9 February 2021. [Google Scholar]
- Guo, M.-H.; Liu, Z.-N.; Mu, T.-J.; Hu, S.-M. Beyond Self-Attention: External Attention Using Two Linear Layers for Visual Tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5436–5447. [Google Scholar] [CrossRef] [PubMed]
- Ausgrid, Smart-Grid Smart-City Customer Trial Data, Online, 2016, data.gov. Available online: https://data.gov.au/dataset/smart-grid-smart-city-customer-trial-data (accessed on 10 March 2023).
- Xavier, L.S.; De Sousa, C.V.; Pereira, H.A.; Mendes, V.F. Design and performance comparisons of power converters for battery energy storage systems. Int. J. Circ. Theor. Appl. 2023; in press. [Google Scholar] [CrossRef]








| Variable | Value |
|---|---|
| Battery capacity (kWh) | 14.0 |
| Depth of discharge (kWh) | 13.5 |
| Maximum charging power (kW) | 5.0 |
| Efficiency | 90% |
| Hyperparameter | Space |
|---|---|
| Input length of encoder | [12-336] |
| Label length of decoder | [4-168] |
| Output length of decoder | [1-96] |
| Batch size | [1-64] |
| Attention heads | [4,8,16] |
| Typical Scenarios | Electricity Demand (kWh) | PV Generation (kWh) |
|---|---|---|
| Scenario 1 | 21.770 | 31.739 |
| Scenario 2 | 19.699 | 9.136 |
| Policies | Cost in Scenario 1 ($) | Cost in Scenario 2 ($) |
|---|---|---|
| Benchmark (no PV-battery) | 6.662 (100%) | 9.660 (100%) |
| MILP | 2.280 (34.2%) | 5.000 (51.8%) |
| LSTM-HEMS | 3.831 (57.5%) | 6.564 (68.0%) |
| Informer-HEMS | 2.650 (39.8%) | 5.650 (58.5%) |
| FastInformer-HEMS | 3.014 (45.2%) | 5.935 (61.4%) |
| Policies | Cost ($/Week) | Cost ($/Month) | Cost ($/4 months) |
|---|---|---|---|
| Benchmark (no PV-battery) | 56.798 (100%) | 248.431 (100%) | 1085.108 (100%) |
| MILP | 24.660 (43.4%) | 114.096 (45.9%) | 554.285 (51.1%) |
| LSTM-HEMS | 35.113 (61.8%) | 155.766 (62.7%) | 157.505 (63.4%) |
| Informer-HEMS | 30.554 (53.8%) | 141.109 (56.8%) | 638.044 (58.8%) |
| FastInformer-HEMS | 31.543 (55.5%) | 144.338 (58.1%) | 645.639 (59.5%) |
| Policies | Time (s) |
|---|---|
| MILP | 10.740 |
| LSTM-HEMS | 0.204 |
| Informer-HEMS | 0.023 |
| FastInformer-HEMS | 0.015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Ning, D. FastInformer-HEMS: A Lightweight Optimization Algorithm for Home Energy Management Systems. Energies 2023, 16, 3897. https://doi.org/10.3390/en16093897
Chen X, Ning D. FastInformer-HEMS: A Lightweight Optimization Algorithm for Home Energy Management Systems. Energies. 2023; 16(9):3897. https://doi.org/10.3390/en16093897
Chicago/Turabian StyleChen, Xihui, and Dejun Ning. 2023. "FastInformer-HEMS: A Lightweight Optimization Algorithm for Home Energy Management Systems" Energies 16, no. 9: 3897. https://doi.org/10.3390/en16093897
APA StyleChen, X., & Ning, D. (2023). FastInformer-HEMS: A Lightweight Optimization Algorithm for Home Energy Management Systems. Energies, 16(9), 3897. https://doi.org/10.3390/en16093897




