Numerical Simulation on the Influence of Inlet Flow Characteristics on the Performance of a Centrifugal Compressor
Abstract
1. Introduction
2. Methodology
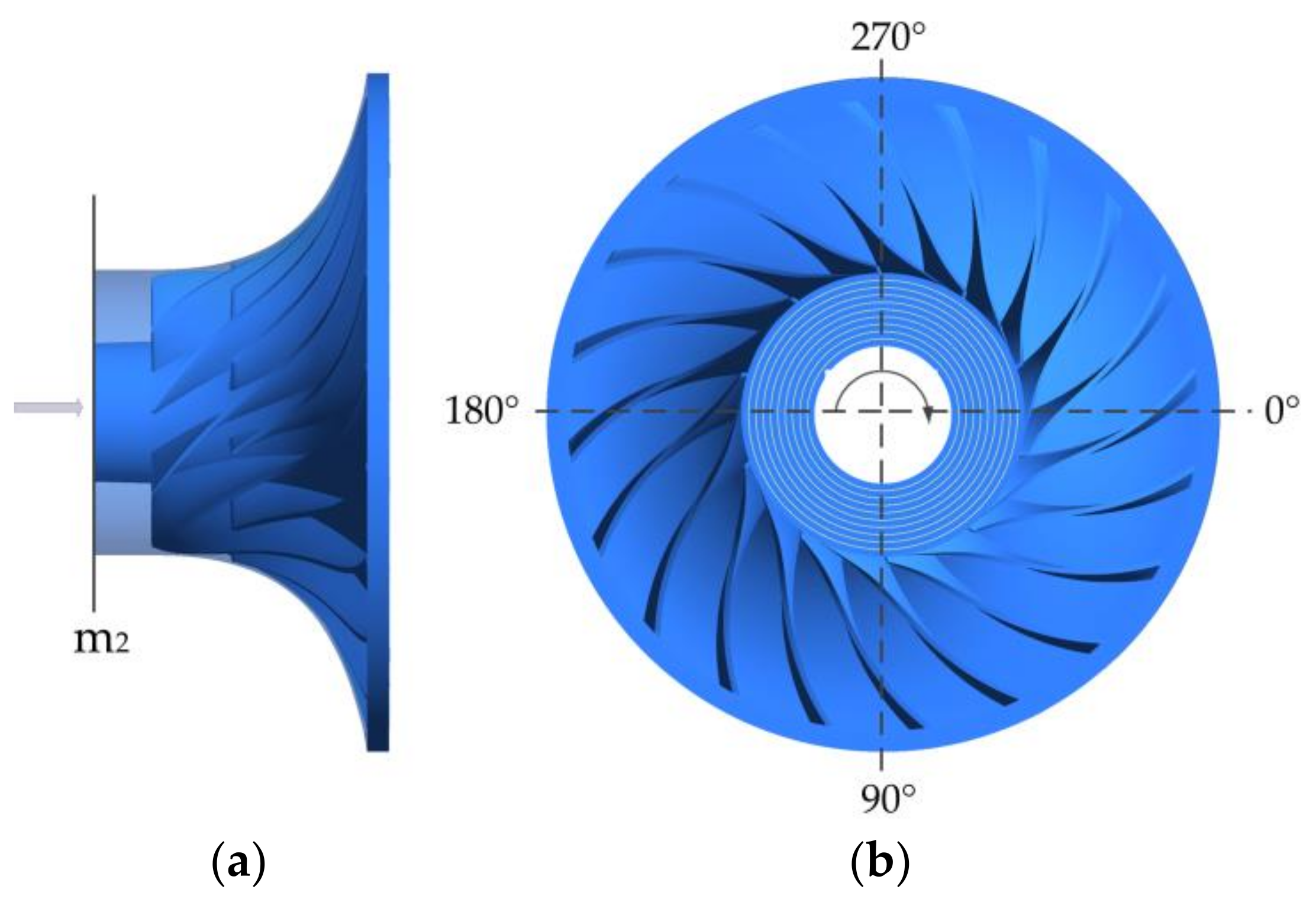
2.1. Model Centrifugal Compressor
2.2. Numerical Simulation Method
2.3. Mesh generation and independence test
3. Numerical Simulations of Centrifugal Compressor with Different Inlet Bent Pipes
3.1. Validation of Numerical Simulation
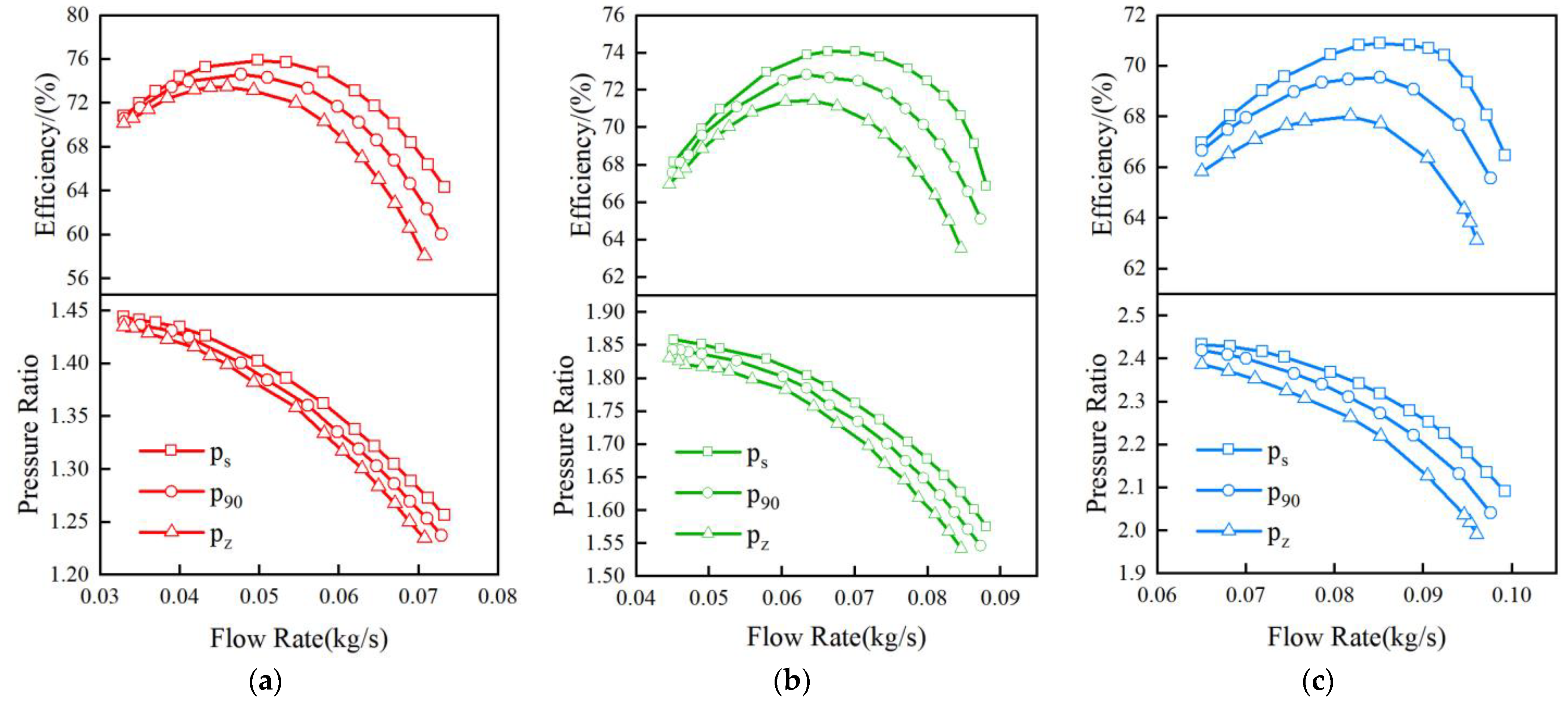
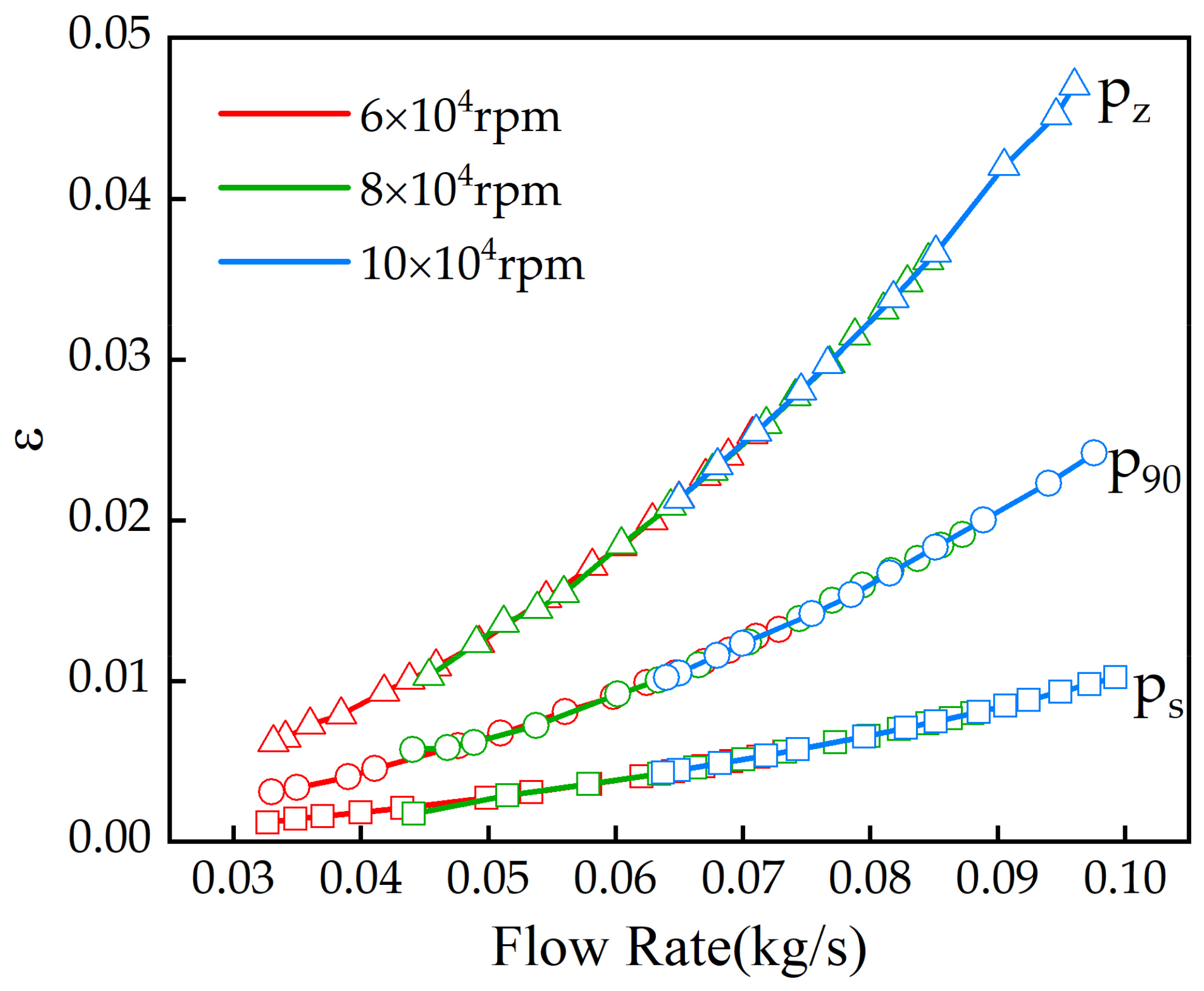
3.2. Analysis of the Performance Difference on the Centrifugal Compressor
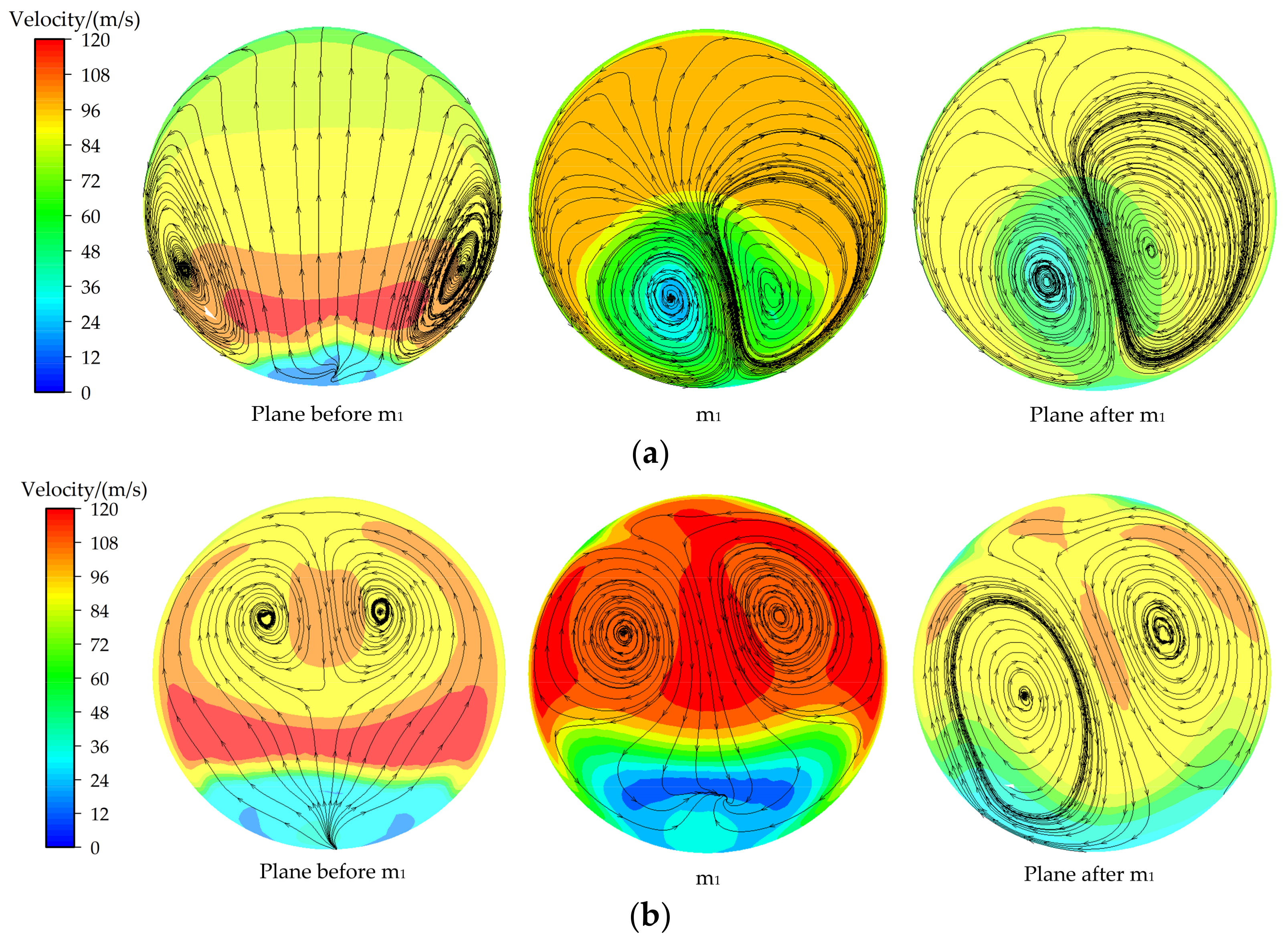
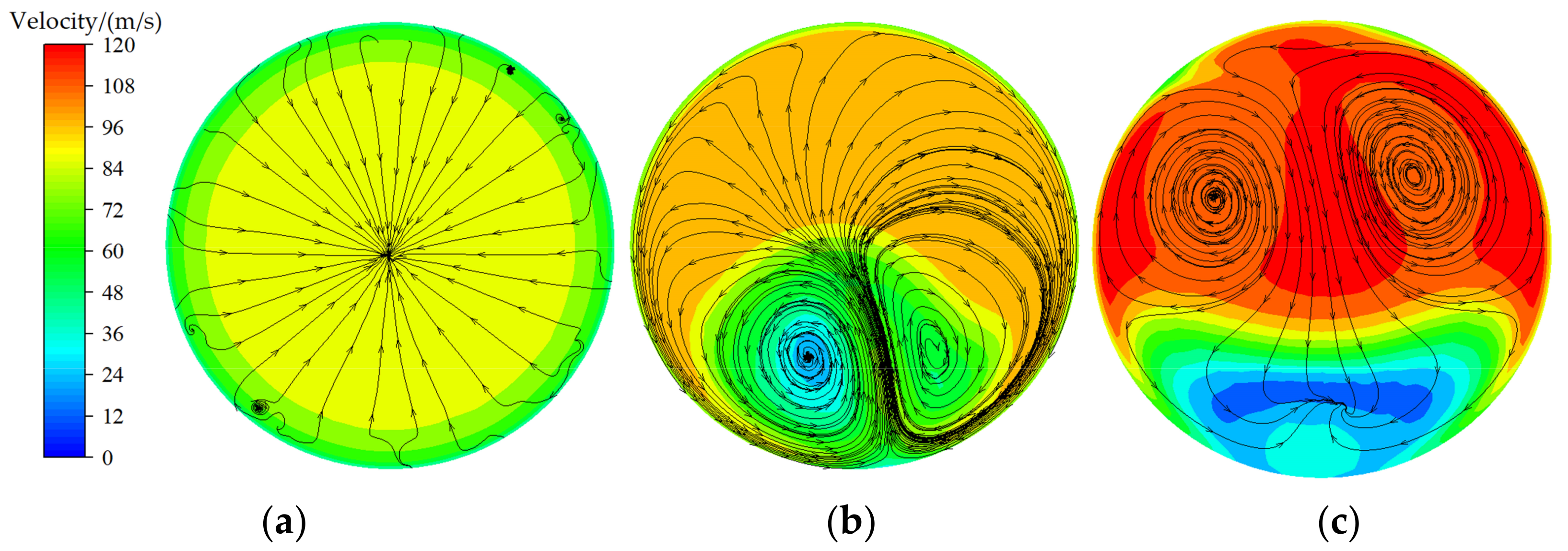
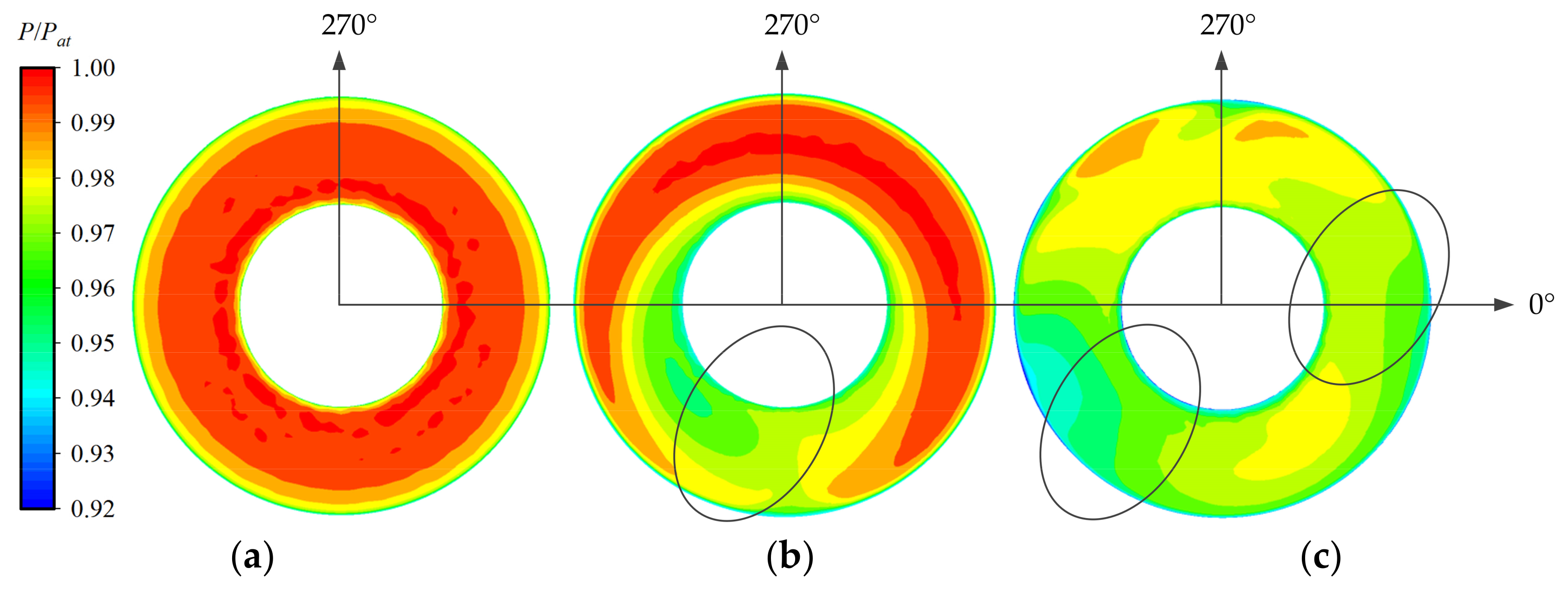
3.3. Distortion Flow Field Analysis of Different Inlet Pipes
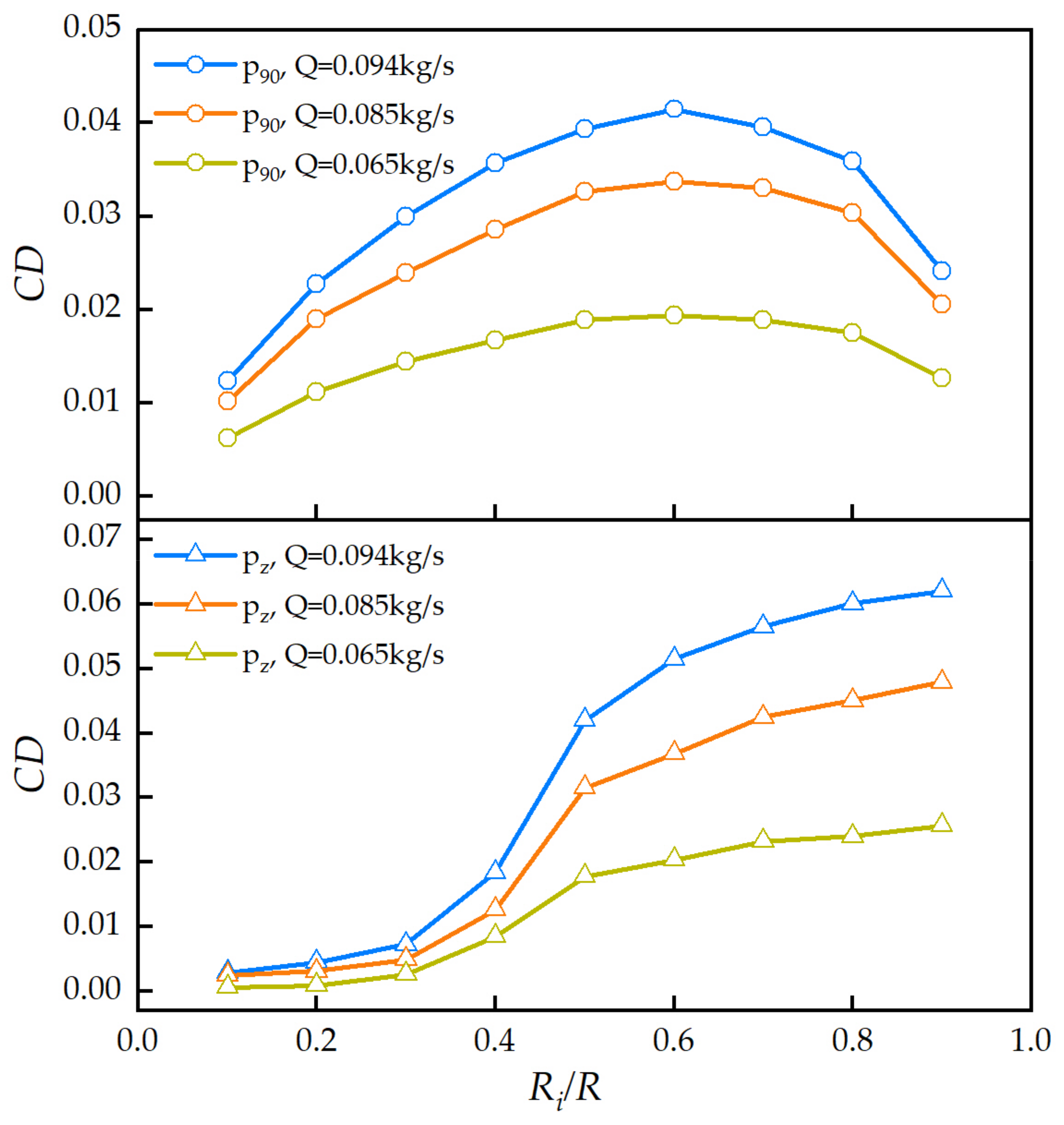
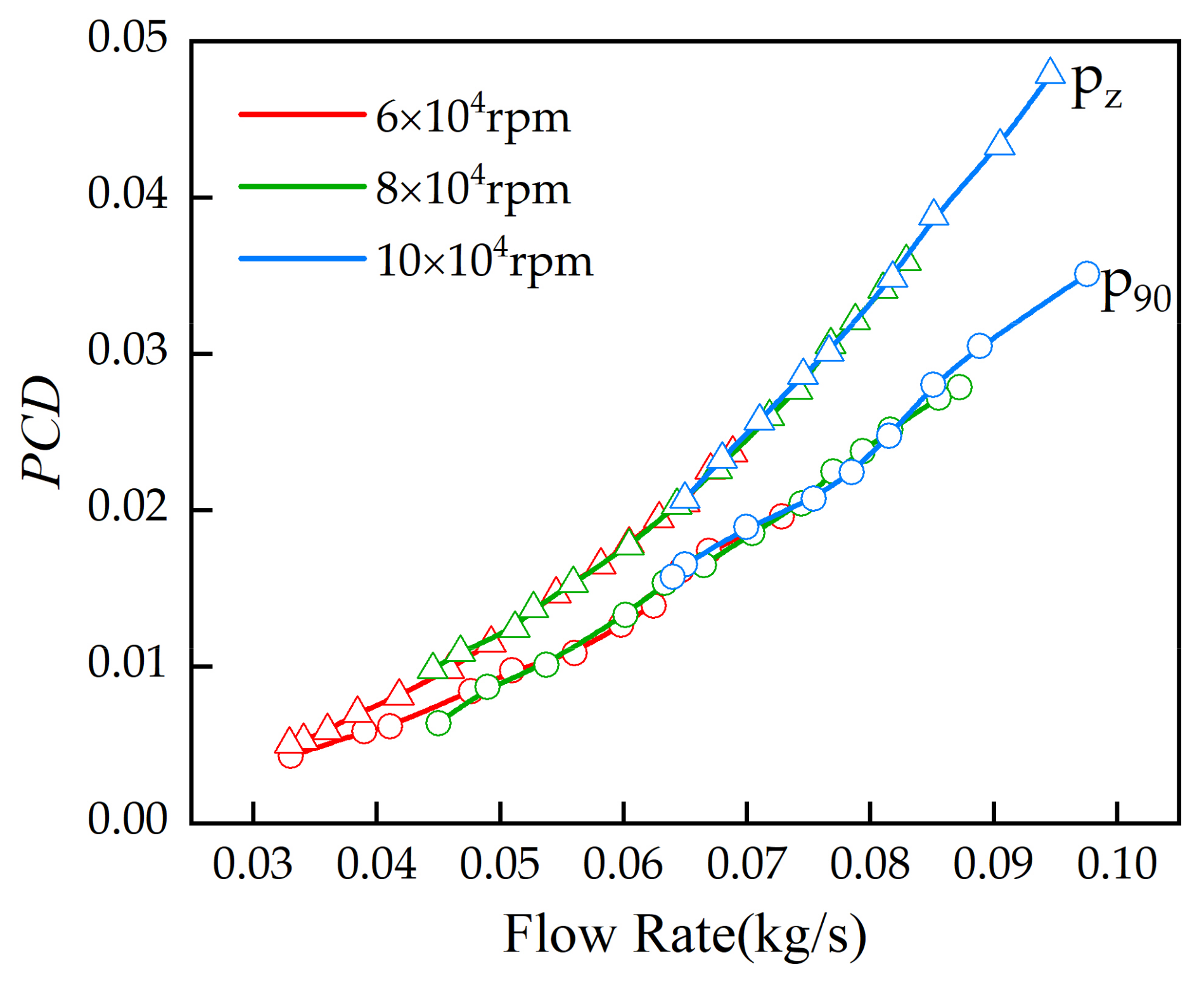
3.4. Quantitative Characterization of the Flow Field at the Outlet of Different Inlet Pipes
4. Analysis of Flow Characteristics in the Impeller of the Centrifugal Compressor
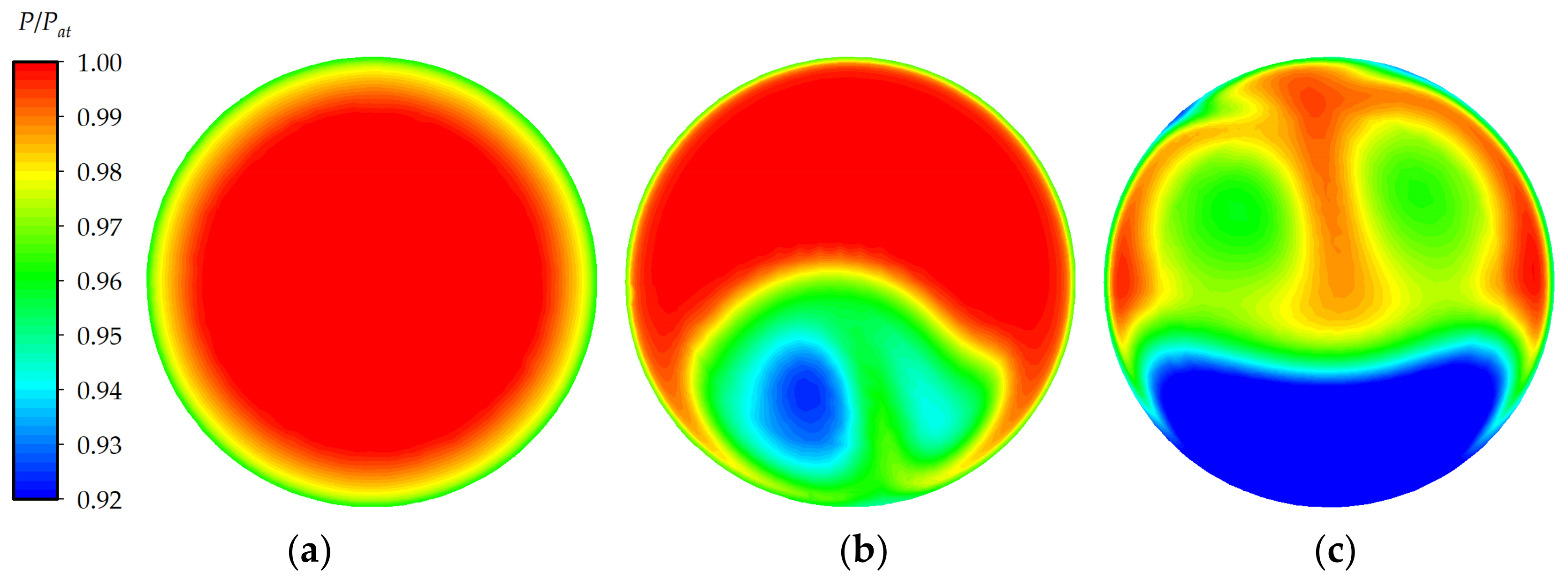
4.1. Total Pressure Distribution at the Inlet of the Impeller
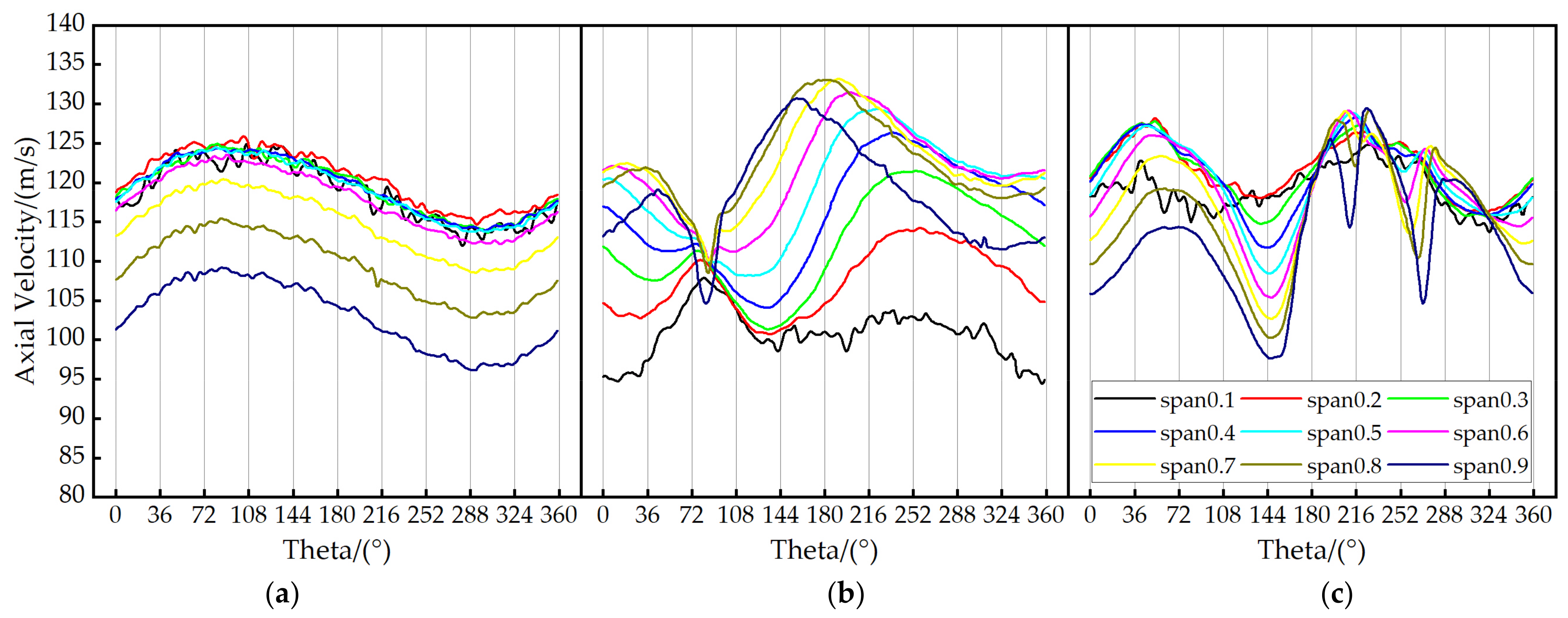
4.2. Axial Velocity Distribution at the Inlet of the Impeller
4.3. Mass Flow Rate Distribution at the Inlet of the Impeller
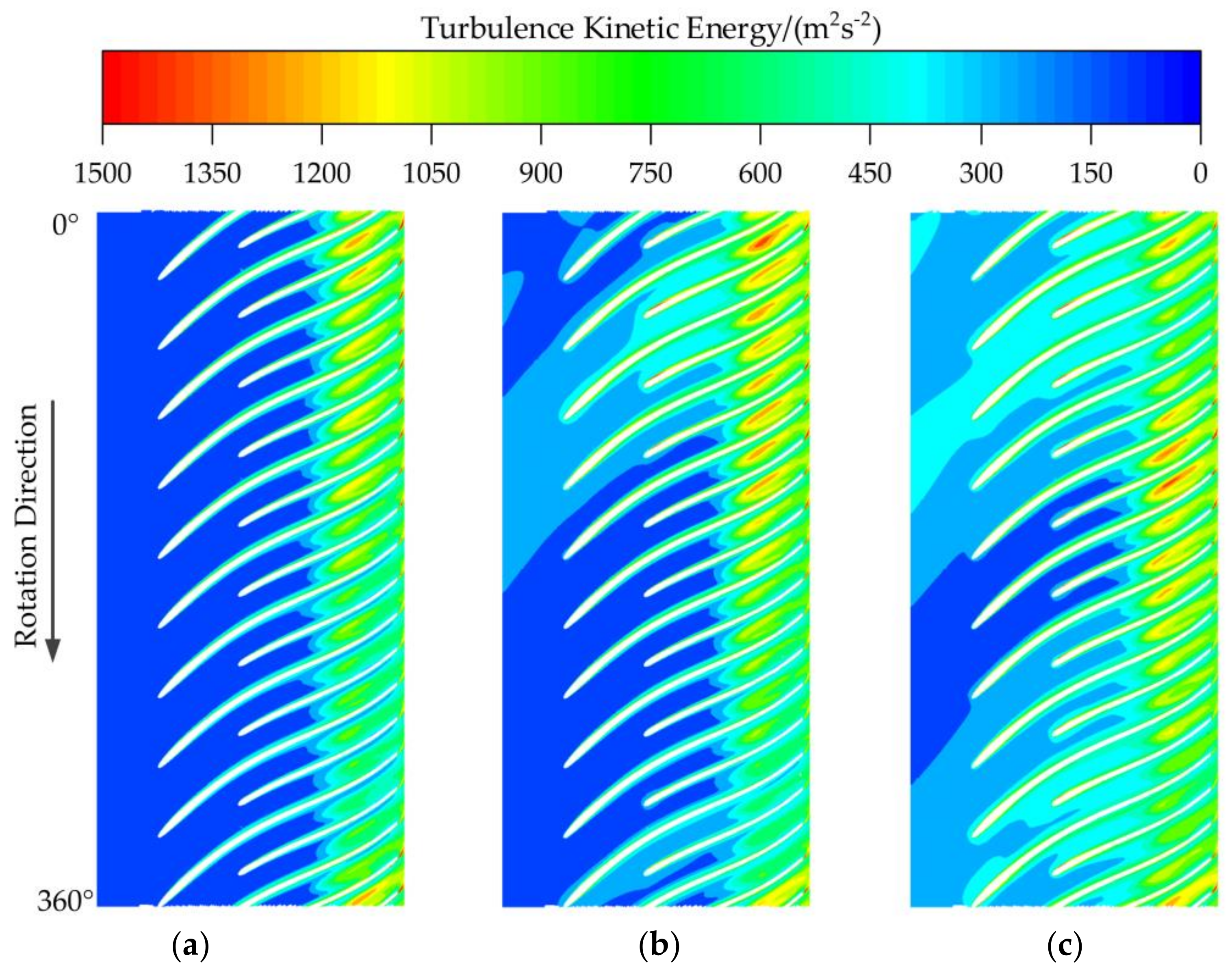
4.4. Distribution of Turbulence Kinetic Energy in the Impeller Passage
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ps | Straight inlet pipe |
| p90 | 90-degree bent pipe |
| pz | Z-shaped bent pipe |
| ε | Total pressure loss coefficient |
| P | Local total pressure (unit: pa) |
| Pat | Local atmospheric pressure (unit: pa) |
| Pin | Pressure of the inlet of the domain (unit: pa) |
| Pout | Pressure of the outlet of the domain (unit: pa) |
| CD | Circumferential distortion degree |
| PCD | Circumferential distortion degree of the plane |
| πc | Pressure ratio of the centrifugal compressor |
| η | Efficiency of the centrifugal compressor |
| δπ | Reduction degree of the pressure ratio |
| δη | Reduction degree of the efficiency |
| Q | Mass flow rate of the centrifugal compressor (unit: kg/s) |
References
- Sun, Z.Z.; Wang, B.T.; Zheng, X.Q.; Kawakubo, T.; Tamaki, H.; Numakura, R. Effect of bent inlet pipe on the flow instability behavior of centrifugal compressors. Chin. J. Aeronaut. 2020, 33, 2099–2109. [Google Scholar] [CrossRef]
- Krain, H. Review of Centrifugal Compressor’s Application and Development. J. Turbomach. 2005, 127, 25–34. [Google Scholar] [CrossRef]
- Li, C.; Bai, S.Z.; Li, Y.Z.; Zhang, J.J.; Zhang, J.M. Effects of curved tube intake on centrifugal compressor efficiency. Intern. Combust. Engine Power Plant 2020, 37, 26–31. [Google Scholar]
- Han, F.H.; Mao, Y.J.; Tan, J.J. Influences of flow loss and inlet distortions from radial inlets on the performances of centrifugal compressor stages. J. Mech. Sci. Technol. 2016, 30, 4591–4599. [Google Scholar] [CrossRef]
- Yang, C.; Wang, W.L.; Zhang, H.Z.; Yang, C.M.; Li, Y.Z. Investigation of stall process flow field in transonic centrifugal compressor with volute. Aerosp. Sci. Technol. 2018, 81, 53–64. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Chu, W.L.; Lu, X.G. Numerical Simulation of Effect of Inlet Total-Pressure Distortion on Subsonic Axial-Flow Compressor. J. Northwestern Polytech. Univ. 2009, 27, 12–17. [Google Scholar]
- Toge, T.D.; Pradeep, A.M. Experimental investigation of stall inception of a low speed contra rotating axial flow fan under circumferential distorted flow condition. Aerosp. Sci. Technol. 2017, 70, 534–548. [Google Scholar] [CrossRef]
- Zhou, S.D.; Wen, Q. The Effects of Inlet Total Pressure Radial Distortions on the Performance Characteristics of a Centrifugal Compressor. Gas Turbine Exp. Res. 2005, 18, 5. [Google Scholar]
- Ariga, I.; Kasai, N.; Masuda, S.; Watanabe, Y.; Watanabe, I. The Effect of Inlet Distortion on the Performance Characteristics of a Centrifugal Compressor. J. Eng. Power 1983, 105, 223–230. [Google Scholar] [CrossRef]
- Dichmann, H.P.; Wimmel, T.S.; Szwedowicz, J.; Filsinger, D.; Roduner, C.H. Unsteady Flow in a Turbocharger Centrifugal Compressor: Three-Dimensional Computational Fluid Dynamics Simulation and Numerical and Experimental Analysis of Impeller Blade Vibration. J. Turbomach. 2006, 128, 455. [Google Scholar] [CrossRef]
- Zemp, A.; Kammerer, A.; Abhari, R.S. Unsteady Computational Fluid Dynamics Investigation on Inlet Distortion in a Centrifugal Compressor. J. Turbomach. 2010, 132, 93–94. [Google Scholar] [CrossRef]
- Kammerer, A.; Abhari, R.S. Blade Forcing Function and Aerodynamic Work Measurements in a High Speed Centrifugal Compressor with Inlet Distortion. J. Eng. Gas Turbines Power 2010, 132, 95–105. [Google Scholar] [CrossRef]
- Li, J.C.; Lei, J.W.; Liu, Y.; Du, J.; Lu, X.X.; Song, Q.B. Distribution characteristics of compressor stall precursor under circumferential distortion. J. Aerosp. Power 2021, 36, 1356–1366. [Google Scholar]
- Zhang, Y.X.; Li, Z.L. Summary of Numerical Simulation Methods for Flow in Fluid Machinery. Fluid Mach. 2006, 34, 6. [Google Scholar]
- Jathar, K.S.; Kulkarni, V.V. An Elementary Study of Computational Fluid Dynamics for Various Engineering Applications—A Review. Int. Res. J. Eng. Technol. 2015, 2, 1292. [Google Scholar]
- Li, D.; Yang, C.; Chen, S.; Qi, M.X. Numerical simulation on inlet distortion of centrifugal compressor with 90° bent pipe. J. Aerosp. Power 2010, 25, 8. [Google Scholar]
- Li, D.; Yang, C.; Chen, S.; Zhang, Z.Q. Unsteady Characteristics on Inlet Distortion of Bend-Pipe of Centrifugal Compressor. Trans. CSICE 2011, 29, 7. [Google Scholar]
- Li, D.; Yang, C.; Zhou, M.; Zhu, Z.F.; Wang, H. Numerical and experimental research on different inlet configurations of high speed centrifugal compressor. Sci. China Technol. Sci. 2012, 55, 174–181. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, H.W.; He, H.; Gu, J.B. Numerical simulation of effects of the inlet pipe on the performance of a centrifugal compressor. J. Aerosp. Power 2009, 24, 7. [Google Scholar]
- Kim, J.; Yadav, M.; Kim, S. Characteristics of Secondary Flow Induced by 90-Degree Elbow in Turbulent Pipe Flow. Eng. Appl. Comput. Fluid Mech. 2016, 8, 229–239. [Google Scholar] [CrossRef]
- Zhao, B.; Sun, H.; Wang, L.L.; Song, M.X. Impact of Inlet Distortion on Turbocharger Compressor Stage Performance. Appl. Therm. Eng. 2017, 124, 393–402. [Google Scholar] [CrossRef]
- Wang, L.L.; Lao, D.Z.; Liu, H.; Zhao, B.; Yang, C. The Influence of Different Installation Angles of 180° Inlet Bend Pipe on the Centrifugal Compressor Performance. J. Eng. Thermophys. 2014, 35, 5. [Google Scholar]
- Wang, Y.H.; Hu, Q.S.; Wang, Z.Y.; Wang, M. Study on the Influence of Distortion Intensity on the Aerodynamic Performance of Compressor. J. Eng. Therm. Energy Power 2021, 36, 110–116. [Google Scholar]
- Tong, D.; Tian, H.Y.; Xing, W.D.; Liu, Y.; Liu, X.Y. Simulation study on the distortion on inlet flow field caused by twin centrifugal compressor sharing a single inlet distortion. Chin. Intern. Combust. Engine Eng. 2020, 41, 63–69. [Google Scholar]
- Zhang, H.G.; Li, Q.; Dong, F.Y.; Chu, W.L. Mechanism of Affecting the Performance and Stability of an Axial Flow Compressor with Inlet Distortion. J. Therm. Sci. 2021, 30, 15. [Google Scholar] [CrossRef]
- Zeng, Y.; Wang, H.B.; Sun, M.B.; Wang, C.; Liu, X. Review on SST turbulence model improvements. Acta Aeronaut. Et Astronaut. Sin. 2023, 44, 027411. [Google Scholar]
- Cravero, C.; Leutcha, P.J.; Marsano, D. Simulation and Modeling of Ported Shroud Effects on Radial Compressor Stage Stability Limits. Energies 2022, 15, 2571. [Google Scholar] [CrossRef]
- An, G.; Fan, Z.; Qiu, Y.; Wang, R.; Yu, X.; Liu, B. Numerical Investigation of the Effect of Hub Gaps on the 3D Flows Inside the Stator of a Highly Loaded Axial Compressor Stage. Energies 2022, 15, 6993. [Google Scholar] [CrossRef]
- Djodikusumo, I.; Diasta, I.N.; Awaluddin, I.S. Geometric Modeling of a Propeller Turbine Runner Using ANSYS BladeGen, Meshing Using ANSYS TurboGrid and Fluid Dynamic Simulation Using ANSYS Fluent. Appl. Mech. Mater. 2016, 842, 164–177. [Google Scholar] [CrossRef]
- Liu, H.L.; Dong, L.; Wang, Y.; Wang, K.; Lu, M.Z. Overview on Mesh Generation Methods in CFD of Fluid Machinery. Fluid Mach. 2010, 38, 32–37. [Google Scholar]
- Tian, H.Y.; Hou, K.; Tong, D.; Liu, X.Y. Effect of Inlet End-Wall Guide Vanes on the Performance of Centrifugal Compressor. Chin. Intern. Combust. Engine Eng. 2021, 42, 95–102. [Google Scholar]
- Xu, Z.L.; Gao, R.Z.; Da, X.Y. Assessment and measurement of total pressure distortion based on five-hole-probe for S-shaped inlet. J. Exp. Fluid Mech. 2018, 32, 9. [Google Scholar]
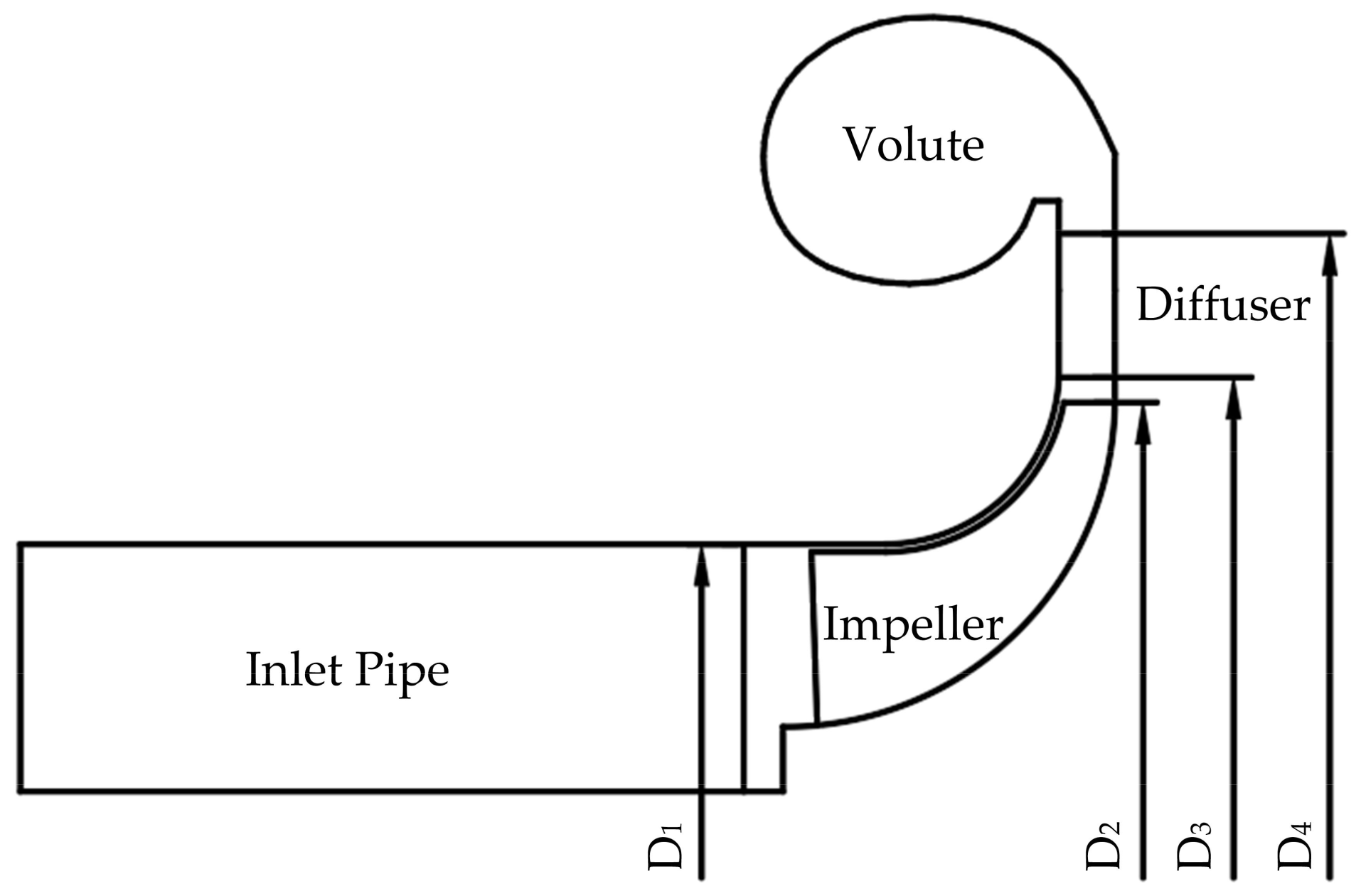
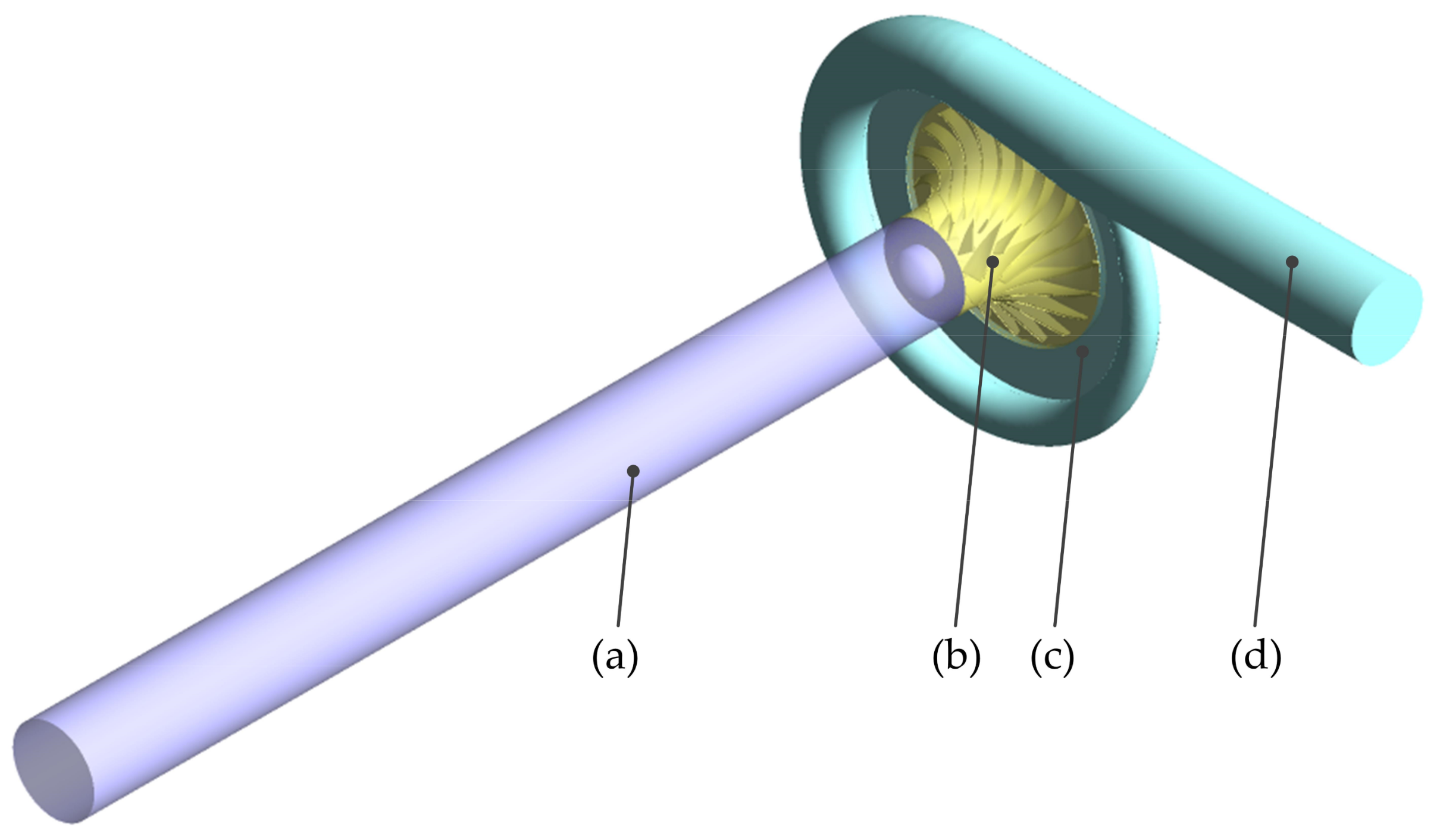


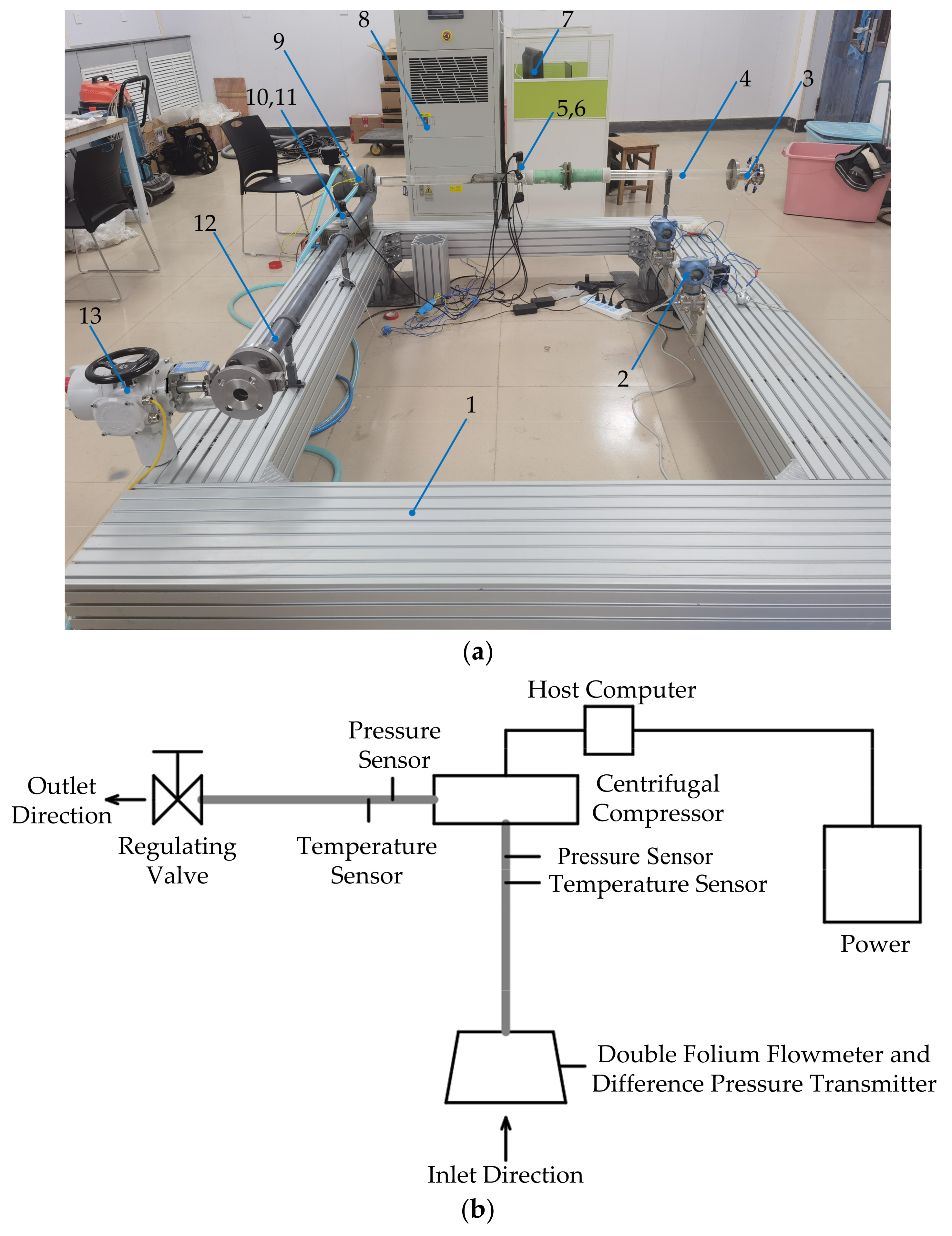








| Parameters | Value |
|---|---|
| Number of impeller main blades | 10 |
| Number of impeller splitter blades | 10 |
| Impeller inlet diameter, D1 (mm) | 34 |
| Impeller outlet diameter, D2 (mm) | 75 |
| Tip clearance (mm) | 0.5 |
| Diffuser inlet diameter, D3 (mm) | 80 |
| Volute inlet diameter, D4 (mm) | 111 |
| Rotational Speed | Location | Boundary Conditions |
|---|---|---|
| 6 × 104 rpm | Inlet of the domain | Pin = 101,325 pa |
| Outlet of the domain | Pout = 122–143 kpa (larger flow rate) | |
| Q = 0.033–0.04 kg/s (lower flow rate) | ||
| 8 × 104 rpm | Inlet of the domain | Pin = 101,325 pa |
| Outlet of the domain | Pout = 153–185 kpa (larger flow rate) | |
| Q = 0.045–0.049 kg/s (lower flow rate) | ||
| 10 × 104 rpm | Inlet of the domain | Pin = 101,325 pa |
| Outlet of the domain | Pout = 205–241 kpa (larger flow rate) | |
| Q = 0.063–0.068 kg/s (lower flow rate) |
| Mesh Schemes | Impeller | Volute | Inlet Pipe | Total Element |
|---|---|---|---|---|
| 1 | 1,371,900 | 495,973 | 613,379 | 2,481,252 |
| 2 | 2,197,980 | 3,307,332 | ||
| 3 | 3,077,680 | 4,187,032 | ||
| 4 | 4,030,240 | 5,139,592 | ||
| 5 | 5,261,100 | 6,370,452 | ||
| 6 | 6,176,680 | 7,286,032 | ||
| 7 | 7,874,300 | 8,983,652 | ||
| 8 | 9,174,520 | 10,283,872 | ||
| 9 | 10,158,200 | 11,267,552 | ||
| 10 | 11,100,320 | 12,209,672 |
| p90-δπ | a | b | Adjusted R-Square |
|---|---|---|---|
| 6 × 104 | 150.028 | 1.130 | 0.998 |
| 8 × 104 | 434.859 | 1.433 | 0.993 |
| 10 × 104 | 2512.410 | 1.973 | 0.986 |
| pz-δπ | a | b | Adjusted R-Square |
| 6 × 104 | 137.537 | 1.016 | 0.998 |
| 8 × 104 | 242.832 | 1.187 | 0.976 |
| 10 × 104 | 635.682 | 1.505 | 0.973 |
| p90-δη | c1 | c2 | d | Adjusted R-Square |
|---|---|---|---|---|
| 6 × 104 | −0.654 | 0.807 | 115.298 | 0.984 |
| 8 × 104 | −0.222 | 0.494 | 84.981 | 0.993 |
| 10 × 104 | −0.150 | 0.253 | 77.510 | 0.964 |
| pz-δη | c1 | c2 | d | Adjusted R-Square |
| 6 × 104 | −2.517 | 2.569 | 72.600 | 0.998 |
| 8 × 104 | −1.317 | 1.661 | 50.668 | 0.998 |
| 10 × 104 | −0.687 | 0.996 | 44.090 | 0.996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Huang, N.; Chen, G.; Zhang, Y.; Zhao, Y.; Zhang, J.; Tong, D. Numerical Simulation on the Influence of Inlet Flow Characteristics on the Performance of a Centrifugal Compressor. Energies 2023, 16, 3869. https://doi.org/10.3390/en16093869
Li X, Huang N, Chen G, Zhang Y, Zhao Y, Zhang J, Tong D. Numerical Simulation on the Influence of Inlet Flow Characteristics on the Performance of a Centrifugal Compressor. Energies. 2023; 16(9):3869. https://doi.org/10.3390/en16093869
Chicago/Turabian StyleLi, Xing, Ning Huang, Guanyan Chen, Yanli Zhang, Yang Zhao, Jie Zhang, and Ding Tong. 2023. "Numerical Simulation on the Influence of Inlet Flow Characteristics on the Performance of a Centrifugal Compressor" Energies 16, no. 9: 3869. https://doi.org/10.3390/en16093869
APA StyleLi, X., Huang, N., Chen, G., Zhang, Y., Zhao, Y., Zhang, J., & Tong, D. (2023). Numerical Simulation on the Influence of Inlet Flow Characteristics on the Performance of a Centrifugal Compressor. Energies, 16(9), 3869. https://doi.org/10.3390/en16093869








