Abstract
The paper presents a physics-based method to calculate in real time the distribution of temperature in the active part of liquid immersed power transformers (LIPT) in a transient thermal processes during grid operation. The method is based on the detailed dynamic thermal-hydraulic network model (THNM). Commonly, up to now, lumped models have been used, whereby the temperatures are calculated at a few points (top-oil and hot-spot), and the parameters are determined from basic or extended temperature-rise tests and/or field operation. Numerous simplifications are made in such models and the accuracy of calculation decreases when the transformer operates outside the range of tested values (cooling stage, loading). The dynamic THNM reaches the optimum of accuracy and simplicity, being feasible for on-line application. The paper presents fundamental equations of dynamic THNM, which are structurally different from static THNM equations. The paper offers the numerical solver for the case of a closed-loop thermosyphon. To apply the method for real transformer grid operation, there is a need to develop details as in static THNM, which has been used to calculate the distribution of the temperatures in LIPT thermal design. The paper proves the concept of dynamic THNM using the experimental results of a closed-loop thermosyphon small-scale model, previously published by authors from McGill University in 2017. The comparison of dynamic THNM with measurements on that model are presented in the paper.
1. Introduction
Liquid immersed power transformers are devices transferring a large amount of electric power with high efficiency. Due to high currents through the winding and the magnetic field through the core, there are heat losses that can reach several hundred thousand kW for large power transformer transformers (>100 MVA). The losses are small compared to the transferred power, meaning the power efficiency of the transformer is high, but the amount of the generated heat is considerable and leads to an increase of temperature inside the transformer. The temperature of the liquid and solid insulation materials should be limited to avoid a sudden failure due to bubbling phenomena or accelerated insulation ageing as a result of the cumulative effect of the increased temperature over a longer time period.
A majority of LIPTs operate in conditions of variable load and ambient temperature. Due to the high thermal inertia of the transformer, there is a time delay between the change of the load and the change of the LIPT components’ temperature. This implies that the temperature will change in time, but more slowly, enabling loading over the rated load during short time periods.
This application is of practical interest and can be used, for example, to overload the transformer during planned daily peak loads, instead of replacing the transformer with a larger one or adding another transformer to the substation. An overload can be useful in emergency cases where the transformer should take over the load due to the outage of some other grid elements. The grid operator needs to take decisions regarding the safe overloading of the transformer and, for this purpose, it is necessary to perform calculations of the critical temperatures inside the transformer, using dynamic thermal models (DTM). The necessity of thermal monitoring, based on the DTMs, in order to optimize the usage and increase the reliability of LIPTs in electrical power systems is presented by Tenbohlen et al. [1].
In order of complexity, the physics-based DTMs can be classified in the following way: (1) ordinary differential equation (ODE), with standard or experimentally determined parameters, (2) detailed dynamic THNM and (3) computational fluid dynamics (CFD) calculations.
Simple ODEs are the preferred approach used in international loading guides (IEC 60076-7 and IEEE C57.91) [2,3]. More precisely, such models consist of a small number of ODEs being solved analytically, when possible, or numerically using finite difference or other solvers. Their main advantage is fast execution, low computational resources, and easy programming. In the loading guides [2,3] ODEs are established as lumped models, where transformer parts are represented with one temperature—the winding with insulation hottest-spot (in further text “hot-spot”) and the top insulation liquid (in further text “top-oil”). The easiest way, but with lower accuracy, is to apply such simple models using the recommended parameters given in standards for different transformer types. In such an approach, complex dependences of the hot-spot and top-oil temperatures on the characteristics of the materials used, the cooling equipment, and the construction of the active part are not considered. An improvement in the accuracy is made after the parameters of the models are determined from the results of the temperature-rise test on a transformer in short-circuit [4], experiments with both winding and core losses [5,6], or field data. Although the individual influences of the above stated parameters are not considered, their cumulative effect on the temperature values is roughly modeled. The model from [3], enhanced by continuously updating parameters based on the transformers’ real-time thermal response [7], is a possibility to overcome some disadvantages of ODEs.
The main problem with the lumped model is to adequately consider the vertical temperature gradient. Since the oil temperature increases along the height of the winding, and the winding hot-spot appears around its top, the majority of the models are based on the mixed top pocket oil temperature (top-oil). As shown in [8], the time variation of the top winding oil consists of one slowly changing component (linked with the bottom-oil temperature) and one small delay with the winding temperature. The thermal model in Annex G [3] is based on the bottom-oil temperature. Although the application of models based on the bottom-oil can better capture the phenomena, none of the models accurately calculates the dynamic change of the vertical winding oil gradient. It depends on the heat transferred from the windings to the oil and the oil flow, which is determined by the equilibrium of the pressure in closed oil circulation loops. Another key issue with existing lumped models is that the heat accumulation is determined according to the change of some local oil or winding temperature. In reality, the temperature over the volume of the parts (winding, core, oil) is changing. Therefore, to determine the complete accumulated heat, the temperature distribution has to be known. Heat accumulation might be roughly modeled by introducing correction coefficients for the mass and specific heat (for example, in [3], for ONAN and ONAF cooling, two thirds of the weight of the tank and 86% of the specific heat of the oil were used) while calculating the thermal capacity in a lumped model. Another possibility is to determine the parameters characterizing heat accumulation using laboratory or field measurements (examples can be found in [9,10]). Some researchers are trying to create hybrid models by combining the lumped models of some transformer parts with the distributed parameter models for the other. This possibility is explored and experimentally validated for the special type of traction transformer [11].
The level of details in THNM enables the calculation of the oil flow distribution needed to determine the vertical oil gradients. The detailed static THNMs [12], implemented in software design tools such as [13], are spreading in transformer engineering practice and can be applied to transformers built with conventional or emerging insulating materials.
Contrary to the static THNM, dynamic THNM is still at a low-level technology readiness level (TRL). Although Seitlinger [14] published in 2000 the idea of application of dynamic THNM and its postulates, being patented in 1999 [15], detailed THNM was not widely used for temperature calculation during dynamic grid operating conditions, although there is a strong technical need for this. The possibility of developing the dynamic detailed THNM of LIPT winding by rearranging the existing static version is proposed in [16], and the further research of winding hydraulic behavior during transients is presented in [17].
One of the discouraging factors for applying detailed dynamic THNM is that detailed construction and the material characteristics are to be known, and that is not often the case, especially for the older transformers. Practically, it is realistic to envisage application to new transformer units, considering that a proper agreement between the transformer producer and the user is met.
Of significant importance in the context of digitalization, the detailed dynamic THNM can be associated with the development of the concept of the transformer digital twin. A digital twin can be defined as a scalable virtual replica of a physical asset that, through automatically updated data and simulation tools, can continuously monitor and predict the condition and behavior of its real-life counterpart, with the goal of optimizing the latter’s performance. The dynamic THNM provides a high-fidelity virtual replica of the thermal behavior of the LIPT.
The modern tendency in different problem-solving areas is the application of artificial intelligence (AI) and deep learning. It can be used in the process of modeling the behavior of technical systems in different operating conditions. Machine learning (ML) and AI are referred to as “black-box” models or data-driven models, as opposed to physics-based models. There are “gray-box” models, or hybrid models, which include more physics and start from a better description of the model structure [18]. Another modern research direction is the application of reduced order modeling (ROM). This is the technique of reducing, for example using AI or other mathematical representations, the complexity of the model (in terms of computational time and used memory) while preserving the model’s accuracy. One of the possibilities is to run off line the CFD calculations and to use their results as the input data for the ROM training, which generates a “black-box” model that mimics the reality. The ROM is valid only within the area of scenarios covered by the set of physics-based simulations (steady and transient states).
More than a hundred years of developments on transformer heat transfer and loading [19] indicate that it is impossible to grasp the complexity of the problem using a small number of ODEs tuned with experimental data. Some of those models are useful in some specific applications, but none of them are general enough to cover all possible scenarios. The key problem is that it is not possible to describe all relevant physical influences with a few differential equations. Although there is much less experience in practical application of ML and AI, due to the same reasons stated for simple lumped models, it is not expected that AI will become a panacea for dynamic thermal model of LIPTs. The detailed dynamic THNM is deeply based on the hydraulic and heat transfer theory and the preliminary findings indicate that it is applicable in real-time operation with variable load, cooling stage, tap position, and cooling medium temperature.
This paper explains the fundamental equations of detailed dynamic THNM. It was found that the dynamic THNM requires a completely different approach to the one used for static THNM [12]. Static THNM is built on the concept that oil ducts and conductors are the elements of the networks, while the solver concept in dynamic THNM is moving towards a 1D finite-element model (FEM).
An important practical issue is the execution time of the developed software that should be shorter than real time. The experimental set-up from McGill University used for the model validation [20] is of moderate complexity but it can be used for the demonstration of the execution time of detailed dynamic THNM applied to a real transformer. The real-time applicability disqualifies the use of CFD. For example, in [21] it has been reported that it would take about 30 days of computational time using 464 processors to simulate 30 min of flow and the thermal behavior in a transformer-scale model. To overcome these limitations of CFD and get results faster, there is a possibility of neglecting a considerable number of physical phenomena [22]. The consequence of this is lower accuracy and a reduced set of results. With such simulations, only the global distribution of the flows and the temperature are obtained.
This paper presents a numerical solver applicable for the transient temperature calculation of a heated solid immersed in liquid circulating in a closed loop. The method is implemented and tested for the case of natural convection fluid flow, which is the most difficult process of the dynamic THNM. The method is tested on a simple experimental set-up with water circulating in a single loop. In the following stage of the research, the model will be expanded using the detailed THNM developed before ([12,23]), to achieve practical application for real transformer operation.
Section 2 briefly revisits the detailed THNM used for steady-state simulation. Section 3 describes the experimental set-up that was used for the validation of the new dynamic THNM. The details of the heat exchanger are reported in Section 4. Section 5 considers the application of the static THNM to the experimental set-up. In Section 6, the basics of dynamic THNM are presented, with emphasized reasons as to why it is not possible to follow the approach of building a model analog to the steady state. The comparison of the static and dynamic THNM simulations with the experimental results is presented in Section 7.
2. About Detailed Thermal-Hydraulic Network Models
In a LIPT, the oil flows up inside the active part of the transformer, increasing its temperature due to the heat transfer from the windings and the core, and then it flows down through the cooler, decreasing its temperature due to the heat transfer to the outer cooling medium (air or water). These heat transfers depend on the temperature differences between the active part and the oil, and between the oil and air (water). The relation between heat transfer and the temperature differences depends on the construction inside the tank and the outer cooling arrangement. Each temperature gradient, especially the vertical oil temperature gradient (∆θovw), depends on the oil flow. Figure 1 shows the simplified temperature diagram of the transformer, for the case of two windings (no core and no oil by-pass in the tank). θbo represents the temperature rise of the bottom oil–oil exiting the cooler and entering the windings, θto the temperature rise of oil entering the cooler, θhs the hot-spot winding temperature rise, g the average winding temperature minus average temperature of oil in the winding, and the hot-spot factor HS. The critical temperature in a transformer with a well guided stray flux transformer appears in one the windings, whereby it depends on the winding constructions and might appear in either HV or LV windings.

Figure 1.
A simplified temperature diagram for the case of two windings.
By using detailed THNM, the flow rate of circulating oil and the distribution of the oil flow and its temperatures at the inlet and outlet of the transformer parts (winding, core, and cooling equipment) can be determined. The detailed THNM is built as a “bottom to top” structure [12], meaning that the networks are first established and solved for each of the elements (windings, core, cooler, etc.), and then they are connected to the global hydraulic network. Solving the global hydraulic network gives the overall distribution of oil. Solving the thermal and hydraulic networks of the transformer elements provides the distribution of the flows inside them, the temperature of the oil in each duct, and for a winding, the temperature of each conductor. The detailed THNM is based on the equations describing: (a) the conservation of heat, (b) the conservation of mass, and (c) the pressure equilibrium in closed loops. Solving the corresponding non-linear equations is a challenging but achievable task.
The most useful result is the location of the winding hot-spot and its temperature under the specified loss distribution. From this result, the hot-spot factors from Figure 1 (HS) can be determined for each winding [23]. The model provides the values of temperatures measured in the standard temperature-rise test, meaning it satisfies the requirements in the transformer design phase. Some examples of its application are presented in [24,25]. Up to now, the static THNM could be applied in transformer thermal design, but not to simulating dynamic grid operating conditions. The fundamental differences between the concepts of building static and dynamic detailed THNMs and the first implementation of dynamic THNM and its testing on a small-scale model [20] are described in the next sections.
3. Description of the Experimental Set-Up
The sketch of the experimental set-up is presented in Figure 2. A photograph of the experimental set-up is given in [20]. It consists of a closed-loop pipe with an inner diameter of 10.21 mm connected to a heater case (containing a heating element) and to a heat exchanger. The heating power can be adjusted. The heated water is cooled in a cooling section (water-to-water heat exchanger using a simple double-pipe counter flow heat exchanger). The flow rate and temperature of the outer cooling water are controlled. The water flow rate in the closed-loop circuit is dictated by a thermosyphon effect. Thus, the water flow rate increases with an increase of heating power and vice versa. The water flow rate in the closed-loop thermosyphon is low. Consequently, the temperature gradient of the outer water is much smaller than the one of the closed-loop water. The outer surfaces of the pipes are well insulated using Armaflex foam insulation. The temperature values of the closed-loop circulating water at different positions are designated with ϑ and the proper index (specified in the nomenclature). Details of the experimental set-up are presented in [20].

Figure 2.
Sketch of the experimental set-up from McGill University [20].
4. Discussion about the Heat Exchanger
The log-mean temperature difference (LMTD) method has been applied. It is based on heat exchanger equations [26]:
In the literature, such as [26], the equations for convection heat transfer coefficients (CHTC) for different geometries can be found. In the experimental set-up, the closed-loop water circulating through the heat exchanger (CHTC αw,hex,ts) flows through a pipe [27], and the outer water circuit (CHTC αw,o,hex) flows through an annulus [28]. In LIPTs, the heat exchanger is more complex (a two-pass shell and tube is often used, where the water flows through the circular tubes and the oil flows across the bank of circular tubes). In the literature [26,29,30], the equations for such cases can be found. The CHTC depends on the flow rate and the fluid temperature and thus these values differ for different operating points. Calculating the CHTC at each transformer operating point is theoretically the ideal approach, but for applying it, the detailed construction of the heat exchanger has to be known. Such data are generally not available for commercial heat exchangers. Another practical issue is the validity and accuracy of the equations for CHTC from the literature. For this reason, a different approach is used herein. After neglecting small heat resistance to heat conduction through the pipe (term in Equation (3)) it can be written:
(Equation (5) is written for the case of a heat exchanger on a transformer, where CHTC on the insulation liquid side is αf and on the water side αw). In general, for optimized design of the heat exchanger at the rated operating point, the αf,r Sf is close to αw,r Sw. For such a case, the following can be written:
The value of kpc,r Sf can be determined from the following relation between the cooling power, the temperatures of the insulation liquid circulating in closed loop (entering ϑf,h and exiting ϑf,c), and the outer water temperatures (entering ϑw,c and exiting ϑw,h) (these data are provided in the catalog for the rated conditions):
Factor F can be determined using the graphs for the specific heat exchanger [26] (a two-pass shell and tube is a typical construction used in LIPTs). Consequently, the cooling power can be determined based on to the following equation for the cooling power:
The ratios of the CHTCs at an arbitrary operating point and a rated operating point (αf/αf,r and αw/αw,r) might be obtained from the corresponding equations from the literature for more accurate calculations, or considered as equal to the rated values, meaning that the influence of the fluid flow and inlet fluid temperatures on the CHTCs is neglected. Similar is valid for the hydraulic resistance to the oil flow through the compact cooler.
For the application of the approach to the experimental set-up, the rated cooler operating point is set using the measurements in steady state for a heating power of 200 W. In this case, the inner and outer pipe surfaces were known and the CHTCs on both surfaces were calculated for the rated 200 W conditions.
5. Application of Detailed Static THNM to Small-Scale Experimental Set-Up
5.1. General about Detailed Static THNM
The basic principles of static THNM applied to LIPTs are presented in [12]. Based on this model, a thermal design software tool has been developed [13]. The tool simulates the heating process and can estimate the temperatures expected in both a temperature-rise test and real transformer operation with the specified constant load, after the steady state is reached. The software is modular and includes numerous construction details of real LIPTs. Due to the modular design, it was possible to re-arrange the code and adapt it to model the small-scale experimental set-up [20], which was built to study the thermosyphon in LIPTs.
5.2. Hydraulic Scheme of the Experimental Set-Up
Figure 3 presents the hydraulic scheme of the experimental set-up. The gravitational pressures are proportional to the density at the average temperature of the element. The hydraulic resistance due to friction, bending, and expansion/contraction (including dynamic change of pressure) are calculated using traditional equations [31], which take into account the geometry, liquid velocity, and liquid properties (the viscosity influence dominates). There is an additional lumped pressure drop modeled by the hydraulic resistance Radd due to the pressure drops on the obstacles, such as the centering plate at the top of the heater and the cable entry to the heater. Its value is determined by calibration, with the criterion to achieve the temperature gradient (ϑw,hp2–ϑw,hp3) measured in steady state in the experiment with 200 W.

Figure 3.
The hydraulic scheme of the experimental set-up.
5.3. Calibration of Heat Transfer Coefficient through the Outer Surface of the Pipes
All the outer surfaces of the thermosyphon were well insulated using Armaflex foam insulation (λArm = 0.04 W∙m–1∙K–1). The thermal resistance to the ambient is mainly due to the conduction heat resistance of Armaflex foam insulation, approximately equal to
and smaller thermal resistances due to the convection from the water to the pipe, from Armaflex to air, the resistance due the conduction through the pipe wall, and thermal contact resistance between the pipe and Armaflex foam insulation. The heat transfer coefficient through these pipes (kpp), covering all four thermal resistances, is determined based on temperatures measured on the experimental set-up for a heating power of 200 W. The option to determine kpp as the sum of dominating component of heat resistance of Armaflex foam insulation (10) and the other four smaller thermal resistances was not applied since there were no exact data about the thickness of Armaflex foam insulation along the loop (in [20] it has been stated that this thickness was between 38 mm and 50 mm). Due to this variable thickness, the applied procedure of the calibration and assuming that kpp is constant along the loop is approximate and will cause a slight calculation error.
The total thermal resistance Rpp and kpp are related as
and kpp is taken to be constant since the dominant Armaflex foam insulation has approximately the same thickness for all outer surface pipes.
5.4. Parameters of the Model Determined from the Results of Experiment with 200 W Heating Power
Supposing the value of kpp is known (its determination is described in the further text), the thermal resistance RppT can be calculated, according to Equation (11), for each of the six pipe sections and each of the three heater case sections, using corresponding lengths and diameters. The heat transferred to these sections, with inlet temperature ϑin and outlet temperature ϑout, is calculated by dividing the average water ((ϑin + ϑout)/2) minus the ambient temperature difference by RppT of that pipe section. Equations (12) and (13) connect the heat taken from the circulating water (left side) and transferred to the ambient air (right side). In zones of pipes excluding the pipe around the heater, the following expression is valid:
For the pipe around the zone of the heating block:
The system of equations containing eight equations of shape (12) (three sections of cold pipe, three sections of hot pipe, heater case below the heater and heater case above the heater) and one equation of shape (13) (heater case in the zone of heater block) describes the change of temperature of circulating water, excluding the pipe in the heat exchanger.
The heat transfer coefficient for the heat exchanger is determined as follows. The temperature gradient in sections of cold pipes is calculated from measured temperatures ϑw,cp2 and ϑw,cp3, and in sections of hot pipes from measured temperatures ϑw,hp2 and ϑw,hp3. Applying these temperature gradients and the section lengths, and starting from measured temperatures ϑw,cp2, ϑw,cp3, ϑw,hp2, and ϑw,hp3, the temperatures at the beginning and end of sections of cold and hot pipes are calculated (results are presented in Table 1). Simultaneously, the value kpp = 6.35 W/(K · m2) is obtained. The sum of the transferred heat, after applying this kpp value, is Pair = 25.8 W. The difference between the heating power in the heater (Ph = 200 W) and Pair represents the power transferred in the heat exchanger to the outer water. In the energy balance for the outer water, there is a small fraction of the heat transferred from the ambient air (ϑa = 21 °C) to the water (its inlet temperature is 11.93 °C). This component, calculated according to kpp, is 4 W. The outlet temperature of the outer water in the cooler (ϑw,o,h) determined from the known flow, and the power (200 –25.8 W) is 12.43 °C; after considering the 4 W transferred from the air to the outer water, this value increases to 12.44 °C. Thus, the effect is negligible, and the value ϑw,o,h = 12.44 °C is used for determining the characteristics of the double-pipe counter flow heat exchanger. Table 2 presents the rated heat exchanger characteristics, established on the measurements at a heating power of 200 W. Using (9) and Sf = π Dp lhex = π·0.01021·0.902 = 0.02893 m2, it is possible to evaluate the heat transfer coefficient for the heat exchanger kpc = 291.2 W/(K · m2).

Table 1.
The estimated static temperatures (°C) of the circulated water at heating power of 200 W.

Table 2.
Parameters used for determining the rated heat exchanger characteristics.
The hydraulic resistance modeling lumped pressure drop on the obstacles Radd (Figure 3) is calculated as
The coefficient C = 2.5 · 109 m–4 is obtained from in a unique iterative procedure, based on Figure 4, by varying C until the calculated temperatures ϑw,hp2 and ϑw,hp3 for the experimental case with 200 W become equal to the measured values. This additional pressure drop corresponds to 25.5% of the total pressure drop over the water circulating loop.
In the software based on detailed static THNM [13], there is no calibration. The objective of this tool is to support transformer design, meaning all dimensions and material characteristics have to be known. Current development of dynamic detailed THNM is based on the same postulate, that all details of the transformer construction are known. Therefore, to be clear, the method can be applied only for a transformer for which detailed construction is known. For the transformers for which there are no detailed data, other approaches have to be applied. These practical issues are discussed in the Introduction section.
Contrary to this, in the case of the experimental set-up considered in the paper, there were two reasons why the calibration has to be applied: there are no precise data about the thickness of Armaflex foam insulation (it varies between 38 mm and 50 mm—see Section 5.3) and the presence of irregular obstacles (centering plate and the cable entry) to oil flow through the heater.
5.5. Flow Chart of the Calculation
The hydraulic and thermal calculations are coupled and are solved in a unique iterative procedure, as presented in Figure 4.

Figure 4.
Flow chart of the static calculation.
6. Dynamic THNM
6.1. The Idea of a Non-Adequate “Quasi-Steady-State” Model
A “quasi-steady-state” model of LIPT starts from a detailed static THNM and is extended by introducing the thermal capacity in the equivalent thermal circuit of metal elements of the transformer (conductors, core, tank, and constructive elements). An example of a transient thermal network in one disc of winding with washers, derived from the static network, presented in [12], is presented in Figure 5. Variables in Figure 5 are: Pγi power loss in each of the conductors; Ci thermal capacity of the conductor; Rαin and Rαout thermal resistances to convection on the axial surface of the inner and outer conductor, respectively; Rαti and Rαbi thermal resistance to convection on top and bottom conductor surfaces, respectively; Rλr and Rλa thermal resistances to conduction in the radial and axial directions, respectively; ϑin and ϑout average temperature of oil near the axial surface of the inner and outer conductors, respectively; ϑti and ϑbi average temperature of oil near the top and bottom conductor surfaces, respectively. In the “quasi-steady-state” approach it is assumed that oil flows and temperatures are determined from the equilibrium of pressure drops in closed oil loops, the same as for the static case, but using the power transferred to oil at a certain moment of the transient process.
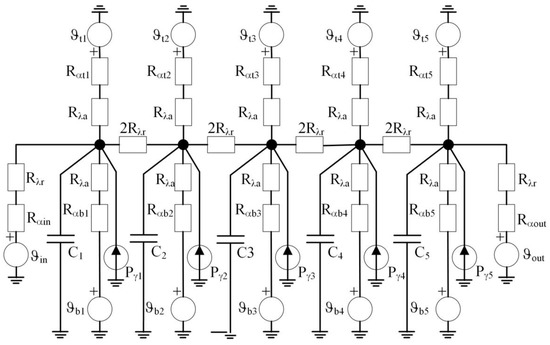
Figure 5.
Illustration of non-adequate concept of transient thermal network of one disc of disc winding with guides.
The challenge is how to include in the model the heat accumulation in the oil. The basic oil equation in steady state (Equation (7) in [12], being fundamentally the same as Equations (12) and (13)) is that the heat transferred from the conductors to the oil is transported by the mass transfer. A fundamental change of the model is needed to include the heat component which is accumulated in the oil during the transient thermal process. The convection−diffusion equation [32,33] has to be employed. Therefore, the initial idea to use a “quasi-steady-state” model (Figure 5 is based on such an approach) was given up. The needed change in the hydraulic part with respect to the static THNM is quite small—it has been extended with the addition of the component due to the change of oil velocity. Details are presented in Section 6.2.
6.2. Basic Equations for Overcoming the Limits of “Quasi-Steady-State” Model
The convection−diffusion equation represents the general energy balance, valid for both solids and fluids [33]:
The first term on the left-hand side of the equation describes the heat accumulation, the second the heat transfer due to the fluid motion, the third the heat conduction, while the term on the right-hand side is the volumetric heat generation. The heat accumulation causes the time delay of the temperatures. This “replaces” traditional application of time constants in the dynamic thermal models. In fluid domains, qv = 0, and in solid domains, the convection term is zero since u(t, X) = 0. In practical engineering problems, this equation is solved after discretization and setting the boundary and initial conditions.
The hydraulic scheme is similar to the static one, with the additional hydraulic resistance considering the time change of the velocity (u), as per [34]. This hydraulic resistance (Rhtr) is added to the friction hydraulic resistance on the element of the length z and is calculated as
6.3. Forming the System of Energy Conservation Equations
There are not many publications of the application of general Equation (15) to the construction of power transformers. Reference [34] deals with this topic but does not offer the complete mathematical model and the solver for fluid circulation in the closed loop.
The following mathematical model is developed and implemented in a software tool. The differential Equation (15) is converted to the discrete form based on the finite volume (FV) approach [35], as illustrated in Figure 6 for a FV of length Δz.

Figure 6.
Energy balance for a finite volume.
The set of Equations (17)–(26) is general, while in the FV of the fluid Pgen = 0, of the solid Pflow = 0, and in case of no heat generation in solid Pgen = 0.
From (17) and (18):
where in the experimental test set-up Padd is applicable only for the last element of the heater block and the first element of the water above the heater block (Equation (31)) and the first element of the heater block and the last element of water below the heater block (Equation (32)).
The above case relates to the situation where the FV is surrounded by two elements of temperatures ϑout,i and ϑin,i, exchanging heat with the observed FV element by convection. The remaining equations to complete the system of equations are:
When modeling complex structures, they should be properly divided into parts and each of them has to be described with FV Equations (17)–(26). For solving this system of equations, boundary and initial conditions are required. This will be explained in detail for the case of a closed-loop thermosyphon small-scale model, which is used for the model validation [20].
6.4. Application of the Dynamic Model to the Small-Scale Experimental Set-Up
The properties of water, for both water circulating in the closed loop and the outer water in the heat exchanger, are considered as temperature-dependent quantities:
The properties of the pipe walls steel are taken to be constant: λFe = 239 W∙m–1∙K–1, cp,Fe = 600 J∙kg−1∙K−1, ρFe = 2470 kg∙m−3. For the heater, it is characteristic that it consists of different materials and the heat properties of the heater are defined according to their percentage participation: λht = 239 W∙m–1∙K–1, cp,ht = 600 J∙kg−1∙K−1, ρht = 2470 kg∙m−3. The heater is considered as the element with uniform material and uniformly distributed losses.
For the water, the temperature at the entry of the element (in the direction of the fluid flow) was taken to be equal to the one at the end of the previous element (for example, the entry to the heater case and the exit from the cold water pipe Section 3—temperature ϑw,cp4 in Figure 2). The boundary conditions at the bottom and at the top of the heater block are resolved by the heat transfer Padd calculated as the convection heat transfer on these surfaces. For the top of the heater block:
This heat is transferred to the first part of the water above the heater block. For the bottom of the heater block:
This heat is transferred to the last part of the water below the heater block. Figure 7 presents the discretization schematics for one element surrounded by two different elements (out and in). Table 3 lists the bodies and surrounding elements for the different parts of the experimental model. The diffusion and the flow heat transfer components are calculated using the top and the bottom surface temperatures of the FV (the diffusion as per (21) and (22), and the flow as per (26)). The heat convection and accumulation are determined using the node temperature representing the volume.

Figure 7.
Schematics of the application of the method.

Table 3.
List of the bodies and surrounding elements for the parts of the experimental set-up.
Numerous different methods for determining surface temperatures from node temperatures have been applied without reaching numerical convergence of the model presented above. The numerical convergence was achieved by the application of an upwind interpolation approximation (upwind differencing scheme—UDS) [35]; the top surface temperature is equalized with the node temperature. Therefore, the bottom surface temperature is inherited from the previous element ϑi,surf,bot = ϑi−1,surf,top for i from 2 to N, where ϑi–1,surf,top = ϑi–1. For fluid ϑ1,surf,bot = ϑbot, where ϑbot is the top surface temperature of the previous part, while for the heater, it is calculated by adding the temperature increase due to Padd.
This approximation implies some changes in (21)–(23). Since ϑi,surf,top = ϑi, (21) will always be equal to zero, and this top diffusion part gets included in Equation (22). As the temperature difference ϑi − ϑi,surf,bot equals to ϑi – ϑi–1, and (22) becomes:
6.5. Flow Chart and the Run Time of the Simulation
The flow chart of the dynamic iterative calculation process is presented in Figure 8. The detail of determining the CHTC (surface of heat exchanger towards the circulating water–pipe, surface of heat exchanger towards outer cooling water and water around heater–annulus, top and bottom surface of the heater–horizontal surface with given temperature) is presented in the flow chart in Figure 9.

Figure 8.
Flow chart of the dynamic calculation.

Figure 9.
Flow chart of the CHTC calculation process (the value of CHTC is calculated using the equations form [26]).
The detail of the algorithm, which is not presented in Figure 8, is the calculation at the start of the simulation with the initial cold start experimental conditions. There were two such experiments, with heating powers of 200 W and 50 W. The initial conditions are: the water temperature in the closed-loop path is uniform (21 °C) and the outer water temperature entering the cooler is 11.93 °C. The outer water starts to flow at the start of the process. Since, at the beginning, the circulating water has a constant temperature, there is no buoyancy and there is no closed-loop water flow. At this period, the CHTC between the water in the closed-loop path and the surface is calculated using the equations for natural convection (for a vertical surface). The change of the water temperature in the closed-loop path appears as a result of the heat transferred from the heater and the heat exchange with the air near pipes and the outer water in the cooler. It has been adopted that this starting period of stagnant water ends when the pressure difference along the closed loop (pressure misbalance) exceeds 10 Pa. This time period lasts 21 s for both the cases with heating powers of 200 W and 50 W. The numerical procedure of flow iteration, starting after the starting period ends, is presented in Figure 8.
The simulation time step was set to 0.1 s, and the scale model parts were divided into elements of about 50 mm in size. With the above specified time and space discretizations, the simulation runtime on a computer with an AMD Ryzen 7 4700U processor (8 cores, base clock 2.0 GHz) for the entire experimental test of about 22 h was 17 min and 50 s (without parallel computing).
7. Results
Two different tests were performed for the newly developed dynamic THNM.
The first test was a comparison of the steady-state temperatures available from the experiments (Exp.) from McGill University [20], with the temperatures calculated using static THNM (Stat.) and the values reached in a steady-state condition with specified constant heating power delivered by the new dynamic THNM (Dyn.). This was the only possibility to make a comparison of static THNM/dynamic THNM and the measurements, since static THNM delivers the temperatures in steady states, i.e., does not calculate the temperatures during transient thermal processes. The dynamic simulations were performed using the same tuned coefficients as the ones for the static calculations (obtained by the calibration procedure on the data of the experiment with 200 W and specified in Section 5.4). The results are presented in Table 4. The differences between results of the static and dynamic THNM are small. The deviations for each of the calculated temperatures from those measured are similar—RMSD (root mean square deviation) values for all four temperatures are (the first number is for static THNM and the second for dynamic THNM): for 200 W 0.40/0.80 °C, for 125 W 0.29/0.24 °C, for 50 W 0.13/0.38 °C. As already explained, the mathematics of the static and dynamic THNMs are completely different. The presented results encourage further development and application of dynamic THNM, since the obtained results are close to the results of static THNM, which is implemented in the design software tool, applied for years in the transformer industry.

Table 4.
Measured [20] and calculated steady-state temperatures.
The second validation test is a comparison of the dynamic THNM simulation results with the values measured during a transient thermal process [20]. Figure 10 compares the results for four step changes of the heating power (50–125 W, 125–200 W, 200–125 W, and 125–50 W). The initial conditions are the steady-state temperatures at a heating power of 50 W. Table 5 shows the characteristic deviations of the calculated from the measured temperatures.

Figure 10.
Measured water temperatures [20] and those calculated by software based on dynamic THNM.

Table 5.
The deviations of calculated from measured temperatures over the complete experiment duration.
Figure 10 indicates a good agreement between the measured and calculated temperatures during all heating up and cooling down processes. The RMSDs (Table 5) are around 1 °C. Figure 11 shows the zoomed-in transient periods for temperatures ϑw,hp2 and ϑw,cp3 (for each transient period 1 h is presented). The differences in steady states are summarized in Table 4—the maximum deviation is 2.06 °C, for ϑw,cp3 in steady state with 200 W.

Figure 11.
Zoomed-in initial periods from Figure 10.
Figure 12 presents the temperatures, the heat transferred from the heater to the water, and the water flow predicted by the dynamic THNM for a cold start scenario and a heating power of 200 W. The following can be observed: (1) There is “dead time” in the change of water temperature at the heater’s top and bottom. At the beginning of the heating process, the heat transferred from the heater is low due to the low heater block temperature. In the initial period with no water flow (ca. 21 s) the heat is transferred through the water by heat conduction, thus the heating of the water slowly propagates inside the heater case, around the heater element toward the measuring points 2 and 3 on the cold and hot pipes. Figure 13 presents zoomed-in initial period. The sharp peak shape of the transferred heat at the very beginning of the process is the consequence of the change of CHTC, which is very low at the beginning and starts to increase when the heater to water temperature gradient establishes (2). After this period, the water flow begins slowly. The temperature drop in the water at the heater bottom (ϑw,cp3) is due to the lower outer cooling water temperature (11.93 °C) compared to the initial temperature of circulating water, being equal to the ambient temperature (21 °C) (3). In the initial period, the heating power is mainly accumulated in the heater block, causing an increase of its temperature (4). With an increase of the heater block temperature, the heat transferred to the water increases and the slope of the heater block temperature decreases (5). During the initial period of low flow rate some time is needed for the water heated in the heater to reach the measuring point (for a velocity of 1 cm/s 156 s are needed—the lengths are presented in Figure 2) causing prolonged “dead time” of the water at the heater top temperature (ϑw,hp2) (6). Further change of ϑw,hp2 is the result of the combination of the effects of the drop in ϑw,cp3, the increase of heat transferred from the heater block to the water, and the change of the water flow (7). As the consequence of the complex hydraulic and thermal phenomena there are peaks in the water flow and heat transferred from the heater to the circulating water. Please note that the heat transferred from the heater to the circulating water exceeds the heat power of the heater. This “paradox” is the consequence of the different inertia phenomena: the flow increase delays the increase of heat transferred to the water, the change of CHTC follows the water flow, causing that the temperature of the heater to exceed the steady-state value corresponding to the heat power (200 W). Similar, somewhat lower, local overshoots in transferred power are noticeable when the heating power is increased from 50 W to 125 W and from 125 W to 200 W (Figure 14).

Figure 12.
Temperatures and the heat transferred from the heater obtained by simulation of the heating from a cold state with 200 W.

Figure 13.
Zoomed-in initial period from Figure 12.

Figure 14.
Change of the transferred heat in step-up power transients.
8. Conclusions
This paper describes the application of the convection−diffusion equation as the base for building a dynamic detailed THNM of LIPT. It has been explained that the heat equations have to be fundamentally changed in respect to static detailed THNM in order to solve the problem of the heat accumulated in insulation liquid. The “quasi-steady-state” model, as a small upgrade of the static THNM, is improper and a conceptual and huge change is needed. Contrary to this, the requested changes in the hydraulic model, defining the equilibrium of pressures in the insulation liquid circulating in closed loops, are small, where only the component of time change of the velocity has to be added. This extension was easy to implement. Although the convection−diffusion equation is basic theoretical knowledge, as far as we know it has not been successfully applied in the development of a dynamic thermal model of LIPT and we do believe the content presented in the paper points to the right research and development direction.
The model delivers the distribution of temperature over the volume of the elements of the active transformer part and oil circulating in the closed loop during transient thermal processes without involving any time constant. As an intermediate value in the calculations, the change of flow rate during the transient process is calculated. The heat accumulation in the components is determined as a distributed value over the volume. The calculation time for the developed software is not high, and thus the model can be used in real time. The simulation run time with 0.1 s time discretization for the experiment on a simple small-scale model of about 22 h was 17 min and 50 s. Based on these data and experience with the run time of detailed static THNM software used for transformer design, a realistic expectation is that the future method applied to a real transformer can satisfy online requirements. This is an essential requirement to apply the detailed dynamic THNM as an improved and more physics-meaningful alternative to the simple lumped models, commonly used in practice but with limited accuracy.
In solving the equations of static detailed THNM in general, there is the problem of convergence of the pressure equilibriums in closed liquid circulation loops. While implementing dynamic detailed THNM, convergence problems were faced and solved using the upwind interpolation approximation (UDS). The method is implemented in the developed software which, for now, models the fluid circulating in the single closed loop of a simple experimental small-scale model. The results of the calculations were compared with the results of measurements published in the literature. The presented results confirm the good agreement between the temperatures calculated by the proposed detailed dynamic THNM and the measurements (the RMSDs of calculated temperatures and the maximum difference in steady states are below 1 °C).
This paper should be understood as a proof of concept for the completely novel approach to the important technical issue of dynamic thermal modeling of LIMT. According to the authors experience in the development of static THNM and its application to transformer design, the key issues in dynamic detailed THNM were solved and the next step is to expand the new principles for real transformer parts, following the structure of the software developed for static detailed THNM. Measurements on a laboratory transformer winding model, and measurements during transformer extended temperature-rise tests, will be used to validate the complete detailed dynamic THNM.
Author Contributions
Conceptualization, Z.R. and P.P.; methodology, Z.R. and M.N.; software, M.N.; validation, Z.R., M.N. and F.T.; writing—review and editing, Z.R., M.N., P.P. and F.T.; visualization, M.N.; supervision, Z.R. and P.P.; project administration, Z.R. and P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No data are available for this work.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Roman Symbols | |
| Δp | Pressure difference (Pa) |
| Δpadd | Additional lumped pressure drop on the obstacles (centering plate and the cable entry) (Pa) |
| A | Area (m2) |
| C | Coefficient of additional hydraulic resistance Radd, (m–4) |
| cp | Specific heat capacity (J∙kg–1∙K–1) |
| D | Diameter (m) |
| F | Factor of the heat exchanger |
| g | The difference between the average winding temperature and the average oil temperature (K) |
| H | Gravitational height (m) |
| h | Height (m) |
| HS | Hot-spot factor |
| kpc | Heat transfer coefficient in the heat exchanger (W∙m–2∙K–1) |
| kpp | Heat transfer coefficient to heat transfer through Armaflex foam insulation to ambient, (W∙m–2∙K–1) |
| l | Length (m) |
| P | Power (W) |
| p | Pressure (Pa) |
| Paccu | Heat accumulated in ith finite volume (W) |
| Padd | Heat transferred by convection on the top / bottom finite volume of the heater block to the water above / below the finite volume (W) |
| Pair | Heat transferred to air (on outer Armaflex insulation) (W) |
| Pconv | Total heat transferred by convection from ith finite volume (W) |
| PconvIn | Heat transferred by convection to ith finite volume from the surrounding element (air, water, or heater, depending on the observed finite volume) at the same ith position (W) |
| PconvOut | Heat transferred by convection from ith finite volume to the surrounding element (air or water, depending on the observed finite volume) at the same ith position (W) |
| PCoolingTot | Total cooling power (W) |
| Pdif | Heat transferred by thermal conduction to the surface (top or bottom) of ith finite volume (W) |
| Pflow | Heat transferred by the water flow from ith finite volume (W) |
| Pgen | Heat generated in ith finite volume (W) |
| Ph | Heating power (W) |
| Ptrans | Total heat transferred in ith finite volume (W) |
| Q | Volumetric flow rate (m3∙s–1) |
| qv | Volumetric heat generation density (W∙m–3) |
| Radd | Hydraulic resistance of the obstacles (centering plate and the cable entry) (Pa∙m–3∙s1) |
| Rfhc | Hydraulic resistance to friction (HRF), 2 contractions and 2 expansions inside heater case (Pa∙m–3∙s) |
| Rfhex | HRF in the heat exchanger (Pa∙m–3∙s) |
| Rfscp1 | HRF in cold pipe section (1) (Pa∙m–3∙s) |
| Rfscp2 | HRF and local banding in cold pipe section (2) (Pa∙m–3∙s) |
| Rfscp3 | HRF in cold pipe section (3) (Pa∙m–3∙s) |
| Rfshp1 | HRF in hot pipe section (1) (Pa∙m–3∙s) |
| Rfshp2 | HRF and local banding in hot pipe section (2) (Pa∙m−3∙s) |
| Rfshp3 | HRF in hot pipe section (3) (Pa∙m–3∙s) |
| Rhtr | Hydraulic resistance due to the change of the velocity (Pa∙m–3∙s) |
| Rpp ArmT | Thermal resistance to heat conduction through Armaflex foam insulation (K∙W–1) |
| RppT | Thermal resistance to heat transfer to ambient (K∙W–1) |
| S | Cooling surface (m2) |
| t | Time (s) |
| u | Fluid velocity (m∙s–1) |
| X | Spatial coordinate (m, m, m) |
| z | Coordinate (m) |
| Greek Symbols | |
| Δθ | Temperature difference (K) |
| Δϑλογ | Logarithmic mean temperature difference in a heat exchanger (℃) |
| α | Convection heat transfer coefficient (CHTC) (W∙m–2∙K–1) |
| δ | Thickness of the cylindrical wall (m) |
| θ | Temperature rise over ambient temperature(K) |
| ϑ | Temperature (℃) |
| λ | Thermal conductivity(W∙m–1∙K–1) |
| ν | Kinematic viscosity (m2∙s−1) |
| ρ | Density (kg∙m–3) |
| Superscripts | |
| n | nth time step |
| T | Thermal |
| Subscripts (combination of more subscripts is possible with “,” as delimiter) | |
| a | Ambient air |
| Arm | Armaflex insulation |
| b, bot | Bottom |
| bo | Bottom oil |
| c | Cold |
| cp (1–4) | Positions at the beginning/end of cold pipe sections (1 to 4) |
| enc | Entry temperature to the cooling zone |
| enh | Entry temperature to the heater zone |
| exc | Exit temperature to the cooling zone |
| exh | Exit temperature to the heater zone |
| f | Insulation liquid in the real transformer heat exchanger |
| Fe | Pipe steel |
| h | Hot |
| hc | Heater case |
| hex | Heat exchanger |
| hp (1–4) | Positions at the beginning/end of hot pipe sections (1 to 4) |
| hs | Hot-spot |
| ht | Heater (block) |
| HV | High-voltage winding |
| i | ith finite volume |
| in | Inner vertical surface (in contact with the finite volume) |
| LV | Low-voltage winding |
| o | Outer water and/or pipe surface towards outer water in the heat exchanger |
| out | Outer vertical surface (in contact with the finite volume) |
| ovw | Vertical temperature gradient of oil inside the winding |
| p | Pipe |
| r | Rated conditions |
| rad | Radiator |
| rel | Relative to the rated value |
| scp (1–3) | Sections of pipe with cold water (cold pipe) (1 to 3) |
| shp (1–3) | Sections of pipe with hot water (hot pipe) (1 to 3) |
| surf | Horizontal surface of ith finite volume (top or bottom) |
| t, top | Top |
| to | Top pocket oil |
| ts | Thermosyphon water and/or pipe surface towards thermosyphon water |
| v | Vertical |
| w | Water |
| win | Winding |
| Constants: | |
| gc | Gravitational constant (m∙s–2) |
References
- Tenbohlen, S.; Coenen, S.; Djamali, M.; Müller, A.; Samimi, M.H.; Siegel, M. Diagnostic Measurements for Power Transformers. Energies 2016, 9, 347. [Google Scholar] [CrossRef]
- IEC 60076-7:2018; Power Transformers—Part 7: Loading Guide for Mineral-Oil-Immersed Power Transformers. IEC Standard: Geneva, Switzerland, 2018.
- C57.91-2011; IEEE Guide for Loading Mineral-Oil-Immersed Transformers and Step-Voltage Regulators. IEEE Standard: New York, NY, USA, 2012.
- Radakovic, Z.; Kalic, D. Results of a novel algorithm for the calculation of the characteristic temperatures in power oil transformers. Electr. Eng. 1997, 80, 205–214. [Google Scholar] [CrossRef]
- Radakovic, Z. Numerical determination of characteristic temperatures in directly loaded power oil transformer. Eur. Trans. Electr. Power 2003, 13, 47–54. [Google Scholar] [CrossRef]
- Vasovic, V.; Lukic, J.; Mihajlovic, D.; Pejovic, B.; Radakovic, Z.; Radoman, U.; Orlovic, A. Aging of transformer insulation—Experimental transformers and laboratory models with different moisture contents: Part I—DP and furans aging profiles. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1840–1846. [Google Scholar] [CrossRef]
- Lachman, M.; Griffin, P.; Walter, W.; Wilson, A. Real-time dynamic loading and thermal diagnostic of power transformers. IEEE Trans. Power Deliv. 2003, 18, 142–148. [Google Scholar] [CrossRef]
- Radakovic, Z.; Feser, K. A new Method for the calculation of the hot-spot temperature in power transformers with ONAN cooling. IEEE Trans. Power Deliv. 2003, 18, 1284–1292. [Google Scholar] [CrossRef]
- Weigen, C.; Chong, P.; Yuxin, Y. Power transformer top-oil temperature model based on thermal–electric analogy theory. Eur. Trans. Electr. Power 2009, 19, 341–354. [Google Scholar] [CrossRef]
- Radakovic, Z.; Radoman, U.; Vukotic, D.; Tenbohlen, S. Dynamic top oil thermal model of oil immersed power transformers with tap changer. In Proceedings of the VDE High Voltage Technology 2016, ETG-Symposium, Berlin, Germany, 14–16 November 2016; VDE Verlag: Berlin, Germany, 2016; pp. 516–521. [Google Scholar]
- You, Y.; Shao, K.; Yi, Z. Dynamic Heat Dissipation Model of Distributed Parameters for Oil-Directed and Air-Forced Traction Transformers and Its Experimental Validation. Entropy 2023, 25, 457. [Google Scholar] [CrossRef] [PubMed]
- Radakovic, Z.; Sorgic, M. Basics of Detailed Thermal-Hydraulic Model for Thermal Design of Oil Power Transformers. IEEE Trans. Power Deliv. 2010, 25, 790–802. [Google Scholar] [CrossRef]
- HoST Calculus 7.1.1 Software. Available online: https://www.hostcalculus.com (accessed on 6 March 2023).
- Seitlinger, W. A thermo-hydraulic transformer model. In Proceedings of the Conference of Electrical Power Supply Industry (CEPSI), Manila, Philippines, 22–27 October 2000. [Google Scholar]
- Seitlinger, W. Method and Arrangement for Ascertaining State Variables. U.S. Patent 6609079B1, 6 May 1999. [Google Scholar]
- Cotas, C.; Goncalves, N.; Santos, R.; Dias, M.; Lopes, J.C.; Quintela, M.; Campelo, H. Development of a dynamic thermal hydraulic network model for core-type power transformers windings. In Proceedings of the CIGRE Paris Session 2018, Paris, France, 26–31 August 2018. [Google Scholar]
- Cotas, C.; Santos, R.; Goncalves, N.; Quintela, M.; Couto, S.; Campelo, H.; Dias, M.; Lopes, J.C. Numerical study of transient flow dynamics in a core-type transformer windings. Electr. Power Syst. Res. 2020, 187, 106423. [Google Scholar] [CrossRef]
- Bragone, F.; Morozovska, K.; Hilber, P.; Laneryd, T.; Luvisotto, M. Physics-informed neural networks for modelling power transformer’s dynamic thermal behaviour. Electr. Power Syst. Res. 2022, 211, 108447. [Google Scholar] [CrossRef]
- Pierce, L.W. Bibliography on Transformer Heat Transfer and Loading 1895–2016; IEEE: New York, NY, USA, 2017; Available online: https://grouper.ieee.org/groups/transformers/info/2017-Bibliography-TransfHeatTransfer&Loading-Pierce.pdf (accessed on 6 March 2023).
- Lokhmanets, I.; Baliga, B.R. Experimental investigation of steady and transient operations of a single-phase closed-loop vertical thermosyphon. Int. J. Therm. Sci. 2019, 145, 105988. [Google Scholar] [CrossRef]
- Torriano, F.; Campelo, H.; Quintela, M.; Labbé, P.; Picher, P. Numerical and experimental thermofluid investigation of different disc-type power transformer winding arrangements. Int. J. Heat Fluid Flow 2018, 69, 62–72. [Google Scholar] [CrossRef]
- Gong, R.; Ruan, J.; Chen, J.; Quan, Y.; Wang, J.; Duan, C. Analysis and Experiment of Hot-Spot Temperature Rise of 110 kV Three-Phase Three-Limb Transformer. Energies 2017, 10, 1079. [Google Scholar] [CrossRef]
- Radakovic, Z.; Radoman, U.; Kostic, P. Decomposition of the Hot-Spot Factor. IEEE Trans. Power Deliv. 2015, 30, 403–411. [Google Scholar] [CrossRef]
- Sorgic, M.; Radakovic, Z. Oil-Forced Versus Oil-Directed Cooling of Power Transformers. IEEE Trans. Power Deliv. 2010, 25, 2590–2598. [Google Scholar] [CrossRef]
- Radakovic, Z.; Sorgic, M.; Van der Veken, W.; Claessens, G. Ratings of Oil Power Transformer in different Cooling Modes. IEEE Trans. Power Deliv. 2012, 27, 618–625. [Google Scholar] [CrossRef]
- Bergman, L.T.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Introduction to Heat Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kays, W.M.; Crawford, M.E. Convection Heat and Mass Transfer, 3rd ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Rohsenow, W.M.; Hartnett, J.P. Handbook of Heat Transfer, 1st ed.; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Grimison, E.D. Correlation and Utilization of New Data on Flow Resistance and Heat Transfer for Cross Flow of Gases over Tube Banks. Trans. ASME 1937, 59, 583–594. [Google Scholar] [CrossRef]
- Zukauskas, A. Heat Transfer from Tubes in Cross Flow. Adv. Heat Transf. 1972, 8, 93–160. [Google Scholar] [CrossRef]
- Idelchik, I.E. Handbook of Hydraulic Resistances, 3rd ed.; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow, 1st ed.; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education: Harlow, UK, 2007. [Google Scholar]
- Van der Veken, W.; Declercq, J.; Baelmans, M.; Van Mileghem, S. New perspectives to overloading with accurate modeling of thermal transients in oil-immersed power transformers. In Proceedings of the 2001 IEEE/PES Transmission and Distribution Conference and Exposition. Developing New Perspectives (Cat. No. 01CH37294), Atlanta, GA, USA, 2 November 2001; pp. 147–152. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).