Abstract
The approaches for predicting output parameters of betavoltaic batteries are reviewed. The need to develop a strategy for predicting these parameters with sufficient accuracy for the optimization of betavoltaic cell design without using the simple trial and error approach is discussed. The strengths and weaknesses of previously proposed approaches for the prediction are considered. Possible reasons for the difference between the calculated and measured parameters are analyzed. The depth dependencies of beta particles deposited energy for Si, SiC, GaN, and Ga2O3 and 20% purity 63Ni and titanium tritide as radioisotope sources are simulated using the Monte Carlo algorithm taking into account the full beta energy spectrum, the isotropic angular distribution of emitted electrons and the self-absorption inside the radioisotope source for homogeneously distributed emitting points. The maximum short circuit current densities for the same semiconductors and radioisotope sources are calculated. The methodology allowing the prediction of betavoltaic cell output parameters with accuracy no worse than 30% is described. The results of experimental and theoretical investigations of the temperature dependence of betavoltaic cell output parameters are briefly discussed. The radiation damage by electrons with the subthreshold energy and the need to develop models for its prediction is considered.
1. Introduction
Betavoltaic microbatteries, comprising a radioactive source and semiconductor structure converting the energy of beta particles into electricity, have attracted considerable research interest for low-power devices due to their high energy density and insensitivity to the environment. Their advantages also include the capability of easy integration, stable output performance, and long working life. While the electronic device and battery size requirements have been continually shrinking over the last several decades, energy density requirements have steadily been increasing at the same time. Betavoltaic batteries have the advantage that they can be made into very small, reliable, and durable power sources for micro scale applications. Due to their high energy density, long lifetime, and anti-jamming capabilities, they can also be used for remote applications including powering Micro Electro Mechanical Systems (MEMS), implantable medical devices, scientific apparatus in spacecraft, in undersea exploration, in the oil and mining industries, underground, in polar regions, in high mountainous regions, in military equipment, in sensor networks for environmental monitoring, and in bridges with embedded sensors. The description of betavoltaic cell operation and their advantages and disadvantages can be found in the recent reviews [1,2,3,4,5,6].
The main elements of betavoltaic batteries are radioisotope source and a semiconductor structure, which converts the kinetic energy of beta particles into electricity (convertor). Therefore, to optimize the battery efficiency, it is necessary not only to select the radioisotope and material of converter, but also to optimize the design of the converter, taking into account the properties of the radioisotope source. As the radioisotope source is the most expensive part of the battery, for the optimization of their design it is useful to develop approaches for predicting battery parameters without using the radioisotope source. Unfortunately, up to now there is no general principle available that can be used to guide the device design for the large number of candidates of semiconductor materials and beta isotope sources. The development of practical models would allow the prediction of output parameters, which can be achieved in betavoltaic cells fabricated of various semiconductor materials and of various designs, and thus would obviate the necessity of their optimization by the simple trial and error approach, which is very time consuming and costly. Despite numerous studies, the efficiency of betavoltaic batteries up to now is far from the predicted one. Thus, the parameters calculated for the particular cells can exceed measured ones on the similar cells more than 5 times [7,8,9]. It seems that this discrepancy is determined both by the non-optimal cell design and the insufficient accuracy of predictions. For instance, the reported short circuit current values for Si-based converters obtained by calculations [9,10,11,12], when normalized to the same source activity of 10 mCi/cm2, varied from 24.4 [11] to 540 nA/cm2 [9]. Taking into account that beta particles undergo numerical collisions inside the radioisotope source, which change not only their total emitted number but also the angular and energy distributions, while the generated excess carriers can recombine inside the converter that decreases their collection efficiency, it should be stated that the processes occurring in the betavoltaic batteries are quite complex. The main obstacle for a development of predictive model is the lack of a detailed understanding the direct conversion mechanisms and insufficient information about real semiconductor structure parameters. A detailed theoretical analysis of betavoltaic mechanisms is therefore in need to accelerate the experimental research and to optimize the betavoltaic battery performance.
A few methodologies to solve the mentioned problems were described in the literature, and they can be divided into two main groups. The first one consists in modeling the energy deposited by beta particles inside a semiconductor convertor, and then the output parameters of betavoltaic cell were calculated using some simulators or using the appropriate device models [8,13,14,15,16,17,18,19,20,21,22,23]. In this approach the material parameters of converters, such as the diffusion length and leakage current should be known. Usually, the used in calculations material parameters have little relation to specific structures, leading to large errors in predicted output parameters of betavoltaic cells. That means that such an approach probably, allows to estimate the limits for the output parameters but not their values in the particular structures and, thus, it hardly can guide the cell design optimization. Additionally, it cannot be used for express characterization of converter prototypes and evaluation of their efficiency, which would speed up and reduce the cost of optimizing their design.
The second main approach consists in using the electron beam of SEM to mimic the radioactive source [24,25,26,27,28,29,30,31,32,33]. At first glance, it seems that this approach allows us to directly obtain the parameters of specific betavoltaic cells. Moreover, it could be expected that it would allow testing converter prototypes under conditions close to those of a betavoltaic cell operation. However, the main disadvantage of this approach consists in the lack of a procedure that allows to choose the parameters of the electron beam, allowing to imitate beta radiation with appropriate accuracy. In the most studies a beam perpendicular to the surface with energy equal to the average energy of beta particles was used in such measurements that, as shown below, is a rather rough approximation.
In the present paper the strengths and weaknesses of the main modeling philosophies applied to prediction of betavoltaic battery efficiency are discussed. The importance of correct estimation of e-h pair generation rate, taking into account the characteristic features of beta radiation and semiconductor convertor parameters, such as top layer thickness, junction depth, doping concentrations etc. is discussed. The calculated by the Monte Carlo simulation depth dependencies of beta particle deposited energy for Si, SiC, GaN and Ga2O3 and 63Ni and titanium tritide as radioactive sources are presented. The upper short-circuit current limit for this material is calculated. Possible reasons for the huge discrepancy between the calculated and measured parameters are considered. The approach allowing to achieve the prediction precision better than 30% using both the calculations and an electron beam of SEM is described in more detail. The radiation damage by electrons with energies less than necessary to knock atoms out of a lattice site is considered.
2. Principles of Betavoltaic Cell Operation
To optimize the design of betavoltaic batteries and understand the limitations and opportunities for improvement of their parameters it is useful to describe the basic principles of betavoltaic battery operation. In these batteries energy from isotope decay is directly converted to electricity, thus the main elements of such batteries are radioisotope source and a semiconductor structure, which converts the kinetic energy of beta particles into electricity (convertor). Typical layouts of betavoltaic cells are presented in Figure 1. As an example, the 63Ni film is shown as the radioisotope source. Besides, the source could contain a substrate and a protective layer, which for the 63Ni film are frequently made from Ni of a natural isotopic abundance. The simplest converter structures are the Schottky barrier (Figure 1a) or p-n junction (Figure 1b). The first one can be formed by a deposition of appropriate metal building up a potential barrier ϕbi at a contact with the semiconductor. A p-n junction is formed by a contact of n- and p-type semiconductors. As the Fermi level must be constant throughout the sample the built-in barrier is formed at the contact providing zero net electron and hole currents. For p-n junctions ϕbi is equal to the difference between the Fermi levels in p- and n-type semiconductors and is close to the bandgap Eg. For the Schottky barriers ϕbi is determined by the difference between the metal work function and the semiconductor electron affinity and by the presence of interface state and usually it is noticeably smaller than Eg. In both structures free carriers are repealed from the contact by the built-in electric field forming the depletion region, which screens the built-in potential. The width W of the depletion region can be described as
for the Schottky barrier and
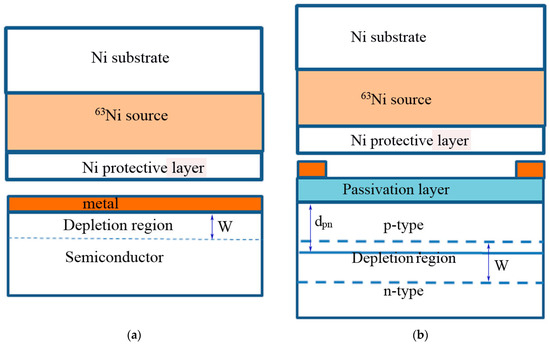
Figure 1.
Schottky (a) and p-n junction (b) betavoltaic battery designs. dpn is the p-n junction depth.
For the p-n junction, where N is the dopant concentration, Na and Nd are the acceptor and donor concentrations, respectively, εs is the semiconductor permittivity and e is the electron charge. As shown below, the leakage current in betavoltaic converters should be as low as possible. Therefore, to reduce the leakage current in p-n junctions the passivation layer (usually thin dielectric film) and the guard ring are used. The passivation layer can also decrease the surface recombination velocity.
The operation mechanism of the conversion is similar to that of solar cell; however, it is more complex because includes also electron scattering inside the source and converter. Therefore, it is more like a formation mechanism of collected current generation in the electron beam induced current (EBIC) mode of scanning electron microscope (SEM). When high energy electrons emitted from the source penetrate the semiconductor converter, they generate electron-hole (e-h) pairs, a number of which exceeds that of primary electrons by a few orders of magnitude. This occurs via numerous elastic and inelastic scattering events, which change the beta particle trajectories and energy. If the electrons in the valence or the deeper bands receive sufficient energy from collisions with the beta particles, they can jump to the conduction bands leaving holes. As their energy after the collision can be high enough to create an e-h pair, they can transfer a part of energy for the additional e-h pair generation. Thus, it is important to note that a relatively low number of high energy beta particles may create a large number of e-h pairs. The higher the beta particle energy, the more pairs are generated by one particle. However, only about a third of beta particle energy is used for electron-hole pair generation. When the electron energy decreases below the threshold for the pair creation, electrons are thermalized by phonon generation. Thus, about two-thirds of the energy is lost mainly due to the phonon generation [34] that is the principal mechanism for reducing the converter efficiency, which should be taken into account under the efficiency analyses. In a quasi-neutral region of semiconductors, the diffusion of thermalized holes and electrons is correlated that allows to describe their transport as ambipolar diffusion [35,36]. Under this approach electron and holes moves with the same ambipolar diffusivity Damb = (n + p)/(n/Dh + p/Dn) and ambipolar mobility μamb = (n − p)/(n/μh + p/μn), where n and p are the electron and hole concentrations, respectively, Dn and Dh are the electron and hole diffusivities, respectively μn and μh are the electron and hole mobilities, respectively. When the electrons and holes reach the depletion region they are separated by the built-in electric field. This field attracts the minority carriers and repeals the majority ones that generate current in the external circuit without an applied bias. Thus, the depletion region plays the role of a collector, which is necessary for the operation of a semiconductor converter. The generated current is the collected current Ic in the EBIC mode and the short-circuit current in the betavoltaic and solar cells. When a load is connected to a cell, the current density in the circuit J for the ideal device can be written as [37]
where J0 is the saturation current, V is the applied bias, R is the load resistance, n is the ideality factor depending on a contribution of recombination current, k is the Boltzmann constant, T is temperature and Jsc is the short-circuit current density, i.e., the current density at R = 0 and V = 0. The sign of V corresponds to the sign of voltage applied to the Schottky barrier on n-type material or to the p-layer of p-n junction. The available voltage at the load is equal to J × R × S, where S is the element area and it cannot exceed the ϕbi value because if it is equal to ϕbi, the depletion region will disappear that will suppress the carrier separation.
Let us define the betavoltaic cell parameters. As follows from Equation (3), the open-circuit voltage Voc can be obtained by setting J = 0. The power of a cell is equal to P = J2 × S2 × R, i.e., it increases with R, however, as follows from Equation (3), J decreases with the R increase. Thus, to calculate the maximum available power of the betavoltaic cell Pm = Rm × (Jm)2 the condition d(R × J2)/dJ = 0 should be used. The additional parameter Fill Factor (FF) is usually used in the solar and betavoltaic cell characterization. It can be defined as FF = Pm/(Isc × Voc).
3. Simulation of Beta Particle Energy Deposition
To calculate the collected current, the energy deposited inside a semiconductor converter and its depth distribution should be known. Many researchers have used different methods for the calculations, such as the Katz-Penfold range equation [25], the Everhart and Hoff range equation [38], the direct chord method [15] etc. However, in the most recent investigations the Monte Carlo method is used because of its comprehensive atomic physics model which obtains better estimates of energy deposition and penetration depth. This method is successfully used for a calculation of depth-dependent energy deposition for electron beams in SEM. However, for realistic description of the energy loss by beta particles it is necessary to take into account a number of features. Thus, the Monte-Carlo algorithm should take into account an isotropic emission of radiation [12,16,19,39,40,41,42,43], the full beta energy spectrum for the isotope [11,12,15,16,19,39,40,41,42,43], the homogeneous distribution of emitting points inside the radioactive source [41] and inelastic and elastic scattering processes in a radioisotope source (self-absorption) [12,16,40,41,42,43]. Additionally, the absorption in passivation and protective layers and top metal contacts, if any, should be estimated.
In the present paper all calculations are carried out for a few semiconductor materials and 20% purity 63Ni and titanium tritide as radioisotope sources using in-house Monte Carlo program based on the algorithm described in [40,44]. The calculation algorithm is specially adapted for the fast simulation of beta particle energy deposition inside multilayer structures. The main advantage is that it can simulate electron trajectories originating uniformly in the radioisotope layer volume with the isotropic angular distribution of emitted electrons. That allows the more precise simulation of self-absorption inside the radioactive source. The full energy spectrum of emitted electrons was used, which according to the Fermi’s golden rule can be approximated as [16]
where E is the beta particle energy, me is the electron mass, Emax is the decay energy and c is the speed of light. If one takes into account coulomb interaction of the beta particles with the atomic nucleus it can change this typical generalized spectrum shape [4,16]. However, the accuracy of calculations using the Equation (4) seems to be acceptable. The advantage of the program is also its ability to self-consistently take into account the backscatter energy and effects of passivation and protective layers. As a result, the depth dependence of beta particle energy deposited inside a semiconductor converter can be calculated with acceptable accuracy for a lot of planar designs of the cell.
63Ni is one of the most attractive radioactive isotopes for specific applications, such for example as remote sensors due to its long half-life (100.2 years). Specific activity of pure 63Ni is of 525 Ci/cm3, however, 63Ni sources with a purity of 20% or lower are usually used due to their commercial availability. The maximum energy of emitting electrons is 67 keV, i.e., it is lower than the threshold energy for a damage of the most of semiconductors. However, it has a rather low specific power of 5.8 mW/g compared to the other beta emitters. Such low value is determined by both long half-life because generally, the specific power of a radioactive source is inversely proportional to its half-life, and relatively low average beta energy. Tritium 3H is probably the most viable source from a practical point of view (e.g., cost, availability and energy density). It is the only radioactive isotope of hydrogen; the nucleus of a tritium atom consists of a proton and two neutrons. It has a rather good specific power of 325 mW/g but a half-life of 12.4 years only. However, tritium is naturally in a gaseous state, and it can create a radiation hazard from leaks (a persistent problem for hydrogen and its isotopes). Additionally, it is difficult to obtain it in high density (e.g., higher pressure can be used), which determines its low effective specific activity per cm3. For these reasons solid sources are preferred in the betavoltaic battery design and 3H was proposed to use in the form of tritiated metals [18,45,46,47] or organic compounds [48]. The calculations below used 20% purity 63Ni and titanium tritide of TiT2 composition.
The isotropic angular distribution of emitted beta particles often was not taken into account. To demonstrate the importance of isotropic angular distribution effect the dependencies of the absorbed energy density dEabs/dz on a depth calculated taking into account the isotropic radiation emission (blue symbols) and under an assumption that all beta particles are emitted perpendicular to the converter surface (magenta lines) are shown in Figure 2 for 10 nm thick TiT2 and 20% purity 63Ni radioisotope sources and 4H-SiC as a converter. It is generally accepted that the depth dependence of e-h pair generation rate h(z) is proportional to the density of deposited energy and can be determined by dividing the distribution of absorbed energy by the mean energy for e-h pair creation Ei, which for 4H-SiC is equal to 8.23 eV [49]. For both isotopes the depth dependencies are qualitatively similar. If the isotropic emission is taken into account that leads to an increase in absorbed energy near the surface and a decrease in depth. It is also seen in Figure 2 that the density of absorbed energy for the isotropic emission case decays noticeably faster than that for the e-beam perpendicular to the surface. Besides, the overall absorbed energy decreases by 21 and 23% for 63Ni and TiT2, respectively, when the isotropic distribution of emission is taken into account due to an increase in backscatter energy with the decrease in incidence angle [16]. The increase in absorbed energy near the surface is also easy to understand, because the decrease in incidence angle should decrease the beta particle penetration depth.
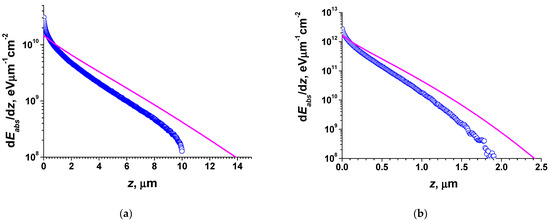
Figure 2.
Deposited energy dependence on depth calculated for 4H-SiC converter and 10 nm thick 20% 63Ni (a) and TiT2 (b) as a radioisotope sources. Calculations were carried out with (blue symbols) and without (magenta lines) taking into account the isotropic angle distribution.
In many works the average energy of beta particles was used to determine the deposited energy and penetration depth, although as shown in [11,12,15,16,19,39,40,41,42,43], the real energy spectrum of sources can essentially affect the deposited energy distribution inside the convertor, thus influencing the prediction accuracy. One of the reasons for the need to take the real spectrum into account is the superlinear dependence of electron range on electron energy R~Eb1.75 that should be considered under averaging, especially for the materials with the diffusion length L smaller than the beta particle penetration depth. Besides, as seen in Figure 3, the depth dependence for the monoenergetic e-beam with the energy equals to the average energy of beta particles essentially differs from the real one, the deposited energy in the case of a monoenergetic beam drops much faster. Additionally, it is seen that the thickness of radioisotope layer not only affects the total number of emitted particles but also the depth dependence of generation rate for both 63Ni and TiT2, especially near the surface (Figure 3 and Figure 4). This means that the elastic and inelastic scattering in the radioisotope layer changes not only a number of emitted particles but also both their spectrum and angle distribution. Thus, it can be concluded that for the correct calculations of deposited energy depth distribution it is insufficient to know the source radioactivity, as it is usually given in papers, but it is necessary additionally to know the radioisotope specific activity or the layer thickness [42] for the correct estimation of source effect. For the same reason, determination of the portion of energy absorbed in the source is insufficient for a complete description of the source, which is necessary for further calculations.
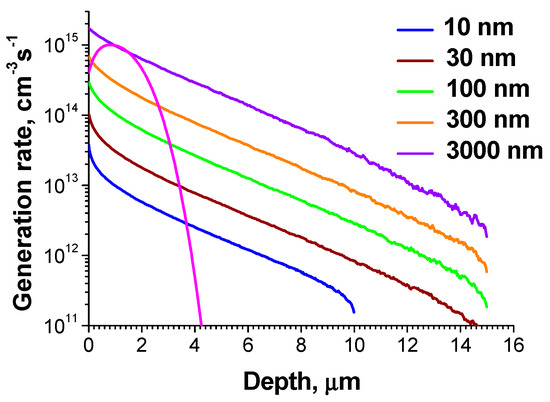
Figure 3.
Dependencies of e-h pair generation rate on depth calculated for 4H-SiC and 20% purity 63Ni film with different thicknesses. The dependence for monoenergetic beam with Eb = 17.4 eV normalized to be represented at the same scale is shown with magenta line.
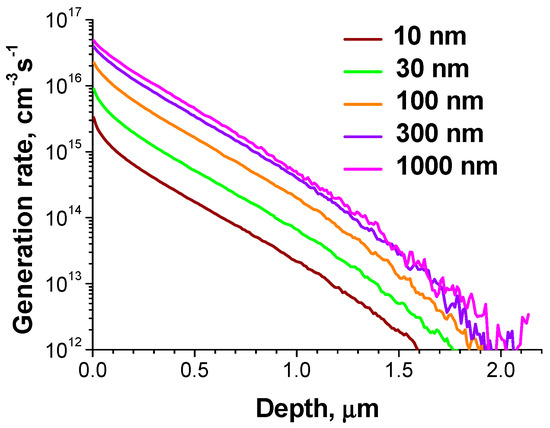
Figure 4.
Dependencies of e-h pair generation rate on depth calculated for 4H-SiC and TiT2 radioisotope film with different thicknesses.
As seen in Figure 4, the energy emitted from the TiT2 radioisotope film is practically saturated for the film thicknesses of 1 μm. For 63Ni the emitted power saturation was observed at about 3 μm [40,50]. Thus, at such thicknesses the maximum power from the sources can be obtained. It can be useful to calculate the depth distribution of excess carrier generation rate for typical semiconductor materials used for the converters and the maximum emitted power. The results for the 5 μm thick 20% purity 63Ni and 2 μm thick TiT2 sources are presented in Figure 5 and Figure 6, respectively. It is seen that the dependencies for GaN and Ga2O3 are similar. The dependencies for 4H-SiC and diamond are also similar, although the difference is larger than for GaN and Ga2O3. Such behavior is easy to understand taking into account that the depth dependence is mainly determined by the material density. As the emitted power is independent of converter material a number of generated carriers will depend on the portion of energy absorbed inside the converter taking into account the backscattered energy, which increases for heavy atoms, and the mean energy for e-h pair creation Ei. It should be noted that the dependencies can be approximated fairly well by exponential functions exp(−z/z0), with z0 values presented in Table 1. The Ei values for Si, 4H-SiC, GaN and Ga2O3 used in calculations of generation rates were taken from [49]. For GaAs and diamond Ei values from [21,51], respectively, were used. It should be mentioned that similar dependencies close to exponential ones were also obtained in many other works [11,15,16,19,21,39].
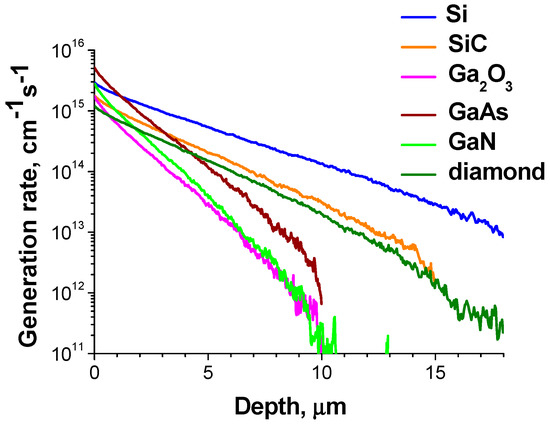
Figure 5.
Dependencies of e-h pair generation rate on depth calculated for 20% 63Ni radioisotope film with a thickness of 5 μm and a few semiconductor materials.
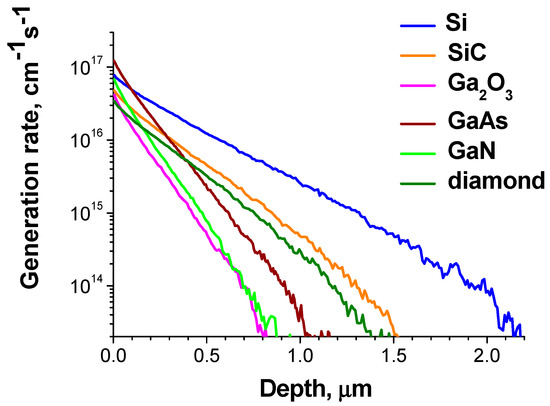
Figure 6.
Dependencies of e-h pair generation rate on depth calculated for TiT2 radioisotope film with a thickness of 2 μm and a few semiconductor materials.

Table 1.
Ei and z0 values for a few semiconductors and 20% purity 63Ni and TiT2 radioisotope sources.
4. Evaluation of Betavoltaic Cell Efficiency
In accordance with [52] the overall betavoltaic cell efficiency η can be written as a product of three terms as
The term ηβ is the radioisotope source efficiency expressing the fraction of all beta particles created that are actually emitted from the source and directed towards the semiconductor converter. It depends on the source design, thickness, protection layer thickness etc. The variable ηc is a coupling efficiency involving properties of both beta source and the semiconductor converter, r is the backscattered energy coefficient and Q is the semiconductor collection efficiency. The term ηs is the semiconductor efficiency, which determines the possible efficiency that can be attained with a given semiconductor coupled to a particular beta radiation source. The mean energy for e-h pair creation Ei can be approximated as [49,53]
The procedure for the Ei estimation from the EBIC measurements and a comparison of Ei values for a several semiconductor materials with the Equation (8) were presented in [49]. The experimental Ei values for a set of semiconductor materials together with Ei(Eg) dependence calculated using Equation (8) are shown in Figure 7. While for Si Ei values obtained in numerous studies are in rather good agreement, for some materials the experimental values differ markedly. Thus, for 4H-SiC they varied from 5.05 eV [54] to 8.6 eV [55]. Nevertheless, it can be stated that the empirical Equation (8) describes Ei(Eg) dependency rather well and it can be used for the Ei estimation. As shown in [49] it described the experimental Ei(Eg) dependency better than other proposed empirical approximations.
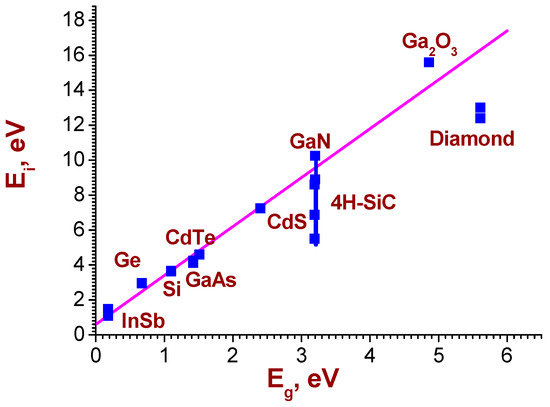
Figure 7.
Experimental values of Ei from [42,49,53,56] (symbols) and the calculated Ei(Eg) dependence calculated using the empirical expression (8) (line).
It is obvious that self-absorption leads to the decrease in beta source efficiency. The curves in Figure 4 clearly demonstrate the saturation of generation rate with the source thickness. That means that the source activity no longer increases with its thickness. As a number of emitted electrons increases in proportion to the source thickness, that means that the source efficiency decreases with the thickness. The results of ηβ simulation for 20% purity 63Ni and TiT2 sources demonstrating the efficiency decrease with the source thickness are shown in Figure 8. It is seen that while for the cell, in which a converter is placed on one side of the source, ηβ is close to 0.5 for thin enough layers, it essentially decreases with the increase in source thickness. On the other side a decrease in radioisotope layer thickness leads to a decrease in battery power. Thus, for any specific application of betavoltaic cells a trade-off between the necessary cell power and efficiency should be reached. It was shown in numerous papers [15,19,31,41,45,47,50] that the power is practically saturated at 3–4 and 0.8–1 μm for 63Ni and TiT2 sources, respectively. These values can be considered as the optimal ones, if the maximum power is required.
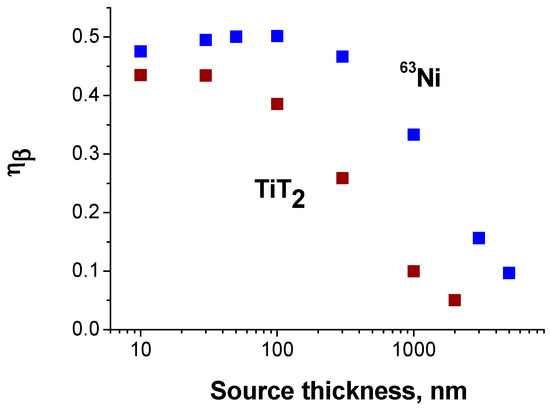
Figure 8.
Dependencies of ηβ on the source thickness calculated for 63Ni and TiT2.
5. Evaluation of Coupling Efficiency
The coupling efficiency of the betavoltaic battery ηc is determined by the degree of matching between the energy deposition range of the radioisotope source inside the converter and the effective excess carrier collection area of the semiconductor converter. The higher the degree of matching, the higher the energy utilization. The main factor determining the coupling efficiency is a relation between the depth dependence of deposited energy and the excess carrier collection efficiency of converter material, which in turn depends on the diffusion length L, depletion region width, p-n junction depth etc. As the diffusion length depends on the crystalline perfection of a converter material and can be only optimized by the choice of suitable material, the effects of other parameters can be optimized by adjusting the converter design. The easiest way for such optimization is to model the dependence of cell parameters on its design. However, the results of such modeling strongly depend on the L value used. In some papers the L value is estimated from its theoretical dependence on the dopant concentration [18,22,57,58] and this value is used to find the optimal dopant concentration. However, in real semiconductors L is mainly determined by deep level defects. Moreover, in some semiconductors, e.g., in GaN, a question about the nature of defects, which determine L values up to now has not been solved [59,60,61]. Therefore, even if the deep level defect concentrations and the capture cross-sections are known in a common case it is impossible to predict the correct excess carrier diffusion length value in semiconductors. Besides, in the p-n junctions the surface recombination should be taken into account, which strongly depends on the semiconductor/passivation layer interface.
For a radioisotope planar source both surfaces, top and bottom, emit power equally, therefore, if a converter is placed on one side of the source the used power cannot exceed a half of the available power, as can be seen in Figure 8. An increase in source thickness further reduces this portion of the available power. A few ways to overcome this restriction were proposed. The obvious one is to use a sandwiched configuration where a radioisotope layer is sandwiched between two semiconductor converters [62,63]. As shown in [63], the portion of available energy can also be increased for one-side cell by depositing a heavy metal film, which backscatters electrons to the source and collector. However, such an approach is efficient for the thin sources only. As the Monte Carlo simulation has shown, for a 100 nm thick 63Ni film deposited on Ni substrate the energy absorbed in Si-based converter increases by 33%. At larger thicknesses the effect decreases and for 1 μm thick Ni film the absorbed energy increase due to backscattering from the substrate is about 5% only (Figure 9). The backscattering effect should be also taken into account for the sandwiched structures, when the beta-radiation source is inserted between two converters for more efficient radiation energy utilization. The estimation has shown that for 0.5 μm thick 63Ni layer placed between two Si converters the short circuit current increases by 8% for every converter as compared with the one-side design. For 1 μm thick 63Ni source this increase is about 4%.
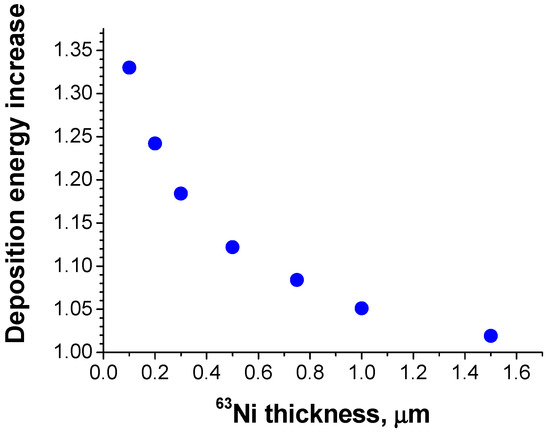
Figure 9.
Calculated relative increase in energy absorbed in Si due to a Ni substrate as a function of radioisotope 63Ni layer thickness.
Another way to increase the available power consists in using stacked multilayer structures [47,58,64]. As seen in Figure 3 and Figure 4 the emitted energy is practically totally absorbed in 4H-SiC layers with a thickness of about 10 and 2 μm for 63Ni and TiT2, respectively. For heavier compounds, such as GaN or Ga2O3 the corresponding thicknesses are about two times smaller [31,41,65]. Thus, using thin radioisotope and converter layers allows essentially improve the battery output power per unit volume. Devices based on a three-dimensional surface structure [6,25,66], a porous material [8,67,68,69] and nanowires [70,71,72,73] have also been proposed for improving the coupling efficiency and achieving higher power density due to an increase in effective surface. Although it should be taken into account that increasing the number of layers in the stacked structure or preparing three-dimensional structures increases the technical difficulty and cost of production and reduces reproducibility. It should be also mentioned rather interesting approach to improve the coupling efficiency by using 35S betavoltaic liquid nuclear battery [74,75] and batteries based on 35S uniformly infused within a semiconductor material [76]. However, a half-life of 35S is only 87.3 days that strongly limited practical application of such batteries.
It should be also mentioned that some protective layers are often deposited on the radioisotope source, especially in the case of 63Ni, and passivation layers are deposited on the semiconductor converter to decrease the surface recombination velocity and leakage current that will additionally decrease ηc [42]. A similar decrease takes place for a top metal contact to a converter. Thus, 100 nm thick Ni protection layer on the source or metal contact on the converter absorbs about 14% of emitted energy, while 500 nm thick layer absorbs about 50%. The effect of SiO2 film is essentially smaller, thus, 200 nm thick film absorbs about 5% of emitted energy. For thin films the portions of energy absorbed in Ni and SiO2 are related as the ratio of their densities [42] that can be used for estimations of covering layer effect for any compound calculating this effect for Ni. It should be also noted that Ni formed the Schottky barrier with n-type 4H-SiC and Ga2O3. Thus, 63Ni layer can be used as the metal forming the Schottky barrier. TiT2 also can form the Schottky barrier with some semiconductors. Additionally, in some structures these metals could form a top metal contact. That allows to eliminate the absorption in the top metal contact. The Monte Carlo simulation routine can effectively predict ηc value for planar structures independent of a number of active or passive layers calculating the energy loss inside every of them. This is also true for the cells in which the radioisotope is distributed uniformly over the converter, as, for example, in [74,75,76] and the stacked multilayer structures. Three-dimensional structures are more complex for calculations nevertheless attempts have been made to evaluate the efficiency for such structures also [8,66,68,70,71,72,73].
Thus, it can be expected that the Monte Carlo program that takes into account all the specific features of beta radiation predicts the ηc value and depth dependence of deposited energy with acceptable accuracy that in turn allows to calculate the maximum short circuit current density Jsc induced by beta irradiation. The maximum short circuit current density assumes that the excess carrier recombination in the converter is neglected, and all e-h pairs generated by beta irradiation contribute to the current. The calculated maximum Jsc values for Si, GaAs, 4H-SiC, GaN, Ga2O3 and diamond are presented in Table 2 together with Ei values used in the calculations. Thick 20% purity 63Ni and TiT2 radioisotope sources (with the 5 and 2 μm thickness, respectively) were used in the calculations to achieve the saturated output power density of the source. It should be noted that the maximum short circuit current density Jsc varies not only due to different Ei values, which increase with Eg according Equation (8), but also due to the different portion of energy r carried out by backscatter electrons. According to estimations for 20 keV e-beam perpendicular to the surface, r is equal to 0.1, 0.095, 0.25, 0.23, 0.22, 0.03 for Si, 4H-SiC, GaAs, GaN, Ga2O3 and diamond, respectively. For e-beam inclined to the surface r increases for all materials.

Table 2.
Ei and the upper limit of Jsc for a few semiconductors and 20% purity 63Ni and TiT2 radioisotope sources.
6. Calculation of Betavoltaic Cell Output Parameters
A rather good correlation of deposited energy depth distributions calculated in different papers [19,41] seems to confirm the above conclusion about the acceptable accuracy of ηc and deposited energy predictions. Thus, if these distributions are approximated with the exponential functions exp(−z/z0), z0 is varied in the range from 2.38 to 5 μm for Si [9,11,15,42], from 1.52 to 2.4 for 4H-SiC [11,21,42] and from 0.88 to 1.2 for GaN [11,21,42]. It should be taken into account that z0 depends on the source thickness (Figure 3 and Figure 4), which can differ in different papers. Thus, it is reasonable to assume that the main reason for the significant discrepancy between the calculated and measured parameters of betavoltaic cells (see references in [42]) is the unsatisfactory accuracy of Jsc and ηs predictions. As these both values depend on the device design and semiconductor properties, it is reasonable to discuss the main approaches for their estimation. As mentioned above, the first one consists in simulation of these parameters by some model calculations or using the device simulators, such as Synopsyss Medici device simulator or COMSOL Multiphysics software. However, in both cases not only the device design but also the converter parameters, such as the diffusion length, surface recombination velocity and leakage current should be known. The converter efficiency is determined by the product of Jsc × Voc × FF. In the real structures the Jsc can be essentially smaller than its upper limit presented in Table 2. In a common case Jsc could decrease if the series resistance is not small enough but in the betavoltaic cells this effect can be neglected due to the small, induced current. Thus, the main factor reducing the Jsc value is carrier recombination decreasing the collection efficiency Q of excess carriers. Q is the portion of generated carriers, which were collected, and it mainly depends on the depletion region width W and the diffusion length L. In some works, it was assumed that the excess carriers are collected only inside the depletion region, therefore, to increase Jsc W should be made as large as possible. Such assumption can be useful for semiconductors with a small L; however, such way of Q improvement has a limit. Indeed, the small L value implies the high recombination rate. If so, at large enough W the electric field inside the depletion region decreases and the recombination inside the depletion region cannot be neglected.
The similarity between the collected current in the EBIC mode Ic and Jsc noted above allows to use for Jsc calculations the approach proposed by Donolato [77,78], which for planar structures gives:
where ψ(z,L) is the collection probability, which is equal to current generated by a unit charge at a depth z. The collection probability can be easily calculated as a solution of homogeneous diffusion [77] or drift-diffusion equations [78], if the diffusion length and device structure are known. If L » W, for the Schottky barrier ψ(z,L) = 1 for z ≤ W and ψ(z,L) = exp[−(z − W)/L] for z > W. If the depth dependence of generation rate is described by the exponential function Jsc can be described as
After integrating Equation (10)
It is seen from Equation (11) that the match between penetration depth of beta particles and the diffusion length will be the critical factor to achieve the high collection efficiency. However, the diffusion lengths in most present state-of-the-art wide-bandgap semiconductors are relatively small. While in 4H-SiC and diamond L can reach values of 10 and 40 μm, respectively [19], and in Si it can approach to 1 mm, in GaN and Ga2O3 it does not exceed 1 μm [79,80,81]. Accordingly, under irradiation by the 63Ni source Jsc in GaN with a donor concentration of 1016 cm−3 and L = 500 nm is less than 50% of its upper limit. The same is true for β-Ga2O3. For a comparison, in Si experimental Jsc value can reach about 97% of its upper limit [42].
As shown in [52], for an ideal device the upper limit of ηs in the Shockley-Queisser approximation can be estimated as
From this expression it follows that the converter efficiency should increase with the bandgap and taking into account Equation (8) for ultra-wide bandgap semiconductors ηs can be estimated as 0.3–0.35. In this regard, it is widely accepted that wide-bandgap semiconductors are more promising for the conversion of beta radiation. In many works Equation (12) is considered as a theoretical limit for ηs. However, as already discussed in [19,82], it is not always true because there are several reasons for the essential efficiency decrease below this limit. One of the reasons mentioned above is the Jsc reduction due to the excess carrier recombination. It should be also pointed out that Equation (12) implies that the upper limit for Voc is Eg. However, such an estimate seems to be too rough. As Voc cannot exceed ϕbi, it is smaller than Eg, even for p-n junctions. For the Schottky barrier structures it is even smaller. The well-known expression for Voc, which can be obtained from Equation (3) by setting J = 0, is [37]
It is seen that Voc increases with Jsc. Taking into account that the induced current in the betavoltaic cells is much lower than that in solar cells it can be expected that Voc should be noticeably lower than Eg because even in the solar cells it never approaches Eg. For wide-bandgap semiconductors J0 is usually determined by the generation in the depletion region and for a p-n junction it can be described as [37]
where ni = (Nc × Nv)0.5exp(−Eg/2kT) is the intrinsic carrier concentration, Nc and Nv are the effective density of states in the conduction and valence bands, respectively, and τ is the generation lifetime. Usually τ is unknown and it can vary by orders of magnitude. If it is estimated from the diffusion length as τ = L2/Damb, with L equals to 10 and 0.5 μm, and Damb equals to 3.3 and 1 cm2/s for 4H-SiC and GaN, respectively, τ can be estimated as 3 × 10−7 and 2.5 × 10−9 s, for 4H-SiC and GaN, respectively. That allows to estimate Voc value due to 20% purity 63Ni irradiation as about 1 V for both materials under an assumption that n = 1 and Jsc is equal to its upper limit. For n > 1, Voc accordingly increases but in any case it is noticeably smaller than Eg. It should be emphasized that a change in τ by one order of magnitude changes Voc by 60 mV, thus, it cannot significantly change the ratio between Voc and Eg.
As shown in [83], FF can be approximated with sufficient accuracy by the following expression:
It is seen from Equation (15) that FF under this approximation is practically independent of n. This allows us to estimate FF as about 0.9 for Voc ~ 1 V. However, state-of-the-art GaN and Ga2O3 contain a lot of defects, which should increase J0. In the Shottky barriers J0 should be several orders of magnitude larger than that in p-n junctions. As follows from Equations (13) and (15), the J0 increase leads to a decrease in both Voc and FF, thus to additional decreasing the cell efficiency. Experimental studies in the most cases also gave for Voc in GaN and 4H-SiC converters values about or below 1 V [84,85,86,87]. Even when measured Voc values were as high as 1.5–2.1 V [38,88,89], FF is rather small (0.5–0.6) that decreases the converter efficiency. Besides, it should be noted that such Voc and FF values contradict Equation (15) if n~1 that could mean the large n value in the studied structures. The large n value indicates the high recombination rate, which in turn should reduce the Jsc. All mentioned effects essentially negate the advantages of wide-bandgap semiconductors. Thus, according to Equation (12), the upper limit of ηs for GaN and Ga2O3 is about 3 and 4.4 times larger than that for Si. However, the collection efficiency in these materials is about 2 times smaller than that for Si, thus only the reduction in the collection efficiency decreases the efficiency of converters based on GaN and Ga2O3 about two times. The analysis carried out in [19,82] showed that if 63Ni or 3H radioisotopes are used as the beta radiation sources the most promising materials for semiconductor converters are SiC and diamond due to the combination of good coupling efficiencies with isotope sources and good electronic transport properties. Probably, Si can be added to them due to the large diffusion length and advanced processing technologies, which may be important for the formation of stacked multilayer structures.
The above discussion shows that the huge uncertainty in the material properties makes a more or less accurate calculation of the cell output parameters and therefore the efficiency of betavoltaic batteries almost impossible. It could be expected that the use of an electron beam to mimic beta radiation would make it possible to obtain more accurate predictions [24,25,26,27,28,29,30,31,32,33]. Moreover, a study of the parameters of converter prototypes could significantly speed up the search for ways to improve them. However, in the most studies a beam perpendicular to the surface with energy equal to the average energy of beta particles was used. As seen in Figure 3, such choice does not reproduce the depth dependence of deposited energy, therefore the prediction accuracy deteriorates, especially in semiconductor materials with low L values. Besides, in many papers the beam current was chosen quite arbitrarily due to a lack of general principles that can be used to choose the appropriate current values. To overcome the shortcomings of both approaches, a hybrid approach was proposed [12,40,41,42,43] that combines calculations and measurements using an electron beam. The approach includes a few steps:
- (a)
- Calculation of the depth distribution of e-h pair generated rate by the Monte Carlo simulation.
- (b)
- Measurement of the Ic dependence on beam energy Eb in the device under study in the EBIC mode of SEM.
- (c)
- Fitting this dependence with that calculated using Equation (9) allows to determine in the real device all parameters necessary to calculate the collection probability ψ(z,L) [79,90]. It should be noted that while for the Schottky barriers only W, L and metal thickness dm should be used as fitting parameters, for p-n junctions a number of fitting parameters increases. Sometimes it could be difficult to separate their contribution to the measured dependence, for example, this happens for the surface recombination velocity and the diffusion length in the upper thin layer of p-n junction. However, this is not very important, since these parameters will be used for further calculation of very similar dependencies. As an example, Figure 10 shows the measured collected efficiency Q dependencies on beam energy Eb for the two Ni/4H-SiC Schottky barriers and GaN p-n junction together with the simulated dependencies. It can be seen that the calculated dependencies well approximate the measured ones.
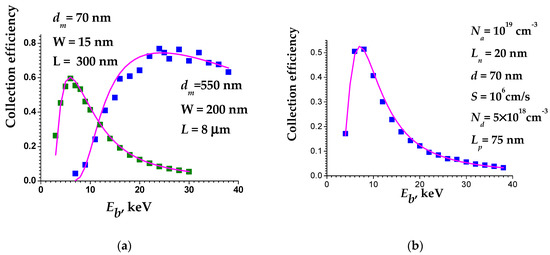 Figure 10. Q dependencies on Eb for the two Ni/4H-SiC Schottky barriers with different dm, W and L values (a) and for GaN p-n junction (b). The parameters obtained by fitting are presented in the Figures. Na and Nd are the acceptor concentration in the top p-type layer and donor concentration in the n-type layer, respectively, Ln and Lp are the excess carrier diffusion length values in p- and n-type layers, respectively, d is the p-n junction depth and S is the surface recombination velocity.
Figure 10. Q dependencies on Eb for the two Ni/4H-SiC Schottky barriers with different dm, W and L values (a) and for GaN p-n junction (b). The parameters obtained by fitting are presented in the Figures. Na and Nd are the acceptor concentration in the top p-type layer and donor concentration in the n-type layer, respectively, Ln and Lp are the excess carrier diffusion length values in p- and n-type layers, respectively, d is the p-n junction depth and S is the surface recombination velocity. - (d)
- The collection probability ψ(z,L) is calculated by a numerical solution of homogeneous diffusion or drift-diffusion equation using the obtained parameters and then Jsc can be calculated using Equation (9). For the planar structures, if the dopant concentration and diffusion length are high enough (the smaller L, the higher dopant concentration should be), as in structures presented in Figure 10, the collection efficiency can be obtained by a solution of homogeneous diffusion equation:with the boundary conditions are ψ(z,W) = 1 and ψ(z,W) → 0 at z → ∞. For such structures the solution of homogeneous drift-diffusion equation [78]where F(z) is the electric field, with the boundary conditions are ψ(0) = 1 and ψ(z,W) → 0 at z → ∞, gives practically the same results. For the structures with the low L values and/or low dopant concentration the excess carrier recombination inside the depletion region cannot be neglected and the drift-diffusion equation should be solved. The Q(Eb) dependence for the Schottky barrier on 4H-SiC with the dopant concentration of about 1014 cm−3 is shown in Figure 11a. Figure 11b shows the depth dependencies of the collection probabilities calculated using the diffusion (blue curve) or drift-diffusion equations (magenta curve). The magenta curve clearly shows that the collection probability inside the depletion region is lower than 1, i.e., the recombination inside the depletion region cannot be neglected. For this reason, the collected probability shown with the blue curve is incorrect. The coincidence of the ψ(z,W) dependencies obtained from the solution of the homogeneous diffusion and drift-diffusion equations can be considered as an indicator of the possibility to neglect recombination inside the depletion region. It should be stressed that using such procedure allows to obtain Jsc value close to real one for any particular converter under study although the upper limit for Jsc can be also calculated as it is shown in Table 2.
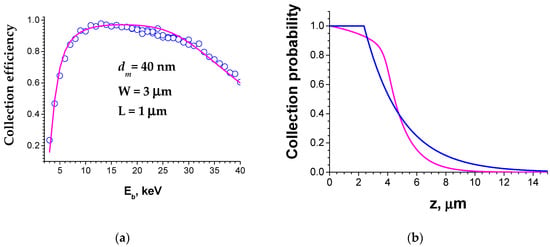 Figure 11. Q dependency on Eb for the Ni/4H-SiC Schottky barrier (a) and ψ(z,W) depth dependencies obtained by the solution of diffusion (blue curve) and drift-diffusion equations (magenta curve) (b). The parameters obtained by fitting are presented in (a).
Figure 11. Q dependency on Eb for the Ni/4H-SiC Schottky barrier (a) and ψ(z,W) depth dependencies obtained by the solution of diffusion (blue curve) and drift-diffusion equations (magenta curve) (b). The parameters obtained by fitting are presented in (a). - (e)
- Finally, the beam current of SEM should be chosen so that the induced current Ic is equal to the calculated Jsc value. As follows from Equations (13) and (15), such choice allows the direct measurements of the open circuit voltage Voc and filling factor FF. This makes it possible to measure Voc and FF for the particular converter under the conditions close to those under beta irradiation.
To check the accuracy of this approach the parameters of betavoltaic cells consisted of two Si-based p-i-n diodes of different design, two 4H-SiC Schottky barriers formed on materials with different diffusion lengths and metal thicknesses, and GaN Shottky barrier were calculated and measured in [42] using the 63Ni radioisotope source with the activity of 2.7 mCi and area of 1 cm2. One of the used Si p-i-n structures had an area of 1 cm2 and consisted of a low doped p-Si, a highly doped top n+ layer and a 20-nm-thick SiO2 protective layer on the top. The p-n junction depth was 300 nm. This structure had an extremely low surface recombination velocity of 30 cm/s and the diffusion length in the top n+ layer of 500 nm. The second Si structure had an area of 81.5 mm2 and consisted of a low doped n-Si, a highly doped p+ top layer and a few nm thick protective SiO2 layer. The p-n junction depth was 70 nm, the surface recombination velocity was about 107 cm/s and the diffusion length in the top p+ layer was about 500 nm. The bulk diffusion length L in both structures exceeded 40 μm, i.e., it was high enough to collect practically all excess carriers generated by beta-radiation from the 63Ni source. The SiC Schottky barriers were prepared by thin Ni layer evaporation on an n-type 4H-SiC. The area, metal thickness, diffusion length, and depletion region width W in the diodes, as obtained from the EBIC measurements, were 4 mm2, 25 nm, 2.6 μm, and 2.3 μm, respectively, for one diode, and 2.77 mm2, 30 nm, 8 μm, and 0.5 μm for other one. The GaN Schottky diode of 1 mm in diameter was formed by Au evaporation on an n-type GaN grown by the hydride vapor phase epitaxy. The diffusion length, metal thickness and depletion region width were 550, 13 and 135 nm, respectively.
For Si diodes the calculated and measured Jsc values were 27.5 and 27 nA/cm2 for the first diode and 25.3 and 26.4 nA/cm2 for the second one. For the 4H-SiC Schottky diodes the calculated and measured Jsc values were 9.5 and 8.15 nA/cm2 for the first and 8.17 and 6.21 nA/cm2 for the second one. For GaN the calculated and measured Jsc values were 2.91 and 3.5 nA/cm2, respectively. It is seen that the difference between the measured and calculated values does not exceed 25%. Moreover, it is seen that the difference between the calculated and measured values increases with decreasing the size of tested diodes that allowed to assume that at least a part of the difference was determined by the source inhomogeneity. As shown in [42], such error in the predicted Jsc values will give the Uoc value with a relative error of about 3–4% and less than a 30% relative error in the maximum power for all structures tested.
7. Temperature Effect on Output Parameters of Betavoltaic Cells
As the radioisotope sources can operate in the wide temperature range and, in particular, at extremely high temperatures, a question arises about the temperature range of betavoltaic batteries. Temperature can essentially affect the semiconductor parameters such as bandgap, carrier mobility, diffusivity and lifetime, thus, influences the collection efficiency. As seen from Equation (14), J0 exponentially increases with temperature, thus decreasing both Voc and FF. It can be expected that in order to extend the temperature range of betavoltaic cells to high temperatures, it is necessary to use wide-bandgap semiconductors in the converter. For using betavoltaic batteries at extreme temperatures it is useful to predict their output parameters to optimize the material choice and device design. A few papers have carried out experimental and theoretical studies of temperature effect on the output parameters of betavoltaic cells [12,54,91,92,93,94,95]. However, the main obstacle to the correct prediction of output parameters of betavoltaic cells as a function of temperature is insufficient information about the real parameters of semiconductor structures and their temperature dependencies. It is in a good correlation with the reasons for the insufficient prediction accuracy of output parameters discussed above. Thus, in [57] the calculated values of Isc and Voc were found to be more than two times larger than measured ones. The calculated values of J0 were about 4 orders of magnitude larger than the measured ones. In [91] the difference between the predicted and measured Voc values was smaller than that in [53], nevertheless, the predicted values were larger than measured ones. It was observed in [93] that Voc and maximum power Pm decreased linearly at low temperatures of 213–273 K and decreased exponentially at high temperatures of 273–333 K in Si-based converters that indicates a change of the mechanism that determines the leakage current. However, in the calculation, the Voc and Pm always decreased linearly at both low and high temperatures. It should be noted that in all calculations, with the exception of [92], Voc also decreased linearly with increasing temperature. Such dependence follows from Equations (13) and (14). Indeed
If W, Nc, Nv and τ weakly depend on T, it follows from Equation (18) that Voc depends on T approximately linearly. This assumption seems to be reasonable for W, Nc and Nv, but for τ it may not hold. The measured Voc(T) dependencies for Si p-i-n diode and the 4H-SiC Schottky barrier, similar to those studied in [42], under irradiation with 63Ni source with the activity of 2.7 mCi are presented in Figure 12. While for Si Voc(T) dependence is indeed close to linear one, for 4H-SiC it noticeably deviates from linear. Moreover, as seen in Figure 12, for the 4H-SiC converter Voc at 300 K is only about two times larger than that for the Si based converter, while about ten times difference was predicted in [94]. To understand the reasons for the observed difference it can be assumed that in 4H-SiC a few components contribute to J0 value and at low temperatures, the component with weaker temperature dependence prevails. A decrease in the difference between Pmax values in Si and SiC converters was also observed in [12]. Thus, it should be concluded that for a complete understanding and reliable prediction of the temperature dependencies of the parameters of betavoltaic cells, additional theoretical and experimental studies are required.
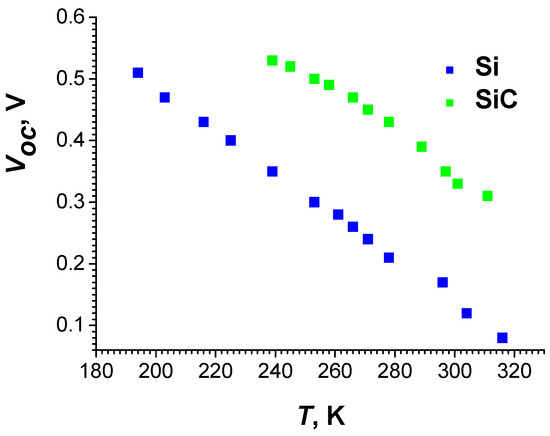
Figure 12.
The experimental Voc(T) dependencies for Si p-i-n diode and the 4H-SiC Schottky barrier under irradiation with 63Ni source with the activity of 2.7 mCi.
8. Prediction of Radiation Damage
As the half-life of betavoltaic batteries is rather long a question about the radiation hardness of semiconductor converter becomes very important. In general, the energy of high-energy particles is spent on the formation of defects by knocking atoms out of lattice sites and on ionization losses. The generated defects can form recombination centers which can reduce the minority carrier lifetime and collection efficiency of the excess carriers. Fortunately, the maximum energy of beta particles emitted from both 3H and 63Ni is essentially lower than the threshold of radiation damage for all semiconductors considered in the present paper. Therefore, it seems that direct formation of lattice defects by knocking out atoms from the lattice sites can be neglected. However, even irradiation with the subthreshold energies can affect the electrical and optical properties of many semiconductor materials and structures (see, e.g., references in [96]). Thus, it is known that low energy electron beam irradiation (LEEBI) with beam energy of about 10 keV enhanced partial dislocation glide in 4H-SiC even at liquid nitrogen temperature [97,98,99,100,101,102,103] and dislocation glide in GaN [104,105,106]. As an example of point defect reconstruction under LEEBI in the materials discussed, the well-known destruction of Mg-H pairs in GaN can be reminded [107,108,109,110]. In Si LEEBI can lead to a destruction of absorbed water film on the surface with following H diffusion into a bulk passivating the existing defects or forming new ones [111]. Taking into account the high hydrogen diffusivity in many semiconductors similar effect can take place also in other materials. LEEBI effect on the optical properties of InGaN/GaN multiple quantum well structures were also well established [112,113,114]. As a result of LEEEBI, the intensity of quantum well-related luminescence increases, and the maximum emission band is shifted to the higher energies. The results were explained by the interplay between the increasing density of nonradiative recombination defects caused by LEEBI and quantum dots inside the InGaN quantum wells and possible stress relaxation in local regions of InGaN quantum wells [115,116].
Additional questions arise if some passivation layer, such as SiO2, was deposited on the converter to decrease the surface recombination velocity and leakage current. Besides well-known charging effect [117,118,119,120,121], LEEBI can create traps in the bulk of SiO2 and at the SiO2/semiconductor interface [122,123,124]. In some structures, it can take place at electron energies lower than 10 keV and doses below 1 μCi/cm2 [124]. Degradation of the Si p-n junction passivated by a SiO2-Si3N4 layer under titanium tritide radioisotope irradiation was already observed in [125]. It was shown that irradiation for 150 h leads to about two times a decrease in Jsc which was explained by charging the passivation layer.
Unfortunately, while the direct formation of lattice defects by knocking out atoms can be simulated and at least the distribution of primary defects can be obtained, for ionization losses, the situation is quite different. It is only possible to obtain a number of e-h pairs and the generation rate distribution. A complete understanding of the device degradation processes stimulated by the excess carriers in almost all cases has not yet been achieved. For example, it is widely accepted that stimulated by irradiation, dislocation motion is determined by the recombination-enhanced dislocation glide mechanism, in which the energy released during recombination at dislocation-related centers is redirected to lowering the barrier for the dislocation glide. However, a microscopic model of such a mechanism has not yet been proposed, which does not allow reliable prediction of dislocation glide and multiplication. Therefore, the behavior of devices under beta irradiation can only be predicted on the base of analysis of experimental studies, a number of which is usually insufficient. Thus, it can be concluded that the converter degradation can occur even under irradiation with subthreshold energy beta particles. However, the reliability of predicting such phenomena is still clearly insufficient.
9. Conclusions
Betavoltaic power sources are promising devices for many applications. However, their technology is now far from maturity, and there is much room for improvement. The development of a strategy for predicting the parameters of betavoltaic cells with sufficient accuracy will simplify cell optimization and thus would obviate the necessity of using the simple trial-and-error approach, which is very time-consuming and costly. For this purpose, it is very important to develop a methodology that allows predicting the parameters of betavoltaic cells according to the characterization data of converter prototypes. Therefore, a sizable number of publications are devoted to this problem. In the present paper, the proposed approaches for predicting output parameters of betavoltaic batteries are reviewed. The advantages and disadvantages of the main of them are discussed. The need to take into account the full beta energy spectrum, the isotropic angular distribution of emitted electrons, and the self-absorption inside the radioisotope source for homogeneously distributed emitting points are demonstrated by the Monte Carlo simulation for 63Ni and 3H radioisotope sources and a few semiconductor converters. The methodology allowing the prediction of betavoltaic cell output parameters with an accuracy no worse than 30% is described in more detail. The necessity of predicting the temperature dependencies of the parameters of betavoltaic cells is shown, although, as the analysis of the literature data shows, the understanding necessary for reliable prediction has not yet been achieved. The analysis of literature data has shown that in spite of rather low beta particle energy for 3H and 63Ni radioisotopes, which is below the threshold for the generation of intrinsic point defects by direct knocking atoms out of a lattice site, some degradation can occur during prolonged irradiation, especially in devices containing dielectric layers. However, the development of models for predicting the degradation of semiconductor converters under long-term irradiation with low-energy electrons is still far from complete. To some extent, this can also be applied to the development of approaches for predicting the temperature dependence of the parameters of betavoltaic cells.
Funding
This work was supported by State Task No. 075-01304-23-00.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The author declares no conflict of interest.
References
- Olsen, L.C.; Cabauy, P.; Elkind, B.J. Betavoltaic power sources. Phys. Today 2012, 65, 35–38. [Google Scholar] [CrossRef]
- Prelas, M.A.; Weaver, C.L.; Watermann, M.L.; Lukosi, E.D.; Schott, R.J.; Wisniewski, D.A. A review of nuclear batteries. Progr. Nucl. Energy 2014, 75, 117–148. [Google Scholar] [CrossRef]
- Revankar, S.T.; Adams, T.E. Advances in Betavoltaic Power Sources. J. Energy Power Sources 2014, 1, 321–329. [Google Scholar]
- Alam, T.R.; Pierson, M.A. Principles of Betavoltaic Battery Design. J. Energy Power Sources 2016, 3, 11–41. [Google Scholar]
- Spencer, M.G.; Alam, T. High power direct energy conversion by nuclear batteries. Appl. Phys. Rev. 2019, 6, 031305. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, J.; Wang, X.; Yang, Y.; Xu, P.; Li, P.; Zhang, L.; Chen, Z.; Feng, H.; Wu, W. Review—Betavoltaic Cell: The Past, Present, and Future. ECS J. Solid State Sci. Technol. 2021, 10, 027005. [Google Scholar] [CrossRef]
- Qiao, D.-Y.; Chen, X.-J.; Ren, Y.; Yuan, W.-Z. A Micro Nuclear Battery Based on SiC Schottky Barrier Diode. J. Microelectromech. Syst. 2011, 20, 685–690. [Google Scholar] [CrossRef]
- Gao, H.; Luo, S.; Zhang, H.; Wang, H.; Fu, Z. Demonstration, radiation tolerance and design on a betavoltaic micropower. Energy 2013, 51, 116–122. [Google Scholar] [CrossRef]
- Gorbatsevich, A.A.; Danilin, A.B.; Korneev, V.I.; Magomedbekov, E.P.; Molin, A.A. Analysis (Simulation) of Ni-63 Beta-Voltaic Cells Based on Silicon Solar Cells. Tech. Phys. 2016, 61, 1053–1059. [Google Scholar] [CrossRef]
- Yao, S.; Song, Z.; Wang, X.; San, H.; Yu, Y. Design and simulation of betavoltaic battery using large-grain polysilicon. Appl. Radiat. Isot. 2012, 70, 2388–2394. [Google Scholar] [CrossRef]
- Zuo, G.; Zhou, J.; Ke, G. A Simple theoretical model for 63Ni betavoltaic battery. Appl. Radiat. Isotop. 2013, 82, 119–125. [Google Scholar] [CrossRef]
- Polikarpov, M.A.; Yakimov, E.B. Study of the Properties of Silicon-Based Semiconductor Converters for BetaVoltaic Cells. Semiconductors 2015, 49, 746–748. [Google Scholar] [CrossRef]
- San, H.; Yao, S.; Wang, X.; Cheng, Z.; Chen, X. Design and simulation of GaN based Schottky betavoltaic nuclear micro-battery. Appl. Radiat. Isotop. 2013, 80, 17–22. [Google Scholar] [CrossRef] [PubMed]
- Munson, C.E., IV.; Arif, M.; Streque, J.; Belahsene, S.; Martinez, A.; Ramdane, A.; El Gmili, Y.; Salvestrini, J.-P.; Voss, P.L.; Ougazzaden, A. Model of Ni-63 battery with realistic PIN structure. J. Appl. Phys. 2015, 118, 105101. [Google Scholar] [CrossRef]
- Gui, G.; Zhang, K.; Blanchard, J.P.; Ma, Z. Prediction of 4H–SiC betavoltaic microbattery characteristics based on practical Ni-63 sources. Appl. Radiat. Isotop. 2016, 107, 272–277. [Google Scholar] [CrossRef] [PubMed]
- Alam, T.R.; Pierson, M.A.; Prelas, M.A. Beta particle transport and its impact on betavoltaic battery modeling. Appl. Radiat. Isotop. 2017, 130, 80–89. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-M.; Lu, J.-B.; Li, X.-Y.; Xu, X.; He, R.; Wang, H.-D. A 4H–SiC betavoltaic battery based on a 63Ni source. Nucl. Sci. Tech. 2018, 29, 168. [Google Scholar] [CrossRef]
- Wu, M.; Wang, S.; Ou, Y.; Wang, W. Optimization design of betavoltaic battery based on titanium tritide and silicon using Monte Carlo code. Appl. Radiat. Isotop. 2018, 142, 22–27. [Google Scholar] [CrossRef] [PubMed]
- Maximenko, S.I.; Moore, J.E.; Affouda, C.A.; Jenkins, P.P. Optimal Semiconductors for 3H and 63Ni Betavoltaics. Sci. Rep. 2019, 9, 10892. [Google Scholar] [CrossRef]
- Zhao, C.; Lei, L.; Liao, F.; Yuan, D.; Zhao, Y. Efficiency prediction of planar betavoltaic batteries basing on precise modeling of semiconductor units. Appl. Phys. Lett. 2020, 117, 263901. [Google Scholar] [CrossRef]
- Zheng, R.; Lu, J.; Wang, Y.; Chen, Z.; Zhang, X.; Li, X.; Liang, L.; Qin, L.; Zeng, Y.; Chen, Y.; et al. Understanding efficiency improvements of betavoltaic batteries based on 4H-SiC, GaN, and diamond. Appl. Phys. Lett. 2022, 121, 103902. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, R.; Lu, J.; Li, X.; Chen, Z.; Zhang, X.; Zhang, Y.; Liang, L.; Zeng, Y.; Qin, L.; et al. Theoretical prediction of output performance of 63NiO-Si heterojunction betavoltaic cell. Appl. Phys. Lett. 2022, 121, 083901. [Google Scholar] [CrossRef]
- Bouzid, F.; Saeed, M.A.; Carotenuto, R.; Pezzimenti, F. Design considerations on 4H-SiC-based p–n junction betavoltaic cells. Appl. Phys. A 2022, 128, 234. [Google Scholar] [CrossRef]
- Chandrashekhar, M.V.S.; Thomas, C.I.; Li, H.; Spencer, M.G.; Lal, A. Demonstration of a 4H SiC betavoltaic cell. Appl. Phys. Lett. 2006, 88, 033506. [Google Scholar] [CrossRef]
- Ulmen, B.; Desai, P.D.; Moghaddam, S.; Miley, G.H.; Masel, R.I. Development of diode junction nuclear battery using 63Ni. J. Radioanal. Nucl. Chem. 2009, 282, 601–604. [Google Scholar] [CrossRef]
- Bao, R.P.; Brand, J.; Chrisey, D.B. Betavoltaic Performance of Radiation-Hardened High-Efficiency Si Space Solar Cells. IEEE Trans. Electron Devices 2012, 59, 1286–1294. [Google Scholar] [CrossRef]
- Delfaure, C.; Pomorski, M.; de Sanoit, J.; Bergonzo, P.; Saada, S. Single crystal CVD diamond membranes for betavoltaic cells. Appl. Phys. Lett. 2016, 108, 252105. [Google Scholar] [CrossRef]
- Tarelkin, S.; Bormashov, V.; Korostylev, E.; Troschiev, S.; Teteruk, D.; Golovanov, A.; Volkov, A.; Kornilov, N.; Kuznetsov, M.; Prikhodko, D.; et al. Comparative study of different metals for Schottky barrier diamond betavoltaic power converter by EBIC technique. Phys. Status Solidi A 2016, 213, 2492–2497. [Google Scholar] [CrossRef]
- Khan, M.R.; Smith, J.R.; Tompkins, R.P.; Kelley, S.; Litz, M.; Russo, J.; Leathersich, J.; Shahedipour-Sandvik, F.; Jones, K.A.; Iliadis, A. Design and characterization of GaN p-i-n diodes for betavoltaic devices. Solid-State Electron. 2017, 136, 24–29. [Google Scholar] [CrossRef]
- Song, Z.; Zhao, C.; Liao, F.; Zhao, Y. Perovskite-Betavoltaic Cells: A Novel Application of Organic–Inorganic Hybrid Halide Perovskites. ACS Appl. Mater. Interfaces 2019, 11, 32969–32977. [Google Scholar] [CrossRef]
- Svintsov, A.A.; Yakimov, E.B.; Dorokhin, M.V.; Demina, P.B.; Kuznetsov, Y.M. Simulation of the Parameters of a Titanium-Tritide-Based Beta-Voltaic Cell. Semiconductors 2019, 53, 96–98. [Google Scholar] [CrossRef]
- Kim, D.-S.; Yoon, Y.J.; Lee, J.S.; Kang, I.M.; Lee, J.-H. Experimental and simulation study of power performance improvement of GaN PIN betavoltaic cell. Int. J. Energy Res. 2021, 45, 17622–17630. [Google Scholar] [CrossRef]
- Heuser, T.; Braun, M.; McIntyre, P.; Senesky, D.G. Electron beam irradiation of gallium nitride-on-silicon betavoltaics fabricated with a triple mesa etch. J. Appl. Phys. 2021, 130, 174503. [Google Scholar] [CrossRef]
- Alig, R.C.; Bloom, S. Electron-Hole-Pair Creation Energies in Semiconductors. Phys. Rev. Lett. 1975, 35, 1522–1525. [Google Scholar] [CrossRef]
- Beck, M.; Streb, D.; Vitzethum, M.; Kiesel, P.; Malzer, S.; Metzner, C.; Döhler, G.H. Ambipolar drift of spatially separated electrons and holes. Phys. Rev. B 2001, 64, 085307. [Google Scholar] [CrossRef]
- Bicknell, W.E. Space charge solution of Rittner photoconductor equation for a HgCdTe detector. Infrared Phys. Technol. 2002, 43, 39–50. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; Wiley: Hoboken, NJ, USA, 2007; pp. 663–741. [Google Scholar]
- Thomas, C.; Portnoff, S.; Spencer, M.G. High efficiency 4H-SiC betavoltaic power sources using tritium radioisotopes. Appl. Phys. Lett. 2016, 108, 013505. [Google Scholar] [CrossRef]
- Zhang, K.; Pathak, P.; Cerrina, F.; Ma, Z. Performance Prediction of Nuclear Micro Power Sources Based on Beta Emitters. ECS Transact. 2009, 19, 45–50. [Google Scholar] [CrossRef]
- Zaitsev, S.I.; Pavlov, V.N.; Panchenko, V.Y.; Polikarpov, M.A.; Svintsov, A.A.; Yakimov, E.B. Comparison of the Efficiency of 63Ni Beta-Radiation Detectors Made from Silicon and Wide-Gap Semiconductors. J. Surf. Investig. X-Ray Synchrotron Neutron Techniq. 2014, 8, 843–845. [Google Scholar] [CrossRef]
- Yakimov, E.B. Prediction of betavoltaic battery output parameters based on SEM measurements and Monte Carlo simulation. Appl. Radiat. Isotop. 2016, 112, 98–102. [Google Scholar] [CrossRef]
- Svintsov, A.A.; Krasnov, A.A.; Polikarpov, M.A.; Polyakov, A.Y.; Yakimov, E.B. Betavoltaic battery performance: Comparison of modeling and experiment. Appl. Radiat. Isotop. 2018, 137, 184–189. [Google Scholar] [CrossRef]
- Dorokhin, M.V.; Vikhrova, O.V.; Demina, P.B.; Kalentyeva, I.L.; Vergeles, P.S.; Yakimov, E.B.; Lesnikov, V.P.; Zvonkov, B.N.; Ved, M.V.; Danilov, Y.A.; et al. GaAs diodes for TiT2-based betavoltaic cells. Appl. Radiat. Isotop. 2022, 179, 110030. [Google Scholar] [CrossRef] [PubMed]
- Svintsov, A.A.; Knyazev, M.A.; Zaitsev, S.I. Calculation of the Absorbed Electron Energy 3D Distribution by the Monte Carlo Method, Presentation of the Proximity Function by Three Parameters α, β, η and Comparison with the Experiment. Materials 2022, 15, 3888. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, Y.; Hu, R.; Yang, Y.; Wang, G.; Zhong, Z.; Luo, S. Simulations about self-absorption of tritium in titanium tritide and the energy deposition in a silicon Schottky barrier diode. Appl. Radiat. Isotop. 2012, 70, 2559–2563. [Google Scholar] [CrossRef]
- Ellis, B.L.; Fritzsche, H.; Patel, J.; Lang, J.; Suppiah, S. Titanium Tritide Films as Betavoltaic Power Sources. Fusion Sci. Technol. 2017, 71, 660–665. [Google Scholar] [CrossRef]
- Alam, T.R.; Spencer, M.G.; Prelas, M.A.; Pierson, M.A. Design and optimization of radioisotope sources for betavoltaic batteries. Int. J. Energy Res. 2018, 42, 2564–2573. [Google Scholar] [CrossRef]
- Russo, J.; Litz, M.; Ray, W., II.; Bayne, S.; Rosen, G.M.; Cho, H.; Yu, J.; Bigio, D.I.; Thomas, C.; Alam, T.R. Demonstration of a Tritiated Nitroxide Nuclear Battery. Appl. Radiat. Isotop. 2019, 144, 93–103. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Polyakov, A.Y.; Shchemerov, I.V.; Smirnov, N.B.; Vasilev, A.A.; Vergeles, P.S.; Yakimov, E.E.; Chernykh, A.V.; Ren, F.; Pearton, S.J. Experimental estimation of electron–hole pair creation energy in β-Ga2O3. Appl. Phys. Lett. 2021, 118, 202106. [Google Scholar] [CrossRef]
- Pavlov, V.N.; Panchenko, V.Y.; Polikarpov, M.A.; Svintsov, A.A.; Yakimov, E.B. Simulation of the Current Induced by 63Ni Beta Radiation. J. Surf. Investig. X-Ray Synchrotron Neutron Techniq. 2013, 7, 852–855. [Google Scholar] [CrossRef]
- Ryan, R.D. Bandgap dependence of the average energy required for electron-hole pair creation in GaAs and in Si. Nucl. Instrum. Methods 1974, 120, 201. [Google Scholar] [CrossRef]
- Olsen, L.C. Review of betavoltaic energy conversion. In Proceedings of the 12th Space Photovoltaic Research and Technology Conference, Cleveland, OH, USA, 20–22 October 1992; pp. 256–267. [Google Scholar]
- Klein, C.A. Bandgap dependence and related features of radiation ionization energies in semiconductors. J. Appl. Phys. 1968, 39, 2029–2038. [Google Scholar] [CrossRef]
- Chandrashekhar, M.V.S.; Thomas, C.I.; Spencer, M.G. Measurement of the mean electron-hole pair ionization energy in 4H SiC. Appl. Phys. Lett. 2006, 89, 042113. [Google Scholar] [CrossRef]
- Lebedev, A.A.; Ivanov, A.M.; Strokan, N.B. Radiation resistance of SiC and nuclearradiation detectors based on SiC films. Semiconductors 2004, 38, 125–147. [Google Scholar] [CrossRef]
- Wrbanek, J.D.; Wrbanek, S.Y.; Fralick, G.C.; Chen, L.Y. Micro-Fabricated Solid State Radiation Detectors for Active Personal Dosimetry; Report No NASA/TM 214674; NASA: Washington, DC, USA, 2007. [Google Scholar]
- Liu, Y.; Tang, X.; Xu, Z.; Hong, L.; Chen, D. Experimental and theoretical investigation of temperature effects on an interbedded betavoltaic employing epitaxial Si and bidirectional 63Ni. Appl. Radiat. Isotop. 2014, 94, 152–157. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Zhang, J. Design and simulation of high conversion efficiency betavoltaic battery based on a stacked multilayer structure. AIP Adv. 2019, 9, 075124. [Google Scholar] [CrossRef]
- Lee, I.-H.; Polyakov, A.Y.; Smirnov, N.B.; Yakimov, E.B.; Tarelkin, S.A.; Turutin, A.V.; Shemerov, I.V.; Pearton, S.J. Electron traps as major recombination centers in n-GaN films grown by metalorganic chemical vapor deposition. Appl. Phys. Express 2016, 9, 061002. [Google Scholar] [CrossRef]
- Lee, I.-H.; Polyakov, A.Y.; Smirnov, N.B.; Yakimov, E.B.; Tarelkin, S.A.; Turutin, A.V.; Shemerov, I.V.; Pearton, S.J. Studies of deep level centers determining the diffusion length in epitaxial layers and crystals of undoped n-GaN. J. Appl. Phys. 2016, 119, 205109. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Smirnov, N.B.; Yakimov, E.B.; Tarelkin, S.A.; Turutin, A.V.; Shemerov, I.V.; Pearton, S.J.; Bae, K.-B.; Lee, I.-H. Deep traps determining the non-radiative lifetime and defect band yellow luminescence in n-GaN. J. Alloys Compd. 2016, 686, 1044–1052. [Google Scholar] [CrossRef]
- Tang, X.B.; Liu, Y.P.; Ding, D.; Chen, D. Optimization design of GaN betavoltaic microbattery. Sci. China Technol. Sci. 2012, 55, 659–664. [Google Scholar] [CrossRef]
- Belghachi, A.; Bozkurt, K.; Ozdemir, O.; Avci, O. Enhancement of Ni-63 planar source efficiency for betavoltaic batteries. J. Phys. D Appl. Phys. 2020, 53, 445501. [Google Scholar] [CrossRef]
- Bormashov, V.S.; Troschiev, S.Y.; Tarelkin, S.A.; Volkov, A.P.; Teteruk, D.V.; Golovanov, A.V.; Kuznetsov, M.S.; Kornilov, N.V.; Terentiev, S.A.; Blank, V.D. High power density nuclear battery prototype based on diamond Schottky Diodes. Diamond Relat. Mater. 2018, 84, 41–47. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Polyakov, A.Y.; Pearton, S.J. Betavoltaic cell based on Ni/β-Ga2O3 and 63Ni source. J. Vac. Sci. Technol. A 2022, 40, 010401. [Google Scholar] [CrossRef]
- Murphy, J.W.; Voss, L.F.; Frye, C.D.; Shao, Q.; Kazkaz, K.; Stoyer, M.A.; Henderson, R.A.; Nikolic, R.J. Design considerations for three-dimensional betavoltaics. AIP Adv. 2019, 9, 065208. [Google Scholar] [CrossRef]
- Sun, W.; Kherani, N.P.; Hirschman, K.D.; Gadeken, L.L.; Fauchet, P.M. Three-dimensional porous silicon pen diode for betavoltaics and photovoltaics. Adv. Mater. 2005, 17, 1230–1233. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Polikarpov, M.A.; Krasnov, A.A. Prediction of Betavoltaic Battery Output Parameters Based on SEM Measurements. J. Nano Electron. Phys. 2016, 8, 04062. [Google Scholar] [CrossRef]
- Krasnov, A.A.; Starkov, V.V.; Legotin, S.A.; Rabinovich, O.I.; Didenko, S.I.; Murashev, V.N.; Cheverikin, V.V.; Yakimov, E.B.; Fedulova, N.A.; Rogozev, B.I.; et al. Development of betavoltaic cell technology production based on microchannel silicon and its electrical parameters evaluation. Appl. Radiat. Isotop. 2017, 121, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Wagner, D.; Novog, D.R.; LaPierre, R.R. Simulation and optimization of current generation in gallium phosphide nanowire betavoltaic devices. J. Appl. Phys. 2019, 125, 165704. [Google Scholar] [CrossRef]
- McNamee, S.; Wagner, D.; Fiordaliso, E.M.; Novog, D.; LaPierre, R.R. GaP nanowire betavoltaic device. Nanotechnology 2019, 30, 075401. [Google Scholar] [CrossRef]
- Wagner, D.; Novog, D.R.; LaPierre, R.R. Design and optimization of nanowire betavoltaic generators. J. Appl. Phys. 2020, 127, 244303. [Google Scholar] [CrossRef]
- Wagner, D.; Novog, D.R.; LaPierre, R.R. Genetic Algorithm Optimization of Core-Shell Nanowire Betavoltaic Generators. Nanotechnology 2020, 31, 455403. [Google Scholar] [CrossRef]
- Meier, D.E.; Garnov, A.Y.; Robertson, J.D.; Kwon, J.W.; Wacharasindhu, T. Production of 35S for a liquid semiconductor betavoltaic. J. Radioanal. Nucl. Chem. 2009, 282, 271–274. [Google Scholar] [CrossRef]
- Movahedian, Z.; Tavakoli-Anbaran, H. Design and optimization of Si-35S betavoltaic liquid nuclear battery in micro dimensions in order to build. Ann. Nucl. Energy 2020, 143, 107483. [Google Scholar] [CrossRef]
- Wacharasindhu, T.; Nullmeyer, B.R.; Kwon, J.W.; Robertson, J.D.; Garnov, A.Y. Mechanisms Leading to Losses in Conventional Betavoltaics and Evolution: Utilizing Composite Semiconductor with Infused Radioisotope for Efficiency Improvement. J. Microelectromech. Syst. 2014, 23, 56–65. [Google Scholar] [CrossRef]
- Donolato, C. A reciprocity theorem for charge collection. Appl. Phys. Lett. 1985, 46, 270–272. [Google Scholar] [CrossRef]
- Donolato, C. An alternative proof of the generalized reciprocity theorem for charge collection. J. Appl. Phys. 1989, 66, 4524–4525. [Google Scholar] [CrossRef]
- Yakimov, E.B. What is the real value of diffusion length in GaN? J. Alloys Compd. 2015, 627, 344–351. [Google Scholar] [CrossRef]
- Yakimov, E.B. Diffusion length measurements in GaN. Jpn. J. Appl. Phys. 2016, 55, 05FH04. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Polyakov, A.Y.; Smirnov, N.B.; Shchemerov, I.V.; Yang, J.; Ren, F.; Yang, G.; Kim, J.; Pearton, S.J. Diffusion length of non-equilibrium minority charge carriers in β-Ga2O3 measured by electron beam induced current. J. Appl. Phys. 2018, 123, 185704. [Google Scholar] [CrossRef]
- Zhao, C.; Liao, F.; Liu, K.; Zhao, Y. Breaking the myth: Wide-bandgap semiconductors not always the best for betavoltaic batteries. Appl. Phys. Lett. 2021, 119, 153904. [Google Scholar] [CrossRef]
- Green, M.A. Accuracy of analytical expressions for solar cell fill factors. Solar Cells 1982, 7, 337–340. [Google Scholar] [CrossRef]
- Li, X.-Y.; Ren, Y.; Chen, X.-J.; Qiao, D.-Y.; Yuan, W.-Z. 63Ni schottky barrier nuclear battery of 4H-SiC. J. Radioanal. Nucl. Chem. 2011, 287, 173–176. [Google Scholar] [CrossRef]
- Wang, G.; Yao, C. Gallium Nitride for nuclear batteries. Adv. Mater. Res. 2012, 343–344, 56–61. [Google Scholar] [CrossRef]
- Kuruoğlu, N.A.; Ozdemir, O.; Bozkurt, K. Betavoltaic study of a GaN p-i-n structure grown by metal-organic vapour phase epitaxy with a Ni-63 source. Thin Solid Film. 2017, 636, 746–750. [Google Scholar] [CrossRef]
- Aydin, S.; Kam, E. Investigation of nickel-63 radioisotope-powered GaN betavoltaic nuclear battery. Int. J. Energy Res. 2019, 43, 8725–8738. [Google Scholar] [CrossRef]
- Eiting, C.J.; Krishnamoorthy, V.; Rodgers, S.; George, T.; Robertson, J.D.; Brockman, J. Demonstration of a radiation resistant, high efficiency SiC betavoltaic. Appl. Phys. Lett. 2006, 88, 064101. [Google Scholar] [CrossRef]
- Cheng, Z.J.; San, H.S.; Feng, Z.H.; Liu, B.; Chen, X.Y. High open-circuit voltage betavoltaic cell based on GaN pin homojunction. Electr. Lett. 2011, 47, 720–722. [Google Scholar] [CrossRef]
- Yakimov, E.B. Study of Wide-Gap Semiconductors Using Electron-Beam Induced Current Method. Crystallogr. Rep. 2021, 66, 581–593. [Google Scholar] [CrossRef]
- Wang, G.; Hu, R.; Wei, H.; Zhang, H.; Yang, Y.; Xiong, X.; Liu, G.; Luo, S. The effect of temperature changes on electrical performance of the betavoltaic cell. Appl. Radiat. Isot. 2010, 68, 2214–2217. [Google Scholar] [CrossRef]
- Butera, S.; Lioliou, G.; Krysa, A.B.; Barnett, A.M. Temperature dependence of an AlInP 63Ni betavoltaic cell. J. Appl. Phys. 2016, 120, 144501. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, X.; Jin, Z.; Tang, X. Temperature dependence of 63Ni–Si betavoltaic microbattery. Appl. Radiat. Isot. 2018, 135, 47–56. [Google Scholar] [CrossRef]
- O’Connor, A.; Manuel, M.V.; Shaw, H. An extended-temperature, volumetric source model for betavoltaic power generation. Trans. Am. Nucl. Soc. 2019, 121, 542–545. [Google Scholar] [CrossRef]
- Novikov, S.G.; Berintsev, A.V.; Alekseev, A.S.; Somov, A.I.; Svetukhin, V.V. Investigation of the Temperature Effect on the Output Parameters of Radioisotope Sources of Electricity Based on Double Energy Conversion of Radiative Decay. Semiconductors 2019, 53, 2040–2043. [Google Scholar] [CrossRef]
- Yakimov, E.B. Low energy electron irradiation effect on optical and electrical properties of InGaN/GaN multiple quantum well structures. Int. J. Nanoparticles 2013, 6, 191–200. [Google Scholar] [CrossRef]
- Chen, B.; Chen, J.; Yao, Y.; Sekiguchi, T.; Matsuhata, H.; Okumura, H. In situ monitoring of stacking fault formation and its carrier lifetime mediation in p-type 4H-SiC. Appl. Phys. Lett. 2014, 105, 042104. [Google Scholar] [CrossRef]
- Orlov, V.I.; Regula, G.; Yakimov, E.B. Low temperature stacking fault nucleation and expansion from stress concentrators in 4H-SiC. Acta Mater. 2017, 139, 155–162. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Yakimov, E.E.; Orlov, V.I.; Gogova, D. Some new insights into the impact of annealing on single stacking faults in 4H-SiC. Superlattices Microstruct. 2018, 120, 7–14. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Sudo, M.; Yao, Y.-Z.; Sugawara, Y.; Kato, M. Expansion of a single Shockley stacking fault in a 4H-SiC (11-20) epitaxial layer caused by electron beam irradiation. J. Appl. Phys. 2018, 123, 225101. [Google Scholar] [CrossRef]
- Yakimov, E.E.; Yakimov, E.B. Radiation-enhanced dislocation glide in 4H-SiC at low temperatures. J. Alloys Compd. 2020, 837, 155470. [Google Scholar] [CrossRef]
- Yakimov, E.E.; Yakimov, E.B. Cathodoluminescence and EBIC investigations of stacking fault expansion in 4H-SiC due to e-beam irradiation at fixed points. J. Phys. D Appl. Phys. 2022, 55, 245101. [Google Scholar] [CrossRef]
- Yakimov, E.E.; Yakimov, E.B. Kink Migration along 30° Si-Core Partial Dislocations in 4H-SiC. Phys. Status Solidi A 2022, 219, 2200119. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Vergeles, P.S.; Polyakov, A.Y.; Lee, I.-H.; Pearton, S.J. Movement of basal plane dislocations in GaN during electron beam Irradiation. Appl. Phys. Lett. 2015, 106, 132101. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Vergeles, P.S.; Polyakov, A.Y.; Lee, I.-H.; Pearton, S.J. Radiation enhanced basal plane dislocation glide in GaN. Jpn. J. Appl. Phys. 2016, 55, 05FM03. [Google Scholar] [CrossRef]
- Vergeles, P.S.; Orlov, V.I.; Polyakov, A.Y.; Yakimov, E.B.; Kim, T.; Lee, I.-H. Recombination and optical properties of dislocations gliding at room temperature in GaN under applied stress. J. Alloy. Compd. 2019, 776, 181–186. [Google Scholar] [CrossRef]
- Amano, H.; Kito, M.; Hiramatsu, K.; Akasaki, I. P-Type Conduction in Mg-Doped GaN Treated with Low-Energy Electron Beam Irradiation (LEEBI). Jpn. J. Appl. Phys. 1989, 28, L2112–L2114. [Google Scholar] [CrossRef]
- Seager, C.H.; Myers, S.M.; Vaandrager, B.; Nelson, J.S. Isotope effects on the rate of electron-beam dissociation of Mg–H complexes in GaN. Appl. Phys. Lett. 2002, 80, 2693–2695. [Google Scholar] [CrossRef]
- Gelhausen, O.; Klein, H.N.; Phillips, M.R.; Goldys, E.M. Influence of low-energy electron beam irradiation on defects in activated Mg-doped GaN. Appl. Phys. Lett. 2002, 81, 3747–3749. [Google Scholar] [CrossRef]
- Juday, R.; Fischer, A.M.; Huang, J.; Huang, J.Y.; Kim, H.J.; Ryou, J.-H.; Dupuis, R.D.; Bour, D.P.; Ponce, F.A. Hydrogen-related, deeply bound excitons in Mg-doped GaN films. Appl. Phys. Lett. 2013, 103, 082103. [Google Scholar] [CrossRef]
- Feklisova, O.V.; Yakimov, E.B.; Yarykin, N.A. Effect of Irradiation in SEM on Electrical Properties of Silicon. Mater. Sci. Engineer. 1996, 42, 274–276. [Google Scholar] [CrossRef]
- Gfrörer, O.; Gemmer, C.; Off, J.; Im, J.S.; Scholz, F.; Hangleiter, A. Direct Observation of Pyroelectric Fields in InGaN/GaN and AlGaN/GaN Heterostructures. Phys. Status Solidi B 1999, 216, 405–408. [Google Scholar] [CrossRef]
- Shmidt, N.M.; Vergeles, P.S.; Yakimov, E.E.; Yakimov, E.B. Effect of low-energy electron irradiation on the cathodoluminescence of multiple quantum well (MQW) InGaN/GaN structures. Solid State Commun. 2011, 151, 208–211. [Google Scholar] [CrossRef]
- Nykänen, H.; Suihkonen, S.; Kilanski, L.; Sopanen, M.; Tuomisto, F. Low energy electron beam induced vacancy activation in GaN. Low energy electron beam induced vacancy activation in GaN. Appl. Phys. Lett. 2012, 100, 122105. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Vergeles, P.S.; Polyakov, A.Y.; Cho, H.-S.; Jang, L.-W.; Lee, I.-H. Microcathodoluminescence spectra evolution for planar and nanopillar multi-quantum-well GaN-based structures as a function of electron irradiation dose. J. Vac. Sci. Technol. B 2014, 32, 011207. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Vergeles, P.S.; Polyakov, A.Y.; Jeon, D.-W.; Lee, I.-H. Low Energy Electron Beam Irradiation Effect on Optical Properties of Nanopillar MQW InGaN/GaN Structures. AIP Conf. Proc. 2014, 1583, 268–271. [Google Scholar] [CrossRef]
- Cazaux, J. Scenario for time evolution of insulator charging under various focused electron irradiations. J. Appl. Phys. 2004, 95, 731–742. [Google Scholar] [CrossRef]
- Di Santo, G.; Coluzza, C.; Flammini, R.; Zanoni, R.; Decker, F. Spatial, energy, and time-dependent study of surface charging using spectroscopy and microscopy techniques. J. Appl. Phys. 2007, 102, 114505. [Google Scholar] [CrossRef]
- Jbara, O.; Fakhfakh, S.; Belhaj, M.; Rondot, S.; Hadjadj, A.; Patat, J.M. Charging effects of PET under electron beam irradiation in a SEM. J. Phys. D Appl. Phys. 2008, 41, 245504. [Google Scholar] [CrossRef]
- Cornet, N.; Goeuriot, D.; Guerret-Piecourt, C.; Juve, D.; Treheux, D.; Touzin, M.; Fitting, H.-J. Electron beam charging of insulators with surface layer and leakage currents. J. Appl. Phys. 2008, 103, 064110. [Google Scholar] [CrossRef]
- Rau, E.I.; Tatarintsev, A.A. Modification of the model of charging dielectrics under electron beam irradiation. J. Appl. Phys. 2022, 132, 184102. [Google Scholar] [CrossRef]
- Oldham, T.R.; McLean, F.B. Total Ionizing Dose Effects in MOS Oxides and Devices. IEEE Trans. Nucl. Sci. 2003, 50, 483–498. [Google Scholar] [CrossRef]
- Schwank, J.R.; Shaneyfelt, M.R.; Fleetwood, D.M.; Felix, J.A.; Dodd, P.E.; Paillet, P.; Ferlet-Cavrois, V. Radiation Effects in MOS Oxides. IEEE Trans. Nucl. Sci. 2008, 55, 1833–1853. [Google Scholar] [CrossRef]
- Vergeles, P.S.; Kulanchikov, Y.O.; Yakimov, E.B. Charging Effects in Al-SiO2-p-Si Structures after Low-Energy Electron Beam Irradiation. J. Electron. Mater. 2020, 49, 5178–5183. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, Y.; Liu, Y.; Li, H.; Wang, G.; Hu, R.; Xiong, X.; Luo, S. The radiation damage of crystalline silicon PN diode in tritium beta-voltaic battery. Appl. Radiat. Isotop. 2014, 90, 165–169. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).