Battery Dynamic Balancing Method Based on Calculation of Cell Voltage Reference Value
Abstract
:1. Introduction
2. Materials and Methods
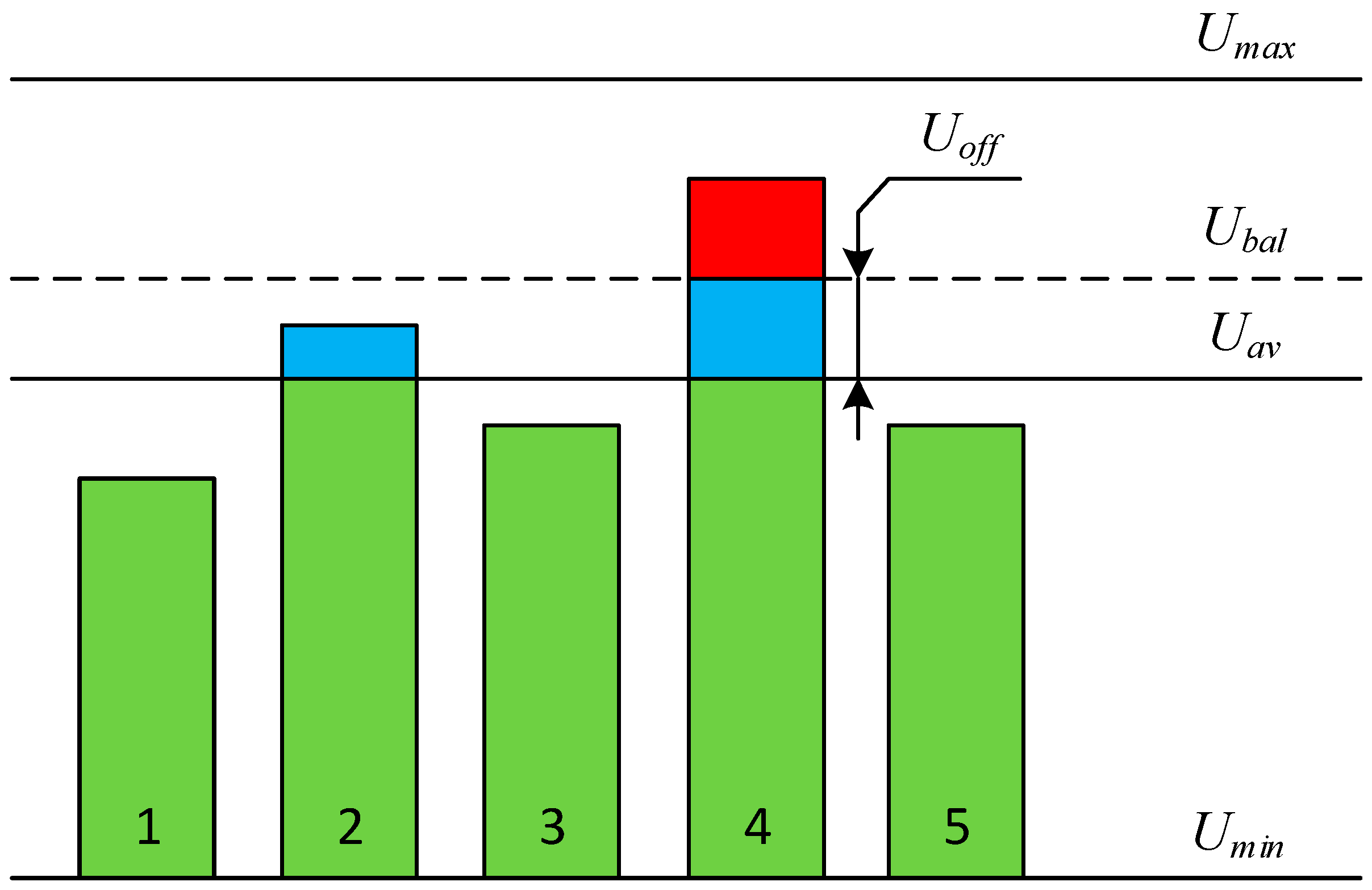
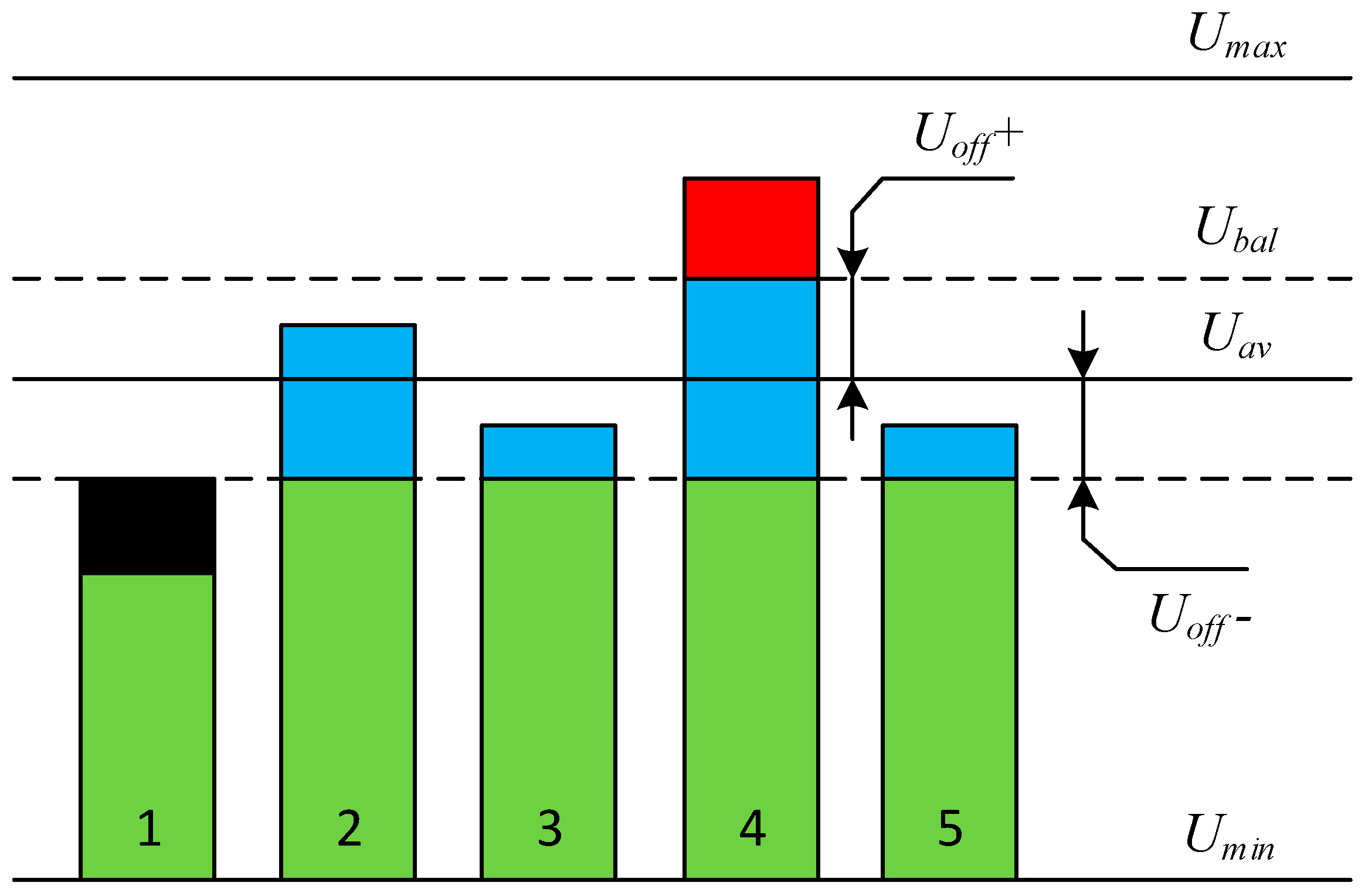
2.1. The Essence of Proposed Method
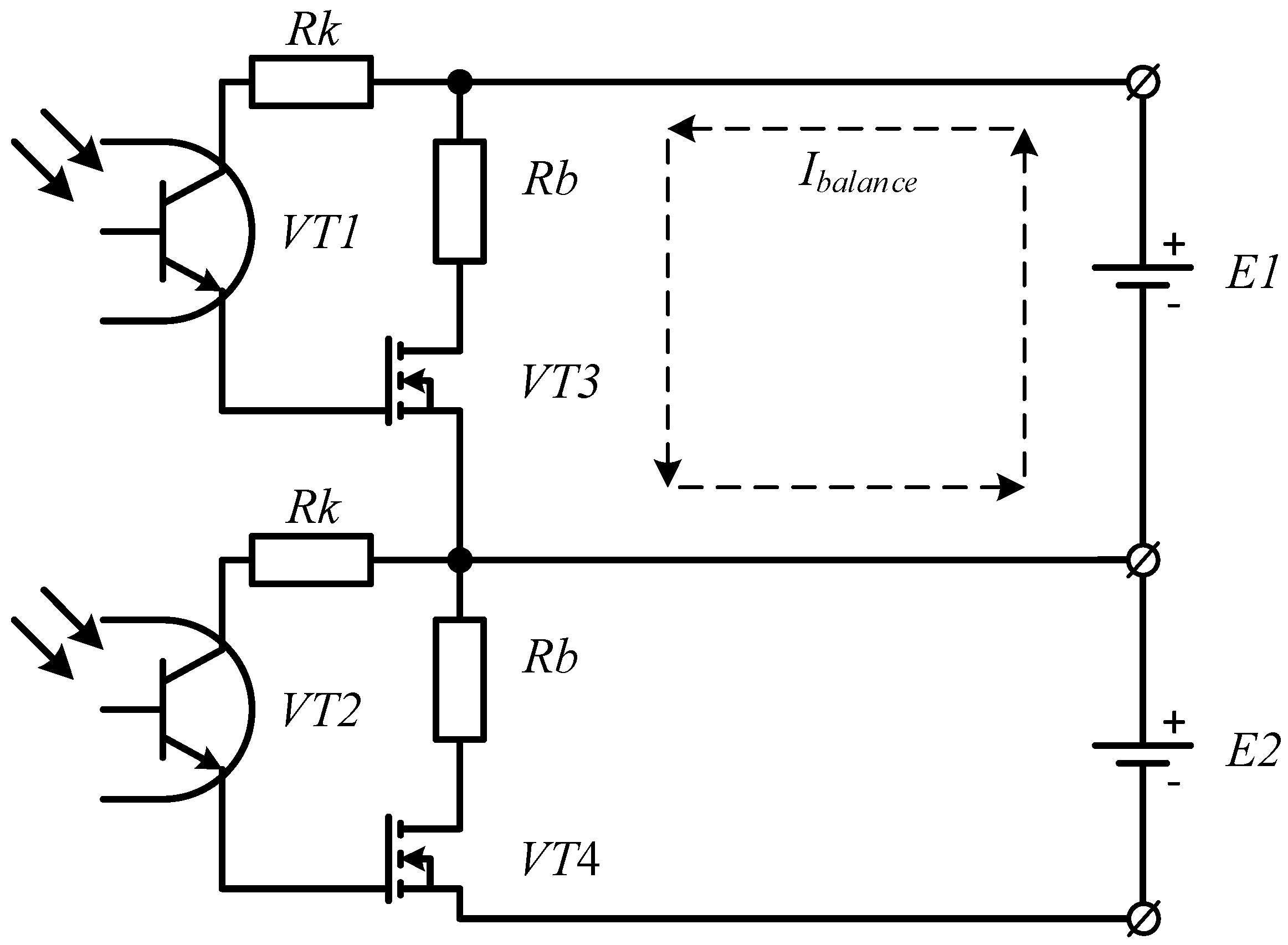
2.2. Block Diagram of Passive Balancing Electronic Nodes Using the Proposed Method
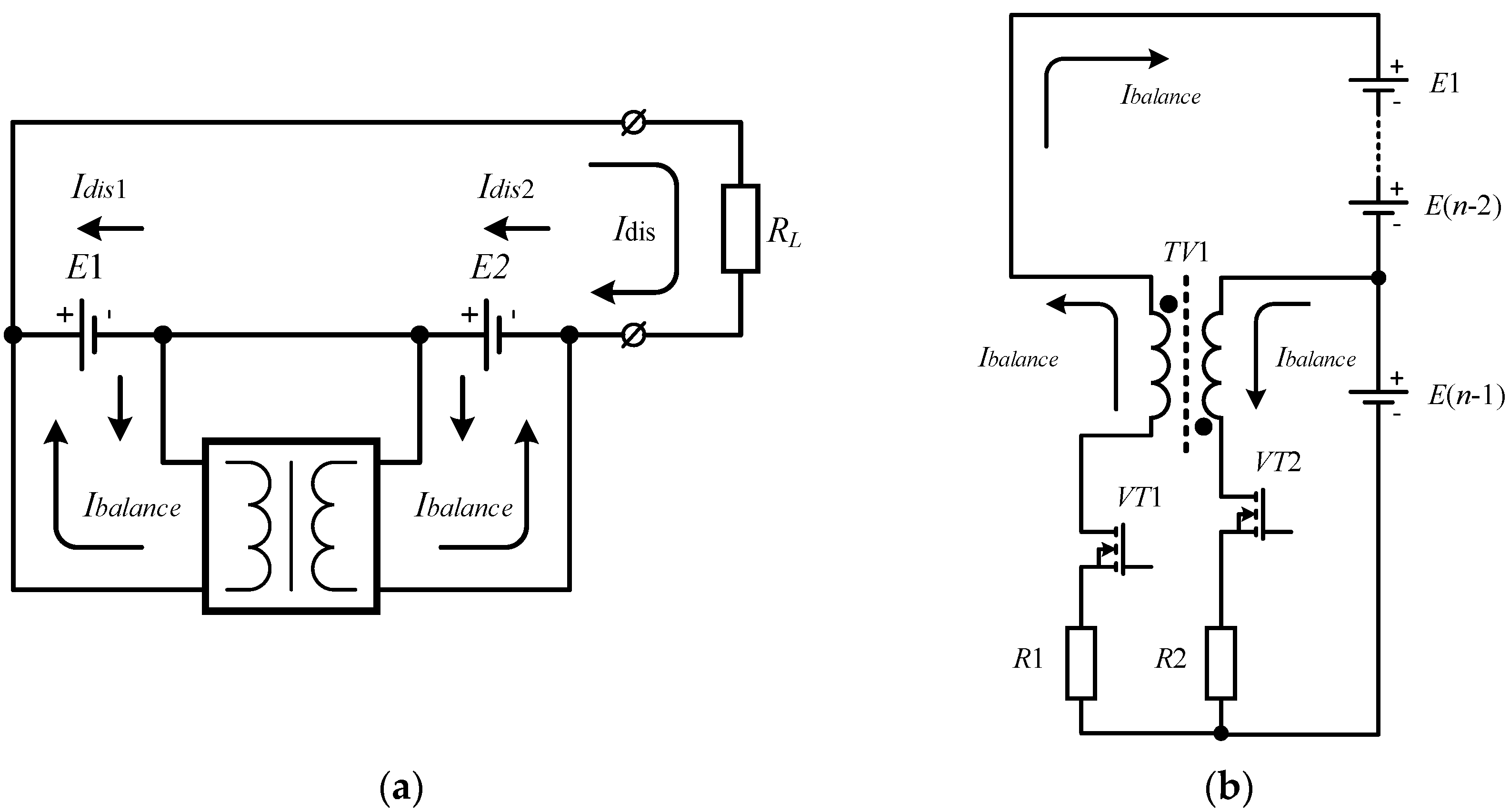
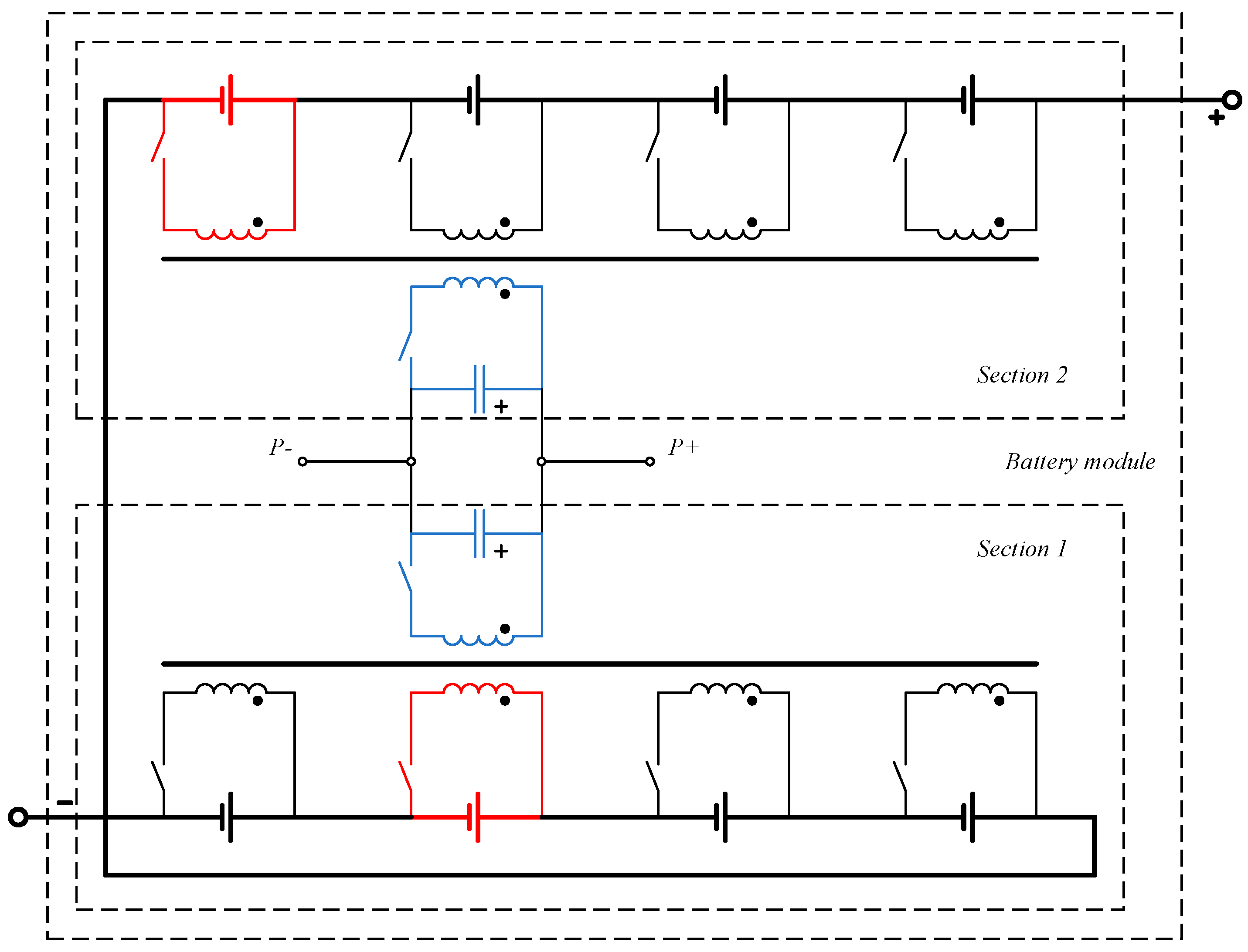
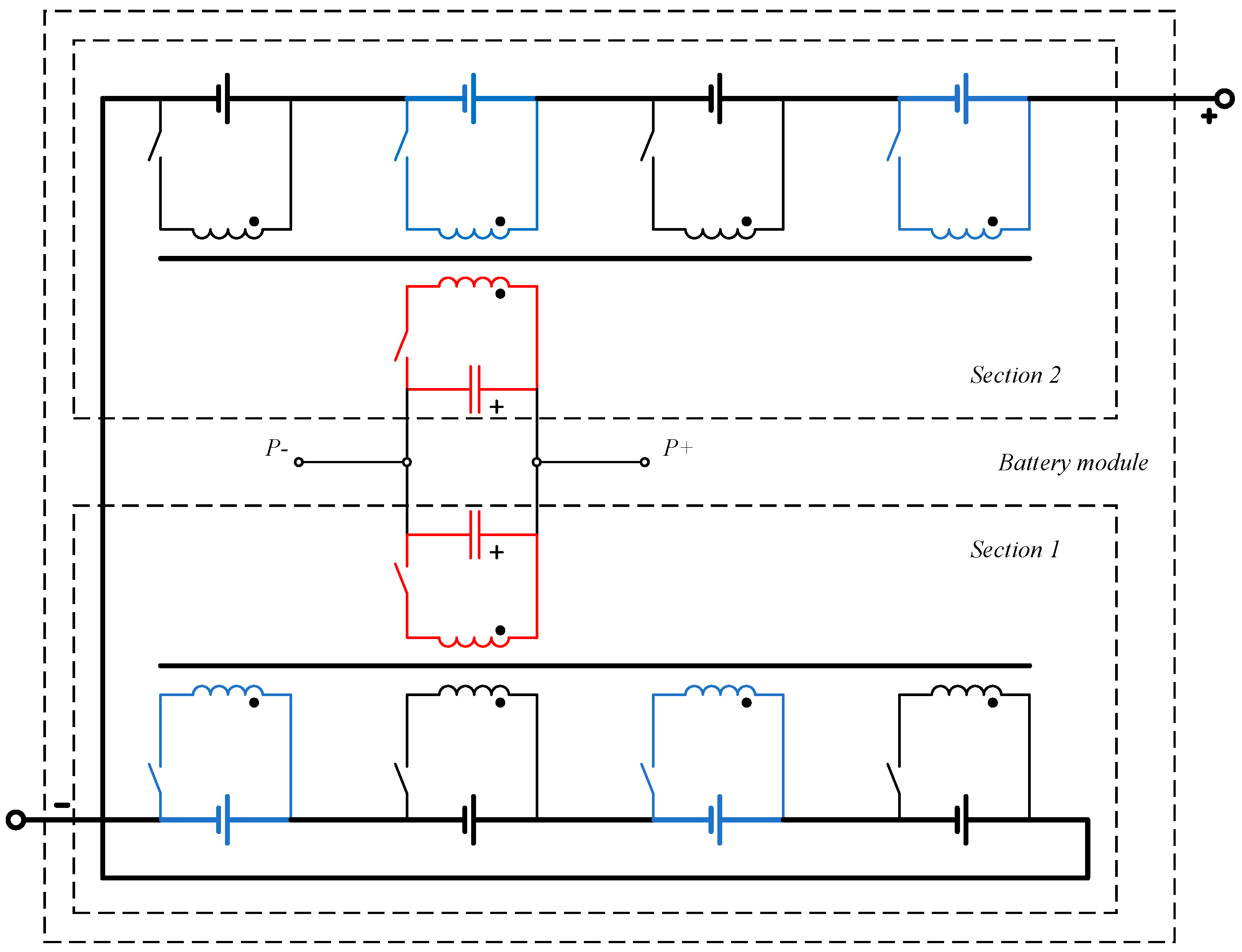
2.3. Multi-Coordinate Energy Transmission Using the Proposed Method Based on Active Balancing Circuit
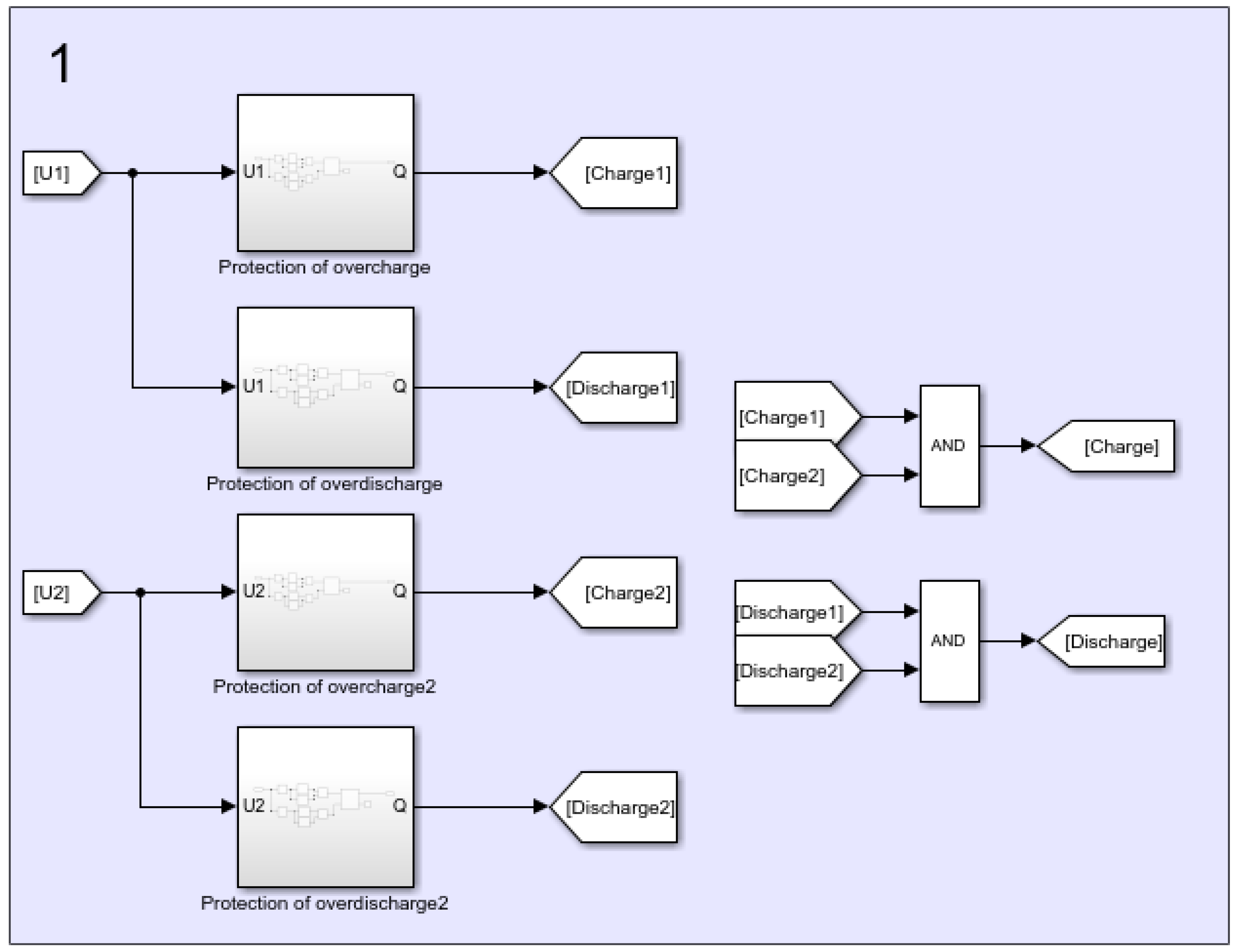
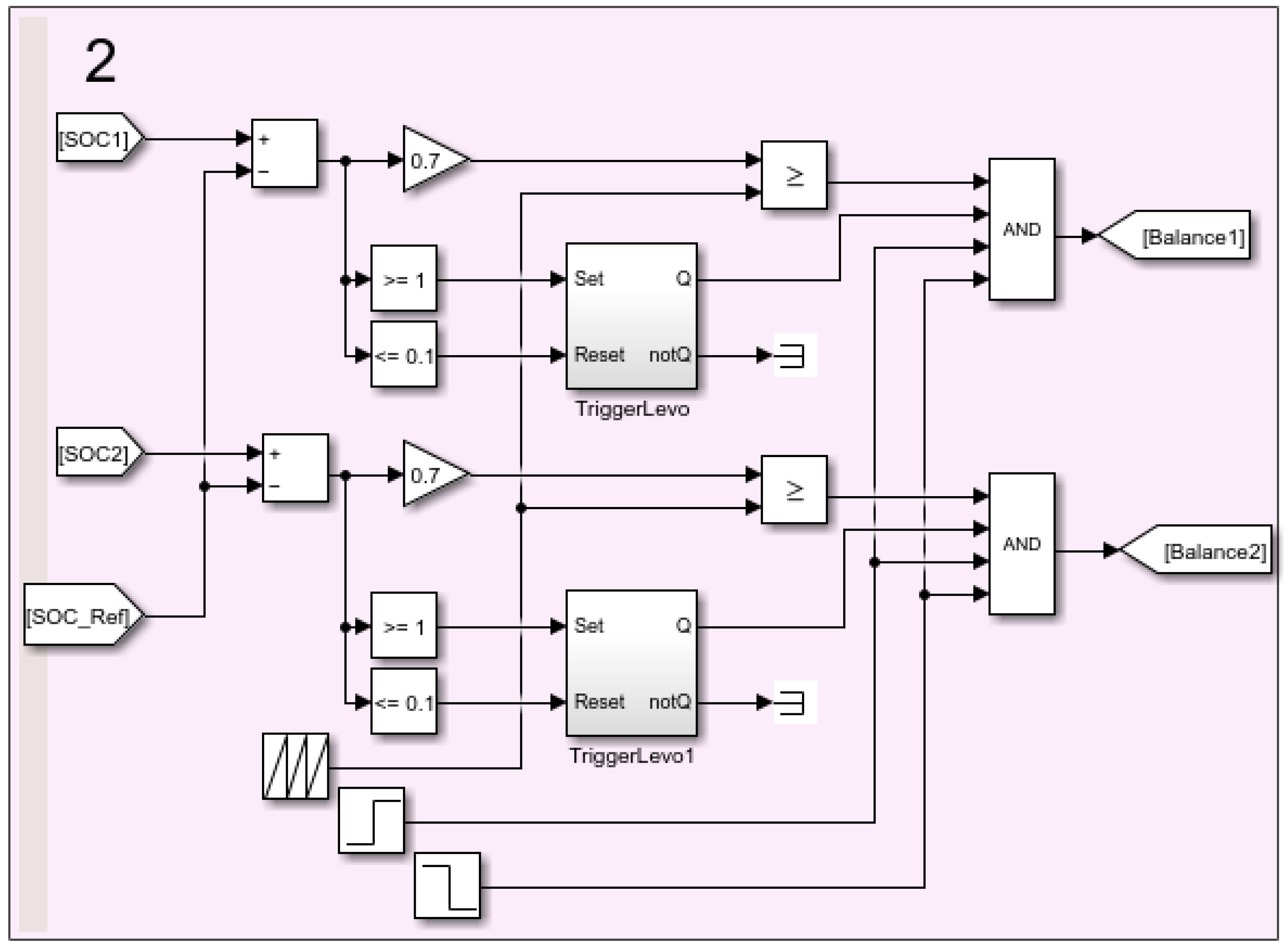
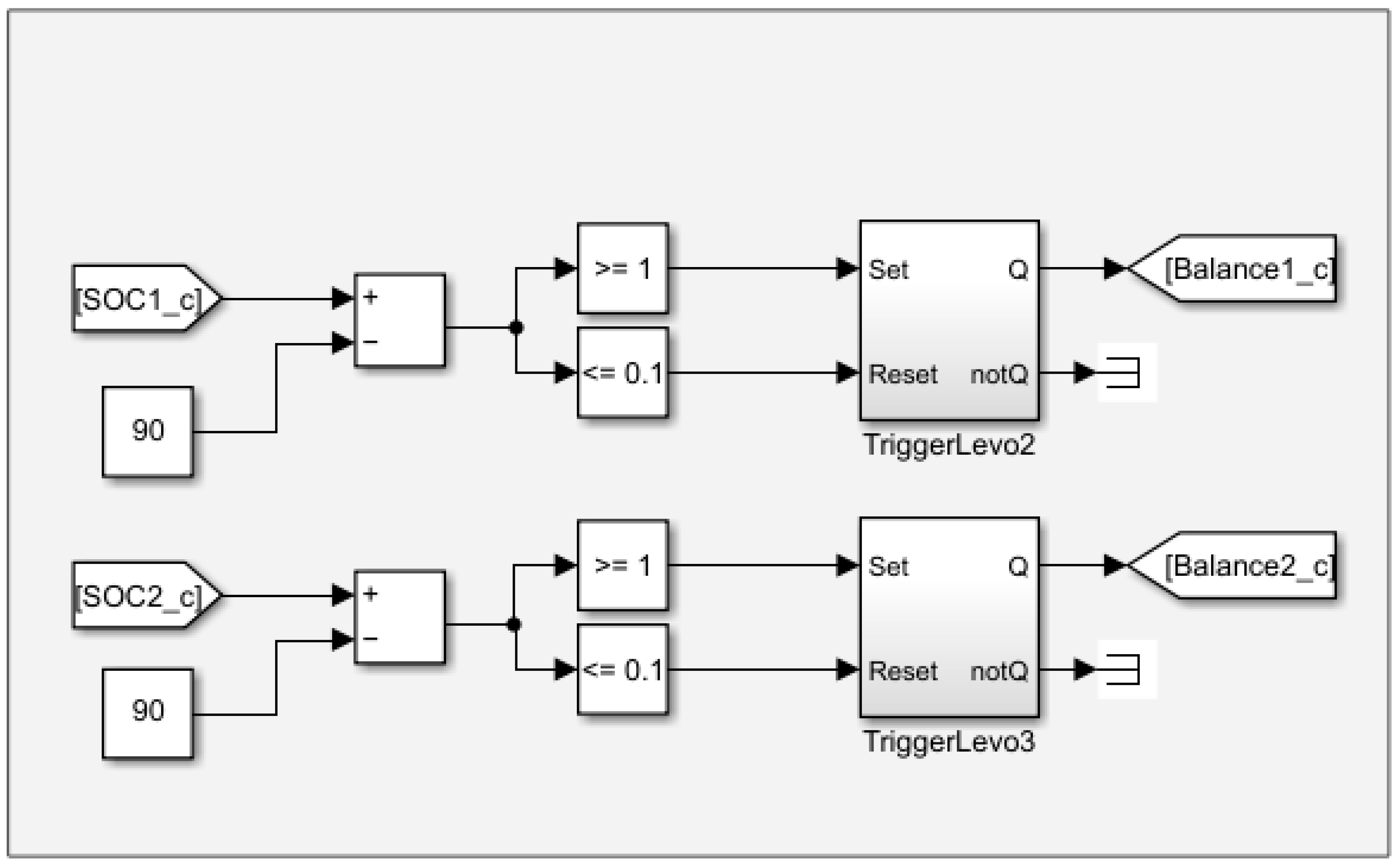
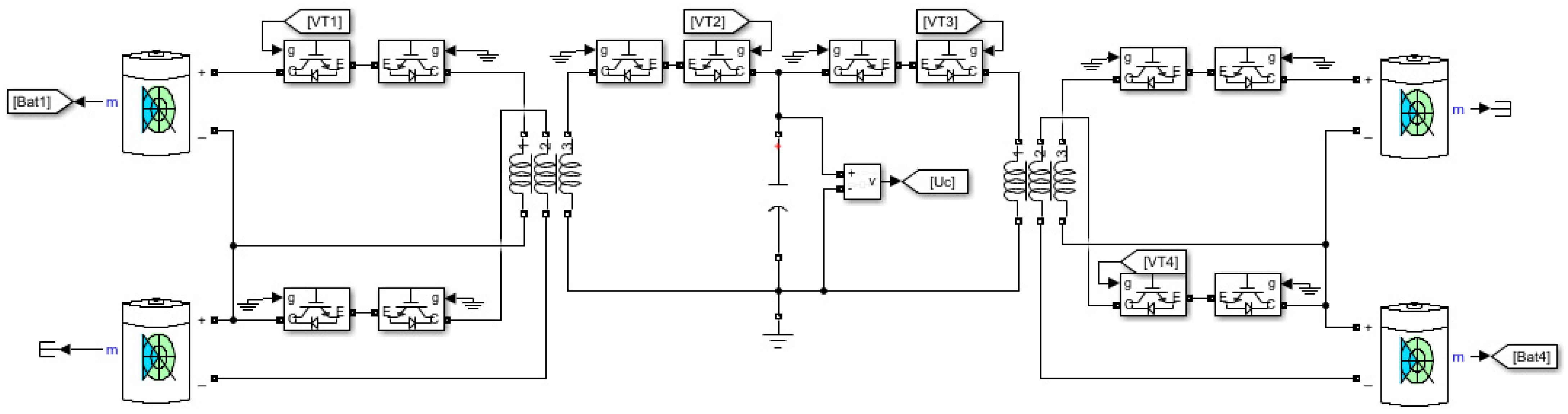
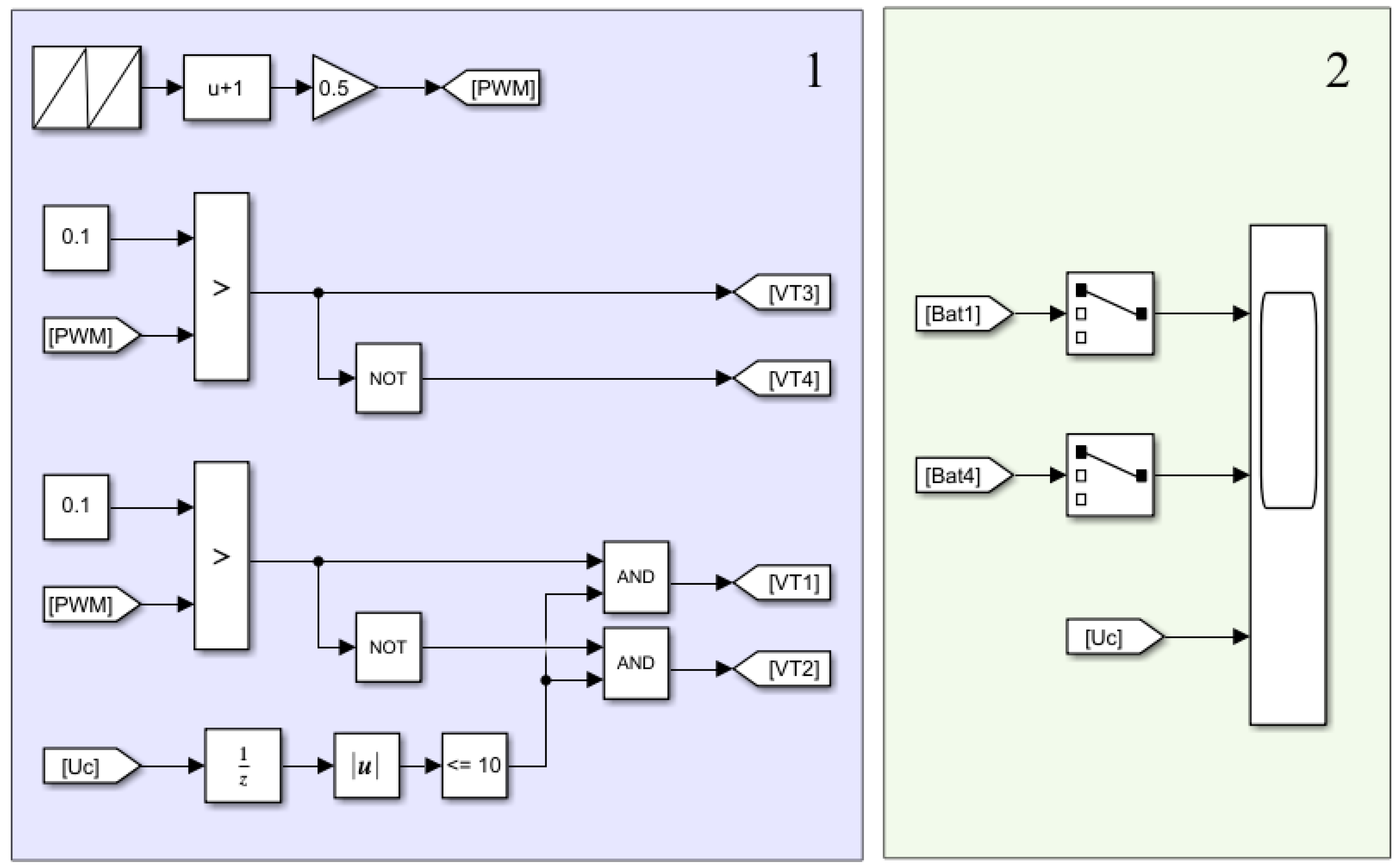
3. Developing Passive and Active Balancing Simulink Models
3.1. Simulink-Passive Balancing Model Using the Proposed Method
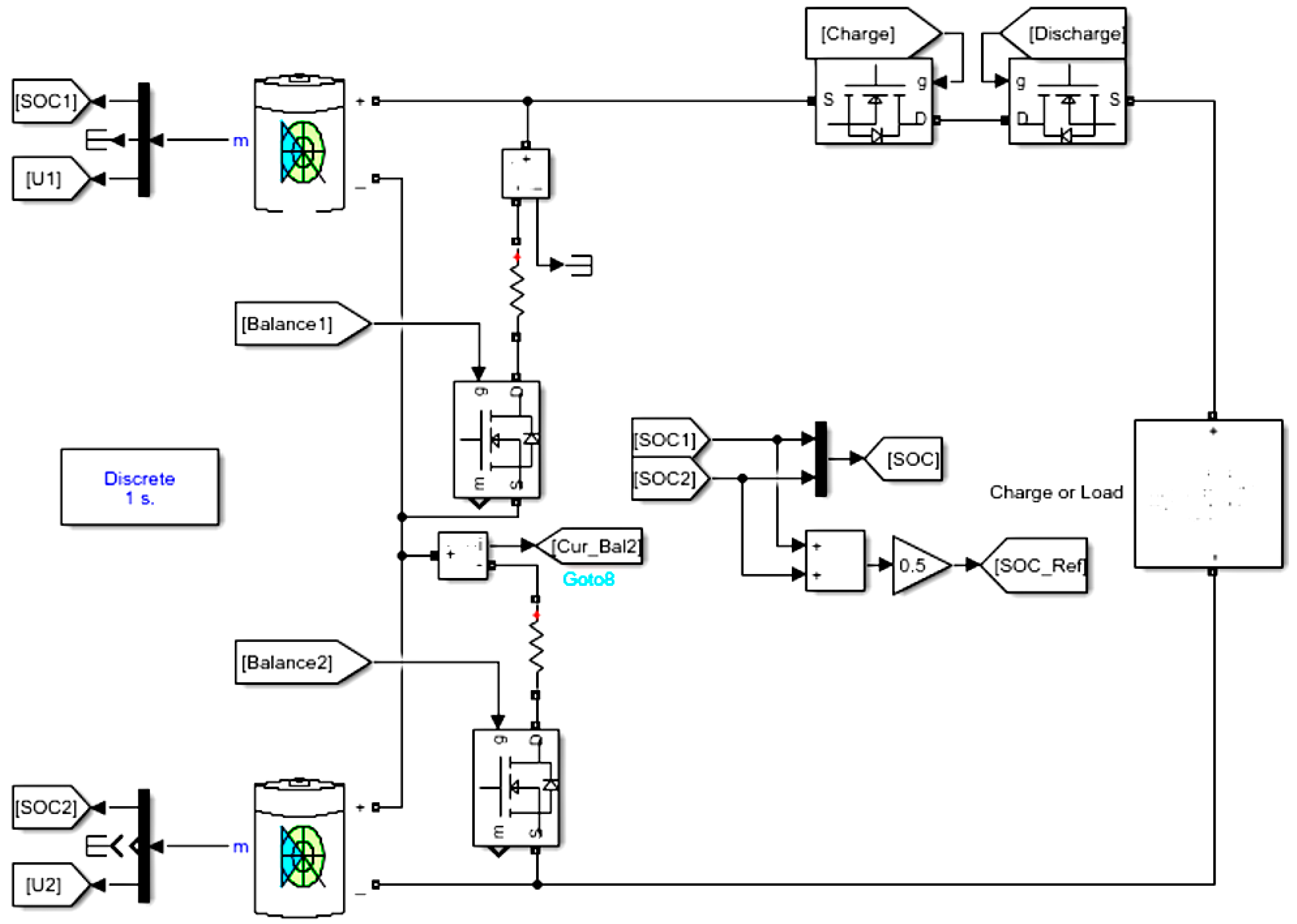
3.2. Active Balancing System Model with Multi-Coordinate Energy Transmission
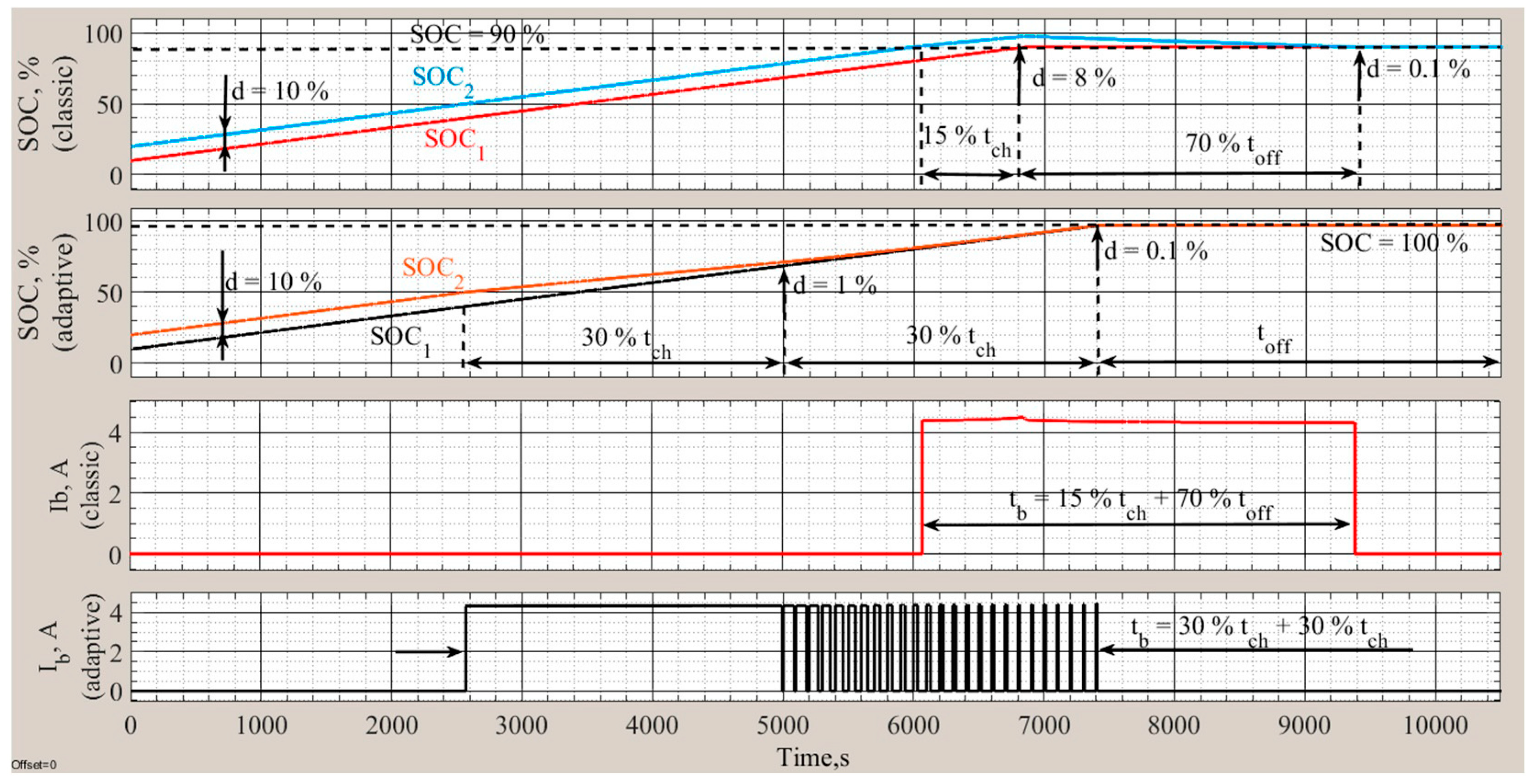
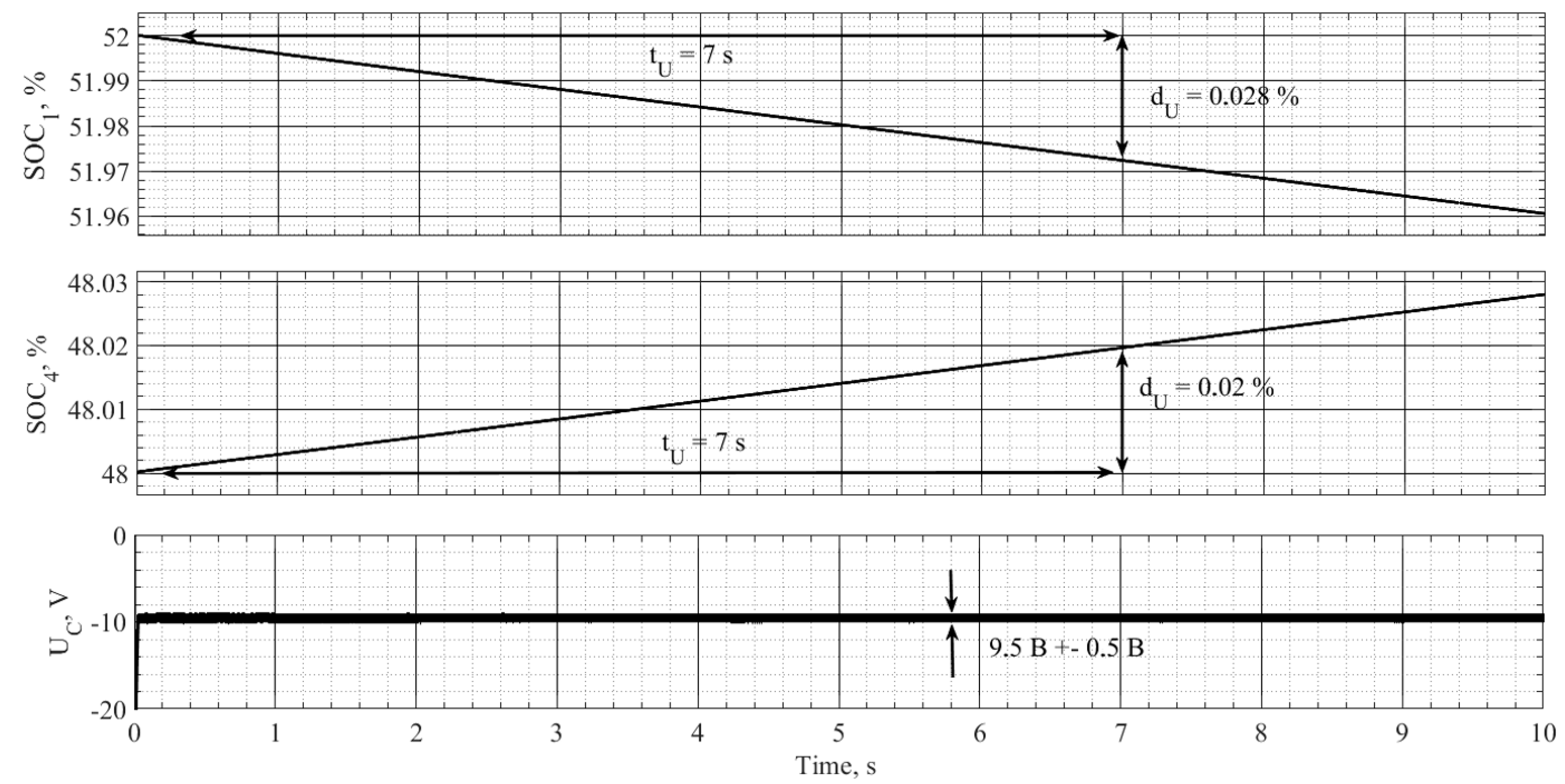
4. Simulation Results
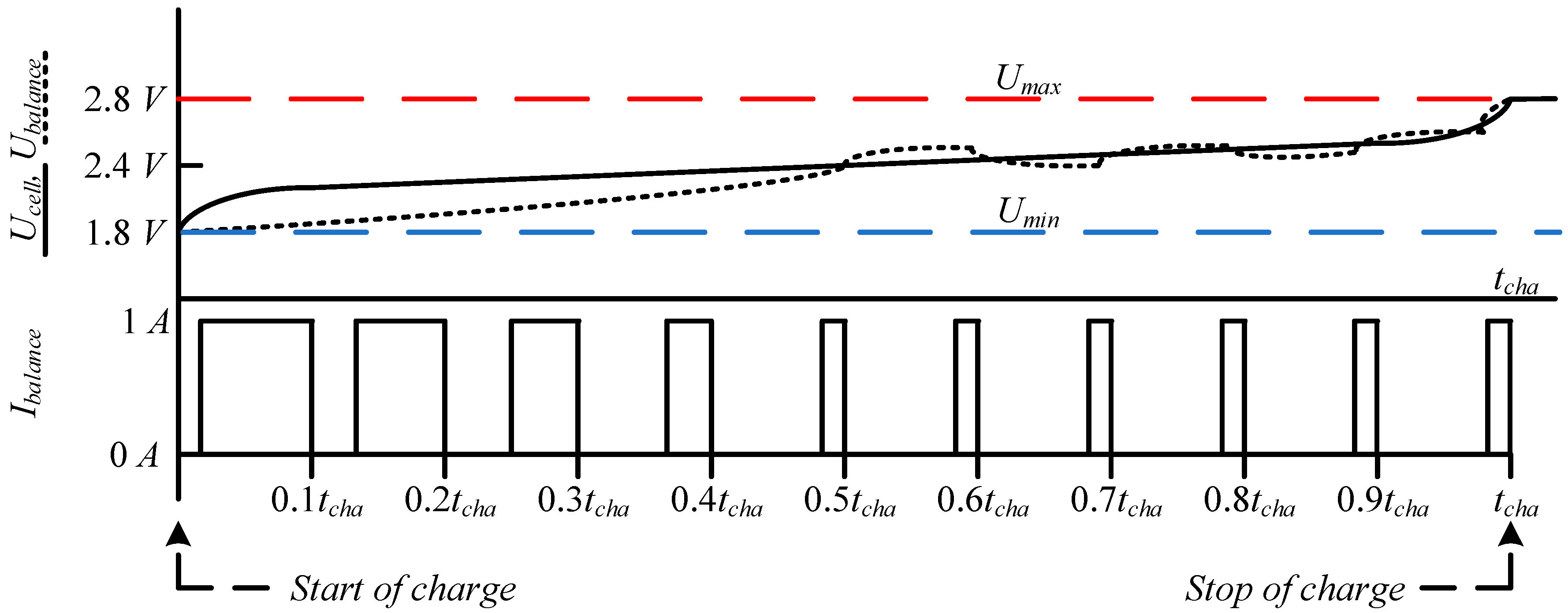
4.1. Passive Balancing Method Simulation Results
4.2. Active Balancing Method Simulation Results
5. Conclusions
- The method allows for speeding up the time of balancing and enhances the accuracy of battery balancing;
- The method excludes the overcharge of individual GCs and provides a uniform charge of all GCs in the battery;
- The method provides for multi-coordinate energy transmission between any GCs in the battery.
Author Contributions
Funding
Conflicts of Interest
References
- Deng, D. Li-ion Batteries: Basics, Progress, and Challenges. Energy Sci. Eng. 2015, 3, 385–418. [Google Scholar] [CrossRef]
- Li, M.; Feng, M.; Luo, D.; Chen, Z. Fast Charging Li-Ion Batteries for a New Era of Electric Vehicles. Cell Rep. Phys. Sci. 2020, 1, 100212. [Google Scholar] [CrossRef]
- Saad, A.A.; Faddel, S.; Mohammed, O. A Secured Distributed Control System for Future Interconnected Smart Grids. Appl. Energy 2019, 243, 57–70. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, G.; Pan, X.; Li, Y.; He, J.; Qi, Y.; Yang, J. High Voltage Electric Pulse Drilling: A Study of Variables through Simulation and Experimental Tests. Energies 2023, 16, 1174. [Google Scholar] [CrossRef]
- Chuang, C.-C.; Yao, C.-J.; Wu, S.-T. Study on Fast Charging Method of Series Connected Lithium-Ion Battery Strings with Intelligent Control. In Proceedings of the 2020 International Conference on Fuzzy Theory and Its Applications (iFUZZY), Hsinchu, Taiwan, 4 November 2020; pp. 1–6. [Google Scholar]
- Streit, L.; Kosan, T.; Hammerbauer, J. CAN Controlled 120 Cells Li-Ion Battery with Integrated BMS and Protection. In Proceedings of the 2022 20th International Conference on Mechatronics—Mechatronika (ME), Pilsen, Czech Republic, 7 December 2022; pp. 1–4. [Google Scholar]
- Cordero, E.; Holt, S.; Dickens, J.; Neuber, A.; Mankowski, J. Implementation of a Battery Management and Protection System for High Power Pulsed Applications. In Proceedings of the 2015 IEEE Pulsed Power Conference (PPC), Austin, TX, USA, 31 May–4 June 2015; pp. 1–4. [Google Scholar]
- Parschau, A.; Degler, D.; Fill, A.; Birke, K.P.; Allmendinger, F. Cycle Tests on the Influence of Different Charging Currents—A Case Study on Different Commercial, Cylindrical Lithium Ion Cells. Batteries 2023, 9, 83. [Google Scholar] [CrossRef]
- Buidin, T.I.C.; Mariasiu, F. Parametric Evaluation of Thermal Behavior for Different Li-Ion Battery Chemistries. Batteries 2022, 8, 291. [Google Scholar] [CrossRef]
- Joshi, B.; Maherchandani, J.K.; Chhipa, A.A. Comparison between Open and Closed Loop Battery Charging Technique for Lithium-Ion Battery. In Proceedings of the 2021 7th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 11 February 2021; pp. 150–155. [Google Scholar]
- Hartono; Sanjaya, K.N. Thermal Monitoring System Phase Change Material Batteries Using Fuzzy Logic. In Proceedings of the 2022 International Conference on Informatics Electrical and Electronics (ICIEE), Yogyakarta, Indonesia, 5 October 2022; pp. 1–8. [Google Scholar]
- Najeeb, M.; Schwalbe, U. Incorporating State of Charge Estimation Methods towards More Accurate Monitoring of Second-Life Lithium-Ion Batteries. In Proceedings of the 2022 13th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 13 December 2022; pp. 1–6. [Google Scholar]
- Kesuma, E.R.; Herman, I.; Rahman, M.M.; Budiman, B.A. Optimization of Electric Vehicle Battery Pack Liquid Cooling. In Proceedings of the 2022 7th International Conference on Electric Vehicular Technology (ICEVT), Bali, Indonesia, 14 September 2022; pp. 214–221. [Google Scholar]
- Fotescu, R.-P.; Burciu, L.-M.; Constantinescu, R.; Svasta, P. Advantages of Using Battery Cell Balancing Technology in Energy Storage Media in Electric Vehicles. In Proceedings of the 2021 IEEE 27th International Symposium for Design and Technology in Electronic Packaging (SIITME), Timisoara, Romania, 27 October 2021; pp. 129–132. [Google Scholar]
- Marathe, S.; Wagh, S. Numerical Investigations on Air Cooled Li-Ion Battery Modules for Effective Thermal Management. In Proceedings of the 2021 IEEE Transportation Electrification Conference (ITEC-India), New Delhi, India, 16 December 2021; pp. 1–6. [Google Scholar]
- Weiss, H.; Volgger, S. Insular Power Supply Battery Manager with Balancing and Protection Unit for Lithium-Ion Batteries. In Proceedings of the 2014 12th International Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Novosibirsk, Russia, 2–4 October 2014; pp. 789–792. [Google Scholar]
- Badrinath, A.S.; Udupa, S.V. Protection Circuitry and Passive Balancing for Battery Management Systems Part I. In Proceedings of the 2017 International Conference on Computation of Power, Energy Information and Commuincation (ICCPEIC), Melmaruvathur, India, 22–23 March 2017; pp. 510–515. [Google Scholar]
- Michael; Sujatmiko, R.P.; Abuzairi, T.; Rizkinia, M.; Kurniawan, T.A. Design of Overcharging Protection and Passive Balancing Circuits Using Dioda for Lithium-Ion Battery Management System. In Proceedings of the 2019 16th International Conference on Quality in Research (QIR): International Symposium on Electrical and Computer Engineering, Padang, Indonesia, 22–24 July 2019; pp. 1–4. [Google Scholar]
- Suryoatmojo, H.; Pamudji, F.A.; Fikri, R.S.; Riawan, D.C.; Adila, A.F.; Mardiyanto, R. Design of Two-Stage Charge Equalizer with Modularized Cell Selection Switches for Series-Connected Lithium-Ion Battery. In Proceedings of the 2022 International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 20 July 2022; pp. 389–394. [Google Scholar]
- Shrivastava, S.; Swarnkar, P. Comparative Study of Cell Balancing Techniques for Battery Module Performance Optimization. In Proceedings of the 2023 IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 18 February 2023; pp. 1–6. [Google Scholar]
- Al-Smadi, M.K.; Abu Qahouq, J.A. Evaluation of Current-Mode Controller for Active Battery Cells Balancing with Peak Efficiency Operation. IEEE Trans. Power Electron. 2023, 38, 1610–1621. [Google Scholar] [CrossRef]
- Tyrpekl, M.; Zavrel, M.; Kindl, V. Comparison of Active and Passive Battery Balancing. In Proceedings of the 2022 20th International Conference on Mechatronics—Mechatronika (ME), Pilsen, Czech Republic, 7 December 2022; pp. 1–6. [Google Scholar]
- Tavakoli, A.; Khajehoddin, S.A.; Salmon, J. A Modular Battery Voltage-Balancing System Using a Series-Connected Topology. IEEE Trans. Power Electron. 2020, 35, 5952–5964. [Google Scholar] [CrossRef]
- Conway, T. An Isolated Active Balancing and Monitoring System for Lithium Ion Battery Stacks Utilizing a Single Transformer Per Cell. IEEE Trans. Power Electron. 2021, 36, 3727–3734. [Google Scholar] [CrossRef]
- Ghaeminezhad, N.; Ouyang, Q.; Hu, X.; Xu, G.; Wang, Z. Active Cell Equalization Topologies Analysis for Battery Packs: A Systematic Review. IEEE Trans. Power Electron. 2021, 36, 9119–9135. [Google Scholar] [CrossRef]
- Tian, L.; Hong, M.; He, Z.; Gao, M. Active Battery Balancing Circuit Based on Optimized Flyback Convertor for Large Lithium-Ion Battery Packs. In Proceedings of the 2018 IEEE 4th International Conference on Control Science and Systems Engineering (ICCSSE), Wuhan, China, 21–23 August 2018; pp. 212–216. [Google Scholar]
- Crespo, M.; Pelaez, I.; Garcia, P.; Georgious, R.; Blanco, C.; Cantero, I. Series/Parallel Li-Ion Battery Modules Active Equalisation Considering Load and No-Load Operation. IEEE Trans. Ind. Appl. 2023, 59, 1–12. [Google Scholar] [CrossRef]
- Ma, H.; Yang, Q. An Online Detection Method of Short Circuit for Battery Packs. In Proceedings of the 2022 4th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 25 March 2022; pp. 594–598. [Google Scholar]
- Mikhaylov, V.V. Protection of Storage Batteries against Short-Circuit Currents in Alternative Power Systems. In Proceedings of the 2022 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 16 May 2022; pp. 148–152. [Google Scholar]
- Heidary, A.; Radmanesh, H.; Rouzbehi, K.; Pou, J. A DC-Reactor-Based Solid-State Fault Current Limiter for HVdc Applications. IEEE Trans. Power Deliv. 2019, 34, 720–728. [Google Scholar] [CrossRef]
- Almutairy, I.; Alluhaidan, M. Protecting a Low Voltage DC Microgrid during Short-Circuit Using Solid-State Switching Devices. In Proceedings of the 2017 IEEE Green Energy and Smart Systems Conference (IGESSC), Long Beach, CA, USA, 6–7 November 2017; pp. 1–6. [Google Scholar]
- Chang, A.H.; Sennett, B.R.; Avestruz, A.-T.; Leeb, S.B.; Kirtley, J.L. Analysis and Design of DC System Protection Using Z-Source Circuit Breaker. IEEE Trans. Power Electron. 2016, 31, 1036–1049. [Google Scholar] [CrossRef]
- Muangjai, W.; Aroonchai, T.; Somsak, T.; Ngaodet, M.; Oranpiroj, K.; Thongpron, J. Analysis of the Effect of Charge and Discharge LiFePO4 Batteries Using BMS with and without Active Balancer. In Proceedings of the 2022 International Electrical Engineering Congress (iEECON), Khon Kaen, Thailand, 9 March 2022; pp. 1–4. [Google Scholar]
- Pawar, A.S.; Chopade, N.B.; Kolte, M.T.; Bendre, V.S.; Harpale, V.K.; Mehta, H. An Overview of Techniques Used for Determination of State-of-Charge of Batteries. In Proceedings of the 2022 6th International Conference on Computing, Communication, Control And Automation (ICCUBEA), Pune, India, 26 August 2022; pp. 1–5. [Google Scholar]
- Thobde, R.R.; Somani, S.B.; Gunale, K.G. State of Charge (SoC) Algorithm for Battery Management System (BMS). In Proceedings of the 2022 13th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kharagpur, India, 3 October 2022; pp. 1–7. [Google Scholar]
- Shimoi, N.; Tohji, K. Simple Diagnosis of Lifetime Characteristics of Used Automotive Storage Battery Cells. Energies 2022, 15, 8814. [Google Scholar] [CrossRef]
- Wang, J.; Meng, J.; Peng, Q.; Liu, T.; Zeng, X.; Chen, G.; Li, Y. Lithium-Ion Battery State-of-Charge Estimation Using Electrochemical Model with Sensitive Parameters Adjustment. Batteries 2023, 9, 180. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the Battery Model and SOC Estimation Method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Castano, S.; Serrano-Jimenez, D.; Sanz, J. BMS Influence on Li-Ion Packs Characterization and Modeling. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar]
- Amin; Ismail, K.; Nugroho, A.; Kaleg, S. Passive Balancing Battery Management System Using MOSFET Internal Resistance as Balancing Resistor. In Proceedings of the 2017 International Conference on Sustainable Energy Engineering and Application (ICSEEA), Jakarta, Indonesia, 23–26 October 2017; pp. 151–155. [Google Scholar]
- Eskandari, R.; Venugopal, P.; Rietveld, G. Advanced Battery Management Systems with Integrated Battery Electronics. In Proceedings of the 2022 IEEE 20th International Power Electronics and Motion Control Conference (PEMC), Brasov, Romania, 25 September 2022; pp. 55–61. [Google Scholar]
- Pannickottu Nivya, K.; Deepa, K. Active Cell Balancing for a 2s Lithium Ion Battery Pack Using Flyback Converter and Push-Pull Converter. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1070, 012097. [Google Scholar] [CrossRef]
- Daowd, M.; Omar, N.; Van Den Bossche, P.; Van Mierlo, J. Passive and Active Battery Balancing Comparison Based on MATLAB Simulation. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–7. [Google Scholar]
- Azad, F.S.; Habib, A.K.M.A.; Rahman, A.; Ahmed, I. Active Cell Balancing of Li-Ion Batteries Using Single Capacitor and Single LC Series Resonant Circuit. Bull. Electr. Eng. Inform. 2020, 9, 1318–1325. [Google Scholar] [CrossRef]
- Chen, W.; Ding, Z.; Liu, J.; Kan, J.; Nazir, M.S.; Wang, Y. Half-Bridge Lithium-Ion Battery Equalizer Based on Phase-Shift Strategy. Sustainability 2023, 15, 1349. [Google Scholar] [CrossRef]
- Qi, X.; Wang, Y.; Wang, Y.; Chen, Z. Optimization of Centralized Equalization Systems Based on an Integrated Cascade Bidirectional DC–DC Converter. IEEE Trans. Ind. Electron. 2022, 69, 249–259. [Google Scholar] [CrossRef]

| Parameter | Primary Winding | Secondary Winding #1 | Secondary Winding #2 | Magnetizing Circuit |
|---|---|---|---|---|
| R, Ohm | 1 | 1 | 1 | 0.1 |
| L, uH | 100 | 100 | 100 | 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vikhorev, N.; Kurkin, A.; Aleshin, D.; Ulyanov, D.; Konstantinov, M.; Shalukho, A. Battery Dynamic Balancing Method Based on Calculation of Cell Voltage Reference Value. Energies 2023, 16, 3733. https://doi.org/10.3390/en16093733
Vikhorev N, Kurkin A, Aleshin D, Ulyanov D, Konstantinov M, Shalukho A. Battery Dynamic Balancing Method Based on Calculation of Cell Voltage Reference Value. Energies. 2023; 16(9):3733. https://doi.org/10.3390/en16093733
Chicago/Turabian StyleVikhorev, Nikolay, Andrey Kurkin, Dmitriy Aleshin, Danil Ulyanov, Maksim Konstantinov, and Andrey Shalukho. 2023. "Battery Dynamic Balancing Method Based on Calculation of Cell Voltage Reference Value" Energies 16, no. 9: 3733. https://doi.org/10.3390/en16093733
APA StyleVikhorev, N., Kurkin, A., Aleshin, D., Ulyanov, D., Konstantinov, M., & Shalukho, A. (2023). Battery Dynamic Balancing Method Based on Calculation of Cell Voltage Reference Value. Energies, 16(9), 3733. https://doi.org/10.3390/en16093733







