Abstract
Proton exchange membrane fuel cells (PEMFC) are a promising clean power source that can be used in a variety of applications such as automobiles, stationary power plants, and portable power devices. The application problem of PEM fuel cells is a multiscale application process involving porous media, consisting of a series of mass, momentum, and energy transfers through gas channels, current transfers through membrane electrode assemblies, and electrochemical reactions at three-phase boundaries. In this paper, the recent research progress of PEMFC in multiscale porous-media mass transfer processes is reviewed, the research progress of fuel cell parameter identification is reviewed, and the future development direction is summarized and analyzed. The purpose of this paper is to provide a comprehensive overview of proton exchange membrane fuel cell mass transfer and parameter identification to reference researchers and engineers in the field of fuel cell systems.
1. Introduction
The reduction of energy consumption and emissions has become a key task for researchers today [1]. With high energy density, long storage time, and other advantages [2], hydrogen energy is considered an important energy carrier for building a diversified energy supply system of clean energy [3]. In terms of hydrogen energy utilization, proton exchange membrane fuel cells have attracted widespread attention due to their advantages such as high power density, zero emissions, and high efficiency [4], and are considered to be one of the most sustainable fuel cells [5]. Hydrogen (chemical energy) is conversion to electrical and thermal energy through electrochemical reactions, where the product is only water [6]. The anode and cathode half-cell reactions (half-cell reaction) of a proton exchange membrane fuel cell and the overall cell reaction are as follows:
Anode (hydrogen oxidation reaction):
Cathode (oxygen reduction reaction):
Overall reaction:
The transmission of hydrogen, oxygen, protons, and electrons is critical to improve the reliability, durability, and performance of PEM fuel cells. Figure 1 shows the structure of a PEMFC and the gas flow through a channel, with mass transfer between the channel and the PEMFC membrane electrode layer. In terms of mass transfer, transport perpendicular to the channel is extremely important in influencing electrochemical reactions, although transport along the channel has also been extensively studied. The latter often includes the former to some extent. Both experimental measurements and numerical simulations have been widely used in the last decades to improve the understanding of PEMFC transport processes. Much of this has focused on the optimization and discovery of membrane electrode assembly (MEA) structures and new materials.
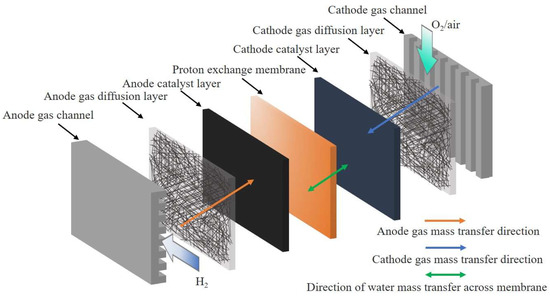
Figure 1.
Mass transfer process of gas between channels and fuel cell membrane electrode layers.
A prominent feature of mass transfer in PEMFC is transportation in multiscale porous media. Since fuel and oxygen/air are continuously supplied in the gas flow channel, the reactant gas species are transported through the gas supply channel, which could be regarded as a particularly porous media with porosity of 1.0 and in the scale of millimeters, a gas diffusion layer (in the scale of 100 μm), and a catalyst layer (in the scale of 10 μm). They then react at the surface of the catalyst, which also involves water transfer through the membrane (in the scale of 10~100 micrometer), and then they are expelled to the gas channel in the opposite direction. Low mass transfer, which has a significant impact on fuel cell performance, is generated by an inadequate supply of reaction gases in the electrochemical reaction and can lead to concentration overvoltage or mass transfer losses. Therefore, research on key areas of mass transfer processes, including mass transfer mechanisms and models, is beneficial to improve PEMFC performance and durability, especially in PEMFC porous media. In the study of relevant transport phenomena, there are also many processes that cannot be solved or decoupled experimentally, and researchers usually model these processes on a continuum, using numerical simulations to achieve understanding and insight into the transport processes [7].
In the case of more accurate model continuity modeling, there are cases where the model parameters are unknown, where they vary considerably with various operating conditions, and where required values of model parameters have not been referenced in the manufacturer’s data sheet. This problem of finding unknown model parameters is known as the “fuel cell model parameter identification problem”. The process of identification of parameters is a very complicated, indispensable, and hard task. In order to simplify the computational process, the problem of identifying fuel cell model parameters is reduced to a mathematical problem and solved by an optimization method [8]. There are various optimization methods, including artificial intelligence techniques, which have been adopted to identify the parameters of unknown PEM fuel cells models [9]. In research, the more accurate the model is, the more accurate the research results are by using appropriate identification methods to accurately identify these parameters, and thus system modeling is often combined with parameter identification.
This paper reviews the progress of research on PEMFC in multiscale porous-media mass transfer processes, starting with a review of modeling and simulation of the mass transfer process, including the main generalized control equations, different modeling approaches, and the different dominant mechanisms in mass transfer. In addition, research on fuel cell parameter identification is summarized, and future directions are analyzed in light of the parameter identification problem in modeling.
2. Modeling and Simulation of Mass Transfer
2.1. Basic Governing Equations
Models are the key to describe the internal mass transfer process of PEMFC. Based on Weber and Newman [10], the model of PEMFC can be described from the following five relationships: (1) the laws of conservation of mass, momentum, energy, species, and charge; (2) the relationships of the constitution of various fluxes; (3) the equations of the kinetics of electrochemical reactions; (4) balance relationships; and (5) supporting or auxiliary relationships, including the definition of variables (e.g., Faraday’s law). All of the relationships are closely related to material properties, empirical relationships, and experimental data [11]. At the level of mass transfer in porous media, physical equations based on the conservation laws of mass, momentum, energy, species, and charge are generally established to model PEMFC behavior in more detail on a continuum scale. In addition, some basic principles and relationships for fluid flow and mass transport are required. It is important to note that the physical properties of most models are similar and the basic physical equations are used in a general form; the differences lie in the scale of the model and the phenomenon under study, the treatment of the various transport properties, and the boundary conditions, and because of this, the equations become more complex [12]. Table 1 presents the basic control equations, including the conservation laws and well-known transport equations, where is the velocity vector, P is the pressure, ε is the porosity, which is determined by the dry porosity and water saturation of the electrode, ρ is the fluid density, μeff is the effective viscosity of the fluid, K is the permeability, T is the temperature, Yi the mass fraction, σs,eff is effective electronic conductivity, σe,eff is effective ionic conductivity, Φ is phase potential, and Deff is the effective diffusion coefficient. As mentioned earlier, in order to demonstrate the generality of the modeled phenomena concisely, the equations shown in the table represent a generalized form of the corresponding modeling approach and are not necessarily used as is.

Table 1.
Basic governing equations.
In general, the first term in the control equation denotes the time-varying properties and is ignored when describing steady-state operation, but the vast majority of PEMFC models do not consider only steady-state models. The term with an operator in the equation represents the change due to the flux into or out of the control section under study. S is called the source term and represents all the processes within the control section that lead to the generation or decay of the property. For example, an oversaturated gas phase can condense in the control section and lead to a decrease in the concentration of the gas phase and an increase in the concentration of the liquid phase. The law of conservation of mass uses Si to represent the rate of consumption of reactant gases such as hydrogen and oxygen, and the source term of mass to represent the transport of water [12]. For gas channels (porous media with a porosity of 1) and GDLs without a volumetric reaction zone, the source term is 0. In addition, the momentum conservation equation is highly coupled to the mass conservation equation. Newton's second law governs the conservation of momentum and can be expressed in terms of the Navier–Stokes (N–S) equations. Other methods for describing the flow of porous media are Darcy's law and Brinkmann's equations, and they can be simplified by the N–S equations without inertial and viscous force. The choice of the appropriate momentum equation for truly porous GDLs and CLs depends on the operating conditions of the fuel cell and the design of the GDL and CL regions. In the absence of bulk fluid motion or advective transport, the reaction gas can only be transported through the GDL and CL by diffusion mechanisms.
2.2. Mechanism of Mass Transfer
Mass species transport describes the movement of substances in the mixture and base fluids and solids. There are two basic types of mass transfer: one is diffusive and the other is convective. Both diffusive and convective mass transfer play an essential role in the transport of reactant gases through flow channels and membrane electrodes. The equation describing mass transfer is known as the transport rate equation and is closely related to and similar to the conservation equation for transport [13].
Diffusion is the transportation of substances caused by a gradient in their concentration, and it exists in any phase in a porous medium. The primary mechanism of gas diffusion is basically the collision between molecules of gases, such as GDL, CL, and flow channels. There are two main types of binary diffusion of substances (hydrogen and water vapor) and multi-component diffusion, and the main equation for calculating the diffusion flux can be expressed as:
where C is the concentration and D is the diffusion coefficient; in practice, the diffusion coefficients are all Fick diffusion coefficients. In binary diffusion the diffusion coefficient is represented by Dij, while multi-component diffusion requires the Maxwell–Stefan model. In addition, consider that the porous and tortuous flow structures of GDL and CL have a diffusion resistance, and corrected or effective diffusion coefficients based on porosity and tortuosity are used.
The above equation can therefore be simplified to:
Another gas diffusion mechanism occurs during CL transfer, considering the presence of small nanoscale pores: namely, Knudsen diffusion (, m2·s−1) due to the collision of gas molecules with the wall, expressed as:
where (m2·s−1) is the reference binary diffusion coefficient; T (K) is the local temperature; R (8314 J kmol−1·K−1) is the universal gas constant; Mi (kg kmol−1) is the molecular weight of gas species I; and d(m) is the pore size
The diffusion coefficient of CL is therefore related to the mechanism of collisions of gas molecules (binary diffusion coefficient , m2·s−1) and collisions of gas molecules with walls (Knudsen diffusion coefficient , m2·s−1), expressed as:
In summary, binary diffusion occurs in GDL, CL, and flow channels, and Knudsen diffusion occurs only in CL.
Convection is the overall movement of a fluid. In PEMFC, the convective force that dominates convective transport is the pressure at the inlet of the flow channel. High flow rates ensure good distribution of reactants (and effective water removal). The convective flow is expressed as:
where is the gas flow velocity. The flow of gas in porous media is calculated by Darcy’s law:
where P is the pressure, K is the permeability, and μ is the dynamic viscosity.
The flow in PEMFC can be predominantly diffusive, convective, or mixed. Figure 2 shows the flow mechanism in GDL when in different flow channel conditions. With the parallel flow channel design, the flow of reactants requires only a small amount of pressure and relatively uniform distribution of pressure within each channel, so the flow within the GDL may be predominantly diffusive. Serpentine flow channels require higher inlet pressures with larger pressure gradients and flow, so that flow can be both diffusion- and convection-based. Cross-finger flow channels in which all flow passes through the GDL have the highest pressure gradient in the flow channel, and therefore flow is predominantly convective in GDL [14].
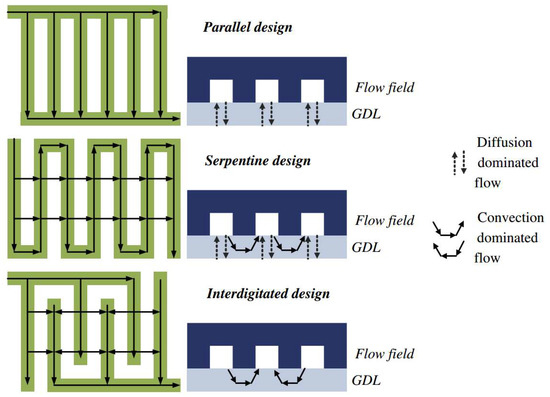
Figure 2.
Flow mechanism of GDL under different flow channel shapes [14].
Considering the transmission process of water within the membrane, the mechanism of water transmission due to electrical resistance is also present. The specific water flux is expressed as:
where nd is the EOD coefficient, which is related to the water content of the membrane, I (A·m−2) is the current density, and F (96,485 C·mol−1) is the Faraday constant. In summary, membrane behavior in mass transfer is described by calculating the membrane water content, water concentration, EOD coefficient, net water flux, and proton conductivity. Two-phase flow can also be calculated by calculating the liquid water saturation and the liquid water flux, involving a water phase change as a function of the molar fraction, partial pressure, and saturation pressure of the gas-phase water as a switching function. In addition, by coupling the mass transfer equation with the reaction kinetic equation (Butler–Volmer or Tafel equation), simulated I-V polarization curves can be constructed. A description of the transfer of species within the MEA is shown in Table 2, where R is the gas constant (J mol−1K−1); T is the temperature (K); z is the direction through the layer thickness; and the effective diffusivity () is the diffusivity corrected by the porosity (ε) and tortuosity (τ) of the porous structure (m2·s−1). xi and xj are the mole fractions of species i and j; Ji and Jj are the molar fluxes (mol m−2s−1); p is the total gas pressure (Pa); ηcathode is the cathode overvoltage (V); j0 and j are the reference and operating current densities (A·cm−2); the 4 in the denominator is the electron valence number for one O2 molecule; and α is the charge transfer coefficient. is the net water flux in the electrolyte membrane (mol m−2s−1); ndrag is the electro-osmotic drag coefficient; λ is the water content in the membrane; ρdry and Mm are the dry density (kg·m−3) and equivalent weight (kg·mol−1) of Nafion; and Dλ is the diffusivity of water. When these control equations are solved, the concentrations of different species, such as H2, O2, and H2O(g), can be obtained for different operating conditions.

Table 2.
Simplified governing equations based on MEA with different region assumptions [15].
2.3. PEMFC Modeling
Models are generally built from different dimensions and using different structures. At the structural level, there are mainly white box, gray box, and black box models, which will be described in Section 4 according to the arrangement of the article. At the dimensional level, model dimensions can be classified as zero-dimensional (0-D), one-dimensional (1-D), two-dimensional (2-D), and three-dimensional (3-D). High-dimensional models are better representations of reality but have correspondingly higher computational cost requirements. Lower dimensional models sacrifice some spatial fidelity but often take into account more complex physical properties. Due to the increase in computational power, more and more multidimensional models are being adopted, and the 1-D+M-D model framework would be a good choice. Figure 3a shows the various model dimensions and the main cell components.
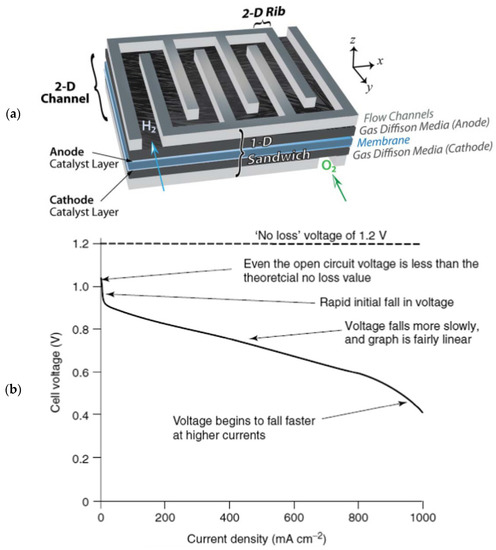
Figure 3.
(a) Schematic representation of different spatial domains and related modeling including PEMFC sandwich [12]; (b) typical polarization curve [16].
The zero-dimensional (0-D) model mainly considers system variables, such as voltage, current, temperature, and pressure, or uses simple empirical correlations without considering any other properties of the spatial domain; therefore, zero-dimensional models do not provide a basic understanding of PEMFC operation, and they have limited applicability in predicting performance or optimizing design under different operating conditions. [17] The typical 0-D model equation is an empirical model describing the polarization curve. The polarization curve diagram, shown in Figure 3b, is represented by the following model [18]:
where ENernst is the calculated open-circuit voltage from the Nernst formula, ignoring the voltage loss due to gas crossings, Vact is the activation overvoltage, Vohm is the ohmic overvoltage, and Vcon is the concentration overvoltage. The model calculates the activation loss, ohmic loss, and concentration loss on the polarization curve, and finally the limiting current due to concentration overpressure. It is worth mentioning that in practical applications, there are still several parameters of the model that need to be identified [18].
The one-dimensional (1-D) models are usually described as physical phenomena spanning one spatial dimension of the PEMFC and can be understood as mass transfer processes in a linear direction. This typically includes electrochemical reactions at porous electrodes, transport of gas and liquid species through porous media, primarily membrane electrode components, and charge transfer processes. In addition to this, one-dimensional models along flow channels focus on the transport and consumption of gases and their influence on the current density [19].
The two-dimensional (2-D) model combines another direction (through or along the channel) on top of the 1-D model, so that the 2-D model can be understood as a mass transfer process in the direction of a face. The cross-channel model is concerned with the cross-section of the gas channel, including the ribs and channels. This method solves the problem that the influence of solid ribs and channels on the distribution of electrons and water in the mass transfer process can be solved. The two-dimensional model along the channel includes the effects of reaction gas consumption and water accumulation generation on the current distribution along the channel and within the cell sandwich. The overall two-dimensional model can therefore predict the distribution of water, temperature, and reaction components within the PEMFC.
The three-dimensional (3-D) models, on the other hand, describe the complete real structure, and with increased computational power, such complex numerical modeling can be achieved. The 3-D models are mainly able to show the distribution of the full three-dimensional space in three dimensions, which helps to improve our overall understanding of the PEMFC operation, but it is clear that a significant computational cost is needed to realize the fully numerical simulation of PEMFC. Therefore, as in references [20,21], utilizing a 1-D+3-D numerical model structure for PEMFC may be the best trade-off between computational cost and model fidelity.
Although the above classification tends towards macroscopic-scale modeling, similar descriptions can be made at microscopic scales.
2.4. PEMFC Simulation
Proton exchange membrane fuel cell models are generally expressed based on the conservation law of mass, momentum, energy, type, and charge, and their basic governing equations are shown in Table 2. The design of the flow field is very important in the study of mass transfer. Ahmed and Sung [22] numerically studied the influence of flow field configuration on battery performance. The local transport characteristics of PEM fuel cells with interfingered gas channel, non-uniform gas channel, and inner baffle are numerically studied, and compared with corresponding straight gas channel fuel cells. The governing equations for modeling and numerical simulation are mainly the mass conservation equation, momentum transport equation, mass transport equation, and energy equation. Shen et al. [23] introduced the field synergy principle based on the enhanced mass transfer theory and applied it to flow channel design. In terms of water management issues related to gas channel mass transfer, Mondal et al. [24] used the three-dimensional computational fluid dynamics (CFD) method combined with the isothermal volume of fluid (VOF) method to track the liquid–gas interface and studied the influence of surface wettability and inlet air velocity on water droplet movement in the flow channel of PEM fuel cells' hydrophilic surfaces. The results show that the droplet motion velocity increases by increasing the air velocity and hydrophilic surface contact angle because of the small liquid wall contact area.
In terms of modeling the gas diffusion layer, as early as 1999, Wang et al. [25] developed a multiphase flow model for PEMFC porous electrodes on a continuum scale based on Darcy's law, but the model used the capillary pressure–saturation Pc–S relationship for two-phase flow in GDL. Because of the lack of an accurate representation of the GDL Pc–S relationship at that time, the Leverett–Udell function was obtained by the current conventional use of homogeneous sand filler [26]. There are many problems with this continuous-scale GDL model, the first of which is the Leverett–Udell function inaccuracy [27]. As a result, researchers began to employ pore-scale studies to better understand the multiphase flows and mass transport within GDL.
In terms of modeling the catalyst layer, it has been reported that there are three commonly used models to describe the electrochemical kinetics of the catalytic layer. The first model is the thin film model [28]. Since the layer of catalyst is much smaller than the thickness of the gas diffusion layer, the simplest description of the catalyst layer is the interface model, which assumes that the catalyst layer is only the interface and does not consider the internal material transport processes. The second is the discrete catalyst model [29], in which the catalyst layer is composed of multiple layers without considering the transport of oxygen through its internal isomerized phases. The third is the agglomeration model [30], which considers the transport process and agglomeration structure of oxygen in the ionomer phase. The true CL thickness is about 10~30 μm, the porosity is about 0.3~0.6, the size of carbon particles is about 20~50 nm, and the carbon aggregates are further formed about 100~600 nm. The thin ionomer film covering the C/Pt surface is typically of several nanometers in thickness [31]. Modeling of the catalyst layer is mainly concerned with CL reconstruction, which has been reported in relevant technical references [32].
As for research on membranes, as early as 1991, Springer et al. [28] numerically studied the mechanism of water transport through membranes and its effect on transport processes. Furthermore, He et al. [33] systematically studied the three-dimensional, multiphysics, mixed-domain model of two-phase transport for PEMFC and an efficient numerical calculation method for it. The three phases of vapor, water in liquid state, and water in the membrane phase are properly explained, enabling numerical studies of water management problems in the presence of condensation/evaporation.
3. Fuel Cell Mass Transfer Research
3.1. In Gas Channels
The mass transfer process and water management in gas channels (GC) are important problems in the study of PEMFC. Figure 4a is a diagram of the fuel cell assembly composition showing the flow path location and the conventional snake flow path. For mass transfer processes, flow field design is an important problem, which greatly affects the reactant/product mass transport process and battery performance. At present, most research is mainly on designing the structure of the flow field and striving for the optimal mass transfer effect. In Afshari’s [34] research, the use of foam metal as a flow field resulted in an improvement in the performance of PEMFC by making the temperature, the gaseous reactants, and the current density distribution more uniform as well as by reducing the mass in the channel and the processing cost. Numerical results based on losses by Yang et al. [35] found that the molar concentration distribution of oxygen at the interface between the catalyst layer and the gas diffusion layer on the cathode side of the M-like channel is more uniform and larger than that of the conventional parallel channel. As a result, more reactants can be involved in the electrochemical reaction at the catalyst layer, which enhances PEMFC performance. Compared with a parallel channel, an M-like channel has better mass transfer performance and comprehensive performance without high voltage drop. In practical applications, optimal obstacle heights and widths were obtained, and performance was improved by 16% over parallel channels. Figure 4b,c shows the characteristic geometric parameters of the bipolar plate and the flow field of an M-like flow field. Qiu et al. [36] provides a three-dimensional air-cooled fuel cell model considering electrochemical simulation to investigate the effect of cathode channel design. Lei et al. [33] proposed three new channels (models 1, 2, and 3) created using two unilateral ramps and one bilateral ramp structure with cone tube lengths of 0.4, 1.2, and 0.8 mm, respectively. Flow channel geometry of the bipolar plate has an important effect with respect to the performance of the PEMFC. In view of this, Wan et al. [37] investigated the optimization of a straight channel flow field by pursuing the minimum entropy yield. Bao et al. [38] reconstructed a three-dimensional flow field morphology based on optical microscope images, and discussed single-phase and two-phase flow characteristics. Recently, a flow field of PEMFC with three-dimensional structures has attracted much attention due to its advantages in mass transmission and water management. One of the most represented is the three-dimensional fine mesh flow field (3D flow field). It is found that the air-guiding effect of a three-dimensional baffle is conducive to the transport of the reactants. At the same time, the liquid–gas separation migration phenomenon was observed, which reduced the liquid covering area on the surface of the gas diffusion layer and provided a larger channel area for mass transfer. In addition, the effects of inlet velocity, droplet size, and baffle contact angle on atomization effect were also discussed. It was found that unless the air velocity was too low, the droplets tended to overcome surface tension and move above the baffle. The water retention capacity of the three-dimensional flow field is limited, which is affected by the wind speed and the contact angle of the baffle. In addition, the three-dimensional baffle's superhydrophobic or superhydrophilic surface may also pose a problem for water management.
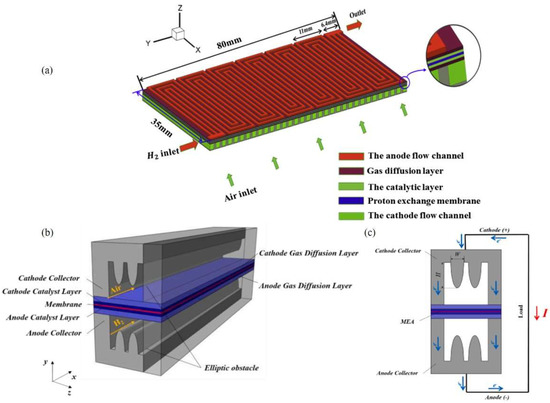
Figure 4.
(a) Fuel cell assembly composition schematic and conventional serpentine flow path [33]. (b) Bipolar plate structure with M-like flow field. (c) Characteristic geometric parameters of M-like flow field and schematic diagram of PEMFC current transmission [34].
In terms of water management, Shen et al. [39] explained in detail the importance of fuel cell water management, especially downstream water management. Fontana et al. [40] numerically investigated the transport of liquid water in the conical gas channel of a PEM fuel cell using a two-dimensional dynamic isothermal model. They observed that liquid water is distributed and transported in the channel depending on the velocity of air. In the vicinity of the channel outlet, because of the high velocity of the gas, a liquid film is formed at the surface of the GDL. In contrast, segment plugs form from the slope of the channel bottom wall, preventing the accumulation of liquid water through the middle of the channel and near the entrance of the channel. The segment plug is the primary drainage mechanism. As the segment plug moves to the channel outlet, it removes adhering droplets, which helps reduce water saturation in the channel, but this results in an additional pressure drop. Qin et al. [41] numerically investigated the water removal and transport processes in the isothermal three-dimensional flow channel of the intermediate hydrophilic plate of a PEM fuel cell using the VOF method. They found that liquid water droplets can be effectively removed from the MEA surface due to the presence of hydrophilic plates, and that once separated from the MEA surface, the liquid water droplets are transported downstream without blocking the reactant gas delivered to the MEA. Wettability, length, and plate height all affect water transport and kinetics and the associated pressure drop in the gas channel. Wettability is expressed as the contact angle of the droplets at the wall. The inclination of a short plate produces a peak pressure drop, while the inclination of a long plate produces a larger pressure drop in the flow channel. The pressure drop is also related to mass transfer. Shen et al. [42] proposed a new efficiency evaluation criterion (EEC) based on the Sherwood number and Euler number to evaluate the relationship between mass transfer and pressure drop. The performance of PEMFC mainly depends on the interaction of mass transfer and reaction. Pan et al. [43] fully revealed these interactions through a "flow field analysis scheme" combining an analysis of theoretical and numerical simulations. There is a relatively comprehensive analysis of the flow field of the gas channel in reference [7]. Other influential works include Barati et al. [44].
3.2. In Gas Diffusion Layers
The GDL provides mechanical support for the CL and transports the reactants and products to and from the CL. The structure and mass transfer process are shown in Figure 5a,b. It also plays a crucial role in heat transmission and water management. The generally used GDL is a porous carbon-fiber-based media with typical diameters of 6~10 μm, with a GDL thickness of 100~300 μm, a porosity of 0.6~0.9, and a pore scale of 10~100 μm [45]. Numerical studies on a large number of pore scales have mostly been performed with the lattice Boltzmann method (LBM). For example, Hao and Cheng [46] investigated the anisotropic permeability of a carbon paper GDL in a PEMFC with multiple reflective solid boundary conditions using a multi-relaxation LBM. Boltzmann's simulation results are shown in Figure 5c. It is found that the in-plane permeability of a carbon fiber GDL is higher than that of through-plane permeability due to its layered structure. The calculated values of permeability are in agreement with the measured values. Some fitting constants were determined by fitting empirical equations for the relationship between permeability and porosity. Based on the pore-scale flow field, the bending degree was calculated. In addition, the relationship between bending degree and porosity is applied to the fractal model of permeability. Yang et al. [47] used a 2-D LBM model to simulate the liquid–liquid process of water transport in a real GDL (considering porosity distribution) and an ideal GDL (neglecting porosity distribution), respectively. The water saturation in real and ideal GDLs is shown in Figure 5d. It was found that the local low-porosity region would significantly influence the transport of water in liquid form in the actual GDL. In the actual GDL, the liquid water saturation limit can be noted with a contact angle of approximately 118°. The porosity distribution of GDLs has a greater influence on hydrodynamics than hydrophobicity, and this needs to be considered in future GDL modeling and design. Chen et al. [48] first analyzed the driving force affecting the droplets on the surface of a gas diffusion layer and found that with the increase of Reynolds number, the influence of the Forchheimer inertia force becomes non-negligible. In addition, an improved two-fluid model is used to study the distribution of liquid water saturation. When considering the influence of the Forchheimer inertia force, the liquid water saturation in the flow channel, gas diffusion layer, and catalyst layer with the flow channel is reduced by 5.69%, 5.56%, and 4.22%, respectively, compared with the results of the traditional two-fluid model. Zhao et al. [49] have investigated the impact of GDL on the operation of AO-LTPEMFC under harsh atmospheric conditions. The effects of PTFE on substrate layers and microporous layer content, microporous layer thickness, and fan pulse width modulation on cell performance and cathode outlet surface temperature distribution were investigated. Yang et al. [50] focus on four key issues of microporous layers (MPL), namely porosity, pore size distribution, wettability, structural design, and durability. Other influential work includes Wijayanti et al. [51].
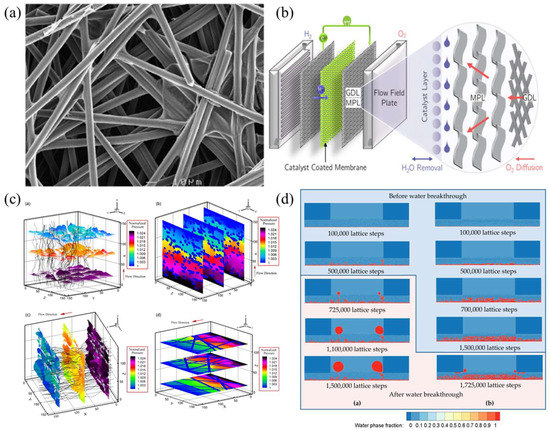
Figure 5.
(a) SEM image of the gas diffusion layer of Toray 060 [46]; (b) schematic diagram of PEMFC and cathode mass transfer process [50]; (c) results of lattice Boltzmann simulations of single-phase flow in a three-dimensional carbon paper GDL, where (a) the velocity and streamline of the flow through the plane. (b) pressure contour of straight-through plane flow. (c) velocity and streamline of flow in the plane. (d) pressure contour of flow in the plane. [46]; (d) ideal GDL (a) and water saturation of actual GDL (b) [47].
3.3. In Catalyst Layers
The catalyst layer (CL) is the site of electrochemical reactions in a fuel cell, and it has many components. It is roughly composed of Pt as a catalyst, a carbon carrier for electron conduction, Nafion ionomer for proton migration, reaction gas, and liquid water, as shown in Figure 6 [31]. Xie et al. [52] reviewed the composition, function, and structure of the CL of an PEMFC. Due to the particularity of the CL, it is a challenge to simulate it accurately. At present, the forefront research of the catalytic layer is to reduce the Pt load, thus saving the cost of PEMFC. Now the mainstream strategy is material innovation. Recently, several reports have shown promising results, especially for cathodes, since promoting oxygen-reduction reactions (ORRs) is essential to reduce the use of Pt in PEMFC. For example, Perng et al. [53] assumed that the catalyst layer was an ultra-thin layer in their study, and used the same composition of the prominent catalyst layer surface on the cathode half-cell of PEMFC to conduct a numerical study on the enhancement of cell performance. The results show that the catalyst layer surface can effectively improve the local cell performance of PEMFC. Chong et al. [54] proposed a co-catalytic method between a core–shell Pt–Co alloy and an Orr-active zeolite imidazole acid skeleton-derived carbon group, which provided 1.08 A mg Pt −1 ORR mass activity in a single cell test; relevant catalyst structure information is shown in Figure 7a. In addition, doped graphene-based cathode catalysts are considered potential competitors for ORR, but have a lower power density compared to Pt-based cathodes, mainly due to their poor mass transport performance. Marinoiu et al. [55] prepared, characterized, and tested a novel electrocatalyst for PEMFC, iodine-doped graphene, and compared it with a typical Pt/C cathode structure. The results show that it increases the electrochemical active area and enhances the mass transfer performance. Scanning electron microscopy (SEM) of iodine-doped graphene nanocomposites is shown in Figure 7b. The performance of carbon nanotubes as catalyst carriers is superior to that of carbon carriers, while the prominent catalytic activity of one-dimensional Pt nanostructures gives them great potential for application in fuel cells. Mardle et al. [56] demonstrated Pt nanorod catalyst electrodes grown on aligned nitrogen-doped carbon nanotubes for PEMFC applications. In this work, Pt nanorod catalyst electrodes grown on aligned nitrogen-doped carbon nanotubes are demonstrated for PEMFC applications. The results show that the nanorods have good durability, which is mainly due to the good structural stability of the nanorods and the enhancement of the N-carbon nanotube carrier.
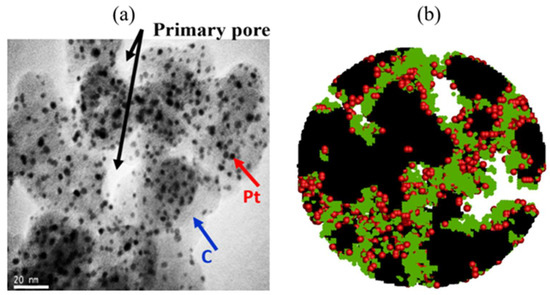
Figure 6.
(a) Transmission electron micrograph of the CL in PEMFC. (b) The reconstructed structure of CL. The black part indicates carbon, the red particles indicate Pt particles, and the green part is the ionomer [31].
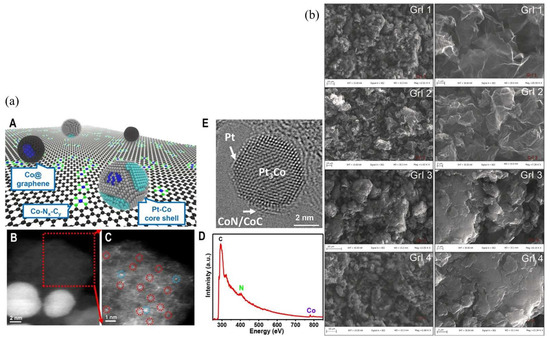
Figure 7.
(a) LP@PF catalyst structure [54], where (A) The schematic diagram of LP@PF shows that Pt-Co NPs, Co@graphene, and Co-N4-C coexist without pgm active sites, (B) HAADF-STEM image of Pt-Co NPs located at LP@PF-1, (C) Pgm-free carrier containing atomically dispersed Co(red circle) and trace Pt(blue circle), (D) EELS analysis of constituent elements in (C), (E) HRTEM image of representative Pt-Co alloy NP with Pt3Co superlattice core and Pt skin partially covered by CoN/CoC terrace.; (b) scanning electron microscopy analysis of iodine-doped graphene nanocomposites to determine the effect of reaction conditions on the morphology of iodine-doped graphene [55].
Another strategy is to optimize the structure of the transmission process. The optimal design of the CL and interlayer interface structure is helpful to improve the utilization rate of Pt, reduce mass transfer loss, and achieve high-performance output of MEA with low Pt load. It is worth noting that the influence of the polyphase transfer process becomes particularly important in the high-current operation of MEA, and the Pt content in the cathode catalyst layer (CCL) drops sharply. The new study shows that the local O2 transport resistance increases dramatically if the Pt loading in the cathode is reduced from 0.4 mg cm−2 to less than 0.1 mg cm−2. This is due to the fact that the active Pt sites are reduced to one-fourth while the current output remains constant, resulting in a transient water yield per Pt site that will be four times higher than before. A large amount of excess water causes microscale "flooding" at the active Pt sites and greatly inhibits local gas transport, leading to a reduction in the limiting current [15]. The pore-scale transport process in the CL was first studied by Wang et al. [57,58], who reconstructed the regular microstructure of the CL, but there were only two components: one was void space and the other was a mixture of electrolyte, carbon, and Pt. The reaction transport process of an ideal CL under different porosity, current density, and CL thickness was numerically studied by using FVM. Such a two-component structure simplifies the complexity of CL structure and is not realistic enough. Some new techniques and methods have been proposed to reconstruct more detailed CL structures. The technique of reconstructing CL structures has been reported in detail in reference [31]. Chen et al. [59] emphatically introduced the importance of the combination design strategy of catalyst layer structures and interlayer structures, and briefly discussed its future development prospects. Other influential work includes Sievers et al. [60].
In conclusion, the speedy development of the recent past suggests that Pt consumption and cost might not be the main obstacles for commercial PEMFC in the sustainable and foreseeable future.
3.4. In Membranes
The water transfer process of membranes is mainly through electric drag force and reverse osmosis. The migration of ions and water is highly coupled. The transport of ions in the proton exchange membrane is not only dependent on water, but also controlled by the nature of water, the interaction of water with the SO3-site in the PFSA, the length and hydrophilicity of the side chains, and the segmental motion of the polymer chains; thus the mesoscale transport network is defined, as shown in Figure 8 [61]. The transport of protons is mainly achieved through the water contained in the membrane and the electric field formed by the electrode. Therefore, the proton conductivity of the membrane is largely dependent on its water content and has a significant impact on cell performance. In addition, membrane hydration is critical for reducing resistivity and ohmic losses in fuel cells. External humidification is often performed at the cathode entrance when the reaction water is insufficient to achieve adequate membrane hydration. However, this causes excess water to build up, which leads to flooding in the CL and leads to a reduction in the active site and a drop in voltage in the reaction region.
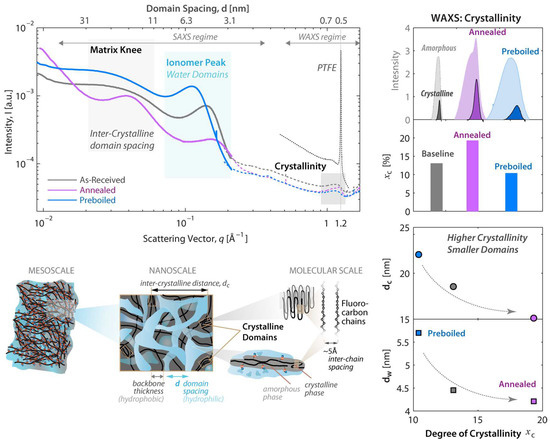
Figure 8.
Nafion scattering: typical SAXS/WAXS profiles of Nafion films in liquefied water at room temperature in AsR (baseline), pre-boiled, and annealed forms. The WAXS peaks in the amorphous and crystalline phases and their characteristic peaks are also shown. The following schematic illustrates the length scales [61].
In terms of membrane research, it is mainly in membrane hydration. Kim et al. [62] found that proper reactant humidification improved membrane hydration and proper stoichiometry increased liquid water removal. They investigated the influence of relative humidity (RH) and the stoichiometry of reactants on water saturation and the local transport processes in PEMFC. The results show that reactant RH and stoichiometry have significant effects on battery performance. Higher anode stoichiometry can enhance fuel cell performance by reducing cathode water saturation through increased water back diffusion. Higher cathode stoichiometry also reduces water saturation and dries more liquid water to increase the local cathode current density. The water state of the membrane has a great impact on the battery performance, so water management is very important, and it also requires timely diagnosis of water faults. In Ren et al. [63], according to the sensitivity of zero-phase ohm resistance to membrane dehydration, a zero-phase ohm resistance measurement method based on impedance was proposed. By adjusting the measurement frequency, the impedance points were limited within the sampling limit range of ±3°, thus ensuring a measurement accuracy of 0.01 mΩ. This provides sufficient information for water fault diagnosis of fuel cells, which is of great significance for fault avoidance and life extension of fuel cells. The most commonly used PEM currently is the Nafion membrane, which shows great proton conductance (σ = 10−1−10−2 S cm−1) at 60–80 °C and 98% relative humidity (RH); however, due to poor thermal stability, dangerous manufacturing process, and high cost, it faces great challenges in large-scale practical application. So far, these inherent flaws have not been solved. Researchers have also been working on developing new PEM models: for example, modified Nafion, various polymers, and composite membranes. Zhang et al. [64] combined polymer with a high-proton-conducting metal-organic skeleton (MOF) to make high-performance PEMs. In the study, it was demonstrated that MOF-801 exhibits significant proton conductance of σ = 1.88 × 10−3 S cm−1 at 298 K and 98% RH, especially with additional stability for hydrochloric acid or diluted sodium hydroxide aqueous solutions and boiling water. In addition, composite membranes (denoted as MOF-801@PP-X, where X represents the mass percentage of MOF-801 in the membrane) were prepared by blending submicron crystal particles of MOF-801 with a polyvinylidene vinylpyrrolidone matrix. These PEMs have high proton conductivity: at 325 K, 98% RH, σ = 1.84 × 10−3 S cm−1. Testing of PEMs as composite membranes in hydrogen fuel cells shows that these membrane materials have great potential for use in PEMs. Song et al. [65] developed a novel porous packed PEM in which a partially fluorinated ionomer with a high crosslinked density is bound to a porous polytetrafluoroethylene (PTFE) substrate.
4. Research Progress of Parameter Identification
Many fields need parameter identification. For applications of PEMFC, a complete system model is often established based on a mechanism or experience, and then the key parameters of the model are identified and determined using appropriate identification methods. The first requirement is for a model to be accurate; commonly used modeling methods have white box, gray box, or black box models. The white box model can be regarded as a different degree of engineering evolution of the Navier–Stokes equation. The gray box model is a semi-physical and semi-empirical model based on experience. The black box model is established according to input and output data, which have nothing to do with the physical mechanism. It is a data-driven modeling method, which has a strong difference ability but ordinary epitaxial performance [66].
In addition to making the model as accurate as possible, the identification of model parameters is another difficult problem in accurate modeling. Different kinds of modeling lead to different parameter identification methods. Among the three modeling methods, parameter identification of whole system models is found more in the related literature, but key parameter identification of a specific object is found less. It should be mentioned that parameter identification corresponding to the black box model is often used to identify the whole system, not just parameters.
4.1. Parameter Identification Is Used for Global Models
Generally, different identification methods for the parameters of PEMFC system models are adopted according to various modeling approaches. However, in addition to the distinction between mechanisms and empirical models, there is also the distinction between dynamic and steady state.
4.1.1. Dynamic State
The dynamic model mainly serves the control aspect. It contains a differential equation in fuel cell modeling, which is difficult to solve by the general identification method. For fuel cells, the real models that can describe physical and electrochemical phenomena are largely differential equations. More importantly, many states in these differential equations are unmeasurable. Both traditional methods based on derivation (such as the fastest descent method, Gauss–Newton method, and Levenberg–Marquardt method) and bionic algorithms are basically ineffective. In this regard, reference [51] first proposed a solution to this problem in a thermal management system, aiming at the identification of unknown parameters with unmeasurable states in the differential equation in the model. The main algorithm flow is shown in Figure 9. In addition, it is worth mentioning another class of semi-empirical methods based on data drive. For example, Li et al. [67] established a relatively comprehensive nine-state model of a fuel cell system, identified its physical parameters, and proposed identification methods for key parameters such as a data-driven stack throttling coefficient and motor voltage change rate considering time delay. The modeling of this process also involved differential equations, and the ultimate goal was to serve the dynamic model.
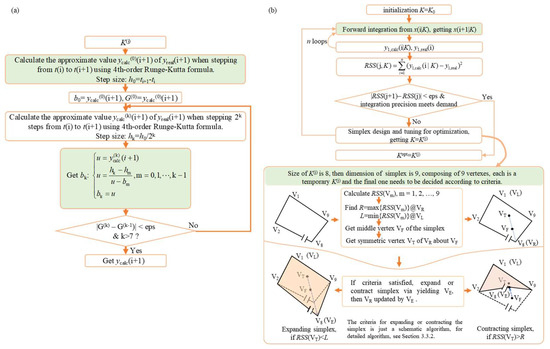
Figure 9.
Schematic diagram of identification algorithm for unknown parameters with unmeasurable state in model differential equations, (a) flow chart of step integration with continued fractions, (b) flow chart of simplex tuning identification algorithm [66].
4.1.2. Steady State
The steady state model is, in fact, the generalized electrochemical model, which is essentially the voltage model of the stack. Although there are many modeling methods, the gray box model developed by Amphlett [68] is accepted for its similarity in predicting the behavior of PEMFC with various operating conditions, where most of the modeling methods reported in the literature are originated. Unlike the white box, such models try to simulate the thermal, mass, and electrochemical phenomena that take place in the stack as a whole. In fact, they predict the effect of different input parameter variations on the volt–current (V–I) characteristics of a fuel cell, but do not have an in-depth understanding of the physical and electrochemical phenomena. Because of this, the stack voltage model can be more convenient to analyze the performance of PEMFC in different working conditions. The complex nature of PEMFC systems makes it difficult to model and describe their performance perfectly from the mechanisms and empirical perspectives. Therefore, the black box model based on data and artificial intelligence (AI) and other methods has also become a choice for PEMFC modeling. System modeling based on artificial neural networks and related robust control is described in the literature [69,70,71].
The key problem of these two modeling methods is that they cannot obtain accurate fuel cell model parameters. With the development of technology, in addition to the traditional gradient algorithm, there are a variety of artificial intelligence/meta-heuristic methods applied to fuel cell parameter estimation. No matter whether the parameter identification is based on traditional derivative methods or on artificial intelligence/meta-heuristic methods, the identification model is still the generalized steady-state electrochemical model (GSSEM). The main model is shown in Formula (13), and there are seven parameters identified: [ξ1, ξ2, ξ3, ξ4, λ, Rc, β]. Currently, the identification of such models mostly uses meta-heuristic search methods, such as genetic algorithm (GA), differential evolution (DE), and particle swarm optimization (PSO) [72]. The algorithm flow chart is shown in Figure 10.
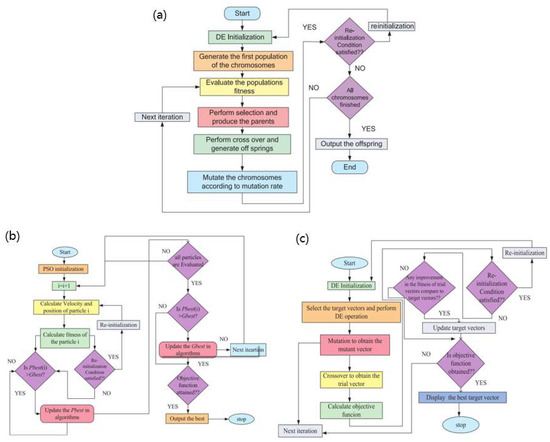
Figure 10.
(a) Flow chart of genetic (GA) algorithm, (b) Flow chart of differential evolution (DE) algorithm, and (c) Flow chart of particle swarm optimization (PSO) algorithm [8].
Traditional derivative methods are also combined with AI for identification. For example, Yang et al. [73] proposed a Levenberg–Marquardt back propagation (LMBP) algorithm for PEMFC parameter identification based on ANNs. See Figure 11 for relevant content. Deng et al. [74] proposed a novel identification method based on nonlinear subspace to model the linear parameter variation of the PEMFC system, and a subspace identification method based on the kernel method was used to identify the PEMFC system’s parameter matrix. Tao et al. [75] used the artificial neural network method to establish a nonlinear system model, taking the flow rate of air (or oxygen) and the operating temperature of the battery as inputs, the voltage and current density of the fuel cell as outputs, and using the Levenberg–Marquardt BP (LMBP) method to identify the whole system. Razmjooy et al. [76] proposed an improved hybrid wavelet neural network for system identification and adopted a hybrid wavelet neural network based on a gravity search algorithm for identification. Hatti et al. [77] and Rezazadeh A et al. [78] also used neural networks for identification.
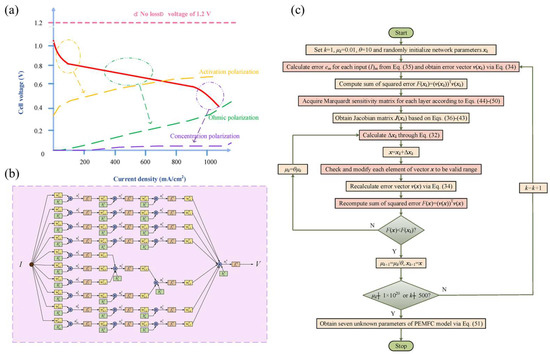
Figure 11.
(a) Polarization curve of PEMFC; (b) the overall structure of neural network PEMFC; (c) overall flow chart of LMBP-based PEMFC parameter identification [73].
In addition, in terms of parameter identification of the meta-heuristic method, Bao et al. [79] proposed the improved monarch optimization algorithm to optimize the parameter selection of the PEMFC voltage model and validated it with 6 kW and 2 kW stacks, respectively. The results are compared with the experimental data and some famous meta-heuristic algorithms (the Chaotic Grasshopper optimization algorithm (CGOA), the grass fiber root optimization algorithm (GRA), and basic monarch butterfly optimization (MBO)), which show the superiority of the proposed method over the comparison method. Salim et al. [80] proposed an off-line parameter identification method based on particle swarm optimization (PSO) for mathematical modeling parameters of a Nexa 1.2kW PEMFC system, and the PEMFC system model obtained by this method was relatively simple and without complicated mathematical formulae. To improve the inherent defects of the particle swarm optimization algorithm (PSO), Li et al. [81] established a PEMFC voltage model based on electrochemistry and proposed an EIA-PSO method based on parameter identification technology. Ahmed et al. [82] used a hybrid vortex search algorithm and differential evolution algorithm to identify optimal parameters of PEMFC. In addition, there are also the improved Crow Search optimizer (ICSO) by Duan et al. [83], the improved hybrid adaptive differential evolution algorithm (HADE) by Sun et al. [18], the two-stage eagle strategy method based on the JAYA algorithm and the Nelder–Mead simplex method by Xu et al. [84], and the improved and developed Artificial Ecosystem Optimizer (IAEO) and other parameter identification method based on optimization methods by Rizk-Allah et al. [9].
4.2. Parameter Identification Is Used for Concrete Objects
Limited by the difficulty of experimental design, there are few articles on parameter identification of each component. Most of the literature on parameter identification is aimed at the whole system. In the field of a specific component, there are not too many articles on the identification of specific objects, and the methods used are described in Section 4.1. However, in addition to the new algorithm, electrochemical impedance spectroscopy and the least-squares method are used to identify specific parameters. Through a lot of data calculation and fitting, a specific parameter value is obtained. For example, Kheirmand et al. [85] used electrochemical impedance spectroscopy analysis to identify parameters of a PEMFC catalyst layer and proposed a finite transmission line of a proton exchange membrane fuel cell reaction layer, in which there was no Faraday current due to the purging of inert gas at the rear of cathode and anode. When charge transfer occurs at the interface between catalyst and electrolyte, a finite transmission line is generated. The electrochemical impedance of the finite transmission line is calculated by MATLAB software. According to the order and type of impedance measured, the relationship to determine and identify the parameters of the model is derived.
Many numerical models have been generated to describe and analyze the internal processes of PEMFC, and the precise identification of many parameters in the models is essential for more accurate prediction of internal physical and electrochemical phenomena. Haslinger et al. [86] demonstrated quasi-3D PEMFC model parameterization using a measurement and numerical optimization algorithm for a stacked experimental bench. Differential evolution and Nelder–Mead simplex algorithms were used to optimize eight material parameters for the membrane, CCL, and GDL. These data will be available for more verified CFD simulations in the future. Measurements were performed at variable operating temperatures and gas inlet pressures to optimize and validate. Because of the lower operating temperature of the stacks, the temperatures related to the control formula were given special attention. Simulation results after optimization of parameters predict the steady-state and transient behavior of the system.
5. Conclusions
This paper reviews the research progress of PEMFC in multiscale porous-media mass transfer and related parameter identification. Firstly, the simplified governing equation for mass transfer of PEMFC is described. The transport characteristics and research progress of GC, GDL, CL, and membranes are discussed on a multiscale. For the nonlinear, multivariate, and strongly coupled characteristics of PEMFC, the characteristic models of PEMFC and the application of various artificial intelligence/meta-heuristic methods in fuel cell parameter identification are described and discussed. The review will help researchers and engineers in the field of fuel cell systems.
The design of the gas channel is an important problem, which greatly affects the mass transport process of reactants/products in fuel cells. Especially for proton exchange membrane fuel cells, reasonable flow field design is particularly important because of the water balance problem. Most studies are focused on the cathode flow channel, and the influence of the flow channel structure on the transport process is analyzed numerically to improve the oxygen quality and the transport process of water discharge. The results of many studies have certain guiding significance for the design and manufacture of fuel cells. The gaseous diffusion layer also plays a crucial role in heat transfer and water management. The GDL model of continuous-scale multiphase flow of PEMFC porous electrodes based on an extended Darcy's law, which has been commonly used at present, is not accurate. As a result, researchers began to employ pore-scale studies to better understand the multiphase flows and mass transport within the GDL. In a large number of pore-scale numerical studies, most of them are carried out by the LBM. There are optimized thickness and porosity combinations for better fuel cell performance. Cutting-edge research in the catalyst layer will reduce Pt load and thus save PEMFC cost. The prevailing strategies are material innovation and structural optimization of the transmission process. Several reports show promising results, especially for cathodes, since promoting ORR is essential to reduce the use of Pt in PEMFC. Doped graphene-based cathode catalysts are considered potential competitors for ORR. Iodo-doped graphene has a larger electrochemically active area and better mass transfer performance when compared with typical Pt/C cathode structures. The surface of the catalyst layer can also effectively improve the local cell performance of PEMFC. The optimal design of the catalyst layer and interlayer interface structure is helpful to improve the utilization rate of Pt, reduce mass transfer loss, and achieve a high performance output of low-Pt-load membrane electrode assembly (MEA). In conclusion, recent rapid developments indicate that Pt consumption and cost may no longer be the major obstacles to the commercialization of PEMFC in the foreseeable future. Membrane hydration is a very important process; the most commonly used PEM is Nafion membrane, but from the perspective of basic and applied research, exploring new applicable PEMs is still frontier research, and there is also a lot of research committed to the development of new PEMs. For example, this includes modified Nafion, various polymers, and composite membranes. This is because, so far, the inherent defects of poor thermal stability, dangerous manufacturing processes, and high cost have not been solved. Therefore, the search for proton conductance with: (1) good (σ = 1.0 × 10−4 S cm−1), (2) potential alternative membranes with excellent thermal and chemical stability in acidic and aqueous environments, (3) good mechanical properties, and (4) low-cost production and simple preparation processes are critical.
With the wide application of PEMFC, people have higher and higher requirements for PEMFC characteristics. More accurate parameter identification is becoming more and more important for models. From traditional derivative methods to artificial intelligence/meta-heuristic methods, fuel cell parameter identification becomes more and more exciting. In the fuel cell parameter extraction problem, it is very important to choose the appropriate recognition method according to different parameters to improve recognition accuracy. Therefore, the appropriate objective function should be selected according to the application situation. The meta-heuristic optimization algorithm has been widely used in PEMFC parameter identification, which highlights the good performance of the meta-heuristic method. Most of what has been identified, however, focuses on the generalized steady-state electrochemical model (GSSEM). The key parameters in specific objects, such as the catalytic layer, gas diffusion layer, and other key parameters in the design of the flow channel optimization methods are still relatively few. However, all the applied optimization techniques try to significantly reduce the relative error between the experimental data and the calculated data. Therefore, the problem of parameter identification can also be extended to other improved PEMFC models. It can be seen that, in the future, the optimization idea of parameter identification can be considered to optimize the design of the structure.
Author Contributions
F.Y.: conceptualization, investigation, writing—original draft, and writing—review and editing. X.X.: conceptualization, investigation, writing—original draft, and writing—review and editing. Y.L.: conceptualization, investigation, writing—original draft, and writing—review and editing. D.C.: writing—original draft preparation and writing—review and editing. S.H.: writing—original draft preparation and writing—review and editing. Z.H.: writing—original draft preparation and writing—review and editing. Y.D.: writing—original draft preparation and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (NO.22005026), and the Fundamental Research Funds for the Central Universities (NO.00007711).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, D.; Pei, P.; Li, Y.; Ren, P.; Meng, Y.; Song, X.; Wu, Z. Proton exchange membrane fuel cell stack consistency: Evaluation methods, influencing factors, membrane electrode assembly parameters and improvement measures. Energy Convers. Manag. 2022, 261, 115651. [Google Scholar] [CrossRef]
- Hu, S.; Guo, B.; Ding, S.; Yang, F.; Dang, J.; Liu, B.; Gu, J.; Ma, J.; Ouyang, M. A comprehensive review of alkaline water electrolysis mathematical modeling. Appl. Energy 2022, 327, 120099. [Google Scholar] [CrossRef]
- Ding, S.; Guo, B.; Hu, S.; Gu, J.; Yang, F.; Li, Y.; Dang, J.; Liu, B.; Ma, J. Analysis of the effect of characteristic parameters and operating conditions on exergy efficiency of alkaline water electrolyzer. J. Power Sources 2022, 537, 231532. [Google Scholar] [CrossRef]
- Chen, D.; Pei, P.; Meng, Y.; Ren, P.; Li, Y.; Wang, M.; Wang, X. Novel extraction method of working condition spectrum for the lifetime prediction and energy management strategy evaluation of automotive fuel cells. Energy 2022, 255, 124523. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Y.; Deng, C.; Chen, J. Research on improving dynamic response ability of 30kW real fuel cell system based on operating parameter optimization. Int. J. Hydrogen Energy 2023, 48, 1075–1089. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel fuel cell/battery/supercapacitor hybrid power source for fuel cell hybrid electric vehicles. Energy 2018, 143, 467–477. [Google Scholar] [CrossRef]
- Wu, H. A review of recent development: Transport and performance modeling of PEM fuel cells. Appl. Energy 2016, 165, 81–106. [Google Scholar] [CrossRef]
- Priya, K.; Sathishkumar, K.; Rajasekar, N. A comprehensive review on parameter estimation techniques for Proton Exchange Membrane fuel cell modelling. Renew. Sustain. Energy Rev. 2018, 93, 121–144. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; El-Fergany, A.A. Artificial ecosystem optimizer for parameters identification of proton exchange membrane fuel cells model. Int. J. Hydrogen Energy 2021, 46, 37612–37627. [Google Scholar] [CrossRef]
- Weber, A.Z.; Newman, J. Modeling Transport in Polymer-Electrolyte Fuel Cells. Chem. Rev. 2004, 104, 4679–4726. [Google Scholar] [CrossRef]
- Siegel, C. Review of computational heat and mass transfer modeling in polymer-electrolyte-membrane (PEM) fuel cells. Energy 2008, 33, 1331–1352. [Google Scholar] [CrossRef]
- Weber, A.Z.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.; Harvey, D.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A Critical Review of Modeling Transport Phenomena in Polymer-Electrolyte Fuel Cells. J. Electrochem. Soc. 2014, 161, F1254–F1299. [Google Scholar] [CrossRef]
- Revankar, S.T.; Majumdar, P. Fuel Cells: Principles, Design, and Analysis; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, J.; Fan, Z.; Tan, W.; Yang, G.; Wang, W.; Zhou, W.; Shao, Z. Understanding and Engineering of Multiphase Transport Processes in Membrane Electrode Assembly of Proton-Exchange Membrane Fuel Cells with a Focus on the Cathode Catalyst Layer: A Review. Energy Fuels 2020, 34, 9175–9188. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A.; McDonald, M.S. Fuel Cell Systems Explained; John Wiley & Sons Ltd.: Chichester, UK, 2003; Volume 2. [Google Scholar]
- Mosdale, R.; Srinivasan, S. Analysis of performance and of water and thermal management in proton exchange membrane fuel cells. Electrochim. Acta 1995, 40, 413–421. [Google Scholar] [CrossRef]
- Sun, Z.; Cao, D.; Ling, Y.; Xiang, F.; Sun, Z.; Wu, F. Proton exchange membrane fuel cell model parameter identification based on dynamic differential evolution with collective guidance factor algorithm. Energy 2021, 216, 119056. [Google Scholar] [CrossRef]
- Bernardi, D.M.; Verbrugge, M.W. A Mathematical Model of the Solid-Polymer-Electrolyte Fuel Cell. J. Electrochem. Soc. 1992, 139, 2477. [Google Scholar] [CrossRef]
- Ferreira, R.B.; Falcão, D.S.; Oliveira, V.B.; Pinto, A.M.F.R. 1D + 3D two-phase flow numerical model of a proton exchange membrane fuel cell. Appl. Energy 2017, 203, 474–495. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, G.; Jiang, Y.; Wang, R.; Sheng, X.; Xi, F.; Zhao, Z.; Chen, W.; Zhu, Y.; Wang, Y.; et al. “3D+1D” modeling approach toward large-scale PEM fuel cell simulation and partitioned optimization study on flow field. Etransportation 2020, 6, 100090. [Google Scholar] [CrossRef]
- Ahmed, D.H.; Sung, H.J. Effects of channel geometrical configuration and shoulder width on PEMFC performance at high current density. J. Power Sources 2006, 162, 327–339. [Google Scholar] [CrossRef]
- Shen, J.; Tu, Z.; Chan, S.H. Enhancement of mass transfer in a proton exchange membrane fuel cell with blockage in the flow channel. Appl. Therm. Eng. 2019, 149, 1408–1418. [Google Scholar] [CrossRef]
- Mondal, B.; Jiao, K.; Li, X. Three-dimensional simulation of water droplet movement in PEM fuel cell flow channels with hydrophilic surfaces. Int. J. Energy Res. 2011, 35, 1200–1212. [Google Scholar] [CrossRef]
- Wang, C.Y.; Wang, Z.H.; Pan, Y. Two-Phase Transport in Proton Exchange Membrane Fuel Cells. In Proceedings of the ASME 1999 International Mechanical Engineering Congress and Exposition, Nashville, TN, USA, 14–19 November 1999; pp. 351–357. [Google Scholar]
- Udell, K.S. Heat transfer in porous media considering phase change and capillarity—The heat pipe effect. Int. J. Heat Mass. Tran. 1985, 28, 485–495. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Lin, G.; Ohn, H.; Wang, X. Measurement of Capillary Pressure Property of Gas Diffusion Media Used in Proton Exchange Membrane Fuel Cells. Electrochem. Solid-State Lett. 2008, 11, B127. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer electrolyte fuel cell model. J. Electrochem. Soc. 1991, 138, 2334. [Google Scholar] [CrossRef]
- Meng, H. Numerical studies of liquid water behaviors in PEM fuel cell cathode considering transport across different porous layers. Int. J. Hydrogen Energy 2010, 35, 5569–5579. [Google Scholar] [CrossRef]
- Moein-Jahromi, M.; Kermani, M.J. Performance prediction of PEM fuel cell cathode catalyst layer using agglomerate model. Int. J. Hydrogen Energy 2012, 37, 17954–17966. [Google Scholar] [CrossRef]
- Chen, L.; He, A.; Zhao, J.; Kang, Q.; Li, Z.; Carmeliet, J.; Shikazono, N.; Tao, W. Pore-scale modeling of complex transport phenomena in porous media. Prog. Energy Combust. 2022, 88, 100968. [Google Scholar] [CrossRef]
- Lei, H.; Huang, H.; Li, C.; Pan, M.; Guo, X.; Chen, Y.; Liu, M.; Wang, T. Numerical simulation of water droplet transport characteristics in cathode channel of proton exchange membrane fuel cell with tapered slope structures. Int. J. Hydrogen Energy 2020, 45, 29331–29344. [Google Scholar] [CrossRef]
- He, M.; Huang, Z.; Sun, P.; Wang, C. Modeling and Numerical Studies for a 3D Two-Phase Mixed-Domain Model of PEM Fuel Cell. J. Electrochem. Soc. 2013, 160, F324–F336. [Google Scholar] [CrossRef]
- Afshari, E. Computational analysis of heat transfer in a PEM fuel cell with metal foam as a flow field. J. Therm. Anal. Calorim. 2020, 139, 2423–2434. [Google Scholar] [CrossRef]
- Yang, C.; Wan, Z.; Chen, X.; Kong, X.; Zhang, J.; Huang, T.; Wang, X. Geometry optimization of a novel M-like flow field in a proton exchange membrane fuel cell. Energy Convers. Manag. 2021, 228, 113651. [Google Scholar] [CrossRef]
- Qiu, D.; Peng, L.; Tang, J.; Lai, X. Numerical analysis of air-cooled proton exchange membrane fuel cells with various cathode flow channels. Energy 2020, 198, 117334. [Google Scholar] [CrossRef]
- Wan, Z.; Quan, W.; Yang, C.; Yan, H.; Chen, X.; Huang, T.; Wang, X.; Chan, S. Optimal design of a novel M-like channel in bipolar plates of proton exchange membrane fuel cell based on minimum entropy generation. Energy Convers. Manag. 2020, 205, 112386. [Google Scholar] [CrossRef]
- Bao, Z.; Niu, Z.; Jiao, K. Analysis of single- and two-phase flow characteristics of 3-D fine mesh flow field of proton exchange membrane fuel cells. J. Power Sources 2019, 438, 226995. [Google Scholar] [CrossRef]
- Shen, J.; Xu, L.; Chang, H.; Tu, Z.; Chan, S.H. Partial flooding and its effect on the performance of a proton exchange membrane fuel cell. Energy Convers. Manag. 2020, 207, 112537. [Google Scholar] [CrossRef]
- Fontana, É.; Mancusi, E.; Ulson De Souza, A.A.; Guelli Ulson De Souza, S.M.A. Flow regimes for liquid water transport in a tapered flow channel of proton exchange membrane fuel cells (PEMFCs). J. Power Sources 2013, 234, 260–271. [Google Scholar] [CrossRef]
- Qin, Y.; Li, X.; Jiao, K.; Du, Q.; Yin, Y. Effective removal and transport of water in a PEM fuel cell flow channel having a hydrophilic plate. Appl. Energy 2014, 113, 116–126. [Google Scholar] [CrossRef]
- Shen, J.; Tu, Z.; Chan, S.H. Evaluation criterion of different flow field patterns in a proton exchange membrane fuel cell. Energy Convers. Manag. 2020, 213, 112841. [Google Scholar] [CrossRef]
- Pan, W.; Wang, P.; Chen, X.; Wang, F.; Dai, G. Combined effects of flow channel configuration and operating conditions on PEM fuel cell performance. Energy Convers. Manag. 2020, 220, 113046. [Google Scholar] [CrossRef]
- Barati, S.; Khoshandam, B.; Ghazi, M.M. An investigation of channel blockage effects on hydrogen mass transfer in a proton exchange membrane fuel cell with various geometries and optimization by response surface methodology. Int. J. Hydrogen Energy 2018, 43, 21928–21939. [Google Scholar] [CrossRef]
- Ozden, A.; Shahgaldi, S.; Li, X.; Hamdullahpur, F. A review of gas diffusion layers for proton exchange membrane fuel cells—With a focus on characteristics, characterization techniques, materials and designs. Prog. Energy Combust. Sci. 2019, 74, 50–102. [Google Scholar] [CrossRef]
- Hao, L.; Cheng, P. Lattice Boltzmann simulations of anisotropic permeabilities in carbon paper gas diffusion layers. J. Power Sources 2009, 186, 104–114. [Google Scholar] [CrossRef]
- Yang, M.; Du, A.; Liu, J.; Xu, S. Lattice Boltzmann Method Study on Liquid Water Dynamic inside Gas Diffusion Layer with Porosity Distribution. World Electr. Veh. J. 2021, 12, 133. [Google Scholar] [CrossRef]
- Chen, H.; Guo, H.; Ye, F.; Ma, C.F. Modification of the two-fluid model and experimental study of proton exchange membrane fuel cells with baffled flow channels. Energy Convers. Manag. 2019, 195, 972–988. [Google Scholar] [CrossRef]
- Zhao, C.; Xing, S.; Liu, W.; Chen, M.; Wang, H. Performance improvement for air-cooled open-cathode proton exchange membrane fuel cell with different design parameters of the gas diffusion layer. Prog. Nat. Sci. Mater. Int. 2020, 30, 825–831. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, X.; Li, B.; Zhang, C. Recent progress of the gas diffusion layer in proton exchange membrane fuel cells: Material and structure designs of microporous layer. Int. J. Hydrogen Energy 2021, 46, 4259–4282. [Google Scholar] [CrossRef]
- Wijayanti, W.; Kusumastuti, R.; Sasmoko, S.; Sasongko, M.N. A numerical study of proton exchange membrane fuel cell performances affected by various porosities of gas difussion layer materials. East. -Eur. J. Enterp. Technol. 2020, 1, 65–75. [Google Scholar] [CrossRef]
- Xie, M.; Chu, T.; Wang, T.; Wan, K.; Yang, D.; Li, B.; Ming, P.; Zhang, C. Preparation, Performance and Challenges of Catalyst Layer for Proton Exchange Membrane Fuel Cell. Membranes 2021, 11, 879. [Google Scholar] [CrossRef]
- Perng, S.; Wu, H. Effect of the prominent catalyst layer surface on reactant gas transport and cell performance at the cathodic side of a PEMFC. Appl. Energy 2010, 87, 1386–1399. [Google Scholar] [CrossRef]
- Chong, L.; Wen, J.; Kubal, J.; Sen, F.G.; Zou, J.; Greeley, J.; Chan, M.; Barkholtz, H.; Ding, W.; Liu, D.J. Ultralow-loading platinum-cobalt fuel cell catalysts derived from imidazolate frameworks. Science 2018, 362, 1276–1281. [Google Scholar] [CrossRef] [PubMed]
- Marinoiu, A.; Raceanu, M.; Carcadea, E.; Varlam, M.; Stefanescu, I. Iodinated carbon materials for oxygen reduction reaction in proton exchange membrane fuel cell. Scalable synthesis and electrochemical performances. Arab. J. Chem. 2019, 12, 868–880. [Google Scholar] [CrossRef]
- Mardle, P.; Ji, X.; Wu, J.; Guan, S.; Dong, H.; Du, S. Thin film electrodes from Pt nanorods supported on aligned N-CNTs for proton exchange membrane fuel cells. Appl. Catal. B Environ. 2020, 260, 118031. [Google Scholar] [CrossRef]
- Wang, G.; Mukherjee, P.P.; Wang, C. Direct numerical simulation (DNS) modeling of PEFC electrodes: Part I. Regular microstructure. Electrochim. Acta 2006, 51, 3139–3150. [Google Scholar] [CrossRef]
- Wang, G.; Mukherjee, P.P.; Wang, C. Direct numerical simulation (DNS) modeling of PEFC electrodes: Part II. Random microstructure. Electrochim. Acta 2006, 51, 3151–3160. [Google Scholar] [CrossRef]
- Chen, M.; Zhao, C.; Sun, F.; Fan, J.; Li, H.; Wang, H. Research progress of catalyst layer and interlayer interface structures in membrane electrode assembly (MEA) for proton exchange membrane fuel cell (PEMFC) system. Etransportation 2020, 5, 100075. [Google Scholar] [CrossRef]
- Sievers, G.; Vidakovic-Koch, T.; Walter, C.; Steffen, F.; Jakubith, S.; Kruth, A.; Hermsdorf, D.; Sundmacher, K.; Brüser, V. Ultra-low loading Pt-sputtered gas diffusion electrodes for oxygen reduction reaction. J. Appl. Electrochem. 2018, 48, 221–232. [Google Scholar] [CrossRef]
- Kusoglu, A.; Weber, A.Z. New Insights into Perfluorinated Sulfonic-Acid Ionomers. Chem. Rev. 2017, 117, 987–1104. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.B. Study on the effect of humidity and stoichiometry on the water saturation of PEM fuel cells. Int. J. Energy Res. 2012, 36, 509–522. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S.; Jia, X. Diagnosis of water failures in proton exchange membrane fuel cell with zero-phase ohmic resistance and fixed-low-frequency impedance. Appl. Energy 2019, 239, 785–792. [Google Scholar] [CrossRef]
- Zhang, J.; Bai, H.; Ren, Q.; Luo, H.; Ren, X.; Tian, Z.; Lu, S. Extra Water- and Acid-StableMOF-801 with High Proton Conductivity and Its Composite Membrane for Proton-Exchange Membrane. ACS Appl. Mater. Inter. 2018, 10, 28656–28663. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Park, J.; Park, J.; Kang, M. Pore-Filled Proton-Exchange Membranes with Fluorinated Moiety for Fuel Cell Application. Energies 2021, 14, 4433. [Google Scholar] [CrossRef]
- Li, Y.; Yang, F.; Chen, D.; Hu, S.; Xu, X. Thermal-physical modeling and parameter identification method for dynamic model with unmeasurable state in 10-kW scale proton exchange membrane fuel cell system. Energy Convers. Manag. 2023, 276, 116580. [Google Scholar] [CrossRef]
- Li, Y.; Pei, P.; Ma, Z.; Ren, P.; Huang, H. Method for system parameter identification and controller parameter tuning for super-twisting sliding mode control in proton exchange membrane fuel cell system. Energy Convers. Manag. 2021, 243, 114370. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Baumert, R.M.; Mann, R.F.; Peppley, B.A.; Roberge, P.R.; Harris, T.J. Performance modeling of the Ballard Mark IV solid polymer electrolyte fuel cell: I. Mechanistic model development. J. Electrochem. Soc. 1995, 142, 1. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, H.; Wei, X.; Ming, P. A novel model-based internal state observer of a fuel cell system for electric vehicles using improved Kalman filter approach. Appl. Energy 2020, 268, 115009. [Google Scholar] [CrossRef]
- Abbaspour, A.; Khalilnejad, A.; Chen, Z. Robust adaptive neural network control for PEM fuel cell. Int. J. Hydrogen Energy 2016, 41, 20385–20395. [Google Scholar] [CrossRef]
- Solsona, M.; Kunusch, C.; Ocampo-Martinez, C. Control-oriented model of a membrane humidifier for fuel cell applications. Energy Convers. Manag. 2017, 137, 121–129. [Google Scholar] [CrossRef]
- Ohenoja, M.; Leiviskä, K. Observations on the Parameter Estimation Problem of Polymer Electrolyte Membrane Fuel Cell Polarization Curves. Fuel Cells 2020, 20, 516–526. [Google Scholar] [CrossRef]
- Yang, B.; Zeng, C.; Wang, L.; Guo, Y.; Chen, G.; Guo, Z.; Chen, Y.; Li, D.; Cao, P.; Shu, H.; et al. Parameter identification of proton exchange membrane fuel cell via Levenberg-Marquardt backpropagation algorithm. Int. J. Hydrogen Energy 2021, 46, 22998–23012. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Q.; Zhang, L.; Zong, Y.; Zhou, K.; Fu, Z. Control oriented data driven linear parameter varying model for proton exchange membrane fuel cell systems. Appl. Energy 2020, 277, 115540. [Google Scholar] [CrossRef]
- Tao, S.; Cao, G.-Y.C.; Zhu, X.-J. Nonlinear modeling of PEMFC based on neural networks identification. J. Zhejiang Univ. -Sci. A 2005, 6, 365–370. [Google Scholar] [CrossRef]
- Razmjooy, N.; Ramezani, M. Training wavelet neural networks using hybrid particle swarm optimization and gravitational search algorithm for system identification. Int. J. Mechatron. Electr. Comput. Technol. 2016, 6, 2987–2997. [Google Scholar]
- Hatti, M.; Tioursi, M. Dynamic neural network controller model of PEM fuel cell system. Int. J. Hydrogen Energy 2009, 34, 5015–5021. [Google Scholar] [CrossRef]
- Rezazadeh, A.; Sedighizadeh, M.; Karimi, M. Proton Exchange Membrane Fuel Cell Control Using a Predictive Control Based on Neural Network. Int. J. Comput. Electr. Eng. 2010, 2, 81–85. [Google Scholar] [CrossRef]
- Bao, S.; Ebadi, A.; Toughani, M.; Dalle, J.; Maseleno, A.; Baharuddin; Yıldızbası, A. A new method for optimal parameters identification of a PEMFC using an improved version of Monarch Butterfly Optimization Algorithm. Int. J. Hydrogen Energy 2020, 45, 17882–17892. [Google Scholar] [CrossRef]
- Salim, R.; Nabag, M.; Noura, H.; Fardoun, A. The parameter identification of the Nexa 1.2 kW PEMFC's model using particle swarm optimization. Renew. Energy 2015, 82, 26–34. [Google Scholar] [CrossRef]
- Li, Q.; Chen, W.; Wang, Y.; Liu, S.; Jia, J. Parameter Identification for PEM Fuel-Cell Mechanism Model Based on Effective Informed Adaptive Particle Swarm Optimization. IEEE Trans. Ind. Electron. 2011, 58, 2410–2419. [Google Scholar] [CrossRef]
- Fathy, A.; Elaziz, M.A.; Alharbi, A.G. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 2020, 146, 1833–1845. [Google Scholar] [CrossRef]
- Duan, F.; Song, F.; Chen, S.; Khayatnezhad, M.; Ghadimi, N. Model parameters identification of the PEMFCs using an improved design of Crow Search Algorithm. Int. J. Hydrogen Energy 2022, 47, 33839–33849. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Wang, Z. Parameter estimation of proton exchange membrane fuel cells using eagle strategy based on JAYA algorithm and Nelder-Mead simplex method. Energy 2019, 173, 457–467. [Google Scholar] [CrossRef]
- Kheirmand, M.; Asnafi, A. Analytic parameter identification of proton exchange membrane fuel cell catalyst layer using electrochemical impedance spectroscopy. Int. J. Hydrogen Energy 2011, 36, 13266–13271. [Google Scholar] [CrossRef]
- Haslinger, M.; Steindl, C.; Lauer, T. Parameter Identification of a Quasi-3D PEM Fuel Cell Model by Numerical Optimization. Processes 2021, 9, 1808. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).