Integrating Hydrokinetic Energy into Hybrid Renewable Energy System: Optimal Design and Comparative Analysis
Abstract
1. Introduction
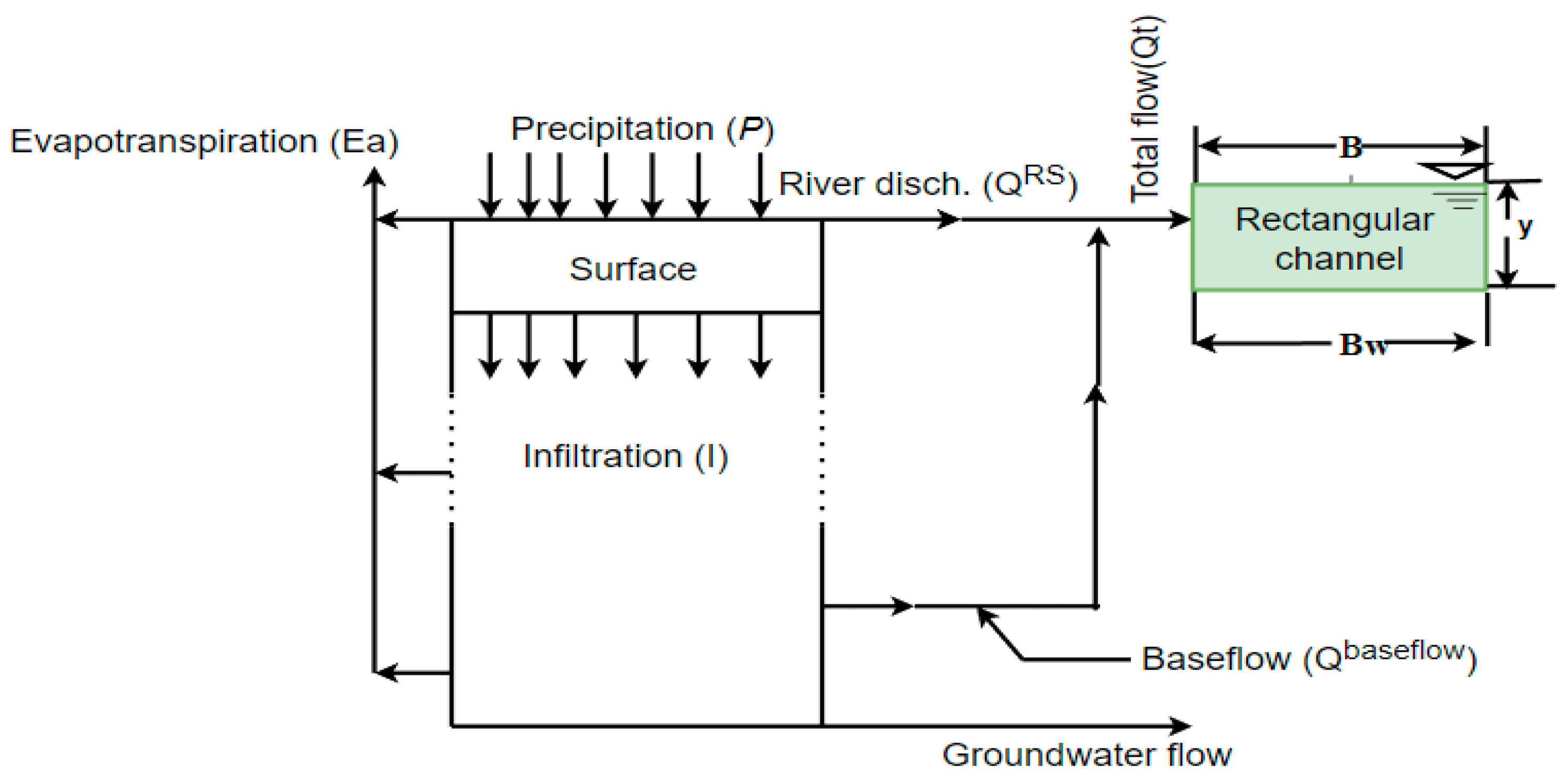
2. Evaluation of Flow Velocity
2.1. Estimation of Cumulative Abstraction
2.2. Estimation of the Evapotranspiration
2.3. Estimation of the Base Flow
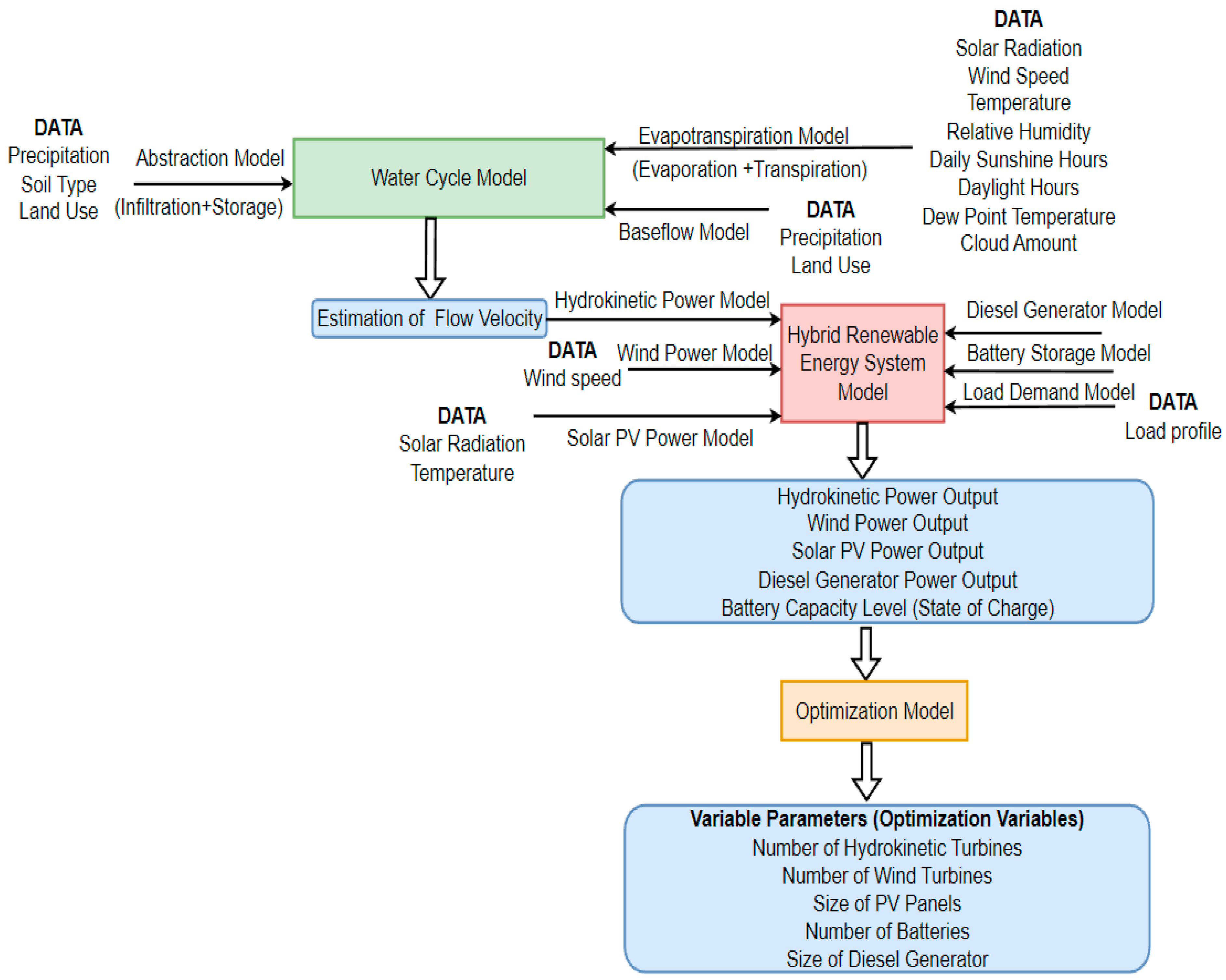
3. System Modeling of the Proposed HRES
3.1. PV Model
3.2. Wind Power Model
3.3. Hydrokinetic Model
3.4. Battery Storage Model
3.5. Diesel Generator Model
3.6. Power Converter Model
4. Problem Formulation and Solution Approach
5. A Case Study
5.1. Data Acquisition for Estimating the Flow Velocity
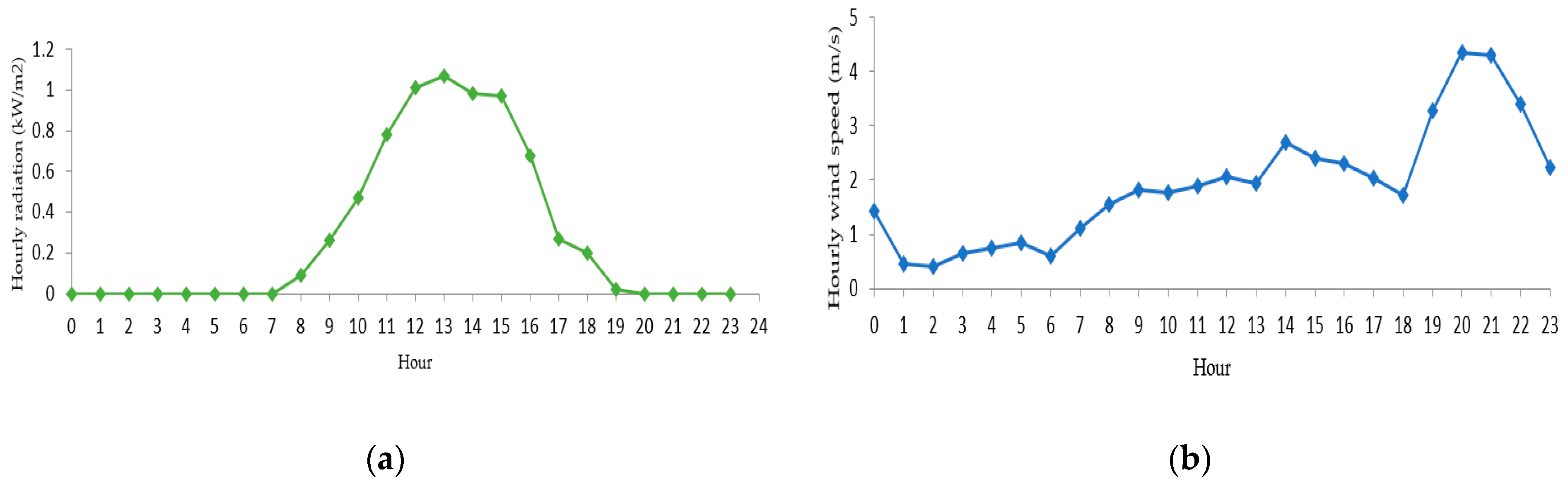
5.2. Meteorological Data for HRES
5.3. Load Demand
5.4. Component Specification of the HRES
6. Results and Discussions
6.1. Results of Flow Velocity
6.2. Results of the Off-Grid HRES
6.2.1. Economic Evaluation
6.2.2. Technical Evaluation
6.2.3. Comparison with the DG-Only System
7. Conclusions
- A detailed model of estimating the flow velocity of a river using the water transportation process has been presented in this study. The discharge results show that the maximum, minimum, and mean annual discharge are 122.90, 0.395, and 14.52 m3/s, respectively. Moreover, our result further indicates that the maximum velocity obtained is 5.12 m/s, while the minimum and mean velocities are 0.017 m/s and 0.71 m/s, respectively. This model-based method will benefit off-grid areas that do not have the requisite manpower to obtain measured or observed data.
- The studied community has the potential to harness both solar and hydrokinetic energy. Moreover, wind technology is not an economically viable option compared to others due to the estimated low wind speed obtained in the area and the high cost of the wind generation component.
- The optimization result using GA shows that the optimal system architecture consists of 320 kW of PV panels, 120 units of 6.91 kWh batteries, two (27 kW) hydrokinetic turbines, 120 kW converters, zero wind turbines, and a 100 kW diesel generator. The total net present cost, cost of energy, and capital cost of the system are USD 1,103,668, 0.2841 USD/kWh and USD 573,320, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEA. SDG7: Data and Projections; IEA: Paris, France, 2019. [Google Scholar]
- IEA. World Energy Outlook 2019; IEA: Paris, France, 2019. [Google Scholar]
- United Nation. Sustainable Development Goals. 2019. Available online: https://www.un.org/sustainabledevelopment/blog/2019/06/growing-at-a-slower-pace-world-population-is-expected-to-reach-9-7-billion-in-2050-and-could-peak-at-nearly-11-billion-around-2100-un-report/ (accessed on 25 June 2022).
- Ghiasi, M. Detailed study, multi-objective optimization, and design of an AC-DC smart microgrid with hybrid renewable energy resources. Energy 2019, 169, 496–507. [Google Scholar] [CrossRef]
- Ember; Energiewende, A. Renewable Energies Overtake Gas and Coal in EU Electricity Generation. 2021. Available online: https://www.agora-energiewende.de/en/press/news-archive/renewables-overtake-gas-and-coal-and-coal-in-eu-electricity-generation-1/#:~:text=For%20the%20first%20time%2C%20more,the%20British%20think%20tank%20Ember (accessed on 13 June 2022).
- Mokhtara, C.; Negrou, B.; Bouferrouk, A.; Yao, Y.; Settou, N.; Ramadan, M. Integrated supply–demand energy management for optimal design of off-grid hybrid renewable energy systems for residential electrification in arid climates. Energy Convers. Manag. 2020, 221, 113192. [Google Scholar] [CrossRef]
- Ighravwe, D.E.; Babatunde, O.M.; Adedoja, O.S.; Okharedia, T.E. Evaluation and selection of hybrid renewable energy systems for healthcare centres in rural areas: A techno-economic approach. In Proceedings of the IEEE International Conference on Adaptive Science and Technology (ICAST), Accra, Ghana, 22–24 August 2018. [Google Scholar] [CrossRef]
- Olatomiwa, L. Optimal configuration assessments of hybrid renewable power supply for rural healthcare facilities. Energy Rep. 2016, 2, 141–146. [Google Scholar] [CrossRef]
- Babatunde, O.M.; Adedoja, O.S.; Babatunde, D.E.; Denwigwe, I.H. Off-grid hybrid renewable energy system for rural healthcare centers: A case study in Nigeria. Energy Sci. Eng. 2019, 7, 676–693. [Google Scholar] [CrossRef]
- Ghenai, C.; Bettayeb, M. Modelling and performance analysis of a stand-alone hybrid solar PV/Fuel Cell/Diesel Generator power system for university building. Energy 2019, 171, 180–189. [Google Scholar] [CrossRef]
- Vishnupriyan, J.; Manoharan, P.S. Optimizing an On-Grid Hybrid Power System in Educational Institution in Tamil Nadu, India. In Green Buildings and Sustainable Engineering; Proceedings of GBSE 2018; Springer: Berlin/Heidelberg, Germany, 2019; pp. 93–103. [Google Scholar]
- Niemelä, T.; Kosonen, R.; Jokisalo, J. Cost-optimal energy performance renovation measures of educational buildings in cold climate. Appl. Energy 2016, 183, 1005–1020. [Google Scholar] [CrossRef]
- Soberanis, M.A.E.; Mithrush, T.; Bassam, A.; Mérida, W. A sensitivity analysis to determine technical and economic feasibility of energy storage systems implementation: A flow battery case study. Renew Energy 2018, 115, 547–557. [Google Scholar] [CrossRef]
- Aderemi, B.A.; Chowdhury, S.P.D.; Olwal, T.O.; Abu-Mahfouz, A.M. Techno-economic feasibility of hybrid solar photovoltaic and battery energy storage power system for a mobile cellular base station in Soshanguve, South Africa. Energies 2018, 11, 1572. [Google Scholar] [CrossRef]
- Amutha, W.M.; Rajini, V. Techno-economic evaluation of various hybrid power systems for rural telecom. Renew. Sustain. Energy Rev. 2015, 43, 553–561. [Google Scholar] [CrossRef]
- Baseer, M.A.; Alqahtani, A.; Rehman, S. Techno-economic design and evaluation of hybrid energy systems for residential communities: Case study of Jubail industrial city. J. Clean Prod. 2019, 237, 117806. [Google Scholar] [CrossRef]
- Hassan, Q. Evaluation and optimization of off-grid and on-grid photovoltaic power system for typical household electrification. Renew Energy 2020, 164, 375–390. [Google Scholar] [CrossRef]
- Tu, T.; Rajarathnam, G.P.; Vassallo, A.M. Optimization of a stand-alone photovoltaic–wind–diesel–battery system with multi-layered demand scheduling. Renew Energy 2019, 131, 333–347. [Google Scholar] [CrossRef]
- Veilleux, G.; Potisat, T.; Pezim, D.; Ribback, C.; Ling, J.; Krysztofiński, A.; Ahmed, A.; Papenheim, J.; Pineda, A.M.; Sembian, S.; et al. Techno-economic analysis of microgrid projects for rural electrification: A systematic approach to the redesign of Koh Jik off-grid case study. Energy Sustain. Dev. 2020, 54, 1–13. [Google Scholar] [CrossRef]
- Johannsen, R.M.; Østergaard, P.A.; Hanlin, R. Hybrid photovoltaic and wind mini-grids in Kenya: Techno-economic assessment and barriers to diffusion. Energy Sustain. Dev. 2020, 54, 111–126. [Google Scholar] [CrossRef]
- Aziz, A.S.; Tajuddin, M.F.N.; Adzman, M.R.; Azmi, A.; Ramli, M.A.M. Optimization and sensitivity analysis of standalone hybrid energy systems for rural electrification: A case study of Iraq. Renew Energy 2019, 138, 775–792. [Google Scholar] [CrossRef]
- Shahzad, M.K.; Zahid, A.; Rashid, T.; Rehan, M.A.; Ali, M.; Ahmad, M. Techno-economic feasibility analysis of a solar-biomass off grid system for the electrification of remote rural areas in Pakistan using HOMER software. Renew Energy 2017, 106, 264–273. [Google Scholar] [CrossRef]
- IEA. Global Energy Review 2020; IEA: Paris, France, 2020. [Google Scholar]
- IEA. Renewables 2019; IEA: Paris, France, 2019. [Google Scholar]
- Jacobson, P.T.; Ravens, T.M.; Cunningham, K.W.; Scott, G. Assssment and Mapping of the Riverine Hydrokinetic Resource in the Continental United States; EPRI: Palo Alto, CA, USA, 2012. [Google Scholar] [CrossRef]
- Kirke, B. Hydrokinetic turbines for moderate sized rivers. Energy Sustain. Dev. 2020, 58, 182–195. [Google Scholar] [CrossRef] [PubMed]
- Olatunji, O.A.S.; Raphael, A.T.; Yomi, I.T. Hydrokinetic energy opportunity for rural electrification in Nigeria. Int. J. Renew. Energy Dev. 2018, 7, 183–190. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Liu, Y.; Wang, S.; Leng, C. Estimating the flow velocity and discharge of ADCP unmeasured area in tidal reach. Flow Meas. Instrum. 2016, 52, 208–218. [Google Scholar] [CrossRef]
- Cruz, J.d.S.; Blanco, C.J.C.; Junior, A.C.P.B. Flow-velocity model for hydrokinetic energy availability assessment in the amazon. Acta Sci. Technol. 2020, 42, e45703. [Google Scholar] [CrossRef]
- Khan, M.J.; Iqbal, M.T.; Quaicoe, J.E. River current energy conversion systems: Progress, prospects and challenges. Renew. Sustain. Energy Rev. 2008, 12, 2177–2193. [Google Scholar] [CrossRef]
- Ibrahim, W.I.; Mohamed, M.R.; Ismail, R.M.T.R.; Leung, P.K.; Xing, W.W.; Shah, A.A. Hydrokinetic energy harnessing technologies: A review Hydrokinetic energy harnessing technologies: A review. Energy Reports 2021, 7, 2021–2042. [Google Scholar] [CrossRef]
- Arango-manrique, A.; Ricardo, N.; Budes, F.A.B. Energy, Economic, and Environmental Evaluation of a Proposed Solar-Wind Power On-grid System Using HOMER Pro:Case Study in Colombia. Energies 2020, 13, 16625. [Google Scholar]
- Yimen, N.; Hamandjoda, O.; Meva’a, L.; Ndzana, B.; Nganhou, J. Analyzing of a photovoltaic/wind/biogas/pumped-hydro off-grid hybrid system for rural electrification in Sub-Saharan Africa—Case study of Djoundé in Northern Cameroon. Energies 2018, 11, 2644. [Google Scholar] [CrossRef]
- Oviroh, P.O.; Jen, T.C. The energy cost analysis of hybrid systems and diesel generators in powering selected base transceiver station locations in Nigeria. Energies 2018, 11, 687. [Google Scholar] [CrossRef]
- Sambhi, S.; Sharma, H.; Bhadoria, V.; Kumar, P.; Chaurasia, R.; Chaurasia, G.S.; Fotis, G.; Vita, V.; Ekonomou, L.; Pavlatos, C.; et al. Economic Feasibility of a Renewable Integrated Hybrid Power Generation System for a Rural Village of Ladakh. Energies 2022, 15, 9126. [Google Scholar] [CrossRef]
- Cabanero, A.; Nolting, L.; Praktiknjo, A. Mini-grids for the sustainable electrification of rural areas in sub-Saharan Africa: Assessing the potential of keymaker models. Energies 2020, 13, 6350. [Google Scholar] [CrossRef]
- Islam, M.R.; Akter, H.; Howlader, H.O.R.; Senjyu, T. Optimal Sizing and Techno-Economic Analysis of Grid-Independent Hybrid Energy System for Sustained Rural Electrification in Developing Countries: A Case Study in Bangladesh. Energies 2022, 15, 6381. [Google Scholar] [CrossRef]
- Costa, T.S.; Villalva, M.G. Technical Evaluation of a PV-Diesel Hybrid System with Energy Storage: Case Study in the Tapajós-Arapiuns Extractive Reserve, Amazon, Brazil. Energies 2020, 13, 2969. [Google Scholar] [CrossRef]
- Miao, C.; Teng, K.; Wang, Y.; Jiang, L. Technoeconomic analysis on a hybrid power system for the uk household using renewable energy: A case study. Energies 2020, 13, 3231. [Google Scholar] [CrossRef]
- Gbadamosi, S.L.; Ogunje, F.S.; Wara, S.T.; Nwulu, N.I. Techno-Economic Evaluation of a Hybrid Energy System for an Educational Institution: A Case Study. Energies 2022, 15, 5606. [Google Scholar] [CrossRef]
- Al-Badi, A.; Al Wahaibi, A.; Ahshan, R.; Malik, A. Techno-Economic Feasibility of a Solar-Wind-Fuel Cell Energy System in Duqm, Oman. Energies 2022, 15, 5379. [Google Scholar] [CrossRef]
- Amupolo, A.; Nambundunga, S.; Chowdhury, D.S.P.; Grün, G. Techno-Economic Feasibility of Off-Grid Renewable Energy Electrification Schemes: A Case Study of an Informal Settlement in Namibia. Energies 2022, 15, 4235. [Google Scholar] [CrossRef]
- Sambhi, S.; Sharma, H.; Kumar, P.; Fotis, G.; Vita, V.; Ekonomou, L. Techno-Economic Optimization of an Off-Grid Hybrid Power Generation for SRM IST, Delhi-NCR Campus. Energies 2022, 15, 7880. [Google Scholar] [CrossRef]
- Samy, M.M.; Barakat, S.; Ramadan, H.S. Techno-economic analysis for rustic electrification in Egypt using multi-source renewable energy based on PV/wind/FC. Int. J. Hydrogen. Energy 2020, 45, 11471–11483. [Google Scholar] [CrossRef]
- Singh, S.S.; Fernandez, E. Modeling, size optimization and sensitivity analysis of a remote hybrid renewable energy system. Energy 2018, 143, 719–731. [Google Scholar] [CrossRef]
- Rodriguez-Gallegos, C.D.; Gandhi, O.; Yang, D.; Alvarez-Alvarado, M.S.; Zhang, W.; Reindl, T. A Siting and Sizing Optimization Approach for PV-Battery-Diesel Hybrid Systems. IEEE Trans. Ind. Appl. 2018, 54, 2637–2645. [Google Scholar] [CrossRef]
- Zhang, W.; Maleki, A.; Rosen, M.A.; Liu, J. Sizing a stand-alone solar-wind-hydrogen energy system using weather forecasting and a hybrid search optimization algorithm. Energy Convers Manag. 2019, 180, 609–621. [Google Scholar] [CrossRef]
- Fodhil, F.; Hamidat, A.; Nadjemi, O. Potential, optimization and sensitivity analysis of photovoltaic-diesel-battery hybrid energy system for rural electrification in Algeria. Energy 2019, 169, 613–624. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R.C. Reliability, economic and environmental analysis of a microgrid system in the presence of renewable energy resources. Appl. Energy 2019, 236, 1089–1114. [Google Scholar] [CrossRef]
- Yuce, M.I.; Muratoglu, A. Hydrokinetic energy conversion systems: A technology status review. Renew. Sustain. Energy Rev. 2015, 43, 72–82. [Google Scholar] [CrossRef]
- Niebuhr, C.M.; van Dijk, M.; Neary, V.S.; Bhagwan, J.N. A review of hydrokinetic turbines and enhancement techniques for canal installations: Technology, applicability and potential. Renew. Sustain. Energy Rev. 2019, 113, 109240. [Google Scholar] [CrossRef]
- Abutunis, A.; Taylor, G.; Fal, M.; Chandrashekhara, K. Experimental evaluation of coaxial horizontal axis hydrokinetic composite turbine system. Renew Energy 2020, 157, 232–245. [Google Scholar] [CrossRef]
- Adeogun, A.G.; Ganiyu, H.O.; Ladokun, L.L.; Ibitoye, B.A. Evaluation of hydrokinetic energy potentials of selected rivers in Kwara state, Nigeria. Environ. Eng. Res. 2020, 25, 267–273. [Google Scholar] [CrossRef]
- Ladokun, L.L.; Sule, B.F.; Ajao, K.R.; Adeogun, A.G. Resource assessment and feasibility study for the generation of hydrokinetic power in the tailwaters of selected hydropower stations in Nigeria. Water Sci. 2018, 32, 338–354. [Google Scholar] [CrossRef]
- Eme, L.C.; Ulasi, J.A.; Tunde, A.I.A.; Odunze, A.C. Hydrokinetic turbines for power generation in Nigerian river basins. Water Pract. Technol. 2019, 14, 71–80. [Google Scholar] [CrossRef]
- John, B.; Thomas, R.N.; Varghese, J. Integration of hydrokinetic turbine-PV-battery standalone system for tropical climate condition. Renew Energy 2020, 149, 361–373. [Google Scholar] [CrossRef]
- Nag, A.K.; Sarkar, S. Techno-economic analysis of a micro-hydropower plant consists of hydrokinetic turbines arranged in different array formations for rural power supply. Renew Energy 2021, 179, 475–487. [Google Scholar] [CrossRef]
- Xia, T.; Rezaei, M.; Dampage, U.; Ali Alharbi, S.; Nasif, O.; Borowski, P.F.; Mohamed, M.A. Techno-economic assessment of a grid-independent hybrid power plant for co-supplying a remote micro-community with electricity and hydrogen. Processes 2021, 9, 1375. [Google Scholar] [CrossRef]
- Islam, M.S.; Das, B.K.; Das, P.; Rahaman, M.H. Techno-economic optimization of a zero emission energy system for a coastal community in Newfoundland, Canada. Energy 2021, 220, 119709. [Google Scholar] [CrossRef]
- Tigabu, M.T.; Guta, D.D.; Admasu, B.T. Economics of Hydro-Kinetic Turbine for Off-Grid Application: A Case Study of Gumara River, Upper Blue Nile, Amhara, Ethiopia. 2019. Available online: https://www.researchgate.net/publication/336148737 (accessed on 17 May 2022).
- Bonakdari, H. Establishment of relationship between mean and maximum velocities in narrow sewers. J. Environ. Manag. 2012, 113, 474–480. [Google Scholar] [CrossRef]
- Ladokun, L.L.; Ajao, K.R.; Sule, B.F. Hydrokinetic Energy Conversion System Nigeria. Int. J. Technol. 2013, 32, 538–549. [Google Scholar]
- Subramanya, K. Engineering Hydrology, 3rd ed.; The McGraw-Hill Companies: New Delhi, India, 2008. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; The McGraw-Hill Companies: New Delhi, India, 1988. [Google Scholar]
- Bhatta, B.; Shrestha, S.; Shrestha, P.K.; Talchabhadel, R. Evaluation and application of a SWAT model to assess the climate change impact on the hydrology of the Himalayan River Basin. Catena 2019, 181, 104082. [Google Scholar] [CrossRef]
- Fan, F.; Deng, Y.; Hu, X.; Weng, Q. Estimating composite curve number using an improved SCS-CN method with remotely sensed variables in guangzhou, China. Remote Sens 2013, 5, 1425–1438. [Google Scholar] [CrossRef]
- Abdi, I.; Meddi, M. Comparison of conceptual rainfall–runoff models in semi-arid watersheds of eastern Algeria. J. Flood Risk Manag. 2021, 14, e01620. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Simplified versions for the Penman evaporation equation using routine weather data. J. Hydrol. 2006, 331, 690–702. [Google Scholar] [CrossRef]
- Khaldi, A.; Khaldi, A.; Hamimed, A. Using the Priestley-Taylor expression for estimating actual évapotranspiration from satellite Landsat ETM + data. Proc. Int. Assoc. Hydrol. Sci. 2014, 364, 398–403. [Google Scholar] [CrossRef]
- Nakamichi, T.; Moroizumi, T. Applicability of three complementary relationship models for estimating actual evapotranspiration in urban area. J. Hydrol. Hydromech. 2015, 63, 117–123. [Google Scholar] [CrossRef]
- Singer, M.B.; Asfaw, D.T.; Rosolem, R.; Cuthbert, M.O.; Miralles, D.G.; MacLeod, D.; Quichimbo, E.A.; Michaelides, K. Hourly potential evapotranspiration at 0.1° resolution for the global land surface from 1981-present. Sci. Data 2021, 8, 224. [Google Scholar] [CrossRef]
- Jabloun, M.; Sahli, A. Evaluation of FAO-56 methodology for estimating reference evapotranspiration using limited climatic data. Application to Tunisia. Agric. Water Manag. 2008, 95, 707–715. [Google Scholar] [CrossRef]
- Poyen, F.B.; Ghosh, A.K.; Kundu, P.; Sen, K. Sensors & Transducers Analysis of Evaluation Stages Involved in Penman Monteith Equation. 2016. Available online: http://www.sensorsportal.com (accessed on 10 April 2022).
- Hobbins, M.T.; Ramírez, J.A.; Brown, T.C.; Claessens, L.H.J.M. The complementary relationship in estimation of regional evapotranspiration: The Complementary Relationship Areal Evapotranspiration and Advection-Aridity models. Water Resour. Res. 2001, 37, 1367–1387. [Google Scholar] [CrossRef]
- Yang, Y.H.; Zhao, N.; Hao, X.H.; Li, C.Q. Decreasing trend of sunshine hours and related driving forces in North China. Theor. Appl. Climatol. 2009, 97, 91–98. [Google Scholar] [CrossRef]
- Dlouhá, D.; Dubovský, V.; Pospíšil, L. Optimal calibration of evaporation models against penman–monteith equation. Water 2021, 13, 1484. [Google Scholar] [CrossRef]
- Sarkar, M.N.I. Estimation of solar radiation from cloud cover data of Bangladesh. Renew Wind Water Sol. 2016, 3, 11. [Google Scholar] [CrossRef]
- Duki, S.R.H.; Seyedian, S.M.; Rouhani, H.; Farasati, M.; Professor, A. Evaluation of Base Flow Separation Methods for Determining Water Extraction (Case study: Gorganroud River Basin). Water Harvest. Res. 2017, 2, 54–70. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Song, J.; Cheng, L. Evaluating relative merits of four baseflow separation methods in Eastern Australia. J. Hydrol. 2017, 549, 252–263. [Google Scholar] [CrossRef]
- Smakhtin, V.U. Estimating continuous monthly baseflow time series and their possible applications in the context of the ecological reserve. Water SA 2001, 27, 213–217. [Google Scholar] [CrossRef]
- Capesius, J.P.; Arnold, L.R. Comparison of Two Methods for Estimating Base Flow in Selected Reaches of the South Platte River, Colorado. 2012. Available online: http://www.usgs.gov/pubprod (accessed on 20 March 2022).
- Buytaert, W.; de Bièvre, B.; Wyseure, G.; Deckers, J. The use of the linear reservoir concept to quantify the impact of changes in land use on the hydrology of catchments in the Andes. Hydrol. Earth Syst. Sci. 2004, 8, 108–114. [Google Scholar] [CrossRef]
- Yang, H.; Choi, H.T.; Lim, H. Applicability assessment of estimation methods for baseflow recession constants in small forest catchments. Water 2018, 10, 1074. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, D.; Jian, S. Baseflow estimation in typical catchments in the Yellow River Basin, China. Water Sci. Technol. Water Supply 2021, 21, 648–667. [Google Scholar] [CrossRef]
- Feldman, A. Hydrologic Modeling System HEC-HMS: Technical Reference Manual. US Army Corps of Engineers, Hydrological Engineering Center. 2000. Available online: https://www.hec.usace.army.mil/software/hec-hms/documentation/HEC-HMS_Technical%20Reference%20Manual_(CPD-74B).pdf (accessed on 2 July 2022).
- Piggott, A.R.; Moin, S.; Southam, C. A revised approach to the UKIH method for the calculation of baseflow. Hydrol. Sci. J. 2005, 50, 911–920. [Google Scholar] [CrossRef]
- Lee, H.; Choi, H.S.; Chae, M.S.; Park, Y.S. A study to suggest monthly baseflow estimation approach for the long-term hydrologic impact analysis models: A case study in south korea. Water 2021, 13, 2043. [Google Scholar] [CrossRef]
- Mandal, S.; Das, B.K.; Hoque, N. Optimum sizing of a stand-alone hybrid energy system for rural electrification in Bangladesh. J. Clean Prod. 2018, 200, 12–27. [Google Scholar] [CrossRef]
- Sgobba, A.; Meskell, C. On-site renewable electricity production and self consumption for manufacturing industry in Ireland: Sensitivity to techno-economic conditions. J. Clean Prod. 2019, 207, 894–907. [Google Scholar] [CrossRef]
- Elkadeem, M.R.; Wang, S.; Sharshir, S.W.; Atia, E.G. Feasibility analysis and techno-economic design of grid-isolated hybrid renewable energy system for electrification of agriculture and irrigation area: A case study in Dongola, Sudan. Energy Convers. Manag. 2019, 196, 1453–1478. [Google Scholar] [CrossRef]
- Zhang, L.; Barakat, G.; Yassine, A. Deterministic optimization and cost analysis of hybrid pv/wind/battery/diesel power system. Int. J. Renew. Energy Res. 2012, 2, 686–696. [Google Scholar]
- Ma, T.; Javed, M.S. Integrated sizing of hybrid PV-wind-battery system for remote island considering the saturation of each renewable energy resource. Energy Convers. Manag. 2019, 182, 178–190. [Google Scholar] [CrossRef]
- Suresh, V.; Muralidhar, M.; Kiranmayi, R. Modelling and optimization of an off-grid hybrid renewable energy system for electrification in a rural areas. Energy Rep. 2020, 6, 594–604. [Google Scholar] [CrossRef]
- Tezer, T.; Yaman, R. Evaluation of approaches used for optimization of stand-alone hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2017, 73, 840–853. [Google Scholar] [CrossRef]
- Anoune, K.; Bouya, M.; Astito, A.; Abdellah, A.B. Sizing methods and optimization techniques for PV-wind based hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2018, 93, 652–673. [Google Scholar] [CrossRef]
- Alramlawi, M.; Gabash, A.; Mohagheghi, E.; Li, P. Optimal operation of hybrid PV-battery system considering grid scheduled blackouts and battery lifetime. Sol. Energy 2018, 161, 125–137. [Google Scholar] [CrossRef]
- Nagapurkar, P.; Smith, J.D. Techno-economic optimization and social costs assessment of microgrid-conventional grid integration using genetic algorithm and Artificial Neural Networks: A case study for two US cities. J. Clean Prod. 2019, 229, 552–569. [Google Scholar] [CrossRef]
- Das, M.; Singh, M.A.K.; Biswas, A. Techno-economic optimization of an off-grid hybrid renewable energy system using metaheuristic optimization approaches—Case of a radio transmitter station in India. Energy Convers. Manag. 2019, 185, 339–352. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Ogunjobi, K.O.; Abolude, A.T.; Sarris, S.C.; Ladipo, K.O. Assessment of Wind Energy Potential for Small Communities in South-South Nigeria: Case Study of Koluama, Bayelsa State. J. Fundam. Renew. Energy Appl. 2017, 7, 1–6. [Google Scholar] [CrossRef]
- Merem, E.C.; Twumasi, Y.; Wesley, J.; Alsarari, M.; Fageir, S.; Crisler, M.; Romorno, C.; Olagbegi, D.; Hines, A.; Ochai, G.S.; et al. Regional Assessment of Climate Change Hazards in Southern Nigeria with GIS. J. Saf. Eng. 2019, 8, 9–27. [Google Scholar] [CrossRef]
- Okiongbo, K.S.; Douglas, R.K. Evaluation of major factors influencing the geochemistry of groundwater using graphical and multivariate statistical methods in Yenagoa city, Southern Nigeria. Appl. Water Sci. 2015, 5, 27–37. [Google Scholar] [CrossRef]
- Lahimer, A.A.; Alghoul, M.A.; Yousif, F.; Razykov, T.M.; Amin, N.; Sopian, K. Research and development aspects on decentralized electrification options for rural household. Renew. Sustain. Energy Rev. 2013, 24, 314–324. [Google Scholar] [CrossRef]
- NASA. Prediction of Worldwide Energy Resources. 2019. Available online: https://power.larc.nasa.gov/ (accessed on 28 November 2020).
- USGS. SRTM 30m Digital Elevation Data. Available online: https://earthexplorer.usgs.gov/ (accessed on 20 September 2020).
- FAO. Digital Soil Map of the World. Available online: https://www.fao.org/land-water/land/land-governance/land-resources-planning-toolbox/category/details/en/c/1026564/ (accessed on 15 September 2020).
- USGS. Landsat Mission Collection 7. Available online: https://www.usgs.gov/landsat-missions/data (accessed on 17 September 2020).
- Kirke, B. Hydrokinetic and ultra-low head turbines in rivers: A reality check. Energy Sustain. Dev. 2019, 52, 1–10. [Google Scholar] [CrossRef]
- Canadian Solar. MAXPOWER 325P Datasheet. Available online: https://luisfgomez.com.do/wp-content/uploads/2017/10/Panel-Solar-Canadian-CS6U-315-330-Watts.pdf (accessed on 5 January 2021).
- Esan, A.B.; Agbetuyi, A.F.; Oghorada, O.; Ogbeide, K.; Awelewa, A.A.; Afolabi, A.E. Reliability assessments of an islanded hybrid PV-diesel-battery system for a typical rural community in Nigeria. Heliyon 2019, 5, e01632. [Google Scholar] [CrossRef]
- EOCYCLE. Wind Turbine. 2020. Available online: https://eocycle.com/our-wind-turbines/ (accessed on 1 May 2020).
- Burwell, W.J. Optimizing and Implementing a Renewable Micro-Grid for a Remote Alaskan Village. Doctoral Dissertation, Harvard University, Ann Arbor, MI, USA, 2018. [Google Scholar]
- Muratoglu, A.; Yuce, M.I. Design of a River Hydrokinetic Turbine Using Optimization and CFD Simulations. J. Energy Eng. 2017, 143, 04017009. [Google Scholar] [CrossRef]
- Laws, N.D.; Epps, B.P. Hydrokinetic energy conversion: Technology, research, and outlook. Renew. Sustain. Energy Rev. 2016, 57, 1245–1259. [Google Scholar] [CrossRef]
- Rolls, B.E. Battery Specification. Available online: https://www.rollsbattery.com/catalog/#renewable_energy (accessed on 18 December 2020).
- Mongird, K.; Viswanathan, V.V.; Balducci, P.J.; Alam, M.J.E.; Fotedar, V.; Koritarov, V.S.; Hadjerioua, B. Energy Storage Technology and Cost Characterization Report; Department of Energy: Washington, DC, USA, 2019. [Google Scholar]
- Leonics. Apollo MTP-410 Series Data Sheet—Three Phase Bidirectional Dual Mode Inverter for Mini-Grid System. Available online: https://www.leonics.com/product/renewable/inverter/dl/MTP-410-091.pdf (accessed on 14 November 2021).
- Oladigbolu, J.O.; Ramli, M.A.M.; Al-turki, Y.A. Feasibility study and comparative analysis of hybrid renewable power system for off-grid rural electrification in a typical remote village located in Nigeria. IEEE Access 2020, 8, 171643–171663. [Google Scholar] [CrossRef]
- CAT. Diesel Generator Set. Available online: https://cdn.shopify.com/s/files/1/0251/0215/5831/files/DE150E0-C_technical_offer.pdf?370 (accessed on 17 December 2021).
- Ericson, S.; Olis, D. A Comparison of Fuel Choice for Backup Generators; NREL/TP-6A50-72509; National Renewable Energy Laboratory: Golden, CO, USA, 2019; p. 59. [Google Scholar]


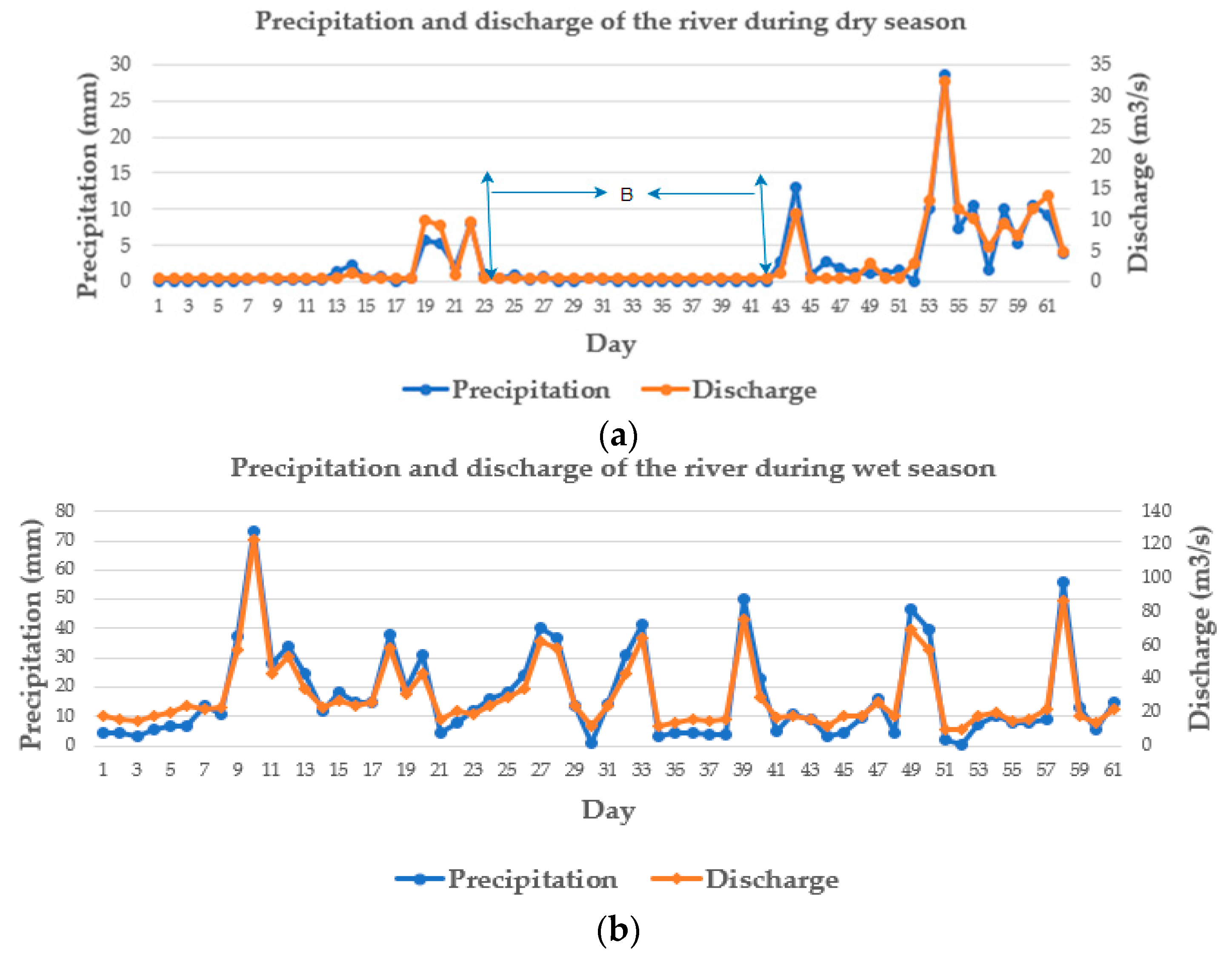
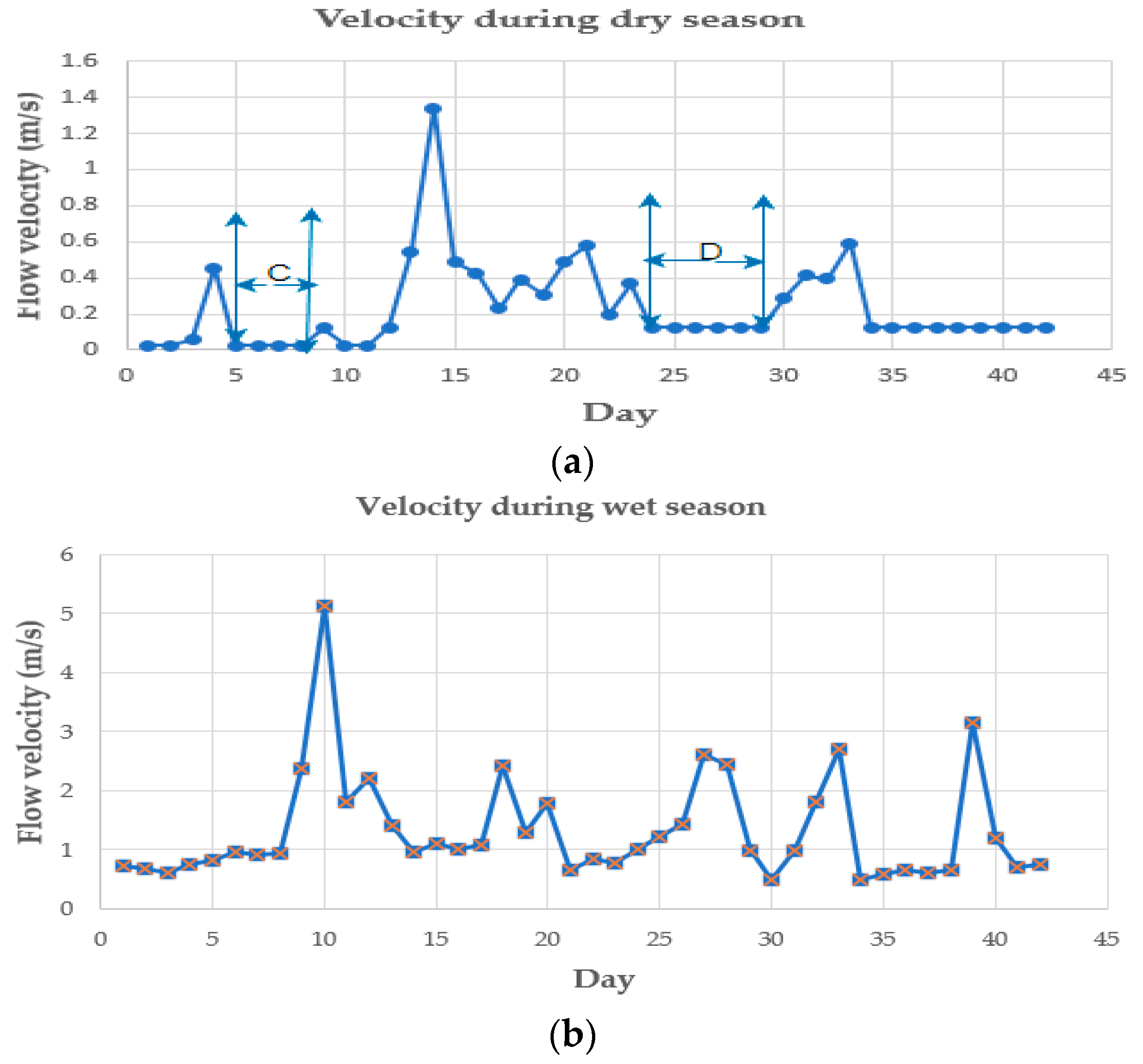
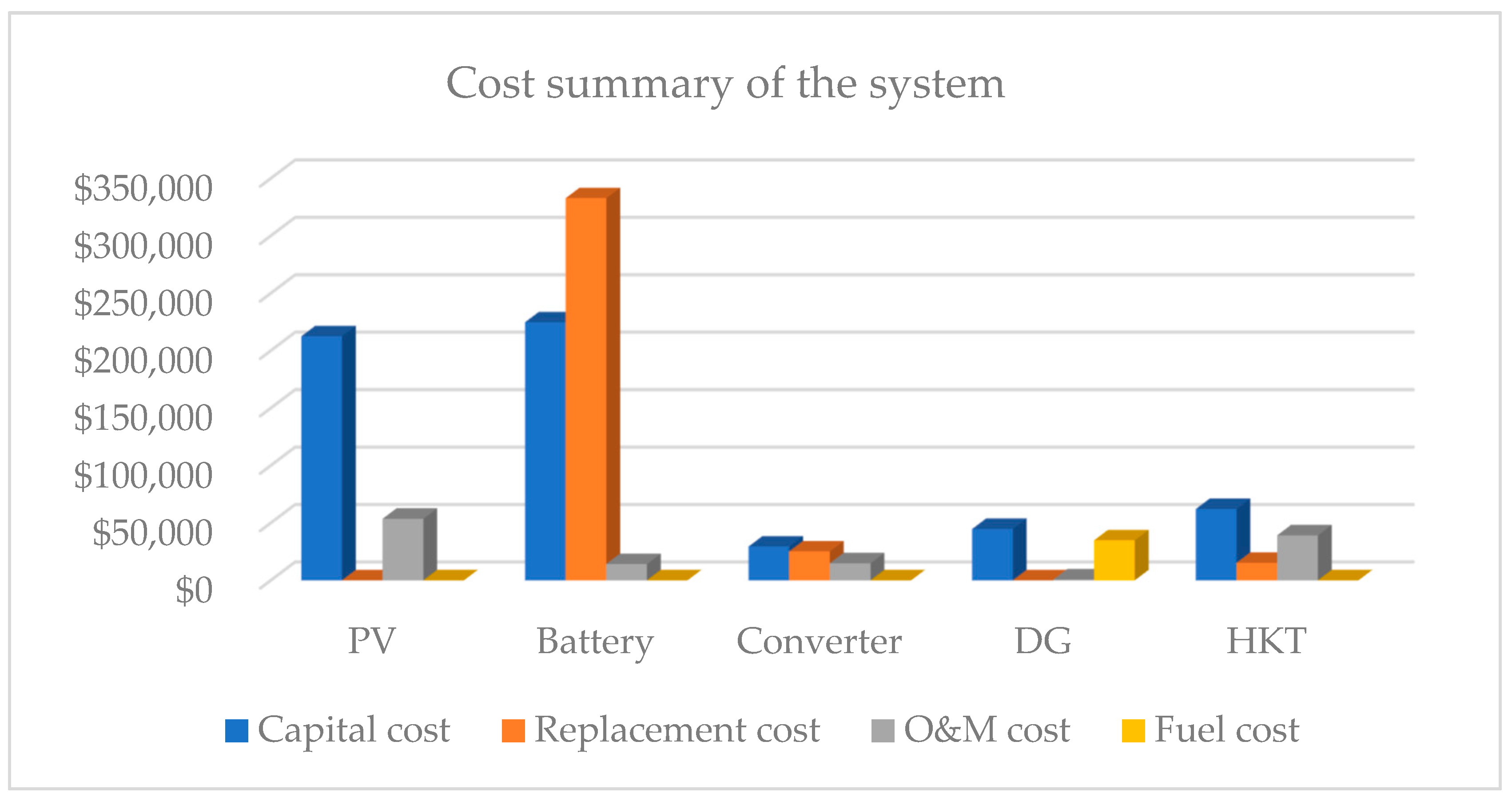


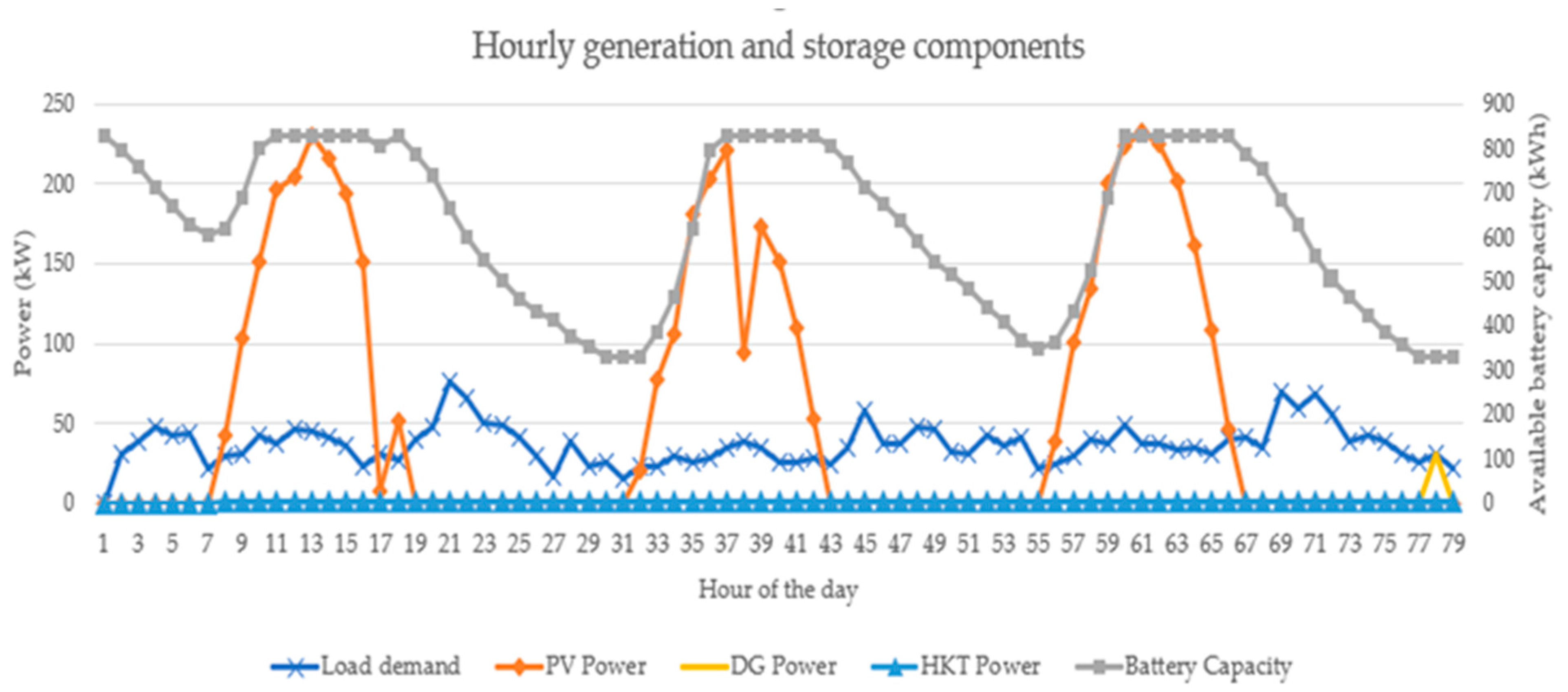
| AMC Level | Total 5-Day Antecedent Rainfall () (mm) | |
|---|---|---|
| Dry season | Wet season | |
| I | ||
| II | ||
| III | ||
| Parameter | (kW) | (Unit) | (Unit) | (Unit) | ||
|---|---|---|---|---|---|---|
| Lower bound | 0 | 0 | 0 | 0 | 80 | 0 |
| Upper bound | 500 | 10 | 5 | 300 | 300 | 2 |
| Parameter | Value |
|---|---|
| Population size | 50 |
| Maximum number of iterations | 500 |
| Crossover fraction | 0.8 |
| Function tolerance | 1e-6 |
| Constraint tolerance | 1e-3 |
| Selection function | Stochastic uniform |
| Data Type | Description | Resolution | Remark | Source |
|---|---|---|---|---|
| Topography map | Digital elevation model (DEM) | 30 m × 30 m | Shuttle Radar Topography Mission | SRTM [104] |
| Land use map | Land use | 30 m | Landsat Mission | Landsat 7 [106] |
| Soil map | Soil type and texture | 10 km | Digital Soil Map of the World | DSMW [105] |
| Weather data | Solar radiation, wind speed, precipitation, etc. | Prediction of Worldwide Energy Resources | NASA [103] |
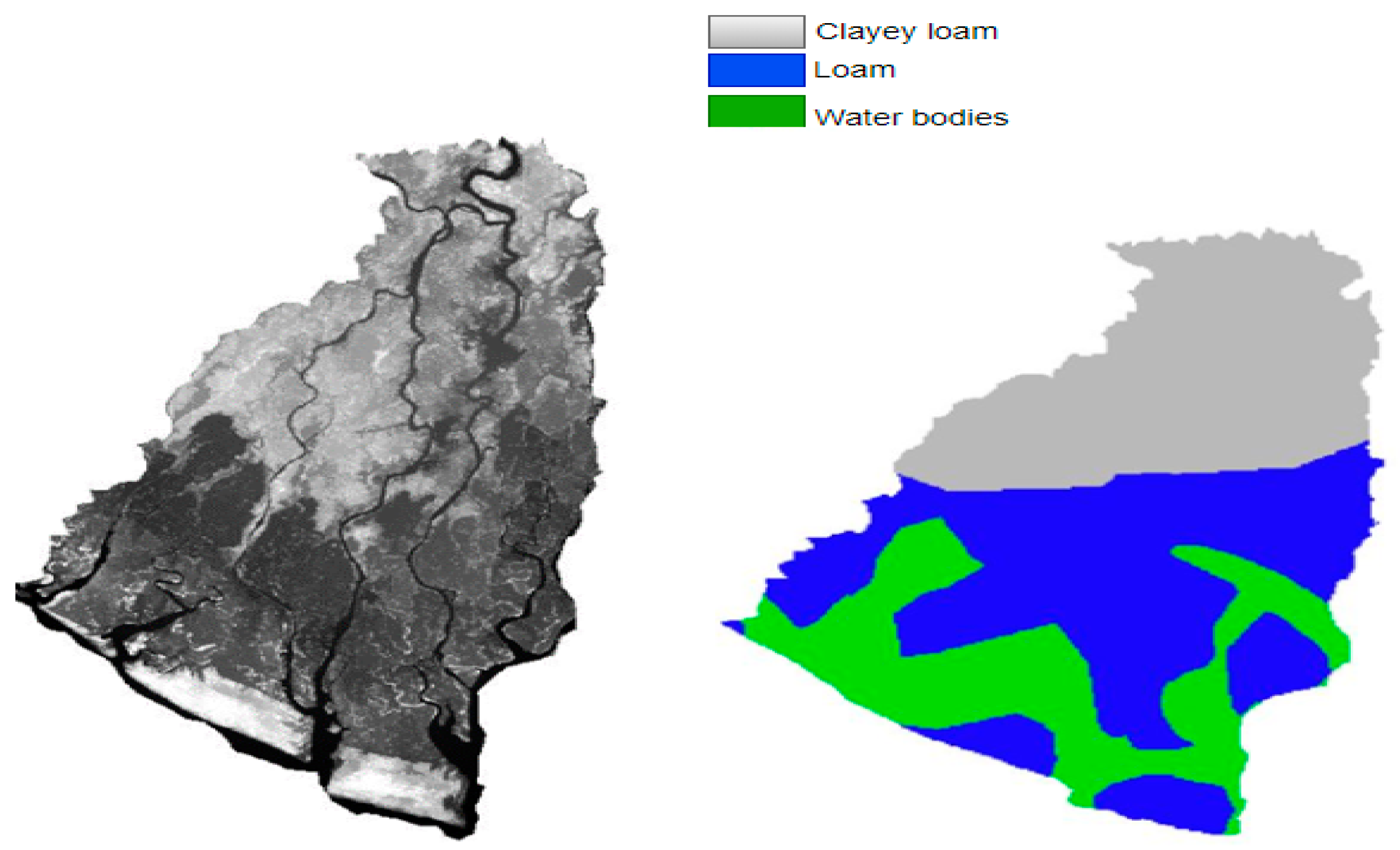
| S/N | Description | Area (km2) | % of the Area |
|---|---|---|---|
| 1 | Clayey loam | 45.32 | 24.52 |
| 2 | Loam | 89.76 | 48.57 |
| 3 | Water bodies | 49.72 | 26.91 |
| S/N | Description | Area (km2) | % of the Area |
|---|---|---|---|
| 1 | Barren land | 10.26 | 5.58 |
| 2 | Residential | 2.28 | 1.24 |
| 3 | Forest, woods, and swamps | 56.08 | 30.48 |
| 4 | Pasture | 30.69 | 16.68 |
| 5 | Agricultural | 41.62 | 22.62 |
| 6 | Bare soil | 27.85 | 15.14 |
| 7 | Water | 15.19 | 8.26 |
| Month | Jan. | Feb. | March | April | May | June | July | Aug. | Sept. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Solar radiation (kWh/m2/d) | 5.79 | 5.91 | 5.49 | 5.29 | 4.60 | 3.67 | 3.64 | 4.33 | 4.30 | 4.76 | 5.40 | 5.60 |
| Wind speed (m/s) | 3.35 | 3.65 | 3.94 | 3.92 | 2.83 | 4.56 | 5.27 | 5.38 | 4.89 | 4.11 | 2.97 | 3.00 |
| Temperature (°C) | 26.17 | 27.07 | 27.32 | 27.16 | 26.78 | 25.88 | 25.10 | 24.85 | 25.09 | 25.59 | 26.23 | 26.30 |
| PV Module | Model: CS6X-325P. Manufacturer: Canadian Solar. Rated capacity: 325 W. Module type: polycrystalline. Efficiency: 16.94%. Temperature power coefficient: −0.41(%/°C). Operating temperature: −40 °C to +85 °C. Lifetime: 25 years [108]. Derating factor: 80%. Capital cost: 664 USD/kW. Replacement cost: 580 USD/kW [109]. Operation and maintenance cost (USD/year): 2% of capital cost. |
| Wind Turbine | Model: EO25III. Manufacturer: Eocycle. Rated capacity: 25 kW. Cut-in wind speed: 2.75 m/s. Cut-out wind speed: 20 m/s. Rotor diameter: 15.8 m. Lifetime: 20 years [110]. Capital cost: USD 175,000 [111]. Replacement cost: USD 120,000. Operation and maintenance (USD/year): 5% of capital cost. |
| Hydrokinetic Turbine | Model: TIGRIS-27 H. Rated capacity: 27 kW@2.7 m/s. Cut-in water velocity: 0.5 m/s. Lifetime: 20 years. Number of blades: 3 Rotor diameter: 3 m. Power coefficient: 0.43 [112]. Capital cost: 1150 USD/kW [113]. Replacement: 1000 USD/kW. Operation and maintenance cost (USD/year): 5% of capital cost. |
| Storage Battery | Model: Surrette 6CS25P. Manufacturer: Rolls. Type: Lead–acid. Nominal voltage: 6V. Nominal capacity: 6.91 kWh. Round trip efficiency: 80%. [114]. Lifetime: 5 years. Capital cost: 271 USD/kWh [115]. Replacement cost: 200 USD/kWh. Operation and maintenance cost (USD/year): 0.5% of the capital cost. |
| Power converter | Model: S219cph. Manufacturer: Leonics. Rated capacity: 5 kW. DC input voltage: 48 Vdc. Efficiency: 96% [116]. Lifetime: 10 years. Capital cost: 245 USD/kW. Replacement cost: 245 USD/kW [117]. Operation and maintenance cost (USD/year): 4% of capital cost. |
| Diesel generator | Model: DE150E0. Manufacturer: CAT. Engine speed: 1500 RPM. Lifetime: 60,000 h. Voltage: 400/230 Vac. Frequency: 50 Hz [118]. Fuel price: 0.7 USD/L. Capital cost: 447 USD/kW [119]. Replacement cost: 400 USD/kW. Operation and maintenance cost (USD/h): 0.4. |
| Month | Jan. | Feb. | March | April | May | June | July | Aug. | Sept. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean discharge (m3/s) | 1.48 | 1.07 | 6.98 | 2.75 | 13.82 | 31.33 | 17.39 | 29.15 | 33.15 | 26.62 | 9.05 | 0.75 |
| Max discharge (m3/s) | 9.82 | 10.91 | 32.18 | 19.51 | 96.57 | 103.4 | 109.6 | 85.10 | 122.9 | 86.92 | 30.04 | 5.33 |
| Min discharge (m3/s) | 0.58 | 0.59 | 2.96 | 1.25 | 4.83 | 10.49 | 5.95 | 10.79 | 11.66 | 9.44 | 3.31 | 0.39 |
| Capital Cost (USD) | Replacement Cost (USD) | OM Cost (USD) | Fuel Cost (USD) |
|---|---|---|---|
| 44,700 | 47,541 | 29,897 | 1,467,800 |
| System | TNPC (USD) | COE (USD/kWh) | Capital Cost (USD) | Fuel Cost (USD) | DG Operation (h/year) | Fuel Consumed (L/year) | Total Load Served (kWh/year) |
|---|---|---|---|---|---|---|---|
| DG-only | 1,589,918 | 0.5182 | 44,700 | 1,467,763 | 5925 | 166,220 | 233,320 |
| Optimal HRES | 1,103,668 | 0.2841 | 573,320 | 34,822 | 141 | 3943.5 | 307,940 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ileberi, G.R.; Li, P. Integrating Hydrokinetic Energy into Hybrid Renewable Energy System: Optimal Design and Comparative Analysis. Energies 2023, 16, 3403. https://doi.org/10.3390/en16083403
Ileberi GR, Li P. Integrating Hydrokinetic Energy into Hybrid Renewable Energy System: Optimal Design and Comparative Analysis. Energies. 2023; 16(8):3403. https://doi.org/10.3390/en16083403
Chicago/Turabian StyleIleberi, Gbalimene Richard, and Pu Li. 2023. "Integrating Hydrokinetic Energy into Hybrid Renewable Energy System: Optimal Design and Comparative Analysis" Energies 16, no. 8: 3403. https://doi.org/10.3390/en16083403
APA StyleIleberi, G. R., & Li, P. (2023). Integrating Hydrokinetic Energy into Hybrid Renewable Energy System: Optimal Design and Comparative Analysis. Energies, 16(8), 3403. https://doi.org/10.3390/en16083403








