Numerical Simulation of Vapor Dropwise Condensation Process and Droplet Growth Mode
Abstract
1. Introduction
2. Method
2.1. Model of the Whole Evolution Process of Dropwise Condensation
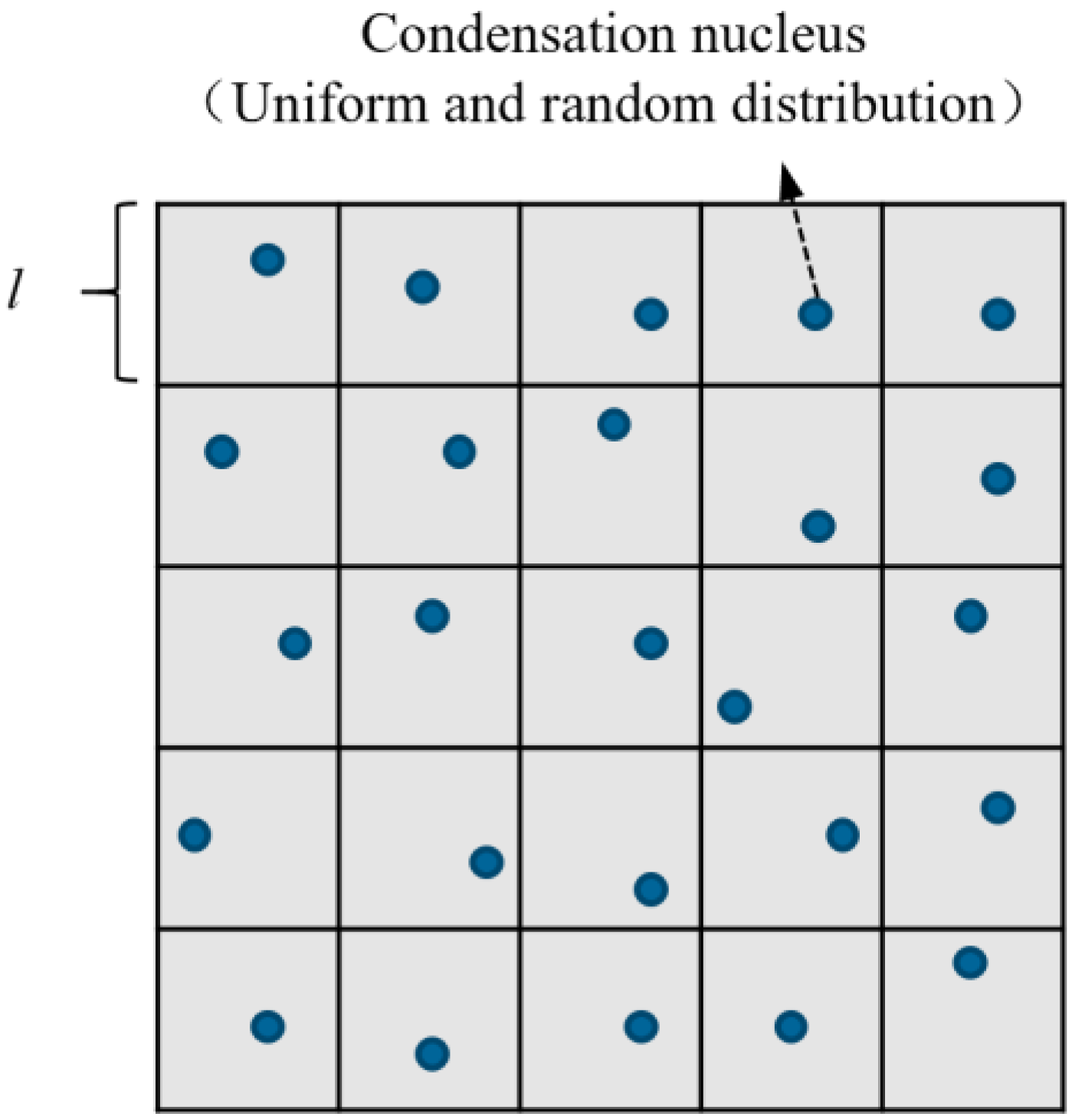
2.1.1. Droplet Nucleation and Renucleation
2.1.2. Droplet Growth
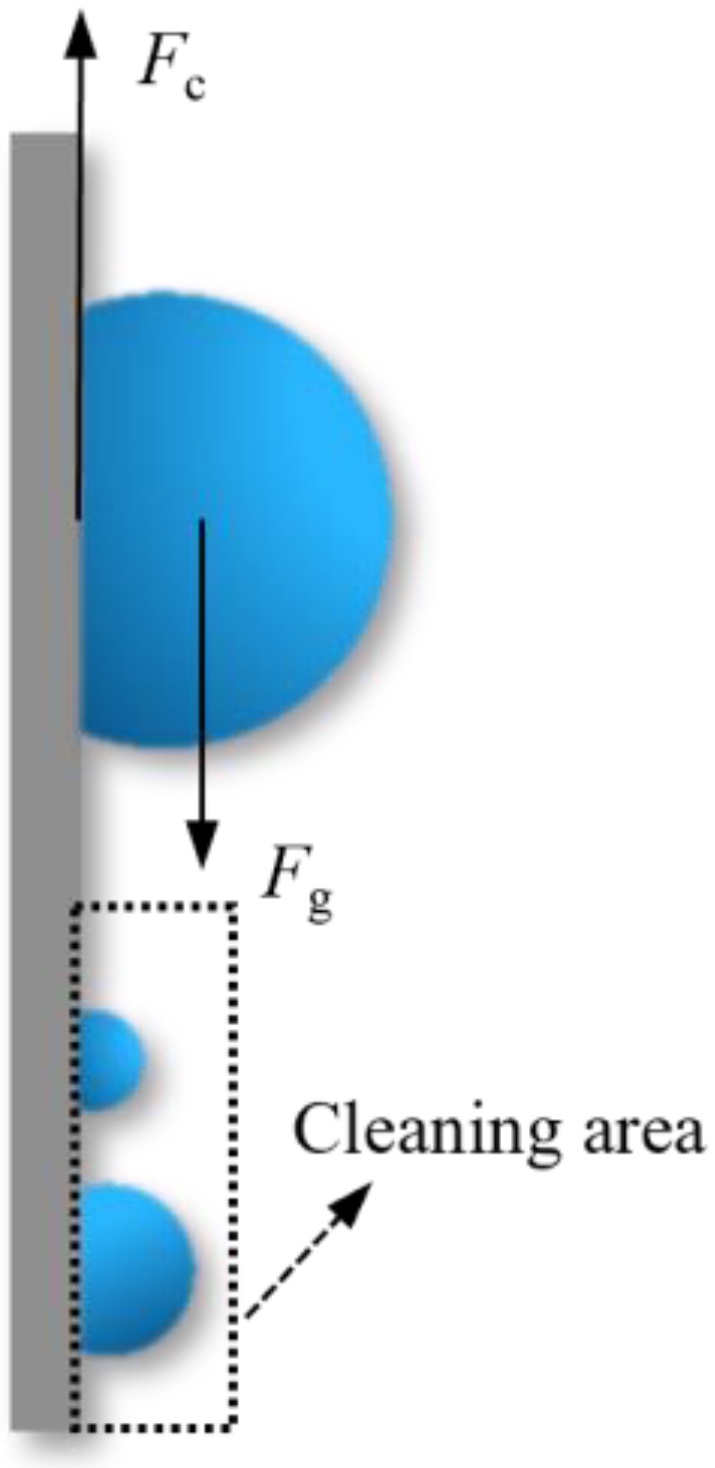
2.1.3. Droplet Departure
2.2. Simulation Method
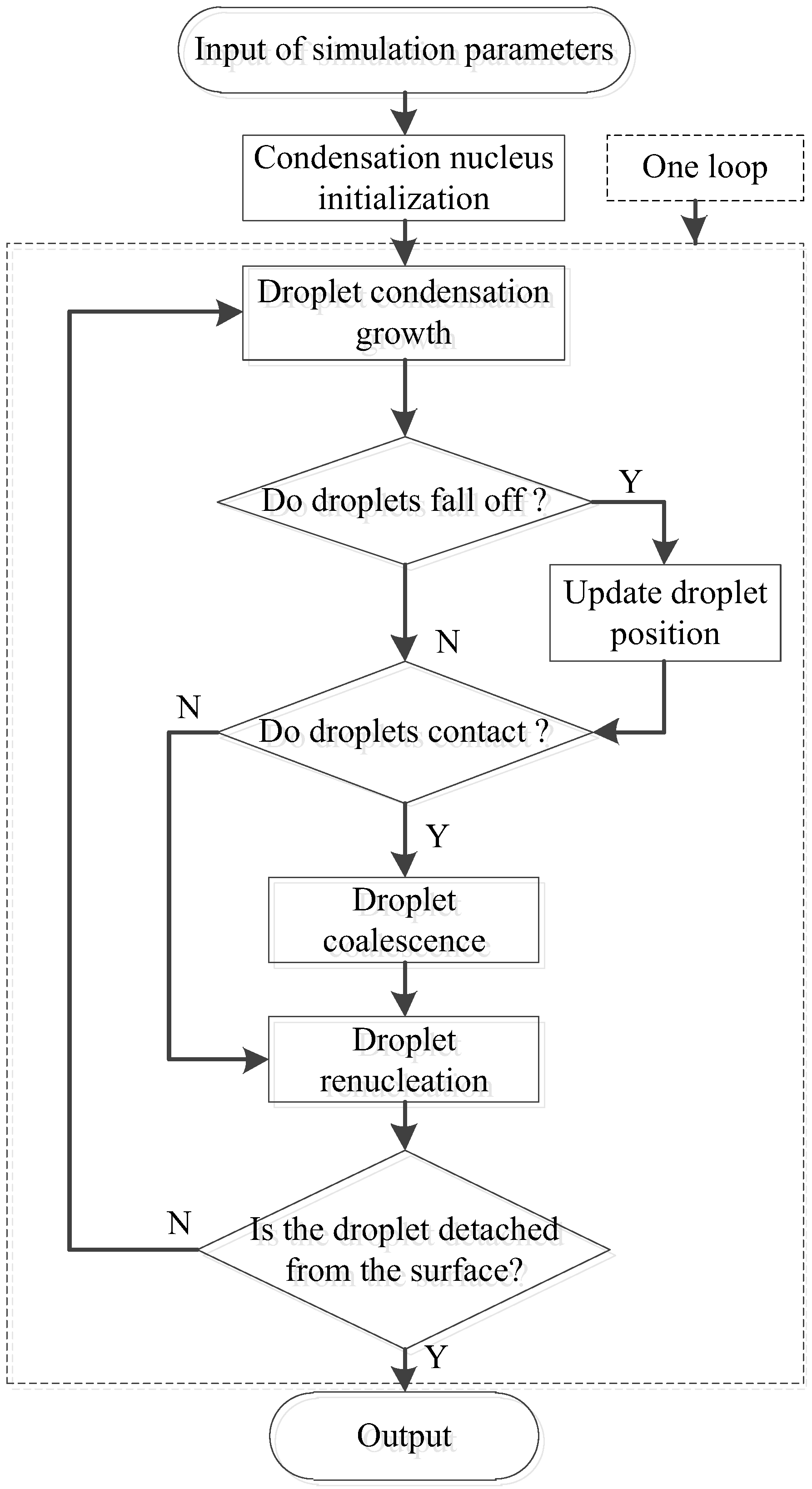
2.2.1. Simulation Procedure and Algorithm
- The formation position of condensation nuclei is fixed, and the condensation nuclei demonstrate uniformly random distribution;
- The droplet is considered an ideal spherical crown when computing its spatial position and size;
- The property of the hydrophobic surface is uniform, and the droplets have the same contact angle.
2.2.2. Simulation Parameters
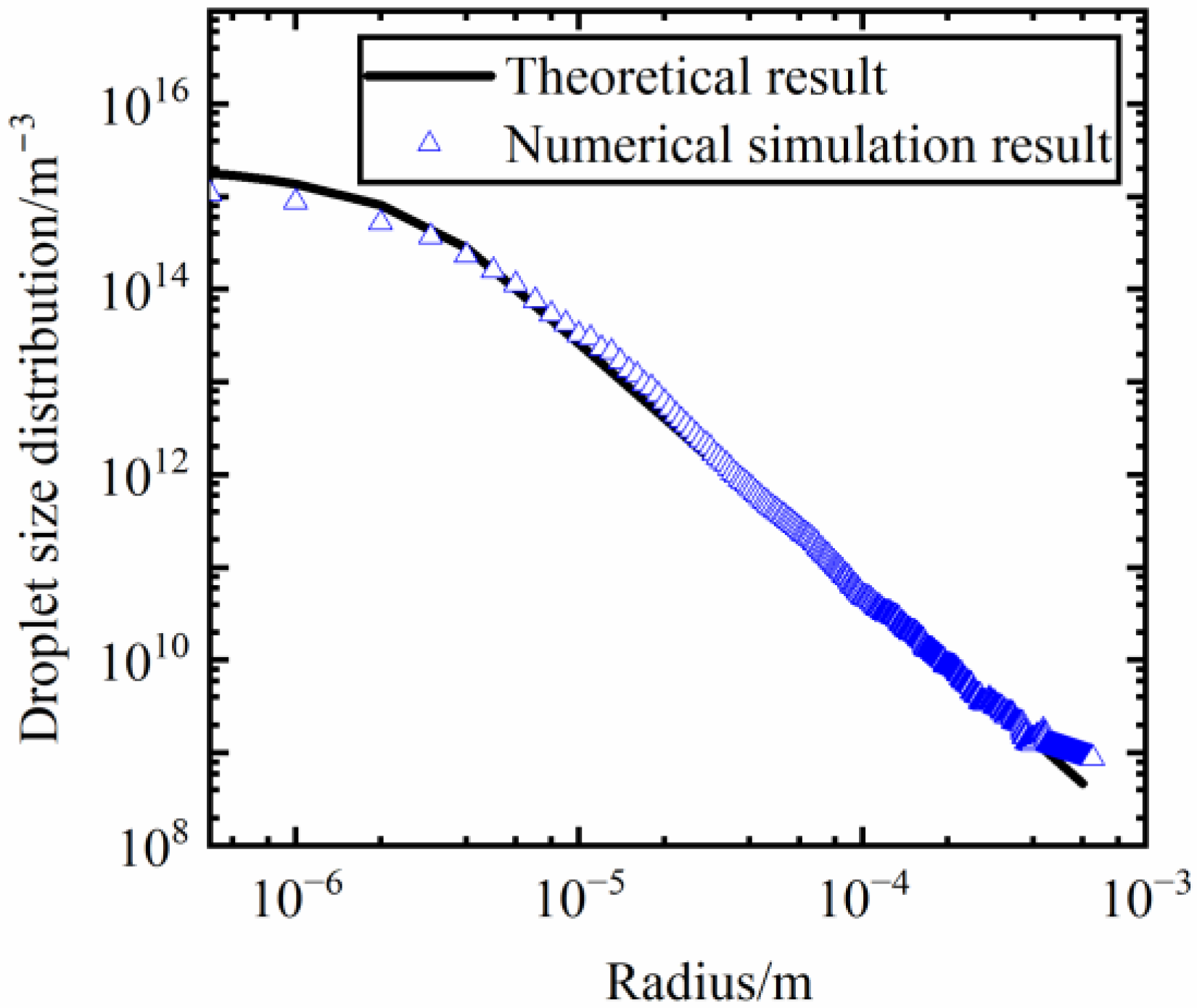
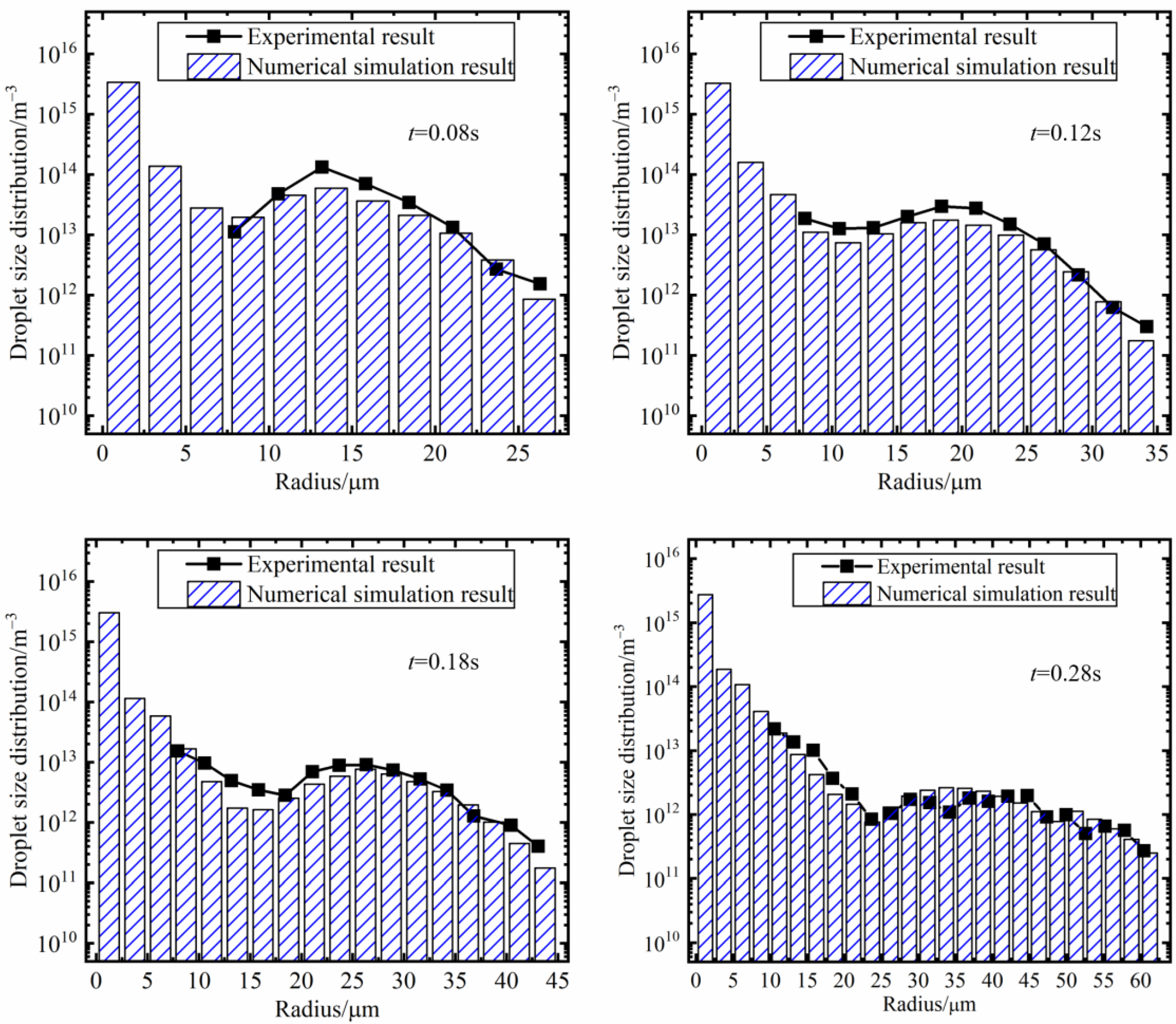
2.3. Reliability Demonstration of the Simulation
3. Results and Discussion
3.1. Dropwise Condensation Process
3.1.1. Droplet Growth and Condensation Evolution
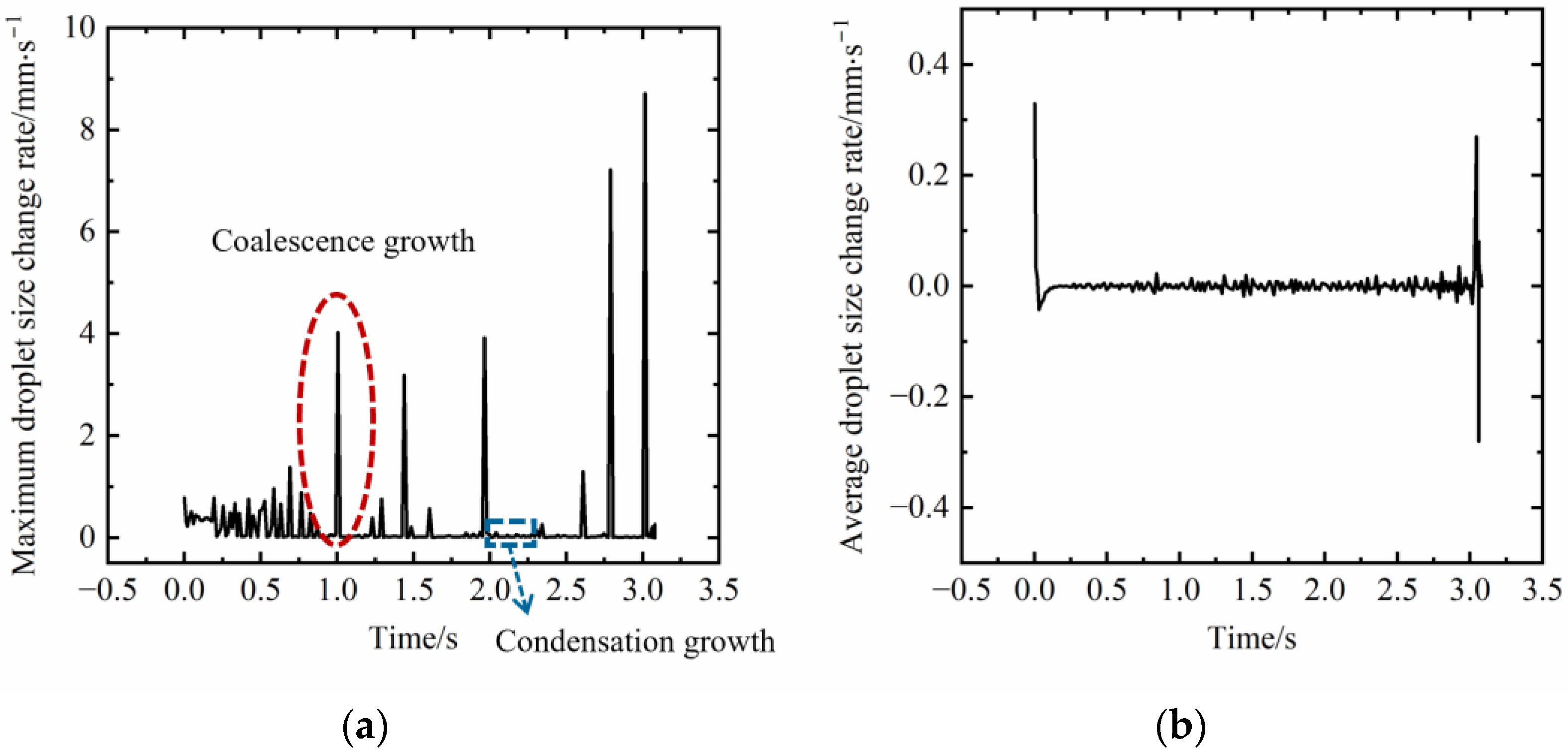
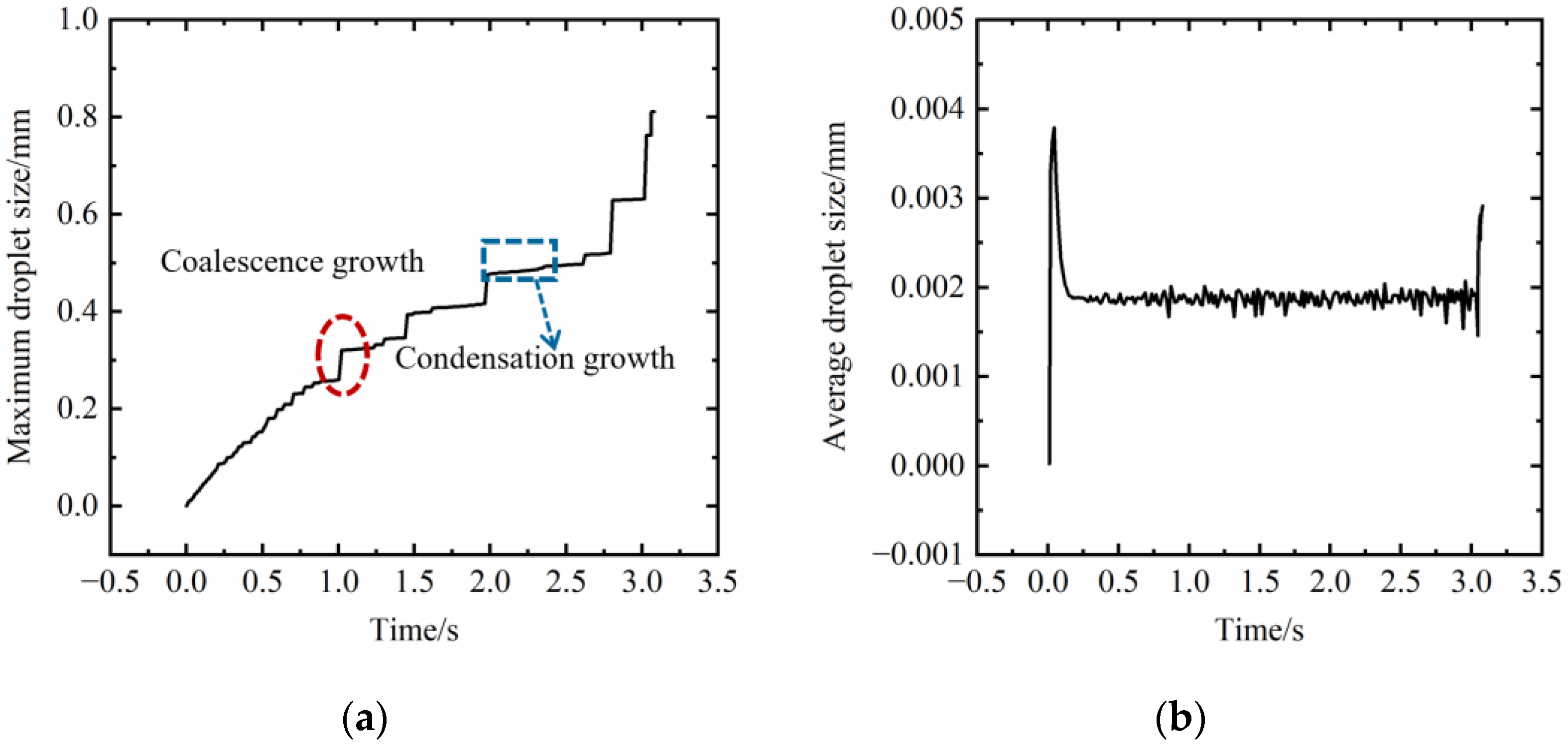
3.1.2. Characterization of the Evolution Rate of Dropwise Condensation Process
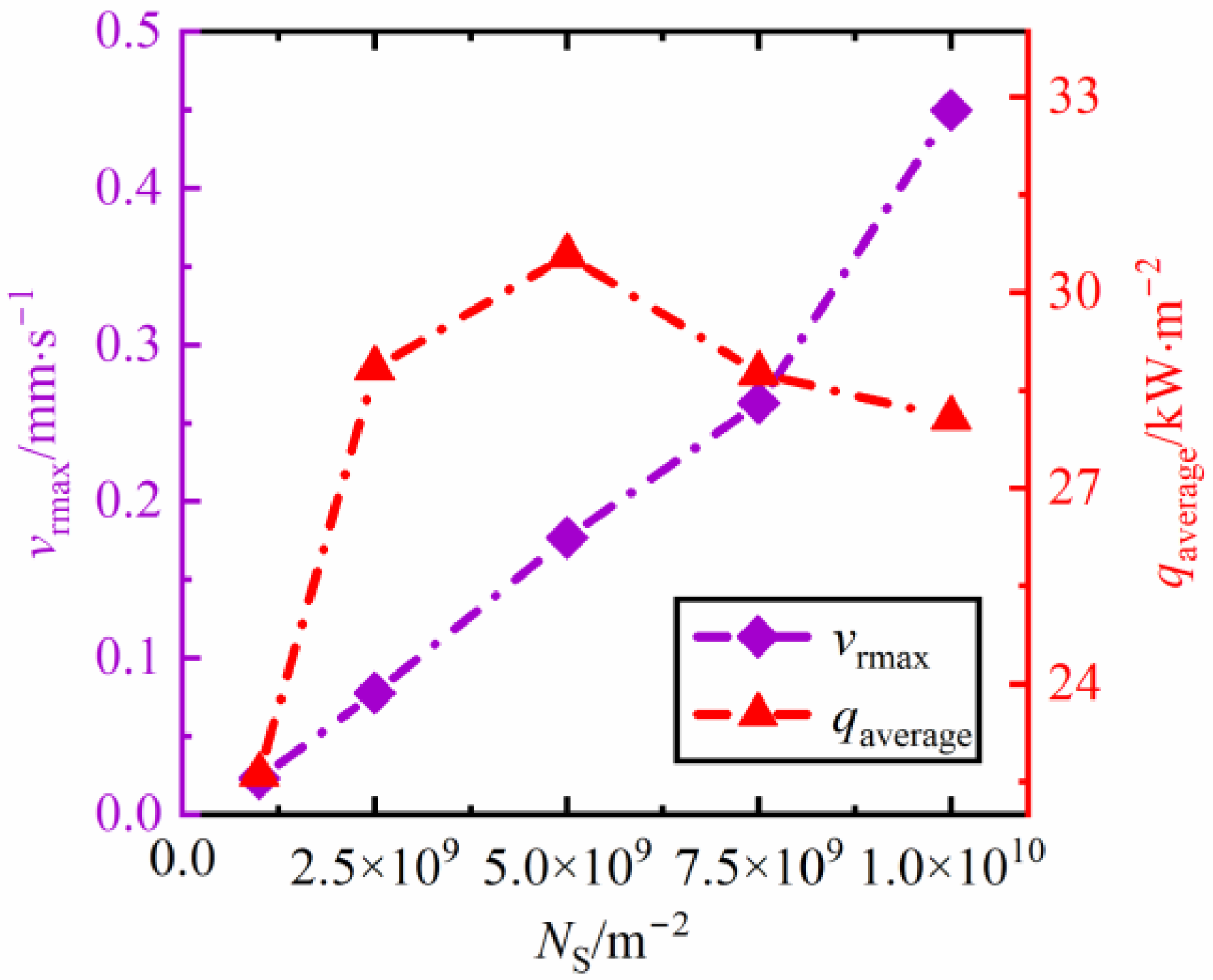
3.2. The influence of Nucleus Densities on the Evolution Rate and Heat Transfer of Dropwise Condensation
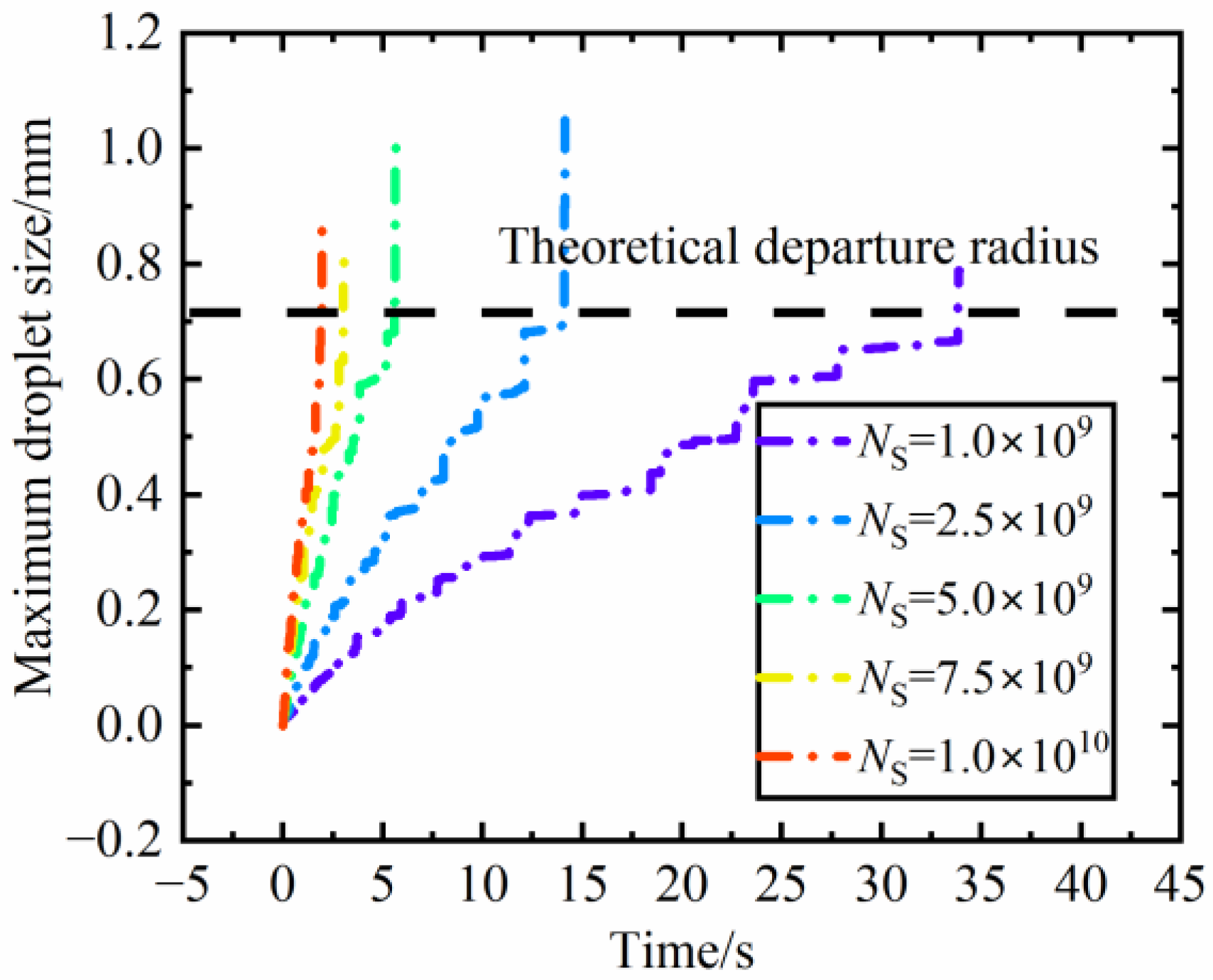
3.2.1. The Influence of Nucleus Densities on the Evolution Rate of Dropwise Condensation
3.2.2. The Influence of Nucleus Densities of Surface Condensation on the Heat Transfer of Dropwise Condensation
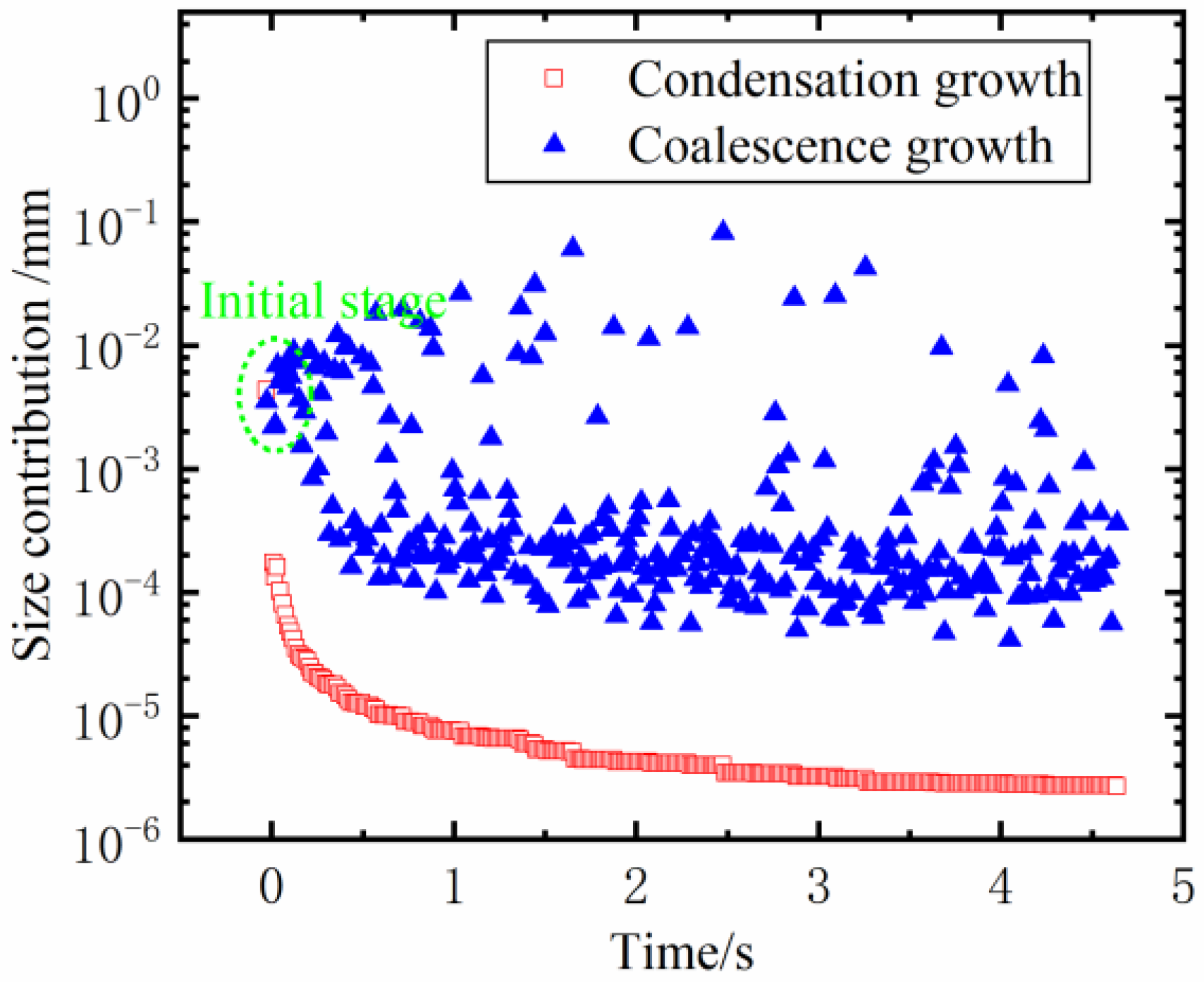
3.3. The Influence of Droplet Growth Modes on the Evolution Process of the Dropwise Condensation
3.3.1. The Contribution of Diverse Growth Modes to the Maximum Droplet Size
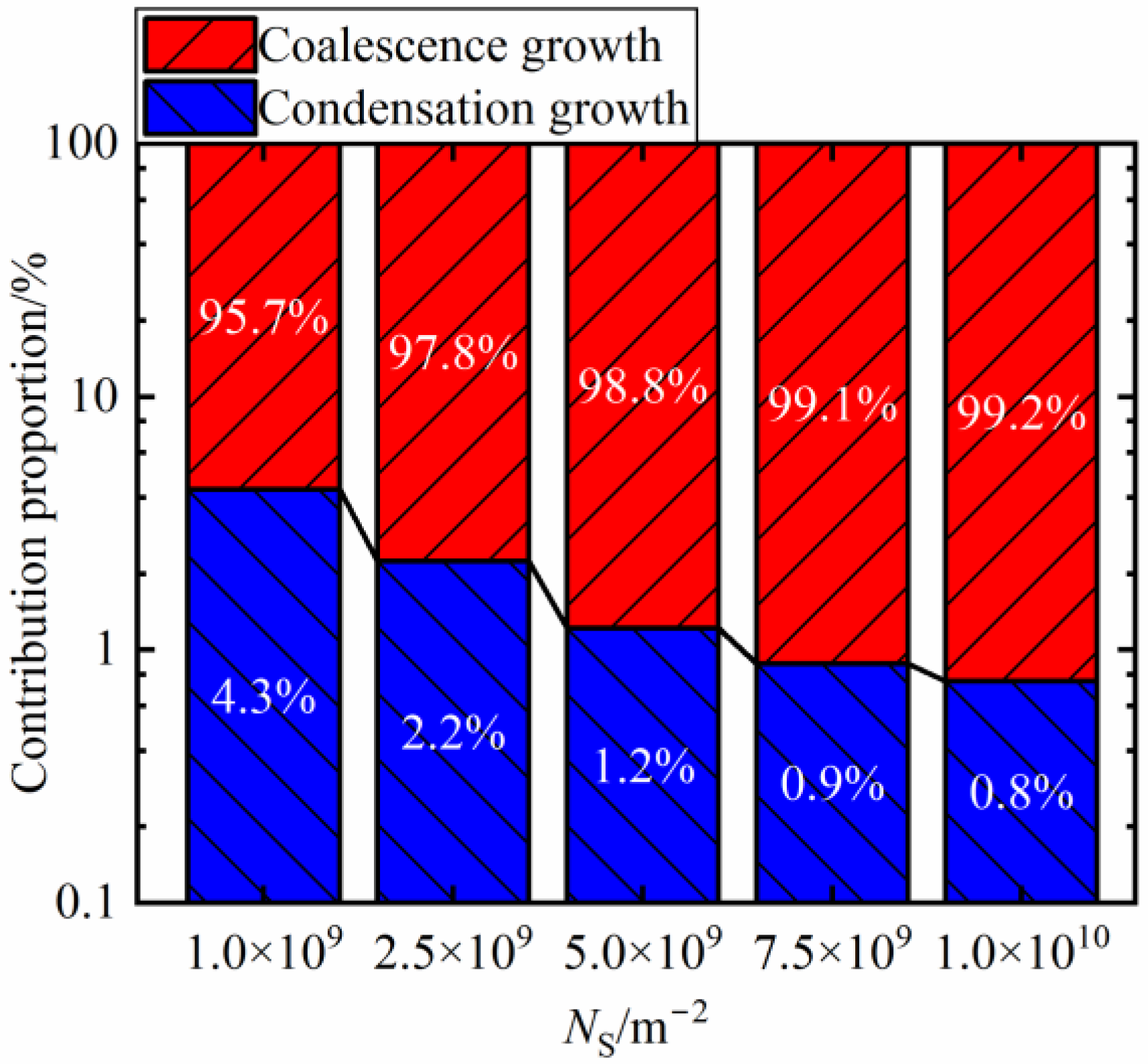
3.3.2. The Contribution Ratio of two Growth Modes under Different Nucleus Densities
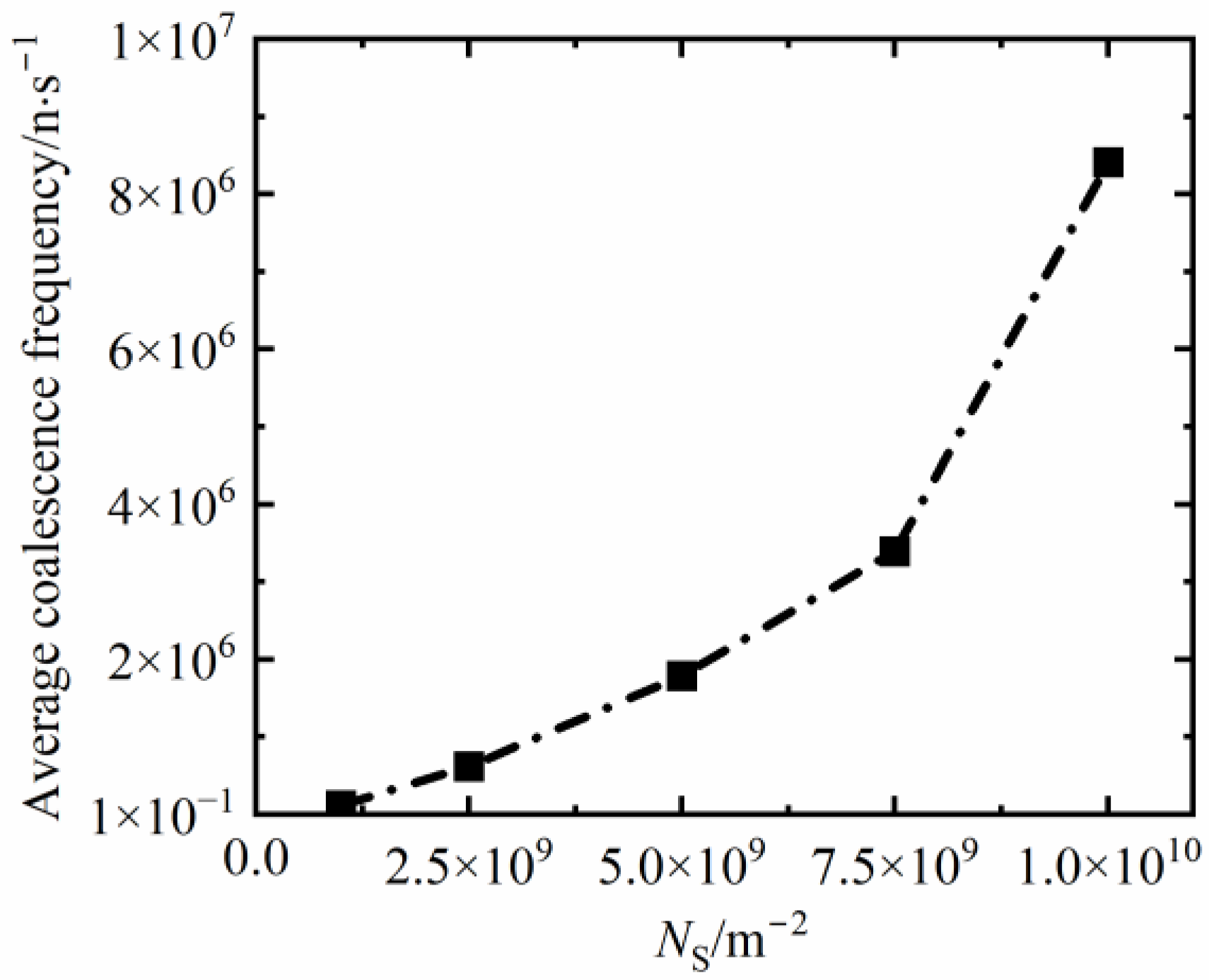
3.3.3. The Coalescence Frequency at Different Nucleus Densities
4. Conclusions
- (1)
- The maximum radius growth rate can better indicate the evolution rate of dropwise condensation than the average droplet size rate;
- (2)
- The enhancement in condensation nucleus density contributes to a linear increase in the evolution rate of dropwise condensation, thereby accelerating the evolution process;
- (3)
- At low condensation nucleus density (less than NS = 5 × 109 m−2), with the increase of condensation nucleus density, the heat transfer capacity of the condensation surface is significantly improved. However, there is a critical value, NS = 5 × 109 m−2. As the nucleus density exceeds such a value, the average heat flux decreases after gradually reaching its peak, qaverage = 30.5 kW·m−2;
- (4)
- Compared to condensation growth, coalescence growth has a more significant effect on the evolution process of dropwise condensation. More than 95% of the maximum droplet size throughout the condensation evolution process originates from coalescence growth, while the effect of condensation growth is minor;
- (5)
- The surfaces with high coalescence frequency can augment the contribution of the coalescence growth to the maximum droplet size more effectively. Conversely, the contribution of condensation growth is weakened, which is less than 1% at the NS = 7.5 × 109 m−2.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | acceleration of the droplet (m/s2) |
| x | x-coordinate of the droplet |
| c | capillary force constant |
| xi | x-coordinate of one of the adjacent droplets (m) |
| Fc | capillary force (N) |
| xj | x-coordinate of the other of the adjacent droplets (m) |
| Fg | gravity force (N) |
| xmin | x-coordinate of the condensation nucleus (m) |
| G | growth rate of dropwise condensation (m/s) |
| xside | x-coordinate of the droplet closest to the condensation nucleus (m) |
| G/g | acceleration of gravity (m/s2) |
| xnew | x-coordinate of new droplet formed by the coalescence (m) |
| Hfg | latent heat of condensed water (J·kg−1) |
| y | y-coordinate of the droplet |
| hi | heat transfer coefficient of gas-liquid section (W·m−2·K−1) |
| yb | y-coordinate of the droplet before the droplet departure within Δt(m) |
| kw | thermal conductivity of water (W·m−1·K−1) |
| yi | y-coordinate of one of the adjacent droplets (m) |
| kδ | thermal conductivity of hydrophobic membrane (W·m−1·K−1) |
| yj | y-coordinate of the other of the adjacent droplets (m) |
| l | mesh spacing (m) |
| ymin | y-coordinate of the condensation nucleus (m) |
| lij | distance between adjacent droplets (m) |
| yn | y-coordinate of the droplet after the droplet departure within Δt(m) |
| NS | condensation nucleus density (m−2) |
| ynew | y-coordinate of new droplet formed by the coalescence (m) |
| qd | droplet heat transfer rate (kW·m−2) |
| yside | y-coordinate of the droplet closest to the condensation nucleus (m) |
| r | radius of the droplet (m) |
| z | z-coordinate of the droplet |
| rb | radius of the droplet before the condensation growth within Δt(m) |
| zi | z-coordinate of one of the adjacent droplets (m) |
| rc | critical radius (m) |
| zj | z-coordinate of the other of the adjacent droplets (m) |
| ri | radius of one of the adjacent droplets (m) |
| zmin | z-coordinate of the condensation nucleus (m) |
| rj | radius of the other the adjacent droplets (m) |
| znew | z-coordinate of new droplet formed by the coalescence (m) |
| rmax(i,j) | the maximum radius of the adjacent droplets (m) |
| zside | z-coordinate of the droplet closest to the condensation nucleus (m) |
| rmin | initial nucleation radius (m) |
| σ | surface tension coefficient (N·m−1) |
| rn | radius of the droplet after the condensation growth within (m) |
| ρ | density of condensate water (kg·m−3) |
| radius of new droplet formed by the coalescence (m) | |
| δ | thickness of hydrophobic coating (m) |
| rside | radius of the droplet closest to the condensation nucleus (m) |
| θ | contact angle of droplet (°) |
| distance of droplet departure within Δt(m) | |
| θr | droplet regression angle (°) |
| Tsat | Saturation temperatures (K) |
| θa | droplet advance angle (°) |
| Vi | volume of one of the adjacent droplets (m3) |
| the size contribution of coalescence growth behavior (m) | |
| Vj | volume of the other the adjacent droplets (m3) |
| Δrl | the size contribution of condensation growth behavior (m) |
| Vnew | volume of new droplet formed by the coalescence (m3) |
| ΔT | surface subcooling (K) |
| vb | initial velocity of the droplet (m/s) |
| Δt | step size (s) |
| vn | the droplet detachment velocity after Δt(m/s) |
References
- Tang, G.; Hu, H. Advances in vapor dropwise condensation heat transfer. Chin. Sci. Bull. 2020, 65, 1653–1676. (In Chinese) [Google Scholar] [CrossRef]
- Wen, F. Microscopic Mechanism of Steam Dropwise Condensation at Low Pressure and Heat Transfer Enhancement. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2014. [Google Scholar]
- Rose, J.W. Dropwise condensation theory and experiment: A review. Proc. Inst. Mech. Eng. Part A 2002, 216, 115–128. [Google Scholar] [CrossRef]
- Peng, Q.; Jia, L. Analysis of droplet dynamic behavior and condensation heat transfer characteristics on rectangular microgrooved surface with CuO nanostructures. Int. J. Heat Mass Tran. 2019, 130, 1096–1107. [Google Scholar] [CrossRef]
- Suss, M.E.; Presser, V. Water desalination with energy storage electrode materials. Joule 2018, 2, 10–15. [Google Scholar] [CrossRef]
- Wen, R.; Xu, S. Capillary-driven liquid film boiling heat transfer on hybrid mesh wicking structures. Nano Energy 2018, 51, 373–382. [Google Scholar] [CrossRef]
- Stark, A.K.; Klausner, J.F. An R&D strategy to decouple energy from water. Joule 2017, 1, 416–420. [Google Scholar] [CrossRef]
- Schmidt, E.; Schurig, W. Condensation of water vapour in film-and drop form. Tech. Mech. Thermodyn. 1930, 1, 53–63. [Google Scholar]
- Graham, C.; Griffith, P. Drop size distributions and heat transfer in dropwise condensation. Int. J. Heat Mass Tran. 1973, 16, 337–346. [Google Scholar] [CrossRef]
- Gose, E.E.; Mucciardi, A.N. Model for dropwise condensation on randomly distributed sites. Int. J. Heat Mass Tran. 1967, 10, 15–22. [Google Scholar] [CrossRef]
- Rose, J.W.; Glicksman, L.R. Dropwise condensation—The distribution of drop sizes. Int. J. Heat Mass Tran. 1973, 16, 411–425. [Google Scholar] [CrossRef]
- Tanasawa, I. Dropwise condensation the way to practical applications. In Proceedings of the International Heat Transfer Conference Digital Library, Toronto, ON, Canada, 7–11 August 1978. [Google Scholar] [CrossRef]
- Chen, J.C. Surface contact—Its significance for multiphase heat transfer: Diverse examples. J. Heat Transfer. 2003, 125, 549–566. [Google Scholar] [CrossRef]
- Peng, B.; Ma, X. Experimental investigation on steam condensation heat transfer enhancement with vertically patterned hydrophobic–hydrophilic hybrid surfaces. Int. J. Heat Mass Tran. 2015, 83, 27–38. [Google Scholar] [CrossRef]
- Chen, X.; Derby, M.M. Combined visualization and heat transfer measurements for steam flow condensation in hydrophilic and hydrophobic mini-gaps. J. Heat Transfer. 2016, 138, 091503. [Google Scholar] [CrossRef]
- Alwazzan, M.; Egab, K. Condensation on hybrid-patterned copper tubes (I): Characterization of condensation heat transfer. Int. J. Heat Mass Tran. 2017, 112, 991–1004. [Google Scholar] [CrossRef]
- Bhattarai, B.; Priezjev, N.V. Wetting properties of structured interfaces composed of surface-attached spherical nanoparticles. Comput. Mater. Sci. 2018, 143, 497–504. [Google Scholar] [CrossRef]
- Ashrafi-Habibabadi, A.; Moosavi, A. Droplet condensation and jumping on structured superhydrophobic surfaces. Int. J. Heat Mass Tran. 2019, 134, 680–693. [Google Scholar] [CrossRef]
- Aili, A.; Ge, Q. How nanostructures affect water droplet nucleation on superhydrophobic surfaces. J. Heat Transfer. 2017, 139, 112401. [Google Scholar] [CrossRef]
- Lefevre, E.J.; Rose, J.W. A theory of heat transfer by dropwise condensation. In Proceedings of the International Heat Transfer Conference Digital Library, Chicago, IL, USA, 7–12 August 1966. [Google Scholar] [CrossRef]
- Maa, J.R. Drop size distribution and heat flux of dropwise condensation. Chem. Eng. J. 1978, 16, 171–176. [Google Scholar] [CrossRef]
- Miljkovic, N.; Enright, R. Modeling and optimization of superhydrophobic condensation. J. Heat Transfer. 2013, 135, 111004. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, P. Dropwise condensation theory revisited: Part I. Droplet nucleation radius. Int. J. Heat Mass Tran. 2015, 83, 833–841. [Google Scholar] [CrossRef]
- Han, X.; Han, Z. Coupled model of heat and mass balance for droplet growth in wet steam non-equilibrium homogeneous condensation flow. Energies 2017, 10, 2033. [Google Scholar] [CrossRef]
- Shang, Y.; Hou, Y. Modeling and optimization of condensation heat transfer at biphilic interface. Int. J. Heat Mass Tran. 2018, 122, 117–127. [Google Scholar] [CrossRef]
- Xie, J.; Xu, J. Dropwise condensation on superhydrophobic nanostructure surface, part II: Mathematical model. Int. J. Heat Mass Tran. 2018, 127, 1170–1187. [Google Scholar] [CrossRef]
- Burnside, B.M.; Hadi, H.A. Digital computer simulation of dropwise condensation from equilibrium droplet to detectable size. Int. J. Heat Mass Tran. 1999, 42, 3137–3146. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, P. Lattice Boltzmann simulation for dropwise condensation of vapor along vertical hydrophobic flat plates. Int. J. Heat Mass Tran. 2013, 64, 1041–1052. [Google Scholar] [CrossRef]
- Pawar, N.D.; Kondaraju, S. Effect of Surface Wettability on Dropwise Condensation Using Lattice Boltzmann Method. In Proceedings of the International Conference on Micro/Nanoscale Heat Transfer, Singapore, 3–6 January 2016. [Google Scholar] [CrossRef]
- Bahrami, H.R.T.; Saffari, H. Theoretical study of stable dropwise condensation on an inclined micro/nano-structured tube. Int. J. Refrig. 2017, 75, 141–154. [Google Scholar] [CrossRef]
- Zhao, C.; Yan, X. Numerical simulation of droplet size distribution in the whole process of droplet condensation. J. Eng. 2020, 41, 1485–1490. (In Chinese) [Google Scholar]
- Azarifar, M.; Budakli, M. On the individual droplet growth modeling and heat transfer analysis in dropwise condensation. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 1668–1678. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.S. On the early and developed stages of surface condensation: Competition mechanism between interfacial and condensate bulk thermal resistances. Sci. Rep. 2016, 6, 35003. [Google Scholar] [CrossRef] [PubMed]
- Niu, D.; Guo, L. Dropwise condensation heat transfer model considering the liquid-solid interfacial thermal resistance. Int. J. Heat Mass Tran. 2017, 112, 333–342. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ghahremanian, S. Effect of solid surface structure on the condensation flow of Argon in rough nanochannels with different roughness geometries using molecular dynamics simulation. Int. Commun. Heat Mass Transfer. 2020, 117, 104741. [Google Scholar] [CrossRef]
- Ghahremanian, S.; Abbassi, A. Investigation the nanofluid flow through a nanochannel to study the effect of nanoparticles on the condensation phenomena. J. Mol. Liq. 2020, 311, 113310. [Google Scholar] [CrossRef]
- Hekmatifar, M.; Toghraie, D. Molecular dynamics simulation of condensation phenomenon of nanofluid on different roughness surfaces in the presence of hydrophilic and hydrophobic structures. J. Mol. Liq. 2021, 334, 116036. [Google Scholar] [CrossRef]
- Cui, H.; Saleem, S. Effects of roughness and radius of nanoparticles on the condensation of nanofluid structures with molecular dynamics simulation: Statistical approach. J. Taiwan Inst. Chem. Eng. 2021, 128, 346–353. [Google Scholar] [CrossRef]
- Ghahremanian, S.; Abbassi, A. Molecular dynamics simulation of annular condensation of vapor argon through a nanochannel for different saturation conditions with focusing on the flow and heat transfer. Int. Commun. Heat Mass Transfer. 2020, 116, 104704. [Google Scholar] [CrossRef]
- Tammann, G.; Boehme, W. Die Zahl der Wassertröpfchen bei der Kondensation auf verschiedenen festen Stoffen. Ann Phys-Berlin. 1935, 414, 77–80. [Google Scholar] [CrossRef]
- Khandekar, S.; Muralidhar, K. Dropwise Condensation on Inclined Textured Surfaces; Springer: New York, NY, USA, 2014; pp. 45–75. [Google Scholar] [CrossRef]
- Abu-Orabi, M. Modeling of heat transfer in dropwise condensation. Int. J. Heat Mass Tran. 1998, 41, 81–87. [Google Scholar] [CrossRef]
- Kim, S.; Kim, K.J. Dropwise condensation modeling suitable for superhydrophobic surfaces. ASME J. Heat Transfer. 2011, 133, 081502. [Google Scholar] [CrossRef]
- Xu, W.; Lan, Z. Droplet size distributions in dropwise condensation heat transfer: Consideration of droplet overlapping and multiple re-nucleation. Int. J. Heat Mass Tran. 2018, 127, 44–54. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, L. Multiscale dynamic growth and energy transport of droplets during condensation. Langmuir 2018, 34, 9085–9095. [Google Scholar] [CrossRef]
- Ristenpart, W.D.; McCalla, P.M. Coalescence of spreading droplets on a wettable substrate. Phys. Rev. Lett. 2006, 97, 064501. [Google Scholar] [CrossRef] [PubMed]
- Wen, R.; Lan, Z. Droplet dynamics and heat transfer for dropwise condensation at lower and ultra-lower pressure. Appl. Therm. Eng. 2015, 88, 265–273. [Google Scholar] [CrossRef]





| Condensation Conditions and Surface Properties | Value |
|---|---|
| Surface subcooling ΔT/K | 1 |
| Saturation temperatures Tsat/K | 359.08 |
| Surface tension coefficient σ/N·m−1 | 0.0616 |
| Condensate water density ρ/kg·m−3 | 968 |
| Latent heat of condensed water Hfg/J·kg−1 | 2.293 × 106 |
| Thickness of hydrophobic coating δ/mm | 0.01 |
| Water thermal conductivity kw/W·m−1·K−1 | 0.6707 |
| Heat transfer coefficient of gas-liquid section hi/W·m−2·K−1 | 106 |
| Thermal conductivity of hydrophobic membrane kδ/W·m−1·K−1 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Wang, R.; Zhao, D.; Gong, L.; Shen, S. Numerical Simulation of Vapor Dropwise Condensation Process and Droplet Growth Mode. Energies 2023, 16, 2442. https://doi.org/10.3390/en16052442
Guo Y, Wang R, Zhao D, Gong L, Shen S. Numerical Simulation of Vapor Dropwise Condensation Process and Droplet Growth Mode. Energies. 2023; 16(5):2442. https://doi.org/10.3390/en16052442
Chicago/Turabian StyleGuo, Yali, Run Wang, Denghui Zhao, Luyuan Gong, and Shengqiang Shen. 2023. "Numerical Simulation of Vapor Dropwise Condensation Process and Droplet Growth Mode" Energies 16, no. 5: 2442. https://doi.org/10.3390/en16052442
APA StyleGuo, Y., Wang, R., Zhao, D., Gong, L., & Shen, S. (2023). Numerical Simulation of Vapor Dropwise Condensation Process and Droplet Growth Mode. Energies, 16(5), 2442. https://doi.org/10.3390/en16052442






