Two-Stage Optimal Scheduling of Highway Self-Consistent Energy System in Western China
Abstract
1. Introduction
- A novel highway self-consistent energy system is proposed. It has been verified that the system can operate stably in areas with low-traffic loads, abundant renewable energy resources and no power grid, such as Western China.
- A two-stage optimal scheduling strategy is proposed, which includes day-ahead stochastic optimization and intra-day rolling optimization. Latin hypercube sampling, which can reduce the impact of uncertainty, is proposed for the generation of typical scenarios. Furthermore, the intra-day rolling optimization is applied to improve the scheduling accuracy. The advantages of the day-ahead and intra-day optimal strategies introduced in this paper are verified through case analysis.
- A definition of the self-consistent coefficient is proposed firstly, which plays a crucial role in day-ahead optimal scheduling. Through a comparable analysis, the necessity for self-consistency of a critical constraint in HSCES day-ahead scheduling is affirmed.
2. HSCES Model
2.1. Distributed Energy Model
2.1.1. Photovoltaic Power Generation
2.1.2. Wind Power Generation
2.2. Battery Model
2.3. Hydrogen Energy System Model
2.3.1. Electrolytic Cell Model
2.3.2. Hydrogen Storage Tank
2.3.3. Hydrogen Fuel Cell
3. Two-Stage Optimal Scheduling Model of the HSCES
3.1. Day-Ahead Long-Time Scale Scheduling
3.1.1. Objective Function
3.1.2. Constraints
- (1)
- Power Balance Constraints
- (2)
- Wind and Photovoltaic Power Generation Constraints
- (3)
- Battery Constraints
- (4)
- Hydrogen Energy System Constraints
- (5)
- Self-Consistent Rate Constraints
3.2. Intra-Day Short-Time Scheduling
3.2.1. Objective Function
3.2.2. Constraints
4. Two-Time Scale Scheduling Solving Process
5. Case Analysis
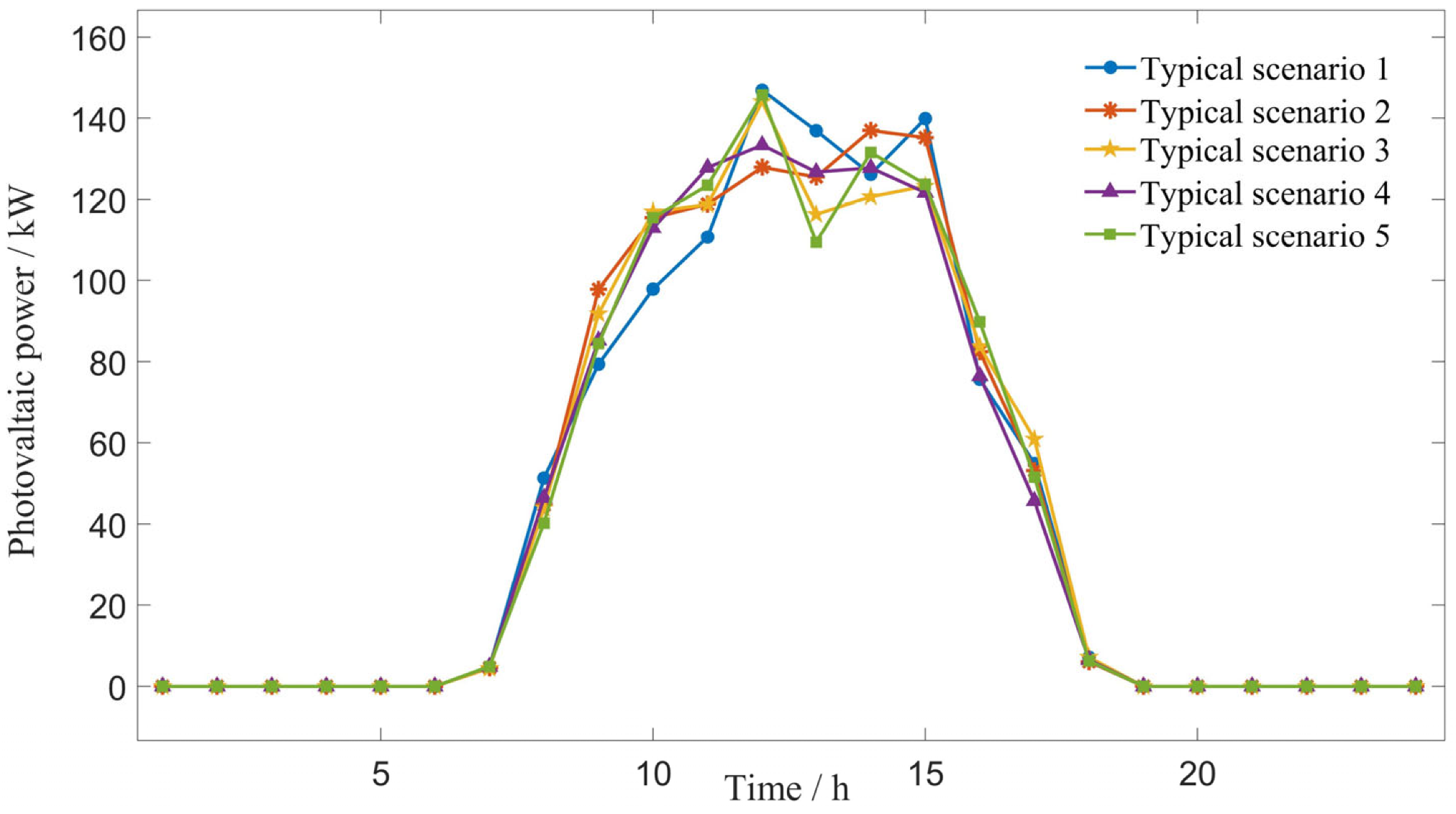
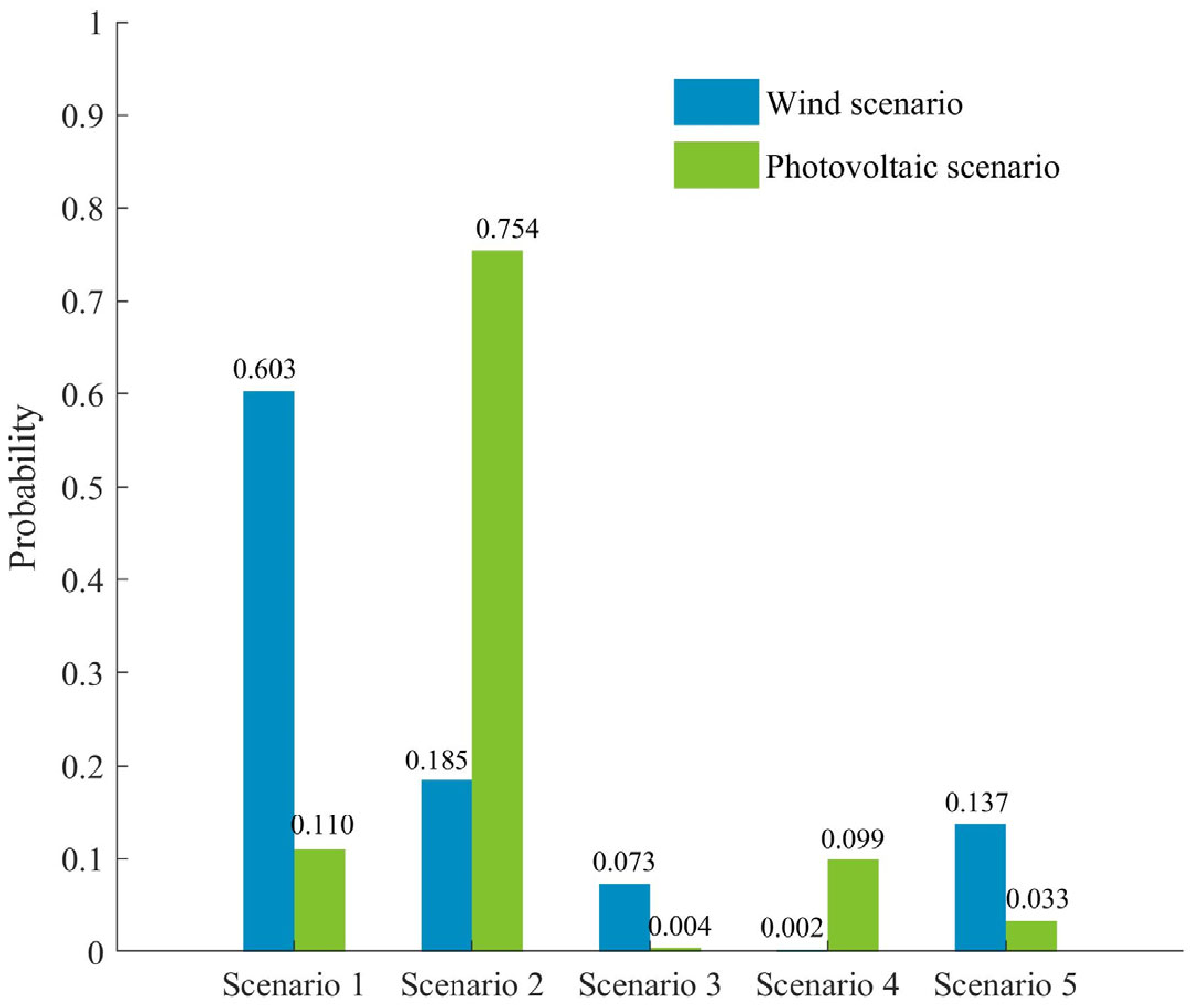
5.1. Scenario Simulation
5.2. Parameters
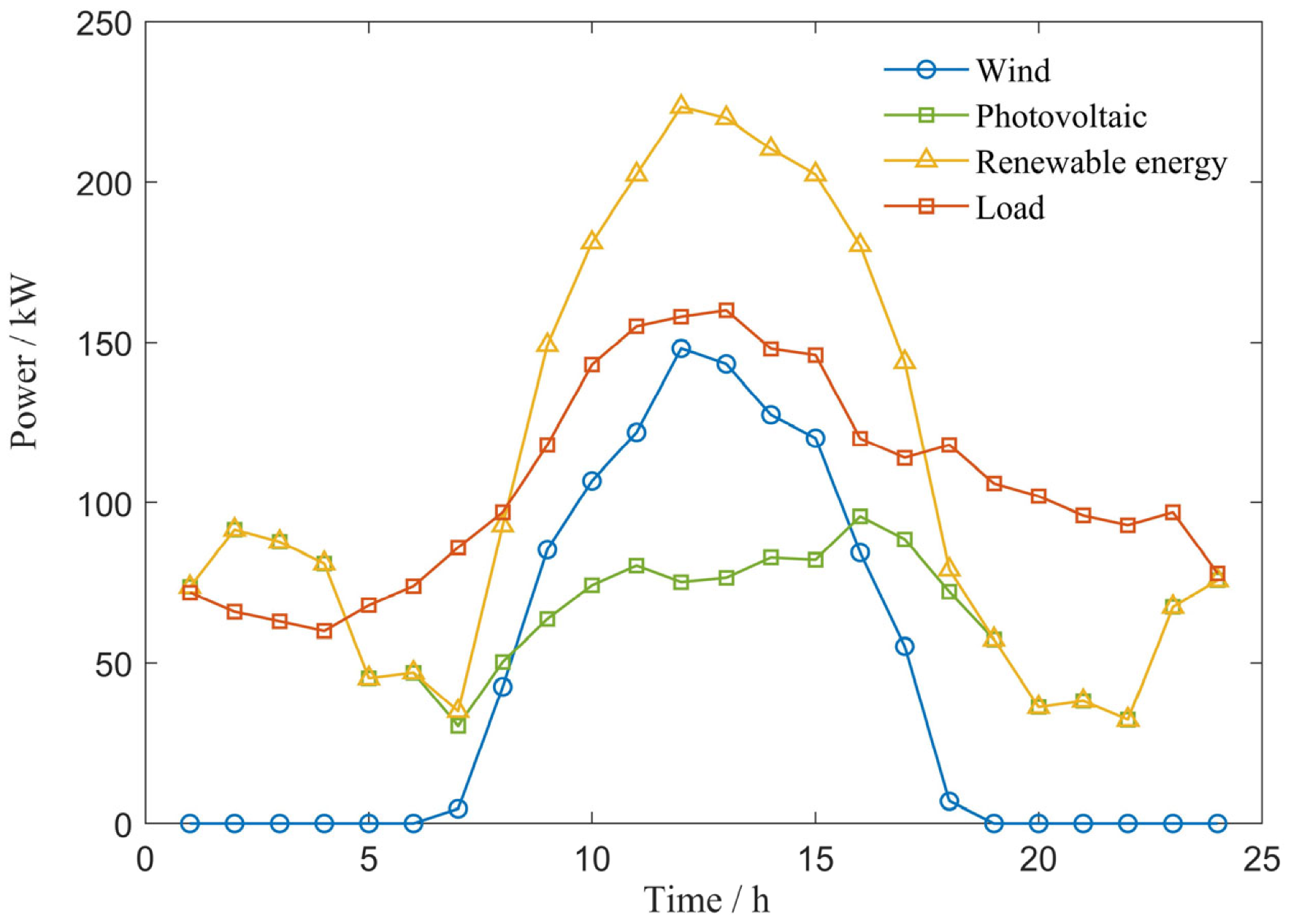
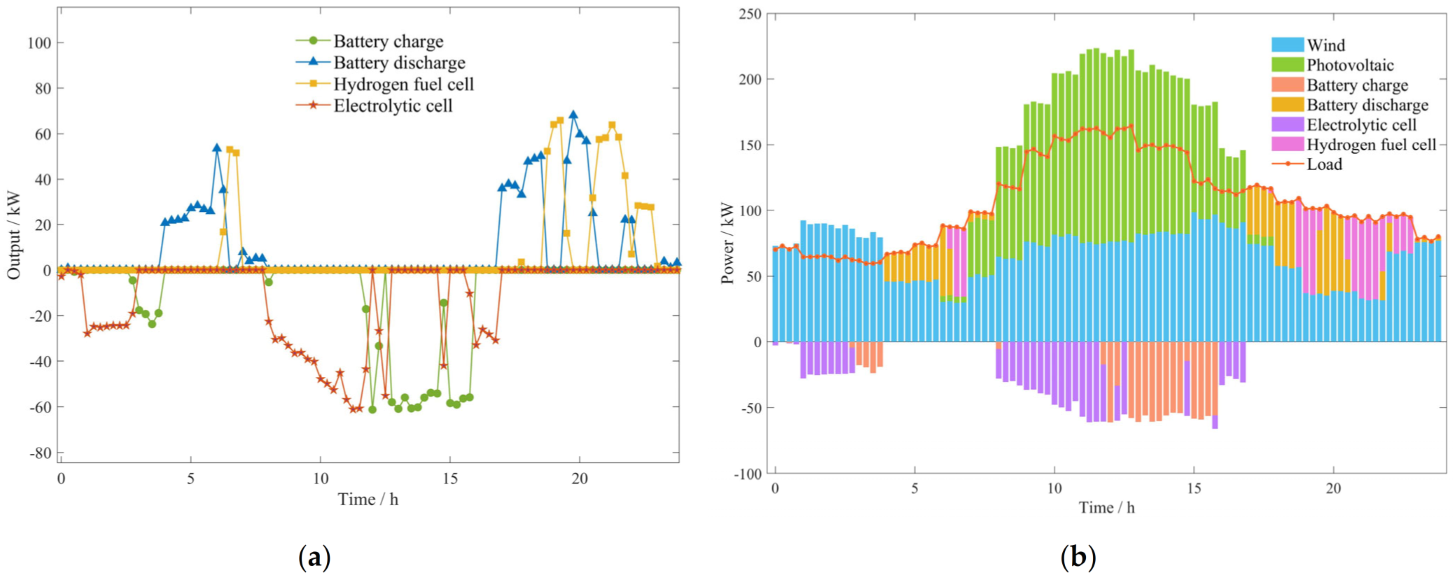
5.3. Result Analysis and Discussion
5.3.1. Day-Ahead Optimal Scheduling Result Analysis
5.3.2. Intra-Day Optimal Scheduling Result Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Rated power of the photovoltaic array | Molar mass of hydrogen | ||
| Surface solar radiation intensity mean value | Conversion constant | ||
| Standard light intensity | Total cost of system operation | ||
| Power temperature coefficient | Wind turbine cost | ||
| T | Actual temperature | Photovoltaic unit cost | |
| Reference temperature | Battery cost | ||
| Wind turbine output power | Hydrogen system cost | ||
| S | Wind turbine actual wind speed | Wind turbine cost coefficient | |
| Cut-in wind speed | Photovoltaic unit cost coefficient | ||
| Cut-out wind speed | Battery cost coefficient | ||
| Rated wind speed | Electrolytic cell cost coefficient | ||
| Rated power | Hydrogen fuel cell coefficient | ||
| Charge state at time t | Wind turbine power at time t | ||
| Charge state at time t − 1 | Photovoltaic unit power at time t | ||
| Battery charging efficiency | Battery charge power at time t | ||
| Battery discharging efficiency | Battery discharge power at time t | ||
| Battery charge power | Electrolytic cell power at time t | ||
| Battery discharge power | Fuel cell power at time t | ||
| Battery rated capacity | Load at time t | ||
| Hydrogen volume | Battery charging state variable at time t | ||
| Electrolytic efficiency | Battery discharging state variable at time t | ||
| Electrolytic cell input power | Hydrogen fuel cell state variable at time t | ||
| Hydrogen storage tank capacity at time t | Electrolytic cell state variable at time t | ||
| Hydrogen storage tank capacity at time t − 1 | Self-consistent coefficient | ||
| Hydrogen storage efficiency | Energy conversion coefficient | ||
| Hydrogen release efficiency | Hydrogen energy conversion efficiency | ||
| Hydrogen storage power at time t | Battery energy conversion efficiency | ||
| Hydrogen release power at time t | Penalty cost | ||
| Fuel cell output power | Resource abandonment amount | ||
| Energy conversion efficiency | Power shortage penalty coefficient | ||
| Hydrogen consumed volume | Resource abandonment penalty coefficient |
References
- Liu, Z.; Deng, Z.; He, G.; Wang, H.; Zhang, X.; Lin, J.; Qi, Y.; Liang, X. Challenges and opportunities for carbon neutrality in China. Nat. Rev. Earth Environ. 2022, 3, 141–155. [Google Scholar] [CrossRef]
- Jia, L.; Ma, J.; Cheng, P.; Liu, Y. A perspective on solar energy-powered road and rail transportation in China. CSEE J. Power Energy Syst. 2020, 6, 760–771. [Google Scholar]
- Zhang, K.; Chen, M.; Yang, Y. Quantifying the photovoltaic potential of highways in China. Appl. Energy 2022, 324, 119600. [Google Scholar] [CrossRef]
- Zhou, B.; Pei, J.; Nasir, D.M.; Zhang, J. A review on solar pavement and photovoltaic/thermal (PV/T) system. Transp. Res. Part D Transp. Environ. 2021, 93, 102753. [Google Scholar] [CrossRef]
- Rezaeeian, S.; Bayat, N.; Rabiee, A.; Nikkhah, S.; Soroudi, A. Optimal Scheduling of Reconfigurable Microgrids in Both Grid-Connected and Isolated Modes Considering the Uncertainty of DERs. Energies 2022, 15, 5369. [Google Scholar] [CrossRef]
- Kim, R.-K.; Glick, M.B.; Olson, K.R.; Kim, Y.-S. MILP-PSO Combined Optimization Algorithm for an Islanded Microgrid Scheduling with Detailed Battery ESS Efficiency Model and Policy Considerations. Energies 2020, 13, 1898. [Google Scholar] [CrossRef]
- Hou, H.; Wang, Q.; Xiao, Z.; Xue, M.; Wu, Y.; Deng, X.; Xie, C. Data-driven economic dispatch for islanded micro-grid considering uncertainty and demand response. Int. J. Elec. Power 2022, 136, 107623. [Google Scholar] [CrossRef]
- Yang, K.; Li, C.; Jing, X.; Zhu, Z.; Wang, Y.; Ma, H.; Zhang, Y. Energy dispatch optimization of islanded multi-microgrids based on symbiotic organisms search and improved multi-agent consensus algorithm. Energy 2022, 239, 122105. [Google Scholar] [CrossRef]
- Lyu, Z.; Yang, X.; Zhang, Y.; Zhao, J. Bi-Level Optimal Strategy of Islanded Multi-Microgrid Systems Based on Optimal Power Flow and Consensus Algorithm. Energies 2020, 13, 1537. [Google Scholar] [CrossRef]
- Ishraque, M.F.; Shezan, S.A.; Ali, M.M.; Rashid, M.M. Optimization of load dispatch strategies for an islanded microgrid connected with renewable energy sources. Appl. Energy 2021, 292, 116879. [Google Scholar] [CrossRef]
- Shezan, S.A.; Ishraque, M.F.; Muyeen, S.M.; Abu-Siada, A.; Saidur, R.; Ali, M.M.; Rashid, M.M. Selection of the best dispatch strategy considering techno-economic and system stability analysis with optimal sizing. Energy. Strateg. Rev. 2022, 43, 100923. [Google Scholar] [CrossRef]
- Li, B.; Wang, H.; Wang, X.; Negnevitsky, M.; Li, C. Tri-stage optimal scheduling for an islanded microgrid based on a quantum adaptive sparrow search algorithm. Energy Convers. Manag. 2022, 261, 115639. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, S.; Li, Q.; Zhang, Y.; Deng, W.; Zhou, L. Optimal Day-ahead Scheduling of Islanded Microgrid Considering Risk-based Reserve Decision. J. Mod. Power Syst. Clean Energy 2021, 9, 1149–1160. [Google Scholar] [CrossRef]
- Javadi, M.; Gong, Y.; Chung, C.Y. Frequency Stability Constrained Microgrid Scheduling Considering Seamless Islanding. IEEE Trans. Power Syst. 2022, 37, 306–316. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Anvari-Moghaddam, A.; Siano, P. Flexible stochastic scheduling of microgrids with islanding operations complemented by optimal offering strategies. CSEE. J. Power Energy Syst. 2020, 6, 867–877. [Google Scholar]
- Hemmati, M.; Mohammadi-Ivatloo, B.; Abapour, M.; Anvari-Moghaddam, A. Optimal Chance-Constrained Scheduling of Reconfigurable Microgrids Considering Islanding Operation Constraints. IEEE Syst. J 2020, 14, 5340–5349. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, C.; Jiang, C.; Liu, X.; Shen, Y. Interval method based optimal scheduling of regional multi-microgrids with uncertainties of renewable energy. IEEE Access 2021, 9, 53292–53305. [Google Scholar] [CrossRef]
- Cui, H.; Xia, W.; Yang, S. Two-time-scale dispatch strategy for networked micro-grids considering uncertainties and demand response. Int. J. Electr. Power Energy Syst. 2023, 145, 108620. [Google Scholar] [CrossRef]
- Li, J.; Zhou, J.; Chen, B. Review of wind power scenario generation methods for optimal operation of renewable energy systems. Appl. Energy 2020, 280, 115992. [Google Scholar] [CrossRef]
- Imeni, M.L.; Ghazizadeh, M.S.; Lasemi, M.A.; Yang, Z. Optimal Scheduling of a Hydrogen-Based Energy Hub Considering a Stochastic Multi-Attribute Decision-Making Approach. Energies 2023, 16, 631. [Google Scholar] [CrossRef]
- Goh, H.H.; Shi, S.; Liang, X.; Zhang, D.; Dai, W.; Liu, H.; Wong, S.Y.; Kurniawan, T.A.; Goh, K.C.; Cham, C.L. Optimal energy scheduling of grid-connected microgrids with demand side response considering uncertainty. Appl. Energy 2022, 327, 120094. [Google Scholar]
- AlDavood, M.S.; Mehbodniya, A.; Webber, J.L.; Ensaf, M.; Azimian, M. Robust Optimization-Based Optimal Operation of Islanded Microgrid Considering Demand Response. Sustainability 2022, 14, 14194. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Carli, R.; Dotoli, M. Robust Optimal Energy Management of a Residential Microgrid Under Uncertainties on Demand and Renewable Power Generation. IEEE Trans. Autom. Sci. Eng. 2021, 18, 618–637. [Google Scholar] [CrossRef]
- Carli, R.; Cavone, G.; Pippia, T.; De Schutter, B.; Dotoli, M. Robust Optimal Control for Demand Side Management of Multi-Carrier Microgrids. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1338–1351. [Google Scholar] [CrossRef]
- Yang, H.; Li, M.; Jiang, Z.; Zhang, P. Multi-time scale optimal scheduling of regional integrated energy systems considering integrated demand response. IEEE Access 2020, 8, 5080–5090. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, D.; Ye, Y.; He, Y.; Fu, X.; Yang, J.; Shi, G.; Zhang, H. Multi-Time Scale Economic Scheduling Method Based on Day-Ahead Robust Optimization and Intraday MPC Rolling Optimization for Microgrid. IEEE Access 2021, 9, 140315–140324. [Google Scholar] [CrossRef]
- Ji, Y.; Xu, Q.; Zhao, J.; Yang, Y.; Sun, L. Day-ahead and intra-day optimization for energy and reserve scheduling under wind uncertainty and generation outages. Electr. Power Syst. Res. 2021, 195, 107133. [Google Scholar] [CrossRef]
- Cheng, Z.; Jia, D.; Li, Z.; Si, J.; Xu, S. Multi-time scale dynamic robust optimal scheduling of CCHP microgrid based on rolling optimization. Int. J. Electr. Power Energy Syst. 2022, 139, 107957. [Google Scholar] [CrossRef]
- Hu, K.; Wang, B.; Cao, S.; Li, W.; Wang, L. A novel model predictive control strategy for multi-time scale optimal scheduling of integrated energy system. Energy Rep. 2022, 8, 7420–7433. [Google Scholar] [CrossRef]
- Yang, M.; Cui, Y.; Huang, D.; Su, X.; Wu, G. Multi-time-scale coordinated optimal scheduling of integrated energy system considering frequency out-of-limit interval. Int. J. Electr. Power Energy Syst. 2022, 141, 108268. [Google Scholar] [CrossRef]
- Chen, J.; Wang, F.; Stelson, K.A. A mathematical approach to minimizing the cost of energy for large utility wind turbines. Appl. Energy 2018, 228, 1413–1422. [Google Scholar] [CrossRef]
- Li, B.; Miao, H.; Li, J. Multiple hydrogen-based hybrid storage systems operation for microgrids: A combined TOPSIS and model predictive control methodology. Appl. Energy 2020, 283, 116303. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Qi, Z. Optimal scheduling of micro-grid for comprehensive hydrogen-electricity supply. Distrib. Util. 2022, 39, 40–46. [Google Scholar]
- Wang, Z.; Hu, J.; Liu, B. Stochastic optimal dispatching strategy of electricity-hydrogen-gas-heat integrated energy system based on improved spectral clustering method. Int. J. Electr. Power Energy Syst. 2021, 126, 106495. [Google Scholar] [CrossRef]
- Chen, H.; Gao, L.; Zhang, Y.; Zhao, C. Optimal scheduling strategy of a regional integrated energy system considering renewable energy uncertainty and heat network transmission characteristics. Energy Rep. 2022, 8, 7691–7703. [Google Scholar] [CrossRef]
- Jia, L.; Shi, R.; Ji, L. Research Report on Integrated Development Strategy of Rail and Road Transportation and Energy—Road; Strategic Consulting Report of Chinese Academy of Engineering: Beijing, China, 2022. [Google Scholar]







| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 1000 W/m2 | 0.5 ¥/(kW h) | ||
| −0.35%/C | 0.5 ¥/(kW h) | ||
| 25 °C | , | 200 kW | |
| , | 90% | , | 0 kW |
| , | 90% | 10% | |
| 80% | 90% | ||
| 80% | , | 0 kW | |
| 0.15 ¥/(kW h) | , | 100 kW | |
| 0.26 ¥/(kW h) | 0.8 | ||
| 0.5 ¥/(kW h) | 0.9 | ||
| 500 kW | |||
| 500 kW |
| CASE | Total Cost/(¥) | Penalty Power/ (kW h) | Resource Abandonment/(kW h) |
|---|---|---|---|
| Case 1 | 1048.5084 | 4.2800 | 94.1994 |
| Case 2 | 984.9163 | 0 | 6.6983 |
| Case 3 | 962.2917 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Shi, R.; Gao, Y.; Ma, X.; Wang, D. Two-Stage Optimal Scheduling of Highway Self-Consistent Energy System in Western China. Energies 2023, 16, 2435. https://doi.org/10.3390/en16052435
Ye Y, Shi R, Gao Y, Ma X, Wang D. Two-Stage Optimal Scheduling of Highway Self-Consistent Energy System in Western China. Energies. 2023; 16(5):2435. https://doi.org/10.3390/en16052435
Chicago/Turabian StyleYe, Yujiang, Ruifeng Shi, Yuqin Gao, Xiaolei Ma, and Di Wang. 2023. "Two-Stage Optimal Scheduling of Highway Self-Consistent Energy System in Western China" Energies 16, no. 5: 2435. https://doi.org/10.3390/en16052435
APA StyleYe, Y., Shi, R., Gao, Y., Ma, X., & Wang, D. (2023). Two-Stage Optimal Scheduling of Highway Self-Consistent Energy System in Western China. Energies, 16(5), 2435. https://doi.org/10.3390/en16052435








