Electromagnetic Design and Analysis in Electrical Power Conversion and Usage

1. Introduction

Electromagnetics is the hidden ‘glue’ that holds together almost all electrical and electronic engineering applications. Whilst end-users are rarely aware of the role of these fields and forces (if they know about them at all), they are the lifeblood of the design and operation of equipment from generation to end-user ‘application’. It is important that any designs of this equipment are undertaken with full cognisance of the performance of the electromagnetic system. Such analysis needs appropriate validation and verification. Often, such validation and verification are undertaken against experiments and/or other relevant numerical analysis, with the results being analysed with the metrics appropriate to that application. This paper examines some recent examples of papers undertaking validation or verification and draws together some general principles for these types of applications. A framework of good practice for validation is presented in the context of the source papers.

Electromagnetics is the foundation of modern society. It underpins convenient ways to provide energy to make things turn, provide lighting, perform calculations, or communicate beyond the range of the human voice. Generating and storing energy, converting it from one level to another, and transmitting it over long distances is also needed; however, this too is underpinned by electromagnetics.

The basis of electromagnetics is electromagnetic force, one of the fundamental forces of nature; from this force, we can derive electromagnetic fields. The properties of that force and those fields dictate, amongst other things, the movement of electrons. From such origins, we can create generators, power transmission, electrical power conversion, and even high-density integrated circuits.

The governing laws of electromagnetics, Maxwell’s equations, are simple and elegant in their formulation, but practical systems are complex, often resulting in intractable solutions. The direct solution of these equations is often only amenable to relatively trivial systems. As a result, a number of numerical methods (simulation techniques) have arisen that allow complex systems to be modelled as an amalgamation of many small elements, where Maxwell’s equations can be applied to each of those small elements independently, with the performance of each of those elements influencing the elements adjacent to it, resulting in an iterative scheme to provide a stable solution. This approach enables one to maintain the behaviour of complex systems as relatively straightforward. The relentless pace of the development of computing power itself enables the performance of more and more complex systems to be obtained on cheaper and more readily available computing platforms.

There are many challenges associated with such simulation approaches. For example, these include selecting elements that are small enough to make the assumption hold that fields vary linearly across them. An element that is too large will exhibit a variation from this assumption of linear behaviour that could propagate through the whole simulation, resulting in a predicted performance that will not be an exact replica of the measured performance. Another challenge is deciding when a simulation is close enough to ‘steady state’ to be able to terminate it and exhibit a low level of error compared to the measured performance.

The upshot of these challenges is that the simulation will only produce an approximation of the performance of the system being analysed. The role of the modeler is to ensure that that approximation is close enough to the real system to be an acceptable analogue. “Close enough” is, of course, a relative term, particularly when it should also be noted that any measurements are themselves only approximations to the behaviour of a system in usage, due to the manner in which the measurements are taken and the loading effects of any additional measurement equipment, amongst other things. However, for the purpose of this paper, it is assumed that any measurements can be taken as acceptable references. Hence, validation of the simulations in order to provide confidence in the model is necessary. From this model confidence, further analysis can be undertaken, designs refined, performance explored in ways that are not available in a physical system, etc.

This Editorial review paper examines some recent papers published in Energies that undertake electromagnetic simulation and verify the performance of the simulation. This is not an exhaustive study, but it provides some relevant examples of how that confidence has been and can be obtained. From this analysis, some common practices are suggested.

In the following sections, the paper first discusses more considerations for verification of the models, takes a number of simulations from motors and actuators, as well as coil-related examples, and derives a good practice framework from these findings.

2. Verification of Model Performance

Motors and actuators are important devices for translating electrical power into motive force. The rise of electric vehicles provides one motivation for the development of more efficient, more reliable, and better controlled motors for drive-train applications. According to research reported in the context of electric drive-train technology in [1], sales of electric vehicles are expected to grow to 21.5 million vehicles in 2030 from a base of 4 million in 2020 (and only 1.4 million in 2017). This represents an approximate growth rate of the sales of vehicles doubling every four years. Thus, while incremental improvements in motor technology can provide valuable improvements in delivered performance, the search for larger scale improvements, or even step-changes, could lead to more profound benefits.

In [2], the authors provide design methods and theoretical analysis for hybrid excitation synchronous motors (HESM). The focus of the work on HESMs is the improvement in motor design for electric vehicles. The novelty of HESMs comes from their design, which is a salient pole rotor with inbuilt dual-V permanent magnets, non-arc pole shoes, and excitation windings. These are being investigated to try to overcome some of the challenges associated with permanent magnet synchronous motors (PMSM), which, despite their high torque density and efficiency, exhibit difficulties in control of the magnetic field. Previous HESM designs have suffered the disadvantages of the presence of axial flux limiting the motor length and the presence of the additional air-gap between the magnetic bridge and the motor core, reducing efficiency. Further, previously investigated HESM designs are more complex than PMSM designs.

Paper [2] studies a motor topology that addresses the relatively poor flux waveform quality and weak flux regulation ability. However, the topology to be investigated does not lend itself to ready calculation using existing analytical solutions, and so a new solution is provided. Amongst other aspects, the paper analyses the operating principle and analytical model, electromagnetic performance, and back EMF. It notes that the rotor technology is more complicated than in previous designs, and the detailed analysis relies on the principle of minimum reluctance and the magnetic equivalent circuit model. In order to verify the performance of the analytical module, the results are compared with both a finite elements model and with the performance of a physical prototype.

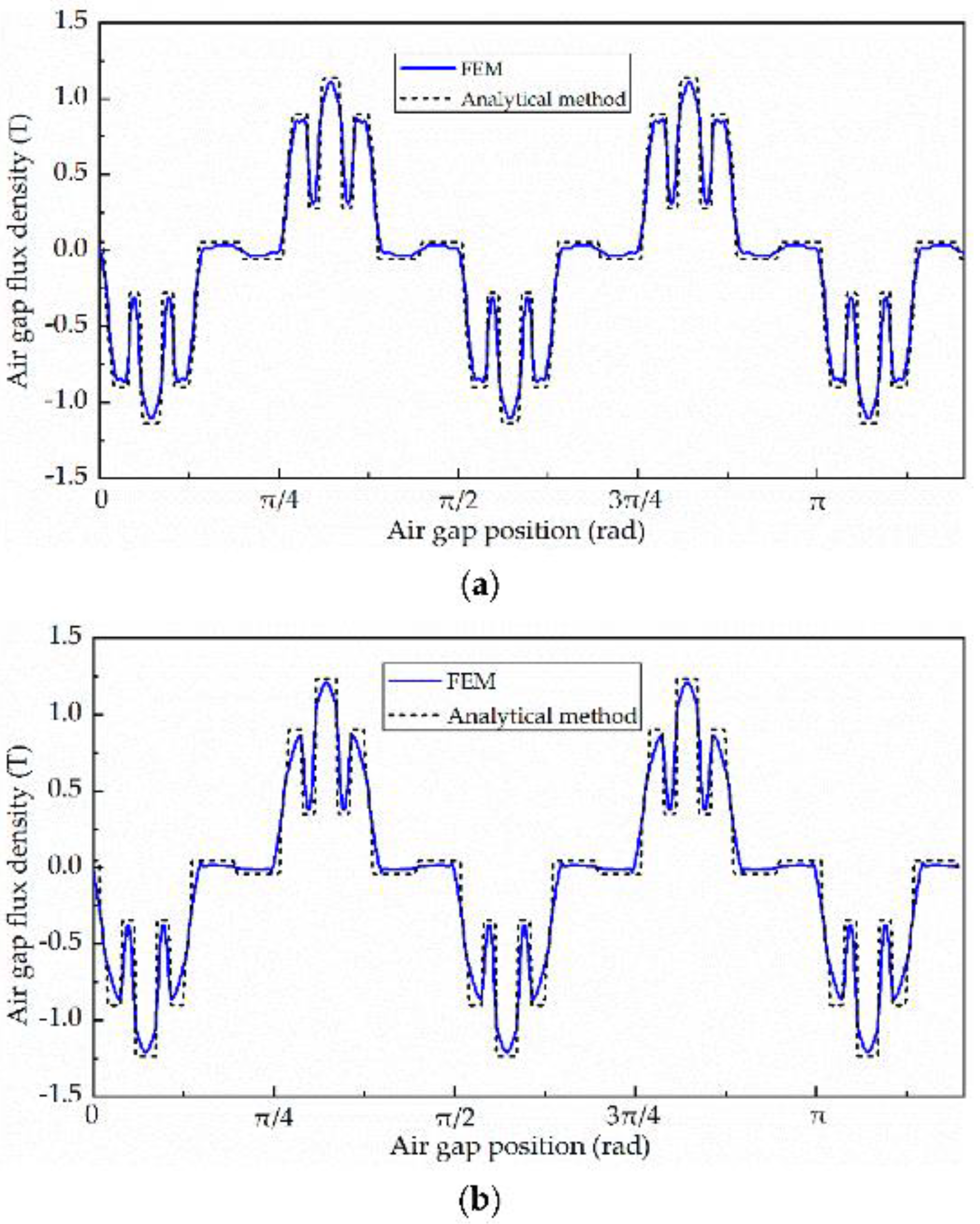
The first step in the validation of the proposed analytical solution was to run a detailed finite element model of various motor structures. From these, the flux density in the air-gap was chosen as a good comparator. Values obtained from the analytical expressions derived in the paper and from the FEM results, acting as a baseline comparator, were compared. These were presented in Figure 9 in [2] and are reproduced here in Figure 1.

The authors note that “… there is a small error between the results of the analytical method and FEM, but the trend is almost the same”. From the point of view of an observer, it is clear that the analytical method provides a very clear envelope of the performance, and the FEM analysis potentially takes account of further (secondary) contributors to the profile; thus, the predicted behaviour of the FEM results is a somewhat ‘smoothed’ version of the analytical envelope.

Obtaining such results from an experimental configuration would be highly problematic, at the very least. As such, further factors need to be considered. In this case, with the experimental prototype, the authors considered parameters that they could readily measure (without artificially changing the prototype structure). In this case, they looked at no-load characteristics including phase voltage versus field current. Figure 2 reproduces their Figure 14a comparing the simulation with the experimental results. The authors note that “…the experimental results are consistent with the simulation results”.

Paper [2] used simulations to verify the accuracy of the analytical framework, as well as experimentation to verify the performance of the simulation (and the analysis on which the design was based). The basis under which the comparisons were undertaken was clear, meaning that simple graphs were the most appropriate way to demonstrate this performance.

As with many papers providing fundamental insight, ref. [2] has become a source paper for other works such as [3], where the authors of that paper are researching techniques to improve the efficiency of traction motors. While it is just one example (of many that could be cited), it shows that the responsibility for ensuring the most robust validation possible is a real and important one.

Paper [3] is concerned with the design of coupling elements in wireless charging systems (WChS). The particular focus of attention is a series–series compensation topology resonant system to be used for automotive battery charging. The authors note that there are still insufficient simulation tools that can help to simplify wireless charging system design and the coupling coil is, naturally, very important and something worth further attention to develop optimized designs. Hence, ref. [3] describes the design and development of a simulation model of the wireless power transfer system. They verify this experimentally, which is the topic of interest in this current paper.

The authors created a 2D axisymmetric model in COMSOL, which was itself composed of four sub models: two for the primary and secondary coil inductances, one for the mutual inductance, and a final one to determine the shape of the transfer characteristics.

Initially, the coil geometric properties were calculated using an appropriate equation set, and an FEM model was used for determining the individual parts of the coil.

The accuracy of the design procedure was verified by comparing the characteristics of coils. One element of good practice in validation can be seen in their work to identify precise transfer characteristics by exploring one of the degrees of freedom in the design (in this case, the separation by varying it at 2 mm steps).

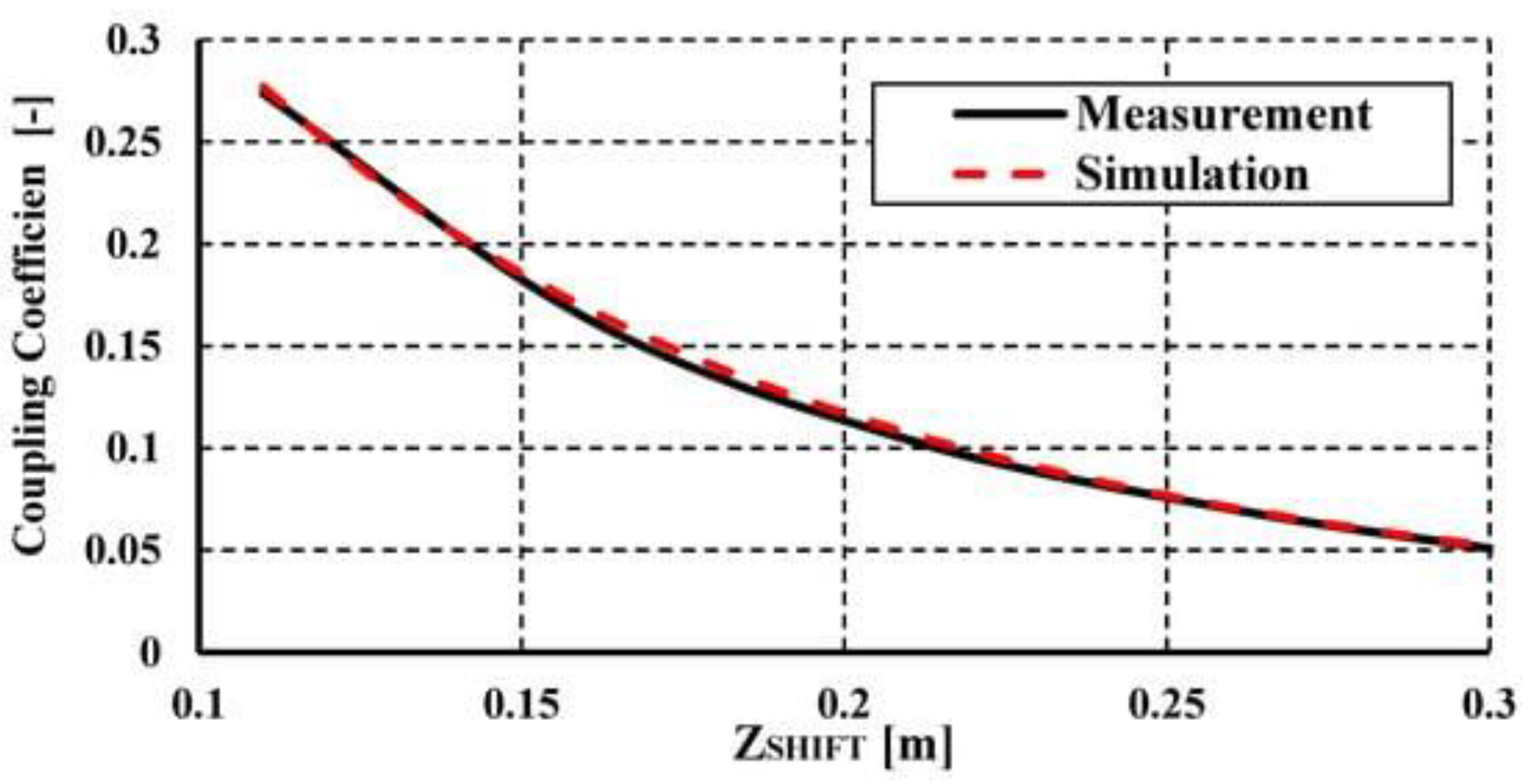
Paper [3] compares various measurement and simulation results using a straightforward graphical representation. Their Figure 5 is reproduced here in Figure 3.

Along with other graphs showing the simulated prediction of transferred power versus frequency for shielded and non-shielded systems, the authors also discuss the maximum difference between the two sets of results as a percentage, noting that “if non-shielded system is under consideration the average accuracy of the proposed model is more than 95%”. The authors also note that that the accuracy of the model they propose is better than 96% for the shielded system.

The paper continues with the validated approach to describe a user interface for loop design that includes the material discussed in the paper.

Paper [4] takes a slightly different approach. Their interest is in displacement and eddy currents. They start with a discussion about the miniaturization of electronic systems and the associated need for (and benefit of) miniaturized convertors. However, a more rigorous understanding of those convertors forms the basis of efficient design and optimization. They have observed that there are multiple papers that discuss the analysis and distribution of the displacement and eddy currents, but none of those papers allow for a detailed time domain study, particularly of the dielectric displacement current.

The paper notes that eddy currents will be induced in ferrites if they are placed in a sufficiently high-frequency electromagnetic field. Clearly, being able to model the fields is important to the authors. They present a 2D Edge Element Method, where the magnetic vector potential is used to describe the elements and, in particular, the integral of the magnetic vector potential along the edge of a finite element.

Paper [5] presents a variety of results, including displacement and eddy current densities in the ferrite cores. To aid visualization, they also provide the time domain behaviour at several points in each core. They note that the eddy currents for sinusoidal waveforms are generally quite low and can be ignored; however, in practice, at higher frequencies, waveforms are rarely pure sinusoidal signals, and trapezoidal or rectangular waves are more common. This, of course, means that these need to be considered in simulations.

The authors’ approach to validation was to compare their proposed solution to COMSOL Multiphysics. Clearly experimental validation would not have been possible here, at least not directly, so their use of an existing commercial technique provides a good triangulation point for their results. They investigated the coils to investigate flux density values in addition to the eddy and displacement currents. While they do not appear to report the values, they do introduce the possibility of using an error distance that they refer to as the Singular Value Decomposition (SVD) ratio, which they define as Equation (1):

$$\mathit{\zeta }=\frac{||{\mathit{I}}_{\mathit{C}}^{\mathit{r}}-{\mathit{I}}_{\mathit{C}}^{\mathbf{0}}||}{{\mathit{I}}_{\mathit{C}}^{\mathit{r}}}$$

(1)

where ${\mathit{I}}_{\mathit{C}}^{\mathit{r}}$ is the coil current reference obtained using COMSOL and ${\mathit{I}}_{\mathit{C}}^{\mathbf{0}}$ is that from the proposed approach. One example of their comparison is shown in Figure 4.

Paper [5] is interested in the challenges of maintaining voltage quality in distribution networks, given that the increasing inclusion of renewable energy is completed using inverters, which can cause significant deformation of the output signals, while harmonics can be caused by nonlinear loads connected to the supply system.

The measurement of power comes with its own challenges, as a measuring voltage transformer adds its own transformation errors to the measured values. Hence, the performance of the voltage transformer is an important factor to be determined. This is particularly important when it is supplied with a distorted voltage. However, it is noted that there is not prior literature that addresses this problem. As a result, the paper uses measurements of a transformer to verify the performance of a 3D model that couples a solution to Maxwell’s equations (obtained through OPERA 3D) with the circuit beyond the transformer model.

In their test system, they use a programmable power supply to feed a step-up transformer to give the reference voltage. This is then passed through (a) the tested voltage transformer and (b) a reference voltage divider, providing a highly accurate output with low distortion.

Rather than a graphical presentation of the results, the authors determine an error metric using the tested voltage output and the reference voltage divider output, according to Equation (2) (modified from Equation (8) in [5]).

$$\Delta U=\frac{{\mathit{U}}_{\mathit{T}\mathit{V}}-{\mathit{U}}_{\mathit{R}\mathit{V}\mathit{D}}}{{\mathit{U}}_{\mathit{R}\mathit{V}\mathit{D}}}\times \mathit{100}\%$$

(2)

where ${\mathit{U}}_{\mathit{T}\mathit{V}}$ is the RMS value of the k-order harmonic a the secondary of the tested transformer, ${\mathit{U}}_{\mathit{R}\mathit{V}\mathit{D}}$ is the k-order harmonic from the reference voltage divider, and $\Delta U$ is the voltage ratio error.

Throughout the paper, the authors demonstrate a voltage ratio error of under 0.2%. They also represent a phase error, which never goes as high as 1% in the results presented.

Paper [5] clearly demonstrates that “the measurement and calculation results are consistent”.

A very different but equally fascinating study comes from [6]. Here, we note that the authors are interested in the flow of electrical current in employees’ bodies when using portable radios. A particular concern is whether induced currents can disrupt endogenous electrophysiological currents, leading to physiological symptoms. While the paper notes that such electrostimulation dominates below 100 kHz, it does cite evidence that phenomena can also occur in the 5–20 MHz range, along with the observation that, above 10 MHz, thermal effects become the dominant phenomenon.

In citing two exposure standards, ref. [6] recognized that exposure can lead to thermal effects but that neither the thermal effects nor the density of induced electric currents exceeds the limits presented in the quoted standards. Here, the authors did not just use the approach of modelling a system and then simulating it; instead, they took two experimental measurements (linked in one theme) and a simulation-based study:

• The electric field was measured near the radios. If this field strength was found to exceed the limit set out in standards, the limb contact current was measured.
• Specific Absorption Rate (SAR) numerical analysis, which used a similar radio performance in the simulation to that in practice and used a human model based on Hugo (one of the commonly used full wave body models originating from a real person).

The authors argue that this approach provides a complementary method of exposure assessment and does so more comprehensively than with either approach individually.

3. A Framework for Validation

The IEEE standard 1597.1 [7] is ostensibly a standard that addresses the validation of computational electromagnetics (CEM) when applied to electromagnetic compatibility (EMC) systems. It does note and recommend several things that support the good practice noted in the papers above and summarized in the Discussion section below. It notes that validation may be performed at a method (e.g., new way to solve Maxwell’s equations), an implementation (a new solver implementation), or a model (system, geometry, etc.) level. Of course, like most validations, the papers described here address validation at a model level. Addressing validation at an individual model level requires some form of reference, which can be provided through closed form equations, canonical problems, comparative modelling techniques (using techniques based on different ways of dealing with the fundamental equations: perhaps using a frequency domain technique in which there is high confidence to validate a time domain approach), or, of course, measurements. It is also noted that self-referencing is possible, but this is often limited to testing the stability of a performance through scenario or sensitivity analysis.

One thing the standard is based on is the unreliability, generally, of simply depending on an overlay of results and saying that the agreement is “good enough”. It should be noted that in EMC data, the results tend to have more visual details than the graphs shown in the papers referenced in this Editorial, which are good examples of the forms of data common to this journal.

A helpful structure from [7] is the discussion of a validation report, the headings for which might help also in the presentation of comparisons within the structure of a paper. A common feature of the articles referenced in this paper is that most of those elements are captured within the papers. The headings are captured here in a condensed form posed as questions to show the flow:

• Where do the data originate?
• Why is it being compared?
• How and why was the reference selected?
• What method was used to quantify the comparison of the data?
• Did the data need to be manipulated before comparison?

The discussions prompted by the above questions can be followed by any additional information that might be thought to be helpful to the reader.

The central comparison technique in IEEE Std 1597.1 is the FSV (Feature Selective Validation) method. It was first described in [8,9] with a large number of papers and other publications being produced describing its use and enhancements, including [10]. Essentially, it is a heuristic technique, closely related to the reliability factors used in low-energy electron diffraction within surface crystallography studies. It decomposes the data into trends and rapidly changing features and, using weighted averages, produces a range of output data ranging from detailed point-by-point analyses to a single valued ‘goodness of fit’.

The original purpose of FSV was to compare data arising from the electromagnetic compatibility (EMC) field. However, it has been applied in many other areas of electromagnetics. One of many interesting examples is [11], which applies it to the comparison of computed and measured radar cross section (RCS) data, and concludes that there is strong evidence for studying the dynamic RCS of manoeuvring targets.

While the FSV technique has been widely used, other approaches have also been proposed. This is particularly important because ‘how’ comparisons are undertaken is less important than ‘why’ they have been undertaken, and that the best approach for the problem at hand has been selected. Most recently, an approach based on factor analysis and the Prony method has been proposed [12]. At the heart of this is identifying a potentially small number of (unknown) factors to describe the observed items through the correlation coefficient matrix or covariance matrix of variables. This method is proposed because it can readily deal with multiple degrees of freedom. The authors simulate the behaviour of a modular multilevel convertor HVDC system. Among the results obtained from their method, the authors verify the performance of their proposed method using FSV and show that it is consistent.

4. Using Numerical Electromagnetics as the Reference

This Editorial focuses on the validation and verification of electromagnetic models using other approaches. However, there are times when electromagnetics can, itself, provide the necessary reference for other analyses. Rather than thinking of these as separate entities, it is highly appropriate to think of them as functionally equivalent. For example, should a simulation be validated with an experiment and the results do not agree, this tells the modeler that there is disagreement, and it is the responsibility of the modeler to understand the nature of said disagreement. The same is true if experiments are compared with models, rather than models with experiments. There are many papers that could be drawn upon to illustrate this. However, for the purpose of this article, we will just make reference to two, with a particular emphasis on the need for care when selecting the reference.

A very good example of consideration of options for the selection of the reference can be found in [13], where the authors review the challenges in using an experimental reference to validate their research. The paper investigates a model to explain bulk current injection. The authors identify the difficulties and challenges imposed by selecting an experimental reference. Given that the model is mathematical, they then use computational electromagnetics as a reference. The careful critique of their needs leads to the discussion about the conflicting needs to terminate each wire to allow measurements but not have the termination modifying the shape of the harness being tested. While this uses electromagnetics as the reference to be compared with rather than as the thing being compared, it is a helpful example of the level of reflection needed to choose the reference to give the highest level of confidence in the outcome.

Similarly, ref. [14] creates a magnetic circuit model to determine on-load field prediction in surface-mounted permanent-magnet machines. Their chosen mode of validation is the use of finite element analysis. A consideration in this validation was to ensure that the linear and nonlinear operation of the magnetic circuit behaved as required; thus, the model was designed with this approach in mind.

5. Discussion

The small number of papers referenced in this Editorial do not represent a comprehensive study of the validation of electromagnetic modelling. There are clearly many more papers that could have been included. However, what they do provide is a number of distinct examples of typical approaches to verifying the performance of simulations or using simulations to verify the performance of measurements. From these, a number of suggestions emerge for good practice when using simulations in this way. They are not all relevant together in all circumstances but do provide some useful food for thought. An IEEE Standard has also been included to help provide further context for that good practice.

The good practice that may be proposed from the papers discussed here is:

• Address the question of “what is needed to demonstrate correct performance?” It is important that there is a clear objective or ‘research question’.
• Measure what can be measured to address #1 without providing a level of ‘loading’ on the system that could materially affect the results. That is, be careful not to create biased results through the act of taking the measurements themselves. This may mean selecting an approach to validation that might be a compromise between what is needed and what can be measured.
• Triangulate where possible between analysis, a plurality of computational techniques (particularly where different bases for the solution of Maxwell’s equations area used) and measurement.
• Vary appropriate parameters to compare precise performance (not just spot measurements where the system has multiple degrees of freedom) in order to improve the overall confidence in the model. Such variation might also include multiple parameters (a scenario analysis), but single values are preferred.
• Graphs can be easy to see but they should be backed up with a quantitative summary where possible, such as percentage errors, or difference value metrics of some type.
• Understand and communicate clearly the reasons for differences. Be prepared to challenge one’s own results but equally accept that differences between the simulation under test and reference can occur without bringing in to question the quality of the method being tested. Remember: such results are rarely absolutely precise and invariant but are points on a distribution. Having, at least, an inherent understanding of the nature of the various distributions arising from the different approaches to generating the results is important to be able to interpret the comparisons.
• Do not ‘over claim’ agreement and mention differences. Anyone who is used to an analytical—simulation—measurement ‘ecosystem’ will be used to a lack of one-to-one correspondence (and may actually be sceptical of excessive agreement).
• It may be more appropriate not to model a system and then measure it but to use a simulation to ‘sense check’ whether the overall electromagnetic environment is consistent with what is expected given the measurements results (of something different but related). This is an approach to providing a more solid backdrop for exercising engineering judgement.

6. Conclusions

This Editorial has taken a handful of other papers published recently in Energies and, from them, has drawn out some examples of good practice that can be applied when validating simulations or similar.

The points of good practice are set out in Section 4. There is no claim that they are complete, but they do provide a useful aide memoire when undertaking comparisons in this way.

With that, some of the key steps are:

• Identify what needs to be compared, how and why this will advance the overall research investigations.
• Be clear about what has been performed and why in a paper.
• Recognize potential shortcomings as a way of strengthening confidence in the conclusions.

The use of simulation is important to allow investigations that would not be possible with measurements; it is an approach that can allow rapid investigation of potential designs and options to allow optimization. Clearly it plays a significant role in the modern electromagnetic engineering toolbox. However, building confidence that the simulations represent reality and that the models are appropriate representations of the physical realm is vital for proper use. By taking a small number of representative papers as source material, this paper has provided a framework that we hope will be useful for other authors so as to help them establish the most appropriate way to represent their model validation for a wider audience.