A Study of the Non-Linear Seepage Problem in Porous Media via the Homotopy Analysis Method
Abstract
1. Introduction
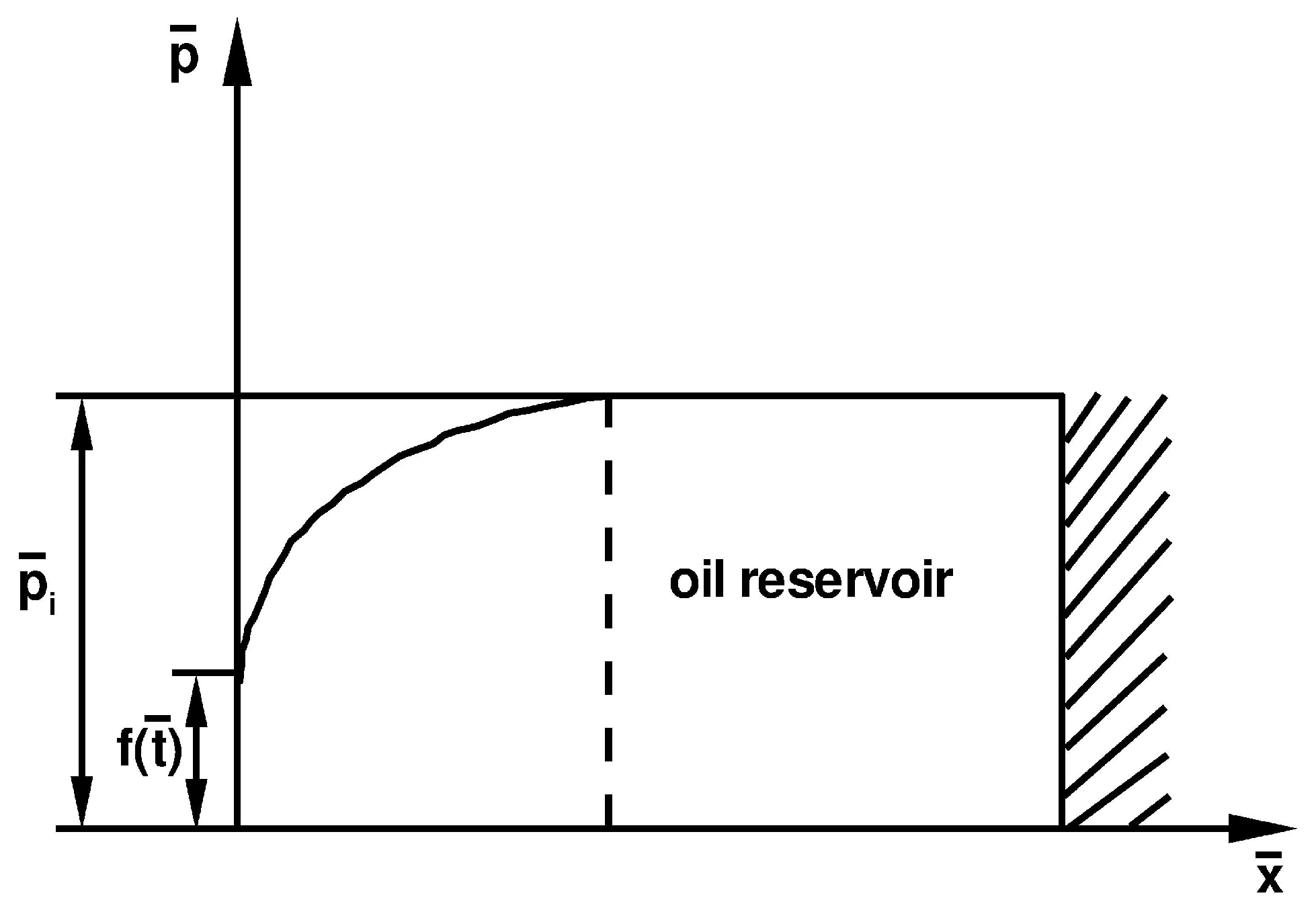
2. Mathematical Models and Methods
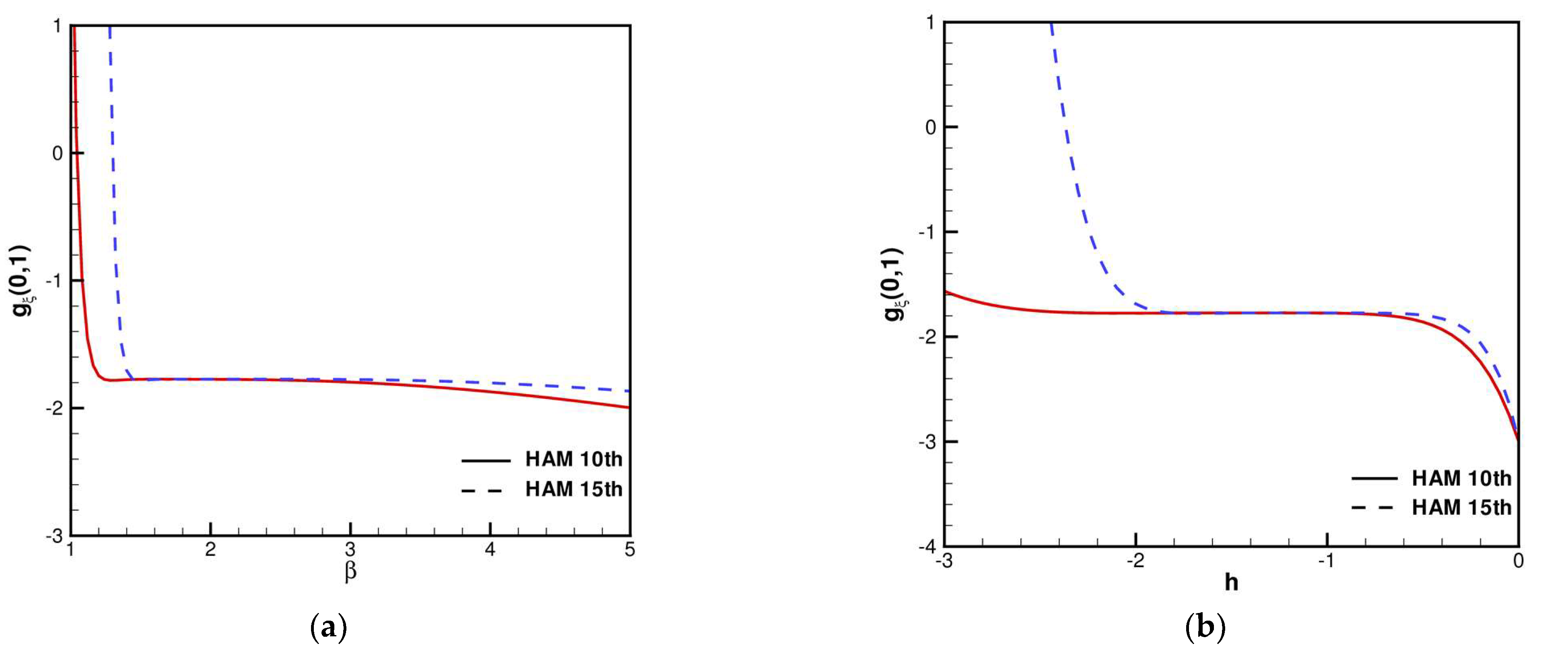
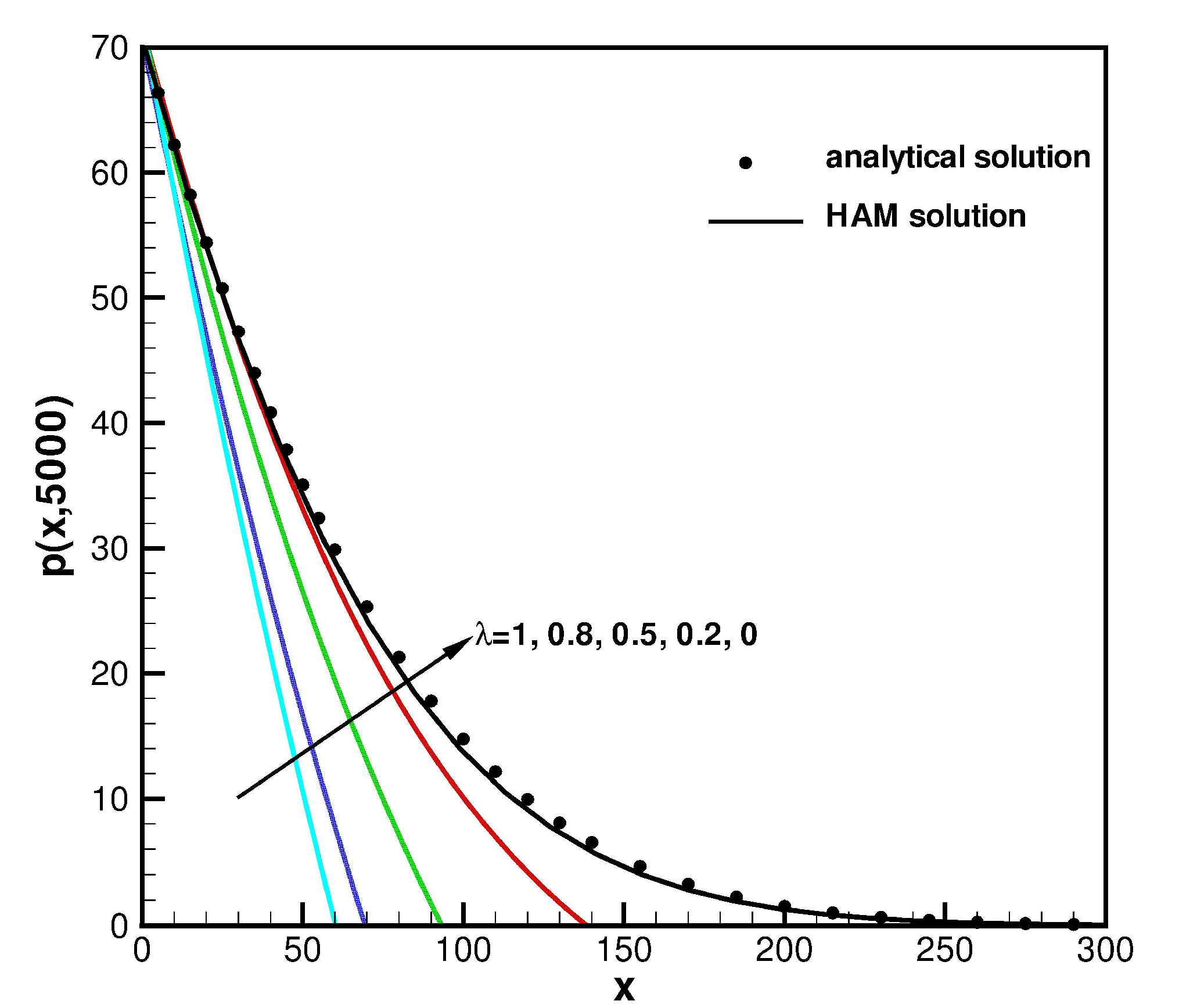
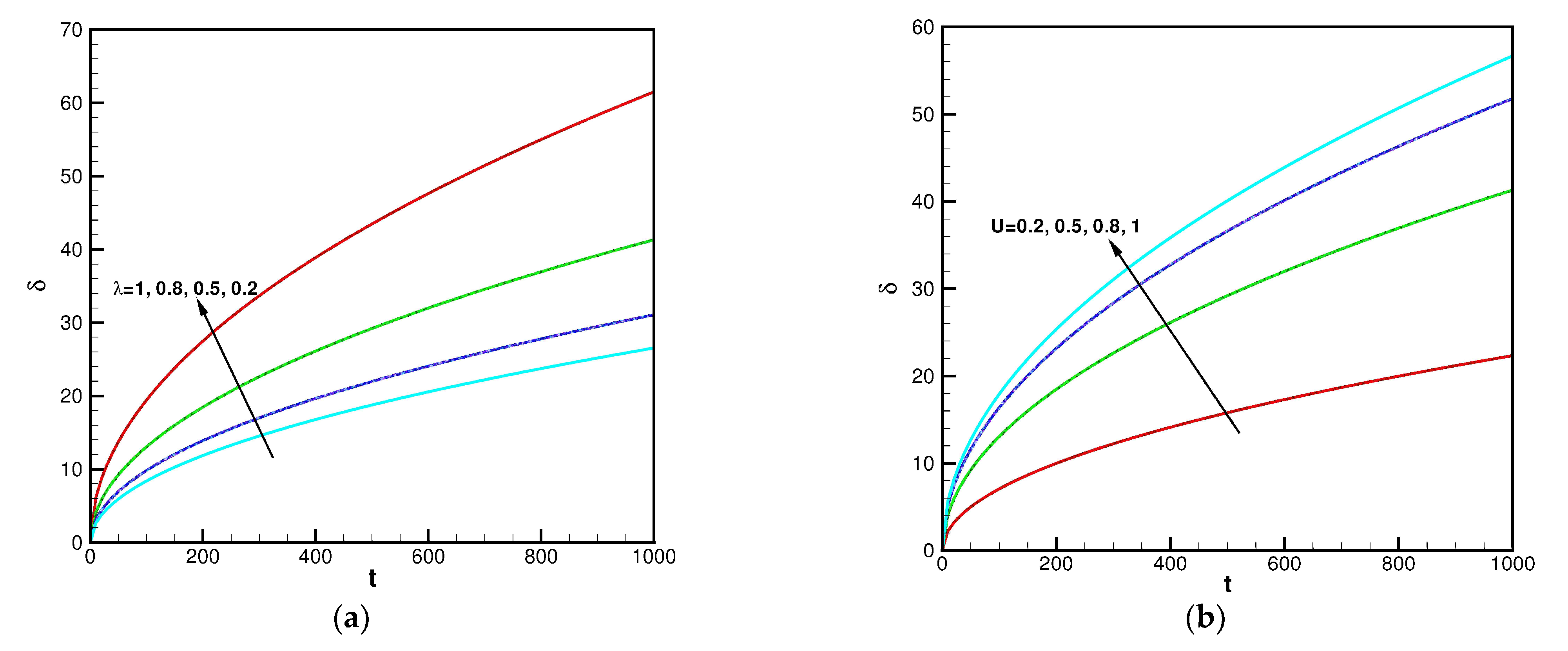
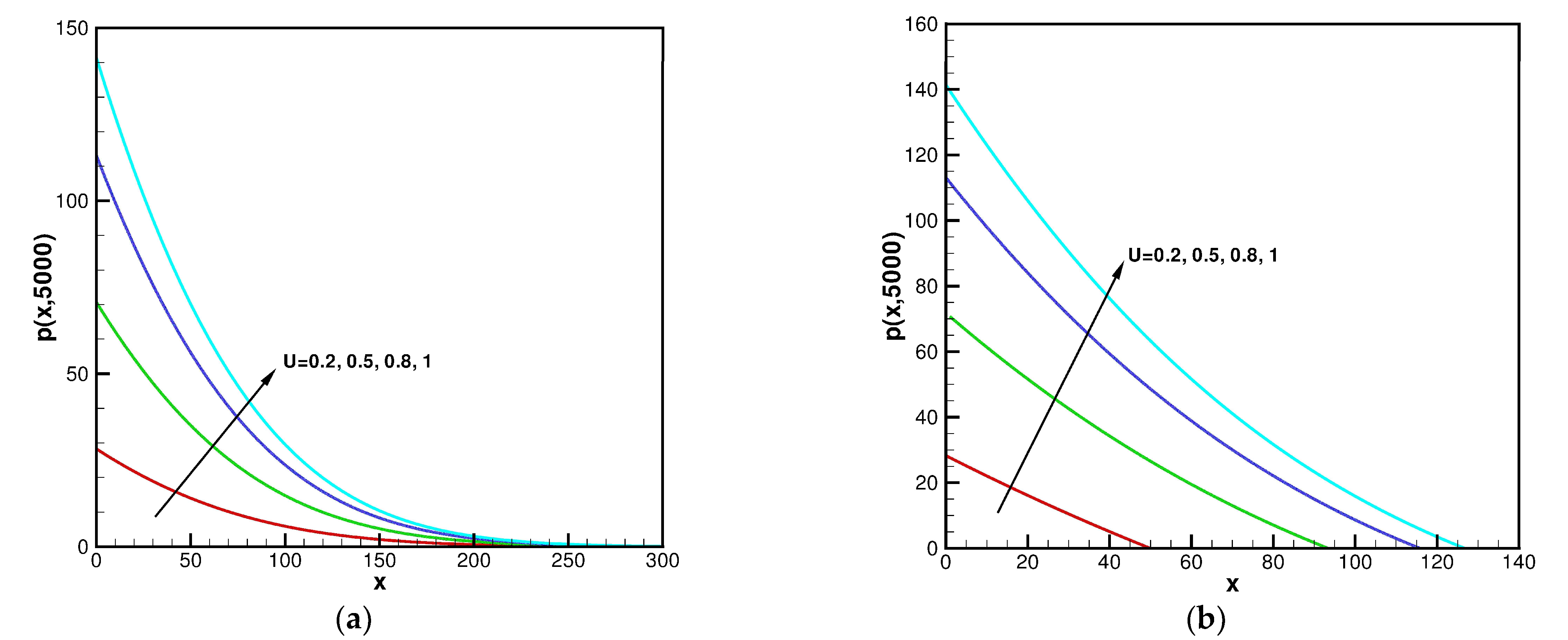
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Formation pressure | |
| Original formation pressure | |
| Fluid compression coefficient | |
| Pore compression coefficient | |
| Seepage velocity | |
| Permeability | |
| Distance | |
| Time | |
| Moving boundary | |
| Comprehensive compression coefficient | |
| Bottom-hole pressure function that changes with time | |
| Distance constant | |
| Non-dimensional distance | |
| Non-dimensional time | |
| Non-dimensional moving boundary | |
| Non-dimensional formation pressure | |
| Non-dimensional positive fitting parameter of production pressure data | |
| Greek Symbols | |
| Fluid density | |
| Initial density of fluid | |
| Porosity | |
| Initial porosity | |
| Fluid viscosity | |
| Threshold pressure gradient | |
| Non-dimensional threshold pressure gradient | |
References
- Cai, J.C. A fractal approach to low velocity non-Darcy flow in a low permeability porous medium. Chin. Phys. B 2014, 23, 044701. [Google Scholar] [CrossRef]
- Wang, F.Y.; Liu, Z.C.; Cai, J.C.; Gao, J. A fractal model for low-velocity non-Darcy flow in tight oil reservoirs considering boundary-layer effect. Fractals 2018, 26, 1850077. [Google Scholar] [CrossRef]
- Ye, W.; Wang, X.; Cao, C.; Yu, W. A fractal model for threshold pressure gradient of tight oil reservoirs. J. Petrol. Sci. Eng. 2019, 179, 427–431. [Google Scholar] [CrossRef]
- Hayat, T.; Yasmin, H.; Ahmad, B.; Chen, B. Simultaneous effects of convective conditions and nanoparticles on peristaltic motion. J. Mol. Liq. 2014, 193, 74–82. [Google Scholar] [CrossRef]
- Yasmin, H.; Iqbal, N. Convective Mass/Heat Analysis of an Electroosmotic Peristaltic Flow of Ionic Liquid in a Symmetric Porous Microchannel with Soret and Dufour. Math. Probl. Eng. 2021, 2021, 2638647. [Google Scholar] [CrossRef]
- Prada, A.; Civan, F. Modification of Darcy’s law for the threshold pressure gradient. J. Petrol. Sci. Eng. 1999, 22, 237–240. [Google Scholar] [CrossRef]
- Tian, W.; Li, A.; Ren, X.; Josephine, Y. The threshold pressure gradient effect in the tight sandstone gas reservoirs with high water saturation. Fuel 2018, 226, 221–229. [Google Scholar] [CrossRef]
- Xiong, W.; Lei, Q.; Gao, S.; Hu, Z.; Xue, H. Pseudo threshold pressure gradient to flow for low permeability reservoirs. Petrol. Explor. Dev. 2009, 36, 232–236. [Google Scholar]
- Zhu, W.; Song, H.; Huang, X.; Liu, X. Pressure characteristics and effective deployment in a water-bearing tight gas reservoir with low velocity non-Darcy flow. Energy Fuel 2011, 25, 1111–1117. [Google Scholar] [CrossRef]
- Yao, T.; Huang, Y.; Li, J. Nonliner flow equations for heavy oil in porous media. Chin. J. Theor. Appl. Mech. 2012, 44, 106–110. [Google Scholar]
- Zhao, L.; Jiang, H.; Wang, H.; Yang, H.; Sun, F.; Li, J. Representation of a new physics-based non-Darcy equation for low-velocity flow in tight reservoirs. J. Petrol. Sci. Eng. 2020, 184, 106518. [Google Scholar] [CrossRef]
- Wei, Q.; Zhou, H.; Yang, S. Non-Darcy flow models in porous media via Atangana-Baleanu derivative. Chaos Solitons Fractals 2020, 141, 110335. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, L.; Wang, T. Analytical solution for one-dimensional non-Darcy flow with bilinear relation in porous medium caused by line source. Appl. Math. Comput. 2021, 392, 125674. [Google Scholar] [CrossRef]
- Nie, R.; Fan, X.; Li, M.; Chen, Z.; Deng, Q.; Lu, C.; Zhou, Z.; Jiang, D.; Zhan, J. Modeling transient flow behavior with the high velocity non-Darcy effect in composite naturally fractured-homogeneous gas reservoirs. J. Nat. Gas Sci. Eng. 2021, 96, 104269. [Google Scholar] [CrossRef]
- Moghimi, H.; Siavashi, M.; Nezhad, M.M.; Guadagnini, A. Pore-scale computational analyses of non-Darcy flow through highly porous structures with various degrees of geometrical complexity. Energy Technol. Assess. 2022, 52, 102048. [Google Scholar] [CrossRef]
- Zhang, X.; Dou, Z.; Wang, J.; Zhou, Z.; Zhuang, C. Non-Darcy flows in layered porous media (LPMs) with contrasting pore space structures. Pet. Sci. 2022, 19, 2004–2013. [Google Scholar] [CrossRef]
- Cheng, S.; Zhang, S.; Huang, Y.; Zhu, W. An integral solution of free-boundary problem of non-Darcy flow behavior. Mech. Eng. 2002, 24, 15–17. [Google Scholar]
- Liu, W.; Yao, J.; Chen, Z.; Liu, Y.; Sun, H. Research on analytical and numerical solution of a moving boundary model of seepage flow in low-permeable porous media. Chin. J. Theor. Appl. Mech. 2015, 47, 605–612. [Google Scholar]
- Liu, W.; Yao, J.; Wang, Y. Exact analytical solutions of moving boundary problems of one-dimensional flow in semi-infinite long porous media with threshold pressure gradient. Int. J. Heat Mass Transf. 2012, 55, 6017–6022. [Google Scholar] [CrossRef]
- Liu, W. Analytical study on a moving boundary problem of semispherical centripetal seepage flow of Bingham fluid with threshold pressure gradient. Int. J. Non-Linear Mech. 2019, 113, 17–30. [Google Scholar] [CrossRef]
- Liu, W. Exact analytical solution of a generalized multiple moving boundary model of one-dimensional non-Darcy flow in heterogeneous multilayered low-permeability porous media with a threshold pressure gradient. Appl. Math. Model. 2020, 81, 931–953. [Google Scholar] [CrossRef]
- Guo, Y.; Zeng, Q.; Wang, Z. Numerical simulation of low permeability flow with moving-boundary using meshless methods. Eng. Mech. 2006, 23, 188–192. [Google Scholar]
- Chen, L.; Ren, S.; Lian, P. Well test analysis on low velocity and non-Darcy flow in dual-porosity reservoir with dynamic boundary. Chin. J. Comput. Mech. 2011, 28, 879–883. [Google Scholar]
- Yao, J.; Liu, W. New method for solution of the model of non-Darcy seepage flow in low-permeability reservoirs with moving boundary. Chin. Q. Mech. 2012, 33, 597–601. [Google Scholar]
- Yao, J.; Liu, W.; Chen, Z. Numerical solution of a moving boundary problem of one-dimensional flow in semi-Infinite long porous media with threshold pressure gradient. Math. Probl. Eng. 2013, 2013, 384246. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Q.; Zhu, W. Numerical simulation of multi-stage fractured horizontal well in low-permeable oil reservoir with threshold pressure gradient with moving boundary. J. Petrol. Sci. Eng. 2019, 178, 1112–1127. [Google Scholar] [CrossRef]
- Xu, H.; Liu, N.; Chen, Y.; Tian, Y.; Guo, Z.; Jiang, W.; He, Y. A novel equivalent numerical simulation method for non-Darcy seepage flow in low-permeability reservoirs. Energies 2022, 15, 8505. [Google Scholar] [CrossRef]
- Liao, S. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S. Beyond Perturbation: Introduction to the Homotopy Analysis Method, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2003; pp. 154–196. [Google Scholar]
- Liao, S. Homotopy Analysis Method in Nonlinear Differential Equations, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 40–86. [Google Scholar]
- Nassar, C.J.; Revelli, J.F.; Bowman, R.J. Application of the homotopy analysis method to the Poisson-Boltzmann equation for semiconductor devices. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2501–2512. [Google Scholar] [CrossRef]
- Vajravelu, K.; Van Gorder, R.A. Nonlinear Flow Phenomena and Homotopy Analysis: Fluid Flow and Heat Transfer; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Sardanyés, J.; Rodrigues, C.; Januário, C.; Martins, N.; Gil-Gómez, G.; Duarte, J. Activation of effector immune cells promotes tumor stochastic extinction: A homotopy analysis approach. Appl. Math. Comput. 2015, 252, 484–495. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Lu, D.C.; Farooq, U. Impact of generalized Fourier’s and Fick’s laws on MHD 3D second grade nanofluid flow with variable thermalconductivity and convective heat and mass conditions. Phys. Fluids 2017, 29, 093102. [Google Scholar] [CrossRef]
- Patel, M.A.; Desai, N.B. Homotopy analysis approach of Boussinesq equation for infiltration phenomenon in unsaturated porous medium. Math. J. Interdiscip. Sci. 2018, 7, 21–28. [Google Scholar] [CrossRef]
- Liu, L.; Rana, J.; Liao, S. Analytical solutions for the hydrogen atom in plasmas with electric, magnetic, and Aharonov-Bohm flux fields. Phys. Rev. E 2021, 103, 023206. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.Y.; Li, Y. On bi-chromatic steady-state gravity waves with an arbitrary included angle. Phys. Fluids 2022, 34, 032107. [Google Scholar] [CrossRef]
- Liao, S. A new non-perturbative approach in quantum mechanics for time-independent Schrödinger equations. Sci. China Phys. Mech. 2020, 63, 234612. [Google Scholar] [CrossRef]
- Liao, S. Avoiding small denominator problems by means of the Homotopy Analysis Method. Adv. Appl. Math. Mech. 2023, 15, 267–299. [Google Scholar] [CrossRef]
- Hayat, T.; Alsaedi, A.; Ahmad, B. Thermo diffusion and diffusion thermo impacts on bioconvection Walter-B nanomaterial involving gyrotactic microorganisms. Alex. Eng. J. 2021, 60, 5537–5545. [Google Scholar] [CrossRef]
- Al-Qudaha, A.; Odibatb, Z.; Shawagfeha, N. A linearization-based computational algorithm of homotopy analysis method for nonlinear reaction-diffusion systems. Math. Comput. Simul. 2022, 194, 505–522. [Google Scholar] [CrossRef]
- Bottona, E.; Greenberga, J.B.; Arad, A.; Katoshevski, D.; Vaikuntanathan, V.; Ibach, M.; Weigand, B. An investigation of grouping of two falling dissimilar droplets using the homotopy analysis method. Appl. Math. Model 2022, 104, 486–498. [Google Scholar] [CrossRef]
- Mehmet, P.; Muhammet, Y. Similarity transformations for partial differential equations. SIAM Rev. 1998, 40, 96–101. [Google Scholar]
- Voller, V.R.; Swenson, J.B.; Paola, C. An analytical solution for a Stefan problem with variable latent heat. Int. J. Heat Mass Tran. 2004, 47, 5387–5390. [Google Scholar] [CrossRef]
- Liao, S. An explicit, totally analytic approximate solution for Blasius’ viscous flow problems. Int. J. Non Linear Mech. 1999, 34, 759–778. [Google Scholar] [CrossRef]
- Liao, S. On the analytical solution of magnetohydrodynamic flows of non-Newtonian fluids over a stretching sheet. J. Fluid Mech. 2003, 488, 189–212. [Google Scholar] [CrossRef]
- Xu, H.; Pop, I. Homotopy analysis of unsteady boundary-layer flow started impulsively from rest along a symmetric wedge. Z. Angew. Math. Mech. 2008, 88, 507–514. [Google Scholar] [CrossRef]
- You, X.; Xu, H.; Liao, S. On the non-similarity boundary-layer flows of second-order fluid over a stretching sheet. J. Appl. Mech. 2010, 77, 021002. [Google Scholar] [CrossRef]
- You, X.; Xu, H.; Pop, I. Free convection along a convectively heated vertical flat sheet embedded in a saturated porous medium. Int. Commun. Heat Mass 2014, 55, 102–108. [Google Scholar] [CrossRef]
- Farooq, U.; Zhao, Y.L.; Hayat, T.; Alsaedi, A.; Liao, S. Application of the HAM-based Mathematica package BVPh 2.0 on MHD Falkner–Skan flow of nano-fluid. Comput. Fluids 2015, 111, 69–75. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Pop, I.; Hendi, A. Stagnation-point flow and heat transfer of a Casson fluid towards a stretching sheet. Z. Nat. A 2015, 67, 70–76. [Google Scholar] [CrossRef]
- Ali, A.; Zaman, H.; Abidin, M.Z.; Shah, S.I.A. Analytic solution for fluid flow over an exponentially stretching porous sheet with surface heat flux in porous medium by means of Homotopy Analysis Method. Am. J. Comput. Math. 2015, 5, 224–238. [Google Scholar] [CrossRef]
- Liu, L.; Li, J.; Liao, S. Explicit solutions of MHD flow and heat transfer of Casson fluid over an exponentially shrinking sheet with suction. Nanomaterials 2022, 12, 3289. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, S. Comparison between homotopy analysis method and homotopy renormalization method in fluid mechanics. Eur. J. Mech. B Fluids 2023, 97, 187–198. [Google Scholar] [CrossRef]
| (10th-Order HAM) | Relative Error (%) | ||
|---|---|---|---|
| 0 | 70.7170 | 70.7107 | 0.0089 |
| 5 | 66.3679 | 66.3589 | 0.0135 |
| 10 | 62.2017 | 62.1848 | 0.0271 |
| 15 | 58.2113 | 58.1879 | 0.0402 |
| 20 | 54.3957 | 54.3672 | 0.0524 |
| 30 | 47.2822 | 47.2482 | 0.0719 |
| 50 | 35.0585 | 35.0304 | 0.0802 |
| 100 | 14.7673 | 14.7895 | 0.1501 |
| 150 | 5.1944 | 5.2046 | 0.1948 |
| 200 | 1.5049 | 1.4704 | 2.3490 |
| 250 | 0.3552 | 0.3463 | 2.5577 |
| 300 | 0.0677 | 0.0660 | 2.6023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, X.; Li, S.; Kang, L.; Cheng, L. A Study of the Non-Linear Seepage Problem in Porous Media via the Homotopy Analysis Method. Energies 2023, 16, 2175. https://doi.org/10.3390/en16052175
You X, Li S, Kang L, Cheng L. A Study of the Non-Linear Seepage Problem in Porous Media via the Homotopy Analysis Method. Energies. 2023; 16(5):2175. https://doi.org/10.3390/en16052175
Chicago/Turabian StyleYou, Xiangcheng, Shiyuan Li, Lei Kang, and Li Cheng. 2023. "A Study of the Non-Linear Seepage Problem in Porous Media via the Homotopy Analysis Method" Energies 16, no. 5: 2175. https://doi.org/10.3390/en16052175
APA StyleYou, X., Li, S., Kang, L., & Cheng, L. (2023). A Study of the Non-Linear Seepage Problem in Porous Media via the Homotopy Analysis Method. Energies, 16(5), 2175. https://doi.org/10.3390/en16052175





