Abstract
Extensive literature is available for modeling and simulating local electricity markets, often called P2P electricity markets, and for pricing local energy transactions in energy communities. Market models and pricing mechanisms provide simulation tools to better understand how these new markets behave, helping to design their main rules for real applications, and assessing the financial compensations of the internal energy transactions. As such, pricing mechanisms are often needed in energy management systems when centralized management approaches are preferred to market-based ones. First, this paper highlights the links between local electricity markets, pricing mechanisms for local electricity transactions, and other approaches to sharing the collective benefits of participating in transactive energy communities. Then, a standard nomenclature is defined to review some of the main pricing mechanisms for local energy transactions, an innovative pricing mechanism based on the economic principles of a post-delivery pool market is proposed, and other relevant approaches for local electricity market simulation such as Nash equilibrium or agent-based simulation are also revisited. The revision was based on systematic searches in common research databases and on the authors’ experience in European and national projects, including local industrial applications for the past five years. A qualitative assessment of the reviewed methods is also provided, and the research challenges are highlighted. This review is intended to serve as a practical guide to pricing mechanisms and market simulation procedures for practical designs of internal financial compensation to share the collective benefits of energy communities.
1. Introduction
The decarbonization of the energy system relies on an efficient combination of strategies and technologies, leading to the more efficient use of energy on the consumer end and to the empowerment of the final users [1,2]. Among those strategies is the decentralization of the energy system, as it is considered in the European Union (EU) regulations and the national energy and climate plans (NECPs) targets [3]. In these plans, the final consumer is presented as an essential participant in the future electricity market, where they should adopt an engaged and active role [4]. In this setting, final consumers can become self-generators (prosumers) of renewable energy [5], for example, by installing rooftop panels, managing their storage and other load flexibilities, and even participating in local collective self-consumption (CSC) and energy communities’ structures, where local electricity markets (LEM) mechanisms can help them to sell their energy surplus or find local supply to their needs. Renewable energy communities (RECs), consisting of the association of prosumers and consumers for producing, consuming, storing, and selling renewable energy, are becoming a promising regulatory tool and organizational structure to promote distributed renewable energy sources (RES) and local energy exchanges [6,7], and to incentivize final consumers to adopt these more active and efficient energy roles.
REC members can sell their electricity surplus to other REC consumers at competitive prices, obtaining an economic benefit compared to feed-in tariff revenues or to direct trading in wholesale electricity markets, which impose considerable entry barriers to their participants [8]. LEM or peer-to-peer (P2P) energy markets appear as feasible local market structures to organize the energy exchanges inside these communities, where the peers freely negotiate the energy exchanges with each other. The development of local markets will contribute to integrating renewable energies at different grid levels, locally improving the energy balance, and, thereby, contributing to the decarbonization strategy of European countries.
These new market structures can host two different profiles of participants, passive consumers, willing to consume renewable energy, and active consumers (prosumers), who produce their renewable energy and share their surplus with their peers, usually in exchange for a financial compensation [9]. In addition to the benefits that LEMs offer consumers, they provide efficient economic signals to adapt their consumption according to the energy price and the local availability of renewable energy supply by accordingly managing their flexibility. Since energy is generated close to where it is consumed, these LEM also contribute to the larger reliability and resilience of the grid, and in most cases, to reduce energy losses [8].
Therefore, driven by the social aspects previously mentioned and the European energy strategy, with an increasing focus on the role of final consumers, there has been progressive growth of RECs and LEMs at an academic level, in pilot demonstrations, and, more recently, in actual implementations. However, internal transaction and financial compensation mechanisms in RECs are still being designed and studied, with few actual implementations of LEM, and concerns and challenges must be addressed. Energy sharing will only develop with the proper economic compensation to those that generate and share their energy with those consuming. However, trading or compensation mechanisms must be simple to implement and generally easy to understand and participate in, and the benefits that participants derive from collective self-consumption must be sufficiently fair compared to what they would derive by behaving individually. Several alternatives can be considered, from pure markets with high levels of flexibility, but also complexity that may disincentivize participation, to centralized management approaches, easing participation, but where the collective benefits must be fairly and transparently shared among the REC members. For example, Shapley approaches [10,11] are often considered in the literature as one of the best approaches to sharing benefits. Still, their conceptual and computational complexity lead to resorting to simple and applicable approaches, often based on ad hoc pricing mechanisms as those described in this review, but still providing fair compensations among REC members. Other approaches use deep learning methods to optimize operations in environments [12].
To date, several local energy projects are in development around the world. However, LEM is still at an early stage where the leading technologies and solutions are still being tested until the products reach a more advanced technology readiness level and the engagement of the final consumers increases. Some examples of LEM projects worldwide, especially in areas where electricity trading is deregulated, were reviewed in [13]. Most of these examples rely on market-based pricing mechanisms. In the United Kingdom, Piclo [14] is developing an electricity trading platform where business consumers can select and directly buy electricity from local renewable suppliers. In the Netherlands, Vanderbron [15] is another electricity trading platform where consumers can directly buy electricity from local independent producers. In Germany, the Sonnen Community is a community whose members entirely cover their energy needs on sunny days from their RES and batteries [16]. Among existing pilot projects, the Brooklyn Microgrid project (BMG project) stands out as the first project worldwide where the members of an energy community could trade locally generated energy with their neighbors over a blockchain platform [17]. In this project, an electrical microgrid was built in addition to the existing distribution network. The energy exchanges inside the community are carried out within the distribution grid, while the physical microgrid is only used for emergencies. Furthermore, community interaction is carried out on a private blockchain platform. There, consumers constantly bid on their price limits and preferred consumed energy resources, whereas prosumers bid on their minimum energy selling price. Regularly, the energy transactions are cleared, and energy exchanges are allocated to the participants trying to maximize their economic benefit. From [17], it is concluded that the rate of participation in the BMG project and the positive social acceptance prove the market potential of local energy communities based on distributed RES generation.
The revision of the literature of this work was conducted based on systematic searches in common research databases using relevant keywords in the current field, but also on the authors experience in European and national projects related to local energy and flexibility markets where previous specific revisions had already been undertaken (such as, for example, [18,19,20,21,22]), also including local industrial applications for the past five years. However, since there is a huge amount of related literature and works, additional criteria have been used to select those papers and works more directly related to the objective of this revision. From the literature reviewed, ref. [23] provides the most comprehensive review on LEM to date. It analyses price formation mechanisms and classifies them into single auction, double auction, negotiation and equilibrium-based, and system-determined mechanisms. These mechanisms are also related to market designs, such as forward markets, real time, and others, such as those settled after delivery or post-delivery [24]. However, it needs to detail the reviewed price mechanisms, missing the opportunity to set a standard nomenclature and mathematical formulation. Common mathematical formulation for LEM proposals has been provided in some other review papers. For example, ref. [25] analyzed LEM simulation methods and algorithms related to market mechanisms. However, it did not focus on specific price formation mechanisms. A review and simulation of auction mechanisms were provided in [26], but relevant aspects of LEM design were ignored. In [27], a framework to test and validate single and multi-unit auctions was proposed for an actual microgrid application, but a comprehensive review of other pricing mechanisms still needs to be included.
Therefore, to our knowledge, no paper to date has provided a comprehensive set of pricing mechanisms related to different market and energy-sharing compensation designs to help researchers in practical cases. In this sense, this paper provides a practical comprehensive revision of the main local electricity pricing mechanisms proposed in the literature for computing the price to compensate for the internal energy transactions within energy communities. Its main contributions are:
- A systematic and practical review of pricing mechanisms for the financial compensations of energy trades within energy communities and LEM, providing a quick and straightforward guide so readers can easily identify them and assess their pros and cons. Since local transaction prices are very much related to LEM simulations, a brief review of the main LEM simulation approaches is also provided.
- A uniform mathematical formulation of the pricing mechanisms with a standard nomenclature so that they can be better understood and compared.
- A conceptual approach to collective benefits sharing that highlights and explains the links among the different alternatives, including LEM, pricing algorithms, and other approaches.
- A practical taxonomy of the pricing mechanisms identified and reviewed.
- The proposal of a new pricing mechanism developed by the authors based on [24] that uses the peers’ opportunity costs and their actual energy delivery, and combines simplicity with market-based principles to provide fair and easy-to-explain financial compensation to the energy transactions.
- A qualitative comparison among the pricing mechanisms reviewed, to help researchers and LEM project developers solve price formation issues for local transaction compensations, both in theoretical and applied fields.
2. Collective Self-Consumption Framework and Nomenclature
The economics of local electricity trading [8] are based on:
- Energy cost savings, since the energy injected back to the grid is typically paid at a lower price (feed-in or selling tariffs) than the retail price (supply, retail, or buying tariffs), so prosumers can profit from locally selling or buying energy.
- Grid cost savings, since energy flows decrease due to local generation and supply matching, and access tariffs for self-consumption are very often only applied to the grid voltage levels used, saving higher voltages grid tariffs. In addition, some regulations (as in Portugal [6]) include additional grid access tariff discounts for the energy locally shared to incentivize the energy decentralization process. Note, however, that tariff redesign may be an issue in guaranteeing long-term power system sustainability.
- Flexibility provision, since new global or local grid services may be provided in the future by aggregated prosumers to balance responsible parties (BRP), transmission system operators (TSO) or distribution system operators (DSO), leading to additional revenue streams.
Figure 1 represents the energy exchanges among the participants in a LEM and with their respective retailers. As an example, it highlights the prices prosumers 1 and 2 face, PBm,h being the retail price prosumer m pays to buy main grid electricity from its retailer for the interval settlement period (ISP) h (which could be an hour or a 15 min interval, as seems to be the standard for self-consumption), PSn,h the price paid by the retailer to the prosumer n for the electricity sold back to main grid, and Pn,m,h the price paid by prosumer n to m for buying local supply.
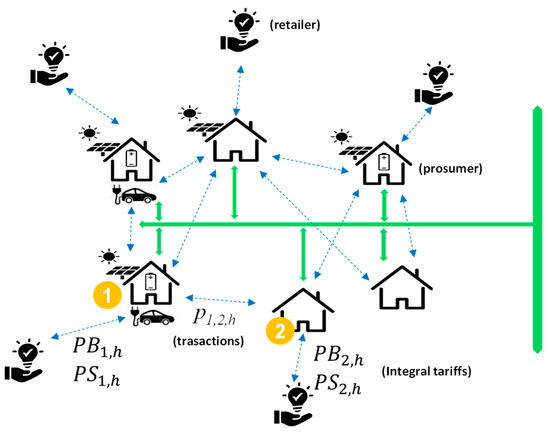
Figure 1.
Overview of electricity exchanges in a local electricity market.
The internal transactions are profitable to all LEM participants if:
Note that other criteria, such as preferences or products differentiation, as described in [28], are not being considered here. In the simplest case, where there is a unique internal trading price ph and all prosumers face the same tariffs PSh and PBh, which is a very common assumption of many related works, Equation (1) becomes:
Let dqn,h be the energy bought (deficit) and eqn,h the energy injected (surplus) by a LEM participant n in an ISP h, i.e.:
where Dn,h is the consumption of participant n and en,h is its self-generation, and where the total energies injected, eqh, and consumed, dqh, by the all the energy community members at ISP h are given by the last two summations of Equation (3).
Variables dqn,h and eqn,h can be decomposed into the energy exchanged with the grid (dqgn,h and eqgn,h, respectively) or within the LEM (dqln,h and eqln,h, respectively), i.e.:
The energy dqln,h bought (or the energy eqln,h sold) by each participant in the LEM is then the sum of the energy em,n,h he sells from (or the energy em,n,h he buys to) all the LEM participants:
Therefore, the total energies internally exchanged, either injected or consumed in the LEM, satisfy:
Finally, the energy balance constraint of each participant sets that its consumption Dn,h must be supplied by its self-generation en,h, plus the energy dqn,h obtained from the LEM or from the main grid, and minus the energy eqn,h injected back to the LEM or to the grid, that is:
3. Collective Benefits Sharing and Pricing Local Electricity Transactions
- Collective benefits sharing is essential to go from individual to collective self-consumption structures, such as energy communities. Indeed, members must see a benefit from joining these structures, which may depend on the existing regulation and subsidies, on the complementarity among the potential members, and on the existence of a fair and straightforward mechanism to share the additional benefits that the community organization may provide to the members, which, as referred to in [29], is a complex issue. Figure 2 shows the main implicit or explicit ways to share these collective benefits among members of a REC.
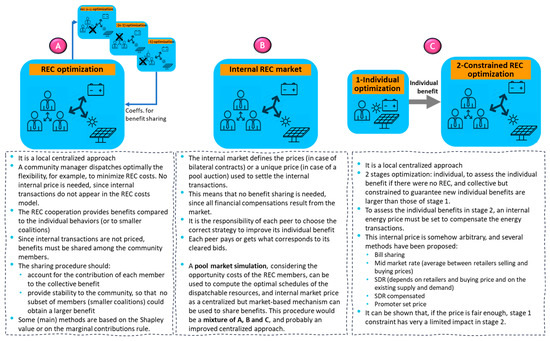 Figure 2. Sharing collective benefits in energy communities, when managed with a centralized optimization approach (A), with an internal local market (B), or with a constraint centralized optimization that guarantees all individual benefit from belonging to the REC (C).
Figure 2. Sharing collective benefits in energy communities, when managed with a centralized optimization approach (A), with an internal local market (B), or with a constraint centralized optimization that guarantees all individual benefit from belonging to the REC (C).
Some approaches (Figure 2A) have proposed centralized optimal management of the REC individual and collective resources, and have proposed to use benefits-sharing mechanisms based on the Shapley value [10,11], or its simplified version, of the marginal contribution of each member [30]. However, these approaches are mathematically and computationally complex, hard to explain to potential REC’s members, and therefore, may be a serious drawback for member engagement.
Market mechanisms (Figure 2B) do not require collective optimizations [24,31]. Indeed, collective benefits generate and are implicitly shared according to the bidding strategies of the REC members, either in bilateral transactions or in a pool system. Hence, the responsibility of fair participation in the collective benefits falls on the bidding decisions of the market participants. While this simplifies the management of the REC, the complexity falls on the side of the REC members, which could also be a barrier to their engagement when the collective benefits do not significantly outweigh the individual ones.
The approach followed in [29] (Figure 2C) proposes a centralized optimization of a REC, but with a constraint to guarantee that the individual benefits that result from the collective optimization (called stage 2) are always equal to or greater than those that would have resulted from the individual optimal behavior (called stage 1). However, although in the collective optimization formulation internal transactions sum zero and do not appear in the objective function, the internal transactions compensations to compute the REC members benefit and guarantee that the individual benefit of stage 1 does require the computation of an internal transactions price. In this sense, ref. [29] did not test different price approaches, but showed how the fairness of the internal price was essential to guarantee, with this multiple stages approach, that efficient energy sharing takes place within the community. Otherwise, when the computed price does not fairly compensate the REC members, the constraint from stage 1 significantly reduces the internal transactions and the benefits of associating, which means that selecting an appropriate pricing mechanism becomes essential for an efficient collective self-consumption.
In this sense, pricing local electricity transactions may have, therefore, two distinct objectives:
- Setting an actual price for the settlement of the local transactions to determine the financial compensations between sellers and buyers, with direct application in centralized REC energy management systems, as shown in Figure 2 or in [29].
- Simulating local electricity markets to understand and validate their designs, and to forecast their behavior for flexible resources management and for optimal strategic bidding. Indeed, centralized management approaches can also be understood as simulation algorithms to assess the behavior a local electricity markets [29].
Figure 3 shows the classification proposed for the main pricing mechanisms. On the left side are the LEM pricing procedures for transaction settlement, including those market-based (either bilateral, pool, or a combination of both) and those based on ad hoc pricing algorithms. While market-based approaches depend on the specific market design, pricing algorithms typically intend to compute a price with sensible economic signals that are either based on collective benefits sharing, or try to reproduce, to some extent, the behavior of actual market prices, such as bill-sharing (BS), mid-market-rate (MMR), or side-demand ratio (SDR). In this case, we added a pricing algorithm based on the clearing of the post-delivery pool market proposed, based on the bilateral post-delivery of [24], and described later in Section 3.1.1 as a significant improvement over the other methodologies described. As already explained, pricing algorithms are often used to determine a transaction price when centralized optimizations are run to compute the setpoints of flexible resources, as in [29], to share the collective benefits derived from the central dispatch.
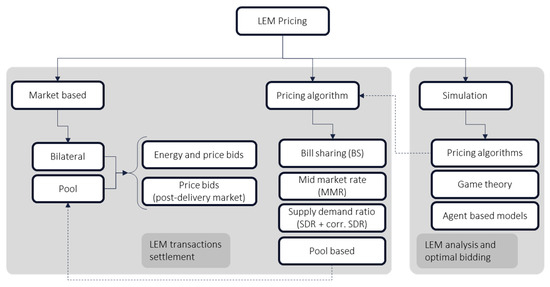
Figure 3.
Classification of LEM pricing mechanisms.
On the right side of Figure 3 are the LEM simulation approaches, such as market equilibrium computations, agent-based simulation algorithms, or the same pricing algorithms of the left side when used for simulation purposes.
3.1. Market-Based LEM Price Computation
In competitive electricity markets [32], bilateral contracts often coexist with a pool-based market:
- In the bilateral clearing, typically, pairs of selling and buying bids are cleared as soon as they are compatible (buying price more significant than the selling price and compatible energy constraints), which means that each transaction is differently priced according to the bids involved. In these cases, no market price exists, and only averages can be computed [33,34].
- In pool-based markets (as is the case of EU wholesale day ahead markets), the aggregated supply and demand curves are built from the individual bids, and their intersection determines the energy traded and the market price applied to all transactions, and the supply and demand bids accepted.
- In general, a combination of bilateral and pool clearing can coexist, which typically implies two processes, a first one for bilateral trading, and a final pool where the energy, not yet negotiated during the bilateral negotiations, can still be offered to the pool.
In the case of competitive pool-based markets, the market price is computed by building the aggregated supply and demand curves from the bids submitted by the participants to buy and sell energy, and the equilibrium price is given by the marginal or opportunity cost of the last supply bid cleared, when the energy supply equals the final consumers’ demand. Competition implies that bid prices should be based on the opportunity costs of the participants [32], and LEM participants will sell or buy depending on their energy needs. In wholesale markets with high penetration of RES with zero marginal costs, this might bring issues regarding low energy equilibrium prices that may not properly remunerate long-run capital costs, which very often implies the need for additional remuneration mechanisms, such as flexibility or capacity markets. However, in LEMs, even if the local generation is from RES with null marginal cost, rational prosumers will only locally buy and sell energy if the LEM price is between its supply and feed-in prices, as in Equation (1), meaning that, instead of marginal generation costs, prosumers face the opportunity costs of not trading their surplus and supplied energy with their retailers or aggregators. In addition, prosumers do not typically have energy schedules agreed with their retailers and aggregators, which act as their BRP on the Wholesale Market (WS), so LEM trades do not have delivery commitments, effectively allowing prosumers to trade energy even after delivery, as proposed in [24].
Figure 4 shows an example of the aggregated demand and supply curves of a LEM under perfect competition, with perfect information and with no entry and exit costs.
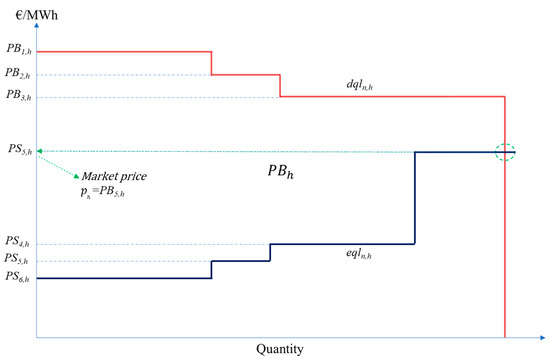
Figure 4.
LEM demand and supply curves based on opportunity costs and benefits.
As can be seen, prosumers 1 to 5, with a surplus of energy, will only be willing to sell their surplus in the LEM if the market price ph is higher than the price they get from their retailer (feed-in-tariff PSn,h. On the other hand, prosumers 1 to 3 that need supply, will only buy energy in the LEM if its price is lower than its retailer selling price PBn,h. Under these incentives, supply and demand curves can be defined as in Figure 4, and the market equilibrium price ph is reached where the curves cross each other, revealing the price that provides the optimal economic signal to the LEM participants. Note that, for example, in case prosumer 5 had no supply to offer, the demand would not be locally supplied, and the market price should be set, instead, by the last supplied demand PB3,h, to properly reflect the current supply scarcity and give the right signal to potential investors in new local generation capacity. Supply prices larger than PB3,h force prosumer 3 to procure energy from its retailer that sells to him more cheaply, generating a local excess supply.
In practice, markets do not usually operate under perfect competition [32]. For instance, information exchange is a relevant challenge in the design of LEM, since prosumers might be inclined to keep their opportunity cost. In addition, small prosumers may also not be willing to invest in advanced technologies to operate with complex trading strategies. Overall, LEM design and simulation tools should provide efficient price signal incentives close to the theoretical equilibrium price.
3.1.1. Post-Delivery LEM Pool Market
We propose a post-delivery pool market based on a fair local market design approach that is easy to implement. In this proposal, the aggregated selling and buying curves can be built after delivery by using, for each prosumer: (1) the energy produced and the corresponding retailer buying price to make its selling bid, and (2) the energy consumed and the corresponding retailer selling price to make its buying bids. Note that a prosumer will only have either a buying or a selling bid per interval settlement period h. The equilibrium is computed as shown in Figure 4. This post-delivery pool market is simple, it does not require participants’ forecasts and previous commitments, and still provides the right economic signals to their participants, based on their opportunity costs. Therefore, the advantages of such a proposal include the following:
- Reduced trading costs, since peers do not have to forecast production and consumption nor design bidding strategies, since they only need to inform the price at which they are willing to buy and sell energy and the energy that comes from the contracts they assign with their retailers and aggregators.
- Works as a market to settle the differences of other markets, so it could be the last round after a previous round of bilateral trading, since it can be integrated with other LEM forward mechanisms, including flexibility markets as described in [35].
3.2. Pricing Algorithms
Pricing algorithms compute local transaction prices based on different ad hoc criteria, usually based on structural or dynamic information of the participants, also considering their opportunity costs. These prices can be used to settle the energy transactions that may result from energy bids or optimal central dispatches of REC flexible resources, as in [29]. Depending on the algorithm selected, the computed price may be known in advance, or only after the energy is delivered as it is for the Bill Sharing (BS), Supply, and Demand Ratio (SDR) [36], and our proposal of post-delivery pool-based pricing algorithms. We next describe these algorithms and compare them in Section 3.2.6.
3.2.1. Bill Sharing (BS)
BS is a method that shares the total energy bill of the REC among its participants, depending on their energy consumption or generation contribution to the total [37]. Everyone pays the same price pbh for the energy consumed and receives the same price psh for the energy exported. In case all REC members have the same supply and feed-in tariffs, and these tariffs have no time discrimination, then these prices are given, for each ISP, by sharing the total cost of the REC purchases among those purchasing, and the total incomes of the REC sales among those buying:
Then, for each REC member, the total energy consumed (bought) dqn,h is priced at pbh and the energy injected (surplus) eqn,h is priced at psh.
If supply and feed-in tariffs depend on the ISP h, then the following extension is straight forward:
In case REC members have different retail prices, and assuming that retailers selling prices are always higher than the feed-in tariffs they apply to the energy sold back to the grid (otherwise arbitrages could take place if regulation allows), these expressions can be extended by using the minimum retailer selling price and the maximum retailer buying price considering all REC members:
Note that the BS method, as described in [37], does not remunerate the REC members that are producing and sharing their energy with other consuming members. If no other payments are arranged for the local transactions, producers share it for free, since necessarily or . In other words, either the consumers pay less for the energy consumed or the producers get less for the energy produced. Therefore, additional internal mechanisms are needed to provide the right economy for local investments and remuneration of the generation resources, since, as it was proposed, this method does not seem to provide fair benefit sharing.
3.2.2. Mid-Market Rate (MMR) and Intermediate-Market Rate (IMR)
The MMR pricing mechanism assumes that the internal energy price ph is the average between the energy buying and selling reference prices. MMR is proposed either to directly determine the bilateral transactions prices between peers [38] or to be a bid reference for these transactions [39]. MMR price ph is computed as the average between the energy buying and selling prices to the grid [37], so that the benefit is somehow equally shared among buyers and sellers. When all REC members have the same supply and feed-in tariffs, this price per ISP is given by:
If different prosumers have different retail prices, these expressions can be extended by using the minimum retailer selling price and the maximum retailer buying price considering all REC members.
We also propose the IMR as a convex linear combination of the minimum retailer selling price and the maximum retailer buying price:
This combination approximates the internal price closer to the retailer selling prices, or to the retailer buying prices.
3.2.3. Supply-Demand Ratio (SDR)
The SDR pricing mechanisms is based on the computation of sdrh [40,41], which is the ratio between the energy available for self-consumption, offered by those prosumers with energy surplus, and the energy demanded by those needing supply:
When sdrh > 1 the REC has a surplus that must be sold to the grid. When sdrh = 1, the energy generated in the REC is the same as the energy demanded, and so, there is no energy exchange with the grid. When 0 < sdrh < 1, there is a deficit of energy in the REC, and it is necessary to buy energy from the grid. Finally, when sdrh = 0 all the energy consumed is bought from the grid, as there is no energy available in the REC.
The SDR pricing mechanism is inspired by the fundamental law of economics that assumes an inverse relationship between the price and sdrh [40]: the higher sdrh is (more energy internally available), the lower the transactions price should be, and the lower sdrh is (less energy available), the higher the LEM price should be. Then, as in [40], assuming same supply and feed-in tariffs for all REC members:
- If sdrh > 1 (more local generation than consumption in the REC), the price ph is the same as the selling price PSh to the grid. Effectively, if ph was lower, prosumers would not internally sell the energy but directly to the grid at PSh. Therefore, all the consumers buy their energy in the LEM at the selling price to the grid:
- If 0 < sdrh < 1 (less local generation than consumption in the REC). The internal energy price is inversely proportional to sdrh. Therefore,
To calculate the coefficients a and b, the boundary conditions of sdrh are used:
- If sdrh = 0, there is no surplus in the REC and all the energy is bought from the grid, and therefore ph = PBh.
- If sdrh = 1, the local generation and demand in the REC are equal, so there is no energy exchange with the grid. Thus, the internal energy price is the lowest possible, i.e., ph = PBh.
By substituting these two points into Equation (16), the following equation set is obtained:
Therefore, the internal SDR energy price is given by:
Since consumers will buy their supply from both the grid and locally in the REC, the resulting energy buying price PBh is the weighted average between the amount of energy purchased from the grid and within the REC, i.e.,
And therefore:
In summary, the internal energy price and average buying price in the REC are defined as a function of sdrh as follows:
Note that these prices not only depend on the energy selling and buying prices from the grid, but also on the generation and demand in the community. Figure 5 represents the relationship between these prices and sdrh.
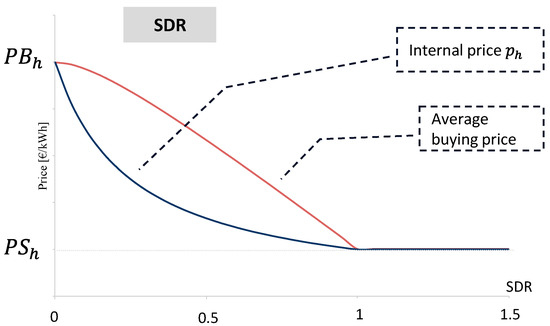
Figure 5.
Relationship between PSh, PBh with the SDR pricing.
If different selling and buying retailers prices exist, PBh can be replaced by maxn(PBn,h) and PSh by minn(PSn,h).
3.2.4. SDR Compensated
According to Equation (21), when there is generation surplus in the REC (sdrh > 1), prosumers obtain the same benefit by either selling their surplus to the grid or within the REC. To incentivize prosumers to sell in the REC, a compensation factor λ such that 0 < λ < PBh − PSh was proposed in [42], so that the benefit of those consuming when there is an excess of local generation is also shared among those prosumers contributing to this local excess. When this compensation is included, the internal energy price and the average buying price become:
Figure 6 represents the relationship between these prices, sdrh and the compensation factor λ.
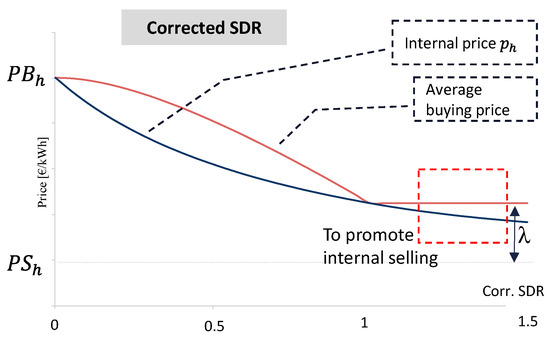
Figure 6.
Relationship between ph, PSh, PBh, λ with the corrected SDR pricing.
Despite the compensation that increases the internal energy price, consuming members still make a profit compared to buying from the grid and will still be willing to pay for their energy ph, lower than PBh. In addition, generating members will still be paid for their energy more than PSh. This ensures that all REC members obtain an economic benefit by staying in the community.
Again, if different selling and buying retailers prices exist, PBh can be replaced by minn(PBn,h) and PSh by maxn(PSn,h).
3.2.5. Post-Delivery Pool-Based Pricing Algorithm
This method is based on the post-delivery market concept of [24], already described in Section 3.1.1, which is an application of auction theory, and finds LEM equilibrium prices [43]. It consists of computing the internal transaction price as the clearing price of a post-delivery pool market, where supply bids are built using the real metered production (for those REC members with net generation) and demand bids using the real metered consumptions (for those REC members with net consumption). Bid prices can be the opportunity costs of the participants to buy or sell, and the market price, as described in Section 3.1, is given by the intersection of the aggregated supply and demand curves. In practice, for simulation purposes, consumption and generation forecasts could be used instead of the measured quantities. While this method set ups a competitive LEM, we also propose it to price the REC transactions that may result from a centrally optimized management approach. Indeed, post-delivery pool simulation is an improvement regarding SDR approaches, since it computes the marginal price of a local market, instead of using arbitrary, even if sensible, criteria to compute ad hoc prices. The pool remunerates participants according to the marginal costs and benefits, effectively pricing the energy for its intrinsic opportunity costs.
When flexible dispatchable resources are present in the community, the computation of their optimal schedule may require transaction price forecasts, as for example in [29]. Since the post-delivery pool price is determined after delivery, this generates a circular problem, since the flexible resources will modify the actual delivery and the pool price. In these cases, we propose a simple iterative resource scheduling algorithm to estimate both the optimal flexible resource schedules and the transaction prices, as shown in Figure 7. Alternatively, a collective welfare maximization may be formulated to simulate, in one optimization step, the dispatch of the flexible resources and the market price.
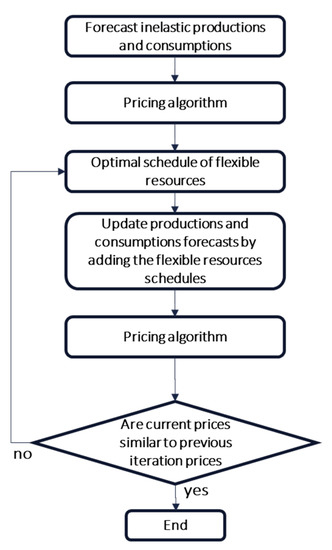
Figure 7.
Iterative pricing algorithm with flexible resources.
3.2.6. Comparison of the Pricing Algorithms
In [44] and in [36] the performance of some of these pricing mechanisms is assessed by measuring how they respond to price signals and how the collective benefits are distributed to the participants. The work in [29] also assesses the transaction price’s impact on the fairness of collective benefits sharing. From this previous works, and assessing selected relevant attributes (as for example does [45] for market designs), some relevant conclusions are first derived, and the qualitative assessment is also proposed in Table 1:

Table 1.
Qualitative comparison of pricing mechanisms.
- According to [40], BS performance is poor, since it only averages the participants’ electricity bill. Hence, the incentives for demand response are low. For real REC applications, potential members need to understand how prices are defined, or, otherwise, they will not join the REC. The BS algorithm may appear to be conceptually simple, but the price computation is not easily traceable since it requires calculating the community’s aggregated costs. In addition, it must be complemented with transaction compensation, increasing its complexity compared to other approaches.
- MR and IMR perform better than BS and slightly worse than SDR when price signals from the retailer fluctuate during the day [36]. MR and IMR are also simple to explain since they can be understood as sharing the benefit that results from the selling and buying price spread. However, they disregard the actual contribution of local load balance in the price formation, meaning that participants have less incentives to manage load and flexibility [41].
- SDR-based mechanisms perform better, since they provide a dynamic internal price that changes depending on the energy availability in the community, and thus, provide good incentives for demand response and better economic signals with more efficient results [41]. Indeed, these methods perform well since they try to reproduce a market-like behavior by setting a dependency on the price with the participants’ opportunity costs and with the available demand and supply.
- The post-delivery pool provides the best economical results to our understanding, since it is based on an optimal market equilibrium, where the prices reflect the actual opportunity costs of the REC for each ISP. In addition, its computation is simple and well-understood in economic theory, and easy to explain and justify to potential REC members. This mechanism, however, can have higher price fluctuations, since prices vary between the retailers’ buying and selling prices.
Based on the assessment above, Table 1 compares the pricing mechanisms based on relevant qualitative attributes by assigning positive and negative marks to each one. The attributes analyzed are the following:
- Conceptual simplicity: refers to how easy it may be for prosumers to understand and accept the price methodology.
- Computation simplicity: measures how easy it is to compute the price, including how affordable and practical is to access input data.
- External price signals relevance: refers to how well the price reflects the real costs and external price signals.
- Economic signal efficiency: measures how the price provides the proper economic signal. The closer the prices are to the opportunity costs, the more efficient the mechanism.
- Price volatility: measures how volatile the prices computed by the mechanism are.
- Sharing fairness: measures to what extent the pricing mechanism accounts for the contribution to each member to the REC benefit. Methods considering supply and demand dynamics or aggregated costs tend to be fairer.
4. Simulation of LEM
LEM can be simulated (or even operated) by defining energy sharing mechanisms to determine the transactions, such as (1) sharing the energy surplus among the participants consuming based on proportionality or other complex arbitrary criteria, and (2) by computing a transaction price based on the pricing algorithms already described, which is a prevalent approach due to its simplicity. These approaches, which may lack depth regarding agents’ behavior and fully economic soundness, are however simple tools which may provide sensible conclusions with lower effort, being acceptable solutions to more practical approaches.
However, more accurate simulations can be performed when the participants’ behavior is represented to compute a market equilibrium. In this case, two main traditional approaches can be found in the literature, those based on game theory, where a system of simultaneous optimization of the individual participants’ benefit must be formulated and solved, and those based on agent-based systems, where iterative algorithms try to reach the market equilibrium by adapting the market agents bids according to pre-defined learning strategies to optimize their objectives.
4.1. Game Theory Approaches
Game theory (GT) is especially suited to simulate LEM and how the actions of one agent influence all others. Reference [46] provides a review of GT models and highlights some fundamental properties of GT LEM simulation techniques:
- Frequency of play: games can happen once or repeatedly.
- Chronology: actions can be simultaneous or sequential amongst players.
- Awareness of players: regarding perfect and imperfect information.
- Knowledge of players: whether the information is complete or incomplete.
GT models can also be divided into two main groups: cooperative game theory and non-cooperative game theory [43,47]. In cooperative game theory, players are considered a unit, and their actions are oriented to maximize the benefit of the group. In LEM simulations, participants must access incentives to justify their presence in the community. The benefit of the community is shared among them according to different rules. Some examples of cooperative game theory have been provided in [48,49,50,51]. Reference [48] showed a LEM where a group of prosumers prioritized cooperation and willingly sold their surplus energy on the local market first to gain further profit. The authors in [51] simulated a P2P LEM through a cooperative game that distributed the benefit according to each participant’s contribution. A Shapley value rule was used to find the transaction prices. Reference [11] compared the benefit sharing in an energy community with investment decisions to other sharing approaches.
In non-cooperative games, participants try to maximize their benefit leading to a collective result that is often only optimal if some economic assumptions, such as perfect competition, hold. These GT models are based on the Nash equilibrium and find individual stable solutions where participants have no advantage in changing their strategies, considering others’ strategies fixed. Some examples of P2P non-cooperative GT models are [52,53].
Reference [52], for example, proposes a non-cooperative equilibrium approach with the following characteristics:
- The LEM has no single internal price, and the prices of each resulting bilateral transaction are dual variables from the optimization problem.
- Not all generation is necessarily traded in the LEM. Participants might not reach an agreement and any untraded energy is sold (bought) to (from) the grid.
The main inputs, following the nomenclature defined in Section 2, are the price PBn,h of the energy bought from the grid, the price PSn,h of the energy sold back to the grid, the bilateral trading costs βn,m imposed by n to m, representing the interest from participant n to sell energy to participant m in [€/kWh]. This trading coefficient represents participants’ preferences such as social values, distance, emissions of the provider, etc., so the following local trading cost is proposed:
The main outputs are the bilateral trading price pn,m,h between participants n and m, which is the dual variable of the trading reciprocity constraint en,m,h = em,n,h, and the congestion price pcn,m,h, which is the dual variable of the capacity trading constraint en,m,h ≤ En,m. Both dual variables are fundamental to determine the nodal price captured by each participant n.
Considering the cost defined in (23), in [28], a multi-bilateral economic dispatch problem with product differentiation was formulated to model a P2P market.
In addition, using this same cost, ref. [52] formulated a non-cooperative game problem with product differentiation, storage capabilities, demand response, and grid restrictions. If Un(dn) is the utility of the final demand dn (considering batteries and its response), the objective function used in both [28,52] works follows, subject to Equations (1)–(7):
4.2. Agent-Based (AB) Simulation Models
In agent-based models to simulate LEM, each virtual market agent bids on a simulation environment while trying to maximize its benefit or other similar goal [54]. Market agents provide buying and selling bids of their demand and generation, as well as their energy prices, after which a coordinator, for example, in a pool market as in [55], determines the final internal energy price. In a pure P2P LEM, any form of a centralized approach to compute an internal price is excluded, and peers must bilaterally communicate their buying and selling bids to generate transactions with their own agreed prices. This may lead to significant computational needs due to the number of iterations, especially for large-scale LEM.
In P2P agent-based simulations, proposals search for ways to reduce the amount of exchanged information to reduce the computational overhead [56]. However, some agent-based P2P simulations solve this overhead issue by escaping from a pure P2P problem with the creation of a coordinator agent which facilitates the optimization problems while simulating some P2P behavior, as in [57]. In addition, pool-based approaches allow some degree of centralization, simplifying the simulation. This is the case of the work in [55], which uses the agent-based simulation example we describe next.
Simulation of AB Model
Figure 8 presents an overview of a pool-based AB model where agents (prosumer, coordinator, and retailer) interact through two main modules, as simulated in [55]. A centralized pricing module operated by the Coordinator Agent interacts with decision-making models simulated for each agent. The retailer is a passive agent that only buys and sells the energy not traded on the LEM.
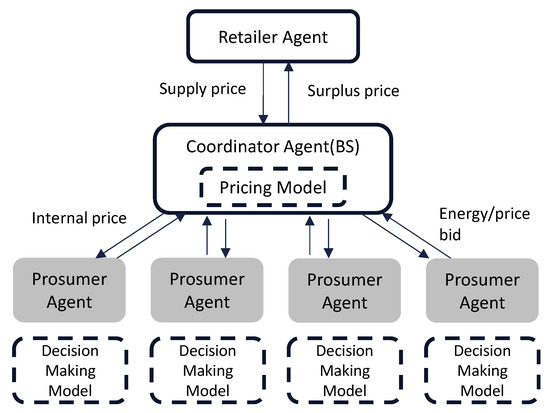
Figure 8.
Overview of the multiagent-based simulation framework, source [55].
The main characteristics of this approach are:
- There is an energy coordinator in the LEM who runs the pricing model.
- A centralized common internal energy price is established for the community, so all participants trade their energy at the same price in the LEM.
- It is assumed that the amount of energy a participant exchanges with the grid is proportionally divided among all participants.
This approach presents a multiagent-based model for a LEM with the possibility of demand response and battery storage capabilities, in which there are three types of agents:
- Prosumer Agents. Who decide how to schedule their consumption from load demand considering PV generation. They may locally buy or sell energy.
- Coordinator Agent. A community representative who determines the internal price and trades with the participants and with the community’s retailer assuring its energy balance.
- Retailer Agent. A typical retailer who buys and sells any surplus or supply required by the coordinator. The retailers’ prices are not considered dynamic.
The decision-making model simulates each prosumer agents’ bids on the local market in response to the price signals sent by the coordinator pricing model. Agents’ energy bids may be given by the generation capabilities, or vary due to demand response and storage systems. The decision-making model can also include price bids from the prosumer agent to the coordinator, and is generally formulated as follows:
s.t.
The above equations are iteratively used, and each agent minimizes its costs of trading with the coordinator by adapting the net energy it offers or buys at each iteration in response to the price signals sent by the coordinator. The energy is therefore computed considering the demand (which can be elastic), the consumption of the battery (if it exists) and the self-generation . In the first iteration, the coordinators might use a mid-market price given by:
Subsequently, the coordinator agent runs a pricing algorithm to propose the internal energy trading prices using the price signals from the grid, and , and the prosumers’ energy bids as inputs, as in Equation (28):
The pricing method function can be any of those described in Section 3.2. In particular, ref. [55] used the SDR algorithm to compute the LEM, by computing as a function of the supply and demand given by as follows:
Iterations last until the energy bids and the internal energy price converge. To guarantee convergence, ref. [55] applied two different techniques: step length control and learning process involvement, and a last-defense mechanism in case it was not achieved.
5. Conclusions
This paper presents a general mathematical view of the main pricing mechanisms found in the literature for transactions within renewable energy communities, whether based on pricing algorithms, market clearing rules, game theory, or agent-based simulation. Pricing mechanisms can be used to set the internal price for the local transactions of an energy community, or to simulate the behavior of local markets.
When pricing mechanisms are used to compute the prices of the internal compensation from those that consume to those that locally generate, several criteria such as conceptual simplicity and fairness become essential. In this sense, those methods that are more closed to market-based approaches, that consider both the existing demand and supply and the opportunity costs of the participants, seem to provide better economic signals. Among them, those based on the demand-supply ratio, and overall, the authors’ proposal of a post-delivery pool market simulation seem to outperform the rest of the alternatives. In addition, the demand-supply ratio is based on sensible but somehow arbitrary criteria, while the post-delivery pool is just a market simulation according to basic economic principles. In this sense, it is easy to understand and, in addition, effortless to compute and verify by the community members.
When pricing mechanisms are used for simulation, simplicity is not an issue, and more complex approaches can be used. Agent-based systems are usually used only for simulation purposes, but the adaptation of the agents’ strategy is not always straightforward and may fail to represent a real market behavior, and the resulting dynamics are often not representative of real market dynamics and can present convergence issues. Nash equilibriums can be an alternative, although in the literature they are often used as a clearing mechanism of a local market. In this case, even if they may allow more flexible clearing mechanisms by including participants’ preferences, arbitrary costs need to be defined and the mathematical complexity becomes an issue indeed. In this sense, the post-delivery pool proposed by the authors is also a proper market equilibrium based on the participants’ opportunity costs, and can also be used to clear a local market.
The systematic analysis and comparison of the different methods is a research challenge, which can be extended to the assessment of the market designs for local markets. The use of arbitrary data or different design principles can make comparison significantly difficult, and very often fairness and simplicity criteria are ignored to incorporate additional flexibility in terms of product or counterpart preferences. However, renewable energy community implementations are still pilot projects, and real implementations are scarce due to regulatory and administrative barriers or inefficiencies, but also due to the low engagement of potential members. In this sense, again, simplicity and fairness, combined with low-cost solutions, seem essential to further develop self-consumption structures. The authors are currently assessing, with quantitative case examples, how the different pricing mechanisms behave in terms of collective benefits sharing when compared to the individual optimum. Methods based on the Shapley value or on the marginal contributions are also being considered, but rather as possible benchmarks for comparison.
Author Contributions
Conceptualization, J.M., F.A.C. and J.V.; methodology, J.M., F.A.C. and J.V.; software, C.d.L. and F.A.C.; validation, C.d.L. and F.A.C.; formal analysis, J.M., C.d.L., F.A.C. and J.V.; investigation, J.M., C.d.L., F.A.C. and J.V.; resources, J.M., F.A.C. and J.V; data curation, C.d.L.; writing—original draft preparation, J.M., C.d.L., F.A.C. and J.V.; writing—review and editing, J.M., F.A.C. and J.V.; visualization, J.M., C.d.L., F.A.C. and J.V.; supervision, J.M., F.A.C. and J.V.; project administration, J.M., F.A.C. and J.V; funding acquisition, J.M., F.A.C. and J.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financed by the ERDF—European Regional Development Fund, through the Operational Programme for Competitiveness and Internationalisation—COMPETE 2020 Programme under the Portugal 2020 Partnership Agreement, within project DIGITALCER, with reference POCI-01-0247-FEDER-047197, and by the Norte Portugal Regional Operational Programme (NORTE 2020), under the PORTUGAL 2020 Partnership Agreement, through the European Regional Development Fund (ERDF), within the DECARBONIZE project under agreement NORTE-01-0145-FEDER-000065.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Indexes | ||
| n, m | Participants in the local electricity market | |
| h | Interval settlement period or ISP | |
| Parameters | ||
| Dn,h | Energy consumption of participant n at ISP h [kWh] | |
| PB, PBh, PBn,h | Price of the electricity bought from the grid (retailer) [€/kWh] | |
| PS, PSh, PSn,h | Price of the electricity sold to the grid (feed-in-tariff) [€/kWh] | |
| 𝜆 | Compensating factor in SDR approaches [€/kWh] | |
| βn,m | Bilateral trading imposed by participant n to participant m [€/kWh] | |
| En,m | Bilateral trading capacity from participant n to participant m [kW] | |
| Variables | ||
| en,h | Energy generated by participant n [kWh] | |
| dqh, dqn,h | Energy deficit (bought from the LEM or the grid) [kWh] | |
| dqgn,h | Energy bought from the grid by participant n [kWh] | |
| dqln,h | Energy bought in the LEM by participant n [kWh] | |
| eqh, eqn,h | Energy surplus (sold in the LEM or to the grid) [kWh] | |
| eqgn,h | Energy sold to the grid by participant n [kWh] | |
| eqln,h | Energy sold in the LEM by participant n [kWh] | |
| p, ph, pn,h | Electricity price of the LEM [€/kWh] | |
| pb, pbh | Electricity price of the energy bought [€/kWh] | |
| ps, psh | Electricity price of the energy sold [€/kWh] | |
| sdrh | Supply-Demand Ratio [pu] | |
| en, en,m,h | Energy sold by participant n and sold to participant m [kWh] | |
| dn, dn,h | Demand of participant n when it is elastic | |
| pn,m,h | Bilateral price of the electricity sold by participant n to m [€/kWh] | |
| pcn,m,h | Congestion price of the electricity sold by participant n to m [€/kWh] | |
| cn, cn,h | Energy from the battery [kWh] | |
| ebidn,h | Electricity bid [kWh] | |
| Functions | ||
| Un | Utility function of participant n | |
| Trading cost function of participant n | ||
| Welfare function of participant n | ||
References
- Xiang, X.; Ma, M.; Ma, X.; Chen, L.; Cai, W.; Feng, W.; Ma, Z. Historical Decarbonization of Global Commercial Building Operations in the 21st Century. Appl. Energy 2022, 322, 119401. [Google Scholar] [CrossRef]
- Ma, M.; Feng, W.; Huo, J.; Xiang, X. Operational Carbon Transition in the Megalopolises’ Commercial Buildings. Build. Environ. 2022, 226, 109705. [Google Scholar] [CrossRef]
- EC National Energy and Climate Plans (NECPs). Available online: https://ec.europa.eu/energy/en/topics/energy-strategy-and-energy-union/national-energy-climate-plans (accessed on 28 September 2021).
- European Union. Directive (EU) 2019/944 of the European Parliament and of the Council of 5 June 2019 on Common Rules for the Internal Market for Electricity and Amending Directive 2012/27/EU (Text with EEA Relevance); The European Parliament and the Council of the European Union: Brussels, Belgium, 2019; Volume 158. [Google Scholar]
- European Union. Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the Promotion of the Use of Energy from Renewable Sources (Text with EEA Relevance); European Union: Brussels, Belgium, 2018; Volume 328. [Google Scholar]
- Rocha, R.; Mello, J.; Villar, J.; Saraiva, J.T. Comparative Analysis of Self-Consumption and Energy Communities Regulation in the Iberian Peninsula, In Proceedings of the 8th International Conference on the European Energy Market, Madrid, Spain, 28 June–2 July 2021.
- Roberts, J.; Frieden, D.; D’Herbemont, S. Compile EU Project—Energy Community Definitions. 2019. Available online: https://main.compile-project.eu/downloads/ (accessed on 14 January 2023).
- Rocha, R.; Villar, J.; Bessa, R.J. Business Models for Peer-To-Peer Energy Markets. In Proceedings of the 16th International Conference on the European Energy Market (EEM), Ljubljana, Slovenia, 18–20 September 2019; pp. 3–8. [Google Scholar]
- IRENA. Peer-to-Peer Electricity Trading Innovation Landscape Brief; IRENA: Masdar City, Abu Dhabi, 2020. [Google Scholar]
- Faia, R.; Pinto, T.; Vale, Z. Fair Remuneration of Energy Consumption Flexibility Using Shapley Value; Springer: Berlin, Germany, 2019. [Google Scholar]
- de Almansa, M.; Campos, F.A.; Doménech, S.; Villar, J. Residential DER Cooperative Investments. In Proceedings of the 2019 16th International Conference on the European Energy Market (EEM), Ljubljana, Slovenia, 18–20 September 2019; pp. 1–6. [Google Scholar]
- Rouzbahani, H.M.; Karimipour, H.; Lei, L. Optimizing Scheduling Policy in Smart Grids Using Probabilistic Delayed Double Deep Q-Learning (P3DQL) Algorithm. Sustain. Energy Technol. Assess. 2022, 53, 102712. [Google Scholar] [CrossRef]
- Park, C.; Yong, T. Comparative Review and Discussion on P2P Electricity Trading. Energy Procedia 2017, 128, 3–9. [Google Scholar] [CrossRef]
- Open Utility Ltd. Piclo—Building Software for a Smarter Energy Future. Available online: https://piclo.energy/ (accessed on 8 March 2021).
- Vandebron. Available online: https://vandebron.nl/ (accessed on 14 January 2023).
- SonnenCommunity. Available online: https://sonnengroup.com/sonnencommunity/ (accessed on 20 January 2021).
- Mengelkamp, E.; Gärttner, J.; Rock, K.; Kessler, S.; Orsini, L.; Weinhardt, C. Designing Microgrid Energy Markets: A Case Study: The Brooklyn Microgrid. Appl. Energy 2018, 210, 870–880. [Google Scholar] [CrossRef]
- Homepage—POCITYF—POCITYF. Available online: https://pocityf.eu/ (accessed on 14 January 2023).
- EUniversal Project Description—The UMEI Concept. EUniversal. Available online: https://euniversal.eu/ (accessed on 14 January 2023).
- Interconnect Consortium Resources—Interconnect Project. Available online: https://interconnectproject.eu/resources/ (accessed on 23 March 2021).
- INESC TEC DIGITAL CER. Digital Energy Platform for Energy Communities—Proposta Projetos Em Copromoção. Available online: https://www.inesctec.pt/en/projects/digitalcer (accessed on 1 February 2023).
- Página Principal » Baterias2030. Available online: https://baterias2030.pt/en_GB (accessed on 9 February 2023).
- Capper, T.; Gorbatcheva, A.; Mustafa, M.A.; Bahloul, M.; Schwidtal, J.M.; Chitchyan, R.; Andoni, M.; Robu, V.; Montakhabi, M.; Scott, I.J.; et al. Peer-to-Peer, Community Self-Consumption, and Transactive Energy: A Systematic Literature Review of Local Energy Market Models. Renew. Sustain. Energy Rev. 2022, 162, 112403. [Google Scholar] [CrossRef]
- Mello, J.; Villar, J.; Bessa, R.J.; Lopes, M.; Martins, J.; Pinto, M. Power-to-Peer: A Blockchain P2P Post-Delivery Bilateral Local Energy Market. In Proceedings of the 2020 17th International Conference on the European Energy Market (EEM20), Ljubljana, Slovenia, 16–18 September 2020; pp. 1–5. [Google Scholar]
- Tsaousoglou, G.; Giraldo, J.S.; Paterakis, N.G. Market Mechanisms for Local Electricity Markets: A Review of Models, Solution Concepts and Algorithmic Techniques. Renew. Sustain. Energy Rev. 2022, 156, 111890. [Google Scholar] [CrossRef]
- Lin, J.; Pipattanasomporn, M.; Rahman, S. Comparative Analysis of Auction Mechanisms and Bidding Strategies for P2P Solar Transactive Energy Markets. Appl. Energy 2019, 255, 113687. [Google Scholar] [CrossRef]
- Teixeira, D.; Gomes, L.; Vale, Z. Single-Unit and Multi-Unit Auction Framework for Peer-to-Peer Transactions. Int. J. Electr. Power Energy 2021, 133, 107235. [Google Scholar] [CrossRef]
- Sorin, E.; Bobo, L.; Pinson, P. Consensus-Based Approach to Peer-to-Peer Electricity Markets with Product Differentiation. arXiv 2018, arXiv:1804.03521v2. [Google Scholar] [CrossRef]
- Rocha, R.; Silva, R.; Mello, J.; Faria, S.; Retorta, F.; Gouveia, C.; Villar, J. A Three-Stage Model to Manage Energy Communities, Share Benefits and Provide Local Grid Services. Energies 2023, 16, 1143. [Google Scholar] [CrossRef]
- Tounquet, F. Energy Communities in the European Union 2014—ASSET Projet; European Comission: Brussels, Belgium, 2019; Available online: https://www.powerpeers.nl/media/1330/asset-energy-comminities-revised-final-report.pdf (accessed on 14 January 2023).
- Mello, J.; Villar, J.; Saraiva, J.T. Concept and Design of a Real Time Walrasian Local Electricity Market. In Proceedings of the 2022 18th International Conference on the European Energy Market (EEM), Ljubljana, Slovenia, 13–15 September 2022; pp. 1–5. [Google Scholar]
- Pérez-Arriaga, I.J. (Ed.) Regulation of the Power Sector; Springer Science & Business Media: Berlin, Germany, 2014. [Google Scholar]
- Imran, K.; Kockar, I. A Technical Comparison of Wholesale Electricity Markets in North America and Europe. Electr. Power Syst. Res. 2014, 108, 59–67. [Google Scholar] [CrossRef]
- Directorate-General for Energy (European Commission); SWECO; TRACTEBEL Advisory and Advanced Analytics; Schumacher, L.; Küpper, G.; Henneaux, P.; Bruce, J.; Klasman, B.; Ehrenmann, A. The Future Electricity Intraday Market Design; Publications Office of the European Union: Luxembourg, 2019; ISBN 978-92-79-88757-4. [Google Scholar]
- Mello, J.; Villar, J. Integrating Flexibility and Energy Local Markets with Wholesale Balancing Responsibilities in the Context of Renewable Energy Communities (Invited Paper for Special Session). In Proceedings of the 2022 5th edition Energy & Environment (ICEE22), Porto, Portugal, 2–3 June 2022; pp. 1–6. [Google Scholar]
- Hadiya, N.; Teotia, F.; Bhakar, R.; Mathuria, P.; Datta, A. A Comparative Analysis of Pricing Mechanisms to Enable P2P Energy Sharing of Rooftop Solar Energy. In Proceedings of the 2020 IEEE International Conference on Power Systems Technology (POWERCON), Kuala Lumpur, Malaysia, 14–16 September 2020; pp. 1–6. [Google Scholar]
- Long, C.; Wu, J.; Zhang, C.; Thomas, L.; Cheng, M.; Jenkins, N. Peer-to-Peer Energy Trading in a Community Microgrid. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 3–7. [Google Scholar]
- Chen, Y.; Lei, X.; Yang, J.; Zhong, H.; Huang, T. Decentralized P2P Power Trading Mechanism for Dynamic Multi-Energy Microgrid Groups Based on Priority Matching. Energy Rep. 2022, 8, 388–397. [Google Scholar] [CrossRef]
- Wang, N.; Liu, Z.; Heijnen, P.; Warnier, M. A Peer-to-Peer Market Mechanism Incorporating Multi-Energy Coupling and Cooperative Behaviors. Appl. Energy 2022, 311, 118572. [Google Scholar] [CrossRef]
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-Sharing Model with Price-Based Demand Response for Microgrids of Peer-to-Peer Prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Umar, A.; Kumar, D.; Ghose, T. Blockchain-Based Decentralized Energy Intra-Trading with Battery Storage Flexibility in a Community Microgrid System. Appl. Energy 2022, 322, 119544. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhou, Y.; Jenkins, N. Peer-to-Peer Energy Sharing through a Two-Stage Aggregated Battery Control in a Community Microgrid. Appl. Energy 2018, 226, 261–276. [Google Scholar] [CrossRef]
- Zheng, B.; Wei, W.; Chen, Y.; Wu, Q.; Mei, S. A Peer-to-Peer Energy Trading Market Embedded with Residential Shared Energy Storage Units. Appl. Energy 2022, 308, 118400. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Long, C.; Cheng, M.; Zhang, C. Performance Evaluation of Peer-to-Peer Energy Sharing Models. Energy Procedia 2017, 143, 817–822. [Google Scholar] [CrossRef]
- Universal Consortium. D5.4 EUniversal: Evaluation of Market Mechanisms: Challenges and Opportunities; Universal Consortium: London, UK, 2021. [Google Scholar]
- Pilz, M.; Al-Fagih, L. Recent Advances in Local Energy Trading in the Smart Grid Based on Game-Theoretic Approaches. IEEE Trans. Smart Grid 2019, 10, 1363–1371. [Google Scholar] [CrossRef]
- de Lorenzo García, C. Modeling the Equilibrium in a Local P2P Energy Market; Universidad Pontificia Comillas, ICAI: Madrid, Spain, 2021. [Google Scholar]
- Tushar, W.; Saha, T.K.; Yuen, C.; Morstyn, T.; McCulloch, M.D.; Poor, H.V.; Wood, K.L. A Motivational Game-Theoretic Approach for Peer-to-Peer Energy Trading in the Smart Grid. Appl. Energy 2019, 243, 10–20. [Google Scholar] [CrossRef]
- Long, C.; Zhou, Y.; Wu, J. A Game Theoretic Approach for Peer to Peer Energy Trading. Energy Procedia 2019, 159, 454–459. [Google Scholar] [CrossRef]
- Han, L.; Morstyn, T.; McCulloch, M. Incentivizing Prosumer Coalitions with Energy Management Using Cooperative Game Theory. IEEE Trans. Power Syst. 2019, 34, 303–313. [Google Scholar] [CrossRef]
- Lee, W.; Xiang, L.; Schober, R.; Wong, V.W.S. Direct Electricity Trading in Smart Grid: A Coalitional Game Analysis. IEEE J. Sel. Areas Commun. 2014, 32, 1398–1411. [Google Scholar] [CrossRef]
- Le Cadre, H.; Jacquot, P.; Wan, C.; Alasseur, C. Peer-to-Peer Electricity Market Analysis: From Variational to Generalized Nash Equilibrium. Eur. J. Oper. Res. 2020, 282, 753–771. [Google Scholar] [CrossRef]
- Amin, W.; Huang, Q.; Umer, K.; Zhang, Z.; Afzal, M.; Khan, A.A.; Ahmed, S.A. A Motivational Game-Theoretic Approach for Peer-to-Peer Energy Trading in Islanded and Grid-Connected Microgrid. Int. J. Electr. Power Energy Syst. 2020, 123, 106307. [Google Scholar] [CrossRef]
- Ringler, P.; Keles, D.; Fichtner, W. Agent-Based Modelling and Simulation of Smart Electricity Grids and Markets—A Literature Review. Renew. Sustain. Energy Rev. 2016, 57, 205–215. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Long, C. Evaluation of Peer-to-Peer Energy Sharing Mechanisms Based on a Multiagent Simulation Framework. Appl. Energy 2018, 222, 993–1022. [Google Scholar] [CrossRef]
- Khorasany, M.; Mishra, Y.; Ledwich, G. A Decentralized Bilateral Energy Trading System for Peer-to-Peer Electricity Markets. IEEE Trans. Ind. Electron. 2020, 67, 4646–4657. [Google Scholar] [CrossRef]
- Babaoglu, O.; Meling, H.; Montresor, A. Anthill: A Framework for the Development of Agent-Based Peer-to-Peer Systems. In Proceedings of the 22nd International Conference on Distributed Computing Systems, Vienna, Austria, 2–5 July 2002; pp. 15–22. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).