Abstract
Low-temperature nitrogen adsorption is a widely used method for the research and evaluation of gas shale’s pore structure. The existing interpretation method, utilizing gas adsorption isotherms to obtain pore size distribution (PSD), is always based on the one-dimensional geometry model, while the void space of gas shale has strong multi-dimensional characteristics. It is necessary to investigate the nitrogen condensation and evaporation behavior in multidimensional structures. In this study, a series of two-dimensional and three-dimensional models based on ink-bottle pores were constructed. A hybrid molecular simulation approach combining grand canonical Monte Carlo (GCMC) and molecular dynamics (MD) is proposed to simulate the low-temperature nitrogen adsorption isotherms. Three aspects have been analyzed in detail. Compared with the conventional understanding that the threshold of cavitation in the ink-bottle pore only relates to throat diameter, this study discloses a wider and more comprehensive range of conditions of cavitation that considers both the throat length and diameter. As pore spaces of shale samples consist of many complex interconnected pores, the multi-stage ink-bottle pore model is more suitable than the single ink-bottle pore model to similarly reproduce the wider cavitation pressure range. A more universal parameter is proposed that quantitatively unifies the influence of cavity diameter and length on condensation pressure and has good applicability in cavities with different shapes. This work quantitatively studies the nitrogen adsorption isotherms of three-dimensional complex nanopore structures using molecular simulation and provides a reasonable explanation for the low-temperature nitrogen adsorption isotherms of gas shale.
1. Introduction
Nanopores are developed in shale gas reservoirs, which are the storage space and migration path for shale gas. To study the pores inside shale, researchers have developed various methods for characterizing micro and nanostructures. The currently mature characterization methods include scanning and transmission electron microscopies (SEM and TEM, respectively), gas physisorption, X-ray diffraction (XRD), mercury porosimetry, nuclear magnetic resonance (NMR), small-angle X-ray (SAXS) and small-angle neutron scattering (SANS). Among these characterization methods, gas physisorption is widely used and is well established. It is relatively inexpensive and is capable of characterizing nanopores with diameters from 0.35 nm to at least 100 nm [1]. Low-temperature nitrogen adsorption is a conventional method by which to obtain the pore size distribution of shale. The nitrogen molecules are used as probes to measure the surface area and volume of the void space of the materials. Briefly, nitrogen condensation occurs in larger pores in which relative pressure increases, and evaporation occurs in smaller pores in which relative pressure decreases. This feature provides a connection between the relative pressure and the size of the void space, and theoretically, the pore size distribution of the void space can be determined with the adsorption and/or desorption isotherms [2,3,4,5].
We have carried out low-temperature nitrogen adsorption experiments on more than 1000 shale samples from Wufeng–Longmaxi formations and different wells from southwest China (See Appendix A for details). Typical adsorption isotherms of shale samples obtained from low-temperature nitrogen adsorption experiments at 77.3 K are depicted in Figure 1a. Considering the adsorption and desorption isotherms, from a morphology perspective, a hysteresis loop can be observed between these two isotherms in a large number of samples, which leads to the problem of branch selection for analysis [6]. Furthermore, another common feature of different isotherms is that there is a sudden change in the desorption branch of the isotherm at a relative pressure of 0.5, while the hysteresis loop is closed at a relative pressure of 0.42.
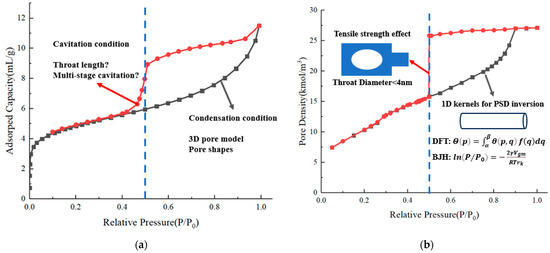
Figure 1.
Typical adsorption isotherms. (a) Low-temperature nitrogen adsorption isotherm of shale. (b) Simulated ink-bottle pore adsorption isotherm from previous works.
There are two main mechanisms that cause hysteresis. One exists in the one-dimensional cylinder pore or slit geometry with both ends open. The meniscus is cylindrical during adsorption, while it becomes hemispherical on desorption, as depicted by Sarkisov and Monson [7]. The curvature of the spherical meniscus is half that of the cylindrical meniscus, so the condensation pressure is higher than the evaporation pressure [8,9,10]. Previous experiments on low-temperature nitrogen adsorption on molecular sieves represented by MCM-41 have found that the hysteresis loops of columnar nanopores are mostly of the H1 type [11]. Another mechanism exists in ink-bottle pores where the wider cavity is controlled by a narrower pore throat, evaporation in the cavity will be delayed until the evaporation in the pore throat or the cavitation happens [12,13,14,15,16,17,18,19]. According to the classification of the hysteresis loops from IUPAC, hysteresis loops of ink-bottle pores are mostly H2 or H3 types [20]. It can be seen that most of the experimental adsorption isotherms have H2-type characteristics, which means that ink-bottle pores are the main pore type of nanopores in shale reservoirs. Meanwhile, through characterization of shale nanopores using techniques such as focused ion beam-scanning electron microscope (FIB-SEM) and micro-computed tomography (CT), it has been found that various types of pores develop in shale, with complex pore shapes, significant differences in pore sizes, and different connectivity modes between pores, and which have strong heterogeneity and anisotropy (Figure 2) [21,22,23,24].

Figure 2.
SEM of organic pores of shale samples from southwest China [24].
In recent years, researchers have continuously investigated the gas condensation and evaporation behavior in multi-dimensional pore structures with molecular simulations. As the basic and most simple unit, the ink-bottle pore is mostly considered. The typical adsorption isotherm obtained by previous simulations of ink-bottle pore is shown in Figure 1b. Via utilization of the molecular simulation of two-dimensional ink-bottle pores, studies have disclosed that the desorption branch in complex structures mainly reflects the size of the controlling pore throat and the volume of the controlled pore cavity, not the size of the pore cavity. The effects of cavity size, throat width, and throat length on the evaporation pressure have been separately discussed [19]. However, the boundary between pore blocking and cavitation type evaporation, considering jointly both throat width and throat length, has not been studied. Furthermore, when cavitation occurs, the predicted declines in desorption branches of single ink-bottle pores are very steep around the same relative pressure, while the window of relative pressure for cavitation for shale samples is wider, as shown in Figure 1. There is a lack of explanation for this phenomenon. Whether it is due to a more complex pore structure is not clear.
As the condensation process is less influenced by the pore structure compared with the evaporation process, it is suggested to analyze the adsorption branch to obtain pore size distribution for gas shale according to standards such as ISO 15901-2:2006 [25], IDT. Clearly, the void space of gas shale has strong multi-dimensional characteristics. However, the interpretation method utilizing gas adsorption isotherm to obtain pore size distribution (PSD) is always based on one-dimensional geometry models, including BJH, NLDFT, QSDFT, etc. [2,26,27,28]. The underlying assumption when applying these models on gas shale is that the condensation or evaporation mechanism in multidimensional pore space should be the same as that in one-dimensional geometry. Quantitatively, one-dimensional pore models with both ends open are applied directly, without a clear understanding of the potential issues with this assumption. The influence of pore length on condensation pressure has been rarely discussed.
In this study, we aim to employ molecular simulation of two-dimensional and three-dimensional models to further investigate the abovementioned problem. The two-dimensional single ink-bottle pores with different throat diameters and lengths are examined to obtain the boundary between pore blocking and cavitation. The three-dimensional parallel and serial-connected ink-bottle pores are constructed to provide an example of gentle decline in the desorption branch. The two-dimensional single ink-bottle pores with different cavity diameters and lengths are simulated to determine a parameter that correlates with the condensation pressure. The paper is organized as follows: the methodology is described in Section 2, while results and discussions are presented in Section 3, and Section 4 concludes the paper.
2. Methodology
2.1. Simulation Cell Construction and Parameters
Graphite is used to represent the wall of organic nanopores in the molecular model [29,30], and nitrogen molecules are randomly distributed in the pore cavity in the initial state. In previous studies, both the united atomic model and the full atomic model were able to accurately obtain the adsorption–desorption process of nitrogen molecules in nanopores. However, compared with the experimental results of MCM-41, the simulation results of the united atomic model were closer to the experimental results [31,32], and the computational efficiency of using the united atomic model was higher, so the united atomic model is used for calculations. The 12-6 Lennard-Jones potential function is used to describe the van der Waals force between molecules, as follows:
where is the intermolecular potential between the two atoms, is the well depth and reflects how strongly the two particles attract each other, is the distance at which the intermolecular potential is zero, and is the distance between the two atoms. Due to the fact that both the united atomic model and the graphite wall are electrically neutral, this model does not consider the effect of charge force. Table 1 lists the force field parameters of the simulations. The Lorentz–Berthelot mixing rules are used to determine force field parameters between different types of molecules.

Table 1.
Force field parameters of the simulation.
The ink-bottle pore model is constructed and taken as a basic unit to construct pores with different connectivity. The basic ink-bottle pore unit contains a cylindrical pore throat and a cylindrical pore cavity. The model of the basic ink-bottle pore unit is shown in Figure 3. The structure is cut from the middle to show its internal wall.

Figure 3.
Schematic diagram of single ink-bottle pore unit.
2.2. Simulation Method and Procedure
In previous studies, the GCMC method was often used to simulate adsorption and desorption in nanopores because of the flexible control of the total number of moving molecules in the simulation cell. However, the computational efficiency of GCMC simulation is fairly low and not easy to run parallelly, and it is difficult to simulate the complex and connected nanopore structures. In this work, a hybrid simulation method combining GCMC and MD is used to simulate the adsorption–desorption process of nitrogen molecules. MD simulation can simulate the movement of nitrogen molecules in the pore space based on potential parameters and Newton’s equation of motion, while GCMC simulation can adjust the total number of nitrogen molecules in the simulation cell to ensure that the chemical potential is consistent with the target bulk value. The computational accuracy of the GCMC–MD method is shown to be acceptable and the efficiency is significantly improved compared with the conventional GCMC method (See Appendix B for details). The use of the hybrid method provides a basis for the calculation of complex connected nanopore structures.
GCMC–MD simulation is implemented by using GCMC and NVT commands in LAMMPS. A complete simulation procedure contains the following steps: the temperature of the simulation system is set to 77.3 K, and the relative pressure point range of the simulation is arranged between 0.05 and 1. The time step is set to 2 fs, and the motion of nitrogen molecules is determined by the MD simulation with the NVT ensemble at each time step. The GCMC cycle is performed every 10 steps, and 1000 random exchanges (insertions or deletions) of nitrogen molecules are attempted in every GCMC cycle to adjust the total number of nitrogen molecules. A total of 1,000,000 steps of MD simulations are performed, and the last 200,000 steps of simulation data are taken for analysis for every relative pressure point.
To investigate the microscopic behavior of nitrogen molecules in nanopores, we analyze the density of fluid molecules in the pores, which is defined as the amount of adsorbate per unit accessible volume of the pores:
where Vacc is the accessible pore volume and Nexcess is the number of excess nitrogen molecules in the pores, defined as the difference between the total number of fluid molecules in the simulation cell and the total number of free-state molecules filling the accessible pore volume under the same conditions:
where ρG is the free-state density of the nitrogen gas under pressure.
3. Results and Discussion
3.1. Nitrogen Evaporation Behaviors in a Single Ink-Bottle Pore
Previous studies have disclosed that, for the ink-bottle pore, there are two kinds of mechanisms that will delay gas evaporation in the pore cavity and lead to an obvious adsorption–desorption hysteresis, including pore blocking and cavitation [12,13,14,15,16]. An obvious difference between these two types is the closure point of the hysteresis loop. For the pore-blocking type, the closure point varies with the diameter of the throat, while for the cavitation type, the closure point is fixed when the diameter of the throat is below a threshold value [33]. In this study, we further quantitatively investigate the boundary between these two mechanisms considering the variation of both the diameter and length of the pore throat. Previous studies with a tubular model have disclosed that the diameter of the throat where cavitation occurs was 3–4 nm. Therefore, we established a collection of ink-bottle pores with throats whose diameters are near this range and whose lengths are variant in a certain range. Firstly, the adsorption–desorption curves of ink-bottle pores with different diameters are simulated with a fixed pore diameter of 6 nm, a fixed pore length of 10 nm, and a fixed throat length of 8 nm. The throat diameter varies from 2 nm to 5.5 nm. The hysteresis loops obtained from the simulations are shown in Figure 4.
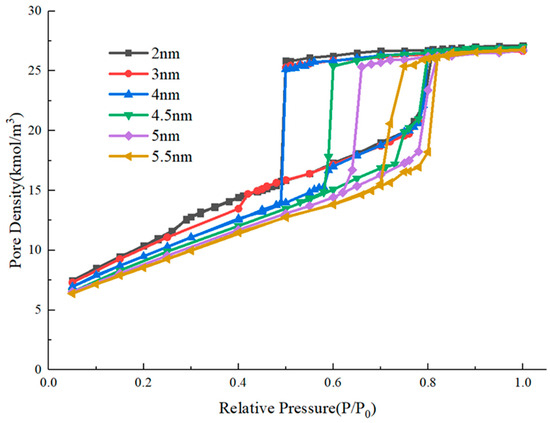
Figure 4.
Adsorption isotherms for nitrogen at 77.3 K of ink-bottle pores with different throat diameters.
As the size of the pore cavity is unchanged, the relative pressure of the adsorption branch for condensation is close. Observing the desorption branch, there are two types of variations of evaporation pressure of the pores with different throat diameters. When the throat diameter is larger than 4 nm, the evaporation pressure decreases with the decrease of throat diameter. When the throat diameter is less than 4 nm, the evaporation pressure is always around 0.5. The molecular snapshots of the system with throat diameters of 4 nm before and 4.5 nm after the evaporation are provided in Figure 5 to further examine the inner differences. When the throat diameter is 4 nm, evaporation occurs firstly in the pore cavity while the throat is still condensed, the pore cavity of the system undergoes evaporation through cavitation. When the throat diameter is 4.5 nm, evaporation takes place first in the throat, followed by the cavity, with the pore cavity evaporating through the gas–liquid two-phase meniscus, also known as pore blocking. There are two aspects in which this study is consistent with previous research, indicating the effectiveness of the simulation method in this study. One is the transition from pore blocking to cavitation as the throat diameters decrease. Another is that the critical throat diameter for cavitation is about 4 nm. Furthermore, the cavitation pressure found here, which is around 0.5, is closer to that observed in the isotherms of gas shale, compared with previous studies whose cavitation pressures are always around 0.2 and 0.3 [13,14,15].
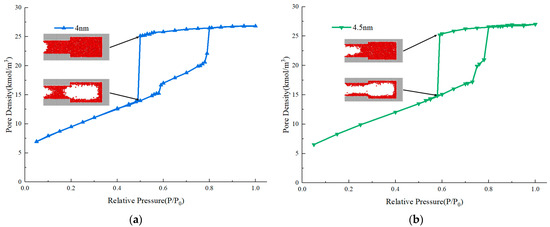
Figure 5.
Adsorption isotherms and molecular snapshots of ink-bottle pores. (a) Throat diameter of 4 nm. (b) Throat diameter of 4.5 nm.
According to Figure 5, the molecular snapshots between and after evaporation can be used to distinguish the underlying mechanism. We further examined the influence of throat length. The simulated adsorption isotherms of ink-bottle pores with different throat lengths and throat diameters of 4 nm and 4.5 nm are depicted in Figure 6. As the length of the throat increases, the evaporation pressure gradually decreases until it approaches a relative pressure of 0.5. For the ink-bottle pores with a throat diameter of 4.5 nm, when the throat length extends from 8 nm to 50 nm, the evaporation pressure changes from 0.57 to 0.5. For the ink-bottle pores with a throat diameter of 4 nm, when the throat length shortens from 8 nm to 2 nm, the evaporation pressure changes from 0.5 to 0.6. Examining the molecular snapshots, it is found that for ink-bottle pores with a throat diameter of 4 nm, evaporation due to cavitation occurs when the throat length is 8 nm and 6 nm, while pore blocking evaporation occurs when the throat length is 4 nm. For the ink-bottle pores with a throat diameter of 4.5 nm, evaporation due to cavitation occurs when the throat length is 50 nm, while pore-blocking evaporation occurs when the throat length is below 30 nm. Based on the above two examples, it can be seen that the transition condition from pore blocking to cavitation is affected by both throat diameter and throat length.
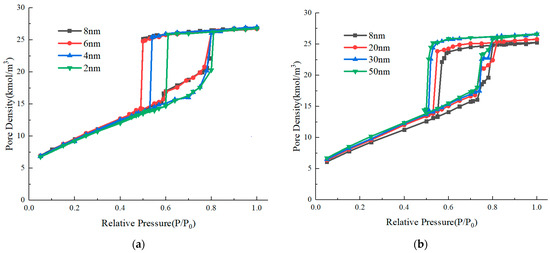
Figure 6.
Adsorption isotherms of ink-bottle pores with different throat lengths (a) Throat diameter of 4 nm. (b) Throat diameter of 4.5 nm.
To further obtain the boundary between these two mechanisms quantitatively, the evaporation processes of ink-bottle pores with pore diameters of 2.5–4.5 nm and different pore lengths are simulated. In Figure 7, each point denotes a simulation model with its x-axis value representing throat diameter and the y-axis value throat length. For the black points, the corresponding simulation model experiences cavitation evaporation, while for the blue points, the corresponding simulation model experiences pore blocking evaporation. The blue line indicates the edge of these two mechanisms, which are identified with the molecular snapshots. There is a boundary, depicted with the blue line in Figure 7, that divides the figure into two zones. In the upper zone, cavitation occurs, while in the lower zone, pore blocking dominates.
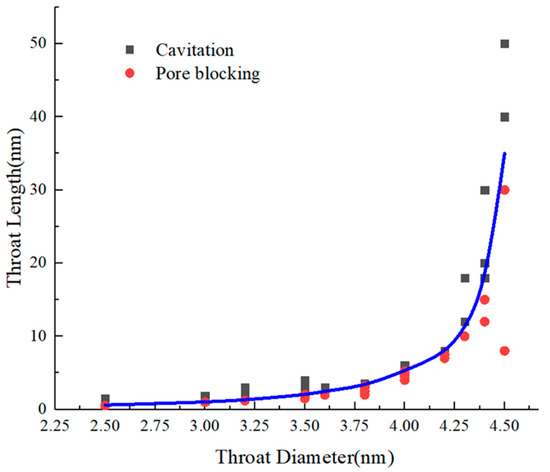
Figure 7.
The evaporation mechanism and boundary of the evaporation mechanism transition for ink-bottle pores with different throat lengths and diameters. The blue line is the exponential function fitting relationship between the critical throat length and throat diameter.
The exponential function is applied to fit the boundary of these two zones, and the fitted formula is:
In a one-dimensional computational model that only considers the diameter of the throat, the throat diameter for which the evaporation mechanism transition occurs is around 4 nm [34]. In the simulation results that comprehensively consider the length and diameter of the throat, based on the characteristics of the exponential function and in the throat with a pore diameter below 3.8 nm, the throat length and diameter comprehensively control the evaporation mechanism. In the throat with a pore diameter above 3.8 nm, the critical throat length for cavitation increases rapidly with the diameter, and the critical condition is mainly controlled by the throat diameter. It must be pointed out that this conclusion is only applicable to systems with throat diameters of 2.5 nm–4.5 nm. In throat diameters less than 2 nm, condensation occurs in the throat at very low pressure. For larger diameter ink-bottle pores, the length of the throat where cavitation occurs exceeds the computational ability of the molecular simulation. Compared with the conventional tubular model the threshold of cavitation only relates to throat diameter, this study discloses a wider range of conditions of cavitation and provides a more comprehensive understanding.
3.2. Nitrogen Evaporation Behaviors in Multi-Stage Ink-Bottle Pores
For a single ink-bottle pore, the decline in the desorption branch is always abrupt in this study and in previous studies within a narrow relative pressure range. However, for gas shale samples, the decline trend is gentle, and the starting point of decline is around 0.5, while the closure point is around 0.42. This indicates that the cavitation process in the nanopores of shale may have a small range of relative pressure, slightly lower than 0.5, rather than being fully completed at the relative pressure of 0.5. From this perspective, simplifying the complex pore space of gas shale so that it is represented by bundles of ink-bottle pores will lose this feature. Therefore, we further consider a series of connected ink-bottle pores.
Firstly, we select three basic ink-bottle pore units with different throat diameters of 3 nm, 4.5 nm, and 5 nm and with throat lengths of the units are all 3 nm. We can obtain the evaporation mechanism of each unit from Section 3.1, wherein the units with throat diameters of 4.5 nm and 5 nm evaporate through the gas–liquid two-phase meniscus, while the units with throat diameters of 3 nm evaporate through cavitation. These three units are connected in different connection sequences. Two systems with these three units connected in series are constructed and named model S1 and S2, while one system with units connected in parallel is constructed and named model P. The common feature of the structure is that the internal structure is connected to the external bulk space through a throat that belongs to the cavitation zone according to Figure 7. The connected structures are shown in Figure 8. The adsorption isotherms of the connected ink-bottle pores are shown in Figure 9.
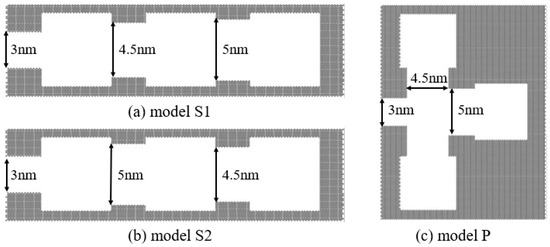
Figure 8.
The connected ink-bottle pores with different throat lengths and diameters: (a) model S1, comprising three units connected in series with throat diameters of 3 nm, 4.5 nm and 5 nm from left to right, respectively. (b) model S2, comprising three units connected in series with throat diameters of 3 nm, 5 nm and 4.5 nm from left to right, respectively. (c) model P, comprising three units connected in parallel.
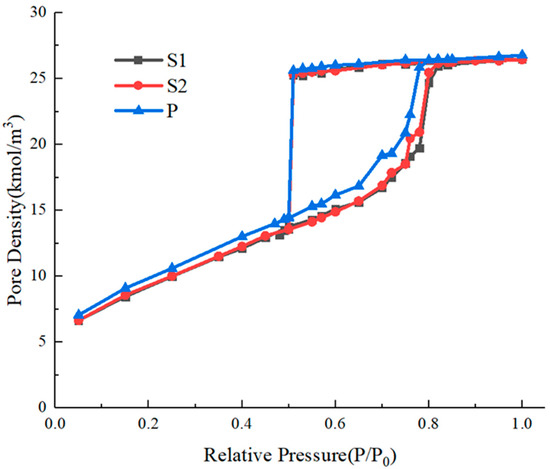
Figure 9.
Nitrogen adsorption isotherms of connected ink-bottle pores.
From the simulated isotherms, we can see that there is only one evaporation process in the simulated system with a main throat diameter of 3 nm, and the relative pressure of evaporation is around 0.5. We obtained snapshots of the molecules in the system under this relative pressure, as shown in Figure 10, indicating that cavitation occurs in all three pore cavities simultaneously.
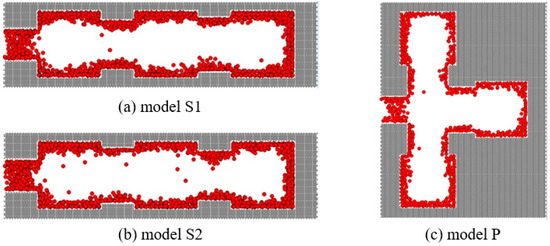
Figure 10.
Nitrogen snapshots of connected ink-bottle pores after cavitation. (a) model S1, comprising three units connected in series with throat diameters of 3 nm, 4.5 nm and 5 nm from left to right, respectively. (b) model S2, comprising three units connected in series with throat diameters of 3 nm, 5 nm and 4.5 nm from left to right, respectively. (c) model P, comprising three units connected in parallel.
The pore structures of the models have similar characteristics that are connected to the external bulk phase through a throat with a diameter and length of 3 nm, so the evaporation process is limited by the throat. Although the connection mode and sequence of ink-bottle pore units are different, evaporation occurs through cavitation in all three systems. When the narrow throat that leads to cavitation exists in the connected pore system, it will control the evaporation process of its internal pore structure that would evaporate through the gas–liquid meniscus at a relative pressure higher than 0.5 without the outer throat. Evaporation through cavitation corresponds with the rapid decline of the desorption branch around the relative pressure of 0.5, and the cavitation pressure does not change with the serially- or parallel-connected pore structure and pore size.
Secondly, we constructed another system in which a portion of the internal throats belong to the cavitation zone. The adsorption isotherm and molecular snapshots of the two-stage cavitation are shown in Figure 11.
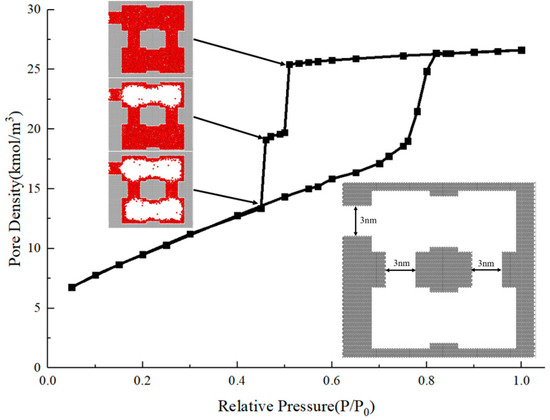
Figure 11.
Nitrogen adsorption isotherms and molecular snapshots at cavitation of a two-layer ink-bottle pore.
The hysteresis loop obtained from the simulation shows that there are two rapid declines in the desorption branch of the system, corresponding with the relative pressures of 0.5 and 0.45. The two-stage evaporation process of the desorption branch occurs both through cavitation, which is controlled by the outermost throat, and the vertical throats connected to the internal structure. The upper cavity evaporates through cavitation when the relative pressure is 0.5, while the lower cavity is controlled by multiple throats that belong to the cavitation zone, and cavitation occurs at the relative pressure of 0.45. In such a structure, a multi-stage cavitation process and the evaporation of some internal structures at a cavitation pressure below 0.5 are observed, which is different from the cavitation pressure in a single-throat ink-bottle pore, which is always 0.5. To further investigate the multi-stage cavitation process, multiple ink-bottle pore units with throat diameters and lengths of 3 nm and cavity diameters and lengths of 6 nm are connected head to tail, representing a multi-stage cavitation structure controlled by multiple narrow throats that can lead to cavitation. For these multilayer structures, we calculated the desorption branches of systems with different unit numbers and compared the results with the hysteresis loop of a single ink-bottle pore unit with a throat of 3 nm. The results are shown in Figure 12.
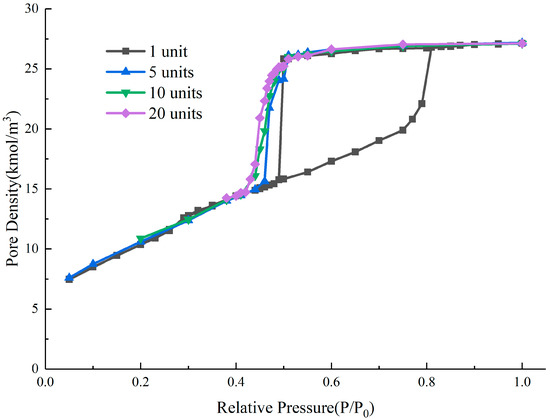
Figure 12.
Nitrogen adsorption isotherms of multilayer ink-bottle pore structure with different unit numbers.
The simulation results of the system show that the narrow throats have a controlling effect which will cause the internal structure to evaporate through cavitation at a lower relative pressure. As the number of units increases, the separated dropping steps appearing in the two-level cavitation structure become smoother, and the hysteresis phenomenon of the cavitation process becomes more obvious, but always within a small relative pressure range. Among them, the multi-stage cavitation structures of 10 units and 20 units both overlap with the adsorption branch around the relative pressure of 0.42. This indicates that the hysteresis phenomenon of multi-level cavitation does not infinitely reduce the relative pressure of cavitation, but rather completely ends around 0.42.
From two-dimensional single ink-bottle pores to three-dimensional connected ink-bottle pores, this study found a type of configuration of ink-bottle pore whose desorption branch gently declines between the relative pressure of 0.42 and 0.5. This decline characteristic is like that of gas shale. For the cavitation in the nanopore which is controlled by the single-hierarchy pore throat, the evaporation process occurs through cavitation at the relative pressure around 0.5, which is close to the abrupt drop of the desorption branch of the shale. In the system with multiple throats to cavitate, the multi-stage cavitation process ends around the relative pressure of 0.42, which is close to the closure position of the hysteresis loop of shale. Considering that pore spaces of shale samples consist of many complex interconnected pores, the multi-stage ink-bottle pores are more suitable than the tubular model to equivalently represent the wider cavitation pressure range.
3.3. Nitrogen Condensation Behavior in the Ink-Bottle Pore
In the adsorption isotherms of ink-bottle pores with different throat diameters, although the evaporation mechanism and pressure are different, the condensation pressure does not change due to the unchanged pore size. The condensation pressure of the ink-bottle pore depends on the size of the cavity and is not affected by the throat and connection sequence. In one-dimensional tubular pore models, the condensation pressure corresponds to the size of pores, and the pore size distribution can be determined. For two-dimensional models, it has been found that condensation pressure is not only related to cavity diameters but also to the length [19]. However, there is a lack of quantitative predictive rules. We designed a series of ink-bottle pore systems with different pore cavity sizes but the same throat diameter and length. The diameter and length of the throat are 3 nm and 8 nm, respectively. Firstly, the diameter of the pore cavity is fixed at 6 nm, and the length changes from 5 nm to 30 nm. The simulated adsorption isotherms are plotted in Figure 13. Secondly, the length of the pore cavity is fixed at 10 nm, and the diameter changes from 6 nm to 8 nm. The simulated isotherms are plotted in Figure 14.
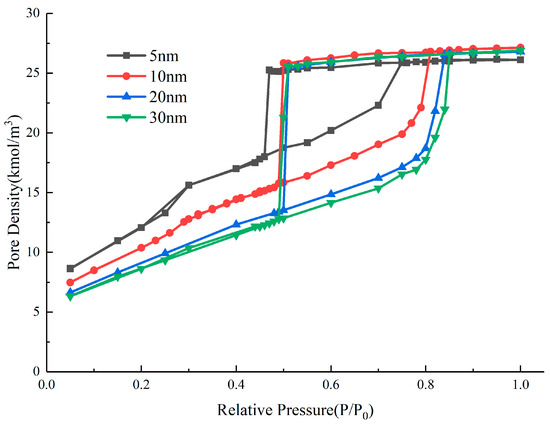
Figure 13.
Nitrogen adsorption isotherms with different cavity lengths.
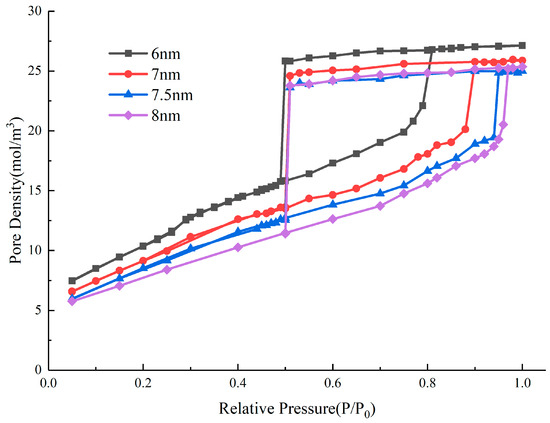
Figure 14.
Nitrogen adsorption isotherms with different cavity diameters.
From the hysteresis loop obtained from the simulation, the variation of condensation pressure with the length and diameter of the cavity in the ink-bottle pore has commonalities, i.e., that, as the length and diameter increase, the condensation pressure increases. The larger the space filled in the cavity during the condensation process, the more difficult the condensation process is, and the higher the condensation pressure. The condensation process is an extension of the multi-layer adsorption layer adsorbed on the wall, so the larger the wall area, the more space where the condensation process occurs, and the faster the condensation progresses. On this basis, we defined RC as related to pore size and investigated the relationship between this parameter and the condensation pressure of the system:
where, V is the total pore volume of the pore cavity, VA is the pore volume occupied by nitrogen molecules in multi-layer adsorption states, S is the surface area of the pore cavity, and is the thickness of the multi-layer adsorption layer.
The key is to determine hA. Considering that the occurrence of a hysteresis loop indicates that the state of nitrogen molecules is in an incomplete equilibrium state, and that the transition point from the multi-layer adsorption layer corresponds with the lower endpoint of the hysteresis loop. Through the simulation in Section 3.1, the cavitation pressure of the ink-bottle pore in which cavitation occurs is about 0.5, which is the transition point. Under saturated vapor pressure, the number of adsorption layers n of adsorbates in micro/nanostructures is limited. Halsey (1969) proposed the equation for describing the adsorption layer of nitrogen at a liquid nitrogen temperature, also known as the Halsey equation [35]:
When the relative pressure is about 0.5, and when substituting the above equation, the thickness of the adsorption layer of nitrogen molecules is about 0.715 nm. Once the size of the cavity is determined, RC can be directly obtained through geometric calculations. RC for the parameters and condensation pressures of different cavity sizes—calculated in Figure 12 and Figure 13, respectively—are summarized in Table 2.

Table 2.
Condensation pressure and RC of ink-bottle pore.
The linear correlation analysis between RC and condensation pressure is shown in Figure 15.
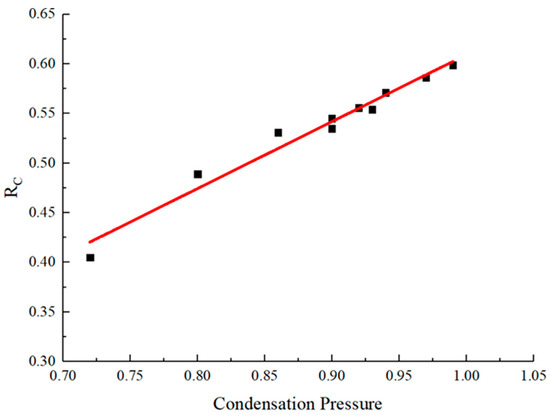
Figure 15.
Linear fitting results of RC and condensation pressure.
From the results of linear fitting, the fitted equation is:
The adjusted R2 of this fitting is 0.97, indicating a strong linear correlation. This indicates that the defined pore parameters, RC, well integrate the effects of cylindrical pore length and diameter on condensation pressure. Compared with a finite cylindrical cavity with the same diameter, the ratio of S and V is smaller for the one-dimensional tubular pore model with two ends open, hence the parameters RC and condensation pressure are higher. For a certain low-temperature nitrogen adsorption isotherm, the pore size distribution obtained using the one-dimensional tubular model will classify the pore volume into smaller pore size ranges.
In addition, among various pore size distribution calculation methods based on the DFT theory, there are different calculation kernels based on slit, cylindrical, and spherical pore shapes, with corresponding pore sizes as follows:. The selection of kernels with different pore shapes will result in different pore size distributions. We simulated the condensation process of ink-bottle pores in which the cavity shapes are slit and spherical, predicted the condensation pressure using the linear fitting equation of RC and the condensation pressure obtained through the cylindrical pore and compared these to obtain Table 3.

Table 3.
Simulated and predicted condensation pressure and RC of nanopores with different shapes.
From the predicted results, the relationship between RC and the condensation pressure obtained through the cylindrical pore cavity is also effective in predicting the condensation pressure of spherical and slit pores, with a maximum prediction error of only 0.011. This further indicates that the condensation process and pressure are directly related to pore space. Compared with pore size, RC is the more universal parameter that relates to condensation pressure.
Beyond that, this relationship provides an approach by which to determine the surface area of a certain pore without assuming its cross-sectional shape. Conventionally, the shape of the pore needs to be selected first, then the size and volume of the pore are determined along with the relationship between them and the relative pressure and condensation gas amount. Finally, the surface area is calculated based on these two quantities according to the predefined pore shape. Here, the parameter RC relates the condensation pressure, volume, and surface area according to Equations (5) and (6). The relative pressure pi corresponds with RCi according to the fitting equation. The increment of nitrogen adsorption is Δvi, and the surface area increment at this relative pressure is:
By accumulating the surface areas of each part, we can obtain the surface area of the pore wall. With this approach, it is possible to break free from the constraints of pore shape assumption and obtain more general calculation results.
The understandings obtained from the former two subsections suggest that for gas shale, there should exist many complex multi-stage ink-bottle-like pore structures. To interpret the pore size distribution, the multi-dimensional model should be applied. However, there is still much effort needed to fulfill this target that is out of the scope of this work and will be addressed in future work. Currently, only the one-dimensional tubular model is mature and optimal selection of the tubular model is more practical. In the ink-bottle-like pore structures, condensation occurs first during the condensation process and could cause the internal structure to condense through the gas–liquid two-phase meniscus rather than the formation of a liquid bridge. Therefore, for the selection of the DFT calculation kernels, it is preferable to use the equilibrium kernel rather than the adsorption kernel to calculate the pore size distribution.
In summary, this study works on statistical adsorption mechanisms, and focuses on the relative pressure of condensation and evaporation feature. The adsorption dynamic is also important and will be investigated in future work [36,37,38].
4. Conclusions
In this study, we constructed a series of two-dimensional and three-dimensional models based on ink-bottle pores, and molecular simulations of low-temperature nitrogen adsorption in nanopores were performed using the GCMC–MD method. This was undertaken in order to provide insights on the nitrogen condensation and evaporation behaviors associated with multi-dimensional pore structures and their implication for the pore size distribution analysis of gas shale. Three aspects have been analyzed in detail.
Firstly, after carefully simulating and examining the evaporation mechanisms of ink-bottle pores with different throat diameters and lengths, the boundary between pore blocking and cavitation has been determined. Compared with the conventional tubular model in which the threshold of cavitation only relates to throat diameter, this study discloses a wider range of conditions of cavitation and provides a more comprehensive understanding.
Secondly, multi-stage ink-bottle pore models have been constructed and it has been found that the cavitation pressure of the inner pore space controlled by multiple-hierarchal cavitation-zone throats is relatively smaller than that of the outer pore space. Considering that pore spaces of shale samples consist of many complex interconnected pores, the multi-stage ink-bottle pores are more suitable than the tubular model to equivalently represent the wider cavitation pressure range.
Thirdly, ink-bottle pore models with different pore cavity diameters and lengths have been constructed and the condensation process differences investigated. A more universal parameter RC is proposed. There is a strong linear relationship between RC and condensation pressure, which not only quantitatively unifies the influence of cavity diameter and length on condensation pressure, but also has good applicability in cavities with different shapes. This breaks free from the constraints of pore shape assumption and obtains more general surface area calculation results. As the condensation process of these pores is carried out through the meniscus formed in the narrow throats, for practical use at this stage, it is more appropriate to use the equilibrium kernels for the calculation of pore size distribution.
Author Contributions
Methodology, Z.C. and W.J.; conceptualization and programming, W.J.; experiment, Z.C.; simulation design, Z.C.; writing, Z.C.; review and editing, M.L. and W.J.; supervision, M.L. and G.C.; funding acquisition, M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the National Natural Science Foundation of China (Grant No. 42030808), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA14010304), the National Natural Science Foundation of China (41690132 and 41872163), and the Technical Innovation Project of Instrument and Equipment Function Development of Chinese Academy of Sciences (2020BA19).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The experimental equipment is supported by Beishide Instrument, Beijing, China.
Conflicts of Interest
We declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
The shale samples for the nitrogen adsorption experiment are selected from the Wufeng–Longmaxi Formation of different blocks in the southern Sichuan Basin. These shale samples are crushed by a compact jaw crusher and sieved between 20 mesh and 40 mesh screens to produce test samples with a particle size of 0.42–0.84 mm. Over 1 g of the sieved sample is loaded into the apparatus for the low-temperature nitrogen adsorption experiment. Before the adsorption procedure, the samples are dried and vacuumed at 110 °C for at least 4 h to fully remove the impurity gas and water in the nanopores. The experimental isotherm is measured at 77.3 K using a surface area and porosity analyzer (3H-2000PS1, Beishide Instrument, Beijing, China). Typical adsorption–desorption curves of shale samples from the Wufeng–Longmaxi Formation are shown in Figure A1.
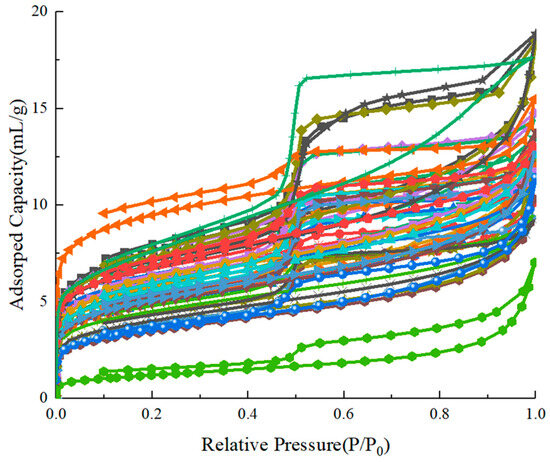
Figure A1.
Low-temperature nitrogen adsorption isotherms of shale samples.
Appendix B
To verify the rationality of the GCMC–MD method, we construct a cylindrical nanopore with a diameter of 5.32 nm and periodic boundary conditions are applied at two ends of the pore to simulate the infinite cylinder pores. The GCMC–MD method and GCMC method are both used to simulate the hysteresis loop of adsorption–desorption with the same molecule model and the same parameters, respectively. Each GCMC cycle performs 1000 changes, which include insertion and deletion only but with equal probability. The cutoff radius is chosen as half of the length of the simulation box. In the GCMC–MD mixed simulation case, the GCMC cycle is performed every 10 steps, and nitrogen molecules are added and deleted with equal probability to adjust the total number of nitrogen molecules. A total of 1,000,000 steps of MD simulations are performed for each relative pressure point, and the last 200,000 timesteps of simulation data are taken for analysis at each relative pressure point. The number of GCMC cycles performed by the two methods is the same, but the GCMC method does not rotate and move the molecules in the mixed simulation. The adsorption–desorption curves are shown in Figure A2.
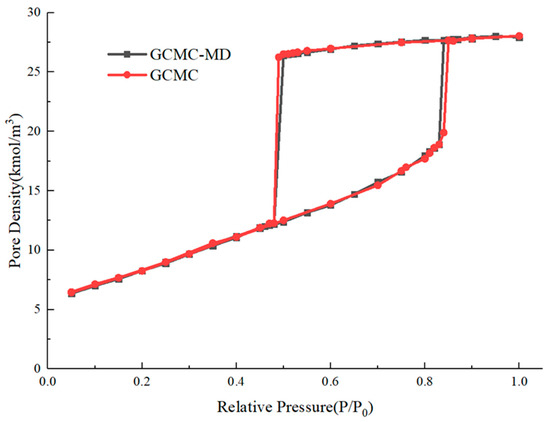
Figure A2.
Nitrogen adsorption–desorption curves of cylinder nanopore with GCMC and GCMC–MD methods.
According to the results obtained by the two methods, both the adsorption and desorption isotherms and the relative pressure point of condensation and evaporation are highly coincident, which indicates that the GCMC–MD simulation method has high reliability. The consumption times of these simulations are listed in Table A1.

Table A1.
Comparison of calculation time of the GCMC and GCMC–MD simulation methods.
Table A1.
Comparison of calculation time of the GCMC and GCMC–MD simulation methods.
| Methods | Calculation Time (h) |
|---|---|
| GCMC | 971 |
| GCMC–MD | 124 |
It can be seen from the calculation time that the calculation efficiency of the GCMC–MD method is much higher than that of the GCMC method under the same conditions. Therefore, the GCMC–MD approach provides a possible means by which to simulate the adsorption–desorption curves of complex nanopore structures.
References
- Zelenka, T.; Horikawa, T.; Do, D.D. Artifacts and misinterpretations in gas physisorption measurements and characterization of porous solids. Adv. Colloid Interface Sci. 2023, 311, 102831. [Google Scholar] [CrossRef] [PubMed]
- Barrett, E.P.; Joyner, L.G.; Halenda, P.P. The determination of pore volume and area distributions in porous substances, I. Computations from nitrogen isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. [Google Scholar] [CrossRef]
- Wang, M.; Li, Z.; Liang, Z.; Jiang, Z.; Wu, W. Method Selection for Analyzing the Mesopore Structure of Shale—Using a Combination of Multifractal Theory and Low-Pressure Gas Adsorption. Energies 2023, 16, 2464. [Google Scholar] [CrossRef]
- Pang, P.; Han, H.; Hu, L.; Guo, C.; Gao, Y.; Xie, Y. The calculations of pore structure parameters from gas adsorption experiments of shales: Which models are better? J. Nat. Gas Sci. Eng. 2021, 94, 104060. [Google Scholar] [CrossRef]
- Medina-Rodriguez, B.X.; Alvarado, V. Use of Gas Adsorption and Inversion Methods for Shale Pore Structure Characterization. Energies 2021, 14, 2880. [Google Scholar] [CrossRef]
- Sing, K.S.W.; Everett, D.H. Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (Recommendations 1984). Pure Appl. Chem. 1985, 57, 603–619. [Google Scholar] [CrossRef]
- Sarkisov, L.; Monson, P.A. Modeling of Adsorption and Desorption in Pores of Simple Geometry Using Molecular Dynamics. Langmuir 2001, 17, 7600–7604. [Google Scholar] [CrossRef]
- Hattori, Y.; Kaneko, K.; Ohba, T. Adsorption Properties. In Comprehensive Inorganic Chemistry II; Elsevier: Amsterdam, The Netherlands, 2013; Volume 5, pp. 25–44. [Google Scholar]
- Pellenq, R.J.M.; Coasne, B.; Denoyel, R.O.; Coussy, O. Simple Phenomenological Model for Phase Transitions in Confined Geometry. 2. Capillary Condensation/Evaporation in Cylindrical Mesopores. Langmuir 2009, 25, 1393–1402. [Google Scholar] [CrossRef]
- Groen, J.C.; Peffer, L.A.A.; Perez-Ramirez, J. Pore size determination in modified micro- and mesoporous materials. Pitfalls and limitations in gas adsorption data analysis. Microporous Mesoporous Mater. 2003, 60, 1–17. [Google Scholar] [CrossRef]
- Barsotti, E.; Piri, M. Effect of Pore Size Distribution on Capillary Condensation in Nanoporous Media. Langmuir 2021, 37, 2276–2288. [Google Scholar] [CrossRef]
- Broekhoff, J.C.; Deboer, J.H. Studies on Pore Systems in Catalysts. 11. Pore Distribution Calculations from Adsorption Branch of a Nitrogen Adsorption Isotherm in Case of Ink-Bottle Type Pores. J. Catal. 1968, 10, 153–165. [Google Scholar] [CrossRef]
- Nguyen, P.T.M.; Do, D.D.; Nicholson, D. Pore connectivity and hysteresis in gas adsorption: A simple three-pore model. Colloids Surf. A—Physicochem. Eng. Asp. 2013, 437, 56–68. [Google Scholar] [CrossRef]
- Klomkliang, N.; Do, D.D.; Nicholson, D. Effects of temperature, pore dimensions and adsorbate on the transition from pore blocking to cavitation in an ink-bottle pore. Chem. Eng. J. 2014, 239, 274–283. [Google Scholar] [CrossRef]
- Phuong, T.M.; Fan, C.Y.; Do, D.D. On the Cavitation-like Pore Blocking in Ink-Bottle Pore Evolution of Hysteresis Loop with Throat Size. J. Phys. Chem. C 2013, 117, 5475–5484. [Google Scholar]
- Nguyen, P.T.M.; Nicholson, D.; Do, D.D. On the Cavitation and Pore Blocking in Cylindrical Pores with Simple Connectivity. J. Phys. Chem. B 2011, 115, 12160–12172. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.J.; Vishnyakov, A.; Thommes, M.; Smarsly, B.M.; Kleitz, F.; Neimark, A. Cavitation in Metastable Liquid Nitrogen Confined to Nanoscale Pores. Langmuir 2010, 26, 10147–10157. [Google Scholar] [CrossRef]
- Loi, Q.K.; Tan, S.J.; Do, D.D.; Nicholson, D. Lower Closure Point for Nitrogen or Argon Adsorption in Mesoporous Solids: Window-Induced Evaporation or Surface-Induced Cavitation? Ind. Eng. Chem. Res. 2021, 60, 15343–15351. [Google Scholar] [CrossRef]
- Zeng, Y.H.; Fan, C.Y.; Do, D.D.; Nicolson, D. Evaporation from an Ink-Bottle Pore: Mechanisms of Adsorption and Desorption. Ind. Eng. Chem. Res. 2014, 53, 15467–15474. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Ji, L.; Lin, M.; Jiang, W.; Cao, G.; Zhou, J. Investigation into the apparent permeability and gas-bearing property in typical organic pores in shale rocks. Mar. Pet. Geol. 2019, 110, 871–885. [Google Scholar] [CrossRef]
- Cao, G.; Lin, M.; Ji, L.; Jiang, W.; Yang, M. Characterization of pore structures and gas transport characteristics of Longmaxi shale. Fuel 2019, 258, 116146. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, Y.; Niu, S.; Wei, X.; Yang, J. Multiscale characterization of pore structure and connectivity of Wufeng-Longmaxi shale in Sichuan Basin, China. Mar. Pet. Geol. 2020, 120, 104514. [Google Scholar] [CrossRef]
- Sun, X.; Luo, C.; Cao, G.H. Differences of Main Enrichment Factors of S1l11-1 Sublayer Shale Gas in Southern Sichuan Basin. Energies 2021, 14, 5472–5493. [Google Scholar]
- ISO 15901-2:2006; Pore Size Distribution and Porosity of Solid Materials by Mercury Porosimetry and Gas Adsorption—Part 2: Analysis of Mesopores and Macropores by Gas Adsorption. International Organization for Standardization: Geneva, Switzerland, 2006.
- Neimark, A.V.; Lin, Y.; Ravikovitch, P.I. Quenched solid density functional theory and pore size analysis of micro-mesoporous carbons. Carbon 2009, 47, 1617–1628. [Google Scholar] [CrossRef]
- Jagiello, J.; Jaroniec, M. 2D-NLDFT adsorption models for porous oxides with corrugated cylindrical pores. J. Colloid Interface Sci. 2018, 532, 588–597. [Google Scholar] [CrossRef] [PubMed]
- Thommes, M.; Cychosz, K.A. Physical adsorption characterization of nanoporous materials: Progress and challenges. Adsorption 2014, 20, 233–250. [Google Scholar] [CrossRef]
- Eugene, A.U. Effect of crystallization and surface potential on the nitrogen adsorption isotherm on graphite A refined Monte Carlo simulation. Carbon 2016, 100, 52–63. [Google Scholar]
- Ambrose, R.J.; Hartman, R.C.; Diaz-Campos, M.; Akkutlu, I.Y.; Sondergeld, C.H. Shale gas-in-place calculations part I: New pore-scale considerations. SPE J. 2012, 17, 219–229. [Google Scholar] [CrossRef]
- Coasne, B.; Galarneau, A.; Di Renzo, F. Molecular Simulation of Nitrogen Adsorption in Nanoporous Silica. Langmuir 2010, 26, 10872–10881. [Google Scholar] [CrossRef]
- Schreiber, A.; Reinhardt, S.; Findenegg, G.H. The lower closure point of the adsorption hysteresis loop of fluids in mesoporous silica materials. Stud. Surf. Sci. Catal. 2002, 144, 177–184. [Google Scholar]
- Nguyen, P.T.M.; Do, D.D.; Nicholson, D. On the Hysteresis Loop of Argon Adsorption in Cylindrical Pores. J. Phys. Chem. B 2011, 115, 4706–4720. [Google Scholar] [CrossRef]
- Lai, W.; Yang, S.; Jiang, Y.; Zhao, F.; Li, Z.; Zaman, B.; Fayaz, M. Artefact peaks of pore size distributions caused by unclosed sorption isotherm and tensile strength effect. Adsorption 2020, 26, 633–644. [Google Scholar] [CrossRef]
- Halsey, G.D. Physical Adsorption of Gases. J. Am. Chem. Soc. 1969, 235, 1214–1225. [Google Scholar] [CrossRef]
- Suzuki, Y.; Ishida, M.; Hata, K.; Ohba, T. Sequential N2 Adsorption by the Nanopore Entrance Filling Scheme in Nanopores of Carbon Nanotubes. Langmuir 2023, 44, 15431–15440. [Google Scholar] [CrossRef] [PubMed]
- Desouza, A.; Monson, P.A. Modeling fluids confined in three-dimensionally ordered mesoporous carbons. Adsorption 2021, 27, 253–264. [Google Scholar] [CrossRef]
- Schneider, D.; Valiullin, R.; Monson, P.A. Filling Dynamics of Closed End Nanocapillaries. Langmuir 2014, 30, 1290–1294. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).