A Semi-Analytical Model for Studying the Transient Flow Behavior of Nonuniform-Width Fractures in a Three-Dimensional Domain
Abstract
:1. Introduction
2. Methodology
2.1. Assumptions
- The reservoir is horizontally infinite, while vertically bounded with upper and lower impermeable boundaries;
- The matrix permeability, matrix porosity, formation thickness, and initial pressure are homogeneous and isotropic in the reservoir;
- The fluid has a constant value of compressibility and viscosity;
- Only single-phase flow is studied in this work;
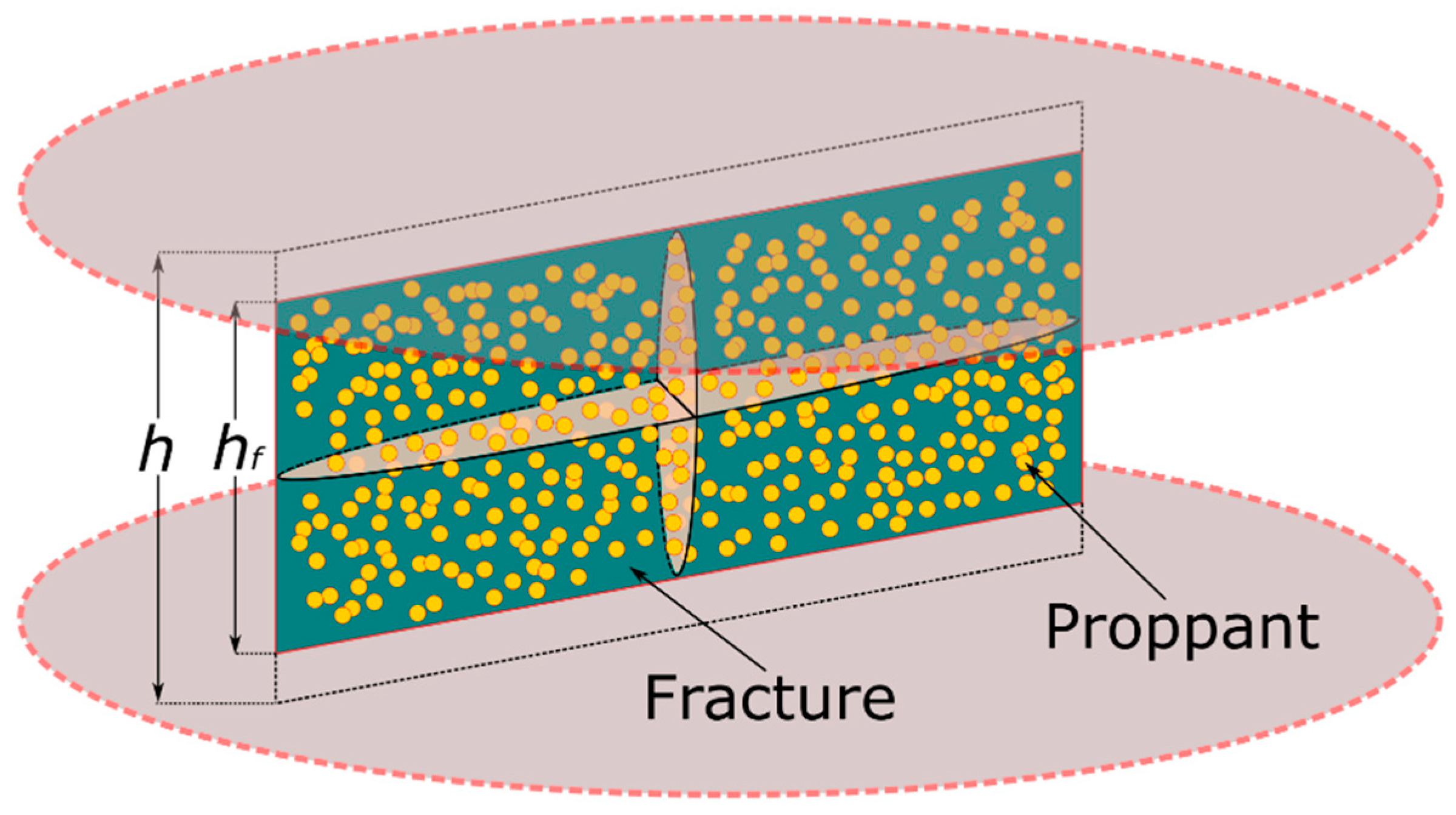
- The fracture is symmetrical with respect to the wellbore along the horizontal direction and located at the center of the reservoir along the vertical direction;
- The effect of leak-off is neglected;
- The fracture is vertical; and
- The fracture width will not change during the production, and the properties of the proppant-pack are uniform.
2.2. Fracture Propagation Model
2.3. Formulation of Fracture Flow
2.4. Formulation of Matrix Flow
2.5. Formulation of Wellbore
3. Validation
4. Results and Discussion
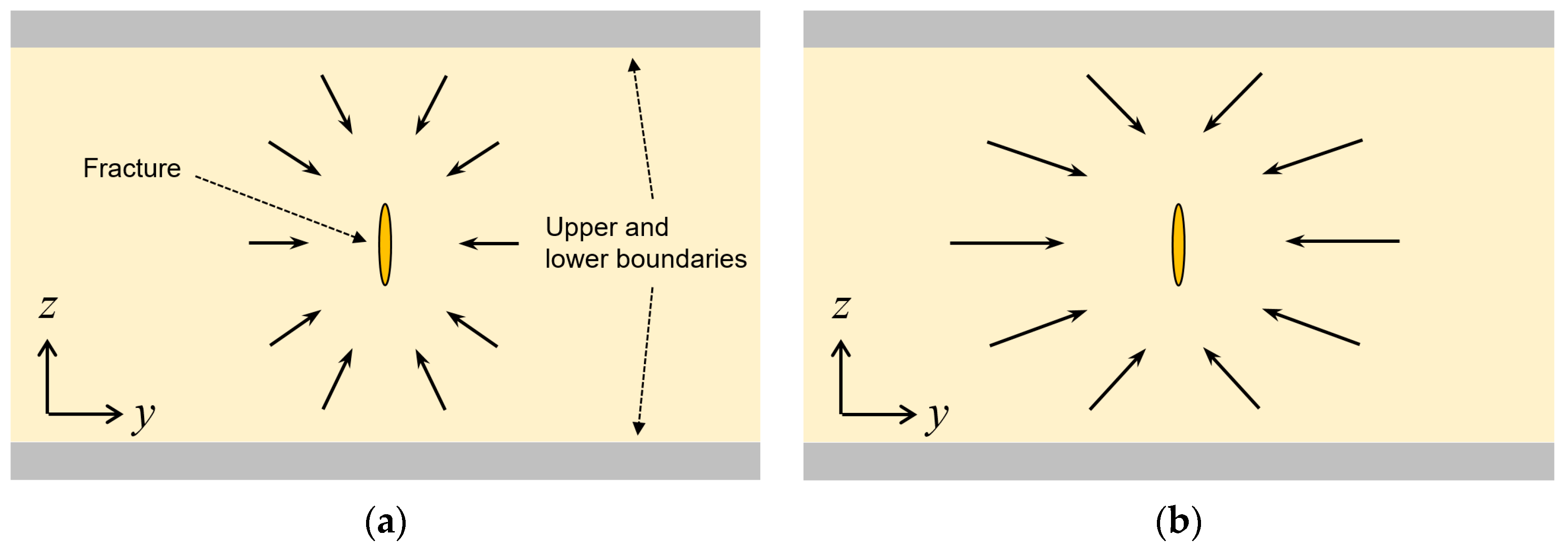
4.1. Flow Regimes
4.2. Sensitivity Analysis
4.3. Fracture Height
4.4. Injection Rate
4.5. Young’s Modulus
5. Conclusions
- If a PKN-type fracture has a sufficiently large height, one can observe the bilinear flow, formation linear flow, and horizontal pseudo-radial flow during the production. If the fracture height is sufficiently small compared to the formation thickness, the vertical flow around the fracture cannot be neglected, and one can observe the vertical elliptical flow and vertical pseudo-radial flow during the production;
- With the same injection volume, a larger fracture height can induce a shorter fracture length. For the scenarios of high fracture permeability (e.g., kf = 1 × 105 md), a longer but lower-height fracture can be more favorable for improving the well productivity;
- A lower injecting rate can render the PKN-type fracture penetrate further into the reservoir, leading to a higher well productivity of the high-permeability fractures. If the fracture permeability is sufficiently small, the injecting rate can only slightly influence the well performance.
- A larger value of Young’s modulus can result in a longer but narrower PKN-type fracture as well as a higher well productivity for high-permeability fractures. The influence of Young’s modulus on the well performance is negligible for the scenarios of low fracture permeability.
- In comparison to the fracture height, the injection rate and Young’s modulus exert a smaller influence on the fracture growth and well productivity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| B | formation volume factor |
| ctf | total compressibility of the fracture system, MPa−1 |
| ctm | total compressibility of the matrix system, MPa−1 |
| E | Young’s modulus, MPa |
| h | formation thickness, m |
| hf | fracture height, m |
| kf | fracture permeability, md |
| nw | number of fracture segments that are connected to the wellbore |
| pf | fracture pressure, MPa |
| q | flux within the fracture, m3/day |
| qf | flux rate from matrix to the fracture, m3/day |
| qf-w | flux rate from the fracture to the wellbore, m3/day |
| qi | injection rate, m3/d |
| qw | well production rate, m3/d |
| Qi | total injection volume, m3 |
| t | time, day |
| ti | injection time, day |
| T | transmissibility, m3/(day MPa) |
| v | Poisson ratio |
| w | fracture width, m |
| W | the maximum fracture width of a cross section of the PKN-type fracture, m |
| x, y, z | x-, y-, z-coordinates, m |
| ∆p | pressure difference, MPa |
| ∆t | time interval, day |
| ∆x | length of the fracture segment along x-axis, m |
| ∆z | length of the fracture segment along z-axis, m |
| β1 | 0.0853, unit conversion factor |
| β2 | 1.01 × 1015, unit conversion factor |
| ηm | β1km/(μϕmctm), diffusivity, m2/day |
| μ | oil viscosity, mPa∙s |
| μi | viscosity of the injection fluid, mPa∙s |
| τ | time the instantaneous source occurs, d |
| ϕf | fracture porosity |
| ϕm | matrix porosity |
References
- Holditch, S.A.; Holcomb, D.L.; Rahim, Z. Using Tracers to Evaluate Propped Fracture Width. In Proceedings of the SPE 26922 Presented at SPE Eastern Regional Meeting, Pittsburgh, PA, USA, 2–4 November 1993. [Google Scholar]
- Wright, E.A.; Davis, E.J.; Golich, G.M.; Ward, J.F.; Demetrius, S.L.; Minner, W.A.; Weijers, L. Downhole Tiltmeter Fracture Mapping: Finally Measuring Hydraulic Fracture Dimensions. In Proceedings of the SPE 46194 Presented at SPE Western Regional Meeting, Bakersfield, CA, USA, 10–13 May 1998. [Google Scholar]
- van Dam, D.B.; Papanastasiou, P.; de Pater, C.J. Impact of Rock Plasticity on Hydraulic Fracture Propagation and Closure. In Proceedings of the SPE 63172 Presented at SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Geertsma, J. Two-dimensional Fracture-propagation Models. Soc. Pet. Eng. AIME J. 1989, 12, 81–94. [Google Scholar]
- Geertsma, J.; Haafkens, R. Comparison of the theories for predicting width and extent of vertical hydraulically induced fractures. J. Energy Resour. Technol. 1979, 101, 8–19. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J. The Use of Source and Green’s Functions in Solving Unsteady-Flow Problems in Reservoirs. SPE J. 1973, 13, 285–296. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J. Unsteady-State Pressure Distributions Created by a Well with a Single Infinite-Conductivity Vertical Fracture. SPE J. 1974, 14, 347–360. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J. Unsteady-State Pressure Distributions Created by a Well with a Single Horizontal Fracture, Partial Penetration, or Restricted Entry. SPE J. 1974, 14, 413–426. [Google Scholar] [CrossRef]
- Rodriguez, F.; Horne, R.N.; Cinco-Ley, H. Partially Penetrating Vertical Fractures: Pressure Transient Behavior of a Finite-Conductivity Fracture. In Proceedings of the SPE 13057 Presented at SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 16–19 September 1984. [Google Scholar]
- Zhou, W.; Banerjee, R.; Poe, B.D.; Spath, J. Semianalytical Production Simulation of Complex Hydraulic-Fracture-Networks. SPE J. 2014, 19, 6–18. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, F.; Styles, J.A.; Gao, J. Performance Evaluation of a Horizontal Well with Multiple Fractures by Use of a Slab-Source Function. SPE J. 2015, 20, 652–662. [Google Scholar] [CrossRef]
- Luo, W.; Tang, C. Pressure-Transient Analysis of Multiwing Fractures Connected to a Vertical Wellbore. SPE J. 2015, 20, 360–367. [Google Scholar]
- Chen, Z.; Liao, X.; Zhao, X.; Lv, S.; Zhu, L. A Semianalytical Approach for Obtaining Type Curves of Multiple-Fractured Horizontal Wells with Secondary-Fracture Networks. SPE J. 2016, 21, 538–549. [Google Scholar] [CrossRef]
- Jia, P.; Cheng, L.; Clarkson, C.R.; Qanbari, F.; Huang, S.; Cao, R. A Laplace-Domain Hybrid Model for Representing Flow Behavior of Multifractured Horizontal Wells Communicating through Secondary Fractures in Unconventional Reservoirs. SPE J. 2017, 22, 1856–1876. [Google Scholar] [CrossRef]
- Xiao, C.; Dai, Y.; Tian, L.; Lin, H.; Zhang, Y.; Yang, Y.; Hou, T.; Deng, Y. A Semianalytical Methodology for Pressure-Transient Analysis of Multiwell-Pad-Production Scheme in Shale Gas Reservoirs, Part 1: New Insights into Flow Regimes and Multiwell Interference. SPE J. 2017, 23, 885–905. [Google Scholar] [CrossRef]
- Teng, B.; Li, H.; Yu, H. A Novel Analytical Fracture-Permeability Model Dependent on Both Fracture Width and Proppant-Pack Properties. SPE J. 2020, 25, 3031–3050. [Google Scholar] [CrossRef]
- Yu, W.; Wu, K.; Sepehrnoori, K. A Semianalytical Model for Production Simulation from Nonplanar Hydraulic-Fracture Geometry in Tight Oil Reservoirs. SPE J. 2016, 21, 1028–1040. [Google Scholar] [CrossRef]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Teng, B.; Li, H.A. A Semi-Analytical Model for Characterizing the Pressure Transient Behavior of Finite-Conductivity Horizontal Fractures. Transp. Porous Med. 2018, 123, 367–402. [Google Scholar] [CrossRef]
- Nordgren, R.P. Propagation of a Vertical Hydraulic Fracture. SPE J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Ertekin, T.; Abou-Kassem, J.H.; King, G.R. Basic Applied Reservoir Simulation; SPE Textbook Series; Society of Petroleum Engineers: Richardson, TX, USA, 2001. [Google Scholar]
- Cinco-Ley, H.; Samaniego-V, F. Transient Pressure Analysis for Fractured Wells. SPE J. 1981, 33, 1749–1766. [Google Scholar] [CrossRef]
















| Parameter | Value | Parameter | Value |
|---|---|---|---|
| qi | 4.32 × 103 m3/day | Qi | 4.32 × 105 m3 |
| μi | 100 mPa∙s | hf | 40 m |
| E | 4.5 × 104 MPa | v | 0.2 |
| ti | 6.94 × 10−3 day | h | 50 m |
| μo | 1 mPa∙s | kf | 1 × 106 md |
| km | 1 × 10−2 md | ctm | 1.12 × 10−3 MPa−1 |
| ctf | 1.12 × 10−3 MPa−1 | ϕm | 0.2 |
| ϕf | 0.2 | pw | 5 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Zhang, X.; Zhou, W.; Li, Q.; Li, J.; Du, Y.; Cai, H.; Teng, B. A Semi-Analytical Model for Studying the Transient Flow Behavior of Nonuniform-Width Fractures in a Three-Dimensional Domain. Energies 2023, 16, 7920. https://doi.org/10.3390/en16247920
Liang Y, Zhang X, Zhou W, Li Q, Li J, Du Y, Cai H, Teng B. A Semi-Analytical Model for Studying the Transient Flow Behavior of Nonuniform-Width Fractures in a Three-Dimensional Domain. Energies. 2023; 16(24):7920. https://doi.org/10.3390/en16247920
Chicago/Turabian StyleLiang, Yanzhong, Xuanming Zhang, Wenzhuo Zhou, Qingquan Li, Jia Li, Yawen Du, Hanxin Cai, and Bailu Teng. 2023. "A Semi-Analytical Model for Studying the Transient Flow Behavior of Nonuniform-Width Fractures in a Three-Dimensional Domain" Energies 16, no. 24: 7920. https://doi.org/10.3390/en16247920
APA StyleLiang, Y., Zhang, X., Zhou, W., Li, Q., Li, J., Du, Y., Cai, H., & Teng, B. (2023). A Semi-Analytical Model for Studying the Transient Flow Behavior of Nonuniform-Width Fractures in a Three-Dimensional Domain. Energies, 16(24), 7920. https://doi.org/10.3390/en16247920







