A High-Precision Error Calibration Technique for Current Transformers under the Influence of DC Bias

Abstract

A bias current in the power system will cause saturation of the measuring current transformer (CT), leading to an increase in measurement error. Therefore, in this paper, we first conducted measurements of the direct current component in a 10 kV distribution system. Subsequently, a reverse extraction method for the CT distorted current under direct current bias conditions based on Random Forest Classification (RFC) and Long Short-Term Memory (LSTM) was proposed. This method involves two stages for the reverse extraction of CT distorted currents under direct current bias conditions. In the offline stage, data samples were generated by changing the operating environment of the CT. The RFC classification algorithm was used to divide the saturation levels of the CT, and for each sub-class, Particle Swarm Optimization–Long Short-Term Memory Network (PSO-LSTM) models were trained to establish the mapping relationship between the secondary distorted current and the primary current fundamental component. In the online stage, the saturated data segments were extracted from the secondary current waveform using wavelet transform, and these segments were input into the offline model for current reverse extraction. The simulation results show that the proposed method exhibited strong robustness under various CT conditions, and achieved high reconstruction accuracy for the primary current.

1. Introduction

Electromagnetic current transformers are important and widely used equipment for measurements and protection in power systems. However, due to the nonlinear electromagnetic characteristics of its core, a CT will be saturated when large current and DC components flow through it [1].With the rapid development of HVDC transmission and the large-scale application of new energy, DC magnetic biases are becoming more and more significant [2], which seriously affects the measurement accuracy of electromagnetic current transformers. Therefore, it is very important to improve the measurement accuracy of CTs through saturation detection and distortion current inversion.

1.1. Literature Overview

In the study of CT saturation detection, the authors of [3,4] developed a traditional detection method based on waveforms obtained from the second and third derivatives to detect the saturation interval. In [5], the utilization of a Lanczos filter for CT saturation was mentioned. Although both methods have a low computation burden, they may not accurately detect the end of some saturation events when there is a smooth current variation at the endpoints of the saturation. In addition, both methods are subject to interference from harmonic signals. Therefore, for practical applications, the signal should be pre-conditioned by a low-pass filter before applying these methods. A novel CT saturation detection method using the least error square (LES) technique was presented in [6]. Another detection method based on symmetrical components was proposed in [7] to determine the saturation duration. In [8], a detection approach based on short-data window impedance and samples taken from the CT and busbar voltage were highlighted. In [9], the analysis of the distance between consecutive points in the plans formed by the difference function of the sampled signal was adopted to detect CT saturation intervals. A technique based on mathematical morphology was proposed in [10] for CT saturation detection and compensation; however, it could not identify saturation under noisy conditions. Discrete wavelet transform (DWT)-based methods were proposed in [11,12] to detect the onset and endpoint of CT saturation. However, the accuracy of saturation detection is determined by the correct selection of the appropriate mother wavelet.

In the study of CT saturation reconstruction, in [13], the excitation current was identified as the fundamental cause of metering errors in CT saturation reconstruction. Although adding the calculated excitation current to the secondary-side current can yield the actual primary-side current, this method neglects the impact of residual magnetic flux in the core, resulting in a complex and challenging calculation process. Meanwhile, in [14], a comprehensive frequency-domain equivalent circuit study was conducted for instrument transformers. However, it was found that the equivalent circuit provided inaccurate results. In [15], wavelet analysis was utilized to detect the distortion caused by core saturation, and subsequently, a regression method was employed to recover the distorted section. The method proposed in [16] classifies the saturated and non-saturated regions. However, these methods heavily rely on human-selected features, which could lead to overfitting issues during validation. In [17,18], the authors introduced other intelligent approaches to differentiate between saturation and non-saturation fragments. Nevertheless, due to unstable convergence in both approaches, the generalization performance of the network was significantly reduced. Additionally, an analysis of CT saturation was thoroughly explored in [19], using decision trees and wavelet transform. While this approach uses signal processing techniques with wavelet decomposition, it requires an extensive scheme for signal processing to extract meaningful and useful features. In contrast, the author in [20] classified the saturation types (no saturation, light saturation, and heavy saturation) based on feature extraction with machine learning and fine-tuning strategies to achieve high accuracy in CT saturation classification. However, this approach failed to detect the endpoints of saturation in each cycle, making it impractical for power system protection.

1.2. Method and Effectiveness

Therefore, this paper proposes a novel method for the saturation detection and primary current reconstruction of CTs used in measurements under DC bias conditions. The method is based on a combination of random forest classification and Long Short-Term Memory neural networks. This approach aims to overcome the limitations of existing methods and improve the accuracy and timeliness of saturation detection and primary current reconstruction in the presence of DC bias. The proposed method consists of two main stages: offline and online. (1) Offline stage: Firstly, the PSCAD/EMTDC V46 is used to generate the one-phase and two-phase current signals of a CT under different operating conditions, which serve as the sample dataset. Then, based on the magnitude of the ratio difference, the secondary current is categorized into different saturation levels. The wave asymmetry coefficient, total harmonic content, and the content of harmonics from the second to fifth order are calculated. Subsequently, a Random Forest Classification (RFC) model is constructed to establish the mapping relationship between each feature and the corresponding saturation level. Finally, for each saturation level, a Particle Swarm Optimization–Long Short-Term Memory Network is developed to reconstruct the saturated current. The PSO-LSTM model is optimized using particle swarm optimization, taking into account the historical context and dependencies of the current waveform. By training the PSO-LSTM model with the corresponding saturated current samples, it learns to reconstruct the primary current accurately. (2) Online stage: The system continuously monitors the secondary current waveform and detects saturation periods in real time. When saturation is detected, the corresponding saturated data segments are fed into the offline model for primary current reconstruction. The reconstructed primary current can then be used for accurate measurement and monitoring purposes. The simulation results of the proposed method demonstrate that it is capable of reconstructing the distorted current of a current transformer under the influence of DC bias within a short timeframe. The accuracy of the reconstruction meets the measurement requirements of 0.2S CT, ensuring high precision. One notable advantage of the proposed method is its independence from the saturation level of the CT. It is capable of accurately reconstructing the distorted current regardless of the saturation level, making it suitable for various operating conditions. This versatility allows the method to meet the measurement requirements of CTs in different scenarios.

2. Transmission Error Analysis of Electromagnetic Transformers under DC Magnetic Bias

2.1. Measurement of DC Content in Transmission Lines

In this study, direct current component testing was conducted on selected grid integration points in the 10 kV distribution network system in Shenzhen area of the China Southern Power Grid, including industrial parks, residential areas, and dedicated transformer users. A total of 408 data samples was collected. The distribution of DC content at the testing points is shown in

Table 1. DC content distribution at test points.

DC Content (%)	Number	Percentage (%)
0–3	338	82.84
3–6	61	14.95
6–9	7	1.71
9–11	2	0.49

. Some of the testing points with a high DC content are presented in

Table 2. DC content of typical testing points.

Testing Point	DC Content (%)
Sha Tau Kok Second living area integrated housing	0.17%
Yantian forest farm public distribution power station	0.57%
Sakai Shinji Industrial Village	1.4%
Shiyan Street Tangtou Vegetable Market	−2.026%
Jiali Hardware Factory Principal variation	−3.8%

.

In the table, DC content was calculated by the ratio of the effective values of the DC component to the effective values of the AC component.

Both indicators are used to illustrate the distribution of DC bias content in the 10 kV distribution system in the South China Grid region. “Number” represents the number of sampling points that meet the corresponding DC bias content, and “Percentage/%” represents the proportion of the DC bias content among all sampling points.

It was observed that approximately 85.05% of the lines have a DC content exceeding 1%, and around 17.16% have a DC content exceeding 3%. This highlights the importance of addressing DC content in modern power systems.

2.2. Analysis of Transmission Characteristics of Current Transformers

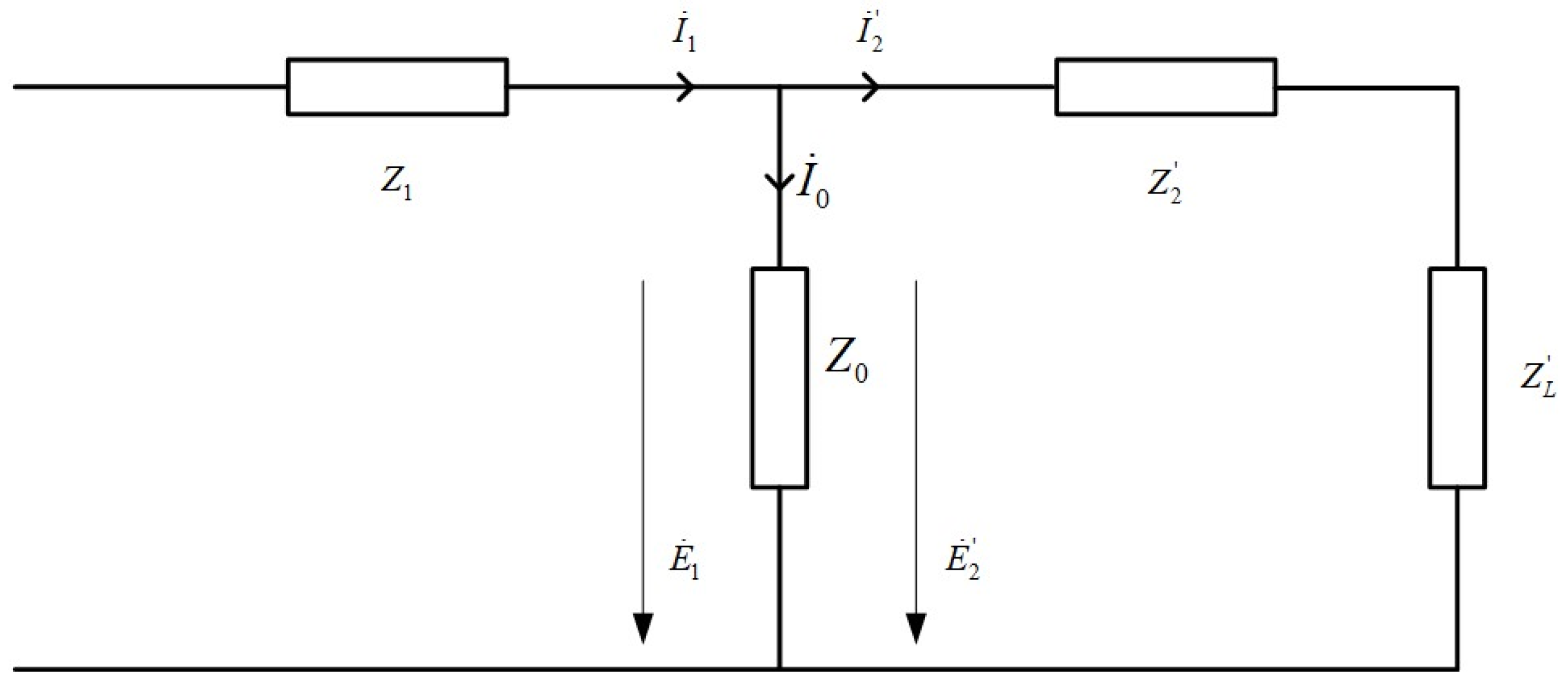
The equivalent circuit of a conventional single-core CT is illustrated in Figure 1.

In the diagram, $Z_1$, $Z_0$, $Z_2^{\prime }=R_2^{\prime }+j{X}_2^{\prime }$ and $Z_L^{\prime }=R_L^{\prime }+j{X}_L^{\prime }$ represent the primary impedance, excitation impedance, leakage impedance converted to the primary side, and the load impedance of the secondary side, respectively. ${\dot{I}}_1$ represents the primary current, ${\dot{I}}_0$ represents the excitation current, and ${\dot{I}}_2^{\prime }$ represents the current on the secondary side converted to the primary side. ${\dot{E}}_1$ represents the induced electromotive force on the primary side, and ${\dot{E}}_2^{\prime }$ represents the induced electromotive force on the secondary side converted to the primary side.

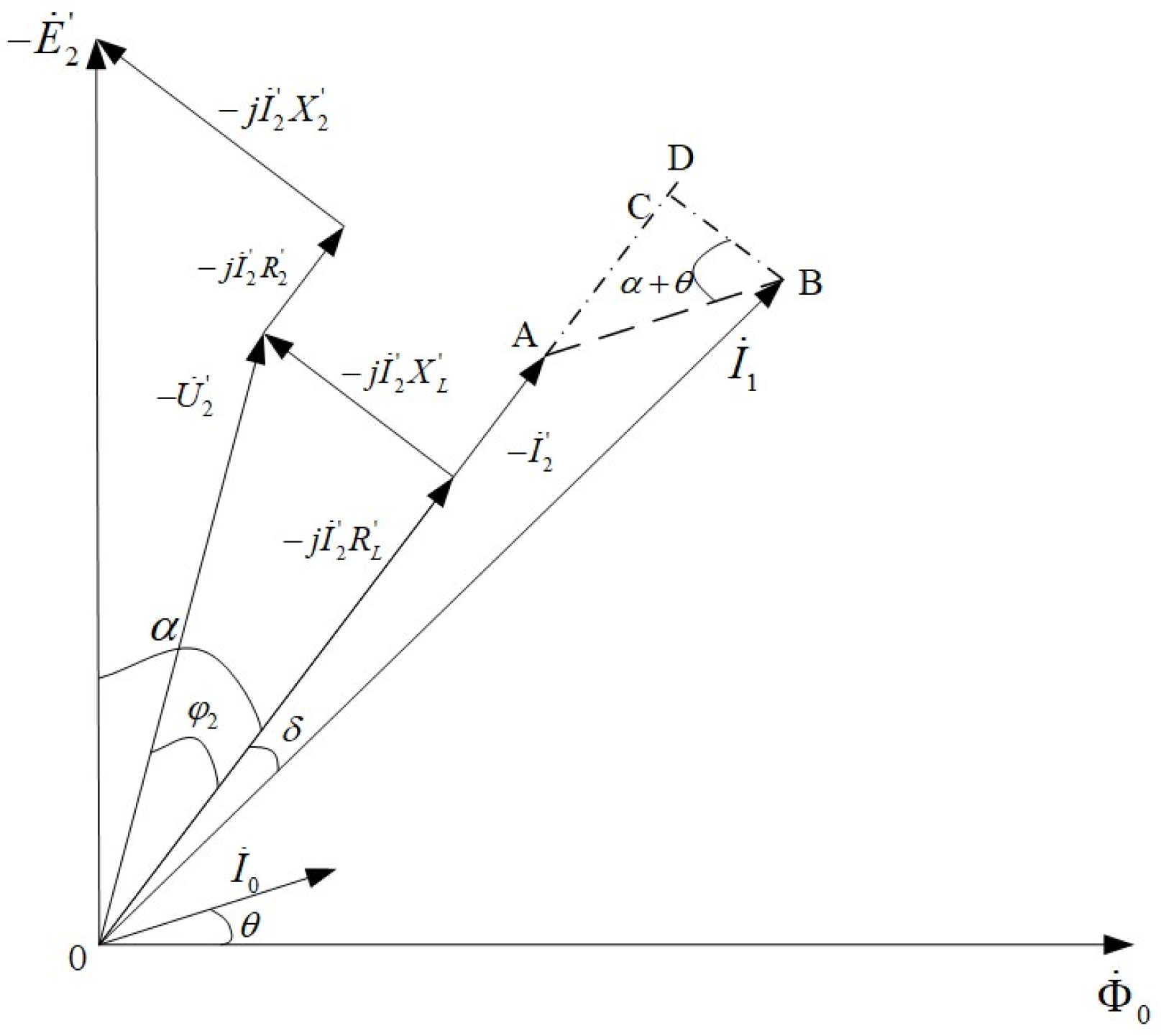
According to the equivalent circuit structure of the current transformer in Figure 1, the phasor diagram of the current transformer can be drawn, as shown in Figure 2.

In the diagram, a is the impedance angle of the second order. $\delta$ is the angle at which the secondary current leads the primary current, indicating the angular difference. $\theta$ is the angle at which the excitation current I₀ leads the magnetic flux ${\dot{\Phi }}_0$, representing the loss angle. It can be derived from the corresponding magnetization curve of the iron core.

When the CT core operates in the linear region, its excitation magnetic flux has the following relationship with the secondary induced electromotive force:

$${\Phi }_0=\frac{\sqrt{2}{E}_2}{2\pi f{N}_2}$$

(1)

In the equation, $E_2=I_2\sqrt{{\left(R_2+R_L\right)}^2+{\left(X_2+X_L\right)}^2}=I_2\left|Z_2\right|$, $\left|Z_2\right|$ represents the modulus of secondary side load. N₂ represents the number of turns in the secondary winding, and f represents the frequency of the AC current.

Combining Ampere’s loop law with Equation (1), we can obtain Equation (2):

$${\Phi }_0=\frac{\sqrt{2}\mu S{I}_0{N}_1}{l_c}$$

(2)

In the equation, l_c represents the effective magnetic path length of the CT core, and N₁ represents the number of turns in the primary winding.

When $\delta$ is very small, combined with the phasor diagram, the geometric expression for CT ratio difference is $\left|\mathrm{AC}\right|/\left|\mathrm{OB}\right|$, the expression for angle difference is $\left|\mathrm{BD}\right|/\left|\mathrm{OB}\right|$, and the mathematical expressions for ratio difference and angle difference are expressed as:

$$\epsilon =-\frac{l_c\left|Z_2\right|}{2\pi f\mu S{N}_2^2}\sin \left(a+\theta \right)\times 100\%$$

(3)

$$\delta =\frac{l_c\left|Z_2\right|}{2\pi f\mu S{N}_2^2}\cos \left(\alpha +\theta \right)\times 3440$$

(4)

To further analyze the transmission performance of current transformers under harmonic conditions and DC bias, this article sets up CT simulation operating conditions in PSCAD based on the regulations on harmonic content in the power grid in IEC-61000-2 and the on-site measurement data of DC components in Table 1. The parameters of CT are shown in

Table 3. The parameters of CT.

Parameter	Value
Turn ratio	5/500
Rated current on the primary side (A)	500
Cross sectional area of iron core (cm2)	26.01
Core magnetic circuit length (cm)	63.77
Secondary side load ($\mathsf{\Omega }$)	0.12 + 0.16j

.

IEC-61000-2 considers the requirement for long-term stable operation of the power grid, and stipulates that the total harmonic distortion should be less than 8%. In the simulation software Matlab 2022, the effective value of harmonics is fixed at 8% of the rated effective value on the primary side, with an initial phase of 0°, which is the same as the fundamental current. The results regarding the impact of harmonic frequency changes from 100 to 500 Hz on the CT fundamental error at a rated current are shown in Figure 3a.

Under the rated current, we adjust the DC component size from 1 to 5% I_N to obtain the ratio difference and angle difference changes of CT, as shown in Figure 3b.

Under harmonic conditions, the ratio difference and phase difference of the current transformer with respect to the fundamental wave remain within a narrow range, without significantly impacting the transmission performance of the current transformer. However, due to the inability to couple the DC component to the secondary side through the iron core, the magnetic flux generated will be superimposed with the same polarity AC magnetic flux, seriously altering the working performance of the iron core. Although Equations (3) and (4) do not directly include the DC component, the magnetic permeability of the iron core under DC bias μ can be regarded as a function of I_DC. When only considering the presence of I_DC in the primary winding, the magnetic induction intensity B generated by the DC component can be obtained as:

$$B=\mu H=\frac{\mu N_1{I}_{DC}}{l_c}$$

(5)

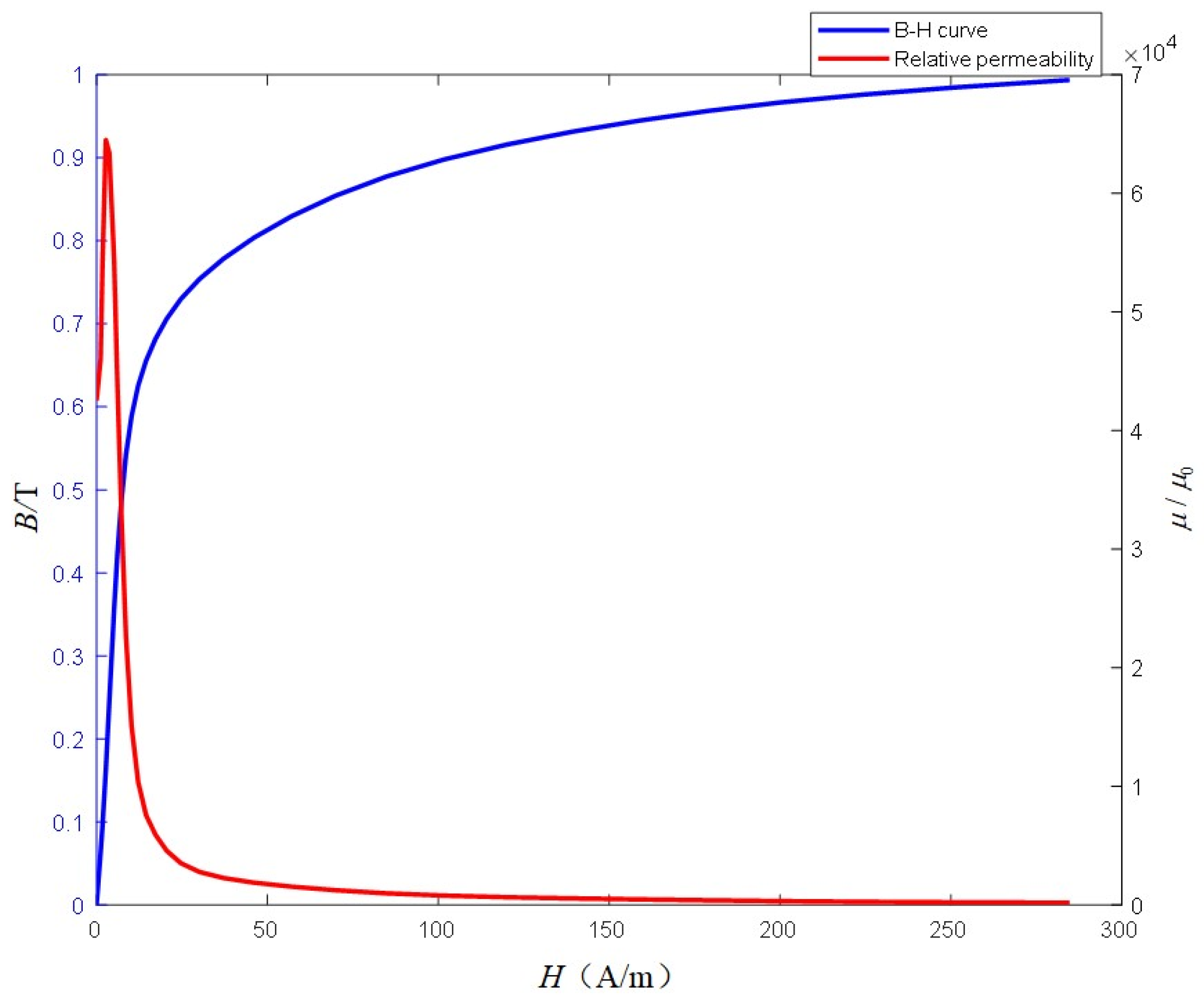
Figure 4 shows the B–H curve and the μ–H curve. When there is no direct current component in the primary coil, H is close to zero. In this situation, the permeability has a high value. According to Equations (3) and (4), the error of the current transformer is small. However, as indicated by Equation (5), the magnetic field intensity value H is directly proportional to the I_DC. With an increase in H, the permeability μ rapidly decreases, resulting in a sharp increase in the measurement error of the current transformer.

To quantitatively analyze the impact of DC bias on the measurement error of the CT, an experimental circuit was constructed, as shown in Figure 5. The experimental circuit independently winds the DC circuit around the tested CT. The standard sampling resistor has a resistance value of 0.1 Ω and a temperature drift of 1 ppm. Assuming a maximum temperature variation of 50 °C, the error caused by the temperature drift in the sampling resistor is at most ±1 ppm/°C × 50 °C = ±0.005%. The digital comparator uses a spectrum analysis algorithm, which provides high accuracy. Even under conditions of frequency offset and non-synchronous sampling, the errors encountered in extracting amplitude and phase from the frequency can reach the order of 10⁻³. The standard current transformer in the diagram possesses a measurement accuracy of 0.01S, which exceeds that of the tested CT by two accuracy classes. This results in a ratio error of no more than 0.01% and a phase error less than 0.2’. In all the tests, the errors of the acquisition system were at most 1/10 of those of the CT under test; therefore, they can be considered negligible [21].

The ratio error and phase error of the LMZ2D metering current transformer under different DC and AC components were measured and are presented in

Table 4. CT (500/5, 0.2S) transmission error data under DC bias.

I (%)	$\mathsf{\epsilon }$ (%)	$\mathit{\delta }$ ($\mathbf{\prime }$)	$\mathit{\epsilon }$ (%)	$\mathit{\delta }$ ($\mathbf{\prime }$)	$\mathit{\epsilon }$ (%)	$\mathit{\delta }$ ($\mathbf{\prime }$)
1	0.1	5.29	0.09	5.04	0.09	6.24
5	0.09	4.99	0.09	13.1	0.07	41.26
20	0.08	26.22	−0.14	112	−0.66	203.12
100	−0.02	44.8	−0.75	137	−1.88	227.03
120	−0.04	45.65	−0.81	138	−1.96	227.25
(IDC/IN)/%	1%		3%		5%

.

In Table 4, it can be observed that when the AC component in the primary circuit is small, the influence of the DC component on the error of the CT is minimal. However, when the AC component in the primary circuit is at the rated current, an increase in the DC component causes the ratio error of the CT to shift in the negative direction and the phase error to shift in the positive direction. A DC component of 3% I_N in the primary circuit can cause the ratio error of the CT to exceed the measurement accuracy requirement of a 0.2S CT.

3. Inverse Propagation Method of CT Distortion Current under DC Magnetic Bias

The algorithm flow of the method for reconstructing the distorted current under a DC bias is shown in Figure 6. The algorithm is divided into two stages: the offline stage and the online stage. In the offline stage, the first step is to establish a PSCAD/EMTDC simulation model based on field measurement data. Under various operating conditions, the primary and secondary current samples of the CT under a DC bias are obtained. The asymmetry, harmonic content, and content of specific harmonics in the secondary current waveform are calculated. An RFC classification model is then built to determine the saturation level of the current transformer. In the next step, the secondary currents for each saturation level are used as input data, and the corresponding primary currents are used as output data to establish a PSO-LSTM nonlinear regression model.

In the online stage, the first step is to use wavelet transform to identify the saturation intervals in the secondary current affected by the DC bias. Then, the relevant indicators of the distorted secondary current are calculated, and they are inputted into a multi-classification model for saturation type determination. Finally, the distorted segments of the current that have been corrected by the PSO-LSTM model are merged with the segments of the current that have not experienced distortion to obtain the final output result of the model.

3.1. Training Sample Generation Method

The main factors that affect the transformation performance of CT include the ratio of DC components to the rated current K_dc, the proportion of the effective value of the AC frequency to the rated current K_ac and the polarity of the bias current pol. Additionally, the primary-side current in the power system inevitably contains harmonic components. This paper also considers two indicators: the proportion of harmonic components to the rated current, K_THD, and the harmonic frequencies, f_i. To better describe the method of generating the training dataset in this paper, this paper defines “F~itr~L” as a way to generate sample data. In this notation, F represents the starting data, L represents the ending data, and itr represents the step size for data generation.

• Based on the field measurement data, which are mainly concentrated in the range of 0–3%, sample data generation for K_dc can be performed using the ranges of 0%~0.2%~3% and 3%~1%~11%;
• Since the impact of DC bias on the measurement error of the primary current of CT is weaker when the primary current is small, the range for K_ac can be set as 10%~10%~150% for thorough exploration;
• We iterate through the harmonic content K_THD, ranging from 0%~0.5%~4%;
• For the sake of simplifying the model’s complexity, each sample considers only one harmonic, and the harmonic frequency f_i is varied from 100 Hz to 50 Hz to 500 Hz;
• To consider the impacts of both positive and negative polarities of the bias current on the transformation performance of the CT, the sample data generation can be conducted for both polarities separately. This will allows for a comprehensive analysis of the performance under different bias current polarities.

By combining the values of the above parameters, we can obtain N different operating conditions for the sampling of the primary and secondary currents of the CT. Each combination represents a specific operating condition that can be used to generate the corresponding sample data.

$$N=N_{K_{dc}}{N}_{K_{ac}}{N}_{K_{THD}}{N}_{f_i}{N}_{pol}$$

(6)

In this equation, $N_{K_{dc}}$, $N_{K_{ac}}$, $N_{K_{THD}}$, $N_{f_i}$ and $N_{pol}$ correspond to the number of iterations for each parameter, where N_pol = 2 represents the two polarities of the bias current.

According to Equation (6), a total of 58,320 potential operating conditions that can cause measurement errors in the current transformer have been generated. These conditions serve as the sample data for offline training.

3.2. Extraction Method of Saturated Period

When a CT saturates, its output secondary-side current waveform becomes distorted. Compared to a normal waveform, the distorted current waveform exhibits certain irregularities. According to the theory of signal singularity detection, the Lipschitz exponent is an important parameter that characterizes the singularity of a signal [22]. Its regularity is related to the decay of the wavelet transform amplitude with scale. The regularity of the Lipschitz exponent of the signal f(x) at any point depends on the attenuation of the wavelet system module $\left|W{T}_f^n\left(b,x\right)\right|$ at the detail scale in the vicinity of the point.

$$W{T}_f^n\left(b,x\right)=f\left(x\right)\ast \left[b\frac{d^n\psi \left(x\right)}{d{x}^n}\right]=b^n\frac{d^n}{d{x}^n}\left[f\left(x\right)\ast \psi \left(x\right)\right]$$

(7)

In the equation, $\psi \left(x\right)$ represents a scaling function associated with the scale factor b, and the symbol * denotes the convolution operation.

If within the local neighborhood $\left(x_0-n\Delta t,x_0+n\Delta t\right)$ of x₀, Equation (8) holds for all. Then, x₀ is a local maximum point in the wavelet transform modulus and a singularity point in the signal f(x). Here, n represents the data window size, and $\Delta t$ is the sampling interval.

$$W{T}_f^n\left(b,x\right)\le \left|W{T}_f^n\left(b,x_0\right)\right|$$

(8)

when n = 1, the modulus of the wavelet coefficients is directly proportional to the first derivative of the signal. Therefore, the singular points of the signal correspond to the local maxima of the modulus. By identifying the local maxima of the signal at a fine scale, we can determine the positions of the singular points, which in turn allows us to recognize the presence of DC components in the secondary current waveform.

This paper has selected the second-generation wavelet basis, Bior3.1, known for its minimal phase distortion and sensitivity to sudden signal changes, as the mother wavelet for signal singularity identification. We utilized a data window size of n = 16. The three-level wavelet decomposition and reconstruction processes were applied to the CT under two conditions: rated current and rated current superimposed with 5% I_N DC bias. The maximum modulus on the first-level detail signal (d1) was used as the criterion to detect CT saturation, and the results are presented in Figure 7.

At the moments of entering and exiting saturation in the CT, distinct modulus maxima are evident on the first-level wavelet detail plots, with a maximum time error of 0.125 ms, signifying a high level of detection precision. Furthermore, on both sides of the modulus maxima obtained from wavelet transformation, the signal exhibits an attenuating nature. The application of a data window prevents the issue of misidentifying pseudo maxima as true maxima due to signal attenuation.

3.3. A Saturation Classification Method for CT Distortion Current Based on RFC

After detecting the saturation interval of the transformer by wavelet transform, the distortion current data in the saturation interval of the transformer should be corrected. When the intelligent algorithm is used to correct the distortion current of the current transformer, the correction time is too long because the data sample is too large and it is difficult for the single model to achieve both generalization and accuracy [23]. Therefore, this paper divides the sample into several clusters to reduce the difficulty of training the correction algorithm.

3.3.1. Extraction of Distorted Current Waveform Features

When the CT reaches saturation, the secondary-side current waveform will display varying levels of distortion and imperfections. This causes the secondary-side current to not only contain fundamental components, but also leads to an increase in harmonic content as the saturation intensifies [16]. Therefore, this paper employs the total harmonic distortion (THD) and the content of specific harmonic orders in the secondary-side current waveform as indicators to assess the degree of transformer saturation.

For a discrete secondary-side current sampling signal, its typical expression is as follows:

$$x\left(n\right)=\sum _{m=1}^K{A}_m\cos \left(2\pi \frac{f_0}{f_s}mn+{\phi }_m\right)$$

(9)

In the equation, m is the number of harmonics; K is the total number of harmonics; f₀ is the fundamental frequency; f_s is the sampling frequency; A_m and ${\phi }_m$ are the amplitude and initial phase of harmonics; n = 0, 1, 2, …, N − 1, and N is the number of sampling points.

By windowing the signal x (n) in the form of Equation (6) with a cosine window function, the discrete Fourier transform expression of the windowed signal can be obtained (only taking the positive frequency part for processing) as follows:

$$\stackrel{-}{X}\left(\left(k-1\right)\Delta f\right)=\frac{A_m}{2}{e}^{j{\phi }_m}W\left[\frac{2\pi \left(k-1\right)\Delta f-f_m}{N}\right]$$

(10)

In the equation, $\Delta f=\frac{f_s}{N}$ is the frequency resolution; $f_m=m{f}_0$; W(f) is the continuous spectrum of the window function.

In asynchronous sampling, the peak frequency f_m does not precisely align with the discrete spectral line frequencies. Let k₁ and k₂ be the spectral lines with the maximum amplitude and the sub-maximum amplitude near the target frequency. In the bispectral interpolation algorithm, k₁ < k_m < k₂ = k₁ + 1, and the amplitudes of these two spectral lines are $y_1=\left|\stackrel{-}{X}\left(\left(k_1-1\right)\Delta f\right)\right|$ and $y_2=\left|\stackrel{-}{X}\left(\left(k_2-1\right)\Delta f\right)\right|$. By introducing variables $\beta =\frac{y_2-y_1}{y_2+y_1}$ and $h=\left(k_m-k_1-0.5\right)\in \left(-\mathrm{0.5,0.5}\right)$, Equation (11) can be derived.

$$\beta =\frac{W\left[\frac{2\pi }{N}\left(0.5-h\right)\right]-W\left[\frac{2\pi }{N}\left(-0.5-h\right)\right]}{W\left[\frac{2\pi }{N}\left(0.5-h\right)\right]+W\left[\frac{2\pi }{N}\left(-0.5-h\right)\right]}$$

(11)

when N is relatively large, Equation (11) is typically simplified to $\beta =g\left(h\right)$. This equation can be solved through a curve-fitting method. Its inverse function is denoted as $h=g^{-1}\left(\beta \right)$. For a given window function, the calculation equation for magnitude is as follows:

$$A_m=\frac{2\left(y_1+y_2\right)}{\left|W\left(\frac{2\pi \left(-h+0.5\right)}{N}\right)\right|+\left|W\left(\frac{2\pi \left(-h-0.5\right)}{N}\right)\right|}$$

(12)

Through Equation (12), the magnitudes of various harmonic frequencies in Equation (9) can be calculated. The content of the m-th harmonic is A_m/A₁ and the total harmonic distortion is $THD=\sqrt{{\displaystyle \sum _{m=2}^{50}}{\left(\frac{A_m}{A_1}\right)}^2}$. Under DC bias, the saturated current in CT will exhibit positive and negative half-wave asymmetry. This is because the DC bias magnetic flux superimposes with the same-polarity AC magnetic flux, increasing the amplitude of the same-polarity AC current. In contrast, it demagnetizes the opposite-polarity AC magnetic flux, reducing the amplitude of the opposite-polarity AC current. To quantitatively analyze this degree of asymmetry, the waveform asymmetry coefficient $\sigma$ is introduced. The area S enclosed by every three sampled points in the positive and negative half-waves with respect to the time axis t is calculated using Simpson’s integration formula.

$$S={\int }_{t_n}^{t_{n+2}}{i}_2\left(t\right)dt=\frac{\Delta t}{3}\left[i_2\left(t_n\right)+4i_2\left(t_{n+1}\right)+i_2\left(t_{n+2}\right)\right]$$

(13)

In the equation $t_n=n\times \Delta t$.

In this paper, the sampling points are traversed, and the maximum area enclosed by each of the three sampling points and the time axis in positive half-wave and negative half-wave is calculated, respectively. The maximum area is defined as S₊ and S₋.

$$\sigma =\frac{S_{+}}{S_{-}}$$

(14)

Taking into consideration the above analysis, this paper comprehensively selects the secondary-side current total harmonic distortion, the contents of second to fifth harmonics, and the waveform asymmetry coefficient as indicators to assess the degree of CT saturation.

3.3.2. RFC Algorithm

Based on the international standard IEC-60044-1 [24], the saturation level of the 0.2S CT is divided into four categories based on the fundamental ratio difference ${\epsilon }^{Fun}$. The saturation conditions corresponding to each operating condition of the CT are shown in Table 4.

$${\epsilon }^{Fun}=\frac{K_n{I}_2^{Fun}-I_1^{Fun}}{I_1}\times 100\%$$

(15)

In this equation, $I_2^{Fun}$ and $I_1^{Fun}$ represent the magnitude of the fundamental effective value in the primary and secondary current waveforms, and K_n represents the turn ratio of the current transformer, while K_n = N₁/N₂.

In

Table 5. Classification of saturation degree.

Degree of Saturation	Serial Number	Sample Size	$\mathbf{Range} \mathbf{of} {\mathsf{\epsilon }}^{\mathit{F}\mathit{u}\mathit{n}}$ (%)
Mild	1	24,000	${\mathsf{\epsilon }}^{Fun}\le 0.2$
Moderate	2	9560	$0.2\le {\mathsf{\epsilon }}^{Fun}\le 0.5$
Severe	3	12,384	$0.5\le {\mathsf{\epsilon }}^{Fun}\le 1$
Profundity	4	12,376	$1\le {\mathsf{\epsilon }}^{Fun}$

, it can be observed that the saturation level classification data of the current transformer vary significantly under different operating conditions. Therefore, this study adopts the random forest classification algorithm, which has advantages such as high classification accuracy, strong resistance to overfitting, and less susceptibility to imbalanced data, to establish a predictive model for the saturation level classification of the current transformer under different operating conditions.

The RFC algorithm first uses the Bootstrap method to perform l iterations of sampling with replacement from the initial sample set M, forming equally sized sample subsets {M₁, M₂, …, M_l}. Then, random feature selection is performed, and the CART algorithm is used to build a decision tree model for each sample subset. Finally, the test data are used to evaluate the l decision trees, and the majority voting method is employed to select the final prediction from the obtained results.

$$T_{pre}\left(x\right)=\mathrm{argmax}\sum _{j=1}^{l}H\left(T_j\left(x\right)=i\right)$$

(16)

In the given equations, $T_{pre}\left(x\right)$ is the final classification result obtained from the random forest; $T_i\left(x\right)$ is the classification result obtained from a single decision tree; H(*) is the indicator function that takes the value of 1 when the output of the decision tree is equal to i and 0 otherwise; and arg max(*) is the statistical function that selects the class with the highest frequency among the outputs of the random forest for a given test sample.

3.4. Saturation Current Inverse Propagation Method Based on PSO-LSTM

To establish the mapping relationship between the distorted secondary current and the fundamental component of the primary current for each saturation level, LSTM models are built. LSTM is a type of recurrent neural network (RNN) that incorporates gated structures to enable the network to forget and delete certain information, making it well-suited for handling time series problems.

Although LSTM has the advantages of fewer iterations, a shorter computation time, and strong data mining capabilities, it still faces challenges in determining network results and selecting the optimal parameters. Therefore, this study adopts PSO to optimize the number of hidden neurons, learning rate, and training iterations in the LSTM model. This optimization process helps determine the optimal parameter combination. The specific steps are as follows (the algorithm flowchart is shown in Figure 8):

(1)

Initialize the parameters and velocities of the particle swarm and randomly generate the initial particle positions G_i = (num, lr, h), where num represents the maximum iteration count of the neural network, lr represents the learning rate of the network, and h represents the number of neurons in the hidden layer. Set the range of values for the three parameters as $num\in \left[\mathrm{100,200}\right]$, $lr\in \left[\mathrm{0.005,0.01}\right]$, and $h\in \left[\mathrm{90,150}\right]$;

(2)

Construct the LSTM network structure, including the input layer, hidden layer, dropout layer, fully connected layer, and regression layer. The number of neurons in the input layer and the fully connected layer is set to 1. The structure of the hidden layer is determined through PSO optimization to avoid overfitting. Set the dropout rate of the dropout layer to 0.2. The regression layer uses the mean squared error (MSE) as the loss function to predict the corresponding half mean square error;

(3)

Use the particles generated in step 1 as the initial parameters of the LSTM hidden layer. Calculate the mean squared error (MSE) between the actual values of the training set and the LSTM output as the fitness function of the particle swarm;

(4)

Compare the fitness value of each particle with its historical best position and the best positions of the particles in its neighborhood. Update the particle positions accordingly;

(5)

If the change in the fitness function resulting from the update of particle positions satisfies the stopping criteria, the optimal parameters for LSTM are considered found. Otherwise, return to step 4;

(6)

Input the parameters optimized through the particle swarm into the LSTM hidden layer and obtain the final model prediction results.

4. Simulation Example

A simulation circuit on the PSCAD/EMTDC simulation platform was built as shown in Figure 9. A DC power source was used to simulate the biased current, injecting it into the system from the grounded neutral point of the transformer. The AC power source had a frequency of 50 Hz and an impedance of (1.2 + 1.6j) $\mathsf{\Omega }$. To investigate the calibration performance of the proposed algorithm under harmonic conditions, a harmonic source was also added to the system. The CT parameters were set according to Table 3. The sampling frequency was f_s = 8 kHz, and the simulation time was 0.5 s.

Based on the CT primary and secondary current signals under different operating conditions, the proposed method was compared with RBF, SVM-SVR, SVM-RBF, and RFC-RBF algorithms in terms of root mean square error (RMSE), average fundamental ratio deviation (${\epsilon }_{ave}^{Fun}$), average fundamental phase angle deviation (${\delta }_{ave}^{Fun}$), and single-cycle average correction time ($t_{ave}$).

To eliminate the influences of different dimensions of the secondary current features on the accuracy of the model predictions and improve convergence speed, the feature variables were standardized using Equation (17) to linearly transform the data to the range of [0, 1].

$$x^{*}=\frac{x-x_{min}}{x_{max}-x_{min}}$$

(17)

In the equation, x* and x represent the values before and after standardization, respectively. x_min and x_max represent the minimum and maximum values of the respective feature samples.

The standardized dataset was divided into training (80%) and testing (20%) sets for model training and testing, respectively. After simulation testing, the RFC algorithm achieved the highest classification accuracy when the number of decision trees n_tree in RFC was set to 100, and the minimum sample count for each leaf node m_split in the classification trees was set to 5.

Accuracy was used to evaluate the classification effect of RFC and SVM. The confusion matrix of the test set classification results for the two algorithms was obtained, as shown in Figure 10.

In the diagram, it can be observed that (1) the classification performance of the RFC algorithm used in this study is significantly better than that of the SVM classification algorithm. The accuracy of the RFC classification algorithm is 91.25%, which is 13.15% higher than the SVM classification algorithm’s accuracy of 78.1%. (2) The RFC algorithm achieved a classification accuracy higher than 90% for each saturation level, outperforming the SVM algorithm in all subcategories. However, there were still cases wherein the saturation level labels were misclassified, particularly at the boundaries between different saturation levels, which makes it challenging for the algorithm to effectively differentiate them.

In Figure 11, the reconstruction performance of the proposed algorithm on current is illustrated under four different operating conditions.

For each saturation level, the PSO-LSTM models were trained, and their correction performances are presented in

Table 6. RFC-PSO-LSTM model’s correction effect on sample data.

Measurement Standard	The Proportion of the Number Reaching the Standard (%)
0.2S CT	91.25%
0.5S CT	96.85%
1.0S CT	97.95%

and

Table 7. Performance comparison between RFC-PSO-LSTM and other methods.

Serial Number	Model	RMSE	${\mathit{\epsilon }}_{\mathit{a}\mathit{v}\mathit{e}}^{\mathit{F}\mathit{u}\mathit{n}}$ (%)	${\mathit{\delta }}_{\mathit{a}\mathit{v}\mathit{e}}^{\mathit{F}\mathit{u}\mathit{n}}$$(\mathbf{\prime }$)	tave (ms)
1	RFC-PSO-LSTM	36.15	0.13	15	17
	SVM-SVR	42.02	0.19	23	34
	SVM-RBF	96.03	0.21	42	55.6
	RFC-RBF	47.55	0.15	27	45.1
	RBF	102.64	1.22	59	67.8
2	RFC-PSO-LSTM	35.72	0.15	13	12.6
	SVM-SVR	89.27	0.44	16	22
	SVM-RBF	102.35	0.51	27	18.6
	RFC-RBF	111.28	0.32	64	36.7
	RBF	152.36	0.98	77	97.6
3	RFC-PSO-LSTM	11.89	0.12	32	14.7
	SVM-SVR	35.62	0.62	26	19
	SVM-RBF	62.33	0.31	29	23.4
	RFC-RBF	88.25	0.33	31	44.7
	RBF	105.36	1.56	62	86.7
4	RFC-PSO-LSTM	42.32	0.17	24	9.8
	SVM-SVR	55.24	0.39	32	12.2
	SVM-RBF	41.33	0.44	40	18.7
	RFC-RBF	88.25	0.30	41	18.9
	RBF	102.55	1.26	45	62.7

. Due to space limitations, one set of the CT’s primary and secondary currents under a randomly selected operating condition, along with the correction results obtained using different methods, is shown in the tables.

Based on the data from Table 6 and Table 7, along with the information provided in Figure 12, it can be observed that the model was improved with the classification approach, exhibiting significant reductions in both the average correction time $t_{ave}$ and the root mean square error (RMSE) when compared to the single RBF model. This indicates that classifying the secondary currents based on saturation level and training separate models for each class can effectively reduce the training difficulty and improve the prediction performance.

Furthermore, the PSO-optimized LSTM model demonstrated strong data mining capabilities and outperformed the other algorithms in terms of reconstructing distorted CT currents. The RFC-PSO-LSTM model showed noticeable improvements in CT measurement errors across different operating conditions. Among the corrected training set samples, 91.25% met the measurement requirements of 0.2S CTs, and 96.85% met the measurement requirements of 0.5S CTs.

5. Conclusions

This paper proposed an RFC-LSTM-based method for reconstructing distorted CT currents under a DC bias, which effectively addresses the issue of increased measurement errors caused by CT saturation under DC biases. The research results demonstrate the following:

(1)

The wavelet transform based on Bior3.1 can effectively extract the saturation periods of a CT, and this method is not affected by the degree of CT saturation, making it highly applicable;

(2)

The PSO-LSTM model establishes an effective mapping relationship between the distorted currents on the secondary side and the fundamental currents on the primary side. The simulation results show that the reconstruction accuracy of distorted currents using the PSO-LSTM method is high, and it outperformed similar methods in terms of accuracy and computational time;

(3)

This method demonstrates good applicability. Under the interference of harmonic components, the CT saturation current caused by direct current bias in the line and the primary side overcurrent can both be accurately reconstructed by the method proposed in this paper;

(4)

The proposed method meets the measurement requirements of 0.2S CTs in 91.25% of the operating conditions and the measurement requirements of 0.5S CTs in 96.85% of the operating conditions.

The proposed method effectively addresses the reconstruction of distorted CT currents under a DC bias, thereby improving the measurement performance of CT. However, the algorithm proposed in this article needs to further optimize its calibration ability in noisy signals and harmonic signals above 1000 Hz, and hardware experiments must be conducted on relevant software.