1. Introduction
Traditionally, the main issue with thermal power plants has been how to increase their efficiency. However, the environmental problem has recently become a global issue. To meet the stringent environmental standards, thermal power plants have an increased need to reduce pollutants such as nitrogen oxides (NOx), sulfur oxides (SOx), carbon monoxide (CO), and fine dust [
1].
Environmental emissions, such as SOx, NOx, and fine dust, are usually reduced by installing abatement facilities in thermal power plants. Despite a lot of research on facility improvements, the reduction of environmental substances through these facilities has been reaching its limits in recent years [
2].
Combustion conditions in the power plant significantly influence the generation of environmental emissions. Some research studies have been reported to model the functional relationship between NOx and operational parameters using a harmony search algorithm [
3], a genetic algorithm [
4], and numerical analysis [
5].
The air to fuel ratio (AFR) in the combustion of thermal power plants directly influences pollutants and thermal efficiency. Low AFR increases CO due to the lack of combustion air, while high AFR increases NOx and heat loss due to excessive air [
6]. An ideal value of AFR varies depending on plant characteristics, operating conditions, and electric load. The ideal value of AFR is usually predetermined by offline tests based on combustion theory and used as the reference signal in online combustion control.
A similar philosophy of AFR control has been applied by most power plant manufacturers. The boiler master demand (BMD) signal is generated with the unit load demand and main steam pressure signal, and it generates the amount of air and fuel demand with the ideal AFR [
7]. This standard control structure has been in use for a long time in thermal power plants.
Nowadays, flexible operations of thermal power plants need to be provided to accommodate more renewable energy [
8]. This flexible operation increases the chance of a transient state in power plants. Although conventional combustion control systems show good performance, their AFR control performance tends to deteriorate, especially under transient conditions [
9].
However, it is hard to find advanced research to update the AFR control performance of standard thermal power plants. For AFR control of vehicle engines, there have been many studies with advanced control techniques, such as supervisory control [
10], feedback control with Kalman filter estimation [
11], generalized predictive control [
12], and fuzzy logic control [
13]. Fuzzy inference with multiple neural networks (NN) is also applied for the AFR control in the heating furnace of a steelmaking plant [
14].
The authors of this paper proposed a supplementary AFR control for thermal power plants [
15]. In that paper, we used dynamic matrix control (DMC) as a supplementary control on a conventional AFR control loop. Though it presented satisfactory simulation results, the formidable DMC online optimization algorithm in [
15] needs an additional computer server in the power plant control room. This additional equipment is a burden in implementation and maintenance in practical power plant operation.
This paper proposes a more practical approach for AFR control without using additional server, which can be implemented in the existing distributed control system (DCS) in the power plant. A one-step ahead control is applied as a supplementary control over the existing conventional combustion control logic for AFR control. The one-step ahead control is a very simple and fast discrete control, therefore it can be applied to a system with a short time constant. In [
16], the one-step ahead controller is used for inductor current control in hybrid electric vehicle applications, showing that it maintains inductor current at a more stable level than conventional PI controllers. The one-step ahead control with a fuzzy based least square estimator was proposed to control voltage and frequency in wind power systems [
17]. In the field of robotics, the one-step ahead control combined with model reference was proposed to control the motion of the humanoid robots, showing effective control with low computation and dependence on model accuracy [
18]. Recently, the one-step ahead control has been applied to coordinated control problems in thermal power plants, resulting in faster power generation output and main steam pressure control than seen in conventional control [
19]. From the view point of practical application, because it maintains the existing control structure, the one-step ahead supplementary control structure has advantages in terms of implementation and maintenance.
The online transfer function model is also applied to the one-step ahead control to improve the control performance in a wide range of operating conditions. These kinds of adaptive strategies have been reported to be efficient for nonlinear systems. An adaptive control combining back stepping control and fuzzy control was proposed to overcome the nonlinearity of permanent magnet synchronous motor, resulting in improved speed control performance even under perturbation [
20]. In addition, the study utilizing radial basis function neural networks and model reference adaptive control has shown high tracking performance in nonlinear systems with the presence of unknown external disturbances [
21]. In this paper, the transfer function for one-step ahead control is interpolated adaptively in real time based on several offline transfer functions.
The paper is organized as follows:
Section 2 describes the overall structure of the proposed adaptive one-step ahead supplementary control for AFR. In
Section 3, the proposed AFR control is applied to a 600 MW oil-fired drum-type power plant and to a 1000 MW ultra supercritical (USC) coal-fired once-through type power plant.
Section 4 presents the simulation results of the proposed AFR control for two different types of thermal power plants, demonstrating a supplementary AFR control in wide range operation with one-step ahead control has a simple structure than the DMC in previous research. Finally, conclusions are drawn in
Section 5 and future works are suggested.
2. System Description of Proposed Supplementary Control
In typical combustion control of a thermal power plant, the BMD signal is generated as a function of the power load demand, turbine speed, and main steam pressure. Then, the BMD signal generates the air flow demand and fuel flow demand, respectively, with an appropriate AFR, which is defined by the air flow mass divided by the fuel flow mass. A “cross limit algorithm” is applied to prevent combustion air starvation and boiler extinguishing, regardless of whether the load increases or decreases. Although conventional combustion control systems show good performance, their AFR control performance tends to deteriorate, especially under transient conditions [
9].
In [
15], DMC manipulates both air demand and fuel demand to improve the performance of conventional AFR control. In this paper, we tried to improve the performance of AFR control while minimizing the impact on the performance of existing combustion control systems. Therefore, in this study, the structure is set up to maintain an ideal AFR by adjusting the air flow demand only, without adjusting the fuel flow demand which can directly affect the thermal conditions of the boiler system.
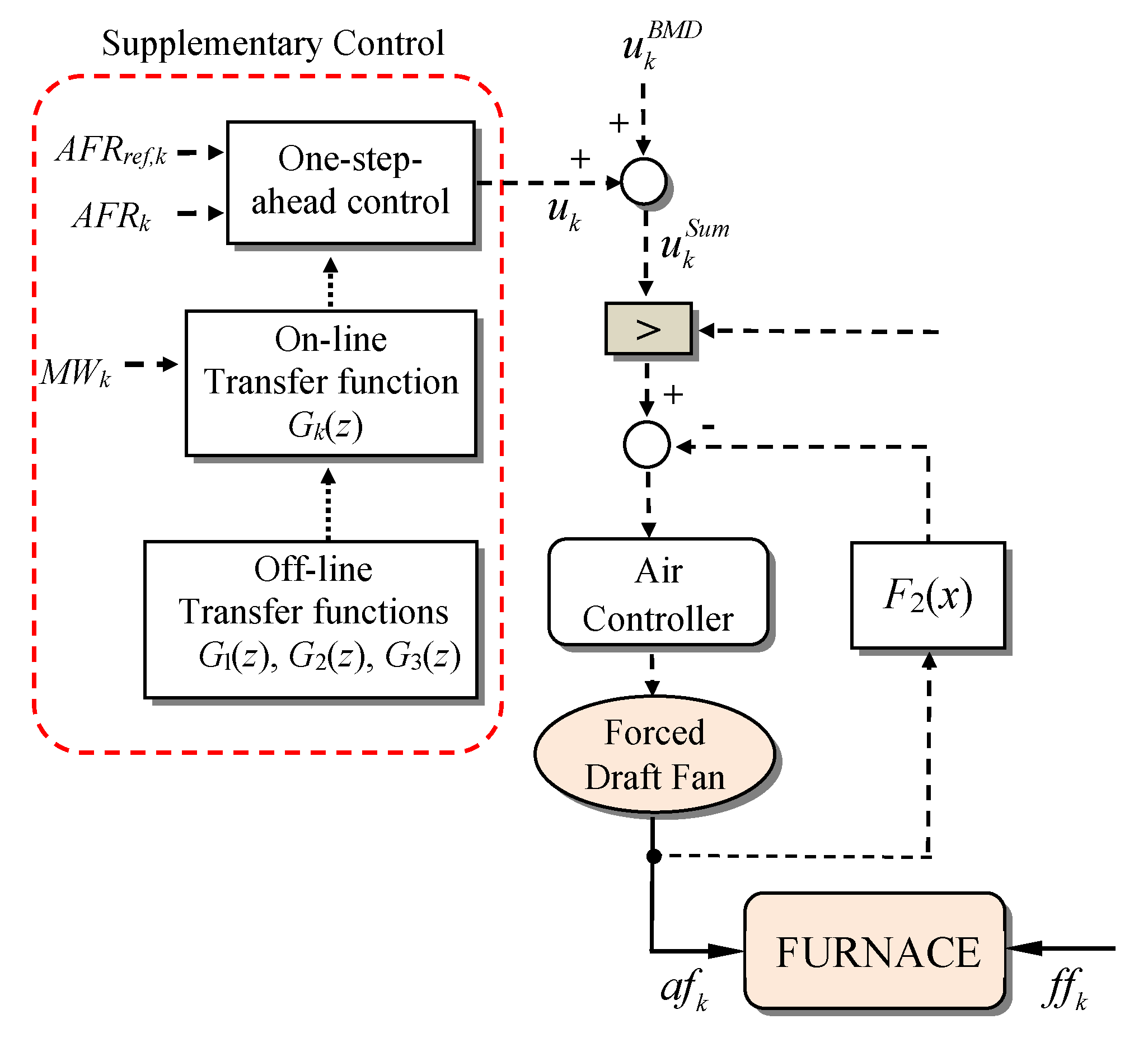
Figure 1 shows the detailed structure of the supplementary control using online interpolated transfer function, which is represented by a dotted red rectangle. In
Figure 1,
AFRref,k is the reference AFR at the
k-th discrete time step.
AFRk is the AFR at the
k-th discrete time step, the plant output or controlled variable (CV). The
MWk is the electric power at the
k-th step.
is the plant input or manipulated variable (MV) at the
k-th step, or the supplementary air flow demand.
For wide range operations at different operating points without loss of generality, three discrete transfer function models, denoted as G1(z), G2(z), and G3(z), are developed at low, medium, and high load, respectively. These models are independently developed offline using plant test data. To consider the operating condition of current load MWk at the k-th step, the transfer function Gk(z) is developed online using pole-zero-gain interpolation of G1(z), G2(z), and G3(z). The transfer function Gk(z) for the current load, the target reference AFRref,k, and the AFRk at the k-th step are used in one-step ahead control to generate the supplementary signal to the existing control structure.
The supplementary control
is added to the air flow demand from the BMD of the conventional multi-loop control as follows:
where
is the BMD control signal of the conventional control system,
is the adaptive one-step ahead supplementary control signal, and
is the sum of two signals.
This supplementary control structure is easy to implement and maintain. In emergency situations, plant operators can immediately remove supplementary control logic and return to the traditional multi-loop control system they are familiar with.
The output
AFRk is then defined as the ratio
where
is the air flow mass at the
k-th step, which is the forced draft fan output, and the fuel flow mass at the
k-th step is
, which is the output of the oil gun or air fan depending on the fuel type.
3. Methodology
The proposed AFR control structure is applied independently to two types of power plants: a 600 MW oil-fired drum-type power plant and a 1000 MW ultra supercritical (USC) coal-fired once-through type power plant.
3.1. AFR Control to 600 MW Oil-Fired Drum-Type Power Plant
3.1.1. Offline Transfer Function Models of 600 MW Plant
In this study, the nonlinear first principles model presented in [
22] is used as the 600 MW power plant model, which has been applied in various ways in several previous studies [
15,
23]. A virtual experiment with a 600 MW plant simulator was performed to get the plant test data. Without loss of generality, three operating points, 350 MW, 450 MW, and 550 MW, are selected as low, medium, and high load, respectively. Step increments of supplementary input
at t = 0 are applied independently from the steady state of low, medium, and high load. The 3% of the normal operation range for
is used as the amplitude of step input
.
Figure 2 shows the responses of the AFR resulting from the step increment tests. From the initial value of 15.35, the AFR is finally increased to 15.63, 15.57, and 15.54 for operating points of 350 MW, 450 MW, and 550 MW, respectively. Because the amount of supplementary air demand is manipulated in the test, these responses include not only the plant dynamics but also the dynamics of the existing conventional control logic.
In
Figure 2, three transient responses show a similar pattern, but the steady-state gain or DC gain is decreased with the increase in electric power. This is because the amount of combustion air and fuel is relatively larger in high load conditions. According to these characteristics, the AFR control problem in the power plant shows nonlinearity as a function of electric power output.
In the single input single output (SISO) discrete time model, output prediction equation is represented as follows [
24]:
The number of output and input history represents the number of poles and zeros of the system.
An identification process is a least square algorithm used to minimize a performance index that represents the error between the plant output data and the model output [
25]. Usually, many parameters in identification show small errors but increases complexity. In this study, the AFR dynamics of a 600 MW plant were identified with 5 poles with a sampling time of 5 s. Then, the prediction Equation (3) is as follows:
The z-transform of (4) is represented with a discrete transform as follows:
where
pj is the
j-th pole of transfer function.
The identification of each response in
Figure 2 is performed independently, and the results are listed in
Table 1 and
Table 2. In the tables,
G1(
z),
G2(
z), and
G3(
z) represent the AFR models at low, medium, and high load in
Figure 2, respectively. The DC gain in
Table 2 was obtained from
Table 1 using the discrete-time final-value theorem.
Figure 3 shows the location of the poles of each model in
Table 2.
Figure 4 shows the comparison of plant output and model output, where the solid line shows the output data, and the dotted line represents the model output. It shows each model captures the major dynamics of plant AFR reasonably.
3.1.2. One-Step Ahead Control with Online Transfer Function for 600 MW Plant
To overcome the nonlinearity of AFR dynamics as a function of the operating point, a suitable model
Gk(
z) at the
k-th step is developed in real time based on the three offline models
G1(
z),
G2(
z), and
G3(
z) in
Table 2.
In case the electric output at the
k-th step,
MWk, is less than 350 MW,
G1(
z) is used as
Gk(
z), while
Gk(
z) is
G3(
z) for larger
MWk than 550 MW. In case
MWk is between 350 MW and 450 MW, the poles and gain of
Gk(
z) are interpolated with those of
G1(
z) and
G2(
z) as follows:
where
is the
j-th pole of
G1(
z),
is the
j-th pole of
G2(
z),
and
are the DC gain of
G1(
z) and
G2(
z), respectively.
In the case where
MWk is between 450 MW and 550 MW, the poles and gain of
Gk(
z) are interpolated with those of
G2(
z) and
G3(
z) as follows:
where
is the
j-th pole of
G3(
z) and
is the DC gain of
G3(
z). This interpolation is performed online at every sampling step with
MWk. Therefore,
Gk(
z) can effectively handle the nonlinearity of AFR dynamics over wide range operations.
To illustrate this interpolation, the
MWk at the
k-step is assumed to be 475 MW. Then,
Gk(
z) interpolated with (9) and (10) is shown in
Table 3. The step response of
Gk(
z) is compared with those of
G2(
z) and
G3(
z) in
Figure 5, where the response of
Gk(
z) is closer to that of
G2(
z) because the present electric output
MWk is near the operating point of
G2(
z).
A simple one-step ahead control is applied with interpolated
Gk(
z) at every sampling step. One-step ahead control is to minimize the control performance of one discrete step,
where
Q is the weight of AFR error,
R is the weight of input adjustment, and
. A large
Q makes the AFR error more significant in performance; moreover, it tends to increase input variation. Contrarily, a large
R decreases the input variation and increases the AFR error. Therefore, there is a trade-off between the two conflicting objectives.
To find the optimal input
, the derivative of Equation (11) using (4) needs to be zero as follows:
Arranging (15) and (16) with
gives,
One-step ahead control is a kind of optimal control that minimizes a certain control performance. However, optimal control is usually designed based on a fixed plant model. In this paper, the plant model is updated online to consider the change of the operating point. Because the proposed control with (7)–(10) and (17) is very simple, it can be directly implemented into the currently operating DCS system without any additional computer server.
3.2. AFR Control to 1000 MW USC Once-Through Power Plant
As a second case study, the same control architecture for a 600 MW plant is applied to a 1000 MW USC coal-fired once-through type plant. Because the once-through boiler does not have a drum, its dynamics are faster than those of the drum-type boiler. In addition, this 1000 MW plant uses coal as fuel, whereas the 600 MW plant uses oil.
For the simulation of 1000 MW plant, the dynamic boiler simulation model (DBSM) of the 1000 MW USC model is used in this paper. This simulator was developed based on the first principle with mass, momentum, and energy balances. It is an industry-proven simulator by DOOSAN company for practical control logic design [
15].
For the 1000 MW plant, the supplementary control is applied to the air controller to drive the secondary air fan. In this coal-fired plant, air flow mass afk in (2) is the sum of the two air flows, secondary air fan and primary air fan, which supplies pulverized coal into the burner.
For three operating points for a 1000 MW plant, without loss of generality, 550 MW, 750 MW, and 950 MW are selected as low, medium, and high load, respectively. While the ideal AFR is a constant in the 600 MW plant, that of DBSM is changed as a function of the load by the internal logic of the DBSM. For example, the setpoints of AFR are 11.5, 11.1, and 11.18 for 550 MW, 750 MW, and 950 MW, respectively.
Figure 6 shows the virtual experiment of DBSM at 550 MW, 750 MW, and 950 MW independently, where the 4% of the respective nominal input is applied as the step input
. Compared with
Figure 2, due to the characteristics of the once-through type, the overall response of 1000 MW is relatively simple and fast. Also, there is a dead time of about 2 s between supplementary
and AFR response. The existing multi-loop control logic is also included in these transient responses.
Compared to
Figure 2, because the once-through boiler does not have a drum, the responses are faster and simpler than those of drum-type boiler. Therefore, the number of poles and sampling time are reduced than (4). The AFR dynamics of a 1000 MW plant are identified with 3 poles and two dead steps, and the sampling time is selected as 1 s. Then the prediction equation and transfer function are as follows:
where
and
are given in two dead step systems. Then, the
z-transform of (18) is represented as
The results of the least square identification are listed in
Table 4 and
Table 5. For adaptability, the online transfer function
Gk(
z) with a
k-th step power output
MWk is also calculated in the same way as that of a 600 MW plant. In case the electric power output at the
k-th step,
MWk, is less than 550 MW,
G1(
z) is used as
Gk(
z), whereas
Gk(
z) is
G3(
z) for
MWk larger than 950 MW. In case
MWk is between 550 MW and 750 MW, the poles and gain of
Gk(
z) are interpolated with those of
G1(
z) and
G2(
z). When
MWk is between 750 MW and 950 MW,
Gk(
z) is interpolated with
G2(
z) and
G3(
z).
A one-step ahead control is also applied with interpolated
Gk(
z) at every sampling step. Control performance with a two dead step system is as follows:
The derivative of Equation (20) using (18) is as follows:
Then,
is as follows:
where,
and
are given in two dead step system.
4. Results and Discussion
The performance evaluation of the proposed one-step ahead supplementary controller is simulated with MATLAB in a personal computer environment for both 600 MW oil-fired drum-type power plant and DBSM, which is a 1000 MW ultra supercritical (USC) coal-fired once-through type power plant. Both simulators were developed and verified using real power plant data and have been applied many times in the existing literature on power plant topic [
15,
23].
The major disturbances of power plant control are nonlinear plant dynamics, highly coupled dynamics among various control loops, electric power load, model mismatch of heat transfer, and exchange coefficients [
26]. The two plant models include severe nonlinear plant dynamics and highly coupled dynamics among various control loops as disturbances. The variation of electric power load is considered as a measured disturbance in the simulation.
The simulation scenario considers two large step changes in the electric power load variations for the wide range operations of power plants. The performance of the conventional multi-loop is compared with that of the proposed adaptive one-step ahead control. For comparison purposes, one-step ahead controls with fixed transfer function models G1(z), G2(z), and G3(z) are also independently simulated for both power plants.
4.1. Simulation Results of 600 MW Drum-Type Thermal Power Plant
The simulation test scenario for a 600 MW plant is presented in
Figure 7. In
Figure 7, the load variation scenario is simulated by reducing the power from 400 MW to 290 MW and then increasing it to 570 MW for wide range operations. The increase/decrease of the load in the simulation is limited to 15 MW/min, which is less than 7% of the total load per minute, referring to the ramping rate of the steam plant [
27]. In this simulation, the ideal AFR of the 600 MW plant model is assumed to be constant, i.e., 15.35 at every electric power load. The design parameters in Equation (11) for four one-step ahead controllers are set as Q = 1 and R = 5 by trial and error.
Figure 8 and
Figure 9 show the AFR responses of the multi-loop control, one-step ahead control with proposed adaptive control, and one-step ahead control with fixed transfer function models
G1(
z),
G2(
z), and
G3(
z), respectively. In these figures, the response of the multi-loop control is indicated by the black line, that of the proposed adaptive control by the red line, while the responses with fixed
G1(
z),
G2(
z), and
G3(
z), by the green, blue, and yellow lines.
In
Figure 8, the responses of the proposed adaptive one-step ahead control show a small error in both first and second step changes compared to that of the existing multi-loop control. Therefore, the AFR control performance was updated by the proposed supplementary control effectively. On the other hand, the response with fixed
G3(
z) shows large oscillations during the first step change, similar to that of adaptive control after 2000s. As
G3(
z) was developed at high load conditions, it is unsuited for low load conditions.
Figure 9 shows the comparison of one-step ahead controls with fixed
G1(
z) and
G2(
z), respectively. The response with fixed
G2(
z) shows large oscillations at the first step change, while it shows a similar response to that of adaptive control at the second step. The response with fixed
G1(
z) is similar to that of the adaptive control during the first step change. However, it shows a relatively larger error at the second step change than that of adaptive control.
The quantitative comparison in terms of the sum of squared errors in
Figure 8 and
Figure 9 is represented in
Table 6. The proposed adaptive control reduced the error sum to 31.84% of existing multi-loop control. Therefore, the AFR control performance of existing multi-loop control can be effectively updated by supplementary control with the proposed adaptive control strategy.
Figure 10 shows the variation of supplementary control of adaptive one-step ahead control. At the beginning of the first step change, from 0 s to 400 s, because the conventional control supplies excessive combustion air in
Figure 8, the supplementary control is negative to reduce the amount of combustion air in
Figure 10. On the other hand, the supplementary control is positive during the second step change, from 1500 s to 2300 s, in order to increase the amount of combustion air of the existing multi-loop control in
Figure 8.
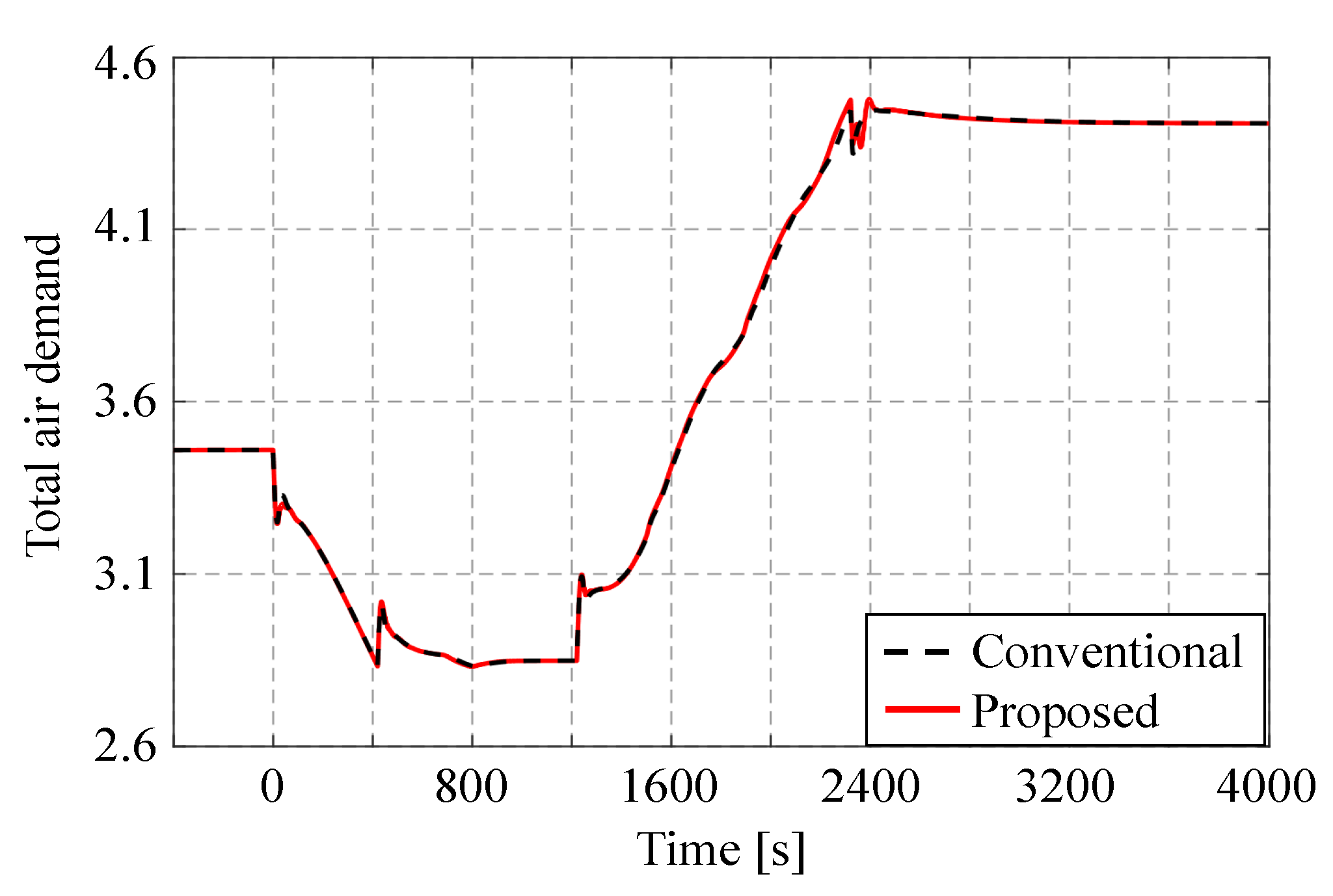
Figure 11,
Figure 12 and
Figure 13 show the comparison of total air demand, fuel demand, and main steam pressure of conventional multi-loop control and that of proposed adaptive control, respectively. Because the amplitude of supplementary control is not so large, total air demands look similar in
Figure 11. Accordingly, main steam pressure, one of the most important variables in power plant operation, is also similar. From
Figure 11,
Figure 12 and
Figure 13, without affecting the existing power plant operation, the proposed adaptive supplementary control can effectively update the AFR control performance.
4.2. Simulation Results of 1000 MW Once-Through Type Thermal Power Plant
A 1000 MW once-through type plant was also simulated in MATLAB and linked with the DBSM simulator in a personal computer.
Figure 14 shows the simulation scenario where the load demand is changed from 650–750 MW at 0 s and changed to 900 MW at 1800 s. In
Figure 14, the load demand change is restricted by the internal logic of the DBSM at each sampling time. In this simulation, the ideal AFR specified by the internal logic of the DBSM is used as the
AFRref for the supplementary control. The design parameters in (20) for four one-step ahead controllers are set as Q = 1500 and R = 10 by trial and error.
Figure 15 shows the AFR responses of the multi-loop control, one-step ahead control with proposed adaptive control, and one-step ahead control with fixed transfer function models
G1(
z),
G2(
z), and
G3(
z), respectively. In the figure, the ideal AFR of DBSM is indicated by a black dotted line, the response of the multi-loop control by the black line, the response of the proposed adaptive control by the red line, and the responses with fixed
G1(
z),
G2(
z), and
G3(
z) by the green, blue, and yellow lines.
In
Figure 15, during the first step change, the response of conventional multi-loop control shows overshoot from 0 s to 200 s, undershoot from 200 s to 400 s and overshoot from 400 s to 800 s, sequentially. And it shows two overshoots and undershoots from the beginning of the second step change. In this simulation, four supplement controllers successfully reduced the AFR error of conventional multi-loop control in a transient state. The response with
G3(
z) among the fixed three transfer functions shows a relatively better performance. The response of the proposed adaptive control shows the smallest error in
Figure 15.
The quantitative comparison in terms of the sum of squared errors in
Figure 15 is represented in
Table 7. The proposed adaptive control showed the best performance and reduced the error sum to 28.59% of the existing multi-loop control in
Table 7. Therefore, the proposed adaptive supplementary control successfully updated the AFR control performance of the existing multi-loop control in the case of a 1000 MW once-through power plant.
Figure 16 shows the variation of supplementary control of adaptive one-step ahead control in a 1000 MW plant simulation. During two overshoots of the first step-change in conventional control, at first 200 s and from 400 s to 800 s, it is negative to reduce the excessive air in
Figure 15. It is positive from 200 s to 400 s during the undershoot of conventional control to increase the combustion air.
To confirm the effect on the overall power plant control,
Figure 17 and
Figure 18 show the comparison of total air demand and main steam pressure for conventional multi-loop control and that of proposed adaptive control, respectively. In both figures, the two responses look similar. Therefore, the overall control of the 1000 MW power plant is not affected by the proposed adaptive control.
5. Conclusions
A supplementary control for tighter control of the AFR was proposed to reduce the environmental emissions of thermal power plants. The amount of combustion air demand of conventional multi-loop control is manipulated using a simple one-step ahead control. For a wide range of operations, three transfer functions at low, medium, and high load conditions have been developed offline. Subsequently, the transfer function for the one-step ahead control is adaptively interpolated in real time based on three offline transfer functions.
Two different types of thermal power plants were considered in the simulations, a 600 MW drum-type oil-fired plant and a 1000 MW once-through type coal-fired plant, and the squared error sum of AFR was reduced to 31.84% and 28.59%, respectively, than that of conventional multi-loop control. The proposed one-step ahead control, without affecting existing combustion control, effectively improved the AFR control performance in wide rage operation.
Compared to the previous work using DMC, the proposed research achieved the following two major contributions:
First, because previous research requires a large amount of real time optimization at every sampling step, an additional computer server is needed for actual implementation. On the other hand, the proposed one-step ahead control is very simple and does not require real time optimization. Therefore, it can be directly implemented into the currently operating DCS of power plants, which reduce costs in implementation and maintenance.
Second, the proposed control structure manipulates the air demand only to control AFR, while previous research manipulated both air demand and fuel demand simultaneously. Because the fuel demand is not manipulated in this paper, the control structure is simpler, and it is expected that the possibility of affecting the existing combustion system will be reduced in real-life application.
It is well known that low AFR increases CO due to the lack of combustion air, while high AFR increases NOx and heat loss due to excessive air. However, emissions depend on a variety of variables for each power plant, and reliable modeling is still a work in progress. Therefore, the measurement of emissions to assess proposed control can be further research work.