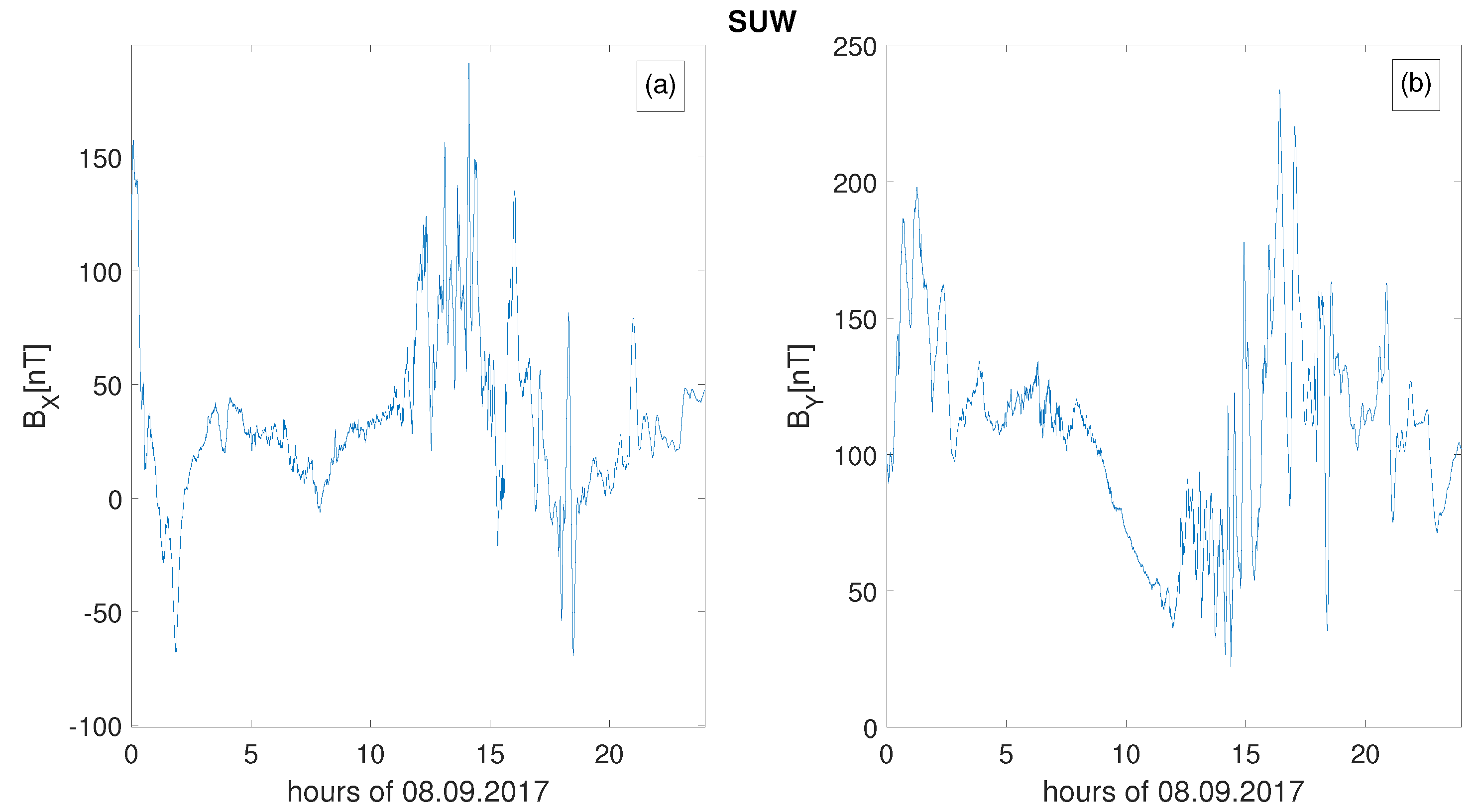Abstract
The Quebec blackout on 13 March 1989, has made geomagnetically induced current (GIC) research a socially important field of study. It is widely recognized that the effects of space weather, which may affect the power infrastructure, threaten countries located at high latitudes. However, in recent years, various studies have shown that countries at lower latitudes may also be at risk. One of the best proxies of GIC variability is the local geoelectric field, as measured in Eskdalemuir, Lerwick, and Hartland, by the British Geological Survey or modeled using, e.g., a 1D layered Earth conductivity model. In our article, we present a review of the issues related to the impact of the GIC on transformers and transmission lines in Central and Southern European countries, from Greece, Spain, and Italy to Slovakia, the Czech Republic, Austria, and Poland. The review underlines the importance of the systematic collection of information about power grid failures and the need for further systematic studies of the GIC’s impact on the operation of power grids in mid-latitude countries.
1. Introduction
Space weather influences many processes through phenomena occurring in near-Earth space. Impacts originating from solar activity can affect astronauts [1,2], the functioning of space probes [3,4], the crews of aircraft [5,6], communication systems [7], ground-based energy systems [8], or even the climate [9], as well as human beings with cardiac diseases [10,11]. This study raises awareness of the importance of solar–terrestrial connections not only from the point of view of increasing our knowledge, but also from the pragmatic point of view [12,13].
Changes occurring on the Sun, observed systematically almost from the Sixteenth Century, affect the Earth to various degrees. Short-term solar variability can lead to powerful magnetic storms, affecting the stable operation of ground-based electronic systems, as well as electrical systems, including transmission line grids, via geomagnetically induced currents (GICs) [14,15,16]. GICs are low-frequency currents induced in conductive systems, like pipelines or power lines, originating from space weather events, (e.g., [17]). These currents, reliant on solar wind conditions and geoelectrical conductance, have been broadly analyzed for many years (e.g., see [17,18,19] and the references therein). The fundamentals of GIC analysis are constructed based on numerous physical characteristics: the parameters of the solar wind, magnetospheric drivers, electrojet indices, and various systematically developed mathematical models. It has to be underlined that several drivers of GIC have been designated [20,21]. Among the drivers of intense GIC episodes are often mentioned huge impulsive events, such as coronal mass ejections (CMEs), solar flares, etc. (e.g., [22,23,24]). Variations differing from the regular geomagnetic field fluctuations, or geomagnetic pulses, have also been recognized as probable GIC drivers [25]. Strong geomagnetically induced currents appearing at low- and mid-latitudes have been related to sudden storm commencement (SSC) and sudden impulses, rather than substorms (e.g., [26]).
At the end of the first half of the Nineteenth Century, it was noticed that, in telegraph equipment, the galvanic batteries were not working. Spontaneous currents were observed in the telegraph cables, occasionally causing large deviations in the directions of the needles [27] (an early review can be found in [28]). More than a hundred years later, for quasi-DC currents emerging during the geomagnetic storms in power systems, the term “solar-induced currents” was used [29].
Geomagnetic storms can also cause satellite damage and interfere with the internal electronics or GPS [30]. These effects are amplified during the maxima of solar activity [31,32,33,34]. Since the Quebec blackout on 13 March 1989, space weather’s impact on transmission lines has become an important issue for our society [35]. Initially, scientists paid particular attention to the Scandinavian countries (e.g., [14,36]). However, several studies have shown that this is not only the case for just most high-latitude countries (e.g., [37,38]). It has to be mentioned that the only blackout that appeared in Europe as an effect of space weather events was the Malmö blackout during the so-called Halloween Storm [39].
In this paper, we present the current stage of the research performed by the European countries to judge the potential influence of GICs on the reliability of the power transmission infrastructure.
The paper is constructed as follows: After the Introduction (Section 1), a brief overview of existing methodologies used to study GICs is presented, in particular indicating the GICs’ proxies (Section 2.1), mentioning the methods of the computation of the geoelectric field induced at the Earth’s surface (Section 2.2), and underlining the problem of GIC modeling (Section 2.3). Section 3 presents the efforts made in seven European countries (Greece, Spain, Italy, Slovakia, the Czech Republic, Austria, and Poland) to estimate the local GICs’ impact on the national power grids.
In Greece, the analysis of transmission line failures during stormy days in the period 1989–2010 was performed. For such a dataset, various statistical techniques were applied. For example, regression and correlation analysis showed that the sunspot number curve was smoother and complied better with the number of transformer failures rather than the K-index curve [40]. In Spain, two new geomagnetic indices were proposed as a proxy for GIC risks: the Local Disturbance index (LDi) and the Local Current index (LCi). Both indices are used by the Spanish Space Weather Service and the European Space Agency on the Space Weather Portal [41]. In Italy, the GIC proxy estimated for over more than 20 years of observations Tozzi et al. [42] showed that, during periods of high magnetic activity, potentially damaging GICs could flow through the power network. Studies of the relationship between space weather events and recorded failures in the Italian transmission grid Berrilli et al. [43] reported that 15% of such malfunctions were observed to coincide with significant geomagnetic disturbances. In the Czech Republic, besides GIC modeling Hejda and Bochníček [44], the anomalies in their electric power grid were analyzed for about 12 years Vybostokova and Svanda [45]. It was noted that the rise in the anomaly rate was more significant after local geomagnetic activity maxima than before them. In a detailed analysis, Svanda et al. [46] showed that substorm-related disturbances and magnetic storms significantly impacted the power grid network. A similar analysis was performed in the adjacent country of Slovakia. In the years 2009–2019, Vybostkova and Svanda [47] examined the relative increase in anomalies in the entire Slovak power transmission grid during the increased geomagnetic activity period. The number of anomalies in the power grid that occurred was significantly dependent on the temperature, which correlated with the K-index due to the semi-annual variations of the geomagnetic field. In Austria, the research concerning GICs started in 2014 with the initiative of the Austrian Power Grid AG. Since then, much work has been performed to measure GICs by the network of DC measurement devices installed in high-voltage power transmission networks Halbedl et al. [48]. The calculated GIC at the transformer’s neutral point was compared with the measurements, revealing a good correlation between the simulated and measured currents. The results of the research in [49] showed that the Austrian power grid is susceptible to large GICs in the tens of amperes, particularly from strong geomagnetic variations in the east–west direction. Studies of the situation in Poland were based on several machine learning methods, such as principal component analysis, neural networks, and hierarchical agglomerative clustering. The authors showed that the solar wind parameters have the most-substantial connections with all the considered types of electric grid failures [50]. Section 4 contains the summary of the presented study. It can be seen that most of the work performed in the mentioned European countries has been completed in the last few years. Unfortunately, many countries have limited access to data on power grid failures. This makes it difficult to reliably assess the impact of GICs on the operation of power grids. From this point of view, much more research should be conducted in the future. Conclusions regarding the current and future work related to the analysis of space weather’s impact on European countries’ energy infrastructure are presented in Section 5.
2. Methodology
GICs are defined as intense, low-frequency (0.0001 Hz–0.1 Hz) quasi-DC currents flowing in ground conductor systems, oil and gas pipelines, communication systems, transmission lines, etc., as a result of rapid geomagnetic field changes (e.g., [51]). In accordance with Faraday’s law of induction, the geomagnetic field fluctuates and induces geoelectric fields that drive GICs in the ground and electrical power systems [17]. In the case of power networks, GICs flow from the transmission lines to the ground via a neutral ground connection of transformers [35]. The GIC is added to the AC exciting current of the transformers, leading, in general, to the rise in reactive power demand, harmonic generation, as well as heating in the transformer. Other subsequent effects mentioned in literature are the maloperation of protective relays, voltage fluctuations, stability issues, and in the very worst-case scenario, the transformer’s damage (e.g., [52]).
One can see that GICs are a vital topic, but also a complex phenomenon related to multiple variables, and to consider them, several data analysis methodologies have been developed (e.g., see [17,19,53] and the references therein).
2.1. Proxies of the Geomagnetically Induced Current Intensity
Most GIC analysis methods focus on geomagnetic field measurement proxies of the geoelectric field and, consequently, the GIC intensity. These proxies are based on geomagnetic data B collected at ground magnetic observatories that are part of extensive international networks: International Monitor for Auroral Geomagnetic Effects (IMAGE) [54,55,56], SuperMAG [57,58], or International Real-time Magnetic Observatory Network (INTERMAGNET) [59]. The geomagnetic field is measured by stations located at a wide range of latitudes (also at mid-latitudes of European countries) with 1 s, 10 s, or 1 min resolution. It is worth mentioning that the spatial distribution of stations is non-uniform and sparse for mid-latitudes, which, next to the time resolution of the measurements, has a direct influence on the possibility of application of some methods (e.g., [60]).
The first, robust approach applied in GIC analysis states the application of various geomagnetic indices, e.g., the K-index, a-index, -index, -index, or SYM-H-index, described and systematically considered in several works (e.g., [46]). In brief, these quantities describe the geomagnetic activity (changes in the Earth’s magnetic field), which is associated with changes in the system of currents of the magnetosphere and ionosphere (e.g., [61] and the references therein). In particular, the storm-time Dst-index or SYM-H-index are low-latitude indicators influenced by ring current variations that drive the GIC there. In contrast, the cumulative mid-latitude index measures auroral and ring current variations [46]. Various studies have confirmed that the geomagnetic indices identifying intense magnetic storms could be treated as indicators of possible GIC exposure (e.g., [46]). The level of change of geomagnetic field variations is treated as the crucial cause of GICs in power grids. Thus, the time derivative of the magnetic field, , its evolution, and statistics have been directly considered in many studies [62,63,64]. Researchers have focused on the horizontal component of the local magnetic field (e.g., [65,66]), where H is calculated using the North Magnetic Field component X () and the east component Y (), i.e.,
It was shown in [67] that GICs are caused by strong variations over typical time scales of 10–1000 s. The significance of the regional variability of geomagnetic disturbances has also been frequently emphasized (e.g., [68,69]). Several works have proposed to estimate GICs at low latitudes by using , which states a measure of the 1-min due to ring current variations, (e.g., [46,67]).
GIC intensity has also been depicted by the GIC index proposed by Marshall et al. [70] and defined as follows:
where is a filter function, f denotes frequency, stands for the Nyquist frequency, is the inverse Fourier transform, while indicates the absolute value. The usefulness of the GIC index has been confirmed by numerous studies [42,71]. This literature review confirms that new geomagnetic indices are still being proposed and used in the context of GIC analysis. Two new geomagnetic indices introduced in [41] are the Local Disturbance index (LDi) and the Local Current index. To determine the LDi, quiet period variations from the horizontal component of the local magnetic field measured by the magnetometer are removed. The LCi index is accepted as the 1 min LDi change rate.
2.2. E-Field Estimation
A more-advanced methodology used to investigate GICs is the approximation of the geoelectric field induced at the Earth’s surface. It is worth underlining that, besides the level and frequency content of the B-field disturbance, the geoelectric field is directly dependent on the location. This is caused by the interaction of the quickly changing geomagnetic field with the conductivity of deep Earth structures. Taking these aspects into account, several approaches have been developed to compute the geoelectric field from the variations of the geomagnetic field, both in the time and frequency domain (e.g., [19]).
One of the basic assumptions is to consider the perturbed B-field to be a vertically incident plane wave at Earth’s surface (plane wave method) and apply simplified models for Earth’s resistivity/conductivity [72,73]. Earth’s conductivity varies in all directions. However, a common assumption is that the most-significant conductivity variation is with the depth [73]. A half-space often replaces the Earth with a flat surface, which is an acceptable approximation since GICs are a regional phenomenon. A uniform ground resistivity model means the Earth’s structure is regionally homogeneous with a constant conductivity . Earth can also be represented by a 1D layered model (e.g., [73]), in the frame of which a group of layers is specified, each defined by its own conductivity and thickness. It is worth mentioning that a set of 1D Earth resistivity models (EURHOM 1D) dedicated to the European region has been proposed and described in detail by Adam et al. [74]. Studies have confirmed that the 1D model can be treated as a valid first-order approximation for modeling the gross resistivity structure and its effect on surface electric fields [34,75]. Multiple studies have underlined, however, that Earth’s internal structure has a complex 3D distribution of electrical resistivity, and taking this fact into consideration, higher-order models are needed (e.g., [19]) and the references therein.
The choice and application of a given Earth resistivity model influence the transfer function K between the B- and E-fields. In the primary step of the E-field estimation, the geomagnetic field is decomposed into its frequency components . Then, they are multiplied by the corresponding transfer function values, that is and , where and stand for the geoelectric field frequency components. In the final step, the inverse Fourier transform is employed to determine the geoelectric field value in the time domain for the northward and eastward components [73,76].
2.3. GIC Modeling
Viljanen and Pirjola Viljanen and Pirjola [77] divided the GIC modeling into two stages. The E-field is estimated in the first, geophysical part (see Section 2.2). In the second engineering part, the E-field is used as an input, the network characteristics are taken into account, and the resulting GICs are estimated.
The Lehtinen–Pirjola method [78] states a base approach in network modeling crucial in the engineering part of GIC modeling. This method assumes a resistive network and known system parameters. Based on the input of the E-field, Kirchoff’s law is applied, and the resulting currents at nodes are calculated. It is worth underlining that, depending on the goal of GIC studies, the power line geometry is only used or complete information about the grounding resistances, as well as transformer characteristics is required. Most studies apply a simplified model of the power grid to determine GICs at the substation level, making at the same time multiple approximations of the details of the power grid system parameters, which are rarely precisely known [19].
In the case of a uniform electric field, GICs are often computed employing the formula:
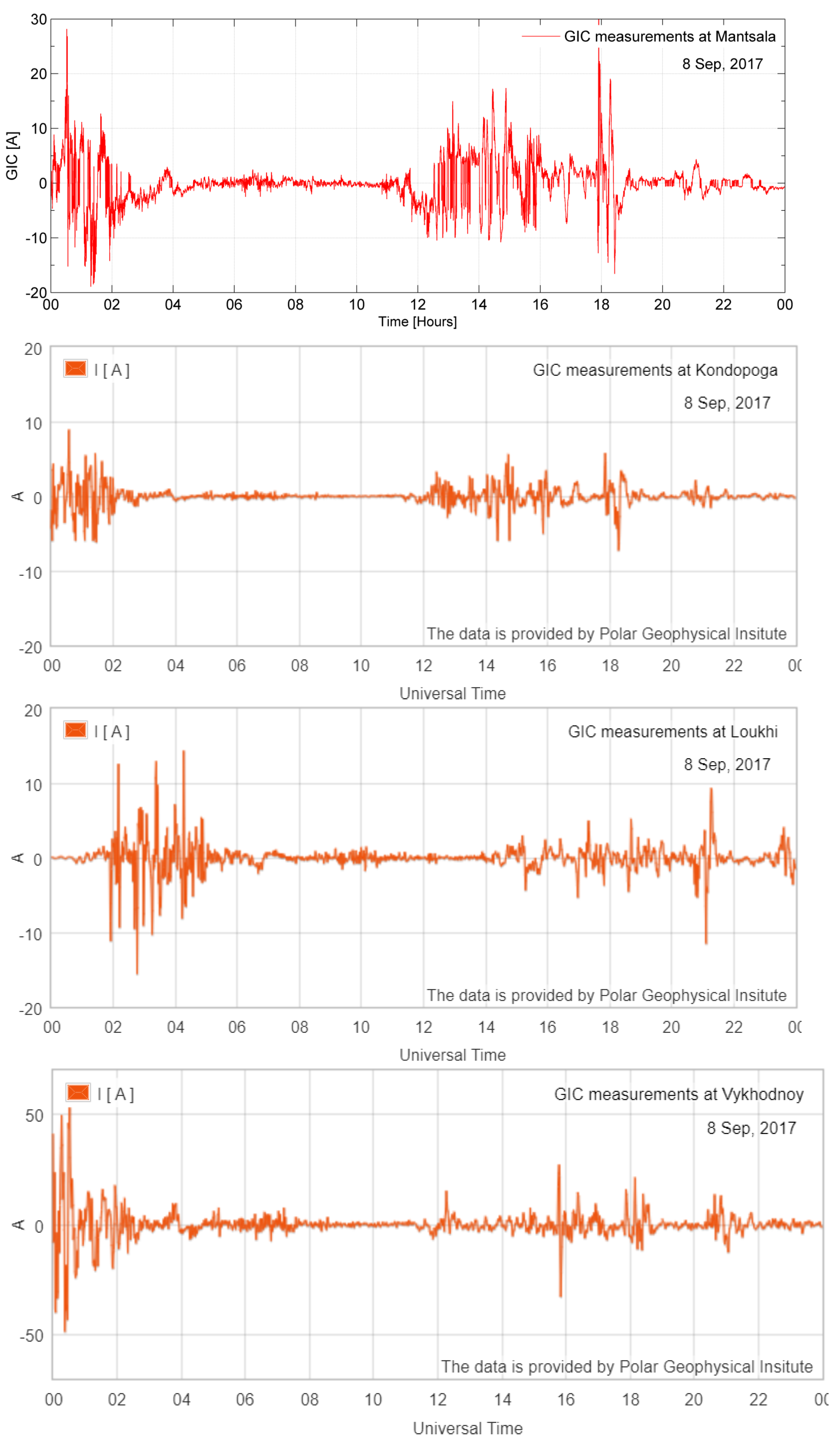
where and are the local geoelectric field’s north–south and east–west components. Coefficients a and b are dependent on the power grid parameters, such as the resistance or the network topology [79]. The details of the simulations enabling the consideration of the individual transformer core saturation process caused by a geomagnetic storm can be found in Ni et al. [80]. As described above, GIC modeling can be validated and compared with direct GIC measurements made along electric power grids and oil and gas pipelines. The most-popular ones are the GIC recordings in the Finnish natural gas pipeline near Mäntsälä presented in the upper panel of Figure 1, during the famous September 2017 geomagnetic storm (e.g., [60]). It is located at subauroral latitudes (57.9 N geomagnetic latitude; 60.6 N geographic latitude, 25.2 E geographic longitude) [60,81]. The other stations that are presented in the next three panels of Figure 1 are Kondopoga, at 58.21 N geomagnetic latitude and 62.22 N geographic latitude, 34.16 E geographic longitude, Loukhi, at 62.31 N geomag. lat. and 66.40 N geogr. lat., and Vykhodnoj, at 65.0 N geomagnetic latitude and 68.83 N geographic latitude, 33.08 E geographic longitude [82]. In the mid-latitude European countries discussed in this review, continuous GIC measurements have not been performed, which is underlined in the further part of this review.
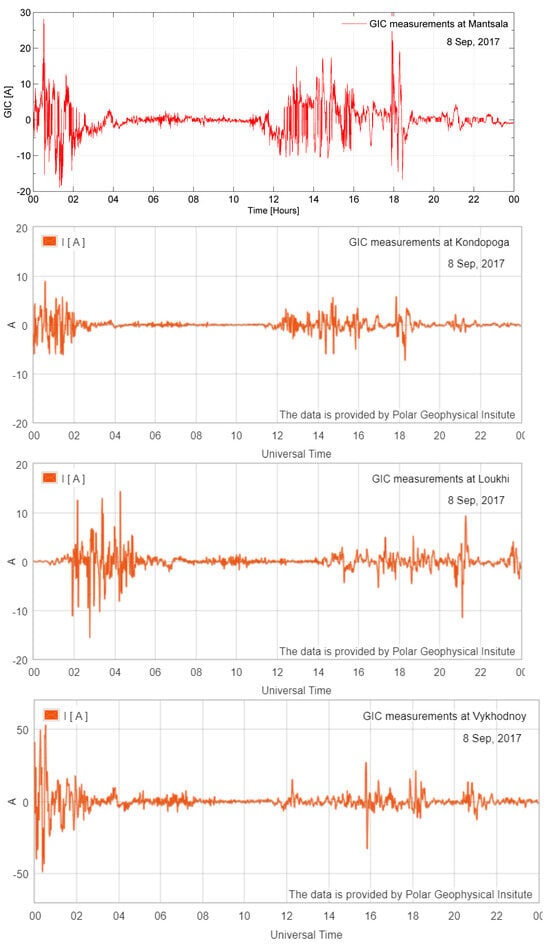
Figure 1.
GIC measurements at four stations located at higher geographic latitudes: Mäntsälä (60.6 N), Kondopoga (62.22 N), Loukhi (66.40 N), and Vykhodnoj (68.83 N) during the geomagnetic storm on 8 September 2017.
More details and an exhaustive description of the methodology applied to the GIC problem can be found in comprehensive reviews, like, e.g., [17,19,51].
3. Issues Connected to the Geomagnetically Induced Currents in Mid-Latitude European Countries
3.1. Greece
The data used to investigate transformer failures in Greece were adapted from the Independent Power Transmission Operator Zois [40] (located in Greece; this is a subsidiary company of the Public Power Corporation). Zois [40] studied the data of the failures obtained from mega and large transformers in the years 1989–2010. Mega and large transformers correspond to 400 kV and 150 kV; in Greece, there are 67 and 501 of them, respectively. The crucial fact that GICs influence transformer failures (TFs) has been well known for a long time in Canada and Scandinavia. In mid-latitude countries like Greece (–), the studies of the geomagnetic storms and their interactions with the Greek electricity transmission network have started only recently. Zois [40] proved that the recorded simple TFs, induced directly by GICs, covered at least of the total sum of the recorded failures in Greece. In his work concerning the Greek power transmission network, the main focus was put on the classic cases of the GICs’ relationship with failures, e.g., the triggering, the destruction of protective relays in transformers, or oil leakage caused by the destruction of the insulation. The author assumed that the TFs connected with the solar activity had to be divided into two groups: short-term (or immediate) effects and long-term ones. Therefore, 3- and 7-day time scales measured after a storm (short-term or immediate) were chosen for the calculations, whereas in the second group, monthly time scales (long-term) were selected. It is worth pointing out that, for stormy days with nT, Zois counted the sum of the failures that occurred during them. Moreover, all the failures that happened during a stormy day, or three days prior, or three days posterior to it were calculated. The same method was applied for 7 days, i.e., 7 days before or after a day with nT. After determining the quantity of the TFs, Zois studied which indices of solar activity affected failures the most. Later, among them, he picked the sunspot number (SSN), K-index, a-index, -index, and -index. The first estimated linear regression model for Greece, between the TF number and SSN, for the long-term effects was presented in Zois [83]. First, the author observed the fact that the failures possessed a periodicity similar to the one of the solar activity (apart from the noise, obviously). According to the solar cycle, the second fact was a “phase delay” of 4–5 years of failures. The author noted that, exactly for the years 1989–2010, the annual number of failures followed the solar activity, and its periodicity was similar to the 11-year solar cycle with a “phase delay”. For example, from 1996 to 2008, the max SSN was recorded in 2000, and 6 years later, in 2006, the maximum number of failures was observed. In Greece, the GICs induce minor disturbances in the power network. The author described solely one period of solar activity, i.e., 1989–2010, the time when this mentioned phenomenon occurred. Moreover, Zois noted that another more-direct and long-term Earth-affecting solar activity index gave a shorter “phase delay”. Subsequently, the results of that article were expanded by various statistical methods like the Shapiro–Wilk test for normality or the Bartlett test for checking the homogeneity of the residuals’ variances. Additionally, Zois determined the models (where TFN is the TF number), both in the case of global indices, for 22 sets of annual data (1989–2010). X is the annual mean of the SSN, -index, -index, and local K-index for Greece (Geomagnetic Observatory of Penteli), and where X equals the annual average of the daily K-index sum. The author presented both linear and non-linear models like logarithmic, polynomial of degree 2 up to 6, hyperbolic, and exponential with the determination coefficient in all cases. Here, Zois [40] obtained an inverse relation between the and X for the linear case of regression, i.e., , , , , , and , where X corresponded to the , the mean of , the mean of , the annual number of days with , the annual number of days with nT, and the annual average of the daily local K-index sum, respectively.
In conclusion, Zois focused on forecasting transformer failure numbers. Still, he noted that this would require local measurements for GICs, defining some long-term index on them and the best statistical methods.
3.2. Spain
The first analysis in north-eastern Spain was conducted by Torta et al. [84]. GICs in a power grid in Spain were the subject of research. Using the records of the Ebro Geomagnetic Observatory, a prediction of the effects of the geomagnetic activity on the Catalonian power transmission system was developed. The area is located at mid-latitudes. The determination of the geoelectric field during the solar cycles indicated amplitudes that were higher than those recorded, for example, in Southern Africa. A network model of the grid was constructed, and the GIC flows in the power network were calculated for such extreme events using the electric field at Ebro. The basic model regarded only the 400 kV electric network of the Spanish grid, including only 23 lines and 17 nodes. The paper [84] was the first step to study and measure GICs in Southern European power grids, a region considered to have a low GIC risk.
Cid et al. [41] developed two new geomagnetic indices, which have been fully approved for on-demand use: the Local Disturbance index (LDi), for now-casting local geomagnetic disturbances, and the Local Current index (LCi), as a proxy for the GIC risks in Spain. The LDi and LCi have been tested and validated using historical databases. Both indices are approved for autonomous use at the Spanish Space Weather Service (accessed on 1 July 2023). (http://www.senmes.es/) and the ESA Space Weather Portal (http://swe.ssa.esa.int/) [41].
Some experiences and recommendations concerning the derivation of GICs by using the differential magnetometry method were considered by Marsal et al. [85]. The authors focused on estimating the GIC, which might be apparent in the Spanish power grid, to validate GIC models. It was shown that the appropriate selection of the instrumentation and installation site of the DMM stations is fundamental due to the GIC signal [85]. Torta et al. [86] focused on mainland Spain and the improvements made after a switch from a homogeneous Earth resistivity to an alternative 3D resistivity distribution approach in geoelectric field computation. Additionally, the authors presented measurement points under power lines used for validating the ground resistivity models. Marsal et al. [87] improved their previously presented methodology. The modeled GIC was obtained using the geomagnetic field measured in Spain and the Earth resistivity models described by Torta et al. [86]. Torta et al. [88] evaluated the GIC hazard in the power networks of the Canary and Balearic archipelagos. The authors constructed models of the real grids and used resistivity models for each group of islands.
3.3. Italy
In Italy, GIC studies mainly have focused on investigating the GIC index, originally presented by Marshall et al. [70]. The GIC index was calculated from geomagnetic field measurements taking into account the dependence on the frequency between the geoelectric field and dBH/dt [89]. This index is known as a geoelectric field proxy because it does not need direct knowledge of the ground conductivity, the geometry of the ionospheric current system, nor significant details of critical infrastructure. The GIC index has been verified in various studies (e.g., [42,71]), concerning mid-latitudes, especially the territory of Italy. Tozzi et al. [42] conducted a preliminary risk assessment regarding GICs for the northernmost Italian region, which is characterized by low ground conductivity.
Tozzi et al. [71] reconstructed a latitudinal profile of maximum GIC indices for six geomagnetic storms. They found that the latitudinal profile of GIC intensity does not vary sensibly from storm to storm, and the latitude threshold boundary can be set at about 45–50 of geomagnetic latitude.
Tozzi et al. [42] estimated the GIC index for over more than 20 years in their observations. They showed that, during periods of high magnetic activity, potentially damaging GICs could flow through the power network, especially at the highest Italian latitudes, which are characterized by a low-conductivity lithosphere. The risk of GIC existence decreases with declining latitude. It decreases considerably at the southernmost latitudes, as was the case with the 2015 St. Patrick’s Day storm, even though edge/coastal effects can significantly increase the GIC amplitude.
Piersanti et al. [90] studied the amplitude of the GIC index on the geomagnetic storms of 25 August 2018 and St Patrick’s Day event on 17 March 2015. A direct comparison indicated that, despite the different storm intensities, the GIC hazard was extreme during August 2018, while only high in March 2015. During the St Patrick’s Day event on 17 March 2015, the geomagnetic storm GIC index grew to very high values above the 60 N geomagnetic latitude. Moreover, for both storms, the GIC index was very low at low–mid-latitudes, suggesting a greater participation of the ring current system.
Regarding the studies of the relationship between space weather events and recorded failures in the Italian transmission grid, Berrilli et al. [43] performed a statistical analysis of the electrical malfunctions on the Italian power grid registered in 2010–2020 in connection with space weather events. It was shown that a fraction of 15% of such breakdowns was observed in coincidence with significant geomagnetic disturbances.
3.4. Czech Republic
Researchers in the Czech Republic have modeled GICs’ effects on oil pipelines [44] and the transmission grid [69], and they selected a period from 24 October to 1 November 2003, for their studies. This time span included the Halloween Storm, and it had varying levels of disturbances such as quiet periods, onsets of great geomagnetic storms, oscillations in the recovery phase, and more. The researchers used a plane-wave model to calculate the geoelectric field and acquired geomagnetic data from the Budkov observation station. They assumed the conductivity to be 0.001 m.
Hejda and Bochníček [44] modeled the geoelectric voltage on the Družba and IKL oil pipelines and compared these modeled voltages with the recorded perturbations of the cathodic protection. To check the cathodic protection on the oil pipelines, the data of geomagnetically induced pipe-to-soil (P/S) voltages were used. The data were taken from three measurement stations (Sv. Katerina, Havl. Brod, Orechov), which are located in different parts of the oil network pipelines in the Czech Republic. After analyzing the collected P/S voltage data, they were able to directly compare them with the calculated geoelectric field. In the P/S voltage from the Sv. Katrina and Orechov stations, the direct impact of geomagnetic disturbances was visible. In the Havl. Brod station, the effect of the geomagnetic storm was less noticeable. Since the induced P/S voltage depends not only on the magnitude of the electric field, but also on the direction of the flow relative to the pipeline, it was also calculated which direction had the most-significant correlation with the P/S voltage. The best fit direction for the Orechov station was in close association with the pipeline direction. For the Sv. Katerina station, ambiguous results were obtained due to the bending of the pipeline near the measuring station. The Havl. Brod station gave a minimal response in each case. The results showed that the electric field’s most-straightforward plane wave and uniform Earth model corresponded very well with the measured P/S voltages.
Svanda et. al. [69] investigated possible GIC amplitudes in the power grid in a mid-to-low-latitude country. The 57 transmission lines with a voltage of 400 kV and 37 substations were analyzed. The GICs were calculated using the Pirjola–Lehtinen method. Studies have shown that the maximum amplitude at the nodes of the Czech transmission grid during a geomagnetic storm similar to the Halloween one is about 15 A. For an “extreme storm”, the expected GIC maxima with a 1 V/km geoelectric field did not exceed 40 A. The obtained GIC amplitude values were too small to cause immediate damage to transformers or other elements of the power grid. However, exposure to repeated GICs of this magnitude could cause aging of the devices and shorten their lifetime.
In addition to GIC modeling, research has also been conducted on the correlation between anomalies in the Czech electric power grid and geomagnetic activity [45], including the search for a quick response of devices to disrupted days of high geomagnetic activity [46]. The analyzed anomaly data in the Czech power grid covered a range of 12 years. However, the span of individual maintenance logs provided by the operators was shorter, varying between 6 and 10 years. In addition, events not related to GICs were excluded from the collection. The data were split into 12 subsets, namely D1 to D12. Each of these sub-datasets was carefully selected to include only events that occurred on devices of similar types and/or with the same voltage level and were registered by the same operating company. This approach ensured that the data were analyzed in a manner that was both efficient and effective, ultimately leading to more-accurate results. The dataset descriptions are shown in Table 1.

Table 1.
The description of the datasets used in the studies Vybostokova and Svanda [45] and Svanda et al. [46] (where ES denotes electrical substations).
According to a study by Vybostokova and Svanda [45], there is a correlation between the anomaly rate rates in the Czech power grid and the geomagnetic activity represented by the K-index. The study used a statistical approach, specifically a binomial test, to test the hypothesis that there is a growth in the anomaly rate around the maxima of geomagnetic activity. This was compared to the anomaly rate at a nearby minimum of activity. The study used measurements from a magnetometer station called Budkov in the Czech Republic. Local minima and maxima in the K-index sequences were searched to test the hypothesis. Then, an interval of the total span of W days was set around each minimum and maximum. These intervals worked as accumulation windows for a series of disturbances in the power grid. The tests were carried out for different values of W. In addition, the number of disturbances immediately before the local maximum was compared with the number of disturbances in the interval of the same length immediately after the maximum. A similar comparison was made for the minimum. Studies have shown that the results strongly depend on the choice of the window size. Only in the sets D1, D7, D10, D11, and D12 associated with disturbances on power lines at high and very high voltage levels was there a statistically significant increase in the anomaly rates in the periods from 30 to 120 days around geomagnetic activity maxima compared to adjacent activity minima. The relative increase was roughly 10% to 70%. In the remaining datasets, the difference was not statistically significant. It was noted that the rise in the anomaly rates was more significant after local maxima than before them. This can indicate that the increase was due to more-significant geomagnetic activity, where the GIC effects appeared with a certain delay.
Therefore, in the following paper, Svanda et al. [46] searched for the rapid and delayed response of power lines and transformers in the Czech electric power grid to disturbed days of high geomagnetic activity. The disturbed days were categorized by different cumulative (time-integrated) parameters based on various magnetic indices such as the cumulative storm time , low-latitude indices, the cumulative high-latitude index, and the cumulative mid-latitude index. The authors studied the relative manifestation of the GIC effects during disturbed days compared to quiet days. They used superposed epoch analysis (SEA). In the next step, using SEA, they determined as precisely as possible the time delay (after the start of the storm), which corresponds to the statistically most-significant increase in anomalies for each of the types of power grid devices analyzed in the D1–D12 sets. The SEA analysis showed that, in the five days following the beginning of the geomagnetic activity, there was an increase of about 5–10% of registered anomalies in power lines and transformers in the Czech power grid. The growth of the anomalies was most likely due to geomagnetic activity nor GICs. An increase in anomalies during strong geomagnetic activity was observed for the D8, D10, and D12 sets for IntDst and D8 and D11 for IntAE. This means that the geomagnetic disturbances most impacted recorded anomalies in long power lines. Also, significant delayed (by 1–2 days) effects were found in the D8 dataset of high-voltage transformers. A significant effect was also observed in the D4 dataset during an intense storm. The results showed that substorm-related disturbances and magnetic storms significantly impacted the power-grid network. The authors also found that days with a minimum 50 nT (which represent about 8% of the stormiest days [91]) were likely to have the most-significant impact on the Czech power grid, resulting in an immediate or slightly delayed (up to several days) increase in anomalies compared to quiet periods.
3.5. Slovakia
Since a relationship was found among the higher rate of anomalies observed during the increase in geomagnetic activity in the Czech Republic, Vybostkova and Svanda [47] assumed that similar behavior would persist in the Slovak distribution network. In their work, the authors used a list of days on which anomalies were registered in the entire Slovak transmission grid. Since the data included not only equipment failure events, but also service anomalies, power outages, and unscheduled switching, anomalies that were not caused by the environment were removed from the set. The dataset of recorded anomalies covered a period of 10 years (2009–2019). Geomagnetic activity was described using the K-index computed for the Geomagnetic Observatory at Hurbanovo in Slovakia. Since periods of increase/decrease in geomagnetic activity were sought, the averaged K-index series was used to identify the local minima and maxima of geomagnetic activity.
It was observed that there was a strong seasonal periodicity in the anomaly rates, which prompted the authors to investigate whether the anomaly rates were dependent on meteorological measurements such as mean daily temperature and daily precipitation amount. Since the mean temperature was found to have a strong correlation with the anomaly rate, a temperature-dependent model was calculated and subtracted from the actual daily anomaly rates. This resulted in a set that could be studied in terms of the statistical dependence of disturbances on geomagnetic activity. Both datasets were tested with a binomial test to determine if there was a difference in the number of anomalies recorded during the local maxima and local minima of activity for the specified dataset and accumulation windows having width W. The analysis was performed for windows W ranging from 10 to 100 days.
Based on the original dataset’s analysis, temperature significantly impacted the number of anomalies observed. This is likely due to the semi-annual variations of the geomagnetic field, which correlates with the K-index. Interestingly, this relationship was observed across all accumulation windows studied. When meteorological effects were removed from the dataset, it became apparent that there were more disturbances during periods of increased geomagnetic activity than during quiet periods. This held true for most accumulation windows, except for those with a length of 30, 40, and 50 days. It was also noted that the rate of anomalies increased for accumulation windows larger than 70 days, possibly due to the fact that larger windows had more recorded disturbances in the power grid. Overall, the relative increase in the anomaly rate was found to be between 10 and 15%, with the percentage increase against a basal failure rate determined from geomagnetically quiet days being around 11%. These findings are essential for understanding the impact of temperature and geomagnetic activity on power grid anomalies and could help inform strategies for mitigating them in the future.
3.6. Austria
As a mid-latitude country, Austria does not expect to experience dangerously large GICs. Although Austria has a similar GIC risk level to Denmark and Scotland, research conducted by [75] highlights that it is more vulnerable to GICs due to highly resistive alpine rocks apparent throughout the country. Subsurface conductivity models support this finding [74].
Consequently, in 2014, Austria started research concerning GICs with the initiative of the Austrian Power Grid AG (APG) and Graz University of Technology. The conducted study investigated any potential DC currents in the high-voltage power transmission network in Austria. To ensure accurate measurements, a measurement system was used that consisted of a Hall sensor, a low-pass filter, and a data logger, which was kept in a temperature-controlled box with a radiator. The data logger had a measurement range of A and recorded data at 1 min intervals. For the APG, measurements of DC are crucial to investigate the nature of the currents and possible effects on transformers, as well as the impact of DC on different equipment such as instrument transformers and protection devices. The data are also used to plan for new transformers’ design criteria. According to the study by Halbedl et al. [48], various frequency components were found in the spectrum, such as DC, slow variations below 1 Hz, 16.7 Hz from the railway system, 50 Hz main, harmonics, and interharmonics. This study investigated the section of the Austrian power grid at the 220 and 380 kV levels, which covers 56 interconnected substations with 6965 km of power lines and 87 transformers. In 2014, some initial test measurements were conducted, and after that, additional DC measurement devices were installed to launch a long-term measurement campaign. The first analysis of the collected data was performed by Halbedl et al. [92]. Along with conducting measurements, simulations of GICs for the Austrian transmission grid were also presented. The GICs calculated in the transformer’s neutral point were compared with the measurements, and the analysis of both simulated and measured current exposed a good correlation, which was robust for the peaks of the GIC analyzed on 22–23 March 2015.
The modeling of the GIC flows through Austria’s national power grid was continued in [49]. The authors used a thin-sheet approach and detailed surface and subsurface conductivity models to compute the induced geoelectric field. They took geomagnetic variations from the Conrad Observatory and a 2D thin-sheet surface conductivity model of Austria provided by the GBA and EURHOM 1D subsurface conductivity models as an input. The resulting measurements of direct currents in a transformer neutral pointshowed very good agreement for short-period variations such as geomagnetic storms. According to the presented results, the Austrian power grid is exposed to large GICs in the range of tens of amperes, predominantly from strong geomagnetic variations in the east–west direction.
The applied model extension and validation with measurements from Austria are presented in [93]. In their analysis, the authors looked at how the choice of local resistivity, especially the surface conductivity in thin-sheet modeling, and the source of geomagnetic variations affect GIC modeling. They also investigated the model’s sensitivity to the accuracy of the network configuration. The results showed that there were only slight improvements with an increase in the degree of detail of the Earth model with the thin-sheet approach. This means that it is not worth the effort to create a more-detailed ground model. However, due to the presence of the Alps, these effects could be more significant in the western part of Austria, where there have been fewer measurements to date. The study also found that the existence of connecting networks in neighboring countries was necessary for the scale of the modeled values, even for stations that were several connections away from the border. Additionally, nodes in the high-voltage (380 kV) network were found to be the most vulnerable to large GICs and to cause significant growths in GICs elsewhere.
According to a recent study by Albert et al. [94], continuous GIC measurements have been taken at transformer neutral points in Austria over five years. The study focused on seven self-designed measurement systems installed in the Austrian 220 and 380 kV transmission levels, which measure currents up to 25 A. An automated algorithm detects GIC events as short-duration peaks caused by switching events and, also, records power grid faults [95]. A GIC event is defined as a current with a peak prominence of at least the mean value plus the standard deviation of the analysis time span, with a half-width duration of at least 100 s. The maximum measured amplitude during the observation period was 13.83 A during the geomagnetic storm on 12 May 2021, with a minimum Dst value of nT. The study also found that the sensitivity of GICs to specific directions of geomagnetic field changes varied depending on location, as evidenced by the evaluation results of the two geomagnetic storms in September 2017 and May 2021. Aside from geomagnetic events and recurrent activity, the study also identified the DC-powered public transportation system as a contributor to the grounded transformer neutral point currents. Other sources, like power electronic devices from renewable energy resources, were also investigated.
In [96], the researchers attempted to use machine learning tools, specifically recurrent neural networks and LSTMs, to predict the GIC at two substations in Austria. They trained their models using solar wind observations at the L1 point as an input to predict two different kinds of output: the geoelectric field components Ex and Ey, as well as the GIC in specific substations. However, while the LSTM model showed promising results in predicting the geoelectric field, translating this into accurate GIC forecasts proved to be complicated. The model was found to have a correlation of around 0.6 with GIC measurements, with a root-mean-squared error of 0.7 A. The probability of detecting mild activity in GICs was assessed to be around 50% and 15% for larger GIC.
3.7. Poland
The structure of the electrical system in Poland is conditioned by the technical status dating back more than half a century. Power plant stations are mostly located near coal mining regions, i.e., central and southwestern Poland. A substantial deficiency in the infrastructure balance negatively impacts the power supply’s stability [97]. However, the probability of a major hazard involving a large part of the country is small. This can only occur due to some hostile conditions, such as high electricity utilization, poor atmospheric conditions, or space weather events.
In Poland, an analysis based on the logs of failures in the part of the Polish transmission network has been performed. The authors, in consultation with experts, classified the causes of failure into six primary clusters: (1) meteorological effects, (2) operational outages, (3) vandalism, (4) failures related to aging of infrastructure elements, (5) failures related to electronic devices, and (6) failures with not specified reasons [16]. As an example, the statistics from 2010 are presented in Table 2.

Table 2.
Main causes of failures of electrical grid elements and their number in 2010 (in southern Poland).
A hypothesis was formulated that failures from Clusters (4)–(6) may have their source in sudden changes in the geomagnetosphere caused by a short-term variability of the Sun [16]. The authors used various methods of statistical inference [16,34,50], time series analysis [16,34], machine learning, such as principal component analysis (PCA) [50], neural networks (self-organizing maps (SOMs)) [34,50], and hierarchical agglomerative clustering (HAC) [50]. The regression analysis showed that the average annual number of failures from Groups (4)–(6) in the period from January 2010 (around the solar activity minimum) to July 2014 (solar maximum) displayed an upward trend. The authors stated that this might indicate a dependency on the solar activity level [16,34].
For instance, some of the considered cases were the SSC one, the occurrence of fast CMEs, and the geomagnetic -index reaching a value not lower than 5 [16]. In particular, a Wilcoxon matched pairs test was used for two groups: (1) failures connected with the days with and (2) -index values ≥ 6. It showed that the greater the value of the geomagnetic -index, the higher the number of recorded electrical grid failures (EGFs) [16].
The analysis of the variability of the number of failures identified in threeclusters: (4) failures linked to the aging of the elements of infrastructure, (5) electronic-device-related failures, and (6) failures whose causes was not determined, showed that, on the day of the occurrence of the SSC, the number of failures almost doubled. When a fast halo coronal mass ejection occurred, the next day, the number of EGFs in Categories (4)–(6) increased by up to two-and-a-half-times the average. On the other hand, when the geomagnetic Kp-index attained a value of at least 5, then, on the same day and/or the day after, there was a considerable increase of the EGF number in the mentioned groups [16]. Similarly, during the cosmic ray Forbush effect recorded by neutron monitors, the number of failures in Categories (4)–(6) increased [98].
Gil et al. [99] presented that the sharp increase in electrical grid failures aligned often with some time lag and heightened geomagnetic activity, as evidenced by the corresponding rise in geoelectric field disturbances recorded for the GICs. This implies a connection with space weather effects. The earlier-mentioned delayed appearance of EGFs could be associated with a cumulative effect resulting from transient states and their propagation within the distribution network. It was also shown that there is a considerable difference in the EGF number in the group related to the aging of infrastructure elements and those of unknown origin in geomagnetically calm periods, when the horizontal component of the local geomagnetic field change is less than 25 nT/min. Statistically, the number of failures is higher during geomagnetic disturbances, i.e., 25 nT/min [34].
Subsequently, intensive geomagnetic storms (according to the definition formulated by Gonzalez, Tsurutani [22]) were considered, accompanied by decreases in the value of the vertical component of the heliospheric magnetic field (below −10 nT for more than 3 h) and decreases in the value of the geomagnetic index (below −100 nT for more than 3 h). It was found that, with such storms, there were considerable increases in the number of failures in Categories (4)–(6). In the above-discussed cases of space weather phenomena, during and/or immediately after them, a significant increase in the number of failures of power grid elements was observed in the groups of failures that may be related to the effects of space weather [16,34].
Research performed using machine learning methods indicated a new, previously not shown, property [34], namely that the growth in the number of power grid failures during or just after intense geomagnetic storms is linked to the variability of the solar wind proton density. However, other solar wind parameters or heliosphere characteristics also have an affect [34]. Gil et al. [50], using cross-correlation, revealed particular delays in the increase of the power grid failures and changes in the geomagnetic, heliospheric, and solar parameters. Those delays were taken into account in the PCA, SOM, and HAC analyses. They revealed that the parameters of the solar wind had the most-substantial connections with all of the considered types of EGFs in southern Poland during all the analyzed storms. The above-mentioned parameters are usually grouped within the same cluster with EGFs in more than 80% of the outcomes.
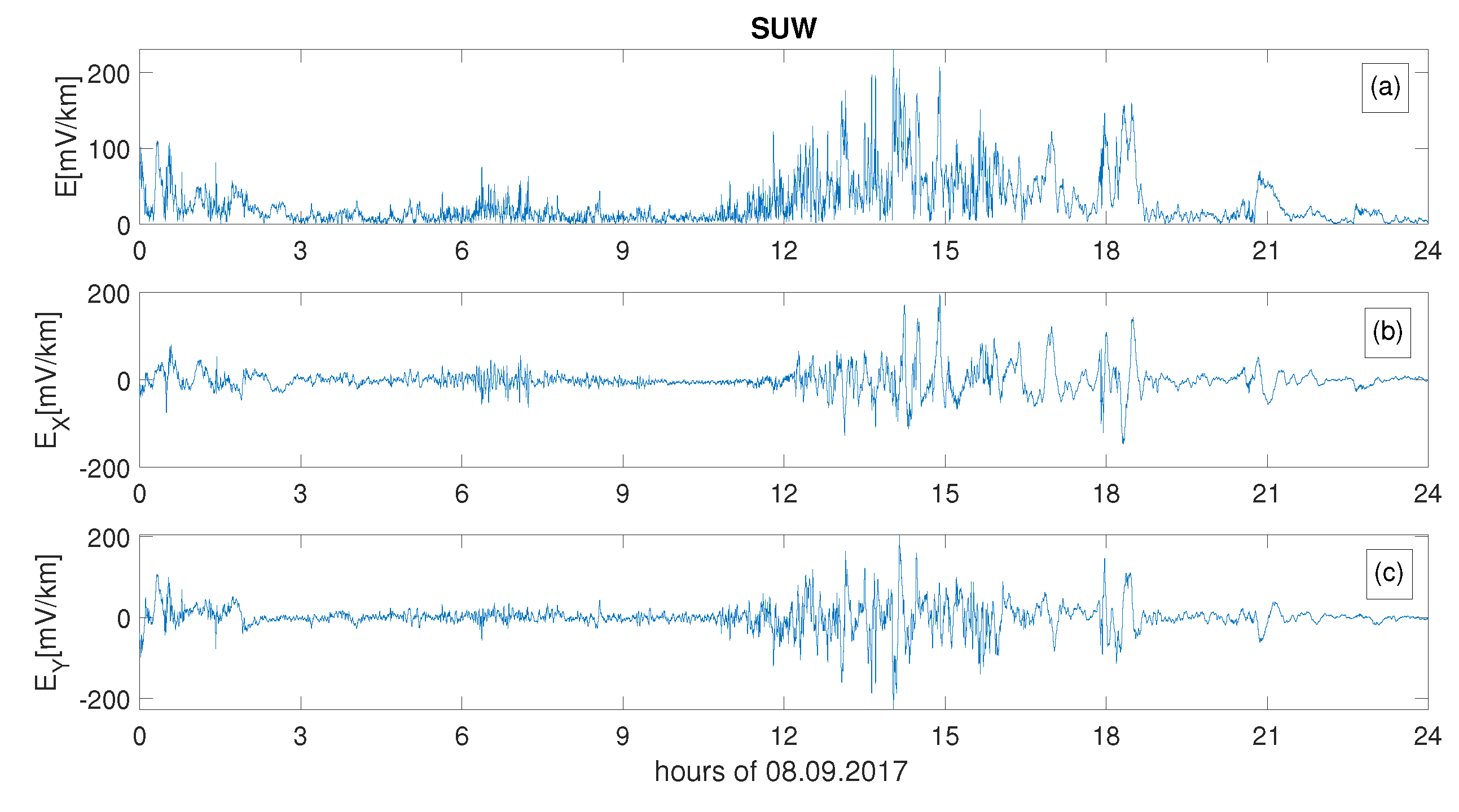
Moreover, for the first time, the local geoelectric field for Poland was determined [100]. The temporal variability of the electric field was calculated using two methods: (1) that proposed by Viljanen and Pirjola [101] and (2) the one-dimensional layered conductivity Earth model (e.g., Boteler et al. [72]). The second method was performed using the conductivity values of the lithospheric layers determined for Poland [74] at individual depths [60,102]. Figure 2 presents the sample of the computed local geoelectric field E and its components, and [60]. The geomagnetic field was computed based on the local geomagnetic field measured by one of the Polish magnetometers located in Suwalki, which is presented in Figure 3. One can observe geomagnetic disturbances mirrored in the strongly fluctuating geoelectric field. It was found that periods of substantial variability of the components of the geoelectric field computed for Poland correspond to the occurrence of strong geomagnetic storms [16,34]. Also, for the first time, the value of the GICs for Poland was roughly estimated [98,103], showing their occurrence in Poland during intense geomagnetic storms.
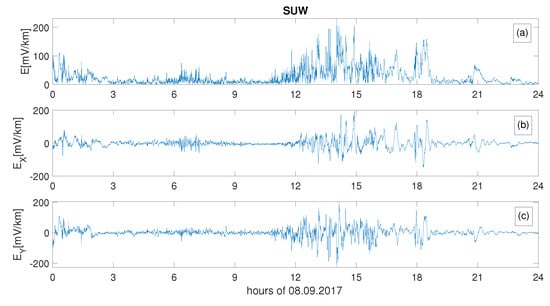
Figure 2.
Geoelectric field, E (a), and its components, (b) and (c), computed for Suwalki, during the geomagnetic storm on 8 September 2017.
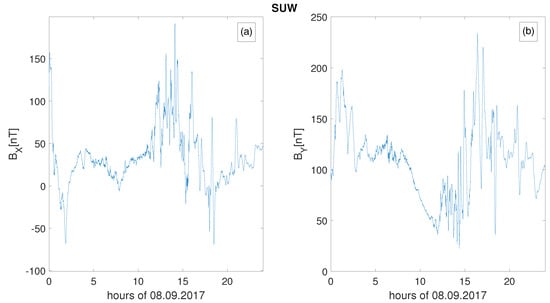
Figure 3.
Horizontal Earth magnetic field components, (a) and (b), measured by the Polish magnetometer located in Suwalki, during the geomagnetic storm on 8 September 2017.
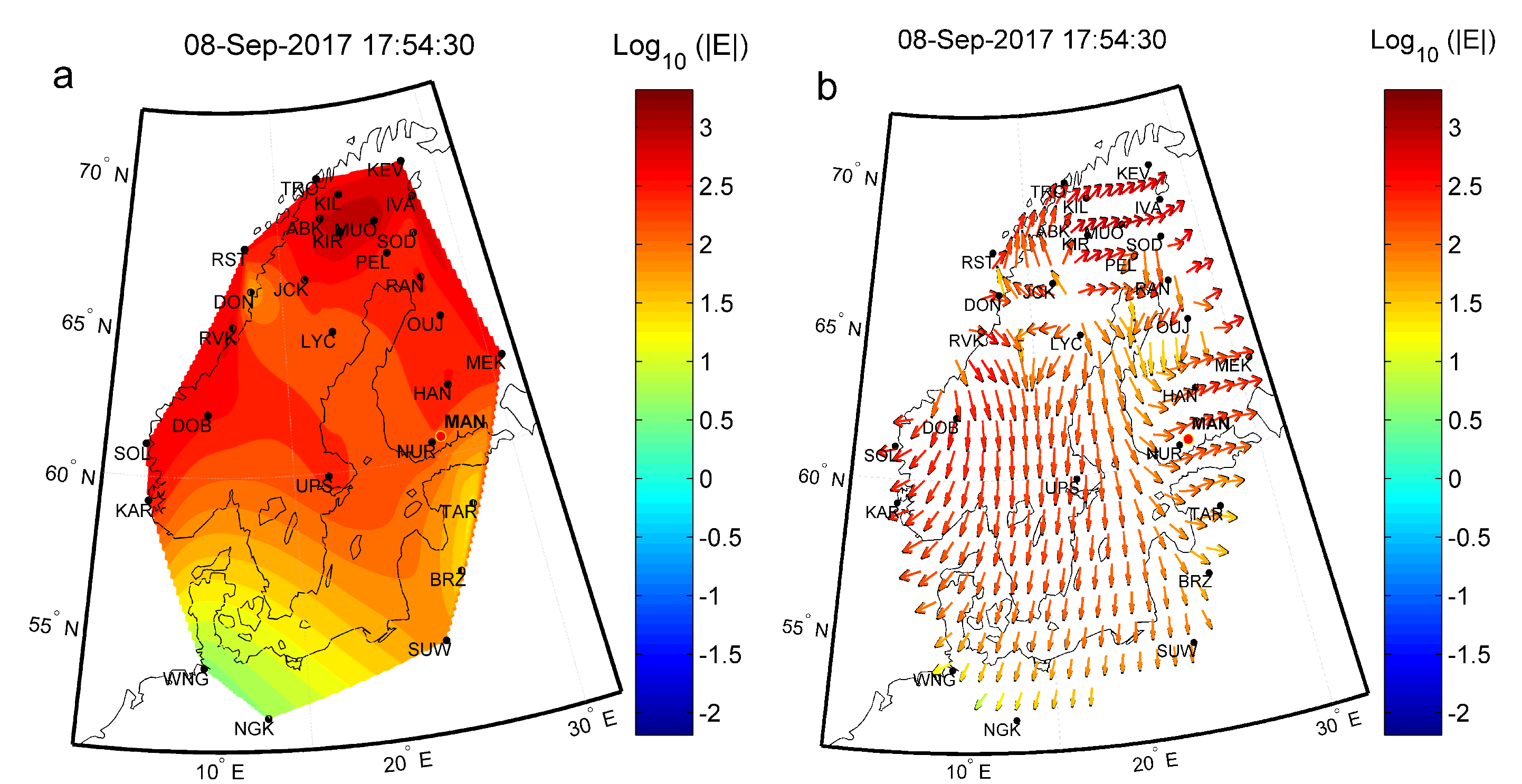
Figure 4 displays maps visualizing the spatial variability of the local geoelectric field E[60] during the September 2017 geomagnetic storm. It shows swift and pronounced fluctuations of the E strength (Figure 4a) and vector (Figure 4b), which is in agreement with Figure 2. It can be seen that, over the mid-latitudes (e.g., Polish Suwalki (SUW)), the strength of the geoelectric field might be temporarily at the same level as at high-latitudes (e.g., Norwegian Dønna (DON)) due to the local effects.
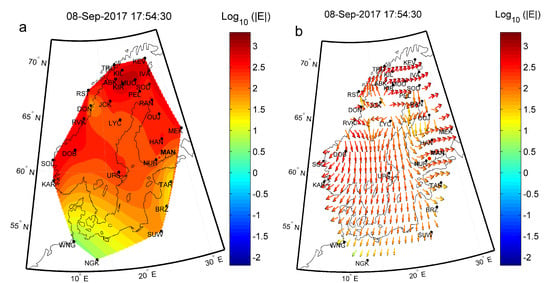
Figure 4.
Geoelectric field strength, E (a), and vector, E (b), during the geomagnetic storm on 8 September 2017 (compare with Figures 6 and 7 of Wawrzaszek et al. [60]).
4. Discussion
As was underlined earlier, the space weather events affecting the Earth’s magnetic field are the causes of GICs [35]. GICs can appear not only at high-latitude regions [104]. They have the potential to lead to power transformer saturation, which is a critical issue for the power transmission network [105]. The fluctuating geomagnetic field induces an electromagnetic field in the transmission networks and the Earth itself. The following are necessary to calculate geomagnetically induced currents in the transmission lines: a ground conductivity model, a power grid topology or transformer neutral point current registrations, and high-temporal-resolution geomagnetic field observations. The current flow path in response to fluctuating external currents in the ionosphere follows both artificial and natural current paths on the ground (e.g., [106]). The artificial current paths consist of power lines, pipelines, etc., while the natural ones include underground conductive structures and nearby water reservoirs. After accounting for the natural current paths, the geoelectric field affects the artificial ones, leading to a quasi-DC (with periods ranging from ten seconds to tens of minutes) in the power networks. These GICs create currents in power transformers, which then operate beyond their designed range, resulting in the saturation of the interior magnetic core material of the transformer. When the core saturates, the transformer loses its ability to provide the electromotive force back, leading to abnormally large voltages and currents in the windings. Based on the transformer’s configuration, this may result in the heating of nearby structures due to induced eddy currents, potentially damaging parts of the transformer. One of the crucial questions is how to postpone the transformer saturation process, which takes from tens of seconds up to even a few minutes, in the face of GICs’ appearance. The core, winding, and tank design characteristics must be considered when evaluating the ability of a transformer to hold off an overexcitation. Furthermore, transformer saturation results in the currents and voltages no longer preserving a simple sine wave form. This, however, can result in the activation of insulating equipment elsewhere in the network and, then, in tripping erroneously. These equipment trips can remove necessary equipment from the line and cause problems with voltage stability [94]. The other concern for the system is that all the saturating transformers come out as a considerable inductive load to the network as a whole. This implies that a system operating close to its peak demand levels prior to the geomagnetic storm might fail to fulfil the entirety of the power demand when the storm occurs, leading to partial or system-wide blackouts [104].
Hence, there are three main strategies for GIC mitigation: (1) preventing their flow, (2) employing or installing equipment that remains unaffected by geomagnetically induced currents, and (3) managing the grid’s operation to reduce the influence of GICs.
The longest-running studies have been conducted in Canada. There, a dramatic example of the repercussion of space weather phenomena on energy infrastructure in March 1989 was recorded. However, apart from the Scandinavian countries, European countries such as Italy and Spain are worth mentioning due to years of experience. Austria is also worth noting in the context of good cooperation between researchers and infrastructure operators.
The most-significant difficulty in developing research conducted in all the described countries is the acquisition of detailed data on instabilities and failures in the power grids of individual countries. This is understandable due to the high attention that is being paid by the national operators to the security of critical infrastructure. Moreover, if finally, as Vybostokova and Svanda [45] wrote: “After years of delicate negotiations, we managed to obtain the maintenance logs from all the operators”, it is difficult to make a comparative analysis between different countries because the form, type, statistics, time intervals, and frequency of data sampling are entirely different. In order to accelerate the development of research on the impact of space weather phenomena on the functioning of power grids in mid-latitudinal European countries, it would be invaluable to create, for instance, within the structures of the European Union, an authority responsible for creating a framework for collecting and processing data on the instability of transmission lines. The absence of regular and extensive GIC measurements in mid-latitude European countries is equally acute. Often, the scientific community uses various types of GIC proxies or indices, performing tremendous and titanic work according to the available resources. We need information on the power grid’s topology and densely located measuring points of the local geomagnetic field to model geomagnetically induced currents accurately.
5. Summary
This review underlined the efforts made in seven European countries (Greece, Spain, Italy, Slovakia, the Czech Republic, Austria, Poland) to estimate the local geomagnetically induced currents’ impact on the national power grids. Three primary approaches to managing GICs involve (1) blocking their transmission, (2) utilizing or installing equipment resistant to GICs’ effects, and (3) overseeing grid operations to mitigate GICs’ impacts.
The performed review showed that:
- 1.
- Mid-latitude countries can be under geomagnetically induced currents’ impact during intense geomagnetic storms.
- 2.
- Modeling the evolution of coronal mass ejections, the geoelectric field, and geomagnetically induced currents needs to be effective and practically available in real-time.
- 3.
- In order to properly validate the models of geomagnetically induced currents and the geoelectric field, there is a requirement for close cooperation between transmission line operators and researchers involved in modeling and forecasting.
- 4.
- To precisely model geomagnetically induced currents, we need information on the power grid topology. Thus, close cooperation between the scientific community and national operators is needed.
- 5.
- There is a need for continuous monitoring of the Earth’s vicinity to build a well-funded system awareness, as the Space Weather Service Network does in the frame of the European Space Agency or the Space Weather Prediction Center of the National Oceanic and Atmospheric Administration.
- 6.
- The development of the research on the impact of space weather phenomena on the functioning of power grids in mid-latitude European countries can be highly accelerated due to the creation within the structures of the European Union of an authority responsible for creating a framework for collecting, unifying, and processing data on the instability of transmission lines.
- 7.
- The absence of regular and extensive geomagnetically induced current measurements in mid-latitude European countries must be resolved.
Author Contributions
The scientific content of the article, text, and discussion have been created by the all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data of geomagnetic field components and were from Suwalki observatory operated by the Institute of Geophysics Polish Academy of Sciences, available at https://www.igf.edu.pl/home.php, the geomagnetic field components were from the International Monitor for Auroral Geomagnetic Effect, available at http://space.fmi.fi/image/, GIC recordings provided by the Finnish Meteorological Institute, available at https://space.fmi.fi/gic/.
Acknowledgments
We thank the researchers and engineers involved in the solar, heliospheric, and geomagnetic measurements and observations, in particular: The data of geomagnetic field components and were from Suwalki observatory operated by the Institute of Geophysics Polish Academy of Sciences (https://www.igf.edu.pl/home.php, accessed on 30 July 2023). The data of the geomagnetic field components were from the International Monitor for Auroral Geomagnetic Effect (IMAGE) (http://space.fmi.fi/image/, accessed on 30 July 2023). The GIC recordings from the Finnish natural gas pipeline near Mäntsälä were from the Finnish Meteorological Institute (https://space.fmi.fi/gic/, accessed on 30 July 2023). The GIC measurements were provided in the frame of the EURISGIC project.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| APG | Austrian Power Grid AG |
| CME | Coronal mass ejection |
| EGF | Electrical grid failure |
| GIC | Geomagnetically induced current |
| HAC | Hierarchical agglomerative clustering |
| LCi | Local Current index |
| LDi | Local Disturbance index |
| LSTM | Long short-term memory network |
| PCA | Principal component analysis |
| P/S | Pipe-to-soil |
| SOM | Self-organizing maps |
| SSC | Sudden storm commencement |
| SSN | Sunspot number |
| TF | Transformer failure |
References
- Di Fino, L.; Romoli, G.; Amantini, S.; Boretti, V.; Lunati, L.; Berucci, C.; Messi, R.; Rizzo, A.; Albicocco, P.; Donato, C.D.; et al. Radiation measurements in the International Space Station, Columbus module, in 2020–2022 with the LIDAL detector. Life Sci. Space Res. 2023, in press. [Google Scholar] [CrossRef]
- Di Fino, L.; Zaconte, V.; Stangalini, M.; Sparvoli, R.; Picozza, P.; Piazzesi1, R.; Narici1, L.; Larosa1, M.; Moro, D.D.; Casolino, M.; et al. Solar particle event detected by ALTEA on board the International Space Station. The March 7th, 2012 X5.4 flare. J. Space Weather Space Clim. 2014, 4, A19. [Google Scholar] [CrossRef]
- Fang, T.W.; Kubaryk, A.; Goldstein, D.; Li, Z.; Fuller-Rowell, T.; Millward, G.; Singer, H.J.; Steenburgh, R.; Westerman, S.; Babcock, E. Space Weather Environment During the SpaceX Starlink Satellite Loss in February 2022. Space Weather 2022, 20, 11. [Google Scholar] [CrossRef]
- Pesnell, D.W. Solar Cycle Predictions (Invited Review). Sol. Phys. 2012, 281, 507–532. [Google Scholar] [CrossRef]
- Meier, M.M.; Berger, T.; Jahn, T.; Matthiä, D.; Plettenberg, M.C.; Scheibinger, M.; Schennetten, K.; Wirtz, M. Impact of the South Atlantic Anomaly on radiation exposure at flight altitudes during solar minimum. Sci. Rep. 2023, 13, 9348. [Google Scholar] [CrossRef]
- Mishev, A.; Usoskin, I. Numerical model for computation of effective and ambient dose equivalent at flight altitudes. Application for dose assessment during GLEs. J. Space Weather Space Clim. 2015, 5, A10. [Google Scholar] [CrossRef]
- Fagundes, P.R.; Cardoso, F.A.; Fejer, B.G.; Venkatesh, K.; Ribeiro, B.A.G.; Pillat, V.G. Positive and negative GPS-TEC ionospheric storm effects during the extreme space weather event of March 2015 over the Brazilian sector. J. Geophys. Res. Space Phys. 2016, 121, 5613–5625. [Google Scholar] [CrossRef]
- Schrijver, C.J.; Kauristie, K.; Aylward, A.D.; Denardini, C.M.; Gibson, S.E.; Glover, A.; Gopalswamy, N.; Grande, M.; Hapgood, M.; Heynderickx, D.; et al. Understanding space weather to shield society: A global road map for 2015–2025 commissioned by COSPAR and ILWS. Adv. Space Res. 2015, 55, 2745–2807. [Google Scholar] [CrossRef]
- Sloan, T.; Wolfendale, A.W. Cosmic rays and climate change over the past 1000 million years. New Astron. 2013, 25, 45–49. [Google Scholar] [CrossRef]
- Mavromichalaki, H.; Papailiou, M.; Dimitrova, S.; Babayev, E.S.; Loucas, P. Space weather hazards and their impact on human cardio-health state parameters on Earth. Nat. Hazards 2012, 64, 1447–1459. [Google Scholar] [CrossRef]
- Alania, M.V.; Gil, A.; Modzelewska, R. On statistical relationship of solar, geomagnetic and human activities. Adv. Space Res. 2004, 34, 1602–1606. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Rosen, I.G.; Tsurutani, B.T.; Verkhoglyadova, O.P.; Meng, X.; Mannucci, A.J. Statistical characterization of ionosphere anomalies and their relationship to space weather events. J. Space Weather Space Clim. 2016, 6, A5. [Google Scholar] [CrossRef]
- Eastwood, J.P.; Biffis, E.; Hapgood, M.A.; Green, L.; Bisi, M.M.; Bentley, R.D.; Wicks, R.; McKinnell, L.A.; Gibbs, M.; Burnett, C. The Economic Impact of Space Weather: Where Do We Stand? Risk Anal. 2017, 37, 206–218. [Google Scholar] [CrossRef] [PubMed]
- Pulkkinen, A.; Viljanen, A.; Pajunpää, K.; Pirjola, R. Recordings and occurrence of geomagnetically induced currents in the Finnish natural gas pipeline network. J. Appl. Geophys. 2001, 48, 219–231. [Google Scholar] [CrossRef]
- Joo, B.S.; Woo, J.W.; Lee, J.H.; Jeong, I.; Ha, J.; Lee, S.H.; Kim, S. Assessment of the Impact of Geomagnetic Disturbances on Korean Electric Power Systems. Energies 2018, 11, 1920. [Google Scholar] [CrossRef]
- Gil, A.; Modzelewska, R.; Moskwa, S.; Siluszyk, A.; Siluszyk, M.; Wawrzynczak, A.; Zakrzewska, S. Does time series analysis confirms the relationship between space weather effects and the failures of electrical grids in South Poland? J. Math. Ind. 2019, 9, 7. [Google Scholar] [CrossRef]
- Lakhina, G.S.; Hajra, R.; Tsurutani, B.T. Encyclopedia of Solid Earth Geophysics; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 523–527. [Google Scholar] [CrossRef]
- Pirjola, R. Review on The Calculation of Surface Electric an Magnetic Fields and of Geomagnetically Induced Currents in Ground-Based Technological Systems. Surv. Geophys. 2002, 23, 71–90. [Google Scholar] [CrossRef]
- Kelbert, A. The Role of Global/Regional Earth Conductivity Models in Natural Geomagnetic Hazard Mitigation. Surv. Geophys. 2019, 41, 115–166. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Hajra, R. The Interplanetary and Magnetospheric causes of Geomagnetically Induced Currents (GICs)>10 A in the Mantsala Finland Pipeline: 1999 through 2019. J. Space Weather Space Clim. 2021, 11, 32. [Google Scholar] [CrossRef]
- Oliveira, D.M.; Arel, D.; Raeder, J.; Zesta, E.; Ngwira, C.M.; Carter, B.A.; Yizengaw, E.; Halford, A.J.; Tsurutani, B.T.; Gjerloev, J.W. Geomagnetically induced currents caused by interplanetary shocks with different impact angles and speeds. Space Weather 2018, 16, 636–647. [Google Scholar] [CrossRef]
- Gonzalez, W.D.; Tsurutani, B.T. Criteria of interplanetary parameters causing intense magnetic storms (Dst < −100 nT). Planet. Space Sci. 1987, 35, 1101. [Google Scholar] [CrossRef]
- Gosling, J.T. Coronal mass ejections: The link between solar and geomagnetic activity. Phys. Fluids B 1993, 5, 2638–2645. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Gonzalez, W.D.; Kamide, Y. Magnetic storms. Surv. Geophys. 1997, 18, 363–383. [Google Scholar] [CrossRef]
- Heyns, M.J.; Lotz, S.I.; Gaunt, C.T. Geomagnetic pulsations driving geomagnetically induced currents. Space Weather 2021, 19, e2020SW002557. [Google Scholar] [CrossRef]
- Marshall, R.A.; Dalzell, M.; Waters, C.L.; Goldthorpe, P.; Smith, E.A. Geomagnetically induced currents in the New Zealand power network. Space Weather 2012, 10. [Google Scholar] [CrossRef]
- Barlow, W.H. On the Spontaneous Electrical Currents Observed in the Wires of the Electric Telegraph. Philos. Trans. R. Soc. Lond. Ser. I 1849, 139, 61–72. [Google Scholar]
- Burbank, J.E. Earth-currents and a proposed method for their investigation. Terr. Magn. Atmos. Electr. (J. Geophys. Res.) 1905, 10, 23. [Google Scholar] [CrossRef]
- Albertson, V.; Thorson, J.; Clayton, R.; Tripathy, S. Solar-Induced-Currents in Power Systems: Cause and Effects. IEEE Trans. Power Appar. Syst. 1973, 92, 471–477. [Google Scholar] [CrossRef]
- Zakharenkova, I.; Cherniak, I. Effects of storm-induced equatorial plasma bubbles on GPS-based kinematic positioning at equatorial and middle latitudes during the September 7–8, 2017, geomagnetic storm. GPS Solut. 2021, 25, 132. [Google Scholar] [CrossRef]
- Gopalswamy, N. History and development of coronal mass ejections as a key player in solar terrestrial relationship. Geosci. Lett. 2016, 3, 8. [Google Scholar] [CrossRef]
- Kataoka, R.; Asaoka, Y.; Torii, S.; Toshio, T.; Shunsuke, O.; Tadahisa, T.; Yuki, S.; Yosui, A.; Masaki, M. Relativistic electron precipitation at International Space Station: Space weather monitoring by Calorimetric Electron Telescope. Geophys. Res. Lett. 2016, 43, 4119–4125. [Google Scholar] [CrossRef]
- Bhaskar, A.; Vichare, G. Forecasting of SYMH and ASYH indices for geomagnetic storms of solar cycle 24 including St. Patrick’s day, 2015 storm using NARX neural network. J. Space Weather. Space Clim. 2019, 9, A12. [Google Scholar] [CrossRef]
- Gil, A.; Berendt-Marchel, M.; Modzelewska, R.; Moskwa, S.; Siluszyk, A.; Siluszyk, M.; Tomasik, L.; Wawrzaszek, A.; Wawrzynczak, A. Evaluating the relationship between strong geomagnetic storms and electric grid failures in Poland using the geoelectric field as a GIC proxy. J. Space Weather Space Clim. 2021, 11, 30. [Google Scholar] [CrossRef]
- Bolduc, L. GIC observations and studies in the Hydro-Québec power system. J. Atmos.-Solar Terr. Phys. 2002, 64, 1793–1802. [Google Scholar] [CrossRef]
- Wik, M.; Viljanen, A.; Pirjola, R.; Pulkkinen, A.; Wintoft, P.; Lundstedt, H. Calculation of geomagnetically induced currents in the 400 kV power grid in southern Sweden. Space Weather 2008, 6, 7. [Google Scholar] [CrossRef]
- Carter, B.A.; Yizengaw, E.; Pradipta, R.; Weygand, J.M.; Piersanti, M.; Pulkkinen, A.; Moldwin, M.B.; Norman, R.; Zhang, K. Geomagnetically induced currents around the world during the 17 March 2015 storm. J. Geophys. Res. Space Phys. 2016, 121, 496–507. [Google Scholar] [CrossRef]
- Anuar, N.M.; Kasran, F.A.M.; Zatul, I.A.L.; Ab Rahim, S.A.E.; Manut, A.; Jusoh, M.H.; Hadi, N.A.; Yoshikawa, A. Estimation of Time Derivative of Horizontal Geomagnetic Component for GIC Assesment in Malaysia during Quiet Period. In Proceedings of the 8th International Conference on System Engineering and Technology (ICSET), Bandung, Indonesia, 15–16 October 2018; Institute of Electrical and Electronics Engineers Inc.: Bandung, Indonesia, 2018; pp. 118–122. [Google Scholar]
- Pulkkinen, A.; Lindahl, S.; Viljanen, A.; Pirjola, R. Geomagnetic storm of 29–31 October 2003: Geomagnetically induced currents and their relation to problems in the Swedish high-voltage power transmission system. Space Weather 2005, 3. [Google Scholar] [CrossRef]
- Zois, J.P. Solar activity and transformer failures in the Greek national electric grid. J. Space Weather Space Clim. 2013, 3, A32. [Google Scholar] [CrossRef]
- Cid, C.; Guerrero, A.; Saiz, E.; Halford, A.J.; Kellerman, A.C. Developing the LDi and LCi geomagnetic indices, an example of application of the AULs framework. Space Weather 2019, 18, e2019SW002171. [Google Scholar] [CrossRef]
- Tozzi, R.; De Michelis, P.; Coco, I.; Giannattasio, F. A preliminary risk assessment of geomagnetically induced currents over the Italian territory. Space Weather 2019, 17, 46–58. [Google Scholar] [CrossRef]
- Berrilli, F.; Bifaretti, S.; Bonaiuto, V.; Consolini, G.; Del Moro, D.; Orrù, L.; Santo, L.; Silletti, F.; Spena, A.; Terlizzi, C. A Statistical Approach to Analyze Possible Correlations Between Space Weather Events and Recorded Failures on the Italian Transmission Grid. In Proceedings of the 2022 AEIT International Annual Conference (AEIT), Rome, Italy, 3–5 October 2022; pp. 1–6. [Google Scholar]
- Hejda, P.; Bochníček, J. Geomagnetically induced pipe-to-soil voltages in the Czech oil pipelines during October–November 2003. Ann. Geophys. 2005, 23, 3089–3093. [Google Scholar] [CrossRef]
- Vybostokova, T.; Svanda, M. Statistical Analysis of the Correlation between Anomalies in the Czech Electric Power Grid and Geomagnetic Activity. Space Weather 2019, 17, 1208–1218. [Google Scholar] [CrossRef]
- Svanda, M.; Mourenas, D.; Zertova, K.; Vybostokova, T. Immediate and delayed responses of power lines and transformers in the Czech electric power grid to geomagnetic storms. J. Space Weather Space Clim. 2020, 10, 26. [Google Scholar] [CrossRef]
- Vybostokova, T.; Svanda, M. Correlation of anomaly rates in the Slovak electric transmission grid with geomagnetic activity. Adv. Space Res. 2022, 70, 3769–3780. [Google Scholar] [CrossRef]
- Halbedl, T.; Renner, H.; Sakulin, M.; Achleitner, G. Measurement and analysis of neutral point currents in a 400-kV-network. In Proceedings of the 2014 Electric Power Quality and Supply Reliability Conference (PQ), Rakvere, Estonia, 11–13 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 65–68. [Google Scholar] [CrossRef]
- Bailey, R.L.; Halbedl, T.; Schattauer, I.; Römer, A.; Achleitner, G.; Beggan, C.D.; Wesztergom, V.; Egli, R.; Leonhardt, R. Modelling geomagnetically induced currents in midlatitude Central Europe using a thin-sheet approach. Ann. Geophys. 2017, 35, 751–761. [Google Scholar] [CrossRef]
- Gil, A.; Berendt-Marchel, M.; Modzelewska, R.; Siluszyk, A.; Siluszyk, M.; Wawrzaszek, A.; Wawrzynczak, A. Analysis of Geoeffective Impulsive Events on the Sun During the First Half of Solar Cycle 24. Sol. Phys. 2023, 298, 26. [Google Scholar] [CrossRef]
- Abda, Z.M.K.; Aziz, N.F.A.; Kadir, M.Z.A.A.; Rhazali, Z.A. A Review of Geomagnetically Induced Current Effects on Electrical Power System: Principles and Theory. IEEE Access 2020, 8, 200237–200258. [Google Scholar] [CrossRef]
- Rajput, V.N.; Boteler, D.H.; Rana, N.; Saiyed, M.; Anjana, S.; Shah, M. Insight into impact of geomagnetically induced currents on power systems: Overview, challenges and mitigation. Electr. Power Syst. Res. 2021, 192, 106927. [Google Scholar] [CrossRef]
- Boteler, D.H.; Pirjola, R.J. Modeling geomagnetically induced currents. Space Weather 2017, 15, 258–276. [Google Scholar] [CrossRef]
- Viljanen, A.; Kauristie, K.; Pajunpää, K. On induction effects at EISCAT and IMAGE magnetometer stations. Geophys. J. Int. 1995, 121, 893–906. [Google Scholar] [CrossRef][Green Version]
- Dimmock, A.P.; Rosenqvist, L.; Hall, J.O.; Viljanen, A.; Yordanova, E.; Honkonen, I.; André, M.; Sjöberg, E.C. The GIC and geomagnetic response over Fennoscandia to the 7–8 September 2017 geomagnetic storm. Space Weather 2019, 17, 989–1010. [Google Scholar] [CrossRef]
- Dimmock, A.P.; Welling, D.T.; Rosenqvist, L.; Forsyth, C.; Freeman, M.P.; Rae, I.J.; Viljanen, A.; Vandegriff, E.; Boynton, R.J.; Balikhin, M.A.; et al. Modeling the geomagnetic response to the September 2017 space weather event over Fennoscandia using the space weather modeling framework: Studying the impacts of spatial resolution. Space Weather 2021, 19, e02683. [Google Scholar] [CrossRef]
- Gjerloev, J.W. The SuperMAG data processing technique. J. Geophys. Res. 2012, 117, A09213. [Google Scholar] [CrossRef]
- Clilverd, M.A.; Rodger, C.J.; Freeman, M.P.; Brundell, J.B.; Mac Manus, D.H.; Dalzell, M.; Clarke, E.; Thomson, A.W.P.; Richardson, G.S.; MacLeod, F.; et al. Geomagnetically induced currents during the 07–08 September 2017 disturbed period: A global perspective. J. Space Weather. Space Clim. 2021, 11, 33. [Google Scholar] [CrossRef]
- Jankowski, J.; Sucksdorff, C. Iaga Guide for Magnetic Measurements and Observatory Practice; International Association of Geomagnetism and Aeronomy: Paris, France, 1996. [Google Scholar]
- Wawrzaszek, A.; Gil, A.; Modzelewska, R.; Tsurutani, B.T.; Wawrzaszek, R. Analysis of Large Geomagnetically Induced Currents During the 7–8 September 2017 Storm: Geoelectric Field Mapping. Space Weather 2023, 21, e2022SW003383. [Google Scholar] [CrossRef]
- Buonsanto, M. Ionospheric Storms—A Review. Space Sci. Rev. 1999, 88, 563–601. [Google Scholar] [CrossRef]
- Boteler, D.H.; Pirola, R.J.; Nevanlinna, H. The effects of geomagnetic disturbances on electrical systems at the Earth’s surface. Adv. Space Res. 1998, 22, 17–27. [Google Scholar] [CrossRef]
- Viljanen, A.; Amm, O.; Pirjola, R. Modeling geomagnetically induced currents during different ionospheric situations. J. Geophys. Res. 1999, 104, 28059–28071. [Google Scholar] [CrossRef]
- Trichtchenko, L.; Boteler, D.H. Modelling geomagnetically induced currents using geomagnetic indices and data. IEEE Trans. Plasma Sci. 2004, 2004 32, 1459–1467. [Google Scholar] [CrossRef]
- Viljanen, A. Relation of Geomagnetically Induced Currents and Local Geomagnetic 700 Variations. IEEE Trans. Power Deliv. 1998, 13, 1285–1290. [Google Scholar] [CrossRef]
- Mac Manus, D.H.; Rodger, C.J.; Dalzell, M.; Thomson, A.W.P.; Clilverd, M.A.; Petersen, T.; Wolf, M.M.; Thomson, N.R.; Divett, T. Long term Geomagnetically Induced Current Observations in New Zealand: Earth return Corrections and Geomagnetic Field Driver. Space Weather 2017, 15, 1020–1038. [Google Scholar] [CrossRef]
- Kappenman, J. Storm sudden commencement events and the associated geomagnetically induced current risks to ground-based systems at low latitude and mid latitude locations. Space Weather 2003, 1, 1016. [Google Scholar] [CrossRef]
- Viljanen, A.; Pirjola, R. Influence of spatial variations of the geoelectric field on geomagnetically induced currents. J. Space Weather. Space Clim. 2017, 7, A22. [Google Scholar] [CrossRef]
- Svanda, M.; Smickova, A.; Vybostokova, T. Modelling of geomagnetically induced currents in the Czech transmission grid. Earth Planets Space 2021, 73, 229. [Google Scholar] [CrossRef]
- Marshall, R.A.; Waters, C.L.; Sciffer, M.D. Spectral analysis of pipe-to-soil potentials with variations of the Earth’s magnetic field in the Australian region. Space Weather 2010, 8, S05002. [Google Scholar] [CrossRef]
- Tozzi, R.; Coco, I.; De Michelis, P.; Giannattasio, F. Latitudinal dependence of geomagnetically induced currents during geomagnetic storms. Ann. Geophys. 2019, 62, GM448. [Google Scholar] [CrossRef]
- Boteler, D.H.; Pirjola, R.J.; Marti, L. Analytic calculation of geoelectric fields due to geomagnetic disturbances: A test case. IEEE Access 2019, 7, 147029. [Google Scholar] [CrossRef]
- Boteler, D.H.; Pirjola, R.J. Numerical calculation of geoelectric fields that affect critical infrastructure. Int. J. Geosci. 2019, 10, 930–949. [Google Scholar] [CrossRef]
- Adam, A.; Pracser, E.; Wesztergom, V. Estimation of the electric resistivity distribution (EURHOM) in the European lithosphere in the frame of the EURISGIC WP2 project. Acta Geod. Geophys. Hung. 2012, 47, 377–387. [Google Scholar] [CrossRef]
- Viljanen, A.; Pirjola, R.; Prácser, E.; Katkalov, J.; Wik, M. Geomagnetically induced currents in Europe: Modelled occurrence in a continent-wide power grid. J. Space Weather. Space Clim. 2014, 4, A09. [Google Scholar] [CrossRef]
- Boteler, D. On choosing Fourier transforms for practical geoscience applications. Int. J. Geosci. 2012, 3, 952–959. [Google Scholar] [CrossRef]
- Viljanen, A.; Pirjola, R.J. Geomagnetically induced currents in the Finnish high-voltage power system. Surv. Geophys. 1994, 15, 383–408. [Google Scholar] [CrossRef]
- Lehtinen, M.; Pirjola, R.J. Currents produced in earthed conductor networks by geomagnetically-induced electric fields. Ann. Geophys. 1985, 1985 3, 479–484. [Google Scholar]
- Pirjola, R.; Lehtinen, M. Currents produced in the Finnish 400 kV power transmission grid and in the Finnish natural gas pipeline by geomagnetically induced electric fields. Ann. Geophys. 1985, 3, 485–491. [Google Scholar]
- Ni, Y.F.; Wang, Z.D.; Jarman, P. GIC Simulation Study for Part of UK Transmission System by ATP/EMTP. In Proceedings of the IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Viljanen, A.; Koistinen, A.; Pajunpää, K.; Pirjola, R.; Posio, P.; Pulkkinen, A. Recordings of Geomagnetically Induced Currents in the Finnish Natural Gas Pipeline-Summary of an 11-year Period. Geophysica 2010, 46, 59–67. [Google Scholar]
- Kozyreva, O.V.; Pilipenko, V.A.; Belakhovsky, V.B.; Sakharov, Y.A. Ground geomagnetic field and GIC response to March 17, 2015, storm. Earth Planets Space 2018, 70, 157. [Google Scholar] [CrossRef]
- Zois, J.P. Solar activity and transformer failures in the Greek national electric grid I: Linear phenomena, talk given during the 8th. In European Space Weather Week-Session 3A, GIC Advances and Developing Mitigation Procedures; University of Namur: Namur, Belgium, 2011. [Google Scholar]
- Torta, J.M.; Serrano, L.; Regué, J.R.; Sánchez, A.M.; Roldán, E. Geomagnetically induced currents in a power grid of northeastern Spain. Space Weather 2012, 10. [Google Scholar] [CrossRef]
- Marsal, S.; Torta, J.M.; Curto, J.J.; Canillas-Pérez, V.; Cid, O.; Ibańez, M.; Marcuello, A. Validating GIC modeling in the Spanish power grid by differential magnetometry. Space Weather 2021, 19, e2021SW002905. [Google Scholar] [CrossRef]
- Torta, J.M.; Marsal, S.; Ledo, J.; Queralt, P.; Canillas-Perez, V.; Pina-Varas, P.; Curto, J.J.; Marcuello, A.; Martí, A. New detailed modeling of GICs in the Spanish power transmission grid. Space Weather 2021, 19, e2021SW002805. [Google Scholar] [CrossRef]
- Marsal, S.; Torta, J.M.; Canillas-Perez, V.; Curto, J.J. A new standalone tool for DC-equivalent network generation and GIC calculation in power grids with multiple voltage levels. Space Weather 2022, 20, e2021SW002984. [Google Scholar] [CrossRef]
- Torta, J.M.; Marsal, S.; Pina-Varas, P.; Hafizi, R.; Marti, A.; Campanya, J.; Canillas-Pérez, V.; Curto, J.J.; Ledo, J.; Queralt, P.; et al. Expected geomagnetically induced currents in the Spanish islands power transmission grids. Space Weather 2023, 21, e2023SW003426. [Google Scholar] [CrossRef]
- Pirjola, R. Electromagnetic induction in the Earth by a plane wave or by fields of line current harmonic in time and space. Geophysica 1982, 18, 1–161. [Google Scholar]
- Piersanti, M.; De Michelis, P.; Del Moro, D.; Tozzi, R.; Pezzopane, M.; Consolini, G.; Marcucci, M.F.; Laurenza, M.; Di Matteo, S.; Pignalberi, A.; et al. From the Sun to Earth: Effects of the 25 August 2018 geomagnetic storm. Ann. Geophys. 2020, 38, 703–724. [Google Scholar] [CrossRef]
- Gonzalez, W.D.; Joselyn, J.A.; Kamide, Y.; Kroehl, H.W.; Rostoker, G.; Tsurutani, B.T.; Vasyliunas, V.M. What is a geomagnetic storm? J. Geophys. 1994, 99, 5771–5792. [Google Scholar] [CrossRef]
- Halbedl, T.; Renner, H.; Bailey, R.L.; Leonhardt, R.; Achleitner, G. Analysis of the impact of geomagnetic disturbances on the Austrian transmission grid. In Proceedings of the 19th Power Systems Computation Conference, Genoa, Italy, 20–24 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Bailey, R.L.; Halbedl, T.; Schattauer, I.; Achleitner, G.; Leonhardt, R. Validating GIC models with measurements in Austria: Evaluation of accuracy and sensitivity to input parameters. Space Weather 2018, 16, 887–902. [Google Scholar] [CrossRef]
- Albert, D.; Schachinger, P.; Bailey, R.L.; Renner, H.; Achleitner, G. Analysis of long-term GIC measurements in transformers in Austria. Space Weather 2022, 20, e2021SW002912. [Google Scholar] [CrossRef]
- Bailey, R.L.; Leonhardt, R. Automated detection of geomagnetic storms with heightened risk of GIC. Earth Planets Space 2016, 68, 716. [Google Scholar] [CrossRef]
- Bailey, R.L.; Leonhardt, R.; Möstl, C.; Beggan, C.; Reiss, M.A.; Bhaskar, A.; Weiss, A.J. Forecasting GICs and geoelectric fields from solar wind data using LSTMs: Application in Austria. Space Weather 2022, 20, e2021SW002907. [Google Scholar] [CrossRef]
- Raport Najwyzszej Izby Kontroli. Informacja o wynikach kontroli. In Zapewnienie Mocy Wytworczych w Elektroenergetyce Konwencjonalnej, KGP-4101-001-00/2014, Nr ewid. 17/2015/P/14/018/KGP, Warszawa; 2015. Available online: https://www.nik.gov.pl/kontrole/P/14/018/KGP/ (accessed on 15 July 2023).
- Gil, A.; Modzelewska, R.; Moskwa, S.; Siluszyk, A.; Siluszyk, M.; Wawrzaszek, A.; Wawrzynczak, A. Signs of geoeffective space weather events in cosmic rays during the first half of the solar cycle 24. In NMDB@Home 2020; Kiel University Publishing: Kiel, Germany, 2021; pp. 119–124. [Google Scholar] [CrossRef]
- Gil, A.; Modzelewska, R.; Moskwa, S.; Siluszyk, A.; Siluszyk, M.; Wawrzynczak, A.; Pozoga, M.; Tomasik, L. The Solar Event of 14–15 July 2012 and Its Geoeffectiveness. Sol. Phys. 2020, 295, 135. [Google Scholar] [CrossRef]
- Gil, A.; Modzelewska, R.; Wawrzaszek, A.; Piekart, B.; Milosz, T. Solar Rotation Multiples in Space-Weather Effects. Sol. Phys. 2021, 296, 128. [Google Scholar] [CrossRef]
- Viljanen, A.; Pirjola, R. Statistics on geomagnetically-induced currents in the Finnish 400 kV power system based on recordings of geomagnetic variations. J. Geomagnet. Geoelectr. 1989, 41, 411–420. [Google Scholar] [CrossRef]
- Gil, A.; Glavan, V.; Wawrzaszek, A.; Modzelewska, R.; Tomasik, L. Katz Fractal Dimension of Geoelectric Field during Severe Geomagnetic Storms. Entropy 2021, 23, 1531. [Google Scholar] [CrossRef] [PubMed]
- Gil, A.; Modzelewska, R.; Moskwa, S.; Siluszyk, A.; Siluszyk, M.; Wawrzynczak, A.; Pozoga, M.; Domijanski, S. Transmission Lines in Poland and Space Weather Effects. Energies 2020, 13, 2359. [Google Scholar] [CrossRef]
- Gaunt, C.T.; Coetzee, G. Transformer failures in regions incorrectly considered to have low GIC-risk. In Power Tech; Institute of Electrical and Electronics Engineers: Lausanne, Switzerland, 2007; pp. 807–812. [Google Scholar] [CrossRef]
- Bejmert, D.; Boehme, K.; Kereit, M.; Rebizant, W. HV Transformer Protection and Stabilization under Geomagnetically Induced Currents. Energies 2020, 13, 4693. [Google Scholar] [CrossRef]
- Panicali, A.R.; Barbosa, C.F. Effect of the integration path on grounding measurements. Electr. Power Syst. Res. 2021, 194, 107062. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).