Abstract
Laves phases crystallize in simple structures and are very common intermetallic phases that can form from combinations of elements throughout the periodic table, giving a huge number of known examples. A special feature of AB2 or AB5 phases is the ability to absorb hydrogen. This study attempts to collect, systematize and summarize the knowledge about RMn2Hx (R: Tb, Gd, Ho, Dy, Er, Sm, Nd and Y) hydrides available in the literature that is mainly related to structural and magnetic transformations. Due to the enormous wealth of data, the analysis focused on hydrides with x < 4.5 H/f.u., i.e., hydrides obtained at relatively low pressure (less than a few bars). The hydrides obtained in this way can be treated as potential hydrogen stores, which undoubtedly accounts for their current attractiveness.
1. Introduction
1.1. Laves Phases
One of the most widespread and most studied groups of solids is the metallic phases. These phases are divided into simple phases (metallic elements), solid solutions and intermetallic phases. Solid solutions include substitution and interstitial solutions. Interstitial solutions are formed when relatively small atoms of a solute element do not occupy atomic positions, but positions in the interstitial voids of the solvent. A characteristic feature of solid solutions is that they retain the crystallographic structure of the solvent. Intermetallic phases assume crystal structures different from those of the individual components of the phase. In general, intermetallic phases are described by the formula AnBm and are divided into the following types according to the adopted classification [1,2,3]:
- Phases with a dense filling of space (Laves phases), which are classified according to the size of atoms/ions;
- Electronic phases, which are classified according to the electron concentration, i.e., the ratio of the number of valence electrons to the number of atoms in the unit cell;
- Phases with mixed, metallic-ionic and metallic-covalent bonds.
The most important properties of the Laves phases include the following:
- They are metal alloys with the general stoichiometric formula AB2;
- The main factor influencing their formation is the ratio of the radii of the component atoms, and rA/rB is equal, theoretically, to 1.225. In fact, this ratio for the Laves phases is within the range of 1.05–1.68 Å. Here, Å refers to larger atoms (e.g., rare earths), and B refers to smaller atoms (e.g., Cu, Zn, Fe, Mn, Cr, etc.);
- They do not create secondary solutions;
- They exhibit an almost purely metallic type of bonding;
- They are phases with the densest space filling;
- They crystallize in one of three homothetic types, C14, C15 and C36, as determined by the value of the electron concentration [4].
The RMn2 intermetallic compounds crystallize either in the hexagonal C14 type for R = Pr, Nd, Sm, Ho, Er, Tm and Lu or in the cubic C15 type for R = Y, Sm, Gd, Tb, Dy and Ho [5,6,7,8,9,10,11,12,13,14]. Other elements (A: La, Ce, Eu and Yb) do not form stable intermetallic compounds with Mn [15].
A more detailed description of the crystal structures of Laves C14 and C15 phases is presented in Supplementary Material.
1.2. Structural and Magnetic Properties of RMn2 Compounds
The RMn2 compounds have been widely studied because of their very interesting structural and magnetic properties. Changes of the unit cells for RMn2 as a function of the temperature are presented in Figure 1a [16]. For the (Tb, Gd, Sm, Nd, Pr, Y)Mn2 compounds, the first-order phase transition is observed, and temperature dilatometer and X-ray diffraction measurements revealed significant increases in the volume of unit cells of these alloys at temperatures below 105 K. The magnetic ordering was also observed below the temperatures of the structural changes [17,18,19]. The largest, an almost 5% change in volume, was recorded for YMn2. This significant magneto-volume effect is related to the appearance of a well-localized magnetic moment in the Mn sublattice (~2.7μB) below the magnetic ordering temperature [20]. The (Er, Ho, Dy)Mn2 compounds do not show changes in the volume cell; they undergo a second-order phase transition in the temperature range of 15–35 K [14,21].
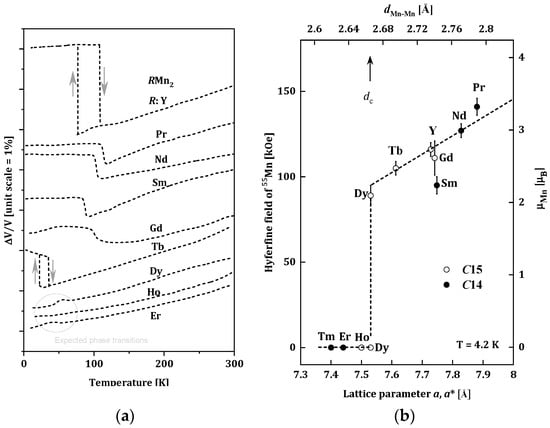
Figure 1.
(a) Changes of the unit cells for RMn2 as a function of the temperature for RMn2 [16]; (b) Relation between the 55Mn hyperfine field Hself and the lattice parameter of RMn2 at 4.2 K. The transferred hyperfine fields from rare-earth moments are subtracted from the observed ones. The effective lattice parameter of C14 compounds (closed circles) is given by aeff = (3a2c)1/3. The scale for the estimated Mn moment from Hself is given on the right-hand side [22].
The type of the phase transition can be related to the occurrence of a magnetic moment of Mn atoms or its absence. The measurements of the hyperfine field on the 55Mn nuclei in RMn2 compounds carried out by Yoshimura (Figure 1b) indicate that below a certain distance of ~2.66 Å between the nearest Mn atoms (dMn-Mn), the localized magnetic moment of the Mn atoms is not observed. This distance is called the critical distance and denoted as dc [22]. Based on the dMn-Mn distance, RMn2 compounds can be divided into three groups [23]:
- dMn-Mn < dc, (LuMn2, ErMn2, TmMn2), where the Mn subnet is non-magnetic, and the Er and Tm sublattices are ferromagnetic [24];
- dMn-Mn > dc, (NdMn2, PrMn2), where the dominant Mn magnetic sublattice is stable and enforces antiferromagnetic ordering in the sublattice of R-atoms with the R-Mn type interaction [25];
- dMn-Mn ~ dc, (GdMn2, TbMn2, DyMn2, HoMn2, YMn2), where the Mn sublattice is on the verge of stability. Generally, non-collinear magnetic structures are observed in this group of compounds. In some cases (TbMn2, DyMn2, HoMn2), only a part of the Mn atoms carries a magnetic moment [20,26,27,28,29,30,31,32,33,34].
The magnetism of the RMn2 compounds is related to the electronic structure of Mn and R atoms. Mn has an unfilled outer 3d electron shell affecting the crystalline field from other ions. However, in the R atoms, the unfilled inner 4f electron shell is shielded by the 5p outer shell, which facilitates the behavior similar to that noted for the free ion.
In the RMn2 compounds, three types of exchange interactions can be distinguished as follows:
- Between 3d–3d magnetic moments (Mn–Mn),
- Between 3d–4f moments (Mn–R),
- Between localized 4f–4f moments (R–R).
The strongest among the above is the 3d–3d exchange interaction, as evidenced by the high temperature of ordering of the magnetic relationship with non-magnetic rare earths (YMn2, TN ≈ 105 K). The band model, which is applicable here, assumes that the difference in concentration between electrons with spins ↓ and ↑ is responsible for the formation of the magnetic moment.
The weakest is the 4f–4f interaction, as indicated by low temperatures of magnetic ordering of the ErMn2 and TmMn2 compounds with the non-magnetic Mn sublattice (Figure 1a,b). The R atoms having an unfilled 4f electron shell are characterized by well-localized magnetic moments; the wave functions that describe them have a short range in comparison to the distance between atoms (magnetic moments). The magnitude of the interaction of 4f–4f depends on the density of the polarized conduction electrons; their oscillating nature as a function of distance is described by the RKKY theory.
The magnetic interaction 3d–4f has an intermediate value between 3d–3d and 4f–4f. It occurs mainly through the polarization of electrons of 5d rare earth atoms [35].
1.3. Hydrogen in Metals
Rare earth (R) metals react with hydrogen forming stable di- and trihydrides. The RH2 dihydrides are very stable, with reported formation enthalpies of about −200 kJ/molH2; thus, they decompose in a vacuum, releasing hydrogen and forming individual RE metals at very high temperatures only [36]. On the other hand, manganese, which is also the main building block of the discussed RMn2Hx structures, behaves differently under the influence of hydrogen in comparison to RHx. At ambient pressure conditions and room temperature, the subhydride Mn2H is the only stable compound. With increasing pressure, MnH is stabilized, and then hydrogen-rich hydrides appear at higher pressure [37].
A simplified scheme of hydrogen penetration into the crystal structure of the metal (intermetallic compound) can be divided into three stages (Figure 2): (a) Physisorption: gaseous hydrogen molecules interact with electrons on the metal surface using weak attractive van der Waals forces; (b) Chemical adsorption: hydrogen molecules dissociate, overcoming the surface energy barrier, and form a metallic hydrogen bond; (c) Absorption: in this step, the chemisorbed hydrogen atom can jump to the subsurface layer to finally diffuse through the crystalline structure of the metallic host [38].
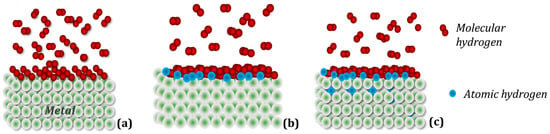
Figure 2.
Simplified mechanism of hydrogen absorption in metal. (a) Physical adsorption: hydrogen molecules adhere to the metal surface, forming several layers; (b) Chemical adsorption: dissociated hydrogen molecules of the layer in direct contact with the metal form chemical bonds with it; (c) Absorption: hydrogen atoms diffuse into the parent metal lattice.
After absorption, the hydrogen atoms/ions remain in the sites of the crystal structure until they are given a surplus of energy necessary to overcome the diffusion barrier as a result of thermal activation. Under these conditions, the diffusion coefficient satisfies the classical Arrhenius relationship: D = D0 exp (−Ea/kT), where D0 is the diffusion constant. Assuming the simple activated diffusion, the typical diffusion constant for H in intermetallic compounds equals 1–103 mm2/s and Ea = 45 kJ/mol at room temperature [39,40]. Researchers also point to the dependence of the D0 and the T on the structure on the structure of the metal. For example, for Pd (fcc structure), D0 = 2.9 × 10−3 cm2/s and Ea = 0.230 eV, while Do = 4.2 × 10−4 cm2/s and Ea = 0.40 eV for Fe (bcc structure) [41].
One of the first experiments indicating the dissociation of H2 molecules in the process of its absorption by metals was the study of the p-c-T relationship (hydrogen pressure-concentration-temperature) [39]. In numerous metal hydrides, hydrogen atoms are characterized by high mobility already at room temperature, especially when the number of available positions is greater than the number of hydrogen atoms. Hydrogen atoms can jump from one position to another without creating a crystallographic ordered structure—the positioning is accidental. The frequency of hydrogen jumps is huge (e.g., in vanadium hydrides at room temperature, it is ~1010–1012 Hz) [39]. With the lowering of the hydride temperature, the frequency decreases. Therefore, it may also happen that hydrogen atoms occupy selected positions in an orderly manner, and they create a superstructure. Skripov states that in many hydrides of the Laves phase, even two types of hydrogen jumping motions with different characteristic jump rates coexist. While the slower jump process is responsible for long-distance diffusion, the faster process corresponds to the localized movement of hydrogen over small groups of interstitial sites. In some of the Laves-phase compounds, the localized hydrogen motion is not ‘frozen out’ on the frequency scale of 107 to 108 Hz down to 20 K [42]. At low temperatures, there is also the possibility of non-activation, tunnel transitions of the hydrogen atom from one position to another [38,43,44].
Figure 3a shows the typical hydrogen absorption isotherms in metal. The isotherms form a phase diagram of the equilibrium pressure as a function of the hydrogen concentration Peq (x), in which three essential areas can be distinguished: (i) the α region is the “solid” solution of hydrogen in the parent metal, where the hydrogen pressure p increases with the hydrogen content x according to Sievert’s law p = (Ks c)2 (K—Sievert’s constant, c—hydrogen concentration), (ii) the two-phase region (α + β) and (iii) the β region—metal hydride. As the temperature increases, the latter narrows and disappears at the critical temperature Tcrit, which is characteristic for a given element. The isotherms in the middle region show a hydride characteristic plateau, corresponding to the equilibrium pressure as a function of the hydrogen concentration.
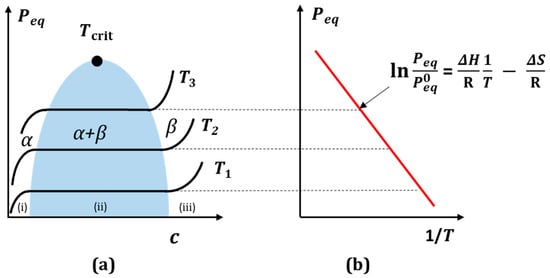
Figure 3.
(a) Schematic plot of hydrogen absorption in metal (p-c-T isotherms). Peq—gas pressure, c—hydrogen concentration in the metal; (b) Construction of the Van’t Hoff relation. Based on [45,46].
The equilibrium pressure zone is ideally suited for the isothermal absorption and desorption of hydrogen from metal. The state of equilibrium can be described by a phase diagram analogous to the Van der Waals diagram of the non-ideal gas. Peq equilibrium pressure is associated with changes in enthalpy (ΔH) and entropy (ΔS) in the two-phase region via the empirical temperature of the Van’t Hoff relationship (Figure 3b) [45,46]. For a typical equilibrium pressure, e.g., for PdHx—hydride at 423 K, it is 0.1 MPa, and it is 1.0 MPa at 518 K. The critical point of this hydride is Tcrit = 565 K at x ≈ 0.25 H/f.u. [39].
The two-phase region characteristic for hydrides is related to the spinodal decomposition, which is a consequence of the long-range, attractive H-H interaction. Two phases with hydrogen concentrations x1 and x2 co-exist when the equilibrium condition is realized:
where μg is the chemical potential of hydrogen gas per molecule, and μα is the chemical potential of hydrogen in solid solution per atom. Critical points (Tcrit and xcrit) determine the condition:
Spinodal decompositions can be related to anomalous changes in the physical properties of hydrides, such as, for example, reductions in diffusion rates, fluctuations of high amplitude density or anomalies in the specific heat [40].
Metal hydrides are hard and brittle (fragile); they are obtained primarily in powder form. Due to the considerable expansion of the unit cell of the metallic element (more than a dozen or so percent) during the hydrogenation process, it is practically impossible to obtain hydride monocrystals (the single crystal is destroyed because of decrepitation). In general, metal hydrides show quite high resistance to weather (atmospheric) conditions, and they are good conductors of electricity [47].
2. RMn2Hx Hydrides
2.1. Localization of Hydrogen
The physical properties of rare earth hydrides with manganese RMn2Hx largely coincide with the properties of metal hydrides (MHx). Also, alloys of RMn2 compounds absorb hydrogen very easily. At close to atmospheric hydrogen pressure and temperatures above 100 °C, it is possible to achieve a hydrogen concentration of ~4.5 H/f.u. [48]. As noted in metal hydrides, hydrogen occupies the interatomic sites of the elements that comprise the RMn2 unit cell. There are three types of tetrahedral sites in RMn2 compounds: A2B2, AB3 and B4, where A and B represent atoms of R and Mn, respectively, surrounding the site (Figure 4). The largest and at the same time most willingly filled by hydrogen site (below x ≈ 3.5 H/f.u.) is the A2B2 type. For x ≳ 3.5 H/f.u., there is also a tendency to fill smaller sites, such as AB3 sites [49,50,51,52]. However, no B4 site filling was observed. The same types of sites occur in both C14 and C15 types of Laves phases. When filling the sites, hydrogen occupies crystallographic positions (Table 1).
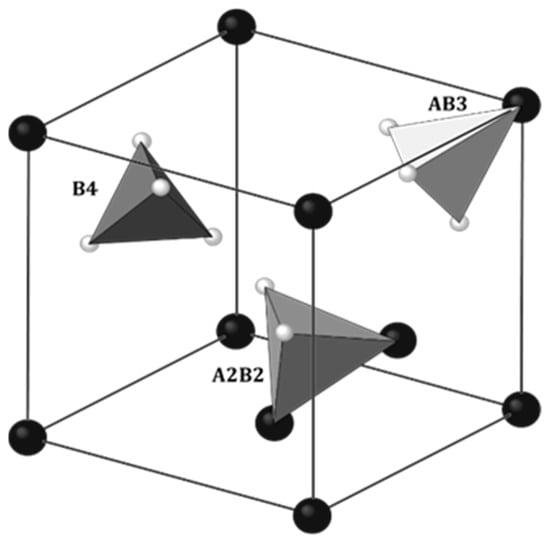
Figure 4.
Three crystallographic positions accessible for hydrogen in C15 Laves phase: 96g (inside of A2B2 tetrahedra), 32e (inside of AB3 tetrahedra) and 8b (inside of B4 tetrahedra). The Fd space group. Some atoms were removed for clarity. Big, dark balls: R; small, bright balls: Mn. Based on [51].

Table 1.
Hydrogen positions in C14 and C15 phases.
Although the number of sites is significant, every site cannot be occupied by hydrogen. Two criteria are useful: (i) the Switendick criterion [53] states that the distance dH-H must be larger than ~2.1 Å and (ii) the Westlake criterion indicates that the radius of the sphere available for hydrogen cannot be less than ~0.37 Å. [54]. As an effect, criteria preclude occupancy of A2B2 tetrahedrons that have a common wall, and the B4 site is not available for hydrogen due to size restrictions. The Switendick criterion, confirmed in neutron measurements [55,56], largely determines the maximum content of absorbed hydrogen. The theoretically determined maximum hydrogen concentration in RT2Hx (R: rare earth, T: transition metal = Y, Mn) compounds is therefore 6.0 H/f.u. [57]. Only the use of ultra-high hydrogen pressures of the order of 103 MPa led to the formation of RMn2H6 hydrides; the first being YMn2H6 [58,59]. Highly hydrogenated (x ≳ 4.5 H/f.u.) compounds show different physical properties compared to low-hydrogen compounds (x ≲ 4.5 H/f.u.) [60,61] and will not be discussed in this study.
2.2. Sample Preparation and Dependence of ΔV/V versus Hydrogen Content
In the discussed hydrides, the sample preparation was similar and usually involved the following scenario.
The host materials (RMn2) were prepared from high purity elements using the standard induction melting technique under argon atmosphere. Next, materials were usually annealed to obtain a single-phase compound. The RMn2 samples were saturated with hydrogen using a standard volumetric method (Sievert) to obtain RMn2Hx hydrides in the typical range of x: 0 < x < 4.3–4.5 [7,8,9,55,62,63,64,65,66,67]. The first test after hydrogen saturation was XRD measurements at 300 K. As a representative example, the HoMn2Hx_C15 diffractogram is presented in Figure 5a. The most visible effect of hydrogen absorption by the sample is the shift of the diffraction lines towards smaller angles (in 2 theta), which means an increase in the distance between atoms in the cell, and consequently an increase in the unit volume of the cell with x.
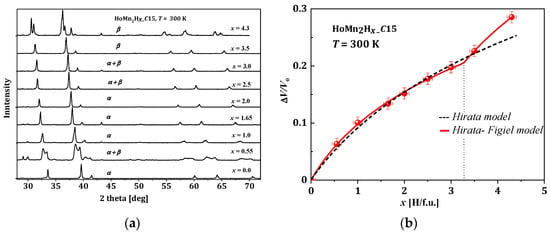
Figure 5.
HoMn2Hx. (a) The XRD patterns for different x; here, α represents the cubic phase (), and β represents the rhombohedral phase (); (b) Relative change in the unit cell volume as a function of x [66].
Even at room temperature, the RMn2Hx hydrides do not persist in the crystallographic structure of the host compound. For the HoMn2Hx_C15 hydride, a combination of the cubic (α) and rhombohedral distortion (β) is observed (Figure 5a). The obtained results are in agreement with [68]. To compare lattice parameters of hydrides with different crystallographic structures, their parameters were converted into parameters of the pseudo-cubic cell considering abundance phases, if the system is not a single-phase system. For example, the lattice parameters of the rhombohedral phase were converted into lattice parameters of the pseudo-cubic phase according to the relationship reported below:
where aδ and cδ are lattice parameters of the rhombohedral phase (space group: , nr166, setting: 1) [66].
The relative volume change in unit cell versus hydrogen content in HoMn2Hx_C15 is depicted in Figure 5b. The first ‘model’ that attempted to describe the relation between ΔV/V0 and x was just a linear relationship. The next one, the Hirata model, only correctly reproduces the lowest range of x (0 < x < 3.0) (Figure 5b, dashed line) [69], and its development was proposed by Figiel et al. [51]. In the last one (farther: Hirata–Figiel model), the authors assume a two-stage approach to occupying interstitial sites (Figure 5b red line). Initially, with a characteristic parameter Xc < 3.0–3.5 H/f.u. (see below), the A2B2 type sites are filled (this part is identical with Hirata model). Next, above Xc > 3.0–3.5 H/f.u., the AB3 type sites are also occupied. It is represented by a characteristic break in the red curve (x~3.2 H/f.u., Figure 5). The Hirata-Figiel model is described according to the relationship described below [51].
where ΔV/V0 is the relative increase in unit cell volume; B0 is a parameter of the lattice contraction, a quantity analogous to the bulk modulus at starting concentration related to the intrinsic pressure; b is the first derivative with respect to concentration x: (Bx = B0 + bx); and P is the probability of filling the AB3 sites by hydrogen atoms for concentrations greater than Xc (P = 0 for x ≤ Xc) [34,51]. Fitted parameters for the RMn2Hx (R: Y, Dy, Gd, Tb, Ho) hydrides are presented in Table 2. For all compounds, the characteristic Xc belongs to the region of ~3.0–3.5 and probabilities of entering the AB3 interstitial sites P~0.6–0.9. This type of filling sites was also postulated in [50,51].

Table 2.
Fitted parameters for the Hirata-Figiel model.
The relative volume increase (ΔV/V0) of unit cells of hydrides determined at room temperature and depending on the hydrogen content in the sample is non-linear and can be described by the same function, indicating that this effect is determined only by the presence of hydrogen. The fits of the Hirata–Figiel model to the change in (ΔV/V0) depending on the hydrogen concentration for the various studied hydrides RMn2Hx are shown in Figure 6.
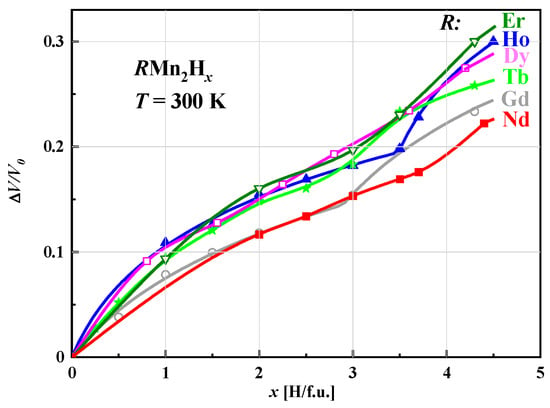
Figure 6.
Comparison of relative volume change in unit cells for RMn2Hx versus hydrogen content at RT = 300 K. Based on [7,51,65,66,67].
For x < 3.0 H/f.u., the curves, except for those corresponding to (Gd and Nd)Mn2Hx, are almost identical. At values greater than x ≈ 3.0 H/f.u., distinct behavior becomes visible with increasing x, especially for concentrations close to the maximum, where the relative increase in volume increases with the atomic number of the rare earth element.
2.3. Examples of Structural and Magnetic Transformations in RMn2Hx
With a temperature change, the RMn2Hx hydrides undergo complex phase transformations in many cases, which, combined with the often occurring multi-phase states, makes the interpretation of their X-ray diffraction magnetic transformation results extremely difficult. Some authors have even argued that it will never be possible [39]. One of the first hydride families to be studied over a wide range of x and temperature changes was YMn2Hx, showing a very wide range of structural transformations as a function of temperature. In contrast, TbMn2Hx hydride families show a very ‘modest’ spectrum of structural transformations. Very interesting are the structural and magnetic properties of HoMn2Hx hydrides, in which the base compound can crystallize in a C14 or C15 Laves phase structure, depending on the sample preparation [10].
2.3.1. YMn2Hx
Due to the similarity of its electronic structure to that of lanthanides, yttrium is classified as rare earth element. The host YMn2 compound shows a large increase (about 5%) in elemental cell volume near 100 K in X-ray diffraction measurements. A temperature hysteresis of several degrees is also observed (compare with Figure 1a). Hydrogen in the YMn2Hx induces a number of structural and magnetic transformations that best are represented by the phase diagram (Figure 7). The structural and magnetic phase diagram for YMn2Hx hydrides can be distinguished into three ranges [50,70,71,72,73,74].
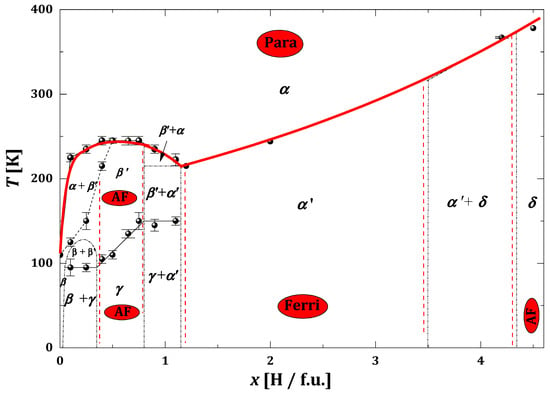
Figure 7.
Structural and magnetic phase diagram of YMn2Hx hydrides as a function of x and temperature. The thick line separates the paramagnetic area from the magnetic ordering are. Para, Ferri and AF correspond to paramagnetic, ferrimagnetic and antiferromagnetic states, respectively. Based on [50,70,71,72,73,74,75,76]. Here, α represents phase type C15; α′ indicates regular phase (P-43m); β represents the tetragonal phase (ε > 0), which is a phase with very low hydrogen content (<0.1 H/f.u.); β′ is like β but with a higher hydrogen content of 0.3 < x < 0.6; γ is a phase with tetragonal distortion but with ε < 0; and δ represents the rhombohedral phase.
- Range 1: x ≲1.2 H/f.u.
A number of phase transformations are observed. In the range of 0.4 ≲ x ≲ 0.8 and below ~245 K, the regular α phase transforms to the tetragonal β′ phase of the same type as noted in the case of YMn2 (at approx. 100 K). In the β′ phase, the lattice parameters satisfy the unequalness ε > 0, where ε = 1 − ctet/atet (atet, ctet—tetragonal structure parameters). On the other hand, below the temperature range ~100–150 K, there is a distortion to the tetragonal phase γ, in which ε < 0. The α → β transformation is accompanied by the antiferromagnetic magnetic ordering of the manganese sublattice. Below x ≈ 0.4 H/f.u. and above x ≈ 0.8 H/f.u., a combination of phases is observed: the host compound (α), the tetragonal (β) with low hydrogen content (x < 0.1 H/f.u.) and the γ phase.
- Range 2: 1.15 ≲ x ≲ 3.5
A very wide range is noted in which hydrides retain the structure of the regular phase. In this area, the hydrides exhibit a ferrimagnetic order. The ordering temperature increases from ~250 K to ~350 K with increasing hydrogen concentration. Neutron diffraction measurements for YMn2D1.15 and YMn2 (H0.64D0.36)1.15 [72,73] indicate a structural transformation from the C15 phase to the regular phase described with lower symmetry (space group: P). From these measurements, it also follows that deuterium is located in A2B2 positions, and magnetic moments of Mn atoms create two magnetic sublattices. One of them forms a non-collinear antiferromagnetic canted structure, and the other one, which is very weak (~0.1 μB), exhibits ferrimagnetic ordering. The abundance of the latter increases linearly as x increases [70].
- Range 3: 3.5 ≲ x ≲ 4.5
Below the temperature range ~300–400 K and along with the increase in hydrogen content, a structural transformation from the regular phase α′ (from the range 2) to the rhombohedral phase δ through the two-phase area (α′ + δ) occurs. The δ phase is a rhombohedral phase belonging to the spatial group [75].
Neutron diffraction studies for YMn2D4.3÷4.5 and YMn2(H0.64D0.36)4.3÷4.5 [71,72,75,76] showed an antiferromagnetic arrangement of the Mn sublattice below 360–398 K with propagation vector k = [½ ½ ½]. Mn atoms occupy two different positions, and their nearest neighbors (H or D) are also different, which explains the alternative ferro- or antiferromagnetic coupling between Mn planes. Moreover, it was also observed that the magnetic ordering of the Mn sublattice and hydrogen/deuterium ordering appeared at the same temperature. Because there are no additional reflections from the deuterium atoms, the deuterium superstructure was described with the k = 0 propagation vector. As the hydrogen content of the sample increases, the magnetic ordering temperature (Tc) of the hydride increases from about 230 K to about 400 K (the red line in Figure 7 conventionally separates the paramagnetic state from the magnetic ordering state). The reason for the increase in Tc is an increase in the elemental cell volume of the sample (by up to 30% compared to YMn2) and, consequently, an increase in the dMn-Mn interatomic distances above the critical distance dc. This results in an increase in the degree of localization of the Mn magnetic moments and therefore an increase in their exchange interaction, leading to an increase in the magnetic ordering temperature.
2.3.2. TbMn2Hx
A characteristic feature of RMn2Hx hydrides is splitting of the structural line into two (or more) components (observed) with decreasing temperature. This process is a spinodal decomposition, as previously mentioned in Chapter 1, and is clearly visible in Figure 8a. With decreasing temperature (below ~360 K), the high-temperature regular phase α splits into two phases (α0 + αr) with different hydrogen contents. In the temperature range of 220–250 K, even the third phase (αm) termed “intermediate” is observed (gray lines). The αo and αr phases occur at the lowest temperatures. Comparing lattice parameters hydrides with x = 0.5 and 1.0 and below 200 K (Figure 8b), it can be noticed that the parameters of the αo phase are very close to these of the host compounds (TbMn2), also reflecting their characteristic behavior (increases in parameters). The αo phase contains negligible amounts of hydrogen, less than ~0.05 H/f.u. This phase can be treated as a solid solution of hydrogen in the metal. The parameters of the second rich-amount hydrogen phase (αr) were estimated as ~1.6–1.8 H/f.u. [9,52]. The process of spinodal decomposition is reversible with temperature.
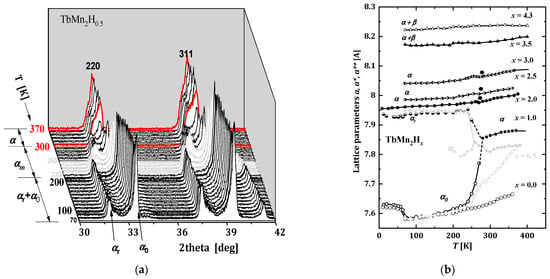
Figure 8.
(a): Evolution of the (220) and (311) XRD lines versus temperature; (b): Lattice parameters for the TbMn2Hx hydrides as a function of temperature. Symbols α and β correspond to cubic and rhombohedral distortion, respectively; αr, α0 and αm correspond to the ‘reach-amount’ hydrogen phase, low-amount hydrogen phase and ‘intermediate’ phase, respectively. The lattice parameters of the rhombohedral structure are expressed in parameters of the pseudo-cubic structure (Equation (3)). Parameters of TbMn2Hx (x = 3.5 and 4.3 H/f.u.) hydrides were determined taking into account the abundance of regular and rhombohedral phases. The dashed lines for x = 1.0 indicate the probable change in parameter values (b). Based on [9,52].
For TbMn2Hx, 1.8 ≲ x ≲ 3.3, hydrides persist one regular phase (α) in the whole temperature range. The increase in parameters for x = 2.0, 2.5, 3.0 is continuous, and weak jumps are observed (marked as black dots) only in the temperature range of 270–280 K (Figure 8b), which corresponds well to magnetic ordering temperature for these hydrides.
In the range 3.2 ≲ x ≲ 4.3 and in addition to the regular α phase, the second phase rhombohedral distortion (β) is observed. This phase, which is initially recognized as an “inclusion” of another phase, becomes dominant at the expense of the α phase as the nominal hydrogen content increases [9].
The spinodal decompositions into two phases (αo + αr) were confirmed using magnetic measurements. Figure 9a shows the dependence of magnetization as a function of temperature for TbMn2Hx (x = 0, 1.0 and 2.0 H/f.u.). The characteristic maximum for TbMn2 at ~50 K (compare the parameters that increase in Figure 1a) is also visible in the magnetization of hydride with x = 1.0 what corresponds to α0 phase. Magnetic ordering of the αr phase is estimated at ~240 K. For x = 2.0, hydride magnetization is a flat curve (100 Oe) in the whole range of temperatures with only exceedingly small irregularities at ~280 K that clearly have been expressed/exposed in the external field of 50 kOe (insert in Figure 9a). This maximum indicates antiferromagnetic ordering, as confirmed in the neutron diffraction study for TbMn2D2.0 [52]. Magnetic ordering temperature increases with increasing hydrogen content x, as represented by the gray thick line in Figure 9b. The increase of magnetic ordering temperature from ~50 K for host TbMn2 to the range of ~200–400 K for its hydrides is fascinating.
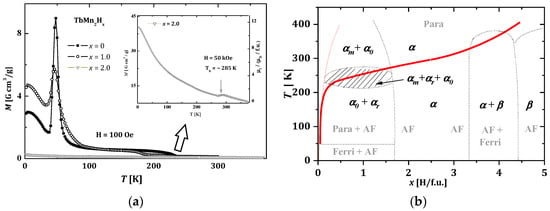
Figure 9.
(a) The dependence of the magnetization of TbMn2Hx hydrides versus temperature in the external magnetic field of 100 Oe and 50 kOe for TbMn2H2.0 (insert). Para, Ferri and AF represent paramagnetic, ferrimagnetic and antiferromagnetic states, respectively; (b) Tentative magnetic and structural hydride phase diagrams for TbMn2Hx. The thick red line separates the paramagnetic state from the state of magnetic ordering. Descriptions in gray correspond to magnetism. Based on [9,52].
This effect is related to the magnetic properties of manganese. For magnetic interactions between the magnetic moments of manganese, an important critical distance is dc = 2.71 Å. Manganese atoms located closer than dc do not form long-distance magnetic ordering, and atoms at a distance greater than dc create large magnetic moments (about 3 μB) and strongly magnetically couple together (compare with Section 1). Because hydrogen causes a strong increase in the volume of the unit cell, it also forces an increase of dMn-Mn above dc, which in turn causes the creation of magnetic order. Because the Mn-Mn interaction is strong and the ordering temperature is proportional to the exchange interaction, magnetic ordering is achieved in these hydrides at such high temperatures. Due to the nature of the exchange interaction, the magnetic moments of manganese are arranged antiferromagnetically. The influence of the interactions coming from rare earth magnetic moments is weak due to the effect of shielding their magnetic moments related to 4f electrons shells. It is reflected in weak dependence of magnetic ordering temperature of hydrides versus rare earth elements (Figure 6) [7,8,9,55,64,65,66,67].
2.3.3. GdMn2Hx
The magnetic (Figure 10a) phase diagram of GdMn2Hx is very similar to that for TbMn2Hx, and one can conventionally identify three x-ranges. In range (i) (x ≲ 1.8 H/f.u.), with decreasing temperature, there is a decay of the high-temperature regular phase into, initially, three phases with different hydrogen contents. The phase with intermediate hydrogen content rapidly disappears with decreasing temperature. The other two clearly segregate into “hydrogen-poor” (x ≲ 0.05 H/f.u.) and “hydrogen-rich” (x ≈ 1.8 H/f.u.) phases. In range (ii), corresponding to 1.8 ≲ x ≲ 3.2, there is only a regular phase throughout the temperature range. In the range (iii) above x ≈ 3.2 H/f.u., the regular phase is transformed to the rhombohedral phase through the area of coexistence of two phases, including the regular phase and the rhombohedral phase [8,55]. Also, the course of changes in lattice parameters versus temperature (Figure 10b) is very similar to those noted for TbMn2Hx. A clear spinodal decomposition is visible for x ≲ 2 H/f.u.
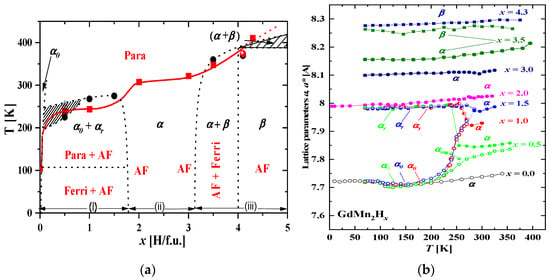
Figure 10.
GdMn2Hx. (a) Composite magnetic and structural hydride phase diagrams for GdMn2Hx. The red line separates the paramagnetic state from the magnetic ordering state. Symbols α and β correspond to cubic and rhombohedral distortion, respectively; αr, α0 and αm correspond to the ‘reach-amount’ hydrogen phase, low-amount hydrogen phase and ‘intermediate’ phase, respectively; (b) The lattice parameters. The rhombohedral structure is expressed in parameters of the pseudo-cubic structure (Equation (3)). Parameters of GdMn2Hx (x = 3.5 and 4.3 H/f.u.) hydrides were determined by taking into account the abundance of regular and rhombohedral phases [8].
2.3.4. DyMn2Hx
Structural hydride studies have also been carried out for a series of DyMn2Hx hydrides [63]. Their structural phase diagram is largely similar to the structural phase diagrams of (Gd or Tb)Mn2Hx, which have been reposted above. The phase diagram of the Dy hydrides (Figure 11) has been described using a combination of two phases: the regular (C15 type) phase denoted as α and the rhombohedral () phase denoted as β. The apostrophes (′) next to the phase symbols refer to the different hydrogen concentrations in the phase or indicate the ordered magnetic state of the sample (e.g., α and α″ for x ≈ 2.0 H/f.u.).
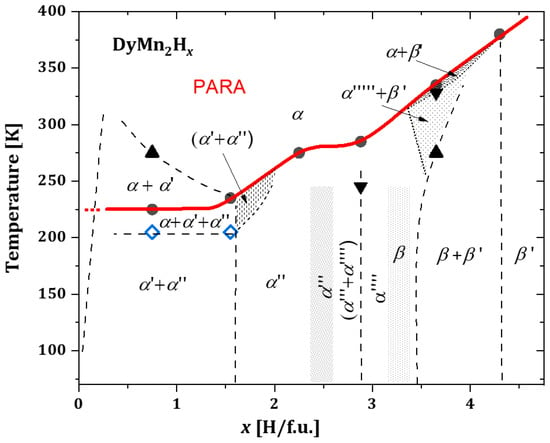
Figure 11.
Structural phase diagram of DyMn2Hx hydrides. Here, α indicates the regular phase of C15 type, and β represents the rhombohedral phase. The red line separates the paramagnetic state from the magnetic ordering state. PARA—paramagnetic state. Based on [63].
For samples with a nominal concentration of x ≲ 1.6 H/f.u., the authors observed spinodal-type decays. For TbMn2Hx (Figure 8b) in a temperature range of ~(200–250) K, a region of up to three regular phases with different hydrogen contents appears. As the temperature decreases (below 200 K), one of them disappears; there is, as already known from previous analyses, a decomposition into two regular phases with a minimum x-value (α′ phase) and a phase with x ≈ 1.6 H/f.u. (α″ phase).
The absence of structural transformations as a function of temperature can be seen for 1.8 ≲ x ≲ 2.8, which is very similar to the hydrides with Tb and Gd. Above x ≈ 2.8 H/f.u., a very narrow interval x is observed in which spinodal type decay is again observed, and it is absent for x ≈ 3.0 H/f.u.. For x ≳ 3.4, rhombohedral β phases with different x were observed below (320–380) K, and these phases transform to a regular α phase with increasing temperature.
The red line separates the paramagnetic span from the state of magnetic order, and the temperature of magnetic order increases with increasing concentration x (Figure 11).
2.3.5. HoMn2Hx_C15 and HoMn2Hx_C14
The structural phase diagrams for HoMn2Hx_C15 and HoMn2Hx_C14 proved to be extremely interesting but at the same time complicated. Although both hydride series share a common HoMn2 host (crystallizing in the Laves C15 or C14 phase), their phase diagrams are quite different from each other [7,66,68,77].
The structural phase diagram of HoMn2Hx_C15 hydrides can be divided into the following main areas (Figure 12a) [66]:
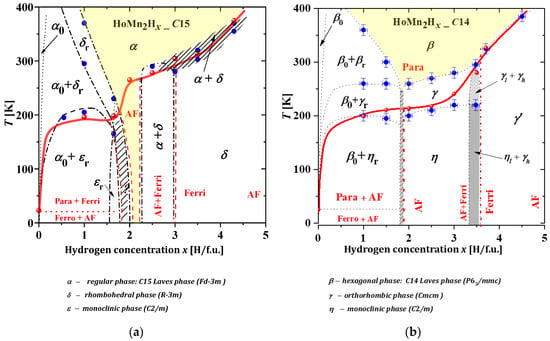
Figure 12.
The proposed phase diagrams for (a) HoMn2Hx_C15 and (b) C14 HoMn2Hx_C14 hydrides (prepared on the basis of HoMn2 host material crystallizing in C15 or C14 Laves types, respectively). The red lines separate the paramagnetic state (Para) from the magnetic ordering state. AF indicates antiferromagnetic, and Ferro and Ferri correspond to ferro- and ferrimagnetic ordering states, respectively. Blue symbols correpond to structural measurements and red ones to magnetic studies. Based on [7,66,77].
- x ≲ 2.0. In this area, two phases are observed at the lowest temperatures: “hydrogen-poor” α0 and “hydrogen-rich” εr. The α0 phase is identical to the C15-type phase of the starting compound HoMn2_C15 and contains a negligible amount of dilute hydrogen (x ≈ 0.04 H/f.u.). The εr phase is monoclinic and contains ~1.6 H/f.u. As the temperature increases (above ~200 K), the εr phase undergoes a structural transformation to a rhombohedral δr phase and further, together with the α0 phase, coexists up to the highest temperatures (for x < 0.5 H/f.u.) or transforms to a single rhombohedral δ phase (for 0.5 ≲ x ≲ 1.6) to finally undergo a structural transformation to a regular α phase. For the hydride x = 1.65, no spinodal type decays were observed, only ε → δ → α type transformations at ~230 K and ~250 K, respectively. For higher concentrations of 1.65 ≲ x ≲ 2.0, a multiphase system is expected and noted as a hatched area;
- An area of an exclusively α phase. This is mainly a high-temperature area with the exception of a low-temperature narrow range of 2.0 ≲ x ≲ 2.2 (yellow area);
- An area of 2.2 ≲ x ≲ 2.8, where again a spinodal type decay is observed. The two phases α and δ occur from the lowest to room temperature;
- An area of x ≳ 2.8. The δ phase occurs from the lowest temperatures up to ~(300–360) K, above which it is transformed to the regular α phase through a narrow two-phase region (α + δ).
In the magnetic part of the diagram, the red line separates the paramagnetic state from the magnetic ordering state. The lowest magnetic ordering temperature of ~200 K is reached by the hydride x ≈ 1.6. As the hydrogen content of the sample increases, Tc increases to ~310 K (x ≈ 3.5 H/f.u.). For x > 3.5, it is expected to increase further. Magnetic measurements indicate that only in hydrides with a hydrogen content close to 2.0 H/f.u. and greater than ~4.2 H/f.u. can relatively simple antiferromagnetic structures be expected. In the remaining cases, we are dealing with either biphasic or monophasic systems with complicated magnetization-temperature dependence M(T), suggesting canted ferrimagnetic ordering [66,77].
In the structural diagram of the HoMn2Hx_C14 hydrides (Figure 12b), the following areas can be distinguished:
- Area x ≲ 1.8, in which there is the coexistence of a ‘hydrogen-poor’ β0 phase that does not undergo any structural transformation from the lowest temperatures to temperatures ~270–400 K and a ‘hydrogen-rich’ phase in which structural transformations of the type (ηr → γr → βr) are observed. The β0 phase is structurally identical to the C14-type phase, with an estimated hydrogen content of less than 0.05 H/f.u. The ηr, γr and βr phases correspond to the monoclinic, orthorhombic and hexagonal phases, respectively, with an estimated hydrogen content of ~1.8 H/f.u.;
- Area 1.8 ≲ x ≲ 3.4, in which the low-temperature monoclinic phase η is transformed to the high-temperature hexagonal phase β via the orthorhombic phase γ. The temperatures of the structural transformations increase almost linearly with the hydrogen content of the sample;
- Area 3.4 ≲ x ≲ 3.6, covering a narrow x-range, in which spinodal-type decay is again observed. Two phases (ηl and γh) with similar hydrogen contents (~ 3.4 H/f.u. and ~3.55 H/f.u) coexist from the lowest temperatures up to ~200 K, above which a structural transformation of the ηl → γl type occurs (during which time γh undergoes no structural transformation). The spinodal type decomposition (γl +γh) disappears above ~300 K;
- Area x ≳ 3.6, in which the low-temperature γ′ phase transforms to the high-temperature β phase in the temperature range ~(320 ÷ 380) K;
- The high-temperature region of the β phase only (yellow area).
The bold line in the magnetic phase diagram of HoMn2Hx_C14 hydrides (Figure 12b) separates the paramagnetic state from the magnetic ordering state. The magnetic ordering temperature increases monotonically (in the range of 200–330 K) with an increasing hydrogen concentration (up to x ≈ 3.7 H/f.u.). Above x ≈ 3.7 H/f.u., it is expected to increase further. In this series of hydrides, “pure” antiferromagnetic (AF) ordering is only to be expected for 1.8 ≲ x ≲ 2.2 and 4.2 ≲ x ≲ 4.5. For the remaining x concentrations, either multiphase systems (with different types of magnetic ordering) or single-phase systems showing non-trivial M(T) relations (including those with possible magnetic moment reorientation) are observed [66,77].
It is interesting to note that in both series, the proportion of single-stranded phases is observed (ε and η) in diagrams described by the same C2/m space group, but with completely different atomic arrangements and unit cell parameters [66,77].
2.3.6. SmMn2H2
The compound SmMn2 crystallizes in the hexagonal structure of the Laves C14 phase type at room temperature. Below a temperature of ~86 K, it undergoes a structural transformation from a hexagonal to an orthorhombic phase with a simultaneous transition to an antiferromagnetic ordering state (see Figure 1) [16]. Although it absorbs hydrogen quite readily, this compound is reluctant to form stable crystal structures for any hydrogen concentration. Figure 13a,b shows temperature X-ray diffractograms of SmMn2H2.0 hydride, the only one of the SmMn2Hx hydrides for which structural properties are reported in the literature [78]. Structural analysis of the diffractograms showed that the hydride, at room temperature, retains a C14-type phase (β), which decomposes into two hexagonal phases (β1 and β2) with slightly different lattice parameters ~1.9 H/f.u. and ~2.1 H/f.u., respectively, below 248 K (Figure 13a). The structural transformation temperature correlates with the magnetic ordering temperature (~248 K) (Figure 13c) [78].
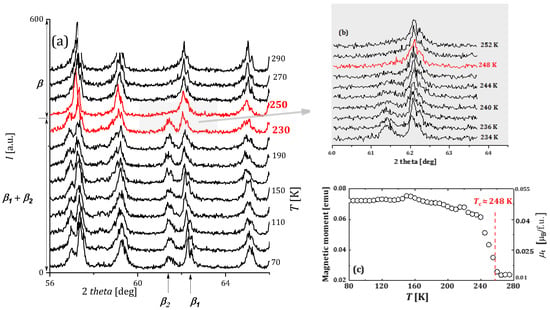
Figure 13.
SmMn2H2: (a,b) Temperature X-ray patterns; (c) Variation in magnetic moment as a function of temperature. Based on [78].
2.3.7. ErMn2Hx
Also in ErMn2Hx hydrides, for x ≲ 1.8 H/f.u., there is observed a characteristic decomposition into a ‘hydrogen-rich’ and a ‘hydrogen-poor’ phase, and the transition is rather complicated. The former phase (as in HoMn2Hx_C14 hydrides) is monoclinic at the lowest temperatures and transforms to a hexagonal phase with increasing temperature (ηr → βr), while the ‘hydrogen-poor’ phase β0 does not undergo structural transformations (Figure 14).
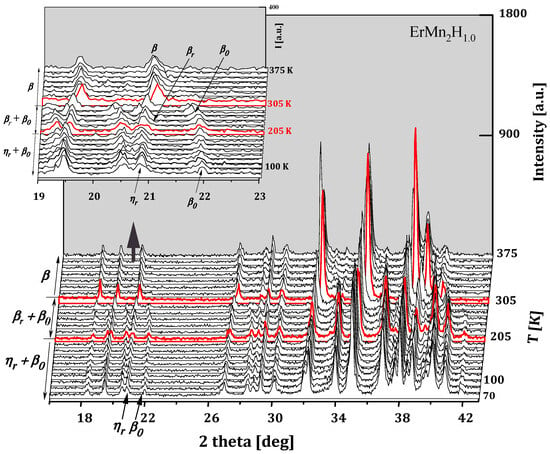
Figure 14.
Diffractograms of ErMn2H1.0 hydride as a function of temperature. Here, β indicates the C14-type phase with nominal hydrogen content (x = 1.0 H/f.u.), β0 represents the C14-type phase with minimal hydrogen content (x < 0.05 H/f.u), βr denotes the ‘rich-hydrogen’ phase with the C14 structure, and ηr represents the monoclinic phase (space group: C2/m). Based on [64].
The ErMn2Hx hydride diagram can be described as an alternation of two-phase and single-phase regions as a function of hydrogen content (Figure 15). At low temperatures and for x ≥ 1.8 H/f.u., only monoclinic phases occur. The hydride x = 2.0 H/f.u. no longer retains the structure of the starting compound in the entire temperature range. At a temperature of ~200 K, it undergoes a structural transformation from the hexagonal phase to the phase with low symmetry along with a temperature decrease through the two-phase region (hexagonal β* + monoclinic η*), as shown by neutron measurements [67]. The sample with maximum hydrogen content, nominally containing 4.3 H/f.u., shows continuous spinodal decomposition into two phases with hydrogen contents of ~3.8 H/f.u. and ~4.6 H/f.u. in the temperature range of 70–385 K (Figure 15).
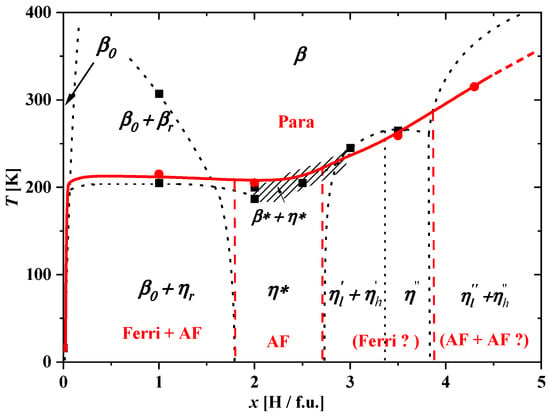
Figure 15.
Structural (in black) and magnetic (in red) phase diagram of ErMn2Hx hydrides. Here, βstands for the contribution of the hexagonal phase, and η stands for the contribution of the monoclinic phase. The red line separates the paramagnetic (Para) state from the magnetic ordering state. Ferri, ferrimagnetic states; AF, antiferromagnetic states. The question marks in (Ferri ?) and (AF+AF ?) denote the presumed occurrence of magnetic states (Ferri) and (AF+AF), respectively. Based on [23,64].
The structural transformations are accompanied by transitions from the paramagnetic state to the magnetic ordering state. The lowest values of magnetic susceptibility are recorded for x = 2.0 H/f.u. (Figure 15). In this sample, antiferromagnetic ordering is also to be expected; however, this has not been clearly demonstrated so far. At higher hydrogen concentrations for x ≈ (2.7–4.0) H/f.u., the hydrides show a complex temperature dependence of magnetization, suggesting a complex magnetic structure including ferrimagnetic canted ordering [64].
The analysis of magnetic results of hexagonal hydrides is not easy or clear. For example, Mössbauer spectroscopy on 166Er nuclei at 4 K showed no magnetic order in the ErMn2H4.6 hydride, so a paramagnetic state of the rare earth sublattice was postulated [79]. On the other hand, neutron diffraction studies on deuterides ErMn2D4.2 and ErMn2D4.6 conducted by Makarova et al. [23] gave a different result—both samples showed antiferromagnetic ordering with the propagation vector k = [1/3, 1/3, 0]. Similar results were obtained for TmMn2D4.6 and (Lu0.4Y0.6)Mn2D4.6 [23].
2.3.8. NdMn2Hx
The NdMn2Hx hydrides undergo structural transformations from the hexagonal phase (C14) to the monoclinic C2/m phase through the Cmcm orthorhombic phase and the disintegration of the spinodal phase. Due to the repeatability of the phases, the symbolism used to describe the HoMn2Hx_C14 and ErMn2Hx hydrides has been retained (β—C14-type phase, γ—orthorhombic phase, η—monoclinic phase).
An example of complex structural transformations is the temperature evolution of the high-temperature line (205) in the NdMn2H2.5 hydride (Figure 16). The high-temperature β phase transforms into the orthorhombic γ phase (~280 K) and then decomposes (~235 K) into two orthorhombic phases γl and γh with different hydrogen contents. With a further slight decrease in temperature, these phases clearly segregate and simultaneously transform into monoclinic phases ηl and ηh. The estimated hydrogen contents in both phases were (at 80 K) ~1.9 H/f.u. and ~2.9 H/f.u, respectively [65].
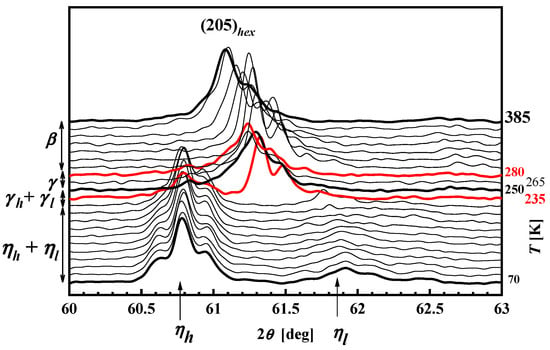
Figure 16.
Temperature evolution of the hexagonal structural line (205) in NdMn2H2.5 hydride. Phase γ occurs between the red lines. Based on [63].
Figure 17 shows a simplified structural phase diagram for NdMn2Hx. Due to difficulties in the preparation of hydrides with x < 2.0 (tendency to form amorphous structures, multiphase systems), this area was not analyzed [65]. Similar difficulties in obtaining hydrides were also encountered with SmMn2Hx samples (Section 2.3.6), which may suggest that RMn2 compounds with light rare earths are reluctant to form structurally stable hydrides with low hydrogen concentrations. All studied NdMn2Hx hydrides undergo a structural transformation according to a general sequence from the high-temperature hexagonal phase of the starting compound through the orthorhombic phase and ending with the low-temperature monoclinic phase (β → γ → η). Hydrides with x = 2.0 and 2.8 ≲ x ≲ 3.5 behave according to this sequence, while the NdMn2Hx hydrides with 2.1 ≲ x ≲ 2.8 and 3.5 ≲ x ≲ 4.3 show spinodal-type decomposition into two phases with different hydrogen contents in different temperature ranges.
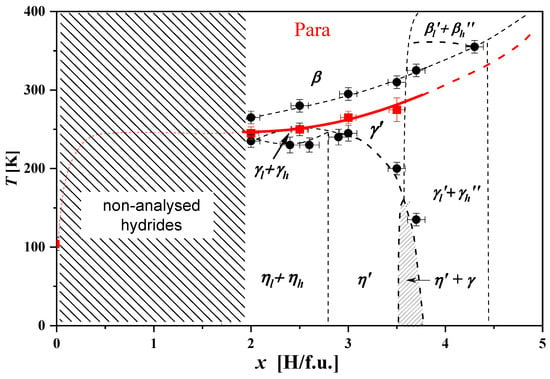
Figure 17.
Structural (in black) and magnetic (in red) phase diagram of NdMn2Hx hydrides. Here, β indicates the presence of a of a hexagonal phase, and η stands for the contribution of the monoclinic phase. The red lines in the region 2 ≤ x < 5 separate the paramagnetic (Para) state from the magnetic ordering state (below lines), and the dashed line in the region x < 2 represents the probable separation of these states. Based on [65].
A red line running through the Tc temperatures was drawn on the structural phase diagram (Figure 17). It separates the paramagnetic state from the magnetic ordering state. The determined Tc temperatures are similar to those observed for other RMn2Hx (Section 2.3.1, Section 2.3.2, Section 2.3.3, Section 2.3.4, Section 2.3.5, Section 2.3.6 and Section 2.3.7) and follow the general trend of their increase with increasing hydrogen concentration in the sample. However, the diagram does not even indicate the proposed magnetic ordering for specific values of x due to the ambiguous interpretation of magnetic measurements.
The transformations discussed here are represented only symbolically; a detailed description of the structural transformation analysis of the magnetic results for NdMn2Hx is presented in [65].
3. Summary
The presented results of structural and magnetic measurements of RMn2Hx hydrides (with x below ~4.5 H/f.u.) indicate great similarity, but also differences depending on the rare earth element. We summarize them below.
3.1. Structural Changes in RMn2Hx Hydrides
1. A linear increase in the relative volume of the unit cell (ΔV/V0) with increasing hydrogen concentration x was not observed in any of the RMn2Hx samples. The saturation of the hydrides is best described by the Hirata-Figiel function (Section 2.2).
2. RMn2 compounds easily absorb hydrogen, which, depending on the concentration in the compound, forces a number of structural transformations. These transformations as a function of temperature are illustrated in structural phase diagrams.
3. The structural phase diagram of GdMn2Hx hydrides is the simplest of all the tested RMn2Hx hydrides. Hydrides of rare earth elements both lighter and heavier than gadolinium show more complicated structural diagrams.
- The phase diagram of GdMn2Hx can be divided into three main areas. In the first area (x ≲ 1.8 H/f.u.), as the temperature decreases, the high-temperature cubic phase decomposes into, initially, three phases with different hydrogen contents. The phase with intermediate hydrogen content quickly disappears as the temperature decreases. The remaining two are clearly segregated into phases: “poor in hydrogen” (x ≲ 0.05 H/f.u.) and “rich in hydrogen” (x ≈ 1.8 H/f.u.). The “hydrogen-poor” phase can be treated as a solid solution of hydrogen in the metal. In the second range, 1.8 ≲ x ≲ 3.2, there is only a cubic phase in the entire temperature range, which is increased in third area.
- The phase diagram of TbMn2Hx is very similar to the hydride diagram of Gd. However, the boundary separating the areas of coexistence of rhombohedral and cubic phases from the highly hydrogenated rhombohedral phase is slightly different.
- In the phase diagram of DyMn2Hx hydrides, below x ≈ 1.6 H/f.u., the same type of phase transformations observed in hydrides with Tb and Gd are noted. However, the middle region (single phase, without structural transformations) narrows (1.6 ≲ x ≲ 2.4). For x ≳ 2.4 H/f.u., additional two-phase regions appear, which are a combination of cubic and rhombohedral phases with different hydrogen contents.
- In hydrides with HoMn2Hx_C14 and C15 and for x ≲ (1.6–1.7) H/f.u., there are, as noted above, spinodal-type decays into two phases “rich and poor in hydrogen” (no “intermediate” phase is observed). However, here the “hydrogen-rich” phase undergoes structural transformations as the temperature increases from the monoclinic through orthorhombic to hexagonal phase.
The central range of occurrence of one phase over the entire temperature range in the C15 series is reduced to an almost symbolic range (2.0 ≲ x ≲ 2.2). In the C14 series, such an area no longer exists. Instead, a wide area (1.8 < x < 3.2) of transformations in structural structures occurs, such as monoclinic phase → orthorhombic phase → hexagonal phase. For higher x, areas dominated by rhombohedral or orthorhombic phases appear in both series.
- Also in ErMn2Hx hydrides, for x ≲ 1.8 H/f.u., there is a decomposition into phases “rich” and “poor” in hydrogen (without the “intermediate” phase). The “hydrogen-rich” phase (as in HoMn2H_C14 hydrides) crystallizes in the monoclinic structure at the lowest temperatures. As the temperature increases, it transforms into the hexagonal phase. The erbium hydride diagram can be described as the alternation of two-phase and single-phase regions as a function of hydrogen content. At low temperatures, only monoclinic phases occur above x ≈ 1.8 H/f.u.
- In the hexagonal hydride SmMn2H2.0, spinodal-type decomposition into two hexagonal phases with slightly different hydrogen contents (~1.9 H/f.u. and ~2.1 H/f.u.) was observed; such a small difference in x concentrations in the area of spinodal decay does not occur for other RMn2Hx.
- The NdMn2Hx phase diagram is filled mainly with two-phase systems, even for x ≈ 4.0 H/f.u., which makes it similar to the erbium hydride diagram in this respect.
4. The occurrence of monoclinic phases is observed only for hydrides with Ho, Er and Nd.
5. The observed decompositions of phases with different hydrogen contents are of the spinodal type.
6. YMn2Hx hydrides behave differently from lanthanide hydrides. In the range of low hydrogen contents (x ≲ 1.15 H/f.u.), the spinodal-type decomposition into two phases with significantly different hydrogen contents, typical of hydrides with lanthanides, does not occur. Instead, a number of structural transformations occur.
7. Based on the conducted research, a synthetic picture of phase transformations under the influence of hydrogen can be presented in the form of a general structural model of the phase diagram of hydrides RMn2Hx (Figure 18), which allows easier understanding of the characteristic features of the observed structural changes.
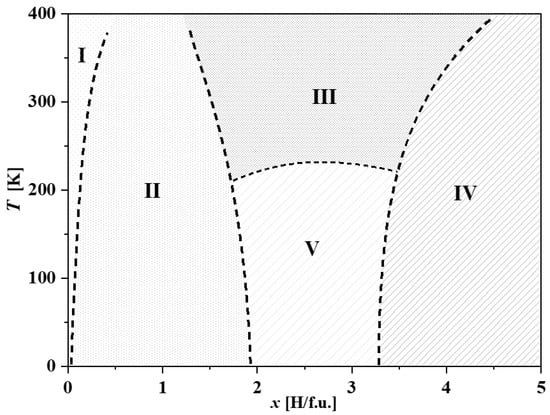
Figure 18.
General sketch of the structural phase diagram for RMn2Hx hydrides. I—Area corresponding to the solid solution of hydrogen in the metal. Estimated hydrogen concentration is below ~0.1 H/f.u. II—Area of occurrence of spinodal-type decomposes into poor and hydrogen-rich phases (Gd, Tb, Dy, Er, Ho)Mn2Hx. For YMn2Hx, this region ends at x ≈ 1.15 H/f.u. and includes more complicated structural changes. III—High-temperature area of occurrence of the phase corresponding to the phase of the starting compound. IV—Area of occurrence of phase combinations of regular/hexagonal and their distortions. V—For RMn2Hx hydrides with R: Y, Gd, Tb, Ho (C15), this area is structurally identical to area III, and the x range has a different width depending on the rare earth element. For other hydrides with R: Ho(C14), Nd and Er, spinodal decays or transformations to monoclinic phases occur in this area.
3.2. Magnetic Transformations and Properties
1. In all discussions on RMn2Hx hydrides, there is a strong increase in the magnetic ordering temperature Tc from the range of 14–105 K corresponding to the starting compounds to the range of ~200–400 K for their hydrides, depending on the hydrogen content. The course of ordering temperatures for RMn2Hx hydrides is shown in Figure 19. The highest magnetic ordering temperatures in the range of 1.5 ≲ x ≲ 4.0 are exhibited by GdMn2Hx hydrides, and the lowest are observed for ErMn2Hx and HoMn2Hx_C14 hydrides. In this x range, the different Tc curves of the HoMn2Hx_C14 and C15 hydrides indicate the influence of the structure of the starting compound on the magnetic properties of the hydrides.
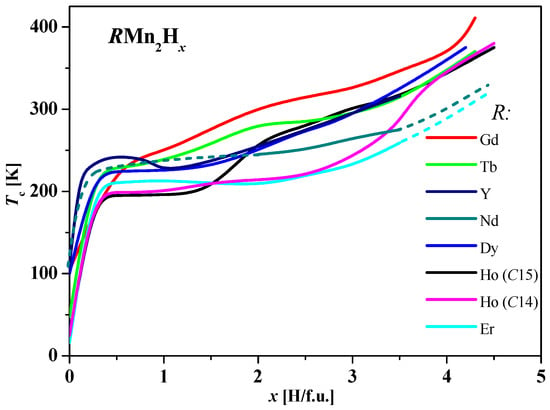
Figure 19.
The course of the magnetic ordering curves of the discussed RMn2Hx hydrides.
2. The reason for the increase in the magnetic ordering temperature of hydrides is the increase in Mn–Mn exchange interactions and a greater degree of localization of the Mn magnetic moments due to the increase in the dMn–Mn distance resulting from hydrogen doping.
3. All the RMn2Hx hydrides in a magnetically ordered state are ferrimagnetic, and their net magnetization strongly depends on the hydrogen concentration.
4. Hydrogen significantly affects the magnetic structure of hydrides/deuterides. In the deuteride TbMn2D2.0, a collinearly ordered antiferromagnetic structure appears with a propagation vector k = [½,½,½], which is significantly simpler than the magnetic structure of the initial compounds. This is one of the most interesting phenomena occurring under the influence of hydrogen in these systems.
5. It can be concluded that the share of f-electron elements in the formation of magnetic properties is similar and depends only slightly on the rare earth element.
6. It can be concluded that the magnetism of hydrogenated RMn2 compounds originates from the electron band.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/en16217383/s1, Figure S1: Arrangement of atoms in C14; Figure S2: Arrangement of atoms in C15; Table S1: Atom positions in C14; Table S2: Atom positions in C15; File S1: C14- and C15-type Laves phases: details of crystal structures. References [4,80,81,82,83,84,85] are cited in the supplementary file.
Author Contributions
A.B.: Conceptualization, Original draft preparation, Writing—Review & Editing, Data Curation, Supervision. J.S.: Reviewing & Editing, Software. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by AGH University of Science and Technology, Krakow, Poland (No 16.16.210.476).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Laves, F. Theory of Alloy Phases; American Society for Metals: Metals Park, OH, USA, 1956; p. 12. [Google Scholar]
- Stein, F.; Palm, M.; Sauthoff, G. Structure and stability of Laves phases. Part I. Critical assessment of factors controlling Laves phase stability. Intermetallics 2004, 12, 713–720. [Google Scholar] [CrossRef]
- Liu, C.T.; Zhu, J.H.; Brady, M.P.; McKamey, C.G.; Pike, L.M. Physical metallurgy and mechanical properties of transition-metal Laves phase alloys. Intermetallics 2000, 8, 1119–1129. [Google Scholar] [CrossRef]
- Stein, F.; Leineweber, A. Laves phases: A review of their functional and structural applications and an improved fundamental understanding of stability and properties. J. Mater. Sci. 2021, 56, 5321–5427. [Google Scholar] [CrossRef]
- YMn2 Crystal Structure, Springer Material. Available online: https://materials.springer.com/isp/crystallographic/docs/sd_0382661 (accessed on 8 October 2023).
- Talik, E.; Kulpa, M.; Winiarski, A.; Mydlarz, T.; Neumann, M. Electronic structure and magnetic properties of HoMn2 single crystals. J. Alloys Compd. 2001, 316, 51–57. [Google Scholar] [CrossRef]
- Budziak, A.; Żurek, M.; Żukrowski, J.; Bałanda, M.; Pacyna, A.; Czapla, M. Influence of hydrogen on structural and magnetic properties of the hexagonal Laves phase HoMn2. J. Magn. Magn. Mater. 2012, 324, 735–741. [Google Scholar] [CrossRef]
- Żukrowski, J.; Figiel, H.; Budziak, A.; Zachariasz, P.; Fisher, G.; Dormann, E. Structural and magnetic transformations in the GdMn2Hx hydrides. J. Magn. Magn. Mater. 2002, 238, 129–139. [Google Scholar] [CrossRef]
- Figiel, H.; Budziak, A.; Żukrowski, J.; Fisher, G.; Kelemen, M.T.; Dormann, E. Structural and magnetic properties of TbMn2Hx hydrides. J. Alloys Compd. 2002, 335, 48–58. [Google Scholar] [CrossRef]
- Nassau, K.; Cherry, L.V.; Wallace, W.E. Intermetallic compounds between lanthanons and transition metals of the first long period: I—Preparation, existence, and structural studies. J. Phys. Chem. Solid 1960, 16, 123–130. [Google Scholar] [CrossRef]
- Wernick, J.H.; Geller, S. Rare-earth compounds with the MgCu2 structure. Trans. Met. Soc. AIME 1960, 218, 866. [Google Scholar]
- Wernick, J.H.; Haszko, S.E. Manganese rare earth compounds with the MgZn2 structure. J. Appl. Phys. 1961, 48, 207–209. [Google Scholar] [CrossRef]
- Hardman, K.; Rhyne, J.J.; Malik, S.; Wallace, W.E. Site magnetization of cubic and hexagonal HoMn2. J. Appl. Phys. 1982, 53, 1944. [Google Scholar] [CrossRef]
- Labroo, S.; Nausahad, A.; Robinson, P. Magnetic properties of RMn2 compounds (R=heavy rare earths). J. Appl. Phys. 1990, 67, 5292–5294. [Google Scholar] [CrossRef]
- Malik, S.K.; Wallace, W.E. Magnetic behavior of cubic Laves phase RMn2 (R = Gd, Dy and Ho) compounds. J. Magn. Magn. Mater. 1981, 24, 23–28. [Google Scholar] [CrossRef]
- Wada, H.; Nakamura, H.; Yoshimura, K.; Shiga, M.; Nakamura, Y. Stability of Mn moments and spin fluctuations in RMn2 (R: Rare earth). J. Magn. Magn. Mat. 1987, 70, 134. [Google Scholar] [CrossRef]
- Shiga, M.; Wada, H.; Nakamura, Y. Magnetism and thermal expansion anomaly of RMn2 (R=Y, Gd, Tb, Ho and Er). J. Magn. Magn. Mat. 1983, 31–34, 119. [Google Scholar] [CrossRef]
- Nakamura, J. Magnetovolume effects in Laves phase intermetallic compounds. J. Magn. Magn. Mat. 1983, 31–34, 829–834. [Google Scholar] [CrossRef]
- Tagawa, Y.; Sakurai, J.; Komura, Y.; Wada, H.; Shiga, M.; Nakamura, Y. X-ray Study of Crystal Distortions in RMn2 Compounds (R: Y, Pr, Nd, Sm and Gd). J. Phys. Soc. Jpn. 1985, 54, 591. [Google Scholar] [CrossRef]
- Shiga, M. Magnetism and spin fluctuations of Laves phase manganese compounds. Phys. B+C 1988, 149, 293–305. [Google Scholar] [CrossRef]
- Gaidukova, I.Y.; Kruglyasher, S.B.; Markosyan, A.S.; Levitin, R.Z.; Pastuschenkov, Y.G.; Snegirev, V.V. Metamagnetism of the manganese subsystem in RMn2 intermetallic compounds. Sov. Phys. JEPT 1983, 57, 1083–1088. [Google Scholar]
- Yoshimura, K.; Shiga, M.; Nakamura, Y. NMR Study of Magnetic State of RMn2 Intermetallic Compounds. II. R=Heavy Rare-Earth. J. Phys. Soc. Jpn. 1986, 55, 3585–3595. [Google Scholar] [CrossRef]
- Makarova, O.L.; Goncharenko, I.N.; Irodova, A.V.; Mirebeau, I.; Suard, E. Interplay of magnetic and hydrogen ordering in the hexagonal Laves hydrides. Phys. Rev B 2002, 66, 104423. [Google Scholar] [CrossRef]
- Felcher, G.P.; Corliss, L.M.; Hastings, J.M. Investigation of the Magnetic Structure of ErMn2, TmMn2, TbNi2 by Neutron Diffraction. J. Appl. Phys. 1965, 36, 1001–1002. [Google Scholar] [CrossRef]
- Ouladdiaf, B.; Ballou, R.; Deportes, J.; Lamaire, R.; Sayet, F. Effects of exchange frustrations in NdMn2. J. Phys. Cond. Matter 1992, 4, 4675–4686. [Google Scholar] [CrossRef]
- Cywinski, R.; Kilcoyne, S.H.; Scott, C.A. Magnetic order and moment stability in YMn2. J. Phys. Cond. Matter 1991, 3, 6473–6488. [Google Scholar] [CrossRef]
- Corliss, L.; Hastings, J. A Neutron Diffraction Investigation of the Magnetic Structure of TbMn2. J. App. Phys. 1964, 35, 1051–1053. [Google Scholar] [CrossRef]
- Brown, P.J.; Ouladdiaf, B.; Ballou, R.; Deportes, J.; Markosyan, A.S. Mn moment instability in the TbMn2 intermetallic compound. J. Phys. Cond. Matter 1992, 4, 1103–1113. [Google Scholar] [CrossRef]
- Ritter, C.; Kilcoyne, S.H.; Cywinski, R. The magnetic structure of DyMn2. J. Phys. Condens. Matter 1991, 3, 727–738. [Google Scholar] [CrossRef]
- Ritter, C.; Cywinski, R.; Kilcoyne, S.H.; Mondal, S. The magnetic structure of HoMn2. J. Phys. Condens. Matter 1992, 4, 1559–1566. [Google Scholar] [CrossRef]
- Ballou, R.; Brown, P.J.; Deportes, J.; Lemaire, R.; Ouladdiaf, B. Exchange frustration and metastability of the magnetic structure of TbMn2. J. Magn. Magn. Mater. 1992, 104–107, 935–936. [Google Scholar] [CrossRef]
- Nakamura, Y.; Shiga, M.; Kawano, S. Antiferromagnetism of YMn2 intermetallic compound. Phys. B+C 1983, 120, 212–215. [Google Scholar] [CrossRef]
- Nakamura, H.; Metoki, N.; Suzuki, S.; Takayanagi, F.; Shiga, M. Helimagnetic structure of YMn2 observed by means of nuclear magnetic resonance and neutron diffraction. J. Phys. Condens Matter 2001, 13, 475–500. [Google Scholar] [CrossRef]
- Deportes, J.; Ouladdiaf, B.; Ziebeck, K.R.A. Thermal dependence of the longitudinal spin fluctuations in YMn2. J. Physigue 1987, 48, 1029–1034. [Google Scholar] [CrossRef]
- Goncharenko, I.N.; Mirebeau, I.; Irodova, A.V.; Suard, E. Magnetic and hydrogen ordering in the frustrated Laves hydrides RMn2 (R = Gd, Tb, Dy, Ho): A neutron-diffraction study. Phys. Rev B 1999, 59, 9324–9331. [Google Scholar] [CrossRef]
- Suwarno, S.; Lototskyy, M.V.; Yartys, V.A. Thermal desorption spectroscopy studies of hydrogen desorption from rare earth metal trihydrides REH3 (RE=Dy, Ho, Er). J. Alloys Compd. 2020, 842, 155530. [Google Scholar] [CrossRef]
- Charraud, J.-B.; Geneste, G.; Torrent, M. Manganese hydrides and superhydrides at high pressure. Phys. Rev. B 2019, 100, 224102. [Google Scholar] [CrossRef]
- Kirchheim, R.; Pundt, A. Hydrogen in Metals. In Physical Metallurgy, 5th ed.; Laughlin, D.E., Hono, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 2597–2705. [Google Scholar] [CrossRef]
- Staliński, B.; Terpiłowski, J. Wodór i wodorki; Wydawnictwa Naukowo–Techniczne: Warszawa, Poland, 1987. [Google Scholar]
- Turnbull, A. 4–Hydrogen diffusion and trapping in metals. In Gaseous Hydrogen Embrittlement of Materials in Energy Technologies; Woodhead Publishing: Cambridge, UK, 2012; pp. 89–128. [Google Scholar] [CrossRef]
- Fukai, Y. The Metal–Hydrogen System: Basic Bulk Properties; Springer Science+Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Skripov, A.V. Hydrogen jump motion in Laves-phase hydrides: Two frequency scales. J. Alloys Compd. 2005, 404–406, 224–229. [Google Scholar] [CrossRef]
- Kehr, K.W. Hydrogen in Metals I–Basic Properties; Alefeld, G., Volkl, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Graubert, H.; Schrober, H.R. Hydrogen in Metals III—Properties and Applications; Wipf, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Coey, J.M.D. Interstitial intermetallics. J. Magn. Magn. Mat. 1996, 159, 80–89. [Google Scholar] [CrossRef]
- Zuttel, A. Materials for hydrogen storage. Mater. Today 2003, 6, 24–33. [Google Scholar] [CrossRef]
- Łodziana, Z.; Dębski, A.; Cios, G.G.; Budziak, A. Ternary LaNi4.75M0.25 hydrogen storage alloys: Surface segregation, hydrogen sorption and thermodynamic stability. Int. J. Hydrogen Energy 2019, 44, 1760–1773. [Google Scholar] [CrossRef]
- Fujiwara, K. Effect of Hydrogen Absorption on the Magnetic Properties of Pseudobinary Intermetallics Y(Mn1-xTx)2 (T=Al, Co and Ni). J. Phys. Soc. Jpn. 1988, 57, 2133. [Google Scholar] [CrossRef]
- Somenkov, V.A.; Irodova, A.V. Lattice structure and phase transitions of hydrogen in intermetallic compounds. J. Less–Common Met. 1984, 101, 481–492. [Google Scholar] [CrossRef]
- Figiel, H.; Lindbaum, A.; Kapusta, C.; Gratz, E. Thermal expansion of YMn2Hx compounds. J. Alloys Comp. 1995, 217, 157. [Google Scholar] [CrossRef]
- Figiel, H.; Osuchowski, S.; Paja, A. Unit cell expansion in Laves phase-type compounds caused by interstitial hydrogen. Phys. Stat. Sol(A) 2007, 204, 3286–3290. [Google Scholar] [CrossRef]
- Budziak, A.; Figiel, H.; Żukrowski, J.; Gratz, E.; Ouladdiaf, B. Magnetic ordering in TbMn2D2. J. Phys. Cond. Matt. 2001, 13, L871. [Google Scholar] [CrossRef]
- Switendick, A.C. Band structure calculations for metal hydrogen systems. Z. Phys. Chem. 1979, 117, 89–112. [Google Scholar] [CrossRef]
- Westlake, D.G. Hydrides of intermetallic compounds: A review of stabilities, stoichiometries and preferred hydrogen sites. J. Less–Common Met. 1983, 91, 1–20. [Google Scholar] [CrossRef]
- Żukrowski, J.; Strecker, M.; Wortmann, G.; Przewoźnik, J.; Krop, K. X-ray diffraction and 155Gd-Mössbauer effect study of GdMn2Hx (0≤ x≤ 4.3). J. Alloys Compd. 1997, 261, 47–53. [Google Scholar] [CrossRef]
- Przewoźnik, J.; Żukrowski, J.; Krop, K. Mössbauer effect study of the magnetic ordering in GdMn2Hx. J. Magn. Magn. Mater. 1998, 187, 337–344. [Google Scholar] [CrossRef]
- Shoemaker, D.P.; Shoemaker, C.B. Concerning atomic sites and capacities for hydrogen absorption in the AB2 Friauf-Laves phases. J. Less-Common Met. 1979, 68, 43–58. [Google Scholar] [CrossRef]
- Wang, C.Y.; Paul-Boncour, V.; Kang, C.C.; Liu, R.S.; Filipek, S.M.; Dorogova, M.; Marchuk, I.; Hirata, T.; Percheron-Guegan, A.; Sheu, H.-S.; et al. The novel YMn2D6 deuteride synthesized under high pressure of gaseous deuterium. Solid State Commun. 2004, 130, 815–820. [Google Scholar] [CrossRef]
- Paul-Boncour, V.; Filipek, S.M.; Dorogova, M.; Bouree, F.; Andre, G.; Marchuk, I.; Percheron-Guegan, A.; Liu, R.S. Neutron diffraction study, magnetic properties and thermal stability of YMn2D6 synthesized under high deuterium pressure. J. Sol. State Chem. 2005, 178, 356. [Google Scholar] [CrossRef]
- Paul–Boncour, V.; Filipek, S.M.; Andre, G.; Bourée, F.; Guillot, M.; Wierzbicki, R.; Marchuk, I.; Liu, R.S.; Villeroy, B.; Percheron-Guégan, A.; et al. Structural, thermal and magnetic properties of ErMn2D6 synthesized under high deuterium pressure. J. Phys. Condens. Matter 2006, 18, 6409. [Google Scholar] [CrossRef]
- Paul–Boncour, V.; Filipek, S.M.; Wierzbicki, R.; Andre, G.; Bouree, F.; Guillot, M. Structural and magnetic properties of DyMn2D6 synthesized under high deuterium pressure. J. Phys. Condens. Matter 2009, 21, 016001. [Google Scholar] [CrossRef]
- Figiel, H.; Przewoźnik, J.; Paul–Boncour, V.; Lindbaum, A.; Gratz, E.; Latroche, M.; Escorne, M.; Percheron-Guegan, A.; Mietniowski, P. Hydrogen induced phase transitions in YMn2. J. Alloys Compd. 1998, 274, 29–37. [Google Scholar] [CrossRef]
- Przewoźnik, J.; Żukrowski, J.; Friendl, K.; Japa, E.; Krop, K. Magnetic and structural properties of DyMn2Hx (0≤x≤4.2). J. Alloys Comp. 1999, 284, 31–41. [Google Scholar] [CrossRef]
- Figiel, H.; Budziak, A.; Zachariasz, P.; Żukrowski, J.; Fisher, G.; Dormann, E. Hydrogen induced structural and magnetic transformations in the hexagonal Laves phase ErMn2. J. Alloys Comp. 2004, 368, 260–268. [Google Scholar] [CrossRef]
- Budziak, A.; Zachariasz, P.; Pełka, R.; Figiel, H.; Żukrowski, J.; Woch, M.W. Structural and magnetic transformations in NdMn2Hx hydrides. J. Alloys Comp. 2012, 525, 175–183. [Google Scholar] [CrossRef]
- Budziak, A.; Zachariasz, P.; Kolwicz-Chodak, L.; Figiel, H.; Pacyna, A.; Żukrowski, J. Structural and magnetic properties of C15 HoMn2 hydrides. J. Alloys Comp. 2011, 509, 1347–1354. [Google Scholar] [CrossRef]
- Maehlen, J.P.; Yartys, V.A.; Riabov, A.B.; Budziak, A.; Figiel, H.; Żukrowski, J. Synchrotron X-ray diffraction study of ErMn2D2. J. Alloys Comp. 2007, 437, 140–145. [Google Scholar] [CrossRef]
- Makihara, Y.; Iwata, Y.; Umeda, K.; Miyairi, Y.; Fujii, H. Structural and Hydriding/Dehydriding Properties of HoMn2Hx with Cubic and Hexagonal Laves Phase Structure. MRS Online Proc. Libr. (OPL) 2006, 927, 0927-EE03. [Google Scholar] [CrossRef]
- Hirata, T.; Dorogowa, M.; Filipek, S. The hydrogen concentration dependence of the unit-cell volume in RMn2Hx (R = Y.; Gd, Tb and Dy). Phys. Stat. Sol(A) 2004, 201, 1458–1462. [Google Scholar] [CrossRef]
- Paul–Boncour, V. Comparison of the influence of hydrogen on the magnetic properties of RMn2 and RFe2 Laves phase compounds. J. Alloys Comp. 2004, 367, 185–190. [Google Scholar] [CrossRef]
- Latroche, M.; Paul-Boncour, V.; Percheron-Guegan, A.; Bouree-Vigneron, F. Temperature dependence study of YMn2D4.5 by means of neutron powder diffraction. J. Alloys Comp. 1998, 274, 59–64. [Google Scholar] [CrossRef]
- Latroche, M.; Paul-Boncour, V.; Percheron-Guegan, A.; Bouree-Vigneron, F.; Andre, G. Neutron diffraction study of YMn2D1.15. Physica B 2000, 276–278, 666–667. [Google Scholar] [CrossRef]
- Latroche, M.; Paul-Boncour, V.; Percheron-Guegan, A.; Bouree-Vigneron, F.; André, G. Structural and Magnetic Properties of Low D Content YMn2 Deuteride. J. State Chem. 2000, 154, 398–404. [Google Scholar] [CrossRef]
- Przewoźnik, J.; Latroche, M.; Percheron-Guegan, A.; Paul-Boncour, V. Neutron diffraction study of YMn2Dx deuterides (1 ⩽ x ⩽ 3.4). J. Alloys Comp. 1995, 225, 436. [Google Scholar] [CrossRef]
- Goncharenko, I.N.; Mirebeau, I.; Irodova, A.V.; Suard, E. Interplay of magnetic and hydrogen orders in the laves hydride YMn2H4.3. Phys. Rev. B 1997, 56, 2580. [Google Scholar] [CrossRef]
- Mirebeau, I.; Goncharenko, I.; Irodova, A.V.; Suard, E. Pressure decoupling of a magneto-structural transition in YMn2D4.3. Physica B 1998, 241–243, 672–674. [Google Scholar] [CrossRef]
- Budziak, A.; Bałanda, M.; Figiel, H.; Kolwicz-Chodak, L.; Tarnawski, Z. Structural and magnetic transformations in HoMn2Hx hydrides. Jt. Eur. Magn. Symp.–JEMS 2010 J. Phys. Conf. Ser. 2011, 303, 012010. [Google Scholar] [CrossRef]
- Figiel, H.; Budziak, A.; Żukrowski, J. Hydrogen induced structural and magnetic transformation in the SmMn2H2 compound. Solid State Comm. 1999, 111, 519–524. [Google Scholar] [CrossRef]
- Viccaro, P.J.; Shenoy, G.K.; Niarchos, D.; Dnulap, B.D. 166Er Mössbauer and X-ray diffraction study of ErMn2 hydrides. J. Less–Common Met. 1980, 73, 265. [Google Scholar] [CrossRef]
- Zhu, J.H.; Liu, C.T.; Pike, L.M.; Liaw, P.K. A thermodynamic interpretation of the size-ratio limits for laves phase formation. Metall. Mater. Trans. A 1999, 30, 1449–1452. [Google Scholar] [CrossRef]
- Thoma, D.J.; Perepezko, J.H. A geometric analysis of solubility ranges in Laves phases. J. Alloys Compd. 1995, 224, 330–341. [Google Scholar] [CrossRef]
- Hahn, T. International Tables for Crystallography, 5th ed.; Springer: Dordrecht, The Netherlands, 2002; Volume A. [Google Scholar]
- Available online: https://next-gen.materialsproject.org/materials/mp-1124/ (accessed on 19 September 2023).
- Chojnacki, J. Metalografia Strukturalna; Wydawnictwo “Śląsk”: Katowice, Poland, 1966. [Google Scholar]
- Available online: https://next-gen.materialsproject.org/materials/mp-1038 (accessed on 19 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).