Quantitative Analysis Study of Effects of Nuclide Concentration Uncertainties on Biases and Bias Uncertainties in Criticality Calculation Method
Abstract
:1. Introduction
2. Methods
2.1. Method for Determination of Isotope Biases and Bias Uncertainties
2.2. Method for Calculation of Bias and Bias Uncertainty in Criticality Calculations
2.2.1. Method for Calculation of Bias and Bias Uncertainty in Criticality Calculations
2.2.2. MC Uncertainty Sampling Method
2.2.3. LHS Method with Isotopic Covariance Matrix
3. Computations and Results
3.1. Introduction to Calculation Codes
3.2. Selection of the SNF Benchmark
3.3. Determination of the Isotopic Bias and Bias Uncertainty in SNF Assembly
3.4. Determination of Isotopic Bias and Bias Uncertainty in SNF Assembly
4. Assessment of Assumptions Used in the MC Uncertainty Sampling Method
4.1. Assessment of the Normal-Distribution Assumption of M/C Concentration Ratio
4.1.1. MC Uncertainty Sampling Method
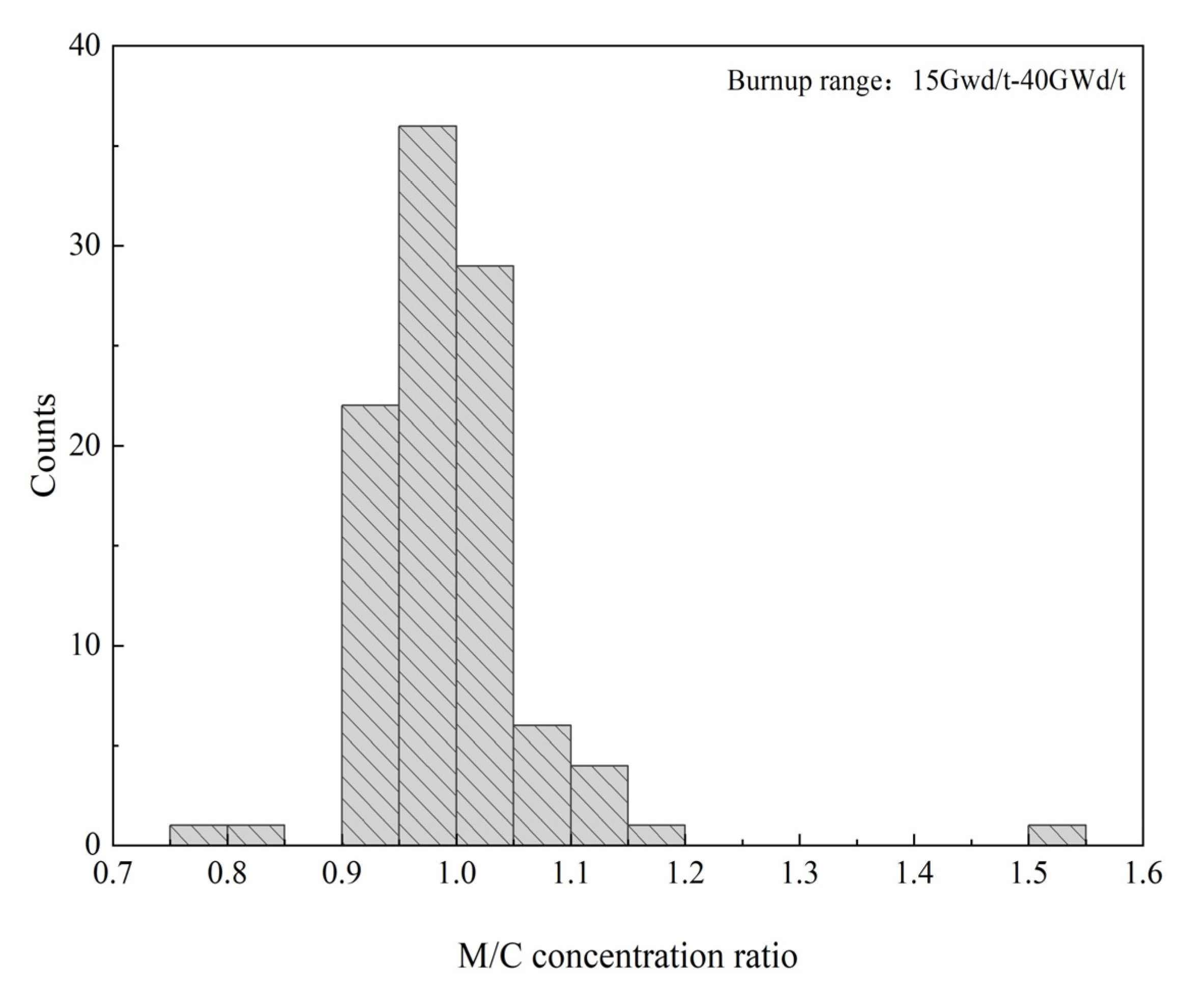
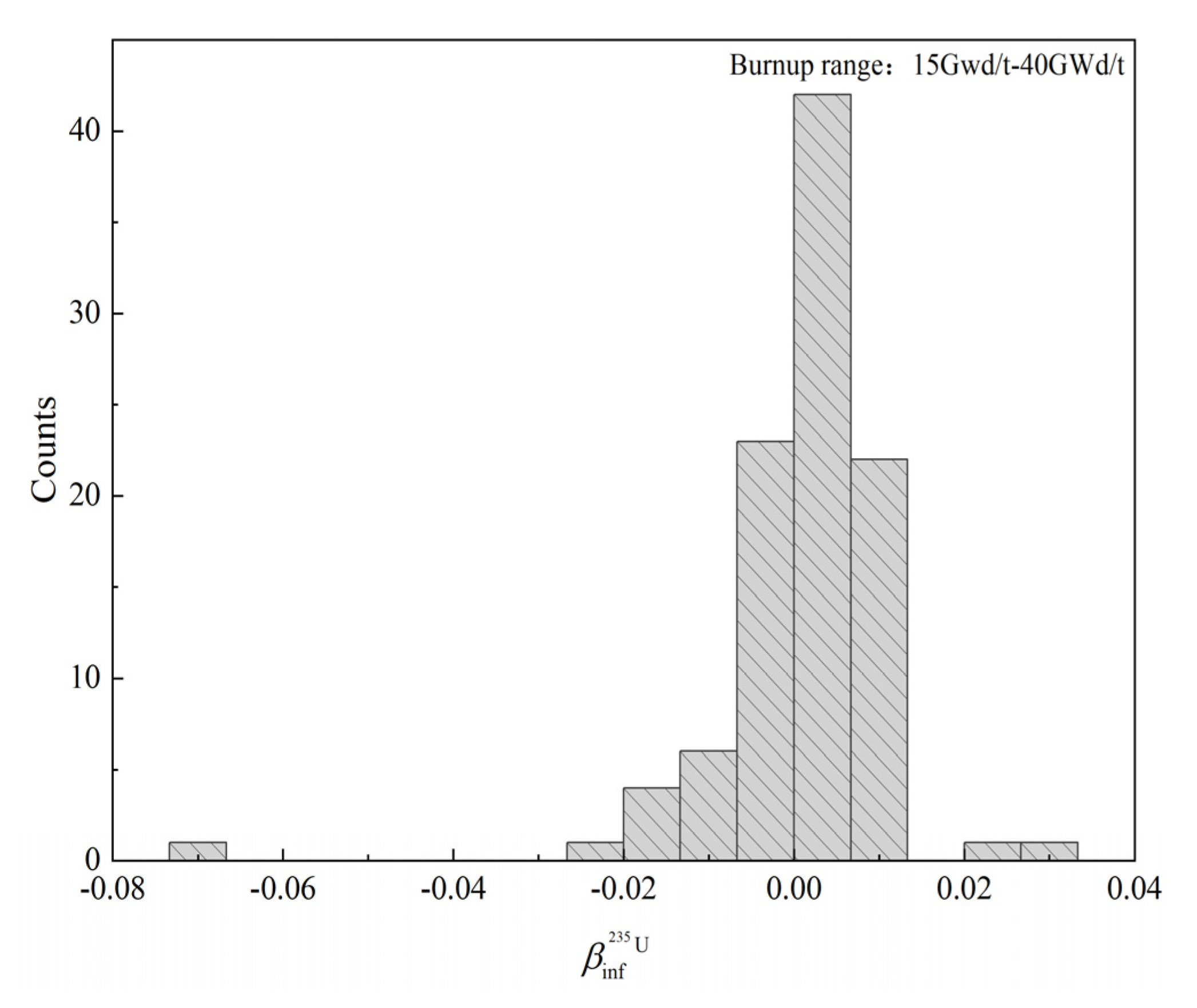
4.1.2. Validation of Assumption for Normal Distribution of Isotopic Bias
4.2. Evaluation of the Uncorrelation Assumption among Isotopes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saqib, A.; Chan, T.-H.; Mikhaylov, A.; Lean, H.H. Are the Responses of Sectoral Energy Imports Asymmetric to Exchange Rate Volatilities in Pakistan? Evidence from Recent Foreign Exchange Regime. Front. Energy Res. 2021, 9, 614463. [Google Scholar] [CrossRef]
- Dinçer, H.; Yüksel, S.; Mikhaylov, A.; Pinter, G.; Shaikh, Z.A. Analysis of Renewable-Friendly Smart Grid Technologies for the Distributed Energy Investment Projects Using a Hybrid Picture Fuzzy Rough Decision-Making Approach. Energy Rep. 2022, 8, 11466–11477. [Google Scholar] [CrossRef]
- Wang, Q.; Su, M.; Li, R.; Ponce, P. The Effects of Energy Prices, Urbanization and Economic Growth on Energy Consumption per Capita in 186 Countries. J. Clean. Prod. 2019, 225, 1017–1032. [Google Scholar] [CrossRef]
- Li, R.; Wang, Q.; Liu, Y.; Jiang, R. Per-Capita Carbon Emissions in 147 Countries: The Effect of Economic, Energy, Social, and Trade Structural Changes. Sustain. Prod. Consum. 2021, 27, 1149–1164. [Google Scholar] [CrossRef]
- Dinçer, H.; Yüksel, S.; Mikhaylov, A.; Barykin, S.E.; Aksoy, T.; Hacıoğlu, Ü. Analysis of Environmental Priorities for Green Project Investments Using an Integrated Q-Rung Orthopair Fuzzy Modeling. IEEE Access 2022, 10, 50996–51007. [Google Scholar] [CrossRef]
- World Nuclear Power Plants in Operation. Available online: https://www.nei.org/resources/statistics/world-nuclear-power-plants-in-operation (accessed on 1 August 2022).
- Silvennoinen, P. Nuclear Fuel Cycle Optimization; Chapter 3—Basic Model of the LWR Fuel Cycle; Pergamon: Oxford, UK, 1982; pp. 34–48. [Google Scholar]
- Alameri, S.A.; Alkaabi, A.K. Nuclear Reactor Technology Development and Utilization; 1—Fundamentals of Nuclear Reactors; Woodhead Publishing: Sawston, UK, 2020; pp. 27–60. [Google Scholar]
- Prieto-Guerrero, A.; Espinosa-Paredes, G. Linear and Non-Linear Stability Analysis in Boiling Water Reactors; 2—Description of Boiling Water Reactors; Woodhead Publishing: Sawston, UK, 2019; pp. 25–55. [Google Scholar]
- Alameri, S.A.; Alrwashdeh, M. Preliminary Three-Dimensional Neutronic Analysis of IFBA Coated TRISO Fuel Particles in Prismatic-Core Advanced High Temperature Reactor. Ann. Nucl. Energy 2021, 163, 108551. [Google Scholar] [CrossRef]
- Zohuri, B. Molten Salt Reactors and Integrated Molten Salt Reactors; Chapter 2—Integral Molten Salt Reactor; Academic Press: Cambridge, MA, USA, 2021; pp. 59–84. [Google Scholar]
- Kooyman, T. Current State of Partitioning and Transmutation Studies for Advanced Nuclear Fuel Cycles. Ann. Nucl. Energy 2021, 157, 108239. [Google Scholar] [CrossRef]
- Baron, P.; Cornet, S.M.; Collins, E.D.; DeAngelis, G.; Del Cul, G.; Fedorov, Y.; Glatz, J.P.; Ignatiev, V.; Inoue, T.; Khaperskaya, A.; et al. A Review of Separation Processes Proposed for Advanced Fuel Cycles Based on Technology Readiness Level Assessments. Prog. Nucl. Energy 2019, 117, 103091. [Google Scholar] [CrossRef]
- Lovecký, M.; Závorka, J.; Jiřičková, J.; Ondráček, Z.; Škoda, R. Fixed Neutron Absorbers for Improved Nuclear Safety and Better Economics in Nuclear Fuel Storage, Transport and Disposal. Nucl. Eng. Technol. 2023, 55, 2288–2297. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, B.; Bi, Y.; Yuan, X.; Zhang, Y.; Tang, H. Investigation and Improvement of the Mini-Max Polynomial Approximation Method for Solving Burnup Equations. Ann. Nucl. Energy 2023, 180, 109482. [Google Scholar] [CrossRef]
- Toit, M.H.D.; Naicker, V.V. Monte Carlo Burnup Oscillations for Thorium-Based EPR Fuel. Ann. Nucl. Energy 2023, 185, 109714. [Google Scholar] [CrossRef]
- Shama, A.; Caruso, S.; Rochman, D. Analyses of the Bias and Uncertainty of SNF Decay Heat Calculations Using Polaris and ORIGEN. Front. Energy Res. 2023, 11, 1161076. [Google Scholar] [CrossRef]
- Herrero, J.J.; Vasiliev, A.; Pecchia, M.; Ferroukhi, H.; Caruso, S. Review Calculations for the OECD/NEA Burn-up Credit Criticality Safety Benchmark. Ann. Nucl. Energy 2016, 87, 48–57. [Google Scholar] [CrossRef]
- Jang, J.; Ebiwonjumi, B.; Kim, W.; Cherezov, A.; Park, J.; Lee, D. Verification and Validation of Isotope Inventory Prediction for Back-End Cycle Management Using Two-Step Method. Nucl. Eng. Technol. 2021, 53, 2104–2125. [Google Scholar] [CrossRef]
- Bess, J.D.; Blaise, P.; Buss, O.; DeHart, M.; Fleming, M.; Hill, I.; Ilas, G.; Ivanova, T.; Ivanov, E.; Marshall, W.J.; et al. Engagement Opportunities in OECD NEA Benchmark Development. Front. Energy Res. 2023, 11, 1085764. [Google Scholar] [CrossRef]
- Ilas, G.; Gauld, I.; Ortego, P.; Tsuda, S. Sfcompo Database of Spent Nuclear Fuel Assay Data—The Next Frontier. EPJ Web Conf. 2021, 247, 10019. [Google Scholar] [CrossRef]
- Hao, C.; Chen, Y.; Guo, J.; Wang, L.; Li, F. Mechanism Analysis of the Contribution of Nuclear Data to the Keff Uncertainty in the Pebble Bed HTR. Ann. Nucl. Energy 2018, 120, 857–868. [Google Scholar] [CrossRef]
- Pecchia, M.; Vasiliev, A.; Ferroukhi, H.; Pautz, A. Criticality Safety Evaluation of a Swiss Wet Storage Pool Using a Global Uncertainty Analysis Methodology. Ann. Nucl. Energy 2015, 83, 226–235. [Google Scholar] [CrossRef]
- Gauld, I.C.; Mertyurek, U. Validation of BWR Spent Nuclear Fuel Isotopic Predictions with Applications to Burnup Credit. Nucl. Eng. Des. 2019, 345, 110–124. [Google Scholar] [CrossRef]
- Yun, H.; Park, K.; Choi, W.; Hong, S.G. An Efficient Evaluation of Depletion Uncertainty for a GBC-32 Dry Storage Cask with PLUS7 Fuel Assemblies Using the Monte Carlo Uncertainty Sampling Method. Ann. Nucl. Energy 2017, 110, 679–691. [Google Scholar] [CrossRef]
- Wang, K.; Li, Z.; She, D.; Xu, Q.; Qiu, Y.; Yu, J.; Sun, J.; Fan, X.; Yu, G. RMC—A Monte Carlo Code for Reactor Core Analysis. Ann. Nucl. Energy 2015, 82, 121–129. [Google Scholar] [CrossRef]
- Sciff, D.; D’agostino, R.B. Practical Engineering Statistics; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
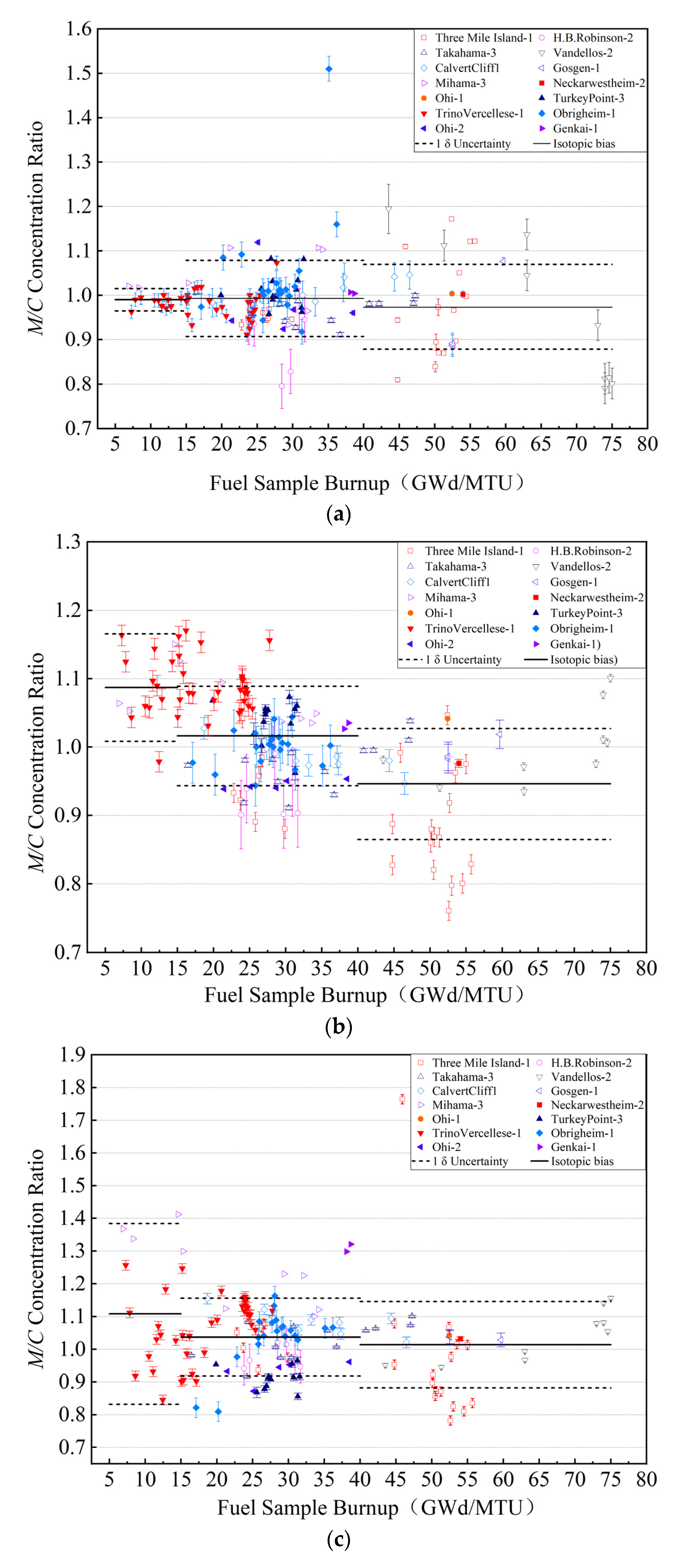



| Reactor | Assembly Design | Enrichment | Burnup (GWd/MTU) | Absorber | Number of Samples |
|---|---|---|---|---|---|
| H.B. Robinson | 15 × 15 | 2.56 wt% | 23.81~31.66 | Control rod | 6 |
| Ohi-2 | 17 × 17 | 3.20 wt% | 21.465~38.5 | Gadolinium-containing fuel | 5 |
| Three Mile Island-1 | 15 × 15 | 4.01 wt% 4.66 wt% | 44.8~55.7 | Control rod Gadolinium-containing fuel | 24 |
| Vandellos-2 | 17 × 17 | 4.50 wt% | 43.52~75 | - | 9 |
| Gosgen-1 | 15 × 15 | 3.50 wt% | 52.5~59.66 | - | 3 |
| Mihama-3 | 15 × 15 | 3.20 wt% 3.21 wt% | 14.6~34.2 | - | 7 |
| Obrigheim-1 | 14 × 14 | 3.00 wt% 3.13 wt% | 15.6~36.2 | - | 20 |
| Ohi-1 | 17 × 17 | 3.20 wt% | 52.434 | - | 1 |
| Trino Vercellese-1 | 15 × 15 | 3.13 wt% 2.72 wt% 3.13 wt% 3.90 wt% | 7.282~27.758 | - | 36 |
| Turkey Point-3 | 15 × 15 | 2.56 wt% | 19.89~31.56 | - | 13 |
| Takahama-3 | 17 × 17 | 4.11 wt% | 16.44~47.25 | Gadolinium-containing fuel | 13 |
| Calvert Cliffs-1 | 14 × 14 | 2.45 wt% 3.04 wt% 2.72 wt% | 18.68~46.46 | - | 9 |
| Genkai-1 | 14 × 14 | 3.42 wt% | 38.1~38.7 | - | 2 |
| Mihama-3 | 15 × 15 | 3.21 wt% | 6.9~8.3 | - | 2 |
| Neckarwestheim-2 | 18 × 18 | 3.80 wt% | 54 | Gadolinium-containing fuel | 1 |
| Nuclide | 5 GWd/MTU < Burnup (a) ≤ 15 GWd/MTU | 15 GWd/MTU < Burnup ≤ 40 GWd/MTU | 40 GWd/MTU < Burnup ≤ 75 GWd/MTU | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No. of Samples | Isotopic Bias | Isotopic Bias Uncertainty (b) | No. of Samples | Isotopic Bias | Isotopic Bias Uncertainty | No. of Samples | Isotopic Bias | Isotopic Bias Uncertainty | |
| 235U | 14 | 0.990 | 0.0249 | 101 | 0.993 | 0.0859 | 36 | 0.974 | 0.0956 |
| 238U | 14 | 1.004 | 0.0136 | 95 | 1.001 | 0.0106 | 15 | 1.006 | 0.0141 |
| 239Pu | 14 | 1.087 | 0.0786 | 101 | 1.016 | 0.0728 | 36 | 0.946 | 0.0811 |
| 240Pu | 14 | 1.101 | 0.1173 | 101 | 1.031 | 0.0641 | 36 | 0.956 | 0.0714 |
| 241Pu | 14 | 1.108 | 0.2763 | 101 | 1.037 | 0.1186 | 36 | 1.014 | 0.1320 |
| 242Pu | 14 | 1.296 | 0.3213 | 101 | 1.105 | 0.1352 | 36 | 1.079 | 0.1506 |
| Nuclide | 5 GWd/MTU < Burnup ≤ 40 GWd/MTU | 40 GWd/MTU < Burnup ≤ 75 GWd/MTU | |||||||
| No. of Samples | Isotopic Bias | Isotopic Bias Uncertainty (b) | No. of Samples | Isotopic Bias | Isotopic Bias Uncertainty | ||||
| 234U | 64 | 0.901 | 0.1737 | 36 | 0.874 | 0.1720 | |||
| 236U | 105 | 1.017 | 0.0633 | 36 | 0.980 | 0.0608 | |||
| 241Am | 62 | 1.451 | 1.1010 | 27 | 1.111 | 1.2581 | |||
| 243Am | 42 | 1.150 | 0.5082 | 27 | 1.020 | 0.4985 | |||
| 237Np | 23 | 1.139 | 0.2945 | 28 | 1.143 | 0.2742 | |||
| 238Pu | 97 | 1.462 | 0.2352 | 36 | 1.218 | 0.2606 | |||
| Nuclide | 5 GWd/MTU < Burnup ≤ 75 GWd/MTU | ||||||||
| No. of Samples | Isotopic Bias | No. of Samples | |||||||
| 109Ag | 17 | 0.597 | 0.3281 | ||||||
| 133Cs | 17 | 0.928 | 0.2719 | ||||||
| 151Eu | 38 | 1.387 | 0.7091 | ||||||
| 153Eu | 40 | 0.995 | 0.1131 | ||||||
| 155Gd | 40 | 1.305 | 0.7218 | ||||||
| 95Mo | 18 | 1.052 | 0.1684 | ||||||
| 143Nd | 71 | 1.081 | 0.8917 | ||||||
| 145Nd | 71 | 1.010 | 0.0779 | ||||||
| 103Rh | 18 | 0.945 | 0.1874 | ||||||
| 101Ru | 15 | 0.990 | 0.1618 | ||||||
| 147Sm | 45 | 1.237 | 0.5030 | ||||||
| 149Sm | 45 | 1.028 | 0.3598 | ||||||
| 150Sm | 45 | 1.035 | 0.0910 | ||||||
| 151Sm | 45 | 0.870 | 0.1174 | ||||||
| 152Sm | 45 | 0.867 | 0.0579 | ||||||
| 99Tc | 31 | 0.993 | 0.1859 | ||||||
| Parameter | Value |
|---|---|
| Fuel assembly design | 17 × 17 |
| Fuel inner radius | 0.4096 cm |
| Inner radius of fuel cladding | 0.418 cm |
| Outer radius of fuel cladding | 0.475 cm |
| Fuel rod center distance | 1.26 cm |
| Inner radius of guide tube | 0.5725 cm |
| Outer radius of guide tube | 0.6225 cm |
| Burnable toxicity types | - |
| Control rod | - |
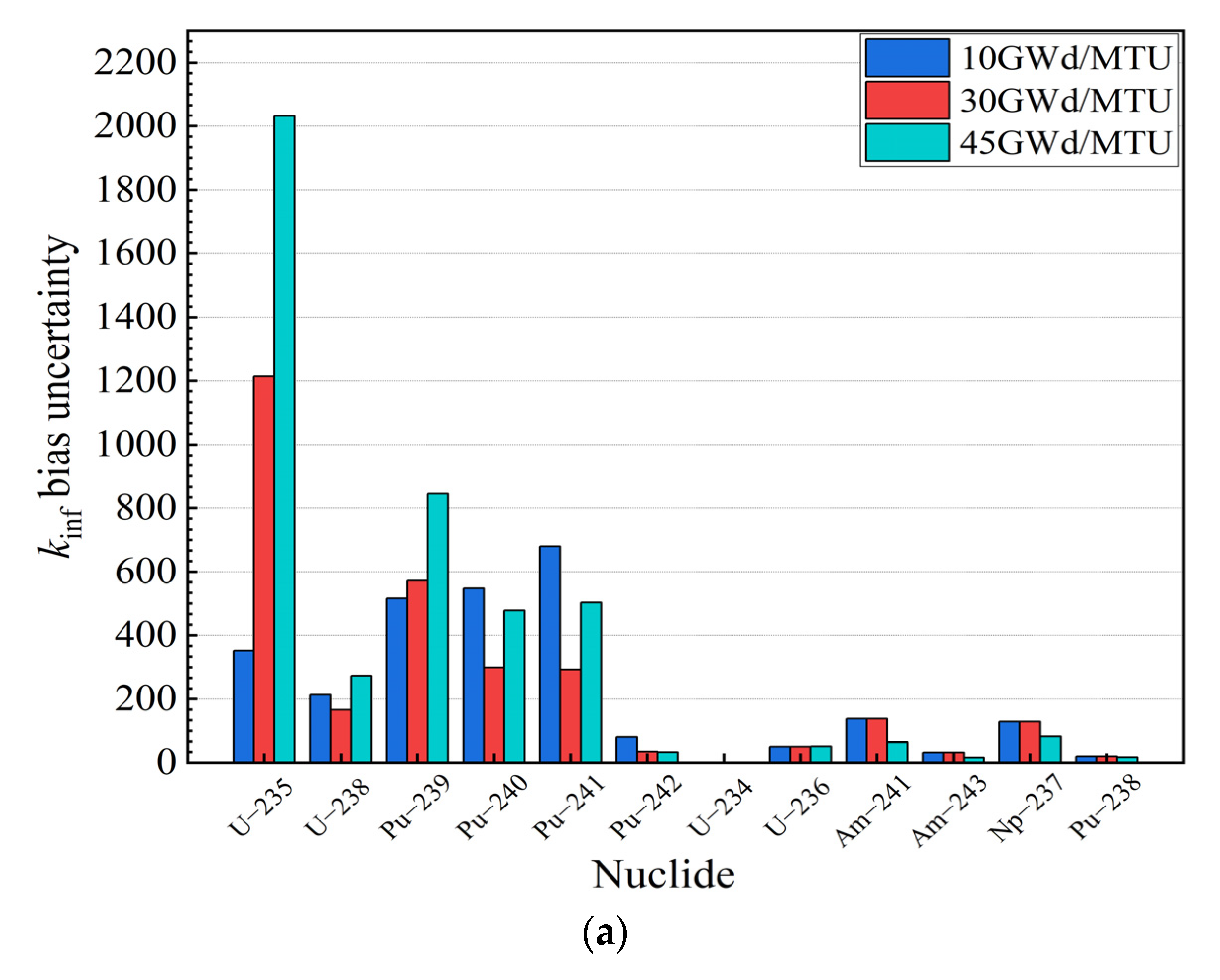
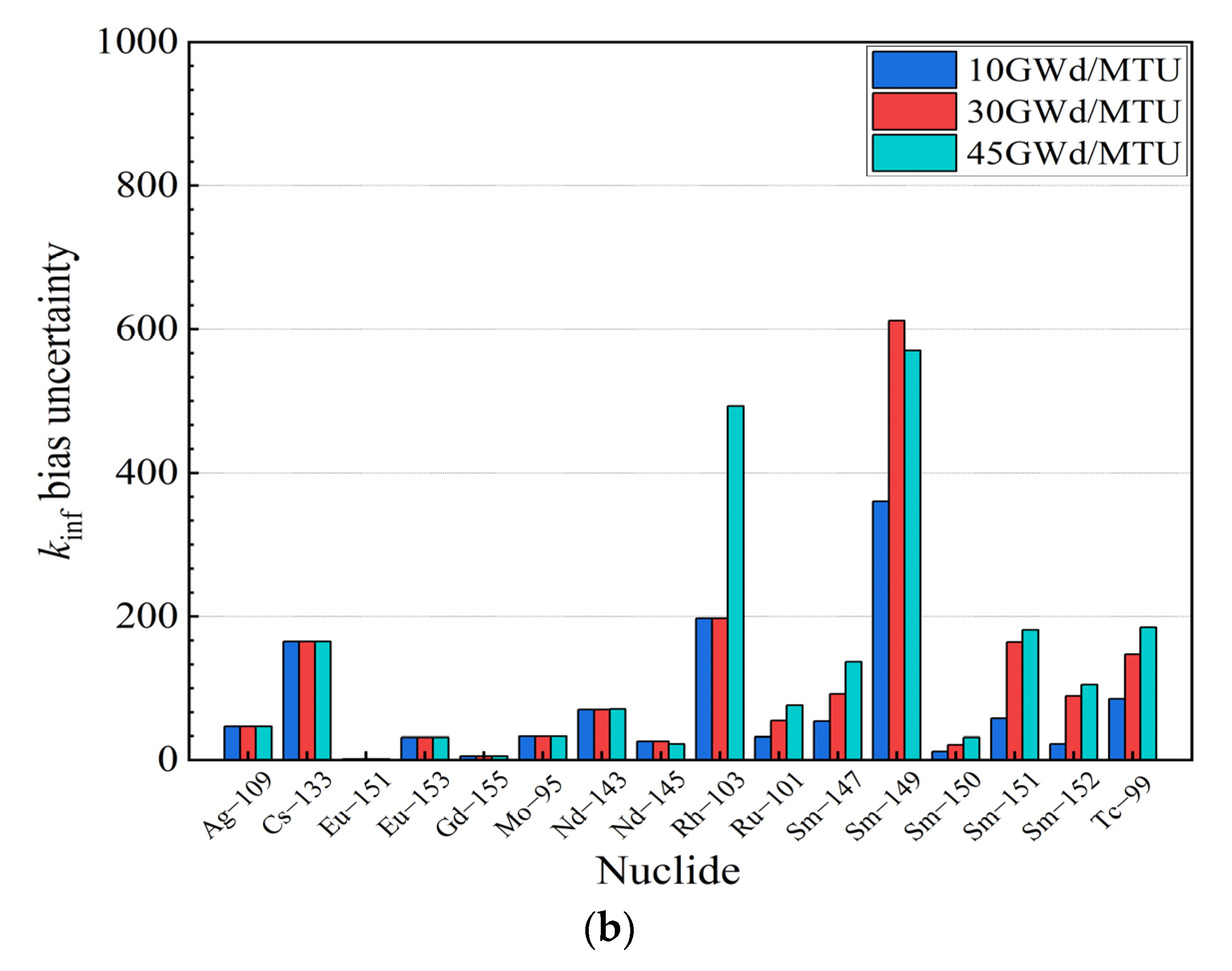
| Burnup | kinf–REF | kinf in ICF Method | Upper Limit of Tolerance Interval | β (pcm) | Δk (pcm) | β + Δk (pcm) | |
|---|---|---|---|---|---|---|---|
| 10 GWd/MTU | 1.2203 | 1.2237 | 1.2813 | 1.2366 | 168 | 1455 | 1455 |
| 30 GWd/MTU | 1.0800 | 1.0819 | 1.6684 | 1.1103 | 191 | 3026 | 3026 |
| 45 GWd/MTU | 0.9869 | 0.9954 | 1.0985 | 1.0334 | 850 | 4644 | 4644 |
| Reactor | Sample ID | Reactor | Sample ID | ||||
|---|---|---|---|---|---|---|---|
| Ohi-2 | 89G01 | 0.94310 | 0.00805 | CalvertCliffs-1 | MKP109-CC | 1.01733 | −0.00245 |
| Ohi-2 | 89G03 | 0.92405 | 0.01074 | CalvertCliffs-1 | MKP109-LL | 1.00734 | −0.00104 |
| Ohi-2 | 89G05 | 1.11899 | −0.01683 | CalvertCliffs-1 | MLA098-BB | 0.99873 | 0.00018 |
| Ohi-2 | 89G08 | 0.96809 | 0.00451 | CalvertCliffs-1 | MLA098-JJ | 0.98305 | 0.00240 |
| Ohi-2 | 89G10 | 0.96075 | 0.00555 | CalvertCliffs-1 | MLA098-P | 0.98545 | 0.00206 |
| ThreeMileIsland-1 | O12S4 | 0.94779 | 0.00738 | CalvertCliffs-1 | NBD107-GG | 1.04068 | −0.00575 |
| ThreeMileIsland-1 | O12S5 | 0.94783 | 0.00738 | CalvertCliffs-1 | NBD107-MM | 1.00000 | 0.00000 |
| ThreeMileIsland-1 | O12S6 | 0.96761 | 0.00458 | Genkai-1 | 87H01 | 1.00395 | −0.00056 |
| ThreeMileIsland-1 | O13S7 | 0.93333 | 0.00943 | Genkai-1 | 87H05 | 1.00646 | −0.00091 |
| ThreeMileIsland-1 | O13S8 | 0.94397 | 0.00792 | H.B. Robinson | A | 0.93564 | 0.00910 |
| ThreeMileIsland-1 | O1S1 | 0.96087 | 0.00553 | H.B. Robinson | B | 0.96535 | 0.00490 |
| ThreeMileIsland-1 | O1S2 | 0.94581 | 0.00766 | H.B. Robinson | B-N | 0.93915 | 0.00861 |
| ThreeMileIsland-1 | O1S3 | 0.96875 | 0.00442 | H.B. Robinson | C-D | 0.94511 | 0.00776 |
| TrinoVercellese-1 | 509-032-E11-4 | 0.95580 | 0.00625 | H.B. Robinson | C-J | 0.79506 | 0.02898 |
| TrinoVercellese-1 | 509-032-E11-7 | 0.93258 | 0.00953 | H.B. Robinson2 | B0-5-E14-C | 0.82821 | 0.02429 |
| TrinoVercellese-1 | 509-032-H9-4 | 1.01829 | −0.00259 | Mihama-3 | 86G03 | 1.10687 | −0.01511 |
| TrinoVercellese-1 | 509-032-H9-7 | 1.01875 | −0.00265 | Mihama-3 | 86G05 | 1.02762 | −0.00391 |
| TrinoVercellese-1 | 509-032-Q15-7 | 0.98684 | 0.00186 | Mihama-3 | 87C03 | 0.93333 | 0.00943 |
| TrinoVercellese-1 | 509-049-A1-7 | 1.01515 | −0.00214 | Mihama-3 | 87C04 | 0.96489 | 0.00496 |
| TrinoVercellese-1 | 509-049-J8-4 | 0.98582 | 0.00201 | Mihama-3 | 87C07 | 1.10659 | −0.01507 |
| TrinoVercellese-1 | 509-049-J8-7 | 0.99286 | 0.00101 | Mihama-3 | 87C08 | 1.10288 | −0.01455 |
| TrinoVercellese-1 | 509-069-A1-1 | 1.00000 | 0.00000 | Obrigheim-1 | 1–86 | 1.00518 | −0.00073 |
| TrinoVercellese-1 | 509-069-A1-7 | 1.07327 | −0.01036 | Obrigheim-1 | 1–88 | 1.01132 | −0.00160 |
| TrinoVercellese-1 | 509-069-E11-2 | 0.95333 | 0.00660 | Obrigheim-1 | 1–91 | 1.00203 | −0.00029 |
| TrinoVercellese-1 | 509-069-E11-4 | 0.91111 | 0.01257 | Obrigheim-1 | 1–92 | 1.00952 | −0.00135 |
| TrinoVercellese-1 | 509-069-E11-5 | 0.93893 | 0.00864 | Obrigheim-1 | 1–94 | 1.00000 | 0.00000 |
| TrinoVercellese-1 | 509-069-E11-7 | 0.92481 | 0.01063 | Obrigheim-1 | 2–87 | 1.01930 | −0.00273 |
| TrinoVercellese-1 | 509-069-E11-8 | 0.94737 | 0.00744 | Obrigheim-1 | 2–89 | 1.01282 | −0.00181 |
| TrinoVercellese-1 | 509-069-E11-9 | 0.97403 | 0.00367 | Obrigheim-1 | 2–90 | 0.99781 | 0.00031 |
| TrinoVercellese-1 | 509-069-E5-4 | 0.98473 | 0.00216 | Obrigheim-1 | 2–93 | 0.97843 | 0.00305 |
| TrinoVercellese-1 | 509-069-E5-7 | 0.96825 | 0.00449 | Obrigheim-1 | 2–95 | 1.01121 | −0.00159 |
| TrinoVercellese-1 | 509-069-E5-9 | 0.96795 | 0.00453 | Obrigheim-1 | E3-P1 | 1.08475 | −0.01198 |
| TrinoVercellese-1 | 509-069-J9-4 | 0.99174 | 0.00117 | Obrigheim-1 | E3-P2 | 1.50984 | −0.07210 |
| TrinoVercellese-1 | 509-069-J9-7 | 1.00000 | 0.00000 | Obrigheim-1 | E3-P3 | 1.16000 | −0.02263 |
| TrinoVercellese-1 | 509-069-L11-4 | 0.98462 | 0.00218 | Obrigheim-1 | E3-P4 | 1.05501 | −0.00778 |
| TrinoVercellese-1 | 509-069-L11-7 | 0.96850 | 0.00445 | Obrigheim-1 | E3-P5 | 1.09174 | −0.01297 |
| TrinoVercellese-1 | 509-069-L5-4 | 1.00000 | 0.00000 | Obrigheim-1 | G7-P1 | 0.97436 | 0.00363 |
| TrinoVercellese-1 | 509-069-L5-7 | 0.96094 | 0.00552 | Obrigheim-1 | G7-P2 | 1.00935 | −0.00132 |
| TurkeyPoint-3 | G10-4 | 1.01248 | −0.00176 | Obrigheim-1 | G7-P3 | 0.91797 | 0.01160 |
| TurkeyPoint-3 | G10-7 | 0.96259 | 0.00529 | Obrigheim-1 | G7-P4 | 1.02747 | −0.00388 |
| TurkeyPoint-3 | G7-15 | 0.99716 | 0.00040 | Obrigheim-1 | G7-P5 | 0.94393 | 0.00793 |
| TurkeyPoint-3 | G7-30 | 1.03161 | −0.00447 | Takahama-3 | SF95-2 | 0.96020 | 0.00563 |
| TurkeyPoint-3 | G7-35 | 1.00000 | 0.00000 | Takahama-3 | SF95-3 | 0.94326 | 0.00802 |
| TurkeyPoint-3 | G7-6 | 1.01459 | −0.00206 | Takahama-3 | SF95-4 | 0.91111 | 0.01257 |
| TurkeyPoint-3 | G9-13 | 1.08250 | −0.01167 | Takahama-3 | SF95-5 | 0.92771 | 0.01022 |
| TurkeyPoint-3 | G9-15 | 1.03351 | −0.00474 | Takahama-3 | SF96-2 | 1.00714 | −0.00101 |
| TurkeyPoint-3 | G9-9 | 0.97178 | 0.00399 | Takahama-3 | SF96-3 | 0.98070 | 0.00273 |
| TurkeyPoint-3 | H6-13 | 0.98991 | 0.00143 | Takahama-3 | SF96-4 | 0.94159 | 0.00826 |
| TurkeyPoint-3 | H9-7 | 1.08140 | −0.01151 | Takahama-3 | SF96-5 | 0.95577 | 0.00626 |
| TurkeyPoint-3 | I9-13 | 0.95798 | 0.00594 | Takahama-3 | SF97-2 | 0.98742 | 0.00178 |
| TurkeyPoint-3 | J8-13 | 0.99712 | 0.00041 |
| Burnup | S/U Method (pcm) | MC Uncertainty Sampling Method (pcm) | Relative Error (%) |
|---|---|---|---|
| 10 GWd/MTU | 1416 | 1455 | 2.75% |
| 30 GWd/MTU | 3005 | 3026 | 0.70% |
| 45 GWd/MTU | 4648 | 4644 | 0.09% |
| Nuclide | 235U | 238U | 239Pu | 240Pu | 241Pu | 242Pu |
|---|---|---|---|---|---|---|
| 235U | 1 | 0.08 | 0.137 | −0.319 | −0.203 | −0.541 |
| 238U | 0.08 | 1 | 0.081 | 0.211 | 0.352 | 0.225 |
| 239Pu | 0.137 | 0.081 | 1 | 0.7 | 0.367 | 0.413 |
| 240Pu | −0.319 | 0.211 | 0.7 | 1 | 0.571 | 0.84 |
| 241Pu | −0.203 | 0.352 | 0.367 | 0.571 | 1 | 0.621 |
| 242Pu | −0.541 | 0.225 | 0.413 | 0.84 | 0.621 | 1 |
| Correlation Coefficients | Correlation Levels |
|---|---|
| 0.8–1.0 | Extremely strong correlation |
| 0.6–0.8 | Strong correlation |
| 0.4–0.6 | Moderate correlation |
| 0.2–0.4 | Weak correlation |
| 0.0–0.2 | Excessively weak correlation or non-existent correlation |
| Nuclide | 235U | 238U | 239Pu | 240Pu | 241Pu | 242Pu |
|---|---|---|---|---|---|---|
| 235U | 1 | 0 | 0 | 0 | 0 | 0 |
| 238U | 0 | 1 | 0 | 0 | 0 | 0 |
| 239Pu | 0 | 0 | 1 | 0.7 | 0 | 0.413 |
| 240Pu | 0 | 0 | 0.7 | 1 | 0.571 | 0.84 |
| 241Pu | 0 | 0 | 0 | 0.571 | 1 | 0.621 |
| 242Pu | 0 | 0 | 0.413 | 0.84 | 0.621 | 1 |
| Nuclide | 235U | 238U | 239Pu | 240Pu | 241Pu | 242Pu |
|---|---|---|---|---|---|---|
| 235U | 1 | 0 | 0 | 0 | 0 | 0 |
| 238U | 0 | 1 | 0 | 0 | 0 | 0 |
| 239Pu | 0 | 0 | 1 | 0.7 | 0 | 0 |
| 240Pu | 0 | 0 | 0.7 | 1 | 0 | 0.84 |
| 241Pu | 0 | 0 | 0 | 0 | 1 | 0.621 |
| 242Pu | 0 | 0 | 0 | 0.84 | 0.621 | 1 |
| Correlation Coefficient Matrix | kinf Values from the Code | kinf Uncertainty from MC Sampling Method (pcm) |
|---|---|---|
| Results without considering isotopic correlation | 1.16792 | 4216 |
| Results excluding negative and weak correlations among isotopes | 1.16792 | 4035 |
| Results considering only strong correlations among isotopes | 1.16792 | 3991 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, Z.; Chen, X.; Xie, J.; Wasaye, M.A.; Yu, T. Quantitative Analysis Study of Effects of Nuclide Concentration Uncertainties on Biases and Bias Uncertainties in Criticality Calculation Method. Energies 2023, 16, 7378. https://doi.org/10.3390/en16217378
Ni Z, Chen X, Xie J, Wasaye MA, Yu T. Quantitative Analysis Study of Effects of Nuclide Concentration Uncertainties on Biases and Bias Uncertainties in Criticality Calculation Method. Energies. 2023; 16(21):7378. https://doi.org/10.3390/en16217378
Chicago/Turabian StyleNi, Zining, Xirong Chen, Jinsen Xie, Muhammad Abdul Wasaye, and Tao Yu. 2023. "Quantitative Analysis Study of Effects of Nuclide Concentration Uncertainties on Biases and Bias Uncertainties in Criticality Calculation Method" Energies 16, no. 21: 7378. https://doi.org/10.3390/en16217378
APA StyleNi, Z., Chen, X., Xie, J., Wasaye, M. A., & Yu, T. (2023). Quantitative Analysis Study of Effects of Nuclide Concentration Uncertainties on Biases and Bias Uncertainties in Criticality Calculation Method. Energies, 16(21), 7378. https://doi.org/10.3390/en16217378






