Effect of Mineral Grain and Hydrate Layered Distribution Characteristics on the Mechanical Properties of Hydrate-Bearing Sediments
Abstract
:1. Introduction
2. Modelling Methodology and Scenarios
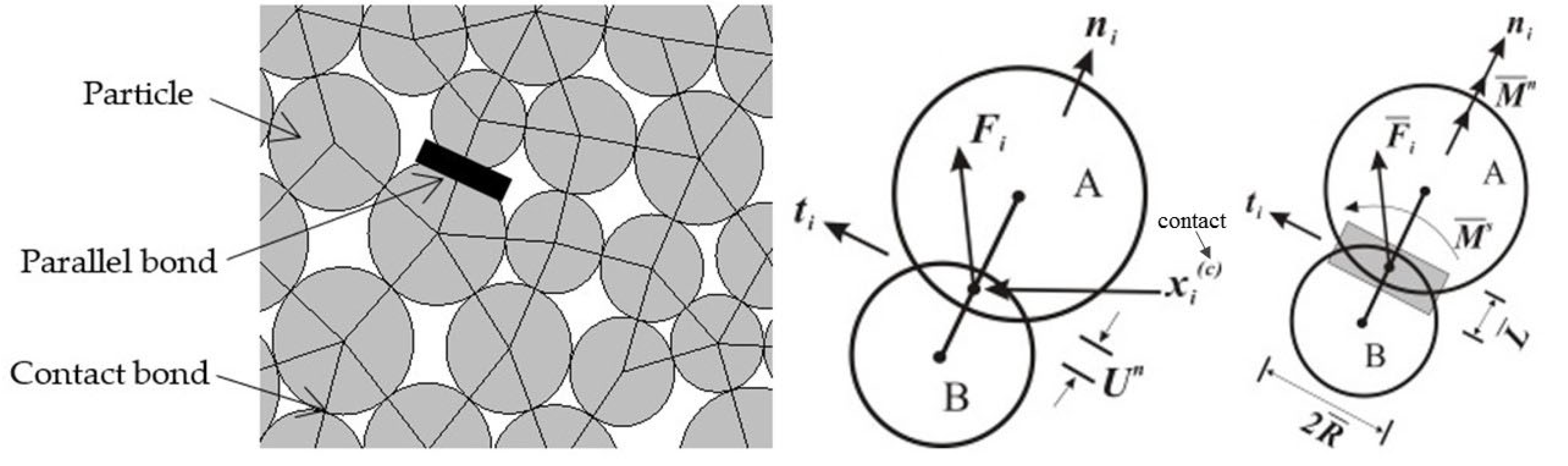
2.1. Methodology
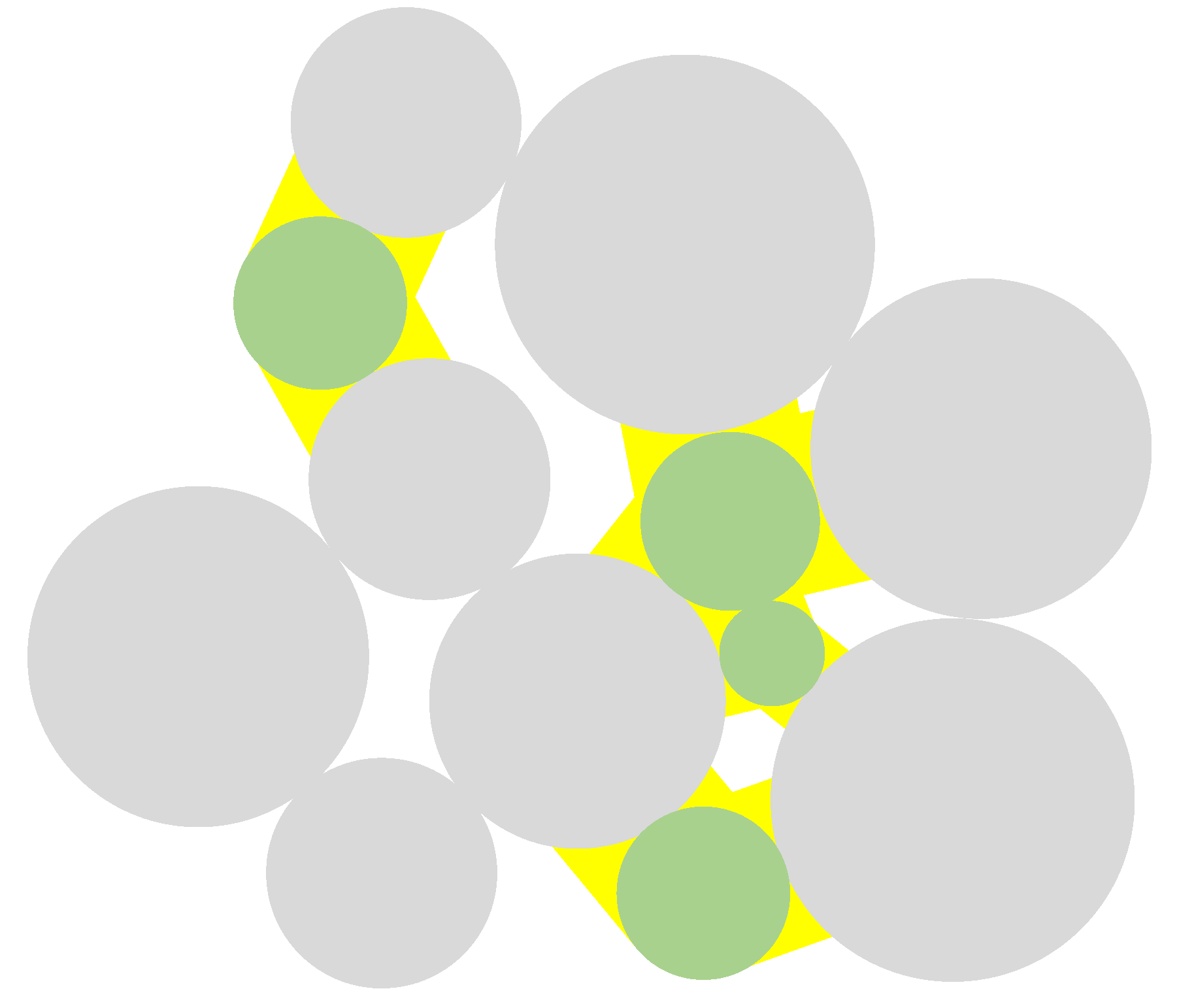
2.2. Model Description
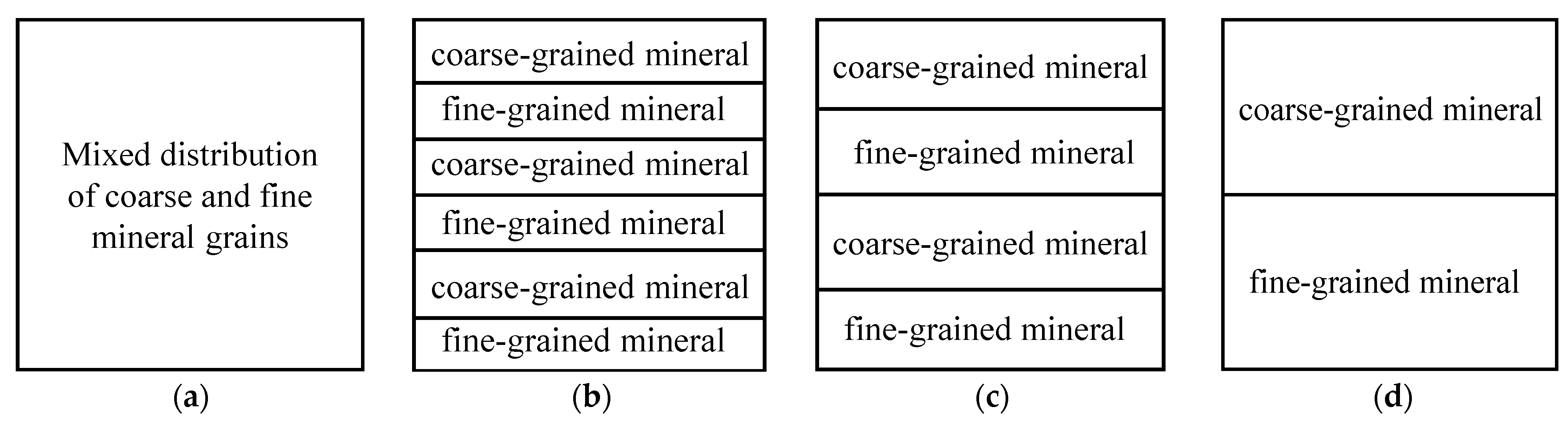
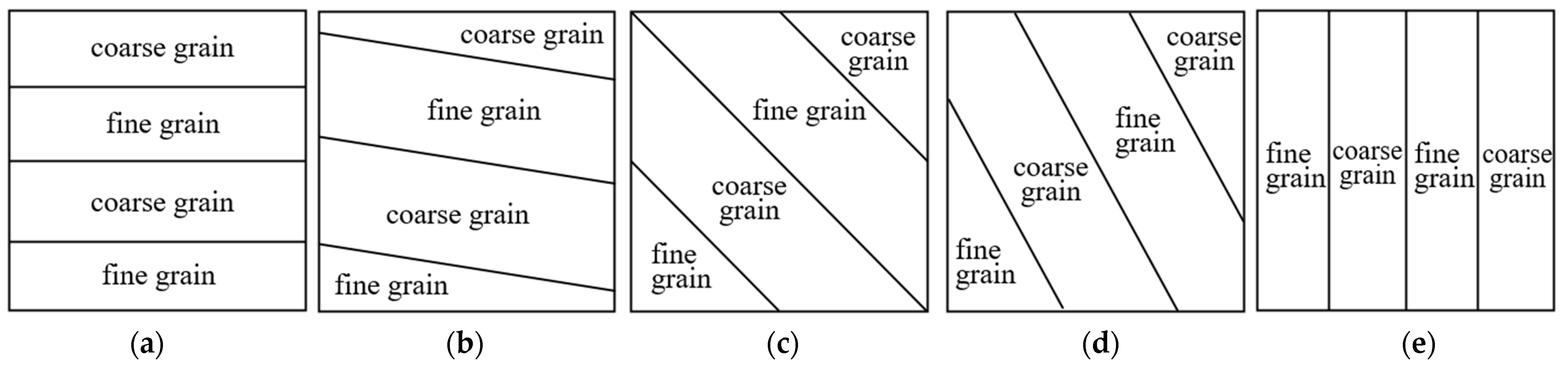
2.3. Modelling Scenarios
- (1)
- Layered models that consider mineral grain size differences
- (2)
- Layered model scenarios considering differences in mineral micromechanical parameters
- (3)
- Layered model scenarios considering anisotropy of the HBS
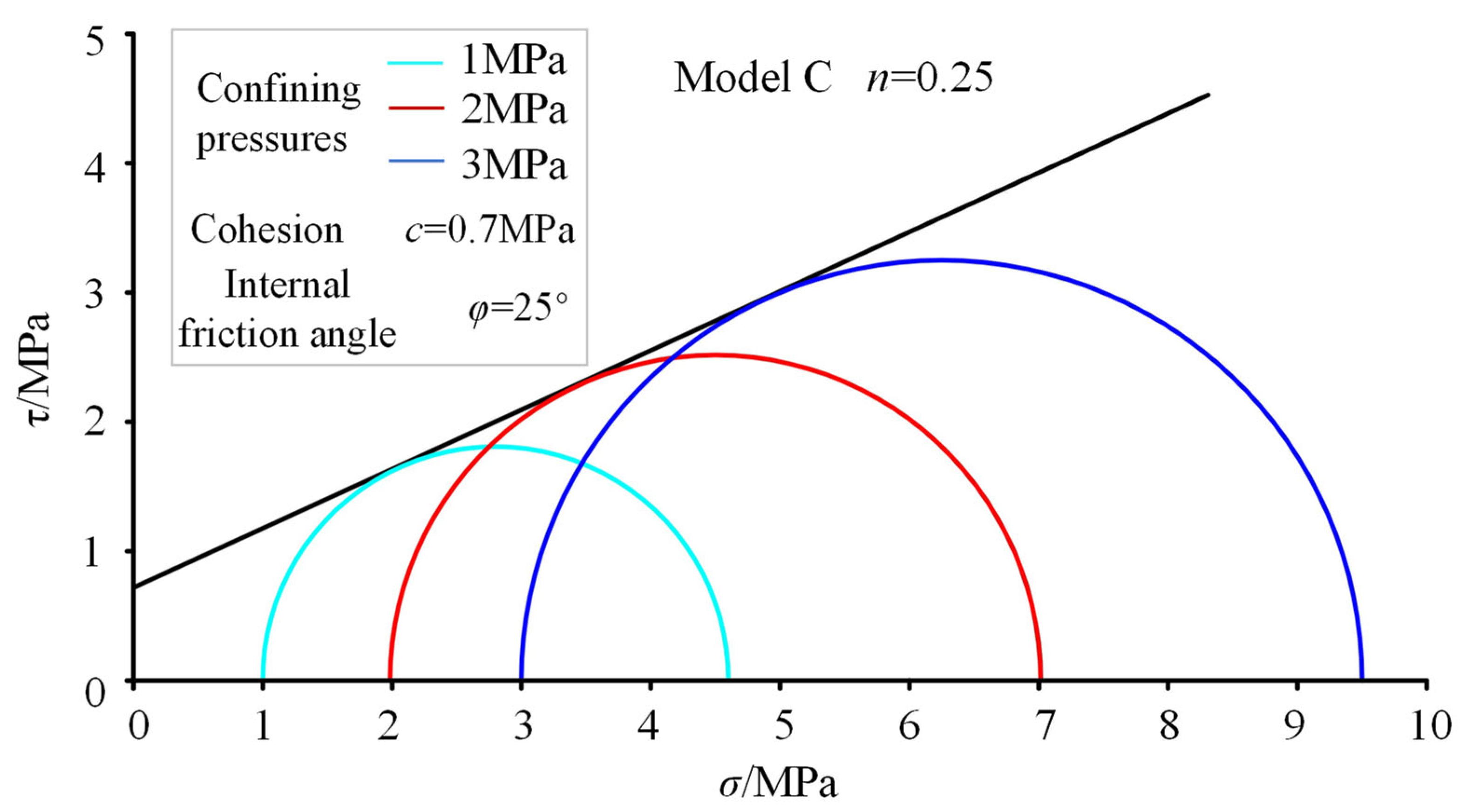
2.4. Microparameter Calibration
3. Influence of Layered Distribution of Sediments and Hydrates
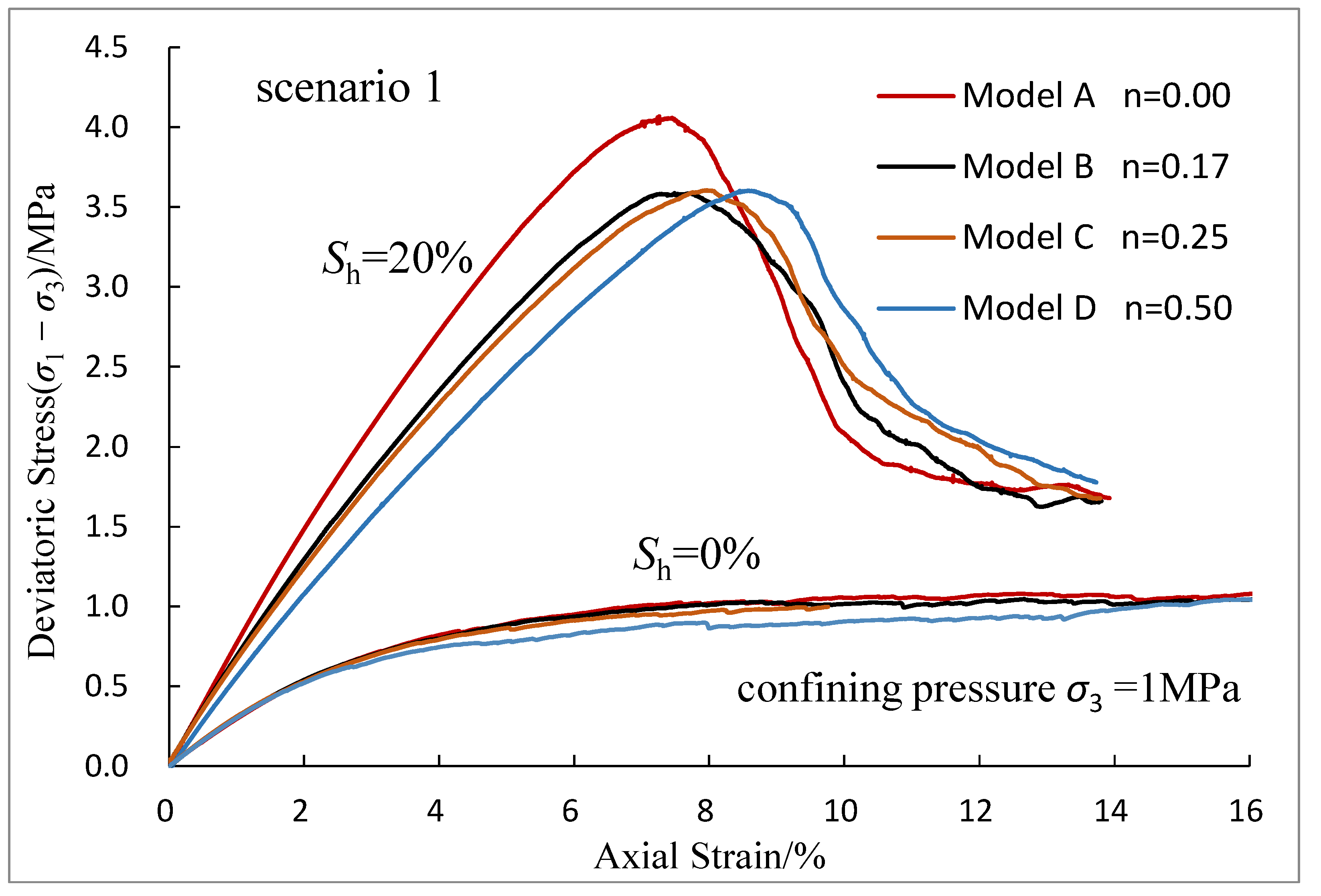
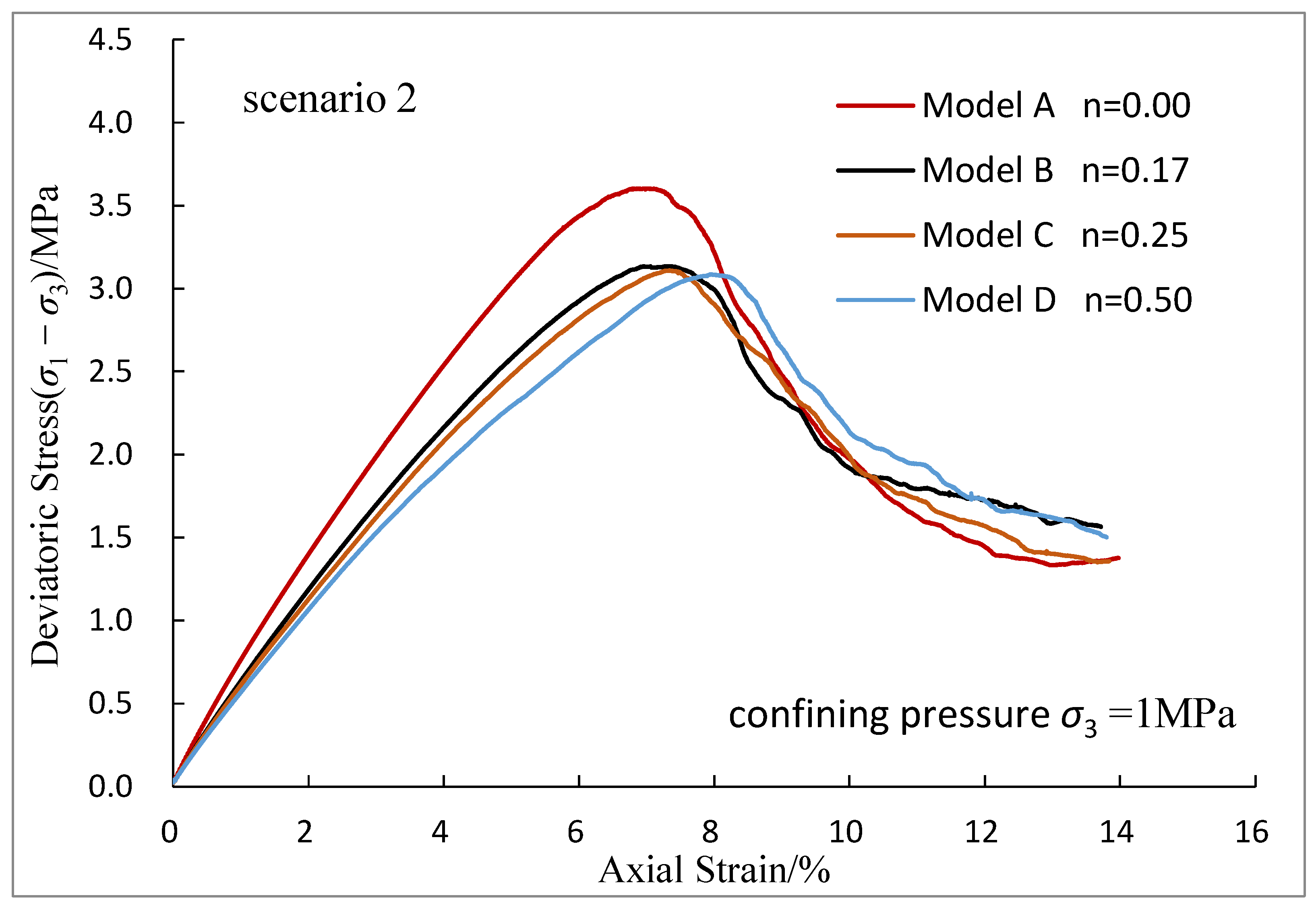
3.1. Effects of Sediment and Hydrate Layering on Deviatoric Stress-Strain Curves
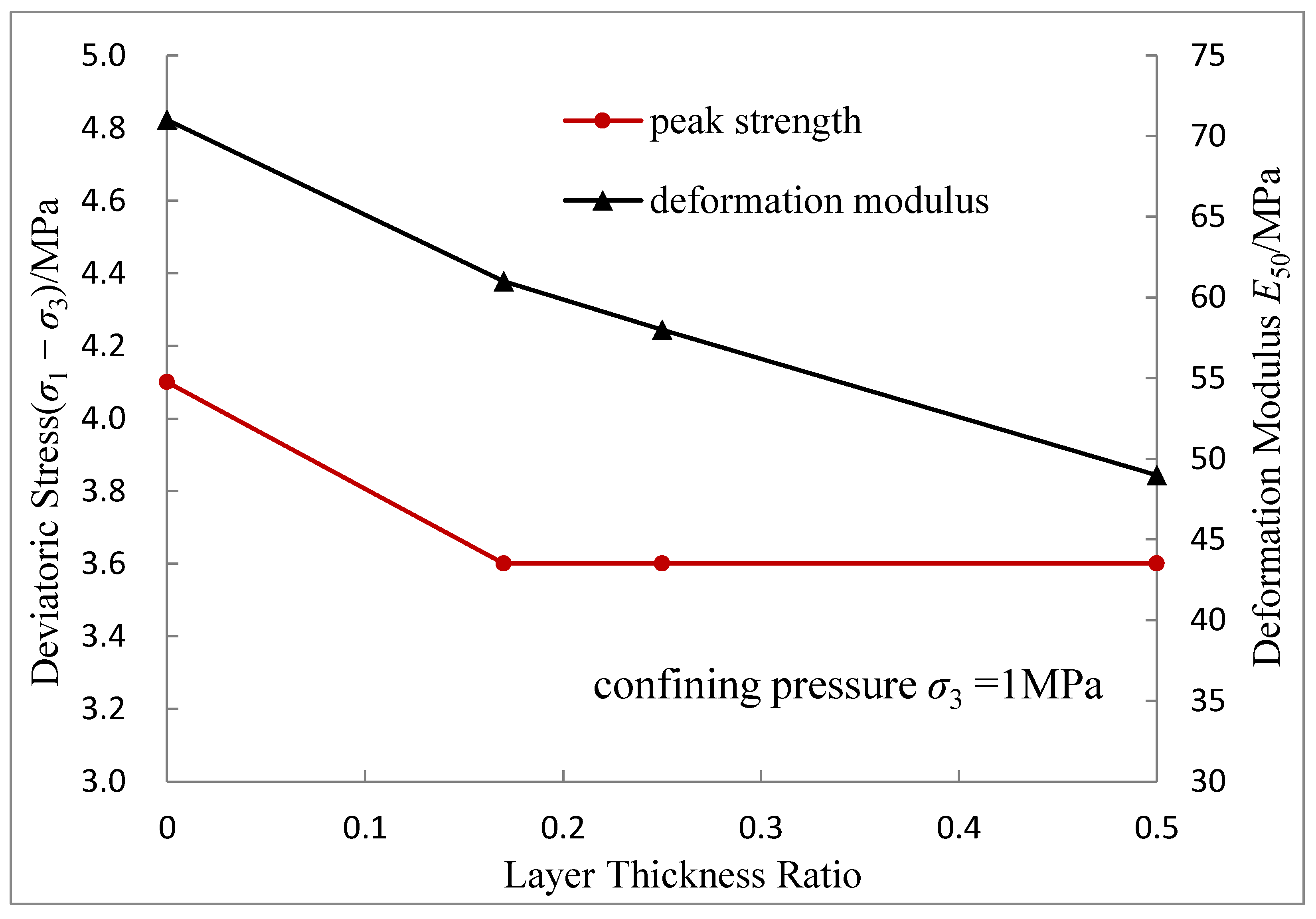
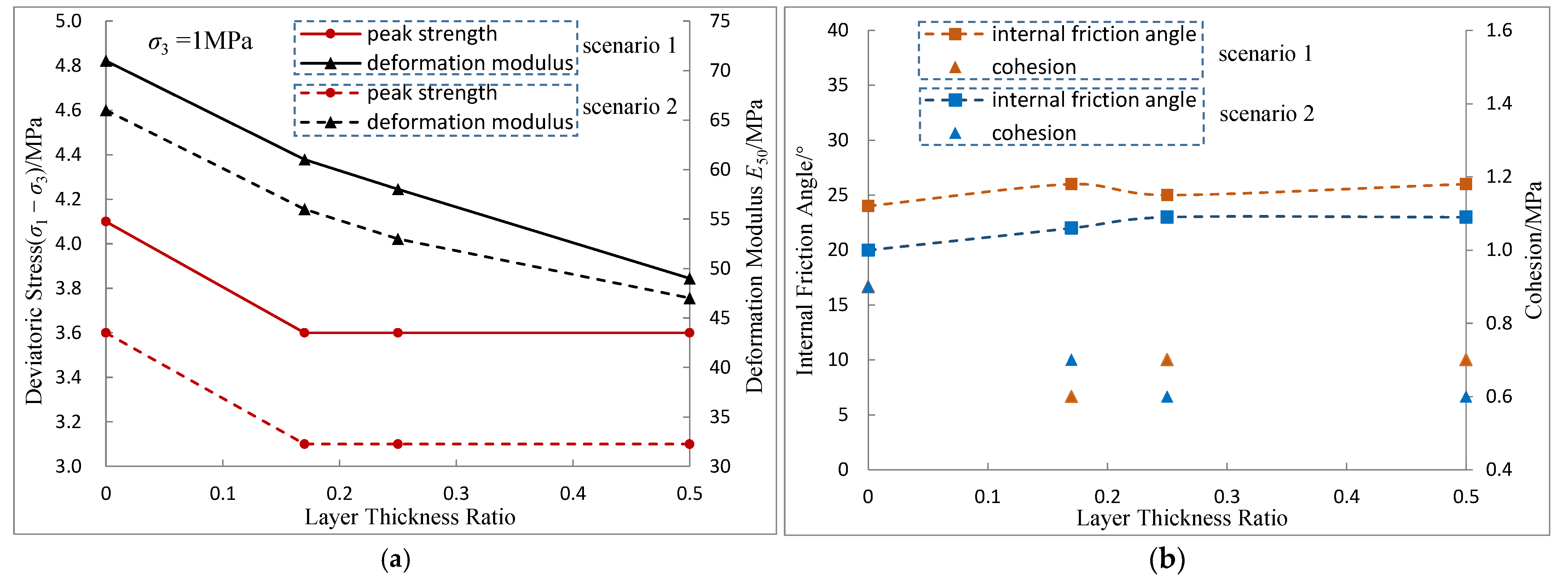
3.2. Effects of Sediment and Hydrate Layering on Peak Strength and Deformation Modulus
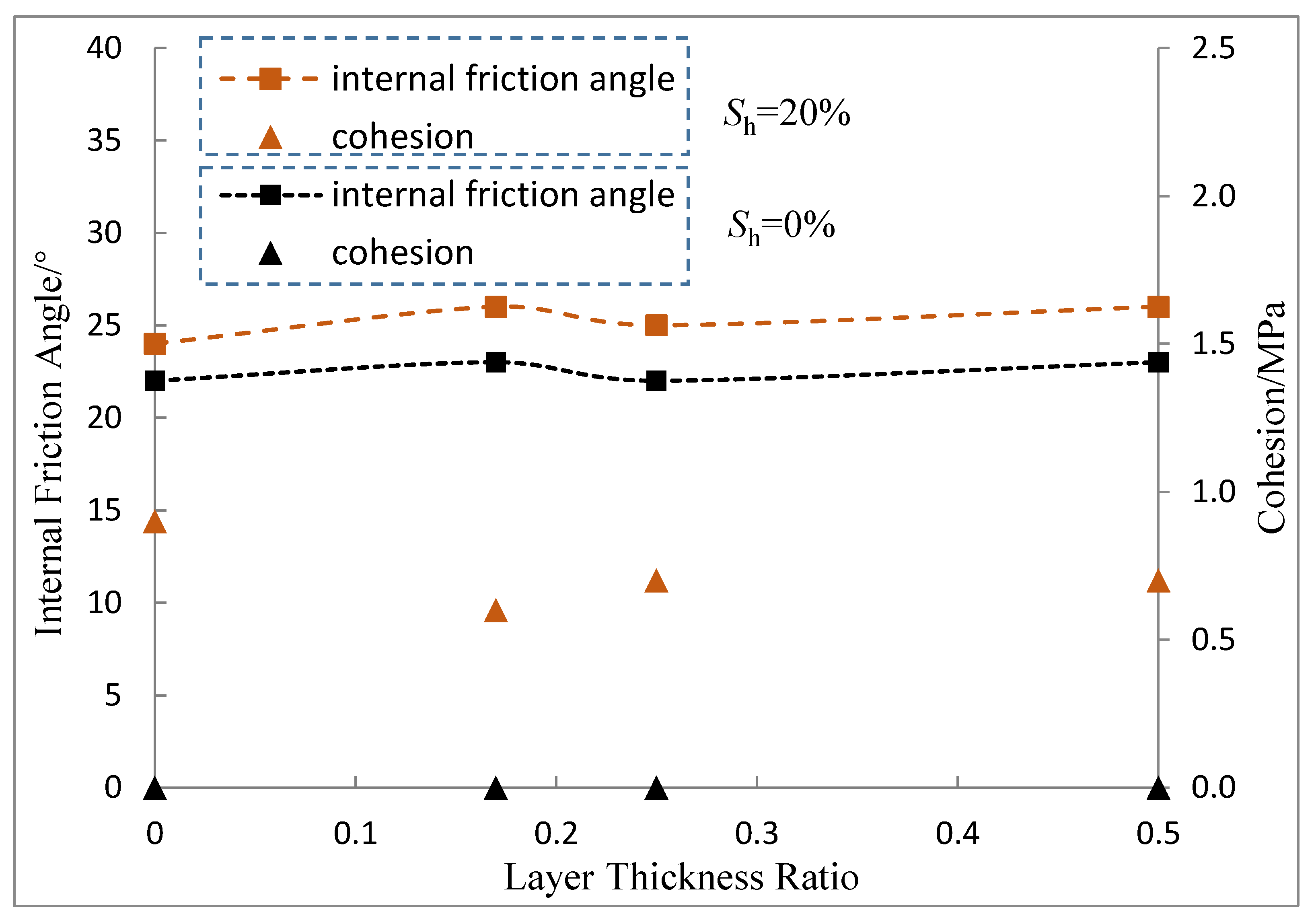
3.3. Effects of Sediment and Hydrate Layering on the Internal Friction Angle and Cohesion
4. Influence of Material Heterogeneity on Mechanical Property of HBS
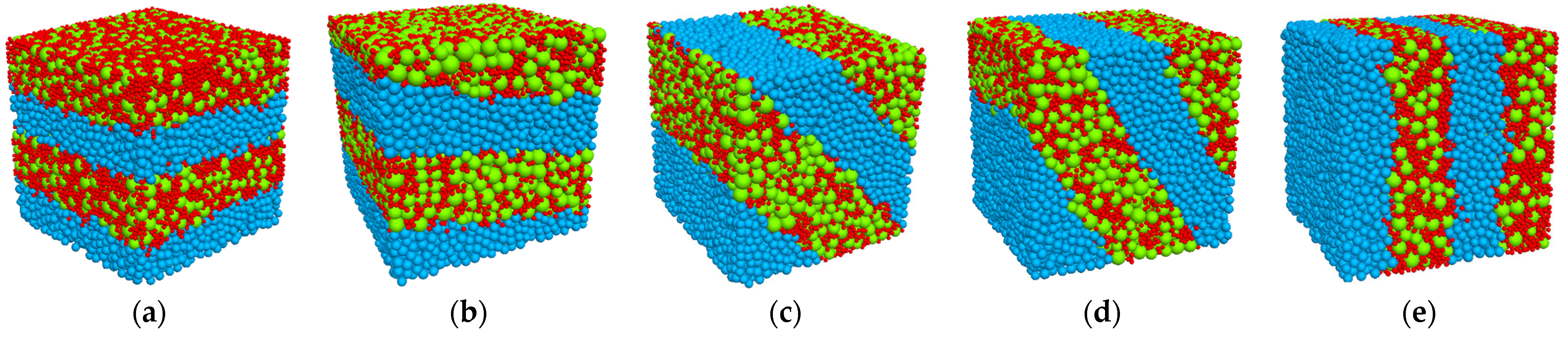
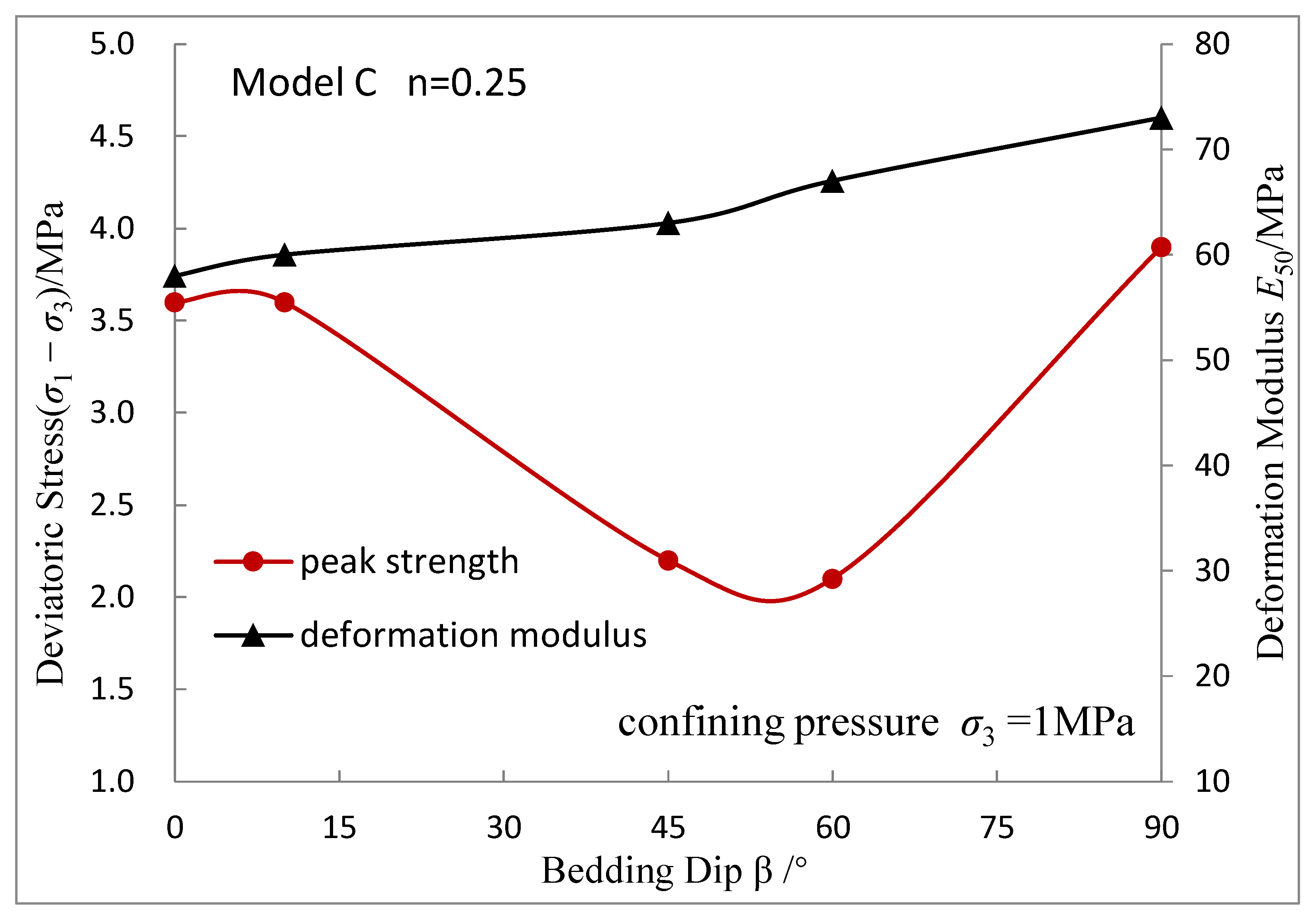
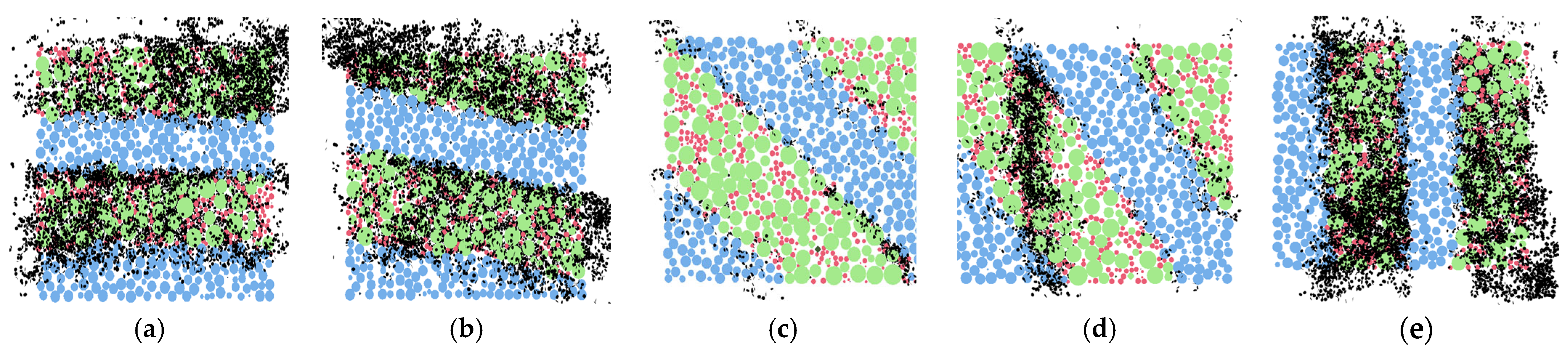
5. Influence of Anisotropy on the Mechanical Properties of HBS
6. Discussion
7. Conclusions
- (1)
- The layered distribution of hydrates has a significant impact on the mechanical behaviour of HBS. Compared with the homogeneous model, the layering of the hydrates reduces the peak strength and cohesion of the sample; however, the number of layers has little effect on the peak strength and cohesion, which is mainly related to the saturation of the hydrates in the model.
- (2)
- Fine-grained mineral layers without hydrates play a major role in controlling the deformation modulus of HBS. When the coarse and fine grains are interlayered and hydrates occur in the coarse-grained layers, there is a good linear positive correlation between deformation modulus and layer number.
- (3)
- When coarse and fine grains correspond to different mineral constituents, the material heterogeneity can further decrease the macroscopic mechanical parameters of HBS, such as peak strength, deformation modulus, and cohesion, which indicate that the mechanical strength will be overestimated if the homogeneous model is used for reservoir evaluation.
- (4)
- The layering of sediment particles and hydrates results in anisotropy of the reservoir. The deformation modulus increases with an increase in the bedding dip angle, and the peak strength first decreases and then increases, with a minimum occurring at an angle of 60°. The anisotropic effect of sediment formation cannot be ignored, when evaluating reservoir strength in the region with complex structural conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chong, Z.R.; Yang, S.H.B.; Babu, P.; Linga, P.; Li, X.S. Review of natural gas hydrates as an energy resource: Prospects and challenges. Appl. Energy 2016, 162, 1633–1652. [Google Scholar] [CrossRef]
- Dong, H.; Wang, J.; Xie, Z.; Wang, B.; Zhang, L.; Shi, Q. Potential applications based on the formation and dissociation of gas hydrates. Renew. Sustain. Energy Rev. 2021, 143, 110928. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, L.; Zhou, J.; Pan, Z.; Wang, S.; Li, R. Effects of Hydrate Occurring Mechanisms and Saturation on the Mechanical Properties of Hydrate-bearing Sediments: Numerical Study based on Simplified DEM simulation. J. Nat. Gas Sci. Eng. 2022, 108, 104804. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, L.; Wang, J. Formation, Exploration, and Development of Natural Gas Hydrates. Energies 2022, 15, 5951. [Google Scholar] [CrossRef]
- Bosikov, I.I.; Klyuev, R.V.; Silaev, I.V.; Pilieva, D.E. Estimation of multistage hydraulic fracturing parameters using 4D simulation. Min. Sci. Technol. 2023, 8, 141–149. [Google Scholar] [CrossRef]
- Brown, N.M.; Brown, M. Tracer dispersion due to non-Newtonian fluid flows in hydraulic fractures with different geometries and porous walls. J. Hydrol. 2023, 622, 129644. [Google Scholar] [CrossRef]
- Manjunath, G.L.; Liu, Z.; Jha, B. Multi-stage hydraulic fracture monitoring at the lab scale. Eng. Fract. Mech. 2023, 289, 109448. [Google Scholar] [CrossRef]
- Locat, J.; Lee, H.J. Submarine landslides: Advances and challenges. Can. Geotech. J. 2002, 39, 193–212. [Google Scholar] [CrossRef]
- Sultan, N.; Cochonat, P.; Foucher, J.R. Effect of gas hydrates melting on seafloor slope instability. Mar. Geol. 2004, 213, 379–401. [Google Scholar] [CrossRef]
- Uchida, S.; Lin, J.-S.; Myshakin, E.M.; Seol, Y.; Boswell, R. Numerical simulations of sand migration during gas production in hydrate-bearing sands interbedded with thin mud layers at site NGHP-02-16. Mar. Pet. Geol. 2018, 108, 639–647. [Google Scholar] [CrossRef]
- Lijith, K.P.; Malagar, B.R.C.; Singh, D.N. A comprehensive review on the geomechanical properties of gas hydrate bearing sediments. Mar. Pet. Geol. 2019, 104, 270–285. [Google Scholar] [CrossRef]
- Bazaluk, O.; Sai, K.; Lozynskyi, V.; Petlovanyi, M.; Saik, P. Research into Dissociation Zones of Gas Hydrate Deposits with a Heterogeneous Structure in the Black Sea. Energies 2021, 14, 1345. [Google Scholar] [CrossRef]
- Rutqvist, J.; Moridis, G.; Grover, T.; Silpngarmlert, S.; Collett, T.; Holdich, S. Coupled multiphase fluid flow and wellbore stability analysis associated with gas production from oceanic hydrate-bearing sediments. J. Pet. Sci. Eng. 2012, 92–93, 65–81. [Google Scholar] [CrossRef]
- Fujii, T.; Suzuki, K.; Takayama, T.; Tamaki, M.; Komatsu, Y.; Konno, Y.; Yoneda, J.; Yamamoto, K.; Nagao, J. Geological setting and characterization of a methane hydrate reservoir distributed at the first offshore production test site on the Daini-Atsumi Knoll in the eastern Nankai Trough, Japan. Mar. Pet. Geol. 2015, 66, 310–322. [Google Scholar] [CrossRef]
- Ye, J.-L.; Qin, X.-W.; Xie, W.-W.; Lu, H.-L.; Ma, B.-J.; Qiu, H.-J.; Liang, J.-Q.; Lu, J.-A.; Kuang, Z.-G.; Cheng, F.; et al. The second natural gas hydrate production test in the South China Sea. China Geol. 2020, 3, 197–209. [Google Scholar] [CrossRef]
- Ye, J.-L.; Qin, X.-W.; Xie, W.-W.; Lu, H.-L.; Ma, B.-J.; Qiu, H.-J.; Liang, J.-Q.; Lu, J.-A.; Kuang, Z.-G. Characterization of gas hydrate reservoirs by integration of core and log data in the Ulleung Basin, East Sea. Mar. Pet. Geol. 2013, 47, 30–42. [Google Scholar] [CrossRef]
- Torres, M.; Tréhu, A.; Cespedes, N.; Kastner, M.; Wortmann, U.; Kim, J.-H.; Long, P.; Malinverno, A.; Pohlman, J.; Riedel, M.; et al. Methane hydrate formation in turbidite sediments of northern Cascadia, IODP Expedition 311. Earth Planet. Sci. Lett. 2008, 271, 170–180. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, H.L.; Liang, J.Q. The methane hydrate accumulation controlled compellingly by sediment grain at Shenhu, northern South China Sea. Chin. Sci. Bull. 2016, 61, 388–397. (In Chinese) [Google Scholar] [CrossRef]
- Yoneda, J.; Oshima, M.; Kida, M.; Kato, A.; Konno, Y.; Jin, Y.; Jang, J.; Waite, W.F.; Kumar, P.; Tenma, N. Pressure core based onshore laboratory analysis on mechanical properties of hydrate-bearing sediments recovered during India’s National Gas Hydrate Program Expedition (NGHP) 02. Mar. Pet. Geol. 2018, 108, 482–501. [Google Scholar] [CrossRef]
- Pecher, I.A.; Holbrook, W.S.; Sen, M.K.; Lizarralde, D.; Wood, W.T.; Hutchinson, D.R.; Dillon, W.P.; Hoskins, H.; Stephen, R.A. Seismic anisotropy in gas-hydrate- and gas-bearing sediments on the Blake Ridge, from a walkaway vertical seismic profile. Geophys. Res. Lett. 2003, 30, 291–305. [Google Scholar] [CrossRef]
- Liu, J.-W.; Li, X.-S.; Kou, X.; Wang, Y.; Li, L.-J. Analysis of Hydrate Heterogeneous Distribution Effects on Mechanical Characteristics of Hydrate-Bearing Sediments. Energy Fuel 2021, 35, 4914–4924. [Google Scholar] [CrossRef]
- Uchida, S.; Soga, K.; Yamamoto, K. Critical state soil constitutive model for methane hydrate soil. J. Geophys. Res. Solid Earth 2012, 117, B03209. [Google Scholar] [CrossRef]
- Hyodo, M.; Li, Y.; Yoneda, J.; Nakata, Y.; Yoshimoto, N.; Nishimura, A.; Song, Y. Mechanical behavior of gas-saturated methane hydrate-bearing sediments. J. Geophys. Res. Solid Earth 2013, 118, 5185–5194. [Google Scholar] [CrossRef]
- Miyazaki, K.; Tenma, N.; Sakamoto, Y.; Yamaguchi, T.; Okubo, S. Effects of Methane Hydrate Saturation and Confining Pressure on Strain-Rate Dependence of Artificial Methane-Hydrate-Bearing Sediment in Triaxial Compression Test. Int. J. Offshore Polar 2012, 22, 90–96. [Google Scholar] [CrossRef]
- Choi, J.H.; Dai, S.; Lin, J.S.; Seol, Y. Multistage Triaxial Tests on Laboratory-Formed Methane Hydrate-Bearing Sediments. J. Geophys. Res. Solid Earth 2018, 123, 3347–3357. [Google Scholar] [CrossRef]
- Priest, J.A.; Hayley, J.L. Strength of laboratory synthesized hydrate-bearing sands and their relationship to natural hydrate-bearing sediments. J. Geophys. Res. Solid Earth 2019, 124, 12556–12575. [Google Scholar] [CrossRef]
- Zhou, M.; Soga, K.; Yamamoto, K. Upscaled Anisotropic Methane Hydrate Critical State Model for Turbidite Hydrate-Bearing Sediments at East Nankai Trough. J. Geophys. Res. Solid Earth 2018, 123, 6277–6298. [Google Scholar] [CrossRef]
- Li, Y.L.; Wu, Q.; Wu, P.; Liu, W.G. Mechanical Properties of Methane Hydrate Interbedded with Clayey Sediments. J. Energy Nat. Res. 2018, 7, 24–31. [Google Scholar] [CrossRef]
- Li, Y.; Dong, L.; Wu, N.; Nouri, A.; Liao, H.; Chen, Q.; Sun, J.; Liu, C. Influences of hydrate layered distribution patterns on triaxial shearing characteristics of hydrate-bearing sediments. Eng. Geol. 2021, 294, 106375. [Google Scholar] [CrossRef]
- Waite, W.F.; Santamarina, J.C.; Cortes, D.D.; Dugan, B.; Espinoza, D.N.; Germaine, J.; Jang, J.; Jung, J.W.; Kneafsey, T.J.; Shin, H.; et al. Physical properties of hydrate-bearing sediments. Rev. Geophys. 2009, 47, 465–484. [Google Scholar] [CrossRef]
- Masui, A.; Haneda, H.; Ogata, Y.; Aoki, K. Effects of methane hydrate formation on shear strength of synthetic methane hydrate sediments. In Proceedings of the Fifteenth International Offshore and Polar Engineering Conference, Seoul, Republic of Korea, 19–24 June 2005; International Society of Offshore and Polar Engineers: Seoul, Republic of Korea, 2005. [Google Scholar]
- Winters, W.; Waite, W.; Mason, D.; Gilbert, L.; Pecher, I. Methane gas hydrate effect on sediment acoustic and strength properties. J. Pet. Sci. Eng. 2007, 56, 127–135. [Google Scholar] [CrossRef]
- Miyazaki, K. Triaxial compressive properties of artificial methane-hydrate-bearing sediment. J. Geophys. Res. Solid Earth 2011, 116, B06102. [Google Scholar] [CrossRef]
- Hyodo, M.; Wu, Y.; Nakashima, K.; Kajiyama, S.; Nakata, Y. Influence of Fines Content on the Mechanical Behavior of Methane Hydrate-Bearing Sediments. J. Geophys. Res. Solid Earth 2017, 122, 7511–7524. [Google Scholar] [CrossRef]
- Kajiyama, S.; Wu, Y.; Hyodo, M.; Nakata, Y.; Nakashima, K.; Yoshimoto, N. Experimental investigation on the mechanical properties of methane hydrate-bearing sand formed with rounded particles. J. Nat. Gas. Sci. Eng. 2017, 45, 96–107. [Google Scholar] [CrossRef]
- Shen, S.; Sun, X.; Wang, L.; Song, Y.C.; Li, Y.H. Effect of Temperature on the Mechanical Properties of Hydrate-Bearing Sand under Different Confining Pressures. Energy Fuel 2021, 35, 4106–4117. [Google Scholar] [CrossRef]
- Liu, W.; Pan, D.; Shen, S.; You, Z.; Zhao, Y.; Sun, X. Experimental Study on Mechanical Properties of Hydrate-Bearing Sand: The Influence of Sand-Water Mixing Methods. Energies 2021, 14, 2554. [Google Scholar] [CrossRef]
- Ginsburg, G.; Soloviev, V.; Matveeva, T.; Andreeva, T. Sediment Grain-Size Control on Gas Hydrate Presence, Sites 994, 995, and 997, Scientific Results, Proc. Ocean Drill. Program Sci. Results 2000, 164, 237–245. [Google Scholar] [CrossRef]
- Uchida, T.; Takeya, S.; Chuvilin, E.M.; Ohmura, R.; Nagao, J.; Yakushev, V.S.; Istomin, V.A.; Minagawa, H.; Ebinuma, T.; Narita, H. Decomposition of methane hydrates in sand, sandstone, clays, and glass beads. J. Geophys. Res. Atmos. 2004, 109, B05206. [Google Scholar] [CrossRef]
- Tréhu, A.; Long, P.; Torres, M.; Bohrmann, G.; Rack, F.; Collett, T.; Goldberg, D.; Milkov, A.; Riedel, M.; Schultheiss, P.; et al. Three-dimensional distribution of gas hydrate beneath southern hydrate ridge: Constraints from ODP leg 204. Earth Planet. Sci. Lett. 2004, 222, 845–862. [Google Scholar] [CrossRef]
- Qin, X.-W.; Lu, J.-A.; Lu, H.-L.; Qiu, H.-J.; Liang, J.-Q.; Kang, D.-J.; Zhan, L.-S.; Lu, H.-F.; Kuang, Z.-G. Coexistence of natural gas hydrate, free gas and water in the gas hydrate system in the Shenhu Area, South China Sea. China Geol. 2020, 3, 210–220. [Google Scholar] [CrossRef]
- Sun, S.-C.; Liu, C.-L.; Ye, Y.-G.; Liu, Y.-F. Phase behavior of methane hydrate in silica sand. J. Chem. Thermodyn. 2014, 69, 118–124. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A Bonded-Particle Model for Rock. Int. J. Rock Mech. Min. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Han, Z.; Zhou, J.; Zhang, L. Influence of Grain Size Heterogeneity and In-Situ Stress on the Hydraulic Fracturing Process by PFC2D Modeling. Energies 2018, 11, 1413. [Google Scholar] [CrossRef]
- Liu, C.; Ye, Y.; Meng, Q.; He, X.; Lu, H.; Zhang, J.; Liu, J.; Yang, S. The characteristics of gas hydrates recovered from Shenhu area in the South China Sea. Mar. Geol. 2012, 307–310, 22–27. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Shen, S.; Liu, T.; Zhao, J. Untrained triaxial tests on water-saturated methane hydrate-bearing clayey-silty sediments of the South China Sea. Can. Geotech. J. 2020, 58, 351–366. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, L.; Azzam, R.; Zhou, J.; Wang, S. A statistical index indicating the degree and mechanical effects of grain size heterogeneity in rocks. Eng. Geol. 2021, 293, 106292. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Shen, S.; Liu, W.; Sun, X.; Liu, Y.; Zhao, J. Mechanical Behaviors of Gas Hydrate-bearing Clayey Sediments of the South China Sea. J. Environ. Geotech. 2019, 9, 210–222. [Google Scholar] [CrossRef]
- Miyazaki, K.; Tenma, N.; Aoki, K.; Yamaguchi, T. A Nonlinear Elastic Model for Triaxial Compressive Properties of Artificial Methane-Hydrate-Bearing Sediment Samples. Energies 2012, 5, 4057–4075. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Y.; Sang, S.; Zeng, Z.; Hua, L.; Kong, L. Triaxial Tests of Hydrate-Bearing Clayey-Silty Sediments Under Different Hydrate Saturations and Effective Confining Pressures. Energy Fuel 2022, 36, 14042–14054. [Google Scholar] [CrossRef]


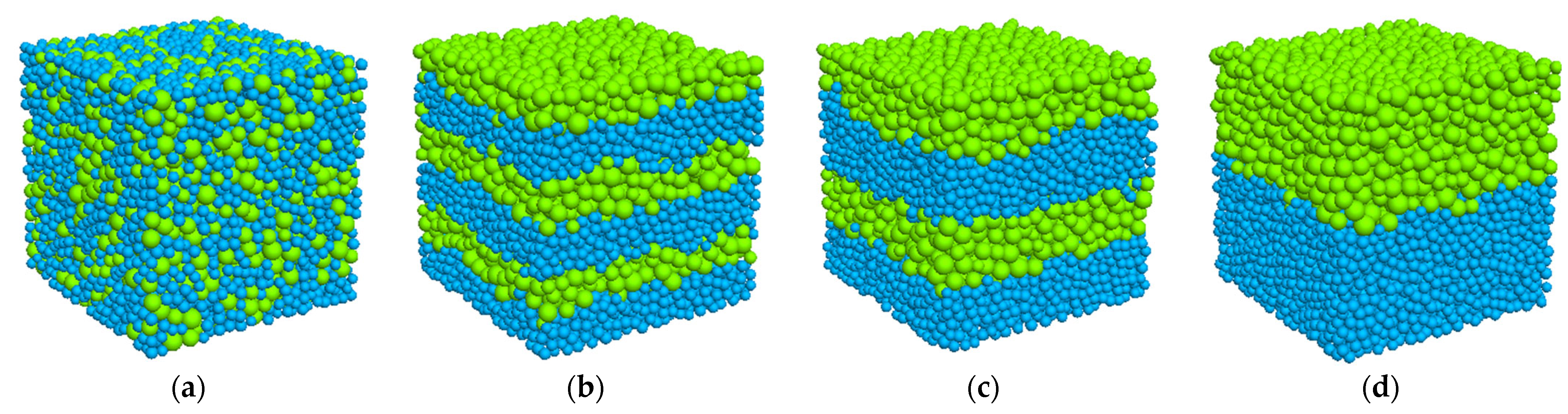
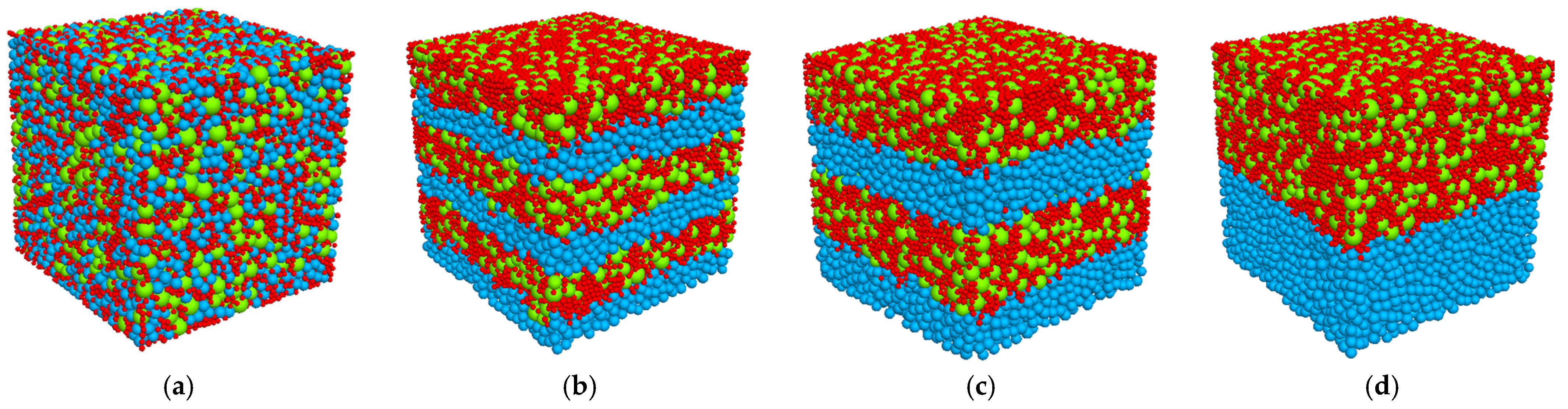

| Scenario | Model | Influence Factors | Confining Pressure/MPa |
|---|---|---|---|
| 1 | A, B, C, D | Mineral grain and hydrate layered distribution, hydrate saturation | 1, 2, 3 |
| 2 | A, B, C, D | Mineral grain and hydrate layered distribution, material heterogeneity | 1, 2, 3 |
| 3 | C | Anisotropy of the HBS | 1 |
| Microparameters | Hydrate | Parameters for Scenario 2 | Parameters for Scenario 1 | ||
|---|---|---|---|---|---|
| Coarse Grain | Fine Grain | Average Value of Coarse and Fine Grain | |||
| Particle | Density/kg/m3 | 300 | 2500 | 2500 | 2500 |
| Modulus/MPa | 50 | 150 | 50 | 100 | |
| Normal-to-shear stiffness | 1.5 | 1.5 | 1.5 | 1.5 | |
| Friction coefficient | 0.5 | 0.8 | 0.2 | 0.5 | |
| Parallel bond | Tension strength/MPa | 3 | |||
| Shear strength/MPa | 3 | ||||
| Normal-to-shear stiffness | 1.5 | ||||
| Modulus/MPa | 50 | ||||
| Friction coefficient | 0.5 | ||||
| Macro-Mechanical Properties | Experimental Results | Simulated Results |
|---|---|---|
| Peak strength/MPa | 0.9–3.5 | 2.1–4.0 |
| Elastic modulus E50/MPa | 40–150 | 50–75 |
| Cohesion/MPa | 0.2–0.9 | 0.5–0.9 |
| Internal friction angle/° | 20–25 | 20–25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Zhang, L.; Zhou, J.; Pan, Z.; Wang, S.; Li, R. Effect of Mineral Grain and Hydrate Layered Distribution Characteristics on the Mechanical Properties of Hydrate-Bearing Sediments. Energies 2023, 16, 7366. https://doi.org/10.3390/en16217366
Han Z, Zhang L, Zhou J, Pan Z, Wang S, Li R. Effect of Mineral Grain and Hydrate Layered Distribution Characteristics on the Mechanical Properties of Hydrate-Bearing Sediments. Energies. 2023; 16(21):7366. https://doi.org/10.3390/en16217366
Chicago/Turabian StyleHan, Zhenhua, Luqing Zhang, Jian Zhou, Zhejun Pan, Song Wang, and Ruirui Li. 2023. "Effect of Mineral Grain and Hydrate Layered Distribution Characteristics on the Mechanical Properties of Hydrate-Bearing Sediments" Energies 16, no. 21: 7366. https://doi.org/10.3390/en16217366
APA StyleHan, Z., Zhang, L., Zhou, J., Pan, Z., Wang, S., & Li, R. (2023). Effect of Mineral Grain and Hydrate Layered Distribution Characteristics on the Mechanical Properties of Hydrate-Bearing Sediments. Energies, 16(21), 7366. https://doi.org/10.3390/en16217366






