Abstract
In recent years, the concept of the negative resistor (NR) has been proposed and applied in the magnetic coupled wireless power transfer (MC-WPT) system to improve the stability of power transfer. However, it remains a fundamental challenge to find the characteristic differences and applications of the four basic NR-based MC-WPT topologies. In this paper, the circuit models of the four basic NR-based MC-WPT topologies: series-series (SS), series-parallel (SP), parallel-parallel (PP), and parallel-series (PS) are established, and their characteristics are analyzed and compared by using circuit theory, which enables engineers to determine and select topologies to suit different applications and requirements. Theoretical analysis shows that the compensation methods of the transmitter and receiver of the NR-based MC-WPT system would affect the operating frequency and output characteristics of the system. Moreover, by comparative analysis, the conditions and applicable ranges for a stable output of different topologies were provided. Finally, the experimental prototypes are set up by using the power electronic inverter and operational amplifier, and the voltage gain ratios of the four basic NR-based WPT topologies under the variations of transfer distance and load are observed. The experimental results validate the correctness of the theoretical analysis.
1. Introduction
Due to its convenience, intelligence, safety and reliability, magnetic coupled wireless power transfer (MC-WPT) technology has been widely studied and applied in various fields, such as consumer electronics, household appliances, electric vehicle charging, and biomedical implants [1,2,3,4,5,6,7,8].
Generally, MC-WPT systems are eager to achieve stable and efficient power transfer characteristics, which are crucial factors to evaluate MC-WPT systems [6,9,10]. However, the output power and transfer efficiency of the conventional MC-WPT systems are sensitive to variations in the coupling strength [11,12,13,14]. Especially for MC-WPT systems in the process of dynamic change, the change in the coupling coefficient is a great challenge to the stable transfer characteristics of MC-WPT systems [15,16,17].
So far, many methods have been investigated to guarantee stable and efficient power transfer to electric devices. The first method is to design a complex coupling mechanism so that the coupling coefficient between the transmitter and receiver does not change with the change of the receiver’s position, so as to obtain stable transfer characteristics [18,19,20,21,22], for example, using a Helmholtz coil, 8-shaped winding structure of coils or a 3-D coupled formed by two orthogonal coils to generate a uniform magnetic field to improve transfer characteristics. The second method is to design the compensation topologies, such as LCL, LCC, CLC, and a combination of series (S) and parallel (P), etc., to improve the misalignment tolerance and thus achieve constant output characteristics [23,24,25,26,27,28,29,30]. The third method is to use the capacitor array to dynamically adjust the resonant frequency, so as to maintain maximum power transfer efficiency in the case of varying coupling coefficients [31]. However, these three methods increase the volume, weight, and cost of the system. The fourth method is to adopt the variable frequency control strategy by tracking the zero-phase angle (ZPA) between the input voltage and current or the input voltage and the receiver’s current, so as to obtain a constant transfer power [12,32,33]. But this method increases the complexity of the system, and the communication delay or interruption between the transmitter and receiver will affect the stable power transfer of the system.
In recent years, some new circuit characteristics have been discovered when adopting new resistive devices in circuit systems, such as a negative resistors (NR) [34] or memristors [35]. Among them, a robust MC-WPT system is proposed by using NR [36], which does not require any communication between the transmitter and receiver, and there are no additional circuits. For the robust MC-WPT system composed of the NR, there are four basic compensation topologies, including series-series (SS), series-parallel (SP), parallel-parallel (PP), and parallel-series (PS). In [35,36], the coupled-mode model of the PP compensation topology of the NR-based MC-WPT system is established and the transfer characteristics of the system are analyzed by the coupled-mode theory, in which the negative resistor is realized by an operational amplifier (op amp) to enable robust wireless power transfer. [37] develops a switch-mode amplifier to construct the negative resistor and applies it to the SP compensation topology of the NR-based MC-WPT system that can wirelessly transfer around 10 W of power to a moving load with a nearly constant transfer efficiency. In [38], the SS compensation topology of the MC-WPT system with the negative resistor constructed by power electronic converter is implemented and successfully applied to a drone-in-flight wireless charging platform. [39,40,41,42] extend the application of the SS compensation topology of the NR-based MC-WPT system to logistic robots, cordless kitchen appliances and electric vehicle charging. [43,44] present the S/PS compensation topology and multiload NR-based MC-WPT systems, which extend the transfer distance with constant output power and transfer efficiency. [45,46] discuss the operating frequency, output power and transfer efficiency of domino NR-based MC-WPT systems based on the coupled-mode theory, in which the output power and transfer efficiency are constant in the strongly coupled region where the operating frequency has multiple solutions. However, the coupled-mode theory is an approximation analytical method, which is suitable for weakly coupling coefficient and higher quality factor [47,48,49]. Furthermore, the comparative analysis between SS, SP, PP, and PS compensation topologies of the NR-based MC-WPT system has been little explored, resulting in a lack of guidelines or references for engineers and researchers to select topologies for different applications.
Therefore, this paper focuses on the comparative analysis of SS, SP, PP and PS topologies for NR-based MC-WPT systems, and the proposed analysis can be generalized to MC-WPT systems with all compensation networks, because other compensation networks can be derived from the combinations or transformations of these four basic topologies. The contributions of this paper are mainly as follows:
- (1)
- Circuit models of the four basic topologies of NR-based MC-WPT systems are established.
- (2)
- The transfer characteristics of the four basic NR-based MC-WPT topologies are systematically compared, and the applicable scenarios for each topology are proposed, providing the reference for the MC-WPT design in the real-world.
- (3)
- Two methods for implementing the NR are compared, and their applicability in different topologies is given, providing the reference for the selection and design of the NR in different MC-WPT topologies.
The remainder of this paper is organized as follows. The basic topologies of the NR-based MC-WPT system are described in Section 2. The circuit models of the four basic NR-based MC-WPT topologies are established in Section 3. The system characteristics of the four basic NR-based MC-WPT topologies are analyzed in Section 4. Section 5 presents the experimental prototypes to compare and analyze the four basic NR-based MC-WPT topologies, and the experimental results validate the theoretical analysis. Finally, Section 6 concludes this paper.
2. Basic Topologies of the WPT System Composed of the Negative Resistor
Currently, WPT systems using a negative resistor have four basic topologies, including an SS, SP, PP and PS topology, as shown in Figure 1. Here, LT and LR denote the inductances of the transmitting and receiving coils, CT and CR denote the capacitances of the transmitting and receiving circuits, and iT and iR are currents flowing through the transmitting and receiving circuits, respectively. −RN in the transmitting circuit is a negative resistor, which is used as a gain source to provide the electrical energy. RL is the load resistance. vin is the voltage across the negative resistor, which is also defined as the input voltage. vo is the voltage across the load resistance, which is also called the output voltage. M is the mutual inductance. Particularly, the coupling strength is defined as k = M/(LTLR)1/2, which always satisfies 0 < k < 1 [50]. The natural frequencies of transmitting and receiving coils are defined as ωT = 1/(LTCT)1/2 and ωR = 1/(LRCR)1/2, respectively [51].
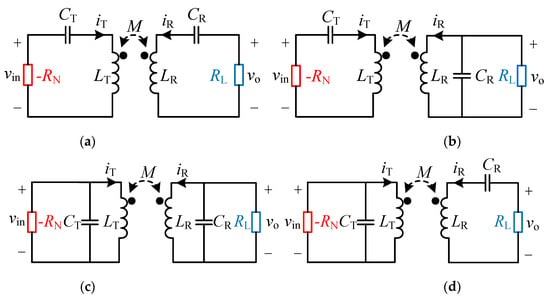
Figure 1.
Basic topologies of the WPT system using a negative resistor. (a) SS topology. (b) SP topology. (c) PP topology. (d) PS topology.
3. Circuit Models
3.1. SS Topology
According to KVL and KCL, the circuit equation of the SS topology shown in Figure 1a can be written as
where j is the imaginary unit, and ω is the operating angular frequency of the WPT system. İT and İR are the phasor forms of iT and iR, respectively. QT = ωTLT/RN and QR = ωRLR/RL are used to represent the quality factors of the negative resistor and load resistor, respectively. The natural frequencies of transmitting and receiving coils are set to be identical, i.e., ωT = ωR = ω0.
Equation (1) has nontrivial solutions only if its coefficient matrix has a zero determinant, that is
Separating the real and imaginary parts of (2) yields
3.2. SP Topology
The circuit equation of the SP topology shown in Figure 1b can be deduced as
Then, the frequency characteristic equation can be written as
Substituting (7) with (6) to eliminate the QT yields
Considering k2 << 1 and << 1 in a general WPT system with an SP topology, (8) can be approximated as
3.3. PP Topology
The circuit equation of the PP topology shown in Figure 1c can be derived as
and the frequency characteristic equation can be written as follows:
3.4. PS Topology
The circuit equation of the PS topology shown in Figure 1d can be written as
Then, the operating frequency can be derived as
Substituting (15) with (14) to eliminate QT yields
Considering k2 << 1 and << 1 in a general WPT system with PS topology, (16) can be approximated as
4. Characteristic Analysis
4.1. SS Topology
From (3) and (4), there are two cases of the operating frequency, as follows:
- (1)
- ω ≠ ω0
In this case, the operating frequency can be derived as
and the negative resistor automatically satisfies
In order to ensure that the operating frequency is positive real, the constraint conditions can be deduced as
where kC is the critical coupling strength, and RLC is the critical load resistance. It can be noted that the region where the operating frequency has multiple positive real solutions is defined as the strongly coupled region, that is k ≥ kC and RL ≤ RLC. In contrast, the region with only one solution of the operating frequency is defined as the weakly coupled region, that is k < kC and RL > RLC.
- (2)
- ω = ω0
In this case, k < kC, the operating frequency works steadily at ω = ω0, and the negative resistor satisfies
By substituting the above solutions of operating frequencies into (1), the current ratio can be written as
where λ = ω/ω0 is the ratio of the operating frequency to the natural frequency, IT and IR are root-mean-square values.
According to Vo = IRRL and Vin = ITRN, the voltage ratio can be derived as
where Vo and Vin are root-mean-square values.
4.2. SP Topology
From (9), it can be found that the operating frequency has two cases, as follows:
- (1)
- ω ≠ ω0
In this case, the operating frequency can be derived as
the negative resistor automatically satisfies
and the constraint conditions can be obtained as
- (2)
- ω = ω0
In this case, k < kC, the operating frequency works steadily at ω = ω0, and the negative resistor satisfies
By substituting the above solutions of operating frequencies with (5), the voltage ratio can be deduced as
4.3. PP Topology
From (11) and (12), the operating frequency has the following two case:
- (1)
- ω ≠ ω0
In this case, the operating frequency can be deduced as
and the negative resistor automatically satisfies
Then, the constraint conditions can be obtained as
- (2)
- ω ≈ ω0
In this case, k < kC and the operating frequency has a steadily solution, that is
Substituting (35) with (11), the negative resistor can be obtained as
Thus, by substituting the above solutions of operating frequencies with (10), the voltage ratio can be deduced as
4.4. PS Topology
From (17), the operating frequency can be found as follows:
- (1)
- ω ≠ ω0
In this case, the operating frequency can be deduced as
the negative resistor automatically satisfies
and the constraint conditions can be obtained as
- (2)
- ω ≈ ω0
In this case, k < kC, the operating frequency has a steadily solution, that is
and the negative resistor satisfies
Hence, by substituting the solutions of operating frequencies with (13), the voltage ratio can be given by
According to the above characteristic analysis, the SS and PP topologies give accurate solutions to the operating frequency, while the operating frequencies of the SP and PS topologies have a certain approximation. Figure 2 shows the comparison between the exact and approximate solutions for the operating frequencies of SP and PS topologies; it can be seen that they are in good agreement, which verifies the correctness of the analytical expressions for the operating frequency shown in (25), (38) and (43). The circuit parameters are shown in Table 1.
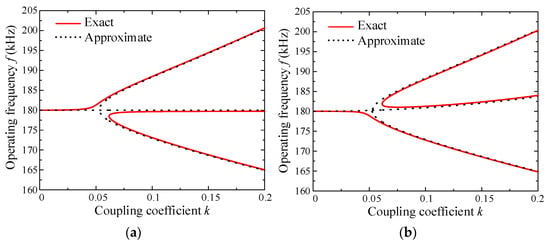
Figure 2.
Comparison between the exact and approximate solutions for the operating frequencies. (a) SP topology. (b) PS topology.

Table 1.
Main circuit parameters.
Furthermore, the operating frequency of the SS and PS topologies are approximately equal, resulting in the same constraint conditions of the coupling coefficient and load resistance, as are the SP and PP topologies.
5. Comparison of Characteristics
Currently, there are two approaches to constructing negative resistor; one is based on operational amplifiers and the other is based on power electronic inverters [34,36,37,38,39,40,41,42,43,44,45,46], whose discrepancies are listed in Table 2.

Table 2.
Comparison of two construction methods of negative resistance.
Due to the limitation of the power level of op amps, the output power provided by the negative resistance based on op amps is small, only at a milliwatt level, which cannot meet the high-power requirements of SS and SP topologies. However, its simple structure and low cost can be used for PS and PP topologies, which are suitable for the wireless charging of low-power devices such as implantable medical devices and sensors. On the contrary, the output power provided by the negative resistance based on power electronic inverters is high, a watt level and even a kilowatt level, which can be applied to SS and SP topologies for the wireless charging of high-power equipment such as electric vehicles and automated guided vehicles. Therefore, SS and SP topologies use a power electronic inverter to achieve negative resistance, while PP and PS topologies adopt an op amp to construct negative resistance.
Figure 3 gives the experimental prototypes of the NR-based MC-WPT systems, and the corresponding schematic diagram of the negative resistance is shown in Figure 4. In Figure 3a, the negative resistance is realized by a full-bridge inverter, which is used for the experiments of SS and SP topologies, and its schematic diagram is shown in Figure 4a, in which the transmitter current signal is sampled by the current trans-former CU8965 and converted into the voltage signal through a high-speed operational amplifier OPA2690, and then fed into the comparator TL3016 to obtain the phase of the transmitter current, and sent to the digital signal processor TMS32028335. The signal processed by the digital signal processor is then sent to the drive circuit (here the drive chip used in the drive circuit is Si8271), and the drive signal generated by the drive circuit ultimately controls the switches S1~S4. In Figure 3b, the negative resistance is constructed by an op amp (LM6172), which is used for the experiments of the PP and PS topologies, and its schematic diagram is shown in Figure 4b, where the negative resistance can be represented by −RN = −VRN/IRN = −RfR1/R2.

Figure 3.
Experimental prototype of the NR-based WPT systems. (a) With the negative resistance constructed by a full-bridge inverter. (b) With the negative resistance constructed by an op amp.
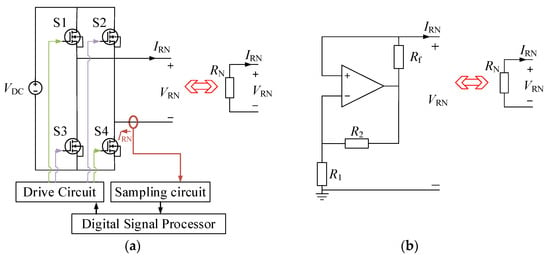
Figure 4.
The schematic diagram of the negative resistance. (a) With the negative resistance constructed by a full-bridge inverter. (b) With the negative resistance constructed by an op amp.
To evaluate the transfer properties of the four basic NR based MR-WPT topologies, the output-input voltage ratios are measured in the experiment. For SS and SP topologies, the input voltage waveform is a square wave, as shown in Figure 5a. Hence, the input fundamental voltage Vin_f of SS and SP topologies can be acquired by fundamental wave analysis method. Therefore, the output-input voltage ratio of SS and SP topologies can be calculated by Vo/Vin_f. For PS and PP topologies, the input and output voltage waveform are sinusoidal, as shown in Figure 5b, so the input voltage Vin and output voltage Vo can be measured with an oscilloscope. Then, the output-input voltage ratio of PS and PP topologies can be calculated by Vo/Vin.
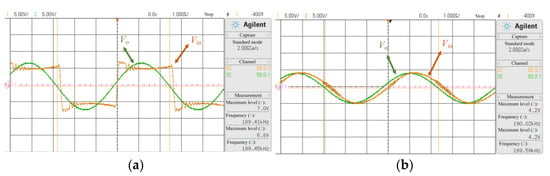
Figure 5.
The waveforms of the input voltage and output voltage of the NR-based MC-WPT system. (a) With the negative resistance constructed by a full-bridge inverter. (b) With the negative resistance constructed by an op amp.
From the above analysis, the operating frequency of SS, SP, PP and PS topologies can be described as shown in Figure 6. It can be seen that the coupling region of the NR-based MC-WPT system can be divided into two parts: the strongly coupled region (k ≥ kC) and the weakly coupled region (k < kC). In the strongly coupled region, the bifurcation of steady solutions of the operating frequency occurs, the operating frequency of the four topologies has two real solutions ω+ and ω−, which are related to the compensation topology of the receiver. When the coupling coefficient decreases, the two real solutions ω+ and ω− coincide at the critical coupling coefficient kC. In addition, the maximum and average errors between the experimental and theoretical values of the four topologies are calculated. The maximum errors of the SS, SP, PP and PS topologies are −0.64%, −0.73%, 1.70% and 0.78%, and the mean errors are −0.17%, −0.17%, 0.34% and 0.18%, respectively. Therefore, the experimental results have a good agreement with the theoretical analytical results.
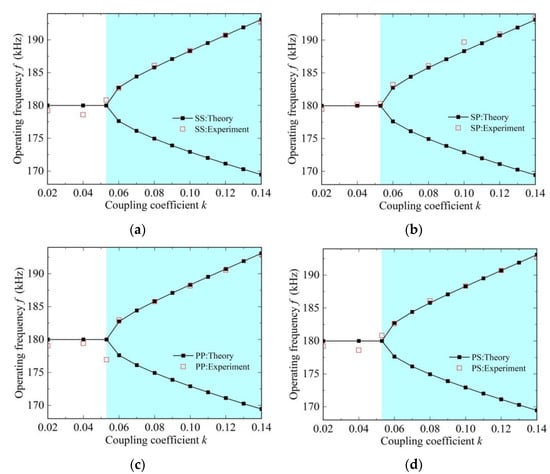
Figure 6.
Operating frequency of the NR-based MC-WPT systems with SS, SP, PP and PS topologies. (a) SS topology. (b) SP topology. (c) PP topology. (d) PS topology.
By changing the distance between the transmitting and receiving coils, the voltage ratio under different coupling coefficients can be obtained. Figure 7 depicts the output-input voltage ratio Vo/Vin of the NR-based MC-WPT system with the SS, SP, PP and PS topologies. It can be seen that the change trend in the voltage ratio Vo/Vin is related to the compensation topology of the transmitter. When the transmitter adopts the S topology, in the weakly coupled region (k < kC), the voltage ratio Vo/Vin decreases rapidly with the increase in the coupling coefficient k, while in the strongly coupled region (k ≥ kC), the voltage ratio Vo/Vin of the SS topology is constant equal to 1, and the voltage ratio Vo/Vin of the SP topology increases slowly with the coupling coefficient k, close to 20. Similarly, when the transmitter adopts the P topology, the voltage ratio Vo/Vin increases rapidly with the increase in the coupling coefficient k in the weakly coupled region (k < kC), but in the strongly coupled region (k ≥ kC), the voltage ratio Vo/Vin of the PP topology remains constant equal to 1, and the voltage ratio Vo/Vin of the PS topology increases slowly with the coupling coefficient k, close to 0.06. Moreover, the maximum and average errors between the experimental and theoretical values of the four topologies are calculated. The maximum errors of the SS, SP, PP and PS topologies are 1.90%, 23.08%, −3.00% and 3.55%, and the average errors are 0.66%, 3.24%, −1.57% and −0.13%, respectively. It can be noted that the 23.08% of the maximum error in the SP topology is due to the larger slope of the voltage ratio of the SP topology in the weakly coupled region. Therefore, the experimental results agree well with the theoretical analysis results.
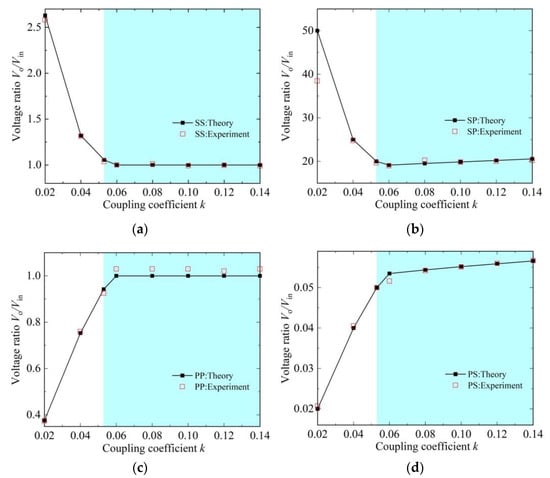
Figure 7.
Voltage ratio as a function of the coupling strength k for the NR-based MC-WPT systems with SS, SP, PP and PS topologies. (a) SS topology. (b) SP topology. (c) PP topology. (d) PS topology.
When the coupling coefficient k is determined to be 0.1, by adjusting the load, the voltage ratio Vo/Vin of the SS, SP, PP and PS topologies as load resistance RL varies is presented in Figure 8, it can be seen that the load changes of the four topologies have different effects on their output characteristics. First, the voltage ratio Vo/Vin of the SS topology remains constant equal to 1 in the range of RL ≤ RLC ≈ 7.58 Ω, but is affected by the load resistance RL in the range of RL > RLC ≈ 7.58 Ω. For the PP topology, the voltage ratio Vo/Vin remains constant equal to 1 in the range of RL ≥ RLC ≈ 753 Ω, but changes with the load resistance RL in the range of RL < RLC ≈ 753 Ω. Furthermore, the voltage ratio Vo/Vin of the PP topology changes in the opposite trend to the SS topology. Second, the SP topology works at ω = ω0 and its voltage ratio Vo/Vin is independent of the load resistance RL in the range of RL < RLC ≈ 753 Ω, but in the range of RL ≥ RLC ≈ 753 Ω, the system’s voltage ratio Vo/Vin is affected by the load resistance RL. Meanwhile, the PS topology with a critical resistance RLC = 14.3 Ω works at , and its voltage ratio Vo/Vin changes in the opposite trend to the SP topology. Third, the critical load resistance RLC is related to the compensation topology of the receiver, where the receiver has the same topology and its critical load resistance is the same. Furthermore, under the same coupling coefficient and circuit parameters, the voltage ratio Vo/Vin of the SP topology is relatively large, but the voltage ratio Vo/Vin of the PS topology is very small. Furthermore, the maximum and average errors between the experimental and theoretical values of the four topologies are calculated. The maximum errors of the SS, SP, PP, and PS topologies are −1.99%, −4.94%, 4.28% and 1.00%, and the mean errors are −0.24%, 0.58%, 1.57% and 0.44%, respectively. Therefore, the experimental results agree well with the theoretical analysis results. As can be seen from the above analysis, in the practical application where the transfer distance is determined, the corresponding compensation topology can be selected according to the working range of the load resistance to obtain stable output characteristics.
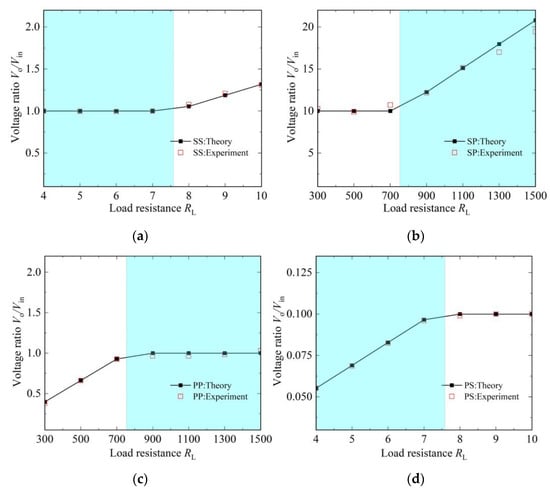
Figure 8.
Voltage ratio as a function of the load resistance RL under k = 0.1 for the NR-based MC-WPT systems with SS, SP, PP and PS topologies. (a) SS topology. (b) SP topology. (c) PP topology. (d) PS topology.
6. Conclusions
This paper systematically compares the transfer characteristics of the four basic NR-based MC-WPT topologies and analyzes the operating principles and applicability of two different NRs. By theoretical analysis and experimental verification, the following conclusions can be obtained.
Firstly, for the NR-based SS or PP topology, as long as the topologies operate in the strongly coupled region, the output-input voltage ratio remains constant (equal to 1 in this paper) even when the coupling coefficient or load changes. Moreover, in the strong coupling region, the load resistance of the PP topology is much greater than (approximately equal to 356.75 times in this paper) that of the SS topology, so the output power of PP topology is much smaller than (approximately equal to 0.0028 times in this paper) that of the SS topology in the strong coupling region.
Secondly, for the NR-based SP or PS topology, as long as the topologies operate in the strongly coupled region, the output-input voltage ratio is robust against the variation in the coupling coefficient, but would vary significantly with changes in the load resistance.
Thirdly, the voltage ratio of the SP topology is much greater than (approximately equal to 333.33 times in this paper) that of the PS topology, making it easier for the SP topology to transmit greater power than the PS topology.
Fourthly, since the NR based on the power converter can output greater power than (approximately equal to 356.75 times in this paper) NR based on operational amplifiers with more efficiency, the the NR based on power converter is suitable for SS and SP topologies, and the NR based on the operational amplifier is suitable for PP and PS topologies.
Finally, based on these four NR-based MC-WPT topologies, more NR-based topologies can be developed, such as domino NR-based topologies or crossed-couple NR-based topologies. Therefore, the above conclusion can also provide a reference for further research into other NR topologies.
Author Contributions
Conceptualization, X.S. and Y.J.; methodology, X.S. and Y.J.; software, G.W. and Y.J.; validation, X.S., Y.J. and G.W.; formal analysis, X.S.; data curation, X.S. and G.W.; writing original draft preparation, X.S. and G.W.; writing review and editing, X.S., Y.J. and G.W.; visualization, X.S. and Y.J.; supervision, X.S. and Y.J.; project administration, Y.J.; funding acquisition, X.S and Y.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by National Natural Science Foundation of China under Grant 62201153, National Natural Science Foundation of China under Grant 52207193 and the Natural Science Foundation of Fujian Province of China under Grant 2021J05136.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Y.; Chen, S.; Li, X.; Tang, Y. Design Methodology of Free-Positioning Nonoverlapping Wireless Charging for Consumer Electronics Based on Antiparallel Windings. IEEE Trans. Ind. Electron. 2022, 69, 825–834. [Google Scholar] [CrossRef]
- Tang, W.; Cheng, Z. A Real-Time Tracking Algorithm for 3D Wireless Maximum Power Transfer to a Moving Device. In Proceedings of the 2020 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Seoul, Republic of Korea, 15–19 November 2020. [Google Scholar]
- Kim, J.; Son, H.C.; Kim, D.H.; Park, Y.J. Optimal design of a wireless power transfer system with multiple self-resonators for an LED TV. IEEE Trans. Consum. Electron. 2012, 58, 775–780. [Google Scholar] [CrossRef]
- Shu, X.; Xiao, W.; Zhang, B. Wireless Power Supply for Small Household Appliances Using Energy Model. IEEE Access 2018, 6, 69592–69602. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, W.; Wang, H.; Shen, Z.; Wu, Y.; Dong, J.; Mao, X. Misalignment-Tolerant Dual-Transmitter Electric Vehicle Wireless Charging System with Reconfigurable Topologies. IEEE Trans. Ind. Electron. 2022, 37, 8816–8819. [Google Scholar] [CrossRef]
- Yan, Z.; Song, B.; Zhang, Y.; Zhang, K.; Mao, Z.; Hu, Y. A Rotation-Free Wireless Power Transfer System with Stable Output Power and Efficiency for Autonomous Underwater Vehicles. IEEE Trans. Power Electron. 2019, 34, 4005–4008. [Google Scholar] [CrossRef]
- Liu, H.; Shao, Q.; Fang, X. Modeling and Optimization of Class-E Amplifier at Sub nominal Condition in a Wireless Power Transfer System for Biomedical Implants. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Qiu, D.; Meng, X.; Zhang, B.; Tang, S.C. Optimized Design of Coils for Wireless Power Transfer in Implanted Medical Devices. IEEE Trans. Ind. Electron. 2018, 2, 277–285. [Google Scholar] [CrossRef]
- Chen, Y.; He, S.; Yang, B.; Chen, S.; He, Z.; Mai, R. Reconfigurable Rectifier-Based Detuned Series-Series Compensated IPT System for Anti-Misalignment and Efficiency Improvement. IEEE Trans. Power Electron. 2023, 38, 2720–2729. [Google Scholar] [CrossRef]
- Fujita, T.; Wada, K. Simultaneous Wireless Data and Power Transfer System Utilizing Frequency Characteristics of Magnetic Resonance with Output Power Fluctuation Suppressed. IEEJ Trans. Electron. Inf. Syst. 2022, 142, 6–14. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M.J.S. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef]
- Sample, A.P.; Meyer, D.T.; Smith, J.R. Analysis, Experimental Results, and Range Adaptation of Magnetically Coupled Resonators for Wireless Power Transfer. IEEE Trans. Ind. Electron. 2011, 58, 544–554. [Google Scholar] [CrossRef]
- Jia, J.; Yan, X. Research on Characteristics of Wireless Power Transfer System Based on U-Type Coupling Mechanism. J. Electr. Comput. Eng. 2021, 2021, 6683800. [Google Scholar]
- Zhu, H.; Zhang, B.; Wu, L. Output Power Stabilization for Wireless Power Transfer System Employing Primary-Side-Only Control. IEEE Access 2020, 8, 63735–63747. [Google Scholar] [CrossRef]
- Kobayashi, D.; Imura, T.; Hori, Y. Real-time coupling coefficient estimation and maximum efficiency control on dynamic wireless power transfer for electric vehicles. In Proceedings of the 2015 IEEE PELS Workshop on Emerging Technologies: Wireless Power (2015 WoW), Daejeon, Republic of Korea, 5–6 June 2015. [Google Scholar]
- Liu, Y.; Feng, H. Maximum Efficiency Tracking Control Method for WPT System Based on Dynamic Coupling Coefficient Identification and Impedance Matching Network. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3633–3643. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.; Hu, Z.; Rong, C.C.; Liu, M.J.I.P.E. Optimization Design for Series-Series Dynamic WPT System Maintaining Stable Transfer Power. IET Power Electron. 2017, 10, 987–995. [Google Scholar] [CrossRef]
- Basar, M.R.; Ahmad, M.Y.; Cho, J.; Ibrahim, F. Stable and High-Efficiency Wireless Power Transfer System for Robotic Capsule Using a Modified Helmholtz Coil. IEEE Trans. Ind. Electron. 2017, 64, 1113–1122. [Google Scholar] [CrossRef]
- Wen-xian, C.; Zhu-ping, C. Optimization on the transmission distance and efficiency of magnetic resonant WPT system. In Proceedings of the CSAA/IET International Conference on Aircraft Utility Systems (AUS 2018), Guiyang, China, 19–22 June 2018. [Google Scholar]
- Kavitha, M.; Bobba, P.B.; Prasad, D. Effect of coil geometry and shielding on wireless power transfer system. In Proceedings of the 2016 IEEE 7th Power India International Conference (PIICON), Bikaner, India, 25–27 November 2016. [Google Scholar]
- Pacini, A.; Costanzo, A.; Aldhaher, S.; Mitcheson, P.D. Load- and Position-Independent Moving MHz WPT System Based on GaN-Distributed Current Sources. IEEE Trans. Microw. Theory Tech. 2017, 65, 5367–5376. [Google Scholar] [CrossRef]
- Liu, D.; Hu, H.; Georgakopoulos, S.V. Misalignment Sensitivity of Strongly Coupled Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2017, 32, 5509–5519. [Google Scholar] [CrossRef]
- Feng, H.; Cai, T.; Duan, S.; Zhao, J.; Zhang, X.; Chen, C. An LCC-Compensated Resonant Converter Optimized for Robust Reaction to Large Coupling Variation in Dynamic Wireless Power Transfer. IEEE Trans. Ind. Electron. 2016, 63, 6591–6601. [Google Scholar] [CrossRef]
- Zhang, P.; Saeedifard, M.; Onar, O.C.; Yang, Q.; Cai, C. A Field Enhancement Integration Design Featuring Misalignment Tolerance for Wireless EV Charging Using LCL Topology. IEEE Trans. Power Electron. 2021, 36, 3852–3867. [Google Scholar] [CrossRef]
- Keeling, N.A.; Covic, G.A.; Boys, J.T. A Unity-Power-Factor IPT Pickup for High-Power Applications. IEEE Trans. Ind. Electron. 2010, 57, 744–751. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Deng, J.; Nguyen, T.D.; Mi, C.C. A Double-Sided LCC Compensation Network and Its Tuning Method for Wireless Power Transfer. IEEE Trans. Veh. Technol. 2015, 64, 2261–2273. [Google Scholar] [CrossRef]
- Gao, W.; Chen, Q.; Geng, Y.; Ren, X.; Wong, S.C. Equivalency analysis of primary series- and series-parallel-compensated contactless resonant converter. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017. [Google Scholar]
- Hou, J.; Chen, Q.; Wong, S.C.; Tse, C.K.; Ruan, X. Analysis and Control of Series/Series-Parallel Compensated Resonant Converter for Contactless Power Transfer. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 124–136. [Google Scholar]
- Hou, J.; Chen, Q.; Wong, S.C.; Ren, X.; Ruan, X. Output current characterization of parallel-series/series compensated resonant converter for contactless power transfer. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015. [Google Scholar]
- Mai, J.; Wang, Y.; Yao, Y.; Xu, D. Analysis and Design of High-Misalignment-Tolerant Compensation Topologies with Constant-Current or Constant-Voltage Output for IPT Systems. IEEE Trans. Power Electron. 2021, 36, 2685–2695. [Google Scholar] [CrossRef]
- Lim, Y.; Tang, H.; Lim, S.; Park, J. An Adaptive Impedance-Matching Network Based on a Novel Capacitor Matrix for Wireless Power Transfer. IEEE Trans. Power Electron. 2014, 29, 4403–4413. [Google Scholar] [CrossRef]
- Seo, D.W.; Lee, J.H. Frequency-Tuning Method Using the Reflection Coefficient in a Wireless Power Transfer System. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 959–961. [Google Scholar] [CrossRef]
- Gati, E.; Kampitsis, G.; Manias, S. Variable Frequency Controller for Inductive Power Transfer in Dynamic Conditions. IEEE Trans. Power Electron. 2017, 32, 1684–1696. [Google Scholar] [CrossRef]
- Assawaworrarit, S.; Yu, X.; Fan, S. Robust wireless power transfer using a nonlinear parity-time-symmetric circuit. Nature 2017, 546, 387–390. [Google Scholar] [CrossRef]
- Buscarino, A.; Fortuna, L.; Frasca, M.; Gambuzza, L.V.; Sciuto, G. Memristive chaotic circuits based on cellular nonlinear networks. Int. J. Bifurc. Chaos 2012, 22, 1250070. [Google Scholar] [CrossRef]
- Schindler, J.; Li, A.; Zheng, M.C.; Ellis, F.M.; Kottos, T.J.P.R.A. Experimental Study of Active LRC Circuits with PT-Symmetries. Phys. Rev. A 2011, 84, 040101. [Google Scholar] [CrossRef]
- Assawaworrarit, S.; Fan, S. Robust and efficient wireless power transfer using a switch-mode implementation of a nonlinear parity–time symmetric circuit. Nat. Electron. 2020, 3, 273–279. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, B.; Xiao, W.; Qiu, D.; Chen, Y. Nonlinear Parity-Time-Symmetric Model for Constant Efficiency Wireless Power Transfer: Application to a Drone-in-Flight Wireless Charging Platform. IEEE Trans. Ind. Electron. 2019, 66, 4097–4107. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, B. Omnidirectional and Efficient Wireless Power Transfer System for Logistic Robots. IEEE Access 2020, 8, 13683–13693. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, B.; Zhou, J. Efficiency Improvement of the Parity-Time-Symmetric Wireless Power Transfer System for Electric Vehicle Charging. IEEE Trans. Power Electron. 2020, 35, 12497–12508. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, B.; Jiang, Y.; Zhou, J. A Robust Parity-Time-Symmetric WPT System with Extended Constant-Power Range for Cordless Kitchen Appliances. IEEE Trans. Ind. Appl. 2022, 58, 1179–1189. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, B.; Jiang, Y. Position-Independent Constant Current or Constant Voltage Wireless Electric Vehicles Charging System Without Dual-Side Communication and DC-DC Converter. IEEE Trans. Ind. Electron. 2022, 69, 7930–7939. [Google Scholar] [CrossRef]
- Qu, Y.; Zhang, B.; Gu, W.; Li, J.; Shu, X. Distance Extension of S-PS Wireless Power Transfer System Based on Parity-Time Symmetry. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2954–2958. [Google Scholar] [CrossRef]
- Luo, C.; Qiu, D.; Gu, W.; Zhang, B.; Chen, Y.; Xiao, W. Multiload Wireless Power Transfer System with Constant Output Power and Efficiency. IEEE Trans. Ind. Appl. 2022, 58, 1101–1114. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, B.; Wei, Z.; Rong, C.; Sun, S. Extended-Distance Wireless Power Transfer System with Constant Output Power and Transfer Efficiency Based on Parity-Time-Symmetric Principle. IEEE Trans. Power Electron. 2021, 36, 8861–8871. [Google Scholar] [CrossRef]
- Sakhdari, M.; Hajizadegan, M.; Chen, P.Y. Robust extended-range wireless power transfer using a higher-order PT-symmetric platform. Phys. Rev. Res. 2020, 2, 013152. [Google Scholar] [CrossRef]
- Kiani, M.; Ghovanloo, M. The Circuit Theory Behind Coupled-Mode Magnetic Resonance-Based Wireless Power Transmission. IEEE Trans. Circuits Syst. I: Regul. Pap. 2012, 59, 2065–2074. [Google Scholar] [CrossRef] [PubMed]
- Haus, H.A.J.P.H. Waves and Fields in Optoelectronics: Prentice-Hall Series in Solid State Physical Electronics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984; pp. 198–234. [Google Scholar]
- Louisell, W.H. Coupled Mode and Parametric Electronics; John Wiley and Sons: Hoboken, NJ, USA, 1961; pp. 1–18. [Google Scholar]
- Su, Y.P.; Liu, X.; Hui, S.Y.R. Mutual Inductance Calculation of Movable Planar Coils on Parallel Surfaces. IEEE Trans. Power Electron. 2009, 24, 1115–1123. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, B.; Liu, G.; Qiu, D. Resonance and Distance Insensitive Wireless Power. Transfer with Parity-Time Symmetric Duffing Resonators. In In Proceedings of the 2018 IEEE Wireless Power Transfer Conference (WPTC), Montreal, QC, Canada, 3–7 June 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).