A Wellbore Pressure Control Method for Two-Layer Coal Seam Gas Coproduction Wells

Abstract

In coal seam gas (CSG) coproduction wells, due to the different production pressures of CSG production layer at different depths, the interlayer interference in wellbore seriously affects the gas production of a coproduction well. To effectively suppress the interlayer interference of the wellbore, a wellbore pressure distribution method for a two-layer coproduction well is proposed. Based on the analysis of the factors influencing the flow pressure distribution in the wellbore of two-layer coproduction wells, a method of coproduction flow pressure adjustment by regulating the wellhead pressure and the depth of the dynamic fluid level was established in this paper. The results show that wellhead pressure can directly affect the production pressure of two layers. The variation in layer 1 output mainly affects the pressure difference between the wellhead pressure and the pressure at the depth of layer 1, which has little effect on the pressure difference between layer 1 and 2. An increase in gas production from layer 2 would not only cause a pressure increase in layer 1, but also result in a reduction of the production pressure at layer 2. The maximum pressure gradient of the gas section is 0.14 MPa/100 m, and the pressure gradient of the gas–liquid section is 0.53–1.0 MPa/100 m.

1. Introduction

As unconventional natural gas, CSG has gradually become a trending topic in gas resource development. As the development of CSG resources has globally accelerated in recent years [1,2], the countries that are making great efforts to develop CSG exploitation include the United States, Australia, Canada, and China, with some fields already in commercial production [3]. Areas of vertical distribution with multiple potential production layers are currently discovered in the Ordos Basin, Qinshui Basin, Eastern Yunnan and western Guizhou in China [4,5,6,7,8]. Similar areas are also found in the United States, Australia and Canada, such as the San Juan Basin [9,10], Black Warrior Basin [11,12], Powder River Basin [13,14], Horseshoe Canyon Basin [15,16], and Bowen-Surat Basin [17,18].

Much attention has been focused on the multilayer coproduction of CSG wells. A multibranch U-shaped well was proposed for two coal seams in one well, which can provide single-layer or two-layer coproduction [19]. Notable progress has been made in physical experiments for multilayer CSG coproduction. The effects of reservoir permeability [1,20], bottom hole pressure [21,22], and coal seam depth [23] on the coproduction have been studied. The difference in reservoir geological properties is a fundamental factor affecting coproduction. While the pressure and fluid flow in the wellbore also affect coproduction, and the interlayer interference coefficient has been proposed to avoid interlayer interference [24,25,26,27,28,29,30]. These results have been verified in field CSG coproduction. However, the current multilayer coproduction efforts have not achieved the ideal result (both layers can produce, and the coproduction is greater than that of a single layer) due to the strong interlayer interference in the wellbore. The effective suppression of interlayer interference in a wellbore remains a challenge for the further development of CSG coproduction.

Due to water production from the CSG layer, the annular space between the tubing and casing is in a gas-liquid two-phase flow state during the coproduction, and there is a dynamic liquid surface [21,31]. The pressure distribution influences the pressure at the depth of different production layers in the wellbore. To solve the calculation of pressure distribution in the annular space, many experimental and theoretical studies have been conducted in recent decades. Sadatomi et al. established a calculation method for the frictional pressure difference of air-water two-phase flow by studying the two phases in the vertical annular space [32]. Hasan and Kabir established a calculation model of the void ratio when the annulus is in bubble flow and slug flow by theoretical and experimental analysis, which can facilitate the calculation of bottom hole pressure (BHP) in pumping wells and the calculation of wellbore pressure for pumping unit well [33]. Kelessidis and Dukler studied the gas-liquid two-phase flow in concentric and eccentric annular spaces and established a basis for determining the flow patterns in concentric and eccentric annuli [34]. Papadimitriou and Shoham studied the case of net-zero liquid flow in the annulus and established a model based on experiments for the bottom pressure in the annulus of a pumping well with net-zero liquid flow [35]. Antonio and Time developed a steady-state model for the pressure drop in concentric annular air–liquid two-phase flow [36]. An, H.-J., et al. studied the effect of liquid viscosity on the pressure drop of gas–liquid two-phase flow at a net-zero liquid flow rate [37].

Compared to single-layer production wells, multilayer coproduction wells have more significant development advantages, which can effectively reduce production costs and increase total gas production from a single well [38,39,40]. The long-term and stable gas production from multilayer CSG coproduction wells has become a technical challenge for coproduction wells. Compared to single-layer production, two production layers at different depths in coproduction wells have different pressures [24]. The fluids from the two layers entering the wellbore cause interlayer interference in the wellbore, which simultaneously affects the gas production capacity of the two production layers during coproduction [41]. Due to interlayer interference, the production capacity of some coproducing gas wells is even lower than that of single-layer production gas wells.

In the case of multilayer coproduction, the wellbore pressure varies at different depths (output pressure for each layer increases with depth). The production status of a single layer is influenced by the pressure at the depth of that layer in the wellbore [41]. Unlike the dry coal seams in the Alberta Basin and Surat-Bowen Basin, the CSG wells in the Ordos Basin and Eastern Yunnan and Western Guizhou Blocks in China have the problem of water production. Reasonable multilayer combination schemes for different block characteristics can effectively reduce interlayer interference in coproduction [31,39,42]. Moreover, due to the presence of multilayer gas systems, there is strong interlayer interference in existing multilayer coproduction wellbores. Effective regulation of the wellbore pressure distribution becomes the key to reasonably controlling the production pressure for both layers. A method to suppress interlayer interference in the wellbore is urgently needed for water-producing coproduction wells. To solve this problem, the key factors influencing the interlayer production pressure difference in the coproduction wellbore were investigated by analyzing the flow pattern of drainage in coproduction wells. A method was proposed to reasonably regulate the production pressure of the two combined production layers by controlling the wellhead pressure and the depth of the dynamic fluid surface. Furthermore, this method can effectively suppress interlayer interference between two layers.

The rest of the paper is organized as follows: in Section 2, the output model of two layers of CSG coproduction and the basic requirements of coproduction pressure distribution are investigated. In Section 3, the method of the coproduction well pressure distribution calculation is presented. Fifteen sets of physical experiments for CSG coproduction were designed and conducted in Section 4. Finally, The results of theoretical analysis and experiments and discussions are in Section 5.

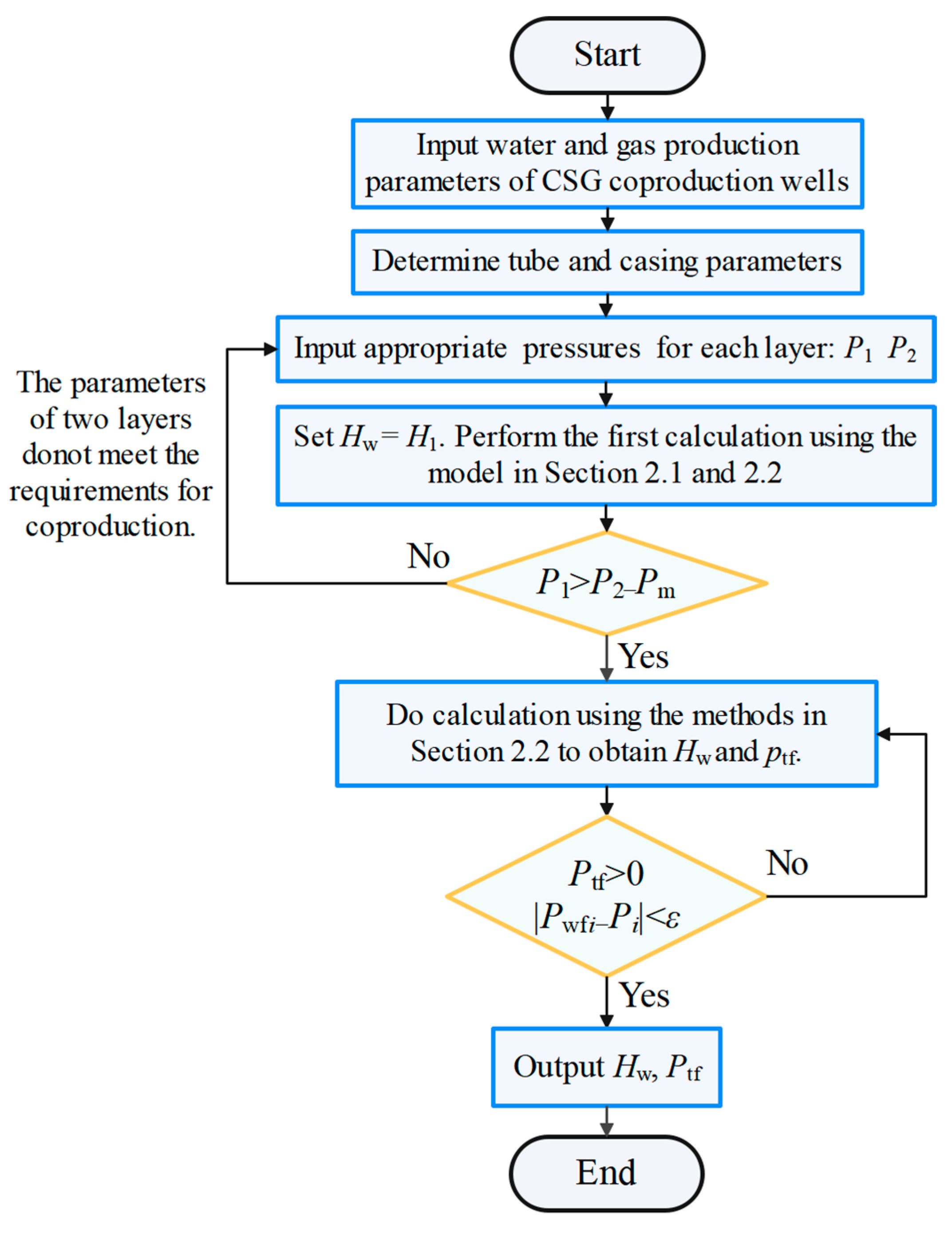
2. Methods

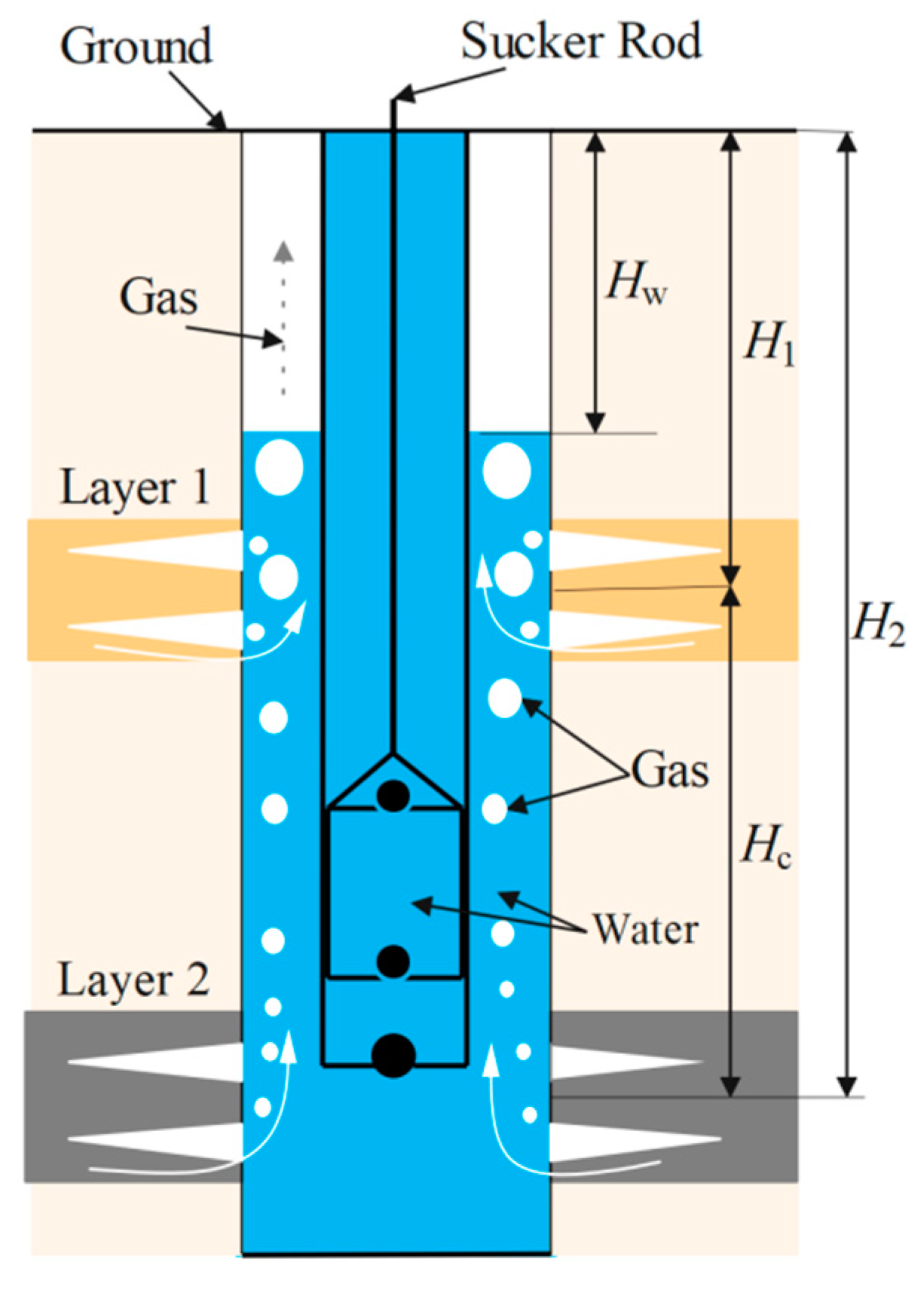
2.1. Production Output and Wellbore Pressure Distribution

According to CSG and conventional natural gas production capacity research [43,44], the capacity equation of the production layer has the following form:

$$q_{\mathrm{g}}=\frac{kHN\left(p_{\mathrm{r}}-p_i\right)}{{141}^2\mu \beta \left(p_{\mathrm{j}i}+S\right)}$$

(1)

$$p_{\mathrm{r}}^2-p_i^2=A{q}_{\mathrm{g}}+B{q}_{\mathrm{g}}^2$$

(2)

$$q_{\mathrm{g}}=C{\left(p_{\mathrm{r}}^2-p_i^2\right)}^n$$

(3)

where: q_g is the daily gas production of a gas well, m³/d; k is the permeability of the CSG reservoir, m²; H is the thickness of the coal seam, m; N is the gas content of the coal seam, m³/t; p_r is the original layer pressure, MPa; p_i is the wellbore pressure at the depth of production layer i, where i = 1, 2, MPa; μ is the viscosity of the fluids, mPa·s; P_ji is the pressure at the beginning of desorption of coalbed methane for layer i, MPa; S is the surface skin of the wellbore; A and B are the laminar flow coefficients and turbulence coefficients, which can be solved based on well test data; C is the gas production index, which is related to the permeability thickness of the production layer, the viscosity of the produced gas and the bottom of the well’s conditions, 10⁴ m³/d(MPa)⁻²ⁿ; n is the gas percolation index and n = 1 for linear percolation; When the fluid percolation rate is large or multiphase percolation occurs, n < 1.

To ensure that both layers can produce normally, the pressure distribution in the wellbore should be:

$$\left\{\begin{array}{l}0<P_{\mathrm{tf}}<P_{\mathrm{wf}}{}_i<P_{ri}i=1, 2\\ P_{\mathrm{wf}1}<P_{\mathrm{wf}2}\end{array}\right.$$

(4)

where P_ri is the original stratigraphic pressure of gas production layer i, MPa; P_tf is the pressure in the annulus at the wellhead, MPa; P_wf1 is the pressure in the annulus at the depth of the layer 1, MPa; P_wf2 is the pressure in the annulus at the depth of layer 2, MPa.

Especially for the desorption production of coalbed methane (CBM):

$$P_{\mathrm{wf}}{}_i<P_{\mathrm{j}i}i=1, 2$$

(5)

To coordinate the production of each layer in multilayer coproduction wells, a detailed study of the pressure distribution in the coproduction wellbore is needed. In this paper, as gas and water flow out from the two layers, an artificial lift device is used for drainage. Water from the layer accumulates in the annulus, which is lifted upward by an artificial lift pump, and then passes through the tubing to the ground. The gas produced from the producing layers enters the wellbore and flows through the annulus of the tubing and casing to the wellhead for output. A two-layer model with distance H_c is supposed to simplify the pressure distribution in the CSG wellbore instead of a multilayer model. The wellbore annulus of the CSG gas well is the three-dimensional annular space, and the wellbore is illustrated in the form of a cross-section in order to clearly express the distribution of fluids in the wellbore. Furthermore, the upper CSG layer is named layer 1, and the lower layer is layer 2, as shown in Figure 1.

The gas in the wellbore below the dynamic liquid level flows up in the water as a bubble or slug flow. The gas above the dynamic liquid level in the wellbore annulus is a single-phase flow. The dynamic fluid level position in the wellbore varies. As shown in Figure 2a–c, influenced by dynamic fluid level depth in the wellbore the pressure relationship for each layer is as follows:

$$\begin{array}{c}\left(\mathrm{a}\right) H_{\mathrm{w}}\le H_1\left\{\begin{array}{l}{P}_{\mathrm{wf}1}=P_{\mathrm{tf}}+\Delta P_{\mathrm{g}}+P_{\mathrm{m}1}\\ P_{\mathrm{wf}2}=P_{\mathrm{tf}}+\Delta P_{\mathrm{g}}+P_{\mathrm{m}1}+P_{\mathrm{m}2}\end{array}\right.\\ (\mathrm{b}) H_1<H_{\mathrm{w}}\le H_2\left\{\begin{array}{l}{P}_{\mathrm{wf}1}=P_{\mathrm{tf}}+\Delta P_{\mathrm{g}1}\\ P_{\mathrm{wf}2}=P_{\mathrm{tf}}+\Delta P_{\mathrm{g}1}+\Delta P_{\mathrm{g}2}+P_{\mathrm{m}2}\end{array}\right.\\ \left(\mathrm{c}\right) H_{\mathrm{w}}>H_2\left\{\begin{array}{l}{P}_{\mathrm{wf}1}=P_{\mathrm{tf}}+\Delta P_{\mathrm{g}1}\\ P_{\mathrm{wf}2}=P_{\mathrm{tf}}+\Delta P_{\mathrm{g}1}+\Delta P_{\mathrm{g}2}\end{array}\right.\end{array}$$

(6)

where: H_w is the distance from the dynamic fluid level in the wellbore to the ground, m; H₁ is the distance from layer 1 to the ground, m; H₂ is the distance from layer 2 to the ground, m; $\Delta P_{\mathrm{g}}$ is the total pressure difference of the gas flow in the annulus, as shown in Figure 2a, MPa; $\Delta P_{\mathrm{g}1}$ is the pressure difference of the gas flow in the annulus at a depth of H₁ to the ground, as shown in Figure 2b,c, MPa; $\Delta P_{\mathrm{g}2}$ is the pressure drop of the gas flow in the annulus at a depth of H_w to H₁, as shown in Figure 2b,c, MPa; $P_{\mathrm{m}1}$ is the pressure drop in gas-liquid mixing zone between the dynamic fluid level and layer 1, as shown in Figure 2a, MPa; and $P_{\mathrm{m}2}$ is the pressure drop in gas-liquid mixing zone between layer 1 and layer 2 as shown in Figure 2a,b, MPa.

From Equation (6), the depth change of the dynamic fluid surface can change the pressure difference between the two layers, while the change in the wellhead pressure could result in the pressure change of layer 1, which could affect the pressure of layer 2. Therefore, a proper wellhead pressure and dynamic fluid surface position can effectively coordinate the production pressure of both layers and suppress interlayer interference.

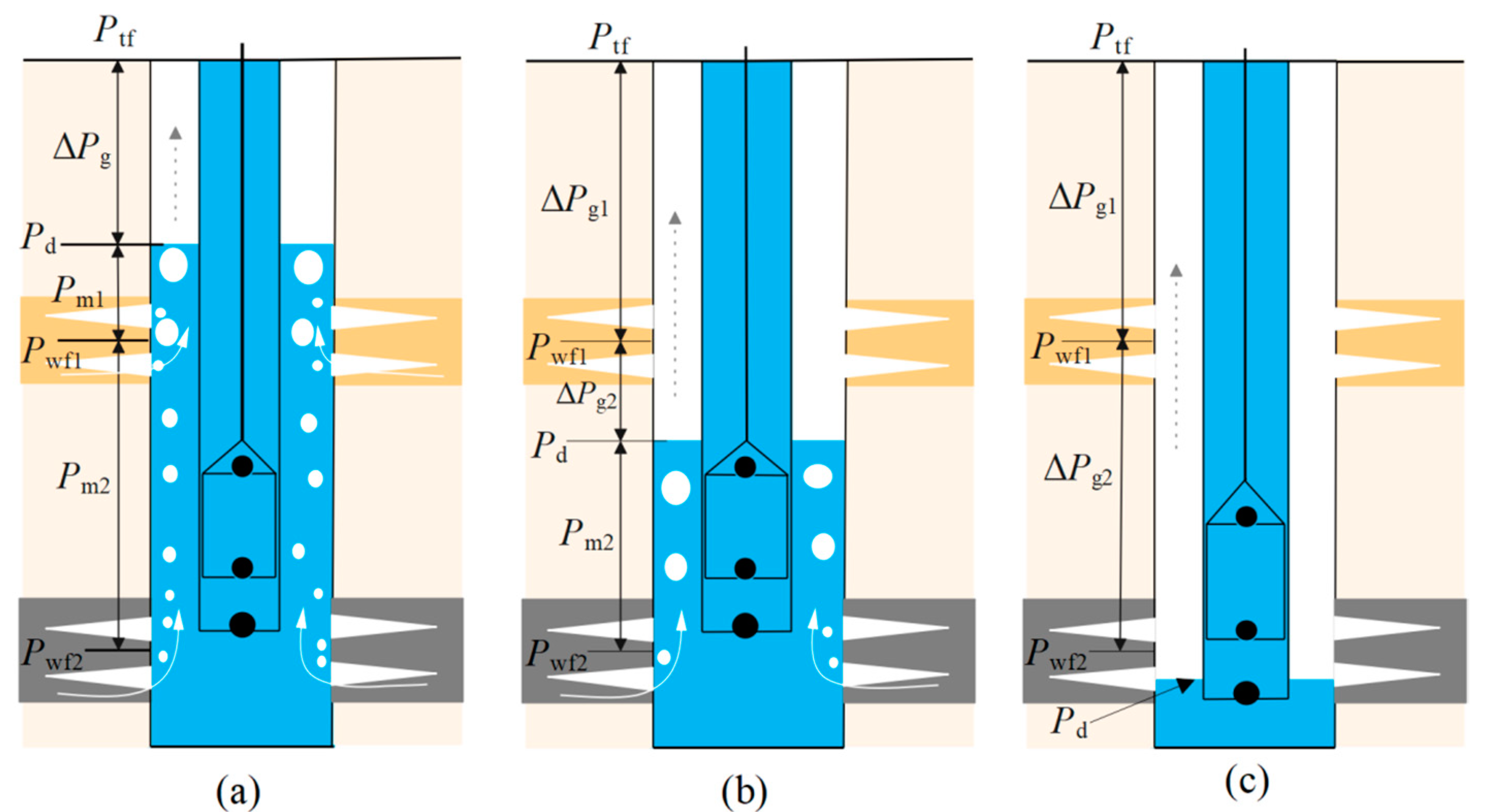
2.2. Calculation for Pressure Distribution in the Wellbore

Detailed calculations of the wellbore pressure distribution are required to obtain the appropriate wellhead pressure and dynamic fluid surface depth. Based on the fluid flow in the two-layer coproduction well, as shown in Figure 1, the following assumptions are made: the wellbore is perpendicular to the surface; the gas in the oil jacket annulus flows steadily; the mass of the fluid at any annulus section is conserved; and the work and heat exchange is constant [44]. The energy equation for fluid flow in the annulus is

$$-\frac{dp}{dh}=\rho v+\frac{dv}{dh}+g\rho +\frac{f\rho v^2}{2d}+dW$$

(7)

where: p is the pressure, Pa; ρ is the fluid density, kg/m³; h is the wellbore length, m; v is the fluid flow velocity, m/s; f is the friction coefficient; and d is the pipe diameter, m.

Taking the dynamic liquid surface as the boundary, the calculation of wellbore pressure distribution was divided into single-phase gas flow and gas-liquid two-phase flow.

2.2.1. Single-Phase Gas Flow

The following assumptions are made in calculating the differential pressure in the flowing gas section: there is no input and output of work in this process (dW = 0) [44]; the kinetic energy loss in the gas flow is neglected (vdv = 0) [45]. Based on these assumptions, Equation (7) can be simplified as

$$\frac{dp}{\rho }+gdh+\frac{f{v}^{2}dh}{2d}=0$$

(8)

The equation of the state of the gas is associated with Equation (8), and the following equation is derived after integrating the separated variables.

$${\displaystyle {\int }_{p_{\mathrm{tf}}}^{p_d}\frac{\frac{p}{ZT}}{{\left(\frac{p}{ZT}\right)}^2+\frac{1.324\times {10}^{-18}f{q}_{\mathrm{sc}}^2}{\left(d_{\mathrm{i}}-d_{\mathrm{o}}\right){\left(d_{\mathrm{i}}^2-d_{\mathrm{o}}^2\right)}^2}}}dp={\displaystyle {\int }_0^{h}0.03415{\gamma }_{g}dh}$$

(9)

where: Z is the gas deviation factor, which can be calculated by the Standing-Katz [46] or Dranchuk-Abu-Kassem [47] model; d_i is the casing ID, mm; d_o is the tubing OD, mm; and q_sc is the daily gas production of the coproduction well, m³.

The wellbore length for which the differential pressure needs to be solved was divided into three sections. The Cullender–Smith method was used to solve Equation (9) [48].

$$F_1=\frac{p}{TZ}, F_2^2=\frac{1.324\times {10}^{-18}f{q}_{\mathrm{sc}}^2}{\left(d_{\mathrm{i}}-d_{\mathrm{o}}\right){\left(d_{\mathrm{i}}^2-d_{\mathrm{o}}^2\right)}^2}, I=\frac{F_1}{F_1^2+F_2^2}$$

(10)

By associating Equation (9) with Equation (10), Equation (11) can be derived.

$${\displaystyle {\int }_{p_{\mathrm{tf}}}^{p_{\mathrm{d}}}Idp}=0.03415{\gamma }_{\mathrm{g}}h$$

(11)

The pressure value at the specified depth can be calculated using the iterative method.

2.2.2. Gas–Liquid Two-Phase Flow

As shown in Figure 2b, there is a mixed gas-water flow below the dynamic liquid surface of the combined production wells. After the gas enters the wellbore, gas flows through a static liquid. Neglecting the kinetic energy loss of the gas and the frictional energy loss of the gas and the liquid and the pipe wall, the expression for the pressure drop in this section can be expressed as

$$\Delta p_{\mathrm{m}}={\displaystyle {\int }_{h_1}^{h_2}{\rho }_{\mathrm{m}}}gdh$$

(12)

where: ${\rho }_{\mathrm{m}}$ is the density of the gas–liquid (water) mixture kg/m³; $h_1$ and $h_2$ are the starting and ending calculated well depths, m, respectively.

Supposing $\varphi$ is the gas void fraction in the water, Equation (12) can be expressed as:

$$\Delta p_{\mathrm{m}}={\displaystyle {\int }_0^h\left[\left(1-\varphi \right){\rho }_{\mathrm{w}}+\varphi {\rho }_{\mathrm{g}}\right]}gdh$$

(13)

or

$$\Delta p_{\mathrm{m}}=g{\displaystyle \sum _1^{\mathrm{n}}\left[\left(1-\varphi \right){\rho }_{\mathrm{w}}+\varphi {\rho }_{\mathrm{g}}\right]}\Delta h_{\mathrm{i}}$$

(14)

where: ${\rho }_{\mathrm{w}}$ is the density of the output water, kg/m³; ${\rho }_{\mathrm{g}}$ is the density of the output gas, kg/m³; and $\Delta h_{\mathrm{i}}$ is the depth of the calculated section of the well, m.

The void fraction $\varphi$ can be calculated using the Hasan and Kabir model in two flow regimes: bubble flow and slug flow [33].

Bubble flow:

$$\varphi =u_{\mathrm{sg}}{\left[\left(1.97+0.371\frac{d_{\mathrm{o}}}{d_{\mathrm{i}}}\right)v_{\mathrm{sg}}+1.50{\left[\frac{g\sigma \left({\rho }_w-{\rho }_g\right)}{{\rho }_w^2}\right]}^{0.25}\right]}^{-1}$$

(15)

Slug flow:

$$\varphi =\frac{v_{\mathrm{sg}}}{\left(1.182+0.9\frac{d_{\mathrm{o}}}{d_{\mathrm{i}}}\right)v_{\mathrm{sg}}+\left(0.3+0.22\frac{d_{\mathrm{o}}}{d_{\mathrm{i}}}\right){\left[\frac{g\left(d_{\mathrm{i}}-d_{\mathrm{o}}\right)\left({\rho }_{\mathrm{w}}-{\rho }_{\mathrm{g}}\right)}{{\rho }_{\mathrm{w}}}\right]}^{0.5}}$$

(16)

The expression for $v_{\mathrm{zb}}$ of the transition from bubble to slug flow is

$$v_{\mathrm{zb}}=\frac{0.375{\left[\frac{g\sigma \left({\rho }_{\mathrm{w}}-{\rho }_{\mathrm{g}}\right)}{{\rho }_{\mathrm{w}}^2}\right]}^{0.25}}{0.5075-0.09275d_{\mathrm{o}}/d_{\mathrm{i}}}$$

(17)

The two-phase section is divided into several sections, and the pressure difference for each section can be calculated. The coefficients in Equations (15)–(17) were determined based on multiple sets of experiments [49,50].

The key parameters (P_tf, H_w) of the coproduction can be obtained by calculation, as shown in Figure 3.

3. Experiments

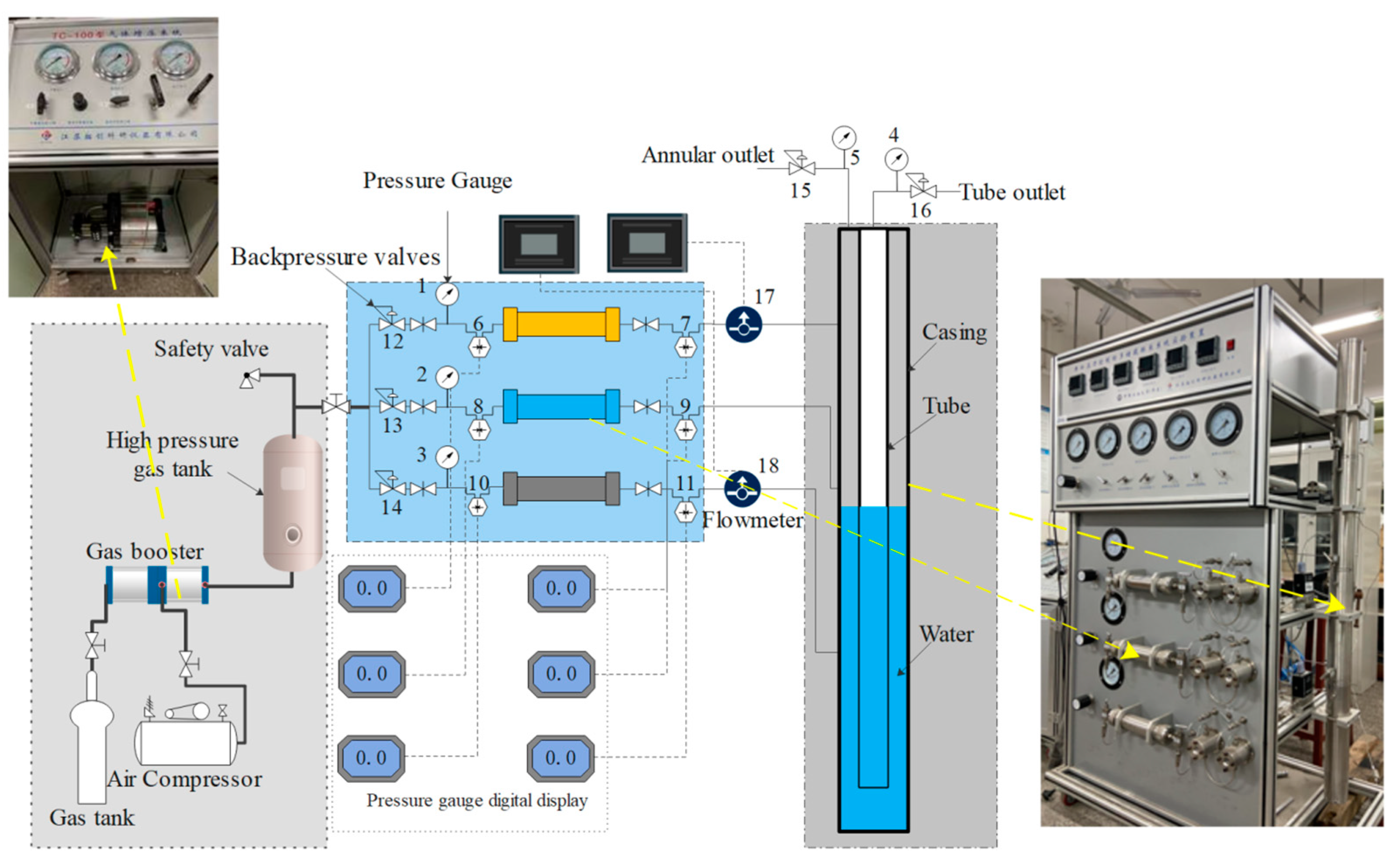
3.1. Device and Method of Experiment

The multilayer physical test device was designed independently and assembled by Jiangsu Tuochuang Scientific Instruments Co. This experimental device can conduct simulations for three layers of CSG coproduction.

The device includes six parts: a gas supply system, a gas flow monitoring system, a pressure monitoring and regulation system, a wellbore simulation unit, and a production layer simulation unit. The gas supply system includes a high-pressure storage tank, an air compressor, a booster system, and a nitrogen tank. The nitrogen tank is a gas resource with a maximum pressure of 12 MPa. The compressed gas is stored in a high-pressure tank with a maximum pressure of 30 MPa. The gas flow monitoring system includes flow meters 17–18. Flow meters 17–18 record the forward gas flow in the upper and lower layer. The pressure monitoring module includes pressure gauges 1–5, with pressure sensors 6–11. The pressure regulation module includes back pressure regulating valves 12–16. Back pressure regulating valves 12–14 are located at the inlet of each of the three core holders and are used to regulate the inlet pressure. The back pressure regulating valve is located at the outlet of the tube and the annulus to regulate the outlet pressure. Pressure sensors 6–11 are located at the front and back of the three core holders to monitor the pressure at the cores. The production layer simulation unit contains three core holders, which can hold φ38 × 200 mm cores. The wellbore simulation unit consists of tubing and casing. The three branches are connected to the casing at different heights, as shown in Figure 4.

As shown in Figure 4, 1–3 are gate valves; 4, 5 are pressure gauges 6–11 are pressure sensors 12–16 are adjustable backpressure valves. 17, 18 are flow sensors. In this device, the rock cores in the holders represent the production layers with different depths. The inlet pressure controlled by back pressure regulating valves 12–14 represents the reservoir pressure, and the pressure monitored by pressure sensors 7, 9 and 11 represents the bottom hole pressure for each layer. The forward gas flow in flowmeters 17–18 represents the flow from the upper and lower layers. The pressures monitored by pressure gauges 5 and 6 represent the casing and tubing pressure at the ground level, respectively. Different volumes of water were injected into the wellbore, which was used to simulate different heights of dynamic fluid levels.

The steps of the experiment were as follows. 1. Prepare the experimental materials and check the sealing performance of the device. 2. Select suitable cores and install the required cores. 3. Conduct the test according to the set parameters and check the sealing performance of the device again. 4. Open the inlet valve of the device and set the inlet pressure of each layer and the outlet pressure of the wellbore according to the set parameters. 5. After the airflow enters a stable state, record the flow data of each layer and the pressure data of each part of the device. 6. After completing all the experiments, analyze the data from different schemes.

3.2. Materials for Experiments and Processing

These experiments use nitrogen instead of methane for the following reasons. First, methane is flammable, explosive, and toxic. Second, methane is close to the molecular diameter of nitrogen. Moreover, the characteristics of nitrogen and methane gas are close in the CSG adsorption and desorption experiments. Since cores with the same properties are extremely difficult to obtain, pulverized coal (20–30 meshes) of different quality was used instead of cores in this experiment, which may make some characters different from the original layer. In addition, the tubing and casing length of the installation is 1.5 m, which is different from the gas well depth (usually more than 500 m). Due to the limitation of size and pressure sensor precision, the device cannot perform experiments of dynamic liquid level with considerable variations.

To investigate the difference between two-layer coproduction and single-layer production and the effect of pressure changes in layer 1 or 2 on coproduction, fifteen sets of experiments were conducted using the device introduced in Section 3.1. The parameters for each group are shown in

Table 1. Pressure parameters for different experiments.

No.	Pr1	Pr2	Ptf	No.	Pr1	Pr2	Ptf
	MPa	MPa	MPa		MPa	MPa	MPa
1	1.0	1.5	0~1.5	9	1.0~2.0	1.5	0.6
2	2.0	3.0	0.7~2.0	10	1.0	-	0~1.0
3	3.0	3.5	1.4~3.0	11	-	1.5	0~1.5
4	2.0	2.0~3.5	1.8	12	2.0	-	0.7~2.0
5	2.0	2.0~3.5	1.5	13	-	3.0	0.7~3.0
6	2.0	2.0~3.5	1.2	14	3.0	-	0.9~3.0
7	1.0~2.0	1.5	1.0	15	-	3.5	0.7~3.5
8	1.0~2.0	1.5	0.8

.

4. Results and Discussion

According to the analysis above, the pressure distribution in the wellbore is the key to the CSG coproduction. Under the condition that the dimensions of the wellbore structure are determined, it can be concluded through the analysis of Equations (7) and (8) that the factors that have an influence on the pressure gradient in the wellbore are the fluid density in the wellbore and the velocity of the fluids. As for the CSG coproduction process, the specific parameters that have influence on the fluid density and velocity in the wellbore are the wellhead pressure, the gas output of each layer, and the depth of the dynamic fluid level. For different parameters, a combination of theoretical calculation and experimental method is used to analyze the influence of different parameters on the pressure distribution of the wellbore.

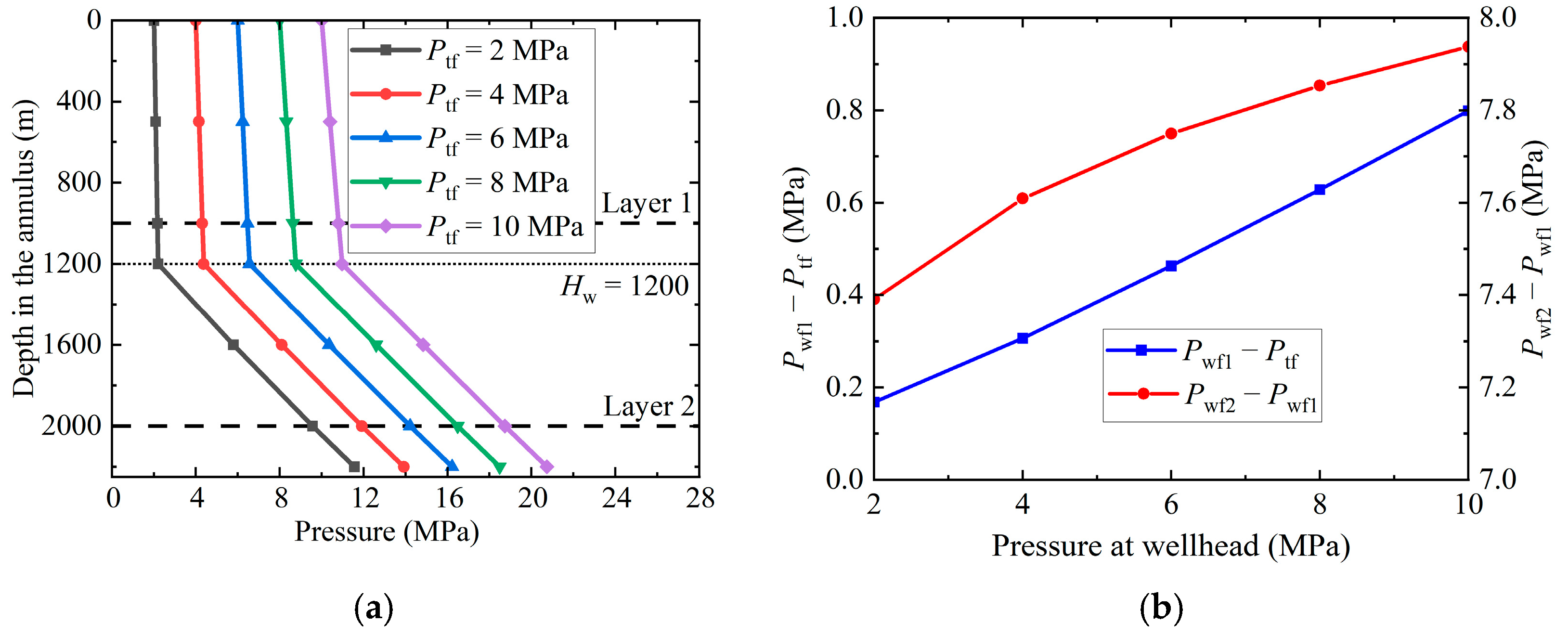
4.1. Pressure at the Wellhead

As the production of CSG production layer is very sensitive to pressure change, wellhead pressure is very important for the production of the CSG combined production well of annular gas production. The effects of wellhead pressure on the pressure distribution and production effect in CSG coproduction wellbore were analyzed by theoretical calculation and experiment.

Based on the calculation model in Section 2.2, the pressure distribution calculation of CSG coproduction well under different wellhead pressure conditions was completed, and the results are shown in Figure 5. Relevant parameters for calculation are set as follows: the gas production of upper and lower layers is set as 0.5 × 10⁴ m³/d. The casing size is 5.5 inches and tubing size is 2.875 inches.

As shown in Figure 5a, the variation in wellhead pressure directly affected the production pressure of the two layers when other parameters were constant. The production pressure increased with the increase in wellhead pressure difference at the depth of both layers. As the dynamic liquid surface is located between layer 1 and layer 2 (H_w = 1200 m), at this time there is a gas–liquid mixed two-phase flow between the two layers, as shown in Figure 2b. Therefore, the change in pressure difference between the two layers is less than that between layer 1 and the wellhead. At the same time, the magnitude of pressure difference between layer 1 and wellhead shows an accelerating trend with the increase in wellhead pressure. While the change of pressure difference between the two layers shows a gradual deceleration trend, as shown in Figure 5b. And this may cause a change in the output gas velocity in both layers.

Nine sets of experiments were carried out for coproduction and independent gas production in each layer, with the parameters and materials of the experimental setup kept unchanged. With different P_tf, the total gas flow rate from coproduction increased with increasing P_e1, as shown in Figure 6a–c. The total gas production from coproduction increases with decreasing P_tf. This is consistent with Equations (1)–(3), thus verifying the validity of the experiments. As shown in Figure 6, with the increase in P_tf, the gas flow rate of both layers showed a downward trend, while the gas production of layer 1 rose significantly faster than that of layer 2, which was due to the difference in the geological properties of the cores used for the two layers.

The gas production rates of each layer independently are more than that of the individual layer produced in coproduction. This is due to the accumulation of gas produced from the other layer in the wellbore during coproduction, causing an increase in the pressure in the wellbore, which in turn suppresses the gas production rate of the two layers in coproduction. At the same time, the gas flow rate of layer 1 increases significantly faster than that of layer 2, as P_tf decreases during coproduction, which is consistent with the calculation results. In other words, while other conditions are constant, the production flow pressure of layer 1 is affected more relative to layer 2 as P_tf decreases, as shown in Figure 5a.

As shown in Figure 6d, the gas production rate of coproduction continues to increase with decreasing wellhead pressure when the wellhead pressure drops below a critical gas production pressure of the coproduction layer, but the gas production rate of coproduction will tend to stabilize after the wellhead pressure drops to less than 50% of the original layer pressure of the low-pressure layer. In field production, the wellhead pressure can be reduced moderately to increase the gas production of the coproduction wells, but it may not be possible to further increase the total gas production rate of the coproduction wells by producing at very low wellhead pressure.

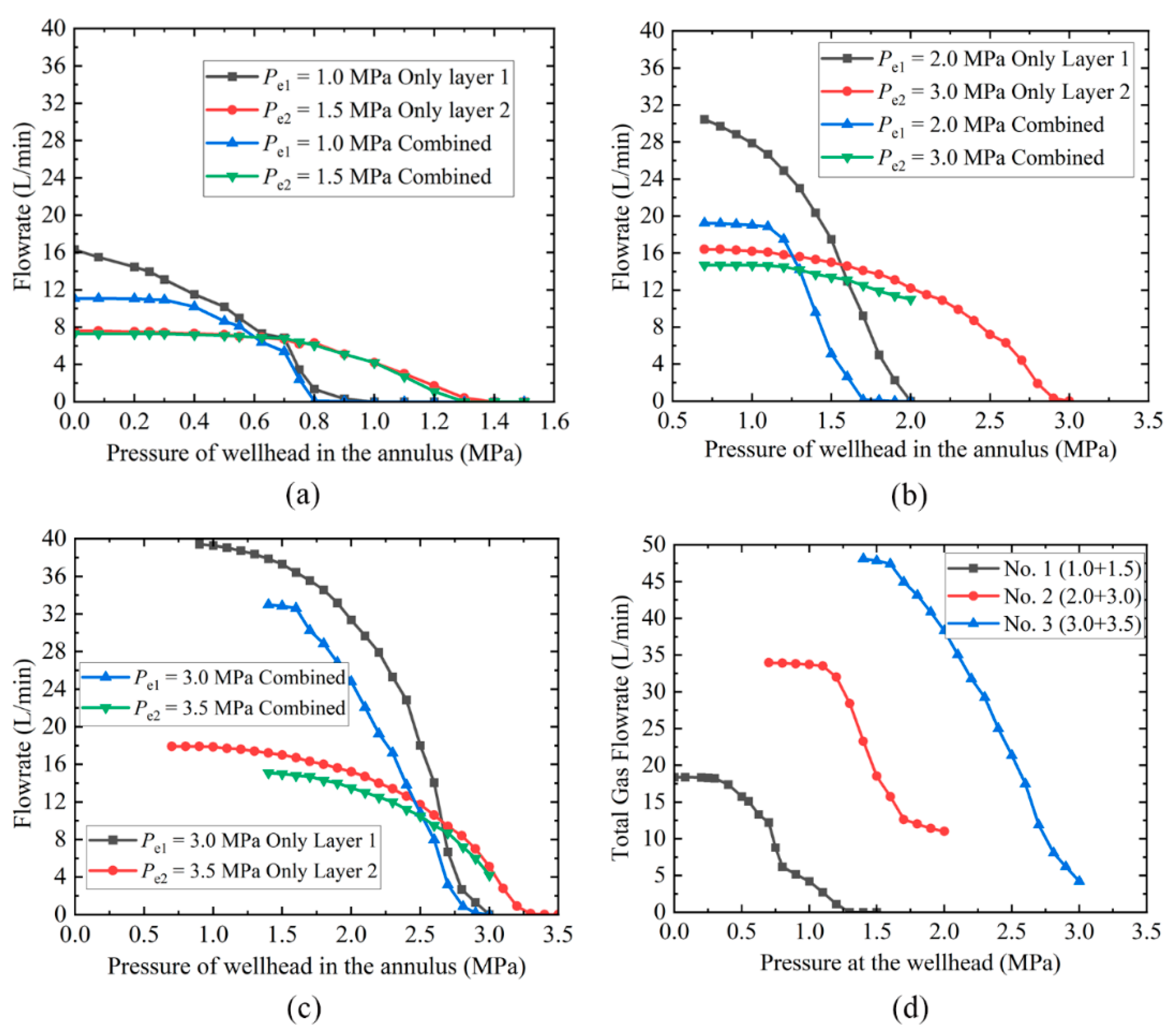
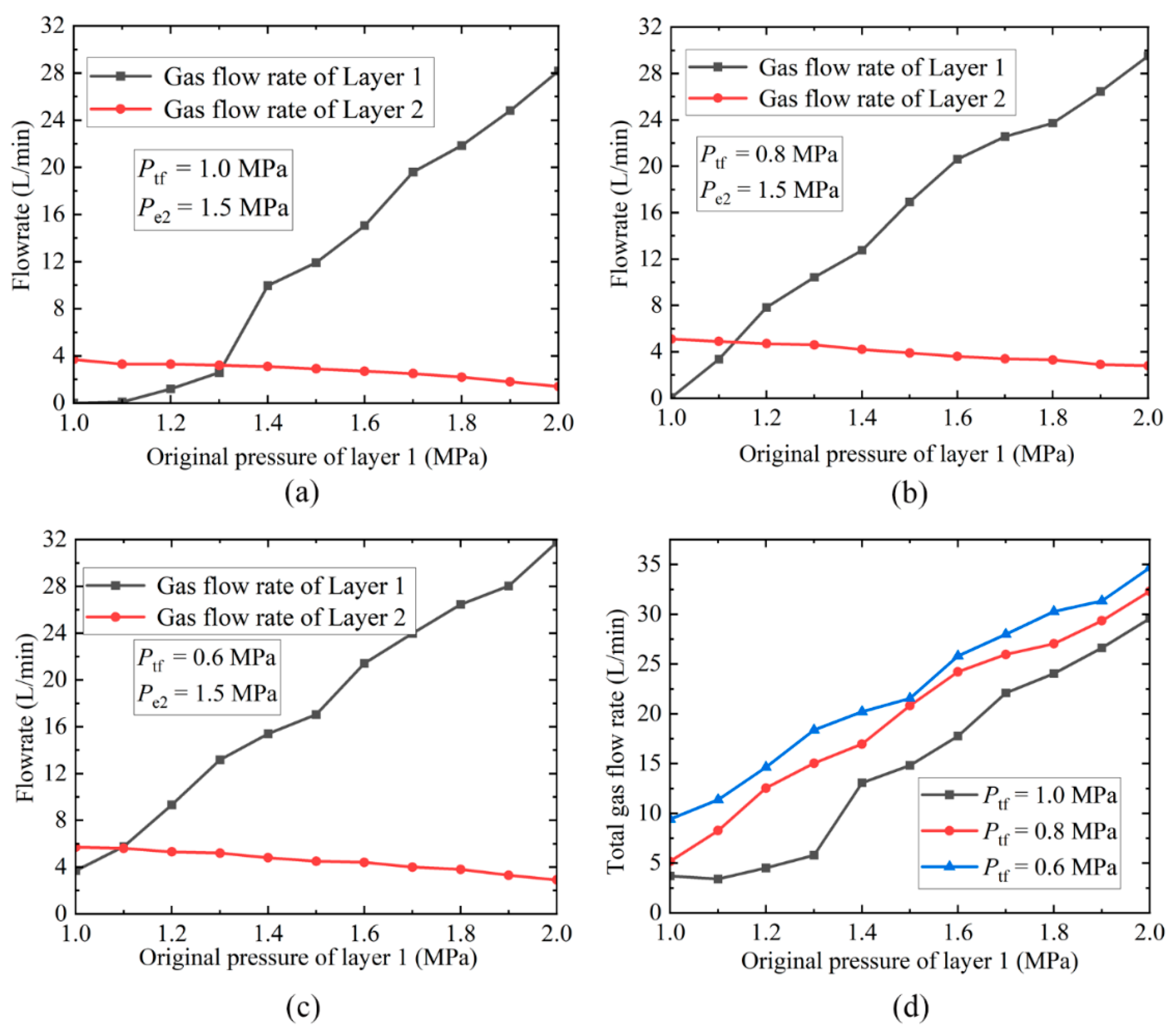
4.2. Output of Layer 1

To investigate the influence of the output of layer 1 on the wellbore annulus pressure distribution and the effect of combined production, two cases of layer 1 fixed pressure production and fixed output production were analyzed respectively. The fixed output production mode was analyzed in a theoretical method, and the results are shown in Figure 7. The fixed pressure production mode was analyzed by experiment, with the results shown in Figure 8.

As shown in Figure 7, the gas production of layer 1 had little effect on the pressure distribution in the annulus with the variation of gas production in the upper layer. When the gas production of layer 1 grows from 500 m³/d to 50,000 m³/d, the pressure difference between P_tf and P_wf1 increases from 0.15 MPa to 0.74 MPa. The increase in P_wf1 − P_tf is 0.59 MPa, an increase of 393.3% relative to the initial pressure difference. At the same time, P_wf2 − P_wf1 increases from 7.39 MPa to 7.46 MPa. P_wf2 − P_wf1 changes by 0.07 MPa with a variation range of less than 1%. The increase in gas production in layer 1 significantly affects the pressure difference between the wellhead and layer 1. As the gas production of layer 1 changes within 10,000 m³/d, the pressure difference between the two layers’ changes less than 0.03 MPa. The effect on the difference in production pressure between the two layers is slight.

As shown in Figure 8a–c, as P_tf decreases from 1.0 MPa to 0.6 MPa, the minimum and maximum gas production of layer 1 increases from 0.0 L/min and 28.2 L/min to 3.7 L/min and 31.8 L/min, respectively, while the minimum and maximum gas production of layer 2 changes from 1.4 L/min and 3.7 L/min to 2.9 L/min and 5.7 L/min, respectively. When the pressure of layer 1 increases, the gas production rate of layer 1 increases, while the gas production rate of layer 2 gradually decreases. The reason is that when the pressure of layer 1 increases, the production pressure difference of layer 1 gradually increases due to the constant P_tf, and the gas production rate of layer 1 increases, which is consistent with Equations (4)–(6). As the production pressure of layer 1 increases, it will cause the production pressure at layer 2 to increase, which makes the production pressure difference of layer 2 decrease, and this would suppress the gas production rate of layer 2. As shown in Figure 8d, when the production pressure of layer 1 increases, the total gas production rate of coproduction increases with decreasing P_tf. When P_tf, decreases from 1.0 MPa to 0.8 MPa, the gas production rate changes more relative to the decrease in P_tf, from 0.8 MPa to 0.6 MPa. This is consistent with the results in Figure 6d. This further verifies that when P_tf, decreases, the total gas production of coproduction will increase rapidly and then slowly with the continuous decrease in wellhead pressure.

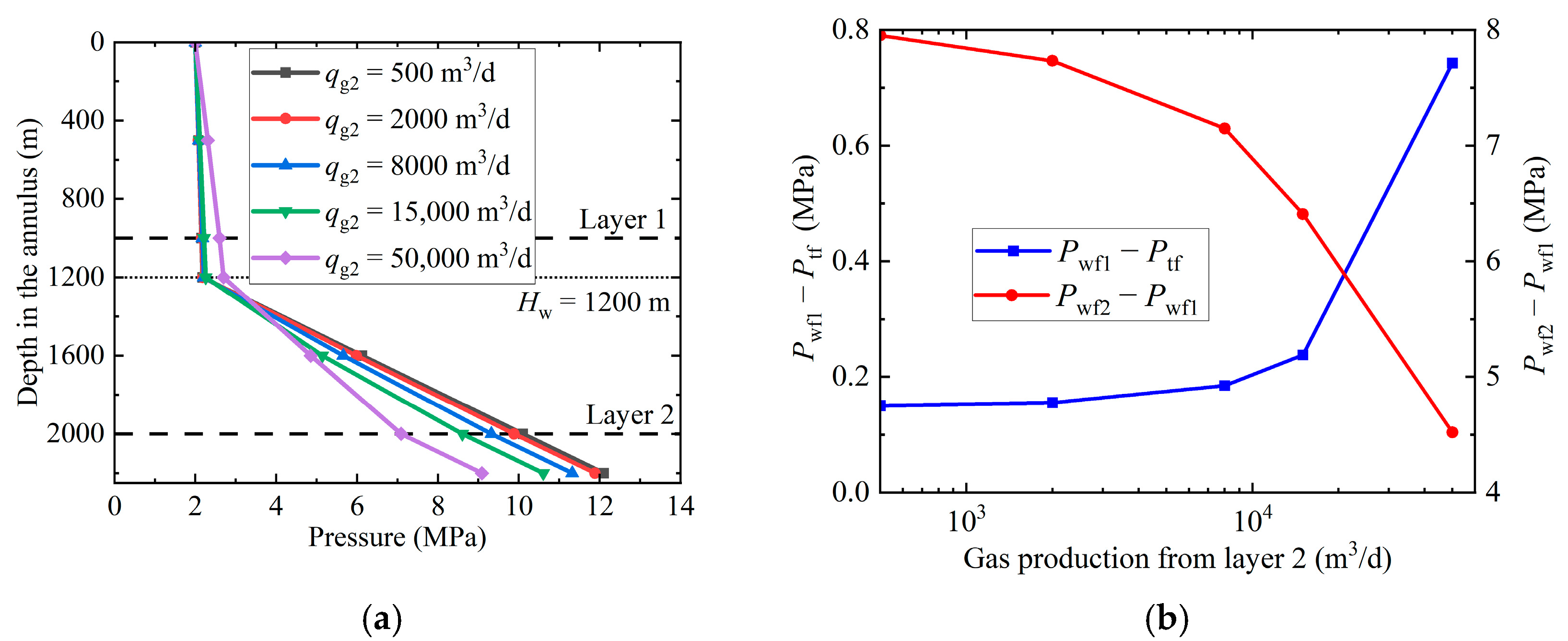
4.3. Output of Layer 2

The gas production and production pressure of layer 2 were analyzed using the same methodology as for layer 1.

As shown in Figure 9a, under the condition that only the gas production of layer 2 varied, the production pressure of layer 1 changed slightly. This is due to the single-phase gas flow in the portion above the depth of layer 1, where the changes in gas production from layer 2 have a small effect on the pressure gradient. However, the production pressure at the depth of layer 2 is greatly varied. The reason for this is the change in the flow regime in the gas–water mixing section between the two layers due to the change in the amount of gas produced from layer 2. As shown in Figure 9b, when q_g2 increased from 500 m³/d to 15,000 m³/d, the pressure difference between P_tf and P_wf1 increases from 0.15 MPa to 0.23 MPa. The increase in P_wf1 − P_tf is 0.08 MPa, an increase of 53.3% relative to the initial pressure difference. At the same time, P_wf2 − P_wf1 decreases from 7.95 MPa to 6.41 MPa. P_wf2 changes by 1.54 MPa with a variation range of 19.4%. While the gas production of layer 2 is 50,000 m³/d, the pressure difference between layer 1 and the wellhead is 0.74 MPa, while the pressure difference between the two layers is 3.43 MPa. These pressure differentials show a large change compared with that of 15,000 m³/d. This is attributed to the change in the flow regime of the gas–water two-phase flow below the dynamic liquid level between the two layers when the gas production grows from 15,000 m³/d to 50,000 m³/d.

The results of the experiments related to the impact of the change in output in layer 2 are shown in Figure 10.

As shown in Figure 10a–c, as the production pressure of layer 2 gradually increases, the gas flow rate of layer 1 gradually decreases. As the wellhead pressure is 1.2 MPa, the flow rate decreases from 21.39 L/min to 12 L/min. while the gas flow rate of layer 2 increases from 5.3 L/min to 16.5 L/min. This is because the production pressure of layer 2 increases and leads to a gradual increase in pressure in the wellbore, which inhibits the output of layer 1. With the increase in the pressure of layer 2, the production pressure drop of layer 2 increases, which results in the increase in the flow rate of layer 2. As the P_tf increases, the total gas production of the two coproduction layers decreases, as shown in Figure 10d.

With P_tf = 1.8 MPa, the total gas output from the coproduction of the two layers gradually increases with the increase in the production pressure of layer 2. At this time, the wellhead pressure is close to the layer production pressure, and the production capacity of the layers is not effectively released. As the pressure in layer 2 increases, the production capacity of layer 2 is gradually released due to the constant P_tf; thus, the gas production rate of layer 2 continues to increase. The pressure in the wellbore also rises simultaneously, thus inhibiting the gas production of layer 1. The reason for this is that when the wellhead pressure is significantly lower than the production pressure of both layers, when the layer pressure of layer 2 increases, it will not only lead to an increase in the gas production rate of layer 2 but also cause an increase in the wellbore pressure, which will in turn inhibit the decrease in the gas production rate of layer 1. Thus, the overall gas production will not show a noticeable increase.

4.4. Dynamic Fluid Level

The theoretical model was used for the calculation of wellbore pressure in the CSG coproduction wells, and the results are shown in Figure 11.

When the depth of the dynamic liquid surface varied, the change in the production pressure of the two layers was significant, as shown in Figure 11. While the dynamic liquid surface was above layer 1, due to the pressure difference between the two phases flow, it would directly increase the production pressure at the depth of layer 1. The magnitude of the increase mainly depended on the value of the depth difference between layer 1 and the dynamic liquid surface. In the case where the dynamic fluid level is between the two layers, the production pressure of layer 1 is mainly affected by the variation in the wellhead pressure of the annular space. However, the production pressure difference between the two layers is affected by the depth variation of the dynamic liquid surface, which means that the production pressure of layer 2 is mainly affected by the depth of the dynamic liquid surface. When the dynamic liquid surface was deeper than layer 2, the dynamic liquid surface mainly affected the pressure distribution below layer 2 in the wellbore annulus. Therefore, the production pressure of the two layers was mainly influenced by the production pressure at the P_tf, H_w and the output pressure of the two layers.

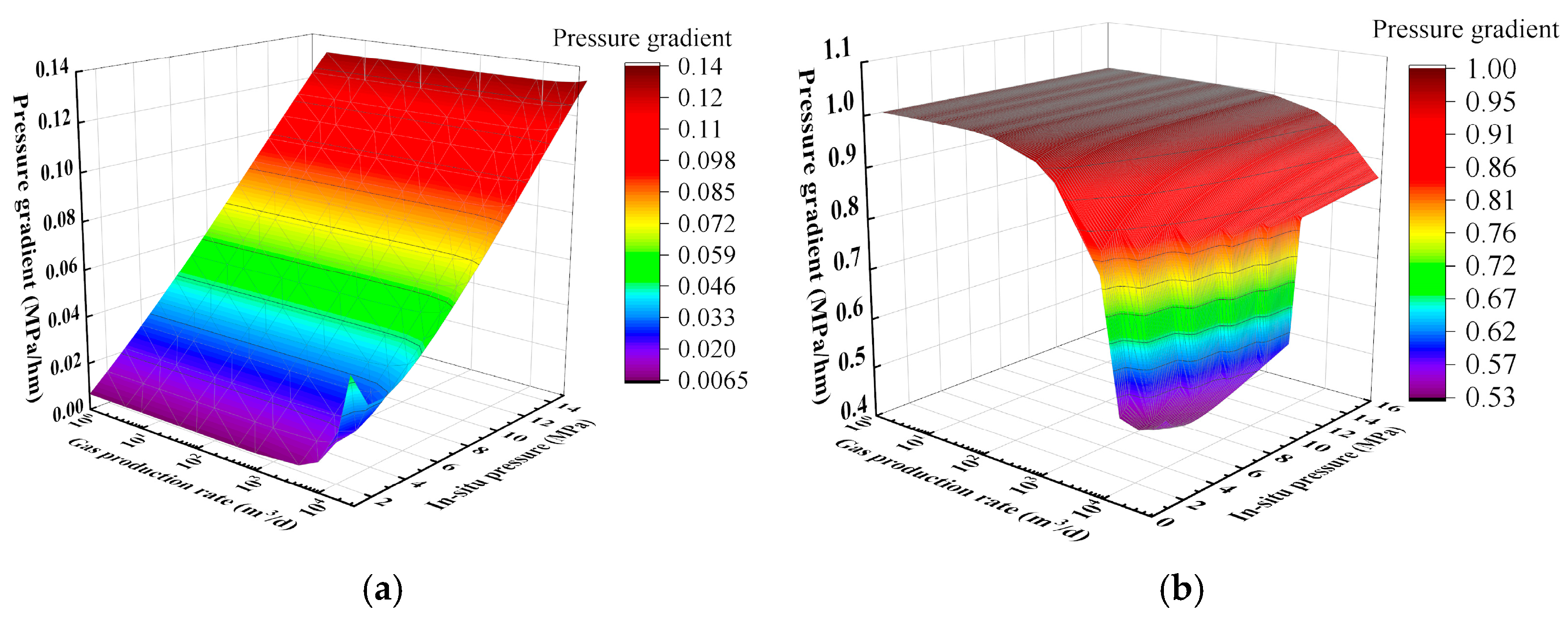
4.5. Pressure Gradient

To facilitate the adjustment of parameters in the field, an analysis of the pressure gradient of the pure gas column and annular gas-liquid two-phase pressure with daily gas production and in-place pressure variation was performed according to the model in Section 3. The range of gas production is 1~50,000 m³/d and the pressure range is 1.0–16.0 MPa. The tubing size in the wellbore is 2.875 inches and the casing size is 5.0 inches. The well depth is set to 2300 m.

The results are shown in Figure 5. The results show that the pressure gradient in the pure gas column section ranges from 6.5 kPa/100 m~0.14 MPa/100 m, while the pressure gradient in the gas-liquid two-phase region ranges from 0.53 to 1.00 MPa/100 m.

As shown in Figure 12a, the pressure drop in the pure gas column section is mainly affected by the pressure, as gas production is below 10,000 m³/d. With an increase in in-situ pressure, the gas density increases, which leads to a linear increase in the pressure drop in the gas column section with gas density. Under the condition of gas production of more than 10,000 m³/d, the increase in frictional resistance in gas flow resulted from an increased gas flow rate. The pressure gradient showed a decreasing and then increasing trend in the range of in situ pressure from 1 to 16.0 MPa. The pressure gradient in the gas column section decreases when the pressure is lower than 4.0 MPa. When the in situ pressure is higher than 4.0 MPa, the gradient change due to frictional resistance gradually decreases as the gas flow velocity gradually slows down due to the pressure increase.

As shown in Figure 12b, when the gas production volume is less than 1000 m³/d, the pressure gradient in the gas-water mixed flow section is mainly influenced by the gravity of both gas and water phases. Moreover, when the gas production volume is greater than 1000 m³/d, the output gas causes the void ratio occupied by the gas in the mixed flow section to increase, which reduces the density of the gas-water mixture in the mixed section. Furthermore, this leads to a rapid decrease in the pressure gradient with the continued growth of gas production. Under this condition, the pressure gradient decreases gradually with an increase in in situ pressure.

The pressure gradient results in the wellbore can effectively guide the adjustment of pressure parameters in the coproduction. This can also provide a basis for determining whether a well should be coproduced through the annulus. Based on the pressure gradient calculation results, the field operator can adjust the wellhead pressure in real time according to the production condition of the coproduction well. Moreover, according to the requirements of the dynamic liquid surface depth, the parameters of the drainage equipment (the stroke and stroke frequency of the pumping unit and the water replenishment flow rate) can be adjusted quickly.

5. Conclusions

It can be obtained from the above analysis that the pressure distribution in the annulus of two-layer CSG coproduction wells is affected by the wellhead pressure, the depth of the dynamic liquid surface, and the gas production rate and gas production pressure of each layer. In order to realize CSG coproduction in the same wellbore annulus, through adjusting the two parameters of wellhead pressure and depth of dynamic liquid surface, a reasonable production pressure difference between the two different pressure system producing layers can be realized, thereby realizing the coproduction of coal system gas. By completing the above study, the following conclusions are concluded:

(1)

Based on the wellbore pressure distribution law of CSG coproduction wells, a production parameter control method is established to effectively inhibit interlayer interference in the wellbore. A calculation method for the key parameter control requirements of the coproduction well is established, which provides a basis for the proper parameter regulation of the coproduction wells with an artificial drainage system.

(2)

For a given CSG coproduction well, the main factors affecting its wellbore pressure distribution are wellhead pressure, depth of the dynamic fluid surface, and the output of layer 1 and layer 2. Among them, the effect of wellhead pressure on the production pressure of the producing layers is the most obvious, but the effect of wellhead pressure on the interlayer pressure difference is small. An increase in wellhead pressure will directly result in an increase in pressure at both layers’ depths. Also, a decrease in wellhead pressure can lead to a decrease in pressure at both layers’ depths.

(3)

Changes in layer 1 output primarily affect the difference between the wellhead pressure and the pressure at the depth of layer 1. It has little effect on the difference between the pressures at the depths of layers 1 and 2. On the other hand, changes in the output of layer 2 affect the production pressure at both layer 1 and layer 2 depths. Therefore, when the dynamic fluid level is located between the two layers, a reasonable dynamic change of the pressure difference between the two layers can be realized by adjusting the depth of the dynamic fluid level. Thus, the interlayer interference in the wellbore can be effectively suppressed.

(4)

Fifteen sets of experiments on the effect of production pressure on coproduction were conducted using a set of two-layer coproduction test devices. The experimental results found that the gas production from the coproduction would be lower than the sum of the gas production from the two separate layers. However, by adjusting the wellhead pressure and dynamic fluid level parameters, it is able to make the gas production from the coproduction greater than the single layer production. Moreover, when the wellhead pressure of the combined production is lower than 50% of the low-pressure production layer, the gas production of the coproduction will not increase significantly.

Through theoretical analysis and laboratory experiments, all set results have been completed. The feasibility of suppressing the interlayer interference in the coproduction wellbore of two layers by adjusting the key parameters was verified, which can effectively improve the development benefit of CSG.