Overview of Common Thermophysical Property Modelling Approaches for Cryogenic Fluid Simulations at Supercritical Conditions
Abstract
1. Introduction
| Fluid | Critical | Critical |
|---|---|---|
| Pressure | Temperature | |
| (MPa) | (K) | |
| Nitrogen-N | 3.3958 | 126.192 |
| Oxygen-O | 5.0430 | 154.581 |
| Methane-CH | 4.5992 | 190.564 |
| Hydrogen-H | 1.2964 | 33.145 |
| Helium-He | 0.22832 | 5.1953 |
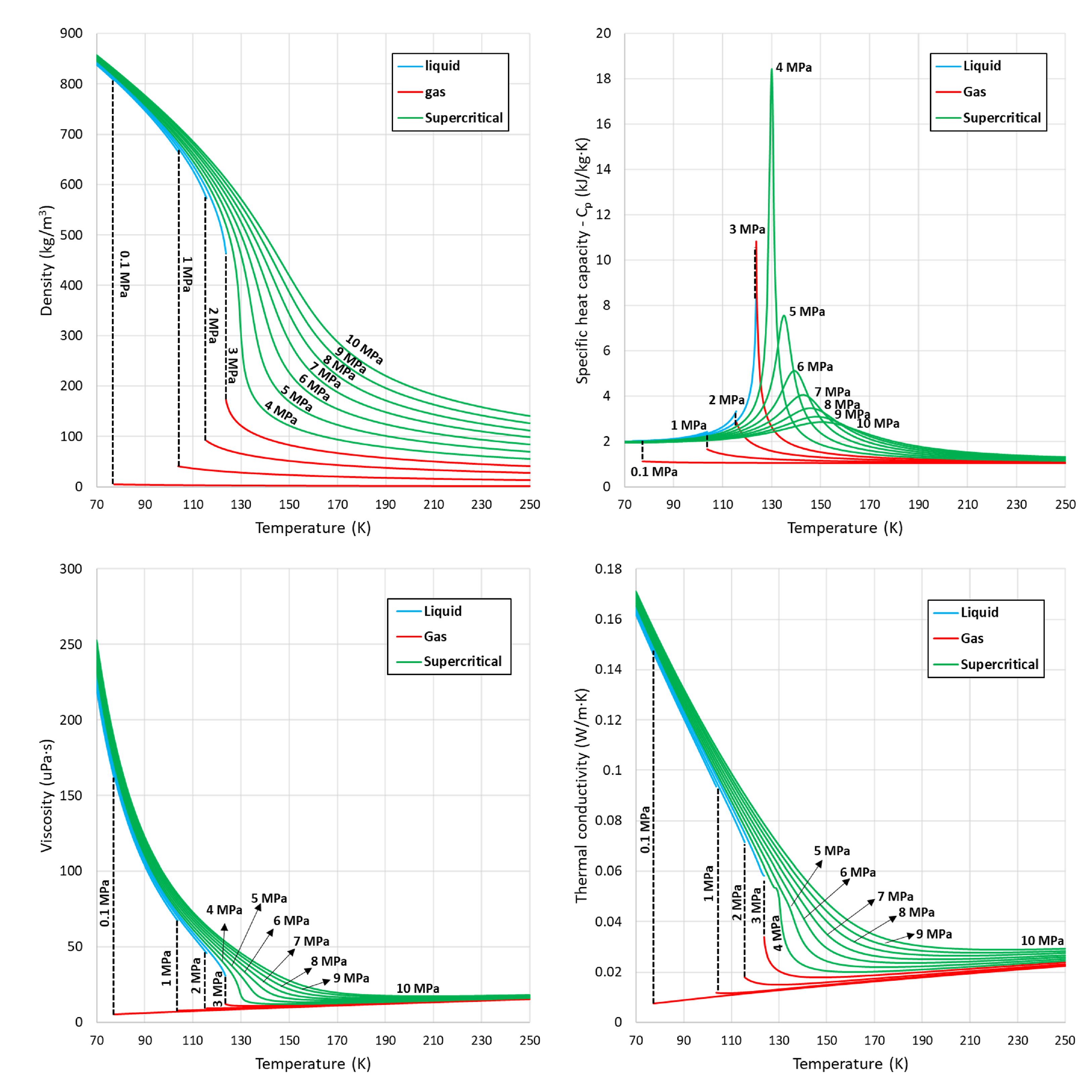
2. Peculiarities of Thermophysical Properties at Supercritical Pressure Conditions
3. Real Fluid Equation of State (EoS)
3.1. Cubic Equations of State
3.2. Non-Cubic Equations of State
SBWR
4. Thermophysical Property Derivation Based on EoS
4.1. Density
4.2. Thermodynamic Properties-Enthalpy and Specific Heat Capacity
4.3. Transport Properties-Viscosity and Thermal Conductivity
5. Predictions of Real Fluid EoS for Various Cryogenic Supercritical Fluids Investigated in CFD Studies
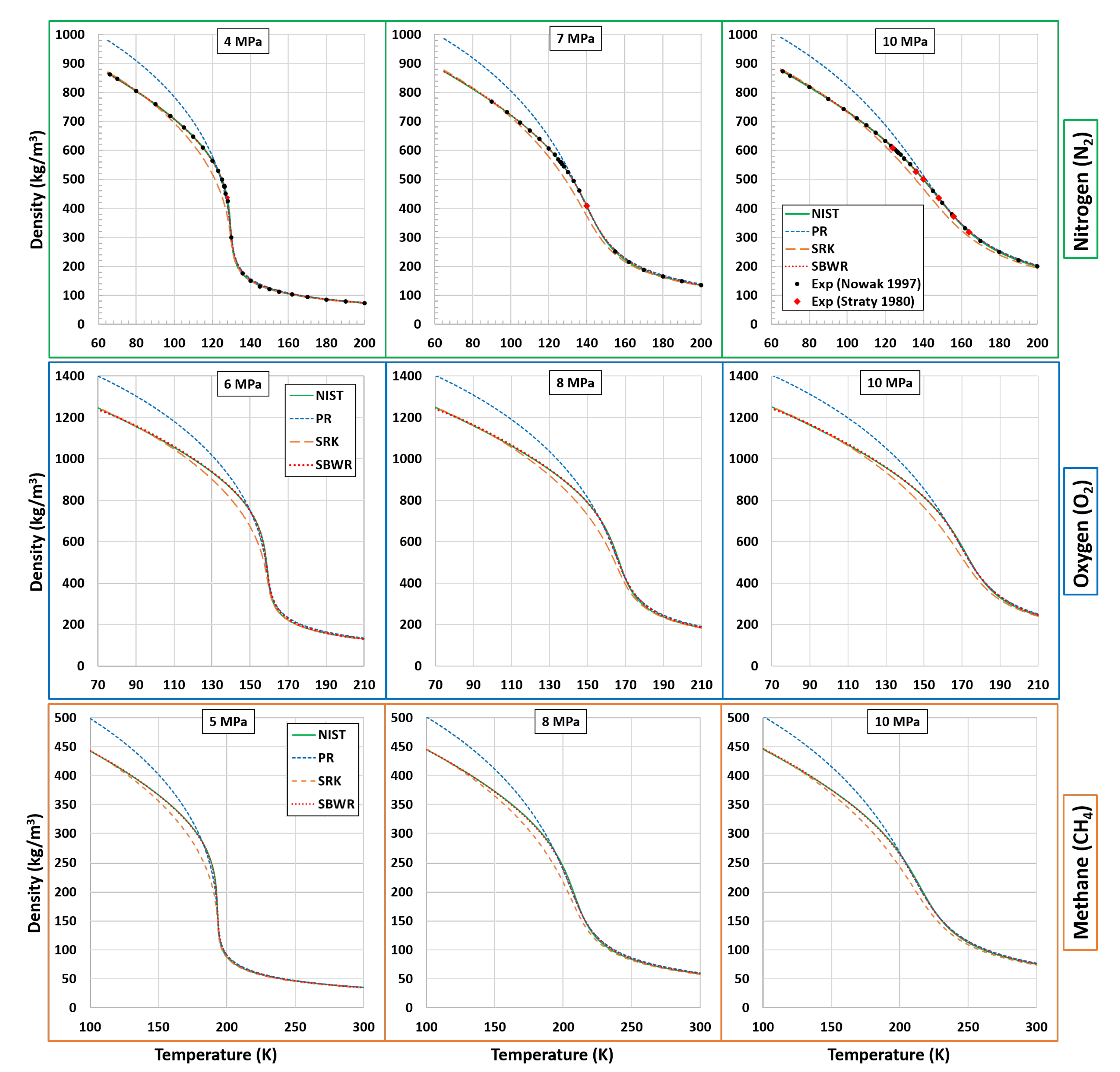
5.1. Density
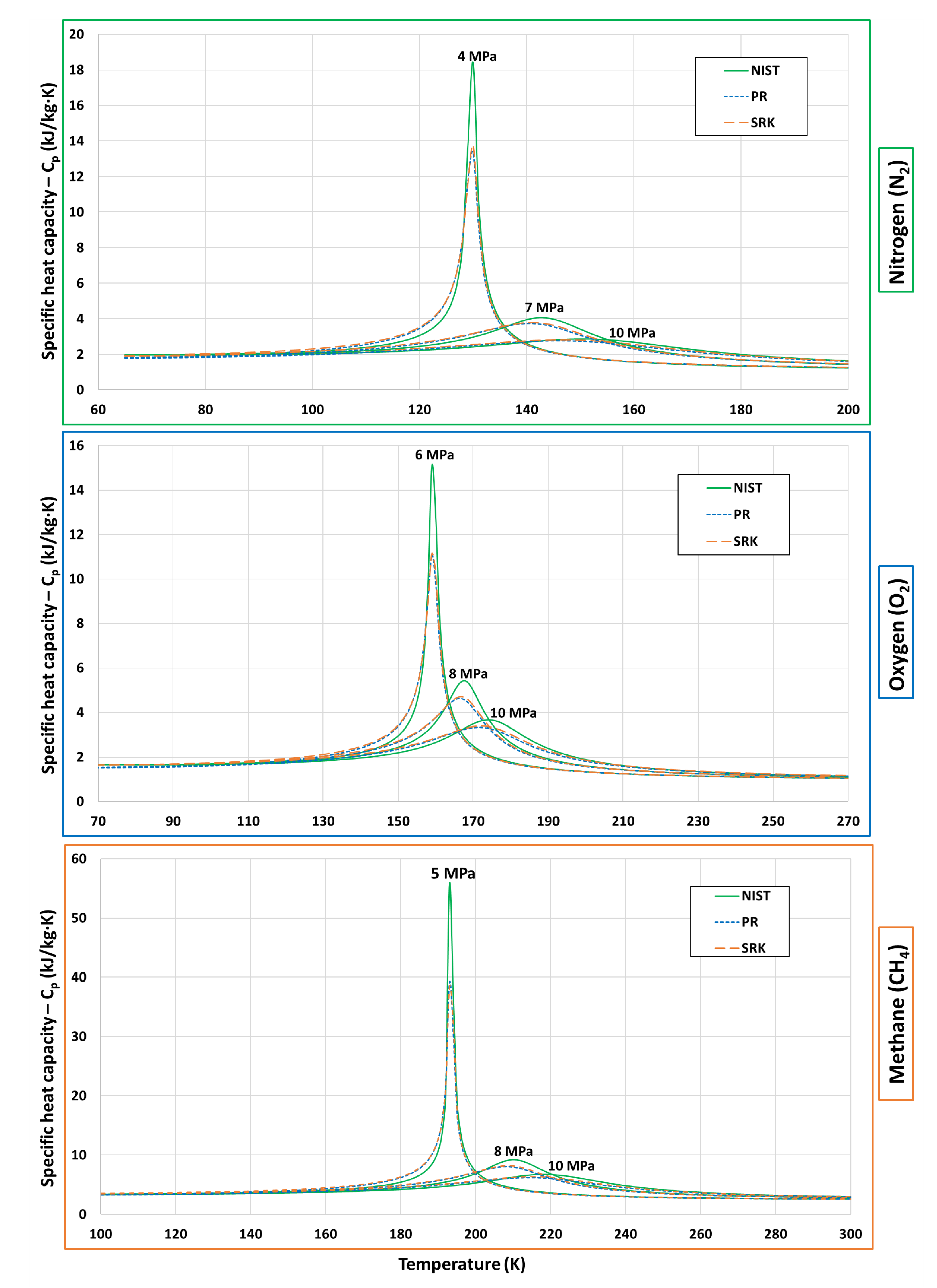
5.2. Thermodynamic Properties-Enthalpy and Specific Heat Capacity
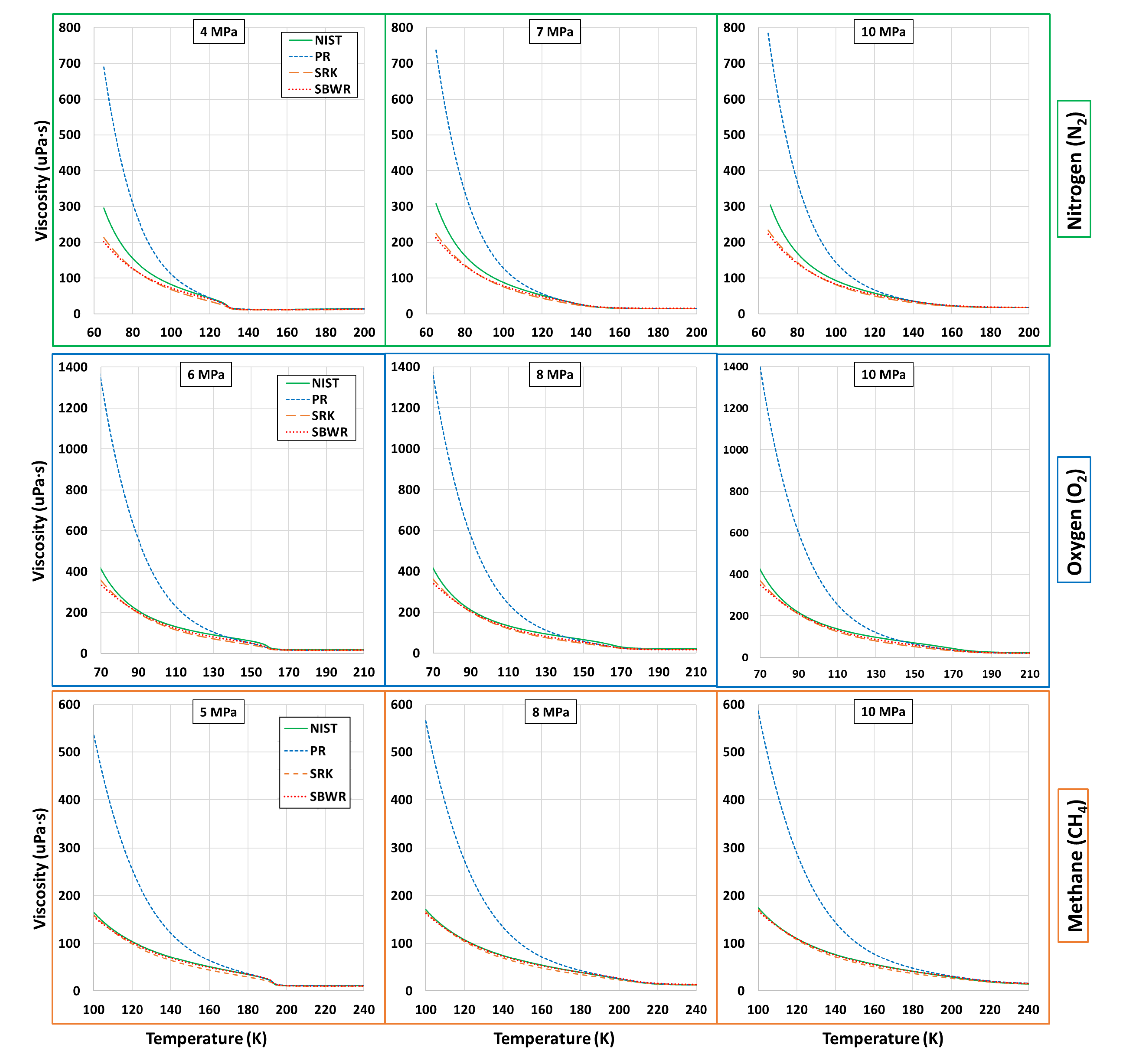
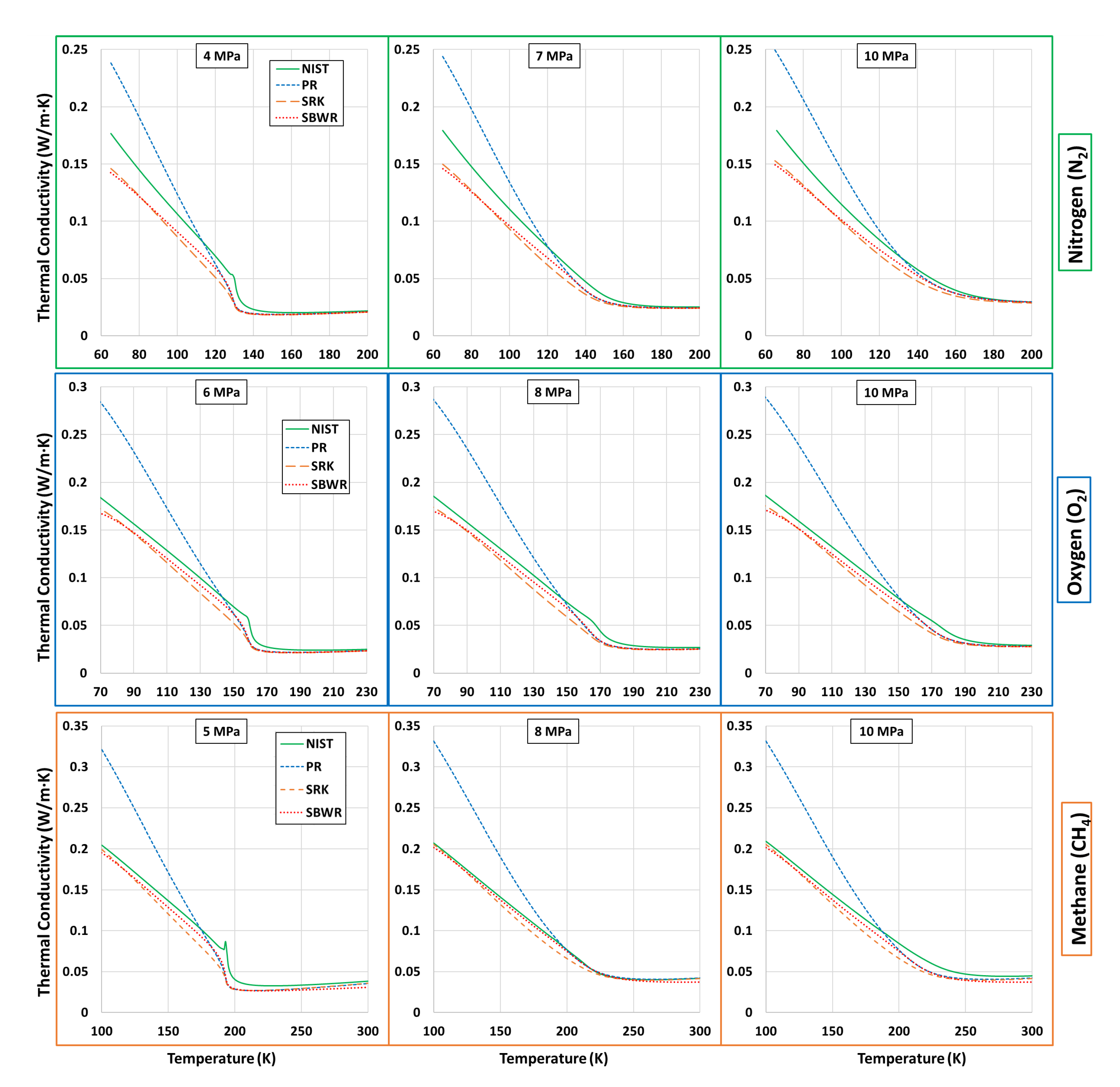
5.3. Transport Properties-Viscosity and Thermal Conductivity
5.4. Summary
6. CFD Simulations of Cryogenic Fluids at Supercritical Pressures
7. Real Fluid EoS in CFD Simulations of Cryogenic Fluids at Supercritical Pressures
| Simulation | EoS | Thermodynamic | Transport | Experiment |
|---|---|---|---|---|
| Properties | Model | Simulated | ||
| Mayer et al. [10] (2003) | Lee-Kesler | Chung et al. [36] | Mayer et al. [10] | |
| Zong et al. [68] (2004) | SRK | SRK derived | 32 term BWR [37,38] | Chehroudi et al. [78] |
| Schmitt et al. [71] (2010) | PR | PR derived | Chung et al. [36] | Mayer et al. [10] |
| Kim et al. [19] (2011) | PR and SRK | PR and SRK | Chung et al. [36] | Telaar et al. [11] |
| derived | Oschwald et al. [15] | |||
| Park [20] (2012) | PR and SRK | PR and SRK | Chung et al. [36] | Telaar et al. [11] |
| derived | Oschwald et al [15] | |||
| Petite et al. [21] (2013) | PR and SRK | PR and SRK | Chung et al. [36] | Mayer et al. [10] |
| derived | ||||
| Pfitzner et al. [73] (2013) | PR | PR derived | Chung et al. [36] | Telaar et al. [11] |
| Mayer et al. [10] | ||||
| Hickey [46] (2014) | PR | PR derived | Chung et al. [36] | Braman et al. [12] |
| Muller et al. [22] (2016) | PR | PR derived | Chung et al. [36] | Mayer et al. [10] |
| Banuti et al. [77] (2016) | MBWR based | MBWR based | MBWR based | Mayer et al. [10] |
| data tabulation | data tabulation | data tabulation [28,29] | Branam et al. [79] | |
| Li et al. [24] (2018) | SRK | SRK derived | Viscosity- | Telaar et al. [11] |
| Zéberg-Mikkelsen et al. [40] | Mayer et al. [10] | |||
| Thermal conductivity | ||||
| -Vasserman et al. [39] | ||||
| Lagarza-Cortés et al. [69] (2019) | SRK | SRK derived | Chung et al. [36] | Mayer et al. [10] |
| Ningegowda et al. [70] (2020) | PR | PR derived | Chung et al. [36] | Mayer et al. [10] |
| Ma et al. [59] (2021) | PR and SRK | PR and SRK | Viscosity- | |
| derived | Zéberg-Mikkelsen et al. [40] | Mayer et al. [10] | ||
| Thermal conductivity | ||||
| -Vasserman et al. [39] |
8. Alternative Approaches of Modelling Thermophysical Properties
8.1. Polynomial Fitting of Data
8.2. Tabulation
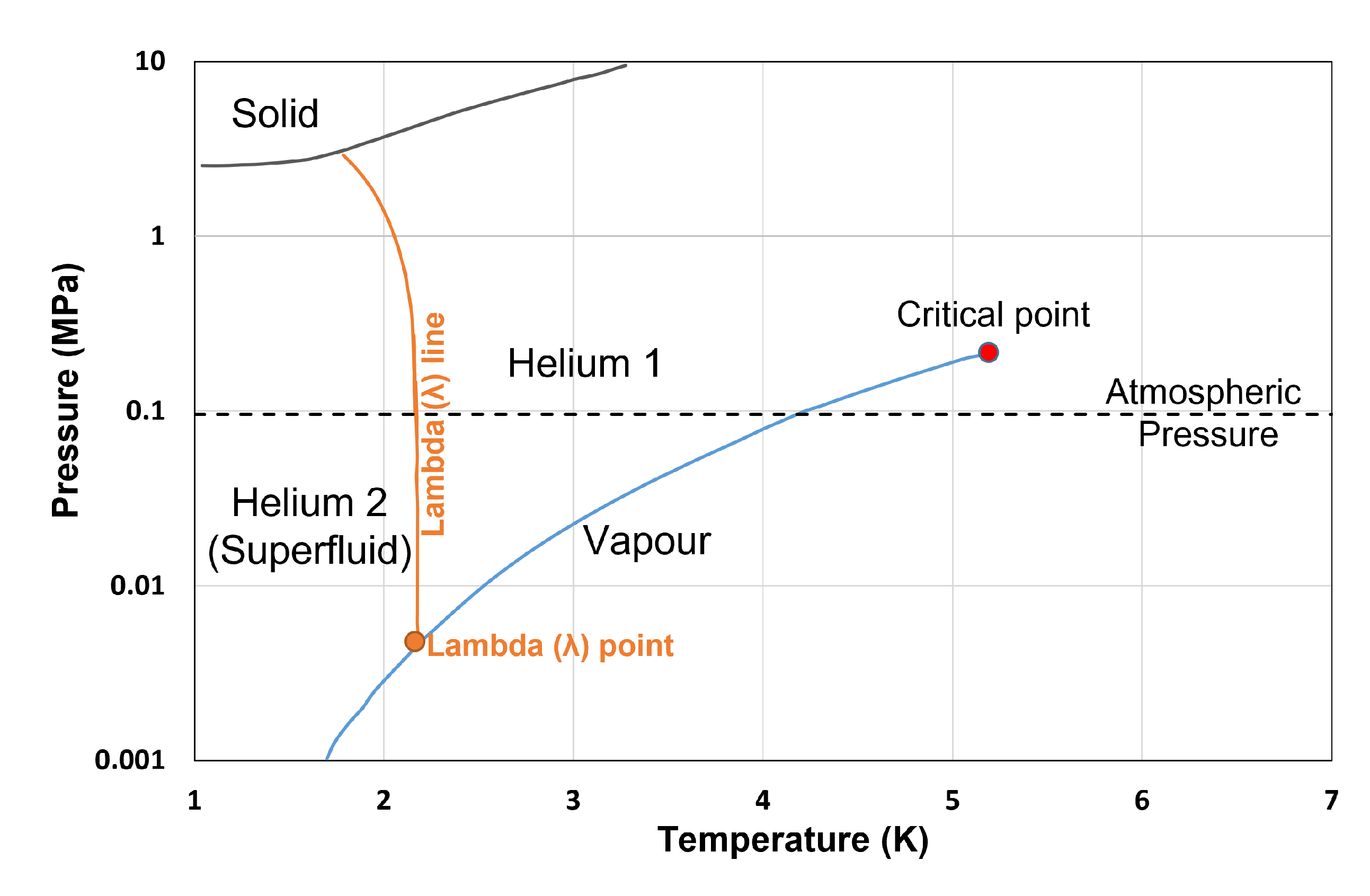
9. Discussion on Cryogenic Fluids with Quantum Effects
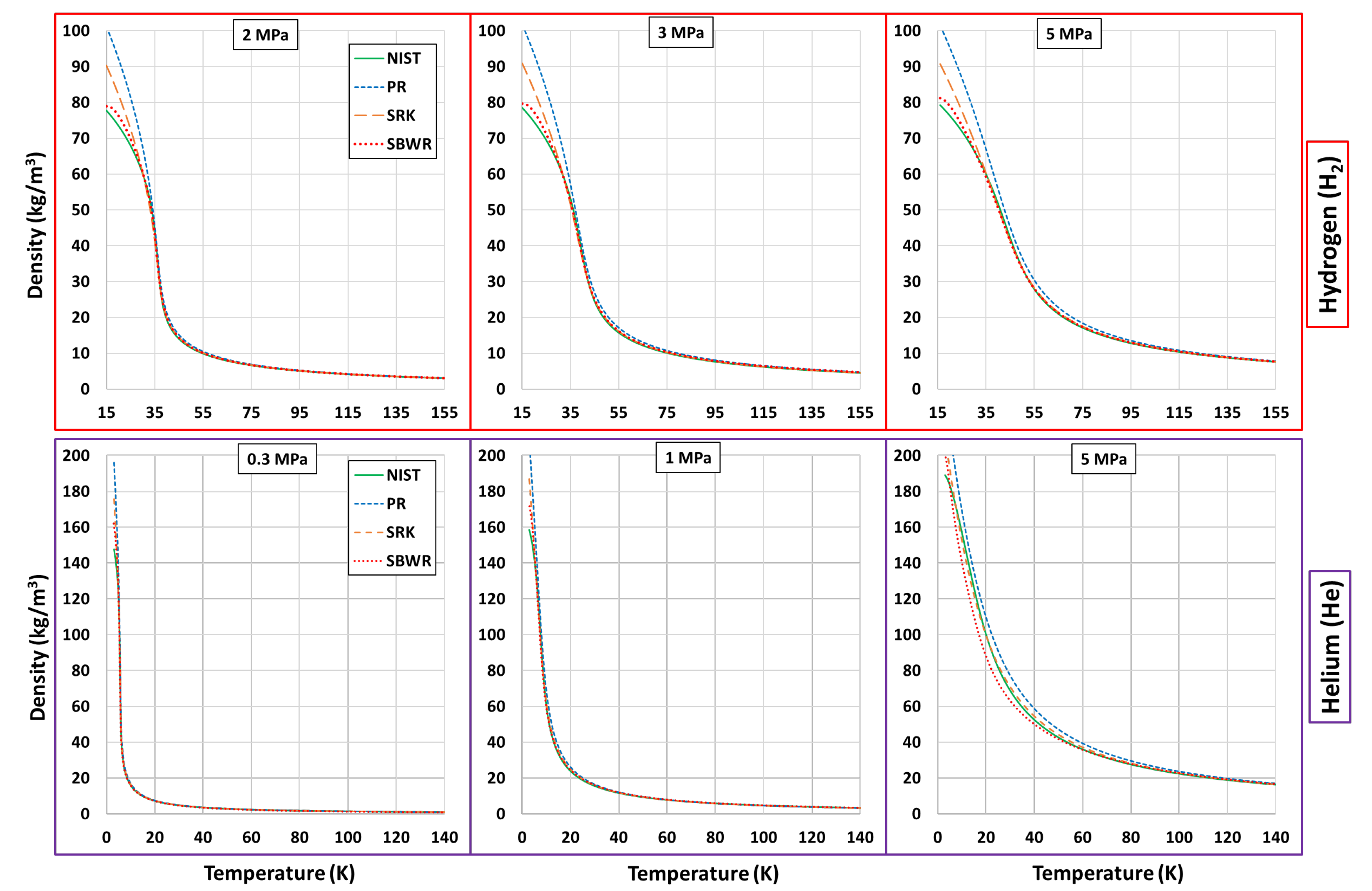
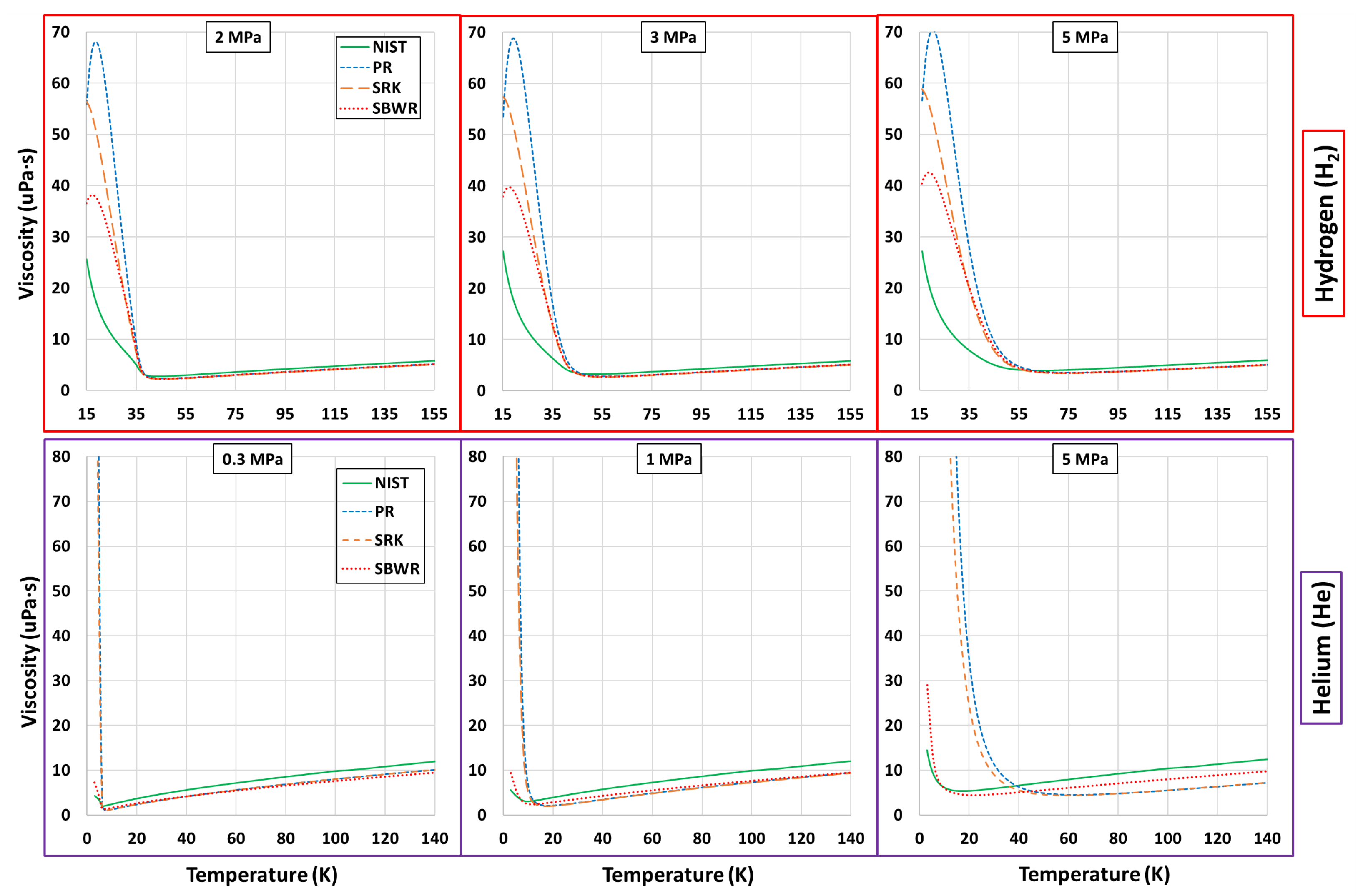
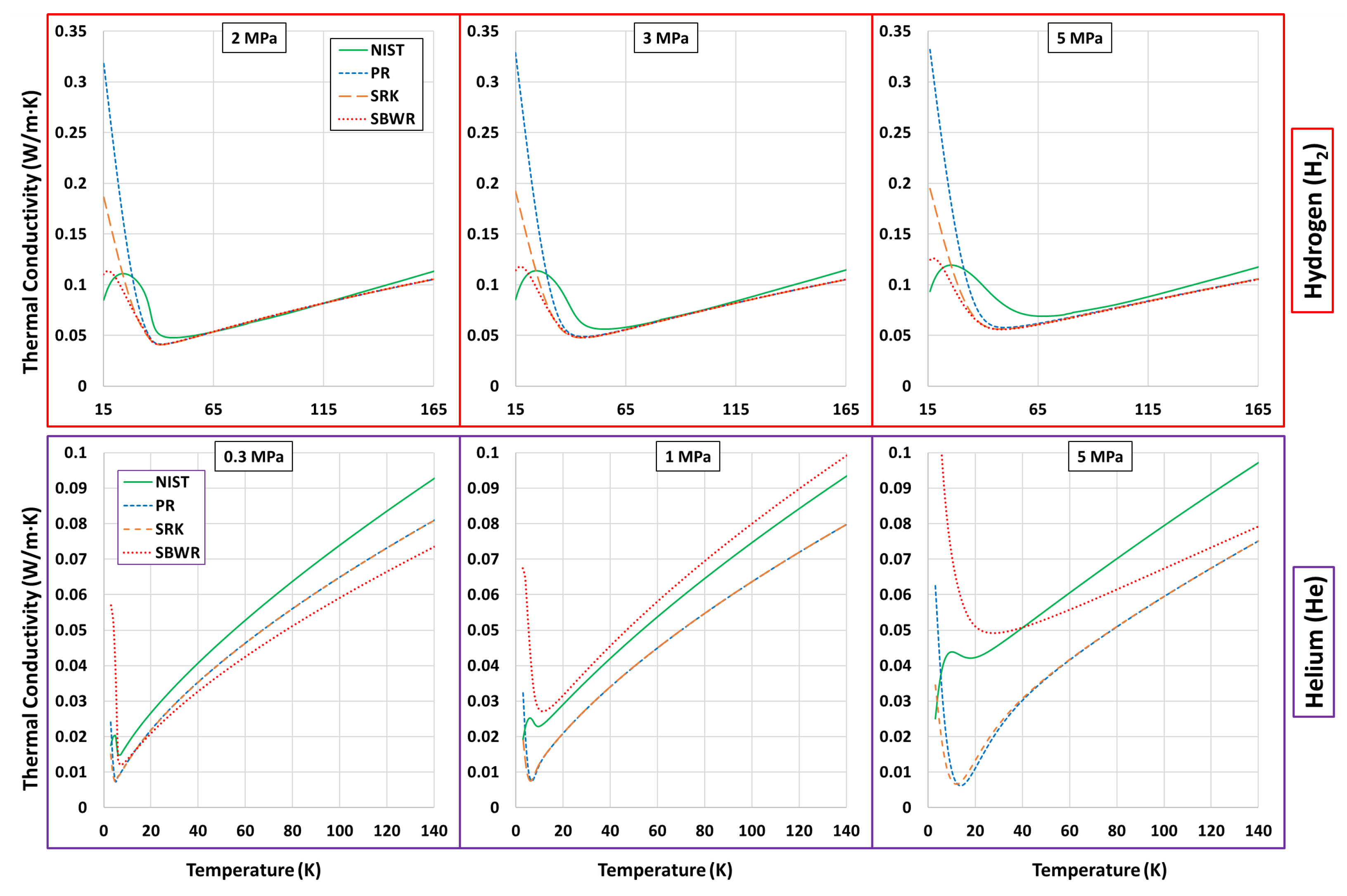
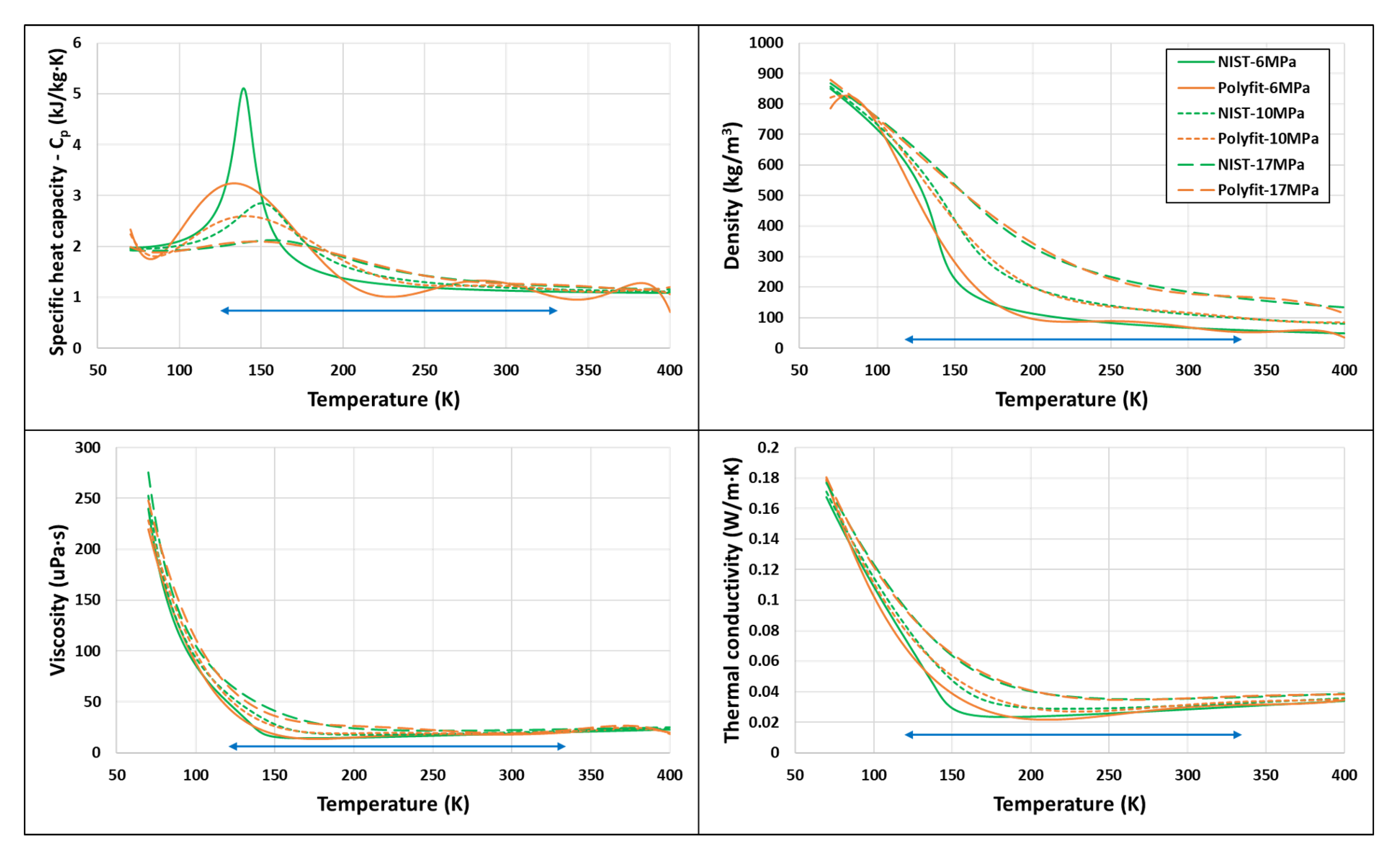
Thermophysical Property Estimation of Hydrogen (H) and Helium (He) Using Common Real Fluid EoS
10. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Thermophysical property estimation methods from PR, SRK and SBWR EoS
Appendix A.1. Thermodynamic Properties—Enthalpy and Specific Heat Capacity
Appendix A.1.1. Real Fluid Enthalpy
Appendix A.1.2. Real Fluid Specific Heat Capacity
Appendix A.2. Transport Properties
Appendix A.2.1. Dilute Gas Viscosity
Appendix A.3. Dilute Gas Thermal Conductivity
Appendix A.4. Dense Gas Viscosity
Appendix A.5. Dense Gas Thermal Conductivity
Appendix B. Estimations of PR, SRK and SBWR for Hydrogen and Helium
References
- Radebaugh, R.; Bar-Cohen, Y. Low Temperature Materials and Mechanisms: Applications and Challenges. In Low Temperature Materials and Mechanisms, 1st ed.; Bar-Cohen, Y., Ed.; CRC Press: Boca Raton, FL, USA, 2016; Chapter 14. [Google Scholar] [CrossRef]
- Owen, N.; Treccarichi, F.; Atkins, A.; Selvaraj, A.; Barnes, D.; Besant, T.; Morgan, R. A Practical Recuperated Split Cycle Engine for Low Emissions and High Efficiency. In Proceedings of the 14th International Conference on Engines & Vehicles, Naples, Italy, 15–19 September 2019. [Google Scholar] [CrossRef]
- Jaya Vignesh, M.; Harvey, S.; Atkins, A.; Atkins, P.; De Sercey, G.; Heikal, M.; Morgan, R.; Vogiatzaki, K. Use of cryogenic fluids for zero toxic emission hybrid engines. In Internal Combustion Engines and Powertrain Systems for Future Transport 2019, 1st ed.; CRC Press: London, UK, 2020; pp. 117–130. Available online: https://www.taylorfrancis.com/books/oa-edit/10.1201/9781003023982/internal-combustion-engines-powertrain-systems-future-transport-2019-imeche (accessed on 15 October 2022). [CrossRef]
- Jaya Vignesh, M.; Tretola, G.; Morgan, R.; Sercey, G.d.; Atkins, A.; Vogiatzaki, K. Understanding Sub and Supercritical Cryogenic Fluid Dynamics in Conditions Relevant to Novel Ultra Low Emission Engines. Energies 2020, 13, 3038. [Google Scholar] [CrossRef]
- Madana Gopal, J.V.; Tretola, G.; Morgan, R.; Sercey, G.d.; Lamanna, G.; Vogiatzaki, K. Unpicking the interplay of turbulence, diffusion, and thermophysics in cryogenic jets at supercritical pressures. Phys. Fluids 2021, 33, 077106. [Google Scholar] [CrossRef]
- Starship. Available online: https://www.spacex.com/vehicles/starship (accessed on 15 October 2022).
- Mayer, W.O.H.; Schik, A.H.A.; Vielle, B.; Chauveau, C.; Gokalp, I.; Talley, D.G.; Woodward, R.D. Atomization and Breakup of Cryogenic Propellants Under High-Pressure Subcritical and Supercritical Conditions. J. Propuls. Power 1998, 14, 835–842. [Google Scholar] [CrossRef]
- Chehroudi, B.; Talley, D.; Coy, E. Visual characteristics and initial growth rates of round cryogenic jets at subcritical and supercritical pressures. Phys. Fluids 2002, 14, 850–861. [Google Scholar] [CrossRef]
- Mayer, W.; Schik, A.; Schweitzer, C.; Schaeffler, M. Injection and mixing processes in high pressure LOX/GH2 rocket combustors. In Proceedings of the 32nd Joint Propulsion Conference and Exhibit, Lake Buena Vista, FL, USA, 1–3 July 1996. [Google Scholar] [CrossRef]
- Mayer, W.; Telaar, J.; Branam, R.; Schneider, G.; Hussong, J. Raman Measurements of Cryogenic Injection at Supercritical Pressure. Heat Mass Transf. 2003, 39, 709–719. [Google Scholar] [CrossRef]
- Telaar, J.; Schneider, G.; Hussong, J.; Mayer, W. Cryogenic Jet Injection: Description of Test Case RCM 1. In Proceedings of the 2nd International Workshop on Rocket Combustion Modeling: Atomization, Combustion and Heat Transfer, Lampoldshausen, Germany, 25–27 March 2001. [Google Scholar]
- Branam, R.; Mayer, W. Length scales in cryogenic injection at supercritical pressure. Exp. Fluids 2002, 33, 422–428. [Google Scholar] [CrossRef]
- Oschwald, M.; Schik, A. Supercritical nitrogen free jet investigated by spontaneous Raman scattering. Exp. Fluids 1999, 27, 497–506. [Google Scholar] [CrossRef]
- Oschwald, M.; Schik, A.; Klar, M.; Mayer, W. Investigation of coaxial LN2/GH2-injection at supercritical pressure by spontaneous Raman scattering. In Proceedings of the 35th Joint Propulsion Conference and Exhibit, Los Angeles, CA, USA, 20–24 June 1999. [Google Scholar] [CrossRef]
- Oschwald, M.; Smith, J.J.; Branam, R.; Hussong, J.; Schik, A.; Chehroudi, B.; Talley, D. Injection of fluids into supercritical environments. Combust. Sci. Technol. 2006, 178, 49–100. [Google Scholar] [CrossRef]
- Chehroudi, B.; Talley, D.; Coy, E. Initial growth rate and visual characteristics of a round jet into a sub- to supercritical environment of relevance to rocket, gas turbine, and diesel engines. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Hampton, VA, USA, 11–14 January 1999. [Google Scholar] [CrossRef]
- Chehroudi, B. Recent Experimental Efforts on High-Pressure Supercritical Injection for Liquid Rockets and Their Implications. Int. J. Aerosp. Eng. 2012, 2012, 121802. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. Thermophysical Properties of Fluid Systems. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. Available online: https://webbook.nist.gov/chemistry/fluid (accessed on 15 October 2022). [CrossRef]
- Kim, T.; Kim, Y.; Kim, S.K. Numerical study of cryogenic liquid nitrogen jets at supercritical pressures. J. Supercrit. Fluids 2011, 56, 152–163. [Google Scholar] [CrossRef]
- Park, T.S. LES and RANS simulations of cryogenic liquid nitrogen jets. J. Supercrit. Fluids 2012, 72, 232–247. [Google Scholar] [CrossRef]
- Petit, X.; Ribert, G.; Lartigue, G.; Domingo, P. Large-eddy simulation of supercritical fluid injection. J. Supercrit. Fluids 2013, 84, 61–73. [Google Scholar] [CrossRef]
- Müller, H.; Niedermeier, C.A.; Matheis, J.; Pfitzner, M.; Hickel, S. Large-eddy simulation of nitrogen injection at trans- and supercritical conditions. Phys. Fluids 2016, 28, 015102. [Google Scholar] [CrossRef]
- Wei, W.; Xie, M.; Jia, M. Large eddy simulation of fluid injection under transcritical and supercritical conditions. Numer. Heat Transf. Part A Appl. 2016, 70, 870–886. [Google Scholar] [CrossRef]
- Li, L.; Xie, M.; Wei, W.; Jia, M.; Liu, H. Numerical investigation on cryogenic liquid jet under transcritical and supercritical conditions. Cryogenics 2018, 89, 16–28. [Google Scholar] [CrossRef]
- Magalhães, L.; Carvalho, F.; Silva, A.; Barata, J. Turbulence Modeling Insights into Supercritical Nitrogen Mixing Layers. Energies 2020, 13, 1586. [Google Scholar] [CrossRef]
- Banuti, D. Thermodynamic Analysis and Numerical Modeling of Supercritical Injection. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2015. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar] [CrossRef]
- Younglove, B.A. Erratum: Thermophysical Properties of Fluids. I. Argon, Ethylene, Parahydrogen, Nitrogen, Nitrogen Trifluoride, and Oxygen. J. Phys. Chem. Ref. Data 1985, 14, 619. [Google Scholar] [CrossRef]
- Younglove, B.A.; Ely, J.F. Thermophysical Properties of Fluids. II. Methane, Ethane, Propane, Isobutane, and Normal Butane. J. Phys. Chem. Ref. Data 1987, 16, 577–798. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed]
- Gross, J.; Sadowski, G. Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Kunz, O.; Group, E.G.R. The GERG-2004 Wide Range Equation of State for Natural Gases and Other Mixtures: GERG TM15 2007. In Fortschrittberichte VDI/6: Energietechnik; VDI-Verlag: Düsseldorf, Germany, 2007. [Google Scholar]
- Kunz, O.; Wagner, W. The GERG-2008 Wide-Range Equation of State for Natural Gases and Other Mixtures: An Expansion of GERG-2004. J. Chem. Eng. Data 2012, 57, 3032–3091. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Chung, T.H.; Ajlan, M.; Lee, L.L.; Starling, K.E. Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Eng. Chem. Res. 1988, 27, 671–679. [Google Scholar] [CrossRef]
- Ely, J.F.; Hanley, H.J.M. Prediction of transport properties. 1. Viscosity of fluids and mixtures. Ind. Eng. Chem. Fundam. 1981, 20, 323–332. [Google Scholar] [CrossRef]
- Ely, J.F.; Hanley, H.J.M. Prediction of transport properties. 2. Thermal conductivity of pure fluids and mixtures. Ind. Eng. Chem. Fundam. 1983, 22, 90–97. [Google Scholar] [CrossRef]
- Vasserman, A.; Nedostup, V. An equation for calculation of the thermal conductivity of gases and liquids. J. Eng. Phys. Thermophys. 1971, 20, 89–92. [Google Scholar] [CrossRef]
- Zéberg-Mikkelsen, C.K.; Quiñones-Cisneros, S.E.; Stenby, E.H. Viscosity Modeling of Light Gases at Supercritical Conditions Using the Friction Theory. Ind. Eng. Chem. Res. 2001, 40, 3848–3854. [Google Scholar] [CrossRef]
- Xu, L.; Kumar, P.; Buldyrev, S.V.; Chen, S.H.; Poole, P.H.; Sciortino, F.; Stanley, H.E. Relation between the Widom line and the dynamic crossover in systems with a liquid–liquid phase transition. Proc. Natl. Acad. Sci. USA 2005, 102, 16558–16562. [Google Scholar] [CrossRef]
- Banuti, D. Crossing the Widom-line—Supercritical pseudo-boiling. J. Supercrit. Fluids 2015, 98, 12–16. [Google Scholar] [CrossRef]
- Banuti, D. The Latent Heat of Supercritical Fluids. Period. Polytech. Chem. Eng. 2019, 63, 270–275. [Google Scholar] [CrossRef]
- Banuti, D.; Raju, M.; Ihme, M. Between supercritical liquids and gases—Reconciling dynamic and thermodynamic state transitions. J. Supercrit. Fluids 2020, 165, 104895. [Google Scholar] [CrossRef]
- Van der Waals, J. Nobel Lectures. Physics 1901–1921; Elsevier Publishing Company: Amsterdam, The Netherlands, 1967. [Google Scholar]
- Hickey, B.J.; Ihme, M. Supercritical mixing and combustion in rocket propulsion. In Annual Research Briefs; Center for Turbulence Research, Stanford University: Stanford, CA, USA, 2013; Available online: https://ctr.stanford.edu/publications/annual-research-briefs/annual-research-briefs-2013 (accessed on 15 October 2022).
- Valderrama, J.O. The State of the Cubic Equations of State. Ind. Eng. Chem. Res. 2003, 42, 1603–1618. [Google Scholar] [CrossRef]
- Lopez-Echeverry, J.S.; Reif-Acherman, S.; Araujo-Lopez, E. Peng–Robinson equation of state: 40 years through cubics. Fluid Phase Equilibria 2017, 447, 39–71. [Google Scholar] [CrossRef]
- Rowlinson, J.; Swinton, F.; Swinton, F. Liquids and Liquid Mixtures, 3rd ed.; Butterworth’s Monographs in Chemistry; Butterworth-Heinemann: Oxford, UK, 1982. [Google Scholar] [CrossRef]
- Hsieh, J. Principles of Thermodynamics; McGraw-Hill Engineering Thermodynamic Book; Scripta Book Company: Fort Worth, TX, USA, 1975. [Google Scholar]
- Tosun, I. Thermodynamics: Principles and Applications, 2nd ed.; World Scientific Publishing Company: Singapore, 2020. [Google Scholar]
- Winterbone, D.E. 7 - Equations of State. In Advanced Thermodynamics for Engineers; Winterbone, D.E., Ed.; Butterworth-Heinemann: Oxford, UK, 1997; pp. 121–134. [Google Scholar] [CrossRef]
- Benedict, M.; Webb, G.B.; Rubin, L.C. An empirical equation for thermodynamic properties of light hydrocarbons and their mixtures I. Methane, ethane, propane and n-butane. J. Chem. Phys. 1940, 8, 334–345. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids; McGraw Hill Book Co.: New York, NY, USA, 1987. [Google Scholar]
- Atkins, P.; De Paula, J.; Keeler, J. Atkins’ Physical Chemistry; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Onnes, H.K. Expression of the equation of state of gases and liquids by means of series. In Through Measurement to Knowledge: The Selected Papers of Heike Kamerlingh Onnes 1853–1926; Gavroglu, K., Goudaroulis, Y., Eds.; Springer: Dordrecht, The Netherlands, 1991; pp. 146–163. [Google Scholar]
- Soave, G.S. A noncubic equation of state for the treatment of hydrocarbon fluids at reservoir conditions. Ind. Eng. Chem. Res. 1995, 34, 3981–3994. [Google Scholar] [CrossRef]
- Soave, G.S. An effective modification of the Benedict–Webb–Rubin equation of state. Fluid Phase Equilibria 1999, 164, 157–172. [Google Scholar] [CrossRef]
- Ma, J.; Liu, H.; Liu, L.; Xie, M. Simulation study on the cryogenic liquid nitrogen jets: Effects of equations of state and turbulence models. Cryogenics 2021, 117, 103330. [Google Scholar] [CrossRef]
- McBride, B.J. NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species; National Aeronautics and Space Administration, John H. Glenn Research Center: Cleveland, OH, USA, 2002. Available online: https://ntrs.nasa.gov/citations/19940013151 (accessed on 15 October 2022).
- Chase, M.W. National Information Standards Organization (US). In NIST-JANAF Thermochemical Tables; American Chemical Society: Washington, DC, USA, 1998; Volume 9. Available online: https://janaf.nist.gov (accessed on 15 October 2022). [CrossRef]
- Aly, F.A.; Lee, L.L. Self-consistent equations for calculating the ideal gas heat capacity, enthalpy, and entropy. Fluid Phase Equilibria 1981, 6, 169–179. [Google Scholar] [CrossRef]
- Chapman, S.; Cowling, T.G.; Burnett, D. The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases; Cambridge university press: Cambridge, UK, 1990. [Google Scholar]
- Guo, X.Q.; Sun, C.Y.; Rong, S.X.; Chen, G.J.; Guo, T.M. Equation of state analog correlations for the viscosity and thermal conductivity of hydrocarbons and reservoir fluids. J. Pet. Sci. Eng. 2001, 30, 15–27. [Google Scholar] [CrossRef]
- Nowak, P.; Kleinrahm, R.; Wagner, W. Measurement and correlation of the (p, ρ, T) relation of nitrogen. I. The homogeneous gas and liquid regions in the temperature range from 66 K to 340 K at pressures up to 12 MPa. J. Chem. Thermodyn. 1997, 29, 1137–1156. [Google Scholar] [CrossRef]
- Straty, G.; Diller, D. (p, V, T) of saturated and compressed fluid nitrogen. J. Chem. Thermodyn. 1980, 12, 927–936. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. Mathematical Description of Physical Phenomena. In The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab; Springer International Publishing: Cham, Switzerland, 2016; pp. 43–83. [Google Scholar] [CrossRef]
- Zong, N.; Meng, H.; Hsieh, S.Y.; Yang, V. A numerical study of cryogenic fluid injection and mixing under supercritical conditions. Phys. Fluids 2004, 16, 4248–4261. [Google Scholar] [CrossRef]
- Lagarza-Cortés, C.; Ramírez-Cruz, J.; Salinas-Vázquez, M.; Vicente-Rodríguez, W.; Cubos-Ramírez, J.M. Large-eddy simulation of transcritical and supercritical jets immersed in a quiescent environment. Phys. Fluids 2019, 31, 025104. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Rahantamialisoa, F.N.Z.; Pandal, A.; Jasak, H.; Im, H.G.; Battistoni, M. Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model. Energies 2020, 13, 5676. [Google Scholar] [CrossRef]
- Schmitt, T.; Selle, L.; Ruiz, A.; Benedicte, C. Large-Eddy Simulation of Supercritical-Pressure Round Jets. AIAA J. 2010, 48, 2133–2144. [Google Scholar] [CrossRef]
- Zeinivand, H.; Farshchi, M. Numerical study of the pseudo-boiling phenomenon in the transcritical liquid oxygen/gaseous hydrogen flame. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 893–911. [Google Scholar] [CrossRef]
- Pfitzner, M.; Müller, H.; Niedermeier, C.; Jarczyk, M.; Hickel, S.; Adams, N. Large Eddy Simulations of Trans- and Supercritical Injection Processes. Prog. Propuls. Phys. 2013, 8, 5–24. [Google Scholar] [CrossRef]
- Harstad, K.G.; Miller, R.S.; Bellan, J. Efficient high-pressure state equations. AIChE J. 1997, 43, 1605–1610. [Google Scholar] [CrossRef]
- Abudour, A.M.; Mohammad, S.A.; Robinson, R.L., Jr.; Gasem, K.A. Volume-translated Peng–Robinson equation of state for saturated and single-phase liquid densities. Fluid Phase Equilibria 2012, 335, 74–87. [Google Scholar] [CrossRef]
- Longmire, N.P.; Banuti, D.T. Limits of Fluid Modeling for High Pressure Flow Simulations. Aerospace 2022, 9, 643. [Google Scholar] [CrossRef]
- Banuti, D.T.; Hannemann, K. The absence of a dense potential core in supercritical injection: A thermal break-up mechanism. Phys. Fluids 2016, 28, 035103. [Google Scholar] [CrossRef]
- Chehroudi, B.; Cohn, R.; Talley, D. Cryogenic shear layers: Experiments and phenomenological modeling of the initial growth rate under subcritical and supercritical conditions. Int. J. Heat Fluid Flow 2002, 23, 554–563. [Google Scholar] [CrossRef]
- Branam, R.; Mayer, W. Characterization of Cryogenic Injection at Supercritical Pressure. J. Propuls. Power 2003, 19, 342–355. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics, Dubrovnik, Croatia, 19–21 September 2007; Volume 1000, pp. 1–20. [Google Scholar]
- Jafari, S.; Gaballa, H.; Habchi, C.; de Hemptinne, J.C. Towards Understanding the Structure of Subcritical and Transcritical Liquid–Gas Interfaces Using a Tabulated Real Fluid Modeling Approach. Energies 2021, 14, 5621. [Google Scholar] [CrossRef]
- Yang, S.; Li, Y.; Wang, X.; Unnikrishnan, U.; Yang, V.; Sun, W. Comparison of Tabulation and Correlated Dynamic Evaluation of Real Fluid Properties for Supercritical Mixing. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017. [Google Scholar] [CrossRef]
- Leachman, J.; Jacobsen, R.; Lemmon, E.; Penoncello, S. Thermodynamic Properties of Cryogenic Fluids, 2nd ed.; Springer International Publishing AG: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Lebrun, P. Superfluid helium as a technical coolant; LHC-Project-Report-125; CERN: Geneva, Switzerland, 1997; Available online: https://cds.cern.ch/record/330851 (accessed on 15 October 2022).
- Rogers, D.W. Concise Physical Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Leachman, J.W.; Jacobsen, R.T.; Penoncello, S.G.; Lemmon, E.W. Fundamental Equations of State for Parahydrogen, Normal Hydrogen, and Orthohydrogen. J. Phys. Chem. Ref. Data 2009, 38, 721–748. [Google Scholar] [CrossRef]
- Kim, T.; Kim, Y.; Kim, S.K. Numerical analysis of gaseous hydrogen/liquid oxygen flamelet at supercritical pressures. Int. J. Hydrog. Energy 2011, 36, 6303–6316. [Google Scholar] [CrossRef]
- Pohl, S.; Jarczyk, M.; Pfitzner, M.; Rogg, B. Real gas CFD simulations of hydrogen/oxygen supercritical combustion. EUCASS Proc. Ser. 2013, 4, 583–614. [Google Scholar] [CrossRef]

| Fluid | Near-Critical | Super-Critical | High | ||||
|---|---|---|---|---|---|---|---|
| P (MPa) | ( P/) | P (MPa) | (P/) | P (MPa) | (P/) | (MPa) | |
| N | 4 | 1.2 | 7 | 2.1 | 3 | 2.9 | 3.396 |
| O | 6 | 1.2 | 8 | 1.6 | 10 | 2 | 5.043 |
| CH | 5 | 1.1 | 8 | 1.7 | 10 | 2.2 | 4.599 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madana Gopal, J.V.; Morgan, R.; De Sercey, G.; Vogiatzaki, K. Overview of Common Thermophysical Property Modelling Approaches for Cryogenic Fluid Simulations at Supercritical Conditions. Energies 2023, 16, 885. https://doi.org/10.3390/en16020885
Madana Gopal JV, Morgan R, De Sercey G, Vogiatzaki K. Overview of Common Thermophysical Property Modelling Approaches for Cryogenic Fluid Simulations at Supercritical Conditions. Energies. 2023; 16(2):885. https://doi.org/10.3390/en16020885
Chicago/Turabian StyleMadana Gopal, Jaya Vignesh, Robert Morgan, Guillaume De Sercey, and Konstantina Vogiatzaki. 2023. "Overview of Common Thermophysical Property Modelling Approaches for Cryogenic Fluid Simulations at Supercritical Conditions" Energies 16, no. 2: 885. https://doi.org/10.3390/en16020885
APA StyleMadana Gopal, J. V., Morgan, R., De Sercey, G., & Vogiatzaki, K. (2023). Overview of Common Thermophysical Property Modelling Approaches for Cryogenic Fluid Simulations at Supercritical Conditions. Energies, 16(2), 885. https://doi.org/10.3390/en16020885









